1. Introduction
According to management theory, the cost is defined as the amount of resources required to produce something or deliver a service. In addition to a managerial technique for measuring energy resources consumption, energy cost accounting must provide a rational method for assessing the production costs and their impact on the environment. There is a broad international agreement that exergy is the most suitable thermodynamic property for cost assessment, at least for energy-intensive systems.
The cost of a product is formed by adding up the resources that have been necessary for its production. Nevertheless, these resources have been products of a previous process, so boundaries must be set that precisely limit its objectivity. There are no cost meters, nor is it a measurable physical property. It is an emergent property that needs an analyst to evaluate it. However, it quantifies how many resources have been necessary to produce something. As nothing is produced in isolation from its waste and co-products and there is always a multiplicity of resources used, cost evaluation is not a trivial activity. Costing looks for the origin of the production process and quantifies it.
The problem of exergy costs allocation was formulated in 1986 by Valero et al. [
1]:
“Given a system whose limits have been defined and a disaggregation level that specifies the subsystems that constitute it, how do we obtain the costs (average costs) of all the flows that become interrelated in this structure?”. The
Exergy Cost Theory [
2] (ECT) answers the question using the following rules:
Resources rule: In the absence of external assessment, the exergy cost of the flows entering the plant equals their exergy.
Cost Conservation Rule: All cost generated by the production process must be included in the final product’s cost. In the absence of an external assessment, we have to assign a zero value for the cost of the losses of the plant.
Unspent Fuel rule: If an output flow of a process is a part of the unspent fuel of this process, the unit exergy cost is the same as that of the input flow from which the output flow comes (also known as F rule).
Co-products rule: If a process has a product composed of several flows, with the same thermodynamic quality, then the same unit exergy cost will be assigned to all of them (also known as P rule).
The
Fuel–Product terminology used in thermoeconomics is due to G. Tsatsaronis [
3]. This idea was a major breakthrough for the detailed cost analysis of industrial energy systems.
The methods based on the direct application of the ECT are well established and widely accepted to account for the exergy costs. One can find examples in [
4]. However, the method has some significant drawbacks:
The original ECT has some shortcomings from a mathematical viewpoint and has limitations and accuracy problems from a software implementation perspective. However, the most notable problem is the allocation of waste costs, which is not dealt with in a rigorous and general way.
Waste is inseparable from production and has always been considered an annoying and hidden part of it. The usual thermoeconomic methods, such as ECT, average cost theory [
5], or the specific cost method of exergy calculation (SPECO) [
6], do not soundly address the problem of waste cost allocation. Other methodologies, such as thermoeconomic functional analysis [
7] or cumulative exergy consumption [
8], provide different waste analysis approaches, but none of them give a general solution to the problem.
Waste thermoeconomic cost accounting has gained importance in the last fifteen years because it allows the discipline to be used as an accounting tool to help assess and design sustainable energy systems [
9,
10,
11].
Torres et al. [
12] highlight the importance of identifying the waste cost formation process to make a correct cost allocation. In this paper, a new rule for cost allocation of waste was proposed:
Waste rule: The exergy cost of a waste stream leaving the system’s boundaries is allocated null (waste cost internalization). Its exergy cost, formed by adding the fuel required to produce it plus the fuel used to carry and dispose of it, is allocated to the processes, which have generated it.
This paper has two main objectives: First, it makes an in-depth reflection on the formation process of waste costs. A new concept, called irreversibility carrier, is introduced to identify the origin, transfer, partial recovery, and disposal of waste and to permit its management as an external irreversibility. It means that waste or external losses should be considered not as flows that leave the system through a dissipative process but as irreversibilities, which originate before, during the production process, but manifest themselves externally.
Second, it introduces a new methodology for calculating exergy costs, which combines graph theory [
13] and productive linear models [
14] with the Exergy Cost Theory, providing a rigorous mathematical approach, a more robust software implementation, and integrating waste cost allocation into the model.
2. Waste from a Thermodynamic Viewpoint
Waste is an unwanted material or energy flow that is generated when something is discarded or produced. It may be characterized by thermal, mechanical, chemical, or other intensive properties, such as radioactive ones. A waste will cease to be a waste when it reaches thermodynamic equilibrium with its surrounding environment. If it does not encounter constraints that prevent it from doing so, it will evolve spontaneously. Thus, if it is hotter or colder, at higher or lower pressure, more concentrated or dilute, or if it has more chemical reactivity than its surroundings, it will dampen its exergy to zero. In general terms, this environment would be Thanatia [
15], a—not so imaginary—state of the completely degraded planet Earth. That is, it might be taken as a general reference of zero exergy.
In other words, first, every residue has exergy with respect to a dead reference environment associated with the biosphere, which we call Thanatia. Second, every residue evolves spontaneously, losing its exergy until it cancels out. That is, its pressure, temperature, and chemical potential are equalized to those of its environment. Although thermodynamics alone cannot estimate its rate, it can predict its final state. This degradation process is not harmless to life on earth, and we call the residue a pollutant as long as it damages the natural environment, i.e., as long as its intensive properties are different from those of the environment.
As examples, we observe that gases coming out of a stack have a different concentration from that of the atmosphere and are diluted in it. They are hotter and cool down, and as they are at higher pressure, they expand to atmospheric pressure. Moreover, wastewater is diluted in rivers, which in turn are diluted in the sea, which acts as a universal dumping ground. Moreover, the lack of lubrication produces noise, which is nothing more than a pressure wave transmitted to the surrounding air from the rubbing materials. Of course, as solid waste is less movable, it is more difficult for it to react, i.e., to be metabolized by the environment, but a landfill is expected to act as a large digester that dampens its chemical reactivity.
As summary, any manufacture of material goods requires exergy resources that are converted into products and waste, both with their exergy. The difference between the exergy of the resources used minus that of the products is called internal irreversibility. When waste crosses the boundaries of the productive system it still has exergy that will irreversibly degrade when it is released into the environment. It is deferred more or less in time, and can potentially damage the biosphere. We call this spontaneous processes external irreversibility. Moreover, at its end-of-life, even products behave as waste, if they do not become recycled.
That is to say, the production of goods and services always generates internal and external irreversibilities both, not only of one type. The first law of thermodynamics applied to the analysis of production systems focuses on the flows that cross the system boundaries. That is, only waste can be counted but does not give clues to locate its origin. In contrast, a conventional view of the second law on the same system focuses on internal exergy losses as an analysis element to improve its efficiency. In other words, attention is focused on internal irreversibilities that allow seeking the causes of internal costs. An integral vision of thermodynamics applied to production systems must consider both internal and external irreversibilities. Therefore, the cost of production should reflect both losses.
The Irreversibility Carrier Concept
As mentioned above, cost quantifies the resource losses incurred to produce something. Therefore, an essential question for cost assessment is how internal and external irreversibilities manifest in a plant and determine its layout. Due to a useless loss of pressure, temperature, or chemical potential, internal irreversibility can be located in any component of a plant, but its effects can appear anywhere as useless heat. It is the case when the location of a cause does not match the location of its effects.
Suppose a Rankine cycle power plant. We know that for each unit and for the plant in general:
, where
is the exergy of the resources required to produce
units of exergy in process
u;
are its internal irreversibilities; and
are the local losses, such as waste heat, noise, or leakage. These losses are usually minor and difficult to measure. Conventionally, the engineer puts insulation in the equipment to minimize them. From a thermoeconomic point of view, these losses are ignored and considered internal irreversibilities,
. Therefore, the above expression can be taken as
Nevertheless, F and P have energy content, and . Then, the first law also states for each and every unit as well as the overall plant, that .
Obviously, the processes are designed to have good thermal and acoustic insulation. Therefore, is not significant in terms of the overall heat released at the overall plant, . In fact, it is observed that for each unit, is released, and an irreversibility is generated, but they are not related one by one, except at the level of the entire plant.
It is worth asking now, where does the heat released caused by each and every one of the units appear? Remarkably, the heat released is detectable, while irreversibility is a conceptual construct with no local manifestation. Therefore, where does such a heat release originate from a second law point of view? What is the best way to understand this fact? How can the the first and the second laws be reconciled? The answer is obvious: at the level of the complete plant, it is true that
As it is well known, most of the heat released in a power plant is rejected in the boiler and condenser-cooling tower subsystem, or in other words, . Note that at the whole power plant, nearly coincide with its exergy F and equals P.
This is an important idea, even though it seems evident. and are located in each and every component. However, released heats appear anywhere on the plant. In other words, , , and are located in each component, while each and every are not. This is a strong argument for using exergy in thermoeconomics. Using the second law allows locating the true causes of degradation in the units where they appear. Therefore, the casualization of inefficiencies is better located.
One cannot pinpoint the causes of inefficiencies simply by looking at the different heat releases and noise that ends as heat to the environment, even if local irreversibilities are eventually dispersed as heat fluxes to the environment. Besides that, it is not an easy way to identify the origin of each degraded heat among the different units in a plant. In any case, these unwanted heats must be eliminated, and they need additional dissipative equipment to achieve it. This is the case of a condenser in a power plant. In other words, internal irreversibilities, sooner or later, generate waste. However, they need a mass medium to manifest. Let us call this medium an irreversibility carrier.
A waste stream has exergy, whether thermal, mechanical, or chemical. In addition, it has its cost of formation, transference, partial recovery, and disposal that must be identified. In parallel with the product cost formation process, there is a waste cost formation process. The irreversibility carrier concept allows us to identify the origin, itinerary, and disposal of any residual stream of the plant regardless it is a mass stream or not. These flows still have exergy that the system does not recover. Instead, one needs to spend additional resources to partially dispose of them in dissipative units. It is the case of the stack and its auxiliary systems for combustion gases. These units avoid a more significant impact on the environment and constitute a technological response to the necessary internalization of the costs of waste produced by industrial processes.
By contrast with internal irreversibilities, in the production of mass waste, waste is itself its carrier. Waste production is easy to find its origin and also easy to follow such stream to the dissipative unit. In terms of mass, the industry produces more waste than commodities and, worse, more types of residual streams than products. For example, in a chemical reaction such as combustion, one is interested in the heat released rather than the reaction’s products. Even in the case of reactors in industrial chemistry, metallurgy and all manufacturing processes in which a reaction product is obtained, the types of unwanted waste are always present. With these basic ideas, we can see how thermoeconomics can assess the costs of waste associated with internal and external irreversibilities. This process is found by following its irreversibility carrier, which identifies its origin, transfer, partial recovery, and disposal. The irreversibility carrier is the generalization of the negentropy concept introduced by C. Frangopoulus [
7]. It now extends not only to steam carrying entropy to be condensed in a Rankine cycle, but to any mass or energy flow that carries a waste to be disposed of in the environment.
Sometimes waste flows are caused by technological limitations imposed by the equipment and processes of the plant. However, it is, unfortunately, typical to overlook the external effects of waste. This practice is called cost outsourcing or cost externalization, that is, letting society or the environment assume the impact of the plant’s waste. This is the case of greenhouse gases produced by combustion processes. Therefore, the techniques of waste allocation or costs internalization will increasingly become a common practice in the near future. Waste flows still have exergy to be recovered or to dispose of them. In any case, one needs to spend additional resources, thus increasing the system’s irreversibility. In accounting terms, as already said, if waste streams cross the system’s boundaries, they can be considered as external irreversibilities. However, appropriate allocation needs to locate which internal process causes them.
For instance, the stack of a combined cycle does not cause the exiting gases. This waste stream has at least three types of waste: rejected heat, CO2, and NOx (plus water, oxygen, nitrogen, and other components of the incoming air, not considered waste). Carbon dioxide and water are produced by the combustion of carbonated fuel, while NOx and excess heat are produced in the combustion chamber. One can compare this combustion chamber to an ideal fuel cell. In such a case, only CO2 and water would be produced. The remaining waste, CO2, and NOx are material streams that need additional dissipative units to get rid of them. Carbon dioxide requires carbon capture and storage techniques, while NOx requires special combustion chambers to prevent its formation. These abatement processes require further fuel and investment whose costs must be added to the plant product(s).
Therefore, the cost of disposing such gases is always associated with the type of equipment and/or fuel used. In general, all the productive components involved in the formation of waste contribute to the cost of the waste. In short, non-material waste streams, like noise, destabilized (or unbalanced) forces that cause vibrations, or excess temperature that turns into rejected heat are internal irreversibilities that eventually turn into waste heat. They need material carriers. However, these carriers easily blur their causal origin. The local entropy generation is the measure of the additional carrying load of the irreversibility carrier.
They are real streams of waste that have an origin, itinerary, and end. Therefore, it is easy to identify their cost formation process as well as its logical disaggregation. Along this way, they add costs: First, of its formation exergy in the chemical reaction, then that of conduction and eventual separation, and finally their abatement costs. Alike the definition of fuel and product, that of waste also depends on the analyst and ultimately on society. In fact, nature does not produce waste because it recycles everything in the short or long term. As long as waste has exergy, it can be recovered. That is, a material stream can be recovered as much as it differs from its reference environment. The distinction between internal and external irreversibilities will also depend on the analyst. However, the cost of any malfunction in the plant must have a single value, independent of the irreversibilities classification.
Therefore, for a proper allocation of the costs of wastes, we must follow their formation process and assess the cost of their formation and disposal to the processes in which they are produced, according to the ideas of irreversibility carrier and polluter pays’ principle. In parallel to the cost formation process of the products, there is a cost formation process of wastes.
From these reflections, one can draw some conclusions. First, as long as waste has exergy, it can be used before going out of the production process. This is achieved with equipment that we call recovery units. Second, if waste cannot be recovered, it is necessary to reduce its exergy. We will do it in dissipative units. Note that the latter units consume exergy in order to dissipate it. In general, they exchange one type of residual exergy for another. Third, complete abatement or total exergy recovery is too costly. Because they follow the law of diminishing returns, in other words, the behavior of this equipment is governed by an entropic behavior. For example, in the separation of a component in a mixture, it is easier to separate a given amount of the minority component if its composition is at 10% than at 1%, which will be less expensive to separate it at a concentration of 0.1%, and so on. This makes total decontamination technically and economically unfeasible and achieving total purity extremely costly. It is an application of the Third Law of Thermodynamics applied to separation processes. As a practical application, a designer of these types of equipment must take into account that there are entropic limits (pinch points) that are neither technically nor economically achievable.
3. The Productive Structure Graph
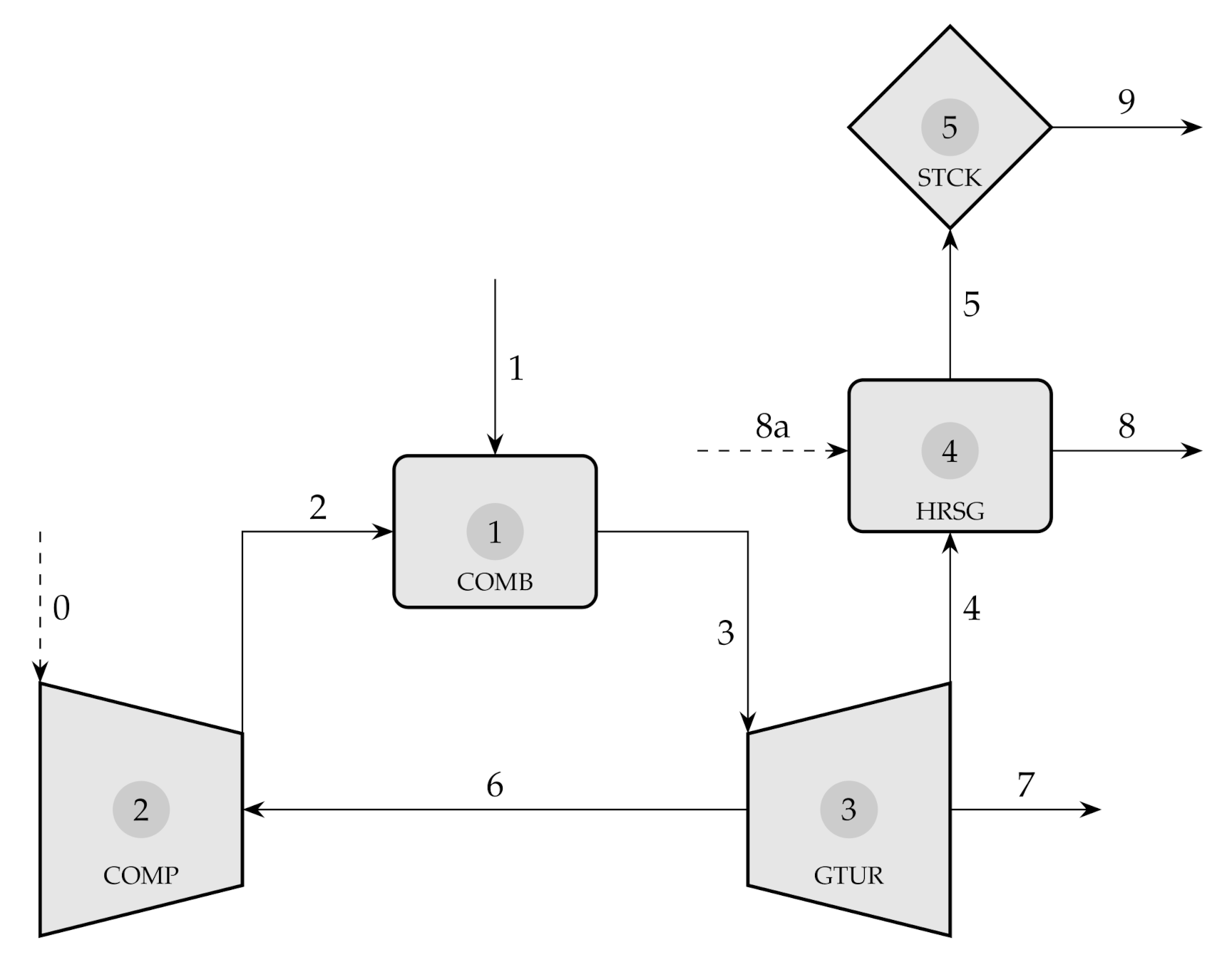
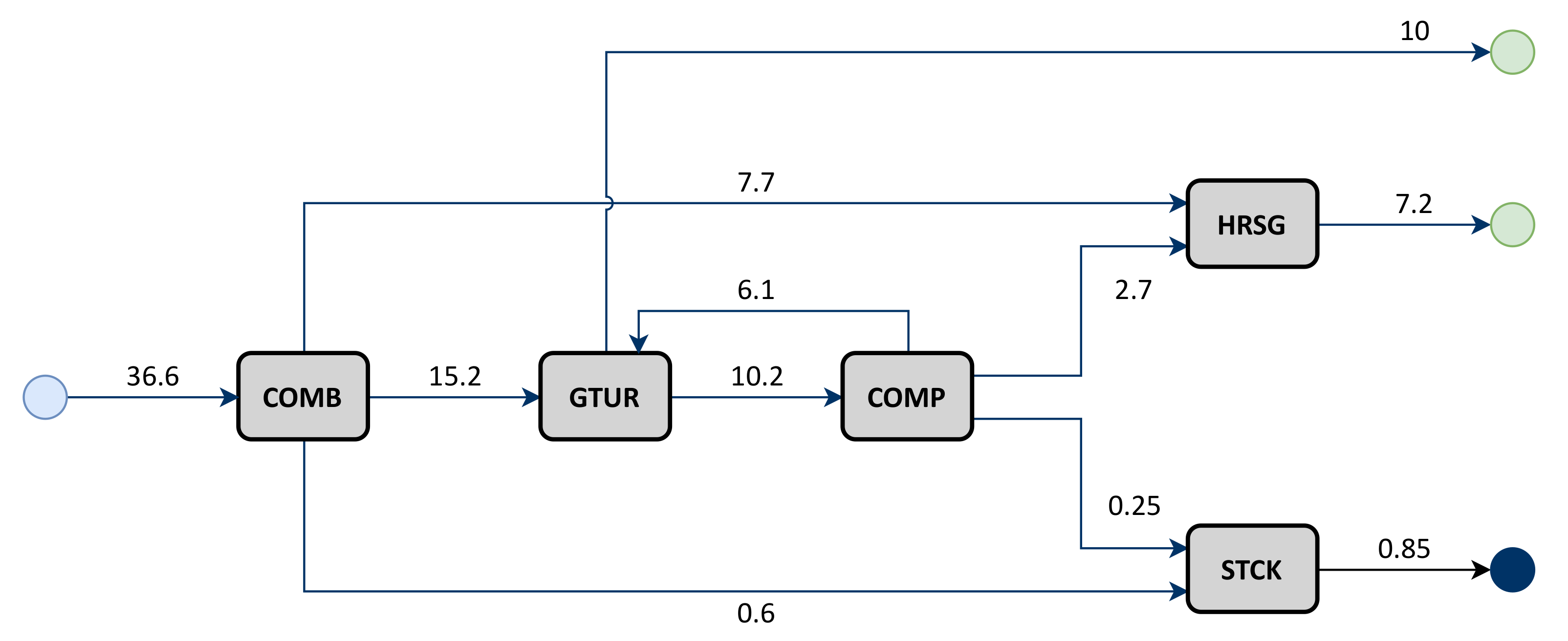
Throughout this paper, a simplified model of a gas turbine cycle with co-generation (hereafter referred to as TGAS) is used as a case study, see
Figure 1.
The TGAS plant uses natural gas (flow #5) to produces 10 MW of electric power (flow #6) and 7.6 kg/s of saturated steam at 20 bar of pressure (flow #8) from freshwater (flow #8a), partially recovering the residual heat of gases (flow #4). Finally, the waste combustion gases are expelled through a stack (flow #9). The combustor has 2% of heat losses, and the isentropic efficiency of the turbine and compressor is 87%. This flowsheet also indicates the system boundaries and the aggregation level. The thermodynamic properties of the plant are shown in
Table 1. To simplify the model, flows #0 and #8a are removed from further analysis because their exergy values equal to zero. We are not considered the pump required to increase the water pressure from 1 to 20 bar because the exergy value of the work flow is negligible (1.8 kW).
From a theoretical viewpoint, an energy system is defined beforehand as a set of subsystems or thermodynamic processes linked to each other and the environment by another set of mass, heat, and work flows, quantified by its exergies. In essence, it constitutes a flow sheet, as it is shown in
Figure 1.
Industrial installations have a productive purpose. Their objective is to obtain one or several products by processing external resources. For each process of the system, it is necessary to identify the flows that constitute their product and the flows required to obtain them called fuel. Energy flows (e.g., heat or work) appear at the process inlet as fuel stream or the process outlet as the product stream. When working with mass streams, it is appropriate to operate with exergy differences associated with each energy transfer between the inlets and the outlets. The output flows that are not part of the production process are considered as unspent or recoverable fuel.
A fuel stream group will consist of
one or several inflows that provide exergy to the process and
input and output flows enter into the process and leave it, after some exergy transfer to the process.
A product stream group will consist of
one or several outflows produced by the process and
output and input flows enter into the process and leave it, after some exergy increase.
The exergetic efficiency of a process
u is defined as the ratio between the exergy obtained or product
and the exergy supplied or fuel
. It measures how reversible a process is. Its inverse value is the exergy unit consumption
, i.e., the amount of resources required per unit of the product obtained:
Table 2 shows the definition of the fuel and product streams of each process in the case of TGAS plant.
3.1. The Production Layer
Let be the set of the n components or processes that constitute the system, for some defined boundaries and aggregation level. The component represents the environment. Let define as the set of the m flows that interchange exergy between the processes. Finally, let be the set of all the productive (fuel and products) groups of the system. Each component of the system has one or more fuel and product streams, let and be the sets of fuel and product streams of the process u, respectively. On the other hand, each stream could have several inputs and output flows. Let us denote and as the sets of input and output streams, respectively, of the productive group ℓ. A fuel stream must have at least one input flow, and a product stream must have at least one output flow.
Defining system boundaries is essential to determine the system costs. For this purpose, the environment is defined as an additional process complementary to the global plant. The system outputs are the fuel of the environment , and the system resources are the product of the environment . A productive group must be defined for each final product and each external resource to ensure the information about them.
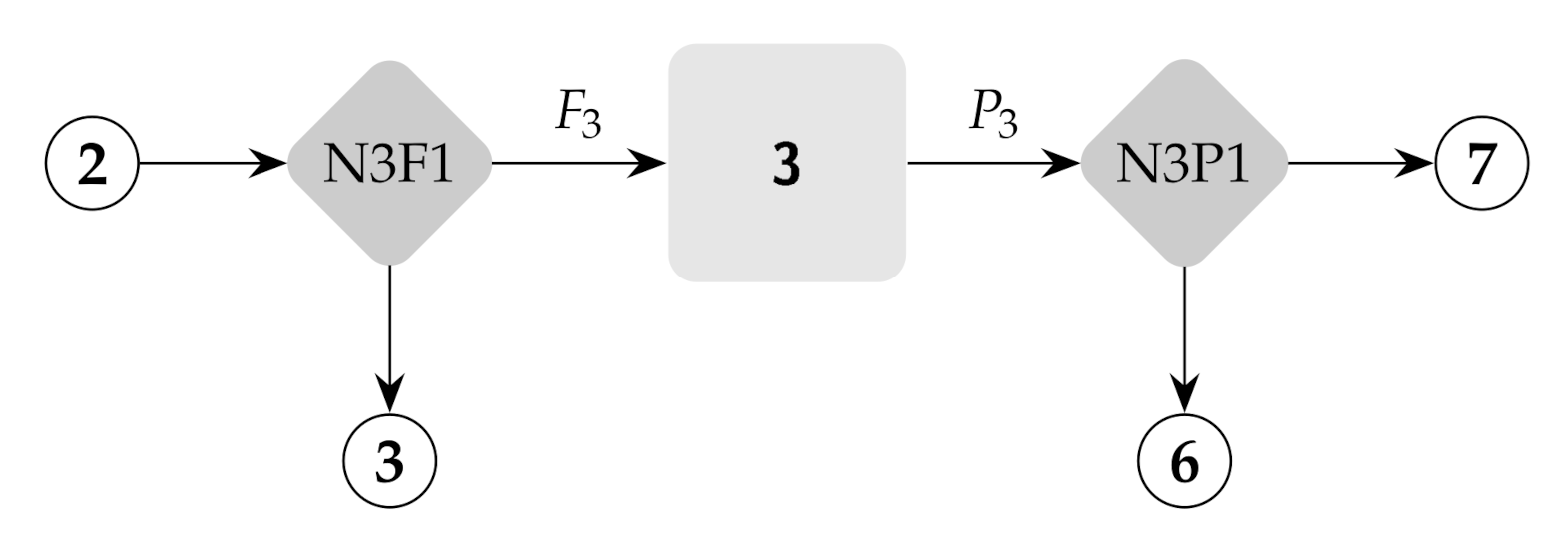
The productive structure is represented as a directed graph, with three types of nodes: processes , flows , and productive groups or streams , and four types of links or connections: process → productive group , productive group → process , flow → productive group , and productive group → flow .
The productive structure graph is built from the definition of the processes efficiency. Each productive structure block is drawn, as shown in
Figure 2. Processes are represented by squares, flows by circles, and productive groups as diamonds.
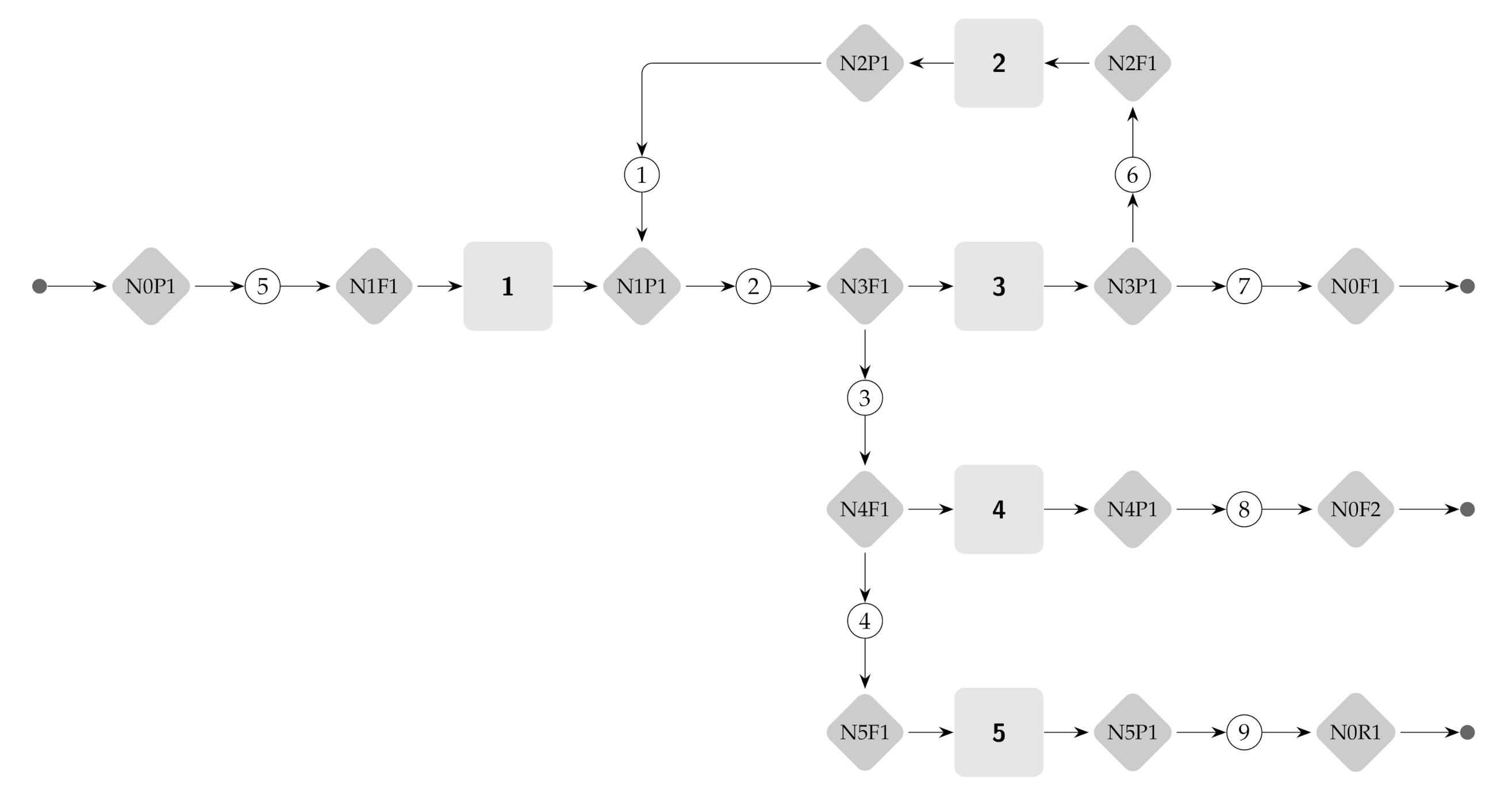
The complete graph of the TGAS system is built by connecting the flows with its processes through the productive groups as shown in
Figure 3. A big dot marks the connection with the environment.
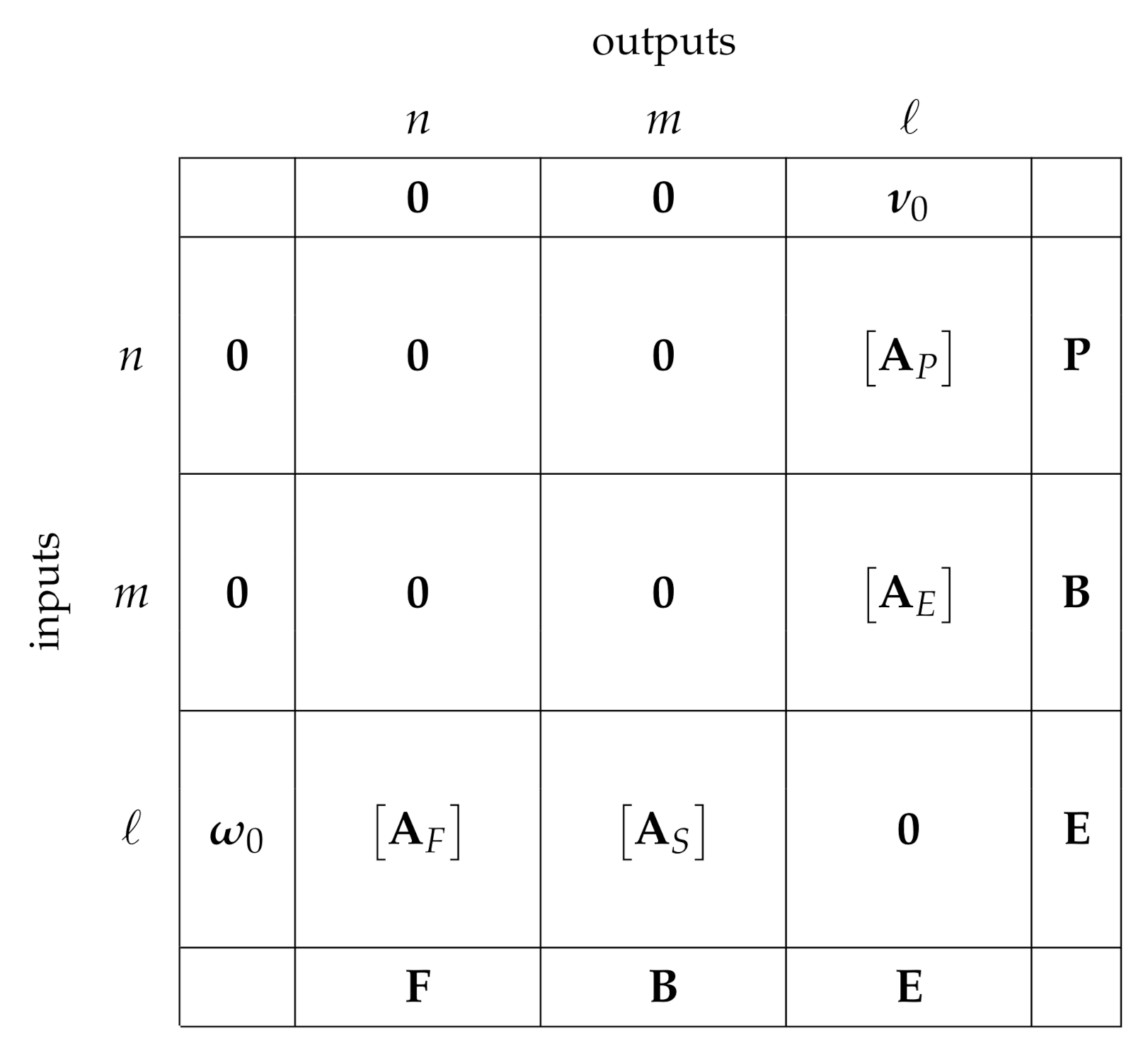
The adjacency matrix of the productive structure graph is called
productive table, see
Figure 4. It is formed by four submatrix corresponding to the four types of links described above.
Let
be a
matrix, containing the exergy of the input flows of productive groups. Each element of the matrix is defined as
Let
be a
matrix, containing the exergy of the output flows of productive groups. Each element of the matrix is defined as
Let
be a
matrix, containing the exergy values of fuels streams of the processes, defined as
Let
to be a
matrix, which contains the exergy values of product streams of the processes, defined as
Vector
contains the exergy values of the external resources, and vector
contains the exergy values of the system outputs:
Let and be vectors, whose elements are the exergy values of fuel and product of the system’s components, and a vector, whose elements are the flows exergy.
The submatrices of the productive table verify the following properties:
where
is a
vector whose elements represent the total exergy processed by each productive group, defined as
The exergy balance in a productive group is conservative, and the exergy of the input streams equals the exergy of the output streams because productive groups are logical or fictitious units. The exergy of a productive group depends on the type of productive group. If the productive group is a fuel stream, its exergy is the sum of the exergy of their input flows and the sum of the exergy of their output flows if it is a product stream group. The exergy balance in a unit process is given by Equation (
1), and it is written in the vectorial form as
where
is a
vector whose elements are the internal irreversibility values
of each system’s component.
Note that to obtain coherent values for processes efficiency, the exergy values of the flows must be non-negative, as well as the exergy values of the fuel and product groups. This condition is evident in nearly all real cases, but if we work with the flow exergy near environment temperature and low pressures, it could take negative values, in this case, the environmental conditions must be revised. Other conditions must be satisfied at process level are and . Obviously, if both are equal to zero, there is no effective process (consider that sometimes bypass and redundant processes are used in complex plants). If and it should be considered as a dissipative unit.
The submatrices that defining the productive structure table for TGAS system, using the Coordinate Sparse Matrix (
row,
col,
value) format, are as follows:
Coordinate Sparse Matrix format is commonly used when the number of non-zero elements represents less than 10% of the total matrix elements. Each column of these matrices determines an element of the matrix in the form (
row, col, value), see
Table 3 to know the index of each productive group.
3.2. The Waste Layer
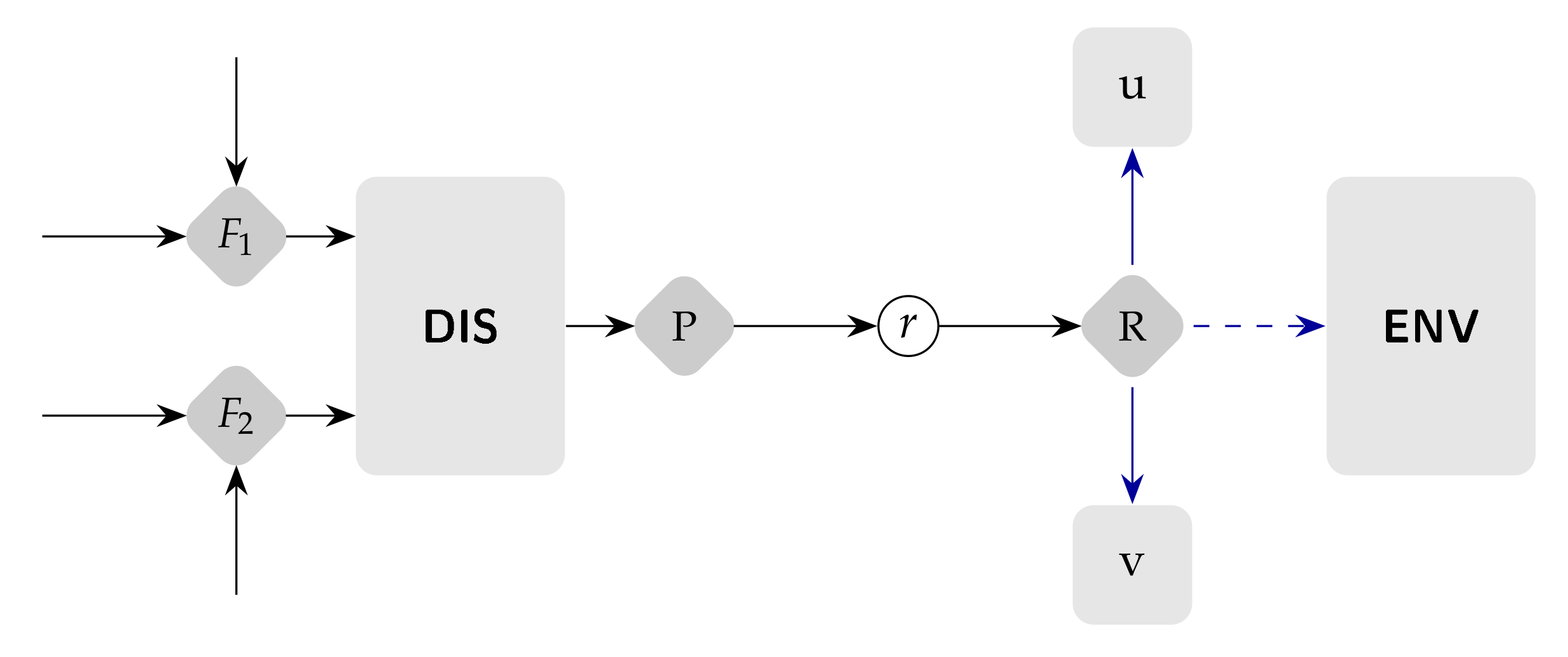
From the viewpoint of processes, we must distinguish among productive components, whose purpose is to make useful products, and dissipative components that not generate any final product but are responsible for disposing of the waste created during the production. Let us denote as the subset of productive units and as the subset of dissipative units. For convenience, each waste flow is defined as the product of a dissipative unit, so the waste cost reallocation could be made from dissipative units to productive components.
Figure 5 shows the cost allocation scheme for dissipative processes and waste flows streams in the productive structure. Flows to be disposed enter as fuel of the dissipative unit (DIS) together with the resources required to eliminate them; the product of the dissipative unit is the removed exergy, flow
, that connects with a waste stream to the environment (ENV), which redistributes the cost among the productive units
and
that produce it. Meanwhile, the flow cost leaving the system (entering the environment) is zero. In other words, waste streams are treated as external irreversibilities of the productive units that generated them. This fact will be formally studied here.
In the case of TGAS example, flow #4 enters on the fuel group , and group is not used in this case, but it could represent the work and electricity flows of the equipment required to extract the gases (forced or induced draft fans). The product of the dissipative unit is the eliminates exergy of output gases . The productive group R, corresponds to index #14. It is a logical node whose function is to redistribute the cost of gases among the processes having contributed to generate the waste flows, in this case, the combustion process #1. Therefore, the cost of waste going outside the plant (entering the environment) is zero, and the remaining exergy will be considered as external irreversibility.
From a conceptual viewpoint, the definition of efficiency in dissipative units would be the same as in a productive unit: the amount of exergy produced divided by the provided exergy resources. However, from an engineering viewpoint, the meaning is different: in a dissipative unit, its production purpose is to eliminate a waste stream (thermal, chemical, or physical), so its product is the exergy we need to dissipate it. As
Figure 5 shows, the fuel has two components. One (
) is the waste stream we want to dispose of, and the other is the additional resources needed to do so, such as labor, electricity, water, cooling air, or chemicals, referred to as
. Therefore, the unit consumption in a dissipative unit could be defined as
. This means that if no additional resources are required, its unit consumption is 1, and the dissipative unit is a simple pipeline. However, in the real world, it always needs additional resources, which increase its unit consumption. The higher the consumption of additional resources for waste disposal, the lower the efficiency of a dissipation unit is.
Waste flows are identified as all the unwanted and unavoidable flows crossing the system boundaries. Let us denote as the subset of output system flows formed by the system’s waste flows. Therefore, the system outputs could be split into two parts: .
Let
be a
vector containing the exergy of the waste flows and
as a
vector containing the exergy of the final products:
Let
be a
matrix, called
waste-process table, whose elements
represent the exergy of waste stream
h generated by the process
u. According to the
Figure 5, the exergy balance is written as
The matrix
verifies the following properties:
where
is a
vector whose elements contain the exergy of the waste generated by each process. Note that, meanwhile, Equation (
6) is an equality based on the definition of the waste process table and Equation (
7) is a definition; the values of
do not correspond to physical flows, but they are identified as external irreversibilities of the processes, as it will be shown in Equation (
32). The waste process table describes the cost formation process of waste, and it is integrated as an additional layer of the productive structure in parallel to the fuel structure.
In the case of the TGAS plant, where only thermal wastes are considered, the waste process table will be
There are not always single criteria to determine the
values. In general, the analyst requires a detailed thermodynamic analysis of processes to identify where the waste is formed, see
Section 10.
Figure 6 describes the waste internalization of a generic component. The value
represents the additional fuel that must be spent to remove waste. It becomes external irreversibilities
of the component
u.
The exergy balance of the global system is written as
where
is the sum of the exergy of external resources
;
is the sum of the exergy of the flows
crossing the system’s boundaries, including both final production and waste; and
is the sum of the internal irreversibilities.
However, when one introduces a productive purpose, part of the outputs of the system can become waste, so the overall exergy balance is rewritten as
the second term of the right side of equation represents the total external irreversibilities
.
On the other hand, if one considers that the costs of the waste leaving the system are zero, because they have no value in the production system, the exergy cost balance on the waste stream will be
where
is the unit exergy cost of the waste stream
, and the cost of the waste generated by each productive component will be
The costs of the waste are internalized and assessed to the productive components that generated them. Therefore, according to
Figure 6, the cost of irreversibilities (internal and external) is zero, and the cost balance for each productive component of the system becomes
It means that the production exergy cost of a process is equal to the cost of the resources required plus the cost of disposed waste that generates.
In conclusion, waste always has a cost, but as it cannot be sold, its cost must be allocated to the final products, or better, to the processes that have produced them. In the same way that there is a cost of formation of products, there is also a cost of formation of waste, which is identified with matrix . Waste is obviously a problem for productive systems, but it also represents an opportunity for energy saving by recovering them to be used in other processes.
4. The Fuel–Product–Waste Cost Allocation Rules
The exergy cost of a flow is an emergent property, that is, one cannot measure it independently of the formation process of a flow stream. Cost is always linked to the production process. Furthermore, this process links a set of internal and external flows. Therefore, a complete set of interrelated cost flows must be determined, not an individual cost. There is not only interesting to find the costs of final products, but it is also valuable to have them for internal products. Then, the cost build-up for each final product could be traced through the energy system. The Fuel–Product (FP) rules offer a procedure for determining the exergy cost of the m flows of an energy plant, building a system of m linear equations with m unknowns, based on the productive structure definition, as it will be shown in this section.
As explained beforehand, given an energy system whose productive structure has been specified, the exergy cost of a flow of that system is defined as the amount of exergy required to produce this flow.
Let us denote
as the exergy cost of the system flow
i and
asthe corresponding exergy cost per unit of product exergy. The cost of the exergy processed on a productive stream
h is defined as
Let us denote
as the cost of exergy processed in a stream, and
its cost per unit of exergy. Therefore, the cost of each fuel and product stream of a generic process
u is defined as
Finally, the exergy cost of fuel and product of the process
u is defined as the sum of the fuel or product streams of the process:
The FP rules that define the exergy cost of the system flow could be written using the notation of the productive structure model, as follows:
Resources rule: The exergy cost is relative to the system boundaries. In the absence of external assessment, the exergy costs of the flows entering the system equal their exergy.
Cost Conservation rule: The exergy cost is a conservative property.
This rule implies all the cost associated to a process, both the spent resources cost and cost of waste generated , must be assessed as a production cost.
Unspent fuel rule: All the outputs of a fuel group have the same unit cost equal to the unit cost of the input fuel streams:
This rule implies that the process irreversibilities will be added to the cost of the output product streams.
Co-production rule: All products of the same quality at the output of a system’s component have the same unit exergy cost.
All the product groups of a process have the same unit exergy cost:
All the outputs streams of a product group have the same unit exergy cost:
The idea of products of the same quality needs a detailed aggregation level of the system.
Waste rule: The exergy cost of waste exiting the analyzed system must be charged to the product of the components that generate them.
This rule implies that the cost of waste flows, leaving the system boundaries, is zero, and then the cost of the non-recoverable exergy of these flows is assessed to the final products by means of the waste internalization.
Let us also define the bifurcation ratio
as
these ratios distribute the cost proportionally to the exergy content. In the case of a fuel group, they define the recoverable fuel rule and, in the case of product groups, they define the co-production rule. Therefore, the unit cost of internal flows equals the unit cost of the productive group the flow comes from.
The Exergy Cost theory provides a set of rational rules based on thermodynamic criteria and the productive purpose. Now, we will prove that the FP rules are necessary and sufficient conditions to unequivocally determine the exergy cost of all flows of a defined energy system.
4.1. Fuel–Product–Waste Rules Matrix Representation
Let and be vectors, whose elements are the exergy cost of fuel and product of the processes related, and a vector, whose elements are the exergy cost of the flows, finally is a vector, whose elements contains the total exergy cost of the productive streams. Let , , and be the corresponding vectors containing the unit costs.
If one applies the Input-Output cost model [
16] to the productive table, one obtains the following equations:
Now, let us prove that the above equations verify the ECT rules of cost allocation:
Equation
16 defines the cost of productive groups, as a linear function of its inputs:
If , i.e., it is a resource stream, by rule FP1:
If
h is a product stream, i.e.,
, we need to verify
by rule FP4P,
, and
Finally, if
h is a fuel stream, i.e.,
, by the stream cost definition, Equation (
16) is verified:
Equation (
17) relates the cost of flows and productive streams. Now, we need to verify for all the flows that
, but by Equation (
15) it is satisfied. It means that the unit costs of a flow equals cost of productive groups the flow comes from.
Equation (
18) defines the cost balances of processes as a linear function of the cost of productive stream groups. By cost balance, rule FP2:
.
By rule FP5R, the second addend of equation is satisfied.
On the other hand, from the first addend, it must satisfy
by definition of fuel stream, and rule FP3, it leads to
therefore, Equation (
18) is satisfied.
The cost balance Equation (
18) could be also written as
This result proves that the FP rules could be expressed using the algebraic relationships (
16)–(
18), which provide a set of
equations with
unknowns that permit to determine the exergy costs of flows and productive streams.
4.2. Exergy Cost Computation
This section explains a new algorithm for calculating the exergy cost of system and process product flows, based on the matrix representation of the ECT rules. First, it calculates the cost of productive groups, then the cost of internal flows Equation (
15)
15, and the processes costs by Equation (
19).
Let be a matrix so that , be a matrix so that . Let be a matrix so that , and similarly, Let be a matrix so that . Finally, let to be a matrix, so that .
These matrices are obtained by scaling the rows of the productive table by the corresponding exergy streams, then Equation (
3) is rewritten as
Let
be a
vector, whose elements indicate if a stream is a system output:
Equation (
5) shows that the system outputs could be separated into final production and waste. Let us define the corresponding adjacency vectors
and
indicating whether the production flows are final products or waste:
The following relationships are verified:
Substituting these matrices into Equation (
16), it leads to the following relationships:
and substituting Equation (
27) into Equation (
26), the following system of
ℓ equations with
ℓ unknowns, to determine the exergy cost of the productive streams
, is obtained:
where
is called
cost characteristic matrix.
To demonstrate that Equation (
28) has a unique solution, we will prove that
is a productive matrix, see
Appendix A, or equivalently that
From Equation (
25), we get
. Therefore, as an energy system has final products, i.e.,
, the exergy costs of the flows can be unequivocally determined by
Once the cost of productive groups are determined, the cost of flows could be obtained by applying Equation (
15), and the production cost of processes by Equation (
27).
Moreover, matrix
is definite positive, see
Appendix A, i.e., all its elements are non-negative. Therefore, the exergy costs are always non-negative because the exergy of external resources is a non-negative magnitude.
Applying the exergy balance, (4), (20) lead to
, and substituting into :
then, right multiplying both sides of Equation (
30) by
, we get the exergy cost of productive streams as a function of the irreversibilities and waste generated by the processes:
Applying Equation (
27), a similar expression for exergy cost of flows is found:
Equation (
31) is essential to understand the process of cost formation. It shows the exergy cost of a flow equals its exergy plus the sum of all exergy destroyed (internal and external irreversibilities) during the production process of that flow. The above equation
represents the local exergy losses assessed to each productive group, and then the cost operator
distributes these values to the remaining processes of the system as additional resources consumption. As it is shown in Equation (
31), waste is considered an irreversibility.
As the last term in Equation (
32) is positive, the exergy cost of a flow is always greatest or equal to its exergy:
for each
i. The equality is satisfied only if there is no irreversibility in the production of such flow. It is the case of the external resources, whose cost is equal to its exergy. Therefore, irreversibility reduction implies production cost decrease and resources saving.
Let us calculate the exergy costs of flows and productive streams of the TGAS plant according to the method exposed above.
The submatrices that define the productive structure table for the TGAS plant, using the sparse coordinate (
row, col, value) format, are
where the bifurcation ratios are
In general, the
matrices are determined as follows:
Then, the cost characteristic matrix compute the exergy cost, by means of Equation (
29), is given by
Note that the cost matrix depends only on the bifurcation ratios. The sum of each row of the internal productive groups is 1, meanwhile if the rows of the system output groups sum to zero, then matrix is productive.
Table 3,
Table 4 and
Table 5 show the exergy and exergy cost values for the TGAS plant for productive groups, physical flows, and processes, calculated using Equation (
29). Each productive stream has an assigned key code that indicates the node to which it belongs and the stream type. Each flow is also defined as the pair of connected productive groups. The global efficiency of the plant is 46.8%, and the unit exergy costs of electricity and heat are 1.8 and 2.59, respectively. Note that the waste stream cost (N5P1) is 1429.7 kW. This means that 4% of natural gas is dissipated to the environment as exhaust gases. This cost is charged to the combustion chamber product and redistributed to the final products of the system. In the next sections, we will explain in detail which part is due to the internal irreversibilities of the processes and which part is due to waste allocation. Observe that the cost balance for the overall system is satisfied
, as well as flows cost overall balance:
.
5. The Generalized Exergy Cost
As mentioned above, the exergy cost is relative to the system boundaries. Therefore, we will distinguish between the thermodynamic system that constitutes the installation and its environment. Exergy cost, also called direct exergy cost, only takes the processes irreversibility (both internal and external) inside the boundaries of the system into account.
From a natural resource management point of view, the system boundaries should be set at the extraction level of non-renewable resources from nature [
17]. The exergy cost of the natural gas processed in a gas turbine will be higher than its exergy due to the extraction, storage, and transportation processes necessary to use it. Moreover, direct exergy cost does not consider the fact that the units that form an installation are functional products, and they have their own exergy cost because to keep them in operation, additional, exergy will be required.
On the other hand, when considering the economic aspects, the perspective is extended with the introduction of two additional factors: the market prices of the fuels (€/MWh) which are not linked to the exergy of the resources processed, and the cost of depreciation, maintenance, and operation of the plant required for the production process Z (€/h).
For these reasons, the
generalized exergy cost concept is introduced as a broader view of direct exergy cost, where the costs of the system flows consider the interactions with the physical and/or economic environment. Therefore, the
Resources rules should be adapted to consider the external valuation of resources
, which could be measured in energy or monetary units per unit of time. If costs consider
Z expenditures, either measured in energy or in monetary units and levelized per time unit, the
Balance Cost Rule must be included this factor and rewritten as follows:
where
,
, and
are the generalized exergy cost of the products, fuels, and waste of each system process, respectively.
According to these ideas, the exergy cost Equations (
16) and (
17) could be rewritten for generalized exergy cost as
where
and
are vectors whose elements contain the generalized exergy cost and unit exergy cost of the productive streams, respectively, and
and
are
vectors whose elements contain the generalized exergy cost and unit exergy cost of flows.
and
are vectors, whose elements contain the generalized exergy cost and the unit exergy cost of the process production.
is a vector whose elements represent the cost of external resources, and is a vector whose elements represent the costs directly allocated to the processes.
Therefore, the generalized exergy cost of flows could be determined as
Note that as the values of the matrix are dimensionless, the measured magnitudes of generalized exergy costs are the same to that of external resources.
Some examples of generalized exergy cost are thermoecological cost [
8], defined as
“The cumulative consumption of non-renewable exergy connected with the fabrication of a particular product, increased by the additional consumption required to compensate for environmental losses caused by the rejection of harmful substances to the environment”, or the exergoeconomic cost [
3], which evaluates the monetary cost of internal flows and products of complex plants. The effects of the environment relations on the generalized exergy cost can be introduced by modifying an external assessment
and
Z, meanwhile, the way to distribute costs, based on exergy, remains unaltered.
6. Process Thermoeconomics
Process Thermoeconomics [
18,
19] (formerly Symbolic Thermoeconomics) is a methodology based on the Exergy Cost theory for the analysis of the productive structure and the natural resources consumption process in energy systems. It was introduced in 1988 [
20] as a technique to obtain general equations that relate the overall efficiency of an energy system and other thermoeconomic variables, such as fuel, product, and exergy cost, with the efficiency and irreversibility of each component which forms it. By using these equations, it is possible to analyze the influence of the individual components on the whole system.
6.1. The Fuel–Product Table
The first stage to identify the cost formation process consists of building a productive scheme, which shows the relationships among the system processes. The problem of productive structure identification at the process level is closely related to the productive structure table previously introduced in this paper.
The Fuel-Product table, also called FP Table, represents the production structure of an energy system at the process level (see
Table 6) and describes how the production processes are related; that is, which processes produce the resources for each process and where each process’s resources come from.
According to this model, the production of one component is used as fuel of another component or as part of the total output of the plant:
where
is the production portion of the
i-th component that fuels the
j-th component. In the above expression, we consider component 0 as the system environment, then
represents the production portion of the component
i which leads to the final product, coming from the environment to the component
i.
On the other hand, the resources entering each component could be expressed as
where
represents the external resources entering the plant, which go into the
i-th component. Moreover, the second law states that the process resources
are always greater or equal to the production of such process
. Finally, the total fuel and product of the system can be expressed as
Table 6 could be expressed in matrix form as follows:
These submatrices satisfy Equations (
33)–(
36):
where
is a
vector which contains the exergy values of the system outputs for each component, and
is a
vector which contains the exergy values of the system inputs for each component.
is a
matrix containing the internal exergy interchange between processes. Its elements
represent the production portion of the
i-th component that fuels the
j-th component.
The FP table could be done graphically in the case of an aggregated system with a few processes under analysis, but in general, this method is not feasible for complex structures and must be derived from the productive structure table described in
Section 3.
From Equations (
20)–(
22) of the productive table, it leads to
It could be proved, from Equation (
25), that the matrix
is productive and its inverse
is non-negative; therefore, Equation (
22) could be rewritten as
then, replacing Equation
37 into Equation
20 leads to
therefore, let define the elements of the FP table as
By construction, all their elements are non-negatives and satisfy Equation (
34). To prove that they define the FP table, we need to check that Equations (
38) to (
40) also satisfies Equation (
33). Indeed, applying Equation (
25) leads to
, and one has
Table 7 shows the FP table of the TGAS plant.
Figure 7 is the corresponding graph representation, which has been obtained using the yEd graph editor software [
21].
This graph shows how the production of the combustion chamber and the compressor are used as fuel of the turbine and the HRSG, and also that a part of its exergy becomes unspent fuel and dissipated out of the stack. The production of the turbine is used part in the compressor, and part becomes the final product. All the production of the HRSG becomes the final product.
6.2. The Dissipative Processes Table
As we have explained, the aim of energy systems is to obtain final products by processing external resources, but in the same way that these products are obtained, waste is also generated. The resources consumed to produce and dispose of these waste streams must be imputed to the final products. Note that waste is called waste only if the flow crosses the system boundaries. Therefore, the system outputs split in two parts
, final products
, and the waste
, so that
where
and
are
vectors, whose elements indicate if the streams group is a final product or a waste, such that
.
Just as there is a productive table for the processes, there is also a table for their waste. Let
be a
matrix, called a
dissipative process table, where its elements
represent the exergy dissipated by the
i process, which has been produced by component
j. This matrix verifies
The dissipative table performs the same function as the waste table, described in previous sections, at the process level, and could be obtained as
The dissipative table represents the waste formation process of the system. This process follows the opposite direction to the production process and identifies where waste has been produced. In the case of the TGAS example, we made the assumption that gases were generated in the combustion chamber, then the table has only one non-zero element: .
6.3. The Cost Equations for the Process Model
The Fuel–Product–Waste tables help to identify the cost formation process. Now, we need to determine the production cost of processes. Let us consider the generalized cost equations of the productive table
and the cost balance equation for the processes
The generalized cost of the productive groups
can be calculated as a function of the production cost of processes as
then, replacing Equation (
51) into Equations Equations (
48) and (
49), and applying the definition of the FP table (
38) leads to
substituting these equations into the cost balance Equation (
50) leads to
where
is a
vector whose elements contain the cost of external resources used in each process.
The above equation allows one to determine the production costs of processes
. Once the production cost are obtained, applying Equation (
51) the costs of the system flows can be determined by means of
Let be
a
matrix whose elements
represents the cost of flow produced by process
i used as fuel to process
j, including the environment process 0. This matrix is called
cost table, and it is defined as
In the next sections, we develop a general methodology to obtain analytical formulae for the production costs that relate the global efficiency and the production costs with its individual components’ efficiency.
7. The Resource-Driven Model
The objective of the resource-driven model is to represent the thermoeconomic variables of a system as a function of the external resources and the efficiency of the individual processes. Let us define the distribution coefficient as the portion of the production of the j-th component used as resource in the i-th component.
Let
be a
matrix whose elements are the distribution coefiecients, defined as
replacing Equation (
57) into Equation (
34) leads to
It shows how the fuel of each component is a linear function of the products that form it.
Let
to be the matrix of waste distribution ratios
, defined as
replacing into the waste table definition Equation (
44) leads to
7.1. Cost Equations in the Resource-Driven Model
In order to compute the production exergy cost, one can replace Equation (
57) into cost balance Equations (
52) to (
54), leading to
Therefore the production exergy cost could be computed as
Note that the matrix operator
includes both information of production cost distribution
and waste allocation
. Besides, the equation of direct exergy cost is given by
Once the exergy costs are calculated, the Fuel–Product cost table can be obtained from Equation (
56).
Table 8 shows this table for the TGAS plant example. Note that the sum of rows equals the sum of columns. The first row and column represent the environment. The total resources entering the system, 36,620 kW, are distributed to the cost of final products: electricity: 18,011.7 kW; heat: 18,608.3 kW. The cost of electricity is 1.8 times the cost of natural gas, and the cost of heat is 2.59 times. The cost of waste gases
kW is charged to the combustor and redistributed to rest of processes. The cost of the stack gases leaving the system is zero.
7.2. Production Cost Decomposition
The production cost of the processes can be calculated using Ëcrefeq:cprd, explained in the previous section. It requires the fuel–product and waste allocation tables. To get a better understanding of the cost formation process, it is necessary to break down the cost into the contributions of internal irreversibilities , and waste .
Let be the base production cost operator, without considering waste allocation.
The matrix of waste distribution ratios can be written as , where is a whose elements are the waste distribution ratios corresponding to the dissipative units (or the active rows of the matrix) and is a matrix, whose columns are the unit vector corresponding to the dissipative component index i.
Therefore, applying the Woodbury formula, see
Appendix B, we can obtain the production cost operator
, from the base production cost operator
, as follows:
where
is a
matrix, and
is the waste cost operator. Therefore, substitution into Equation
64 leads to
where:
Equations (
66) to (
68) allows one to determine the production cost as the sum of the contribution of process irreversibilities and waste allocation. First, we compute the base production cost operator to determine the production cost due to internal irreversibilities
. Once it is determined, the production cost due to waste is computed employing the waste cost operator Equation (
68).
This expression can also be written as
and
where
represents both the cost of waste allocated to each process and the equivalent resources required to abate the waste generated by each process. Therefore, the production cost due to waste could be computed as
The cost decomposition values for TGAS example are shown in
Table 9.
8. The Demand-Driven Model
In the previous section, we studied the representation of the system’s thermoeconomic variables as a function of its components’ efficiency, the distribution coefficients, and the external resources. The optimization and diagnosis analysis of a thermal system requires studying the productive structure’s behavior as a function of the total production or demand objectives. This section presents an alternative representation that relates the thermoeconomic variables of the system with the total plant production, the efficiency of its components, and a new type of parameter called junction ratio.
We define, in a analogous way to distribution coefficients, the
junction coefficients
as the portion of the resources of the
j-th component coming from the
i-th product.
Let
be a
matrix, so that
and
is a
vector, so that
. Their elements
, called
junction ratios, represent the ratio of production of process
j used as fuel on process
i. They verify
Similarly, let
be a
matrix, so that
and considering that
is a
vector, so one obtains that
. Their elements
, are dubbed
technical coefficients or unit consumption ratios, and represent the amount of resources provided by process
j needed to obtain one unit of the process product
i. They verify
where
, which verifies
. Note that the unit consumption of the process
i equals to the sum of its technical coefficients. Therefore,
and
contain the information about the efficiency of local components.
Replacing these matrices into Equation (
33) leads to
and therefore:
By construction,
is a productive matrix, therefore it has inverse
, and it verifies that
These formulas allow the fuel, product, and internal irreversibility of the system components to be related in terms of unit exergy consumption and system outputs, including both final products and waste.
On the other hand, let
be a
matrix, so that
, whose elements
represent the waste streams generated by a process per unit produced. By definition of the waste table, Equation (
42) it leads
, therefore
and replacing into Equation (
70), we get:
Therefore, we can relate the fuel, product, and irreversibility of the system components as a function of the final demand:
Note that production operators do not only depend on local unit consumption, but also on waste generation ratios.
The total system resources can also be expressed, according to the definition of the technical coefficients, as follows:
or in matrix notation:
depending on whether waste is considered or not.
For example, the total fuel of the TGAS system could be written in terms of their unit local consumptions, and the system outputs
The effect of waste on total fuel consumption is given by the term .
Finally, the external irreversibilities of the system
, could be also related to its final demand, by means of the relationship
In the previous section, we can obtain the production operator
from the base production operator
. In a similar way, the waste generation ratios matrix could be decomposed in the form
, where
is a
corresponding to the non null rows of
matrix. Applying the Woodbury formula, see
Appendix B, leads to
where
is a
matrix, and the waste operator is computed as
Cost Equations in the Demand-Driven Model
Dividing both sides of the cost balance (
64) by
, it could be written in terms of the demand-driven model as
therefore, the unit exergy cost of product can be obtained as
where
is a
vector, whose elements are the external resources costs per unit of fuel consumed in the process. The direct unit exergy cost is calculated as
Applying to Equation (
72) and (
73) to (
74) leads to
In the same way as the resource-driven model, the unit production cost could be decomposed into the amount due exclusively to
irreversibilities plus the amount due to waste
.
The cost balance of the system could be written from Equation (
71) as
Table 9 shows the production cost of the processes of the TGAS plant. As can be seen, the production cost due to waste allocation represents near 4% of the total production cost of the system.
The values of
show the impact of waste on the final production cost. However, waste could also be partially used in other processes, i.e., recycled. The limit of these costs is given by
. Exergy cost theory could be applied to Industrial Ecology [
22], which can help to solve several significant problems such as the identification of integration, efficiency improvement, quantification of benefits obtained by integration, or determination of prices based on physical roots [
23].
We have explained two different ways of evaluating the production cost—the resource-driven and the demand-driven model—as functions of the components’ efficiencies, the external resources, and the distribution or junction coefficients. The demand-driven model is used in local optimization and diagnosis. Meanwhile, the resource-driven model is used in processes integration and waste cost allocation.
The information in the resource-driven model representation has the direction of the production process. If the external resources are known, the remaining thermoeconomic properties can be evaluated. The demand-driven model representation uses an equivalent logical structure, but the information has the opposite direction. If we know the demand or the final products of a plant, it is possible to determine the resources needed to obtain any internal product and their unit costs. Both representations are complementary and figure out the complete picture of the production process and cost formation. The operators of both models could be related by using the relationships
then, production operators are similar matrices, with the same values in the diagonal, and they are related by
This formulation has been widely applied in different thermoeconomic fields like cost accounting [
24,
25,
26,
27], local optimization [
28,
29], and diagnosis of energy systems [
30,
31,
32].
9. The Irreversibility Cost Formula
As explained above, the exergy cost depends on the cost of external resources. If no external evaluation is considered, the exergy cost of the flows entering the system is equal to their exergies. This indicates that, once the system boundaries are defined, the production costs only take into account the internal and external irreversibilities of the system. The direct exergy cost does not take into account physical or economic interactions with other systems and only depends on the efficiency of the local components, and thus on the local irreversibilities.
In a previous section, we have obtained the relationship (
32) between the cost of flows and the irreversibilities of processes. As irreversibility is a property of processes, it is interesting to relate it to the cost of production.
Consider the direct exergy cost Equation (
65) of the resources-driven model:
On the other side, from Equation (
58), the exergy of resources could be expressed as
using the relation
, and replacing into Equation (
65), leads to
therefore, by definition of operator
, we get
It means that the cost of exergy production is equal to its exergy plus all the internal irreversibilities and waste generated by each process generated to obtain this product. The matrix operator is the footprint of the exergy destruction of the energy systems .
One can prove that
, therefore Equation (
77) could be expressed as
therefore
, and it follows that the unit production cost of a process is always greatest or equal to the unit local consumption:
A similar expression from unit direct exergy can be obtained by applying Equation (
76) to the irreversibility cost formula Equation (
77):
This equation is an alternative to computing the unit exergy production cost of processes, decomposed by the contribution of irreversibilities and waste. The irreversibility operator could be computed from the base operator as
where
are the columns of the irreversibility operator corresponding to the dissipative units and
are the active rows of the waste operator
.
The irreversibility cost formula makes it possible to explain the process of product cost formation of an energy system and trace the destruction of exergy from external resources to final products. By construction, this formula is only valid for the direct cost of exergy. Next, an extension of this formula is presented, taking into account physical and economic interactions, and not only the exergy of external resources.
Equation (
78) can be extended to include the cost of external resources by introducing the
irreversibility cost factor vector
such as
In order to determine the irreversibility cost factor independently of the exergy cost, we take the following relationship:
combining with Equations (
74) and (
79), we get the following system of linear equations:
Equation (
80) allows one to determine the irreversibility cost factor from the internal productive structure
and the cost of external resources. Note that, in the case of direct exergy cost,
, and by definition of exergy junction ratios, the irreversibility cost ratio
, corresponds to the expression of Equation (
78).
The irreversibility cost factor
obtained from Equation (
80) can be interpreted as the minimum costs for a given value of external resources, obtained when one makes the hypothesis that the system has no internal and external irreversibilities, i.e.,
and
.
If we want to distinguish the exergy cost due to internal irreversibilities from the cost due to waste allocation, the former can be obtained directly from Equation (
79), taking
equal to zero.
The generalized irreversibility cost formula allows for a breakdown of the contribution of external resources to exergy destruction. The irreversibility cost factor plays two roles in the formula: First, it is the cost of the inputs to the system used in each process, i.e., it accounts for irreversibilities outside the system boundaries, and second, it is the cost of exergy destruction of the processes within the boundaries.
To illustrate the application of this formula, we will calculate the thermo-ecological cost footprint for the TGAS plant. The system boundaries have been extended to consider the extraction, processing, and transport to the plant of natural gas, as well as the reduction in CO2.
The following assumptions are made to calculate the TEC of external resources [
17]: a value of 1.082 kW/kW NG (domestic Natural Gas including CO
2 emissions) for the unit cost of NG, and a value of 0.238 kW/kW NG for the cost of CO
2 abatement. Finally, we also include the depreciation, maintenance, and operating costs of the plant’s processes
. They have been calculated from the work in [
33] and converted to energy units using a natural gas price of 20 MWh as the conversion factor. In this example, the costs of reducing CO
2 are considered as an external cost that is allocated to the stack process. These values are summarized in
Table 10.
Table 11 and
Figure 8 show the TEC costs of the TGAS plant using the external resource cost values from the Table. One can see the importance of CO
2 emissions.
In the case of direct exergy cost, the unit resource cost is one. Meanwhile, in the case of thermo-ecological costs, the unit resource cost is greater than one. Rows I represent the contribution of the irreversibility of the i-th process to the unit cost, and row R represents the contribution of the external irreversibility of both hot gases and CO2 emissions. The exergy cost of the flue gas is 12.8 times the exergy of the dissipated gases. This cost is redistributed to the final products of the plant and accounts for about 20% of the total cost.
10. Methods for Cost Allocation of Waste
As we have seen, there is not a general criterion to allocate the cost of the system waste. It depends on the type and the nature of the waste flows. For example, in the case of the heat dissipated in the condenser of a Rankine cycle, we can distribute the cost proportionally to the entropy generated by each process. Meanwhile, the combustion gases eliminated by the combined cycle stack are allocated to the combustion process. The allocation of waste costs should be based on the following criteria [
34]:
- (a)
The cost of waste must be charged to the productive units that have generated it. Here, it is essential to establish a conceptual difference between the exergy of waste and its cost. Costs also encompass exergy consumption to be involved in the elimination of the system waste. Therefore, it is the cost, not its exergy, that is of actual interest. This raises a need that is expressed in the second premise.
- (b)
It is needed to identify the process of cost formation of waste. This process is parallel to the process of production cost formation because waste is eliminated in the dissipative components, but formed along with the productive processes.
- (c)
The responsibility of a productive component for waste generation lies in its contribution to the formation cost of waste.
To identify waste flows at the process level, it is necessary to relate each waste flow with the physical and chemical processes taken place in dissipative units. We must define as many dissipative units as waste flows. Dissipative units are defined in such a way that the output product stream is a waste flow, and input fuel streams are these flows that one wants to be eliminated and the resources required to do that. The irreversibility carriers allow one to identify the origin, path, and end of waste streams and then build the dissipative table .
The FP table helps to explain the cost formation process of system products and waste. In this section, we will propose four methods to obtain the values of the elements of matrix , based on the productive structure information at the processes level:
Method A (Exergy distribution): It is directly based on the information provided by the FP table [
12]. Then, we consider the values of the table
as the exergy provided by the component j that is disposed in the dissipative unit r:
This method looks for the immediate cause and distributes the waste’s costs to the components that have produced it directly and in proportion to their exergy.
The next methods are based on the contribution of the productive units to the direct exergy cost of waste. As the unit production cost has not been determined yet, we will consider the value of the unit cost due to irreversibilities and the values of the production cost operator instead. In all cases, direct exergy cost is considered.
Method B (Exergy cost distribution): This allocation method is similar to the previous one, but it distributes the cost in proportion to their exergy cost instead of exergy. Note that in many cases, the exergy of waste is not relevant but their cost. According to (
52), if
is a dissipative unit,
Equation (
52) means that the production cost is equal to the sum of the cost of exergy streams eliminated in this dissipative unit, and the waste cost must be allocated to the processes have produced them.
Method C (Irreversibility–cost distribution): A more complex method considers the complete chain of production cost [
34]. It is based on Equation (
77):
where
is the corresponding element in matrix
. Decomposing the exergy of waste by its individual contributions, we get
therefore, the waste cost distribution parameters could be defined as
This method combines the first one with the irreversibility cost formula, to distribute the cost according to the irreversibility carriers of waste streams. This method takes into account the full path of the waste cost formation.
Method D (Resources distribution): The last proposed method is based on the idea of cost definition, i.e., the cost of waste is the amount of external resources spent to produce it, and then allocate the cost of waste proportionally to the resources consumed:
and the waste distribution parameters are defined as
This method allocates the waste cost to the overall system according to the proportion of each external resource used to produce the waste. This method is used in the TGAS example. It is equivalent to increasing the cost of natural gas by a factor of 1.0609 (6%), determined by calculation of , and therefore the cost of all streams is increased by the same factor.
Table 12 shows the values of waste costs allocated to each process
and the unit production cost of each component due to waste for each of the proposed methods. The total cost of waste and the unit production cost of final products are the same for methods one, two, and four, and the method based on irreversibility carrier allocation is slightly different.
As discussed throughout this paper, the formation of the cost of waste is parallel to the production cost. The process model can help provide methods for the first approximation to the allocation of the waste cost, but in general, the construction of waste tables is usually external to calculating production costs. In this line, several researchers have proposed different waste cost allocation methods in recent years [
35,
36,
37,
38].
11. Recycling Saving Accounting
As long as these residual streams have exergy, they can be retrieved in recovery units; it is the case of the heat recovery steam generator (HRSG) in the TGAS example. These recovery units are integrated into the plant and constitute productive units that, instead of expending exergy to dispose of waste, their exergy is recovered to produce some other by-product. In the case of the TGAS plant, the recovery unit produces saturated steam.
The potential savings from waste recycling can be estimated if one knows the production costs due to external irreversibilities. The production cost due to waste indicates the maximum amount of resources that could be saved if waste were recycled.
It is well known that not all waste could be saved for technical and economic reasons, but through the process integration and Industrial Symbiosis [
39], it is possible that other systems convert this waste into resources. The exergy cost theory allows evaluating the cost of waste, accounting for the resources savings and providing fair prices to waste becoming by-products.
Let
to be the percentage of waste
i that could be reused or
recycling ratio, in these conditions
. Therefore, the waste allocation matrix can be recalculated as
where
is a
diagonal matrix whose elements contain the
recycling ratios of the system. By introducing this matrix, it is possible to recalculate the waste operators, as
and the production cost as a function of the recycling ratios is given by
The waste rule in a recovery unit is the with Cost Conservation rule. The exergy cost of final waste plus that of the obtained by-product is the cost of entering waste plus the spent fuel to abate them. This reduces the cost of final waste, then at the end of the analysis, only these final waste costs add to the final costs of the plant product(s). Clearly, recovering the exergy of waste saves exergy and reduces the cost of products.
Consider the TGAS plant again, and suppose there is not an HRSG to recover part of the escape gases of the turbine. In this situation, the cost of electricity will be 3.662 kW of natural gas for one kW of electricity produced. Moreover, we have lost 11.7 MW in hot gases leaving the gas turbine.
The cost of electricity and flue gas as a function of recycling rates can be obtained using the formulation introduced in this section, as shown in
Figure 9. The unit cost of electricity is 3.662 if turbine escape gases are not recovered. It is near two times more than the turbine with heat recover steam generator, that recover 92.86% of escape gases.
The unit cost of electricity as function of the recycling ratio
is
This function is not linear, and its slope is decreasing, which means that the exergy saving decreases when the recirculation ratio increases. If we want to recover more than 90% of the energy from the exhaust gases, the decrease in the unit cost of electricity is not relevant, and possibly the investment cost to do so is much higher than the natural gas savings obtained.
As shown in this simple example, the use of
recycling or recovering units as productive processes is a key practice for energy saving. The work in [
40] shows another example of Process Thermoeconomics applying to recycling saving by system integration.
12. Conclusions
This paper reviews the fundamentals of the Exergy Cost Theory, an energy cost accounting methodology for assessing physical costs that incorporates both the production of products and their associated waste. Besides, a mathematically and computationally useful formulation is presented, which will allow the practitioner to carry out studies on productive systems regardless of their structural complexity.
The process of waste cost formation is presented from a thermodynamic perspective that contrasts with the conventional economists’ approach. It is proposed to consider waste as external irreversibilities whose origin is in plant processes.
We propose to generalize the idea of waste, and consequently we have created a theory to evaluate its cost in any production process. Waste is an unwanted effluent of matter or energy, which leaves the plant and will sooner or later dissipate into the environment. It is clear that waste has exergy, as its temperature, pressure, concentration, or composition differs from the same properties of the environment. Therefore, waste can be utilized before going outside through the use of recovery units. However, if this waste cannot be recovered, it is necessary to reduce their exergy using dissipation units. Logically, a waste will cease to be waste when it reaches complete thermodynamic equilibrium with its environment.
The conventional classification [
41] of
waste as solid waste and
emissions as gaseous waste, wastewater, particulate matter, noise, and emissions of different wavelengths (i.e., pollutants) does not make sense from the point of view of thermodynamics. They are all
outflows that give rise to external irreversibilities. Moreover, they are inherent to production. All production has its associated waste. Waste is generally more voluminous and entropically complex than the manufactured products.
The current perception of the effects of waste on climate change, water pollution, the constant growth of landfills, and the consequent depletion of raw materials has led to scientific attention being paid to its minimization and abatement and the internalization of its costs. Thus, prices should reflect the resources consumed and the external impact of waste generation.
This mindset change leads to a revision of the current theories of optimization and diagnosis of industrial processes. For example, the definition of process efficiency must reflect both internal and external irreversibilities.
The objective function to be minimized is the production cost plus the combined minimization of waste and its associated abatement costs, both inside and outside the production plant’s boundaries. Optimization of production processes should not use cost externalization. Unfortunately, cost externalization is, and has been, a common practice in the economies of developed countries and, in general, it is an economic practice that transfers the costs of external impacts to society, to developing countries or future generations.
The main contribution of the new model presented in this article is the integration of the different methodologies derived from ECT with the productive linear models of Input–Output analysis. The cost equations of ECT, the characteristic equations of Structural Theory, and the formulation of Symbolic Exergoeconomics can be obtained from the production structure table.
Furthermore, it allows proving the existence, uniqueness, and positiveness of the solution to the exergy cost allocation problem in a mathematically rigorous way. It provides a set of numerical procedures and general formulae, valid for any state of the system, which solely depends on the productive structure and its interaction with the environment. They serve as a guideline to develop software for thermoeconomic analysis of energy systems. The TGAS plant results illustrating the methodology of this paper have been obtained using TAESS (Thermoeconomic Analysis of Energy System Software). It is freely available on the web site [
42].
As a summary, the following algorithms and formulae are introduced:
The Fuel–Product table Equations (
38)–(
40).
Internal and external cost decomposition. Both
direct or
generalized exergy cost Equations (
66)–(
68)
The Fuel–Product cost table Equation (
56)
Irreversibility-cost formula, both for direct and generalized costs Equations (
79) and (
80).
Cost of physical flows. The same tables that in the case of processes can be obtained Equation (
55).
All thermoeconomic or exergoeconomic theories should take this new formulation into account because they use a partial view of the Second Law by concentrating their discussions on internal irreversibilities and their impact on the other components that can be located within the production structure. Parallel to the product cost formation process, there is a waste cost formation process. For this purpose, the concept of irreversibility carrier has been defined, which identifies the origin, transfer, recovery, abatement, and disposal of a waste output stream. As the physical waste leaves the plant, the waste cost is added back to the final production cost of the plant. This process is called cost internalization.
Another concept that has been outlined and should be developed is the
pinch point of waste recoverability. It is essential to know that as the generalized force gradients relative to the temperature, pressure or chemical potentials of a waste stream approach those of the environment, the exergy transfer kinetics, and thus the exergy recoverability of waste, decrease to zero. If one looks at
Figure 9, every time a percentage of the waste is recycled, the total system’s efficiency improves further. However, when the proportion of waste recycling increases, efficiency does not increase linearly. The production cost of the gas turbine as a function of recycling gases is convex, i.e., the exergy savings at the beginning of the recycling process are quite remarkable. However, as one approaches its theoretical limit—the reference environment, the exergy saving nullifies. This means that each additional increase in recycling corresponds to a smaller efficiency gain. Similarly, complete waste abatement or full exergy recovery is too costly and yields low results.
In fact, this is the law of diminishing returns governed by entropic behavior. From a global point of view, our economic system will never wholly reduce all its pollution. Pollutants can be minimized and diluted but not avoided. Therefore, neither the toxicity to life nor the degradability of the environment will disappear. However, low doses lengthen the deterioration time. The theory developed here allows explaining mathematically and physically this type of reflection.