Learning to Calibrate Battery Models in Real-Time with Deep Reinforcement Learning
Abstract
1. Introduction
2. Related Work
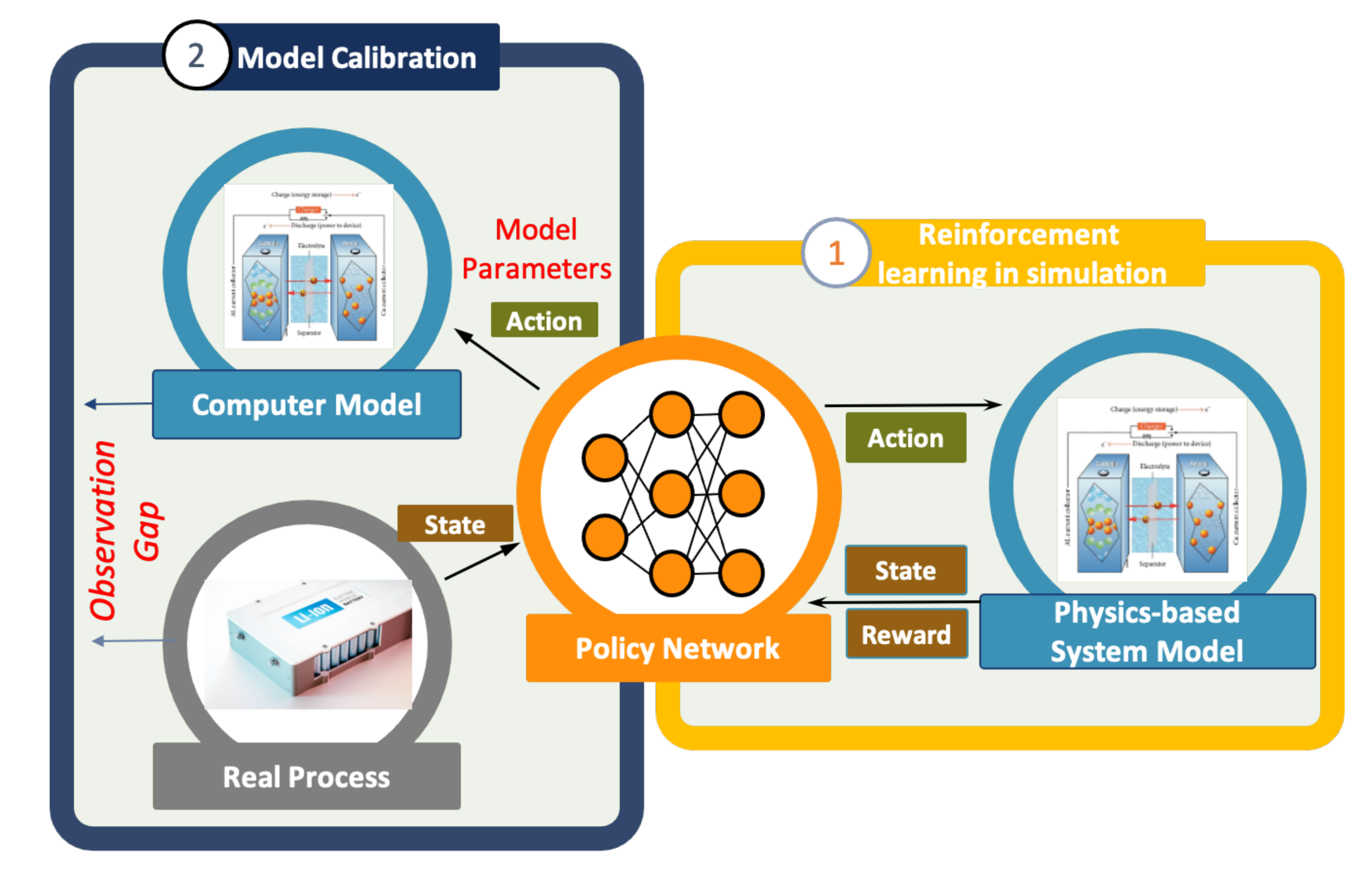
3. Materials and Methods
3.1. Battery Discharge Model
3.2. Markov Decision Process and Reinforcement Learning
3.3. Lyapunov-Based Actor–Critic
4. Experiment Datasets and Models
4.1. Dataset Generation
4.2. Hyperparameters of the RL Framework
4.3. Compared Methods
4.3.1. Unscented Kalman Filter (UKF)
4.3.2. Direct Mapping
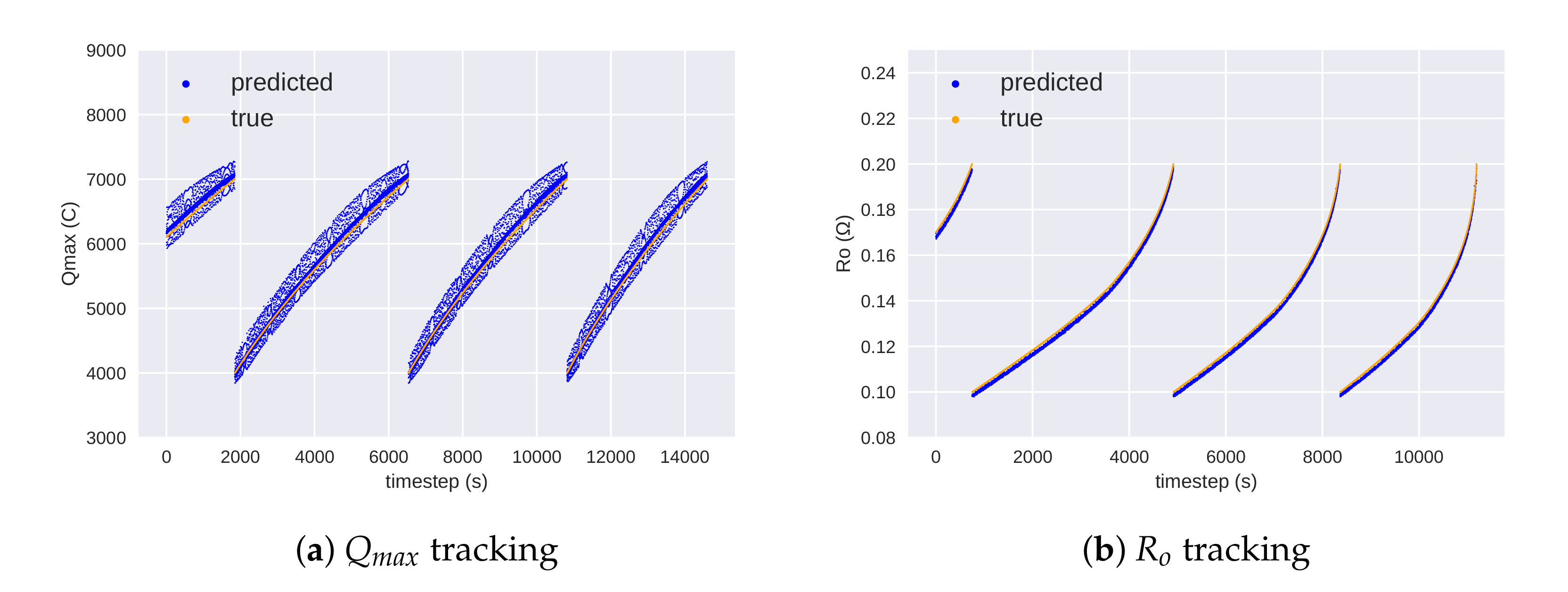
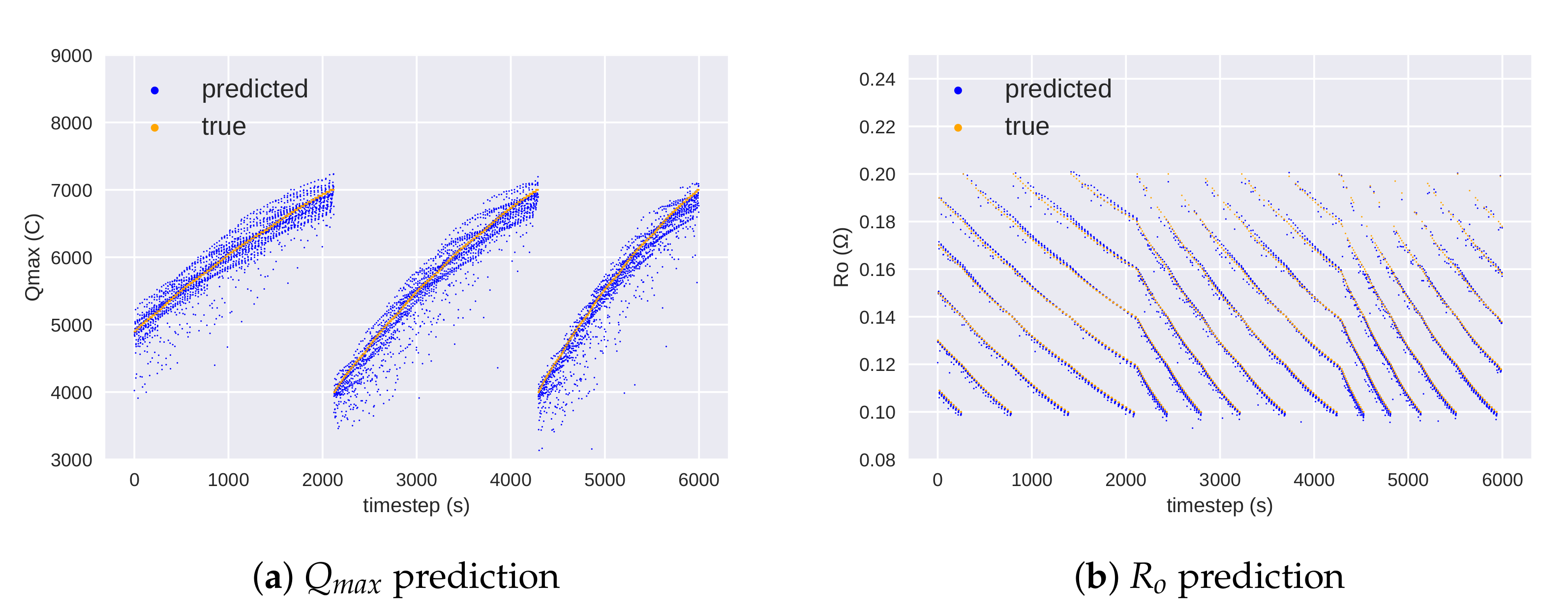
5. Results
5.1. Discussion
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Code for the Experiments
Appendix A. Dataset Generation
References
- Chen, W.; Liang, J.; Yang, Z.; Li, G. A review of lithium-ion battery for electric vehicle applications and beyond. Energy Procedia 2019, 158, 4363–4368. [Google Scholar] [CrossRef]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-ion battery storage for the grid—A review of stationary battery storage system design tailored for applications in modern power grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef]
- Bugga, R.; Smart, M.; Whitacre, J.; West, W. Lithium ion batteries for space applications. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007. [Google Scholar]
- Hussein, A.A.H.; Batarseh, I. An overview of generic battery models. In Proceedings of the IEEE PES General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Sun, K.; Shu, Q. Overview of the types of battery models. In Proceedings of the 30th IEEE Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 3644–3648. [Google Scholar]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Hinz, H. Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation. Inventions 2019, 4, 41. [Google Scholar] [CrossRef]
- Daigle, M.; Kulkarni, C.S. End-of-discharge and End-of-life Prediction in Lithium-ion Batteries with Electrochemistry-based Aging Models. In Proceedings of the AIAA Infotech@Aerospace, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Wu, T.H.; Moo, C.S. State-of-Charge Estimation with State-of-Health Calibration for Lithium-Ion Batteries. Energies 2017, 10, 987. [Google Scholar] [CrossRef]
- Ning, G.; Popov, B.N. Cycle life modeling of lithium-ion batteries. J. Electrochem. Soc. 2004, 151, A1584. [Google Scholar] [CrossRef]
- Ning, G.; White, R.E.; Popov, B.N. A generalized cycle life model of rechargeable Li-ion batteries. Electrochim. Acta 2006, 51, 2012–2022. [Google Scholar] [CrossRef]
- Andre, D.; Nuhic, A.; Soczka-Guth, T.; Sauer, D.U. Comparative study of a structured neural network and an extended Kalman filter for state of health determination of lithium-ion batteries in hybrid electricvehicles. Eng. Appl. Artif. Intell. 2013, 26, 951–961. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.S.; Daigle, M. Adaptation of an Electrochemistry-Based Li-Ion Battery Model to Account for Deterioration Observed under Randomized Use; Technical Report; SGT, Inc.: Mountain View, CA, USA, 2014. [Google Scholar]
- Saha, B.; Goebel, K. Modeling Li-ion battery capacity depletion in a particle filtering framework. In Proceedings of the Annual Conference of the PHM, San Diego, CA, USA, 27 September–1 October 2009; pp. 2909–2924. [Google Scholar]
- Nuhic, A.; Bergdolt, J.; Spier, B.; Buchholz, M.; Dietmayer, K. Battery health monitoring and degradation prognosis in fleet management systems. World Electr. Veh. J. 2018, 9, 39. [Google Scholar] [CrossRef]
- Buşoniu, L.; de Bruin, T.; Tolić, D.; Kober, J.; Palunko, I. Reinforcement learning for control: Performance, stability, and deep approximators. Annu. Rev. Control. 2018, 46, 8–28. [Google Scholar] [CrossRef]
- Kumar, V.; Gupta, A.; Todorov, E.; Levine, S. Learning dexterous manipulation policies from experience and imitation. arXiv 2016, arXiv:1611.05095. [Google Scholar]
- Han, M.; Tian, Y.; Zhang, L.; Wang, J.; Pan, W. Reinforcement Learning Control of Constrained Dynamic Systems with Uniformly Ultimate Boundedness Stability Guarantee. arXiv 2020, arXiv:2011.06882. [Google Scholar]
- Bhattacharya, B.; Lobbrecht, A.; Solomatine, D. Neural networks and reinforcement learning in control of water systems. J. Water Resour. Plan. Manag. 2003, 129, 458–465. [Google Scholar] [CrossRef]
- Treloar, N.J.; Fedorec, A.J.; Ingalls, B.; Barnes, C.P. Deep reinforcement learning for the control of microbial co-cultures in bioreactors. PLoS Comput. Biol. 2020, 16, e1007783. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Q.; Huang, Z.; Li, W.; Dai, D.; Yang, M.; Wang, J.; Fink, O. Off-policy reinforcement learning for efficient and effective GAN architecture search. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020; pp. 175–192. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Han, M.; Tian, Y.; Zhang, L.; Wang, J.; Pan, W. Hinf Model-free Reinforcement Learning with Robust Stability Guarantee. arXiv 2019, arXiv:1911.02875. [Google Scholar]
- Tian, Y.; Arias Chao, M.; Kulkarni, C.; Goebel, K.; Fink, O. Real-Time Model Calibration with Deep Reinforcement Learning. arXiv 2020, arXiv:2006.04001. [Google Scholar]
- Daigle, M.J.; Kulkarni, C.S. Electrochemistry-Based Battery Modeling for Prognostics; NASA Ames Research Center: Moffett Field, CA, USA, 2013. [Google Scholar]
- Available online: https://github.com/nasa/PrognosticsModelLibrary (accessed on 30 October 2020).
- Li, L.; Saldivar, A.A.F.; Bai, Y.; Li, Y. Battery remaining useful life prediction with inheritance particle filtering. Energies 2019, 12, 2784. [Google Scholar] [CrossRef]
- Kim, M.; Kim, K.; Kim, J.; Yu, J.; Han, S. State of charge estimation for lithium Ion battery based on reinforcement learning. IFAC-PapersOnLine 2018, 51, 404–408. [Google Scholar] [CrossRef]
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep Reinforcement Learning-Based Energy Storage Arbitrage With Accurate Lithium-Ion Battery Degradation Model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. In Proceedings of the NeurIPS, Denver, CO, USA, 27 November–2 December 2000; pp. 1008–1014. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor–critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv 2018, arXiv:1801.01290. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor–critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D. Battery Thermal-and Health-Constrained Energy Management for Hybrid Electric Bus based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2020. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Wang, J.; Li, P. Video Recommendation with Multi-gate Mixture of Experts Soft Actor Critic. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 25–30 July 2020; pp. 1553–1556. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Zhao, W.; Queralta, J.P.; Westerlund, T. Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: A Survey. In Proceedings of the IEEE SSCI, Canberra, ACT, Australia, 1–4 December 2020; pp. 737–744. [Google Scholar]
- Ghavamzadeh, M.; Mannor, S.; Pineau, J.; Tamar, A. Bayesian reinforcement learning: A survey. arXiv 2016, arXiv:1609.04436. [Google Scholar]
| Method | Single Parameter | Multi Parameter | ||
|---|---|---|---|---|
| Qmax | Ro | Qmax | Ro | |
| RL-LAC (ours) | 5.16 | 2.07 | 8.39 | 1.51 |
| UKF | 19.91 | 4.08 | 19.75 | 7.54 |
| Direct Mapping | 0.01 | 10.2 | 1.86 | 2.5 |
| Method | |||
|---|---|---|---|
| RL-LAC | UKF | Direct Mapping | |
| Time (ms) | 1.99 | 4.55 | 0.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unagar, A.; Tian, Y.; Chao, M.A.; Fink, O. Learning to Calibrate Battery Models in Real-Time with Deep Reinforcement Learning. Energies 2021, 14, 1361. https://doi.org/10.3390/en14051361
Unagar A, Tian Y, Chao MA, Fink O. Learning to Calibrate Battery Models in Real-Time with Deep Reinforcement Learning. Energies. 2021; 14(5):1361. https://doi.org/10.3390/en14051361
Chicago/Turabian StyleUnagar, Ajaykumar, Yuan Tian, Manuel Arias Chao, and Olga Fink. 2021. "Learning to Calibrate Battery Models in Real-Time with Deep Reinforcement Learning" Energies 14, no. 5: 1361. https://doi.org/10.3390/en14051361
APA StyleUnagar, A., Tian, Y., Chao, M. A., & Fink, O. (2021). Learning to Calibrate Battery Models in Real-Time with Deep Reinforcement Learning. Energies, 14(5), 1361. https://doi.org/10.3390/en14051361








