Collapse of n Point Vortices, Formation of the Vortex Sheets and Transport of Passive Markers
Abstract
1. Introduction
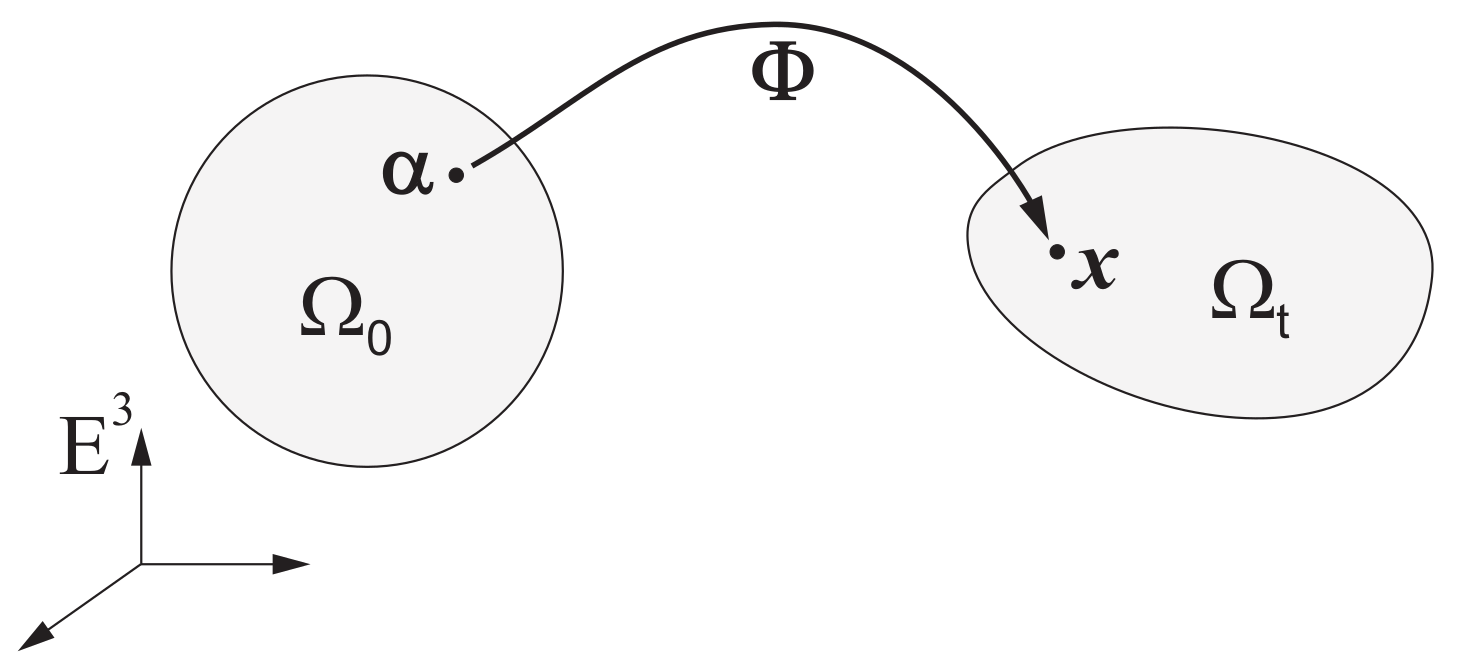
2. Equations of Motion for n Vortices
3. Self Similar Motions of n-Vortices
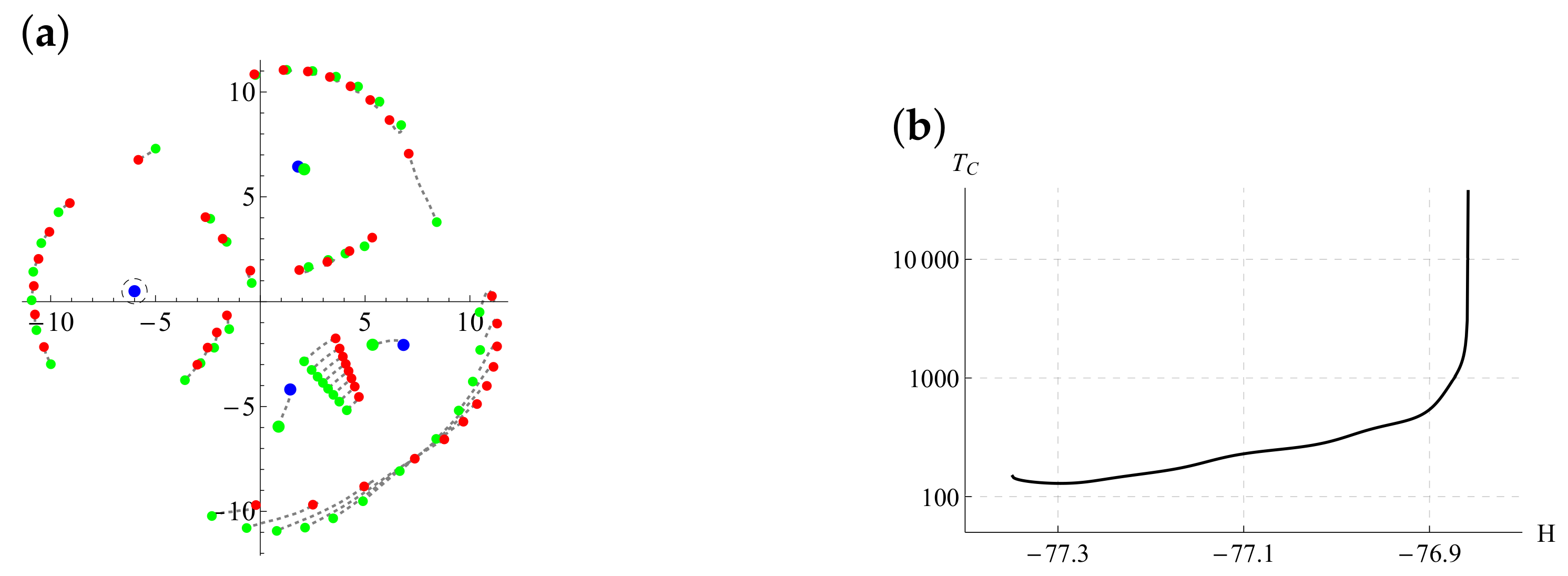
4. Algebraic Equations for Collapse Locations of Vortices
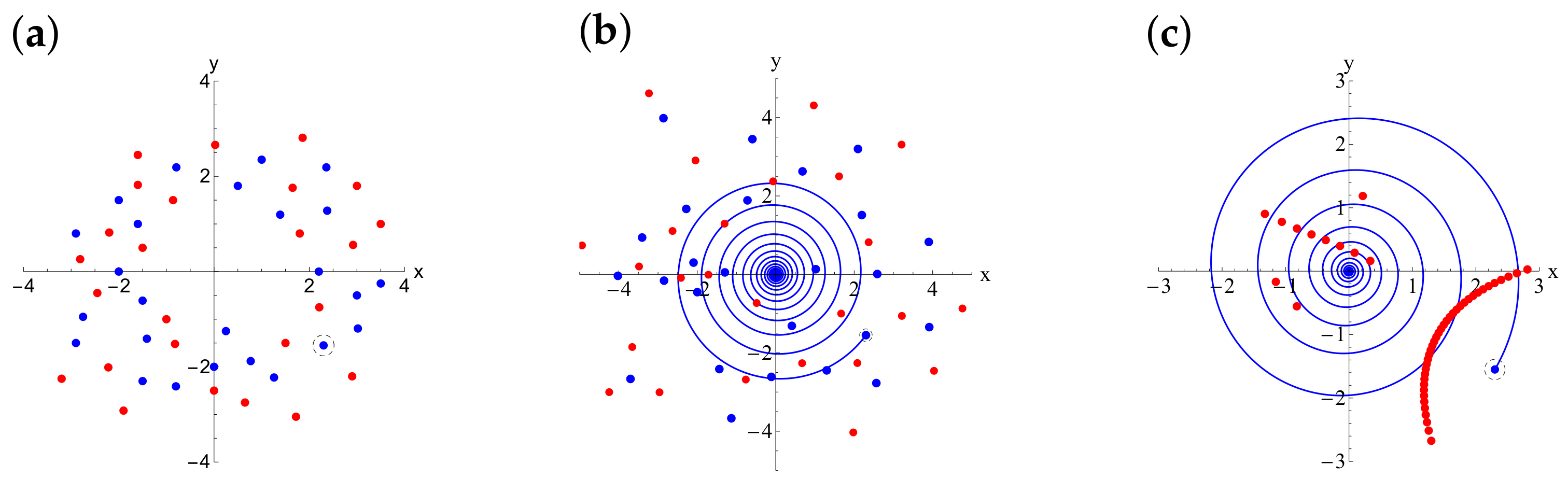
5. Numerical Examples
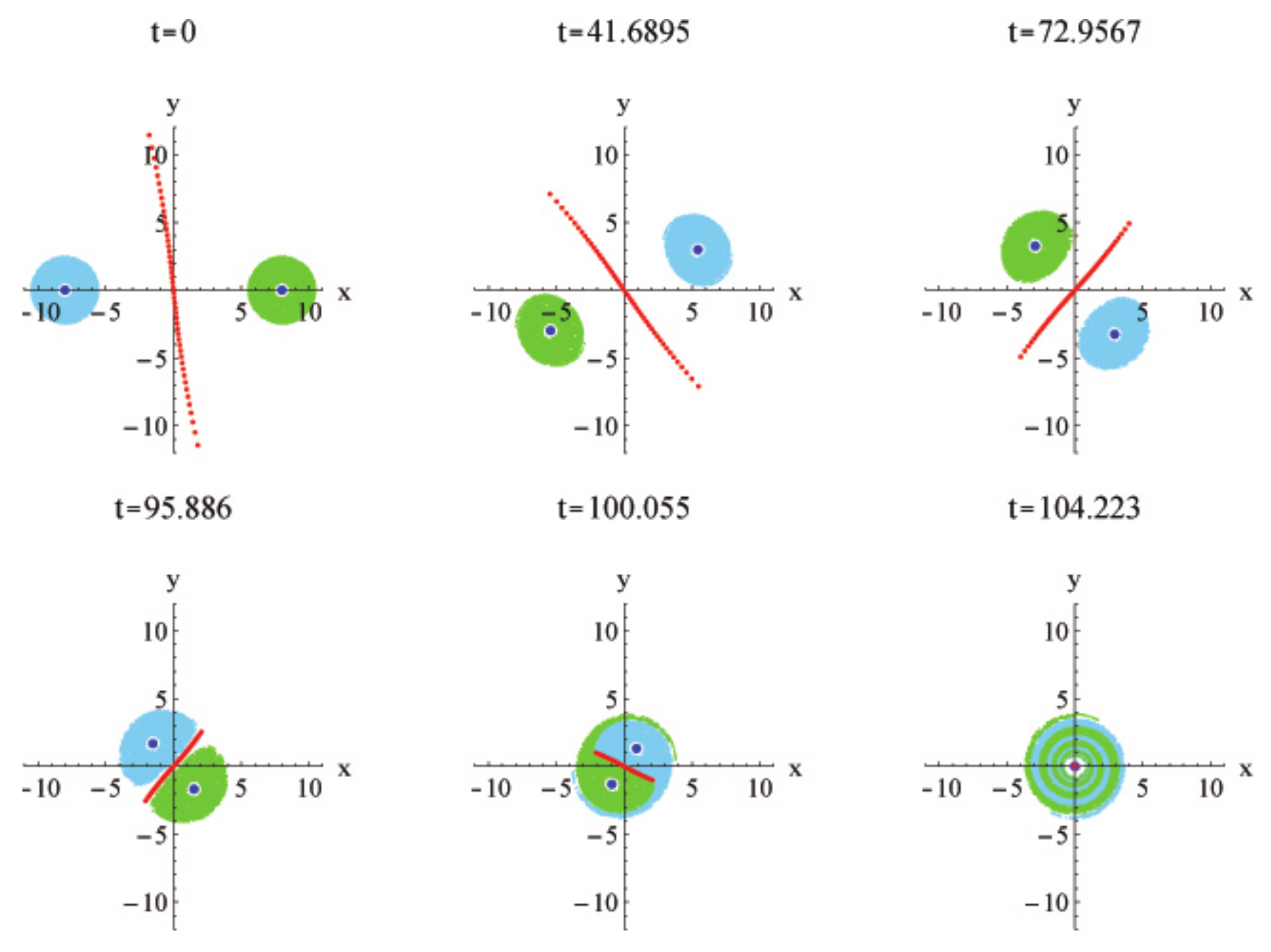
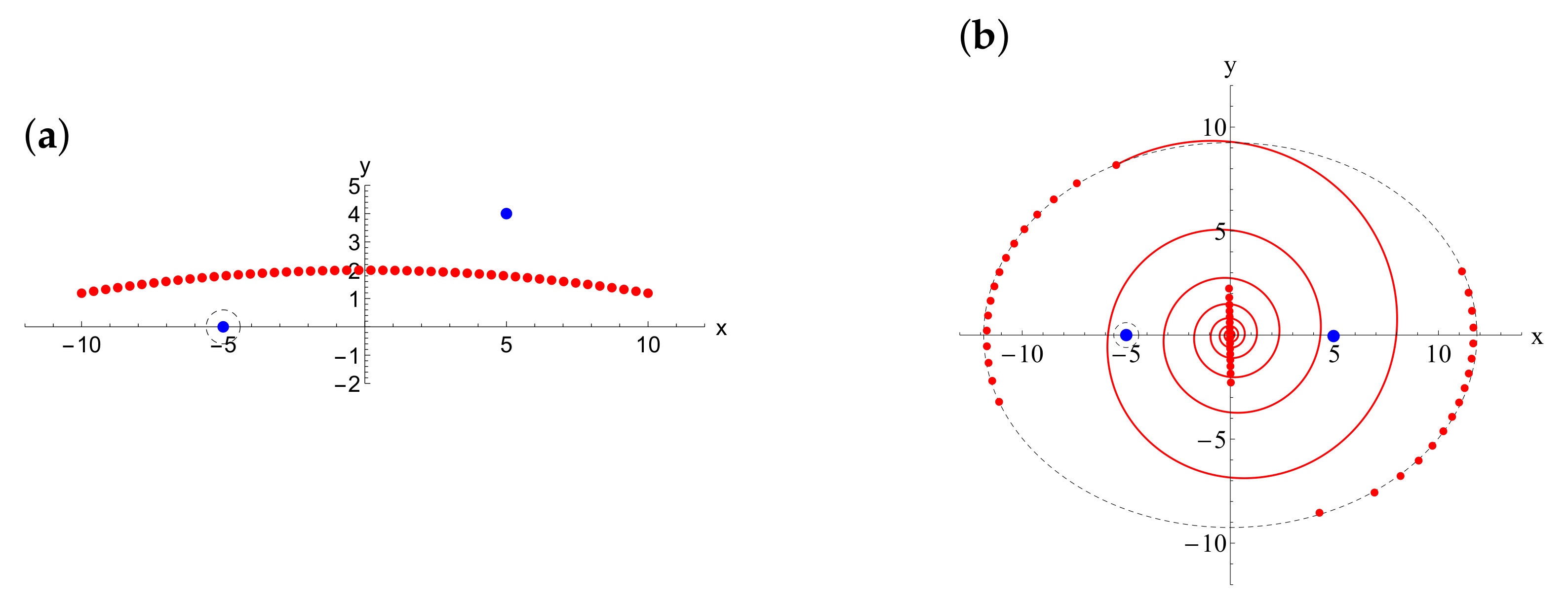
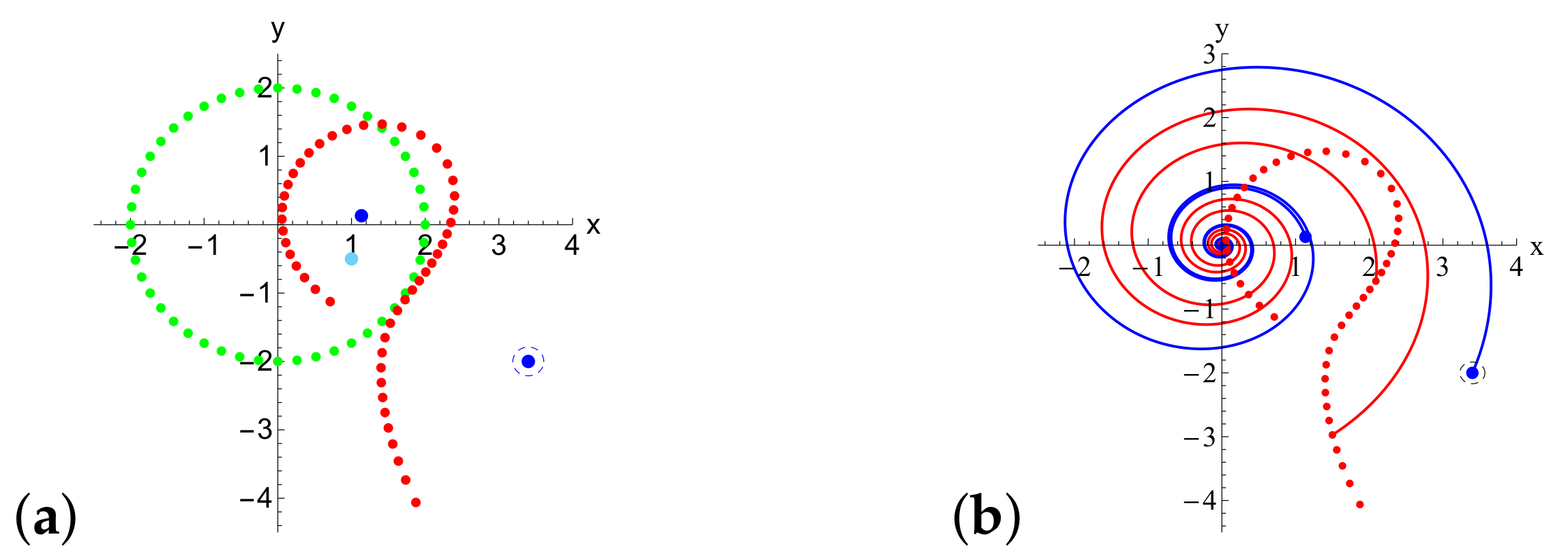
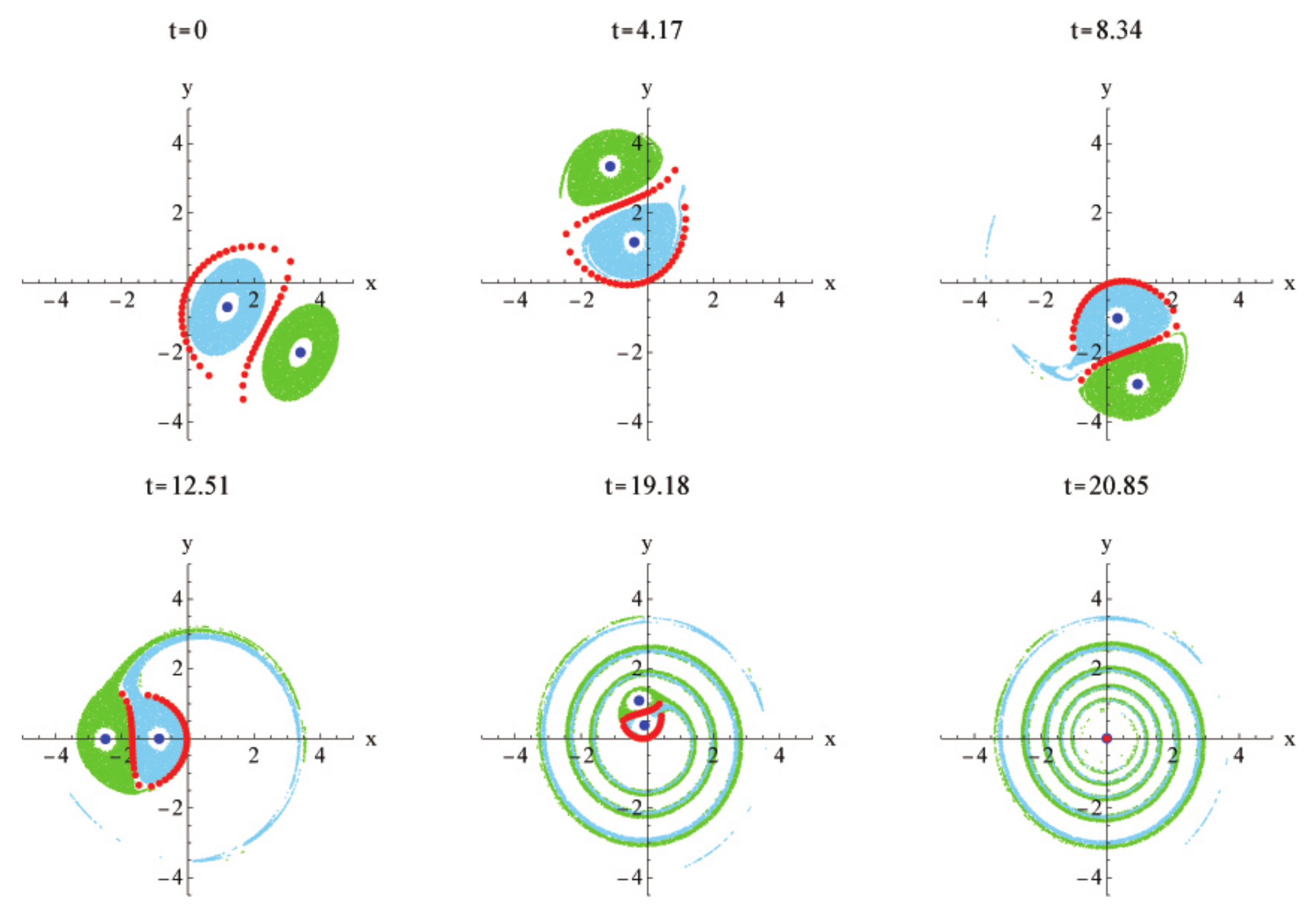
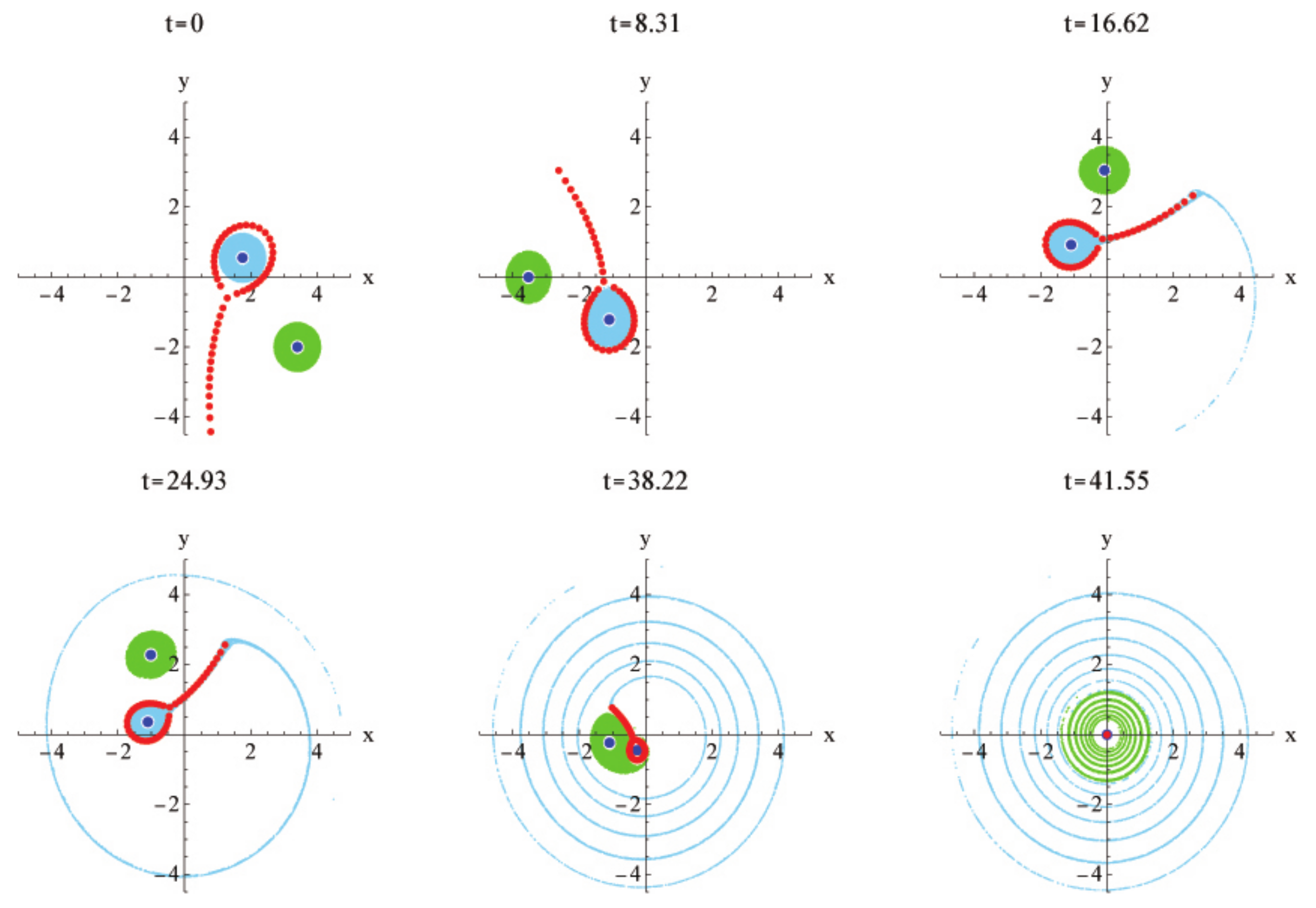
5.1. Prelude Example
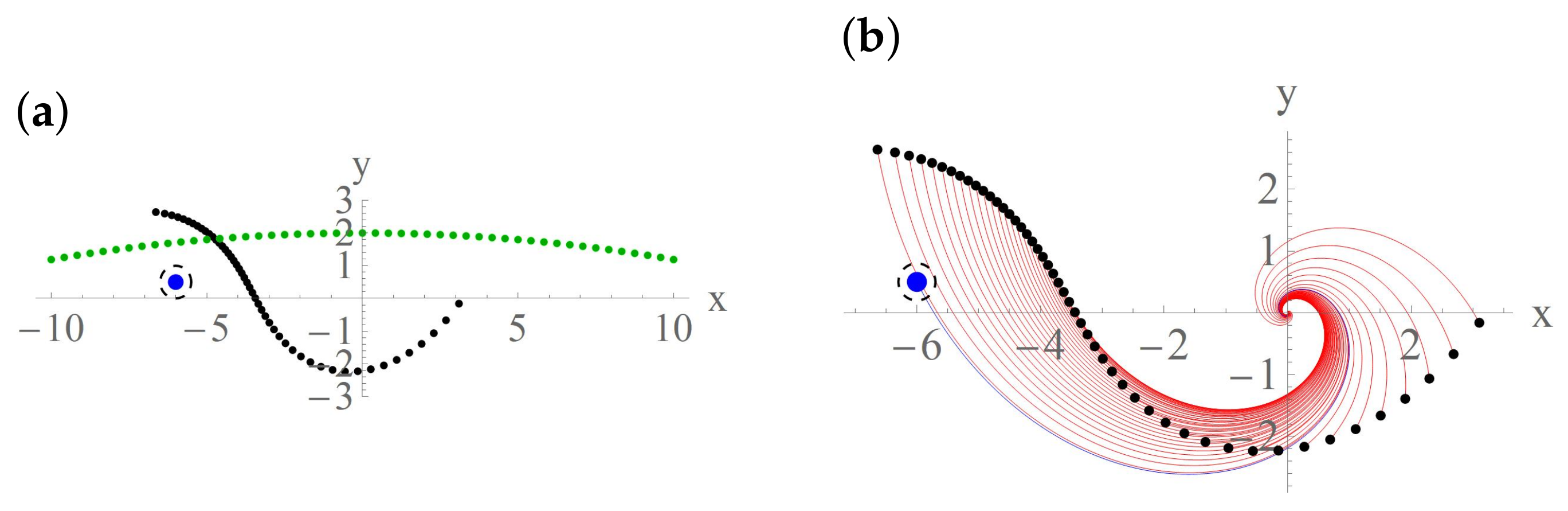
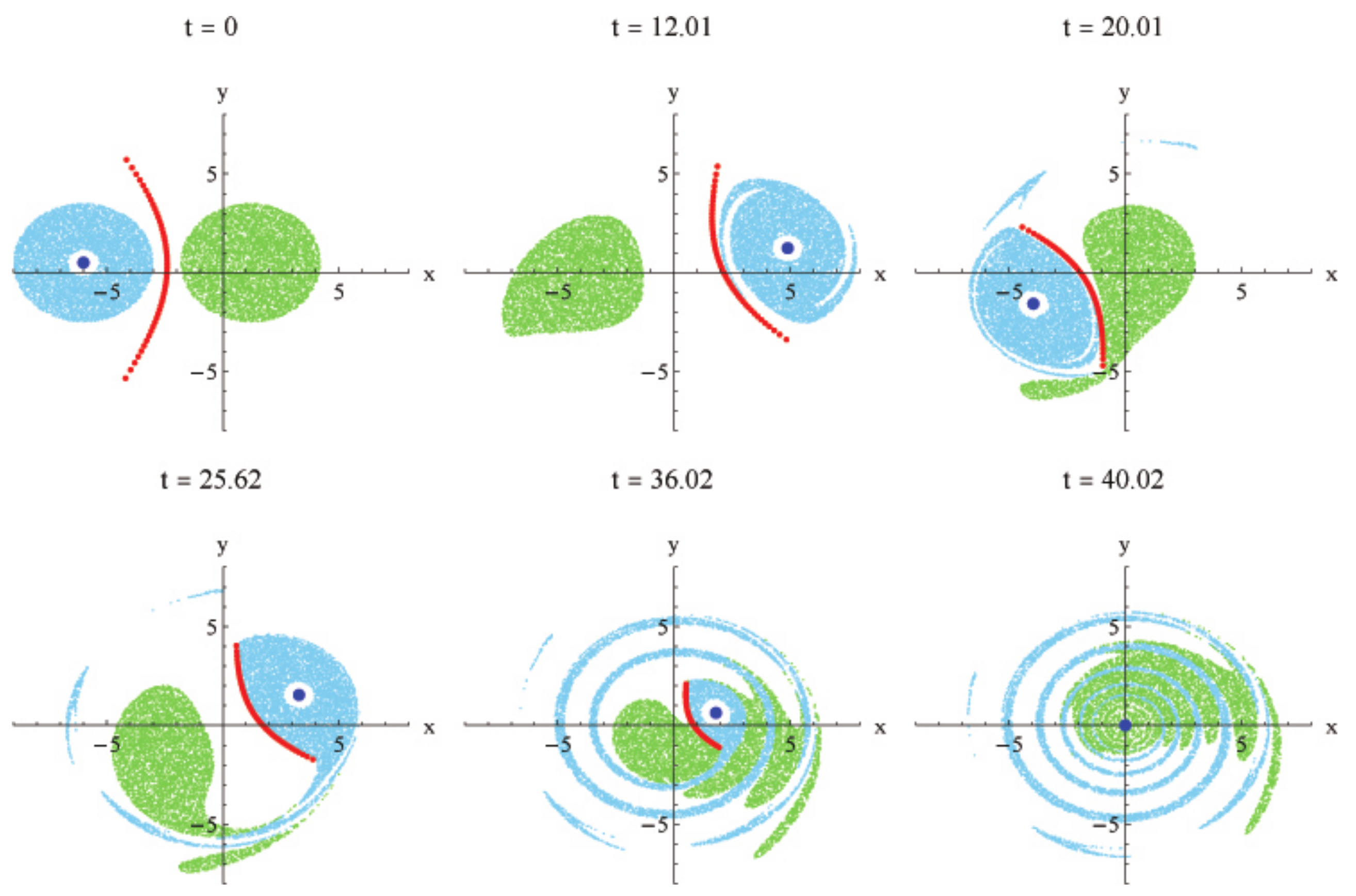
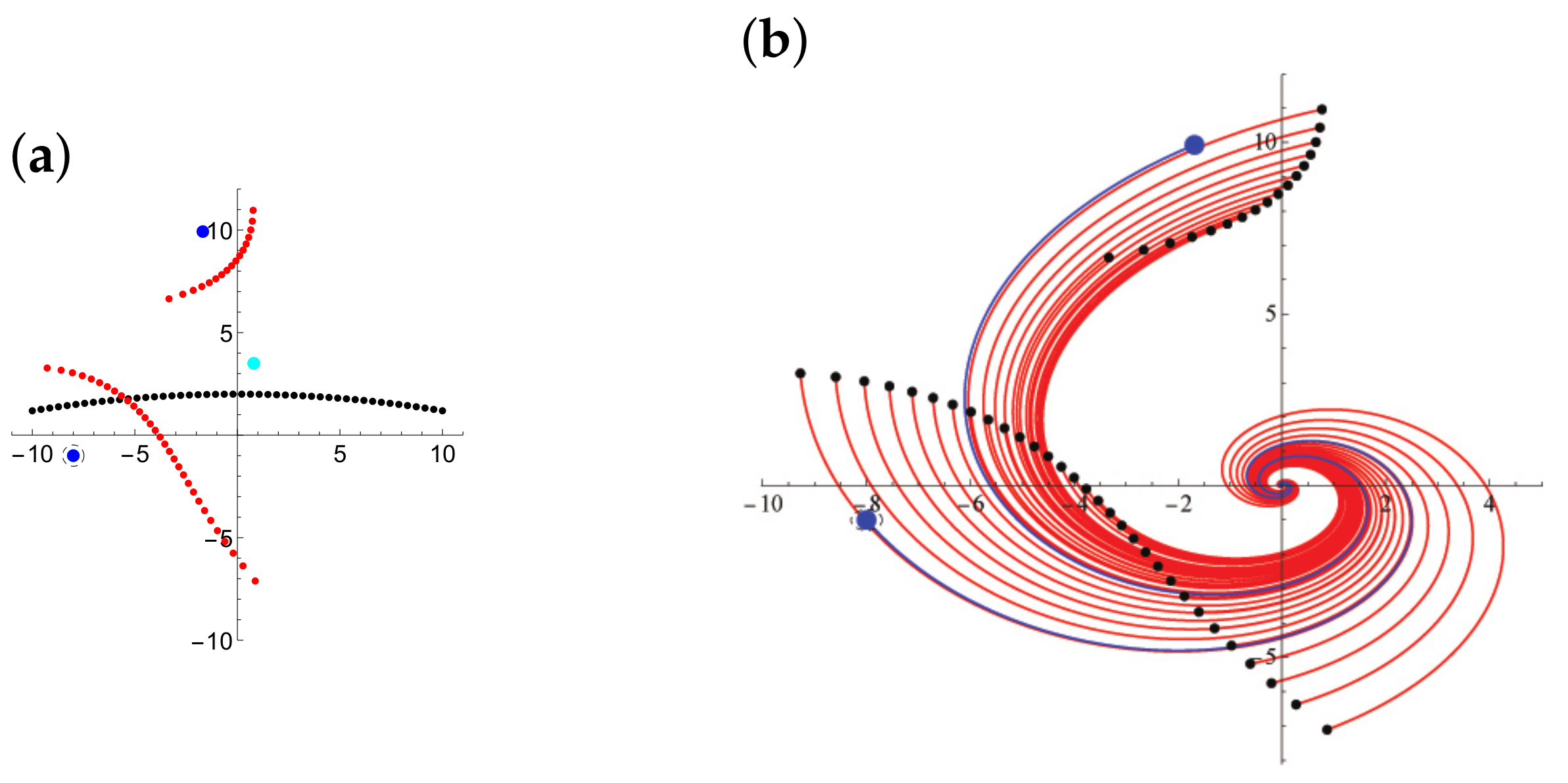
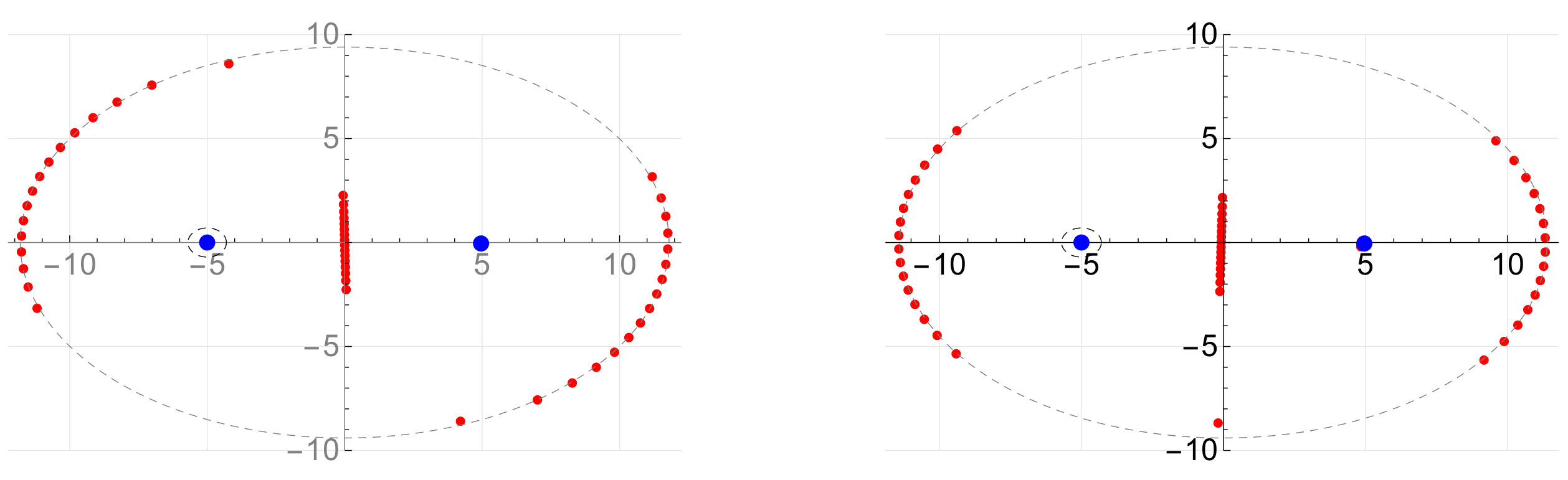
5.1.1. Dynamics of Passive Tracers
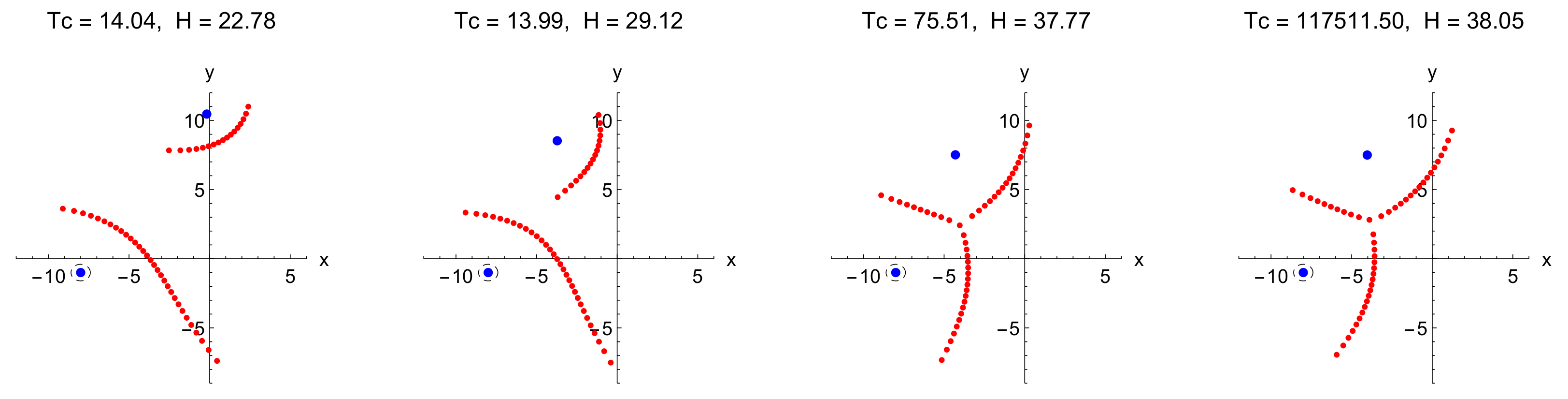
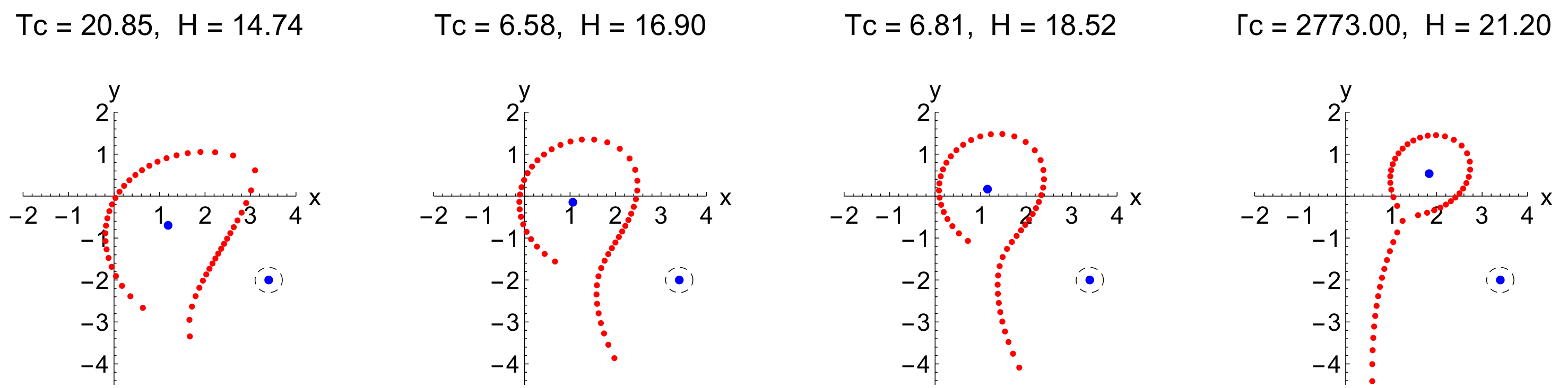
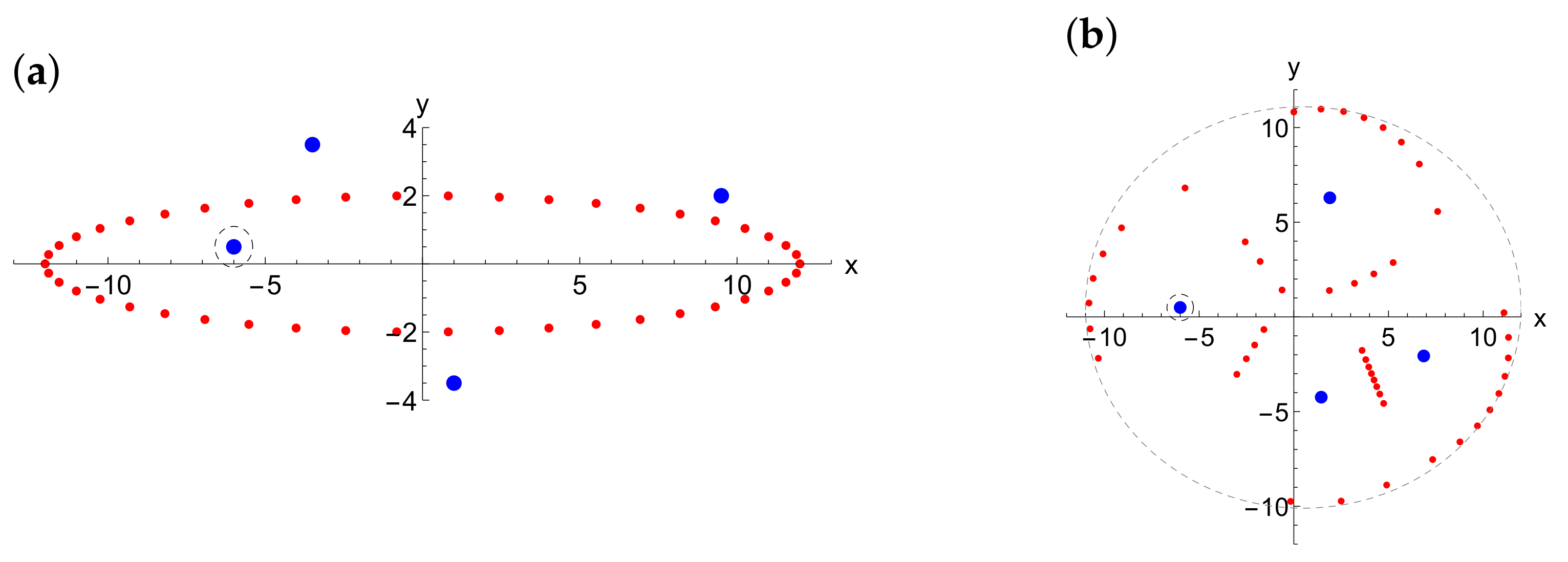
5.1.2. Remarks on the Determination of the Values of Strong Vortices
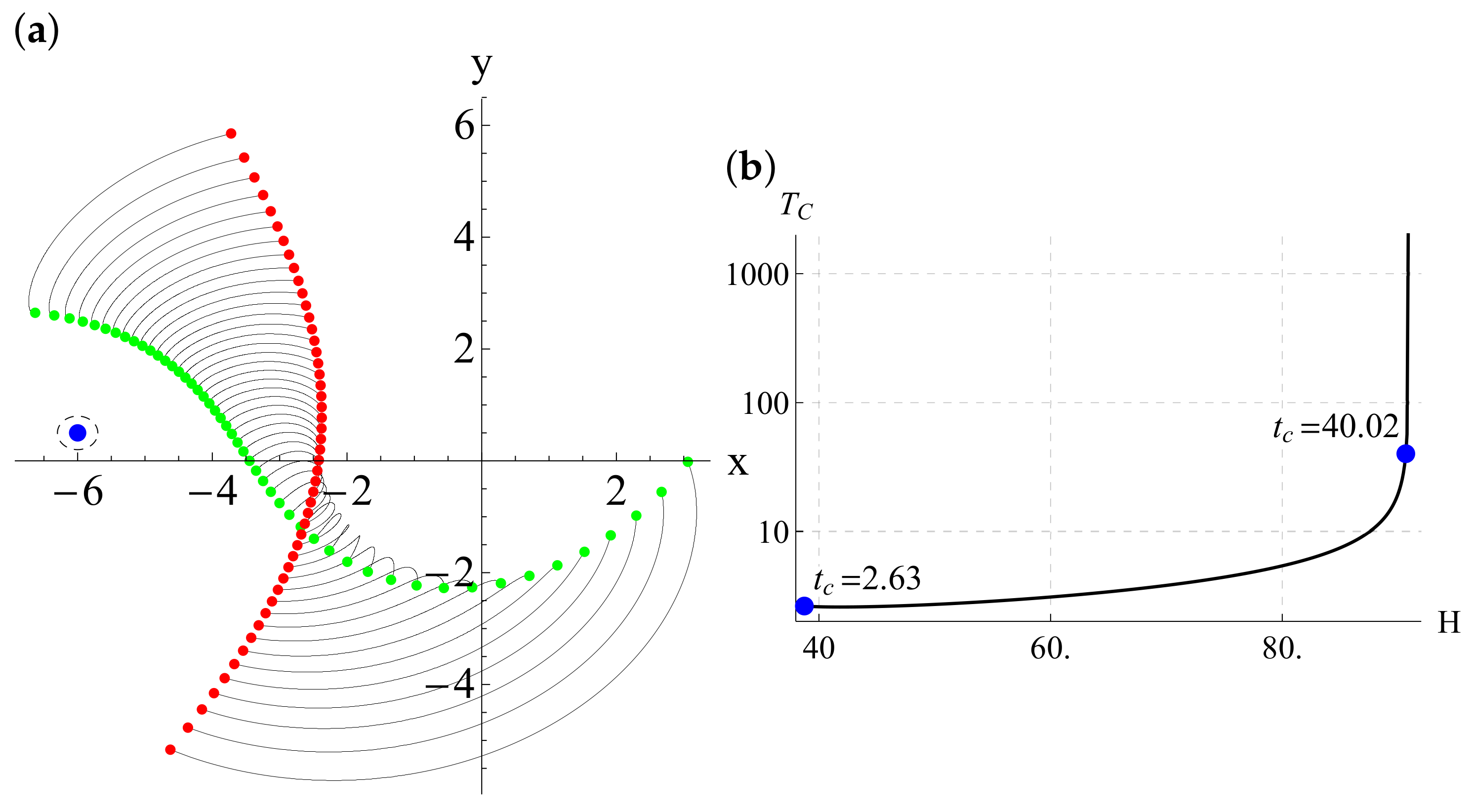
5.2. Numerical Results for the Collapse of 50 Vortices with One Strong Vortex
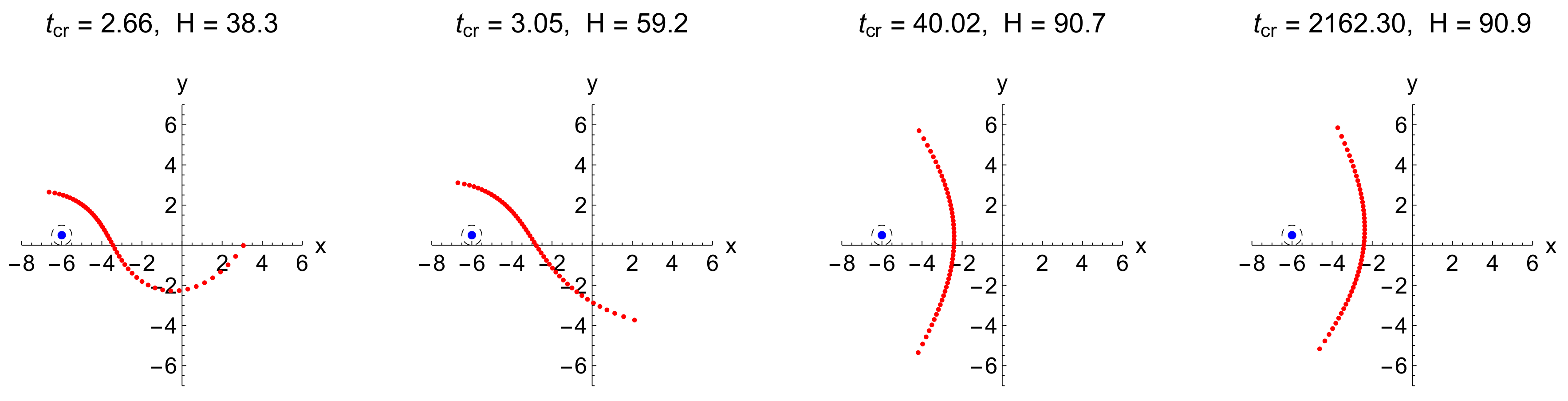
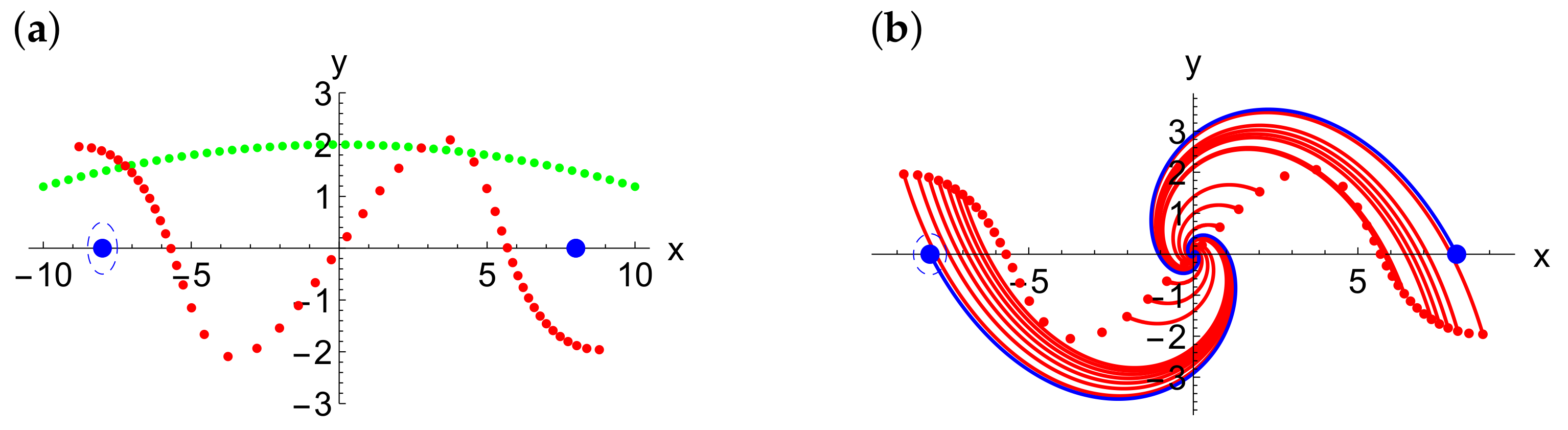
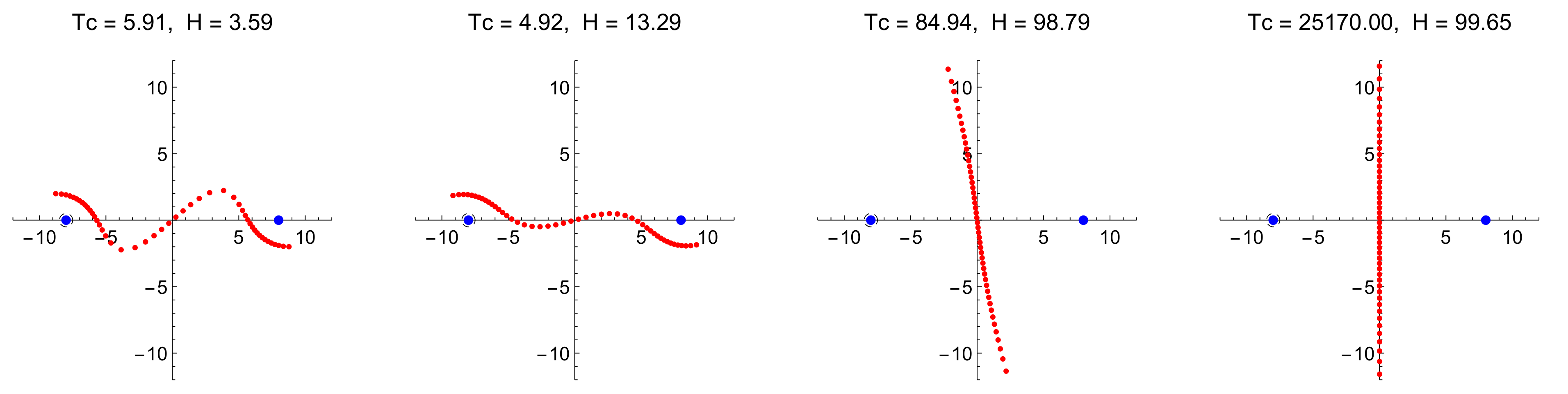
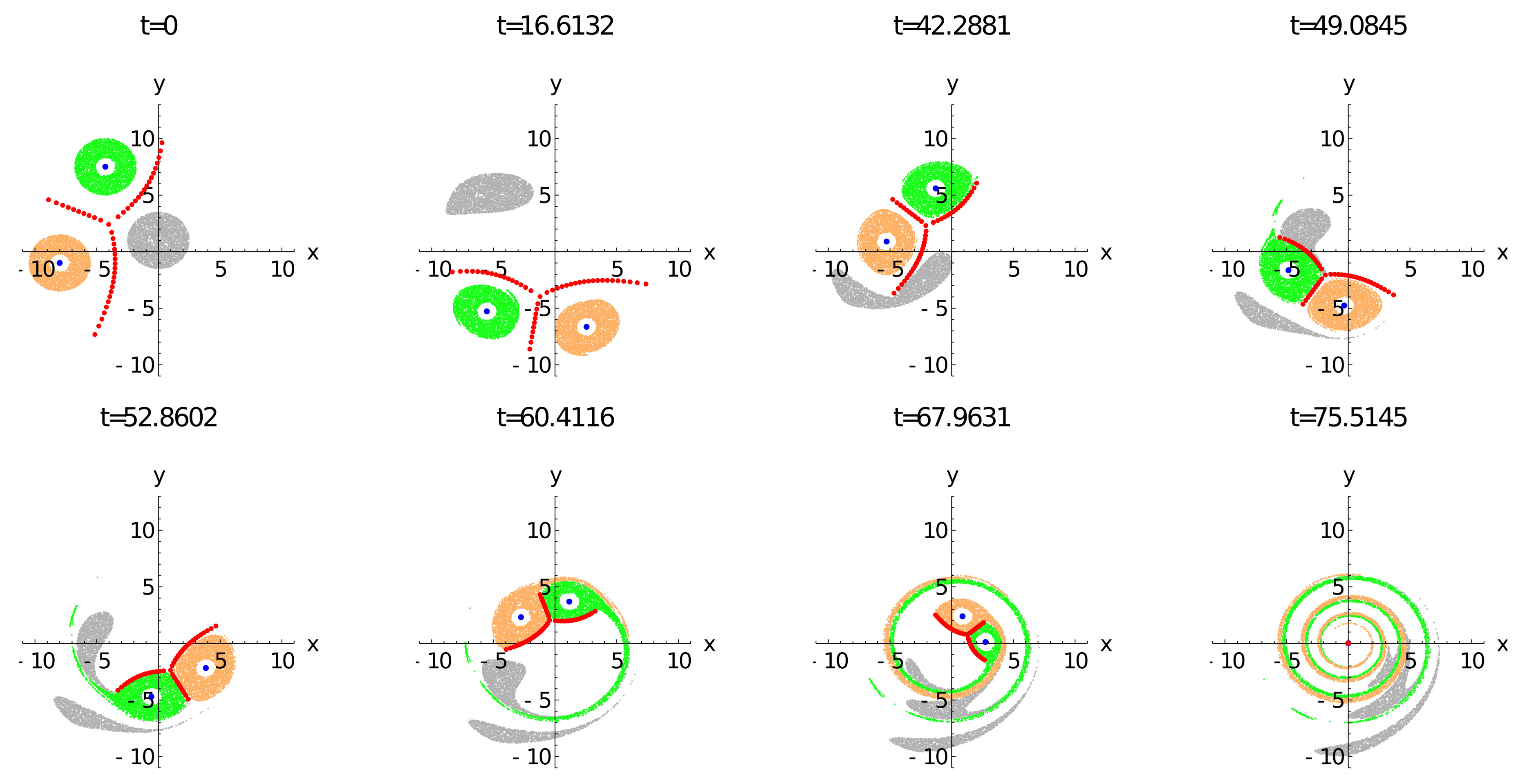
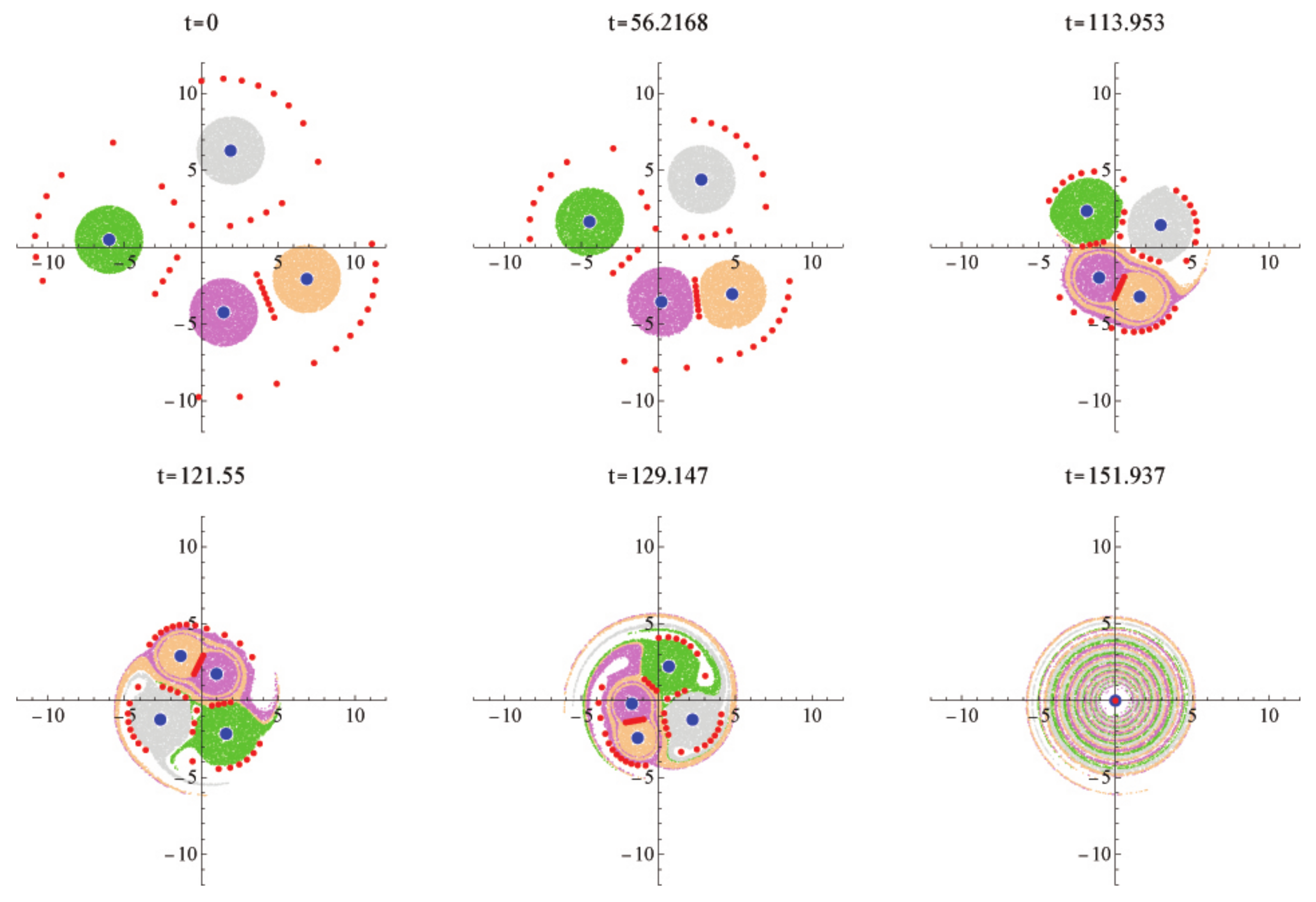
6. Collapse of 50 Vortices with Two Strong Vortices
6.1. The Case
6.2. The Case
6.3. The Case
6.4. The Case
6.5. The Case
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Helmholtz Equations
References
- Von Helmholtz, H. Über Integrale der hydro-dynamischen Gleichungen, welche den Wirbeldewegungen entrsprechen. J. Reine Angew. Math. 1858, 55, 25–55. [Google Scholar]
- Aref, H. Integrable, choatic, and turbulent vortex motion in two dimesnional flows. Ann. Rev. Fluid Mech. 1983, 15, 345–389. [Google Scholar] [CrossRef]
- O’Neil, K. Stationary Configurations of point vorticies. Trans. Amer. Math. Soc. 1987, 302, 383–425. [Google Scholar] [CrossRef]
- Aref, H.; Newton, P.; Stremler, M.; Tokieda, T.; Vainchtein, D. Vortex crystals. Adv. Appl. Mech. 2002, 39, 1–79. [Google Scholar]
- Badin, G.; Barry, A.M. Collapse of generalized Euler and surface quasigeostrophic point vortices. Phys. Rev. E 2018, 98, 023110-1–023110-11. [Google Scholar] [CrossRef] [PubMed]
- Wayne, E. Vortices and two-dimensional fluid motion. Not. AMS 2011, 58, 10–19. [Google Scholar]
- Weiss, J.B.; Provenzale, A.; McWilliams, J.C. Lagrangian dynamics in high-dimensional point-vortex systems. Phys. Fluids 1998, 10, 1929–1941. [Google Scholar] [CrossRef][Green Version]
- Gotoda, T. Self-similar motions and related relative equilibria in the N-point vortex system. J. Dyn. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P. Vortex Methods. Theory and Practice; Cmabridge Univesity Presss: Cmabridge, UK, 2000. [Google Scholar]
- Kozlowski, T.; Kudela, H. Transitions in the vortex wake behid the plunging profile. Fluid Dyn. Res. 2014, 46, 1–15. [Google Scholar] [CrossRef]
- Kudela, H.; Malecha, Z. Eruption of a boundary layer induced by a 2D vortex patch. Fluid Dyn. Res. 2009, 41, 1–18. [Google Scholar] [CrossRef]
- Goodman, J.; Hou, T.Y.; Lowengrub, J. Convergence of the Point Vortex Method for the 2-D Euler Equations. Comm. Pure Appl. Math. 1990, 43, 415–430. [Google Scholar] [CrossRef]
- Boatto, S.; Crowdy, D. Point-Vortex Dynamics. In Encyclopedia of Mathematical Physics; Françoise, J.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 66–79. [Google Scholar]
- Kosior, A.; Kudela, H. The 3D vortex particle method in parallel computations on many GPUs. Comput. Fluids 2014, 92, 274–280. [Google Scholar] [CrossRef]
- Gröbli, W. Specielle Probleme über die Bewegung Geradliniger Paralleler Wirbelfäden; Zurich und Furrer: Zurich, Switzerland, 1877. [Google Scholar]
- Aref, H. Motion of three vortices. Phys. Fluids 1979, 22, 393–400. [Google Scholar] [CrossRef]
- Novikov, E.A. Dynamics and statistics of a system of vortices. Zh. Eksp. Teor. Fiz. 1975, 68, 1868–1882. [Google Scholar]
- Novikov, E.A.; Sedov, Y.B. Vortex collapse. Zh. Eksp. Teor. Fiz. 1979, 77, 588–597. [Google Scholar]
- Novikov, E.A. Stochastization and collapse of vortex systems. Ann. N. Y. Acad. Sci. 1980, 357, 47–54. [Google Scholar] [CrossRef]
- Kimura, Y. Similarity solution of two-dimensional point vortices. J. Phys. Soc. Jpn. 1987, 56, 2024–2030. [Google Scholar] [CrossRef]
- Vosbeek, P.; van Geffen, J.H.G.M.; Meleshko, V.; van Heijst, G.J.F. Collapse interactions of finite-sized two-dimensina vortices. Phys. Fluids 1997, 11, 3315–3322. [Google Scholar] [CrossRef]
- Kevlahan, N.K.R.; Farge, M. Vorticiry filaments in two-dimensional turbulence: Creation, stability and effect. J. Fluid Mech. 1997, 346, 49–76. [Google Scholar] [CrossRef]
- Leoncini, X.; Kuznetsov, L.; Zaslasky, G.M. Motion of threee vortices near collapse. Phys. Fluids 2000, 12, 1911–1927. [Google Scholar] [CrossRef][Green Version]
- Krishnamurthy, V.; Stremler, M.A. Finite-time collapse of three point vortices in the plane. Regul. Chaotic Dyn. 2018, 23, 530–550. [Google Scholar] [CrossRef]
- Kudela, H. Collapse of n-point vortices in self-similar motion. Fluid Dyn. Res. 2014, 46, 031414. [Google Scholar] [CrossRef][Green Version]
- Kudela, H. Self-similar collapse of n point vortices. J. Nonolinear Sci. 2014, 25, 913–933. [Google Scholar] [CrossRef]
- Provenzale, A. Transport by coherent barotropic vortices. Annu. Rev. Fluid Mech. 1999, 31, 55–93. [Google Scholar] [CrossRef]
- McWilliams, J. The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 1984, 146, 21–43. [Google Scholar] [CrossRef]
- O’Neil, K. Collapse and concetration of vortex sheets in two-dimensional flow. Theor. Comput. Fluid Dyn. 2010, 24, 39–44. [Google Scholar] [CrossRef]
- Kochin, N.E.; Kibel, I.A.; Roze, N.V. Theoretical Hydromechanics; Interscience Publishers: New York, NY, USA, 1965. [Google Scholar]
- Batchelor, G. An Introduction to Fluid Dynamcis; Cambridge Univeristy Press: Cambridge, UK, 2005. [Google Scholar]
- Newton, P. The N Vortex Problem; Springer: Berlin, Germany, 2001. [Google Scholar]
- Demina, M.V.; Kudryashov, N.A. Rotation, collapse, and scattering of point vortices. Theor. Comput. Fluid Dyn. 2014, 28, 357–368. [Google Scholar] [CrossRef]
- Synge, J.L. On the motion of three vortices. Can. J. Math. 1949, 1, 257–270. [Google Scholar] [CrossRef]
- Kelley, C. Solving Nonlinear Equations with Newton’s Method; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Ruskeepää, H. Mathematica Navigator, Mathematics, Statiscics, and Graphics; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Boatto, S.; Pierrehumber, R.T. Dynamics of a passive tracer in a velocity filed of four identicaal point vorticies. J. Fluid Mech. 1999, 394, 137–174. [Google Scholar] [CrossRef]
- Sofroniou, M.; Knapp, R. Wolfram Mathematica© Tutorial Collection. Advanced Numerical Differential Equation Solving in Mathematica; Wolfram Resarch, Inc.: Champaign, IL, USA, 2008. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudela, H. Collapse of n Point Vortices, Formation of the Vortex Sheets and Transport of Passive Markers. Energies 2021, 14, 943. https://doi.org/10.3390/en14040943
Kudela H. Collapse of n Point Vortices, Formation of the Vortex Sheets and Transport of Passive Markers. Energies. 2021; 14(4):943. https://doi.org/10.3390/en14040943
Chicago/Turabian StyleKudela, Henryk. 2021. "Collapse of n Point Vortices, Formation of the Vortex Sheets and Transport of Passive Markers" Energies 14, no. 4: 943. https://doi.org/10.3390/en14040943
APA StyleKudela, H. (2021). Collapse of n Point Vortices, Formation of the Vortex Sheets and Transport of Passive Markers. Energies, 14(4), 943. https://doi.org/10.3390/en14040943





