Analysis of the Ignition Behavior Based on Similarity Factor Method

Abstract

The chemical kinetics mechanism is an important factor to accurately predict the combustion characteristics of constant-volume bomb (CVB). In this study, an n-heptane oxidation mechanism constructed by Wang et al. is introduced to study the correlation of the ignition behaviors with the mechanism constructed by Chang et al. The effects of the similarity factor method in the analysis of ignition behaviors of fuel in CVB were repeatedly verified by changing the important spraying parameters: injection pressure and hole diameter. Through further verification, it was found that the combustion process was controlled at approximately 850 K and stoichiometric ratio mixture of fuel/air in CVB, which corresponds to the negative temperature coefficient region at stoichiometric ratio mixture in shock tube (ST). The mechanism verified by the experiment under the condition in ST can reflect the chemical ignition in CVB. In addition, the similarity factor method was less dependent on the chemical reaction mechanism and boundary conditions.

1. Introduction

The ignition phenomenon in an internal combustion engine is considerably complex and is a collection of physical and chemical processes. The groups of Di Blasio [1] and Mueller [2] gained remarkable achievements in the research field of improving fuel efficiency and reducing exhaust emissions through adopting various advanced technologies and alternative fuels. Because the operating state of internal combustion engines is continuous, the in-cylinder reaction conditions in the previous cycle influences the next one, such as the residual gas, residual pressure, and several other factors. These factors may have numerous effects on the initial combustion conditions in the next cycle, which makes it considerably difficult to directly study the ignition and combustion characteristics in internal combustion engines. To stabilize the combustion boundary conditions, many experimental devices have been designed that can reproduce the operating conditions of internal combustion engines, including shock tube, rapid compression machine (RCM) and constant-volume bomb (CVB). The CVB is an experimental platform between basic experiments and engine experiments that can effectively integrate engine experiment and numerical simulation method for a comprehensive analysis of the combustion process. There are many different types of CVB for different experimental purposes; however, it is essentially a simplified internal combustion engine block with a simple structure and easy operation. It is designed to study the combustion phenomena near the top dead center of internal combustion engines, such that the piston compression structure is eliminated, which makes the gas in the cylinder of the bomb unaffected by compression. Thus, its flow and heat transfer are relatively stable and uniform, which helps reproduce the various phenomena in the combustion process of internal combustion engines. One of the classic devices for studying the ignition and combustion characteristics of internal combustion engines is the CVB, and several international research organizations have established the Engine Combustion Network (ECN) [3] to study combustion with the help of CVB. Currently, most of the experimental data of CVB come from ECN, among which the data from the Sandia [4] National Laboratories are the most common. Unless otherwise indicated, all data in this study are also based on Sandia’s constant-volume combustion experiments.

To gain insights into the combustion process within CVB, Computational Fluid Dynamics (CFD) models are commonly used to numerically simulate the combustion process within a CVB [5,6,7,8]. Fu and Aggarwal [7] used numerical simulations to study the detailed effects of fuel unsaturation on the emission characteristics of spray combustion and describe detailed characteristics of combustion over time. Pei et al. [8] used global sensitivity analysis to analyze the effects of parameter uncertainty on the simulation results. These data have been presented and the relatively important parameters among them have been revealed. Recently, Payri et al. [6] used experimental and numerical simulation to analyze the effects of operating conditions in a volumetric bomb on the ignition delay (ID) and flame rise height of a diesel characterization fuel mixture of n-dodecane and m-xylene. Because the combustion process in CVB is different from that in the shock tube, it is not only related to the chemical reaction kinetics, but also mixed with the spraying and evaporation of the fuel, the collision and fragmentation of liquid droplets, the heat transfer and diffusion of combustion, and many other physical factors. Therefore, the numerical simulation of the CVB must rely on the combination of the CFD model and chemical reaction kinetics to obtain a reliable fit. When the flow model is combined with chemical kinetics, it is necessary to reflect the consistency of energy conservation and to ensure that the chemical reaction has mass conservation properties. The coupled complete model is simulated by CFD software according to experimental parameters and compared with validation metrics. The validation analysis is used to determine whether the fluid model or kinetic mechanism of the chemical reaction is reasonable. Numerical simulations of CVB are often used to measure ignition delay, flame lift-off length, liquid penetration, and vapor penetration [9]. This is not the same as the validation of combustion models in basic experiments; the difference is caused by the different purposes of the validation because the objectives of the CVB study are more focused on the flow, morphology, and emission of combustion.

The simulation of the CVB is not only influenced by the physical model [10], but also by the chemical kinetic mechanism [11]. Som et al. [12], in their analysis of the factors influencing the numerical simulation in a CVB, found that in addition to the physical model predicting the results, different mechanisms also have a significant impact on the prediction results, even if these mechanisms have passed the correlation validation of the basic reactor. This indicates that the reliability of the chemical kinetic mechanism is also important for simulations of CVB. Moreover, the analysis by the chemical kinetic mechanism exhibited the significant discrepancies for the ignition behaviors prediction of one specific fuel among different mechanisms [13]. One of the reasons is that the selection of mechanism parameters is based on the experimental and theoretical data, which is determined by the mechanism characteristics [14]. On one hand, with the publication of new experimental results, the previous mechanisms need be updated and adjusted to improve the prediction ability [15,16,17]. Therefore, chemical mechanisms can hardly be established and developed without proper experimental data [18]. At present, almost all mechanisms are verified by the experimental data from shock tubes and other basic reactors [19], which are considered the conventional mechanism. However, the recognition scope of such mechanisms is limited [20]. At the same time, there are few mechanisms constructed based on CVB experiments, so the ignition behavior of fuels in CVB usually cannot be accurately described by the conventional mechanism. For example, although the n-dodecane skeleton mechanism in Chang et al. [21] has passed the basic reactor validation, it cannot accurately predict ignition delay of n-dodecane in CVB. Prediction performances of different mechanisms under different conditions vary widely indicating that the mechanism should be adjusted continually [22].

Additionally, the treatment of the mechanism in the numerical simulation of the CVB is usually different from that of the physical model. For the physical model, if it fails the test, it needs to be improved and then sent to the software for calibration until the desired results are obtained. However, for chemical mechanisms, only mechanisms that have been verified by the basic reactor are screened in numerical simulation of CVB, and direct analysis is rarely performed. Inappropriate mechanisms are sent back to the basic experimental verification stage for correction. On the one hand, the complex combustion process in a CVB determines the difficulty of analyzing chemical reaction kinetics. On the other hand, the mechanism determined by the CVB needs to be verified by the basic reactor. Therefore, the above treatment is the most common solution. However, this approach tends to cause studies on CVB to primarily focus on the influence of physical parameters and models on the predictions of various indicators, and lack studies on the influence of chemical processes, especially those detailing the role of chemical kinetic mechanisms. Moreover, most of the applicable chemical kinetic mechanisms are constructed based on basic experimental data [23]. The specific reasons for the differences in the performance of the mechanisms in two reactors, and how to use the basic experiments to guide the mechanism construction while also considering the role of other experimental platforms such as the CVB, have not been fully investigated. How to identify informative experiments for mechanism discrimination efficiently [20]? That is the key, which needs to be considered at the beginning of the mechanism construction. This study will focus on the strategy of mechanism construction, which is suitable for CVBs.

The ignition behaviors of fuel include autoignition temperature (AIT), ID and low/intermediate/high-temperature ignition. The chemical kinetic mechanism is the key for researching these [24]. Comparing the validation targets between CVB and other basic experiments, ignition delay is the most consistent and most closely related combustion characteristic. Therefore, this group preliminarily [25,26] by analyzing the commonality between the ignition characteristics in the CVB and the ignition characteristics in the shock tube [25,26] investigated the generality of the mechanism in different reactors, so that the mechanism construction can better consider the characteristics and needs of different reactors, to solve the problem that some of the mechanism is verified by the basic experimental data, but cannot accurately predict ignition delay in the CVB. In the process of studying the ignition characteristics of the fuel in a CVB, the group analyzed the temporal temperature and heat release rate (HRR) evolution during the ignition process [25,26], and considered the low-temperature exothermic trigger point as the determinant of the final thermal ignition. Additionally, in analyzing the sensitivity coefficients of ignition delay in shock tubes and CVBs, the group adopted the constructed similarity factor method [25,26] to obtain shock-tube reaction conditions with similar ignition characteristics to those of the main reaction conditions in CVB, which can be used to fine-tune the simulation mechanism of the ignition behavior in the CVB.

2. Definition of the Ignition Delay in a CVB

Kwak et al. [27] have compared the differences in fire delay data measured in shock tubes and CVB. In their study, except for the negative temperature coefficient region, the ignition delay in CVB was almost always slower than that in a shock tube. This is because fuel ignition in CVB is affected by both chemical and physical delay [28,29,30], whereas the shock tube is largely dominated by chemical delay. Additionally, the ignition delay in the CVB does not have a significant negative temperature coefficient region. This indicates a difference in the ignition delay of the fuel in two reactors. This study attempts to investigate the common conditions for the ignition characteristics in the two reactors. In the discussion of ignition delay definitions in the Introduction section of this paper, examples of ignition delay definitions using different metrics are given, including mainly pressure change definitions, substance concentration change definitions, and optical intensity threshold definitions. Vasu et al. [31] showed the pressure values and OH concentration variation values for ignition delay in shock tube. The ECN summarized the definitions of the fire delay for CVB at the 4th meeting in 2015 [32], with the main definitions of pressure, optical substance definition, optical intensity definition, OH mass fraction definition, and rate of warming definition. Among them, the pressure definition [33] and the optical intensity definition are the most typical. Fraser et al. [34] adopted the pressure trajectory extension intersection method to define ignition delay of CVB, and Lapuerta et al. [35] performed a comparative analysis of different pressure ignition delay definitions within CVB, with an improved extension intersection definition, which is similar to the pressure intersection definition [31]. Based on the characteristic of predicting the pressure variation of the shock tube in Chemkin Pro, this study combines the above pressure-defining ignition delay method to define the ignition delay in CVB as the time from the moment of fuel injection to the time when the rate of boost reaches 0.02 MPa/ms. This method considers the ignition delay characteristics of both reactors.

Figure 1 shows the results of the ignition delay of n-heptane in CVB obtained from the definition of the boost rate threshold determined in this study at 800 and 1000 K, respectively, as well as the ignition delay obtained from the generic pressure-crossing line definition. The experimental conditions were selected for the Sandia n-heptane ambient density of 14.8 kg/m³. As seen in Figure 1, the two definitions maintain a high degree of agreement. The definition adopted in this study, in contrast, facilitates automatic value taking and is consistent with the definition of the ignition delay of shock tube by Burke et al. [36]. Compared with the predicted results for all operating conditions, the average absolute error of the two ignition delay definitions is 0.0141 ms and the average relative error is 2.19%, which is much smaller than the uncertainty of ignition delay introduced by the experimental uncertainty as pointed out by Burke et al. [36].

Using the optimization mechanism, this group analyzed the ignition characteristics in the CVB in previous work and constructed a similar factor method to analyze the role of the chemical reaction kinetic mechanism in the CVB by studying the correlation between the ignition delay in two reactors. Among them, the main analysis is to analyze the condition where we found the highest correlation between the CVB and the shock tube, to determine which condition the mechanism verified by the exciter tube is most applicable to the simulations with CVB [25,26]. Additionally, in the previous study of the distribution of cylinder temperatures and exotherms at different times to analyze the evolution of ignition in the CVB, the group used the analysis of exotherm distribution and Φ-T diagrams as the key to study the ignition evolution of CVB based on Bhattacharjee and Haworth [37] and Fu and Aggarwal [7], who both used the analysis of exotherm distribution and Φ-T diagrams as the key to study the ignition evolution of CVB and adopted the exotherm variation analysis to identify the low-temperature exotherms and the ignition evolution of CVB. At the time of ignition, a local HRR of 30 kJ/cm³∙s is used as the calibration threshold for the onset of low- and high-temperature exotherm, to improve automatic program recognition.

3. Similarity Factor Method

In this study, the similarity factor method [25] is used to analyze the ignition behavior in different reactors at wide conditions. The method is based on the sensitivity coefficient of different reactors, which is derived using Formula (1) [36]:

$$Se{n}_i=\frac{\ln \left({\tau }_{i, +}/{\tau }_{i, -}\right)}{\ln \left(k_{+}/k_{-}\right)}$$

(1)

where $Se{n}_i$ is the sensitivity coefficient of the i-th reaction; ${\tau }_{i, +}$ and ${\tau }_{i, -}$ indicate that the ignition delay using the mechanism with the pre-exponential factor of ith reaction is multiplied by 2 or divided by 2, respectively; and $k_{+}$ and $k_{-}$ are taken as 2.0 and 0.5, respectively.

In the previous study, the sensitivity coefficient of different reactors was different. To eliminate that, the similarity factor method describes the similarity of sensitivity coefficients between different reactors using Formula (2):

$$S_i=\frac{Se{n}_i}{|Se{n}_{ max}|}$$

(2)

where $Se{n}_{max}$ is the sensitivity coefficient with the maximum absolute value among all the large-molecule reactions.

By introducing the normalized sensitivity coefficients, a similarity factor can be obtained by the Formula (3) [38], which can be used to analyze the similarity of ignition behavior in different reactors.

$$\mathrm{Similarity}\mathrm{Factor}=1-\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(S_{CVB, T_j, i}-S_{ST, T_k, i }\right)}^2}$$

(3)

where $S_{CVB, T_j, i}$ is the normalized sensitivity coefficient of the ith reaction in CVB at the initial temperature of $T_j$; $S_{ST, T_k, i }$ is the normalized sensitivity coefficient of the ith reaction in shock tubes at the temperature $T_k$; and $N$ is the total number of the large-molecule reactions.

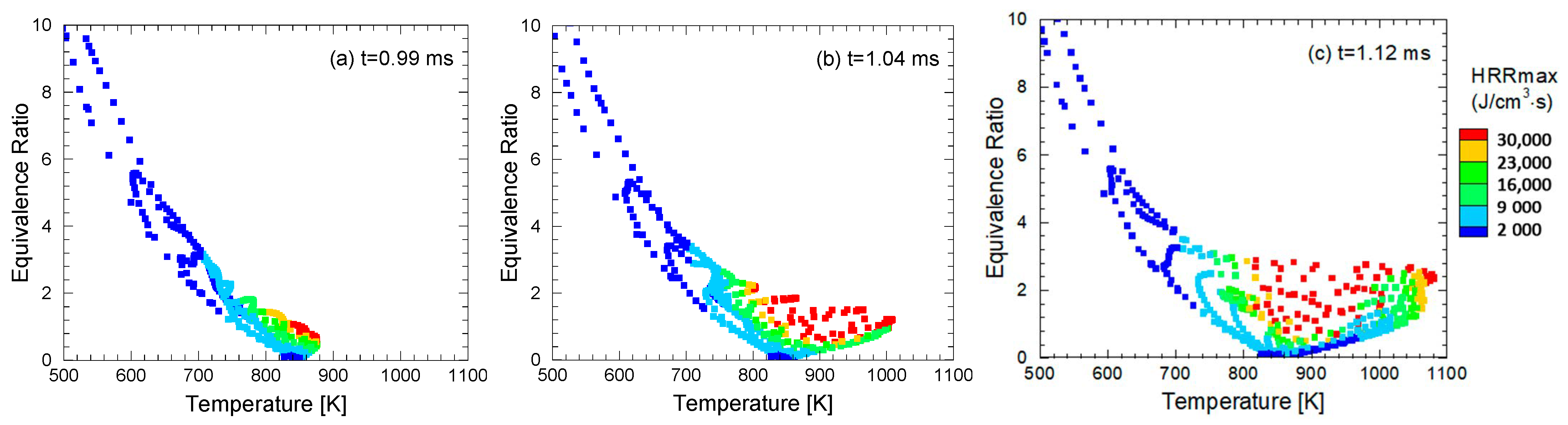
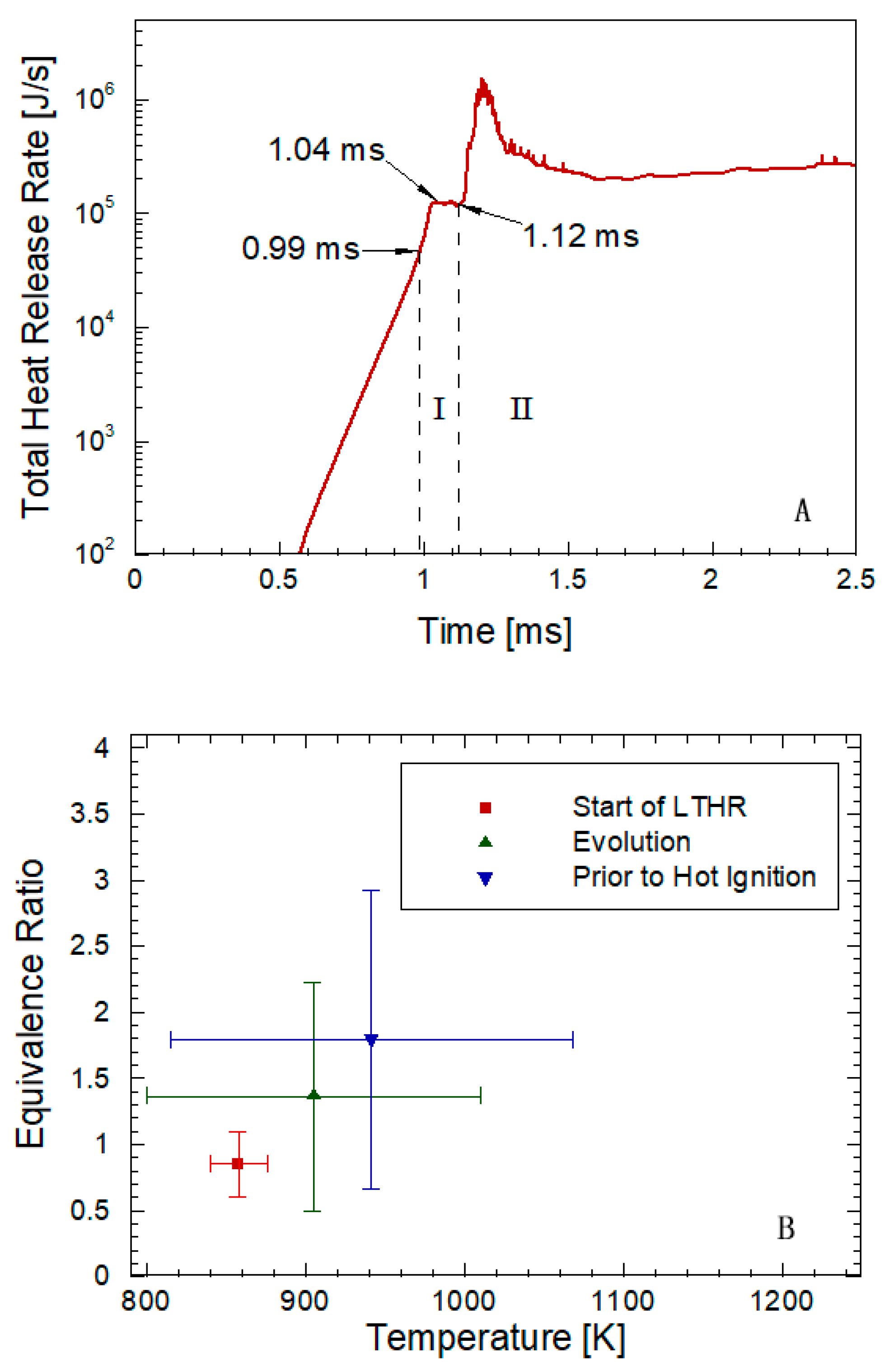
4. Expanded Application Research of the Similarity Factor Method

4.1. Validation by Different Mechanisms

Based on the need for CFD numerical simulation in this study, the chemical reaction kinetic mechanism used in the coupling of KIVA-3V and Chemkin Pro should be kept at a reasonable scale. Otherwise, it will affect the computational efficiency. Moreover, because this study focuses on the pre- and post-fire changes, the selected mechanism should be able to better predict the ignition and combustion characteristics of the relevant fuel in CVB. The ignition delay and fuel HRR under different conditions are dominant. Additionally, the selected mechanism should accurately describe two HRR stages of fuel combustion in a CVB. Moreover, as the mechanism does not have strict requirements for predictions such as emission characteristics, the sub-mechanisms involving emission and other characteristics can be excluded to improve the computational efficiency as much as possible without affecting the other prediction performance of the mechanism. According to the above principles, to test whether the similar factor method proposed by our group applies to different chemical reaction mechanisms, this study will compare the above analysis results between the simplified n-heptane mechanism constructed by Wang et al. [39] and the n-heptane skeleton mechanism proposed by Chang et al. [40].

In this study, the similar method was used to study ignition behavior measured by Fu and Bhattacharjee [7,37]. Figure 2 shows the Φ-T diagram for the n-heptane mechanism of Wang et al. [39] at an initial temperature of 850 K. As shown in the Figure 3A, region I from 0.64 ms to 1.20 ms is the period for low-temperature exothermic reaction, which includes the entire development of Figure 2. Region II is the high-temperature exothermic region, where high-temperature exothermic reactions take place. Figure 3B describes the conditions of each key point of heat release quantitatively. This is helpful to understand the initial condition of two-stage heat release.

As seen from the evolutionary process in Figure 2, at 0.64 ms (see Figure 2a), the first HRR above the threshold appears, which is depicted in Figure 3A. The first peak locates around 0.84 ms in Figure 3A, which is the moment of maximum heat release in the first stage (see Figure 2b and Figure 3A). Accordingly, Figure 3B shows the range of exothermic temperature and equivalence ratio for the first stage ignition. It starts with the region of equivalence ratio about 0.7 and temperature around 850 K, which is shown as the red cross. Then, it reaches its peak at 0.84 ms, which is the green cross in Figure 3B. At 1.20 ms (see Figure 2c), the second exothermic stage occurs, which exhibits two different exothermic regions. As shown in Figure 3A, the moment at 1.20 ms corresponds to the inflection point of rapid heat release. The second stage causes intense heat release in a wider range of conditions as shown in Figure 3B (the blue cross). All ignition behaviors are highly consistent with the previous study [25,26], especially revealing the same HRR hierarchical structure.

4.2. Injection Pressure Verification

To test the influence of the similar factor method in this study by the variation of physical parameters and the effect of the physical delay in the CVB on the results of the sensitivity analysis of the chemical mechanism ignition characteristics, this section re-validates the important parameters affecting the spray, the injection pressure (DP_inj) adjusted from 150 MPa to 100 MPa and the injection duration adjusted accordingly, following the Refs. [25,26] analysis procedure. Figure 4 shows the temperature and HRR distribution for the injection pressure of 100 MPa. In order to describe the ignition behavior, the temperature and exotherm distribution at all critical moments in the CVB were shown in Figure 4 colored by the distributions of temperature and HRR. Thus, the evolution of ignition has been clearly described. Despite the substantial change in injection pressure, it has limited effects on the temperature and HRR distribution at the three moments of the low-temperature exothermic trigger, accumulated exothermic and thermal ignition. The adjustment of injection pressure only slightly delays all moments. Figure 5 shows the evolution of HRR with the Φ-T plot after adjusting the injection pressure. As seen in the figure, all the evolutionary processes are identical to those in Figure 2.

As mentioned above, Figure 6 accurately describes the evolution of HRR and exothermic region, and recognizes the conditions of each critical moment roughly. Compared to Figure 3, Figure 6 depicts the following process more accurately: The exothermic region expands from the low-temperature, stoichiometric ratio to the high-temperature, high-equivalent ratio and finally reaches the thermal ignition in CVB. The results indicate that the trigger point of the red cross determines the subsequent hot ignition. The reaction condition is about 840 K and stoichiometric ratio mixture.

Figure 7 is a comparison of the normalized sensitivity coefficients between CVB and ST with similar factors at 100 MPa injection pressure, corresponding to an initial temperature of 800 K for ST and an ambient temperature of 850 K for the CVB. As seen in Figure 7, the normalized sensitivity coefficients to the moment of ignition can be kept very similar to the normalized sensitivity coefficients of the mechanism in the CVB. However, the overall trend of the normalized sensitivity coefficients of the two reactors remained highly consistent under the high similarity factor condition, indicating that under this condition, the adjustment of the mechanism based on the validation data of ST can also be well-fed back to the sensitivity of the ignition delay in CVB with the mechanism.

4.3. Verification of Nozzle Diameter

In this section, another important parameter of nozzle diameter affecting spraying process is adjusted from 0.1 to 0.15 mm, and the spraying duration was adjusted accordingly and re-validated following the analytical procedure described above. Figure 8 shows the temperature and HRR distribution for a nozzle diameter of 0.15 mm. From Figure 8, the moments are similar to Figure 4. Moreover, the temperature and HRR distributions of the low-temperature exothermic trigger point, accumulated exothermic, and thermal ignition moments in both Figure 8 and Figure 9 are consistent.

Figure 9 shows the Φ-T plot after increasing the nozzle diameter. As seen in Figure 9, all the evolutionary processes remain highly consistent with the Injection pressure variation, except for the extended ignition delay in CVB. It can be seen that the change of the nozzle diameter has less influence on the ignition behavior and temperature distribution at the three moments, and the distribution of the exothermic region is also almost consistent. This higher stability is beneficial to the similarity factor method.

The trend and range of conditions shown in Figure 10 are consistent with those in Figure 6. Although the variation of nozzle diameter changes both the fuel injection before ignition and the intensity of the thereafter reaction, this change has less impact on the HRR and temperature analysis method used in this study, which shows the relatively stable characteristics. The reaction condition of the red cross in Figure 10 is about 860 K with equivalence ratio about 0.7. The ignition behavior was controlled at approximately 850 K and stoichiometric ratio mixture of fuel/air in CVB.

Figure 11 shows the comparison of the highest normalized sensitivity coefficients with similarity factors between CVB and ST at the diameter of 0.15 mm, corresponding to an initial temperature of 850 K for ST and an ambient temperature of 1000 K for CVB, which maintains a high similarity with Figure 7. It is concluded that even though the boundary conditions have been changed, highly consistent conditions for validation in basic reactors still can be found by using the method proposed in this study.

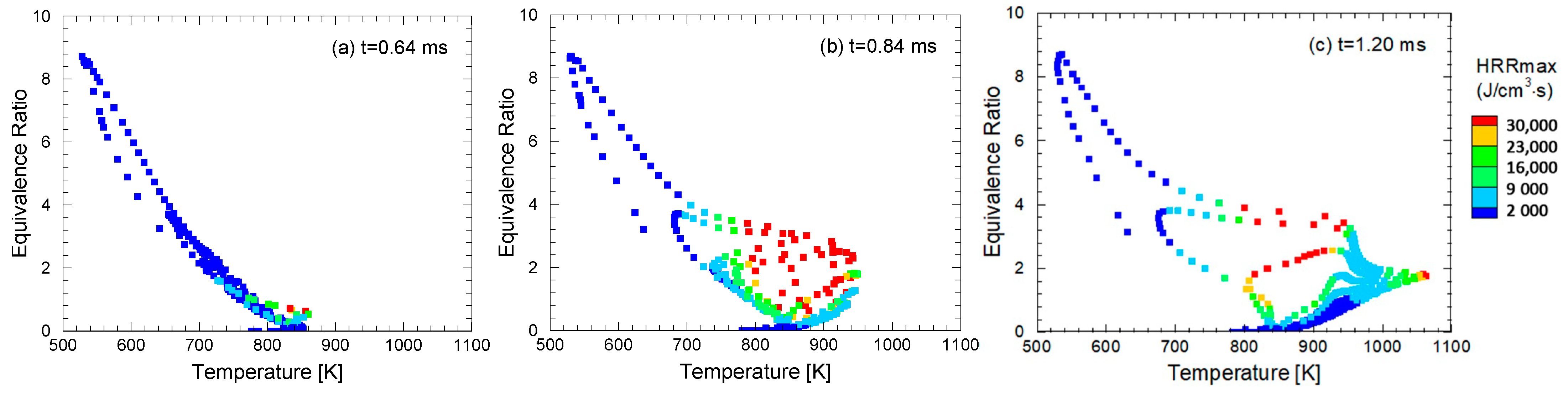
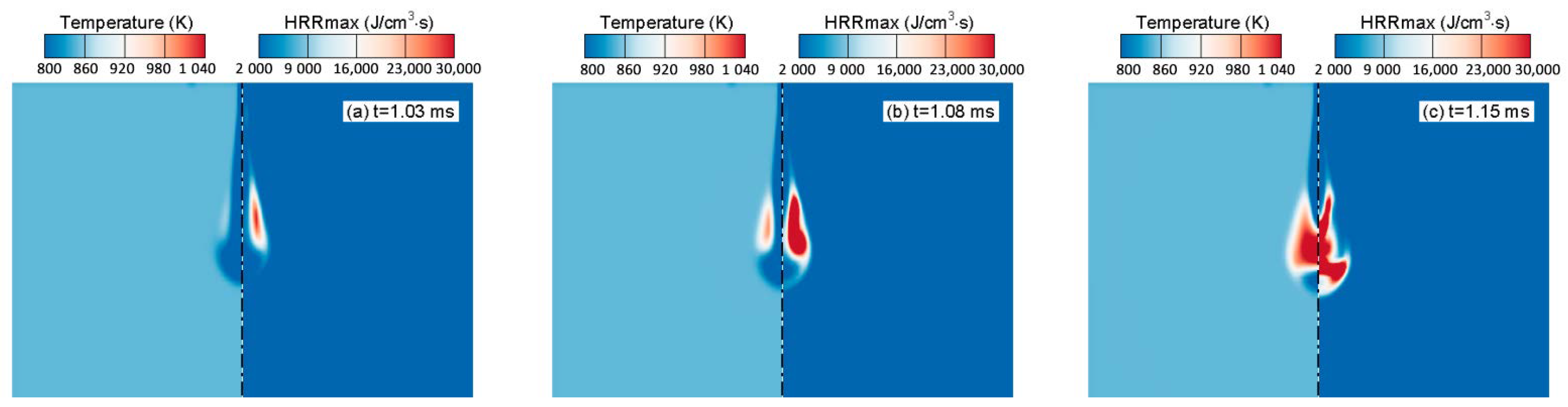
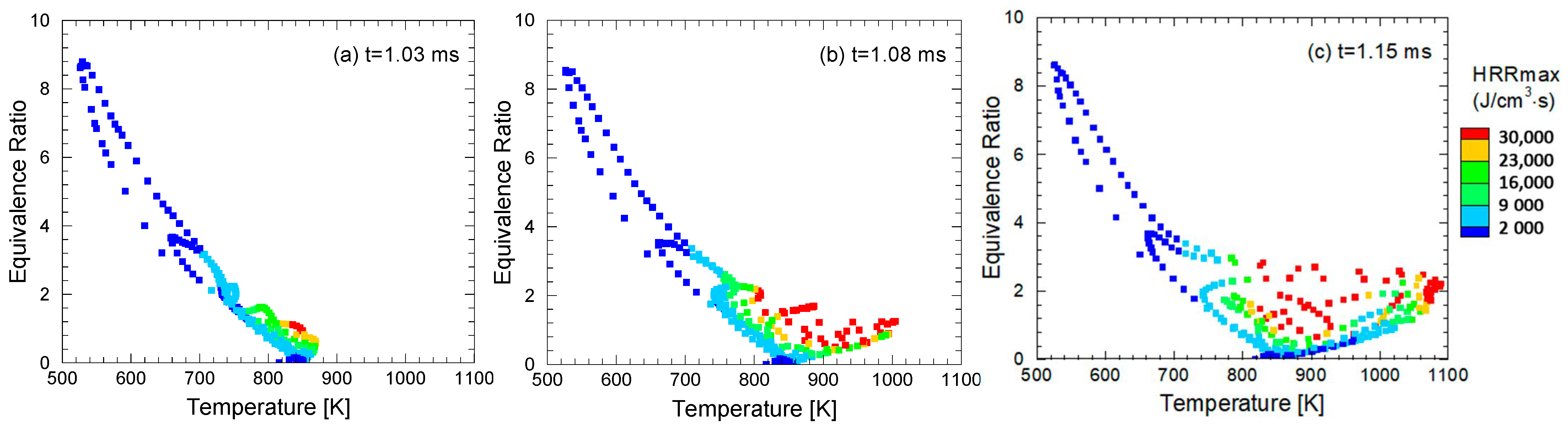
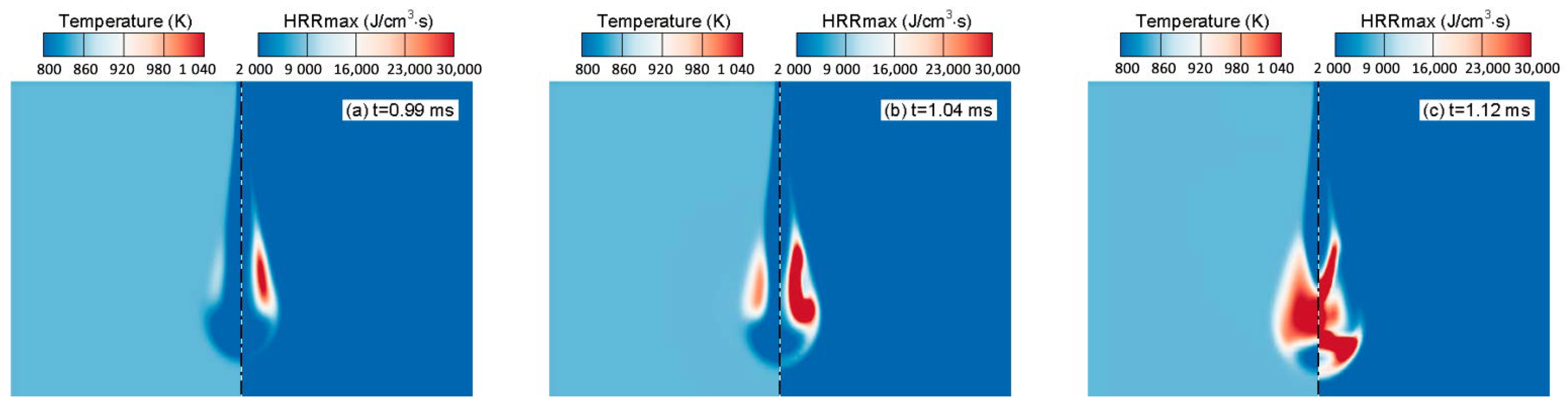
4.4. Comparison of Similarity Factors

Figure 12 shows the temperature distribution of high similarity factor in CVB and ST under different conditions, which classifies the different similarity of the above cases and the previous one [25] by different color lines. Here, the red lines represent the results of Chang’s mechanism [40], the blue lines represent the results of Wang’s mechanism [39], the green lines represent the results of Chang’s mechanism [40] with the injection pressure of 100 MPa, and the orange lines represent the results of Chang’s mechanism [40] with the nozzle diameter of 0.15 mm. The main areas of high similarity factor are shaded in the figure. For shock tube, the high-factor mainly locates at the temperature between 800–950 K, while a wider range of 800–1100 K is observed in CVB. Combined with the above analysis of ignition behavior, the trigger point of two-stage ignition was also developed from approximate 850 K with stoichiometric ratio mixture. According to the previous studies [26], the key condition in ST is less affected by equivalence ratio. Therefore, the experimental conditions in ST used for mechanism verification should concentrate on the negative temperature coefficient region and stoichiometric ratio mixture.

5. Conclusions

To understand the results of the similarity factor method for constructing different mechanisms and applying the methods under different working parameter conditions, we compared the n-heptane mechanism of Wang et al. [39] and repeatedly observed results detailed in the present study; and it can be concluded that the main conclusions of this study are not subject to the actual adoption of the mechanism. After the comparative testing of the boundary conditions that affect spraying, such as injection pressure and orifice diameter, we can see that the similarity analysis method proposed in this study can better exclude the interference of the variation of physical parameters.

On the one hand, two-stage exothermic expands from the low-temperature, stoichiometric ratio to the high-temperature, high-equivalent ratio and finally reaches the thermal ignition in CVB, which keeps the relatively stable analytical results. On the other hand, it also determines the universality of the similarity factor method. Although the combustion process is conducted under a wide range of temperature and equivalence ratio conditions in CVB, the specific conditions at approximately 850 K and stoichiometric ratio mixture are important to control the ignition and combustion process, which is the key to construct the chemical kinetic mechanism suitable for CVB. The corresponding condition in shock tube is negative temperature coefficient region and stoichiometric ratio mixture.

Additionally, by comparing the similar factors of the normalized sensitivity coefficients of the shock tube and the HCCI engine, we found that the shock tube can well reflect the overall trend in HCCI engines [26]. Under the reaction conditions filtered using similar factors, the mechanism validated by the ignition delay in shock tube has a higher reference value for the numerical simulation of ignition behavior in different reactors.