Optimal Shape of Non-Linear Partially Wet Annular Fins for Maximum Efficiency
Abstract
1. Introduction
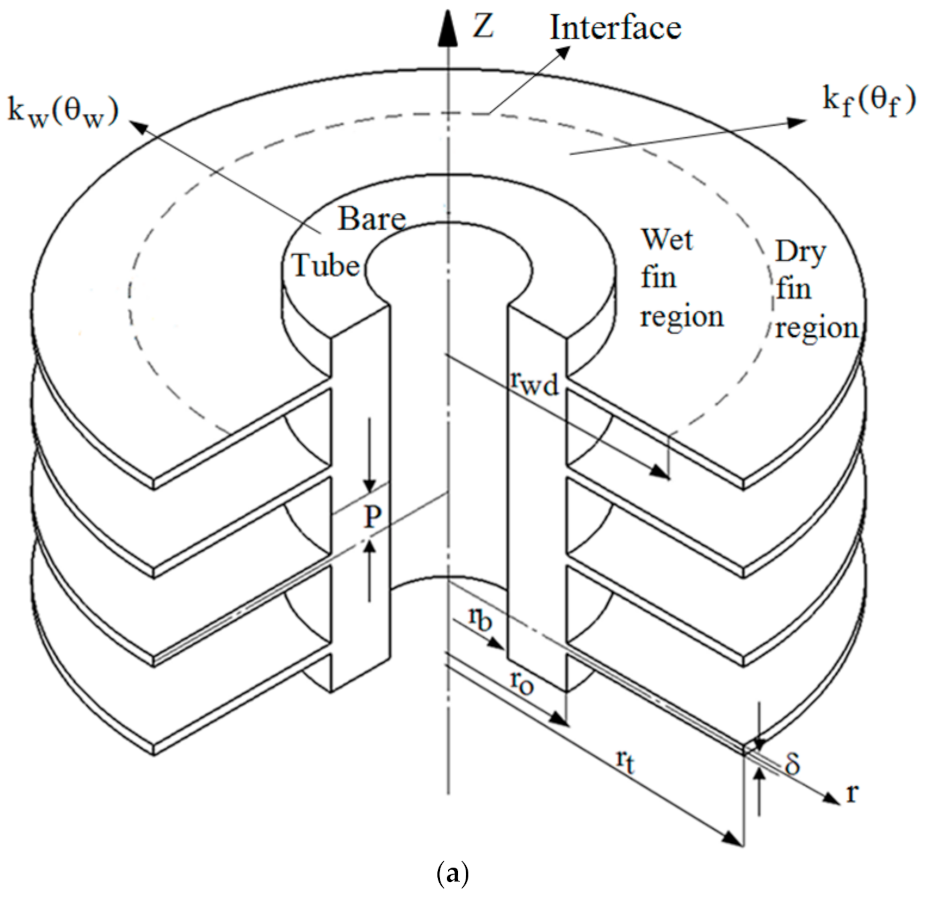
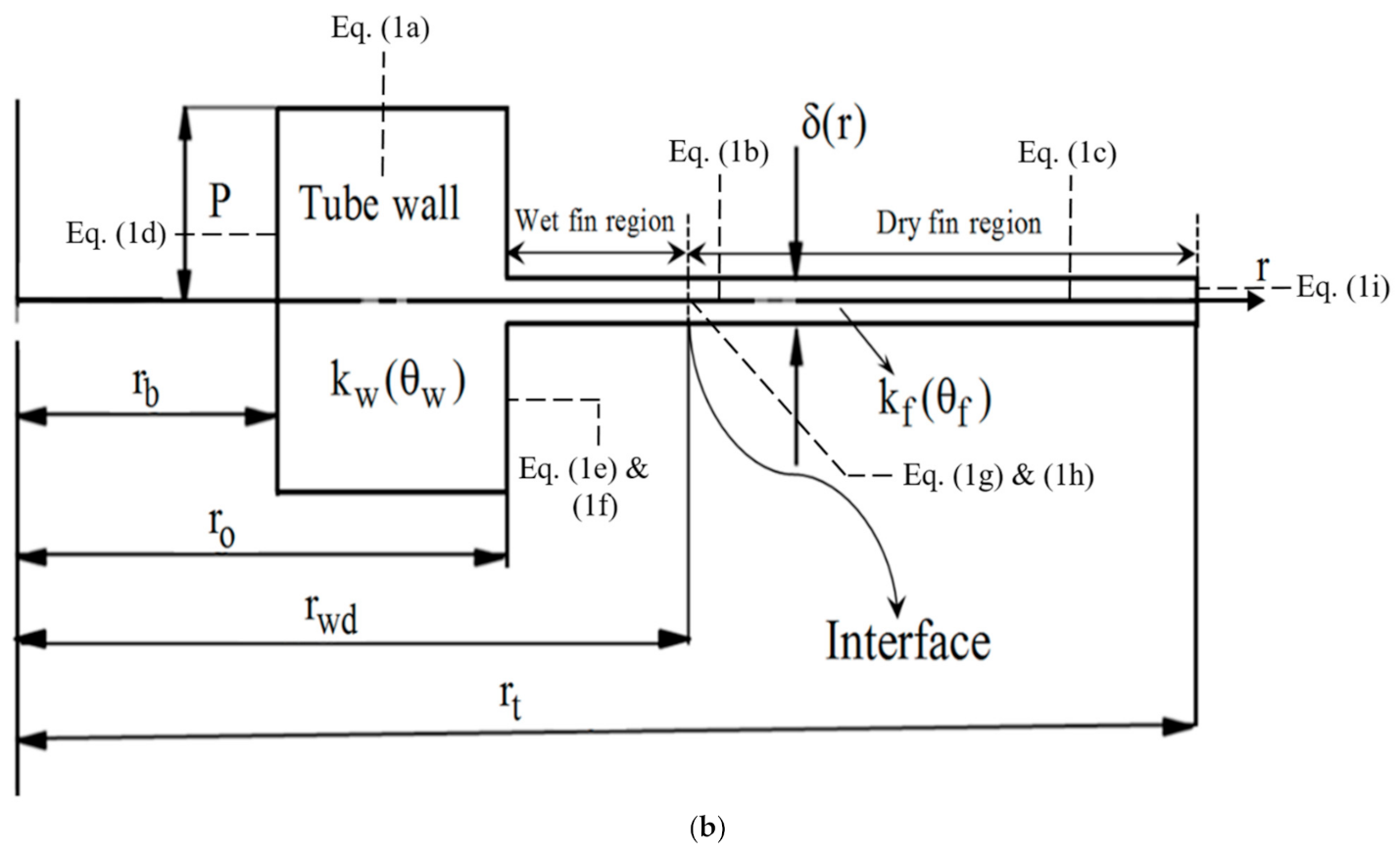
2. The Direct Problem
3. The Fin Design Problem
4. Iterative Process with CGM
5. The Sensitivity Problem
6. The Adjoint Problem
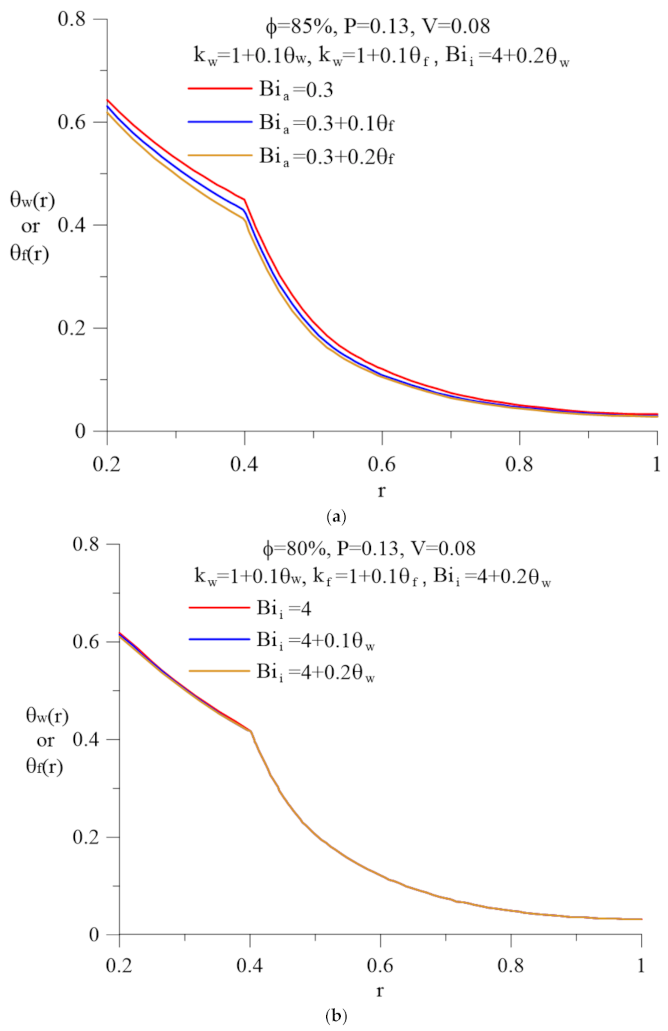
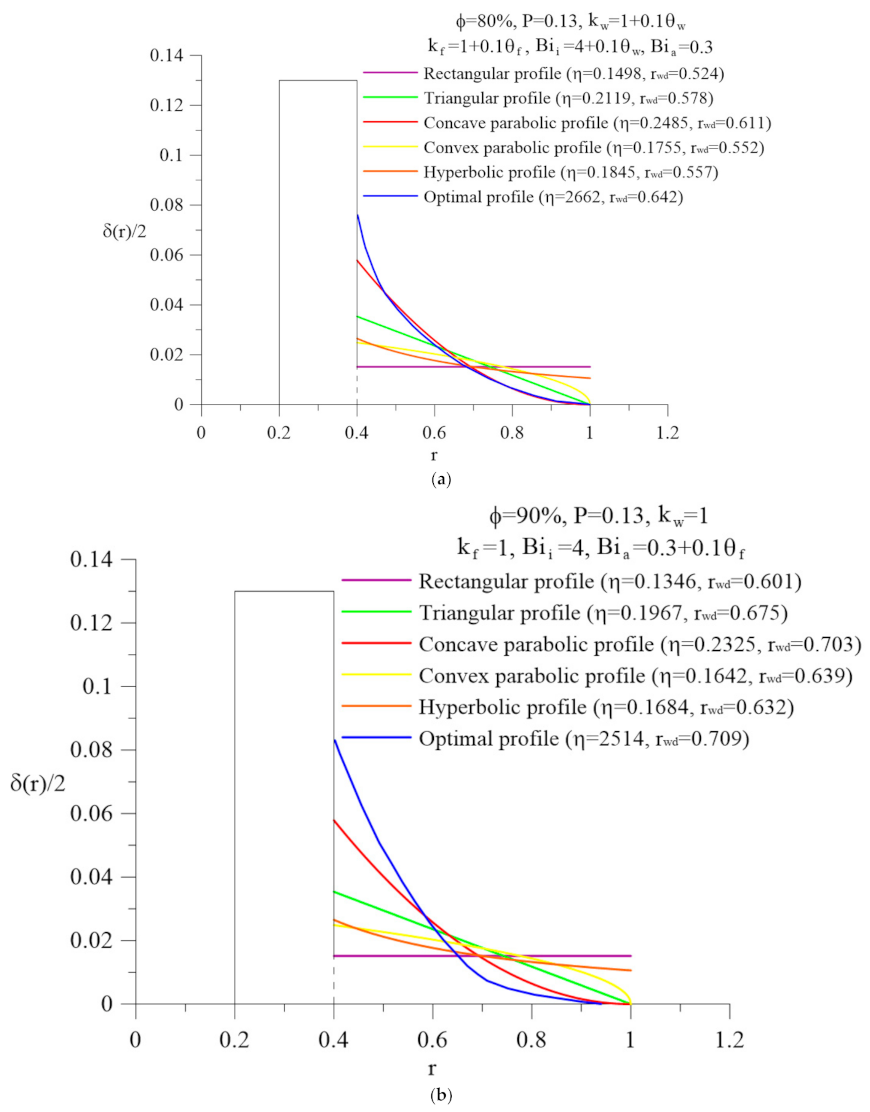
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fin cross-sectional area (m2) | |
| Bia(θf), Bii(θw) | Biot number |
| , | convective heat transfer coefficient (Wm−2K−1) |
| , | temperature-dependent thermal conductivity (Wm−1K−1) |
| , | dimensionless temperature-dependent thermal conductivity |
| mass transfer coefficient (kgm−2s−1) | |
| latent heat of condensation of moisture (Jkg−1) | |
| constant pressure specific heat for moist air (Jkg−1K−1) | |
| J | cost function defined by Equation (3) |
| J′ | gradient of the cost function defined by Equation (15) |
| Le | Lewis number |
| pn | search direction |
| half fin pitch (m) | |
| Pr | Prandtl number |
| q | actual heat transfer rate of fin |
| Q | ideal heat transfer rate of fin |
| , | inner and external tube radius (m) |
| interfacial radius between wet and dry fin domains (m) | |
| external fin radius (m) | |
| fin perimeter (m) | |
| Sc | Schmidt number |
| , , | tube wall, wet fin and dry fin surfaces temperatures (K) |
| , , | fin, refrigerant and air temperatures (K) |
| u (.) | unit step function |
| v(δ) | estimated fin volume |
| V | specified fin volume |
| Greek symbols | |
| α | damping coefficient |
| β | search step size |
| γ | conjugate coefficient |
| δ(r) | fin thickness |
| θw(r), θf,w(r), θf,d(r) | temperatures defined by Equation (2) |
| Δθw(r), Δθf,w(r), Δθf,d(r) | sensitivity functions defined by Equation (7) |
| Δλw(r), Δλf,w(r), Δλf,d(r) | adjoint functions given by Equation (13) |
| Γ (.) | Dirac delta function |
| Φ | desired fin efficiency |
| η | computed fin efficiency |
| ϕ | relative humidity |
| ε | stopping criterion |
| specific humidity of air on the fin surface | |
| specific humidity of the surrounding air | |
| Superscripts | |
| n | index of iteration |
| _ | dimensional variables |
| Subscripts | |
| f | fin |
| w | wall |
| f,d | dry fin |
| f,w | wet fin |
References
- Charters, W.W.S.; Theerakulpisut, S. Efficiency equations for constant thickness annular fins. Int. Commun. Heat Mass Transf. 1989, 16, 547–558. [Google Scholar] [CrossRef]
- Mokheimer, E.M.A. Performance of annular fins with different profiles subject to variable heat transfer coefficient. Int. J. Heat Mass Transf. 2002, 45, 3631–3642. [Google Scholar] [CrossRef]
- Iborra, A.A.; Campo, A. Approximate analytic temperature distribution and efficiency for annular fins of uniform thickness. Int. J. Therm. Sci. 2009, 48, 773–780. [Google Scholar] [CrossRef][Green Version]
- McQuiston, F.C. Fin efficiency with combined heat and mass transfer. ASHRAE Trans. 1975, 81, 350–355. [Google Scholar]
- Toner, M.; Kilic, A.; Onat, K. Comparison of rectangular and triangular fins when condensation occurs. Heat Mass Transf. 1983, 17, 65–72. [Google Scholar] [CrossRef]
- Schmidt, E. Die Warmeubertragung durch Rippen. Z. VDI 1926, 70, 885–947. [Google Scholar]
- Kern, D.Q.; Kraus, A.D. Extended Surface Heat Transfer; MacGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Jang, Y.J.; Choi, D.J.; Kim, S.; Hyun, M.T.; Lee, Y.G. Enhancement of condensation heat transfer rate of the air-steam mixture on a passive condenser system using annular fins. Energies 2017, 10, 1777. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, Y.; Yang, H.; Mao, H.; Yu, Z.; Li, R. One convenient method to calculate performance and optimize configuration for annular radiator using heat transfer unit simulation. Energies 2020, 13, 271. [Google Scholar] [CrossRef]
- Wu, G.; Bong, T.Y. Overall efficiency of a straight fin with combined heat and mass transfer. Am. Soc. Heat. Refrig. Air-Cond. Eng. Trans. 1994, 100, 367–374. [Google Scholar]
- Naphon, P. Study on the heat transfer characteristics of the annular fin under dry-surface, partially wet-surface, and fully wet-surface conditions. Int. Commun. Heat Mass Transf. 2006, 33, 112–121. [Google Scholar] [CrossRef]
- Pirompugd, W.; Wang, C.C.; Wongwises, S. Finite circular fin method for heat and mass transfer characteristics for plain fin-and-tube heat exchangers under fully and partially wet surface conditions. Int. J. Heat Mass Transf. 2007, 50, 552–565. [Google Scholar] [CrossRef]
- Rosario, L.; Rahman, M.M. Analysis of heat transfer in a partially wet radial fin assembly during dehumidification. Int. J. Heat Fluid Flow 1999, 20, 642–648. [Google Scholar] [CrossRef]
- Kang, H.S. Optimization of a rectangular profile annular fin based on fixed fin height. J. Mech. Sci. Technol. 2009, 23, 3124–3131. [Google Scholar] [CrossRef]
- Brown, A. Optimum dimensions of uniform annular fins. Int. J. Heat Mass Transf. 1964, 8, 655–662. [Google Scholar] [CrossRef]
- Huang, C.H.; Hsiao, J.H. A non-linear fin design problem in determining the optimum shape of spine and longitudinal fins. Commun. Numer. Methods Eng. 2003, 19, 111–124. [Google Scholar] [CrossRef]
- Alifanov, O.M. Solution of an inverse problem of heat conduction by iteration methods. J. Eng. Phys. 1974, 26, 471–476. [Google Scholar] [CrossRef]
- Huang, C.H.; Chung, Y.L. Optimal Design of Annular Fin Shapes with Temperature-Dependent Properties. AIAA J. Thermophys. Heat Transfer. 2018, 32, 18–26. [Google Scholar] [CrossRef]
- Huang, C.H.; Chung, Y.L. A Nonlinear Fin Design Problem in Determining the Optimum Shapes of Fully Wet Annular Fins. Appl. Therm. Eng. 2016, 103, 195–204. [Google Scholar] [CrossRef]
- Huang, C.H.; Chung, Y.L. An inverse problem in determining the optimum shapes for partially wet annular fins based on efficiency maximization. Int. J. Heat Mass Transf. 2015, 90, 364–375. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Zubair, S.M. Efficiency and optimization of an annular fin with combined heat and mass transfer—An analytical solution. Int. J. Refrig. 2007, 30, 751–757. [Google Scholar] [CrossRef]
- Threlkeld, J.L. Thermal Environmental Engineering, 2nd ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
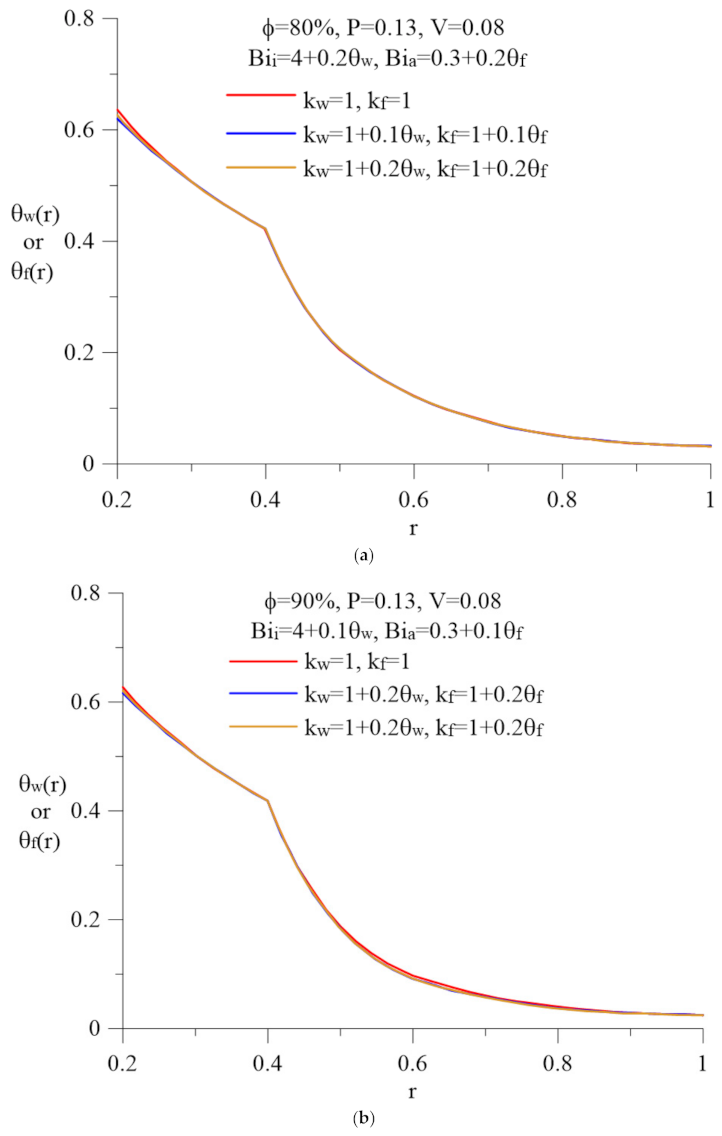
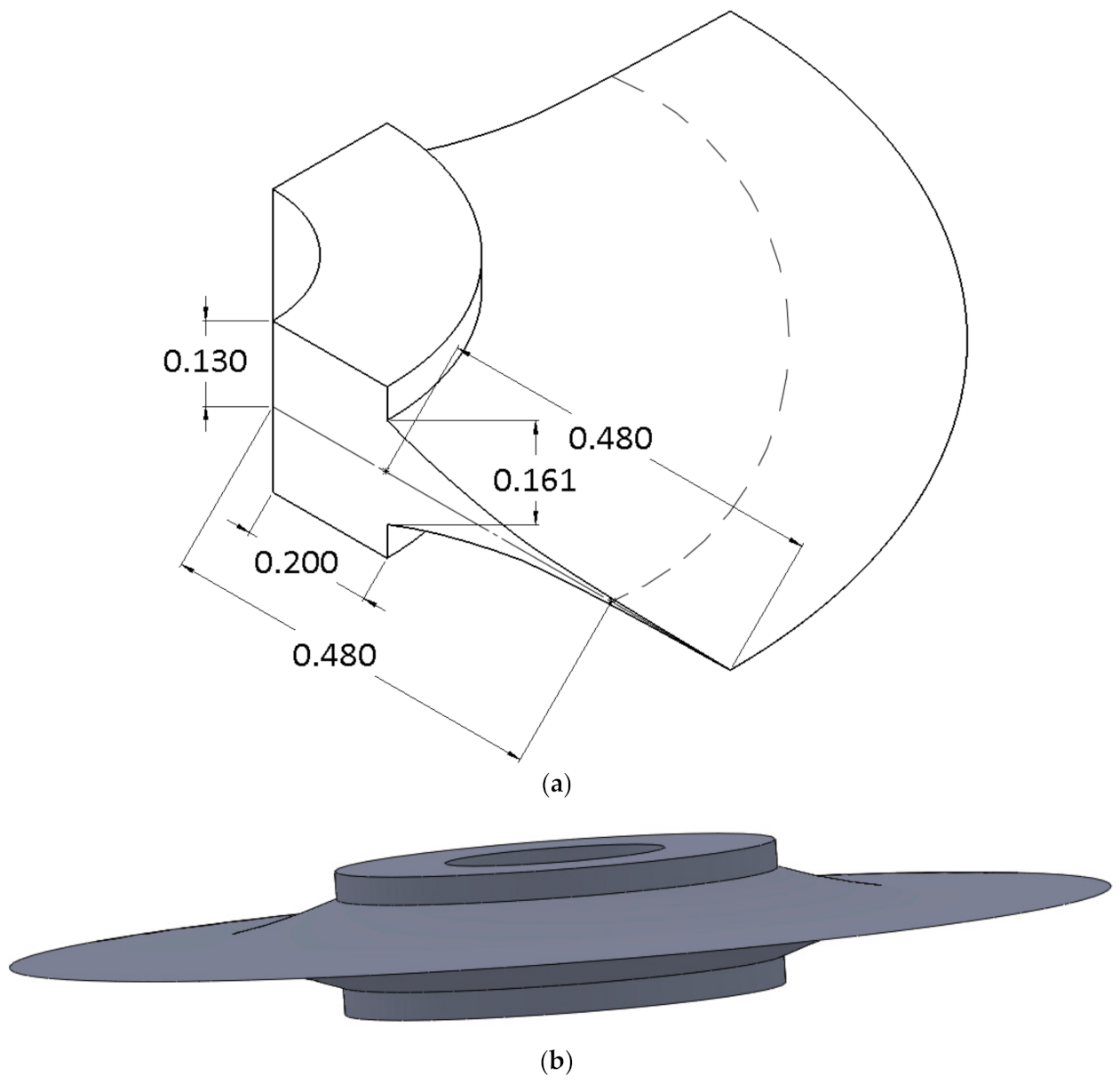

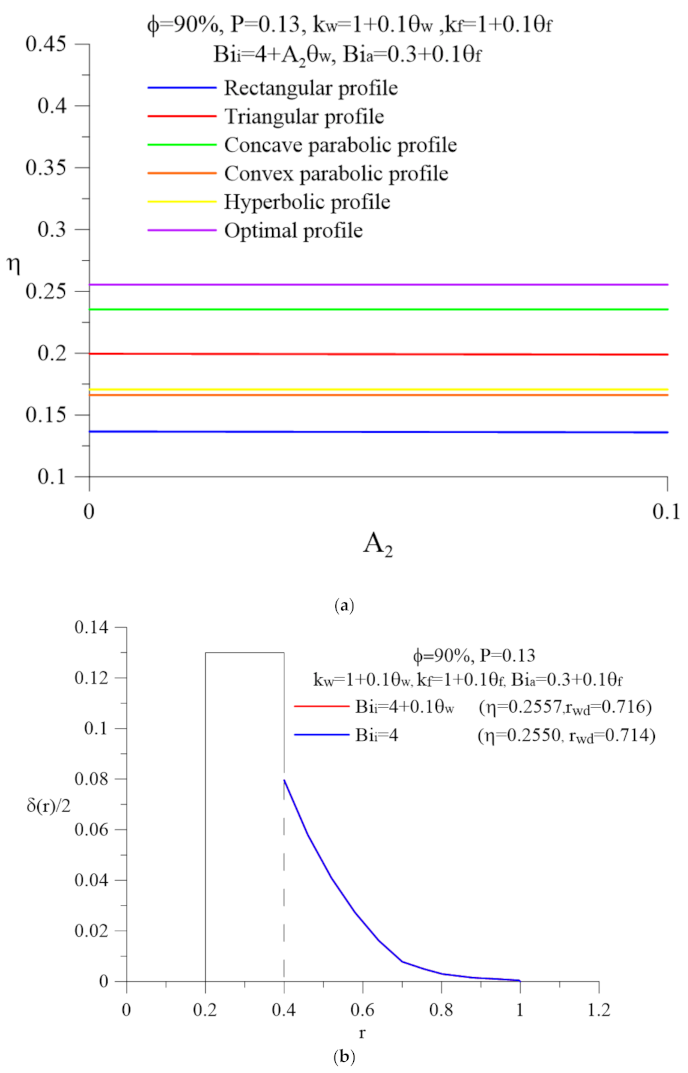
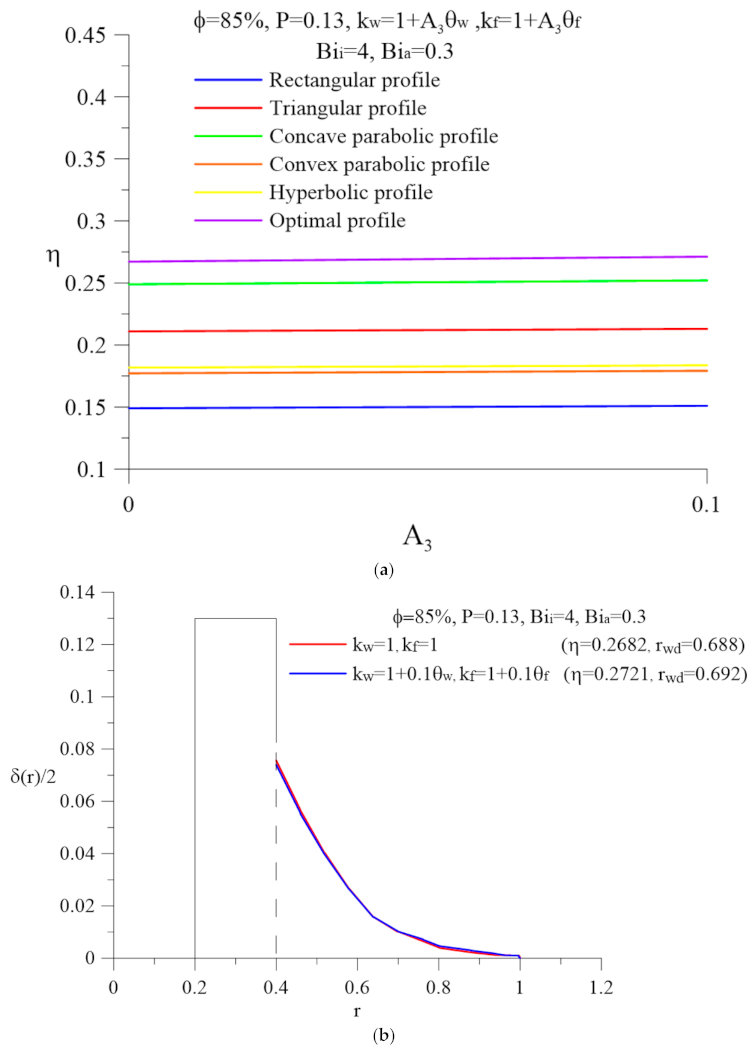
| η | Number | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| of Iterative | |||||||||||||||
| Φ | V | α | φ | kw | kf | Bii | Bia | V | Rectangular | Triangular | Concave | Convex | Hyperbolic | Optimal | N |
| 0.3 | 0.08 | 625 | 0.8 | 1 | 1 | 4 | 0.3 | 0.08 | 0.1472 | 0.2086 | 0.2450 | 0.1726 | 0.1815 | 0.2624 | 425 |
| 0.3 + 0.1θf | 0.1336 | 0.1924 | 0.2272 | 0.1576 | 0.1661 | 0.2443 | 382 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1473 | 0.2088 | 0.2452 | 0.1727 | 0.1817 | 0.2625 | 556 | |||||||
| 0.3 + 0.1θf | 0.1338 | 0.1927 | 0.2275 | 0.1578 | 0.1663 | 0.2445 | 448 | ||||||||
| 1 + 0.1θw | 1 + 0.1θf | 4 | 0.3 | 0.1497 | 0.2117 | 0.2483 | 0.1753 | 0.1843 | 0.2659 | 326 | |||||
| 0.3 + 0.1θf | 0.1355 | 0.1945 | 0.2302 | 0.1601 | 0.1683 | 0.2466 | 201 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1498 | 0.2119 | 0.2485 | 0.1755 | 0.1845 | 0.2662 | 710 | |||||||
| 0.3 + 0.1θf | 0.1357 | 0.1947 | 0.2305 | 0.1604 | 0.1686 | 0.2468 | 365 | ||||||||
| 0.85 | 1 | 1 | 4 | 0.3 | 0.1478 | 0.2117 | 0.2488 | 0.1774 | 0.1830 | 0.2682 | 476 | ||||
| 0.3 + 0.1θf | 0.1342 | 0.1955 | 0.2305 | 0.1624 | 0.1675 | 0.2501 | 655 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1479 | 0.2119 | 0.2490 | 0.1775 | 0.1832 | 0.2684 | 399 | |||||||
| 0.3 + 0.1θf | 0.1344 | 0.1958 | 0.2308 | 0.1627 | 0.1678 | 0.2509 | 395 | ||||||||
| 1 + 0.1θw | 1 + 0.1θf | 4 | 0.3 | 0.1503 | 0.2148 | 0.2521 | 0.1801 | 0.1858 | 0.2721 | 549 | |||||
| 0.3 + 0.1θf | 0.1363 | 0.1974 | 0.2334 | 0.1651 | 0.1699 | 0.2528 | 307 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1504 | 0.2150 | 0.2523 | 0.1803 | 0.1860 | 0.2725 | 811 | |||||||
| 0.3 + 0.1θf | 0.1365 | 0.1977 | 0.2337 | 0.1654 | 0.1702 | 0.2537 | 388 | ||||||||
| 0.9 | 1 | 1 | 4 | 0.3 | 0.1482 | 0.2139 | 0.2508 | 0.1792 | 0.1838 | 0.2704 | 664 | ||||
| 0.3 + 0.1θf | 0.1346 | 0.1967 | 0.2325 | 0.1642 | 0.1684 | 0.2514 | 582 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1483 | 0.2142 | 0.2511 | 0.1794 | 0.1840 | 0.2710 | 486 | |||||||
| 0.3 + 0.1θf | 0.1347 | 0.1970 | 0.2328 | 0.1644 | 0.1687 | 0.2521 | 421 | ||||||||
| 1 + 0.1θw | 1 + 0.1θf | 4 | 0.3 | 0.1507 | 0.2170 | 0.2541 | 0.1819 | 0.1866 | 0.2740 | 628 | |||||
| 0.3 + 0.1θf | 0.1367 | 0.1994 | 0.2354 | 0.1666 | 0.1707 | 0.2550 | 766 | ||||||||
| 4 + 0.1θw | 0.3 | 0.1508 | 0.2172 | 0.2543 | 0.1821 | 0.1867 | 0.2742 | 729 | |||||||
| 0.3 + 0.1θf | 0.1369 | 0.1996 | 0.2356 | 0.1669 | 0.1711 | 0.2557 | 606 | ||||||||
| Rwd | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Φ | V | α | φ | kf | kw | Bii | Bia | V | Rectangular | Triangular | Concave | Convex | Hyperbolic | Optimal |
| 0.3 | 0.08 | 625 | 0.8 | 1 | 1 | 4 | 0.3 | 0.08 | 0.521 | 0.573 | 0.606 | 0.547 | 0.552 | 0.637 |
| 0.3 + 0.1θf | 0.511 | 0.555 | 0.591 | 0.532 | 0.540 | 0.620 | ||||||||
| 4 + 0.1θw | 0.3 | 0.521 | 0.574 | 0.607 | 0.548 | 0.553 | 0.638 | |||||||
| 0.3 + 0.1θf | 0.512 | 0.556 | 0.592 | 0.533 | 0.541 | 0.621 | ||||||||
| 1 + 0.1θf | 1 + 0.1θw | 4 | 0.3 | 0.524 | 0.576 | 0.610 | 0.551 | 0.556 | 0.641 | |||||
| 0.3 + 0.1θf | 0.514 | 0.558 | 0.595 | 0.535 | 0.543 | 0.625 | ||||||||
| 4 + 0.1θw | 0.3 | 0.524 | 0.578 | 0.611 | 0.552 | 0.557 | 0.642 | |||||||
| 0.3 + 0.1θf | 0.515 | 0.559 | 0.596 | 0.540 | 0.544 | 0.627 | ||||||||
| 0.85 | 1 | 1 | 4 | 0.3 | 0.561 | 0.616 | 0.655 | 0.592 | 0.589 | 0.688 | ||||
| 0.3 + 0.1θf | 0.546 | 0.610 | 0.643 | 0.580 | 0.584 | 0.672 | ||||||||
| 4 + 0.1θw | 0.3 | 0.562 | 0.617 | 0.656 | 0.593 | 0.590 | 0.689 | |||||||
| 0.3 + 0.1θf | 0.546 | 0.611 | 0.644 | 0.581 | 0.585 | 0.673 | ||||||||
| 1 + 0.1θf | 1 + 0.1θw | 4 | 0.3 | 0.564 | 0.619 | 0.660 | 0.596 | 0.593 | 0.692 | |||||
| 0.3 + 0.1θf | 0.549 | 0.614 | 0.646 | 0.584 | 0.587 | 0.676 | ||||||||
| 4 + 0.1θw | 0.3 | 0.565 | 0.520 | 0.661 | 0.597 | 0.593 | 0.693 | |||||||
| 0.3 + 0.1θf | 0.549 | 0.615 | 0.648 | 0.585 | 0.588 | 0.678 | ||||||||
| 0.9 | 1 | 1 | 4 | 0.3 | 0.612 | 0.677 | 0.714 | 0.651 | 0.642 | 0.726 | ||||
| 0.3 + 0.1θf | 0.601 | 0.675 | 0.703 | 0.639 | 0.632 | 0.709 | ||||||||
| 4 + 0.1θw | 0.3 | 0.613 | 0.678 | 0.715 | 0.652 | 0.643 | 0.727 | |||||||
| 0.3 + 0.1θf | 0.601 | 0.676 | 0.704 | 0.640 | 0.633 | 0.711 | ||||||||
| 1 + 0.1θf | 1 + 0.1θw | 4 | 0.3 | 0.615 | 0.681 | 0.717 | 0.655 | 0.646 | 0.730 | |||||
| 0.3 + 0.1θf | 0.604 | 0.679 | 0.706 | 0.643 | 0.635 | 0.714 | ||||||||
| 4 + 0.1θw | 0.3 | 0.616 | 0.682 | 0.718 | 0.656 | 0.647 | 0.731 | |||||||
| 0.3 + 0.1θf | 0.605 | 0.680 | 0.707 | 0.644 | 0.636 | 0.716 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-H.; Chung, Y.-L. Optimal Shape of Non-Linear Partially Wet Annular Fins for Maximum Efficiency. Energies 2021, 14, 844. https://doi.org/10.3390/en14040844
Huang C-H, Chung Y-L. Optimal Shape of Non-Linear Partially Wet Annular Fins for Maximum Efficiency. Energies. 2021; 14(4):844. https://doi.org/10.3390/en14040844
Chicago/Turabian StyleHuang, Cheng-Hung, and Yun-Lung Chung. 2021. "Optimal Shape of Non-Linear Partially Wet Annular Fins for Maximum Efficiency" Energies 14, no. 4: 844. https://doi.org/10.3390/en14040844
APA StyleHuang, C.-H., & Chung, Y.-L. (2021). Optimal Shape of Non-Linear Partially Wet Annular Fins for Maximum Efficiency. Energies, 14(4), 844. https://doi.org/10.3390/en14040844






