A Methodology for Provision of Frequency Stability in Operation Planning of Low Inertia Power Systems
Abstract
1. Introduction
1.1. Motivation
1.2. Overview of Available Countermeasures for Supporting Low Inertia
1.3. Paper Contribution
2. Background
2.1. Classic Inertia
2.2. Synthetic Inertia
3. Synthetic Inertia Aimed for Large Disturbances and RoCoF Limitation
3.1. Derivation of the Method
3.2. Tuning of Synthetic Inertia Controller
3.3. Synthetic Inertia Concept Verification Based on Simple Theoretical Model of a Power System
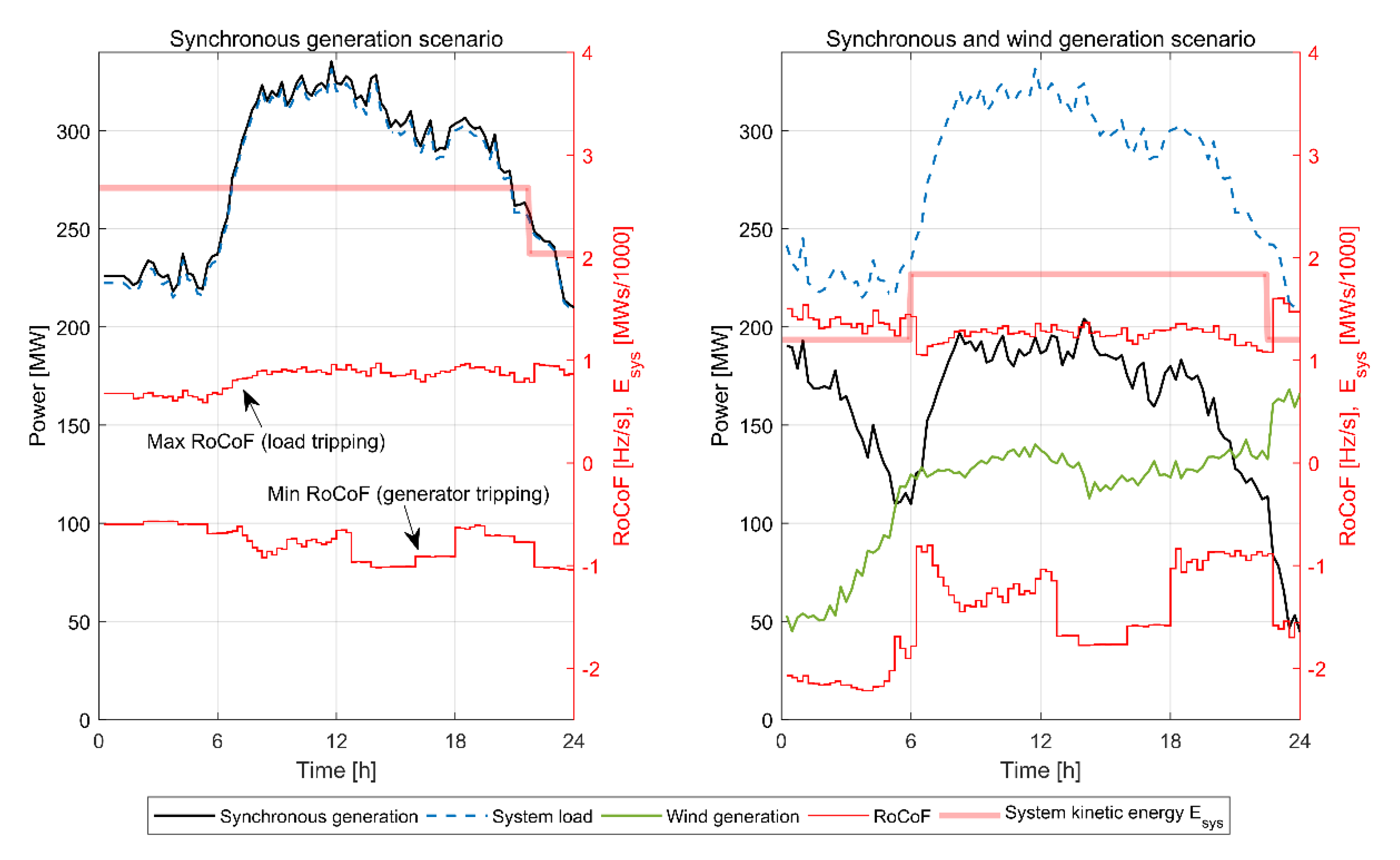
4. System Operation Planning Methodology with Focus on RoCoF
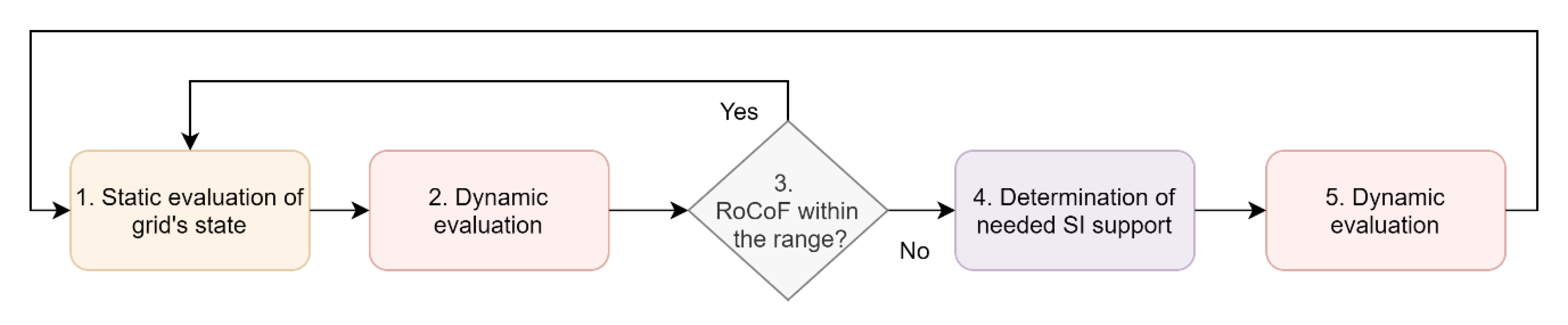
- For each time step of the forecast the algorithm starts with static evaluation of the grid’s state through a load flow. In this stage equivalent, system inertia is calculated according to Equation (2), and based on Equation (3), maximum and minimum RoCoF are calculated for load and generation tripping, respectively. ΔP in this equation is the largest possible active power imbalance found in the load flow data.
- In the second stage, dynamic evaluation is performed. This step might be considered optional for Scenario 1 but is a must for Scenario 2, if wind generation or other devices operating in the power system are equipped with synthetic inertia. The purpose is to accurately determine RoCoF through dynamic simulation of a power system model that encompasses dynamic responses of relevant elements to frequency changes.
- Step three is a simple check—if the resulting value of RoCoF is within the predefined range, the algorithm moves to another time step, as the system is able to withstand the largest possible outage in given grid operation conditions. If not, Step 4 is executed.
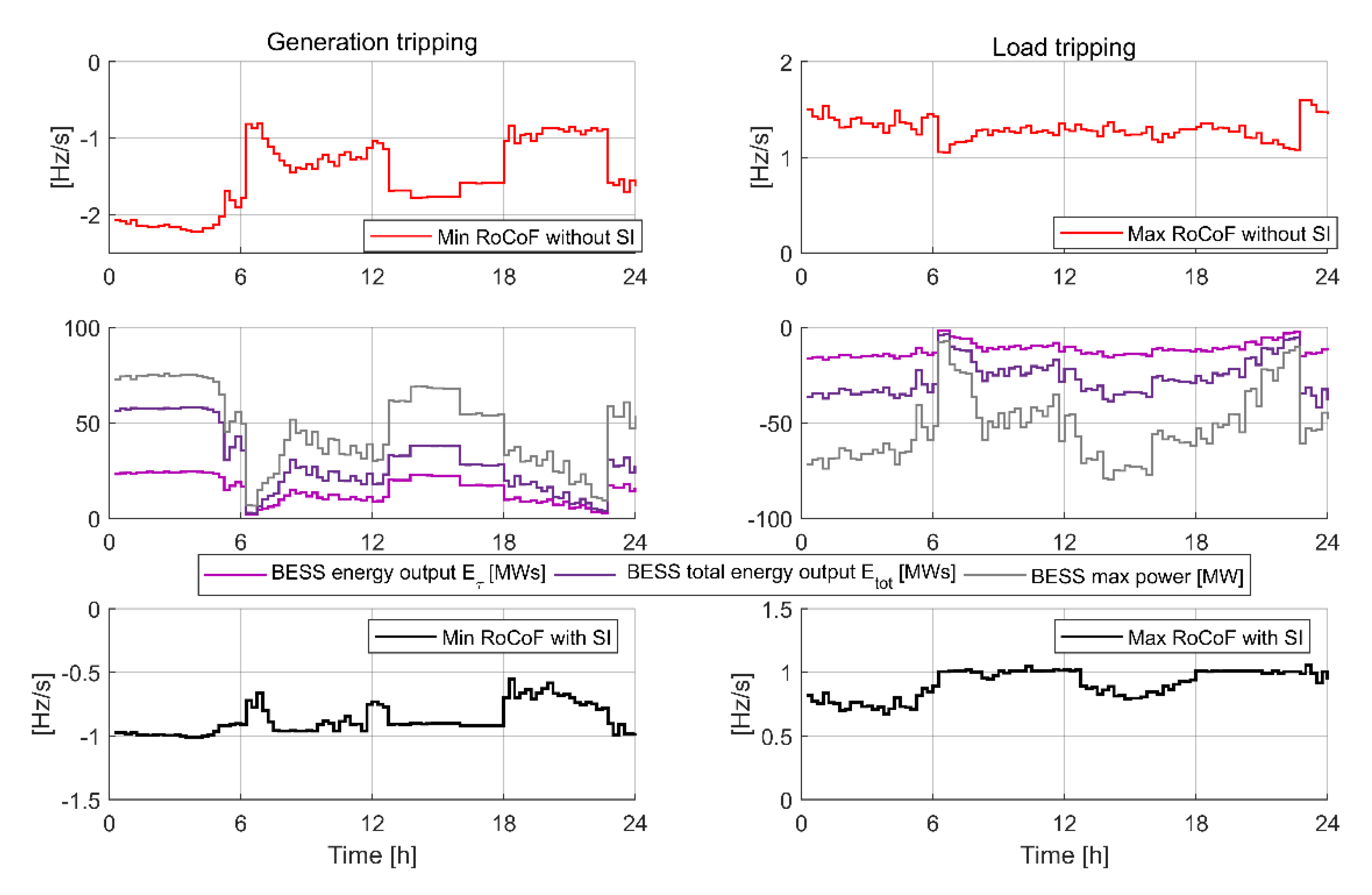
- Step four consists in determining necessary additional inertia to keep RoCoF in the assumed range, i.e., between RoCoFmin for generation trip and RoCoFmax for load trip. The methodology is demonstrated using BESS, which are used for SI service due to their excellent controllability but support from other devices is also possible. Then, based on Equations (10) and (13), controller parameters are calculated. In fact, controller’s time constants do not have to be updated often. They could even be hardcoded in the SI controllers based on average inertia level in the power system and response time of fast frequency control of the frequency-governing devices. On the other hand, the overall SI gain needs to be calculated for every time step, as it influences the contribution level of SI.
- In Step five, the SI is distributed among selected assets by assigning a weighting factor to each device so that the sum of weighting factors is equal to 1, and final dynamic simulation is performed to confirm the calculations. It has to be noted that more than one BESS or other device can take part in SI service. Calculated energy ΔEτ can be distributed among available units arbitrarily by the TSO, e.g., by engaging units being furthest from their respective limits, or by typical market mechanisms, such as merit order or long-term contracts, etc.
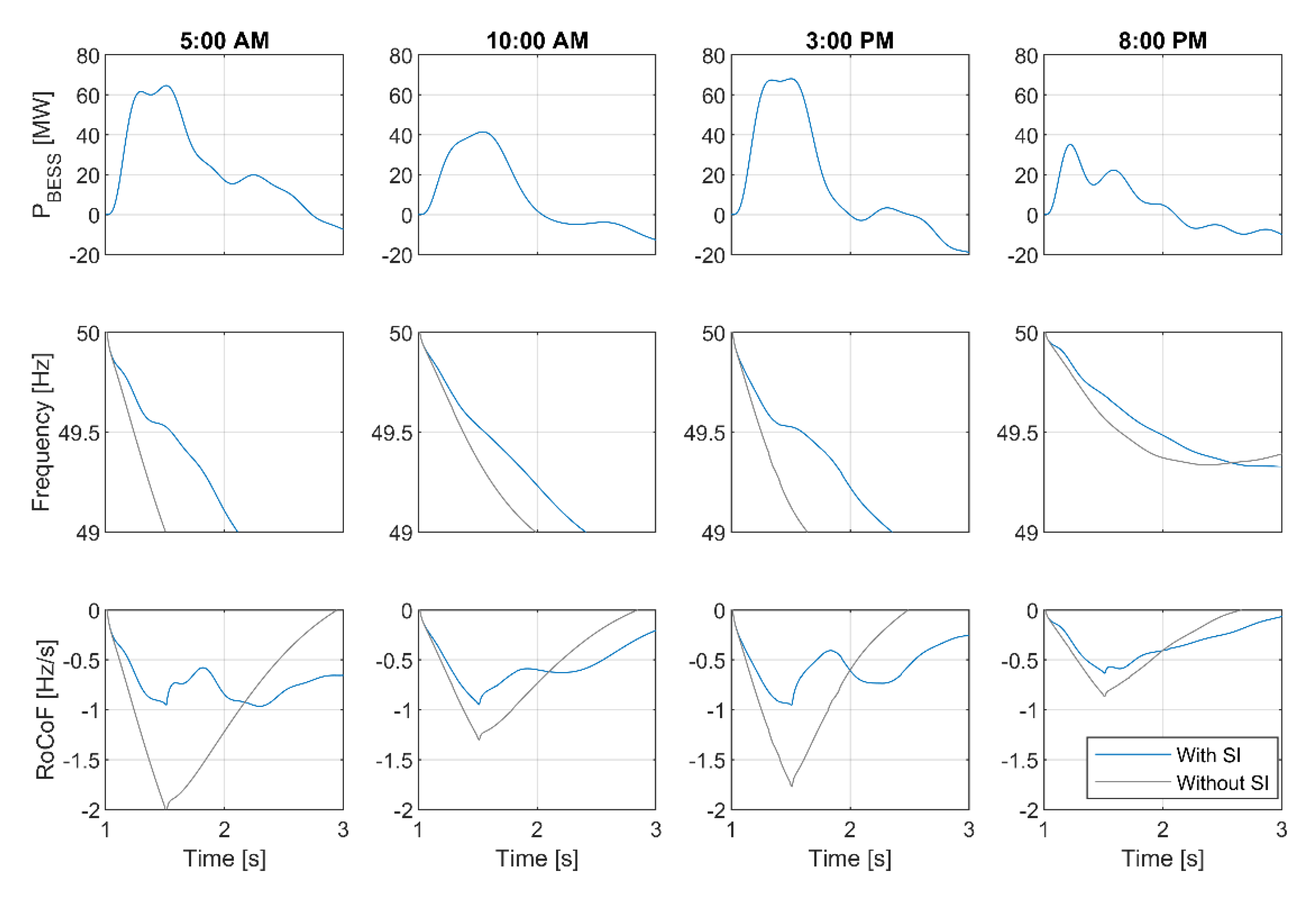
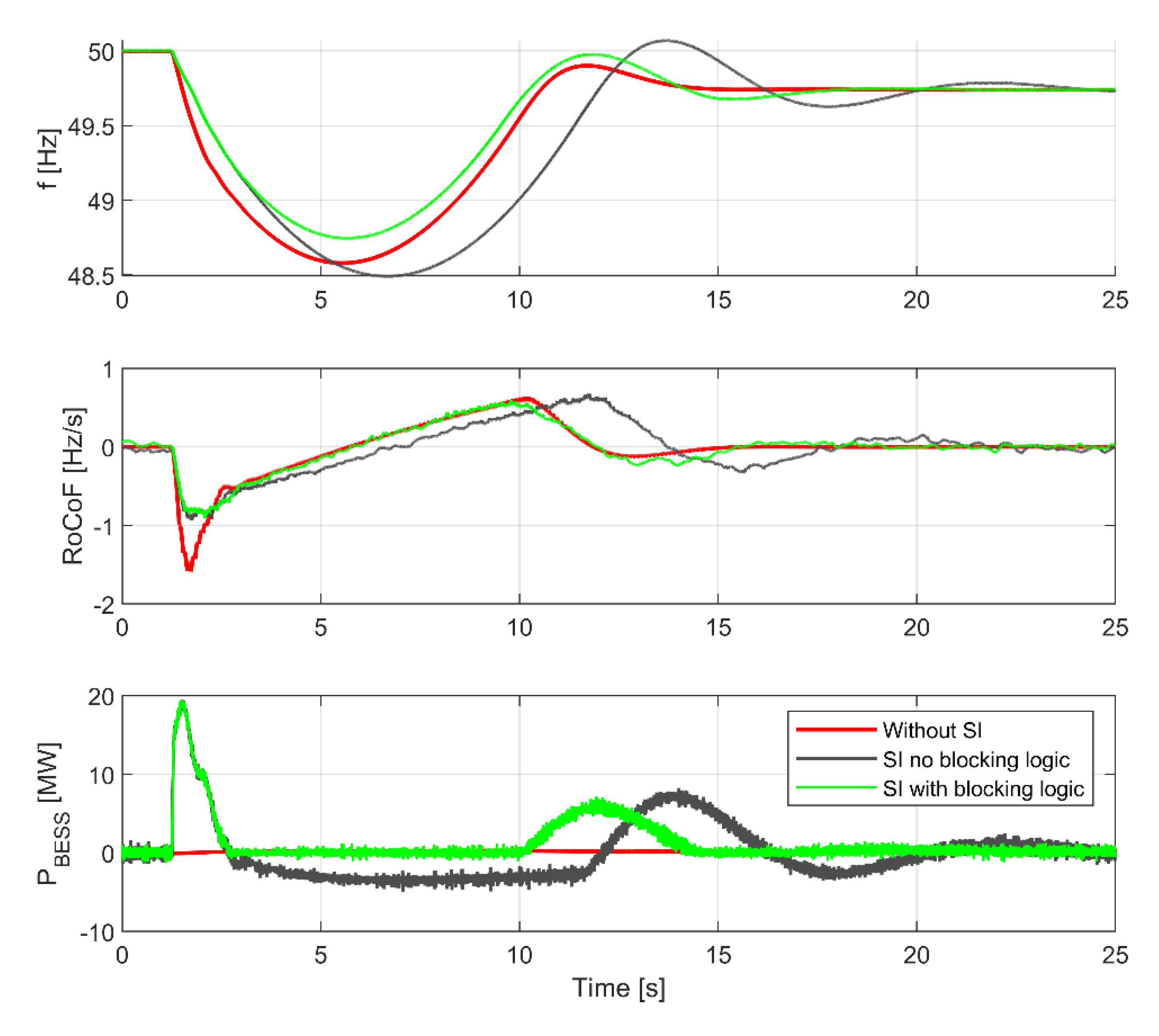
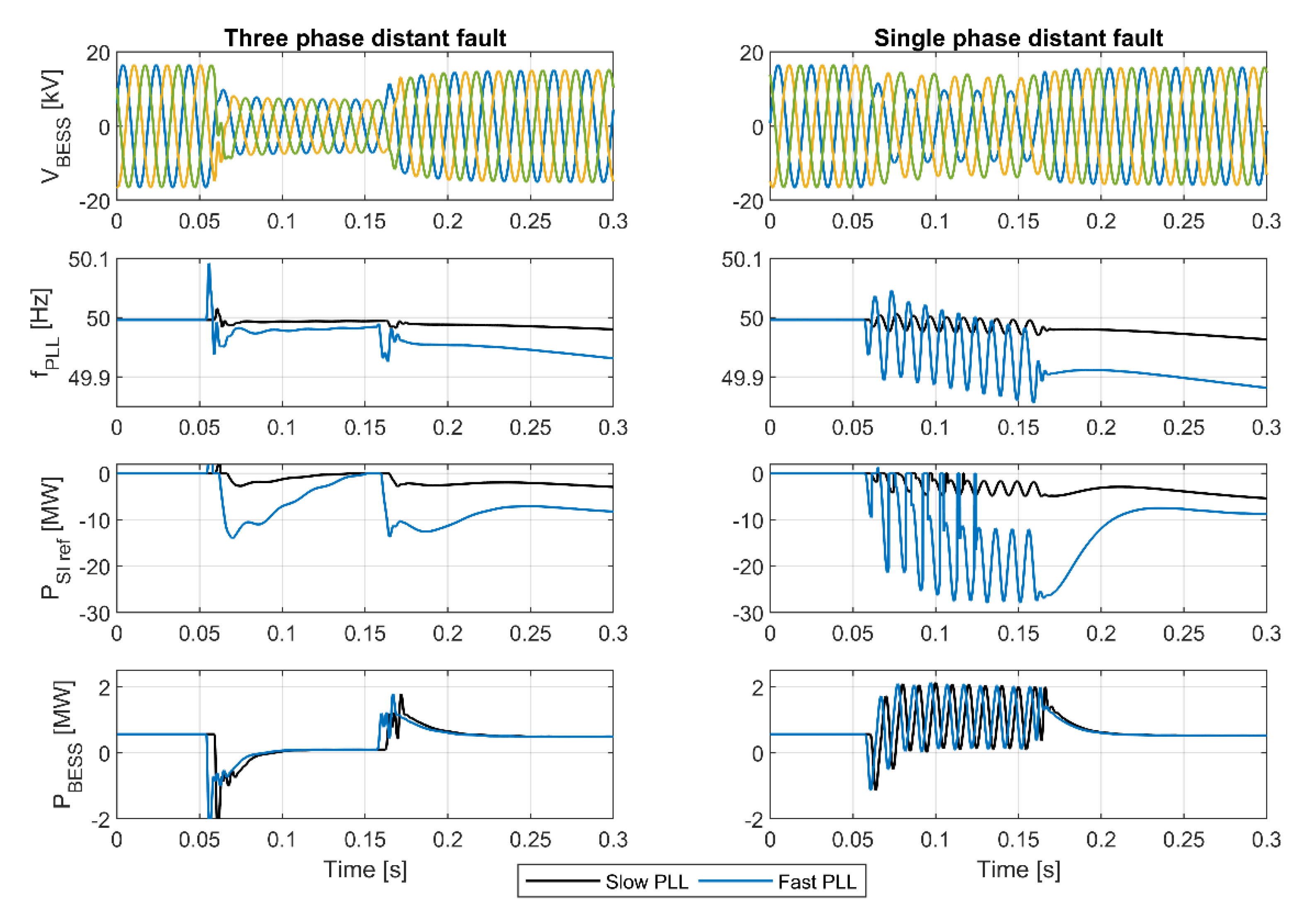
5. Validation of the Synthetic Inertia Concept in Real-Time Simulation Environment
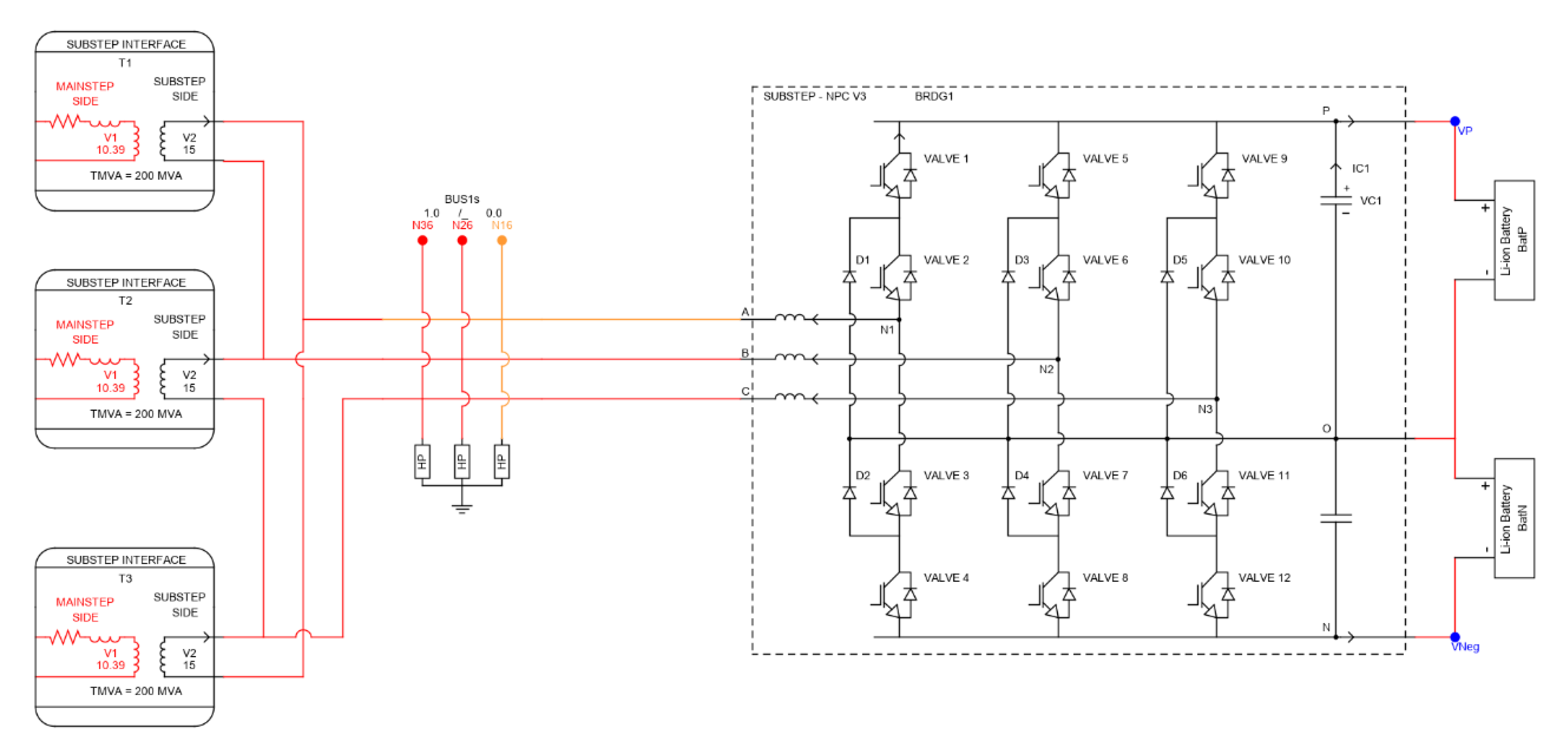
5.1. Real-Time Simulation Environment
5.2. Battery Energy Storage System Model
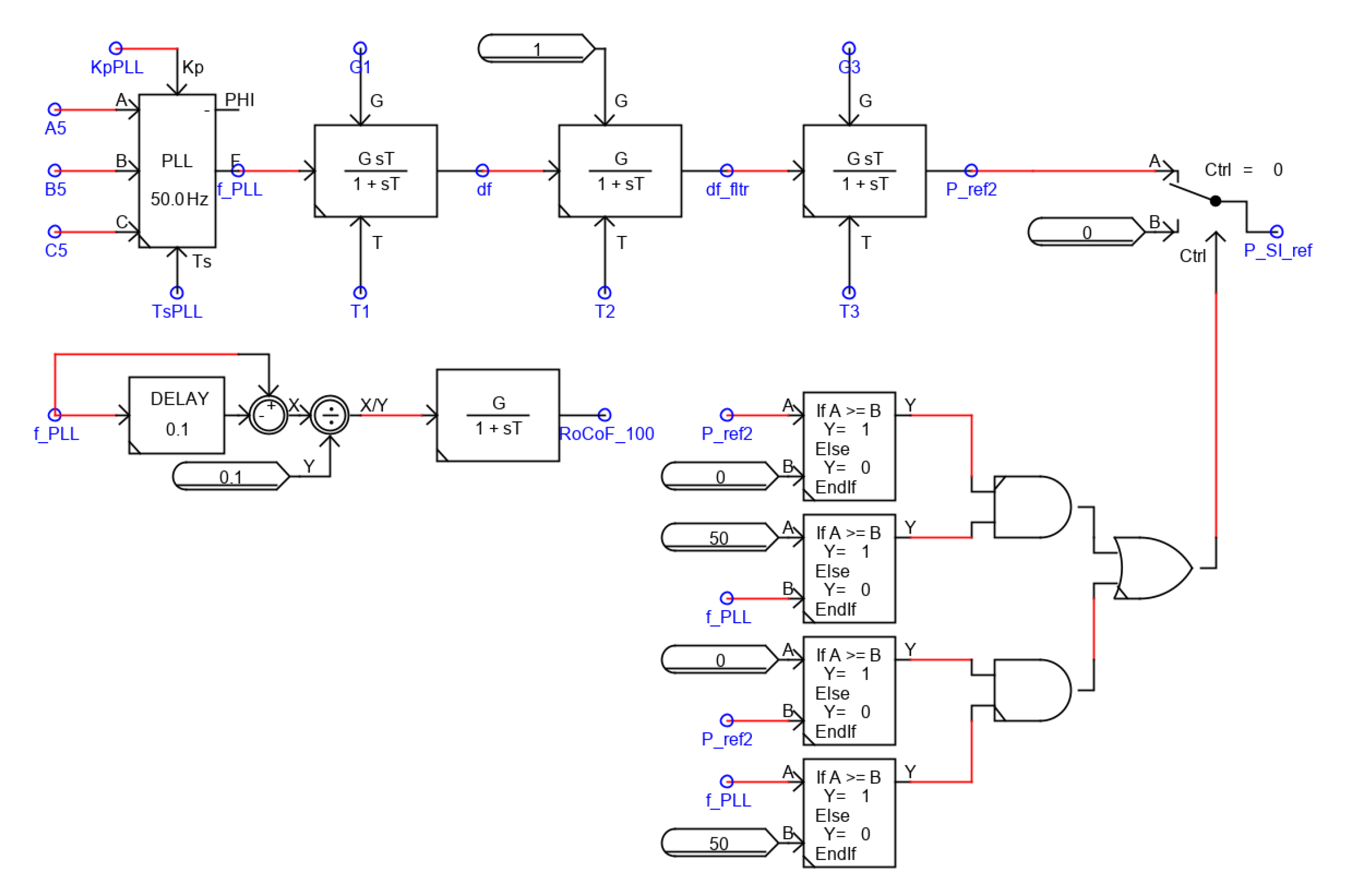
5.3. Synthetic Inertia Controller in RTDS
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- ENTSO-E. Ten Year Network Development Plan (TYNDYP); 2020 Scenario Report; ENTSO-E: Brussels, Belgium, 2020. [Google Scholar]
- ENTSO-E; Technical Group on High Penetration of Power Electronic Interfaced Power Sources. High Penetration of Power Electronic Interfaced Power Sources and the Potential Contribution of Grid Forming Converters; Technical Report; ENTSO-E: Brussels, Belgium, 2020. [Google Scholar]
- Austalian Energy Market Operator. Black System, South Australia, 28 September 2016—Final Report; Australian Energy Market Operator: Melbourne, Australia, 2017. [Google Scholar]
- O’Conell, B.; Cunniffe, N.; Eager, M.; Cashman, D.; O’Sullivan, J. Assessment of Technologies to Limit the Rate of Change of Grid Frequency on an Island System; CIGRE: Paris, France, 2018. [Google Scholar]
- ENTSO-E. European Power System 2040: Completing the Map. System Needs Analysis, Part of ENTSO-E’s 2025, 2030, 2040 Network Development Plan 2018; ENTSO-E: Brussels, Belgium, 2019. [Google Scholar]
- ENTSO-E. High Penetration of Power Electronic Interfaced Power Sources (HPoPEIPS) ENTSO-E Guidance Document for National Implementation for Network Codes on Grid Connection; ENTSO-E: Brussels, Belgium, 2017. [Google Scholar]
- Machowski, J.; Lubośny, Z. Stabilność Systemu Elektroenergetycznego; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2018; ISBN 978-83-01-20006-0. [Google Scholar]
- ENTSO-E. Need for Synthetic Inertia (SI) for Frequency Regulation: ENTSO-E Guidance Document for National Implementation for Network Codes on Grid Connection; ENTSO-E: Brussels, Belgium, 2018. [Google Scholar]
- European Commission. Commission Regulation (EU) 2016/631 of 14 April 2016 Establishing a Network Code on Requirements for Grid Connection of Generators (Text with EEA Relevance); European Commission: Brussels, Belgium, 2016. [Google Scholar]
- European Commission. Commission Regulation (EU) 2016/1447 of 26 August 2016 Establishing a Network Code on Requirements for Grid Connection of High Voltage Direct Current Systems and Direct Current-Connected Power Park Modules (Text with EEA Relevance); European Commission: Brussels, Belgium, 2016. [Google Scholar]
- European Commission. Commission Regulation (EU) 2016/1388 of 17 August 2016 Establishing a Network Code on Demand Connection; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- ENTSO-E. Rate of Change of Frequency (RoCoF) Withstand Capability ENTSO-E Guidance Document for National Implementation for Network Codes on Grid Connection; ENTSO-E: Brussels, Belgium, 2018. [Google Scholar]
- National Grid ESO. Operability Strategy Report; National Grid ESO: Warwick, UK, 2019. [Google Scholar]
- Energy Networks Association. The Accelerated Loss of Mains Change Programme: Stakeholder Event; National Grid ESO: Warwick, UK, 2019. [Google Scholar]
- You, S.; Liu, Y.; Tan, J.; Gonzalez, M.T.; Zhang, X.; Zhang, Y.; Liu, Y. Comparative Assessment of Tactics to Improve Primary Frequency Response Without Curtailing Solar Output in High Photovoltaic Interconnection Grids. IEEE Trans. Sustain. Energy 2019, 10, 718–728. [Google Scholar] [CrossRef]
- Sami, S.S.; Meng, C.; Jianzhong, W. Modelling and Control of Multi-Type Grid-Scale Energy Storage for Power System Frequency Response. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–25 May 2016; pp. 269–273. [Google Scholar]
- Knap, V.; Sinha, R.; Swierczynski, M.; Stroe, D.; Chaudhary, S. Grid Inertial Response with Lithium-Ion Battery Energy Storage Systems. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1817–1822. [Google Scholar]
- Eriksson, R.; Modig, N.; Elkington, K. Synthetic Inertia versus Fast Frequency Response: A Definition. IET Renew. Power Gener. 2017, 12. [Google Scholar] [CrossRef]
- Gao, Q.; Preece, R. Improving Frequency Stability in Low Inertia Power Systems Using Synthetic Inertia from Wind Turbines. In Proceedings of the 2017 IEEE Manchester PowerTech; IEEE: Manchester, UK, June 2017; pp. 1–6. [Google Scholar]
- Gonzalez-Longatt, F.M. Effects of the Synthetic Inertia from Wind Power on the Total System Inertia: Simulation Study; IEEE: Manchester, UK, 2012; p. 8. [Google Scholar]
- Gevorgian, V.; Koralewicz, P.J.; Villegas Pico, H.N.; Shah, S.D.; Wallen, R.B.; Corbus, D.A.; Keller, J.A.; Hovsapian, R.; Mohanpurkar, M.; Kadavi, R.; et al. WGRID-49 GMLC Project Report: Understanding the Role of Short-Term Energy Storage and Large Motor Loads for Active Power Controls by Wind Power; OSTI: Oak Ridge, TN, USA, 2019.
- Jiebei, Z.; Booth, C.D.; Adam, G.P.; Roscoe, A.J. Inertia Emulation Control of VSC-HVDC Transmission System. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection; IEEE: Beijing, China, 2011; pp. 1–6. [Google Scholar]
- Debbarma, S.; Hazarika, C.; Singh, K.M. Virtual Inertia Emulation from HVDC Transmission Links to Support Frequency Regulation in Presence of Fast Acting Reserve. In Proceedings of the 2018 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE), Meghalaya, India, 1–2 June 2018; pp. 1–6. [Google Scholar]
- Haileselassie, T.M.; Uhlen, K. Primary Frequency Control of Remote Grids Connected by Multi-Terminal HVDC. In Proceedings of the IEEE PES General Meeting; IEEE: Minneapolis, MN, USA, 2010; pp. 1–6. [Google Scholar]
- Gonzalez-Longatt, F.M. Activation Schemes of Synthetic Inertia Controller on Full Converter Wind Turbine (Type 4). In Proceedings of the 2015 IEEE Power & Energy Society General Meeting; IEEE: Denver, CO, USA, 2015; pp. 1–5. [Google Scholar]
- Chamorro, H.R.; Riaño, I.; Gerndt, R.; Zelinka, I.; Gonzalez-Longatt, F.; Sood, V.K. Synthetic Inertia Control Based on Fuzzy Adaptive Differential Evolution. Int. J. Electr. Power Energy Syst. 2019, 105, 803–813. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Malik, N.R.; Gonzalez-Longatt, F.; Sood, V.K. Evaluation of the Synthetic Inertia Control Using Active Damping Method. In Proceedings of the 2017 6th International Conference on Clean Electrical Power (ICCEP); IEEE: Santa Margherita Ligure, Italy, 2017; pp. 269–274. [Google Scholar]
- Chamorro, H.R.; Sanchez, A.C.; Overjordet, A.; Jimenez, F.; Gonzalez-Longatt, F.; Sood, V.K. Distributed Synthetic Inertia Control in Power Systems. In Proceedings of the 2017 International Conference on ENERGY and ENVIRONMENT (CIEM); IEEE: Bucharest, Hungary, 2017; pp. 74–78. [Google Scholar]
- Knap, V.; Chaudhary, S.K.; Stroe, D.; Swierczynski, M.; Craciun, B.; Teodorescu, R. Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency Reserve. IEEE Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Stenclik, D.; Richwine, M.; Miller, N.; Hong, L. The Role of Fast Frequency Response in Low Inertia Power Systems; CIGRE: Paris, France, 2018. [Google Scholar]
- EIRGRID. System Operator for Northern Ireland. RoCoF Modification Proposal—TSOs’ Recommendations; EIRGRID: Dublin, Ireland, 2012. [Google Scholar]
- Pourbeik, P. Simple Model Specification for Battery Energy Storage System; EPRI: Washington, DC, USA, 2015. [Google Scholar]
- Freris, L.L.; Sasson, A.M. Investigation of the Load-Flow Problem. Proc. Inst. Electr. Eng. 1968, 115, 1459–1470. [Google Scholar] [CrossRef]
- Report, I.C. Excitation System Models for Power System Stability Studies. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 494–509. [Google Scholar] [CrossRef]
- Report, I.C. Dynamic Models for Steam and Hydro Turbines in Power System Studies. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1904–1915. [Google Scholar] [CrossRef]
- Min, C.; Rincon-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I-V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]

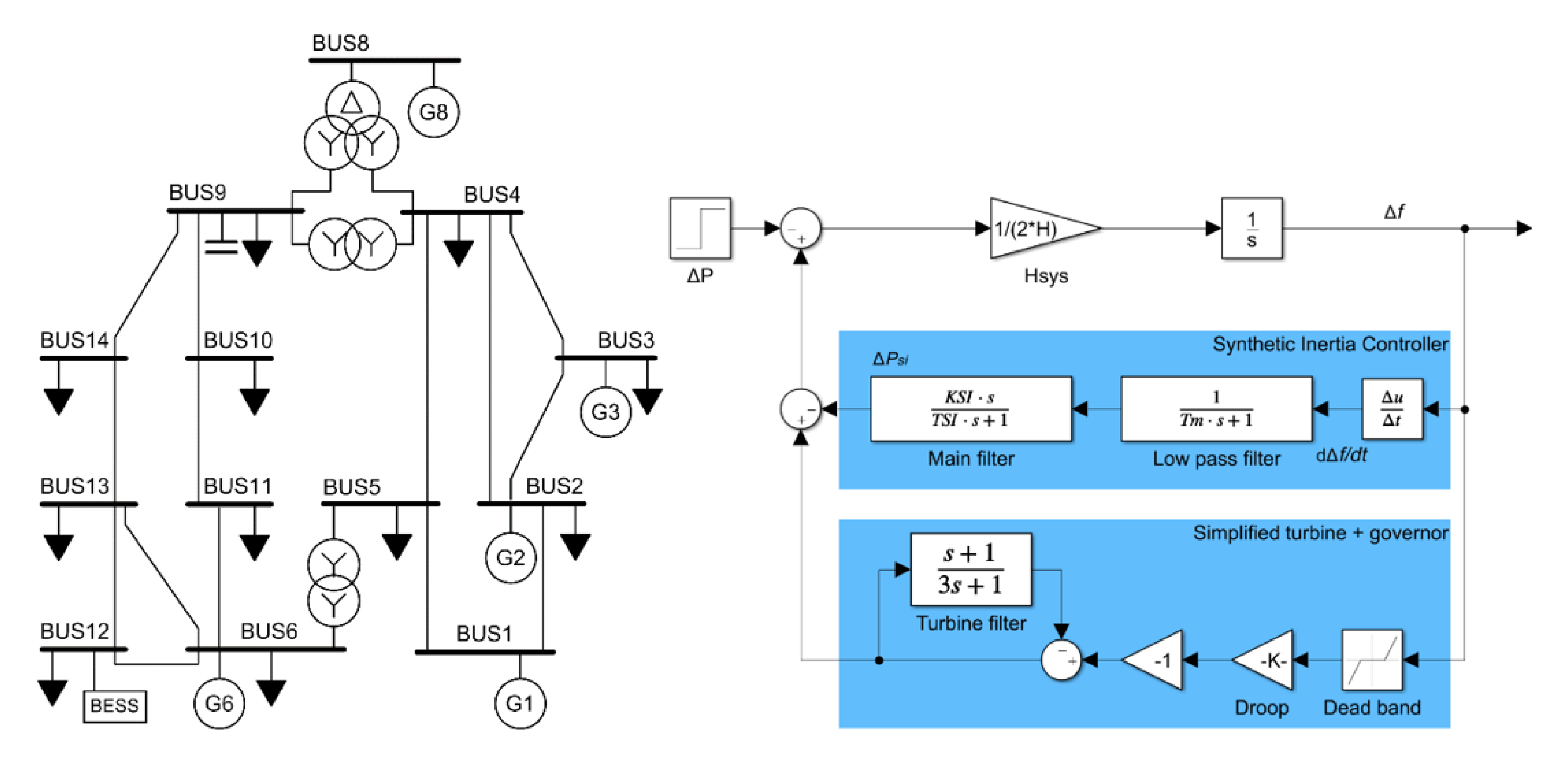

| Gen 1 | Gen 2 | Gen 3 | Gen 6 | Gen 8 | |
|---|---|---|---|---|---|
| Type | Synchronous | Synchronous | Synchronous | Wind | Wind |
| Rating [MVA]/Load [MW] | 200/50 | 220/30 | 160/117 | 72/49 | 100/77 |
| H [s] | 3.2 | 4.0 | 2.0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosmecki, M.; Rink, R.; Wakszyńska, A.; Ciavarella, R.; Di Somma, M.; Papadimitriou, C.N.; Efthymiou, V.; Graditi, G. A Methodology for Provision of Frequency Stability in Operation Planning of Low Inertia Power Systems. Energies 2021, 14, 737. https://doi.org/10.3390/en14030737
Kosmecki M, Rink R, Wakszyńska A, Ciavarella R, Di Somma M, Papadimitriou CN, Efthymiou V, Graditi G. A Methodology for Provision of Frequency Stability in Operation Planning of Low Inertia Power Systems. Energies. 2021; 14(3):737. https://doi.org/10.3390/en14030737
Chicago/Turabian StyleKosmecki, Michał, Robert Rink, Anna Wakszyńska, Roberto Ciavarella, Marialaura Di Somma, Christina N. Papadimitriou, Venizelos Efthymiou, and Giorgio Graditi. 2021. "A Methodology for Provision of Frequency Stability in Operation Planning of Low Inertia Power Systems" Energies 14, no. 3: 737. https://doi.org/10.3390/en14030737
APA StyleKosmecki, M., Rink, R., Wakszyńska, A., Ciavarella, R., Di Somma, M., Papadimitriou, C. N., Efthymiou, V., & Graditi, G. (2021). A Methodology for Provision of Frequency Stability in Operation Planning of Low Inertia Power Systems. Energies, 14(3), 737. https://doi.org/10.3390/en14030737











