Interval Load Flow for Uncertainty Consideration in Power Systems Analysis
Abstract
1. Introduction
2. Interval Arithmetic
3. Interval Load Flow
3.1. Algorithm Description
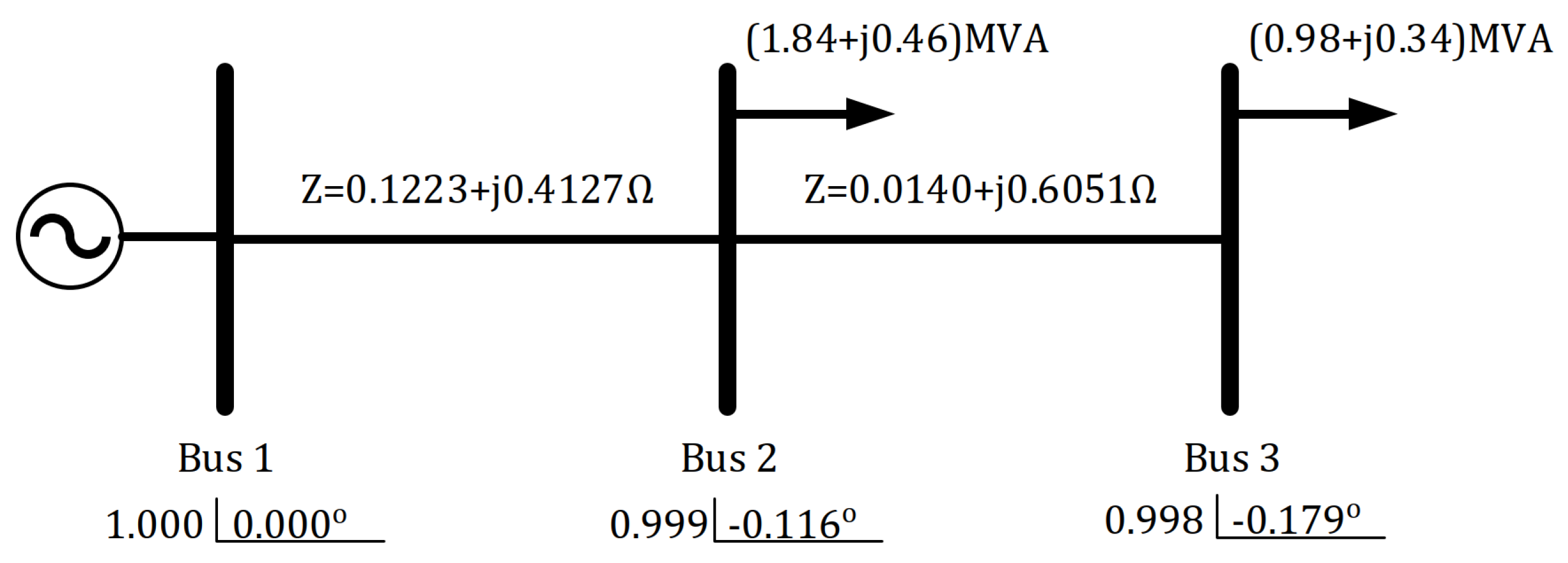
3.2. Illustrative Example
4. Probabilistic Load Flow
5. Test and Results
5.1. IEEE 34-Bus Radial TEST System
5.2. IEEE 69-Bus Distribution Network
5.3. 192-Bus Brazilian Distribution Network
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Monticelli, A.J. Fluxo de Carga em Redes de Energia Eletrica; Edgar Blucher Ltda: São Paulo, Brazil, 1983. [Google Scholar]
- Allan, R.N.; Al-Shakarchi, M.R.G. Probabilistic A.C. Load Flow. Proc. Inst. Electr. Eng. 1976, 123, 531–536. [Google Scholar] [CrossRef]
- Borkowska, B. Probabilistic Load Flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 752–759. [Google Scholar] [CrossRef]
- Primadianto, A.; Lu, C. A Review on Distribution System State Estimation. IEEE Trans. Power Syst. 2017, 32, 3875–3883. [Google Scholar] [CrossRef]
- de Oliveira, L.W.; Seta, F.D.S.; de Oliveira, E.J. Optimal reconfiguration of distribution systems with representation of uncertainties through interval analysis. Int. J. Electr. Power Energy Syst. 2016, 83, 382–391. [Google Scholar] [CrossRef]
- Pereira, L.; da Costa, V.; Rosa, A. Interval arithmetic in current injection power flow analysis. Int. J. Electr. Power Energy Syst. 2012, 43, 1106–1113. [Google Scholar] [CrossRef]
- Araujo, B.M.C.; da Costa, V.M. New Developments in the Interval Current Injection Power Flow Formulation. IEEE Latin Am. Trans. 2018, 16, 1969–1976. [Google Scholar] [CrossRef]
- Seta, F.d.S.; de Oliveira, L.W.; de Oliveira, E.J. Distribution System Planning with Representation of Uncertainties Based on Interval Analysis. J. Control Autom. Electr. Syst. 2020, 31, 494–510. [Google Scholar] [CrossRef]
- Del Monego, A.; Fernandes, T. Optimal Power Flow Analysis with Interval Mathematics-the Krawczyk Method. In Proceedings of the 12th Latin-American Congress on Electricity Generation and Transmission-Clagtee 2017, Mar del Plata, Argentina, 12–15 November 2017. [Google Scholar]
- Moore, R.E. Interval Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Mori, H.; Yuihara, A. Calculation of multiple power flow solutions with the Krawczyk method. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems (ISCAS), Orlando, FL, USA, 30 May–2 June 1999; Volume 5, pp. 94–97. [Google Scholar] [CrossRef]
- Rasmussen, T.B.; Yang, G.; Nielsen, A.H. Interval estimation of voltage magnitude in radial distribution feeder with minimal data acquisition requirements. Int. J. Electr. Power Energy Syst. 2019, 113, 281–287. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic Load Flow Evaluation With Hybrid Latin Hypercube Sampling and Cholesky Decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Fu, C.; Xu, Y.; Yang, Y.; Lu, K.; Gu, F.; Ball, A. Response analysis of an accelerating unbalanced rotating system with both random and interval variables. J. Sound Vib. 2020, 466, 115047. [Google Scholar] [CrossRef]
- Cheng, W.; Cheng, R.; Shi, J.; Zhang, C.; Sun, G.; Hua, D. Interval Power Flow Analysis Considering Interval Output of Wind Farms through Affine Arithmetic and Optimizing-Scenarios Method. Energies 2018, 11, 3176. [Google Scholar] [CrossRef]
- Luo, L.; Gu, W.; Wang, Y.; Chen, C. An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation. Energies 2017, 10, 1794. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z.; Dou, X.; Hu, M.; Xu, Y. Interval power flow analysis via multi-stage affine arithmetic for unbalanced distribution network. Electr. Power Syst. Res. 2017, 142, 1–8. [Google Scholar] [CrossRef]
- Wang, C.; Liu, D.; Tang, F.; Liu, C. A clustering-based analytical method for hybrid probabilistic and interval power flow. Int. J. Electr. Power Energy Syst. 2021, 126, 106605. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Shi, K.; Qiu, M.; Hua, D.; Ngan, H. An Interval Power Flow Analysis Through Optimizing-Scenarios Method. IEEE Trans. Smart Grid 2018, 9, 5217–5226. [Google Scholar] [CrossRef]
- Liao, X.; Liu, K.; Zhang, Y.; Wang, K.; Qin, L. Interval method for uncertain power flow analysis based on Taylor inclusion function. Transm. Distrib. IET Gener. 2017, 11, 1270–1278. [Google Scholar] [CrossRef]
- Liu, B.; Huang, Q.; Zhao, J.; Hu, W. A Computational Attractive Interval Power Flow Approach with Correlated Uncertain Power Injections. IEEE Trans. Power Syst. 2020, 35, 825–828. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Ngan, H.; Yang, P.; Hua, D. A Mixed Interval Power Flow Analysis Under Rectangular and Polar Coordinate System. IEEE Trans. Power Syst. 2017, 32, 1422–1429. [Google Scholar] [CrossRef]
- Tang, K.; Dong, S.; Zhu, C.; Song, Y. Affine Arithmetic-Based Coordinated Interval Power Flow of Integrated Transmission and Distribution Networks. IEEE Trans. Smart Grid 2020, 11, 4116–4132. [Google Scholar] [CrossRef]
- Wang, Z.; Alvarado, F.L. Interval arithmetic in power flow analysis. IEEE Trans. Power Syst. 1992, 7, 1341–1349. [Google Scholar] [CrossRef]
- Dimitrov, N.; Markov, S.; Popova, E. Extended interval arithmetics: New results and applications. In Computer Arithmetic and Enclosure Methods; North-Holland: Amsterdam, The Netherlands, 1992; pp. 225–232. [Google Scholar]
- Tinney, W.F.; Hart, C.E. Power Flow Solution by Newton’s Method. IEEE Trans. Power Appar. Syst. 1967, PAS-86, 1449–1460. [Google Scholar] [CrossRef]
- Dopazo, J.F.; Klitin, O.A.; Sasson, A.M. Stochastic load flows. IEEE Trans. Power Appar. Syst. 1975, 94, 299–309. [Google Scholar] [CrossRef]
- Allan, R.N.; Grigg, C.H.; Al-Shakarchi, M.R.G. Numerical techniques in probabilistic load flow problems. Int. J. Numer. Methods Eng. 1976, 10, 853–860. [Google Scholar] [CrossRef]
- Van Ness, J.E.; Griffin, J.H. Elimination Methods for Load-Flow Studies. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1961, 80, 299–302. [Google Scholar] [CrossRef]
- Prakash, D.; Lakshminarayana, C. Optimal siting of capacitors in radial distribution network using Whale Optimization Algorithm. Alex. Eng. J. 2017, 56, 499–509. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Brigatto, G.A. Modelo De Decisão Multiobjetivo Para a Busca De Estratégias Ótimas De Inserção De Empreendimentos Em Geração Distribuída. Ph.D. Thesis, Universidade Federal de Santa Catarina, Florianopolis, Brazil, 2011. [Google Scholar]




| Bus | Method | Lower Angle (°) | Upper Angle (°) | Deterministic Angle (°) |
|---|---|---|---|---|
| 5 | MCS | 0.23615 | 0.35810 | 0.31588 |
| ILF | 0.26275 | 0.36900 | ||
| 9 | MCS | 0.48285 | 0.67387 | 0.61611 |
| ILF | 0.53320 | 0.69891 | ||
| 23 | MCS | 0.70353 | 1.00872 | 0.90243 |
| ILF | 0.78490 | 1.01959 | ||
| 27 | MCS | 0.79289 | 1.13820 | 1.00895 |
| ILF | 0.88240 | 1.13499 | ||
| 33 | MCS | 0.52957 | 0.72857 | 0.66792 |
| ILF | 0.58067 | 0.75503 |
| Bus | Method | Lower Magnitude (p.u.) | Upper Magnitude (p.u.) | Deterministic Magnitude (p.u.) |
|---|---|---|---|---|
| 5 | MCS | 0.97556 | 0.97868 | 0.97603 |
| ILF | 0.97479 | 0.97729 | ||
| 9 | MCS | 0.96113 | 0.96639 | 0.96197 |
| ILF | 0.95999 | 0.96396 | ||
| 23 | MCS | 0.94417 | 0.95144 | 0.94601 |
| ILF | 0.94318 | 0.94885 | ||
| 27 | MCS | 0.93963 | 0.94997 | 0.94166 |
| ILF | 0.93861 | 0.94474 | ||
| 33 | MCS | 0.95896 | 0.96466 | 0.95992 |
| ILF | 0.95784 | 0.96201 |
| Bus | Method | Lower Angle (°) | Upper Angle (°) | Deterministic Angle (°) |
|---|---|---|---|---|
| 2 | MCS | −0.00140 | −0.00089 | −0.00122 |
| ILF | −0.00133 | −0.00223 | ||
| 29 | MCS | −0.00587 | −0.00421 | −0.00530 |
| ILF | −0.00578 | −0.00482 | ||
| 48 | MCS | −0.06559 | −0.03440 | −0.05247 |
| ILF | −0.05724 | −0.04770 | ||
| 54 | MCS | 0.00461 | 0.37110 | 0.19470 |
| ILF | 0.12409 | 0.26530 | ||
| 63 | MCS | 0.33813 | 187.126 | 112.526 |
| ILF | 0.90650 | 134.402 |
| Bus | Method | Lower Magnitude (p.u.) | Upper Magnitude (p.u.) | Deterministic Magnitude (p.u.) |
|---|---|---|---|---|
| 2 | MCS | 0.99996 | 0.99997 | 0.99996 |
| ILF | 0.99996 | 0.99997 | ||
| 29 | MCS | 0.99984 | 0.99987 | 0.99985 |
| ILF | 0.99984 | 0.99986 | ||
| 48 | MCS | 0.99840 | 0.99883 | 0.99854 |
| ILF | 0.99847 | 0.99980 | ||
| 54 | MCS | 0.96770 | 0.97738 | 0.97141 |
| ILF | 0.96985 | 0.97296 | ||
| 63 | MCS | 0.89464 | 0.93411 | 0.91165 |
| ILF | 0.90679 | 0.91652 |
| Bus | Method | Lower Angle (°) | Upper Angle (°) | Deterministic Angle (°) |
|---|---|---|---|---|
| 8 | MCS | −0.24610 | −0.21364 | −0.24170 |
| ILF | −0.27692 | −0.20648 | ||
| 36 | MCS | −0.90111 | −0.76996 | −0.87943 |
| ILF | −100.956 | −0.75299 | ||
| 64 | MCS | −0.44769 | −0.38699 | −0.43892 |
| ILF | −0.50307 | −0.37477 | ||
| 113 | MCS | −0.86144 | −0.73693 | −0.84702 |
| ILF | −0.97206 | −0.72197 | ||
| 187 | MCS | −0.91812 | −0.78600 | −0.89612 |
| ILF | −102.858 | −0.76365 |
| Bus | Method | Lower Magnitude (p.u.) | Upper Magnitude (p.u.) | Deterministic Magnitude (p.u.) |
|---|---|---|---|---|
| 8 | MCS | 0.98727 | 0.98888 | 0.98795 |
| ILF | 0.98732 | 0.99176 | ||
| 36 | MCS | 0.95602 | 0.96027 | 0.95686 |
| ILF | 0.95461 | 0.95911 | ||
| 64 | MCS | 0.97824 | 0.97994 | 0.97827 |
| ILF | 0.97713 | 0.97939 | ||
| 113 | MCS | 0.95754 | 0.96171 | 0.95849 |
| ILF | 0.95632 | 0.96066 | ||
| 187 | MCS | 0.95603 | 0.95959 | 0.95612 |
| ILF | 0.95612 | 0.95842 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nogueira, W.C.; Garcés Negrete, L.P.; López-Lezama, J.M. Interval Load Flow for Uncertainty Consideration in Power Systems Analysis. Energies 2021, 14, 642. https://doi.org/10.3390/en14030642
Nogueira WC, Garcés Negrete LP, López-Lezama JM. Interval Load Flow for Uncertainty Consideration in Power Systems Analysis. Energies. 2021; 14(3):642. https://doi.org/10.3390/en14030642
Chicago/Turabian StyleNogueira, Wallisson C., Lina Paola Garcés Negrete, and Jesús M. López-Lezama. 2021. "Interval Load Flow for Uncertainty Consideration in Power Systems Analysis" Energies 14, no. 3: 642. https://doi.org/10.3390/en14030642
APA StyleNogueira, W. C., Garcés Negrete, L. P., & López-Lezama, J. M. (2021). Interval Load Flow for Uncertainty Consideration in Power Systems Analysis. Energies, 14(3), 642. https://doi.org/10.3390/en14030642









