An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand
Abstract
1. Introduction
- Proposing a novel operation and management framework for the reconfigurable microgrids considering the high penetration of HEVs (with two different charging schemes) and renewable energy sources;
- Developing a novel hybrid prediction model based on SVR and MDA for accurate estimation of the total charging demand of HEVs in the microgrid;
- Proposing a new optimization method based on DA and a three phase modification method to enhance its search ability for the optimization applications.
2. Machine Learning Based Policy Development and Energy Management Framework
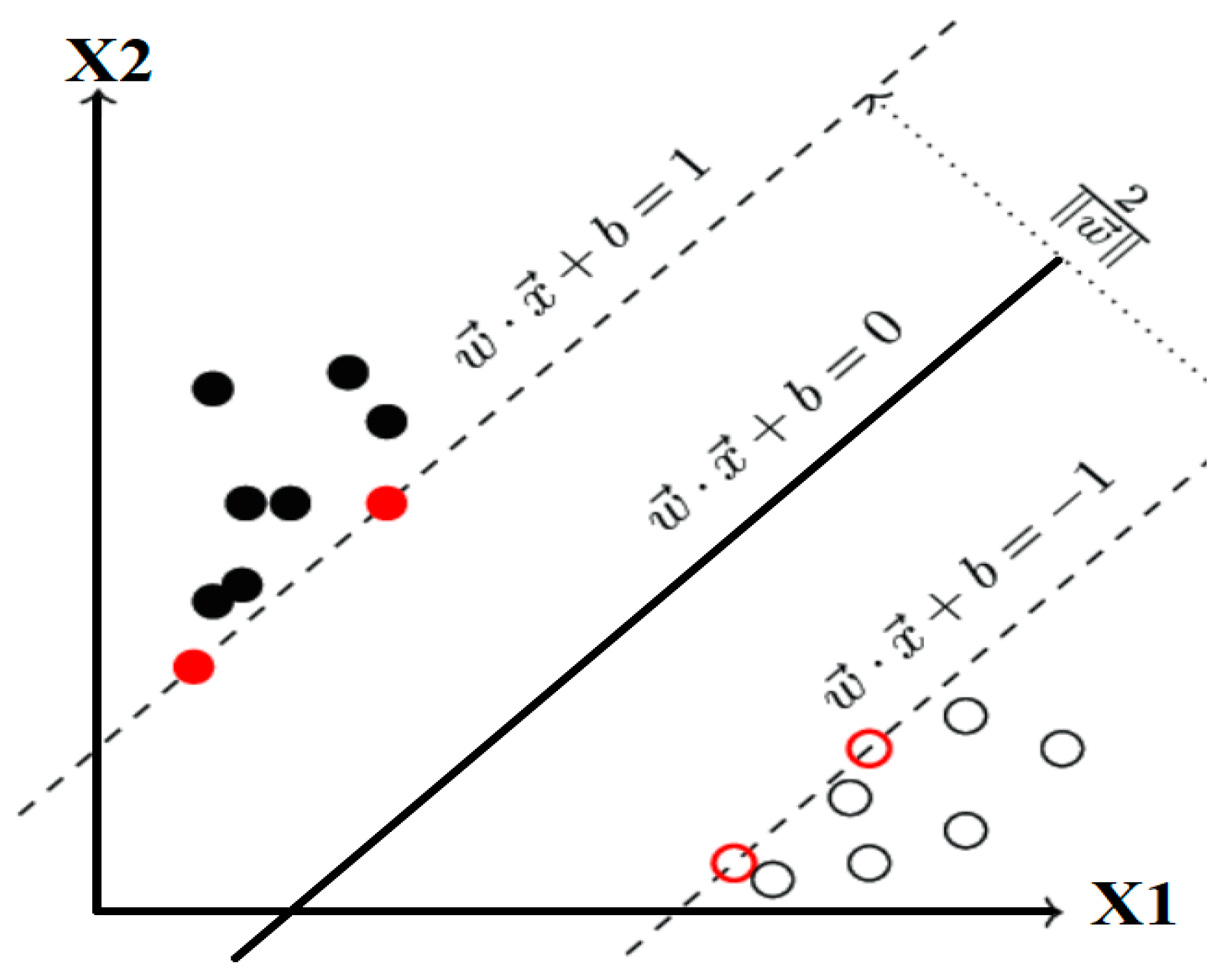
2.1. Machine Learning Based on SVR
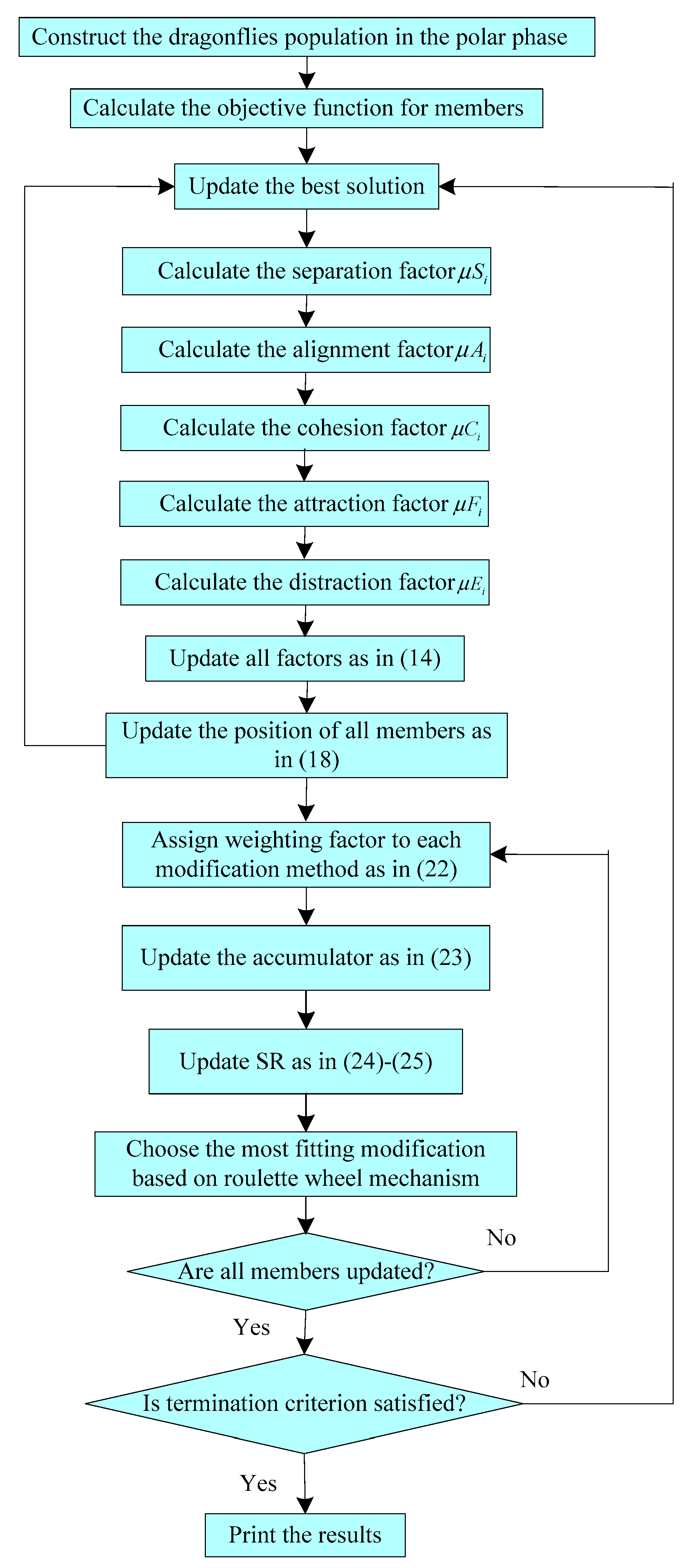
2.2. Improved Optimization Based on MDA
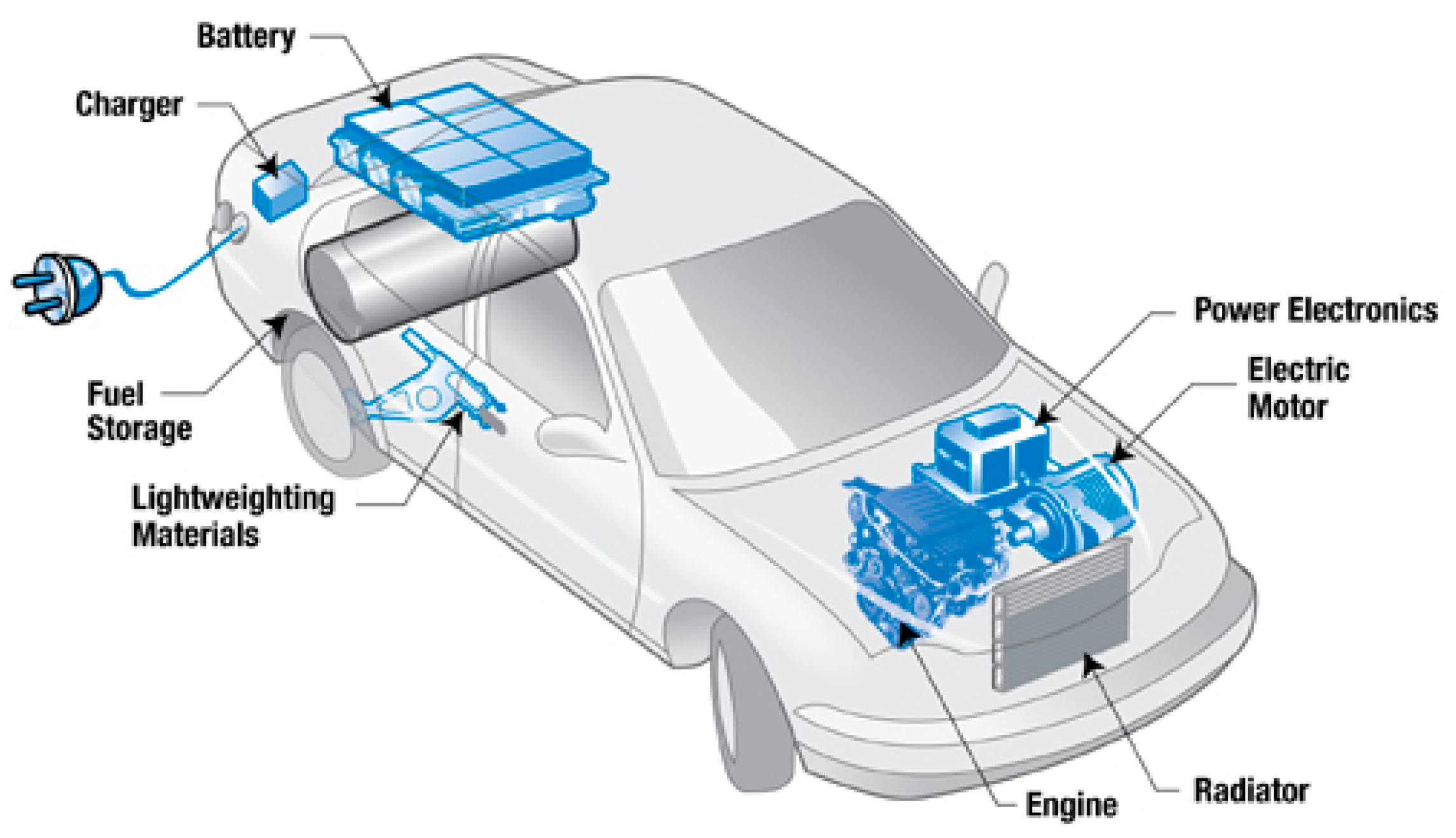
3. Charging Modeling of HEVs
4. Problem Formulations
- -
- Active and reactive power limit of DGs:
- -
- Ramp up/down limits:
- -
- Minimum up and down time limit:
- -
- Charging/discharging limit of battery storage:
- -
- Adjustable load demand:
- -
- Bus voltage limit:
- -
- Main grid power limit:
- -
- Reconfiguration using the remote switches:Optimal switching is a strategic tool for altering the power flow path in the microgrid using the tie (normal open) switches and sectionalizing (normal closed). To this end the binary variable is used, which can get 0 and 1 to show the closed or open status of a line:
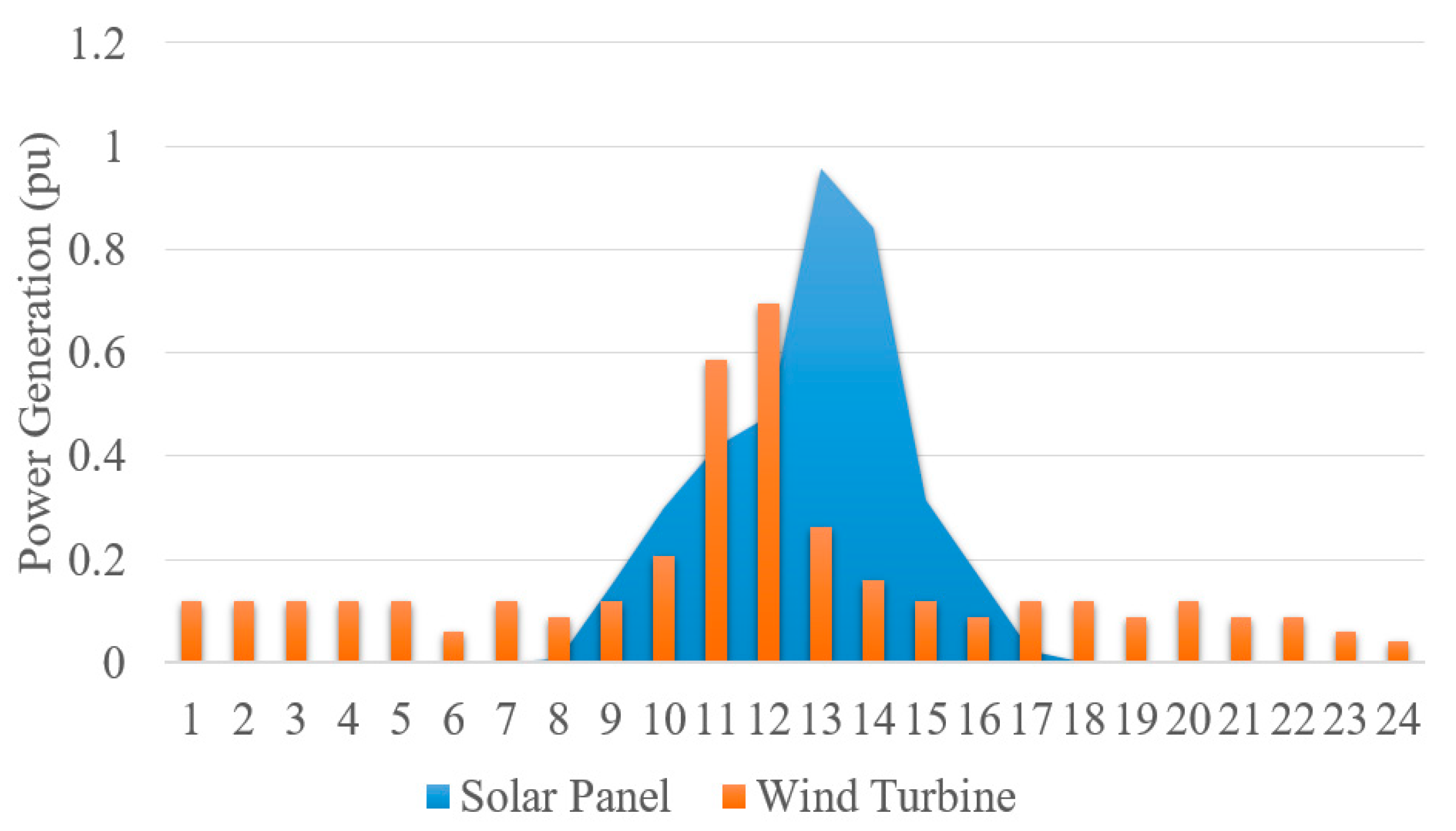
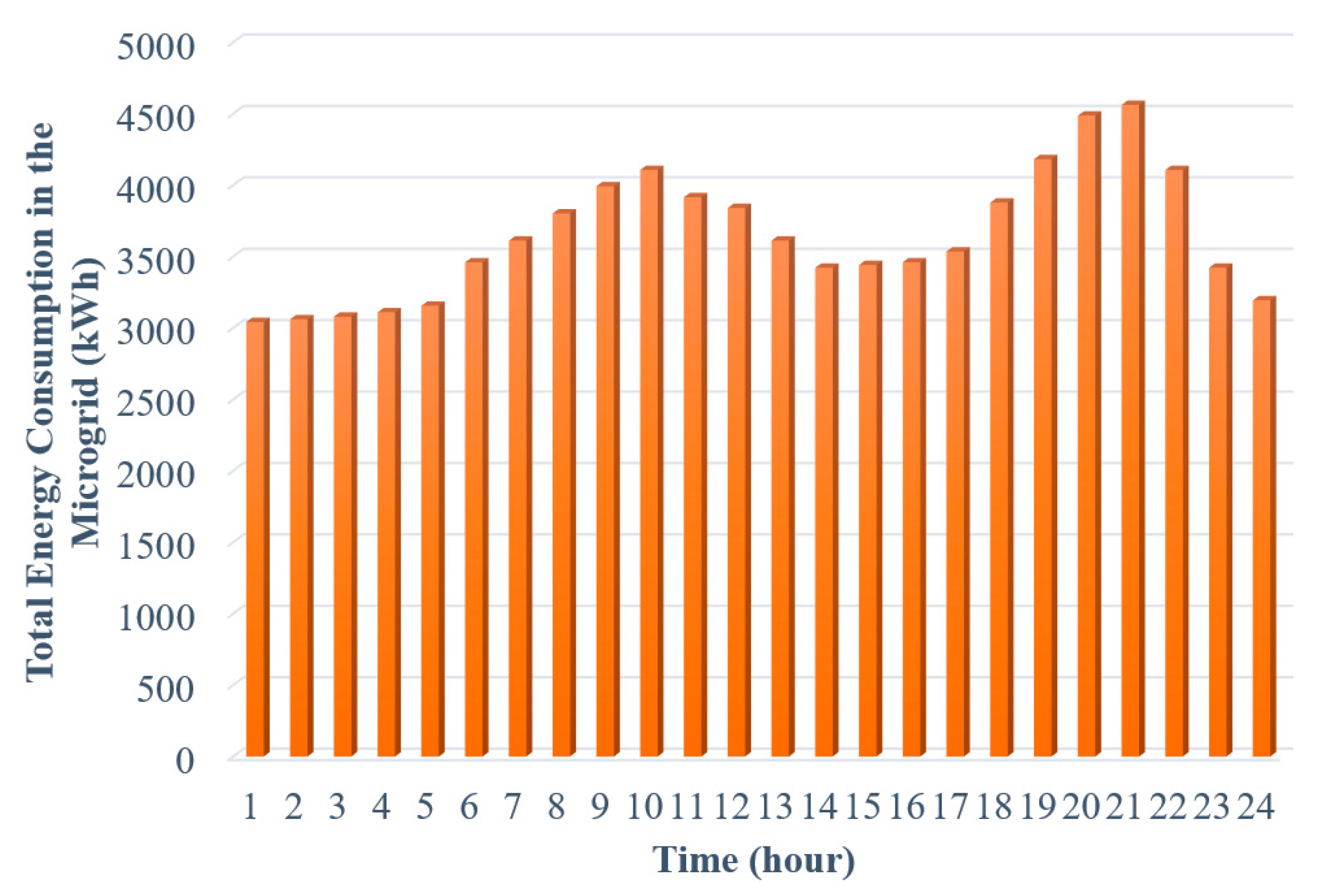
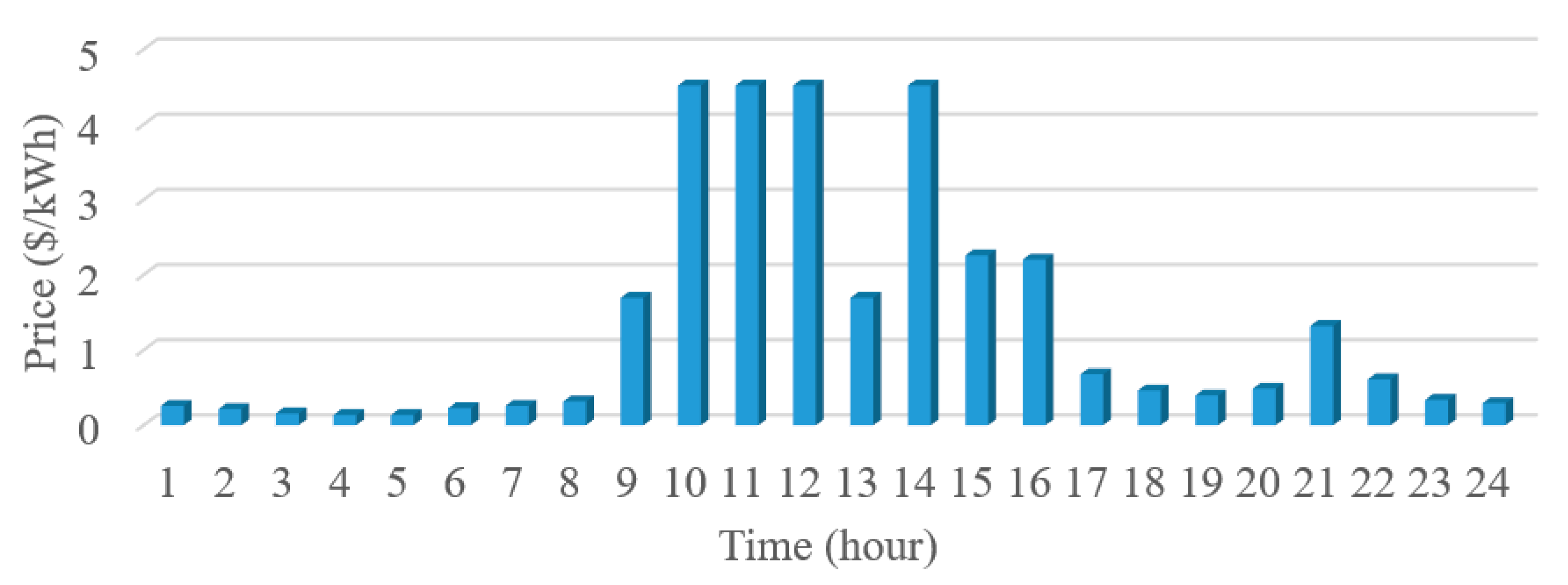
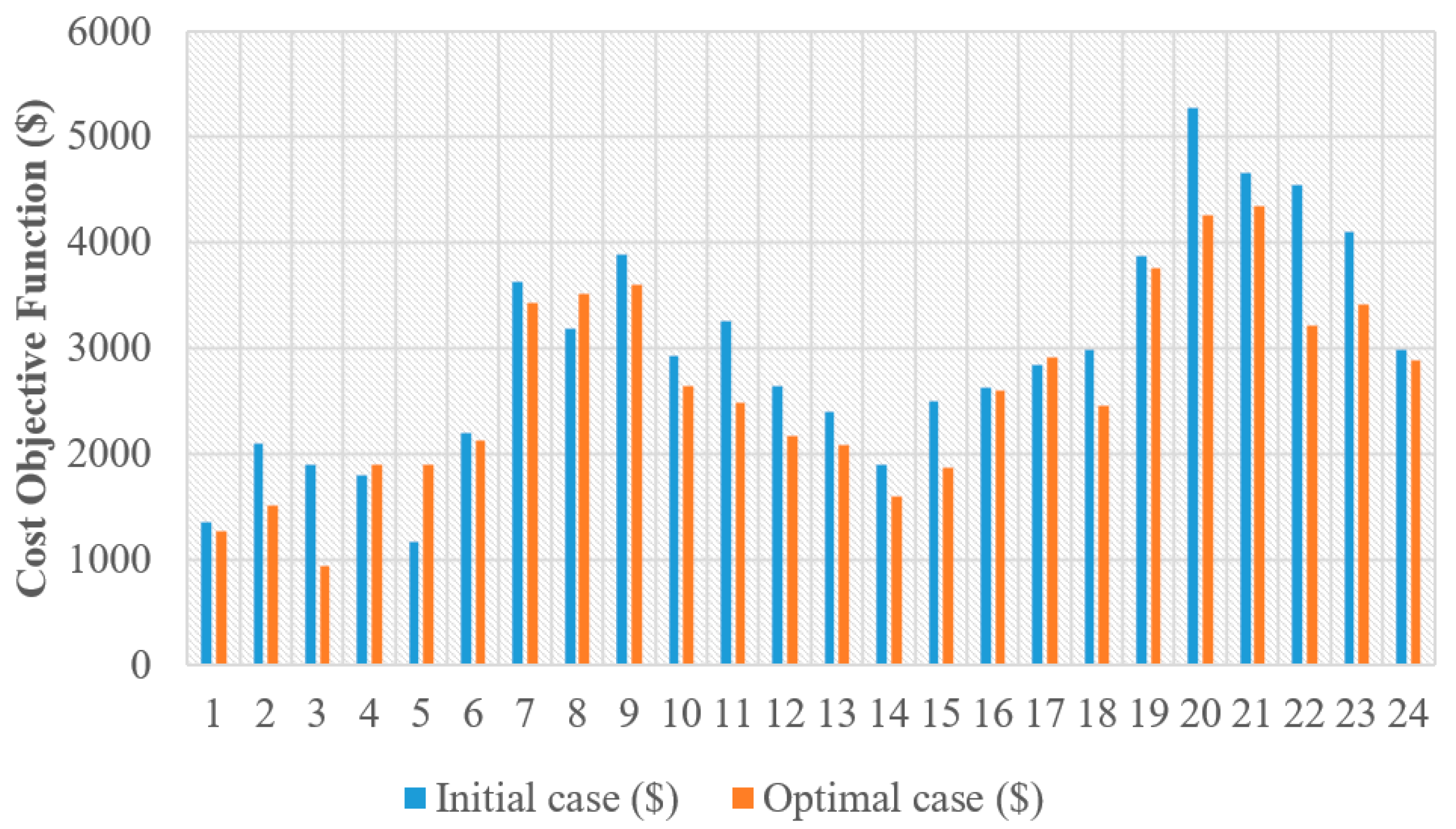
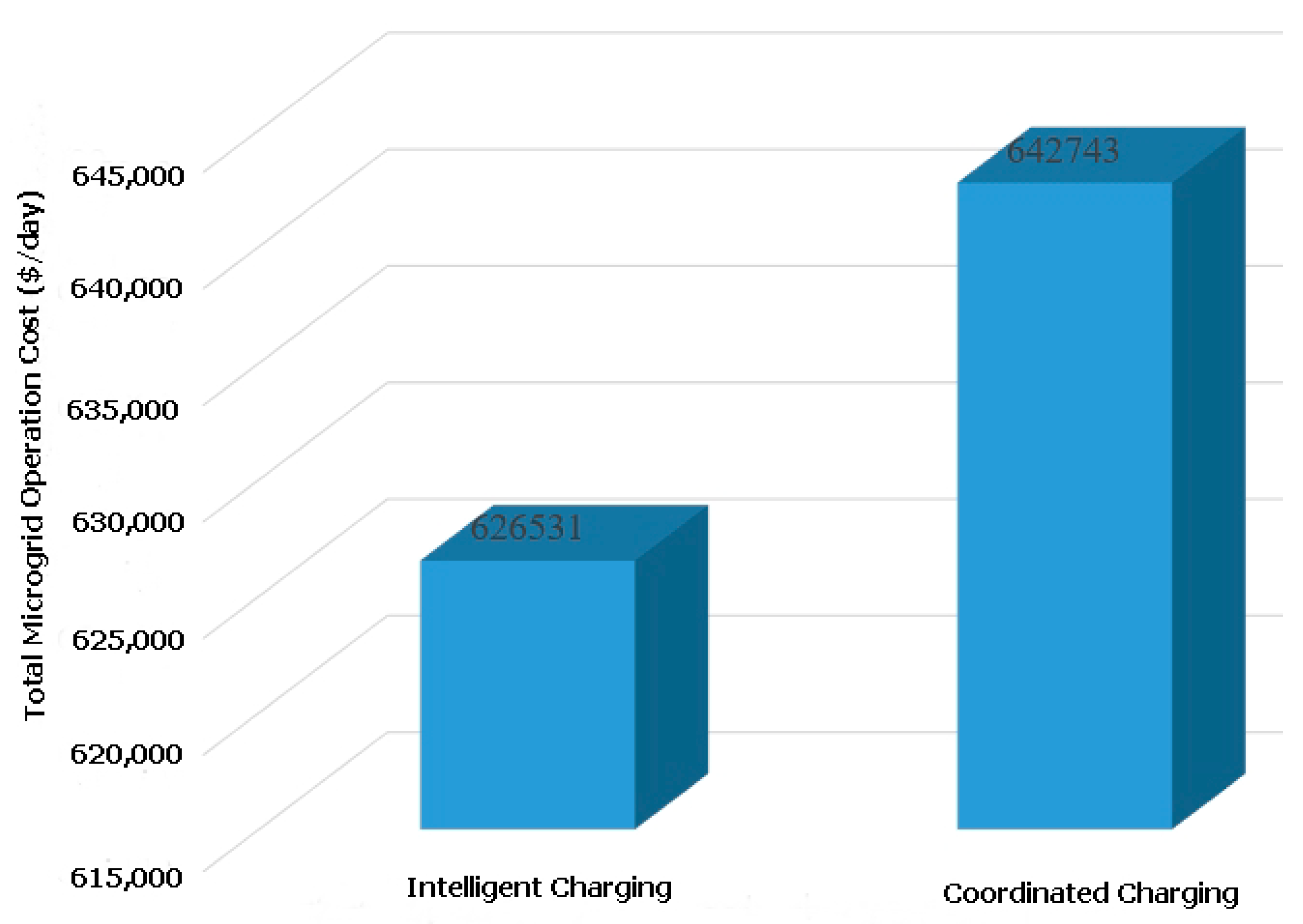
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Amount of energy stored in mth storage at time t | |
| Capacity of battery in HEVs | |
| Minimum charging time | |
| Depth of discharge in HEVs | |
| Minimum down time limits for DG | |
| Minimum discharging time for storage | |
| Eloc | The enemy’s scene |
| Total energy required by the adjustable load | |
| ER | Total electric range in HEVs |
| Floc | Location of the nourishment basis |
| Current flow in line between the buses n and m | |
| Iter | Iteration number. |
| m | Distance passed by HEVs |
| Min/max of battery capacity in HEVs | |
| N | Number of population |
| Nv | Number of forecast samples for Charging demand of HEVs |
| Battery charging power rate | |
| Power generation by DG. | |
| Amount of power generated by the main grid | |
| Amount of power charging demand of HEV | |
| and | Amount of active and reactive power generated by mth DG at time t |
| Charging power of storage | |
| Discharging power of the storage | |
| Load demand on but m at time t | |
| Active power flow on line connecting buses l to m | |
| and | Active and reactive load demand on bus m |
| Amount of power generated/consumed by the main grid at time t | |
| s, a, c, f, and e | Weighting factor for the relevant motivation factors |
| r | Random value |
| and | Ramp up and down limits for mth DG |
| Resistance connecting buses m and n | |
| ri | Random number in the range [0,1] |
| s | Indicator of modification |
| Set of modification | |
| SoC | Depth of discharge in HEVs |
| tstart | Starting time for the charging |
| tD | Charging length for HEVs |
| Minimum up time of the load | |
| Minimum up time limits for DG | |
| vj | Speed of the neighbor |
| Voltage value of bus m | |
| Line status, 0 or 1 | |
| ON/OFF status of the DG | |
| Forecast/real value of the total charging demand sample of HEV | |
| Charging status of the battery | |
| Discharging status of the battery | |
| ON/OFF status of the load demand | |
| Fictional current flow of distribution lines | |
| Fictional current flow of utility grid | |
| Fictional current flow demand | |
| Charging efficiency in HEVs | |
| Cost of power purchasing from the DG | |
| Cost of power purchasing from the main grid | |
| Time interval (here 1 h) | |
| ith solution in the DA | |
| / | Mean/standard deviation of battery in HEVs |
| Set of buses with installed DG | |
| Set of operation time horizon (here 24 h) | |
| Set of lines | |
| Charging efficiency | |
| Discharging efficiency |
Appendix A
| Branch No. | From Bus | To Bus | R (ohm) | X (ohm) |
|---|---|---|---|---|
| 1 | 1 | 2 | 0.0005 | 0.0012 |
| 2 | 2 | 3 | 0.0005 | 0.0012 |
| 3 | 3 | 4 | 0.0015 | 0.0036 |
| 4 | 4 | 5 | 0.0251 | 0.0294 |
| 5 | 5 | 6 | 0.366 | 0.1864 |
| 6 | 6 | 7 | 0.3811 | 0.1941 |
| 7 | 7 | 8 | 0.0922 | 0.0470 |
| 8 | 8 | 9 | 0.0493 | 0.0251 |
| 9 | 9 | 10 | 0.8190 | 0.2707 |
| 10 | 10 | 11 | 0.1872 | 0.0691 |
| 11 | 11 | 12 | 0.7114 | 0.2351 |
| 12 | 12 | 13 | 1.0300 | 0.3400 |
| 13 | 13 | 14 | 1.0440 | 0.3450 |
| 14 | 14 | 15 | 1.0580 | 0.3496 |
| 15 | 15 | 16 | 0.1966 | 0.0650 |
| 16 | 16 | 17 | 0.3744 | 0.1238 |
| 17 | 17 | 18 | 0.0047 | 0.0016 |
| 18 | 18 | 19 | 0.3276 | 0.1083 |
| 19 | 19 | 20 | 0.2106 | 0.0696 |
| 20 | 20 | 21 | 0.3416 | 0.1129 |
| 21 | 21 | 22 | 0.0140 | 0.0046 |
| 22 | 22 | 23 | 0.1591 | 0.0526 |
| 23 | 23 | 24 | 0.3463 | 0.1145 |
| 24 | 24 | 25 | 0.7488 | 0.2745 |
| 25 | 25 | 26 | 0.3089 | 0.1021 |
| 26 | 26 | 27 | 0.2732 | 0.0572 |
| 27 | 3 | 28 | 0.0044 | 0.0108 |
| 28 | 28 | 29 | 0.0640 | 0.1565 |
| 29 | 29 | 30 | 0.3978 | 0.1315 |
| 30 | 30 | 31 | 0.0702 | 0.0232 |
| 31 | 31 | 32 | 0.3510 | 0.1160 |
| 32 | 32 | 33 | 0.839 | 0.2816 |
| 33 | 33 | 34 | 1.7080 | 0.5646 |
| 34 | 34 | 35 | 1.474 | 0.4673 |
| 35 | 3 | 36 | 0.0044 | 0.0108 |
| 36 | 36 | 37 | 0.0640 | 0.1565 |
| 37 | 37 | 38 | 0.1053 | 0.1430 |
| 38 | 38 | 39 | 0.0304 | 0.0355 |
| 39 | 39 | 40 | 0.0018 | 0.0021 |
| 40 | 40 | 41 | 0.7283 | 0.8509 |
| 41 | 41 | 42 | 0.310 | 0.3623 |
| 42 | 42 | 43 | 0.0410 | 0.0478 |
| 43 | 43 | 44 | 0.0092 | 0.0116 |
| 44 | 44 | 45 | 0.1089 | 0.1373 |
| 45 | 45 | 46 | 0.0009 | 0.0012 |
| 46 | 4 | 47 | 0.0034 | 0.0084 |
| 47 | 47 | 48 | 0.0851 | 0.2083 |
| 48 | 48 | 49 | 0.2898 | 0.7091 |
| 49 | 49 | 50 | 0.0822 | 0.2011 |
| 50 | 8 | 51 | 0.0928 | 0.0473 |
| 51 | 51 | 52 | 0.3319 | 0.1114 |
| 52 | 9 | 53 | 0.1740 | 0.0886 |
| 53 | 53 | 54 | 0.2030 | 0.1034 |
| 54 | 54 | 55 | 0.2842 | 0.1447 |
| 55 | 55 | 56 | 0.2813 | 0.1433 |
| 56 | 56 | 57 | 1.5900 | 0.5337 |
| 57 | 57 | 58 | 0.7837 | 0.2630 |
| 58 | 58 | 59 | 0.3042 | 0.1006 |
| 59 | 59 | 60 | 0.3861 | 0.1172 |
| 60 | 60 | 61 | 0.5075 | 0.2585 |
| 61 | 61 | 62 | 0.0974 | 0.0496 |
| 62 | 62 | 63 | 0.1450 | 0.0738 |
| 63 | 63 | 64 | 0.7105 | 0.3619 |
| 64 | 64 | 65 | 1.0410 | 0.5302 |
| 65 | 11 | 66 | 0.2012 | 0.0611 |
| 66 | 66 | 67 | 0.0047 | 0.0014 |
| 67 | 12 | 68 | 0.7394 | 0.2444 |
| 68 | 38 | 69 | 0.0047 | 0.0016 |
| Bus No. | Active Power (kW) | Reactive Power (kVar) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 2.60 | 2.2 |
| 7 | 40.4 | 30 |
| 8 | 75 | 54 |
| 9 | 30 | 22 |
| 10 | 28 | 19 |
| 11 | 145 | 104 |
| 12 | 145 | 104 |
| 13 | 8 | 5.50 |
| 14 | 8 | 5.50 |
| 15 | 0 | 0 |
| 16 | 45.50 | 30 |
| 17 | 60 | 35 |
| 18 | 60 | 35 |
| 19 | 0 | 0 |
| 20 | 1 | 0.60 |
| 21 | 114 | 81 |
| 22 | 5.30 | 3.50 |
| 23 | 0 | 0 |
| 24 | 28 | 20 |
| 25 | 0 | 0 |
| 26 | 14 | 10 |
| 27 | 14 | 10 |
| 28 | 26 | 18.6 |
| 29 | 26 | 18.6 |
| 30 | 0 | 0 |
| 31 | 0 | 0 |
| 32 | 0 | 0 |
| 33 | 14 | 10 |
| 34 | 19.5 | 14 |
| 35 | 6 | 4 |
| 36 | 26 | 18.55 |
| 37 | 26 | 18.55 |
| 38 | 0 | 0 |
| 39 | 24 | 17 |
| 40 | 24 | 17 |
| 41 | 1.2 | 1 |
| 42 | 0 | 0 |
| 43 | 6 | 4.3 |
| 44 | 0 | 0 |
| 45 | 39.22 | 26.3 |
| 46 | 39.22 | 26.3 |
| 47 | 0 | 0 |
| 48 | 79 | 56.4 |
| 49 | 384.7 | 274.5 |
| 50 | 384.7 | 274.5 |
| 51 | 40.5 | 28.3 |
| 52 | 3.6 | 2.7 |
| 53 | 4.35 | 3.5 |
| 54 | 26.4 | 19 |
| 55 | 24 | 17.2 |
| 56 | 0 | 0 |
| 57 | 0 | 0 |
| 58 | 0 | 0 |
| 59 | 100 | 72 |
| 60 | 0 | 0 |
| 61 | 1244 | 888 |
| 62 | 32 | 23 |
| 63 | 0 | 0 |
| 64 | 227 | 162 |
| 65 | 59 | 42 |
| 66 | 18 | 13 |
| 67 | 18 | 13 |
| 68 | 28 | 20 |
| 69 | 28 | 20 |
References
- Shayeghi, H.; Shahryari, E.; Moradzadeh, M.; Siano, P. A survey on microgrid energy management considering flexible energy sources. Energies 2019, 12, 2156. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Abdullah, H.M.; Al-Sumaiti, A.S.; El-Meligy, M.A.; Sharaf, M.; Soliman, A.T. Towards Energy Management Negotiation between Distributed AC/DC Networks. IEEE Access 2020, 8, 215438–215456. [Google Scholar] [CrossRef]
- Gong, X.; Dong, F.; Mohamed, M.A.; Awwad, E.M.; Abdullah, H.M.; Ali, Z.M. Towards distributed based energy transaction in a clean smart island. J. Clean. Prod. 2020, 273, 122768. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Guerrero, J.M. Hybrid machine intelligent SVR variants for wind forecasting and ramp events. Renew. Sustain. Energy Rev. 2019, 108, 369–379. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Zhu, C.; Yang, Y.; Abdullah, H.M.; Mohamed, M.A. Stochastic management of hybrid AC/DC microgrids considering electric vehicles charging demands. Energy Rep. 2020, 6, 1338–1352. [Google Scholar] [CrossRef]
- Rezaei, M.; Naghdi-Khozani, N.; Jafari, N. Wind energy utilization for hydrogen production in an underdeveloped country: An economic investigation. Renew. Energy 2020, 147, 1044–1057. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, Y.S.; El-Sayed, A.H.M.; Mohamed, M.A.; Elghaffar, A.N.A. Power Quality and Reliability Considerations of Photovoltaic Distributed Generation. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 1–21. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Jin, T.; Su, W. Multi-agent energy management of smart islands using primal-dual method of multipliers. Energy 2020, 208, 118306. [Google Scholar] [CrossRef]
- Duan, Q.; Quynh, N.V.; Abdullah, H.M.; Almalaq, A.; Duc Do, T.; Abdelkader, S.M.; Mohamed, M.A. Optimal Scheduling and Management of a Smart City Within the Safe Framework. IEEE Access 2020, 8, 161847–161861. [Google Scholar] [CrossRef]
- Wang, R.; Hsu, S.-C.; Zheng, S.; Chen, J.-H.; Li, X.I. Renewable energy microgrids: Economic evaluation and decision making for government policies to contribute to affordable and clean energy. Appl. Energy 2020, 274, 115287. [Google Scholar] [CrossRef]
- Qamar, S.B.; Janajreh, I. Renewable energy sources for isolated self-sufficient microgrids: Comparison of solar and wind energy for UAE. Energy Procedia 2016, 103, 413–418. [Google Scholar] [CrossRef]
- Fioriti, D.; Poli, D. A novel stochastic method to dispatch microgrids using Monte Carlo scenarios. Electr. Power Syst. Res. 2019, 175, 105896. [Google Scholar] [CrossRef]
- Geng, S.; Vrakopoulou, M.; Hiskens, I.A. Chance-constrained optimal capacity design for a renewable-only islanded microgrid. Electr. Power Syst. Res. 2020, 189, 106564. [Google Scholar] [CrossRef]
- Liu, J.; Jia, R.; Li, W.; Ma, F.; Abdullah, H.M.; Ma, H.; Mohamed, M.A. High precision detection algorithm based on improved RetinaNet for defect recognition of transmission lines. Energy Rep. 2020, 6, 2430–2440. [Google Scholar] [CrossRef]
- Kumar, J.; Agarwal, A.; Singh, N. Design, operation and control of a vast DC microgrid for integration of renewable energy sources. Renew. Energy Focus 2020, 34, 17–36. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Balas, V.E. Supervised Machine Learning in Wind Forecasting and Ramp Event Prediction; Academic Press: New York, NY, USA, 2020. [Google Scholar]
- Dey, B.; Roy, S.K.; Bhattacharyya, B. Solving multi-objective economic emission dispatch of a renewable integrated microgrid using latest bio-inspired algorithms. Eng. Sci. Technol. Int. J. 2019, 22, 55–66. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Jin, T.; Su, W. An effective stochastic framework for smart coordinated operation of wind park and energy storage unit. Appl. Energy 2020, 272, 115228. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Han, Y.; Zhao, Q. Coordination dispatch of electric vehicles charging/discharging and renewable energy resources power in microgrid. Procedia Comput. Sci. 2017, 107, 157–163. [Google Scholar] [CrossRef]
- Gong, X.; Dong, F.; Mohamed, M.A.; Abdalla, O.M.; Ali, Z.M. A secured energy management architecture for smart hybrid microgrids considering PEM-fuel cell and electric vehicles. IEEE Access 2020, 8, 47807–47823. [Google Scholar] [CrossRef]
- Al-Saud, M.; Eltamaly, A.M.; Mohamed, M.A.; Kavousi-Fard, A. An intelligent data-driven model to secure intravehicle communications based on machine learning. IEEE Trans. Ind. Electron. 2019, 67, 5112–5119. [Google Scholar] [CrossRef]
- Patel, P.; Shandilya, A.; Deb, D. Optimized hybrid wind power generation with forecasting algorithms and battery life considerations. In Proceedings of the 2017 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 23–24 February 2017; pp. 1–6. [Google Scholar]
- Osório, G.J.; Shafie-khah, M.; Coimbra, P.D.L.; Lotfi, M.; Catalão, J.P.S. Distribution system operation with electric vehicle charging schedules and renewable energy resources. Energies 2018, 11, 3117. [Google Scholar] [CrossRef]
- Mortaz, E.; Valenzuela, J. Optimizing the size of a V2G parking deck in a microgrid. Int. J. Electr. Power Energy Syst. 2018, 97, 28–39. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Almalaq, A.; Awwad, E.M.; El-Meligy, M.A.; Sharaf, M.; Ali, Z.M. A modified balancing approach for renewable based microgrids using deep adversarial learning. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- Kavousi-Fard, A. Modeling uncertainty in tidal current forecast using prediction interval-based SVR. IEEE Trans. Sustain. Energy 2016, 8, 708–715. [Google Scholar] [CrossRef]
- Li, J.; Lu, J.; Yao, L.; Cheng, L.; Qin, H. Wind-Solar-Hydro power optimal scheduling model based on multi-objective dragonfly algorithm. Energy Procedia 2019, 158, 6217–6224. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Almalaq, A.; Awwad, E.M.; El-Meligy, M.A.; Sharaf, M.; Ali, Z.M. An effective energy management approach within a smart island considering water-energy hub. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Chabok, H.; Awwad, E.M.; El-Sherbeeny, A.M.; Elmeligy, M.A.; Ali, Z.M. Stochastic and distributed scheduling of shipboard power systems using MθFOA-ADMM. Energy 2020, 206, 118041. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A. Optimal sizing and designing of hybrid renewable energy systems in smart grid applications. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 231–313. [Google Scholar]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, S.; Wei, R. Support vector machine with composite kernels for time series prediction. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2007; pp. 350–356. [Google Scholar]
- Acı, Ç.İ.; Gülcan, H. A Modified Dragonfly Optimization Algorithm for Single and Multiobjective Problems Using Brownian Motion. Comput. Intell. Neurosci. 2019, 2019, 6871298. [Google Scholar] [CrossRef]
- Khalil, H.A.; Darwish, S.; Ibrahim, Y.M.; Hassan, O.F. 3D-MRI Brain Tumor Detection Model Using Modified Version of Level Set Segmentation Based on Dragonfly Algorithm. Symmetry 2020, 12, 1256. [Google Scholar] [CrossRef]
- Avatefipour, O.; Al-Sumaiti, A.S.; El-Sherbeeny, A.M.; Awwad, E.M.; Elmeligy, M.A.; Mohamed, M.A.; Malik, H. An intelligent secured framework for cyberattack detection in electric vehicles’ CAN bus using machine learning. IEEE Access 2019, 7, 127580–127592. [Google Scholar] [CrossRef]
- Rostami, M.-A.; Kavousi-Fard, A.; Niknam, T. Expected cost minimization of smart grids with plug-in hybrid electric vehicles using optimal distribution feeder reconfiguration. IEEE Trans. Ind. Inform. 2015, 11, 388–397. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Tajik, E.; Awwad, E.M.; El-Sherbeeny, A.M.; Elmeligy, M.A.; Ali, Z.M. A two-stage stochastic framework for effective management of multiple energy carriers. Energy 2020, 197, 117170. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Muresan, V.; Balas, V.E. Wake management in wind farms: An adaptive control approach. Energies 2019, 12, 1247. [Google Scholar] [CrossRef]
- Deb, D.; Ambekar, A.K.; Sagi, D.R. Method and System for Hybrid Wind Power Generation. U.S. Patent 10,066,604, 4 September 2018. [Google Scholar]
- Mohamed, M.A.; Al-Sumaiti, A.S.; Krid, M.; Awwad, E.M.; Kavousi-Fard, A. A Reliability-Oriented Fuzzy Stochastic Framework in Automated Distribution Grids to Allocate ηPMUs. IEEE Access 2019, 7, 33393–33404. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khodaei, A. Efficient Integration of Plug-in Electric Vehicles via Reconfigurable Microgrids. Energy 2016, 111, 653–663. [Google Scholar] [CrossRef]
- Energy Information Administration. Electric Power Annual. 2017. Available online: https://www.eia.gov/electricity/annual/ (accessed on 6 December 2019).
- Kavousi-Fard, A.; Niknam, T.; Golmaryami, M. Short term load forecasting of distribution systems by a new hybrid modified FA-backpropagation method. J. Intell. Fuzzy Syst. 2014, 26, 517–522. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Muresan, V.; Unguresan, M.-L. Multi-criteria decision making approach for hybrid operation of wind farms. Symmetry 2019, 11, 675. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A. A novel software for design and optimization of hybrid power systems. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1299–1315. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A.; Alolah, A.I. A novel smart grid theory for optimal sizing of hybrid renewable energy systems. Sol. Energy 2016, 124, 26–38. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D. Decision and Control in Hybrid Wind Farms; Springer: Singapore, 2020. [Google Scholar]
- Mohamed, M.A.; Eltamaly, A.M.; Farh, H.M.; Alolah, A.I. Energy management and renewable energy integration in smart grid system. In Proceedings of the 2015 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–6. [Google Scholar]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiah, A.K.; Kim, H.-J. An improved routing schema with special clustering using PSO algorithm for heterogeneous wireless sensor network. Sensors 2019, 19, 671. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Jin, T.; Mohamed, M.A.; Chen, T. A Minimum Hitting Set Algorithm with Pre-Judging Mechanism for Model-Based Fault Diagnosis in Distribution Networks. IEEE Trans. Instrum. Meas. 2020, 69, 4702–4711. [Google Scholar] [CrossRef]
- Gojiya, A.; Deb, D.; Iyer, K.K.R. Feasibility study of power generation from agricultural residue in comparison with soil incorporation of residue. Renew. Energy 2019, 134, 416–425. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. Sizing and techno-economic analysis of stand-alone hybrid photovoltaic/wind/diesel/battery power generation systems. J. Renew. Sustain. Energy 2015, 7, 063128. [Google Scholar] [CrossRef]
- Jin, T.; Chen, Y.; Guo, J.; Wang, M.; Mohamed, M.A. An effective compensation control strategy for power quality enhancement of unified power quality conditioner. Energy Rep. 2020, 6, 2167–2179. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Anand, P.; Deb, D. Wavelet transform and variants of svr with application in wind forecasting. In Innovations in Infrastructure; Springer: Singapore, 2019; pp. 501–511. [Google Scholar]
- Rezaei, M.; Khalilpour, K.R.; Jahangiri, M. Multi-criteria location identification for wind/solar based hydrogen generation: The case of capital cities of a developing country. Int. J. Hydrogen Energy 2020, 45, 33151–33168. [Google Scholar] [CrossRef]
- Mostafa, M.; Abdullah, H.M.; Mohamed, M.A. Modeling and Experimental Investigation of Solar Stills for Enhancing Water Desalination Process. IEEE Access 2020, 8, 219457–219472. [Google Scholar] [CrossRef]
- Kapoor, D.; Sodhi, P.; Deb, D. Solar panel simulation using adaptive control. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 1124–1130. [Google Scholar]
- Eltamaly, A.M.; Mohamed, M.A.; Al-Saud, M.S.; Alolah, A.I. Load management as a smart grid concept for sizing and designing of hybrid renewable energy systems. Eng. Optim. 2017, 49, 1813–1828. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D. Wake management based life enhancement of battery energy storage system for hybrid wind farms. Renew. Sustain. Energy Rev. 2020, 130, 109912. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Awwad, E.M.; El-Sherbeeny, A.M.; Nasr, E.A.; Ali, Z.M. Optimal scheduling of reconfigurable grids considering dynamic line rating constraint. IET Gener. Transm. Distrib. 2020, 14, 1862–1871. [Google Scholar] [CrossRef]



| Charger Type | Input Voltage | Maximum Power (kW) |
|---|---|---|
| Level 1 | 120 VAC | 1.44 |
| Level 2 | 208–240 VAC | 11.5 |
| Level 3 | 208–240 VAC | 96 |
| Level 3 (DC) | 208–600 VDC | 240 |
| Class | Market Share | Min Cbat (kWh) | Max Cbat (kWh) |
|---|---|---|---|
| Micro Car | 0.2 | 8 | 12 |
| Economy Car | 0.3 | 10 | 14 |
| Mid-Size Car | 0.3 | 14 | 18 |
| SUV | 0.3 | 19 | 23 |
| Time (Day) | 1–8 | |||||||
|---|---|---|---|---|---|---|---|---|
| Charging demand (MWh) | 2.3928 | 2.1667 | 2.2810 | 2.3690 | 2.4564 | 2.4876 | 2.2998 | 2.1136 |
| Time (day) | 9–16 | |||||||
| Charging demand (MWh) | 2.1185 | 2.1678 | 2.4336 | 2.1663 | 2.4215 | 2.1614 | 2.4739 | 2.2099 |
| Time (day) | 17–24 | |||||||
| Charging demand (MWh) | 2.1401 | 2.1649 | 2.3312 | 2.2661 | 2.2107 | 2.4290 | 2.3172 | 2.3010 |
| Time (day) | 25–30 | |||||||
| Charging demand (MWh) | 2.4684 | 2.1807 | 2.3955 | 2.3939 | 2.2238 | 2.2783 | ||
| Storage | Bus | Capacity (kWh) | Min-Max Charging/Discharging Power (kW) | Min Charging/Discharging Time (h) |
|---|---|---|---|---|
| DES | 15 | 1500 | 50–250 | 4 |
| Load | Type | Bus | Min-Max Capacity (kW) | Required Energy (kWh) | Initial Start/End Time (h) | Min Up Time (h) |
|---|---|---|---|---|---|---|
| L1 | S | 28 | 0–60 | 240 | 11–14 | 1 |
| L2 | S | 56 | 0–60 | 240 | 15–19 | 1 |
| L3 | S | 18 | 20–60 | 240 | 16–19 | 1 |
| L4 | C | 35 | 10–40 | 200 | 1–24 | 24 |
| L5 | C | 59 | 20–60 | 300 | 13–24 | 12 |
| Method | MAPE (%) | MARPE | RMSE |
|---|---|---|---|
| ARMA | 2.08753 | 6.25845 | 2.63238 |
| ANN | 2.26421 | 6.56019 | 2.86453 |
| SVR | 1.36508 | 3.40989 | 1.45778 |
| SVR-DA | 1.16523 | 3.11277 | 1.44568 |
| Proposed SVR-MDA Method | 0.97752 | 1.88198 | 1.04481 |
| Method | Cost ($) (×105) | ||||
|---|---|---|---|---|---|
| Average | Worst | Best | Standard Deviation | CPU Time (s) | |
| GA | 6.6927 | 7.8865 | 6.5364 | 0.1524 | 17.269 |
| PSO | 6.5378 | 7.9124 | 6.4473 | 0.1325 | 15.703 |
| Original DA | 6.5085 | 7.5295 | 6.4527 | 0.1358 | 14.275 |
| Proposed MDA | 6.4163 | 6.5946 | 6.2653 | 0.1063 | 13.276 |
| Wind Turbine 1 (kW) | Wind Turbine 2 (kW) | Solar Panel 1 (kW) | Solar Panel 1 (kW) | HEV Charging Demand (Coordinate) | HEV Charging Demand (Intelligent) |
|---|---|---|---|---|---|
| 16.898 | 29.7500 | 0 | 0 | 233.02 | 275.78 |
| 16.898 | 29.7500 | 0 | 0 | 106.52 | 289.04 |
| 16.898 | 29.7500 | 0 | 0 | 77.76 | 227.24 |
| 16.898 | 29.7500 | 0 | 0 | 72.00 | 210.00 |
| 16.898 | 29.7500 | 0 | 0 | 60.48 | 159.68 |
| 8.662 | 15.2500 | 0 | 0 | 50.40 | 136.68 |
| 16.898 | 29.7500 | 0 | 0 | 40.32 | 84.92 |
| 12.354 | 21.7500 | 1.6000 | 1.6000 | 28.80 | 53.28 |
| 16.898 | 29.7500 | 30.000 | 30.000 | 20.16 | 43.20 |
| 29.252 | 51.5000 | 60.200 | 60.200 | 11.52 | 41.74 |
| 83.070 | 146.250 | 83.600 | 83.600 | 8.64 | 38.86 |
| 98.548 | 173.5000 | 95.600 | 95.600 | 2.88 | 23.04 |
| 37.062 | 65.2500 | 191.20 | 191.20 | 1.44 | 20.16 |
| 22.436 | 39.5000 | 168.40 | 168.40 | 0 | 12.96 |
| 16.898 | 29.7500 | 63.000 | 63.000 | 0 | 7.20 |
| 12.354 | 21.7500 | 33.8000 | 33.8000 | 0 | 2.88 |
| 16.898 | 29.7500 | 4.4000 | 4.4000 | 0 | 0 |
| 16.898 | 29.7500 | 0 | 0 | 0 | 4.32 |
| 12.325 | 21.7000 | 0 | 0 | 0 | 17.26 |
| 16.898 | 29.7500 | 0 | 0 | 0 | 20.14 |
| 12.311 | 21.6750 | 0 | 0 | 113.6 | 50.34 |
| 12.311 | 21.6750 | 0 | 0 | 432.78 | 152.42 |
| 8.6620 | 15.2500 | 0 | 0 | 578.00 | 240.10 |
| 5.8220 | 10.2500 | 0 | 0 | 440.02 | 167.10 |
| Storage | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 |
| L1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| L2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| L3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| L4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| L5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Hours | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Sectionalizing Switches | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 18 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 20 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 26 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 33 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 36 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 38 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 47 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 49 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Tie Switches | 69 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 70 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 71 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 72 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 73 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, T.; Jermsittiparsert, K.; T. Alrashood, S.; Rezaei, M.; Al-Ghussain, L.; A. Mohamed, M. An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand. Energies 2021, 14, 569. https://doi.org/10.3390/en14030569
Lan T, Jermsittiparsert K, T. Alrashood S, Rezaei M, Al-Ghussain L, A. Mohamed M. An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand. Energies. 2021; 14(3):569. https://doi.org/10.3390/en14030569
Chicago/Turabian StyleLan, Tianze, Kittisak Jermsittiparsert, Sara T. Alrashood, Mostafa Rezaei, Loiy Al-Ghussain, and Mohamed A. Mohamed. 2021. "An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand" Energies 14, no. 3: 569. https://doi.org/10.3390/en14030569
APA StyleLan, T., Jermsittiparsert, K., T. Alrashood, S., Rezaei, M., Al-Ghussain, L., & A. Mohamed, M. (2021). An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand. Energies, 14(3), 569. https://doi.org/10.3390/en14030569










