Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty
Abstract
:1. Introduction
- Quantification of the Option Value of investing in energy storage across India, covering the period 2020–2060.
- Presentation of key investment insights and notable conclusions for India’s electricity system covering the period 2020–2060.
- Application of an advanced decomposition approach to overcome the increased complexity related to the application of stochastic optimization under multi-dimensional uncertainty, to the India context.
2. Energy Storage and Option Value in the India Context
3. Planning Model Formulation and Solution Procedure
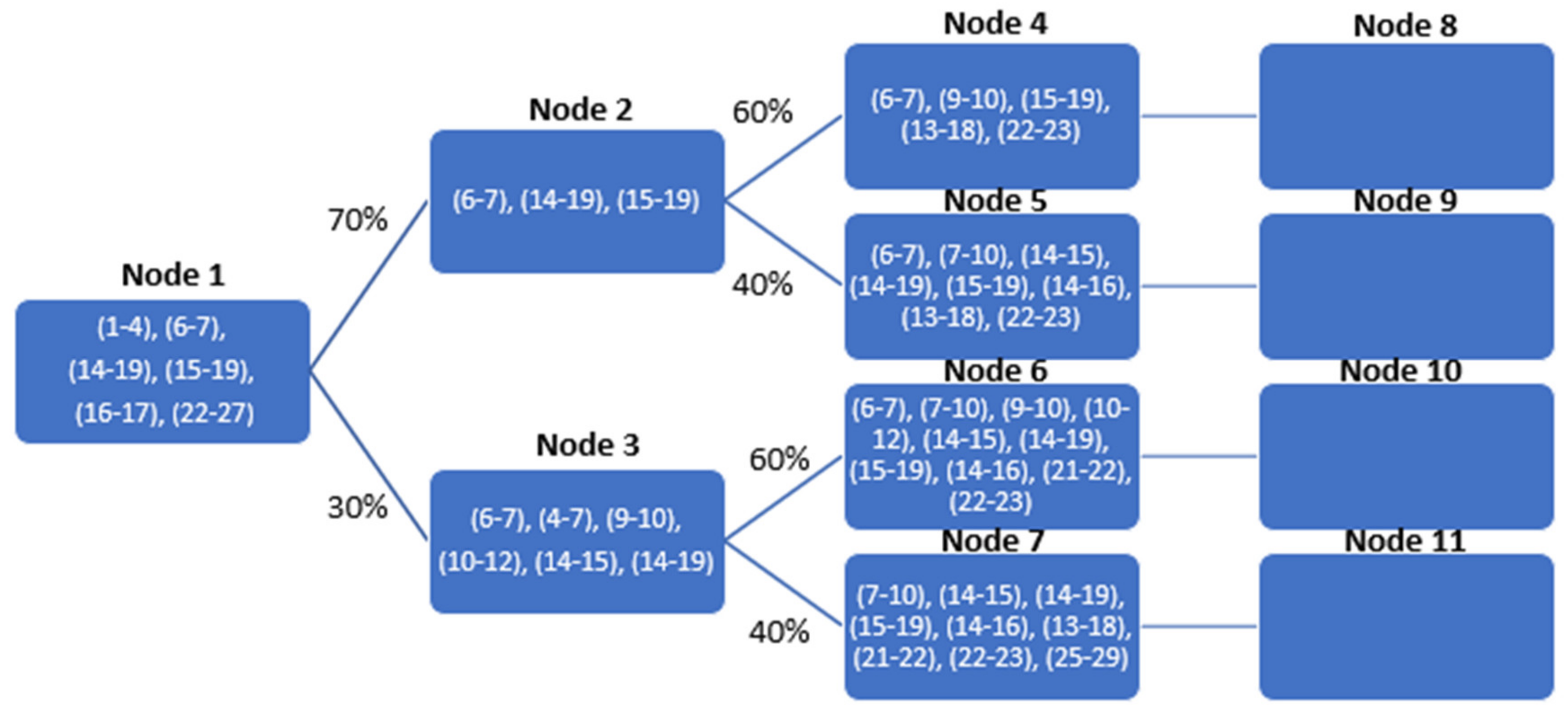
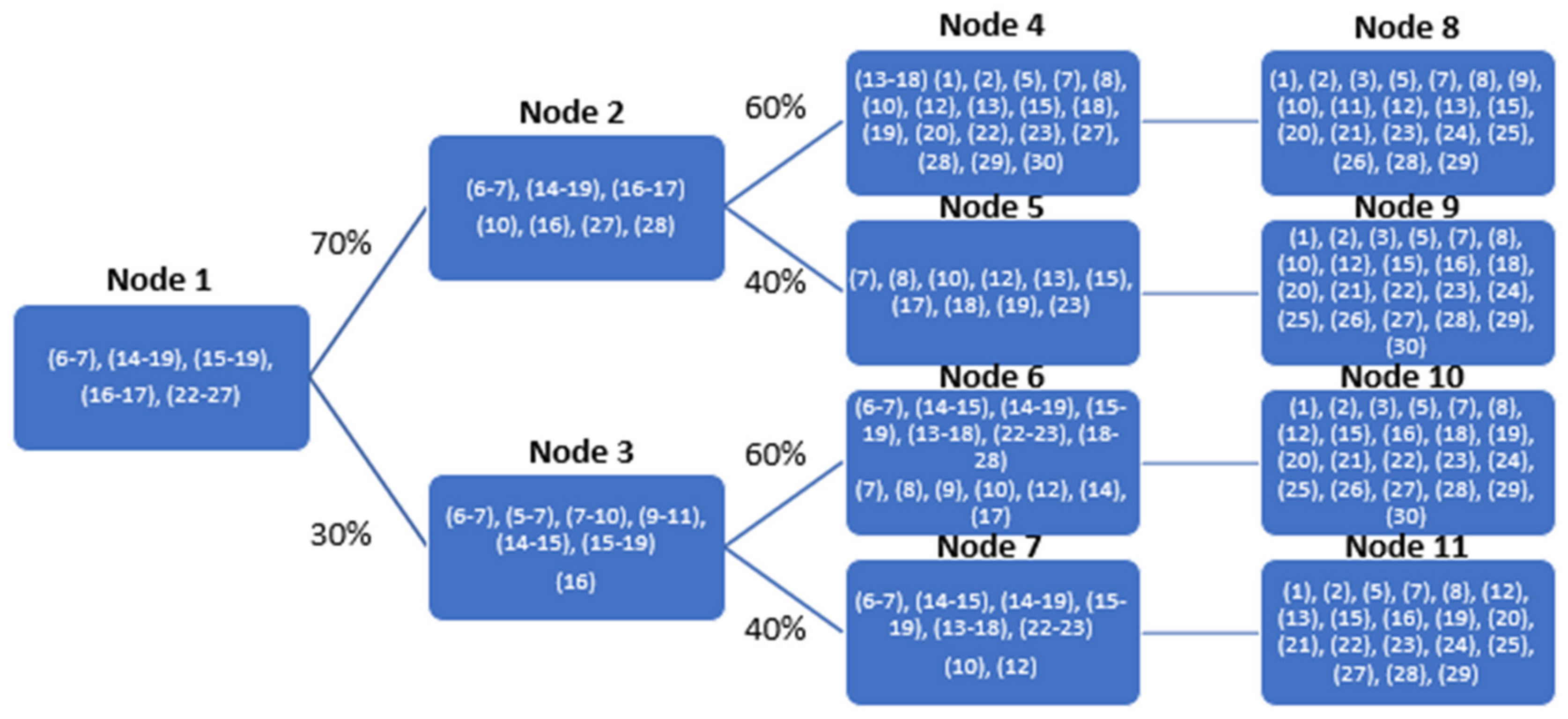
3.1. Advanced Decompostion of the Large-Scale Transmission Planning Problem
3.2. Mathematical Formulation
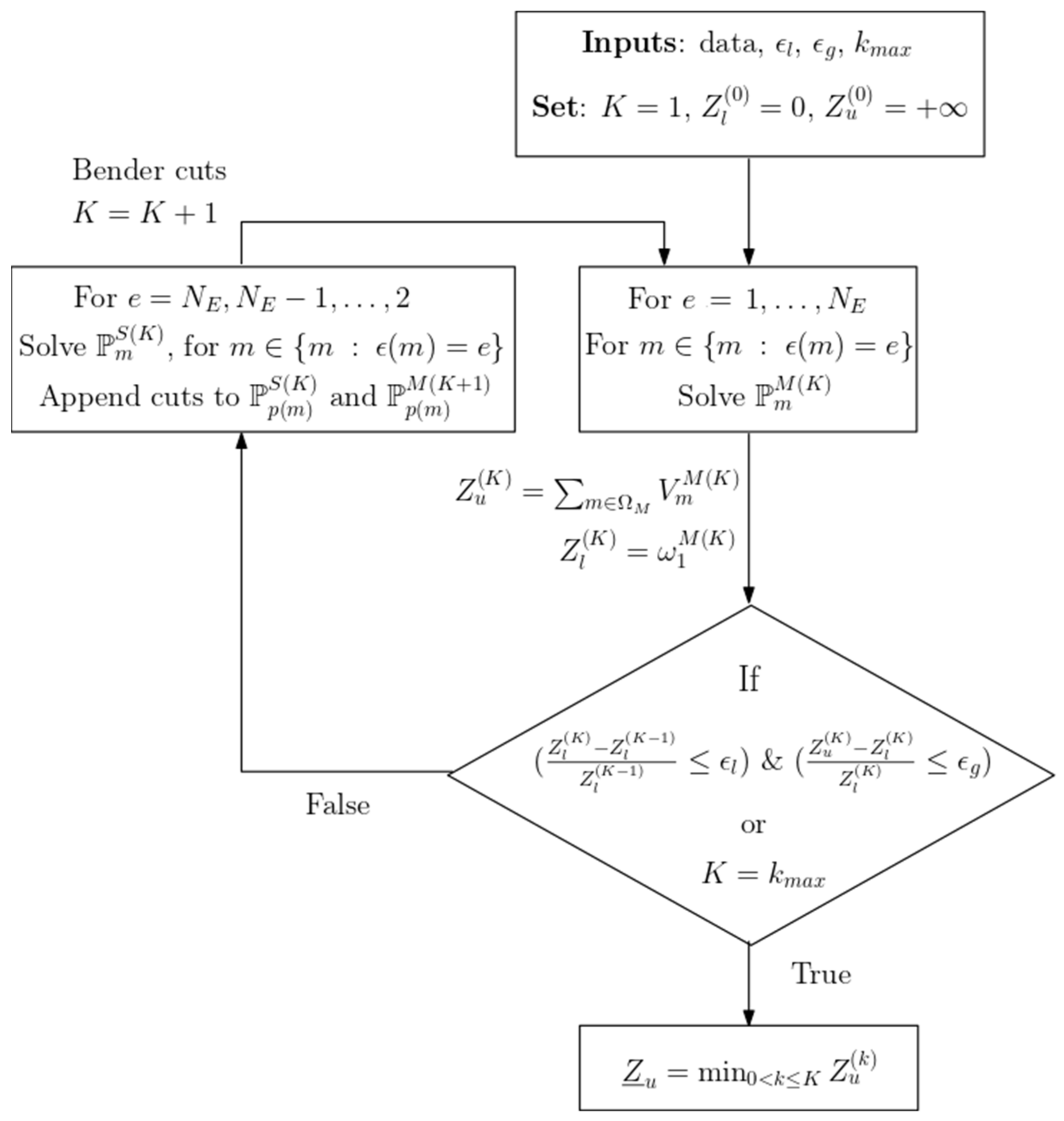
3.3. Solution Algorithm and Convergence
4. Case Study
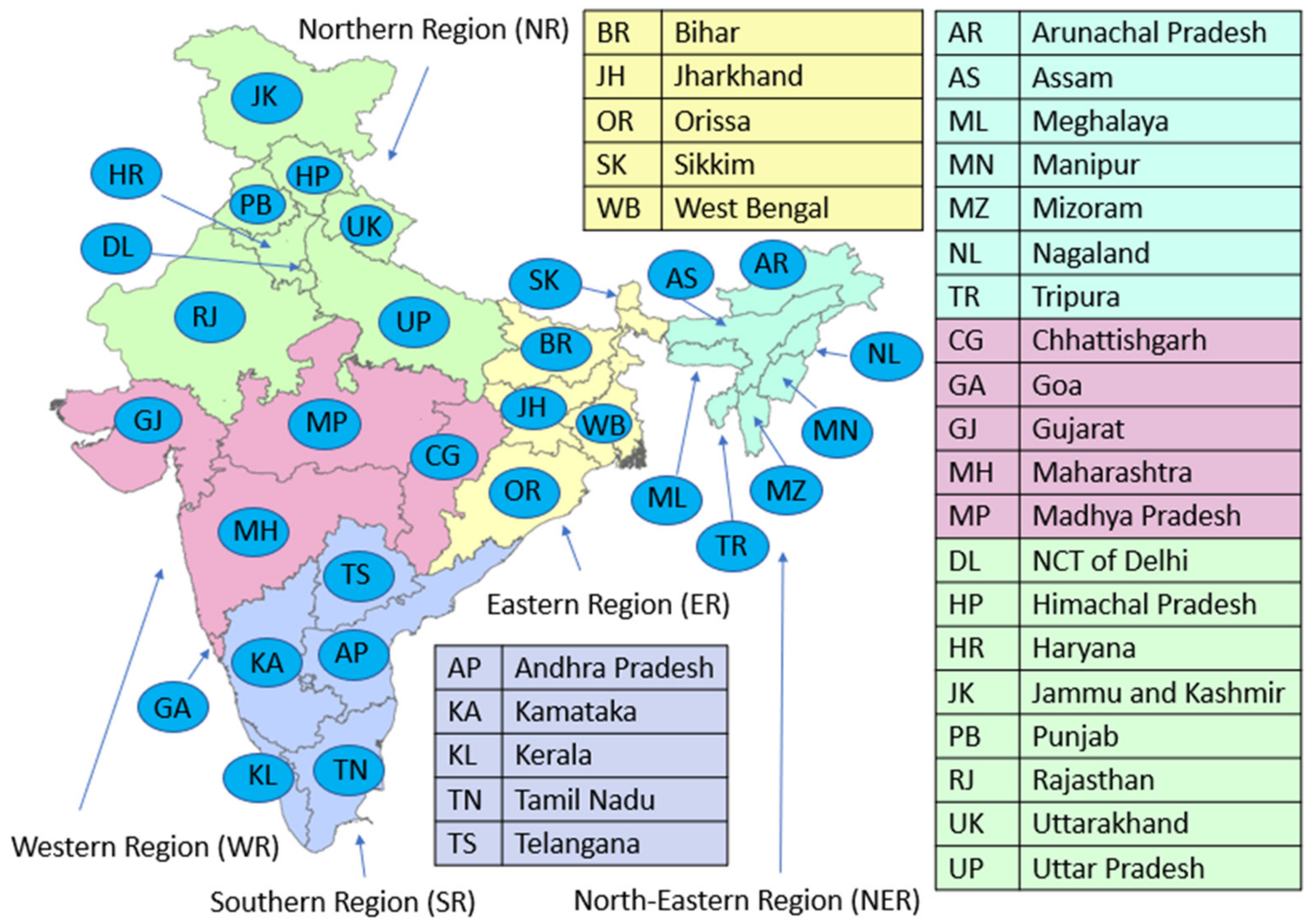
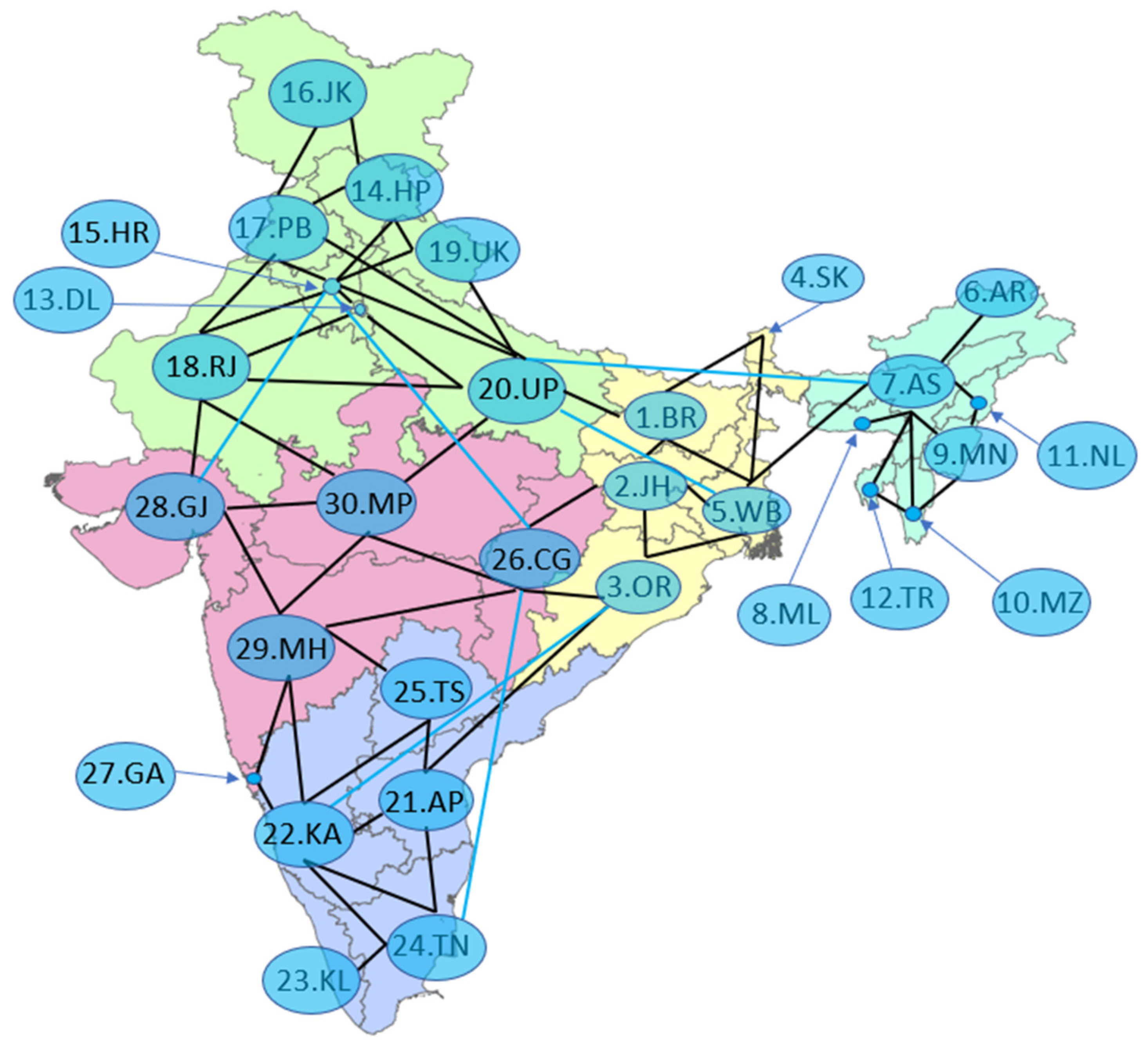
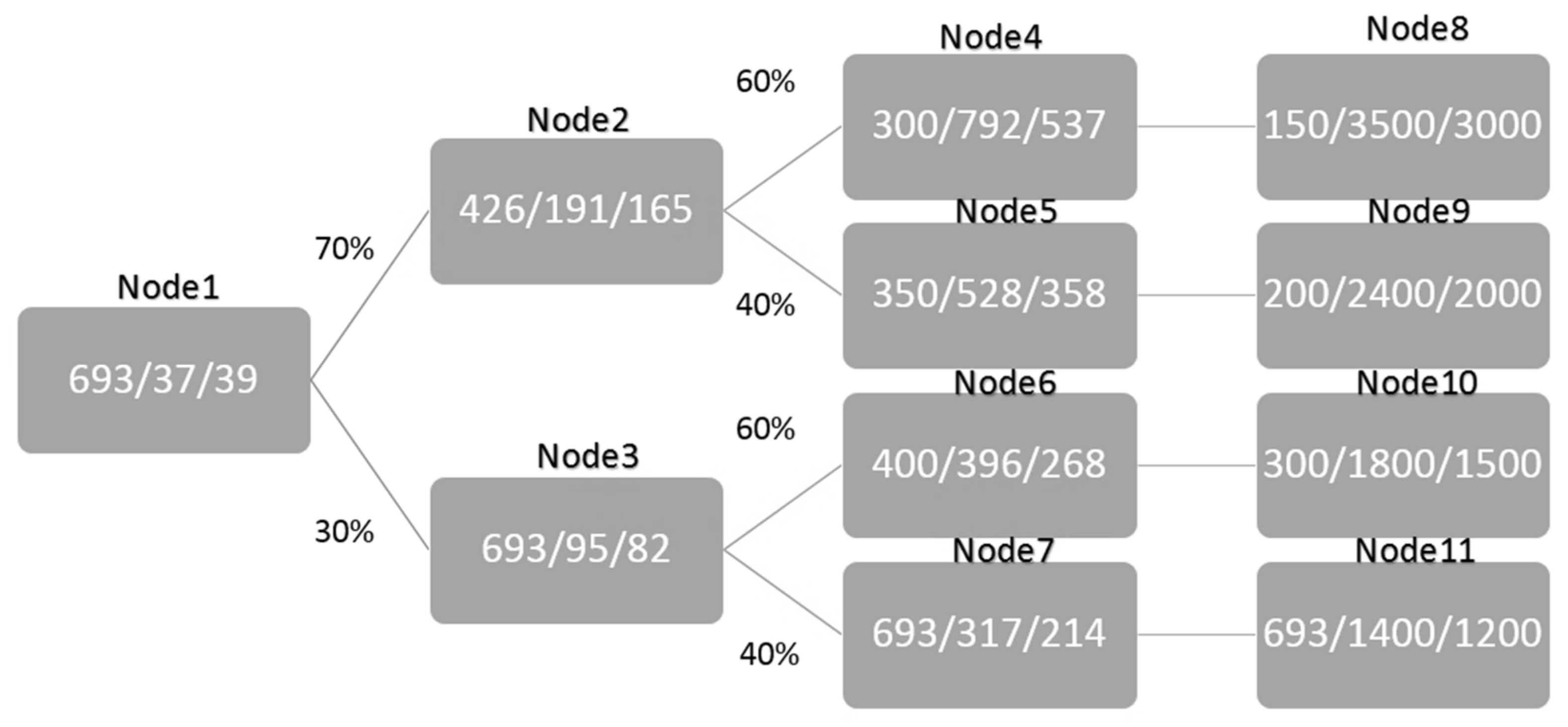
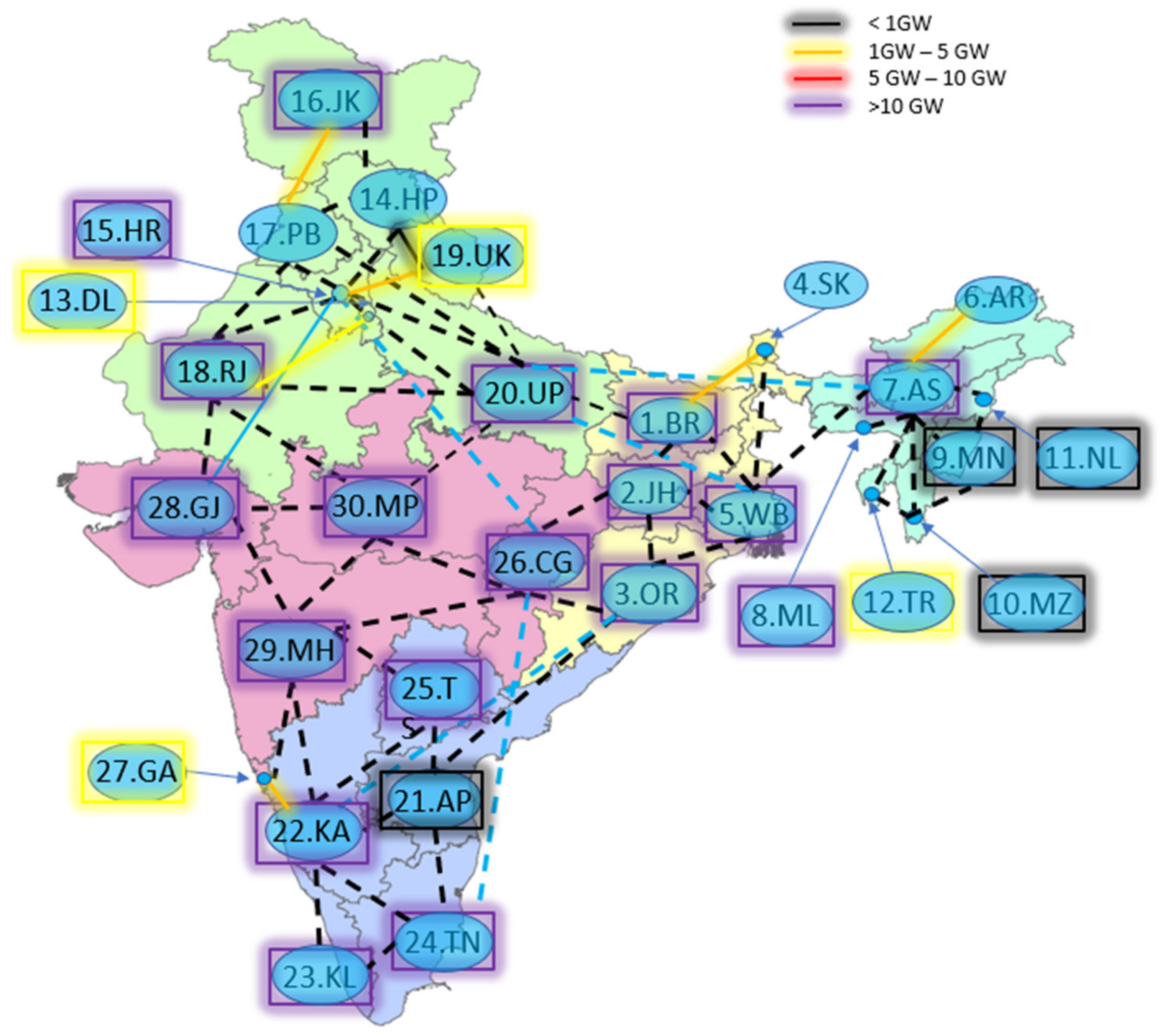
4.1. Description
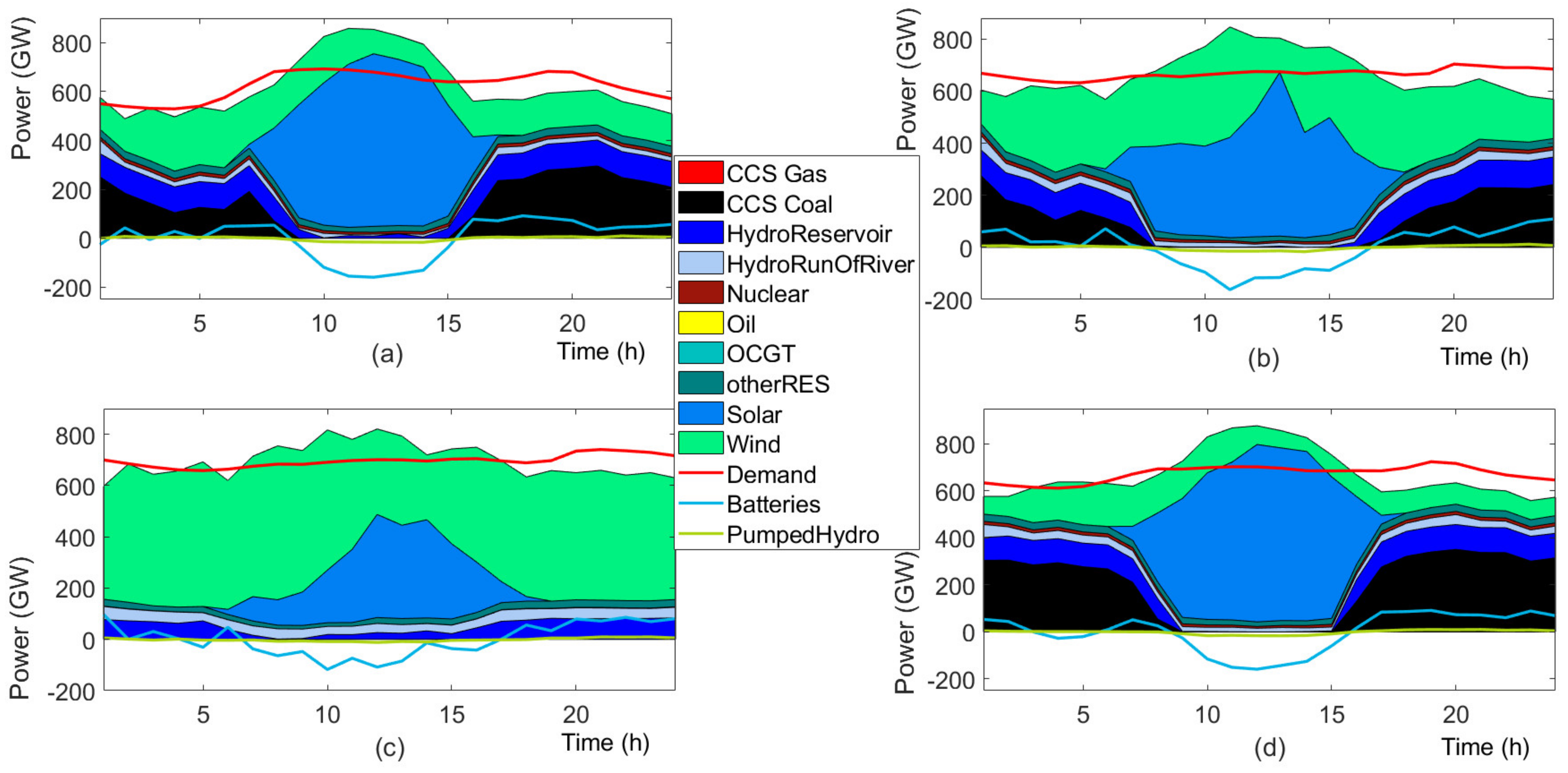
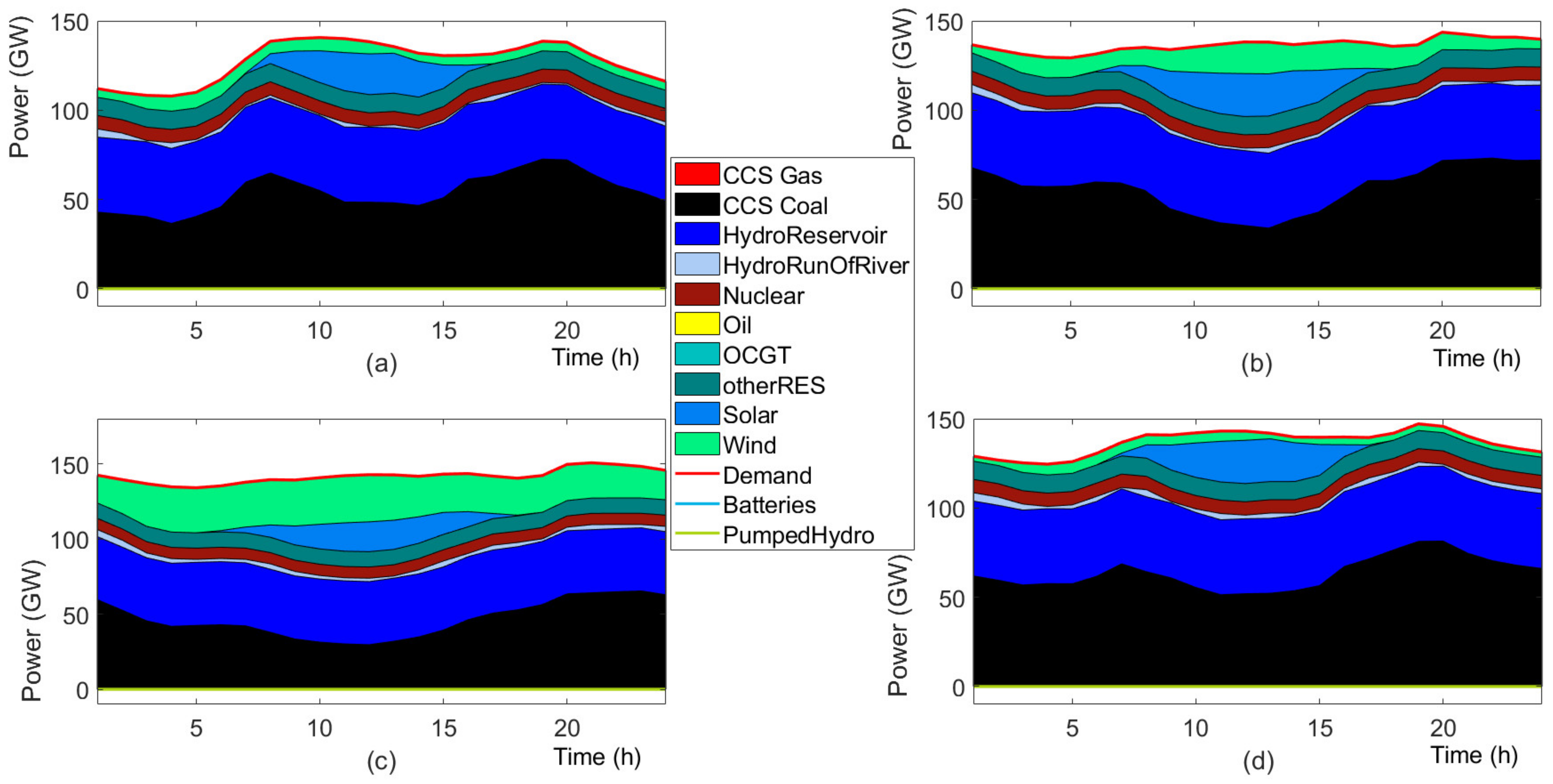
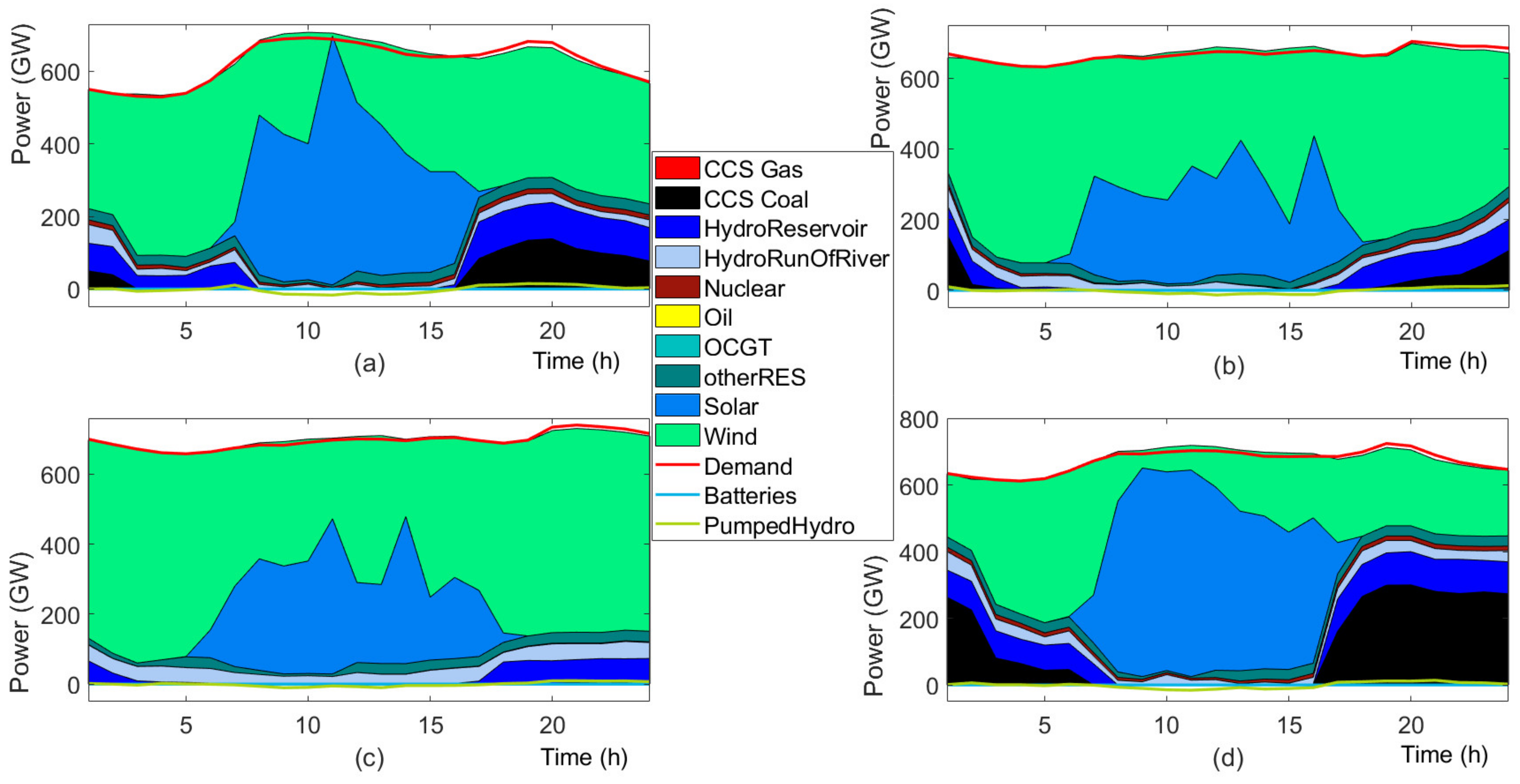
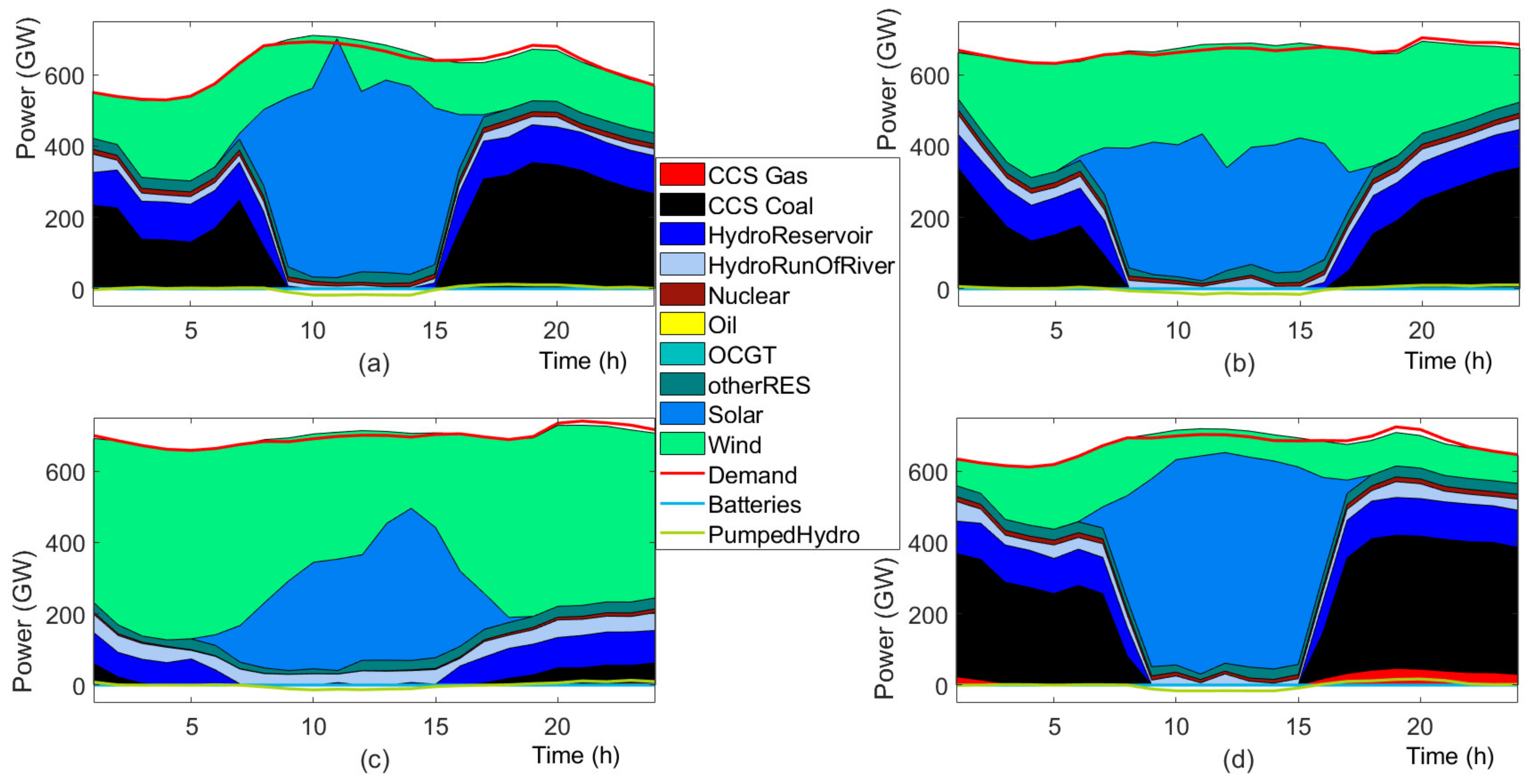
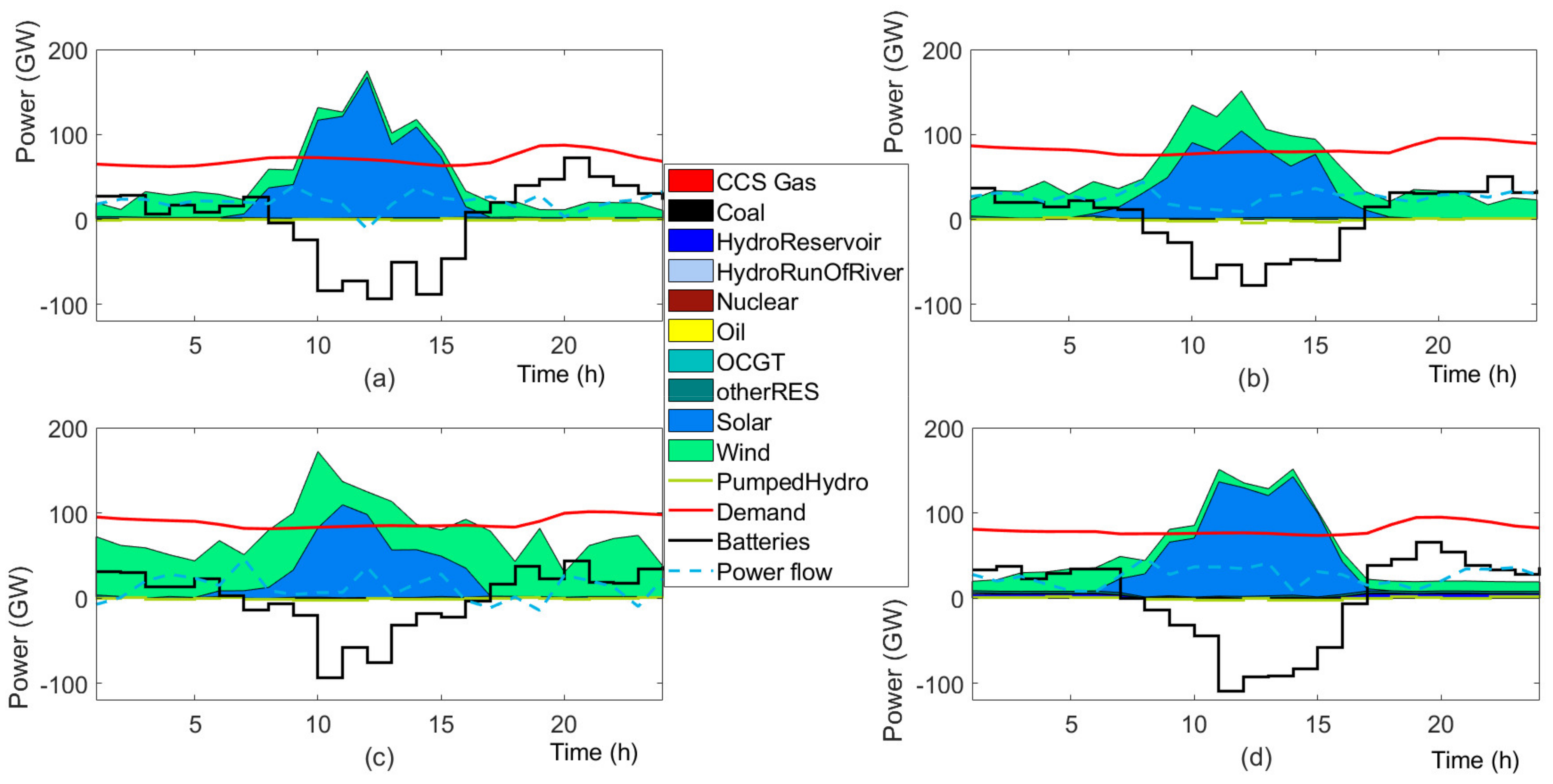
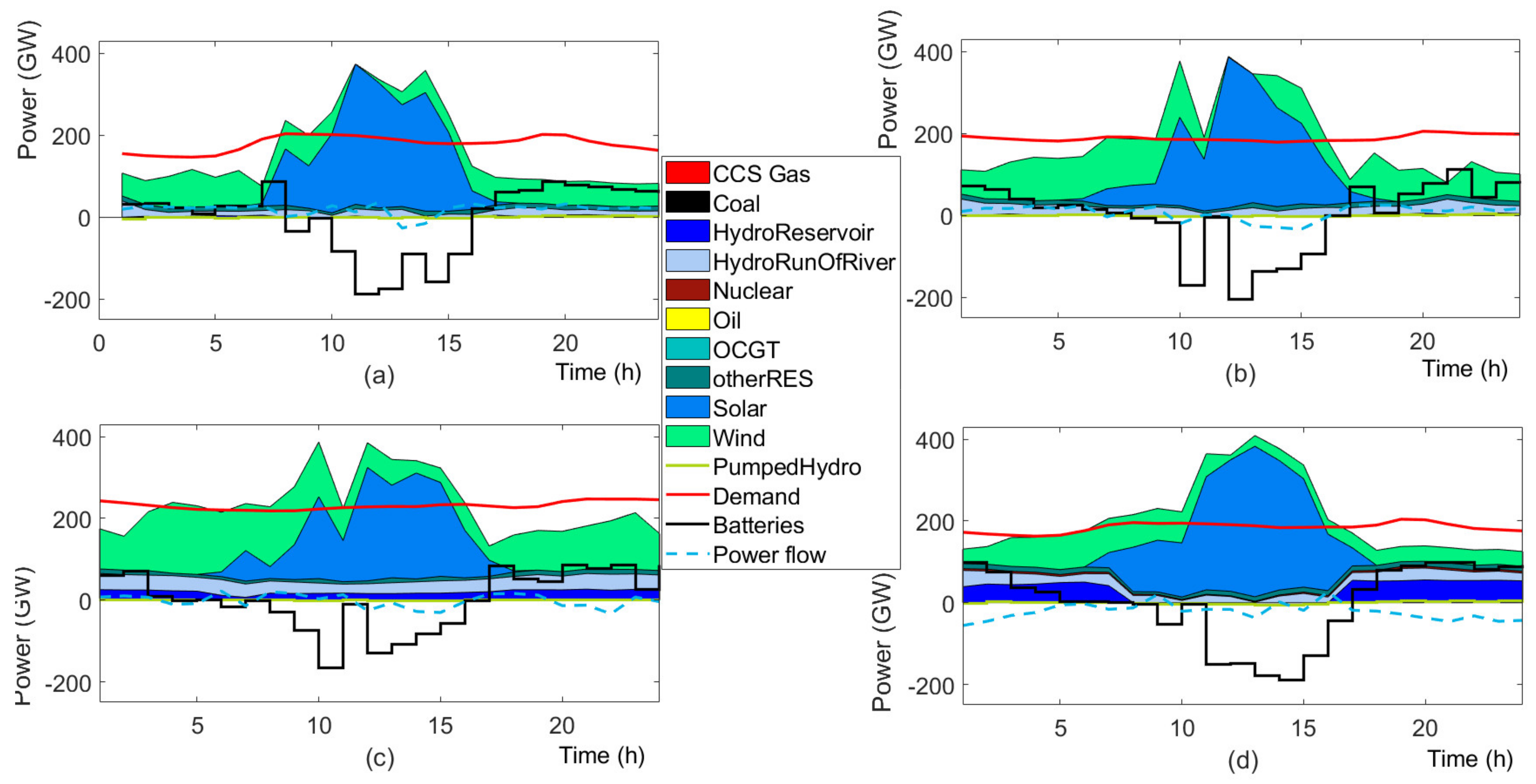
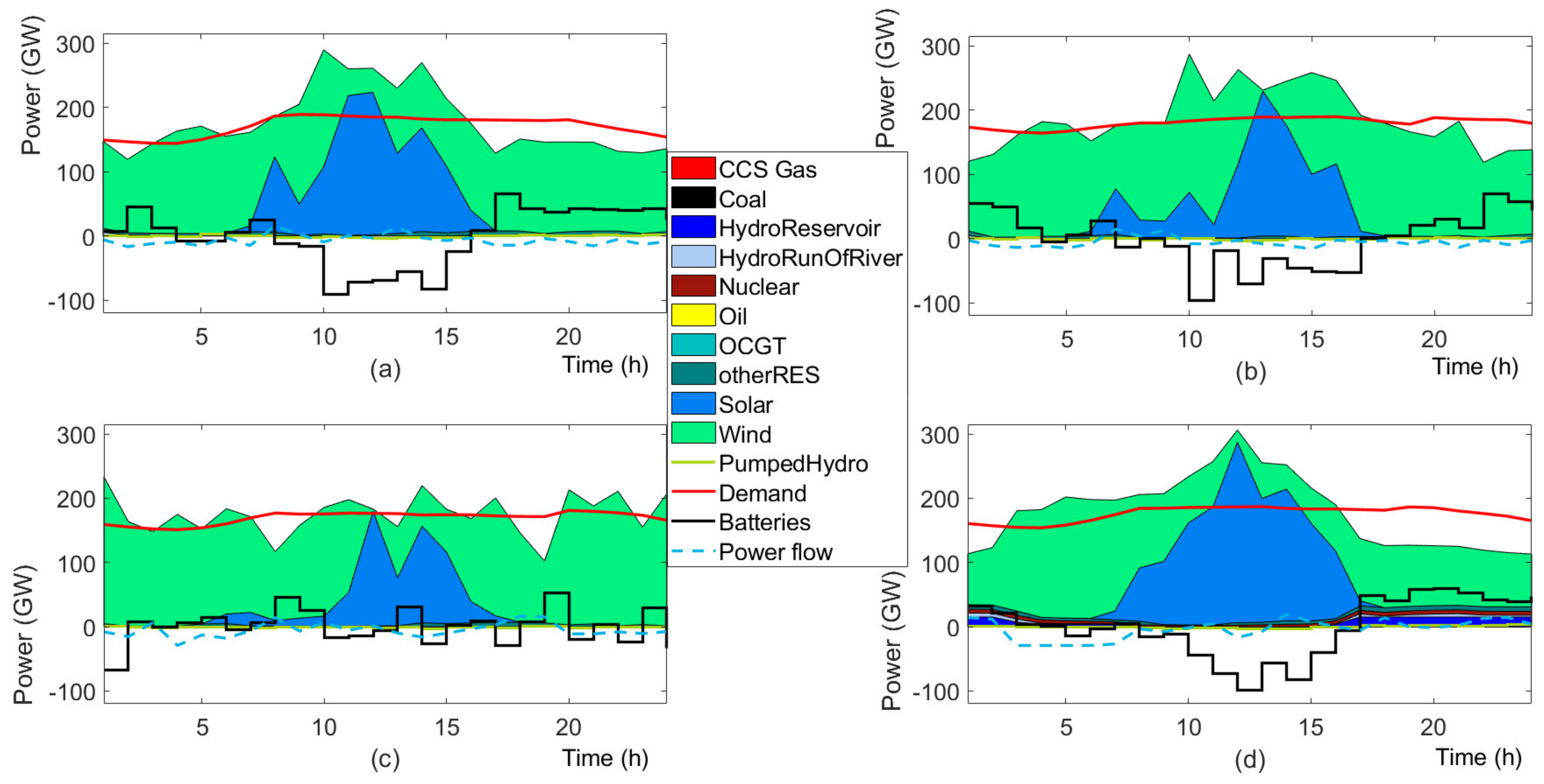
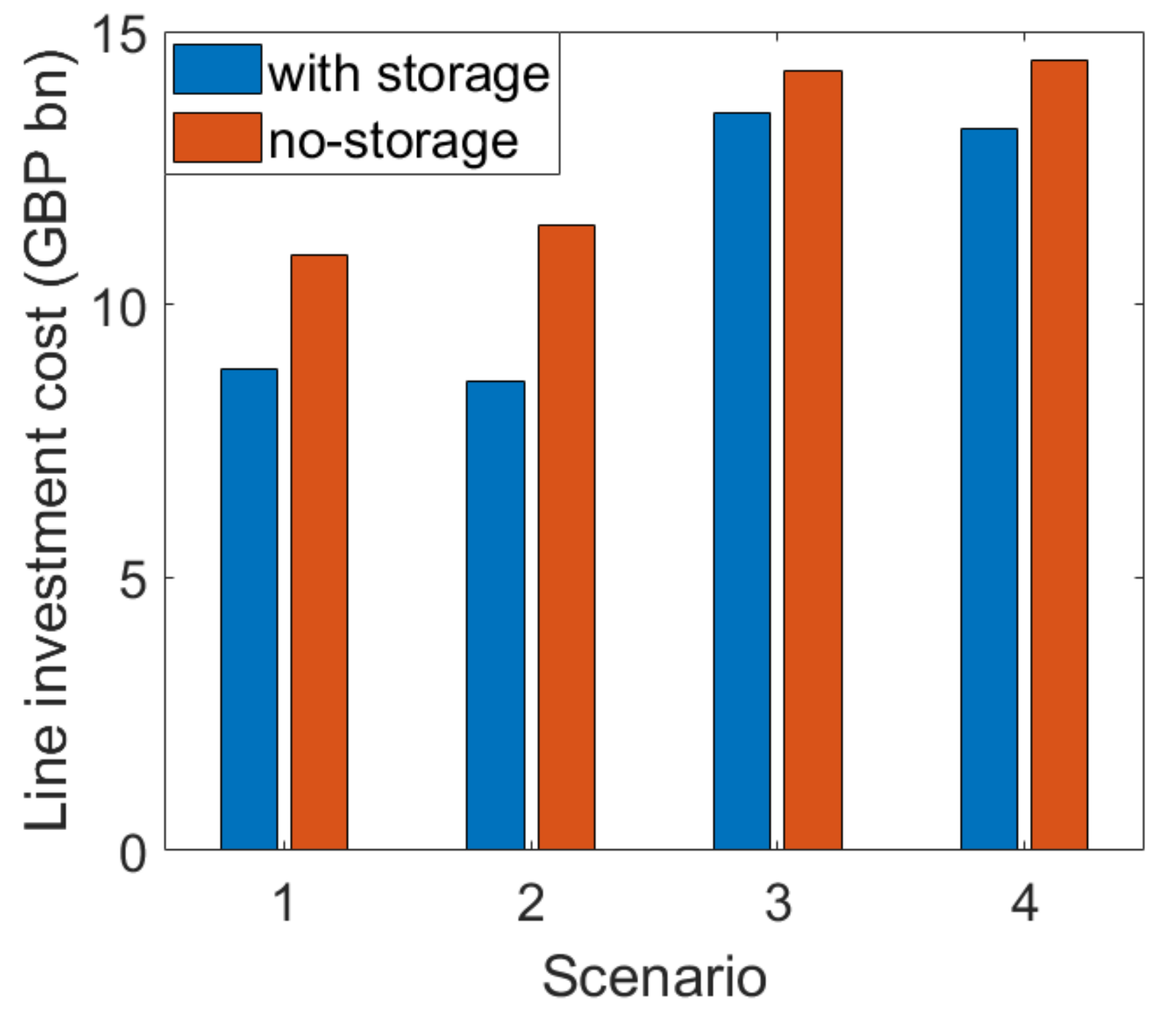
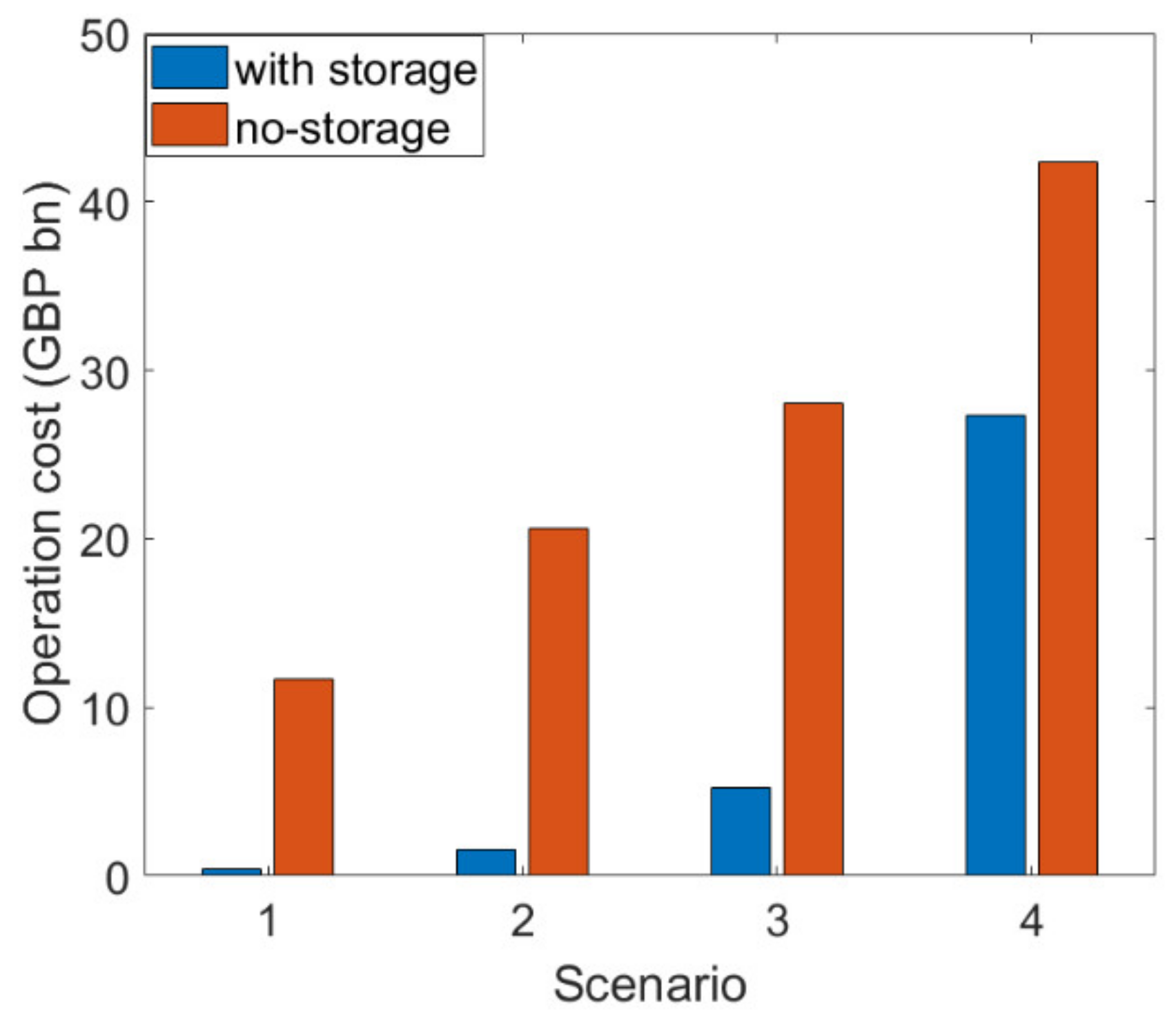
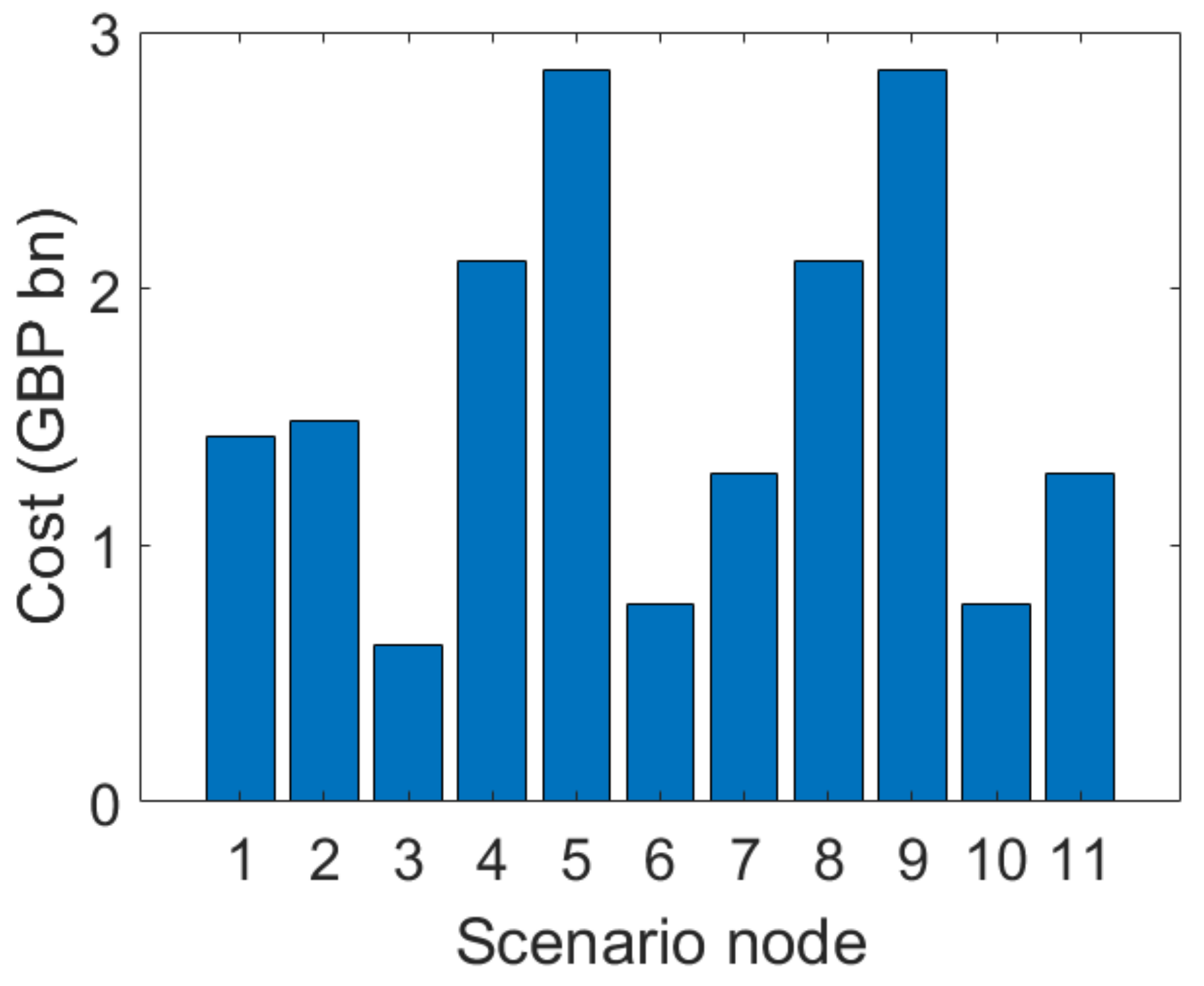
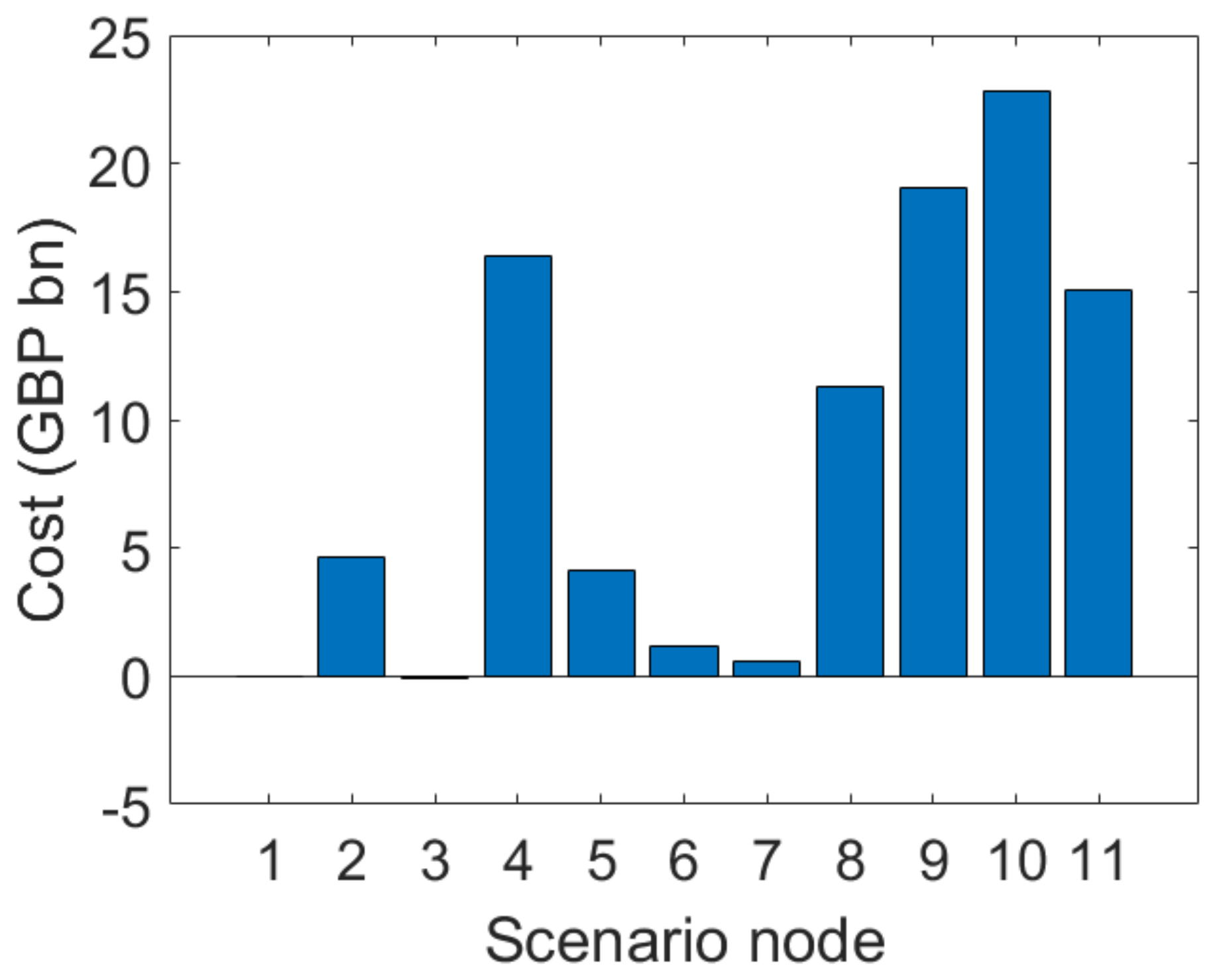
4.2. Results
4.3. Discussion
4.3.1. Investment Flexibility
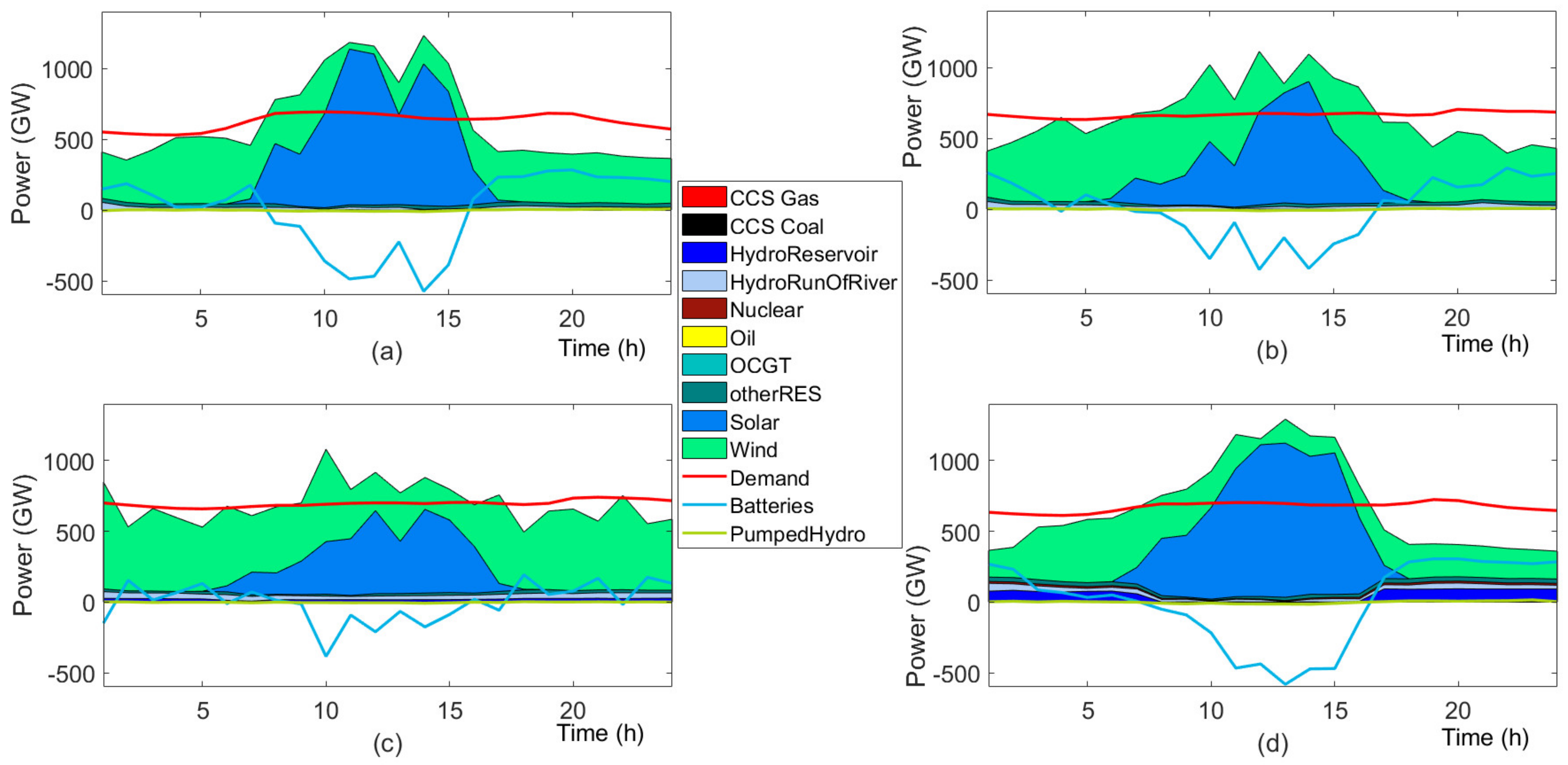
4.3.2. Future Generation Mix
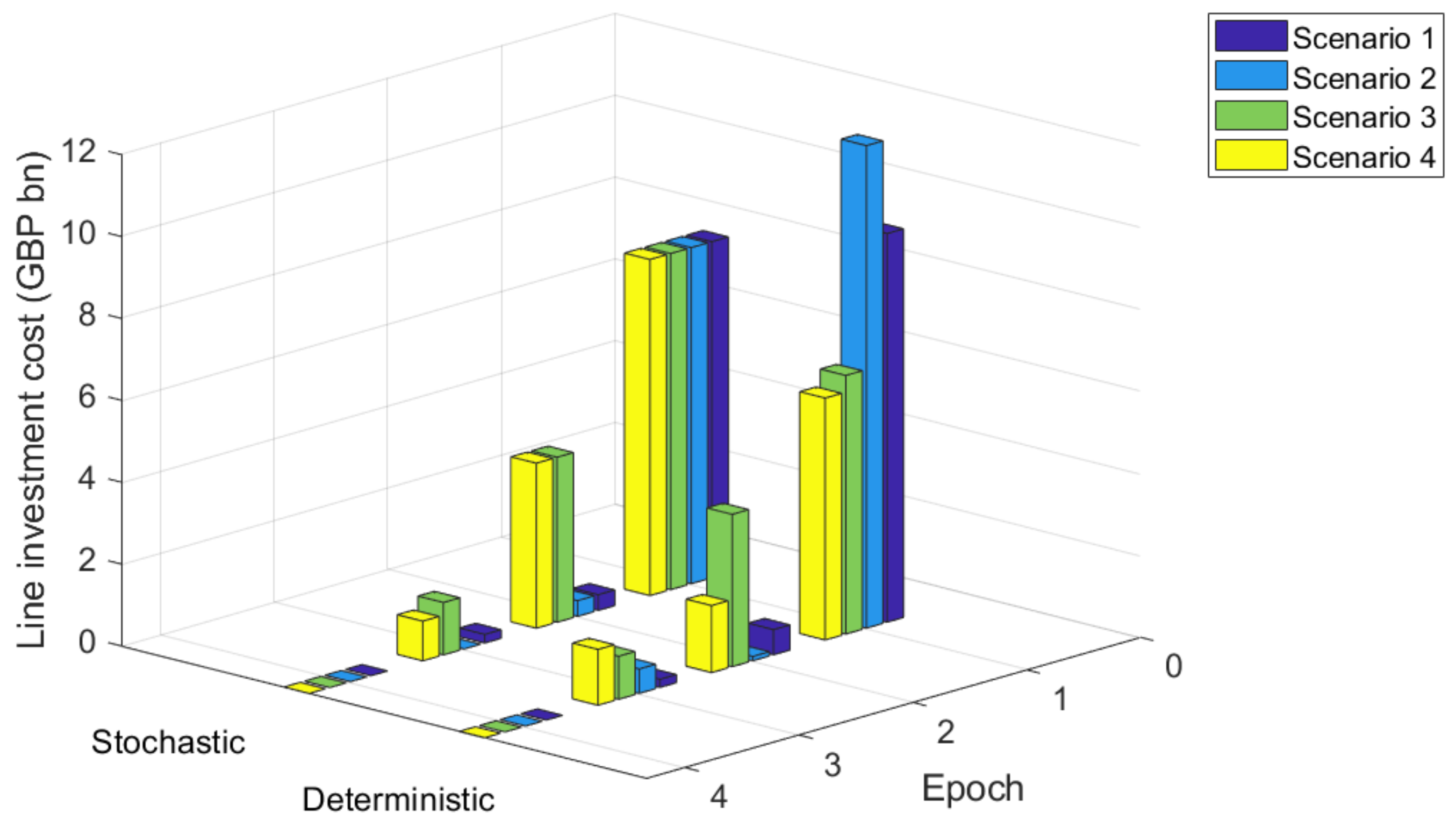
4.3.3. Stochastic versus Deterministic Planning
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets and indices | |
| Set of all demand blocks, indexed b | |
| Set of all generation units, indexed g | |
| Set of all hydro run of river generation units | |
| Set of all hydro reservoir generation units | |
| Set of all storage units, indexed h | |
| Set of candidate storage technologies, indexed h | |
| Set of all transmission lines, indexed l | |
| Set of all AC transmission lines | |
| Set of all scenario-tree nodes, indexed m | |
| Set of all stages, indexed by e | |
| Set of all system buses, indexed n | |
| Set of all time periods in demand block b, indexed t | |
| Set of all conventional expansion options, indexed ω | |
| Number years in the planning horizon | |
| Set of all children nodes of scenario-tree node m | |
| Parent node of scenario-tree node m | |
| Stage to which scenario-tree node m belongs | |
| First year of stage e | |
| Parameters | |
| Demand at bus n for 0 operating point (m,t) in demand block b | |
| Minimum energy capacity storage equivalent of hydro generation unit g at time t, where q ∈ {rr,res} for run of river and reservoir units, respectively | |
| Maximum energy capacity storage equivalent of hydro generation unit g at time t, where q ∈ {rr,res} for run of river and reservoir units, respectively | |
| Initial transmission capacity of line l | |
| Maximum capacity upgrade of option for line | |
| Bus-to-storage incidence matrix | |
| Bus-to-generator incidence matrix | |
| Bus-to-line incidence matrix | |
| Maximum output of generation unit for operating point (m,t) | |
| Ramp-down capability (MW/h) for generation technology g | |
| Ramp-up capability (MW/h) for generation technology g | |
| Hourly water inflow (capacity) for hydro d ∈ {rr,res}, generation unit g at time t | |
| Maximum charge rate of storage device h (MW) | |
| Maximum discharge rate of storage device h (MW) | |
| Maximum storage investment size of technology h in one stage (MW) | |
| Rated discharge duration (energy over power capacity) of a new storage unit (h) | |
| Weighting of demand block b | |
| Reactance of transmission line l | |
| Generation cost of unit g (GBP/MWh) | |
| Value of lost load (GBP/MWh) | |
| Cumulative discount factor for line investments in epoch ϵ(m) | |
| Cumulative discount factor for storage investments in technology h in epoch ϵ(m) | |
| Cumulative discount factor for system operation in epoch ϵ(m) | |
| Interest rate | |
| Start bus of line l | |
| End bus of line l | |
| Charging efficiency of storage technology h | |
| Discharging efficiency of storage technology h | |
| Build time for line l and expansion option ω | |
| Build time of candidate storage technology | |
| Lifespan of candidate storage technology h | |
| Annual fixed investment cost of line l and option ω (GBP/yr) | |
| Annual variable investment cost of line l and option ω (GBP/MW yr) | |
| Annual variable investment cost of storage h in node m (GBP/MW yr) | |
| State probability of scenario-tree node m | |
| Time duration of a demand period t | |
| Decision variables | |
| Note that the vector x represents all decision variables involved in the optimization problem. | |
| Equivalent amount of stored energy of hydro generation unit at operating point (m,t), where q ∈ {rr,res} for run of river and reservoir units, respectively | |
| Transmission line capacity upgrade for line l using option ω at node m | |
| Aggregate transmission line capacity upgrades of line at node | |
| Output of generation unit g at operating point (m,t) | |
| Charging power of storage device h at operating point (m,t) | |
| Discharging power of storage device h at operating point (m,t) | |
| Output of hydro generation unit g at operating point (m,t), where q ∈ {rr,res} for run of river and reservoir units, respectively | |
| Water shed equivalent of hydro generation unit for at operating point (m,t) | |
| Decision variable modelling investment in storage asset h at node m | |
| Aggregate storage capacity investment for asset h at node m | |
| Demand curtailment at bus n and operating point (m,t) | |
| Power flow on line l at operating point (m,t) | |
| Decision vector coupling investments in node with those in its parent node , where for line investment decisions, transmission capacity investment, aggregate transmission capacity investment, storage investment decisions, and storage decommissioning decisions, respectively | |
| Linear combination of , where for line investment decisions, transmission capacity investment, aggregate transmission capacity investment, storage investment decisions, and storage decommissioning decisions, respectively | |
| Binary decision variable modelling investment in transmission capacity in line using option ω at node m | |
| Voltage angle at bus n at operating point (m,t) | |
| State of charge of storage device h at operating point (m,t) | |
References
- Krishnan, R.; Sanjay, J.; Gnanaseelan, C.; Mujumdar, M.; Kulkarni, A.; Chakraborty, S. Assessment of Climate Change over the Indian Region: A Report of the Ministry of Earth Sciences (MoES), Government of India. 2020. Available online: https://link.springer.com/book/10.1007%2F978-981-15-4327-2 (accessed on 1 November 2021). [CrossRef]
- Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 1 November 2021).
- Available online: https://www.eia.gov/international/content/analysis/countries_long/India/india.pdf (accessed on 1 November 2021).
- Available online: https://saubhagya.gov.in/ (accessed on 1 November 2021).
- The Times of India. Power distribution plan soon to ensure 24X7 electricity supply for all. 16 July 2019; Live Mint. Govt’s 100-day plan aims to re-energize India’s power sector. The Times of India. 12 June 2019, p. 6.
- International Energy Agency. World Energy Outlook 2019, Annexes; BP Statistical Review of World Energy 2019; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Available online: https://niti.gov.in/writereaddata/files/175-GW-Renewable-Energy.pdf (accessed on 1 November 2021).
- Available online: https://data.worldbank.org/indicator/EN.ATM.CO2E.PC?locations=IN (accessed on 1 November 2021).
- Strbac, G.; Konstantelos, I.; Pollitt, M.; Green, R. Report for the UK National Infrastructure Commission: Delivering Future-Proof Energy Infrastructure. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/507256/Future-proof_energy_infrastructure_Imp_Cam_Feb_2016.pdf (accessed on 30 January 2020).
- Available online: https://www.iea.org/reports/india-2020 (accessed on 1 November 2021).
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option value of dynamic line rating and storage. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Giannelos, S.; Konstantelos, I.; Strbac, G. Option Value of Demand-Side Response Schemes Under Decision-Dependent Uncertainty. IEEE Trans. Power Syst. 2018, 33, 5103–5113. [Google Scholar] [CrossRef]
- Konstantelos, I.; Giannelos, S.; Strbac, G. Strategic Valuation of Smart Grid Technology Options in Distribution Networks. IEEE Trans. Power Syst. 2017, 32, 1293–1303. [Google Scholar] [CrossRef]
- Andrychowicz, M. The Impact of Energy Storage along with the Allocation of RES on the Reduction of Energy Costs Using MILP. Energies 2021, 14, 3783. [Google Scholar] [CrossRef]
- Andrychowicz, M. RES and ES Integration in Combination with Distribution Grid Development Using MILP. Energies 2021, 14, 383. [Google Scholar] [CrossRef]
- Laha, P.; Chakraborty, B. Cost optimal combinations of storage technologies for maximizing renewable integration in Indian power system by 2040: Multi-region approach. Renew. Energy 2021, 179, 233–247. [Google Scholar] [CrossRef]
- Frerk, M. Investing for Net Zero in the Face of Uncertainty: Real Options and Robust Decision-Making; The Oxford Martin School Programme on Integrating Renewable Energy; Working Paper; March 2021. Available online: https://www.oxfordmartin.ox.ac.uk/downloads/academic/Oxford-strategic-investment-150321.pdf (accessed on 1 November 2021).
- Giannelos, S.; Djapic, P.; Pudjianto, D.; Strbac, G. Quantification of the Energy Storage Contribution to Security of Supply through the F-Factor Methodology. Energies 2020, 13, 826. [Google Scholar] [CrossRef] [Green Version]
- Pudjianto, D.; Aunedi, M.; Djapic, P.; Strbac, G. Whole-Systems Assessment of the Value of Energy Storage in Low-Carbon Electricity Systems. IEEE Trans. Smart Grid 2014, 5, 1098–1109. [Google Scholar] [CrossRef]
- Alvarado, D.; Moreira, A.; Moreno, R.; Strbac, G. Transmission Network Investment with Distributed Energy Resources and Distributionally Robust Security. IEEE Trans. Power Syst. 2019, 34, 5157–5168. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Maris, T.I. Power quality improvement in power grids with the integration of energy storage systems. Int. J. Eng. Res. Technol. 2016, 5, 438–443. [Google Scholar]
- Papadaskalopoulos, D.; Pudjianto, D.; Strbac, G. Decentralized Coordination of Microgrids with Flexible Demand and Energy Storage. IEEE Trans. Sustain. Energy 2014, 5, 1406–1414. [Google Scholar] [CrossRef]
- Agamah, S.; Ekonomou, L. Energy storage system scheduling for peak demand reduction using evolutionary combinatorial optimization. Sustain. Energy Technol. Assess. 2017, 23, 73–82. [Google Scholar]
- Available online: https://www.iea.org/commentaries/india-is-going-to-need-more-battery-storage-than-any-other-country-for-its-ambitious-renewables-push (accessed on 1 November 2021).
- Giannelos, S.; Konstantelos, I.; Strbac, G. Investment Model for Cost-effective Integration of Solar PV Capacity under Uncertainty using a Portfolio of Energy Storage and Soft Open Points. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019. [Google Scholar] [CrossRef]
- Binder, W.R.; Paredis, C.J.J.; Garcia, H.E. The Value of Flexibility in the Design of Hybrid Energy Systems: A Real Options Analysis. IEEE Power Energy Technol. Syst. J. 2017, 4, 74–83. [Google Scholar] [CrossRef]
- Kauppinen, L.; Siddiqui, A.S.; Salo, A. Investing in Time-to-Build Projects with Uncertain Revenues and Costs: A Real Options Approach. IEEE Trans. Eng. Manag. 2018, 65, 448–459. [Google Scholar] [CrossRef]
- Moreira, A.; Pozo, D.; Street, A.; Sauma, E.; Strbac, G. Climate-aware generation and transmission expansion planning: A three-stage robust optimization approach. Eur. J. Oper. Res. 2021, 295, 1099–1118. [Google Scholar] [CrossRef]
- Moreira, A.; Strbac, G.; Fanzeres, B. An ambiguity averse approach for transmission expansion planning. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019. [Google Scholar] [CrossRef]
- Moreira, A.; Strbac, G.; Moreno, R.; Street, A.; Konstantelos, I. A Five-Level MILP Model for Flexible Transmission Network Planning Under Uncertainty: A Min–Max Regret Approach. IEEE Trans. Power Syst. 2018, 33, 486–501. [Google Scholar] [CrossRef]
- Falugi, P.; Konstantelos, I.; Strbac, G. Planning with Multiple Transmission and Storage Investment Options Under Uncertainty: A Nested Decomposition Approach. IEEE Trans. Power Syst. 2018, 33, 3559–3572. [Google Scholar] [CrossRef]
- Conejo, A.J.; Baringo, L.; Kazempour, S.J.; Siddiqui, A.S. Investment in Electricity Generation and Transmission: Decision Making under Uncertainty; Springer: New York, NY, USA, 2016. [Google Scholar]
- Long Term Electricity Demand Forecasting; Tech. Rep.; Central Electricity Authority, Ministry of Power, Government of India: New Delhi, India, 2019. Available online: https://cea.nic.in/old/reports/others/planning/pslf/Long_Term_Electricity_Demand_Forecasting_Report.pdf (accessed on 28 August 2021).
- Pradhan, G.B.; Singhal, A.K.; Bakshi, A.S.; Iyer, M.K. Determination of Transmission Tariff for 2014–15 Tariff Period; Petition No. 173/TT/2016; Central Electricity Regulatory Commission: New Delhi, India, 2017. Available online: https://cercind.gov.in/2017/orders/173_TT.pdf (accessed on 28 August 2021).




| Conventional Reinforcement Only | Conventional Reinforcement and Storage Investment | |
|---|---|---|
| Expected investment cost (GBP) | 12,097,947,208 | 26,732,242,295 |
| Conventional reinforcement (GBP) | 12,097,947,208 | 10,123,219,872.03 |
| Energy storage (GBP) | / | 16,609,022,423 |
| Expected system operation cost (GBP) | 507,853,578,872 | 480,318,047,587 |
| Expected total system cost (GBP) | 519,951,526,080 | 507,050,289,882 |
| Option Value (GBP) | / | 12,901,236,198 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannelos, S.; Jain, A.; Borozan, S.; Falugi, P.; Moreira, A.; Bhakar, R.; Mathur, J.; Strbac, G. Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty. Energies 2021, 14, 7813. https://doi.org/10.3390/en14227813
Giannelos S, Jain A, Borozan S, Falugi P, Moreira A, Bhakar R, Mathur J, Strbac G. Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty. Energies. 2021; 14(22):7813. https://doi.org/10.3390/en14227813
Chicago/Turabian StyleGiannelos, Spyros, Anjali Jain, Stefan Borozan, Paola Falugi, Alexandre Moreira, Rohit Bhakar, Jyotirmay Mathur, and Goran Strbac. 2021. "Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty" Energies 14, no. 22: 7813. https://doi.org/10.3390/en14227813
APA StyleGiannelos, S., Jain, A., Borozan, S., Falugi, P., Moreira, A., Bhakar, R., Mathur, J., & Strbac, G. (2021). Long-Term Expansion Planning of the Transmission Network in India under Multi-Dimensional Uncertainty. Energies, 14(22), 7813. https://doi.org/10.3390/en14227813







