Abstract
Nowadays, robust and efficient solid waste collection is crucial to motivate citizens to participate in the circular economy by sorting recyclable solid waste. Vocational vehicles, including garbage trucks, contribute significantly to CO emissions; therefore, it is strongly recommended, and in the European Union it is mandatory, to replace conventional-fuel-based garbage trucks with electric ones. For providing sustainable and energy-efficient solid waste collection with a heterogeneous fleet, in-depth mathematical computations are needed to support solving complex decision-making problems, including crew rostering and vehicle routing, because the distance and capacity of electric garbage trucks differ from conventional-fuel-based ones. However, the literature on solid waste collection using electric garbage trucks is still relatively scarce. The main contribution of this paper is developing an optimization problem for balancing travel distance assigned to each garbage truck of a heterogeneous fleet. The problem is based on specific requirements of the Municipal Solid Waste Management in Cracow, Poland, where the working time of routes is balanced and the total time of collection service can be minimized. For the problem, an MIP program was developed to generate optimal crew schedules, so that the hitherto network of segregated solid waste pickup nodes can be served using a heterogeneous fleet in which the share of electric garbage trucks is up to 30%. We study the impact of the changed composition of the fleet on modifications in crew rostering due to the shorter range of an electric vehicle compared to a conventional-fuel-based one.
1. Introduction
The selected solid waste collection process has been the subject of numerous research as it is an increasingly urgent and important issue faced by municipalities all over the world, because effective Solid Waste Management (SWM) is considered as an essential method for resource and energy recovery [,,,]. The existing substantial literature particularly concentrates on the Vehicle Routing Problem for garbage trucks performing the service of solid waste collection. Practical aspects of application OR-based methods (the most frequently VRPs) for improving decision-making in SWM were studied using cases of different municipalities, e.g., Rio de Janeiro, Brazil []; Austin, Texas, USA []; Malaga, Spain []; Mashhad, Iran []; Cracow, Poland [,,,]; La Palma, Spain []; Ipoh City, Malaysia []; Wageningen, the Netherlands []; and many cities in Portugal [].
According to the The European Green Deal, the EU Member Countries are obliged to achieve climate neutrality by 2050 []; therefore, it is strongly recommended—and in the European Union, to some extent, even mandatory—to replace conventional-fuel-based vocational vehicles, including garbage trucks with zero-emission ones, e.g., electric vehicles [,]. In Poland, where electromobility still holds a small share of the transportation sector [], the Act on Electromobility and Alternative Fuels obliges municipal service providers to guarantee that 30% of their fleets are comprised of zero-emission vehicles (ZEV) by 2028; the act foresees the following thresholds to reach: 5% by 2021, 10% in 2022, and 20% in 2025 []. Fleet management finds augmenting the share of electric vehicles (EV) challenging, due to the differences in the main characteristics of an electric truck compared to conventional ones [,,], e.g., range, capacity, or noise level. In terms of municipal solid waste collection, electric garbage truck performance may result in rerouting (because of the shorter electric vehicle range) and rescheduling as solid waste collection at night can be allowed (because of electric vehicles’ low noise level). With the growing share of electric garbage trucks in the fleet, the need for effective tools for routing a heterogeneous fleet also becomes more urgent. As solid waste management is getting increasingly complicated due to laws and regulations, there is a need for robust and efficient decision support systems in this area. Although the VRP for a heterogeneous fleet has been widely studied (e.g., by Coelho et al. [], Schneider et al. [], Taillard [], Matthopoulos and Sofianopoulou [], Li et al. [], Berghida and Boukra [], Kaewman and Akararungruangkul [], Liu and Cao [], Baldacci et al. [], Toth and Vigo [], Sousa et al. [], Liong et al. []) the body of knowledge on the VRPs dedicated to solid waste management is still not impressive; to the authors’ best knowledge, the garbage truck routing as a combinatorial optimization problem has neither been studied from the perspective of balancing the workload assigned to garbage trucks crew nor balancing the routes assigned to vehicles [,,,,].
There are numerous approaches to organizing the municipal segregated solid waste collection system [,,,,,]. Roughly two approaches to selected recyclables collection can be distinguished. The first system is based on picking up segregated solid waste packed separately in dedicated bin bags directly from private pickup points, i.e., an individual real estate such as a private house, an apartment house, organization headquarters, companies, office buildings and other public facilities. This system is suitable for smaller towns or agglomeration districts dominated by detached residential houses. The second system uses a network of open access pickup points equipped with big recycling bins (BRB) dedicated to segregating different types of recyclable waste. BRB locations are not linked to any real estate and citizens have unlimited open access to them. Such a system works effectively in cities or districts which are built up with residential towers. In this paper, we concentrate only on the segregated solid waste collection based on BRBs in the form adopted in the municipality of Cracow, Poland. We formulate the Recyclables Collection Route Balancing Problem (RCRBP) and solve it using Mixed-Integer Programming (MIP) for an SWM with heterogeneous fleet. The main contribution of this paper is the adoption of an objective function representing the aim to balance the route kilometrage of the serving BRBs, i.e., balancing the workload on serving BRBs assigned to garbage collector teams. Such an approach is not typical for the VRPs, but is crucial for satisfying the specific requirements of the segregated solid waste collection system under investigation [,].
The remainder of this paper is as follows: In Section 2, we briefly review the recent advantages in Solid Waste Management, i.e., selective recyclable waste collection and sustainable energy-efficient fleet management including using green garbage trucks. We give special attention to optimization models dealing with routing problems with heterogeneous fleets, as these problems are crucial for decision making in Solid Waste Management (SWM) when reaching the mandatory share of ZEV within the fleet. In Section 3, we present the newly developed Recyclables Collection Route Balancing Problem. The problem fulfils the specific requirements of the BRB service performed by the Municipal Solid Waste Management in Cracow, Poland; therefore, it aims at balancing the workload assigned to each garbage truck instead of minimizing the total cost, which makes this approach unique among the VRPs. Next, in Section 4, we formulate an extension of the Recyclables Collection Route Balancing Problem, so that the requirements of using a heterogeneous fleet composed of conventional-fuel-based and electric garbage trucks can be met. Then, the results of computational experiments are reported and discussed. As the share of ZEV in the fleet serving solid waste collection is expected to grow and have a significant impact on SWM, in Section 5 we highlight some directions for future research.
2. Recent Advances in Decision Support Systems for Solid Waste Management
The SWM becomes an increasingly complex system and that makes it more expensive and requires elaborating logistics management using in-depth mathematical computation. Electric garbage trucks become increasingly popular in agglomerations all over the world as a cleaner alternative to conventional-fuel-based vehicles. As already mentioned, the European Union obliges member countries to use green garbage trucks, which significantly influences crew rostering and vehicle routing where the solid waste collection fleet is engaged. Such a situation results in further advances on decision support tools based on modeling processes in SWM systems and the VRPs with a heterogeneous fleet (i.e., mix VRP). A detailed review in this area is provided by Hannan et al. [] and Sulemana et al. [], which cover different types of optimization, objectives and constraints on solid waste collection, optimization methods and techniques, as well as research gaps, key issues, and challenges in this field.
On the table are both well-known and completely new issues. An example of the former is the trade-off between cost optimization and risk minimization in an integrated municipal SWM network, which is addressed by Yousefloo and Babazadeh [] using a multi-objective mixed integer linear programming (MILP) model, solved using the -constraint method. The authors also included environmental aspects in the proposed model. Dolinina et al. [] propose a mathematical model for rerouting in a solid waste collection system, while Puspita et al. [] use an open capacitation VRP. An SWM is studied by Gdowska et al. [] from another perspective. Selective solid waste collection is performed by a heterogeneous fleet and the kilometrage assigned to the collector crew must be balanced. Markov et al. [] approach the recyclable waste collection problem as a vehicle routing problem with intermediate facilities, so that a heterogeneous fixed fleet and a flexible assignment of destination depots can be integrated. The problem is modeled as an MILP with several valid inequalities. Asefi et al. [] investigate a VRP for a heterogeneous fleet with the aim of cost optimization by flexibly adjusting the fleet size. The problem is modeled with a bi-objective MILP model minimizing the transportation cost in the entire waste management system and the total deviation from the fair load allocation to transfer stations.
A new problem is introduced by Kang et al. [], where modeling SWM is focused on the selective collection process of electric and electronics, because the amount of electric waste grows and becomes a challenge due to toxic chemicals and heavy metals in it. On the other hand, electric waste is considered as a valuable source of precious and base metals. The authors discuss the e-waste collection model for smart collection systems. Another innovation is proposed by Nowakowski et al. [], where an algorithm and a productive model of the online system for scheduling solid waste collection are presented. The system includes parametric models of simulated annealing, tabu search, greedy, and bee colony optimization. An Internet platform enables comprehensive communication for people that request waste equipment for collection, registering of data, and solving the vehicle routing problem with time windows (VRPTW).
Erdinç et al. [] present a Mixed-Integer Linear Programming (MILP)-based route optimization model as the first attempt explicitly for the waste-collection-oriented electric garbage truck routing process. The objective is to minimize total energy consumption, so that the solid waste collection process can be greener. Another mathematical model developed by Bányai et al. [] combines routing, assignment, and scheduling problems for the solid waste collection process. The authors concentrated on optimizing the assignment of waste sources to garbage trucks, scheduling the waste collection through routing of each garbage truck to minimize the total operation cost, and increasing reliability, meanwhile considering comprehensive environmental indicators that have great impact on public health. A binary bat algorithm is used for solving the problem. Earlier, a simulation-based approach was used to model VRPs with a heterogeneous fleet partially composed with electric garbage trucks; Vonolfen et al. [] presented simulation models for analyzing the scenarios of replacing conventional trucks with electric ones in the collection process of municipal glass waste.
3. Methodology and Materials
In this section, we present the Recyclables Collection Route Balancing Problem (RCRBP), which is the next one in the series of solid waste collection problems presented in the previous publications [,,,]. Here we consider a selective recyclables collection system which separates collection from open access BRBs and collection from recycling bins belonging directly to real estate (private pickup points); it means that to each recyclable collection route belong either BRB locations or pickup points located at real estates. The recyclables collection service is performed by one company for the entire agglomeration. The company uses a heterogeneous fleet of garbage trucks dedicated to collecting recyclables separately: (1) if a garbage truck is assigned to collect paper, it collects paper along the routes comprised of BRB locations as well as along the routes to which belong private pickup points, but (2) if a garbage truck is assigned to collect paper during the given go, it can be assigned to collect plastic on the next go, certainly after cleanup. During a working day, a garbage collector team can serve both a route in the BRB network and a route to which belong only private pickup points. In this paper, we focus exclusively on the emptying service dedicated to the network of open access BRBs. The BRB network is served with a heterogeneous fleet in which the share of electric garbage trucks constantly increases. We consider an SWM with a heterogeneous fleet of garbage trucks in which ZEVs can occupy any share. The objective is to find recyclables collection routes to be performed during a planning horizon (i.e., a certain number of planning periods), so that (1) every type of recyclable must be collected from every BRB location, (2) the working time of routes is balanced, and (3) the total time of collection service can be minimized.
We assume the demand for emptying service is deterministic, because it is estimated using historical data on filling in dynamics. The average fill level of BRBs was used also to set the frequency of emptying service during the planning horizon. The proposed approach does not consider the stochastic filling level of BRBs, because the monitoring of this index is out of the scope of the routing problem. In the SWM system on which our research is based, the filling level is not monitored by another unit and they set the size of BRBs in every location and the frequency of emptying them. For the routing problem, the size of BRBs and the frequency of service is a parameter, whose value cannot be changed. In our case, the frequency of emptying each BRB is once in a week (7 days), because the company found out that during a week the average filling level reaches ca. 60–80%. Moreover, garbage collector teams visually inspect the fill level every time and report it, so if BRBs in a given location are repeatedly filled below 50% or are overfilled, the management can analyze the data and undertake some actions, e.g., replace BRBs with smaller or bigger ones, relocate BRBs, increase the emptying frequency, etc. Finally, the analysis can show the need to reroute recyclables’ collection.
In 2019, in the agglomeration of Cracow, Poland, BRBs were located in 639 locations. According to GIS data, the distance between BRB locations ranges from 1 km to 29 km, with the average equal to 7.3 km. In every location, the citizens could dump three types of recyclable material (): plastic and metal (yellow BRBs), paper and cardboard (blue BRBs), and glass (green BRBs). The recyclable collection service was provided everyday on weekdays (from Monday until Friday), so the schedule of segregated recyclable collection comprised of 5 days (i.e., five planning periods, ). The service was performed by 12 garbage trucks (). Moreover, according to the SWM requests, each BRBs location can visit at most once a day, so that the citizens may not consider this service too arduous. There is a simplification adopted by decision makers to enable generating schedules manually without any dedicated decision support tool: each garbage truck has a fixed assignment to one type of recyclables as well as every garbage truck should serve only one route every day, so that balancing the working time of routes can be easier to obtain.
Using their knowledge and experience, the decision makers developed a Formula (1) for estimating the number of routes that guarantee collecting types of recyclables with the fleet of vehicles in planning. Note that is not proved to be the minimum number of balanced routes to serve the area. If decision makers are not supported with any optimization tool capable of minimizing the number of balanced routes of recyclables collection from BRBs, they can take it for granted that is a reasonable number of feasible routes to be performed in a relatively short time and the working time of each route is similar. Formula (1) should rather be considered as a useful tool for making a quick decision on the number of routes to design and the number of garbage trucks to engage in serving BRBs.
In the SWM system under investigation, , , and , hence , which means that in the network of 639 BRB locations we should find 20 balanced routes for the selected recyclables collection. In Table 1, we present an exemplary schedule of the selected recyclable collection prepared by decision makers using manual tools. The fleet of 12 vehicles (i.e., 12 garbage collectors teams) is divided into three groups and each group is assigned to one recyclable: Teams 1–4 to plastic, Teams 5–8 to paper, and Teams 9–12 to glass. Roman numbers (I–XX) represent 20 routes which cover 639 BRB locations. Each route is used three times a week: for collecting separately plastic, paper, and glass. Routes are assigned to teams and vehicles with respect to the total pickup demand of the route, vehicle capacity, vehicle range, etc.

Table 1.
An exemplary weekly assignment of 20 routes for selected recyclables collection (I–XX) to 12 garbage collectors teams and vehicles in the agglomeration of Cracow, Poland.
Note that in the schedule presented in Table 1 each garbage collector team (i.e., each vehicle) has a fixed assignment to one recyclable. After careful analysis of fleet capacity, fleet range, distances between BRB locations, and historical data on pickup demand that the number of vehicles engaged in serving BRBs should be reasonably low (and not necessarily minimum), but must guarantee proper service at every BRB location. Moreover, a route assigned to a garbage truck must be performed in one go. This is why Teams 1–12 every day serve only one route each, because for the rest of the working day the collectors teams and vehicles are engaged in performing other activities.
The heuristic method of assignment and routing presented above is handy and provides feasible solutions with acceptable effort and computation time. However, the obtained solutions cannot be considered optimal, because the method assumes using every available collectors team and vehicle, even if a smaller number of teams was sufficient to perform the service. Moreover, the method does not guarantee indisputable balancing the working time assigned to routes, because the routing is separated from the assignment problem. For these reasons, we would like to propose an OR-based hierarchical approach combining clustering BRB locations and balancing the working time of garbage collectors teams engaged in serving BRBs.
4. Recyclables Collection Route Balancing Problem
In our research, we take the SWM system described in Section 3 as the reference for formulating the optimization problem called the Recyclables Collection Route Balancing Problem (RCRBP). The objective is to find routes for segregated solid waste collection to be performed in planning horizon . Recyclables are represented by set , so the decision maker may decide on the number of recyclables to be picked up separately basing on the specific features of the installation for processing segregated recyclables. Recyclables are collected by a fleet of garbage trucks ( ). The recyclables collection system is represented by a graph , where is the set of nodes, and is the set of edges. In set nodes represent pickup points (BRB locations), except nodes 0 and n; node 0 is the depot where all the garbage trucks start and end their routes, while n represents a recycling center, which must be visited by every garbage truck to unload the collected recyclables.
The problem is deterministic, and for each recyclable r we know in advance the amount to be picked up from pickup point j during the whole planning horizon (). Each garbage truck v has its characteristic capacity . Note that parameters and have the same unit based on the volume after compression. The RCRBP is less restrictive and allows the vehicle v to collect different types of recyclables during the planning horizon on condition that the vehicle is assigned to only one type each day. For each edge, , we know the travel time between nodes i and j (), so we can easily compute the distance between i and j. For each garbage truck v we know its maximum working time ; as working time is equal to driving time of garbage truck v, we can use to compute the maximum range of vehicle v.
Binary variable yields value 1, if garbage truck v goes from node i to node j to collect recyclable r; otherwise, variable yields value 0. The binary variable is equal to 1 if garbage truck v collects recyclable r in planning period t, otherwise is equal to 0. Non-negative variable represents the moment of the arrival of garbage truck v at pickup point j in planning period t.
Using the notation presented above, we can define the following MIP model for the Recyclables Collection Route Balancing Problem:
The objective function (2) minimizes the average working time (i.e., distance) in the system, so that the working time (i.e., kilometrage) assigned to each garbage truck (collector crew) can be balanced. Such an approach is typical for lot scheduling problems (such as the key performance indicator ) but it is unusual for VRPs. Such an objective function suits the RCRBP as it is mandatory to use all vehicles in the fleet and exploit them to the same extent and intensity.
Constraints (3) assure that in the planning period, t, at most one garbage truck, v, collecting recyclables, r, traverses edge, , i.e., garbage truck v goes from pickup point i directly do pickup point j. Moreover, in the planning period, t vehicle v is allowed to collect only recyclable r from pickup point j, to which the garbage truck comes directly from pickup point i (4). Constraints (5) guarantee that recyclables of all types are collected from each node during the planning horizon, while constraints (6) assure that in each planning period vehicle v is allowed to collect recyclables of one type r top. In the planning period t, the amount of collected recyclables cannot exceed maximum capacity of vehicle v (); it means that the capacity of a garbage truck A assigned to the route Z must be at least equal to the total capacity of BRBs to be collected along this rout. In other words, even if all BRBs belonging to the route Z are 100% filled, the capacity of garbage truck A is large enough to empty all bins. Constraint (7) guarantees that in planning period tdemand for collecting recyclables r () cannot exceed capacity of vehicle v (). This constraint requires the restrictive assumption that in the planning period t vehicle v can visit the recycling center and get unloaded only once. Such a simplification is allowed when the problem is adjusted to the specific requirements of a segregated solid waste collection system with BRBs in Cracow, Poland, where each garbage truck serves one type of recyclables in a given day and collects them from BRBs belonging to one route. The last location belonging to the route is the recycling center. For the rest of the day, the garbage truck is used for other tasks, e.g., collecting recyclables from detached houses in a residential district, but these tasks are out of the scope of the research to which this paper refers.
Constraints (8) assure that loops from node i to node i are avoided, while constraints (9) guarantee that loops in the route of vehicle v are also forbidden. Constraints (10) guarantee that in the planning period t picking point i is served at most once no matter what type of recyclables is collected from this node; in other words, at most one type of recyclables can be picked up from node i in planning period t. Flow constraints (11) assure that if vehicle v enters picking point i, in the planning period, the t must also leave it.
Constraints (12)–(14) integrate the model by establishing the relationship between decision variables and . If in the planning period t, garbage truck v picks up recyclables r from pickup point i, then this garbage truck in this planning period can collect only recyclable r. Constraints (13) guarantee that each garbage truck has a mandatory stop at node n, where the vehicle is unloaded. To reinforce the mutual dependencies between decision variables, constraints (14) narrow the feasible region.
Constraints (15) and (16) enable the computation of the arrival time (i.e., distance) of garbage truck v at pickup point i in planning period t. Arrival times are computed only if in the planning period t garbage truck v traverses edge , otherwise big constant M makes these contracts “inactive”. Constraints (17) set arrival at node 0 to 0, which is interpreted as departure from depot and the beginning of the route of vehicle v in planning period t. Similarly, constraints (18) forbid the use of vehicle v after the end of working day .
The newly developed MIP model for RCRBP shows that it is possible to solve a real decision-making problem using an exact method after adjusting it to the requirements of the selected solid waste collection system. Here, an innovation is the adoption of an objective function representing balanced working time, i.e., balancing the routes assigned to garbage collectors teams. Therefore, the RCRBP can be used as a part of the decision support system in SWM for generating optimal weekly schedules of serving BRBs, despite the computation time for an MIP model potentially being relatively long. The weekly schedule of collecting segregated recyclables from BRBs is not frequently modified. Moreover, the locations of BRBs hardly change over a long time, so that the citizens may not change their habit of segregating recyclables with BRBs in fixed locations.
Due to the fact that this scheduling problem belongs to strategic decision making, we can invest some time in computations to obtain an optimal or suboptimal solution using an exact method. Therefore, despite RCRBP for large-size instances cannot be solved in polynomial time, it still can be a useful decision support tool, because after clustering we can obtain small- and medium-size instances, for which the optimal solution can be found in acceptable computational time. The MIP model can also be the point of reference for effective heuristics or meta-heuristics, which can find suboptimal solutions in a reasonable time.
4.1. RCRBP Adapted for Using Electric Garbage Trucks
Adjusting the RCRBP for the fleet partially composed electric garbage trucks some alterations are needed: (1) Removing the index t from decision variable , so it can be replaced with new decision variable . Variable yields value 1, if garbage truck v collects recyclables r during entire planning horizon, otherwise is equal to 0. (2) Constraints need to be modified in the way presented in Formulas (19)–(22).
Modified constraints (19) assure that during the entire planning horizon, vehicle v serves only one type of recyclables r. Constraints (20) were modified by introducing variables and . If a garbage truck v departs from the depot to pickup point j to collect the recyclables r, then this vehicle is allowed to collect exclusively recyclables r during the entire planning horizon. Modified constraints (21) guarantee that every garbage truck travels to the recycling center (node n) where it can get unloaded. Constraints (22) still narrow the feasible region by strengthening the relationship between decision variables and .
When the minimum requested number of routes (e.g., computed using Formula (1)), next two constraints—(23) and (24)—must be added to the MIP model. If each garbage truck is assigned to at most one type of garbage, it is sufficient to only add constraints (24).
4.2. Computational Experiments
Computational experiments were conducted with the aim to find the size of instance of the RCRBP for which the presented MIP model can be solved using a standard computer, because the model is supposed to be used in the company using typical available computational power. We used solver GUROBI 9.0.1 and a computer equipped with a two-core processor Intel Core i7-4710HQ CPU @2.50 GH and RAM 16 GB. There was no expectation to find a ready-to-implement route merely to test the RCRBP for an aggregated BRB network and its flexibly changed composition of the heterogeneous garbage truck fleet.
To conduct experiments with a clustering algorithm, we randomly generated a BRB network using an empirical probability distribution based on historical data. Randomly generated instances were used for validating and verifying the model, so that we could demonstrate its universal applicability for problems of the RCRBP family. In the recyclable collection system with BRBs, the distances between BRB locations were in the range 1–29 km, distances between with the average equal to 7.3 km (see Section 3). In Table 2, we present real distances, their standardized values, frequencies, and cumulative frequency; the data were used for developing the probability distribution function used for generating random instances. The obtained probability distribution was standardized and then the cumulative distribution function was computed (see Table 2). The empirical distribution of historical data is presented in Figure 1, while Figure 2 shows the probability distribution function fitted to the empirical distribution.

Table 2.
Data used to develop cumulative distribution function of the distances between pickup points (BRB locations) used for generating random instances for computational experiments.
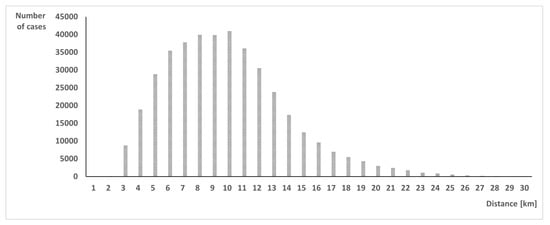
Figure 1.
Empirical distribution of the distance between BRB locations—historical data.
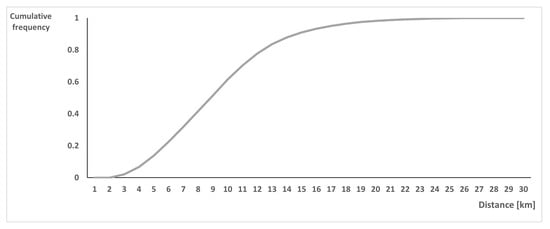
Figure 2.
Cumulative distribution function of the distance between pickup points (BRB locations) used for generating random instances for computational experiments.
Similarly to the referential SWM system in the agglomeration of Cracow, Poland, the instance data are comprised of three types of recyclables to be collected during the five-day planning horizon. We adopt a strong simplification assuming that the demand for collection service is identical in every pickup point and it is equal to 1. Selective recyclables collection was to be performed by a fleet of 12 garbage trucks. We assume that 5 vehicles (i.e., ca. 40% of the fleet) are replaced by electric garbage trucks, whose range is up to 150 km, when the average route in the system under investigation is ca. 219 km. We assume the range of conventional-fuel-based vehicles has no upper limit. The total capacity of the fleet must (according to the problem description) be at least equal to the total demand. Therefore, there should not be a situation when the total demand is greater than the total vehicle capacity. Moreover, we assume that the BRB service frequency is adjusted to BRB fill level, so the amount of recyclables to be picked up never exceeds the BRB capacity. As it has already been mentioned, the filling level is monitored by another unit, so we can assume that the location and sizes of BRB answer properly the citizens’ needs.
As the network of 639 BRB locations can be considered as a large-size instance, we used the clustering algorithm to aggregate BRB locations to get smaller instances of, respectively, 10, 15, and 20 pickup points (see Figure 3). Clustering is indispensable for getting instances solvable on a standard computer, as the VRPs are not solvable in polynomial time []. For clustering, we used the k-mean algorithm (the centroid algorithm). After clustering, the demand of clustered BRB points was aggregated. Certainly, any other clustering algorithm can be used for this problem with the same efficacy, because the goal is not to find routes but only to verify and validate the MIP model. A much more efficient approach is to obtain an optimal solution for a small-sized instance of clustered BRB location using an exact method (i.e., MIP) and then find a route within the cluster using an efficient heuristic algorithm.
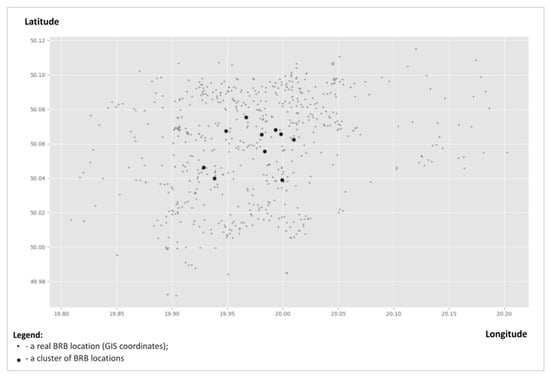
Figure 3.
Clustering 639 BRBs locations to 10 pickup points using k-mean algorithm.
For further experiments with the MIP model, we selected three instances of the following size: 10, 15, and 20 clusters, i.e., aggregated BRB locations. Instances were generated using the probability distribution function described at the beginning of this subsection. We considered two types of the RCRBP: (A) when each garbage truck has a fixed assignment of one type of recyclables, and (B) when the minimum number of routes is defined. Note that the RCRBP(A) is far less restrictive than the way of generating pickup schedules adopted by the decision makers of the company (see Section 3), while the RCRBP(B) is an attempt to mirror the decision makers’ approach with the predefined number of routes. The aim was to determine the recyclable collection routes, so that the total working time (based on distance) is minimized, i.e., the routes are balanced in terms of working time. Parameters used for the performed computations are presented in Table 3: we have instances of three sizes: 10, 15, and 20 aggregated pickup points to be served by maximum 12 garbage trucks including five ZEVs. In experiments with the RCRBP(B), we assume that the minimum number of routes is 20. Certainly, due to the clustered working time (distance) and aggregated pickup demand, we can expect that routes usually consist of one clustered pickup point. An interesting thing to observe will be the number of vehicles used to serve the system and their assignment to recyclables and routes. Here we can expect differences from the solutions generated manually by the decision makers. This is also the area where savings on vehicle usage and kilometrage can be made.

Table 3.
Parameters used in computational experiments.
Obtained results are presented in Table 4. The quality of solutions were assessed using measurement, which is the gap between the obtained feasible MIP solution and the best estimation for the problem being solved for the given data instance.
where:
—the best estimation for the instance,
—the best MIP solution for the instance.

Table 4.
Summarization of the results of computational experiments.
Table 4.
Summarization of the results of computational experiments.
| Instance | I | II | III | ||||
|---|---|---|---|---|---|---|---|
| Type of the RCRBP | A | B | A | B | A | B | |
| Instance size | |||||||
| Number of rows | 37,525 | 37,917 | 82,915 | 83,582 | 146,305 | 147,247 | |
| Number of columns | 18,780 | 18,636 | 41,580 | 41,436 | 73,380 | 73,236 | |
| The quality of obtained solution after 600, 1800 and 3600 s of computations | |||||||
| GAP [%] for | 600 [sec.] | 83.5 | 80.1 | 86.7 | 87.5 | 93.7 | 91.3 |
| 1800 [sec.] | 77.7 | 79.8 | 85.2 | 83.9 | 91.1 | 90.4 | |
| 3600 [sec.] | 77.7 | 76.5 | 85.1 | 83.5 | 90.4 | 90.2 | |
In Table 4, the obtained results are presented. The first and foremost observation is the exponential growth of the size of instances: for 10 clusters (instance I) the size of RCRBP(A) as the MIP problem is 37,525 × 18,780, for 15 clusters—82,915 × 41,520, and for 20 clusters—146,305 × 73,380. Moreover, the gap between MIP solutions obtained after 600, 1800, and 3600 s of computation and the optimal solution found for the linearized problem is great and range from 77.7% up to 93.7%. The gap increases with the growth of instance size. These observations confirm that the problem can be solved with exact methods only for small-sized instances and there is a great need for efficient algorithms for clustering and routing to be used to obtain applicable schedules based on the initial solutions found using MIP model.
We would like to emphasize that the assumption which helps the decision maker in generating recyclables pickup schedules using manual tools, i.e., computing the minimum number of routes (), may make the MIP model more almost imperceptibly less complicated. We can compare the size of instances for RCRBP(A) and RCRBP(B) for the same case: in case I (10 clusters), the number of columns of the RCRBP(A) is 18,780 while the the number of columns of the RCRBP(B) is 18,636; in case II (15 clusters) they are, respectively, 41,580 and 41,436; in case III (20 clusters) they are, respectively, 73,380 and 73,236. Nevertheless, introducing the required minimum number of routes to the problem can change significantly the obtained results, i.e., the number of routes and the assignment of collectors teams to routes and to recyclables. As a consequence, it may have a relevant impact on the total operational costs.
5. Conclusions
To summarize the obtained results, we must clearly state that research on the SWM systems with the fleet fully of partially consisting of ZEVs is scarce but urgently required. Thr presented example of the use of an exact method for decision system support is possible, despite the obvious limitations of them. However, on the level of strategic decision-making, these limitations can be overcome and the results may be used for such fleet routing, which results in decreasing energy usage and carbon footprint of segregated recyclables collection.The RCRBP presented in this paper has already been utilized for solving instances based on historical data, but future research should concentrate on testing the schedules obtained with the RCRBP in a real system.
The RCRBP and the developed MIP model can serve as a useful tool for assessing the fulfillment of the SWM’s requirements and goals. Using the model, we cannot receive the ready-to-implement recyclables collection schedules, because of the complexity of the problem. However, optimal solutions for small-sized instances with clustered BRB locations can be used as the initial solutions for other efficient routing algorithms, so that recyclables collection routes and schedules can be easily modified if changes in pickup demand occurred.
This paper justifies the need for new models for routing the fleet serving a segregated recyclable collection system. Due to the different requirements of SWMs, also atypical approaches to defining the problem can be successfully launched, such as the one used for the RCRBP.
Apart from developing tools based on exact methods, computer simulations are needed to enable experiments with real data on the fleet (number of vehicles, their range, and capacity), crew (different team sizes), operational costs (travel costs, staff costs, etc.) as well as stochastic recyclables’ pickup demand.
The future research in this area should be focused on including more flexible garbage trucks in the problem, e.g., vehicles with compartments which can collect separately two types of recyclables in one go. Moreover, the BRBs in the SWM under consideration are not equipped with sensors monitoring the filling level, so for the time being, the collection system is not included in the Internet of Things. The fill level is visually inspected by collectors at every emptying service and reported to the management. These data are taken into consideration by decision makers during developing a routing strategy and changing BRBs locations or capacity. Data collected constantly could have brought interesting insights into the BRB filling dynamics and could have resulted in new routing strategies. Finally, the research should be concentrated on minimizing operational costs influenced by environmental decisions such as renewing the garbage trucks fleet with ZEVs.
Author Contributions
Conceptualization, R.K., K.G. and A.K.; methodology, K.G. and R.K.; software, R.K.; validation, R.K., A.K. and K.G.; formal analysis, A.K.; investigation, K.G., R.K. and A.K.; resources, A.K.; data curation, A.K.; writing—original draft preparation, K.G.; writing—review and editing, K.G., R.K. and A.K.; visualization, R.K.; supervision, A.K.; project administration, A.K.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the AGH University of Science and Technology with the grant for the maintenance of research potential. Research project supported by the program Excellence initiative—research university” at the AGH University of Science and Technology in Cracow, Poland.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funding institution had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BRB | Big Recycling Bin |
| DM | Decision Making |
| EV | Electric Vehicle |
| GIS | Geographic Information System |
| MIP | Mix Integer Programming |
| OR | Operations Research |
| RCRBP | Recyclables Collection Route Balancing Problem |
| SWM | Solid Waste Management |
| VRP | Vehicle Routing Problem |
| ZEV | Zero Emission Vehicle |
References
- Parameswari, K.; Majid Salim Al Aamri, A.; Gopalakrishnan, K.; Arunachalam, S.; Ali Said Al Alawi, A.; Sivasakthivel, T. Sustainable landfill design for effective municipal solid waste management for resource and energy recovery. Mater. Today Proc. 2021, 47, 2441–2449. [Google Scholar] [CrossRef]
- Kaur, A.; Bharti, R.; Sharma, R. Municipal solid waste as a source of energy. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Kundaria, N.; Sabyasachi Mohanty, S.; Varjani, S.; Hao Ngo, H.; Wong, J.W.; Taherzadeh, M.J.; Chang, J.S.; Yong Ng, H.; Kim, S.H.; Bui, X.T. A review on integrated approaches for municipal solid waste for environmental and economical relevance: Monitoring tools, technologies, and strategic innovations. Bioresour. Technol. 2021, 342, 125982. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, U.R.; Aparecida Neto, L.; Abreu, P.A.F.; Fernandes, V.A. Risk management applied to the reverse logistics of solid waste. J. Clean. Prod. 2021, 296, 126517. [Google Scholar] [CrossRef]
- Franca, L.S.; Ribeiro, G.M.; Chaves, G.d.L.D. The planning of selective collection in a real-life vehicle routing problem: A case in Rio de Janeiro. Sustain. Cities Soc. 2019, 47, 101488. [Google Scholar] [CrossRef]
- Vu, H.L.; Ng, K.T.W.; Fallah, B.; Richter, A.; Kabir, G. Interactions of residential waste composition and collection truck compartment design on GIS route optimization. Waste Manag. 2019, 102, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, J.; Alba, E. BIN-CT: Urban waste collection based on predicting the container fill level. Biosystems 2019, 186, 103962. [Google Scholar] [CrossRef] [PubMed]
- Erfani, S.M.H.; Danesh, S.; Karrabi, S.M.; Shad, R.; Nemati, S. Using applied operations research and geographical information systems to evaluate effective factors in storage service of municipal solid waste management systems. Waste Manag. 2018, 79, 346–355. [Google Scholar] [CrossRef]
- Jakubiak, M.; Hanczar, P. Optymalizacja tras zbiórki odpadów komunalnych na przykładzie MPO Kraków / Optimization of municipal solid waste collection and transportation routes on the example of MPO Cracow. Pr. Nauk. Uniw. Ekon. Wrocławiu 2016, 446, 83–92. [Google Scholar] [CrossRef]
- Jakubiak, M. The Improvement in Collection of Municipal Waste on the Example of a Chosen Municipality. Transp. Res. Procedia 2016, 16, 122–129. [Google Scholar] [CrossRef][Green Version]
- Korcyl, A.; Ksia̧żek, R.; Gdowska, K. A MILP Model for the Municipal Solid Waste Selective Collection Routing Problem. Decis. Mak. Manuf. Serv. 2019, 13, 17–35. [Google Scholar] [CrossRef]
- Gdowska, K.; Ksia̧żek, R.; Korcyl, A. Fleet Optimization for a Selective Solid Waste Collection System. In Challanges and Modern Solution in Transportation; Stajniak, M., Kopeć, M., Adrianna Toboła, M.S., Eds.; Instytut Naukowo-Wydawniczy Spatium: Radom, Poland, 2019; pp. 121–134. [Google Scholar]
- Expósito-Márquez, A.; Expósito-Izquierdo, C.; Brito-Santana, J.; Moreno-Pérez, J.A. Greedy randomized adaptive search procedure to design waste collection routes in La Palma. Comput. Ind. Eng. 2019, 137, 106047. [Google Scholar] [CrossRef]
- Malakahmad, A.; Bakri, P.M.; Mokhtar, M.R.M.; Khalil, N. Solid Waste Collection Routes Optimization via GIS Techniques in Ipoh City, Malaysia. Procedia Eng. 2014, 77, 20–27. [Google Scholar] [CrossRef]
- Bing, X.; Keizer, M.; Bloemhof-Ruwaard, J.M.; van der Vorst, J.G.A.J. Vehicle routing for the eco-efficient collection of household plastic waste. Waste Manag. 2014, 34, 719–729. [Google Scholar] [CrossRef]
- Ramos, T.R.P.; Morais, C.S.; Barbosa-Póvoa, A.P. The smart waste collection routing problem: Alternative operational management approaches. Expert Syst. Appl. 2018, 103, 146–158. [Google Scholar] [CrossRef]
- European Commission. A Clean Planet for All, A European Strategic Long Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52018DC0773&from=EN (accessed on 15 September 2021).
- Koiwanit, J.; Hamontree, C. Greenhouse gas emissions comparison of solid waste transportation system: A case study in Thailand. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Changchun, China, 21–23 August 2020; Volume 424. [Google Scholar] [CrossRef]
- Schmid, F.; Taube, L.; Rieck, J.; Behrendt, F. Electrification of Waste Collection Vehicles: Technoeconomic Analysis Based on an Energy Demand Simulation Using Real-Life Operational Data. IEEE Trans. Transp. Electrif. 2021, 7, 604–615. [Google Scholar] [CrossRef]
- Skowrońska-Szmer, A.; Kowalska-Pyzalska, A. Key Factors of Development of Electromobility AMONG Microentrepreneurs: A Case Study from Poland. Energies 2021, 14, 764. [Google Scholar] [CrossRef]
- Polish Parliament. Ustawa z Dnia 11 Stycznia 2018 r. o Elektromobilności i Paliwach Alternatywnych. Available online: http://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20180000317 (accessed on 15 September 2021).
- Elangovan, R.; Kanwhen, O.; Dong, Z.; Mohamed, A.; Rojas-Cessa, R. Comparative Analysis of Energy Use and Greenhouse Gas Emission of Diesel and Electric Trucks for Food Distribution in Gowanus District of New York City. Front. Big Data 2021, 4. [Google Scholar] [CrossRef]
- California Air Resources Board. California Air Resources Board. Battery Electric Truck and Bus Energy Efficiency Compared to Conventional Diesel Vehicles. Available online: https://ww2.arb.ca.gov/resources/documents/carb-technical-analysis-evcharging-infrastructure-nonresidential-calgreen (accessed on 15 September 2021).
- MSW Management. Preparing for the Future of Electric Garbage Trucks. Available online: https://www.mswmanagement.com/collection/collection-vehicles/article/21213526/preparing-for-the-future-of-electric-garbage-trucks (accessed on 15 September 2021).
- Coelho, V.; Grasas, A.; Ramalhinho, H.; Coelho, I.; Souza, M.; Cruz, R. An ILS-based algorithm to solve a large-scale real heterogeneous fleet VRP with multi-trips and docking constraints. Eur. J. Oper. Res. 2016, 250, 367–376. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Taillard, É.D. A heuristic column generation method for the heterogeneous fleet VRP. RAIRO Oper. Res. 1999, 33, 1–14. [Google Scholar] [CrossRef]
- Matthopoulos, P.P.; Sofianopoulou, S. A firefly algorithm for the heterogeneous fixed fleet vehicle routing problem. Int. J. Ind. Syst. Eng. 2019, 33, 204–224. [Google Scholar] [CrossRef]
- Li, J.; Wang, M.G.; Tang, L.X.; Song, J.H. Special kind of vehicle routing problem. Dongbei Daxue Xuebao/J. Northeast. Univ. 2001, 22, 245–248. [Google Scholar]
- Berghida, M.; Boukra, A. Quantum Inspired Algorithm for a VRP with Heterogeneous Fleet Mixed Backhauls and Time Windows. Int. J. Appl. Metaheuristic Comput. 2016, 7, 18–38. [Google Scholar] [CrossRef]
- Kaewman, S.; Akararungruangkul, R. Heuristics Algorithms for a Heterogeneous Fleets VRP with Excessive Demand for the Vehicle at the Pickup Points, and the Longest Traveling Time Constraint: A Case Study in Prasitsuksa Songkloe, Ubonratchathani Thailand. Logistics 2018, 2, 15. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, B. Solving full-vehicle-mode vehicle routing problems using ACO. In ICCL 2018: Computational Logistics; Springer: New York, NY, USA, 2018; pp. 306–315. [Google Scholar]
- Baldacci, R.; Battarra, M.; Vigo, D. Routing a heterogeneous fleet of vehicles. In The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: Boston, MA, USA, 2008; pp. 3–27. [Google Scholar]
- Toth, P.; Vigo, D. Vehicle Routing; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014. [Google Scholar] [CrossRef]
- Sousa, J.C.; Biswas, H.A.; Brito, R.; Silveira, A. A Multi Objective Approach to solve Capacitated Vehicle Routing Problems with Time Windows Using Mixed Integer Linear Programming. Int. J. Adv. Sci. Technol. 2011, 28, 1–8. [Google Scholar]
- Liong, C.Y.; Wan Rosmanira, I.; Khairuddin, O.; Mourad, Z. Vehicle Routing Problem: Models and Solutions. J. Qual. Meas. Anal. 2008, 4, 205–218. [Google Scholar]
- Hannan, M.A.; Akhtar, M.; Begum, R.A.; Basri, H.; Hussain, A.; Scavino, E. Capacitated vehicle-routing problem model for scheduled solid waste collection and route optimization using PSO algorithm. Waste Manag. 2018, 71, 31–41. [Google Scholar] [CrossRef] [PubMed]
- Nowakowski, P.; Szwarc, K.; Wala, M. Investigation of the sustainable waste transportation in urban and rural municipalities—Key environmental parameters of the collection vehicles use. In Circular Economy and Sustainability; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Ghiani, G.; Laganà, D.; Manni, E.; Musmanno, R.; Vigo, D. Operations research in solid waste management: A survey of strategic and tactical issues. Comput. Oper. Res. 2014, 44, 22–32. [Google Scholar] [CrossRef]
- Kargin, R.V.; Yakovlev, I.A.; Shemshura, E.A. Modeling of Workflow in the Grip-Container-Grip System of Body Garbage Trucks. Procedia Eng. 2017, 206, 1535–1539. [Google Scholar] [CrossRef]
- Lobov, N.V.; Maltsev, D.V.; Genson, E.M. Improving the process of transport of solid municipal waste by automobile transport. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; Volume 632. [Google Scholar] [CrossRef]
- Soni, A.; Patil, D.; Argade, K. Municipal Solid Waste Management. Procedia Environ. Sci. 2016, 35, 119–126. [Google Scholar] [CrossRef]
- Asefi, H.; Shahparvari, S.; Chhetri, P. Advances in sustainable integrated solid waste management systems: Lessons learned over the decade 2007–2018. J. Environ. Plan. Manag. 2020, 13, 1–26. [Google Scholar] [CrossRef]
- Bernstad Saraiva, A.; Souza, R.G.; Mahler, C.F.; Valle, R.A. Consequential lifecycle modelling of solid waste management systems—Reviewing choices and exploring their consequences. J. Clean. Prod. 2018, 488–496. [Google Scholar] [CrossRef]
- Ahsan, A.; Alamgir, M.; El-Sergany, M.M.; Shams, S.; Rowshon, M.K.; Daud, N.N.N. Assessment of Municipal Solid Waste Management System in a Developing Country. Chin. J. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- ElSaid, S.; Aghezzaf, E.H. A progress indicator-based assessment guide for integrated municipal solid-waste management systems. J. Mater. Cycles Waste Manag. 2018, 20, 850–863. [Google Scholar] [CrossRef]
- Rodrigues, J.; Gondran, N.; Beziat, A.; Laforest, V. Application of the absolute environmental sustainability assessment framework to multifunctional systems—The case of municipal solid waste management. J. Clean. Prod. 2021, 322, 129034. [Google Scholar] [CrossRef]
- Hanczar, P. Wspomaganie decyzji w obszarze wyznaczania tras pojazdów. Decyzje 2010, 13, 55–83. [Google Scholar]
- Gdowska, K.; Ksia̧żek, R.; Korcyl, A. Solving the garbage truck routing problem for collecting recyclables from big recycling bins using the VRP spreadsheet solver. Sci. Bull. Flight Acad. Sect. Econ. Manag. Law 2020, 2, 63–72. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hossain Lipu, M.S.; Akhtar, M.; Begum, R.A.; Al Mamun, M.A.; Hussain, A.; Mia, M.S.; Basri, H. Solid waste collection optimization objectives, constraints, modeling approaches, and their challenges toward achieving sustainable development goals. J. Clean. Prod. 2020, 277, 123557. [Google Scholar] [CrossRef]
- Sulemana, A.; Donkor, E.A.; Forkuo, E.K.; Oduro-Kwarteng, S. Optimal Routing of Solid Waste Collection Trucks: A Review of Methods. J. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Yousefloo, A.; Babazadeh, R. Designing an integrated municipal solid waste management network: A case study. J. Clean. Prod. 2020, 244, 118824. [Google Scholar] [CrossRef]
- Dolinina, O.; Pechenkin, V.; Gubin, N.; Aizups, J.; Kuzmin, A. Development of semi-adaptive Waste Collection Vehicle Routing Algorithm for agglomeration and urban settlements. In Proceedings of the 2019 IEEE 7th IEEE Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Liepaja, Latvia, 15–16 November 2019. [Google Scholar] [CrossRef]
- Puspita, F.M.; Hartono, Y.; Syaputri, N.Z.; Yuliza, E.; Pratiwi, W.D. Robust Counterpart Open Capacitated Vehicle Routing (RC-OCVRP) Model in Optimization of Garbage Transportation in District Sako and Sukarami, Palembang City. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 4382–4390. [Google Scholar] [CrossRef]
- Markov, I.; Varone, S.; Bierlaire, M. Integrating a heterogeneous fixed fleet and a flexible assignment of destination depots in the waste collection VRP with intermediate facilities. Transp. Res. Part B Methodol. 2016, 84, 256–273. [Google Scholar] [CrossRef]
- Asefi, H.; Shahparvari, S.; Chhetri, P.; Lim, S. Variable fleet size and mix VRP with fleet heterogeneity in Integrated Solid Waste Management. J. Clean. Prod. 2019, 230, 1376–1395. [Google Scholar] [CrossRef]
- Kang, K.D.; Kang, H.; Ilankoon, I.; Chong, C.Y. Electronic waste collection systems using Internet of Things (IoT): Household electronic waste management in Malaysia. J. Clean. Prod. 2020, 252, 119801. [Google Scholar] [CrossRef]
- Nowakowski, P.; Szwarc, K.; Boryczka, U. Vehicle route planning in e-waste mobile collection on demand supported by artificial intelligence algorithms. Transp. Res. Part D Transp. Environ. 2018, 63, 1–22. [Google Scholar] [CrossRef]
- Erdinç, O.; Yetilmezsoy, K.; Erenoğlu, A.K.; Erdinç, O. Route optimization of an electric garbage truck fleet for sustainable environmental and energy management. J. Clean. Prod. 2019, 234, 1275–1286. [Google Scholar] [CrossRef]
- Bányai, T.; Tamás, P.; Illés, B.; Stankevičiūtė, Ž.; Bányai, Á. Optimization of Municipal Waste Collection Routing: Impact of Industry 4.0 Technologies on Environmental Awareness and Sustainability. Int. J. Environ. Res. Public Health 2019, 16, 634. [Google Scholar] [CrossRef]
- Vonolfen, S.; Affenzeller, M.; Beham, A.; Wagner, S.; Lengauer, E. Simulation-based evolution of municipal glass-waste collection strategies utilizing electric trucks. In Proceedings of the 3rd IEEE International Symposium on Logistics and Industrial Informatics, Budapest, Hungary, 25–27 August 2011. [Google Scholar] [CrossRef]
- Korcyl, A.; Gdowska, K.; Ksia̧żek, R. Optymalizacja tras odbioru odpadów komunalnych z wykorzystaniem różnych typów pojazdów i ograniczeniami czasowymi w obsłudze klienta. Logistyka 2015, 4, 9202–9211. [Google Scholar]
- Korcyl, A.; Gdowska, K.; Ksia̧żek, R. A MILP Model for Route Optimization Problem in a Municipal Multi-Landfill Waste Collection System. In Proceedings of the ICIL 2016: 13th International Conference on Industial Logistics, Zakopane, Poland, 28 September–1 October 2016; pp. 109–118. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).