Formation of Characteristic Polynomials on the Basis of Fractional Powers j of Dynamic Systems and Stability Problems of Such Systems
Abstract
1. Introduction
2. Analysis of the Influence of the Roots’ Location of a Characteristic Polynomial on the System Stability
2.1. All Roots Are Real Numbers and Are Located on the Left Half-Plane
2.2. The Case When Even One Real Root Is Placed in the Right Half-Plane
2.3. The Case When All Roots Are Complex-Conjugate Numbers with Negative Real Part
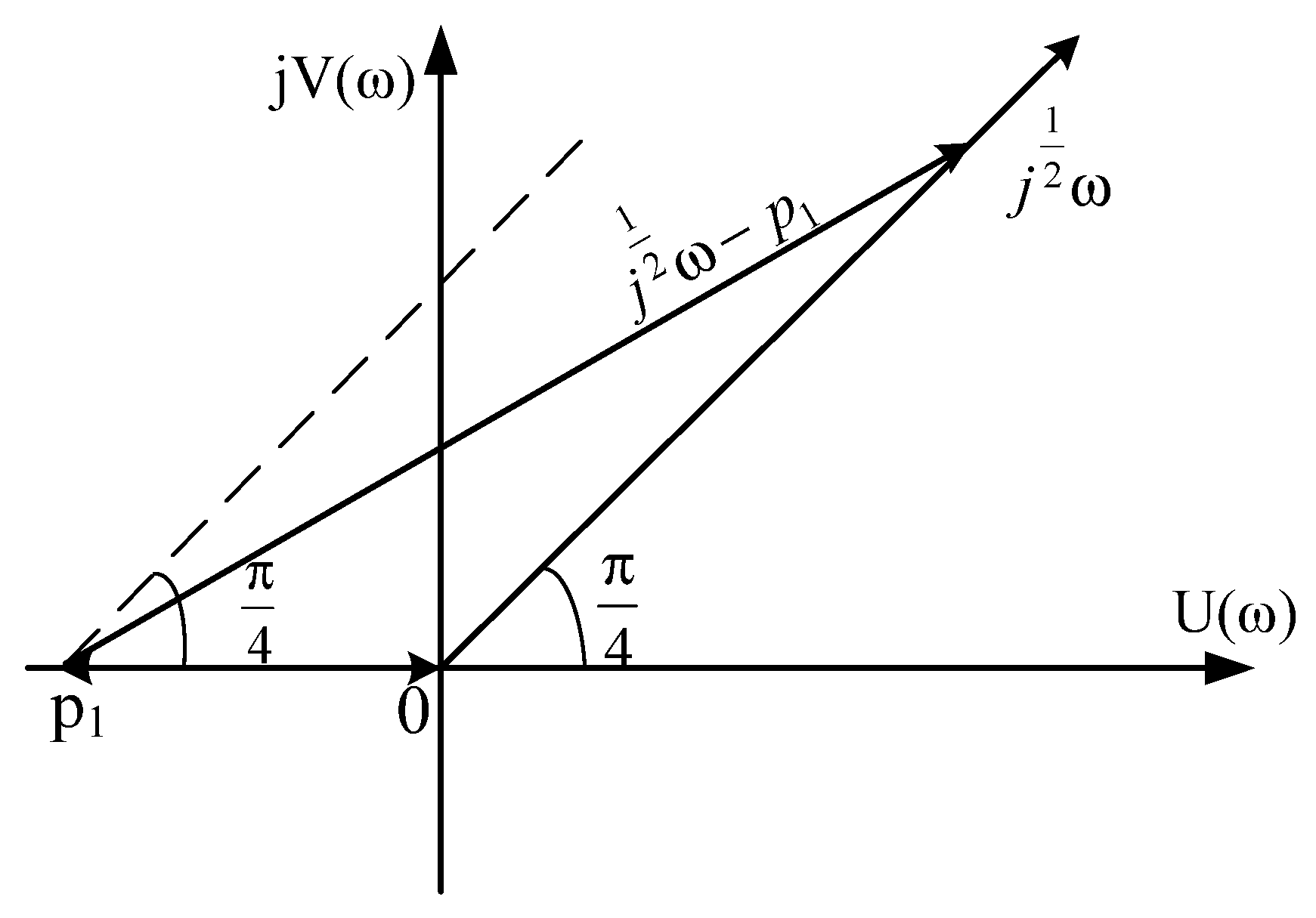
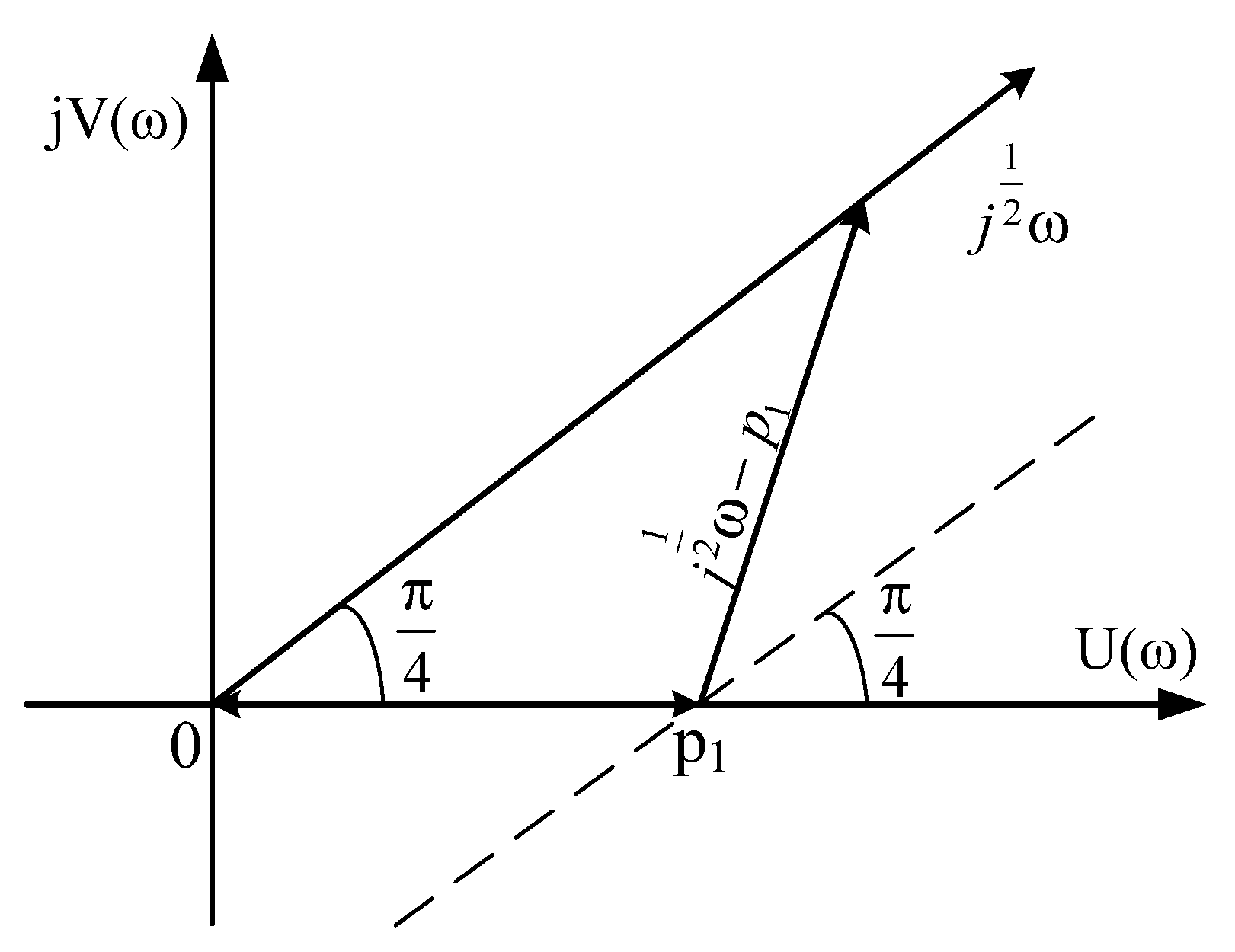
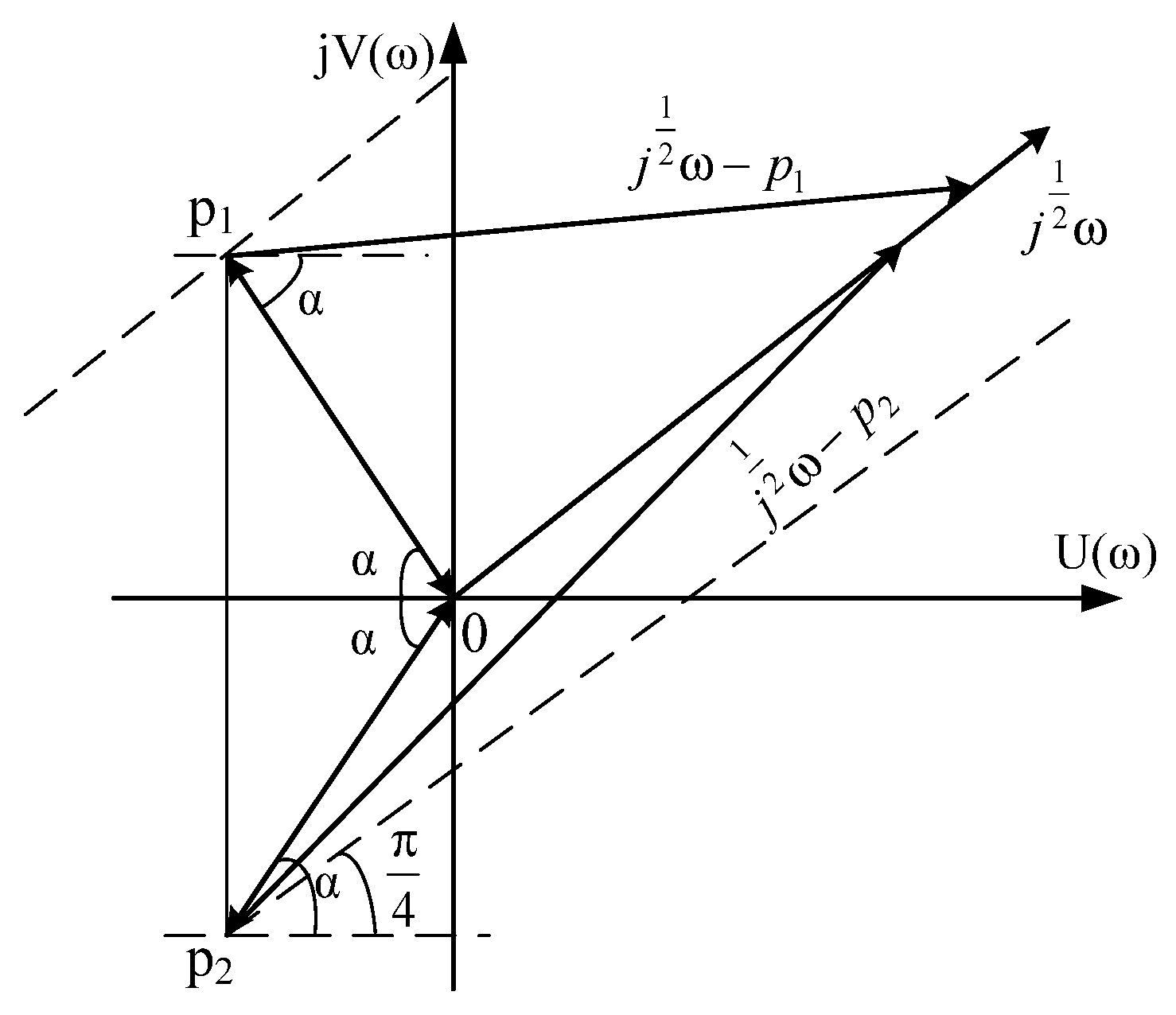
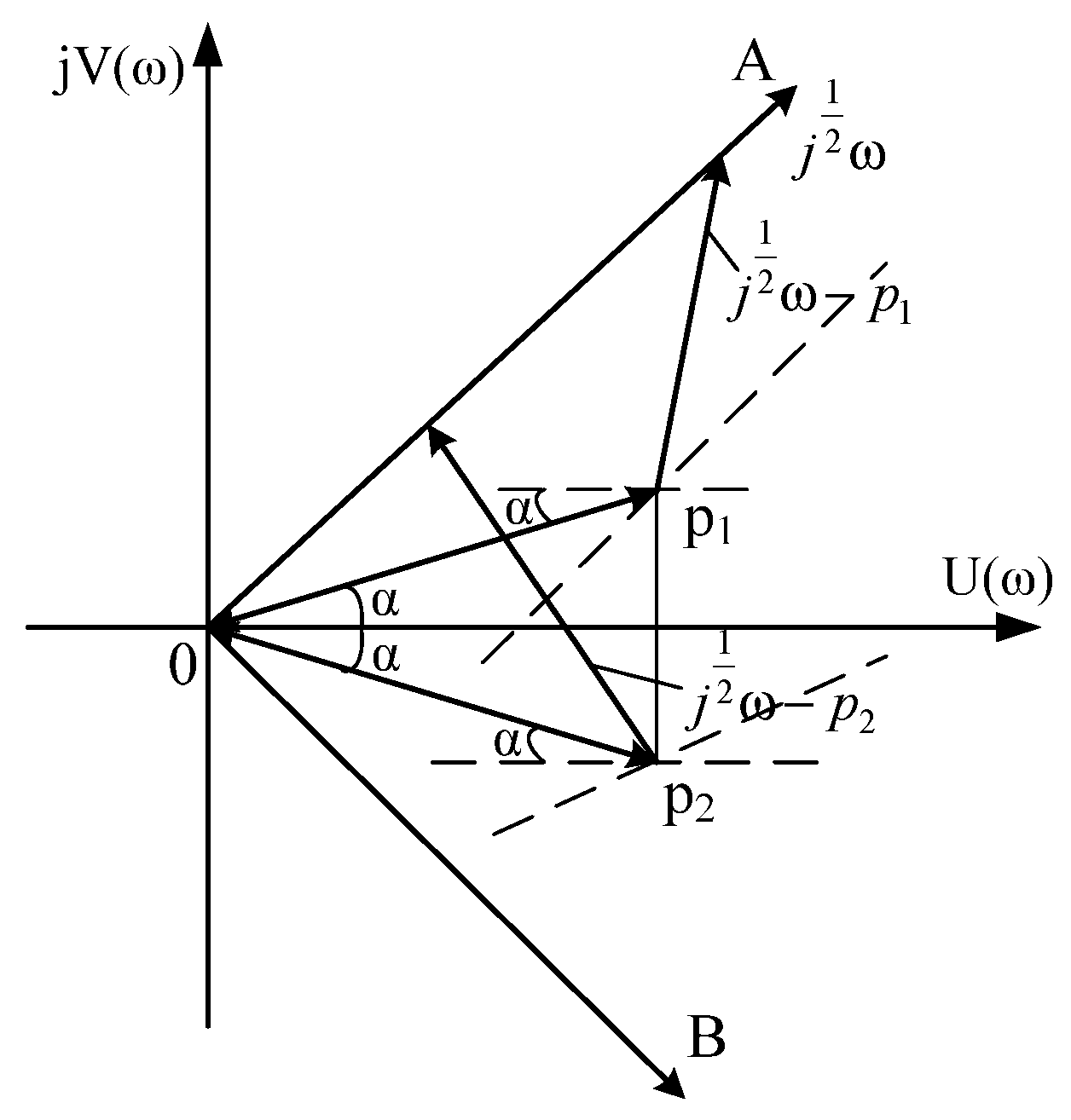
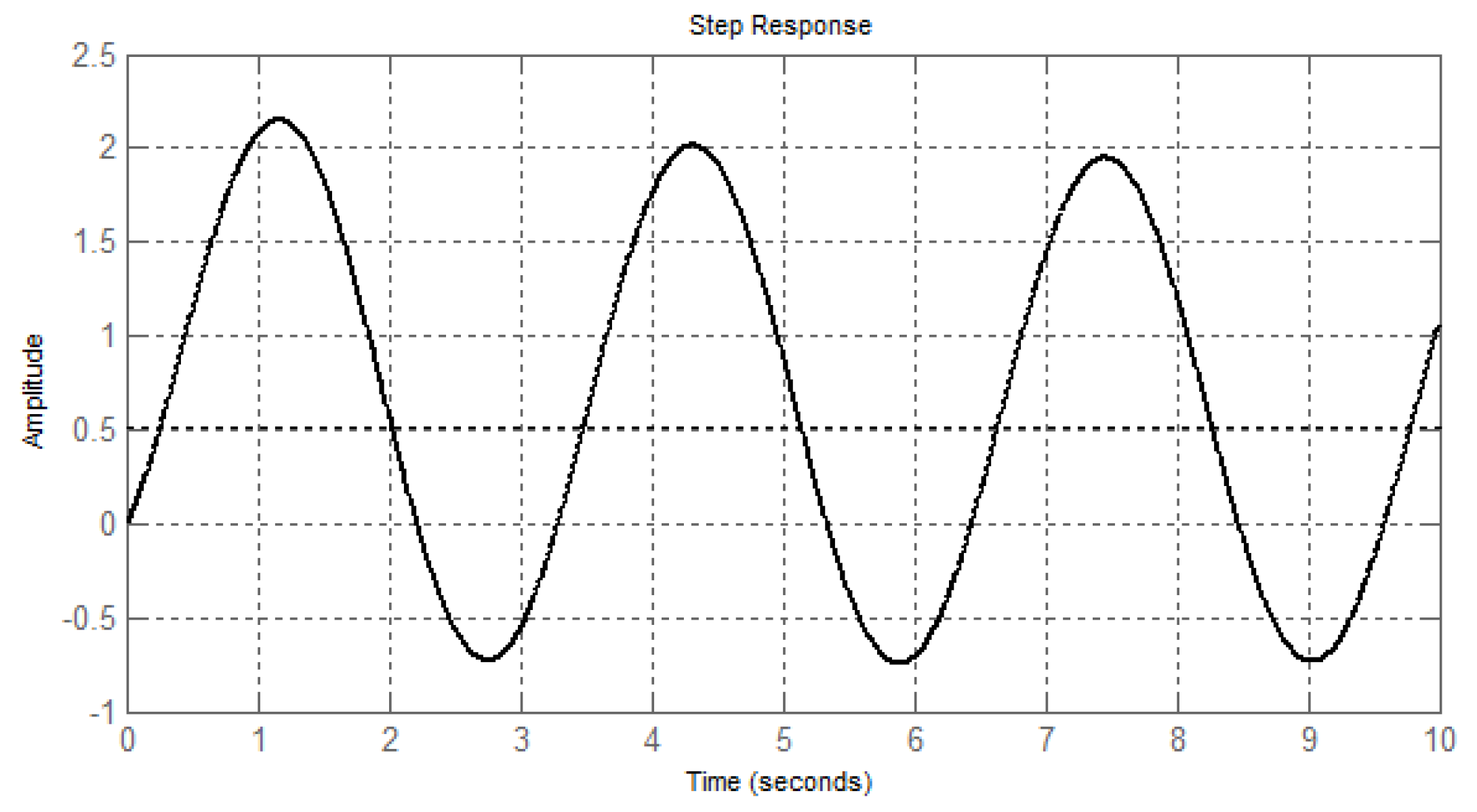
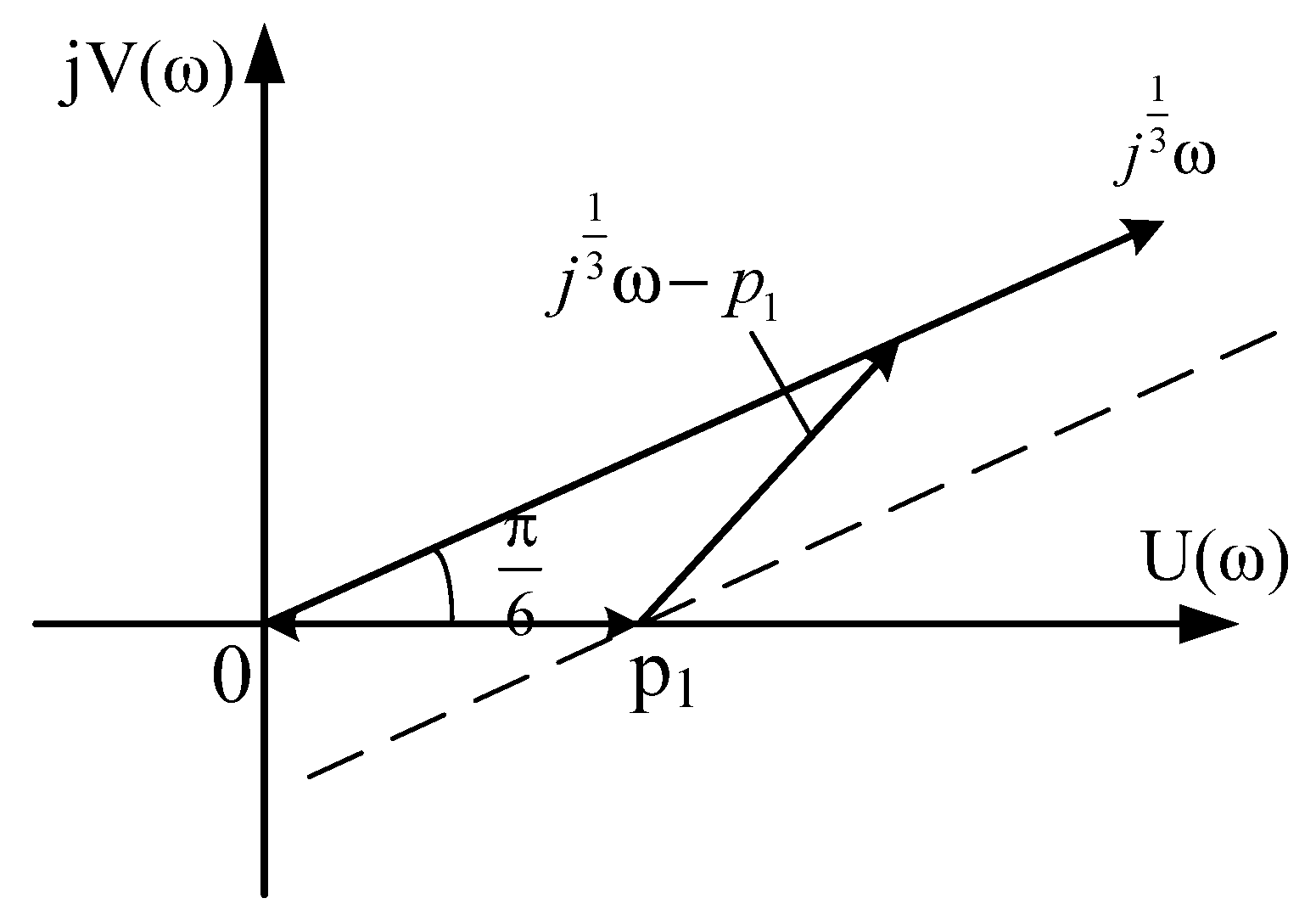
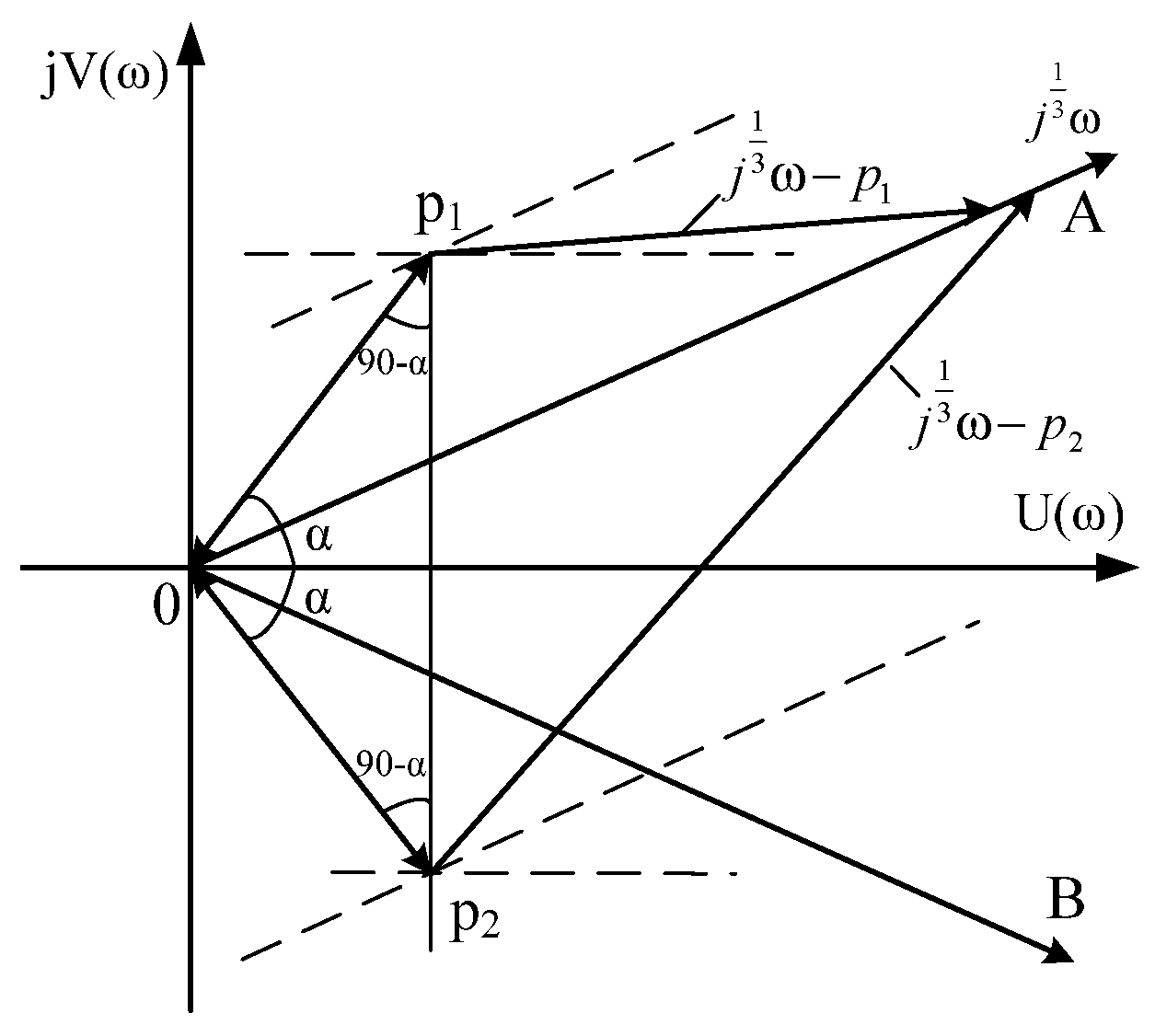
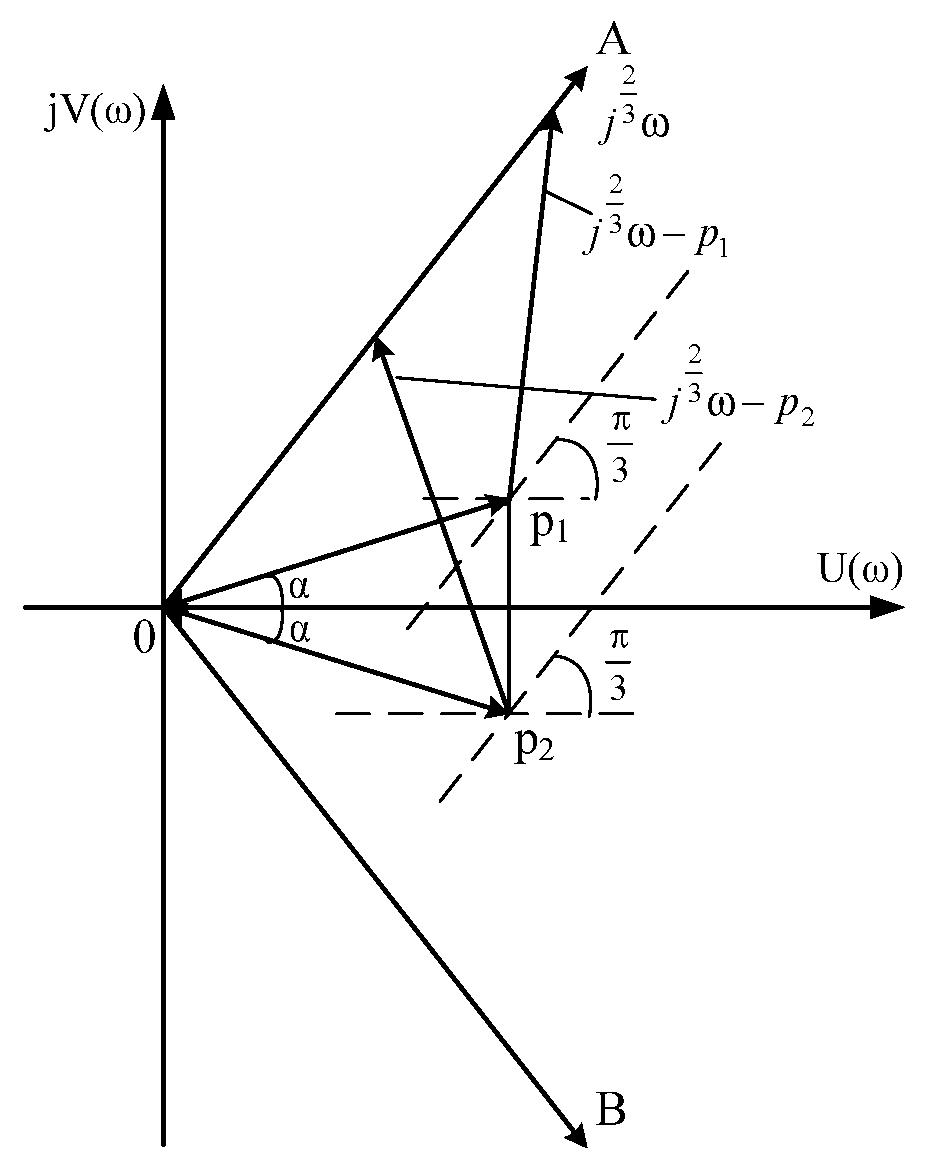
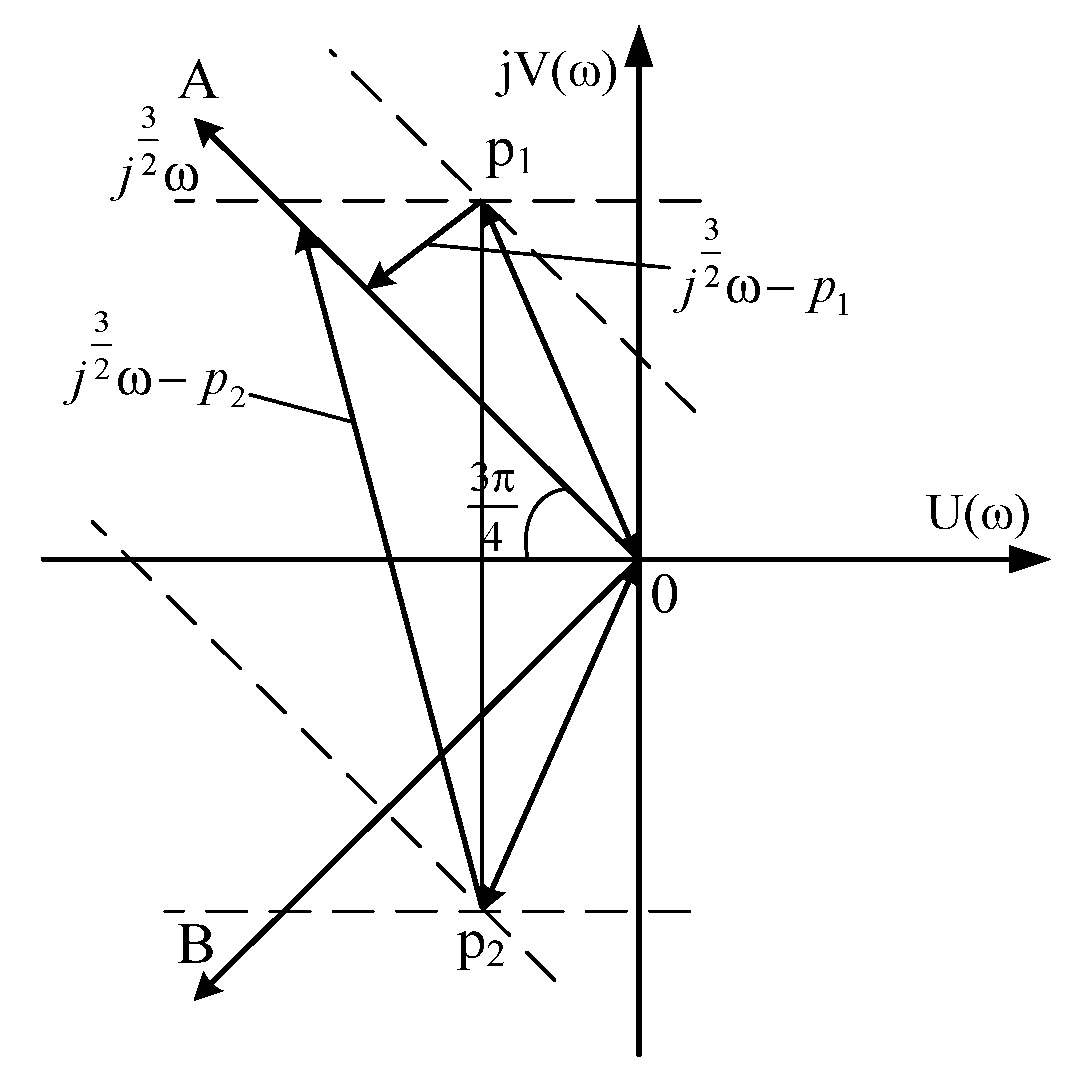
2.4. The Case When Even One Pair of Roots are Complex-Conjugate Numbers with a Positive Real Part (The Roots Are in the Sector AOB)
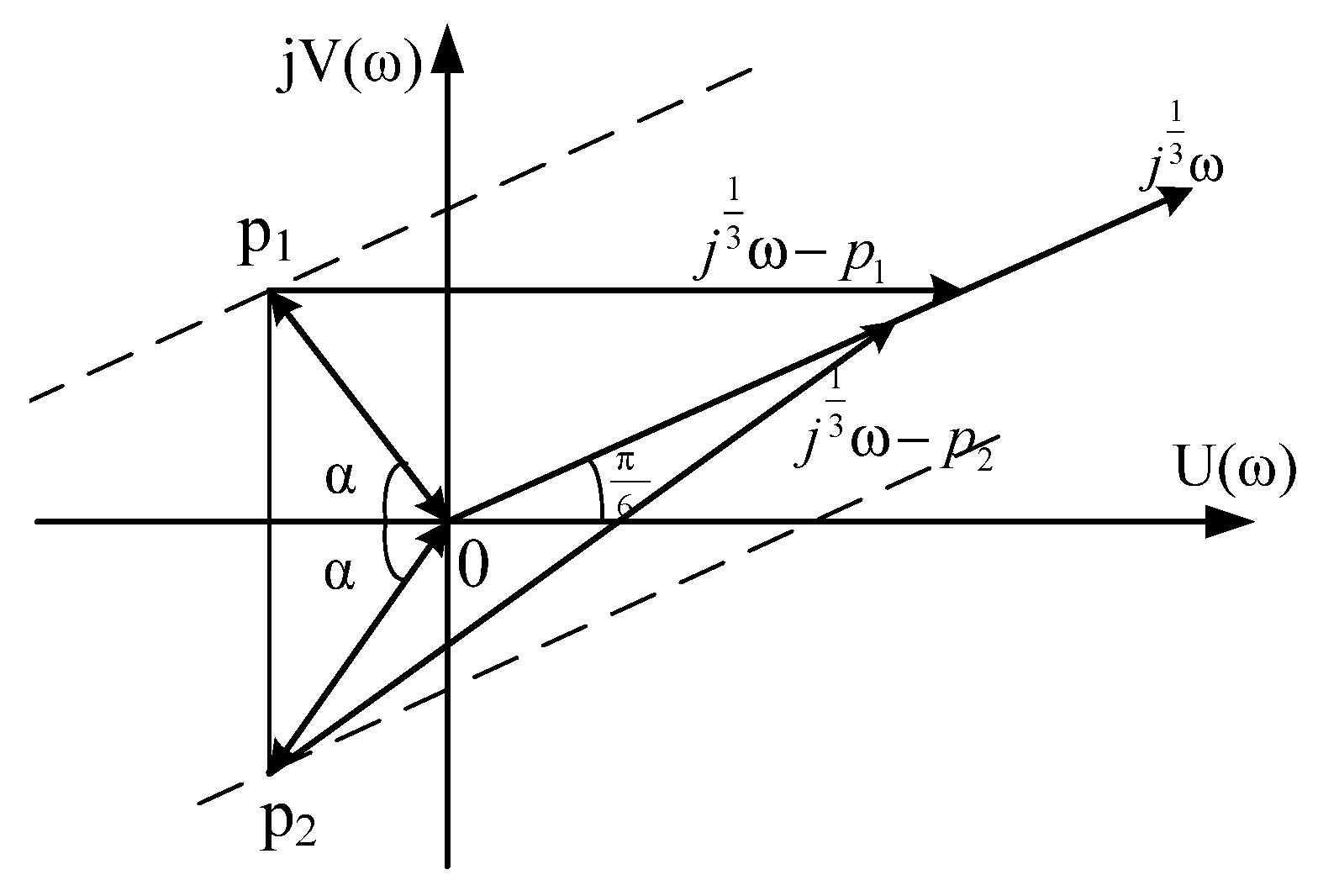
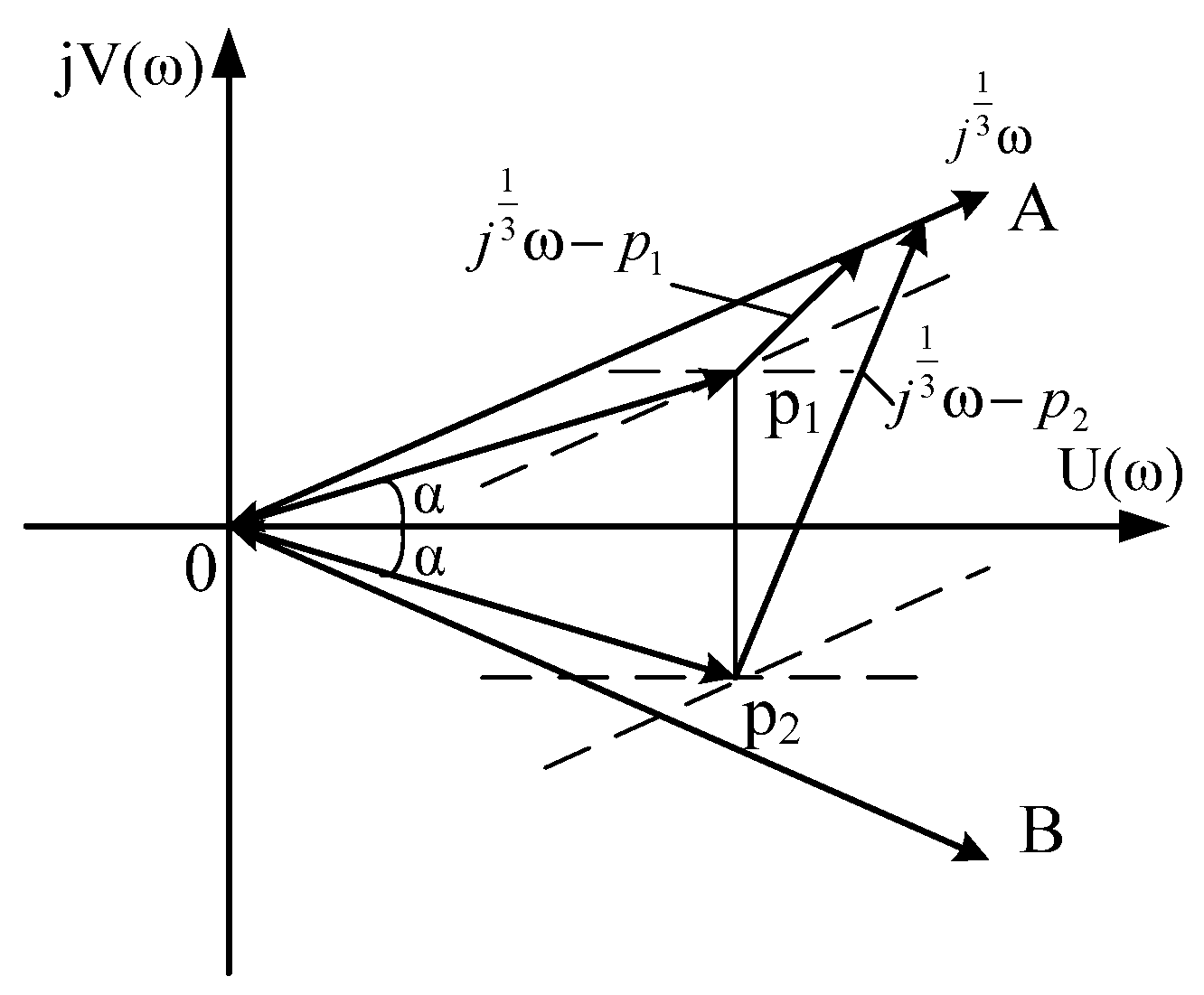
2.5. The Case of Complex-Conjugate Roots with a Positive Real Part (The Roots Are Outside the Sector AOB)
- a.
- Hodograph of the second-order system
- b.
- Hodograph of the third-order system
- c.
- Fifth-order hodograph
3. Analysis of the Influence of Roots’ Location of a Characteristic Polynomial on the System Stability
3.1. All Roots Are Real Numbers and Are Located on the Left Half-Plane
3.2. The Case When Even One Real Root Is Placed in the Right Half-Plane
3.3. The Case When All Roots Are Complex-Conjugate Numbers with a Negative Real Part
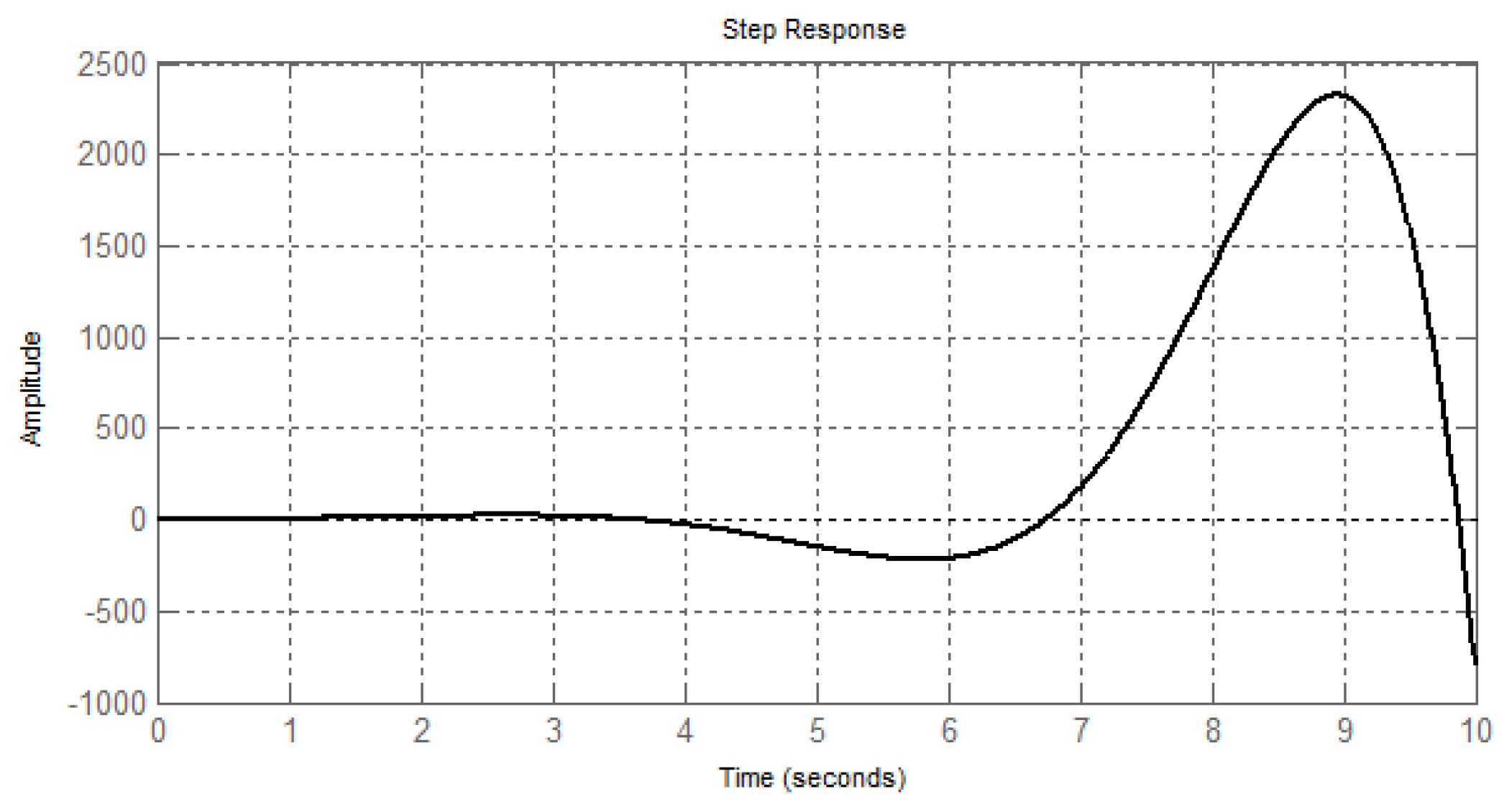
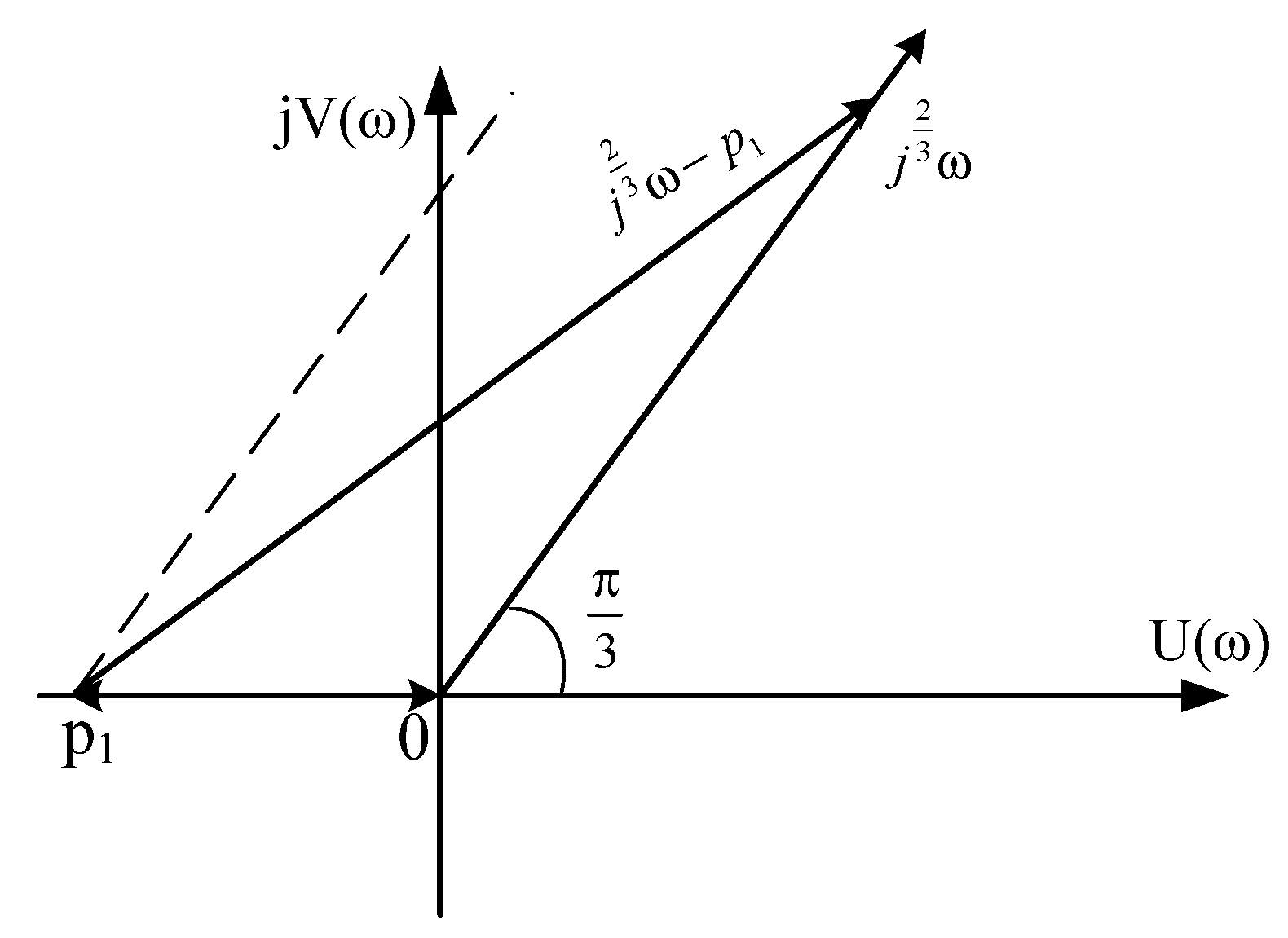
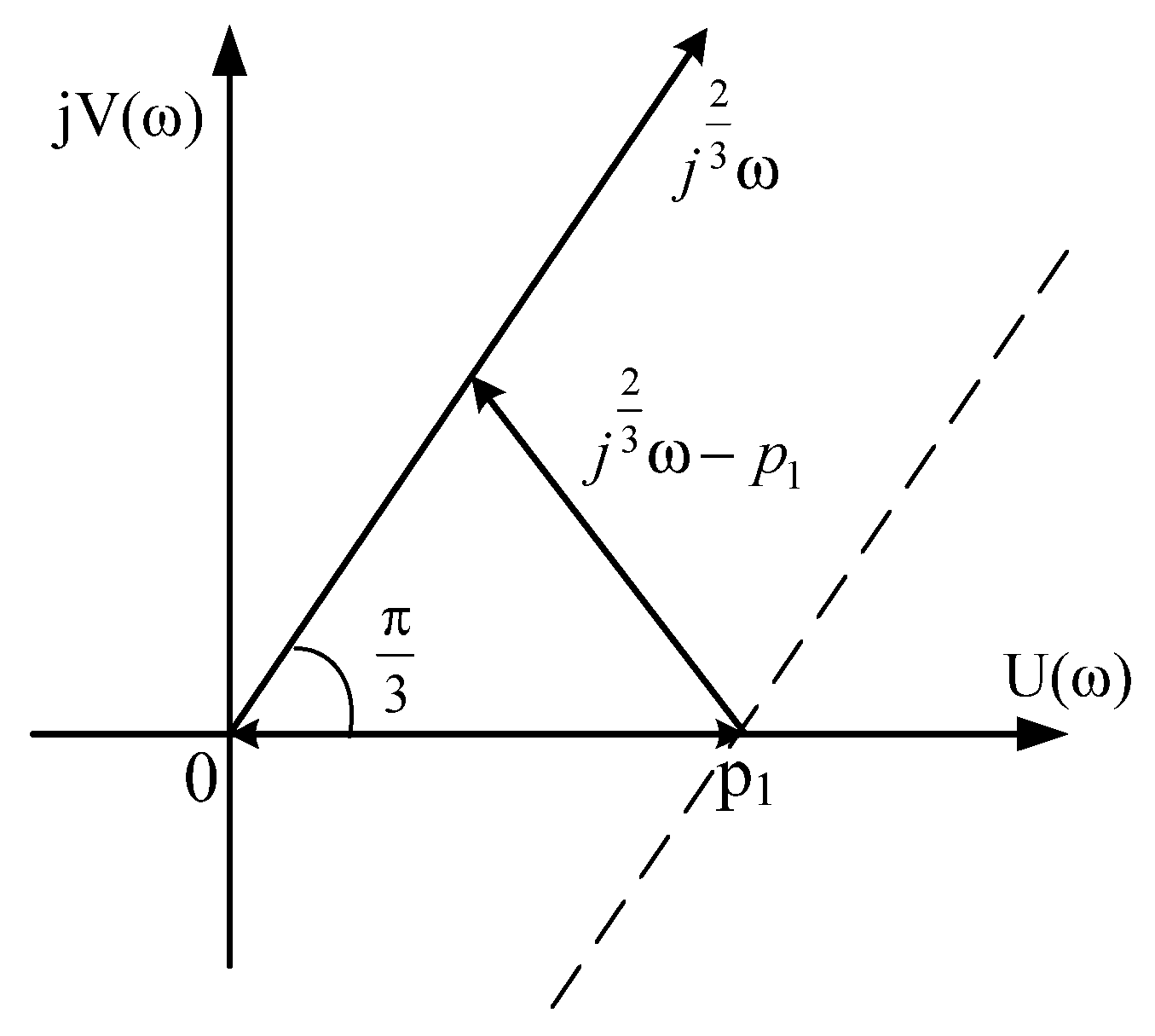
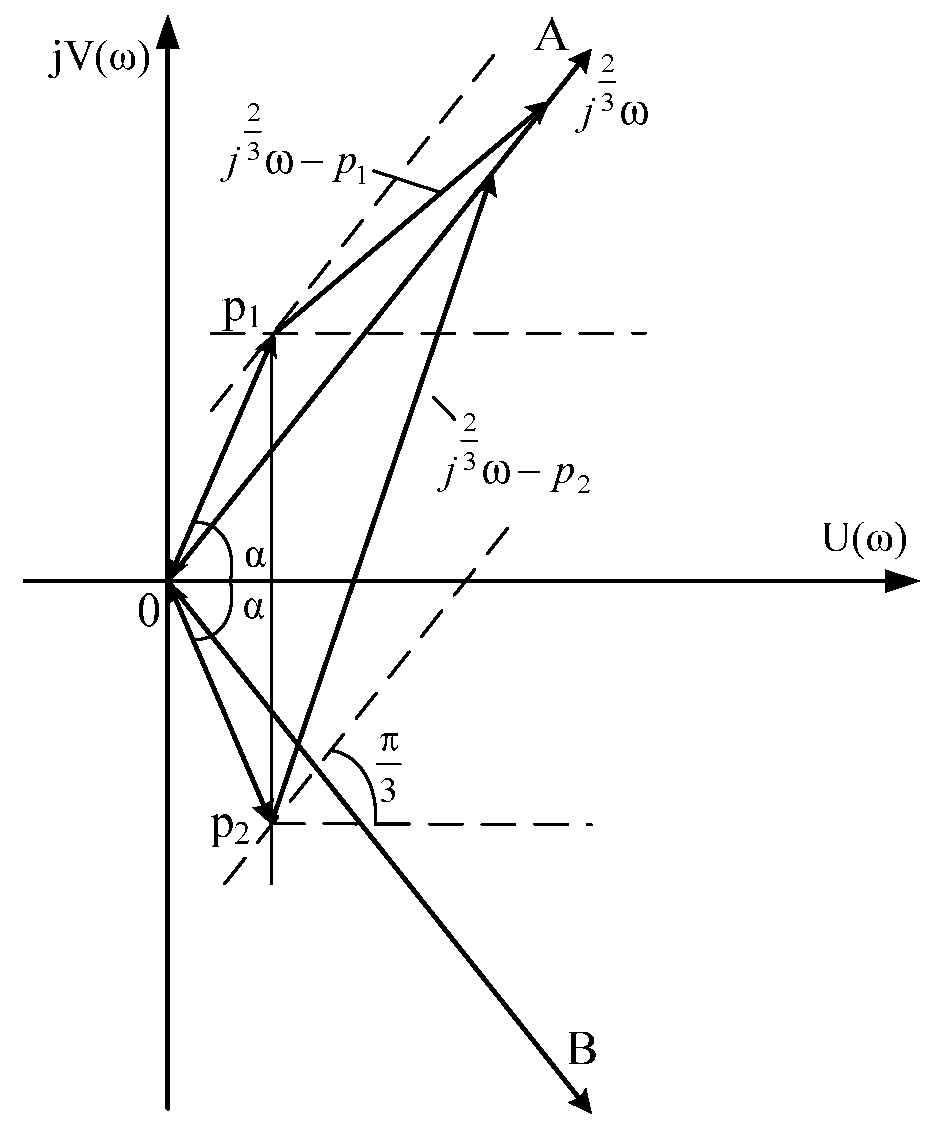
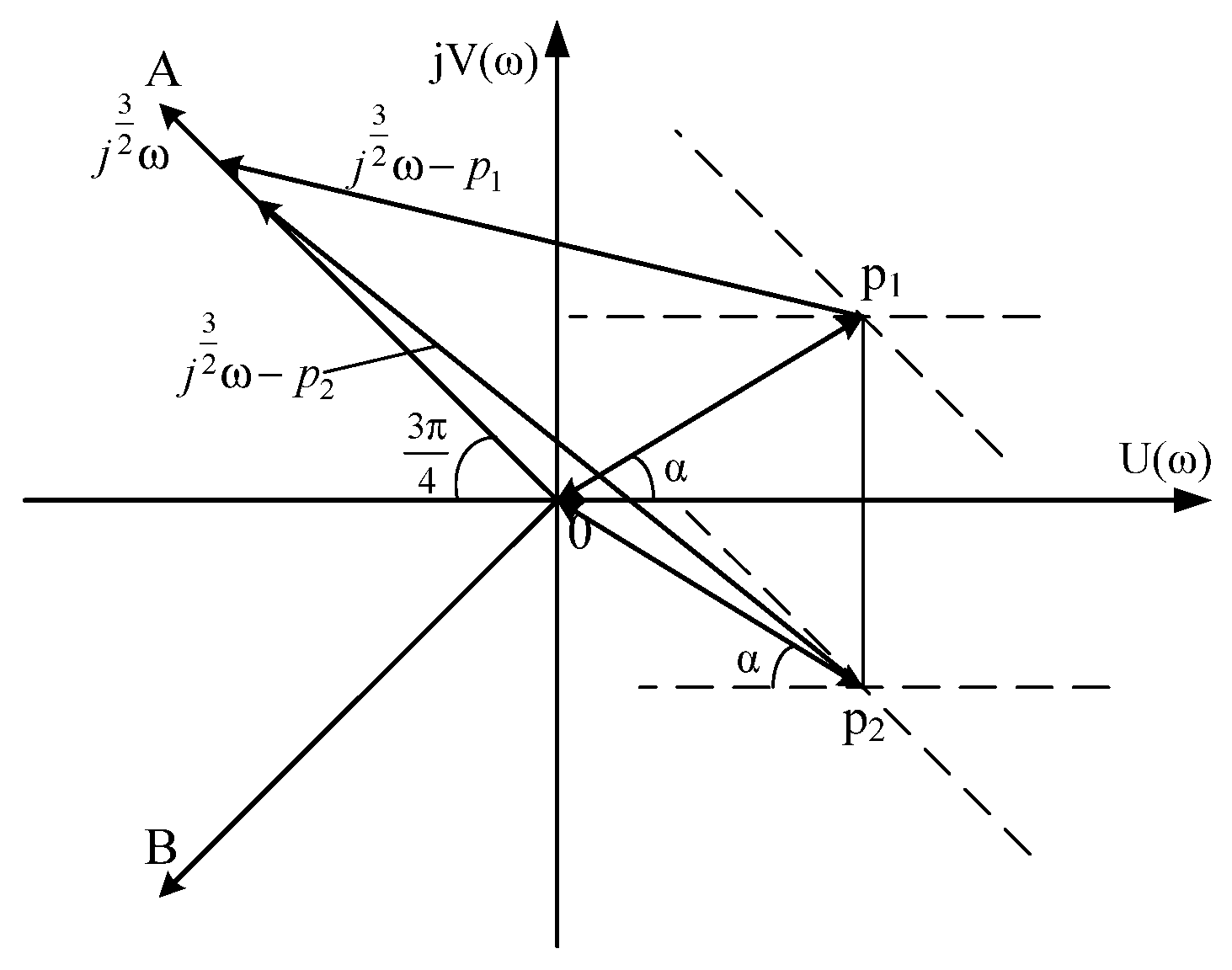
3.4. The Case When Even One Pair of Roots is Complex-Conjugate Numbers with a Positive Real Part (The Roots Are in the Middle of the Sector AOB)
3.5. The Case of Complex-Conjugate Roots with a Positive Real Part (The Roots Are Outside the Sector AOB)
- a.
- Hodograph of the second-order system
- b.
- Hodograph of the third-order system
- c.
- Fifth-order hodograph
4. Analysis of the Influence of the Characteristic Polynomial Roots’ Location on System Stability
4.1. All Roots Are Real Numbers and Are Located on the Left Half-Plane
4.2. The Case When Even One Real Root Is Located in the Right Half-Plane
4.3. The Case When All Roots Are Complex-Conjugate Numbers with a Negative Real Part
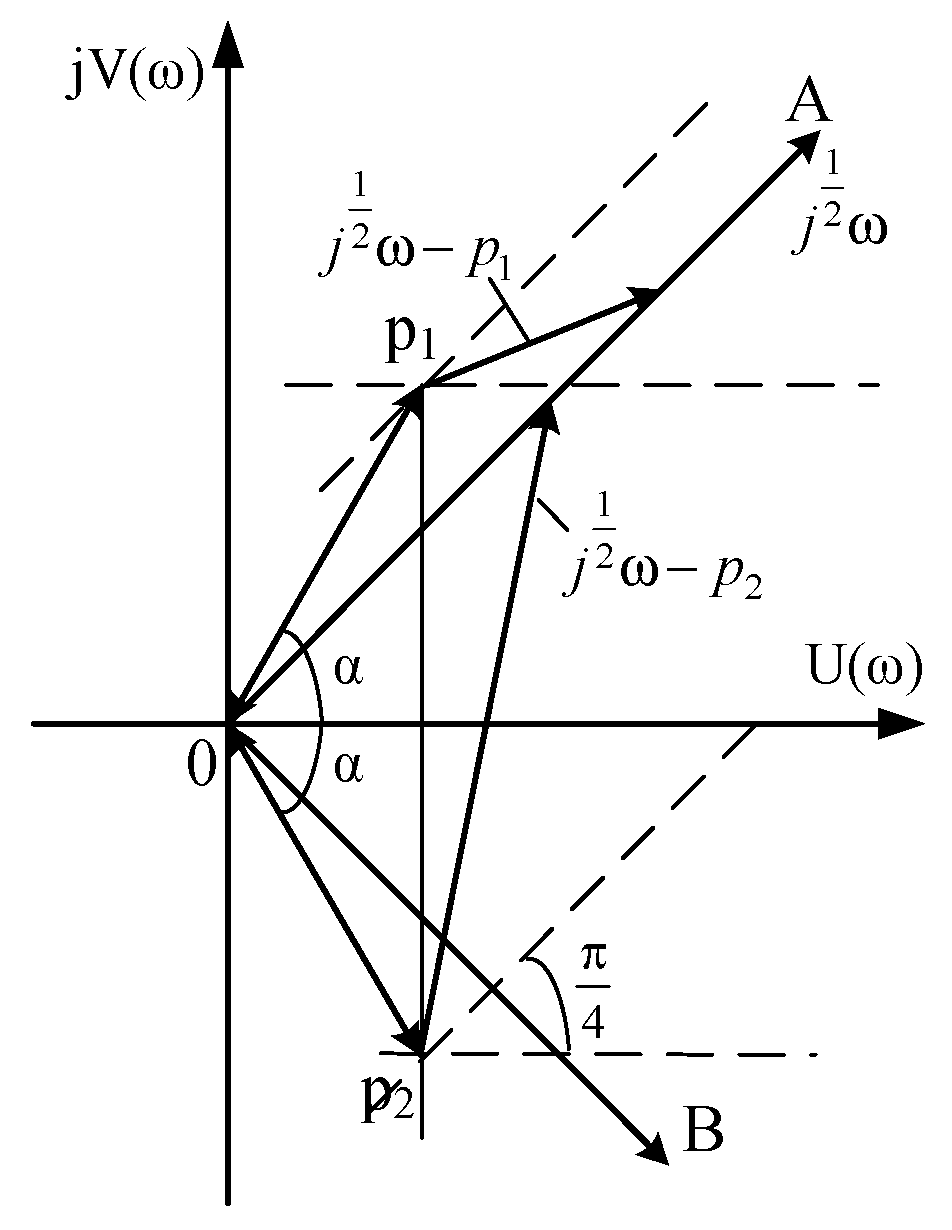
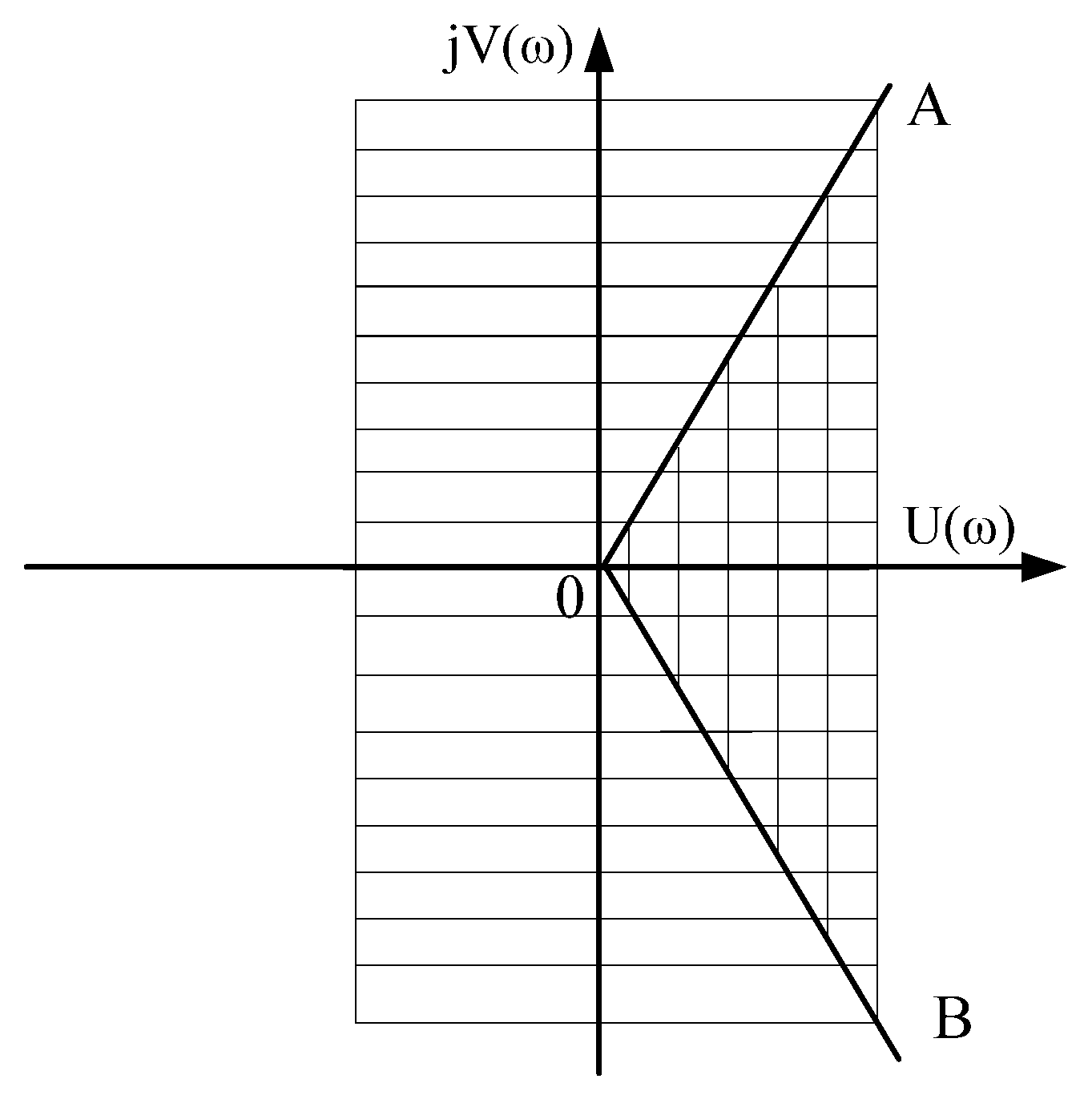
4.4. The Case When Even One Pair of Roots is Complex-Conjugate Numbers with a Positive Real Part (The Roots Are in the Sector AOB)
4.5. The Case of Complex-Conjugate Roots with a Positive Real Part (The Roots Are Outside the AOB Sector)
- a.
- Hodograph of the second-order system
- b.
- Hodograph of the third-order system
- c.
- Hodograph of the fifth-order system
5. Analysis of the Influence of the Roots’ Location of the Characteristic Polynomial on System Stability
5.1. All Roots Are Real and Placed on the Left Half-Plane
5.2. The Case Where Even One Real Root Is in the Right Half-Plane
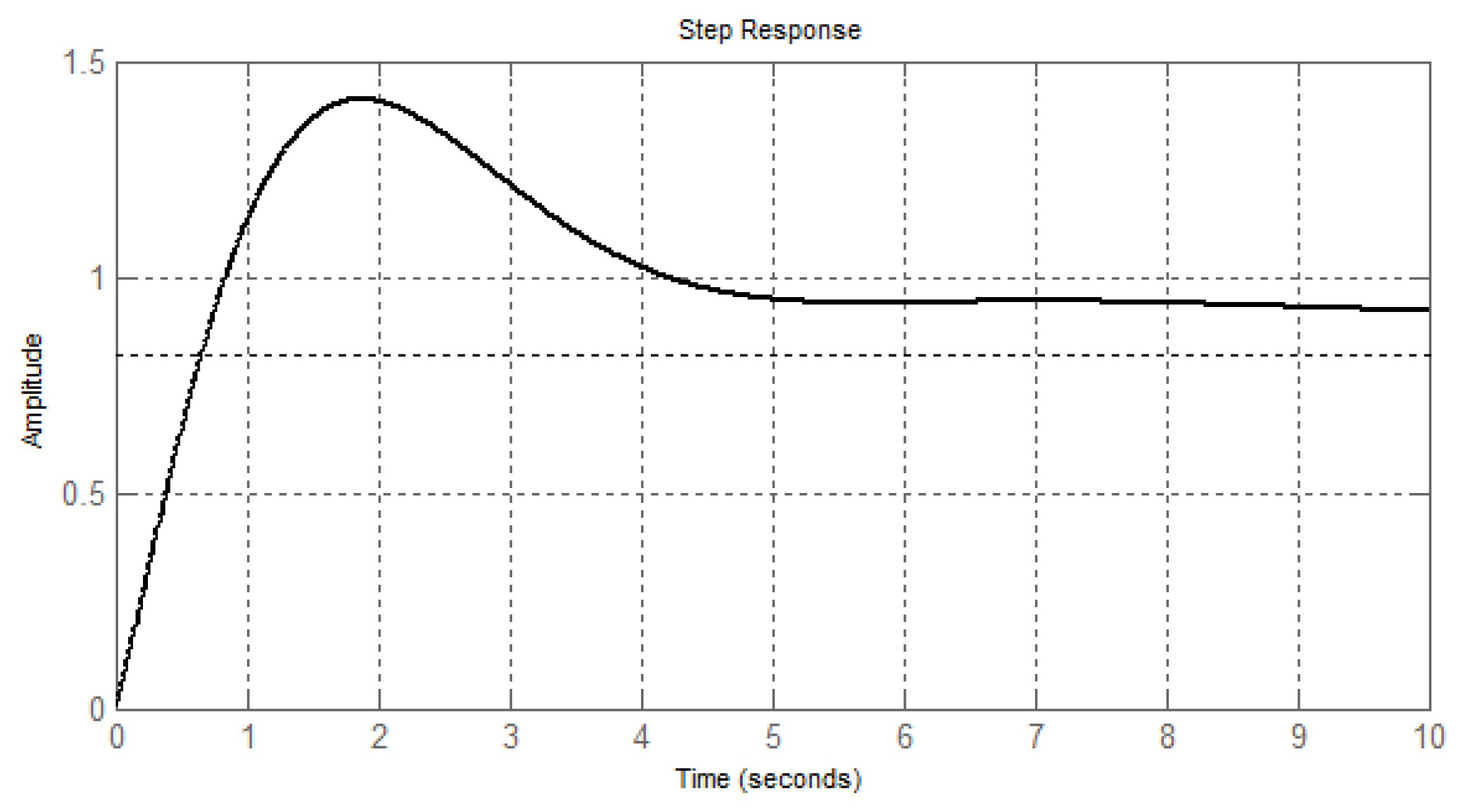
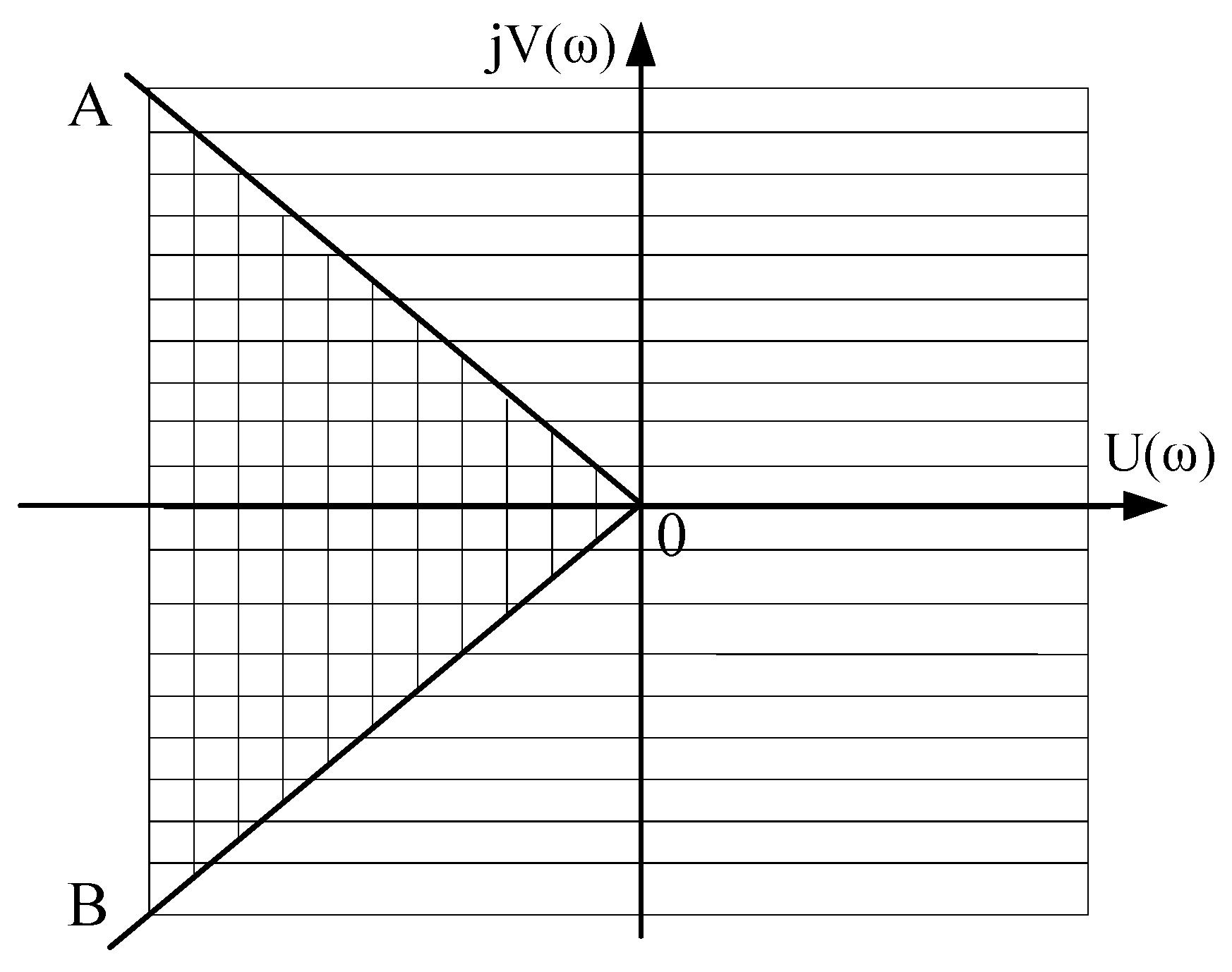
5.3. The Case Where All Roots Are Complex-Conjugate with Negative Real Part (Roots Are in the Sector AOB)
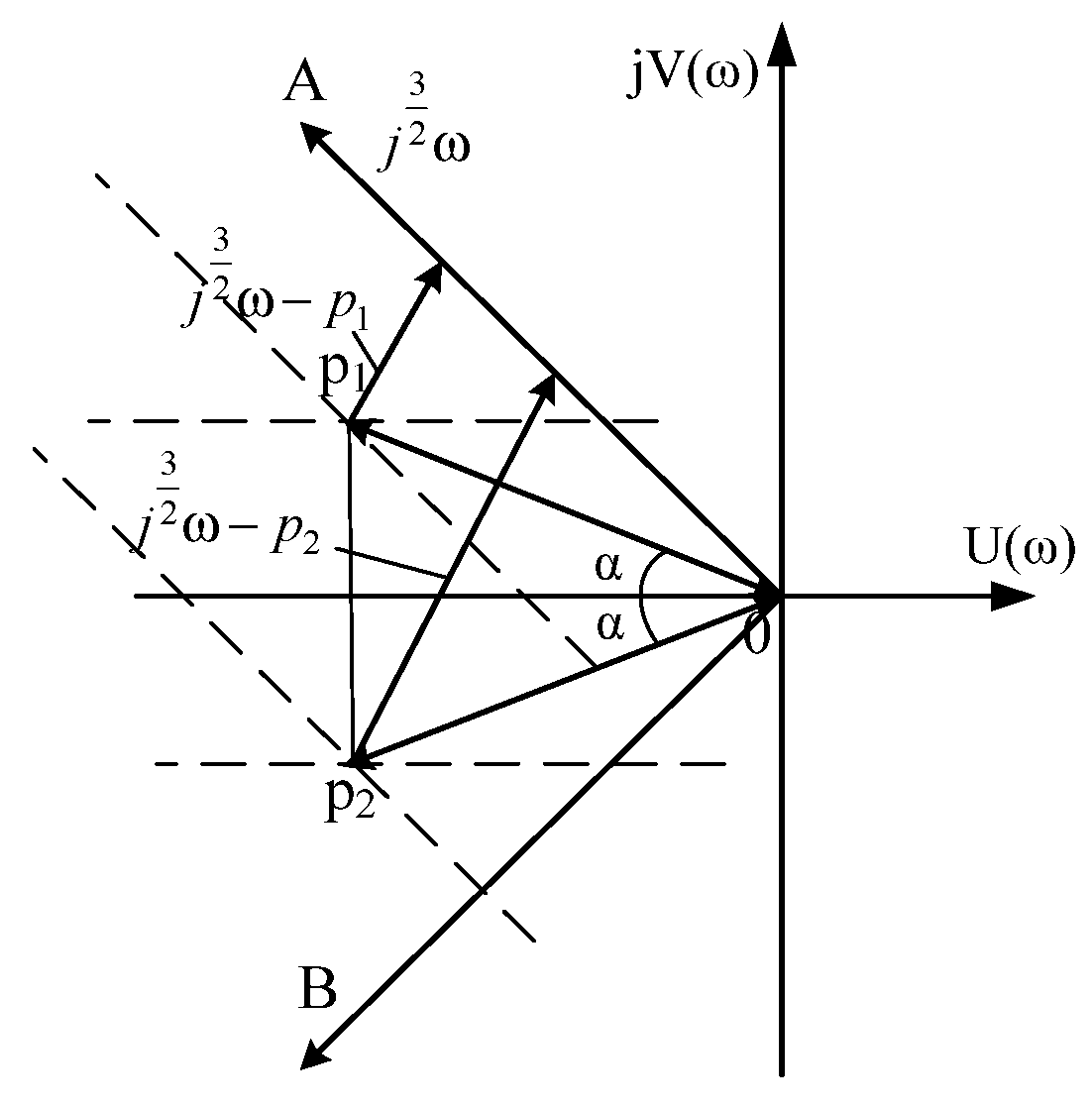
5.4. The Case Where Even One Pair of Roots is a Complex-Conjugate Number with a Negative Real Part (The Roots Are Outside the Sector AOB)
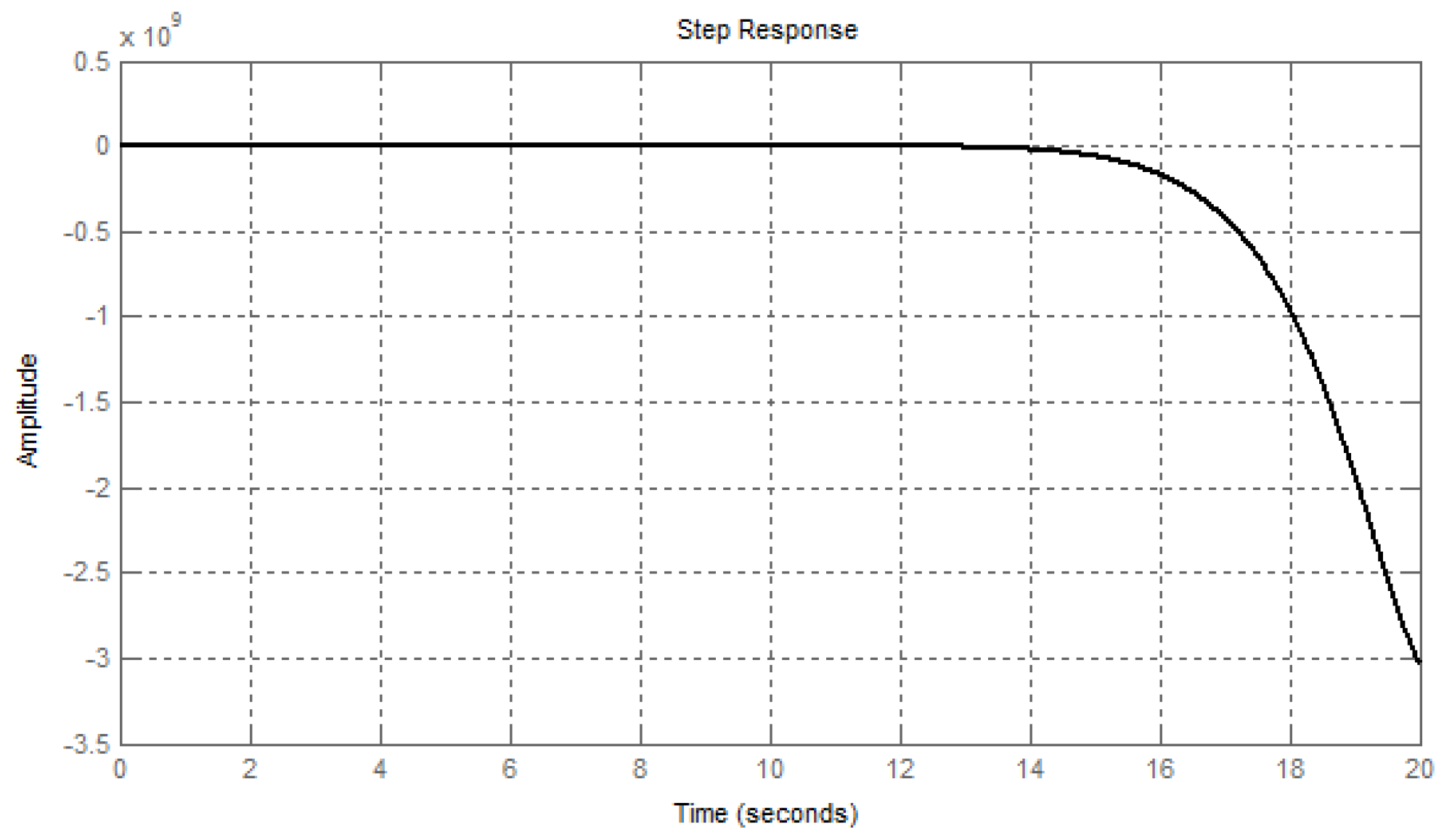
5.5. The Case of Complex-Conjugate Roots with a Positive Real Part (The Roots Are Outside the Sector AOB)
- a.
- Hodograph of second-order system
- b.
- Hodograph of third-order system
- c.
- Hodograph of fifth-order system
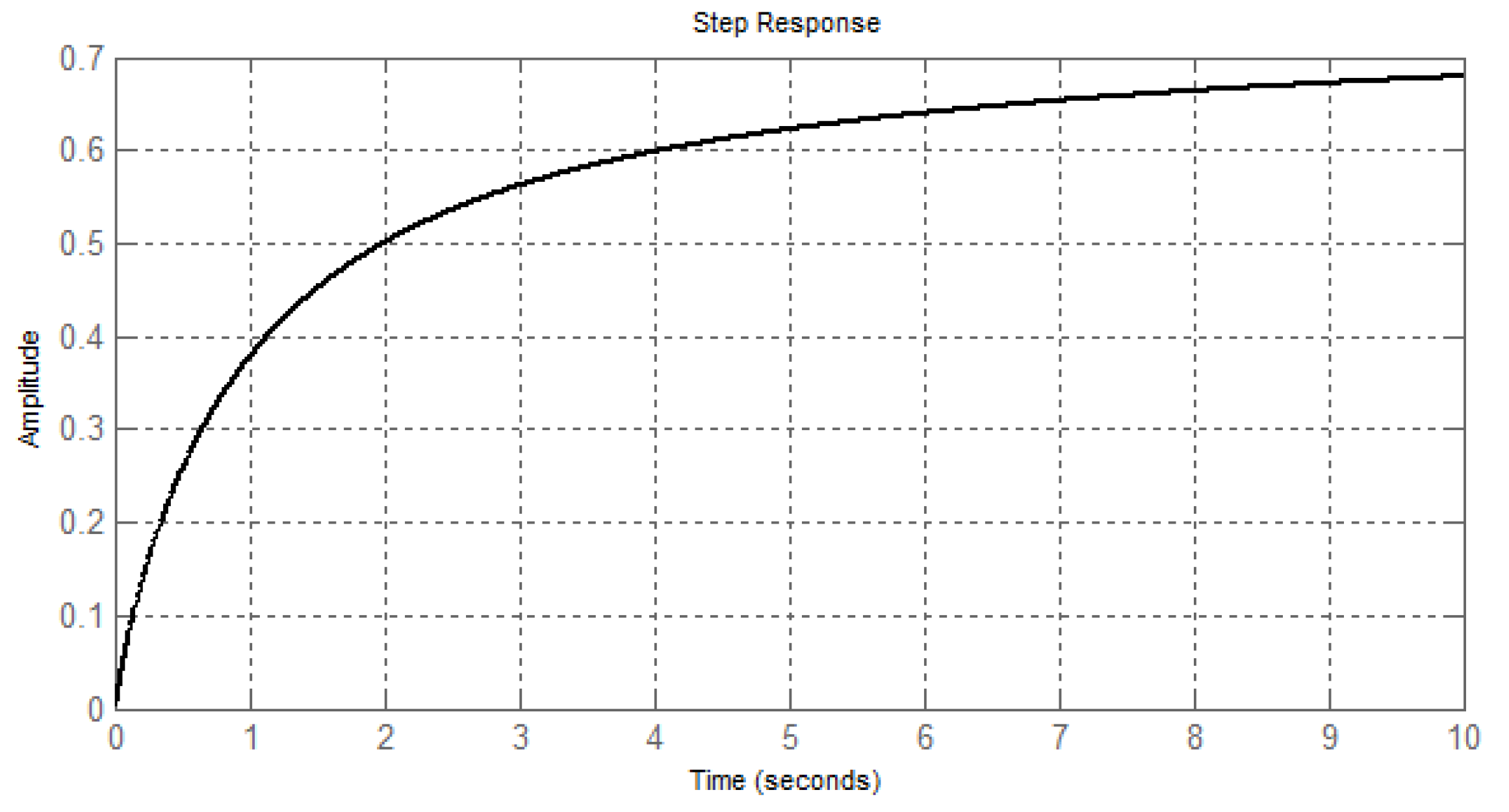
6. Conclusions
- 1.
- Polynomial based on
- -
- hodograph by second order, first quadrant
- -
- hodograph by third order, second quadrant
- -
- hodograph by fifth order, third quadrant
- 2.
- Polynomial based on
- -
- hodograph by second order, first quadrant
- -
- hodograph by third order, first quadrant
- -
- hodograph by fifth order, second quadrant
- 3.
- Polynomial based on
- -
- hodograph by second order, second quadrant
- -
- hodograph by third order, second quadrant
- -
- hodograph by fifth order, fourth quadrant
- 4.
- Polynomial based on
- -
- hodograph by second order, third quadrant
- -
- hodograph by third order, first quadrant
- -
- hodograph by fifth order, fourth quadrant
- 1.
- Polynomial which is formed in the basis , would be described as:The real part of this polynomialand, accordingly, the imaginary part
- 2.
- Polynomial which is formed in the basis , would be described as:
- 3.
- Polynomial which is formed in the basis would described as:
- 4.
- Polynomial which is formed in the basis , can be represented as:
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matignon, D. Stability result on fractional differential equations with applications to control processing. In Proceedings of the International Meeting on Automated Compliance Systems and the International Conference on Systems, Man, and Cybernetics (IMACS-SMC ’96), Lille, France, 9–12 July 1996; pp. 963–968. [Google Scholar]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional Order Control, A Tutorial. In Proceedings of the American Control Conference Hyatt Regency Riverfront, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Radwan, A.; Soliman, A.; Elwakil, A.; Sedeek, A. On the stability of linear system with fractional order elements. Chaos Solut. Fractals 2009, 40, 2317–2328. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simul. 2009, 79, 1566–1576. [Google Scholar] [CrossRef]
- Rivero, M.; Rogosin, S.V.; Tenreiro Machado, J.A.; Trujillo, J.J. Stability of fractional order systems. Math. Probl. Eng. New Chall. Fract. Syst. 2013, 2013, 356215. [Google Scholar] [CrossRef]
- Shu, L.; Cheng, P.; Yong, W. Improved linear matrix inequalities stability criteria for fractional order systems and robust stabilization synthesis: The 0 < α < 1 case. Control Appl. 2013, 30, 531–535. [Google Scholar]
- Benzaouia, A.; Hmamed, A.; Mesquine, F.; Benhayoun, M.; Tadeo, F. Stabilization of continuous-time fractional positive systems by using Lyapunov function. IEEE Trans. Autom. Control. 2014, 59, 2203–2208. [Google Scholar] [CrossRef]
- Lozynskyy, O.Y.; Kalenyuk, P.I.; Lozynskyy, A.O.; Kasha, L.V. Frequency criterion for stability analysis of the systems with derivatives of fractional order. Math. Model. Comput. 2020, 7, 389–399. [Google Scholar] [CrossRef]
- Kopchak, B.; Marushchak, Y.; Kushnir, A. Devising a procedure for the synthesis of electromechanical systems with cascade-enabled fractional-order controllers and their study. East. Eur. J. Enterp. Technol. Inf. Technol. Ind. Control Syst. 2019, 5, 65–71. [Google Scholar] [CrossRef]
- Marushchak, Y.; Kopchak, B.; Kasha, L. Robust stability of fractional electromechanical systems. In Electrical Power and Electromechanical Systems; Publishing House of Lviv Polytechnic National University: Lviv, Ukraine, 2018; pp. 47–51. [Google Scholar]
- Drałus, G.; Dec, G.; Mazur, D. One day ahead forecasting of energy generating in photovoltaic systems, Computing in Science and Technology (CST). In Proceedings of the ITM Web of Conferences, Rzeszów, Poland, 11–14 June 2018. [Google Scholar] [CrossRef][Green Version]
- Piotrowski, P. Analysis of variable selection in the task of forecasting ultra-short-term production of electricity in solar systems. Electrotech. Rev. 2014, 90, 5–9. [Google Scholar]
- Kudo, M.; Takeuchi, A.; Nozaki, Y.; Endo, H.; Sumita, J. Forecasting electric power generation in a photovoltaic power system for an energy network. Electr. Eng. Jpn. 2009, 167, 16–23. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, J.; Liu, C.; Xu, X.; Wang, W.; Zhou, X. Comparative study of power forecasting methods for PV stations. In Proceedings of the International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Yona, A.; Senjyu, T.; Saber, A.Y.; Funabashi, T.; Sekine, H.; Kim, C.H. Application of neural network to 24-hour-ahead generating power forecasting for PV system. In Proceedings of the Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
- Kluska, J. Analytical Methods in Fuzzy Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gergaud, O.; Multon, B.; Ahmed, H.B. Analysis and Experimental Validation of Various Photovoltaic System Models. In Proceedings of the Electrimacs, Montreal, QC, Canada, 18–21 August 2002; p. 6. [Google Scholar]
- Durisch, W.; Bitnar, B.; Mayor, J.C.; Kiess, H.; Lam, K.H.; Close, J. Efficiency model for photovoltaic modules and demonstration of its application to energy yield estimation. Sol. Energy Mater. Sol. Cells 2007, 91, 79–84. [Google Scholar] [CrossRef]
- Ross, R.G. Interface design considerations for terrestrial solar cell modules. In Proceedings of the 12th Photovoltaic Specialists Conference, Conference Record. (A78-10902 01-44), New York, NY, USA, 15–18 November 1976; Institute of Electrical and Electronics Engineers, Inc.: Piscataway, NJ, USA, 1976; pp. 801–806. [Google Scholar]
- MATLAB Release 2012a (7.14.0.739); The MathWorks, Inc.: Natick, MA, USA, 2012.
- Piegat, A. Modeling and Fuzzy Control; Akademicka Oficyna Wydawnicza EXIT: Warszawa, Poland, 2015. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-Network-based Fuzzy Inference Systems. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Bermejo, J.F.; Fernández, J.F.G.; Pino, R.; Márquez, A.C.; López, A.J.G. Review and Comparison of Intelligent Optimization Modelling Techniques for Energy Forecasting and Condition-Based Maintenance in PV Plants. Energies 2019, 12, 4163. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Leva, S.; Pavan, A.M.; Mellit, A.; Lughi, V.; Dolara, A. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies 2019, 12, 1621. [Google Scholar] [CrossRef]
- Kim, T.; Ko, W.; Kim, J.; Kim, T. Analysis and Impact Evaluation of Missing Data Imputation in Day-ahead PV Generation Forecasting. Appl. Sci. 2019, 9, 204. [Google Scholar] [CrossRef]
- Mei, F.; Pan, Y.; Zhu, K.; Zheng, J. A Hybrid Online Forecasting Model for Ultrashort-Term Photovoltaic Power Generation. Sustainability 2018, 10, 820. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Wang, B.; Mi, Z. Comparative Study on KNN and SVM Based Weather Classification Models for Day Ahead Short Term Solar PV Power Forecasting. Appl. Sci. 2017, 8, 28. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A Physical Hybrid Artificial Neural Network for Short Term Forecasting of PV Plant Power Output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
- Ogliari, E.; Grimaccia, F.; Leva, S.; Mussetta, M. Hybrid Predictive Models for Accurate Forecasting in PV Systems. Energies 2013, 6, 1918–1929. [Google Scholar] [CrossRef]
- Son, J.; Park, Y.; Lee, J.; Kim, H. Sensorless PV Power Forecasting in Grid—Connected Buildings through Deep Learning. Sensors 2018, 18, 2529. [Google Scholar] [CrossRef]
- Jamro, M.; Rzońca, D.; Sadolewski, J.; Stec, A.; Świder, Z.; Trybus, B.; Trybus, L. CPDev Engineering Environment for Modeling, Implementation, Testing, and Visualization of Control Software, Advances in Intelligent Systems and Computing. In Recent Advances in Automation, Robotics and Measuring Techniques; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 267, pp. 81–90. [Google Scholar]
- Kamali, G.A.; Moradi, I.; Khalili, A. Estimating solar radiation on tilted surfaces with various orientations: A study case in Karaj (Iran). Theor. Appl. Clim. 2005, 84, 235–241. [Google Scholar] [CrossRef]
- Trybus, B. Development and Implementation of IEC 61131-3 Virtual Machine. Theor. Appl. Inform. 2011, 23, 21–35. [Google Scholar] [CrossRef][Green Version]








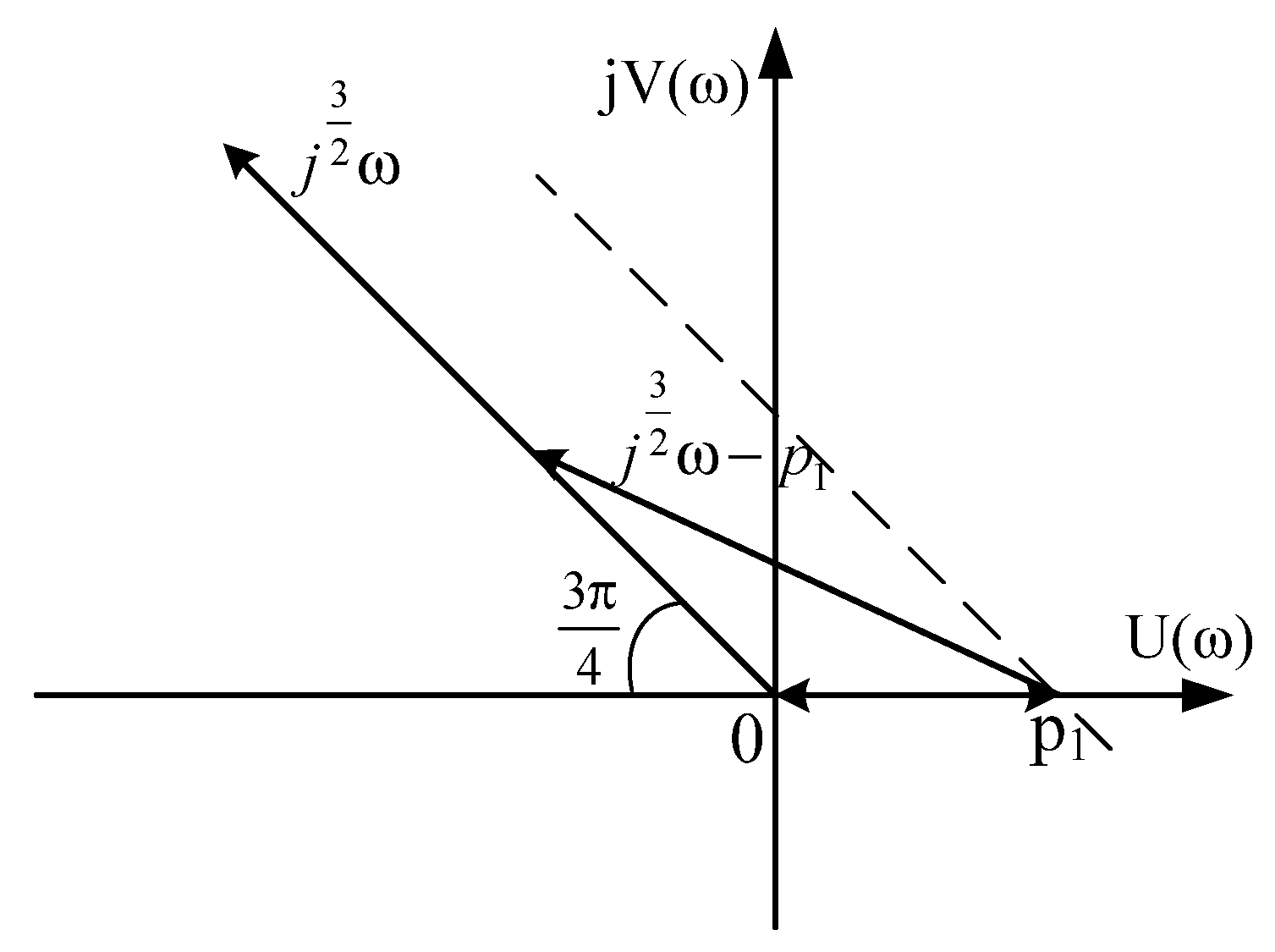


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozynskyy, O.; Mazur, D.; Marushchak, Y.; Kwiatkowski, B.; Lozynskyy, A.; Kwater, T.; Kopchak, B.; Hawro, P.; Kasha, L.; Pękala, R.; et al. Formation of Characteristic Polynomials on the Basis of Fractional Powers j of Dynamic Systems and Stability Problems of Such Systems. Energies 2021, 14, 7374. https://doi.org/10.3390/en14217374
Lozynskyy O, Mazur D, Marushchak Y, Kwiatkowski B, Lozynskyy A, Kwater T, Kopchak B, Hawro P, Kasha L, Pękala R, et al. Formation of Characteristic Polynomials on the Basis of Fractional Powers j of Dynamic Systems and Stability Problems of Such Systems. Energies. 2021; 14(21):7374. https://doi.org/10.3390/en14217374
Chicago/Turabian StyleLozynskyy, Orest, Damian Mazur, Yaroslav Marushchak, Bogdan Kwiatkowski, Andriy Lozynskyy, Tadeusz Kwater, Bohdan Kopchak, Przemysław Hawro, Lidiia Kasha, Robert Pękala, and et al. 2021. "Formation of Characteristic Polynomials on the Basis of Fractional Powers j of Dynamic Systems and Stability Problems of Such Systems" Energies 14, no. 21: 7374. https://doi.org/10.3390/en14217374
APA StyleLozynskyy, O., Mazur, D., Marushchak, Y., Kwiatkowski, B., Lozynskyy, A., Kwater, T., Kopchak, B., Hawro, P., Kasha, L., Pękala, R., Ziemba, R., & Twaróg, B. (2021). Formation of Characteristic Polynomials on the Basis of Fractional Powers j of Dynamic Systems and Stability Problems of Such Systems. Energies, 14(21), 7374. https://doi.org/10.3390/en14217374







