Effect of Semiconductor Parasitic Capacitances on Ground Leakage Current in Three-Phase Current Source Inverters
Abstract
:1. Introduction
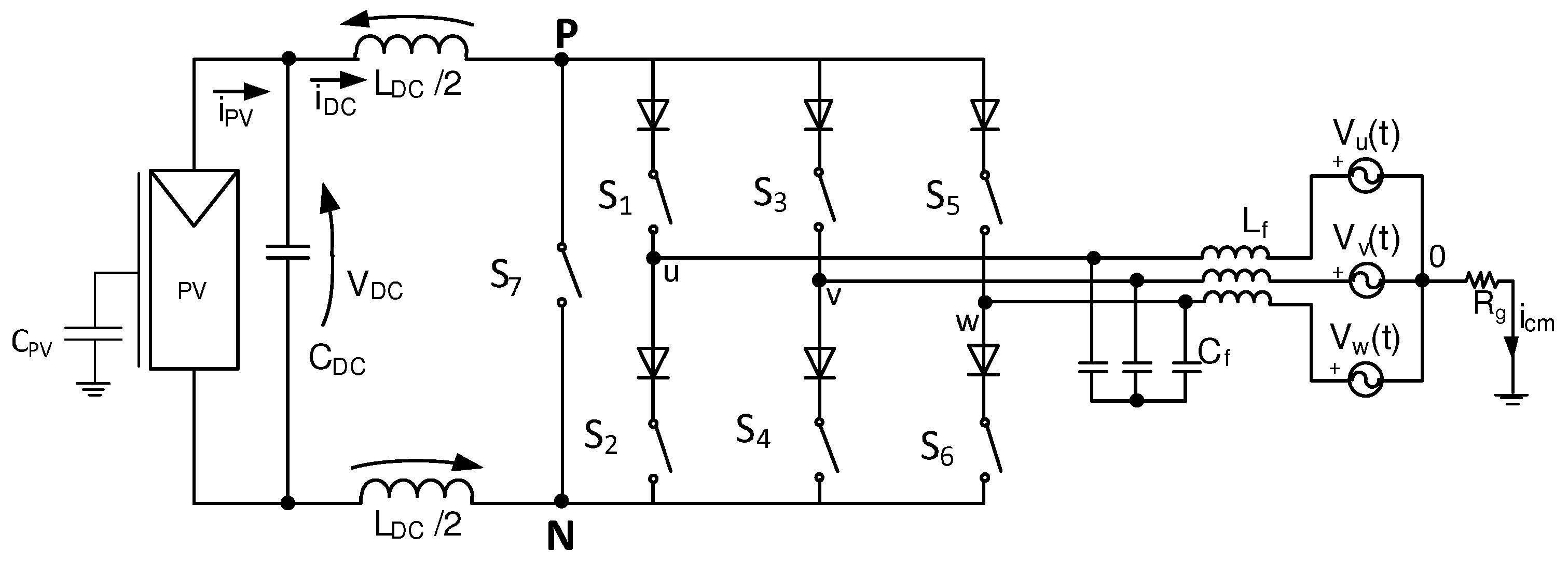
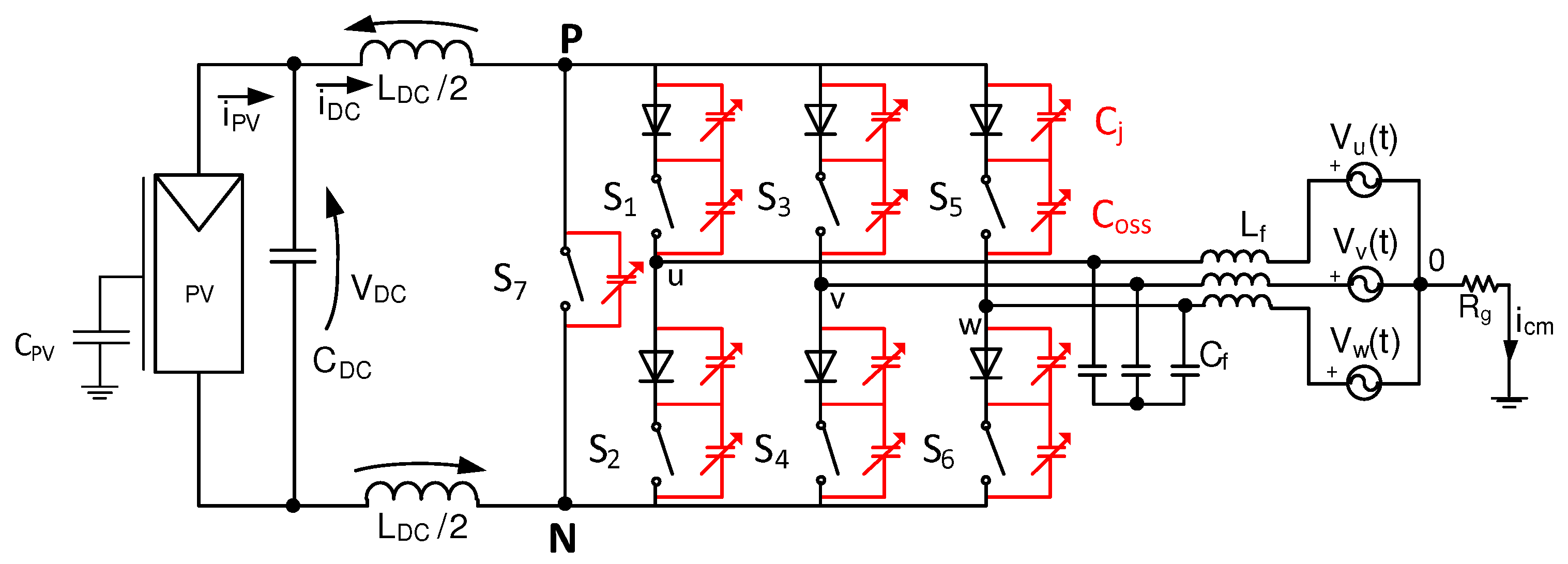
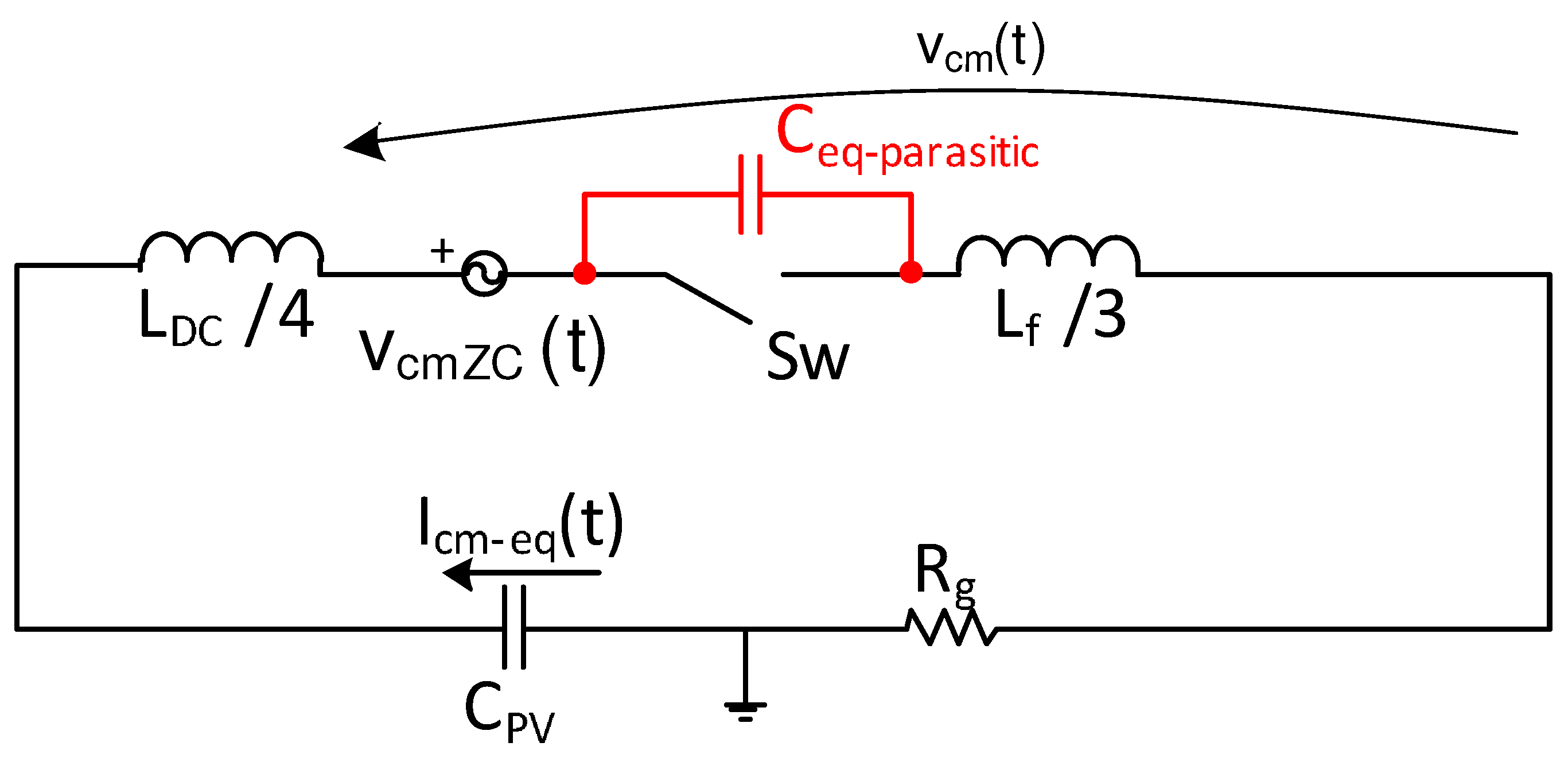
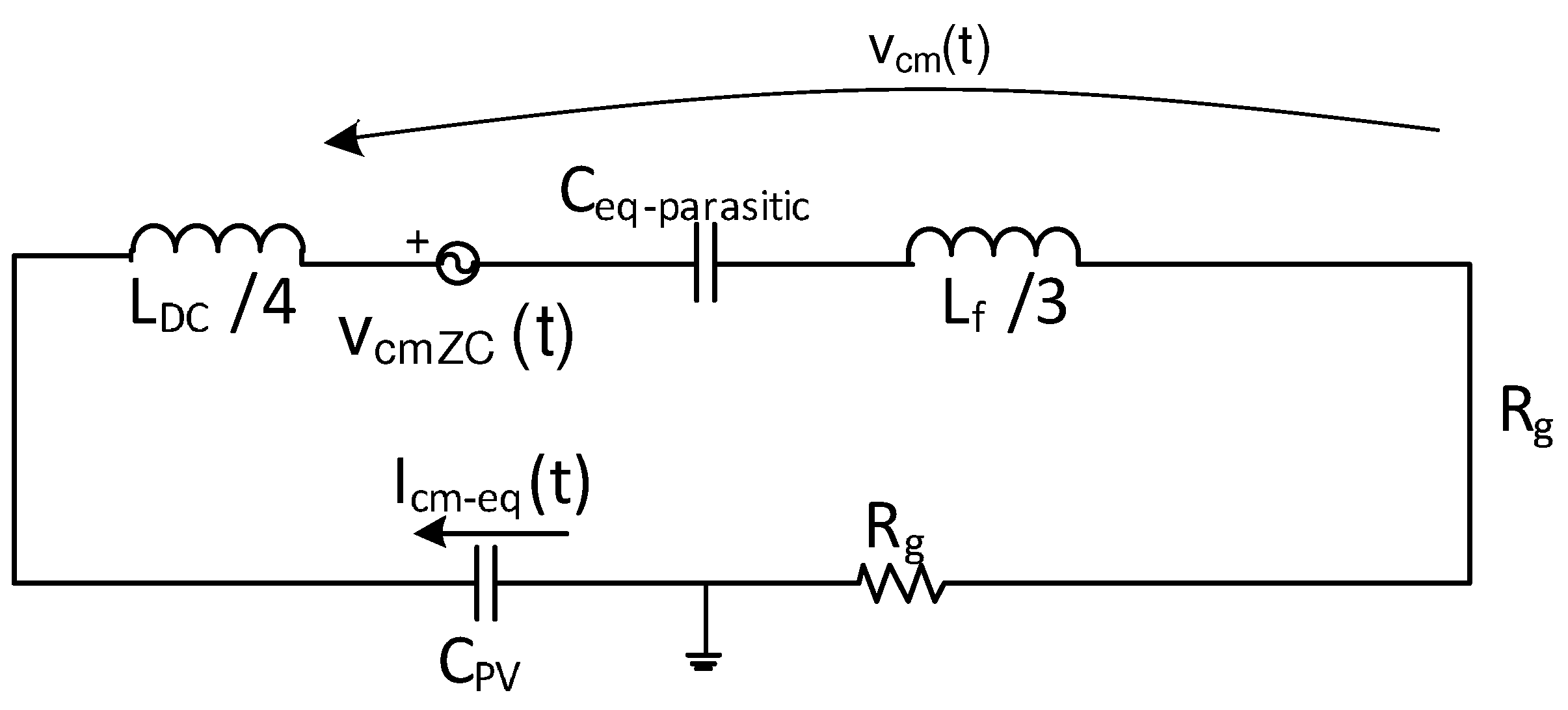
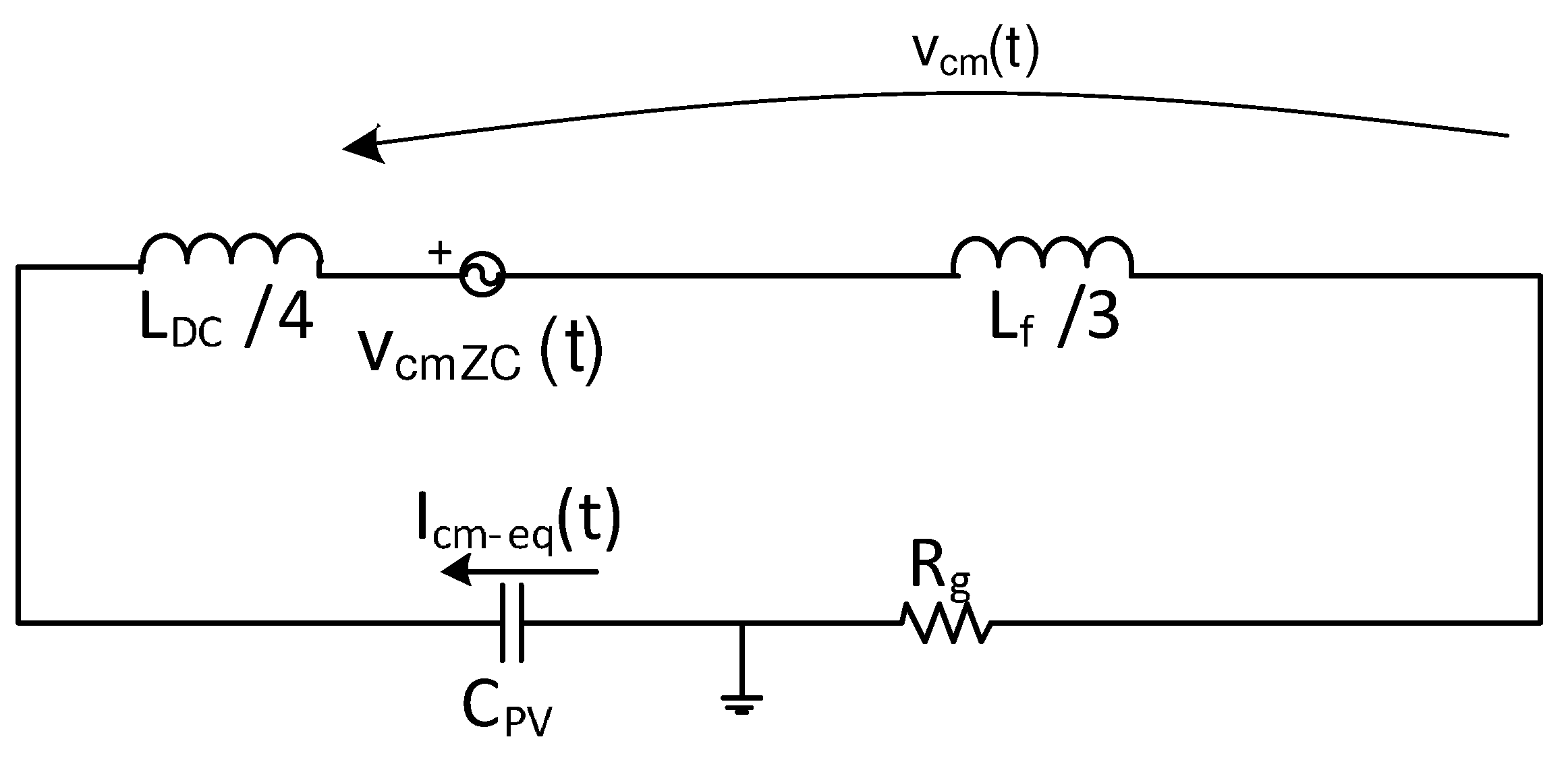
2. Considerations on Parasitic Components
3. Numerical Simulations
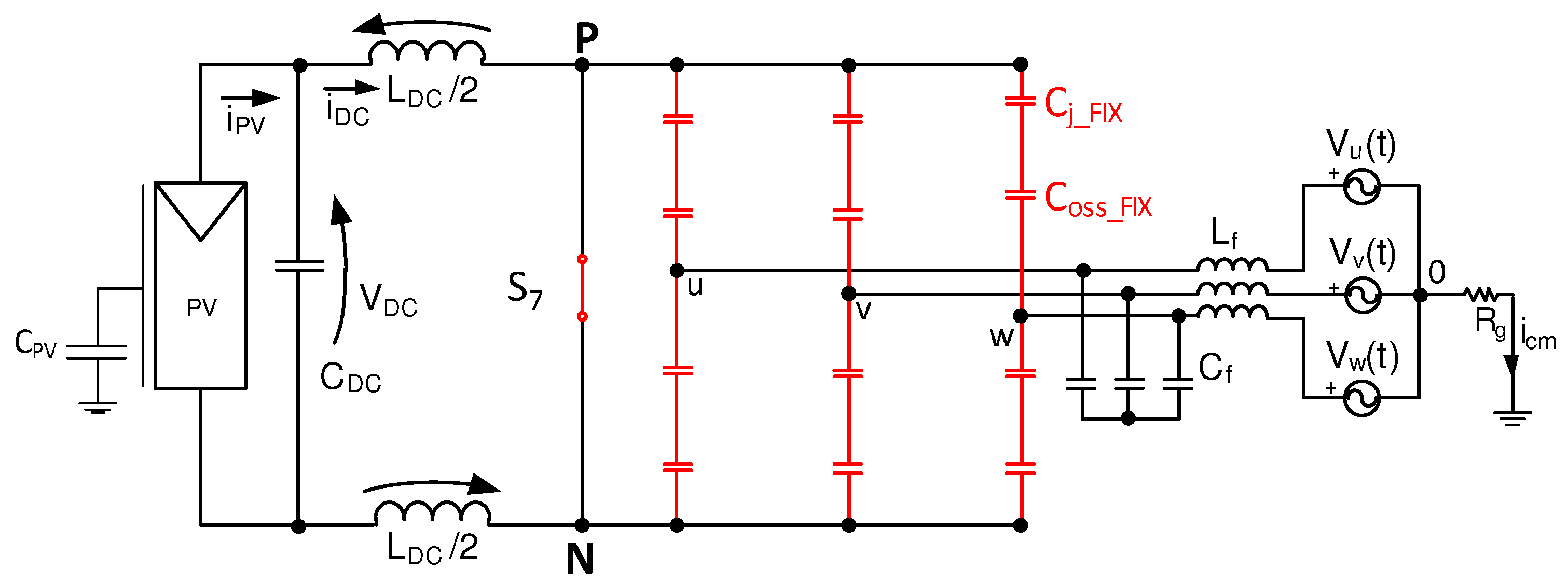
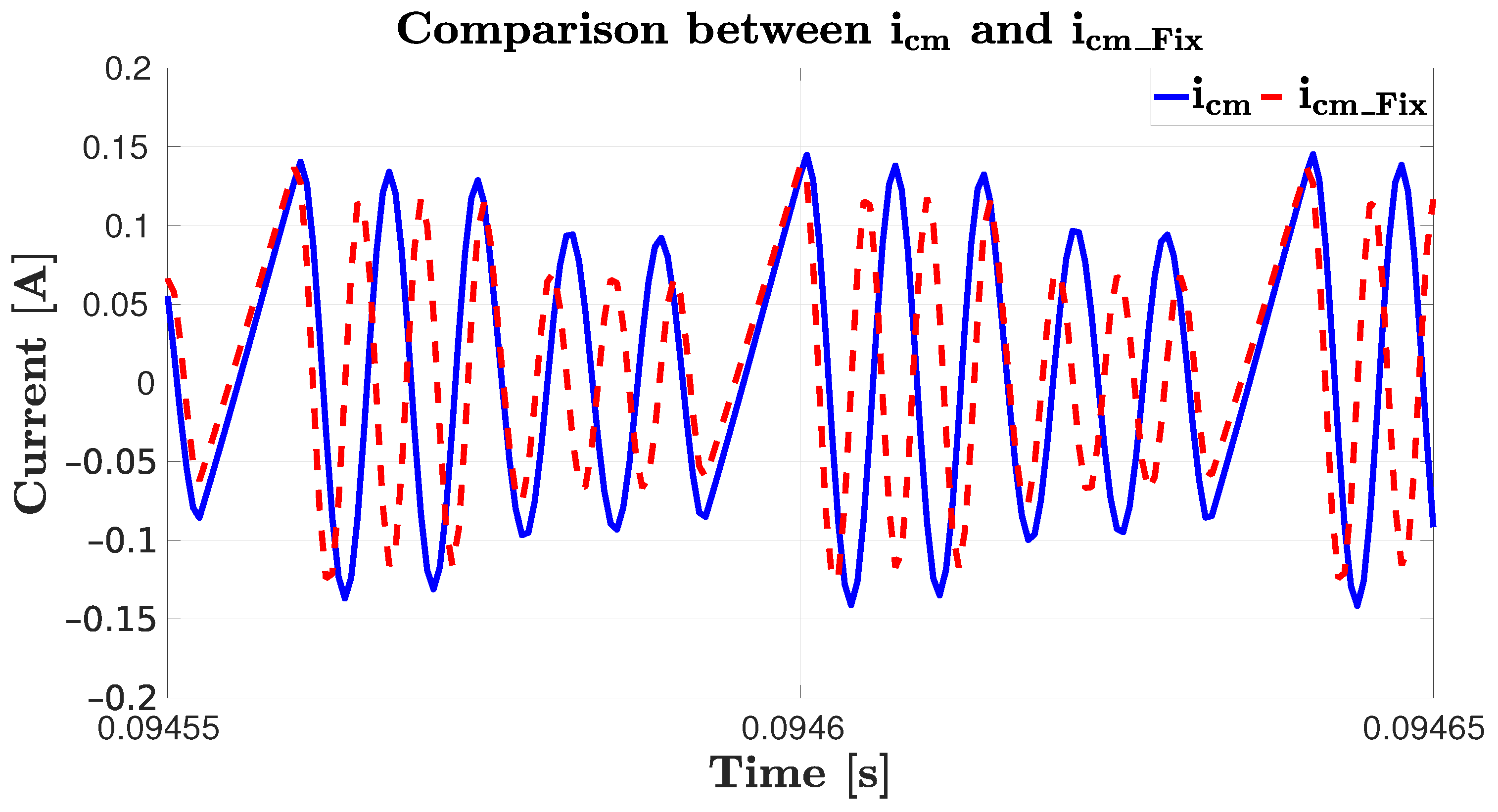
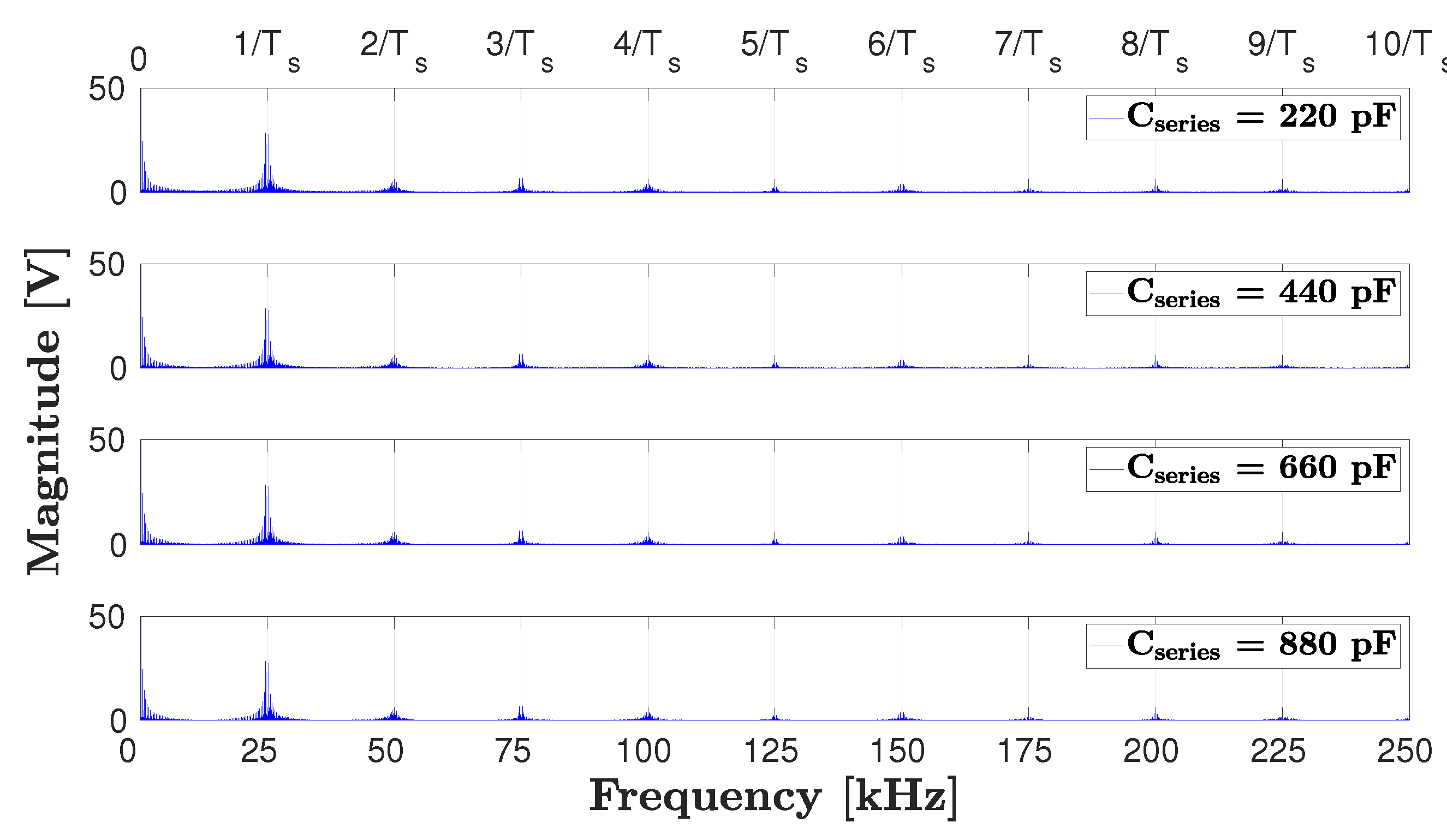
3.1. Matching between Variable and Fixed Capacitances
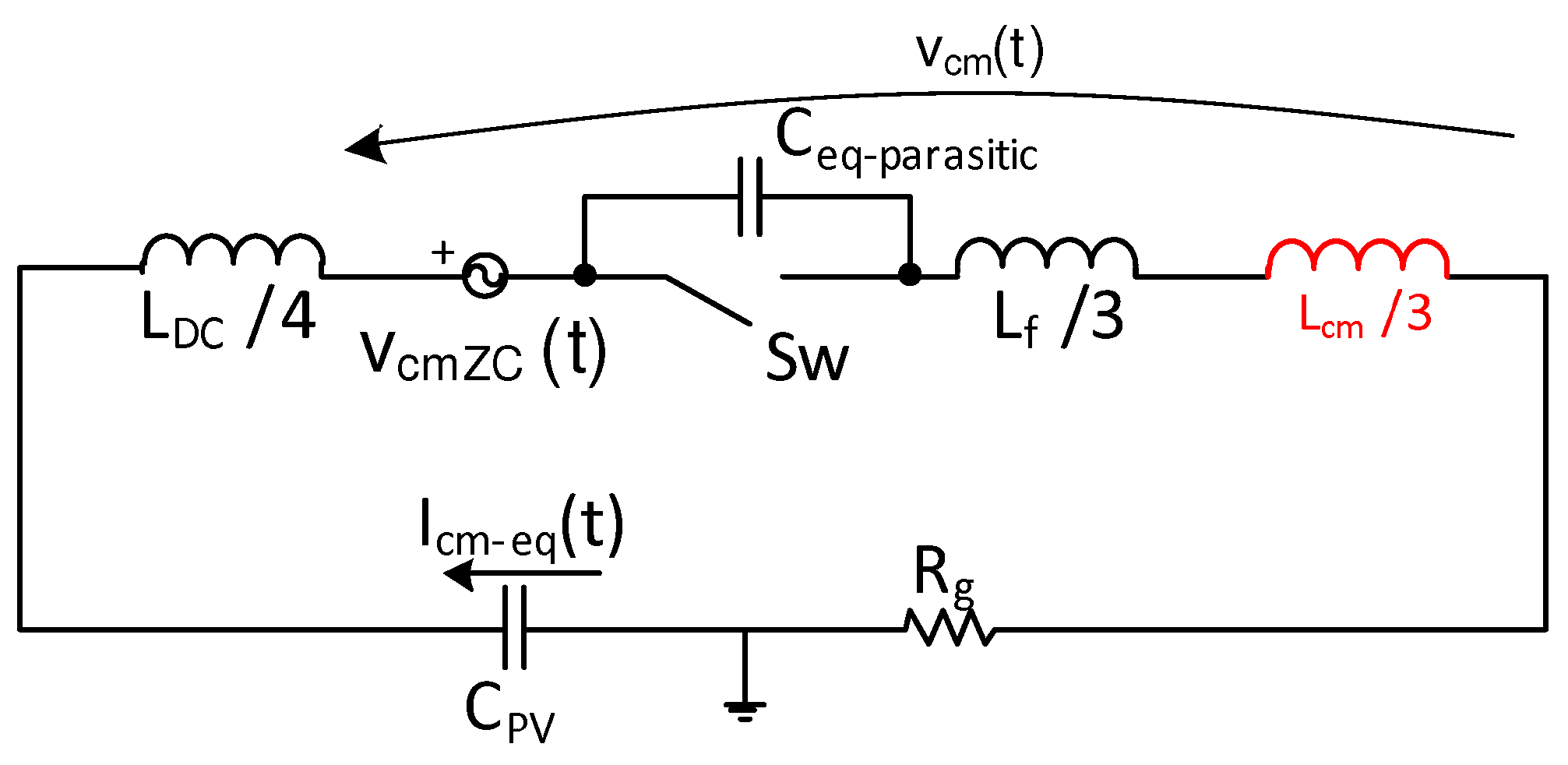
3.2. Validation of the Equivalent Common-Mode Circuit
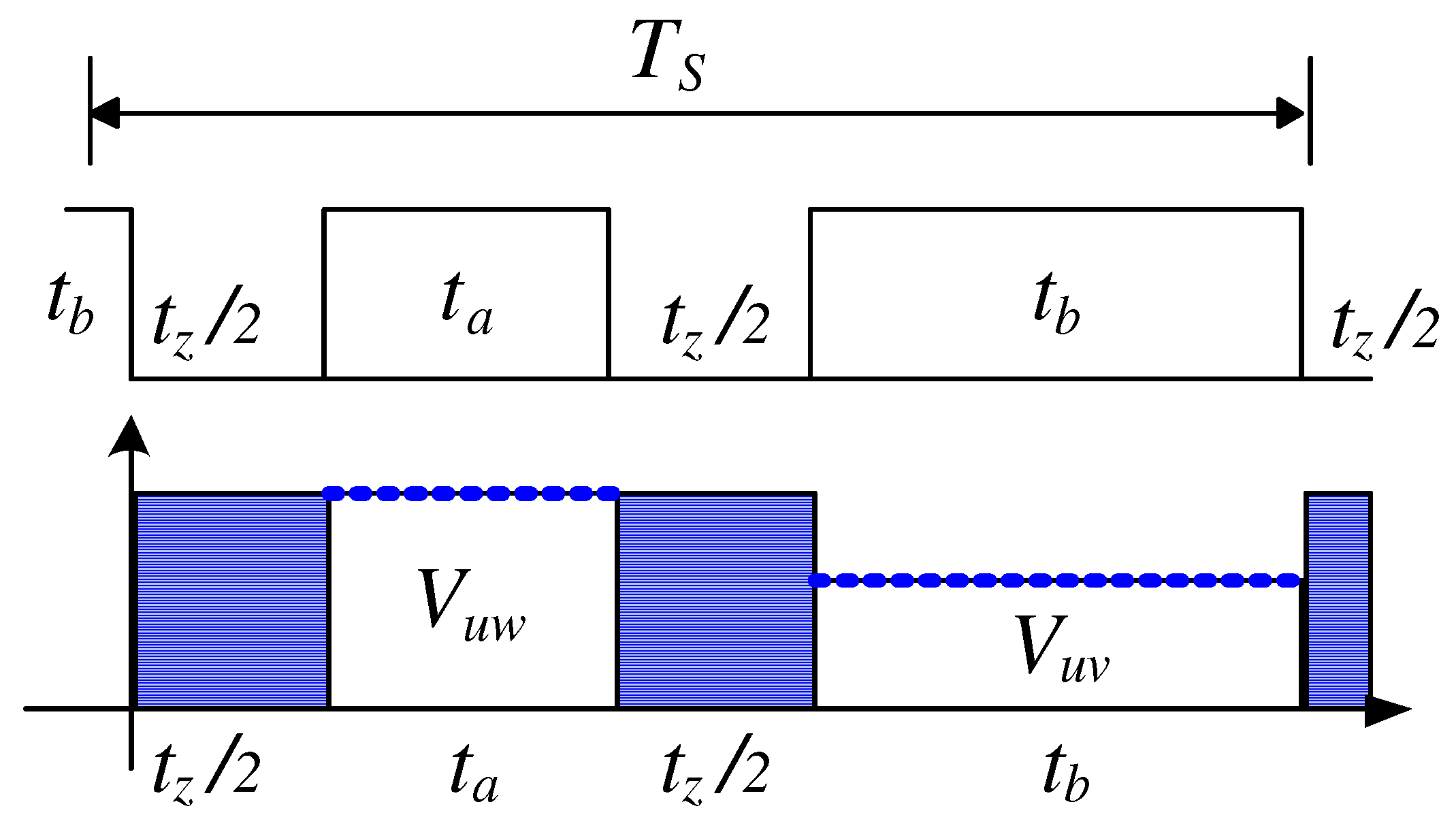
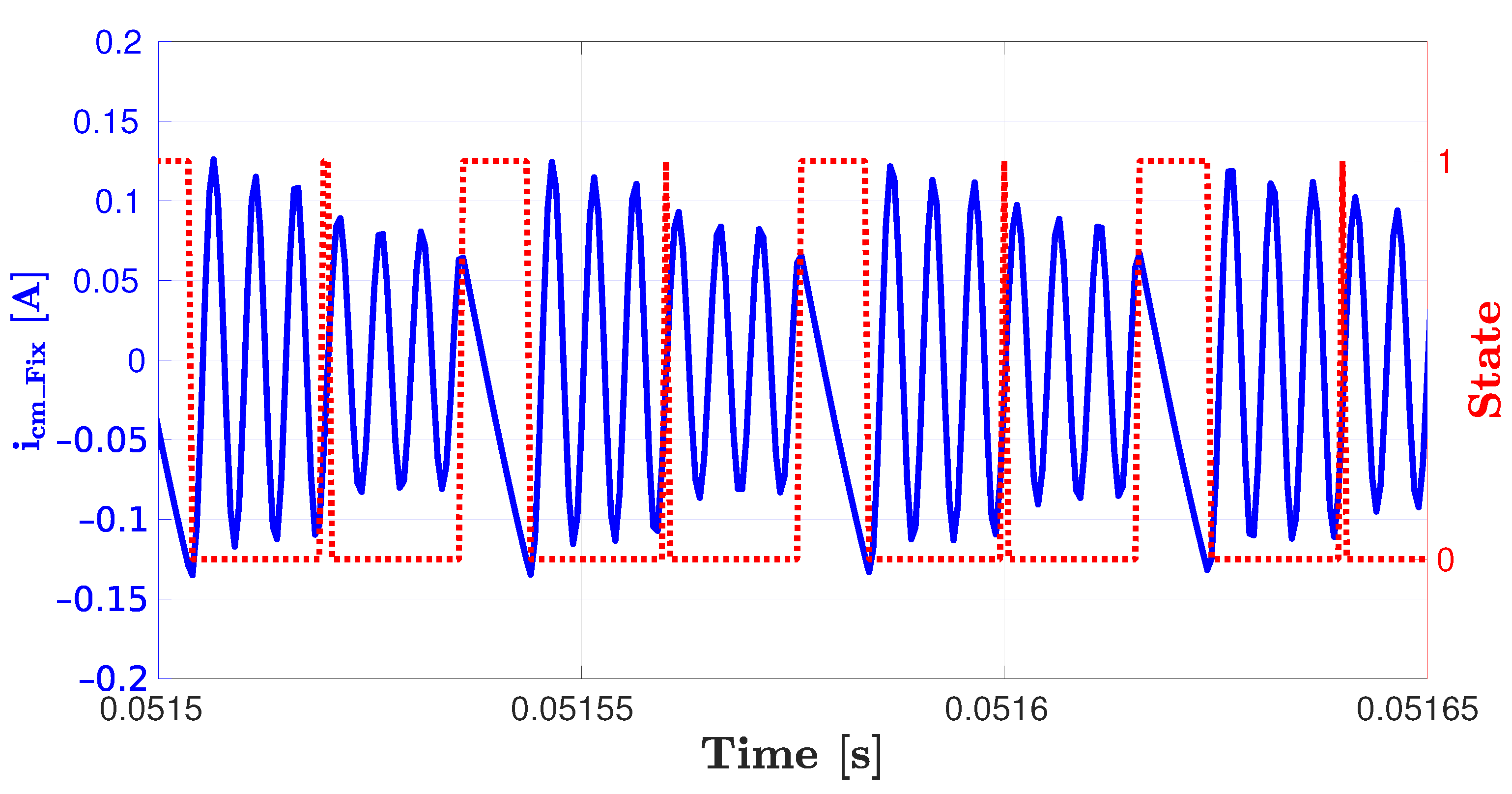
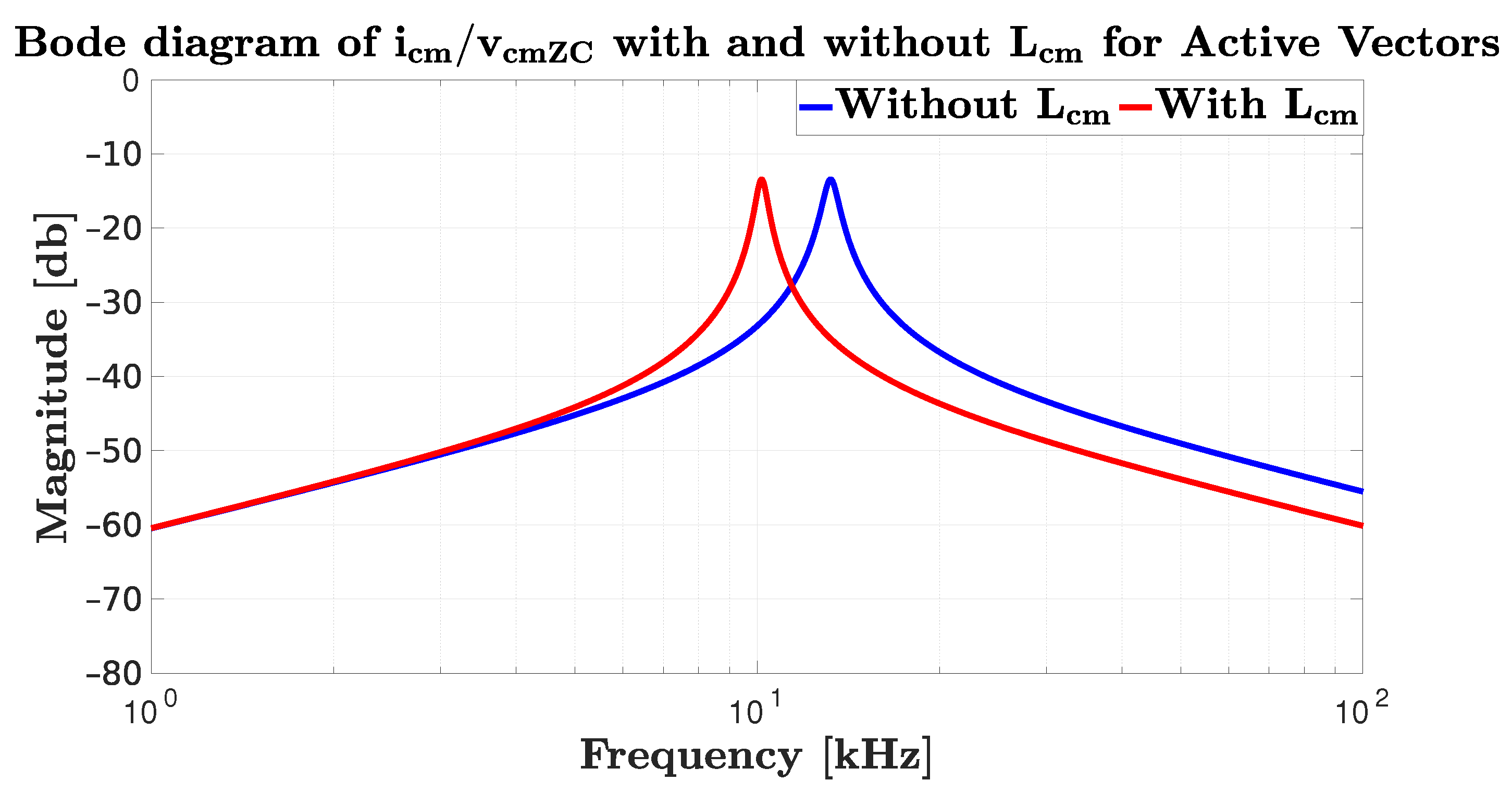
3.3. Critical Aspects of the Resonant Frequency
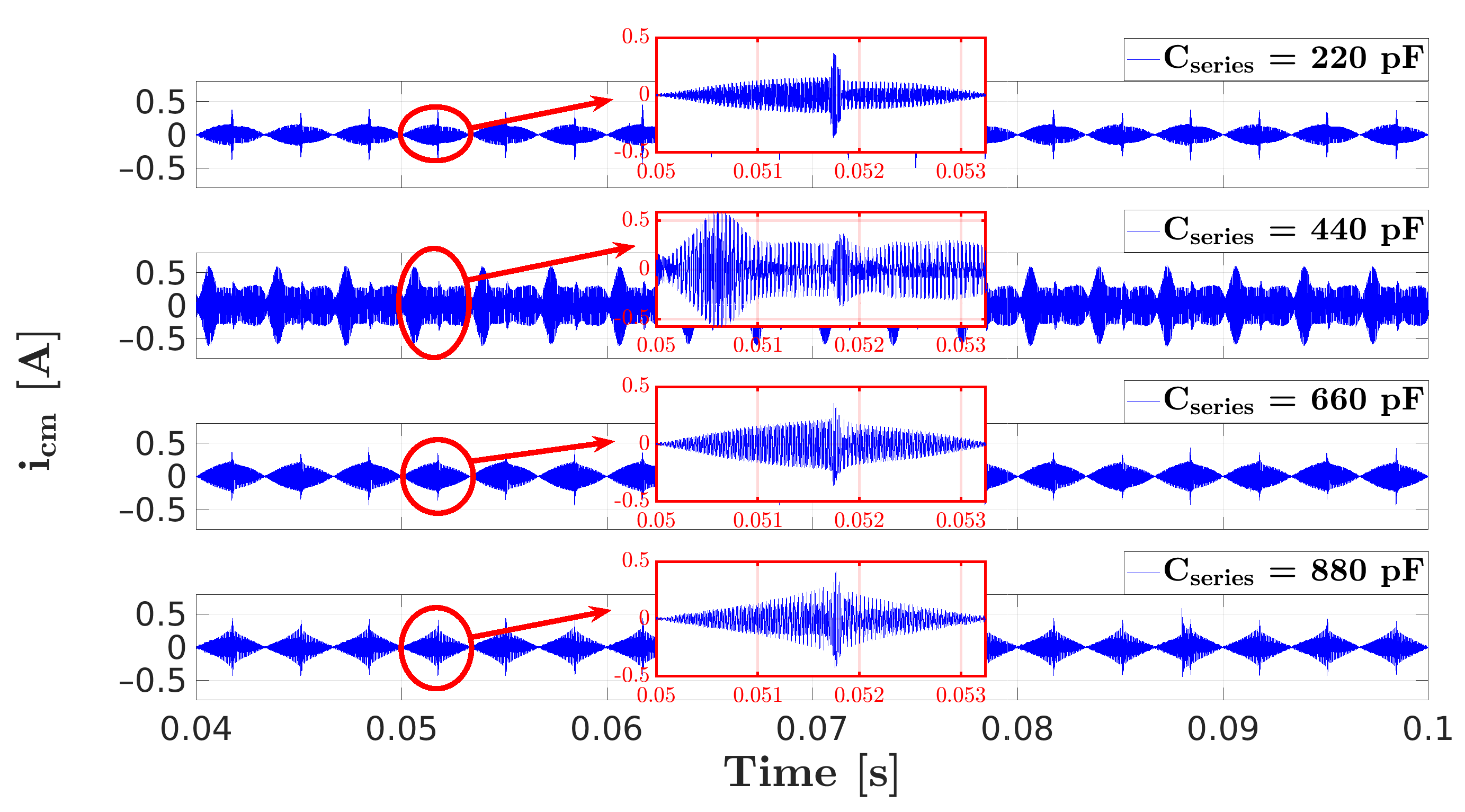
3.4. Mitigation of the Resonance Problem
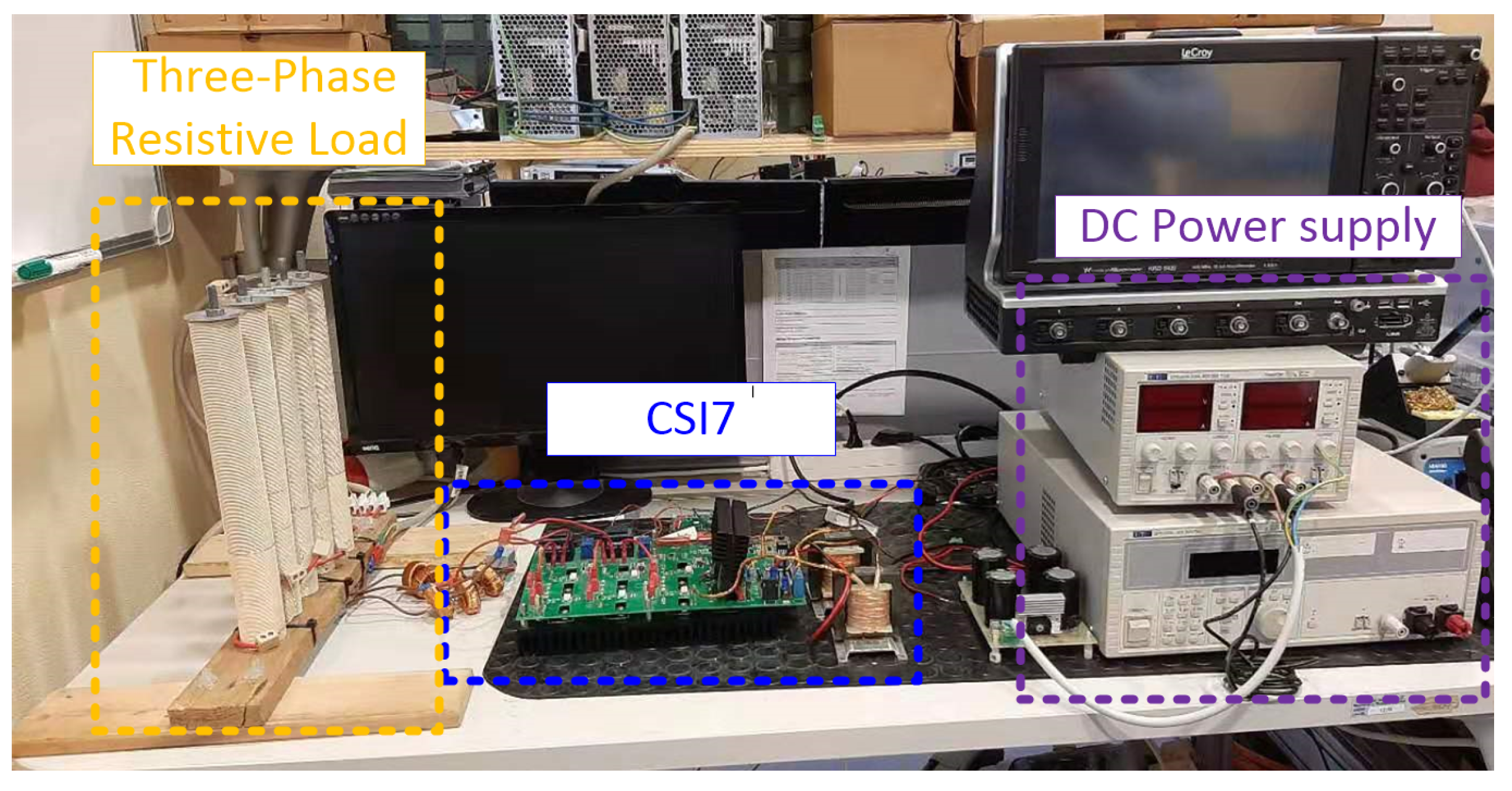
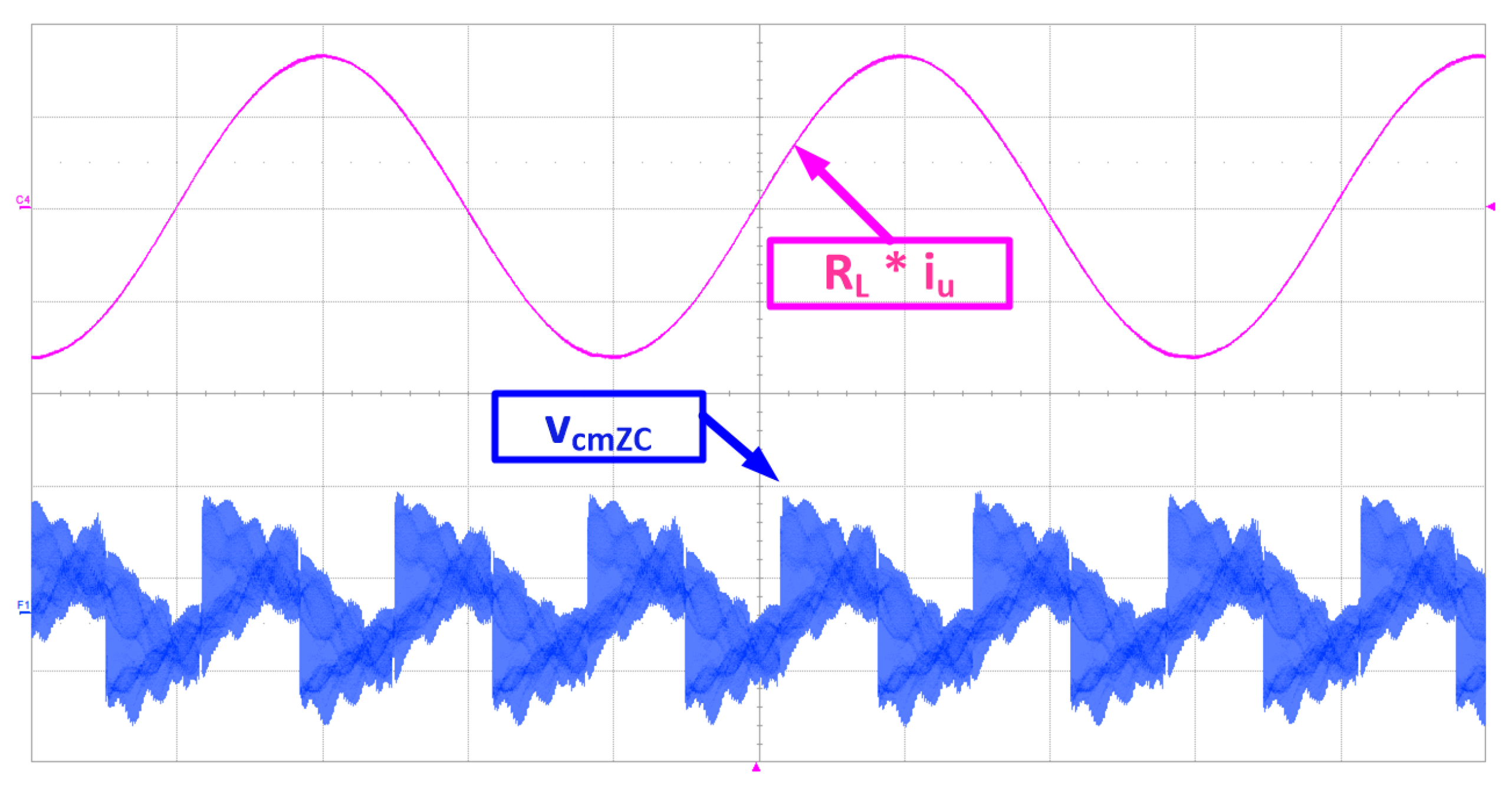
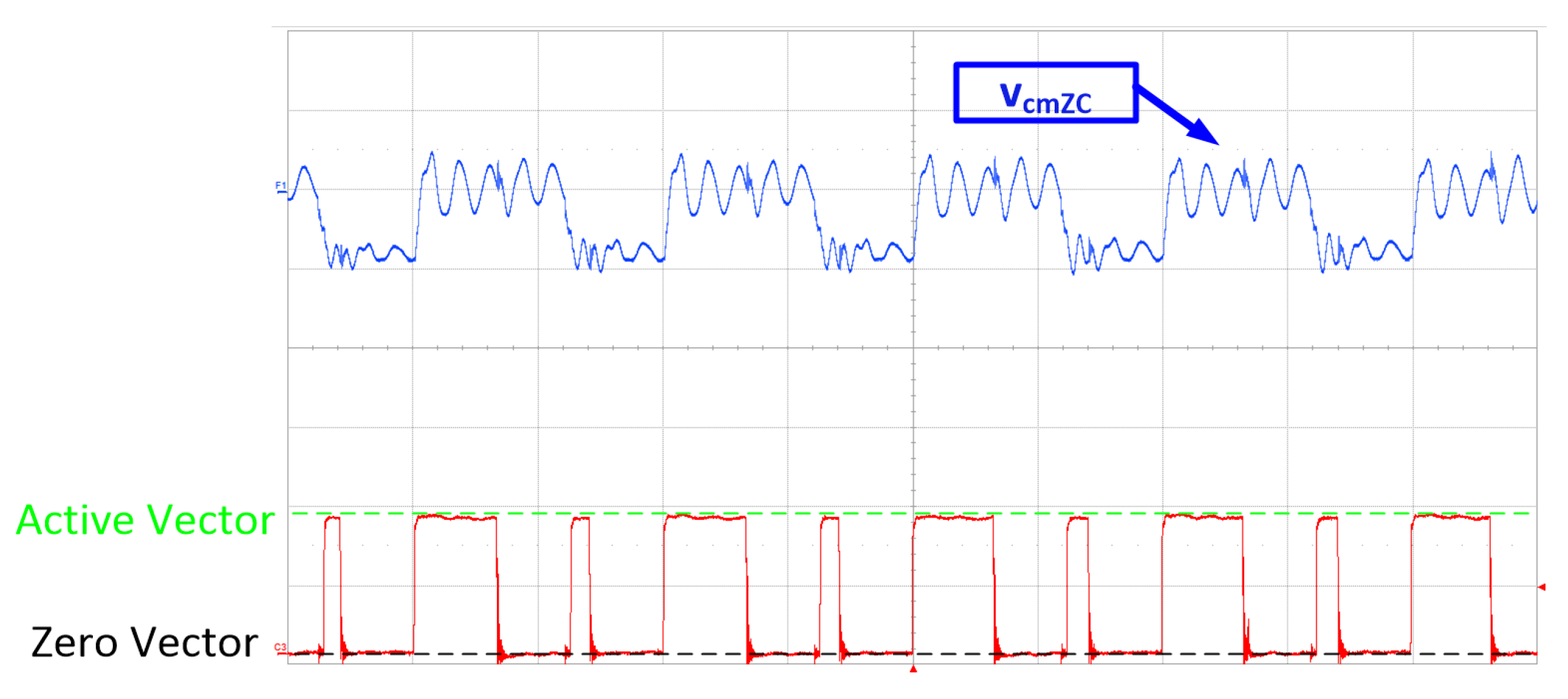
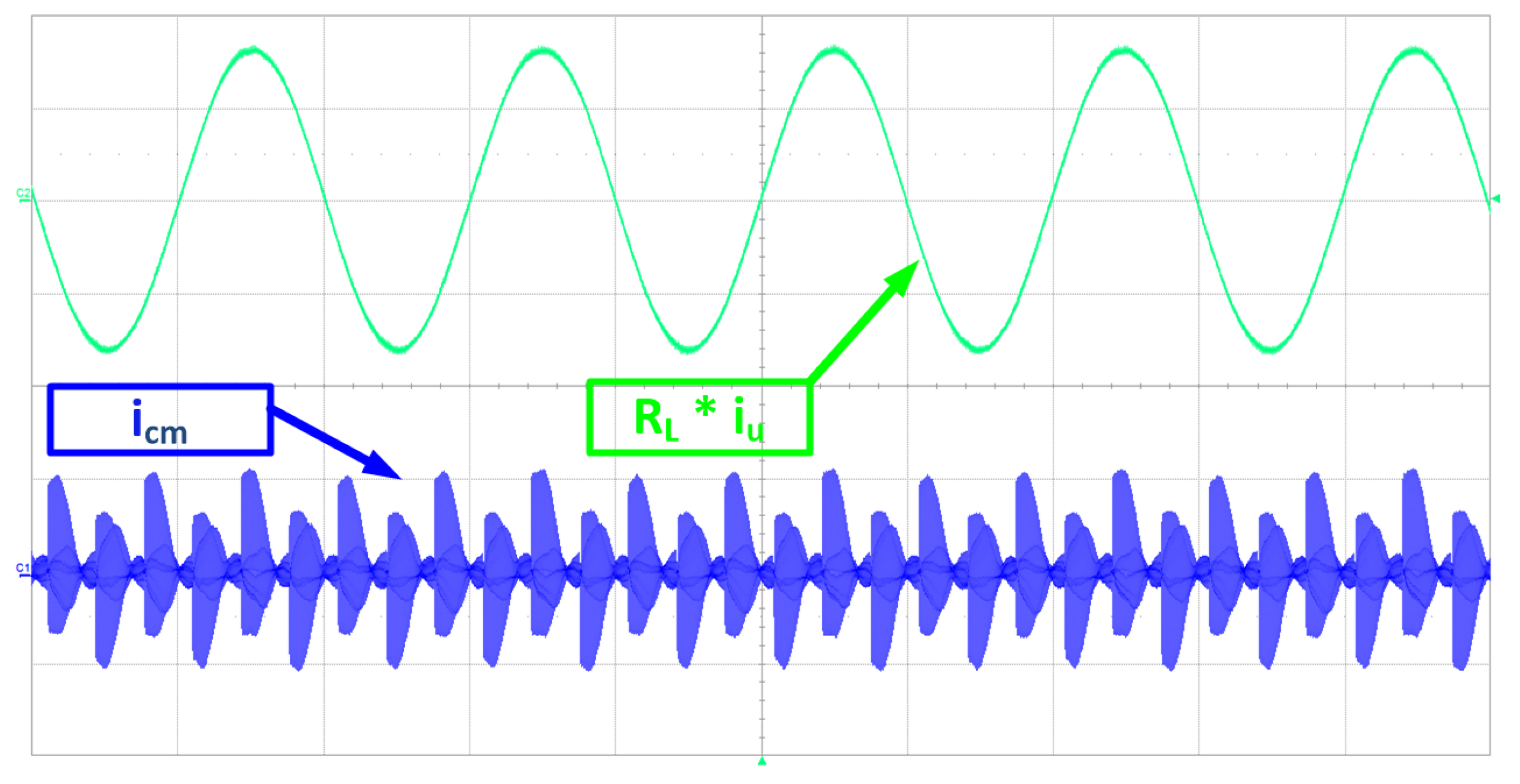
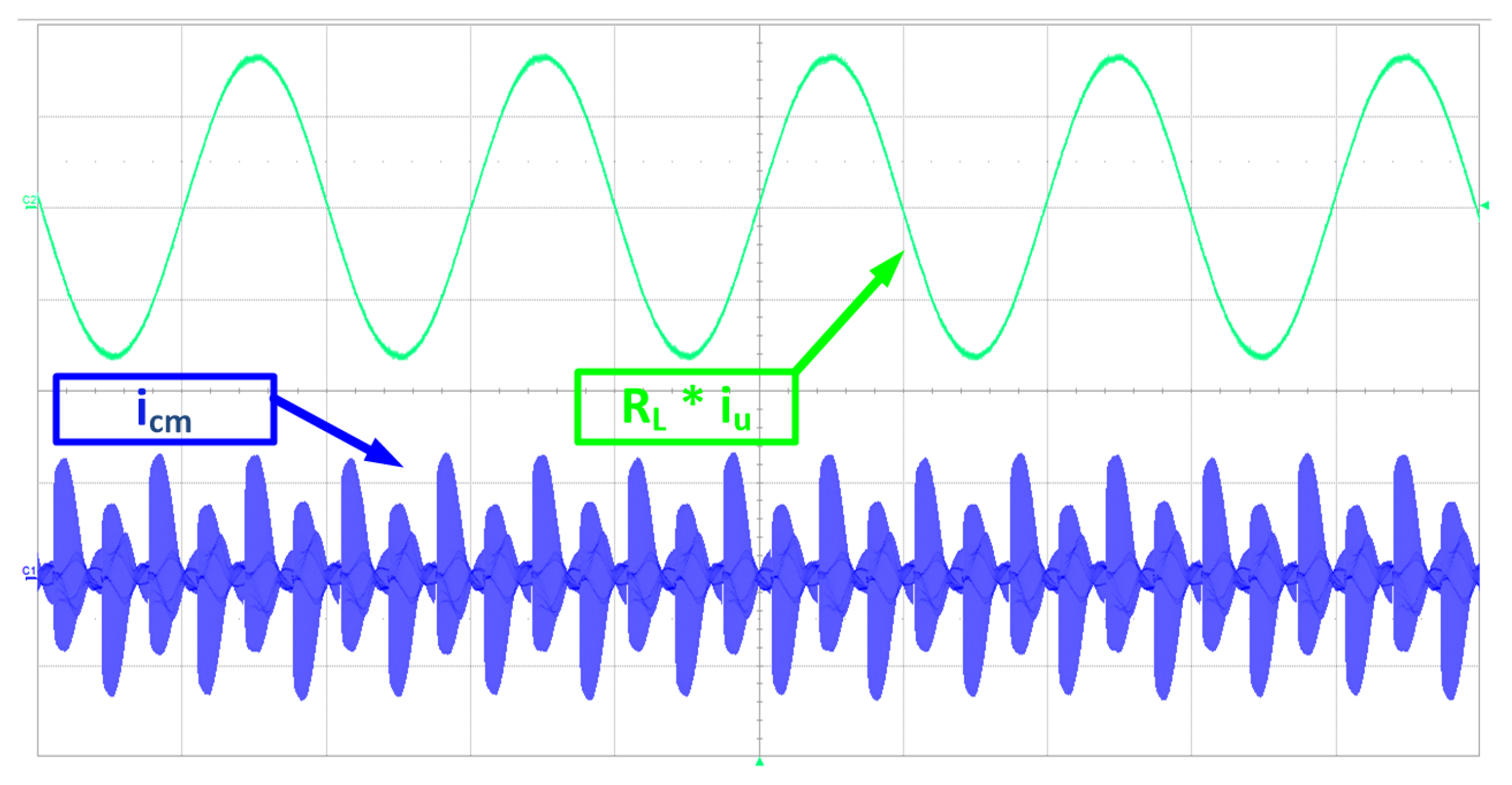
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Sahan, B.; Vergara, A.N.; Henze, N.; Engler, A.; Zacharias, P. A Single-Stage PV Module Integrated Converter Based on a Low-Power Current-Source Inverter. IEEE Trans. Ind. Electron. 2008, 55, 2602–2609. [Google Scholar] [CrossRef]
- Bendre, A.; Wallace, I.; Nord, J.; Venkataramanan, G. A Current Source PWM Inverter with Actively Commutated SCRs. IEEE Trans. Power Electron. 2002, 17, 461–468. [Google Scholar] [CrossRef]
- Migliazza, G.; Carfagna, E.; Bernardi, F.; Lorenzani, E. Ground Leakage Current in Three-Phase Current Source Inverters Depending on Power Semiconductors Parasitic Capacitances. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 2125–2130. [Google Scholar] [CrossRef]
- Lorenzani, E.; Immovilli, F.; Migliazza, G.; Frigieri, M.; Bianchini, C.; Davoli, M. CSI7: A Modified Three-Phase Current-Source Inverter for Modular Photovoltaic Applications. IEEE Trans. Ind. Electron. 2017, 64, 5449–5459. [Google Scholar] [CrossRef]
- Wang, W.; Gao, F.; Yang, Y.; Blaabjerg, F. Operation and Modulation of H7 Current-Source Inverter With Hybrid SiC and Si Semiconductor Switches. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 387–399. [Google Scholar] [CrossRef]
- Gao, F.; Loh, P.C.; Blaabjerg, F.; Vilathgamuwa, D.M. Five-Level Current-Source Inverters With Buck–Boost and Inductive-Current Balancing Capabilities. IEEE Trans. Ind. Electron. 2010, 57, 2613–2622. [Google Scholar] [CrossRef]
- Espinoza, J.R.; Joos, G. A Current-Source-Inverter-Fed Induction Motor Drive System with Reduced Losses. IEEE Trans. Ind. Appl. 1998, 34, 796–805. [Google Scholar] [CrossRef]
- Li, Y.W.; Pande, M.; Zargari, N.R.; Wu, B. DC-Link Current Minimization for High-Power Current-Source Motor Drives. IEEE Trans. Power Electron. 2009, 24, 232–240. [Google Scholar]
- Lee, H.; Jung, S.; Sul, S. A Current Controller Design for Current Source Inverter-Fed AC Machine Drive System. IEEE Trans. Power Electron. 2013, 28, 1366–1381. [Google Scholar] [CrossRef]
- Migliazza, G.; Buticchi, G.; Carfagna, E.; Lorenzani, E.; Madonna, V.; Giangrande, P.; Galea, M. DC Current Control for a Single-Stage Current Source Inverter in Motor Drive Application. IEEE Trans. Power Electron. 2021, 36, 3367–3376. [Google Scholar] [CrossRef]
- Morya, A.K.; Gardner, M.C.; Anvari, B.; Liu, L.; Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Wide Bandgap Devices in AC Electric Drives: Opportunities and Challenges. IEEE Trans. Transp. Electrif. 2019, 5, 3–20. [Google Scholar] [CrossRef]
- Shen, J.; Qin, X.; Wang, Y. High-Speed Permanent Magnet Electrical Machines—Applications, Key Issues and Challenges. CES Trans. Electr. Mach. Syst. 2018, 2, 23–33. [Google Scholar] [CrossRef]
- Buticchi, G.; Bozhko, S.; Liserre, M.; Wheeler, P.; Al-Haddad, K. On-Board Microgrids for the More Electric Aircraft—Technology Review. IEEE Trans. Ind. Electron. 2019, 66, 5588–5599. [Google Scholar] [CrossRef] [Green Version]
- Madonna, V.; Migliazza, G.; Giangrande, P.; Lorenzani, E.; Buticchi, G.; Galea, M. The Rebirth of the Current Source Inverter: Advantages for Aerospace Motor Design. IEEE Ind. Electron. Mag. 2019, 13, 65–76. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Li, C.; He, J. Common-Mode Voltage Reduction and Fault-Tolerant Operation of Four-Leg CSI-Fed Motor Drives. IEEE Trans. Power Electron. 2021, 36, 8570–8574. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Liu, P.; Zhang, Y.; He, J. Zero-Voltage-Switching Current Source Inverter Fed PMSM Drives With Reduced EMI. IEEE Trans. Power Electron. 2021, 36, 761–771. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Xu, D.; Zargari, N.R. Hybrid PWM for High-Power Current-Source-Inverter-Fed Drives With Low Switching Frequency. IEEE Trans. Power Electron. 2011, 26, 1754–1764. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Xu, D.; Zargari, N.R. A Current-Source-Converter-Based High-Power High-Speed PMSM Drive With 420-Hz Switching Frequency. IEEE Trans. Ind. Electron. 2012, 59, 2970–2981. [Google Scholar] [CrossRef]
- Wu, B.; Narimani, M. High-Power Converters and AC Drives; John Wiley & Sons: Hoboken, NJ, USA, 2017; Volume 59. [Google Scholar]
- Lorenzani, E.; Migliazza, G.; Immovilli, F.; Buticchi, G. CSI and CSI7 Current Source Inverters for Modular Transformerless PV Inverters. Chin. J. Electr. Eng. 2019, 5, 32–42. [Google Scholar] [CrossRef]
- Grandi, G.; Casadei, D.; Reggiani, U. Common- and Differential-Mode HF Current Components in AC Motors Supplied by Voltage Source Inverters. IEEE Trans. Power Electron. 2004, 19, 16–24. [Google Scholar] [CrossRef]
- Magdun, O.; Binder, A. High-Frequency Induction Machine Modeling for Common Mode Current and Bearing Voltage Calculation. IEEE Trans. Ind. Appl. 2014, 50, 1780–1790. [Google Scholar] [CrossRef]
- Rodriguez, J.; Moran, L.; Pontt, J.; Osorio, R.; Kouro, S. Modeling and Analysis of Common-Mode Voltages Generated in Medium Voltage PWM-CSI Drives. IEEE Trans. Power Electron. 2003, 18, 873–879. [Google Scholar] [CrossRef] [Green Version]
- Lorenzani, E.; Migliazza, G.; Immovilli, F.; Gerada, C.; Zhang, H.; Buticchi, G. Internal Current Return Path for Ground Leakage Current Mitigation in Current Source Inverters. IEEE Access 2019, 7, 96540–96548. [Google Scholar] [CrossRef]









| Name | Value | Unit | Name | Value | Unit |
|---|---|---|---|---|---|
| Input inductance | 2 | Capacitor filter | 1.5 | ||
| Switching Period | 40 | PV panels capacitance | 150 | ||
| Overlap time | 1 | DC bus voltage | 120 | ||
| Line-to-line voltage | 400 | Mosfet parasitic capacitance | 224 | ||
| Inductance filter | 1.4 | Diode parasitic capacitance | 191 | ||
| Ground resistance | 4.7 | Ω | Equivalent parasitic capacitance | 619 | |
| Grid frequency | 50 | Phase current | 0.91 |
| Case | RMS Current [] |
|---|---|
| 0.0650 | |
| 0.0556 |
| [] | RMS Current [] |
|---|---|
| 0.07119 | |
| 0.18296 | |
| 0.09214 | |
| 0.08938 |
| [] | RMS Current [] |
|---|---|
| 0.0396 | |
| 0.0715 | |
| 0.0836 | |
| 0.1360 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Migliazza, G.; Carfagna, E.; Buticchi, G.; Immovilli, F.; Lorenzani, E. Effect of Semiconductor Parasitic Capacitances on Ground Leakage Current in Three-Phase Current Source Inverters. Energies 2021, 14, 7364. https://doi.org/10.3390/en14217364
Migliazza G, Carfagna E, Buticchi G, Immovilli F, Lorenzani E. Effect of Semiconductor Parasitic Capacitances on Ground Leakage Current in Three-Phase Current Source Inverters. Energies. 2021; 14(21):7364. https://doi.org/10.3390/en14217364
Chicago/Turabian StyleMigliazza, Giovanni, Emilio Carfagna, Giampaolo Buticchi, Fabio Immovilli, and Emilio Lorenzani. 2021. "Effect of Semiconductor Parasitic Capacitances on Ground Leakage Current in Three-Phase Current Source Inverters" Energies 14, no. 21: 7364. https://doi.org/10.3390/en14217364
APA StyleMigliazza, G., Carfagna, E., Buticchi, G., Immovilli, F., & Lorenzani, E. (2021). Effect of Semiconductor Parasitic Capacitances on Ground Leakage Current in Three-Phase Current Source Inverters. Energies, 14(21), 7364. https://doi.org/10.3390/en14217364










