Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review
Abstract
:1. Introduction
1.1. Energy Storage Systems Overview, Main Techniques, Classifications, and Control Architecture
- Lithium-ion: The typical lithium-ion battery energy storage consists of four main components: a cathode, anode, electrolyte, and a separator. All the components collaborate in accomplishing the objective of storing excess energy. The growing demand of the energy storage market encourages a progressed development of commercial lithium-ion to achieve batteries with higher energy densities, better safety, lower cost, and more prolonged life [7].
- Fuel cell: It is an energy storage technique that converts the stored chemical energy to electrical energy via an electrochemical process. Polymer Electrolyte Membrane (PEM) fuel cells are the major application of fuel-cells, and are recently widely desired because of their low operation temperature, high power density, high efficiency, and low emissions [8].
- Flow battery: The flow battery is a fully rechargeable electrolyte-based electrical energy storage technique, in which fluids are pumped through a cell in order to enhance reduction/oxidation at the ion exchange layer. A redox flow battery is considered a distinguished storage unit because of its high capability of storing electricity, which makes it more desirable than traditional batteries [9].
- Compressed air: It is typically a technique to store energy through compressed air during low-demand times, and this air can be used later to rotate a motor-generator and generate electricity [10].
- Flywheel: This technique is based on storing energy in the form of kinetic energy in a vacuum, and then using it to rotate a motor-generator and generate electricity [11].
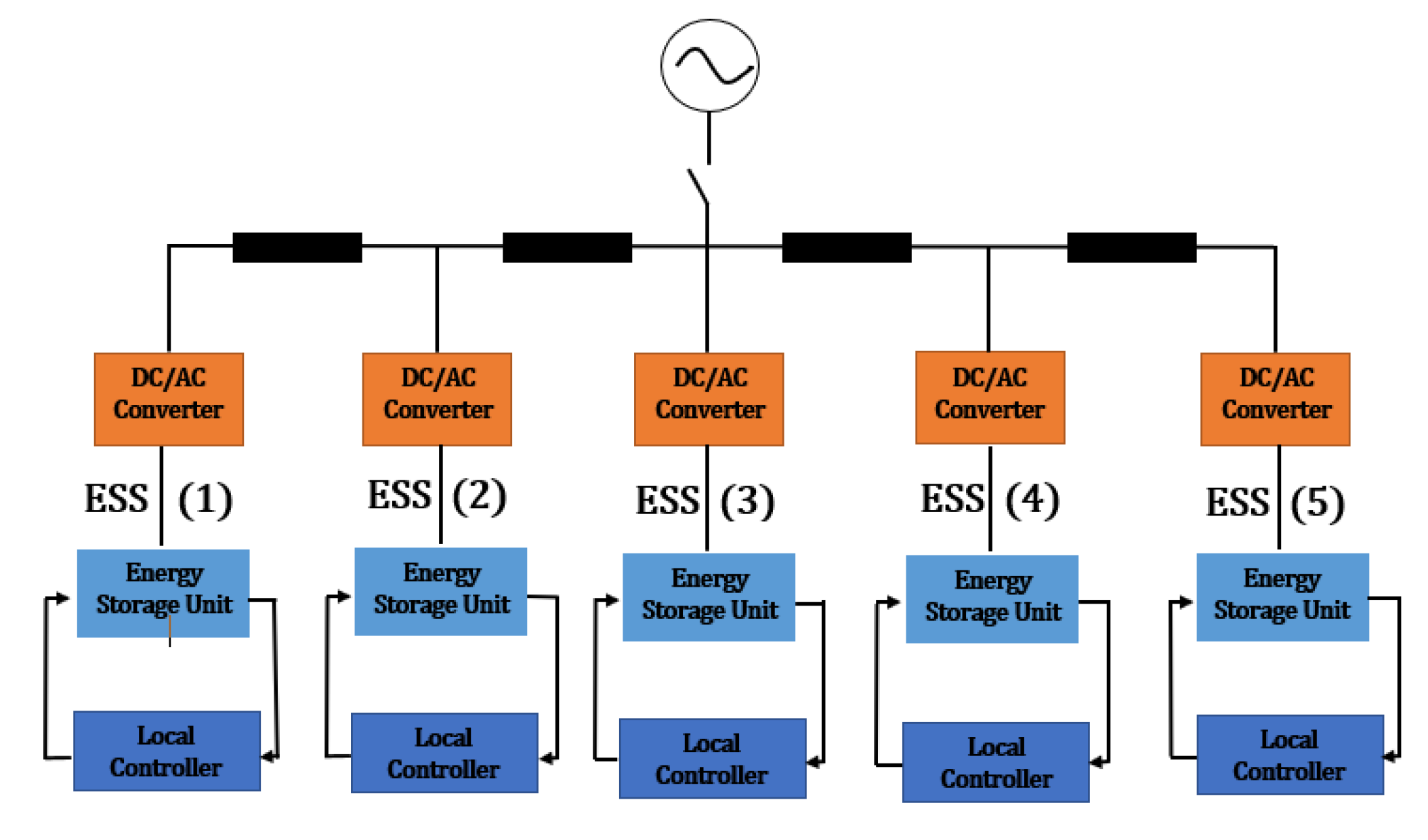
- Aggregated: Modelling is simplified when all ESSs are in one location of a predetermined microgrid network [12].
- Distributed: Distributed ESSs are scattered around different locations within a predetermined microgrid network [13].
- Hybrid: A combined application of ESSs with different storage technologies, which is necessary due to the lack of any ESS technologies which can individually provide all the mandatory characteristics [14].
- The urgent necessity to increase the introduction of renewable energy resources, such as photovoltaics and wind generators, has simulated the movement toward decentralized distributed ESS [16]; consequently, it has paved the way for a successful and beneficial transition to smart microgrid networks and reduced pollution [17].
- The gradual degradation of ESSs cost has prompted an increase in their use, for the purpose of storing excess energy, and other purposes [18].
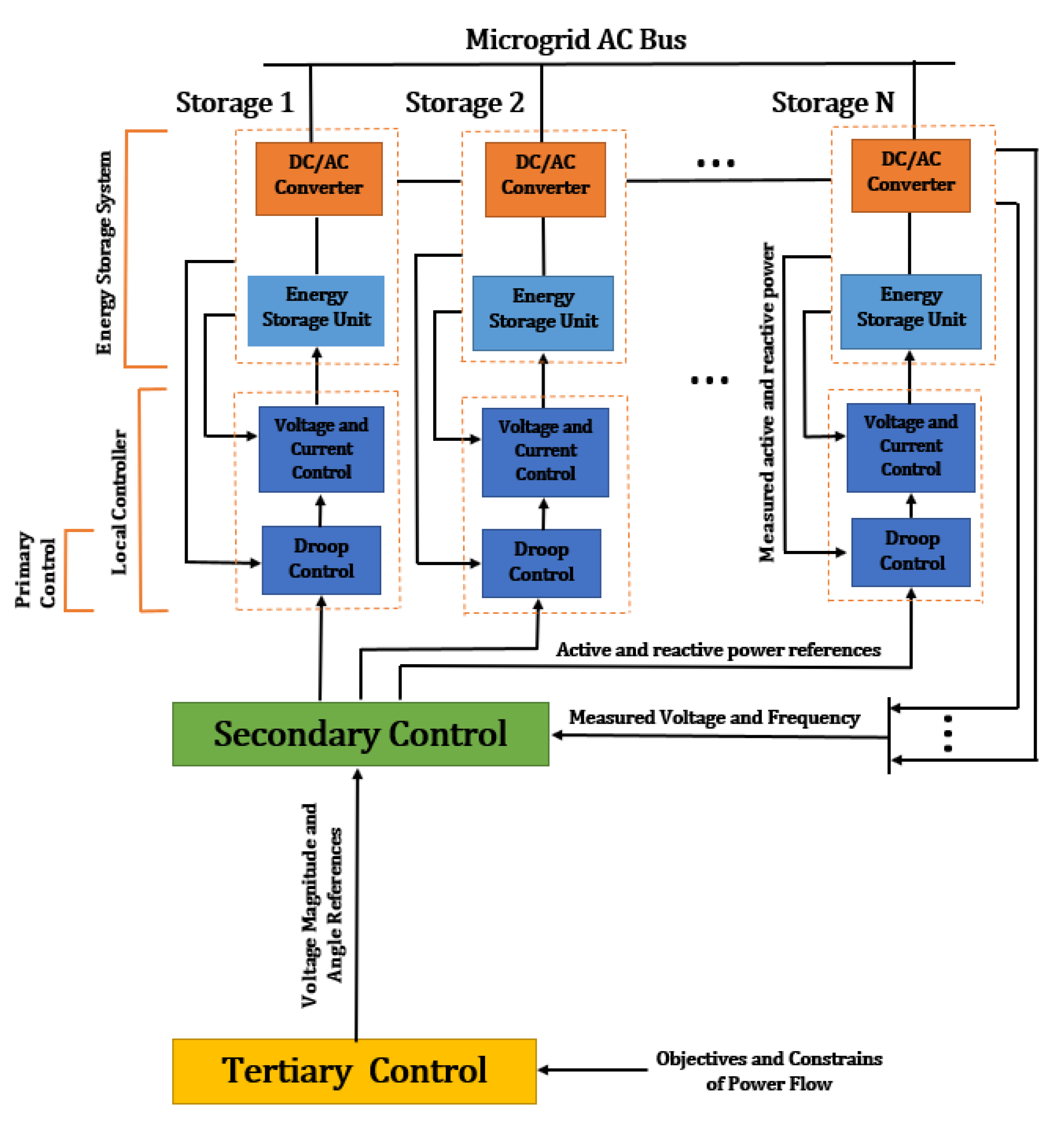
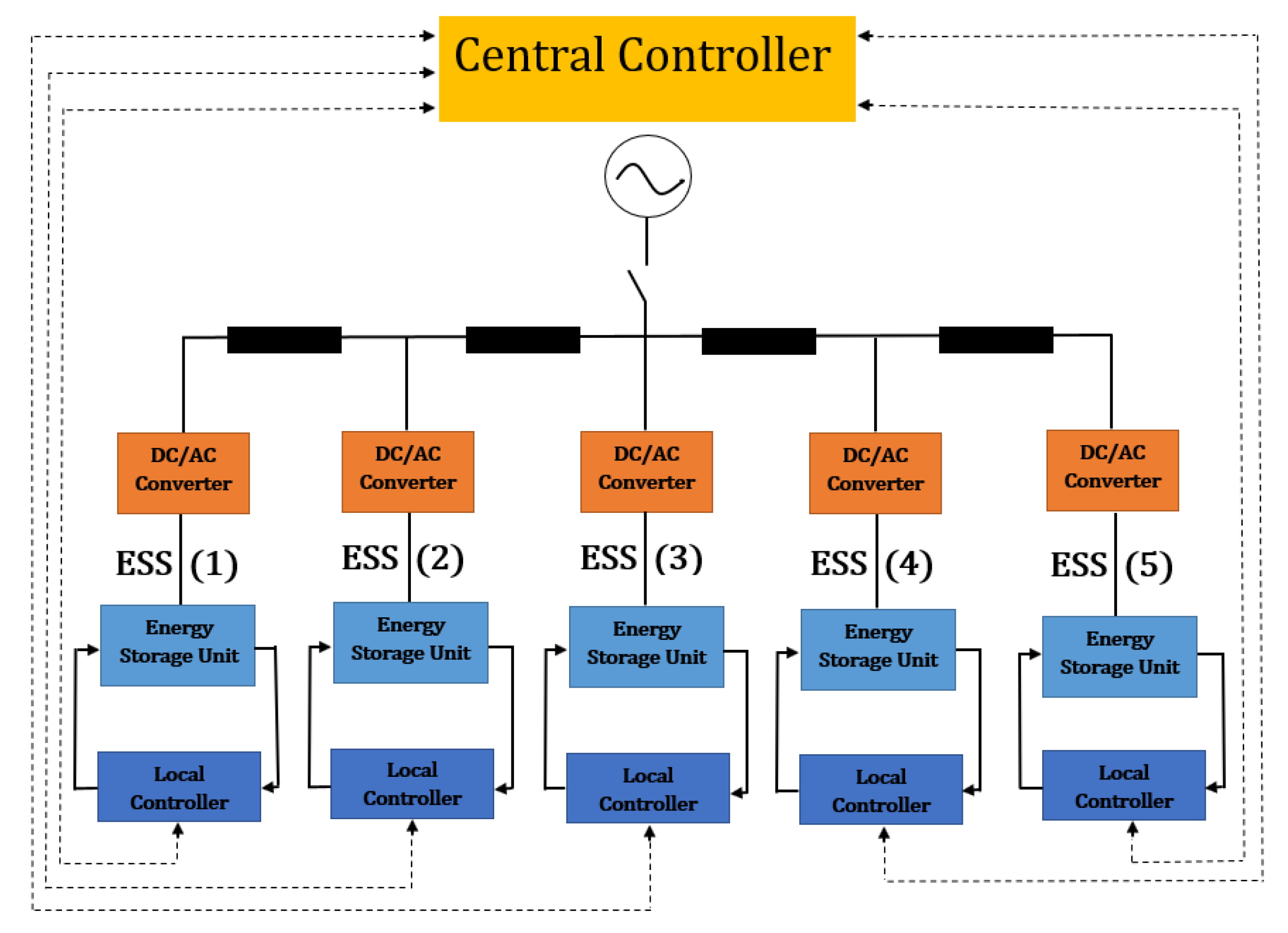
- Primary Decentralized Control: The objective of this level is to regulate the load sharing of distributed energy resources and storage, via the control of their linked converters output voltage and frequency, to attain balanced and autonomous operation of these distributed systems [19,20]. The most typical strategy of this is droop control, which is responsible for implementing balanced load sharing for the distributed resources and storage, with no necessity for time-critical communication links [21]. As demonstrated in the AC microgrid of Figure 1, droop control is present at each distributed ESS as a primary control. It receives measured active and reactive power and creates voltage and frequency offsets for the local controller. This, in turn, implements load participation that accomplishes the overall balance of the load sharing in the microgrid.
- Secondary Centralized Control: Centralized secondary control has the responsibility of correcting voltage and frequency offsets that are achieved by the primary control. Therefore, it plays the role of an observer for the primary control. Moreover, it offers some additional roles, such as reactive power-sharing, accurate frequency regulation, and PQ compensation [22,23]. The application of an AC microgrid in Figure 1 illustrates the role of secondary control in correcting droop control offsets to the nominal microgrid references provided by tertiary control. The correction is based on the measured output voltage and frequency offered by each ESS.
- Tertiary Centralized Control: This is the highest control level of the control hierarchy. Typically, it is liable of two major objectives. Firstly, adjusting voltage setpoints, or providing optimal voltage references. Secondly, managing power entering or leaving microgrid, or solve optimal power flow problem (OPF) [24]. In addition, it operates in conjunction with other entities to implement overall objectives of providing balanced and sustainable load sharing [25,26]. Figure 1 clarifies how tertiary control in AC microgrid receives power flow management constraints and objectives, and then creates voltage magnitude and angle references that implement optimal power flow management.
1.2. Energy Storage Systems Roles and Objectives of Microgrid
- Grid voltage support: Means power provided by ESS of a microgrid network, for the objective of maintaining voltage within a mandatory level, or acceptable range. This can be accomplished through the control of distributed ESS reactive power based on real energy generated.
- Grid Frequency Support: It is active power that can be delivered by distributed ESS in a microgrid network, to compensate for any imbalance of frequency that is due to a sudden increase in load or generation.
- Grid stability: ESS offers the opportunity of decreasing oscillation from the rapid introduction of an event during microgrid operation.
- Peak shaving: Typically, the energy generated during the availability of generation or during off-peak times is stored in ESS and shafted to support during high demand time or absence of generation. Furthermore, distributed ESS can implement a short-term demand independently with no obligation of generation. This, in turn, provides excellent support to distributed renewable energy resources, such as photovoltaic and wind turbines.
- Spinning reverse: ESS offers support backup power for islanding.
- Enhancing quality of power: ESS participates in improving power quality, through the involvement of reducing typical issues related to it, such as maintaining voltage and frequency offsets, reducing harmonics, maintaining the balance of voltage, and improving power factor.
- Support reliability: ESS is collaborating on enhancing system reliability in implementing consumer demand.
- Ride through support: ESS can offer essential energy during the conditions of a disturbance or voltage sag, which affects system reliability. This, in turn, helps to keep electric units connected for the duration of these disturbances.
- Compensation of unbalanced load: The collaboration of ESS through the individual injection/absorption of power supports the compensation of an unbalanced load.
1.3. Contribution and Paper Structure
2. Decentralized Control Strategies of Distributed ESSs
2.1. Traditional Droop Control
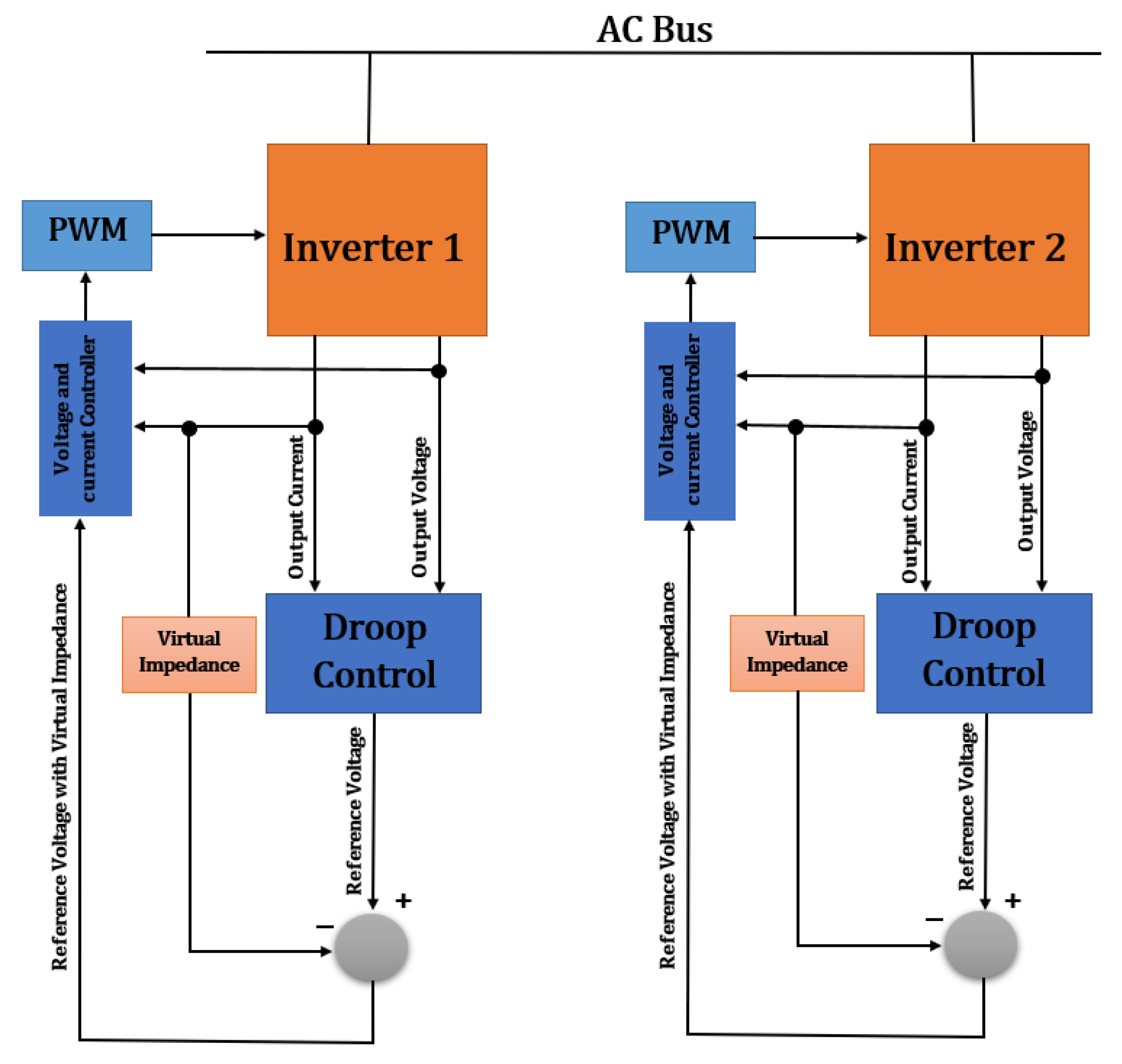
2.2. Virtual Impedance Droop Control
2.3. Droop Control-Based SOC
2.4. Fuzzy Logic Droop Control
2.5. Droop Control of Different Technology-Distributed ESSs
2.6. SOC Balancing of Modular Multilevel Converter Energy Storage System
3. Centralized Control Strategies of Distributed ESSs
3.1. Centralized Secondary Control
3.2. Centralized Tertiary Control of AC Microgrid
3.2.1. Single/Aggregated Distributed ESSs
3.2.2. Ideal Real Power Transfer
3.2.3. Convex Approximation
3.2.4. Non-Convex Approximation
3.3. Centralized Tertiary Control of DC Microgrid
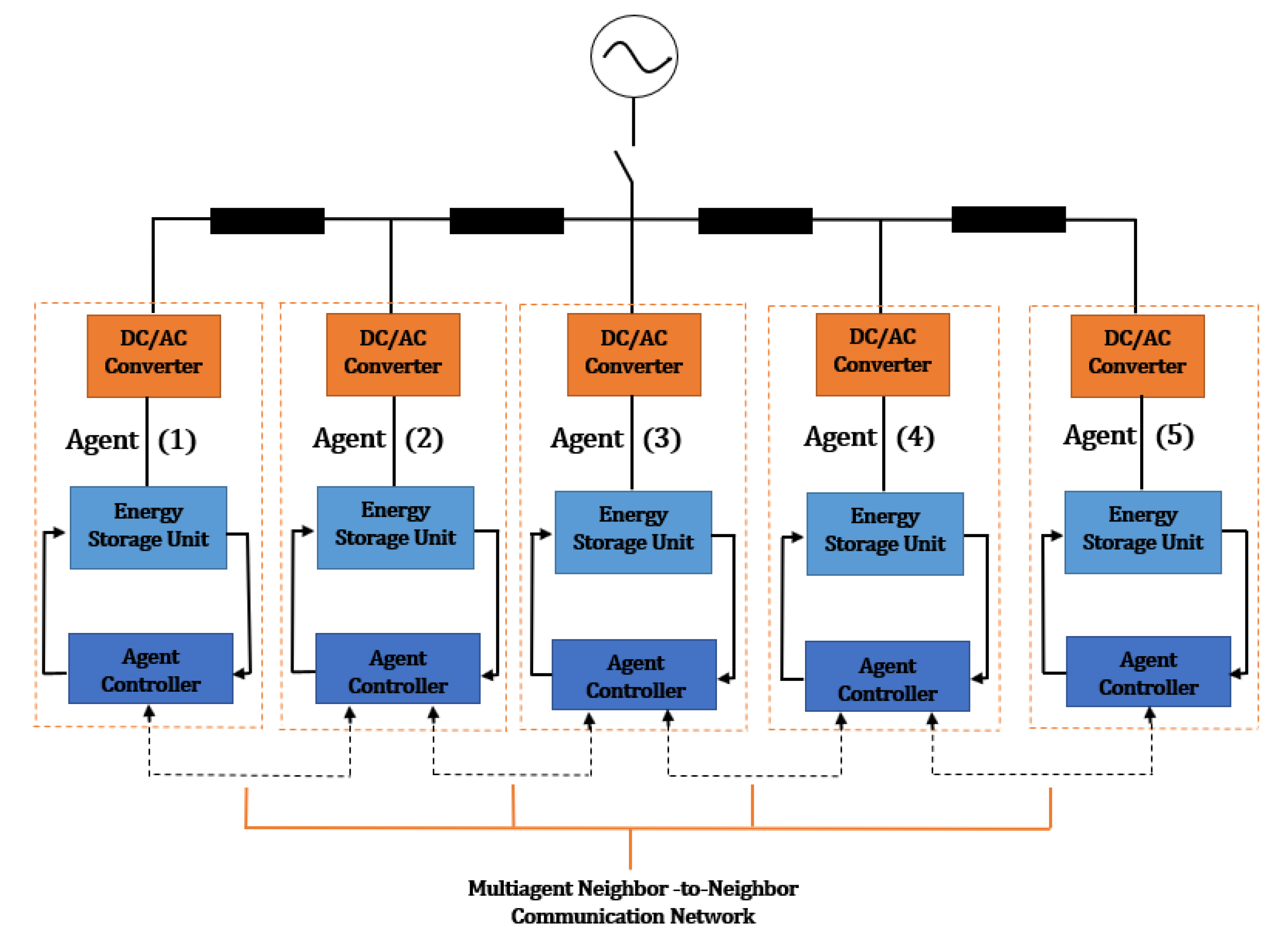
4. Distributed Control Strategies Based on Multiagent Communication of Controlling Distributed ESSs
4.1. Secondary Multiagent of Controlling Distributed ESSs
4.2. Tertiary Cooperative Multiagent Based Strategies of Distributed ESSs
4.2.1. Hierarchical Tertiary Multiagent Strategies of Implementing DOPF of Distributed ESSs
4.2.2. Topology-Based Multiagent DOPF Solutions
4.2.3. Fully Distributed Tertiary Multiagent DOPF Solutions
4.3. Tertiary Competitive Multiagent Solutions
4.4. Combined Cooperative Competitive Multiagent Solutions
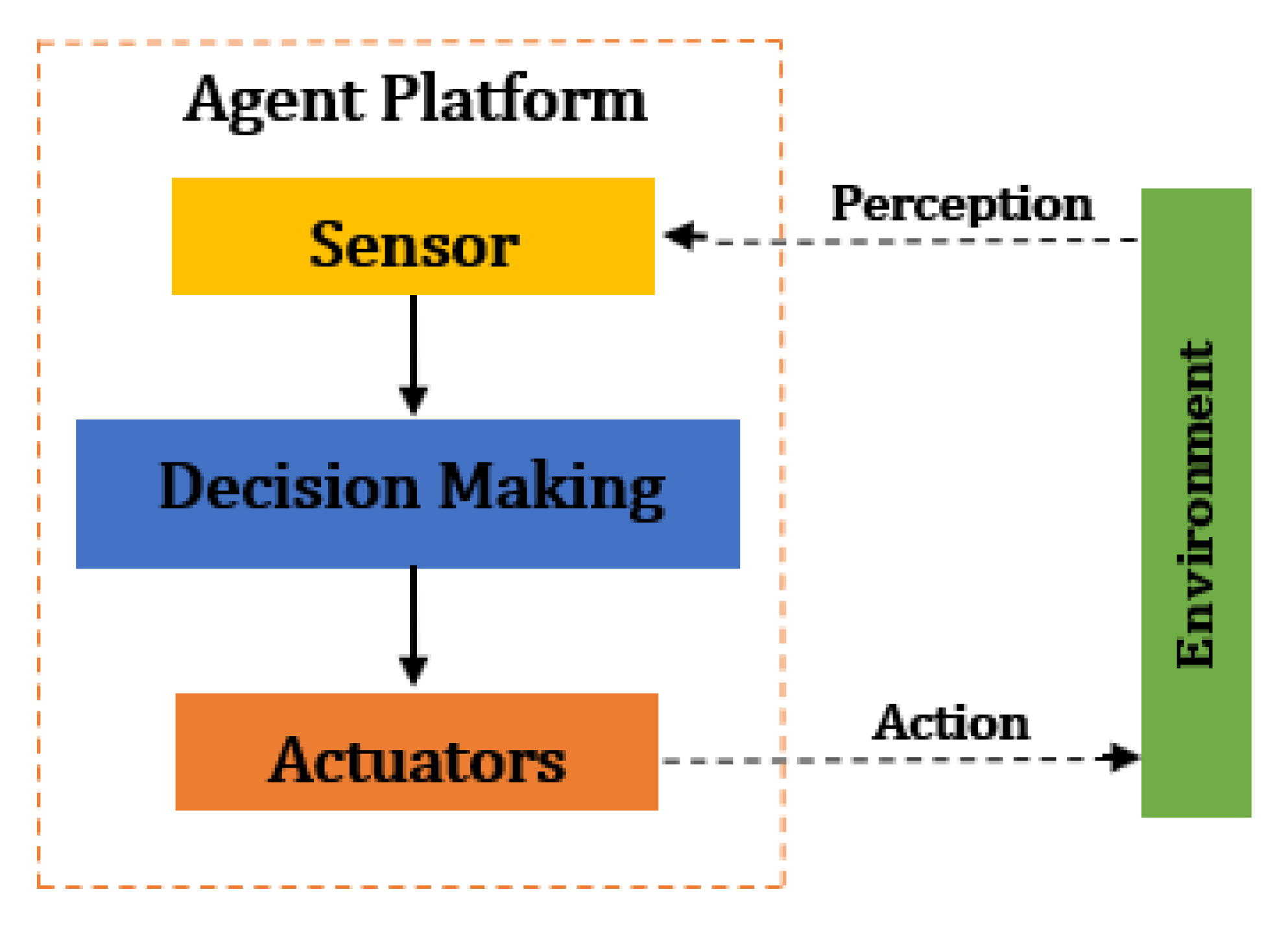
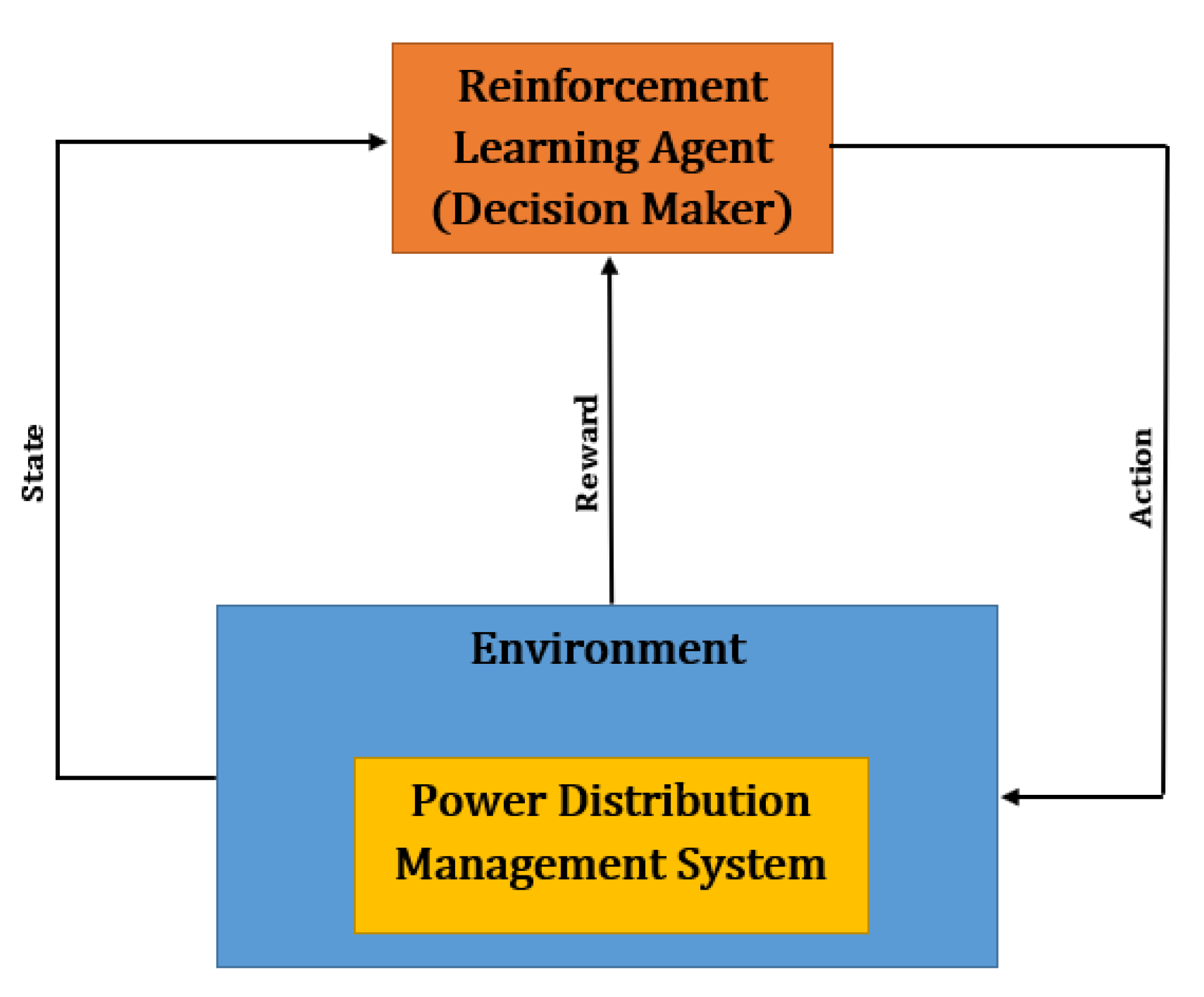
5. Intelligent Control-Based Reinforcement Learning
5.1. Balance of Exploration and Exploitation
E-Greedy Policy
5.2. Q-Learning
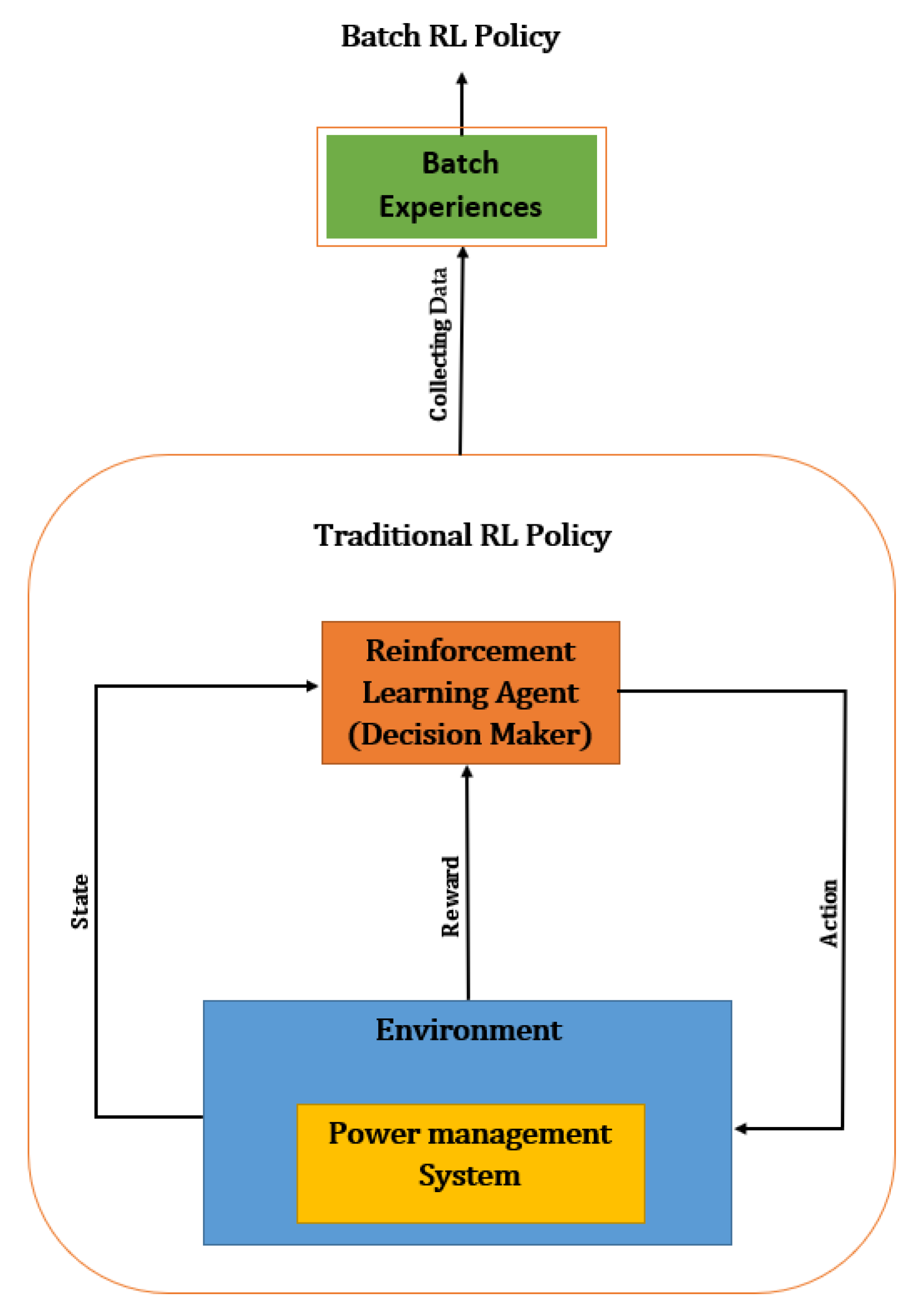
5.3. Batch Reinforcement Learning
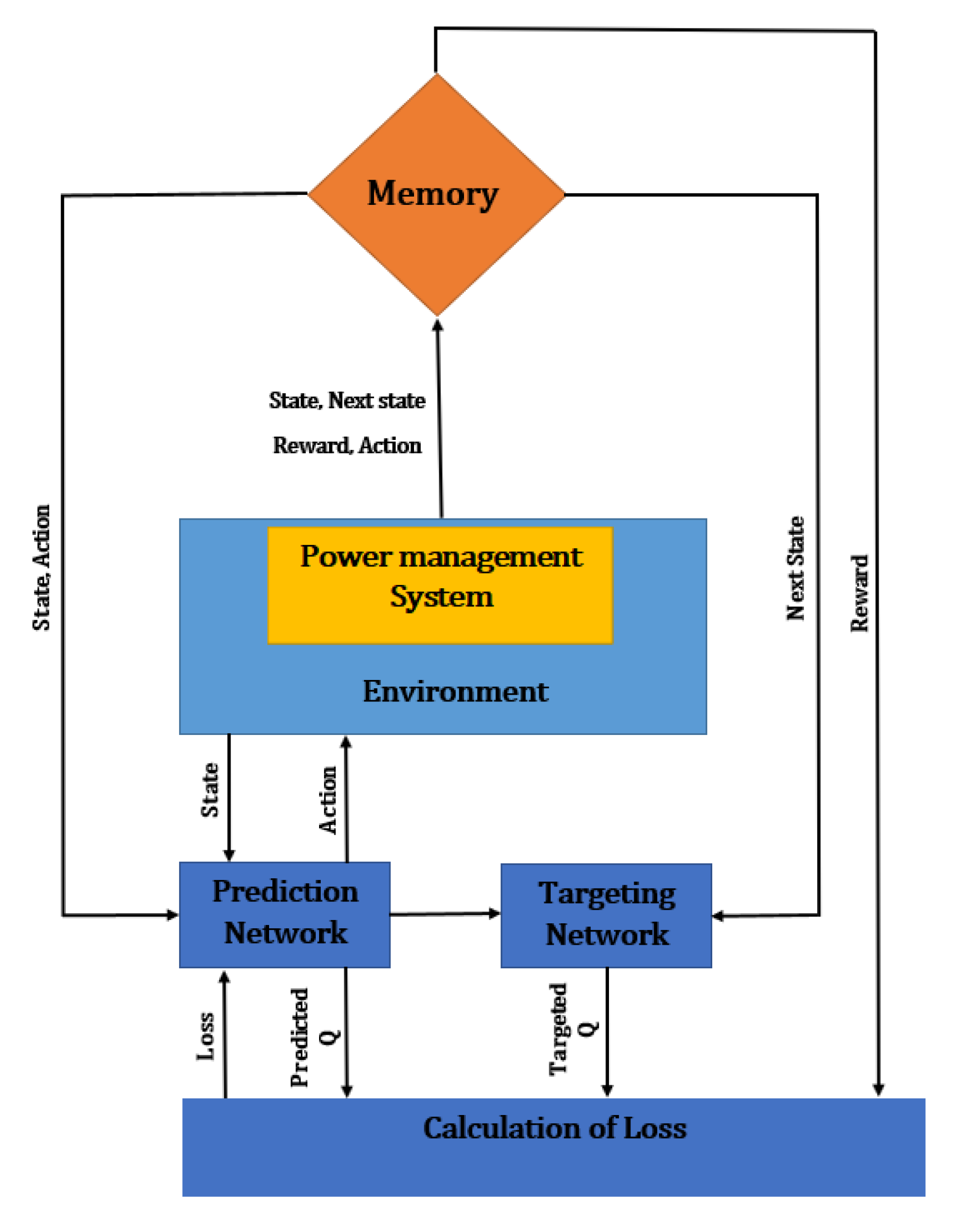
5.4. Deep Q-Learning
5.5. Actor-Critic Algorithms
6. Emerging Reinforcement Learning Techniques of Power Management in Micro and Smart Grids
7. Conclusions and Recommendations
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| SOC | State of charge |
| ESS/ESSs | Energy storage system, systems |
| FIS | Fuzzy inference system. |
| MPC | Module predictive control |
| EMS | Energy system management |
| DG | Distributed Generation |
| BESS/BESSs | Battery energy storage system, systems |
| OPF | Optimum power flow |
| DOPF | Dynamic optimal power flow |
| RL | Reinforcement learning |
| EV/EVs | Electric vehicle, vehicles |
| SEMS | Superconducting magnetic energy storage |
| HPFD | High pass filter-based droop |
| VCD | Virtual capacitance droop |
| SC | Super capacitor |
| PCC | Point of common coupling |
| THD | Total harmonic distortion |
| SLB | Sensitive load bus |
| MSOGI-FLL | Multiple-second order generalized integers and frequency locked loop |
| RBC | Rule-based control |
| EMPC | Economic module predictive control |
| EMS | Energy management system |
| EMU | Energy management unit |
| GCC | Global central controller |
| UC | Unity commitment |
| ED | Economic dispatch |
| MINLP | Mixed integer nonlinear formulation problem |
| MILP | Mixer integer linear programming |
| SUC | Stochastic unit commitment |
| SHOPF | Shrinking horizon optimal power flow |
| HESS | Hybrid energy storage system |
| PV | Photovoltaic |
| MGCC | Microgrid global central controller |
| SMG | Smart Microgrid |
| PLA | Power Link |
| DDS | Data distribution service |
| RTPS | Real time publish subscribe. |
| TPM | Transition probability matrix |
| MACA | Mobility-aware control algorithm |
| V2G | Vehicle to grid |
| OEM | Optimal energy management |
| DDPG | Deep deterministic policy gradient |
| A3C | Asynchronous advantage actor-critic |
| A2C | Synchronous actor-critic version |
| MARLA | Multiagent reinforcement learning |
| DP | Dynamic programming |
| TRPO | Trust-Region Policy Optimization |
| PWM | Pulse width modulation |
| PEM | Polymer Electrolyte membrane |
| NDO | Nonlinear disturbance observer |
| FC | Fuel cell |
| Tariff | How energy provider charges consumers for using energy |
| UCE | Unit control error |
| MMC | Modular multi-level converter |
| MMC-ESS | Modular multi-level converter energy storage system |
| X/R | Reactance to resistance ratio |
| AI | Artificial Intelligence |
| Active power droop coefficient | |
| Reactive power coefficient | |
| First and second inverter virtual impedances | |
| First and second line impedances | |
| Discharge/Charge droop coefficients | |
| Exponential of the computed SOC | |
| Discharge/Charge Droop control action | |
| Fuzzy logic droop control virtual resistance | |
| Fuzzy droop control correction | |
| , | Battery and SMES droop coefficients |
| Critical-up frequency | |
| Critical-low frequency | |
| Deviation resistance | |
| Voltage in dq frame | |
| Total harmonic compensation signal | |
| Modified total harmonic compensation signal | |
| Battery rated capacity | |
| Charge/Discharge efficiency | |
| Power flow of the distributed ESS at time K | |
| Charge, discharge power at time K | |
| Microgrid reference voltage | |
| Voltage control action | |
| Energy control action | |
| SOC at of agent i at time t | |
| Average neighbors’ agents SOC of agent i | |
| Participation current of agent i per unit energy storage | |
| Maximum current of agent i per unit energy storage | |
| Communication weight from node j to node i. | |
| Power supplied by the main grid at time K | |
| Power injected to the main grid at time K | |
| Rule or policy | |
| Value of state | |
| The immediate reward | |
| Value function (degree of goodness of taking an action a) | |
| Action | |
| Constant power loads |
References
- Butt, O.M.; Zulqarnain, M.; Butt, T.M. Recent advancement in smart grid technology: Future prospects in the electrical power network. Ain Shams Eng. J. 2021, 12, 687–695. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Hussain, A.; Mansor, M.B.; Blaabjerg, F. Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Ceglia, F.; Marrasso, E.; Roselli, C.; Sasso, M. Small renewable energy community: The role of energy and environmental indicators for power grid. Sustainability 2021, 13, 2137. [Google Scholar] [CrossRef]
- Fichera, A.; Marrasso, E.; Sasso, M.; Volpe, R. Energy, environmental and economic performance of an urban community hybrid distributed energy system. Energies 2020, 13, 2545. [Google Scholar] [CrossRef]
- Huang, P.; Sun, Y.; Lovati, M.; Zhang, X. Solar-photovoltaic-power-sharing-based design optimization of distributed energy storage systems for performance improvements. Energy 2021, 222, 119931. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.; Wong, M.D. Dynamic power allocation of battery-supercapacitor hybrid energy storage for standalone PV microgrid applications. Sustain. Energy Technol. Assess. 2017, 22, 55–64. [Google Scholar] [CrossRef]
- Wu, F.; Maier, J.; Yu, Y. Guidelines and trends for next-generation rechargeable lithium and lithium-ion batteries. Chem. Soc. Rev. 2020, 49, 1569–1614. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Diaz, D.F.R.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells–a review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, C. Cost-effective iron-based aqueous redox flow batteries for large-scale energy storage application: A review. J. Power Sour. 2021, 493, 229445. [Google Scholar] [CrossRef]
- Alirahmi, S.M.; Mousavi, S.B.; Razmi, A.R.; Ahmadi, P. A comprehensive techno-economic analysis and multi-criteria optimization of a compressed air energy storage (CAES) hybridized with solar and desalination units. Energy Convers. Manag. 2021, 236, 114053. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Xue, H. A novel capacity configuration method of flywheel energy storage system in electric vehicles fast charging station. Electr. Power Syst. Res. 2021, 195, 107185. [Google Scholar] [CrossRef]
- Miao, Z.; Xu, L.; Disfani, V.R.; Fan, L. An SOC-based battery management system for microgrids. IEEE Trans. Smart Grid 2013, 5, 966–973. [Google Scholar] [CrossRef]
- Toledo, O.M.; Oliveira Filho, D.; Diniz, A.S.A.C. Distributed photovoltaic generation and energy storage systems: A review. Renew. Sustain. Energy Rev. 2010, 14, 506–511. [Google Scholar] [CrossRef]
- Xu, Q.; Hu, X.; Wang, P.; Xiao, J.; Tu, P.; Wen, C.; Lee, M.Y. A decentralized dynamic power sharing strategy for hybrid energy storage system in autonomous DC microgrid. IEEE Trans. Ind. Electron. 2016, 64, 5930–5941. [Google Scholar] [CrossRef]
- Rehmani, M.H.; Reisslein, M.; Rachedi, A.; Erol-Kantarci, M.; Radenkovic, M. Integrating renewable energy resources into the smart grid: Recent developments in information and communication technologies. IEEE Trans. Ind. Inform. 2018, 14, 2814–2825. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. Decentralized control for residential energy management of a smart users’ microgrid with renewable energy exchange. IEEE/CAA J. Autom. Sin. 2019, 6, 641–656. [Google Scholar] [CrossRef]
- Olsen, D.J.; Kirschen, D.S. Profitable emissions-reducing energy storage. IEEE Trans. Power Syst. 2019, 35, 1509–1519. [Google Scholar] [CrossRef] [Green Version]
- Dinh, H.T.; Yun, J.; Kim, D.M.; Lee, K.-H.; Kim, D. A home energy management system with renewable energy and energy storage utilizing main grid and electricity selling. IEEE Access 2020, 8, 49436–49450. [Google Scholar] [CrossRef]
- Muhtadi, A.; Pandit, D.; Nguyen, N.; Mitra, J. Distributed energy resources based microgrid: Review of architecture, control, and reliability. IEEE Trans. Ind. Appl. 2021, 57, 2223–2235. [Google Scholar] [CrossRef]
- Legry, M.; Dieulot, J.-Y.; Colas, F.; Saudemont, C.; Ducarme, O. Non-linear primary control mapping for droop-like behavior of microgrid systems. IEEE Trans. Smart Grid 2020, 11, 4604–4613. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.-L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2012, 60, 1254–1262. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, J.; Song, H.; Nawaz, A.; Qu, Y. Nonlinear secondary voltage control of islanded microgrid via distributed consistency. IEEE Trans. Energy Convers. 2020, 35, 1964–1972. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Zhang, R.; Savkin, A.V.; Hredzak, B. Centralized nonlinear switching control strategy for distributed energy storage systems communicating via a network with large time delays. J. Energy Storage 2021, 41, 102834. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N. Control techniques in AC, DC, and hybrid AC–DC microgrid: A review. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 738–759. [Google Scholar] [CrossRef]
- Mohammed, A.; Refaat, S.S.; Bayhan, S.; Abu-Rub, H. Ac microgrid control and management strategies: Evaluation and review. IEEE Power Electron. Mag. 2019, 6, 18–31. [Google Scholar] [CrossRef]
- Khan, K.A.; Khalid, M. Improving the transient response of hybrid energy storage system for voltage stability in DC microgrids using an autonomous control strategy. IEEE Access 2021, 9, 10460–10472. [Google Scholar] [CrossRef]
- Mohd, A.; Ortjohann, E.; Schmelter, A.; Hamsic, N.; Morton, D. Challenges in Integrating distributed energy storage systems into future smart grid. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 1627–1632. [Google Scholar]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Control strategies for microgrids with distributed energy storage systems: An overview. IEEE Trans. Smart Grid 2016, 9, 3652–3666. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2019, 7, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Moslemi, R.; Mohammadpour, J. Accurate reactive power control of autonomous microgrids using an adaptive virtual inductance loop. Electr. Power Syst. Res. 2015, 129, 142–149. [Google Scholar] [CrossRef]
- Tayab, U.B.; Roslan, M.A.B.; Hwai, L.J.; Kashif, M. A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 2017, 76, 717–727. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L. State-of-charge balance using adaptive droop control for distributed energy storage systems in DC microgrid applications. IEEE Trans. Ind. Electron. 2013, 61, 2804–2815. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.; Kumar, K.; Dutta, V. Droop based control strategy for balancing the level of hydrogen storage in direct current microgrid application. J. Energy Storage 2021, 33, 102106. [Google Scholar] [CrossRef]
- Bi, K.; Yang, W.; Xu, D.; Yan, W. Dynamic SOC balance strategy for modular energy storage system based on adaptive droop control. IEEE Access 2020, 8, 41418–41431. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, M.; Jiang, H.; Chen, Z.; Wang, Q. Improved droop control based on State-of-Charge in DC microgrid. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1509–1513. [Google Scholar]
- Gavriluta, C.; Candela, J.I.; Citro, C.; Rocabert, J.; Luna, A.; Rodríguez, P. Decentralized primary control of MTDC networks with energy storage and distributed generation. IEEE Trans. Ind. Appl. 2014, 50, 4122–4131. [Google Scholar] [CrossRef]
- Wang, J. SoC-based dynamic droop control for battery energy storage systems in DC microgrids feeding CPLs. J. Phys. Conf. Ser. 2021, 1754, 012060. [Google Scholar] [CrossRef]
- Diaz, N.L.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. In Fuzzy-logic-based gain-scheduling control for state-of-charge balance of distributed energy storage systems for DC microgrids. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 2171–2176. [Google Scholar]
- Diaz, N.L.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Intelligent distributed generation and storage units for DC microgrids—A new concept on cooperative control without communications beyond droop control. IEEE Trans. Smart Grid 2014, 5, 2476–2485. [Google Scholar] [CrossRef] [Green Version]
- Díaz, N.L.; Wu, D.; Dragičević, T.; Vásquez, J.C.; Guerrero, J.M. In Fuzzy droop control loops adjustment for stored energy balance in distributed energy storage system. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 728–735. [Google Scholar]
- Li, J.; Xiong, R.; Yang, Q.; Liang, F.; Zhang, M.; Yuan, W. Design/test of a hybrid energy storage system for primary frequency control using a dynamic droop method in an isolated microgrid power system. Appl. Energy 2017, 201, 257–269. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Gomis-Bellmunt, O. Participation of wind power plants in system frequency control: Review of grid code requirements and control methods. Renew. Sustain. Energy Rev. 2014, 34, 551–564. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, J.; Hu, X.; Wang, P.; Lee, M.Y. A decentralized power management strategy for hybrid energy storage system with autonomous bus voltage restoration and state-of-charge recovery. IEEE Trans. Ind. Electron. 2017, 64, 7098–7108. [Google Scholar] [CrossRef]
- Bharathi, G.; Kantharao, P.; Srinivasarao, R. Fuzzy logic control (FLC)-based coordination control of DC microgrid with energy storage system and hybrid distributed generation. Int. J. Ambient Energy 2021, 1–17. [Google Scholar] [CrossRef]
- Liu, J.; Dong, D.; Zhang, D. A hybrid modular multilevel converter family with higher power density and efficiency. IEEE Trans. Power Electron. 2021, 36, 9001–9014. [Google Scholar] [CrossRef]
- Zhang, D.; Jiang, J.; Zhang, L.; Zhou, Z. Grid-connected control strategy of modular multilevel converter–battery energy storage system based on VSG. J. Eng. 2019, 2019, 1502–1505. [Google Scholar] [CrossRef]
- Yuan, Q.; Yang, F.; Li, A.; Ma, T. A novel hybrid control strategy for the energy storage modular multilevel converters. IEEE Access 2021, 9, 59466–59474. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, L.; Zhou, Q.; Chen, M.; Xu, T.; Hu, S. State-of-charge balancing control strategy of battery energy storage system based on modular multilevel converter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 15–18 September 2014; pp. 2567–2574. [Google Scholar]
- Liang, H.; Guo, L.; Song, J.; Yang, Y.; Zhang, W.; Qi, H. State-of-charge balancing control of a modular multilevel converter with an integrated battery energy storage. Energies 2018, 11, 873. [Google Scholar] [CrossRef] [Green Version]
- Golsorkhi, M.S.; Hill, D.J.; Baharizadeh, M. A secondary control method for voltage unbalance compensation and accurate Load sharing in networked microgrids. IEEE Trans. Smart Grid 2021, 4, 2822–2833. [Google Scholar] [CrossRef]
- Andishgar, M.H.; Gholipour, E.; Hooshmand, R.-A. Improved secondary control for optimal total harmonic distortion compensation of parallel connected DGs in islanded microgrids. IET Smart Grid 2019, 2, 115–122. [Google Scholar] [CrossRef]
- Guan, Y.; Vasquez, J.C.; Guerrero, J.M. Coordinated secondary control for balanced discharge rate of energy storage system in islanded AC microgrids. IEEE Trans. Ind. Appl. 2016, 52, 5019–5028. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-S.; Hwang, C.-S.; Kim, E.-S.; Cho, C. State of charge-based active power sharing method in a standalone microgrid with high penetration level of renewable energy sources. Energies 2016, 9, 480. [Google Scholar] [CrossRef]
- Dragičević, T.; Guerrero, J.M.; Vasquez, J.C.; Škrlec, D. Supervisory control of an adaptive droop regulated DC microgrid with battery management capability. IEEE Trans. Power Electron. 2013, 29, 695–706. [Google Scholar] [CrossRef] [Green Version]
- Meng, T.; Lin, Z.; Shamash, Y.A. Distributed cooperative control of battery energy Storage systems in DC microgrids. IEEE/CAA J. Autom. Sin. 2021, 8, 606–616. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K. Distributed cooperative control of battery energy storage system in AC microgrid applications. J. Energy Storage 2015, 3, 43–51. [Google Scholar] [CrossRef]
- Jin, Z.; Meng, L.; Guerrero, J.M.; Han, R. Hierarchical control design for a shipboard power system with DC distribution and energy storage aboard future more-electric ships. IEEE Trans. Ind. Inform. 2017, 14, 703–714. [Google Scholar] [CrossRef] [Green Version]
- Teleke, S.; Baran, M.E.; Bhattacharya, S.; Huang, A.Q. Rule-based control of battery energy storage for dispatching intermittent renewable sources. IEEE Trans. Sustain. Energy 2010, 1, 117–124. [Google Scholar] [CrossRef]
- Wang, G.; Ciobotaru, M.; Agelidis, V.G. Power management for improved dispatch of utility-scale PV plants. IEEE Trans. Power Syst. 2015, 31, 2297–2306. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Bang, Y.H.; Di Noto, V. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Etxeberria, A.; Vechiu, I.; Baudoin, S.; Camblong, H.; Kreckelbergh, S. Control of a vanadium redox battery and supercapacitor using a three-level neutral point clamped converter. J. Power Sour. 2014, 248, 1170–1176. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, T.; Ma, F. A multi-agent based hierarchical control system for DERs management in islanded micro-grid. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1371–1376. [Google Scholar]
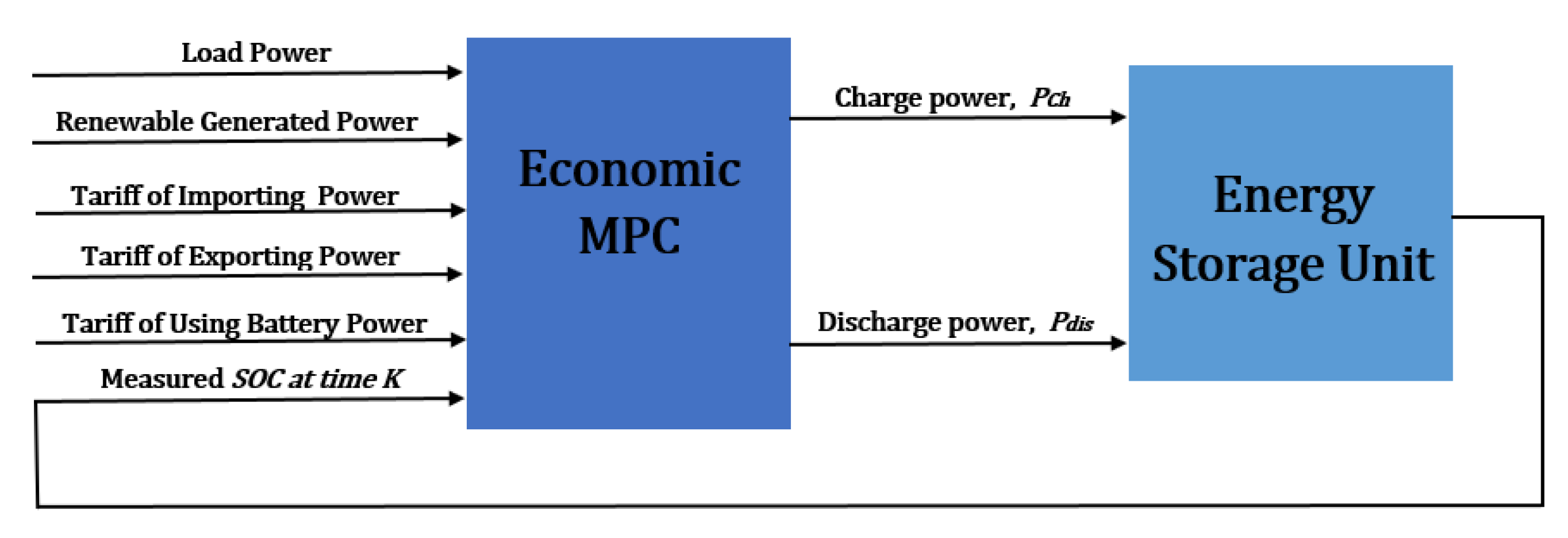
- Banfield, B.; Robinson, D.A.; Agalgaonkar, A.P. Comparison of economic model predictive control and rule-based control for residential energy storage systems. IET Smart Grid 2020, 3, 722–729. [Google Scholar] [CrossRef]
- Halilbašić, L.; Pinson, P.; Chatzivasileiadis, S. Convex relaxations and approximations of chance-constrained AC-OPF problems. IEEE Trans. Power Syst. 2018, 34, 1459–1470. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Xu, Y.; Cheng, K.W.; Guerrero, J.M. A model predictive control strategy of PV-Battery microgrid under variable power generations and load conditions. Appl. Energy 2018, 221, 195–203. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A model predictive control approach to microgrid operation optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Dessaint, L.; Sacile, R. Coordinated model predictive-based power flows control in a cooperative network of smart microgrids. IEEE Trans. Smart Grid 2015, 6, 2233–2244. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Bordons, C. Optimal economical schedule of hydrogen-based microgrids with hybrid storage using model predictive control. IEEE Trans. Ind. Electron. 2015, 62, 5195–5207. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M. Stochastic optimization of renewable-based microgrid operation incorporating battery operating cost. IEEE Trans. Power Syst. 2015, 31, 2289–2296. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Optimal power flow on DC microgrids: A quadratic convex approximation. IEEE Trans. Circuits Syst. II Express Br. 2018, 66, 1018–1022. [Google Scholar] [CrossRef]
- Giraldo, J.S.; Castrillon, J.A.; López, J.C.; Rider, M.J.; Castro, C.A. Microgrids energy management using robust convex programming. IEEE Trans. Smart Grid 2018, 10, 4520–4530. [Google Scholar] [CrossRef]
- Garifi, K.; Baker, K.; Christensen, D.; Touri, B. Convex relaxation of grid-connected energy storage system models with complementarity constraints in DC OPF. IEEE Trans. Smart Grid 2020, 11, 4070–4079. [Google Scholar] [CrossRef]
- Bai, W.; Zhu, X.; Lee, K.Y. Dynamic optimal power flow based on a spatio-temporal wind speed forecast model. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 136–143. [Google Scholar]
- Shuai, H.; Fang, J.; Ai, X.; Yao, W.; Wen, J.; He, H. On-line energy management of microgrid via parametric cost function approximation. IEEE Trans. Power Syst. 2019, 34, 3300–3302. [Google Scholar] [CrossRef]
- Olivares, D.E.; Cañizares, C.A.; Kazerani, M. A centralized energy management system for isolated microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Olivares, D.E.; Lara, J.D.; Cañizares, C.A.; Kazerani, M. Stochastic-predictive energy management system for isolated microgrids. IEEE Trans. Smart Grid 2015, 6, 2681–2693. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Dynamic optimal power flow for DC microgrids with distributed battery energy storage systems. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Gulin, M.; Matuško, J.; Vašak, M. Stochastic model predictive control for optimal economic operation of a residential DC microgrid. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 505–510. [Google Scholar]
- Zhang, J.; Csank, J.T.; Soeder, J.F. Hierarchical control of distributed battery energy storage system in a DC microgrid. In Proceedings of the 2021 IEEE Fourth International Conference on DC Microgrids (ICDCM), Virtual Conference, Arlington, VA, USA, 18–21 July 2021; pp. 1–8. [Google Scholar]
- Fax, J.A.; Murray, R.M. Information flow and cooperative control of vehicle formations. IEEE Trans. Autom. Control 2004, 49, 1465–1476. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Lewis, F.L.; Das, A. Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback. IEEE Trans. Autom. Control 2011, 56, 1948–1952. [Google Scholar] [CrossRef]
- Mondal, S.; Srivastava, A.; Maji, A.; Chakraborty, R.; Roy, D.S.; Mukherjee, S. A distributed fixed-time consensus for battery storage systems. In Proceedings of the 2021 Innovations in Energy Management and Renewable Resources (52042), Kolkata, India, 5–7 February 2021; pp. 1–5. [Google Scholar]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Communication delay robustness for multi-agent state of charge balancing between distributed AC microgrid storage systems. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, NSW, Australia, 21–23 September 2015; pp. 181–186. [Google Scholar]
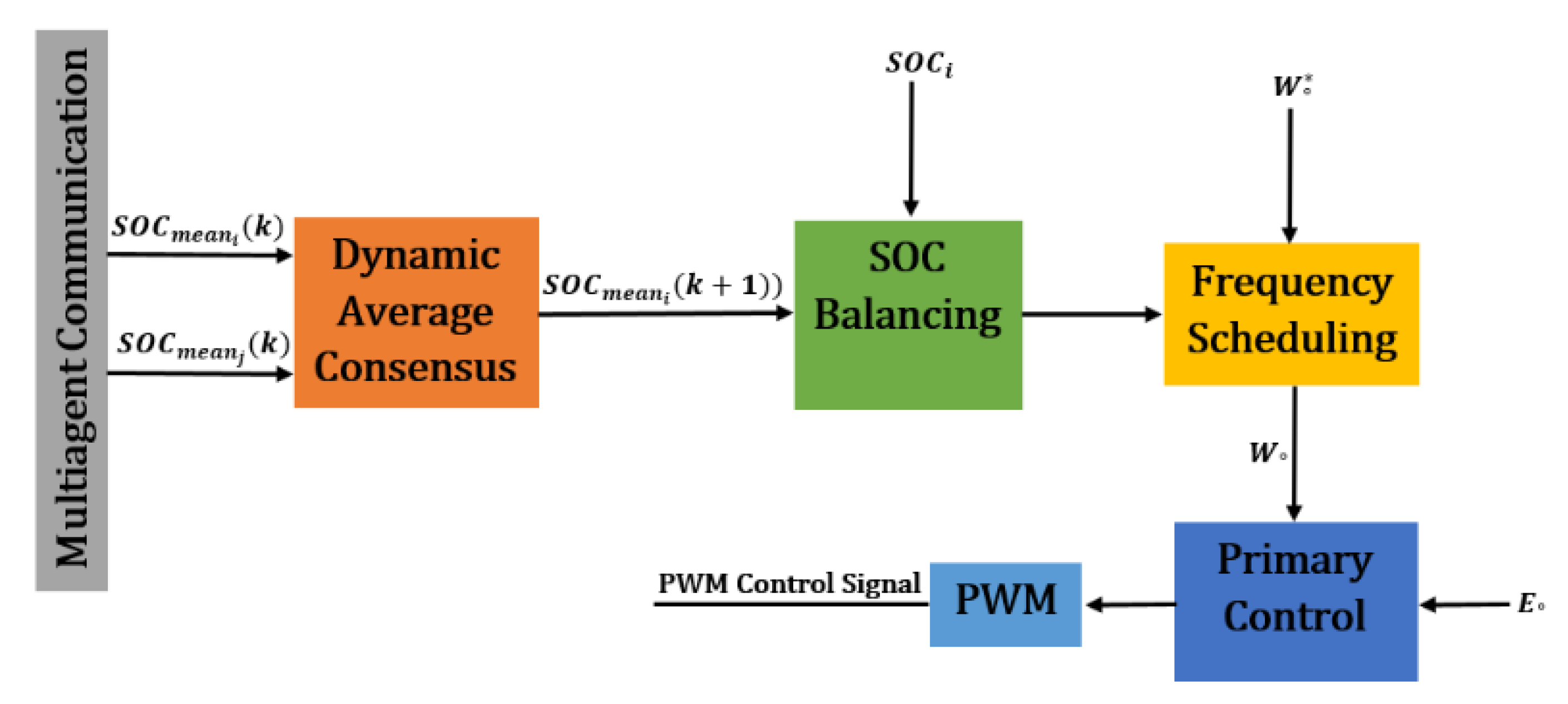
- Li, C.; Coelho, E.A.A.; Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C. Multiagent-based distributed state of charge balancing control for distributed energy storage units in AC microgrids. IEEE Trans. Ind. Appl. 2016, 53, 2369–2381. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Zhou, H.; Yao, R.; Chen, S. Frequency synchronization and soc balancing control in AC microgrids. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3365–3370. [Google Scholar]
- Morstyn, T.; Hredzak, B.; Demetriades, G.D.; Agelidis, V.G. Unified distributed control for DC microgrid operating modes. IEEE Trans. Power Syst. 2015, 31, 802–812. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Cooperative multi-agent control of heterogeneous storage devices distributed in a DC microgrid. IEEE Trans. Power Syst. 2015, 31, 2974–2986. [Google Scholar] [CrossRef]
- Li, C.; Dragicevic, T.; Plaza, M.G.; Andrade, F.; Vasquez, J.C.; Guerrero, J.M. Multiagent based distributed control for state-of-charge balance of distributed energy storage in DC microgrids. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2180–2184. [Google Scholar]
- Morstyn, T.; Savkin, A.V.; Hredzak, B.; Agelidis, V.G. Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC microgrid. IEEE Trans. Smart Grid 2017, 9, 4735–4743. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Xia, Y.; Wang, L.; Wei, W. Multiagent based distributed control with time-oriented SoC balancing method for DC microgrid. Energies 2020, 13, 2793. [Google Scholar] [CrossRef]
- Almada, J.B.; Leão, R.P.; Almeida, R.G.; Sampaio, R.F. Microgrid distributed secondary control and energy management using multi-agent system. Int. Trans. Electr. Energy Syst. 2021, 31, e12886. [Google Scholar] [CrossRef]
- Worthmann, K.; Kellett, C.M.; Braun, P.; Grüne, L.; Weller, S.R. Distributed and decentralized control of residential energy systems incorporating battery storage. IEEE Trans. Smart Grid 2015, 6, 1914–1923. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Cheng, Z.; Zhang, Z.; Sun, M.; Deng, R.; Cheng, P.; Chow, M.-Y. A multi-agent system based hierarchical control framework for microgrids. In Proceedings of the 2021 IEEE PES General Meeting, Washington, DC, USA, 16 February 2021. [Google Scholar]
- He, Y.; Wang, W.; Wu, X. Multi-agent based fully distributed economic dispatch in microgrid using exact diffusion strategy. IEEE Access 2019, 8, 7020–7031. [Google Scholar] [CrossRef]
- Dagdougui, H.; Sacile, R. Decentralized control of the power flows in a network of smart microgrids modeled as a team of cooperative agents. IEEE Trans. Control Syst. Technol. 2013, 22, 510–519. [Google Scholar] [CrossRef]
- Kang, W.; Chen, M.; Li, B.; Chen, F.; Lai, W.; Lin, H.; Zhao, B. Distributed reactive power control and SOC sharing method for battery energy storage system in microgrids. IEEE Access 2019, 7, 60707–60720. [Google Scholar] [CrossRef]
- Hug, G.; Kar, S.; Wu, C. Consensus+ innovations approach for distributed multiagent coordination in a microgrid. IEEE Trans. Smart Grid 2015, 6, 1893–1903. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Network topology independent multi-agent dynamic optimal power flow for microgrids with distributed energy storage systems. IEEE Trans. Smart Grid 2016, 9, 3419–3429. [Google Scholar] [CrossRef] [Green Version]
- Cintuglu, M.H.; Martin, H.; Mohammed, O.A. Real-time implementation of multiagent-based game theory reverse auction model for microgrid market operation. IEEE Trans. Smart Grid 2015, 6, 1064–1072. [Google Scholar] [CrossRef]
- Russel, S.; Norvig, P. Artificial Intelligence—A Modern Approach, 2nd ed.; Pearson Education: Bergen, NJ, USA, 2003. [Google Scholar]
- Mondal, A.; Misra, S.; Obaidat, M.S. Distributed home energy management system with storage in smart grid using game theory. IEEE Syst. J. 2015, 11, 1857–1866. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, H. Real-time multiobjective microgrid power management using distributed optimization in an agent-based bargaining framework. IEEE Trans. Smart Grid 2017, 9, 6318–6327. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, H. An agent-based hierarchical bargaining framework for power management of multiple cooperative microgrids. IEEE Trans. Smart Grid 2017, 10, 514–522. [Google Scholar] [CrossRef] [Green Version]
- Esfahani, M.M.; Hariri, A.; Mohammed, O.A. A multiagent-based game-theoretic and optimization approach for market operation of multimicrogrid systems. IEEE Trans. Ind. Inform. 2018, 15, 280–292. [Google Scholar] [CrossRef]
- Arwa, E.O.; Folly, K.A. Reinforcement learning techniques for optimal power control in grid-connected microgrids: A comprehensive review. IEEE Access 2020, 8, 208992–209007. [Google Scholar] [CrossRef]
- Erick, A.O.; Folly, K.A. Energy trading in grid-connected PV-battery electric vehicle charging station. In Proceedings of the 2020 International SAUPEC/RobMech/PRASA Conference, Cape Town, South Africa, 29–31 January 2020; pp. 1–6. [Google Scholar]
- Liu, T.; Hu, X. A bi-level control for energy efficiency improvement of a hybrid tracked vehicle. IEEE Trans. Ind. Inform. 2018, 14, 1616–1625. [Google Scholar] [CrossRef] [Green Version]
- Ko, H.; Pack, S.; Leung, V.C. Mobility-aware vehicle-to-grid control algorithm in microgrids. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2165–2174. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, X.; Xie, B.; Wang, D.; Liu, B.; Yu, T. Fast learning optimiser for real-time optimal energy management of a grid-connected microgrid. IET Gener. Transm. Distrib. 2018, 12, 2977–2987. [Google Scholar] [CrossRef]
- Erick, A.O.; Folly, K.A. Power flow management in electric vehicles charging station using reinforcement learning. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Lange, S.; Gabel, T.; Riedmiller, M. Batch reinforcement learning. In Reinforcement Learning; Springer: Berlin, Germany, 2012; pp. 45–73. [Google Scholar]
- Mbuwir, B.V.; Ruelens, F.; Spiessens, F.; Deconinck, G. Battery energy management in a microgrid using batch reinforcement learning. Energies 2017, 10, 1846. [Google Scholar] [CrossRef] [Green Version]
- Shi, G.; Liu, D.; Wei, Q. Echo state network-based Q-learning method for optimal battery control of offices combined with renewable energy. IET Control Theory Appl. 2017, 11, 915–922. [Google Scholar] [CrossRef] [Green Version]
- Vrancois, V. Contributions to Deep Reinforcement Learning and Its Applications in Smart Grids. Ph.D. Thesis, University of Liège, Liège, Belgium, 2017. [Google Scholar]
- Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-time energy management of a microgrid using deep reinforcement learning. Energies 2019, 12, 2291. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Xiao, X.; Xiao, L.; Dai, C.; Peng, M.; Poor, H.V. Reinforcement learning-based microgrid energy trading with a reduced power plant schedule. IEEE Internet Things J. 2019, 6, 10728–10737. [Google Scholar] [CrossRef]
- Desportes, L.; Fijalkow, I.; Andry, P. Deep reinforcement learning for hybrid energy storage systems: Balancing lead and hydrogen storage. Energies 2021, 14, 4706. [Google Scholar] [CrossRef]
- Zsembinszki, G.; Fernández, C.; Vérez, D.; Cabeza, L.F. Deep learning optimal control for a complex hybrid energy storage system. Buildings 2021, 11, 194. [Google Scholar] [CrossRef]
- Awate, Y.P. Policy-gradient based actor-critic algorithms. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, Washington, DCM, USA, 19–21 May 2009; pp. 505–509. [Google Scholar]
- Chen, P.; Liu, M.; Chen, C.; Shang, X. A battery management strategy in microgrid for personalized customer requirements. Energy 2019, 189, 116245. [Google Scholar] [CrossRef]
- Yu, L.; Xie, W.; Xie, D.; Zou, Y.; Zhang, D.; Sun, Z.; Zhang, L.; Zhang, Y.; Jiang, T. Deep reinforcement learning for smart home energy management. IEEE Internet Things J. 2019, 7, 2751–2762. [Google Scholar] [CrossRef] [Green Version]
- Joshi, A.; Tipaldi, M.; Glielmo, L. An actor-critic approach for control of residential photovoltaic-battery systems. IFAC-PapersOnLine 2021, 54, 222–227. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Kyriakides, G.; Margaritis, K.G. Neural architecture search with synchronous advantage actor-critic methods and partial training. In Proceedings of the 10th Hellenic Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2018; pp. 1–7. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Berlin, Germany, 2021; pp. 321–384. [Google Scholar]
- Zhou, S.; Zhou, L.; Mao, M.; Xi, X. Transfer learning for photovoltaic power forecasting with long short-term memory neural network. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Korea, 19–22 February 2020; pp. 125–132. [Google Scholar]
- Cao, X.; Wan, H.; Lin, Y.; Han, S. High-value prioritized experience replay for off-policy reinforcement learning. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1510–1514. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. A brief survey of deep reinforcement learning. arXiv 2017, arXiv:1708.05866 2017. [Google Scholar] [CrossRef] [Green Version]
- De Abril, I.M.; Kanai, R. Curiosity-driven reinforcement learning with homeostatic regulation. In Proceedings of the 2018 International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]

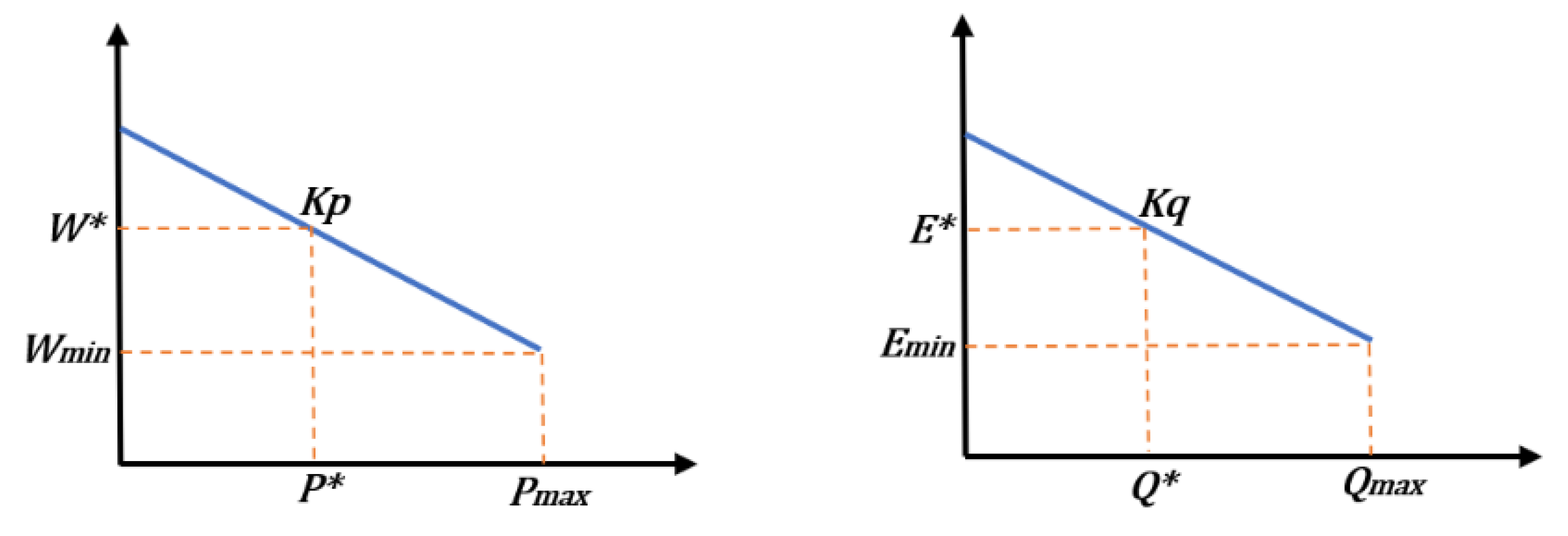



| Scheme | Strengths | Weaknesses |
|---|---|---|
| [30] DC | Decentralization. A maintained mismatch of lines impedances. | No consideration to SOC balance. A fast operation cannot be achieved, due to unavoidable initial current peaks. |
| [32] AC | Improved transient response. Effective of sharing a non-linear load. Optimized active/reactive power-sharing without deviation of frequency and voltage amplitude. | A fast operation cannot be achieved, due to unavoidable initial current peaks. |
| [33] DC | Balanced SOC. Decentralization. Extendable to AC microgrid. | In the case of AC implementation, transmission lines impedance mismatch should be considered. The dependency of SOC exponent on many parameters, (power rating, maximum DC voltage deviation, accuracy of power-sharing). |
| [35] AC | The accomplishment of SOC balance. Decrease in cost for control and communication infrastructure. Fault-tolerant control capability. Reduced data for communication and control. | No improvement over other strategies, in terms of energy loss reduction. |
| [36] DC | Enhanced current sharing in the case of load fluctuations. Compensated DC voltage deviation. | An existing minor current fluctuation. |
| [37] AC | Generic to different operating states. Decentralization. Balanced SOC (considered of determining droop coefficients). | An existing drop of bus voltage but within the acceptable limit. |
| [38] DC | An achieved system stability and rapidity. Balanced SOC. A disconnection of BESS with low SOC (less than 10%). | A constant power loads (CPLs) (load fluctuation has not been considered). |
| [39] DC | A developed fuzzy control strategy that can do more than one control objective. Reduced voltage deviation. The same controller can be selected for different values of Rd (virtual resistance loop). Good balance of SOC (faster than fixed virtual resistance strategy). Decentralization. | An existing minor deviation of voltage but within an acceptable limit. |
| [40] DC | Self-controlled (based on local parameters) with good SOC balance. Modular and expandable. Decentralization. Multi-objective control. Faster charge. | A prioritization of SOC balancing over the regulation of voltage deviation. An existing minor voltage deviation, but within an acceptable limit. |
| [41] AC | Decentralization. Good SOC balance. No obliged modification for the introduction of a new active generator. Asymptotic approximation to SOC during storage operation. Fast charge compared with the traditional method. Furthermore, a reduced depth of discharge. FIS is applicable for DC microgrid. | An existing minor voltage deviation between batteries. Good SOC balance but to an extant (still some unbalance exists). |
| [42] AC | Good frequency balance. An improved SOC balance of battery. Longer battery life. | A minor fluctuation of battery SOC. No consideration to bus voltage. |
| [44] DC | Decentralization. Elimination of a voltage deviation. Bus voltage restoration. Supercapacitor, SOC recovery. The accomplishment of transient power-sharing with no effect of voltage and SOC. | Still, a high snap of supercapacitor current when the load fluctuates. A little instability of battery current. |
| [45] DC | Quick power balance. Maintained system performance with different dynamic situations. | No consideration to temperature effect. |
| [49] MMC-BESS | Balanced SOC. Suppression of circulating current. Suppression of grid DC current. | High total simulation time (17.5 s) due to computer limitation. |
| [50] MMC-BESS | SOC balance of all battery modules. Improvement to utilization of second-life BESS. | An existing minor deviation of SOC estimation, which is affecting the final SOC convergence. |
| Strategy Microgrid Type | Strengths | Weaknesses |
|---|---|---|
| [51] AC | Accurate sharing of an unbalanced load. Balanced output voltage. Active power flow. | An existing voltage deviation and unbalance when load fluctuates (compensate in 2 s). |
| [52] AC | Successful in compensating THD. No additional equipment has been installed. Less complexity control structure. Fast tunning. | No improvement in terms of the results than the previous strategies. Same objectives have been gained but a simpler control structure. |
| [53] AC | Control DG based on ESS capacity and SOC level (prevent overcurrent). Capable of balancing SOC. Fast transient/Good robustness. | Only applicable for AC Microgrid. There was a communication cost. |
| [54] AC | Balanced SOC and not affected by power fluctuations. Maintained frequency to a nominal value and not affected by power fluctuations. | Communication failure of BESS when changing control mode. Difficult recognizing of DG role due to the intermittent change of their output power. |
| [55] DC | The capability of coordinating a multiple charged battery. Balanced SOC of the batteries. | Despite SOC balance, there was some fluctuation and instability. |
| [56] DC | Balanced SOC of all batteries. Total batteries power of charge/discharge was adequate for the desired operation. | Unclear if circulating current was existing or not during the convergence of SOC (during discharge convergence, the response shows some batteries discharge while the other charge). |
| [57] AC | Balanced SOC. Newly developed droop control has been achieved. | Life and protection of batteries have not been mentioned. |
| [58] AC | Balanced power-sharing of different resources depending on their actual power and energy rather than the rated capacity. Efficient fuel consumption to a limited extent. Accomplished power-sharing of onboard sources independent of load conditions. | A degrade of fuel efficiency under load variations. |
| [59] DC | Balanced SOC within the mandatory levels. The battery current has been directed to the renominated limits. Great catch on for injected power to set points. Better performance than the wind case method. | Limited exploitation to batteries capacity (30–100%). |
| [60] AC | The capability of dealing with solar forecasting error up to 60% with no brake to dispatch rules. Optimized dispatch performance than basic control (delta-balance). Active, less-complex computation, and easy for practical application. Adapted to other electricity markets. | Thresholds and HESS are required to be re-evaluated. |
| [63] AC | Optimized power management-based hierarchical control. Plug and play of loads and sources. | Frequency fluctuations exist until steady at 50 Hz. Voltage fluctuations exist until steady at 311 V. |
| [64] DC | Greater reduction in the annual cost compared to standalone PV and ESS that uses rule-based controller. More battery prolonged life compared to rule-based control. The greater annual saving in all operational scenarios. Capability of flattening the aggregated feeder of 30 consumers for one day. Evening demand reduced by 20% compared to the rule-based. | Limited to one PV and one ESS. |
| [65] AC | Convergence has been assured. Effective computation compared to other strategies. Providing solutions with linear and nonlinear solvers. AC viable recovery of SOC-OPF design. | Expected convergence issues. Inaccurate approximation. |
| [66] AC/DC | Stable voltage in both islanded and grid-connected modes. The good exploitation of reactive power in supporting main grids against voltage variation. Balanced power management. Proper charge/discharge balance. | There was an overshoot of current when transfer from autonomous to the grid-connected. |
| [67] AC | Optimized economical operation compared to other existing strategies. An advantageous tradeoff between peak demands and consumers has been achieved through an acceptable restriction. | No consideration for heat recovery. No demonstration for reactive power exploitation. |
| [68] Smart | Future planning of, power exchange, and charge/discharge profile, of each ESS, among different Microgrid networks, has been predicted via an MPC-based algorithm. | Real-time communication failure with some grids of the system. |
| [69] AC | Optimized operational scheduling (because price variation with time). The effect of ESS towards a dispatchable generation. MPC has minimized the cost function. | Formulation complexity under the use of MPC. |
| [70] AC | Economic dispatch has been achieved without the introduction of a further objective function. An optimized operation with day-ahead scheduling and high probability. | Due to the limitation of batteries’ discharge depth, they barely discharge for only some hours at night. Electricity price has not been considered. |
| [72] AC | More flexible and faster than stochastic. The applicability of offline solutions, since implementation has proved that execution times are steady with expectations of mixed-integer programming. | Convenient for short-term energy management scenarios (this could be an advantage or disadvantage based on the purpose). |
| [73] DC | Satisfied ESS charge/discharge in the situation of a taken relaxation. Reduction in computation time. Negligible influence of penalty time. | Unsatisfied charging/discharging in the case of non-simultaneous ESS. No participation of load in demand response. |
| [75] AC | Improvement of performance. Uncomplicated implementation. Less computation time. Active in implementing large system solutions. Reduction of the cost compared to MPC. | Convergence was after 1000 iterations. However, stability value was 0.4 < 1, which improves the activity of large system solutions. |
| [76] AC | Reduced computation time. The decomposition of the MINLP problem has enabled the solution to be solved within the desired time. | The quality of solutions needs to be improved. Specifically, the impact of primary controllers. More robustness against uncertainties is mandatory. |
| [77] AC | Improved total operational cost. Qualified accounting of uncertainty in power predictions. Improved computation time. | Convergence failure. |
| [78] DC | An optimized operation, because of the accomplished scalable solution. Good interaction between the proposed controller and the local controllers. Lower average solution time. | Slight improvement of power consumption than non-convex QP (0.036%). |
| [79] DC | Allows more flexibility, through an advantageous tradeoff between constrains violations and the achieved revenue. Minimized microgrid operation cost. | Penalizing any constraint with higher/lower prices for importing/exporting energy will not prevent constraints violation but keep it as small as possible (violation is still existing). |
| [80] DC | Balanced SOC. Successful restoration of DC voltage. Accurate sharing of batteries current. System effectiveness has been accomplished. | Tested only for two batteries. |
| Strategy Application | Strengths | Weaknesses |
|---|---|---|
| [83] 2nd order multiagent system | Synchronization of energy and power levels of the battery during the charging/discharging mode. Achieved energy and power fixed time consensus regardless of charging/discharging. Robustness. | Neglect of the dynamics of the system, inner loops, control of secondary frequency, and control of power, to simplify the design. |
| [84] AC microgrid/multiagent system | Balanced SOC. | A negative influence of frequency control if neighbors tracking error is suddenly changed. |
| [85] AC microgrid/multiagent system | Balanced SOC. Robustness against communication failure. Plug and play. Active for different topologies. Unaffected by Communication failure. | A slight disturbance of the consensus result of during communication disconnection of unit 3 and 1. Visible delay of frequency, in the case of an increasing delay time. A high time delay because of the low pass filter. Power network topology and lifetime maximization have not been considered. |
| [86] AC microgrid/multiagent system | Balanced SOC. Active restoration of frequency to the nominal at steady state. | Short oscillation of the controller before steady state. |
| [87] DC microgrid/multiagent system | Robust, extensible, and flexible. Regulated DC voltage in all operational modes. Accurate demand implementation. | Intermittent of renewable generation. Delay of communication. |
| [88] DC microgrid/multiagent system | Decentralized coordination of heterogeneous storage systems. A high-frequency load has been provided by ultracapacitor, while short frequency load was by battery. | The minimum voltage achieved (367.5 V) is still above the minimum microgrid rating (360 V). |
| [89] DC microgrid/multiagent system | Balanced SOC. Regulated bus voltage to a specific range. Less communication dependency. | Communication fail (multiagent communication topology is changeable). |
| [90] DC microgrid/multiagent system | Balanced SOC. No circulating current between the participated BESSs. No overloading of any of the participated BESS and plug and play. | Despite balanced SOC, the overloading problem has been prioritized over the accuracy of SOC synchronization, to reduce sliding mode chattering. |
| [91] DC Microgrid/multiagent system | Elimination of average voltage deviation based on nominal voltage. Balanced SOC at the limits. Smooth transfer from charge to discharge and vice versa. Robust against, load fluctuations and different ESS capacities. | A difference in nodes voltage is existing, but the average of the microgrid is balanced. SOC is only balanced when reach limits (90% higher, 20% lower). |
| [92] Multiagent-based microgrid network | Active for both connected and standalone modes. More realistic environment for microgrid control and management. Optimized power flow. | Frequency deviation when switching to transfer from an operating mode to the other. |
| [93] Residential ESSs. (multi-microgrid network) | Optimized performance. Lowering local optimization problems. | The optimized performance level that provided by MPC does not last, because of the fast increase in an optimization problem with the expansion of the network. |
| [94] Multiagent-based microgrid network | Highly robust to link failure. Excellent scalability. | Current sharing cannot be implemented, as the failed link will isolate the agent. |
| [95] Multiagent-based microgrid network | Faster convergence. Economic and stable operation. Robust to the changes in communication topology. Plug and play of distributed systems. Guarantee optimal operation of resources with economic optimization. | Transmission losses are not considered. |
| [96] Smart Microgrids (SMGN) | Effective computation, even if the number of Smart grids is increased. Individual cooperation over Smart grid operation (no need for information for other Smart grids status). Scalable and robust. | The increase in PLAs iterations with the increase in involved smart grid number. Thus, computation time will be increased. |
| [97] Multiagent-based microgrid network | Normal variation of voltage, and within the mandatory range. Fast convergence balanced SOC. Balanced load sharing of BESSs. Easy-designed control strategy. Battery health and life were enhanced. | Packed losses are existing. Delay of communication, and link failure. |
| [98] Multiagent-based microgrid network | Arbitrage behavior of storage has reduced generation level. Economical operation. Optimal utilization of storage. | Optimal communication has not been considered. Instead, extra communication links were introduced. Power flow constraints have not been considered. |
| [99] Multiagent-based microgrid network | Expandable to many distributed ESSs networks (network topology was not an effective parameter of control). More flexibility and enhanced robustness. | Reduction in power quality due to the VSC references. Slight increase in power consumption, compared to central (0.13%). |
| [100] Multiagent based grid connected Microgrid | Compatible with industry applications. The possibility of large-scale implementations for the proposed microgrid has been proven. | A voltage drop at PCC is recognizable but small. |
| [102] Multi-microgrid multi-consumer network | Enhancement to energy adequality. Economical operation of each microgrid of the network. | A delay in energy supply. |
| [103] Multiagent microgrid applications. | The multi-objective power management (MOPM) problem has been solved for a grid connected and islanded microgrids. | Limitation of exported power to 4.2 MW, lower than congestion limit 7.5 MW |
| [104] Multiagent-based multi-Microgrid network | Lower computational load per iteration. Active for wide-scale applications in real-time. | Computational delays. |
| [105] Multiagent multi-microgrid network | Minimized, implementation time. Capable of using all of the agents’ capacity to minimize cost, in addition, to raising system flexibility for deregulated fields. Less dependence on utility. | A minor real-time mismatch. |
| Strategy Application | Strengths | Weaknesses |
|---|---|---|
| [108] Hybrid tracked vehicle | Balanced SOC trajectory to the level of DP-based. Good fuel consumption. Faster computation. | No improvement of SOC trajectory over the other strategies. |
| [109] Vehicle-to-grid microgrid | Achieved microgrid autonomy. Optimal charge/discharge management. | Battery health and life has not been considered. |
| [110] Grid-connected microgrid | High-quality optimization. Fast computation. Qualified real-coded memory. | Convergence is the same as the classical method. |
| [111] Electric vehicle charging station | Higher reward achievement compared to conventional. Lower cost by 14% compared to conventional. | Dimensionality, and lack of policy. |
| [113] Microgrid network | Enhanced learning. Improved control policy. Economic benefits. An increase in battery usage rate. | Increase in computation time. |
| [114] Office distribution network | Optimal battery charge/discharge. Significant reduction in cost. | An existing error of modeling includes renewable energy errors, errors of energy demand, and the error of electricity ratings. |
| [116] Microgrid network | The capability of predicting uncertainty without a specific model. Economical operation. | A side effect exists in reducing batch size, which is that the full advantage of samples was not taken and leads to an ineffective Q-network. This reduces the performance. |
| [117] Smart grid consisting of N microgrids | Convergence has been achieved. Effective strategy (decrease power plant introduction and increase microgrids utility). Less computation time. | A tradeoff between computational complexity and power plant scheduling. |
| [118] Distribution network (storage, PV, and building) | Successful monitoring of hybrid storage. Long-term minimization of carbon impact at least 35% (minimum is one year). Active with storage models comprising a non-linearity. | Cannot assess a day or an hour because of similar or near consumptions; for example, cannot distinguish between 1 am and 4 am at night because these times are showing the same consumption. Or between cloudy summer and clear winter because of the similar consumption. |
| [119] Residential building | A successful deal with system complexity. Better system management. Significant cost reduction and energy saving. | Lack of accuracy. More identification of project feasibility is needed. |
| [121] Microgrid network | Action space is continuous. Cost reduction. Improved SOC. | Islanded mode was disregarded. Only daily consideration to the reduction in cost and improvement of SOC. Furthermore, they were limited. User favoriting is not considered. Power losses are existing. |
| [122] Smart home | Effective and robust. Increase and stabile average reward. Reduction of energy cost. Reduced temperature deviation. An effective tradeoff between thermal comfort and cost of energy. | A variation of performance for the same system parameters. |
| [123] Residential household fed by PV-battery system. | Active battery scheduling. Less computational tame compared to the existing strategies. Reduced electricity cost. Enhanced role of the consumer in the management policy. | Limited to one consumer (as consumer role is enhanced, it is advantageous in reducing electricity cost to achieve the decision of several consumers). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saadi, M.; Al-Greer, M.; Short, M. Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review. Energies 2021, 14, 7234. https://doi.org/10.3390/en14217234
Al-Saadi M, Al-Greer M, Short M. Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review. Energies. 2021; 14(21):7234. https://doi.org/10.3390/en14217234
Chicago/Turabian StyleAl-Saadi, Mudhafar, Maher Al-Greer, and Michael Short. 2021. "Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review" Energies 14, no. 21: 7234. https://doi.org/10.3390/en14217234
APA StyleAl-Saadi, M., Al-Greer, M., & Short, M. (2021). Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review. Energies, 14(21), 7234. https://doi.org/10.3390/en14217234








