Application of Gene Expression Programming (GEP) in Modeling Hydrocarbon Recovery in WAG Injection Process
Abstract
:1. Introduction
2. Theory and Background
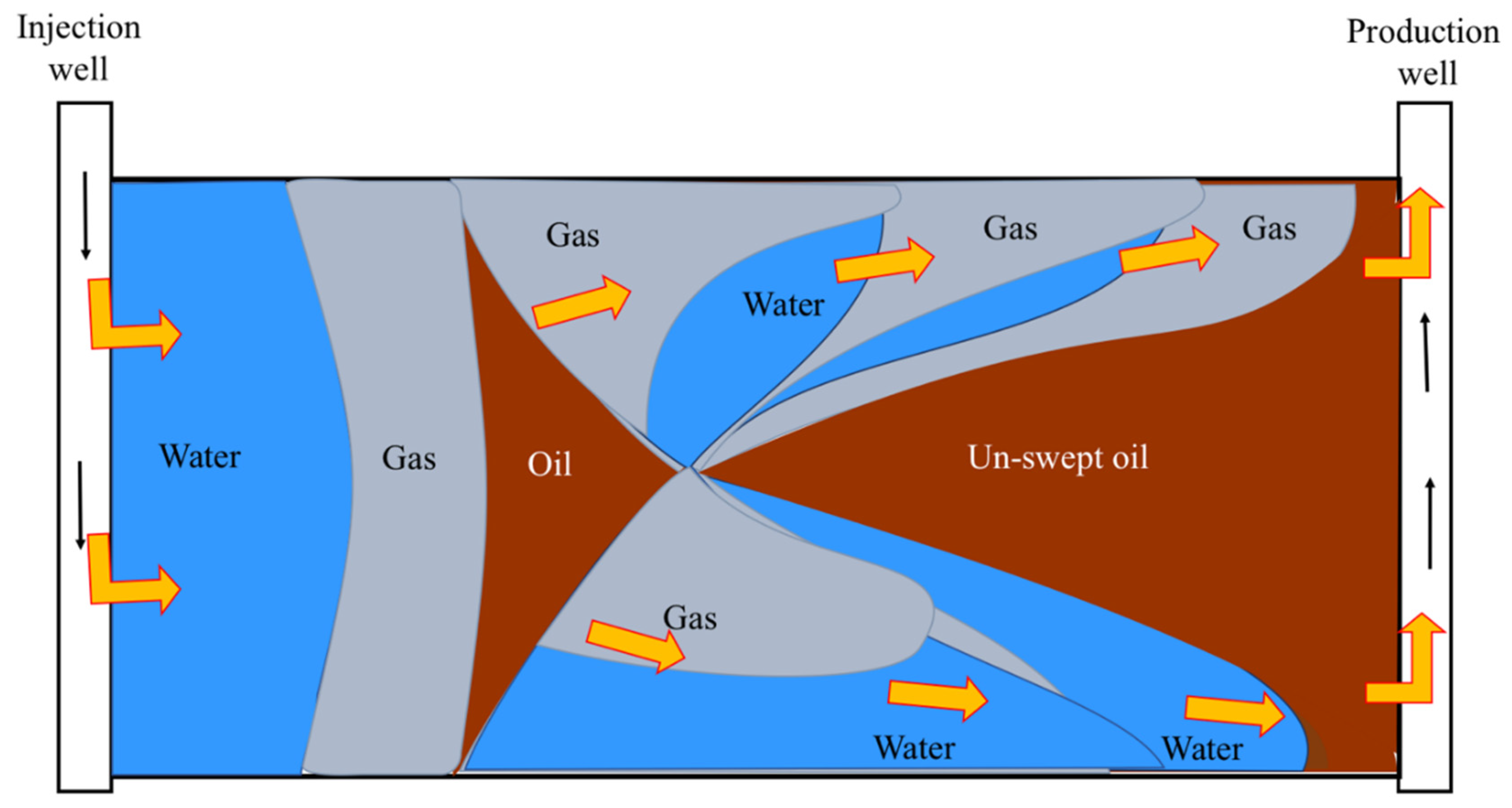
2.1. WAG Mechanisms
2.2. Dimensional Analysis
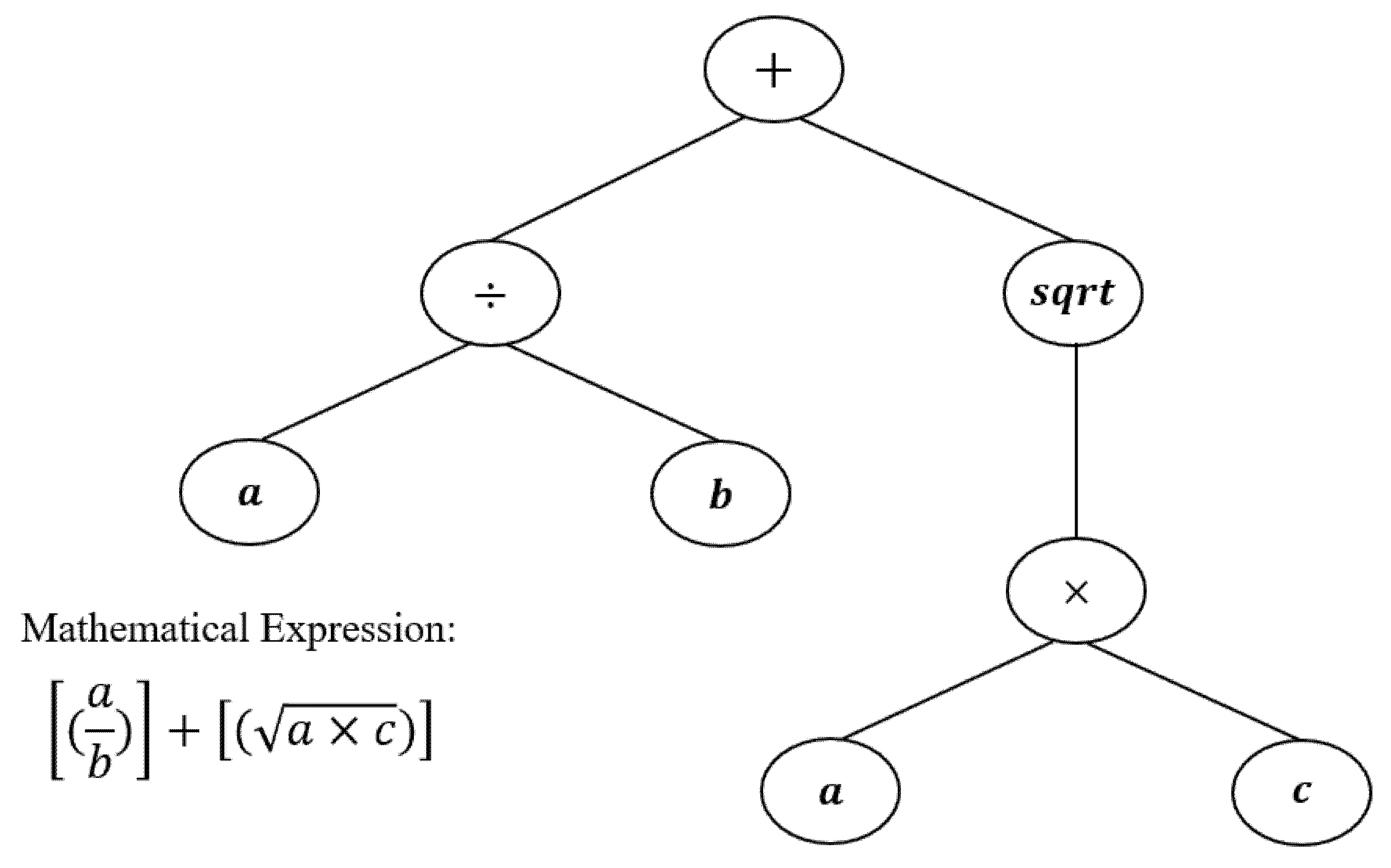
2.3. Fundamentals of GEP
3. Methodology
3.1. Data Collection
3.2. Governing and Auxiliary Equations
3.3. Model Assumptions and Limitations
- Gravity forces are neglected.
- The flow direction is considered as 1D horizontal in the system.
- The core and fluids are considered incompressible.
- Core is strongly water-wet and homogeneous.
- The equilibrium of capillary forces is held in the system.
- The temperature of the system is 38 °C and the thermal equilibrium holds in the system.
- The capillary end effects are neglected.
3.4. Design of Experiment (DOE)
3.5. Dimensionless Scaling Groups
3.6. Analysis of Variance (ANOVA)
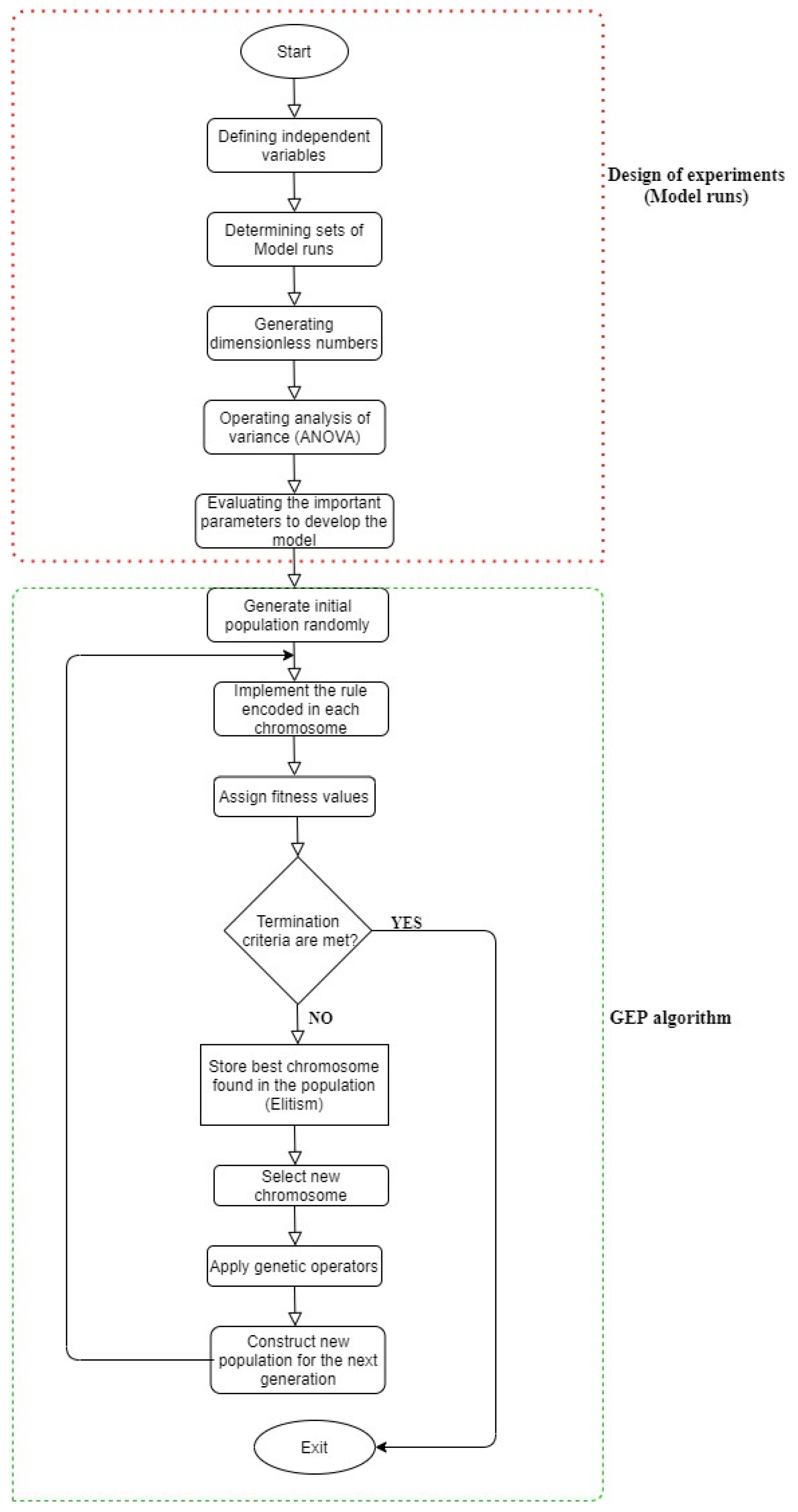
3.7. GEP Procedure
- Initializing the population through generating random chromosomes of a certain number of individuals.
- Fitting the population individuals according to the fitness functions.
- Selecting some individuals and copying them for the next generation based on their fitness (simple elitism) [96].
- Applying the same procedure for the new population including the selection of the environment, expression of genomes, selection of the population individuals, and reproduction with modification.
- Repeating the previous steps until the termination criteria are met.
3.8. Model Development Steps
- Generating the population using random chromosome individuals and applying correlation formats as pars trees using the functions or operators (×, +, −), and terminals which are functions of input variables and output results (RF of WAG).
- Computing the fitness value for each individual of the generated population using the following objective function (OF):
- Applying the genetic operators on selected chromosomes, including:
- -
- Replication operator: This operator copies the chromosome’s structure selected in step 3.
- -
- Mutation operator: As the most important step in the GEP algorithm, the mutation can occur anytime and at any position in a genome, as long as the mutated chromosome meets the validity criteria. The mutation operator changes the head and tail terminals, while the original structure of the chromosome is preserved.
- -
- Inversion: The inversion operator is only applied to the heads of genes, where any sequence is randomly selected and employed. The inversion operator selects the chromosome, the gene to be modified, and the initiation and termination points of the sequence to be inverted at random.
- Transposition and insertion sequence elements: A portion of the genomes, which can be activated and jump to another place in the chromosome, are called the transposable elements of the GEP program. Ferreira [45] divided these elements into three types: “short fragments with either a terminal or function in the first position transpose to the head of genes, short fragments with a function in the first position that transpose to the rest of the head of genes (root IS elements or RIS elements), and entire genes that transpose to commencing of chromosomes.”
- Recombination: This step normally involves two parent chromosomes to produce two new chromosomes through combining various parts of the parents through three approaches: linking one-point recombination, two-point recombination, and gene recombination [35]. Accordingly, the new generation will be reproduced, and the procedure is continued until the termination criteria are met.
4. Results and Discussions
4.1. Model Development
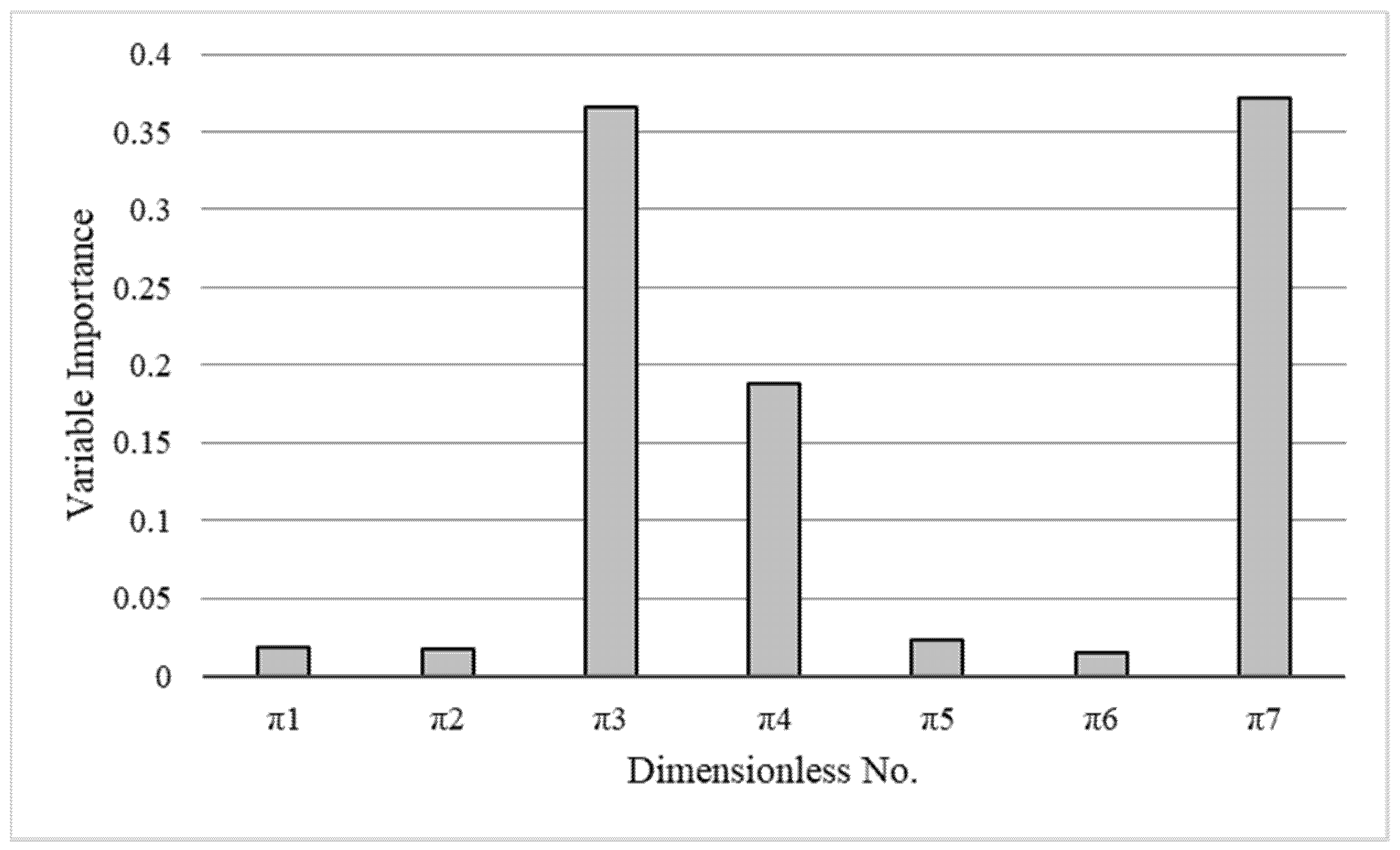
4.2. Relative Importance (RI) of Input Variables
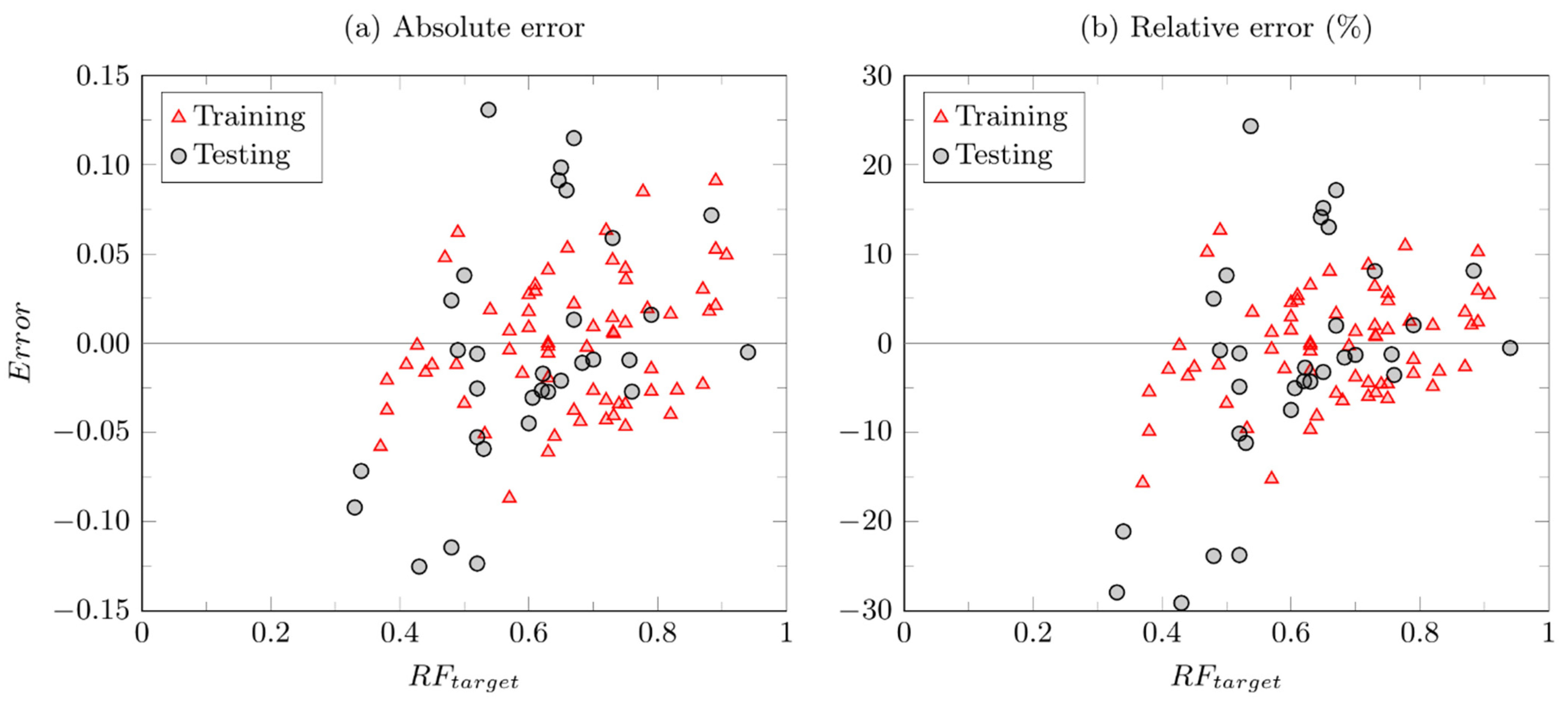
4.3. Evaluation of Developed Correlation
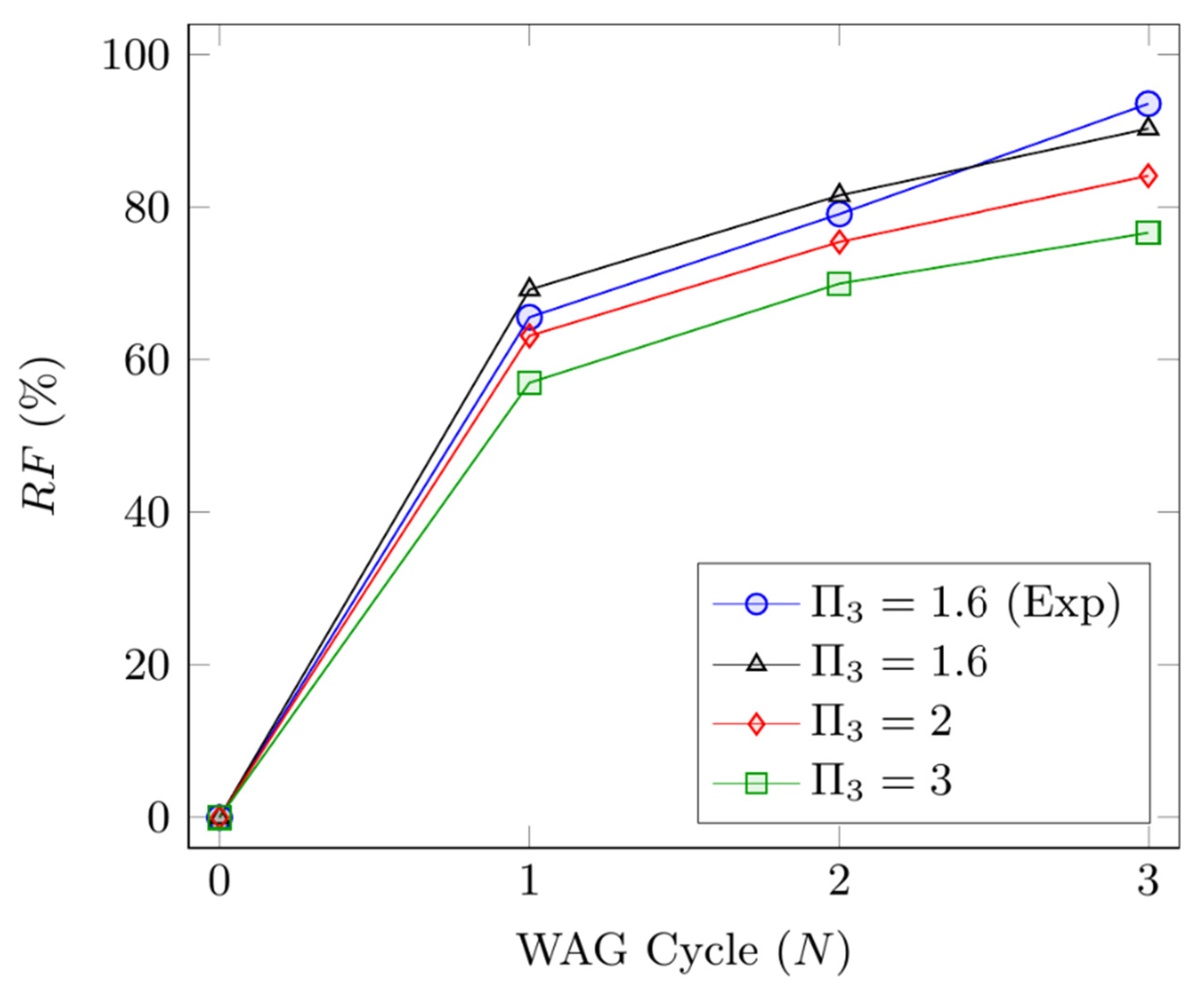
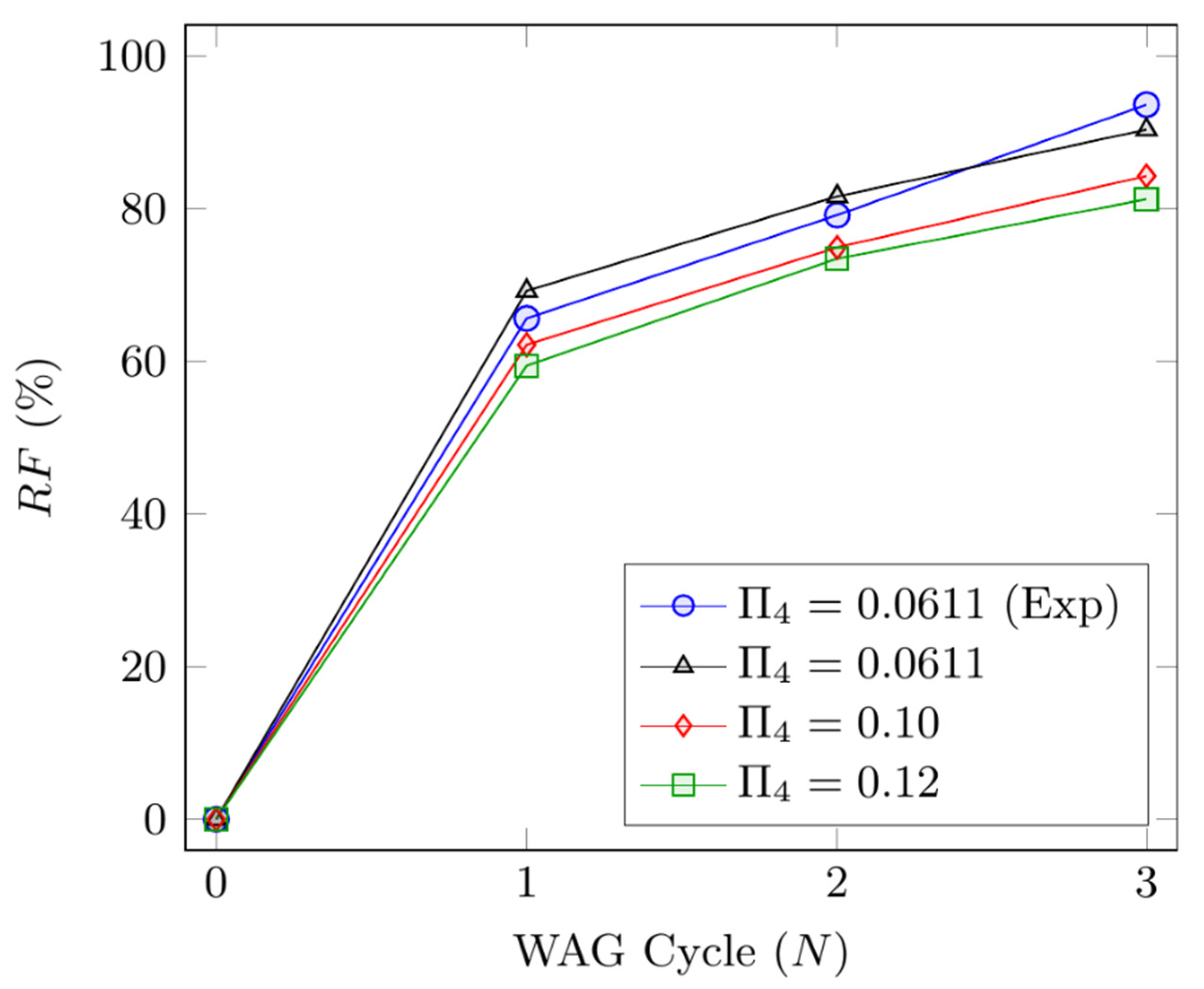
4.4. Effect of Capillary Number
4.5. Effect of Viscosity Ratio ()
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| Acronyms | |
| ANOVA | Analysis of variance |
| CCD | Central composite design |
| DCI | Dimensionless CO2 injection |
| DCP | Dimensionless CO2 production |
| DEOR | Dimensionless tertiary oil recovery |
| DOE | Design of experiment |
| DTI | Dimensionless total injection |
| EOR | Enhanced oil recovery |
| ET | Expression tree |
| GA | Genetic algorithm |
| GEP | Gene expression programming |
| GI | Gas injection |
| GP | Genetic programming |
| IFT | Interfacial tension |
| IOR | Improved oil recovery |
| IMPES | Implicit-pressure-explicit-saturation |
| M | Mobility ratio |
| MMP | Minimum miscible pressure |
| MSE | Mean square error |
| N | Number of injected cycles |
| OF | Objective function |
| PSO | Particle swarm optimization |
| PVI | Pore volume injection |
| RAE | Relative absolute error |
| RF | Recovery factor |
| RI | Relative importance |
| RMSE | Root-mean-square error |
| RSE | Residual standard error |
| WF | Waterflooding |
| WAG | Water-alternating-gas |
| Variables and Parameters | |
| a | Capillary exponent |
| Cij | Correlation constant values |
| Ci | Capillary constant [Pa] |
| F | The main effect of factors in ANOVA |
| K | Absolute permeability [md] |
| kri | Relative permeability of phase i |
| p | Pressure [Pa] |
| p value | The interaction effect of factors in ANOVA |
| q | Flowrate [m3/h] |
| R2 | Coefficient of determination |
| si | Saturation of phase i |
| t | Time [h] |
| v | velocity [m/h] |
| x | Length [m] |
| Greek Letters | |
| µ | Viscosity [cP] |
| ρ | Density [kg/m3] |
| σ | Interfacial tension [N/m] |
| ϕ | Porosity |
| θ | Contact angle |
| Dimensionless number | |
| Subscripts and Superscripts | |
| ave | Average |
| ca | Capillary |
| D | Drainage |
| ed | Displaced phase (oil) |
| exp | Experiment |
| g | Gas phase |
| ing | Displacing phase |
| I | Imbibition |
| nw | Nonwetting phase |
| o | Oil phase |
| og | Oil–gas system |
| ow | Oil–water system |
| r | Residual phase |
| w | Wetting phase |
Appendix A
| Parameter | Description |
|---|---|
| Capillary pressure (in a three-phase system) | |
| Interfacial tension | |
| Contact angle | |
| , | Capillary entry pressure |
| s | Saturation |
| Capillary exponent | |
| nw, w | Nonwetting and wetting phases, respectively. |
| i, j | Existing phases (oil, water, or gas) |
References
- Afzali, S.; Rezaei, N.; Zendehboudi, S. A comprehensive review on enhanced oil recovery by water alternating gas (WAG) injection. Fuel 2018, 227, 218–246. [Google Scholar] [CrossRef]
- Christensen, J.R.; Stenby, E.H.; Skauge, A. Review of WAG field experience. In Proceedings of the International Petroleum Conference and Exhibition of Mexico, Villahermosa, Mexico, 3 March 1998. [Google Scholar]
- Skauge, A.; Stensen, J.Å. Review of WAG field experience. In Proceedings of the Oil Recovery–2003, 1st International Conference and Exhibition, Modern Challenges in Oil Recovery, Moscow, Russia, 19–23 May 2003; pp. 19–23. [Google Scholar]
- Al-Mamari, F.; Al-Shuraiqi, H.; Al-Wahaibi, Y.M. Numerical simulation and experimental studies of oil recovery via first-contact miscible water alternating gas injection within shaley porous media. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, United Arab Emirates, 28–31 October 2007. [Google Scholar]
- Bequette, B.W. Nonlinear control of chemical processes: A review. Ind. Eng. Chem. Res. 1991, 30, 1391–1413. [Google Scholar] [CrossRef]
- Agada, S.; Geiger, S. Wettability, trapping and fracture-matrix interaction during WAG injection in fractured carbonate reservoirs. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 12–16 April 2014. [Google Scholar]
- Larsen, J.A.; Skauge, A. Simulation of the immiscible WAG process using cycle-dependent three-phase relative permeabilities. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Duchenne, S.; de Loubens, R.; Petitfrere, M.; Joubert, T. Modeling and simultaneous history-matching of multiple WAG coreflood experiments at reservoir conditions. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015. [Google Scholar]
- Dale, E.I.; Skauge, A. Fluid Flow Properties of WAG Injection Processes. In Proceedings of the 13th European Symposium on Improved Oil Recovery, Budapest, Hungary, 25–27 April 2008. [Google Scholar]
- Juanes, R.; Patzek, T.W. Analytical solution to the Riemann problem of three-phase flow in porous media. Transp. Porous Media 2004, 55, 47–70. [Google Scholar] [CrossRef] [Green Version]
- Stone, H. Probability model for estimating three-phase relative permeability. J. Pet. Technol. 1970, 22, 214–218. [Google Scholar] [CrossRef]
- Kulkarni, M.M.; Rao, D.N. Experimental investigation of miscible and immiscible Water-Alternating-Gas (WAG) process performance. J. Pet. Sci. Eng. 2005, 48, 1–20. [Google Scholar] [CrossRef]
- Larsen, J.; Skauge, A. Methodology for numerical simulation with cycle-dependent relative permeabilities. SPE J. 1998, 3, 163–173. [Google Scholar] [CrossRef] [Green Version]
- Delshad, M.; Pope, G.A. Comparison of the three-phase oil relative permeability models. Transp. Porous Media 1989, 4, 59–83. [Google Scholar] [CrossRef]
- Fenwick, D.H.; Blunt, M.J. Network modeling of three-phase flow in porous media. SPE J. 1998, 3, 86–96. [Google Scholar] [CrossRef]
- Shahverdi, H.; Sohrabi, M. Relative Permeability Characterization for Water-Alternating-Gas Injection in Oil Reservoirs. SPE J. 2016, 21, 0799–0808. [Google Scholar] [CrossRef]
- Spiteri, E.J.; Juanes, R. Impact of relative permeability hysteresis on the numerical simulation of WAG injection. J. Pet. Sci. Eng. 2006, 50, 115–139. [Google Scholar] [CrossRef]
- Giordano, R.; Redman, R.; Bratvedt, F. A new approach to forecasting miscible WAG performance at the field scale. SPE Reserv. Eval. Eng. 1998, 1, 192–200. [Google Scholar] [CrossRef]
- Kohata, A.; Willingham, T.; Yunus Khan, M.; Al Sowaidi, A. Extensive miscible water alternating gas WAG simulation study for a giant offshore oil field. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13–16 November 2017. [Google Scholar]
- Afzali, S.; Ghamartale, A.; Rezaei, N.; Zendehboudi, S. Mathematical modeling and simulation of water-alternating-gas (WAG) process by incorporating capillary pressure and hysteresis effects. Fuel 2020, 263, 116362. [Google Scholar] [CrossRef]
- Belazreg, L.; Raub, M.R.A.; Hanifah, M.A.B.; Ghadami, N. WAG cycle dependent hysteresis modelling through an integrated approach from laboratory to field scale, Malaysia oil fields. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Jakarta, Indonesia, 17–19 October 2017. [Google Scholar]
- Sanchez, N.L. Management of water alternating gas (WAG) injection projects. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Caracas, Venezuela, 21–23 April 1999. [Google Scholar]
- Belazreg, L.; Mahmood, S.M. Water alternating gas incremental recovery factor prediction and WAG pilot lessons learned. J. Pet. Explor. Prod. Technol. 2020, 10, 249–269. [Google Scholar] [CrossRef] [Green Version]
- Jaber, A.K.; Awang, M.B.; Lenn, C.P. Box-Behnken design for assessment proxy model of miscible CO2-WAG in heterogeneous clastic reservoir. J. Nat. Gas Sci. Eng. 2017, 40, 236–248. [Google Scholar] [CrossRef]
- Jaber, A.K.; Alhuraishawy, A.K.; AL-Bazzaz, W.H. A Data-Driven Model for Rapid Evaluation of Miscible CO-WAG Flooding in Heterogeneous Clastic Reservoirs. In Proceedings of the SPE Kuwait Oil & Gas Show and Conference, Mishref, Kuwait, 13–16 October 2019. [Google Scholar]
- Gharbi, R.B. Neural Network Prediction Model of Miscible Displacements in Heterogeneous Reservoirs. In Proceedings of the Middle East Oil Show, Manama, Bahrain, 9–12 June 2003. [Google Scholar]
- Ghiasi, M.M.; Shahdi, A.; Barati, P.; Arabloo, M. Robust modeling approach for estimation of compressibility factor in retrograde gas condensate systems. Ind. Eng. Chem. Res. 2014, 53, 12872–12887. [Google Scholar] [CrossRef]
- Le Van, S.; Chon, B.H. Evaluating the critical performances of a CO2–Enhanced oil recovery process using artificial neural network models. J. Pet. Sci. Eng. 2017, 157, 207–222. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Sasaki, K. Application of artificial neural network for predicting the performance of CO2 enhanced oil recovery and storage in residual oil zones. Sci. Rep. 2020, 10, 18204. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Shafiei, A.; Bahadori, A.; James, L.A.; Elkamel, A.; Lohi, A. Asphaltene precipitation and deposition in oil reservoirs–Technical aspects, experimental and hybrid neural network predictive tools. Chem. Eng. Res. Des. 2014, 92, 857–875. [Google Scholar] [CrossRef]
- Ghiasi, M.M.; Zendehboudi, S.; Mohsenipour, A.A. Decision tree-based diagnosis of coronary artery disease: CART model. Comput. Methods Programs Biomed. 2020, 192, 105400. [Google Scholar] [CrossRef]
- Eshraghi, S.E.; Rasaei, M.R.; Zendehboudi, S. Optimization of miscible CO2 EOR and storage using heuristic methods combined with capacitance/resistance and Gentil fractional flow models. J. Nat. Gas Sci. Eng. 2016, 32, 304–318. [Google Scholar] [CrossRef]
- Kamari, A.; Bahadori, A.; Mohammadi, A.H.; Zendehboudi, S. Evaluating the unloading gradient pressure in continuous gas-lift systems during petroleum production operations. Pet. Sci. Technol. 2014, 32, 2961–2968. [Google Scholar] [CrossRef]
- Kamari, A.; Mohammadi, A.H.; Bahadori, A.; Zendehboudi, S. Prediction of air specific heat ratios at elevated pressures using a novel modeling approach. Chem. Eng. Technol. 2014, 37, 2047–2055. [Google Scholar] [CrossRef]
- Dashti, A.; Raji, M.; Razmi, A.; Rezaei, N.; Zendehboudi, S.; Asghari, M. Efficient hybrid modeling of CO2 absorption in aqueous solution of piperazine: Applications to energy and environment. Chem. Eng. Res. Des. 2019, 144, 405–417. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Zahedi, G.; Bahadori, A.; Lohi, A.; Elkamel, A.; Chatzis, I. A dual approach for modelling and optimisation of industrial urea reactor: Smart technique and grey box model. Can. J. Chem. Eng. 2014, 92, 469–485. [Google Scholar] [CrossRef]
- Rajabzadeh, A.R.; Ruzich, N.; Zendehboudi, S.; Rahbari, M. Biomass leachate treatment and nutrient recovery using reverse osmosis: Experimental study and hybrid artificial neural network modeling. Energy Fuels 2012, 26, 7155–7163. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Bahadori, A.; Lohi, A.; Elkamel, A.; Chatzis, I. Practical and economic aspects of the ex-situ process: Implications for CO2 sequestration. Energy Fuels 2013, 27, 401–413. [Google Scholar] [CrossRef]
- Hamedi, H.; Ehteshami, M.; Mirbagheri, S.A.; Zendehboudi, S. New deterministic tools to systematically investigate fouling occurrence in membrane bioreactors. Chem. Eng. Res. Des. 2019, 144, 334–353. [Google Scholar] [CrossRef]
- Sun, Q.; Ampomah, W.; You, J.; Cather, M.; Balch, R. Practical CO2—WAG Field Operational Designs Using Hybrid Numerical-Machine-Learning Approaches. Energies 2021, 14, 1055. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Nguele, R.; Sasaki, K. Robust optimization of CO2 sequestration through a water alternating gas process under geological uncertainties in Cuu Long Basin, Vietnam. J. Nat. Gas Sci. Eng. 2020, 76, 103208. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin, Germany, 2006. [Google Scholar]
- Gharagheizi, F.; Ilani-Kashkouli, P.; Farahani, N.; Mohammadi, A.H. Gene expression programming strategy for estimation of flash point temperature of non-electrolyte organic compounds. Fluid Phase Equilibria 2012, 329, 71–77. [Google Scholar] [CrossRef]
- Rostami, A.; Hemmati-Sarapardeh, A.; Mohammadi, A.H. Estimating n-tetradecane/bitumen mixture viscosity in solvent-assisted oil recovery process using gep and gmdh modeling approaches. Pet. Sci. Technol. 2019, 37, 1640–1647. [Google Scholar] [CrossRef]
- Rostami, A.; Arabloo, M.; Kamari, A.; Mohammadi, A.H. Modeling of CO2 solubility in crude oil during carbon dioxide enhanced oil recovery using gene expression programming. Fuel 2017, 210, 768–782. [Google Scholar] [CrossRef]
- Kamari, A.; Arabloo, M.; Shokrollahi, A.; Gharagheizi, F.; Mohammadi, A.H. Rapid method to estimate the minimum miscibility pressure (MMP) in live reservoir oil systems during CO2 flooding. Fuel 2015, 153, 310–319. [Google Scholar] [CrossRef]
- Umar, A.A.; Saaid, I.M.; Sulaimon, A.A.; Pilus, R.M. Predicting the Viscosity of Petroleum Emulsions Using Gene Expression Programming (GEP) and Response Surface Methodology (RSM). J. Appl. Math. 2020, 2020, 6215352. [Google Scholar] [CrossRef] [Green Version]
- Kamari, A.; Sattari, M.; Mohammadi, A.H.; Ramjugernath, D. Reliable method for the determination of surfactant retention in porous media during chemical flooding oil recovery. Fuel 2015, 158, 122–128. [Google Scholar] [CrossRef]
- Rostami, A.; Raef, A.; Kamari, A.; Totten, M.W.; Abdelwahhab, M.; Panacharoensawad, E. Rigorous framework determining residual gas saturations during spontaneous and forced imbibition using gene expression programming. J. Nat. Gas Sci. Eng. 2020, 84, 103644. [Google Scholar] [CrossRef]
- Mostafa, M.M.; El-Masry, A.A. Oil price forecasting using gene expression programming and artificial neural networks. Econ. Model. 2016, 54, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Mashayekhizadeh, V.; Kord, S.; Dejam, M. EOR potential within Iran. Spec. Top. Rev. Porous Media Int. J. 2014, 5, 325–354. [Google Scholar] [CrossRef]
- Ahmed, T. Reservoir Engineering Handbook; Elsevier: Austin, TX, USA, 2006. [Google Scholar]
- Pudugramam, V.S. A Numerical Study of CO2-EOR With Emphasis on Mobility Control Processes: Water Alternating Gas (WAG) and Foam; The University of Texas at Austin: Austin, TX, USA, 2013. [Google Scholar]
- Holm, L. Propane-gas-water miscible floods in watered-out areas of the adena field, Colorado. J. Pet. Technol. 1972, 24, 1264–1270. [Google Scholar] [CrossRef]
- Moffitt, P.; Zornes, D. Postmortem analysis: Lick creek meakin sand unit immiscible CO2 waterflood project. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar]
- Esene, C.; Rezaei, N.; Aborig, A.; Zendehboudi, S. Comprehensive review of carbonated water injection for enhanced oil recovery. Fuel 2019, 237, 1086–1107. [Google Scholar] [CrossRef]
- Watts, R.J.; Conner, W.D.; Wasson, J.A.; Yost, A.B. CO2 injection for tertiary oil recovery, Granny’s Creek Field, Clay County, West Virginia. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, OK, USA, 4–7 April 1982. [Google Scholar]
- Gharbi, R.; Peters, E.; Elkamel, A. Scaling miscible fluid displacements in porous media. Energy Fuels 1998, 12, 801–811. [Google Scholar] [CrossRef]
- Shahverdi, H. Characterization of Three-Phase Flow and WAG Injection in Oil Reservoirs; Heriot-Watt University: Edinburgh, UK, 2012. [Google Scholar]
- Birkhoff, G. Hydrodynamics, a study in logic, fact, and similitude. Bull. Am. Math. Soc. 1951, 57, 497–499. [Google Scholar]
- Ruark, A.E. Inspectional analysis: A method which supplements dimensional analysis. J. Elisha Mitchell Sci. Soc. 1935, 51, 127–133. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation, Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Peters, E.J.; Afzal, N.; Gharbi, R. On scaling immiscible displacements in permeable media. J. Pet. Sci. Eng. 1993, 9, 183–205. [Google Scholar] [CrossRef]
- Collins, R.E. Flow of Fluids Through Porous Materials; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1976.
- Greenkorn, R. Flow models and scaling laws for flow through porous media. Ind. Eng. Chem. 1964, 56, 32–37. [Google Scholar] [CrossRef]
- Li, D.; Lake, L.W. Scaling fluid flow through heterogeneous permeable media. SPE Adv. Technol. Ser. 1995, 3, 188–197. [Google Scholar] [CrossRef]
- Loomis, A.G.; Crowell, D.C. Theory and Application of Dimensional and Inspectional Analysis to Model Study of Fluid Displacements in Petroleum Reservoirs; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1964.
- Nielsen, R.L.; Tek, M. Evaluation of scale-up laws for two-phase flow through porous media. Soc. Pet. Eng. J. 1963, 3, 164–176. [Google Scholar] [CrossRef]
- Rapoport, L.; Leas, W. Properties of linear waterfloods. J. Pet. Technol. 1953, 5, 139–148. [Google Scholar] [CrossRef]
- Shook, M.; Li, D.; Lake, L.W. Scaling immiscible flow through permeable media by inspectional analysis. In Situ (United States) 1992, 16, 311. [Google Scholar]
- Sorbie, K.; Feghi, F.; Pickup, G.; Ringrose, P.; Jensen, J. Flow regimes in miscible displacements in heterogeneous correlated random fields. SPE Adv. Technol. Ser. 1994, 2, 78–87. [Google Scholar] [CrossRef]
- Waggoner, J.; Castillo, J.; Lake, L.W. Simulation of EOR processes in stochastically generated permeable media. SPE Form. Eval. 1992, 7, 173–180. [Google Scholar] [CrossRef]
- Wygal, R. Construction of models that simulate oil reservoirs. Soc. Pet. Eng. J. 1963, 3, 281–286. [Google Scholar] [CrossRef]
- Leverett, M.; Lewis, W.; True, M. Dimensional-model studies of oil-field behavior. Trans. AIME 1942, 146, 175–193. [Google Scholar] [CrossRef]
- Engleberts, W.; Klinkenberg, L. Laboratory Experiments on the Displacement of Oil by Water From Packs of Granular Materials. In Proceedings of the 3rd World Petroleum Congress, The Hague, The Netherlands, 28 May–6 June 1951. [Google Scholar]
- Asghari, K.; Dong, M.; Shire, J.; Coleridge, T.J.; Nagrampa, J.; Grassick, J. Development of a correlation between performance of CO2 flooding and the past performance of waterflooding in Weyburn oil field. SPE Prod. Oper. 2007, 22, 260–264. [Google Scholar] [CrossRef]
- Liu, S.; Sahni, V.; Hsu, C.-F. A novel method of forecasting CO2 flood performance for various WAG injection schemes by analyzing injection pulses. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 12–16 April 2014. [Google Scholar]
- Chung, S.H.; Chan, H.K. A two-level genetic algorithm to determine production frequencies for economic lot scheduling problem. IEEE Trans. Ind. Electron. 2011, 59, 611–619. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Huang, H.-C.; Chan, C.-K. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation. IEEE Trans. Ind. Electron. 2011, 58, 4813–4821. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, S.; Chen, D.; Li, X. Fast covariance matching with fuzzy genetic algorithm. IEEE Trans. Ind. Inform. 2011, 8, 148–157. [Google Scholar] [CrossRef]
- Varadan, V.; Leung, H. Reconstruction of polynomial systems from noisy time-series measurements using genetic programming. IEEE Trans. Ind. Electron. 2001, 48, 742–748. [Google Scholar] [CrossRef]
- Teodorescu, L.; Sherwood, D. High energy physics event selection with gene expression programming. Comput. Phys. Commun. 2008, 178, 409–419. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Abbasi, R.; Tirandazi, B. Prediction of Henry’s law constant of organic compounds in water from a new group-contribution-based model. Ind. Eng. Chem. Res. 2010, 49, 10149–10152. [Google Scholar] [CrossRef]
- Virnovsky, G.; Vatne, K.; Iversen, J.; Signy, C. Three-phase capillary pressure measurements in centrifuge at reservoir conditions. In Proceedings of the International Symposium of the Society of Core Analysts, Abu Dhabi, United Arab Emirates, 5–9 October 2004. [Google Scholar]
- Neshat, S.S.; Pope, G.A. Compositional Three-Phase Relative Permeability and Capillary Pressure Models Using Gibbs Free Energy. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar]
- Skjaeveland, S.; Siqveland, L.; Kjosavik, A.; Hammervold, W.; Virnovsky, G. Capillary pressure correlation for mixed-wet reservoirs. In Proceedings of the SPE India Oil and Gas Conference and Exhibition, New Delhi, India, 17–19 February 1998. [Google Scholar]
- Lorenzen, T.; Anderson, V. Design of Experiments: A No-Name Approach; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Safa, Y.; Bhatti, H.N. Biosorption of Direct Red-31 and Direct Orange-26 dyes by rice husk: Application of factorial design analysis. Chem. Eng. Res. Des. 2011, 89, 2566–2574. [Google Scholar] [CrossRef]
- Antony, J. Training for design of experiments using a catapult. Qual. Reliab. Eng. Int. 2002, 18, 29–35. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.C. Design and Analysis of Experiments; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- George, E.; Hunter, J.S.; Hunter, W.G.; Bins, R.; Kirlin IV, K.; Carroll, D. Statistics for Experimenters: Design, Innovation, and Discovery; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Chen, Y.; Chen, D.; Khan, S.U.; Huang, J.; Xie, C. Solving symbolic regression problems with uniform design-aided gene expression programming. J. Supercomput. 2013, 66, 1553–1575. [Google Scholar] [CrossRef]
- Ferreira, C. Function finding and the creation of numerical constants in gene expression programming. In Advances in Soft Computing; Springer: Berlin/Heidelberg, Germany, 2003; pp. 257–265. [Google Scholar]
- Cândida, F. GeneXproTools; Gepsoft Ltd.: Capelo, Portugal. Available online: https://www.gepsoft.com/ (accessed on 27 August 2020).
- Agbalaka, C.C.; Dandekar, A.Y.; Patil, S.L.; Khataniar, S.; Hemsath, J. The effect of wettability on oil recovery: A review. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 20–22 October 2008. [Google Scholar]
- Delshad, M.; Bhuyan, D.; Pope, G.; Lake, L. Effect of capillary number on the residual saturation of a three-phase micellar solution. In Proceedings of the SPE Enhanced Oil Recovery Symposium, Tulsa, OK, USA, 20–23 April 1986. [Google Scholar]
- Bethel, F.; Calhoun, J.C. Capillary desaturation in unconsolidated beads. J. Pet. Technol. 1953, 5, 197–202. [Google Scholar] [CrossRef]
- Chatzis, I.; Morrow, N.R. Correlation of capillary number relationships for sandstone. Soc. Pet. Eng. J. 1984, 24, 555–562. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 245, 312–329. [Google Scholar]



| Governing Equations | Auxiliary Equations | ||
|---|---|---|---|
| Density of the fluid | |||
| Rock permeability | Capillary pressure | ||
| Relative permeability of phase i | Pressure of the nonwet phase | ||
| μ | Viscosity of the fluid | Pressure of the wet phase | |
| Pressure | Saturation of phases | ||
| Spatial location | o | Oil phase | |
| q | Source/sink term | w | Water phase |
| Time | g | Gas phase | |
| Factors | Level | |
|---|---|---|
| Low (−1) | High (+1) | |
| (Pa.h) | 1.11 × 10−8 | 1.11× 10−7 |
| (m3/h) | 25 × 10−6 | 40 × 10−6 |
| (m3/h) | 25 × 10−6 | 40 × 10−6 |
| K (mD) | 65 | 200 |
| PVI | 0.5 | 1 |
| N | 1 | 3 |
| Variables | Fixed Parameters | Response Variable |
|---|---|---|
| (cP) | (N/m) | RF |
| qw (m3/h) | (N/m) | |
| qg (m3/h) | (cP) | |
| K (mD) | (cP) | |
| PVI | ||
| N |
| Source | Sum Sq | d.f | F | p |
|---|---|---|---|---|
| 0.0092 | 2 | 6.66 | 0.0018 | |
| 0.0159 | 1 | 10.45 | 0.0010 | |
| 0.0100 | 4 | 200.24 | <0.0001 | |
| 0.0153 | 1 | 40.34 | 0.0013 | |
| 0.0189 | 1 | 12.39 | 0.0007 | |
| 0.0635 | 1 | 4.67 | 0.0023 | |
| 0.0614 | 4 | 348.21 | <0.0001 | |
| Error | 0.1564 | 8 | ||
| Total | 0.1942 | 22 |
| Configuration | Value |
|---|---|
| Population size | 96 |
| No. of chromosomes | 33 |
| Head size | 8 |
| No. of genes | 4 |
| Fitness function | OF |
| Map operators | |
| No. of constants per gene | 10 |
| Statistical Measures | Training | Testing |
|---|---|---|
| MSE | 1.38 × 10−3 | 4.30 × 10−3 |
| RMSE | 3.72 × 10−2 | 6.56 × 10−2 |
| MAE | 3.06 × 10−2 | 5.25 × 10−2 |
| RSE | 7.15 × 10−2 | 23.29 × 10−2 |
| RAE | 26.85 × 10−2 | 47.87 × 10−2 |
| Correlation coefficient (%) | 96.36 | 87.68 |
| R2 (%) | 92.85 | 91.93 |
| Constant | Value |
|---|---|
| C13 | −4.7530 |
| C15 | −5.4106 |
| C18 | −7.5887 |
| C11 | 6.7068 |
| C10 | 2.2652 |
| C28 | 11.5608 |
| C29 | 0.7480 |
| C22 | −59.7849 |
| C35 | −7.7281 |
| C32 | 9.5931 |
| C49 | 0.0875 |
| C42 | 0.4019 |
| Attribute | |||||||
|---|---|---|---|---|---|---|---|
| Importance | 1.89 | 1.70 | 3.66 | 1.88 | 2.30 | 1.53 | 3.71 |
| Minimum | 3.16 | 4.71 | 1.61 | 6.17 | 6.25 | 5.00 | 1.00 |
| Maximum | 1.56 | 2.32 | 16.09 | 6.17 | 1.60 | 1.00 | 3.00 |
| Average | 8.22 | 1.25 | 8.62 | 3.30 | 1.06 | 7.58 | 2.14 |
| Median | 7.39 | 1.10 | 1.61 | 6.17 | 1.00 | 1.00 | 2.00 |
| Standard deviation | 4.63 | 7.19 | 7.29 | 2.79 | 3.58 | 2.52 | 8.33 |
| R2 (vs. Response) | 2.62 | 2.30 | 3.24 | 3.24 | 4.51 | 4.12 | 5.67 |
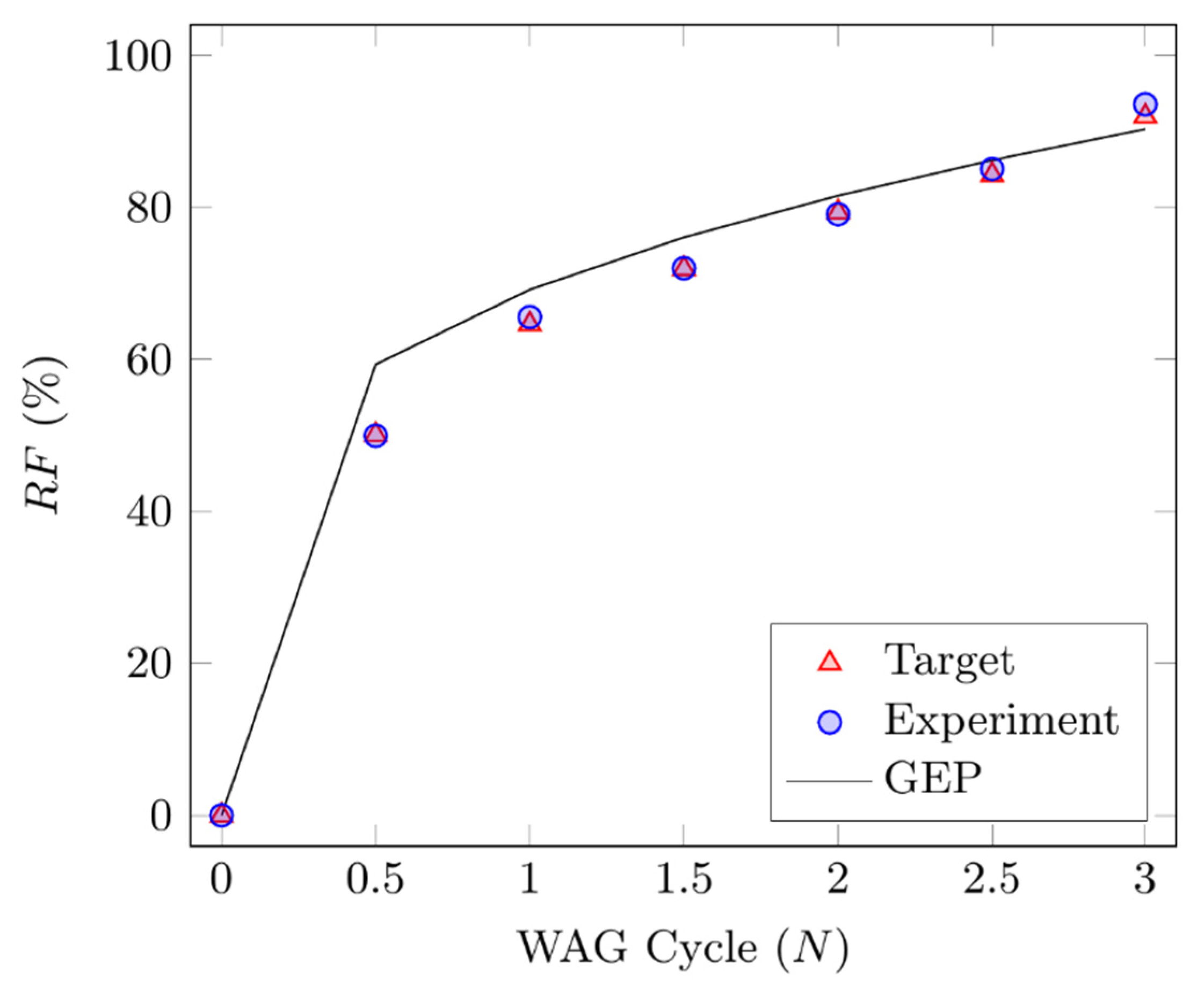
| N | RFGEP (%) | Relative ErrorGEP-Exp (%) | RFTarget (%) | Relative ErrorGEP-Target (%) | RFExp (%) |
|---|---|---|---|---|---|
| 0.5 | 59.35 | 18.77 | 50.08 | 18.51 | 49.97 |
| 1 | 69.20 | 5.50 | 64.64 | 7.05 | 65.59 |
| 1.5 | 76.08 | 5.65 | 71.94 | 5.75 | 72.01 |
| 2 | 81.56 | 3.08 | 79.37 | 2.76 | 79.12 |
| 2.5 | 86.22 | 1.33 | 84.30 | 2.28 | 85.09 |
| 3 | 90.32 | 3.48 | 92.00 | 1.83 | 93.58 |
| N | RF (%) | RF (%) | ||
|---|---|---|---|---|
| 1.59 | 1 | 69.20 | 0.0611 | 69.20 |
| 2 | 81.56 | 81.56 | ||
| 3 | 90.32 | 90.32 | ||
| 2.00 | 1 | 63.15 | 0.100 | 62.14 |
| 2 | 75.46 | 74.89 | ||
| 3 | 84.14 | 84.25 | ||
| 3.00 | 1 | 57.00 | 0.120 | 59.40 |
| 2 | 70.00 | 73.42 | ||
| 3 | 76.66 | 81.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afzali, S.; Mohamadi-Baghmolaei, M.; Zendehboudi, S. Application of Gene Expression Programming (GEP) in Modeling Hydrocarbon Recovery in WAG Injection Process. Energies 2021, 14, 7131. https://doi.org/10.3390/en14217131
Afzali S, Mohamadi-Baghmolaei M, Zendehboudi S. Application of Gene Expression Programming (GEP) in Modeling Hydrocarbon Recovery in WAG Injection Process. Energies. 2021; 14(21):7131. https://doi.org/10.3390/en14217131
Chicago/Turabian StyleAfzali, Shokufe, Mohamad Mohamadi-Baghmolaei, and Sohrab Zendehboudi. 2021. "Application of Gene Expression Programming (GEP) in Modeling Hydrocarbon Recovery in WAG Injection Process" Energies 14, no. 21: 7131. https://doi.org/10.3390/en14217131
APA StyleAfzali, S., Mohamadi-Baghmolaei, M., & Zendehboudi, S. (2021). Application of Gene Expression Programming (GEP) in Modeling Hydrocarbon Recovery in WAG Injection Process. Energies, 14(21), 7131. https://doi.org/10.3390/en14217131







