Model Predictive Controller Design for Vehicle Motion Control at Handling Limits in Multiple Equilibria on Varying Road Surfaces
Abstract
:1. Introduction
2. Vehicle Modeling and Simulation Setup
2.1. Vehicle Modeling
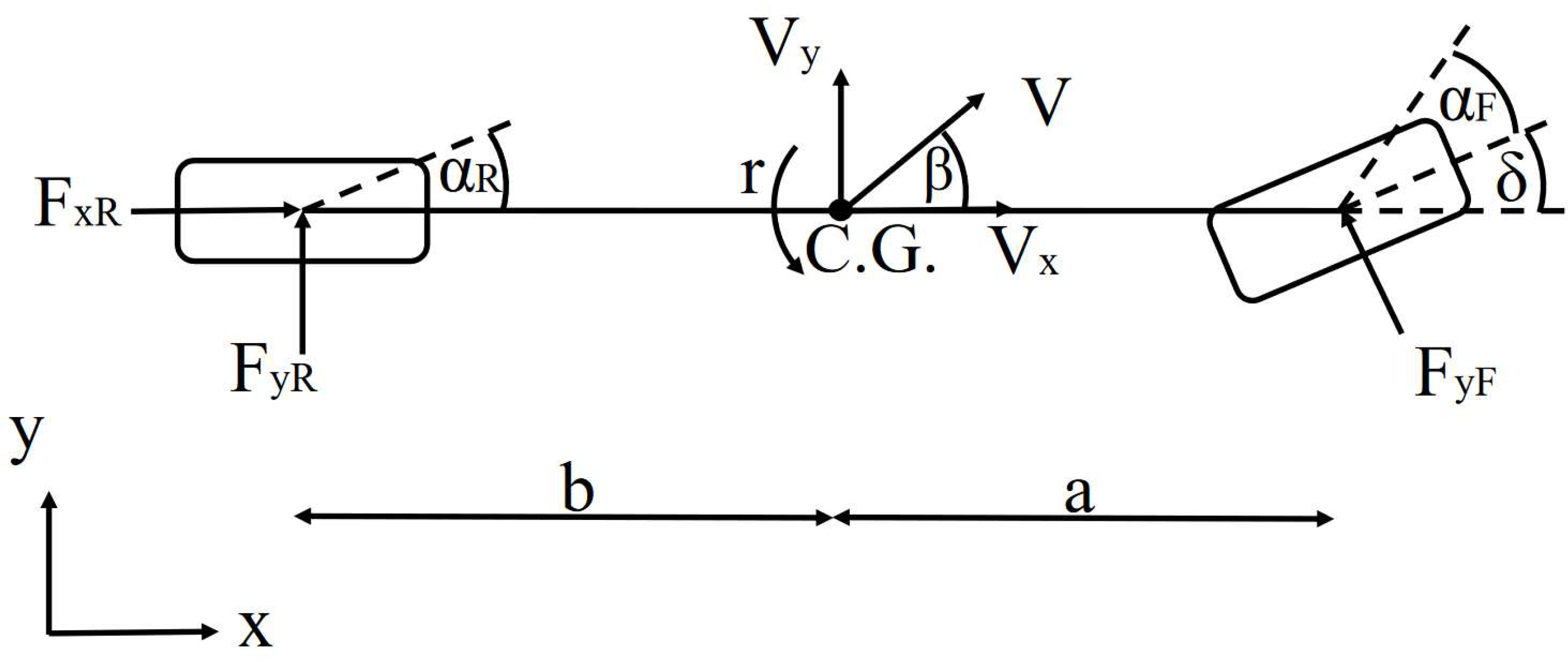
2.1.1. Two-Wheel Planar Vehicle Dynamics
2.1.2. Nonlinear Tire Model
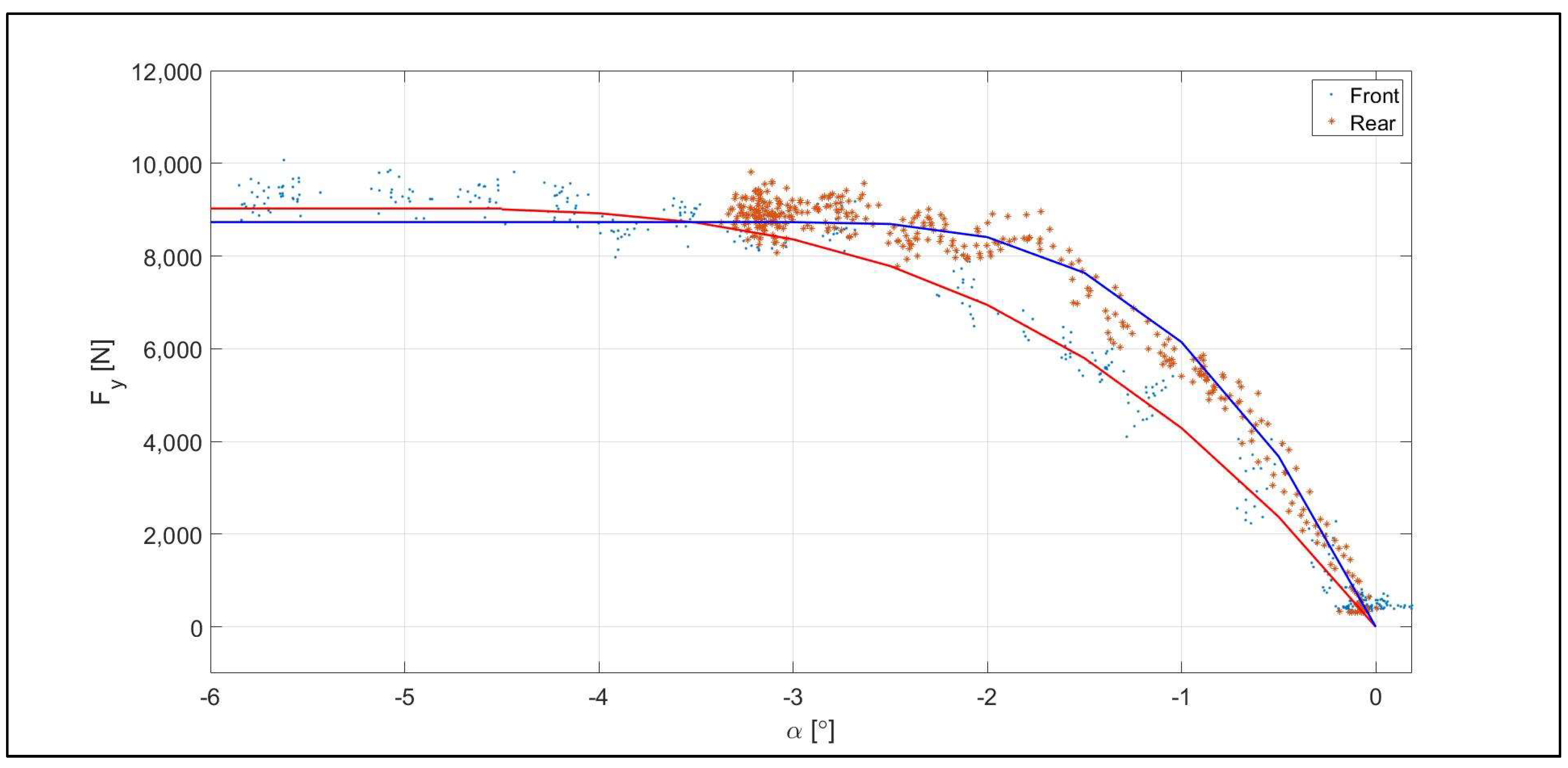
2.2. Model Parameter Identification Measurements
3. Equilibrium Analysis
4. Controller Design
4.1. MPC Formulation
4.2. Successive Linearization
5. Simulation Results
5.1. Steady-State Drift in a Single Equilibrium
5.2. Steady-State Drift in Multiple Equilibria
5.3. Drifting on Varying Road Surfaces
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Name | Sign | Dimension |
|---|---|---|
| mass of the vehicle | m | kg |
| vehicle moment of inertia around z-axis | Iz | kg·m2 |
| lateral force | Fy | N |
| lateral force at front wheel | FyF | N |
| lateral force at rear wheel | FyR | N |
| normal load on the front wheels | FzF | N |
| normal load on the rear wheels | FzR | N |
| drive force at the rear wheel | FxR | N |
| drive force at the front wheel | FxF | N |
| air drag | FA | N |
| applied torque at the center of gravity | Mz | Nm |
| yaw-rate | r | rad/s |
| longitudinal velocity | Vx | m/s |
| lateral velocity | Vy | m/s |
| distance between center of gravity and front axle | a | m |
| distance between center of gravity and rear axle | b | m |
| derating factor | - | |
| cornering stiffness of the front tire | CαF | N/rad |
| cornering stiffness of the rear tire | CαR | N/rad |
| air drag coefficient | CA | - |
| frontal cross-section surface of the vehicle | A | m2 |
| air density | ρ | kg/m3 |
| front tire sideslip angle | αF | rad |
| rear tire sideslip angle | αR | rad |
| sideslip boundary angle of the front tire | rad | |
| sideslip boundary angle of the front rear | rad | |
| friction coefficient | µ | - |
| vehicle sideslip angle at center of gravity | β | rad |
| steering angle | δ | rad |
| state vector | x | - |
| input vector | u | - |
| continuous time state matrices | Ac, Bc, Cc, Dc | - |
| discrete time state matrices | Ad, Bd, Cd, Dd | - |
References
- Ágoston, G.; Madleňák, R. Road Safety Macro Assessment Model: Case Study for Hungary. Period. Polytech. Transp. Eng. 2021, 49, 89–92. [Google Scholar] [CrossRef] [Green Version]
- Ghadi, M.Q.; Török, Á. Evaluation of the Impact of Spatial and Environmental Accident Factors on Severity Patterns of Road Segments. Period. Polytech. Transp. Eng. 2020, 49, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Hegedűs, T.; Németh, B.; Gáspár, P. Challenges and Possibilities of Overtaking Strategies for Autonomous Vehicles. Period. Polytech. Transp. Eng. 2020, 48, 320–326. [Google Scholar] [CrossRef]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Wu, N.; Huang, W.; Song, Z.; Wu, X.; Zhang, Q.; Yao, S. Adaptive dynamic preview control for autonomous vehicle trajectory following with ddp based path planner. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1012–1017. [Google Scholar]
- Bacha, S.; Saadi, R.; Ayad, M.Y.; Aboubou, A.; Bahri, M. A review on vehicle modeling and control technics used for autonomous vehicle path following. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar]
- Zhang, B.; Chen, G.; Zong, C. Path tracking of full drive-by-wire electric vehicle based on model prediction control. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 868–873. [Google Scholar]
- Velenis, E.; Frazzoli, E.; Tsiotras, P. On steady-state cornering equilibria for wheeled vehicles with drift. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 3545–3550. [Google Scholar]
- Velenis, E.; Frazzoli, E.; Tsiotras, P. Steady-state cornering equilibria and stabilisation for a vehicle during extreme operating conditions. Int. J. Veh. Auton. Syst. 2010, 8, 10. [Google Scholar] [CrossRef]
- Hindiyeh, R.Y. Dynamics and Control of Drifting in Automobiles. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Bardos, A.; Domina, A.; Szalay, Z.; Tihanyi, V.; Palkovics, L. MIMO controller design for stabilizing vehicle drifting. In Proceedings of the IEEE Joint 19th International Symposium on Computational Intelligence and Informatics and 7th IEEE International Conference on Recent Achievements in Mechatronics, Automation, Computer Sciences and Robotics, Szeged, Hungary, 14–16 November 2019. [Google Scholar]
- Wachter, E.; Alirezaei, M.; Bruzelius, F.; Schmeitz, A. Path control in limit handling and drifting conditions using State Dependent Riccati Equation technique. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 783–791. [Google Scholar] [CrossRef]
- Xu, D.; Wang, G.; Qu, L.; Ge, C. Robust Control with Uncertain Disturbances for Vehicle Drift Motions. Appl. Sci. 2021, 11, 4917. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D. UniTire: Unified tire model for vehicle dynamic simulation. Veh. Syst. Dyn. 2007, 45, 79–99. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Li, K. A New Path Tracking Method Based on Multilayer Model Predictive Control. Appl. Sci. 2019, 9, 2649. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Guo, J.; Guo, C.; Chen, C.; Zhang, Y.; Wang, J. Adaptive Cruise Control for Cut-In Scenarios Based on Model Predictive Control Algorithm. Appl. Sci. 2021, 11, 5293. [Google Scholar] [CrossRef]
- Zhang, X.; Göhlich, D. Integrated Traction Control Strategy for Distributed Drive Electric Vehicles with Improvement of Economy and Longitudinal Driving Stability. Energies 2017, 10, 126. [Google Scholar] [CrossRef] [Green Version]
- Zhai, L.; Hou, R.; Sun, T.; Kavuma, S. Continuous Steering Stability Control Based on an Energy-Saving Torque Distribution Algorithm for a Four in-Wheel-Motor Independent-Drive Electric Vehicle. Energies 2018, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Jang, I.G.; Hwang, S.-H. Torque Distribution Algorithm for an Independently Driven Electric Vehicle Using a Fuzzy Control Method: Driving Stability and Efficiency. Energies 2018, 11, 3479. [Google Scholar] [CrossRef] [Green Version]
- Joa, E.; Cha, H.; Hyun, Y.; Koh, Y.; Yi, K.; Park, J. A new control approach for automated drifting in consideration of the driving characteristics of an expert human driver. Control. Eng. Pr. 2020, 96, 104293. [Google Scholar] [CrossRef]
- Reza, N.J. Advanced Vehicle Dynamics; Springer: Cham, Switzerland, 2019; pp. 143–144. ISBN 978-3-030-13060-2. [Google Scholar]
- Lugaro, C.; Alirezaei, M.; Konstantinou, I.; Behera, A. A Study on the Effect of Tire Temperature and Rolling Speed on the Vehicle Handling Response; SAE Technical Paper 2020-01-1235; SAE International: Warrendale, PA, USA, 14 April 2020. [Google Scholar]
- Helnwein, P.; Liu, C.; Meschke, G.; Mang, H. A new 3-d finite element model for cord-reinforced rubber composites application to analysis of automobile tires. Finite Elem. Anal. Des. 1993, 14, 1–16. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1992, 21 (Suppl. S1), 1–18. [Google Scholar] [CrossRef]
- Fiala, E. Lateral forces on rolling pneumatic tires. Z. VDI 1954, 96, 973–979. [Google Scholar]
- Hadekel, R. The mechanical characteristics of pneumatic tyres. In Sand T Memo TPA3/TIB; National Association of Housing & Redeve: Washington, DC, USA, 1952. [Google Scholar]
- Szalay, Z.; Hamar, Z.; Nyerges, Á. Novel design concept for an automotive proving ground supporting multilevel CAV development. Int. J. Veh. Des. 2019, 80, 1–22. [Google Scholar] [CrossRef]
- Bardos, A.; Domina, A.; Tihanyi, V.; Szalay, Z.; Palkovics, L. Implementation and experimental evaluation of a MIMO drifting controller on a test vehicle. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1472–1478. [Google Scholar]
- Varga, B.; Tettamanti, T.; Kulcsár, B. Optimally combined headway and timetable reliable public transport system. Transp. Res. Part C Emerg. Technol. 2018, 92, 1–26. [Google Scholar] [CrossRef]
- Zhakatayev, A.; Rakhim, B.; Adiyatov, O.; Baimyshev, A.; Varol, H.A. Successive linearization based model predictive control of variable stiffness actuated robots. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1774–1779. [Google Scholar]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control. In Nonlinear Model Predictive Control: Theory and Algorithms; Springer: Cham, Switzerland, 2017; pp. 45–69. [Google Scholar]
- Roubal, J.; Husek, P.; Stecha, J. Linearization: Students Forget the Operating Point. IEEE Trans. Educ. 2009, 53, 413–418. [Google Scholar] [CrossRef]
- Panahandeh, G.; Ek, E.; Mohammadiha, N. Road friction estimation for connected vehicles using supervised machine learning. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1262–1267. [Google Scholar]
- Roychowdhury, S.; Zhao, M.; Wallin, A.; Ohlsson, N.; Jonasson, M. Machine Learning Models for Road Surface and Friction Estimation using Front-Camera Images. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Fényes, D.; Németh, B.; Gáspár, P.; Szabó, Z. Road surface estimation based LPV control design for autonomous vehicles. IFAC-PapersOnLine 2019, 52, 120–125. [Google Scholar] [CrossRef]
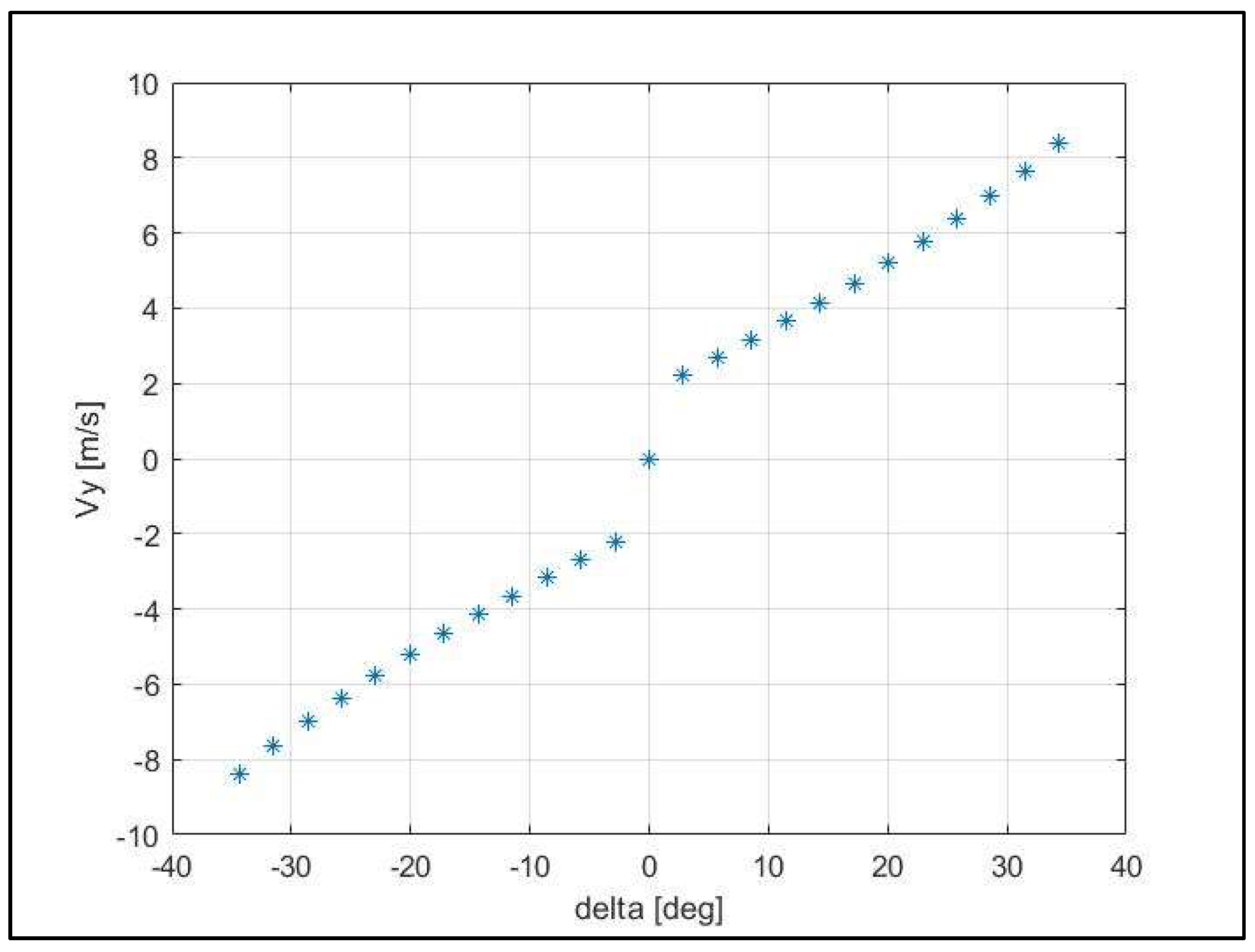

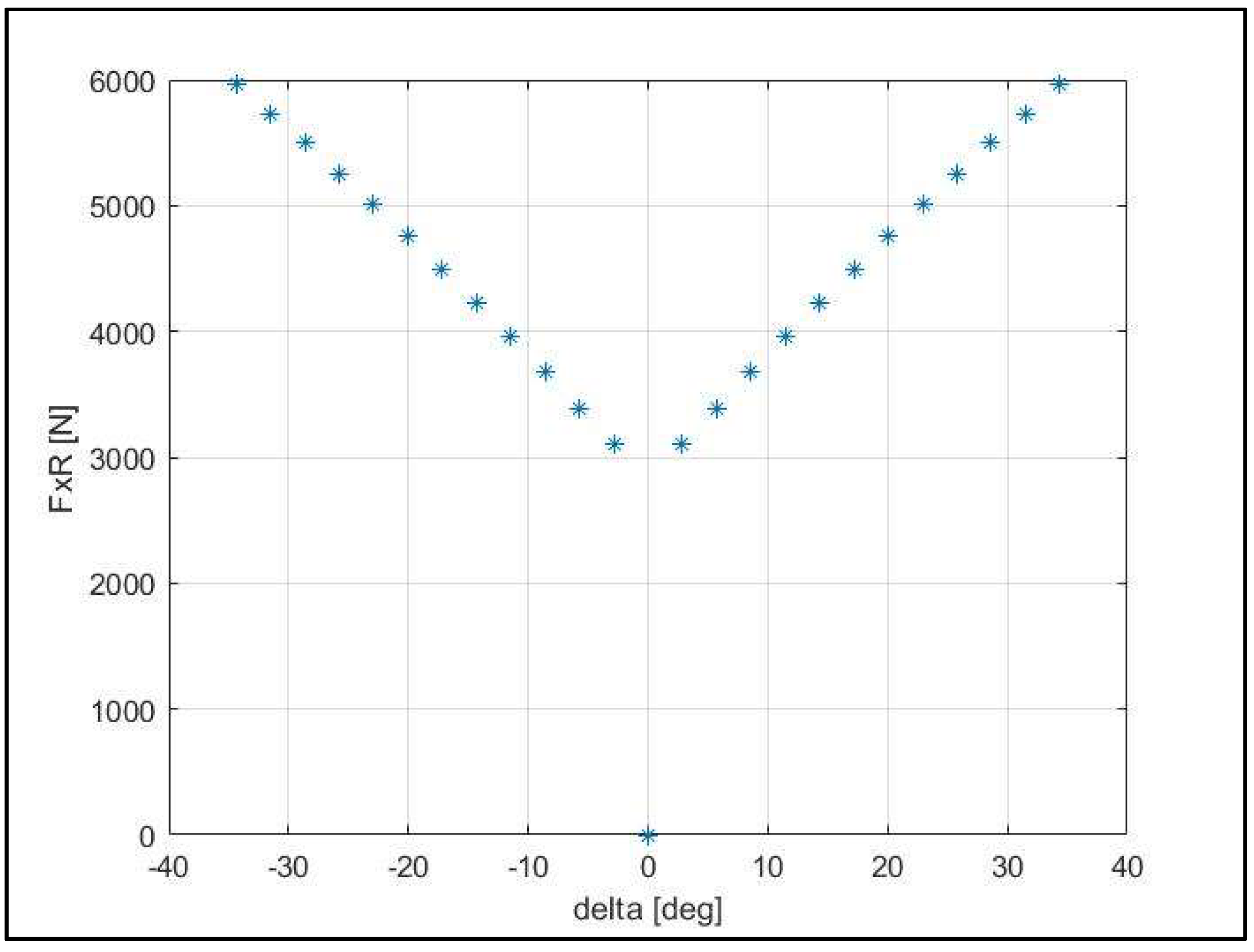

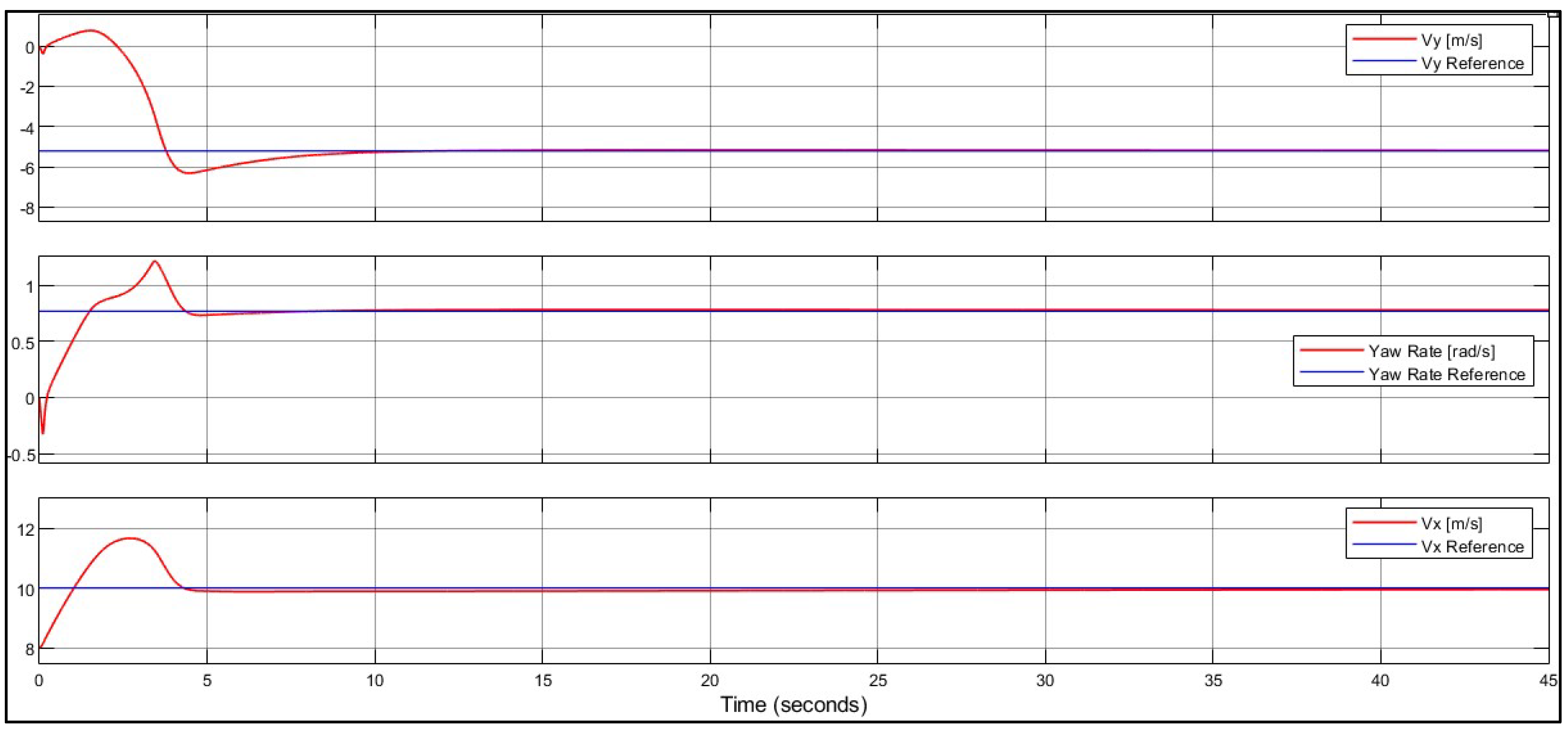
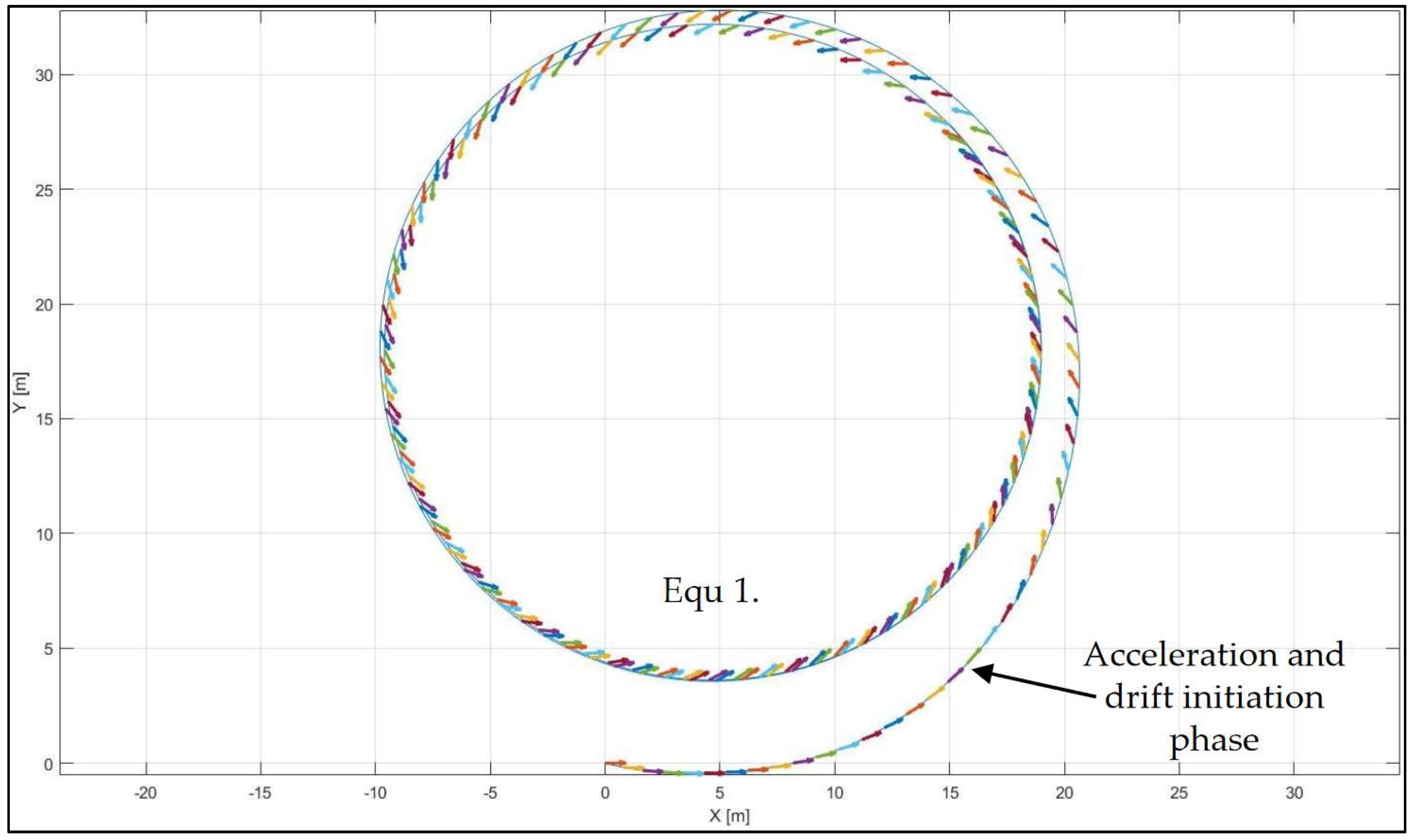
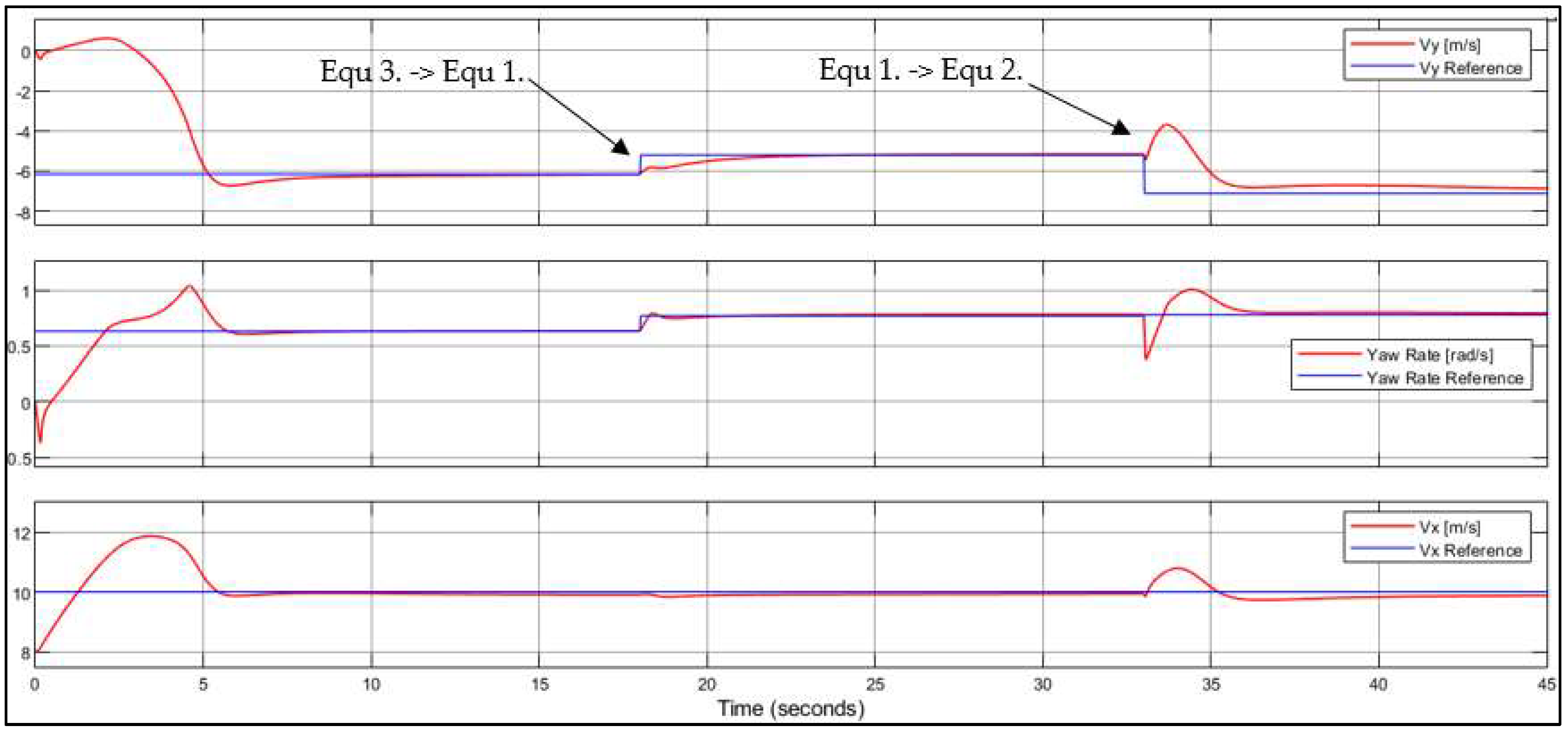
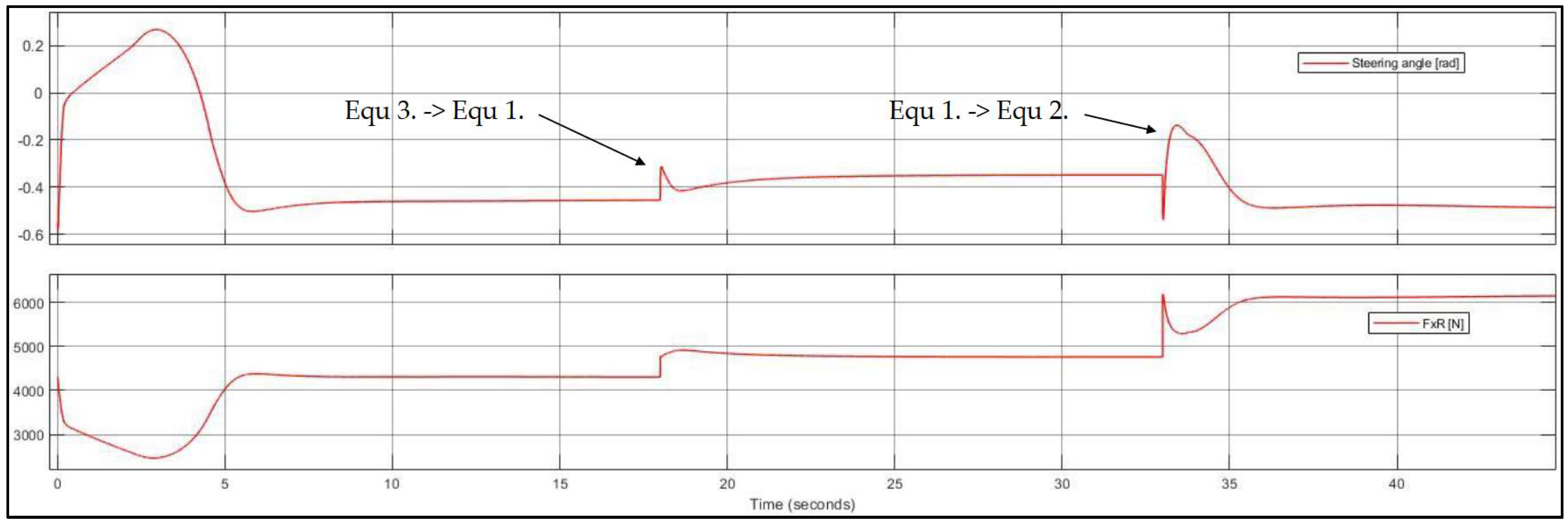
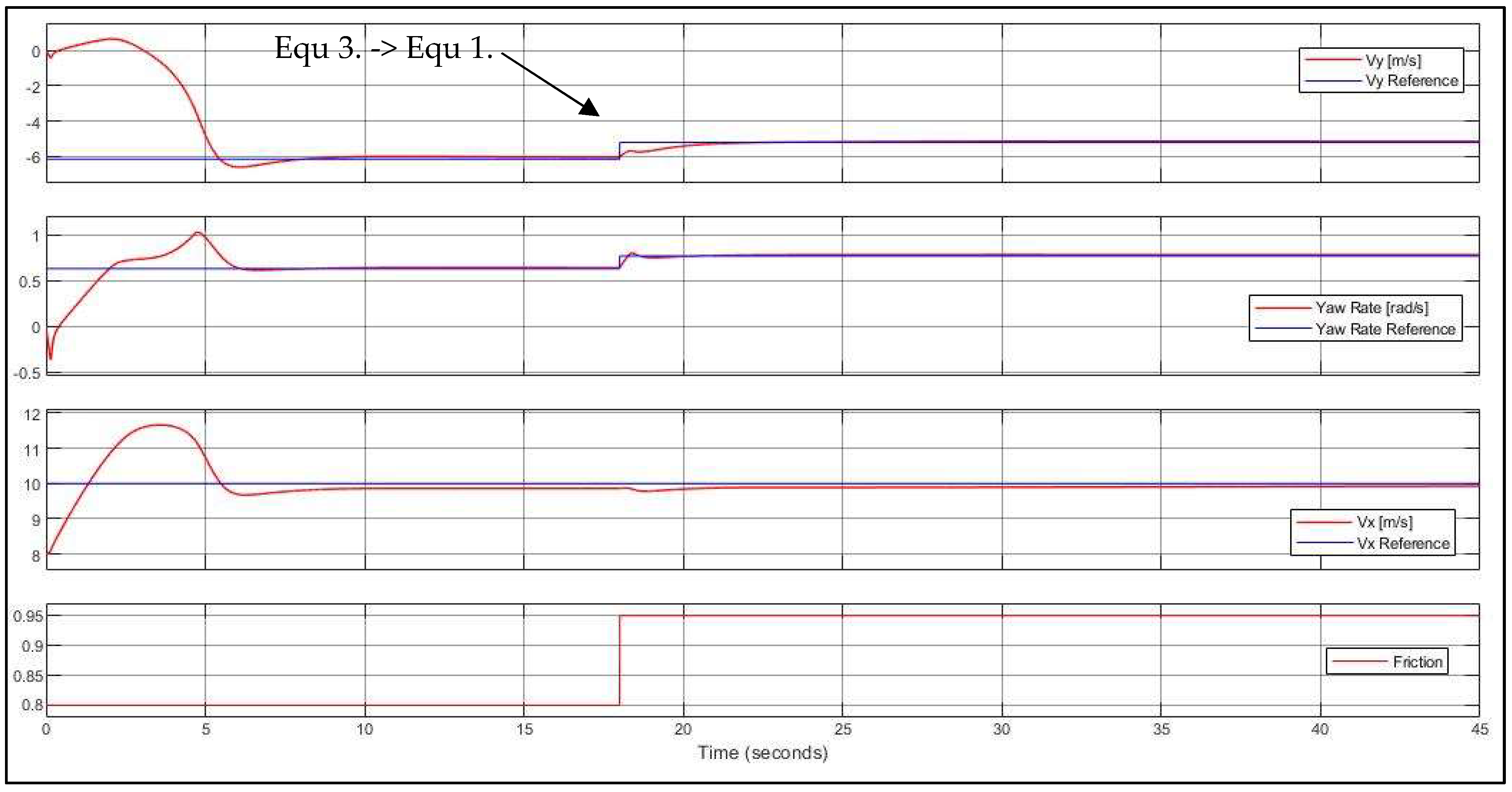
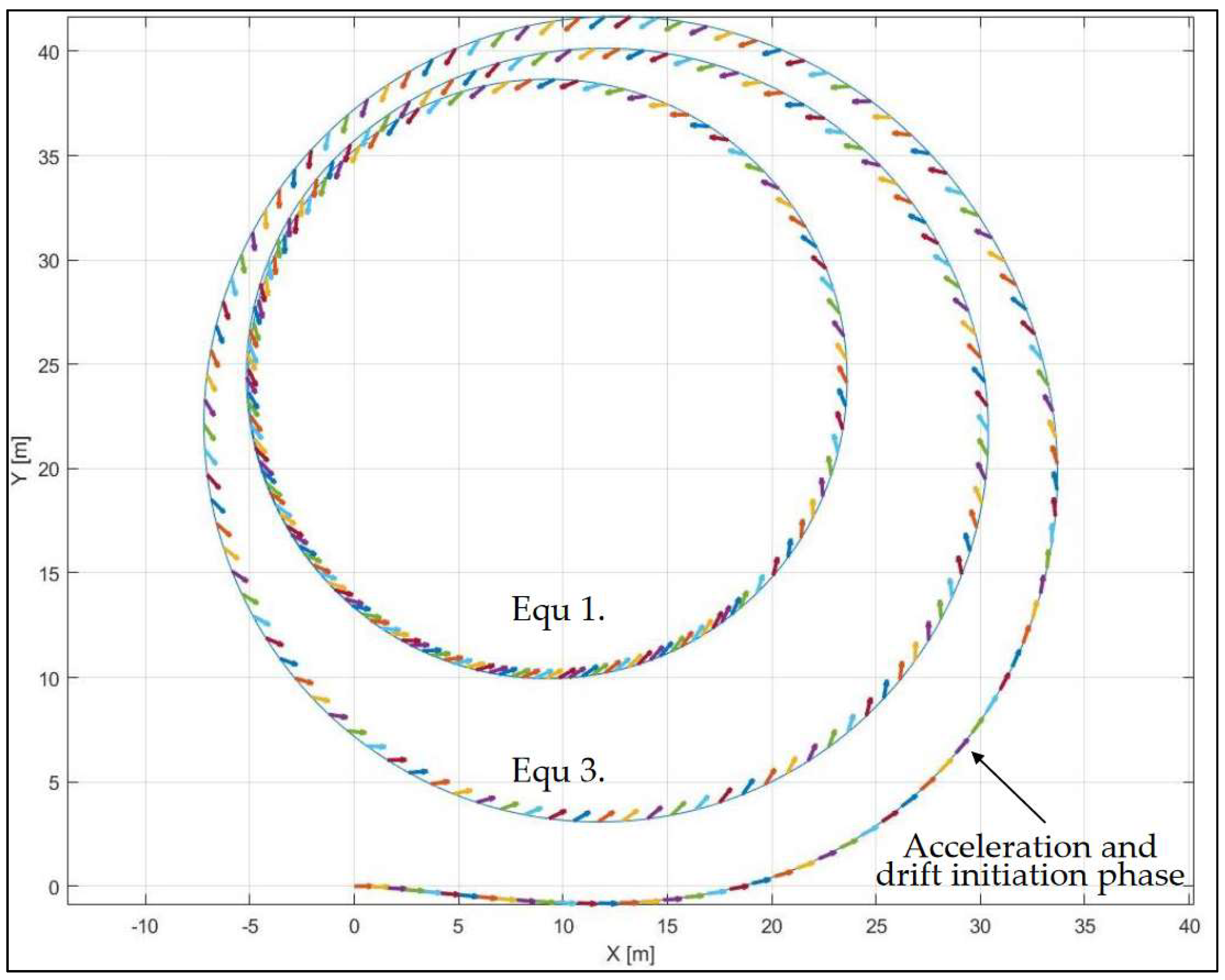
| Case No. | δ (°) | FxR (N) | Vy (m/s) | r (rad/s) | Vx (m/s) |
|---|---|---|---|---|---|
| 1 | −20.05 | 4753 | −5.21 | 0.776 | 10 |
| 2 | −28.65 | 5500 | −6.99 | 0.713 | 10 |
| 3 | −22.92 | 5254 | −6.36 | 0.735 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czibere, S.; Domina, Á.; Bárdos, Á.; Szalay, Z. Model Predictive Controller Design for Vehicle Motion Control at Handling Limits in Multiple Equilibria on Varying Road Surfaces. Energies 2021, 14, 6667. https://doi.org/10.3390/en14206667
Czibere S, Domina Á, Bárdos Á, Szalay Z. Model Predictive Controller Design for Vehicle Motion Control at Handling Limits in Multiple Equilibria on Varying Road Surfaces. Energies. 2021; 14(20):6667. https://doi.org/10.3390/en14206667
Chicago/Turabian StyleCzibere, Szilárd, Ádám Domina, Ádám Bárdos, and Zsolt Szalay. 2021. "Model Predictive Controller Design for Vehicle Motion Control at Handling Limits in Multiple Equilibria on Varying Road Surfaces" Energies 14, no. 20: 6667. https://doi.org/10.3390/en14206667
APA StyleCzibere, S., Domina, Á., Bárdos, Á., & Szalay, Z. (2021). Model Predictive Controller Design for Vehicle Motion Control at Handling Limits in Multiple Equilibria on Varying Road Surfaces. Energies, 14(20), 6667. https://doi.org/10.3390/en14206667






