A GRASP Approach for Solving Large-Scale Electric Bus Scheduling Problems
Abstract
:1. Introduction
2. Model Outline
- There are N locations and the corresponding set of locations is represented by set .
- There is a single depot .
- The distance between any two locations is known and is equal to .
- The schedule is done over P time periods and a corresponding set of time periods is denoted by .
- A timetable trip is a 4-tuple , where origin-destination pairs are in the set of existing locations, that is, and other parameters are part of time periods, that is . The timetable is a set of timetable trips. For simplicity of notation, we will use for each trip to indicate the time of its completion.
- An EB has a battery capacity that provides a fixed range R. It is assumed that all EBs have the same range.
- The objective is to find the minimal number of EBs that can perform all the trips in the timetable.
- An EB can only be charged at a depot.
- An EB is fully charged at the first time period.
- There is a charging rate , i.e., how much a battery is charged in one time period.
- Charging of an EB is always done to full capacity.
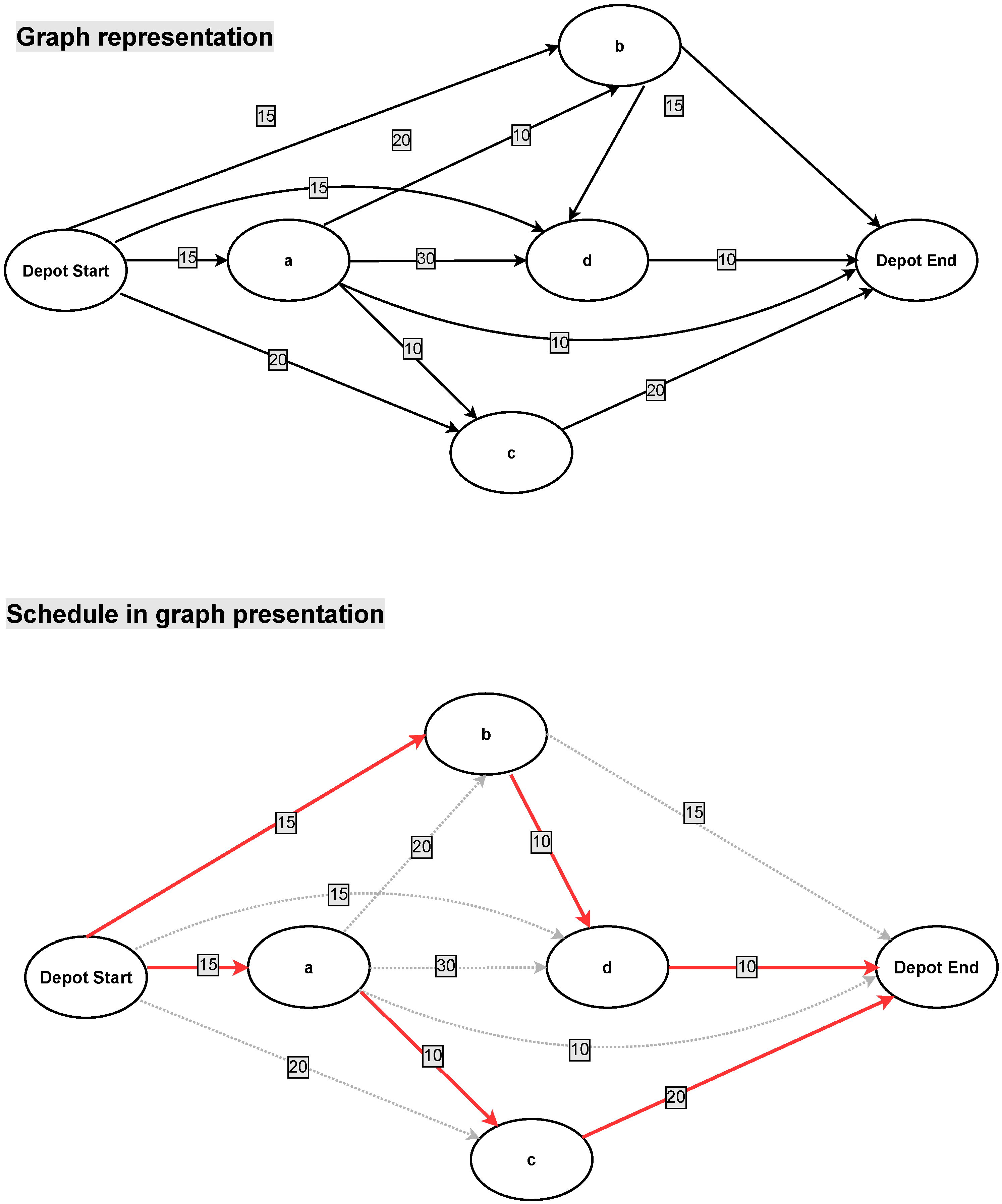
3. Graph Formulation
4. Mathematical Model
- The distance between any two trips is known and is equal to which is calculated as described in the previous section.
- For each trip i there is a starting time and a duration . For simplicity of notation, let us define as the time when trip i is completed.
- The charging rate per time period is denoted by .
- Battery usage per time period is denoted by .
- The battery capacity of all EBs is denoted by G.
- For each let us define a binary variable which states whether some EB performs a trip j after i.
- For each trip let us define as the state of the battery of the EB when it has arrived at the origin of trip i but before performing it.
- For each let us define a binary variable which states whether the EB that performs trip i charges its battery after completing it.
5. GRASP Algorithm
5.1. Greedy Algorithm
| Algorithm 1 Greedy Algorithm |
Generate initial solution using Equation (22) |
whiledo |
Generate set of valid candidates for , |
Expand with candidate |
end while |
5.2. GRASP Extension
| Algorithm 2 Path Removal |
functionRelocatePath(, P) |
Set R to all trips in P |
while do |
Select random |
if |
end if |
end while |
return |
end function |
| Algorithm 3 Local Search |
functionLocalSearch() |
repeat |
while do |
Select random |
if then |
break |
end if |
end while |
until No Improvement |
end function |
5.3. Implementation
| Algorithm 4 GRASP algorithm |
while () do |
Generate solution using |
Check if is new best solution |
end while |
6. Results
6.1. Synthetic Data Experiments
6.2. Case Studies
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Batur, İ.; Bayram, I.S.; Koc, M. Impact assessment of supply-side and demand-side policies on energy consumption and CO2 emissions from urban passenger transportation: The case of Istanbul. J. Clean. Prod. 2019, 219, 391–410. [Google Scholar] [CrossRef] [Green Version]
- Meyer, D.; Wang, J. Integrating ultra-fast charging stations within the power grids of smart cities: A review. IET Smart Grid 2018, 1, 3–10. [Google Scholar] [CrossRef]
- Rahman, I.; Vasant, P.M.; Singh, B.S.M.; Abdullah-Al-Wadud, M.; Adnan, N. Review of recent trends in optimization techniques for plug-in hybrid, and electric vehicle charging infrastructures. Renew. Sustain. Energy Rev. 2016, 58, 1039–1047. [Google Scholar] [CrossRef]
- Jovanovic, R.; Bayhan, S.; Bayram, I.S. A multiobjective analysis of the potential of scheduling electrical vehicle charging for flattening the duck curve. J. Comput Sci. 2021, 48, 101262. [Google Scholar] [CrossRef]
- Song, Z.; Liu, Y.; Gao, H.; Li, S. The underlying reasons behind the development of public electric buses in China: The Beijing case. Sustainability 2020, 12, 688. [Google Scholar] [CrossRef] [Green Version]
- Malnaca, K.; Gorobetz, M.; Yatskiv (Jackiva), I.; Korneyev, A. Decision-making process for choosing technology of diesel bus conversion into electric bus. In Reliability and Statistics in Transportation and Communication; Kabashkin, I., Yatskiv (Jackiva), I., Prentkovskis, O., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 91–102. [Google Scholar]
- Topal, O.; Nakir, İ. Total cost of ownership based economic analysis of diesel, CNG and electric bus concepts for the public transport in Istanbul City. Energies 2018, 11, 2369. [Google Scholar] [CrossRef] [Green Version]
- Quarles, N.; Kockelman, K.M.; Mohamed, M. Costs and benefits of electrifying and automating bus transit fleets. Sustainability 2020, 12, 3977. [Google Scholar] [CrossRef]
- Feng, W.; Figliozzi, M. Vehicle technologies and bus fleet replacement optimization: Problem properties and sensitivity analysis utilizing real-world data. Public Transp. 2014, 6, 137–157. [Google Scholar] [CrossRef]
- Zahedmanesh, A.; Muttaqi, K.M.; Sutanto, D. A cooperative energy management in a virtual energy hub of an electric transportation system powered by PV generation and energy storage. IEEE Trans. Transp. Electrif. 2021, 7, 1123–1133. [Google Scholar] [CrossRef]
- Vuelvas, J.; Ruiz, F.; Gruosso, G. Energy price forecasting for optimal managing of electric vehicle fleet. IET Electr. Syst. Transp. 2020, 10, 401–408. [Google Scholar] [CrossRef]
- Gallo, J.B.; Bloch-Rubin, T.; Tomić, J. Peak Demand Charges and Electric Transit Buses; U.S. Department of Transportation Federal Transit Administration: Washington, DC, USA, 2014. [Google Scholar]
- Dreier, D.; Rudin, B.; Howells, M. Comparison of management strategies for the charging schedule and all-electric operation of a plug-in hybrid-electric bi-articulated bus fleet. Public Transp. 2020, 12, 363–404. [Google Scholar] [CrossRef]
- Foster, B.A.; Ryan, D.M. An integer programming approach to the vehicle scheduling problem. J. Oper. Res. Soc. 1976, 27, 367–384. [Google Scholar] [CrossRef]
- Desaulniers, G.; Hickman, M.D. Public transit. Handb. Oper. Res. Manag. Sci. 2007, 14, 69–127. [Google Scholar] [CrossRef]
- Wen, M.; Linde, E.; Ropke, S.; Mirchandani, P.; Larsen, A. An adaptive large neighborhood search heuristic for the electric vehicle scheduling problem. Comput. Oper. Res. 2016, 76, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Freling, R.; Paixão, J.M.P. Vehicle scheduling with time constraint. In Computer-Aided Transit Scheduling; Daduna, J.R., Branco, I., Paixão, J.M.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 130–144. [Google Scholar] [CrossRef]
- Haghani, A.; Banihashemi, M. Heuristic approaches for solving large-scale bus transit vehicle scheduling problem with route time constraints. Transp. Res. Part A Policy Pract. 2002, 36, 309–333. [Google Scholar] [CrossRef]
- Desaulniers, G.; Desrosiers, J.; Solomon, M.M.; Soumis, F.; Villeneuve, D. A unified framework for deterministic time constrained vehicle routing and crew scheduling problems. In Fleet Management and Logistics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 57–93. [Google Scholar]
- Perumal, S.S.; Dollevoet, T.; Huisman, D.; Lusby, R.M.; Larsen, J.; Riis, M. Solution approaches for integrated vehicle and crew scheduling with electric buses. Comput. Oper. Res. 2021, 132, 105268. [Google Scholar] [CrossRef]
- Iliopoulou, C.; Kepaptsoglou, K.; Vlahogianni, E. Metaheuristics for the transit route network design problem: A review and comparative analysis. Public Transp. 2019, 11, 487–521. [Google Scholar] [CrossRef]
- Durán-Micco, J.; Vansteenwegen, P. A survey on the transit network design and frequency setting problem. Public Transp. 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Z. Robust planning of dynamic wireless charging infrastructure for battery electric buses. Transp. Res. Part C Emerg. Technol. 2017, 83, 77–103. [Google Scholar] [CrossRef]
- Xylia, M.; Leduc, S.; Patrizio, P.; Kraxner, F.; Silveira, S. Locating charging infrastructure for electric buses in Stockholm. Transp. Res. Part C Emerg. Technol. 2017, 78, 183–200. [Google Scholar] [CrossRef]
- Wang, J.; Kang, L.; Liu, Y. Optimal scheduling for electric bus fleets based on dynamic programming approach by considering battery capacity fade. Renew. Sustain. Energy Rev. 2020, 130, 109978. [Google Scholar] [CrossRef]
- Ji, J.; Bie, Y.; Shen, B. Vehicle scheduling model for an electric bus line. In Smart Transportation Systems 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 29–39. [Google Scholar]
- Liu, T.; Ceder, A.A. Battery-electric transit vehicle scheduling with optimal number of stationary chargers. Transp. Res. Part C Emerg. Technol. 2020, 114, 118–139. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Wang, Y.; Avalos, R.; Liu, Z. Electric bus scheduling under single depot dynamic wireless charging infrastructure planning. Energy 2020, 213, 118855. [Google Scholar] [CrossRef]
- Tang, X.; Lin, X.; He, F. Robust scheduling strategies of electric buses under stochastic traffic conditions. Transp. Res. Part C Emerg. Technol. 2019, 105, 163–182. [Google Scholar] [CrossRef]
- Van Kooten Niekerk, M.E.; van den Akker, J.; Hoogeveen, J. Scheduling electric vehicles. Public Transp. 2017, 9, 155–176. [Google Scholar] [CrossRef]
- Janovec, M.; Koháni, M. Exact approach to the electric bus fleet scheduling. Transp. Res. Proc. 2019, 40, 1380–1387. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, D.; Zhao, X.; Lu, C. Collaborative optimization of vehicle and charging scheduling for a bus fleet mixed with electric and traditional buses. IEEE Access 2020, 8, 8056–8072. [Google Scholar] [CrossRef]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar] [CrossRef]
- Li, L.; Lo, H.K.; Xiao, F. Mixed bus fleet scheduling under range and refueling constraints. Transp. Res. Part C Emerg. Technol. 2019, 104, 443–462. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. Greedy randomized adaptive search procedures. J. Global Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef] [Green Version]
- Li, J.Q. Transit bus scheduling with limited energy. Transp. Sci. 2014, 48, 521–539. [Google Scholar] [CrossRef]
- Stakić, Đ.; Anokić, A.; Jovanovic, R. Comparison of different grasp algorithms for the heterogeneous vector bin packing problem. In Proceedings of the 2019 China-Qatar International Workshop on Artificial Intelligence and Applications to Intelligent Manufacturing (AIAIM), Doha, Qatar, 1–4 January 2019; pp. 63–70. [Google Scholar] [CrossRef]
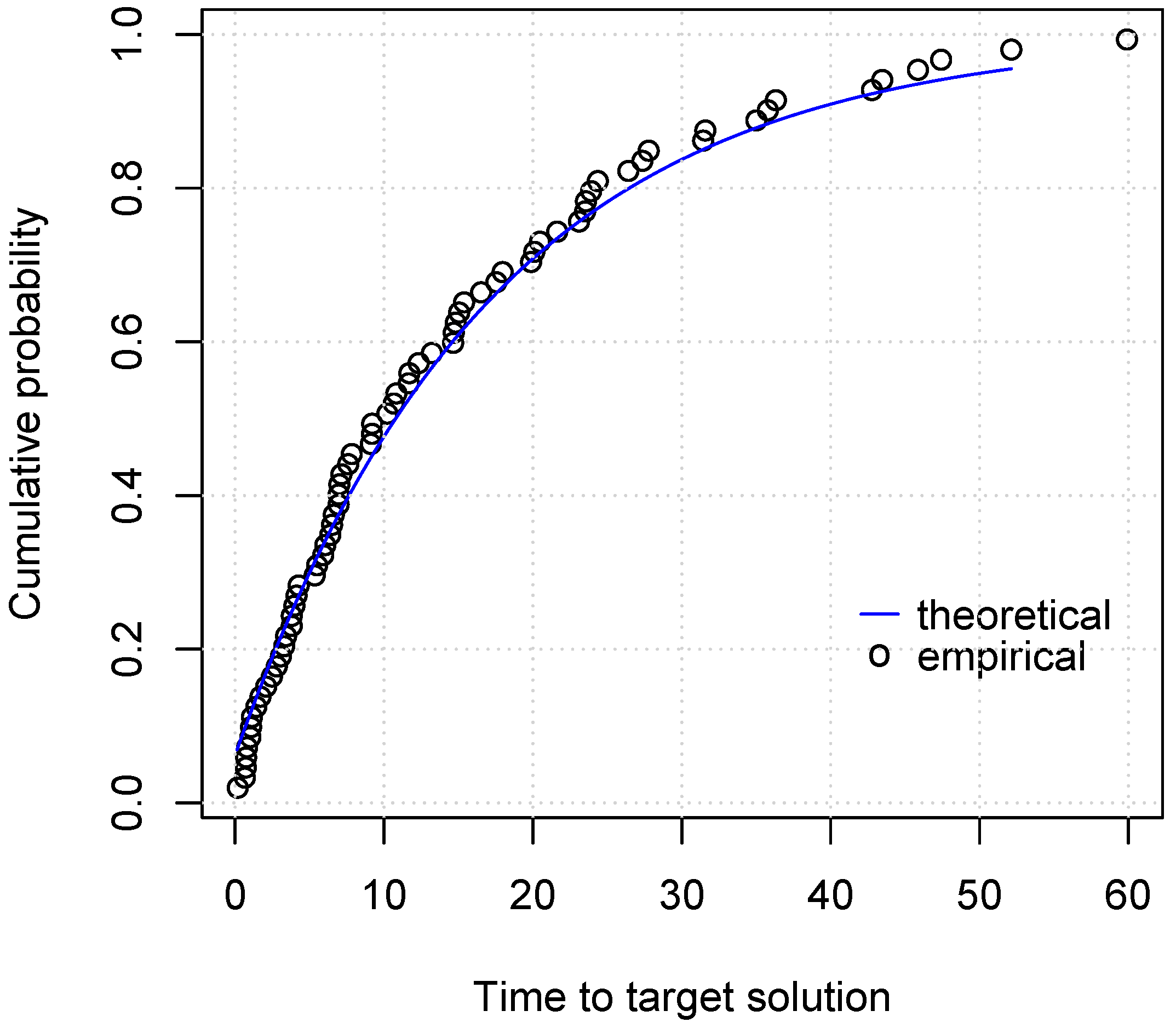
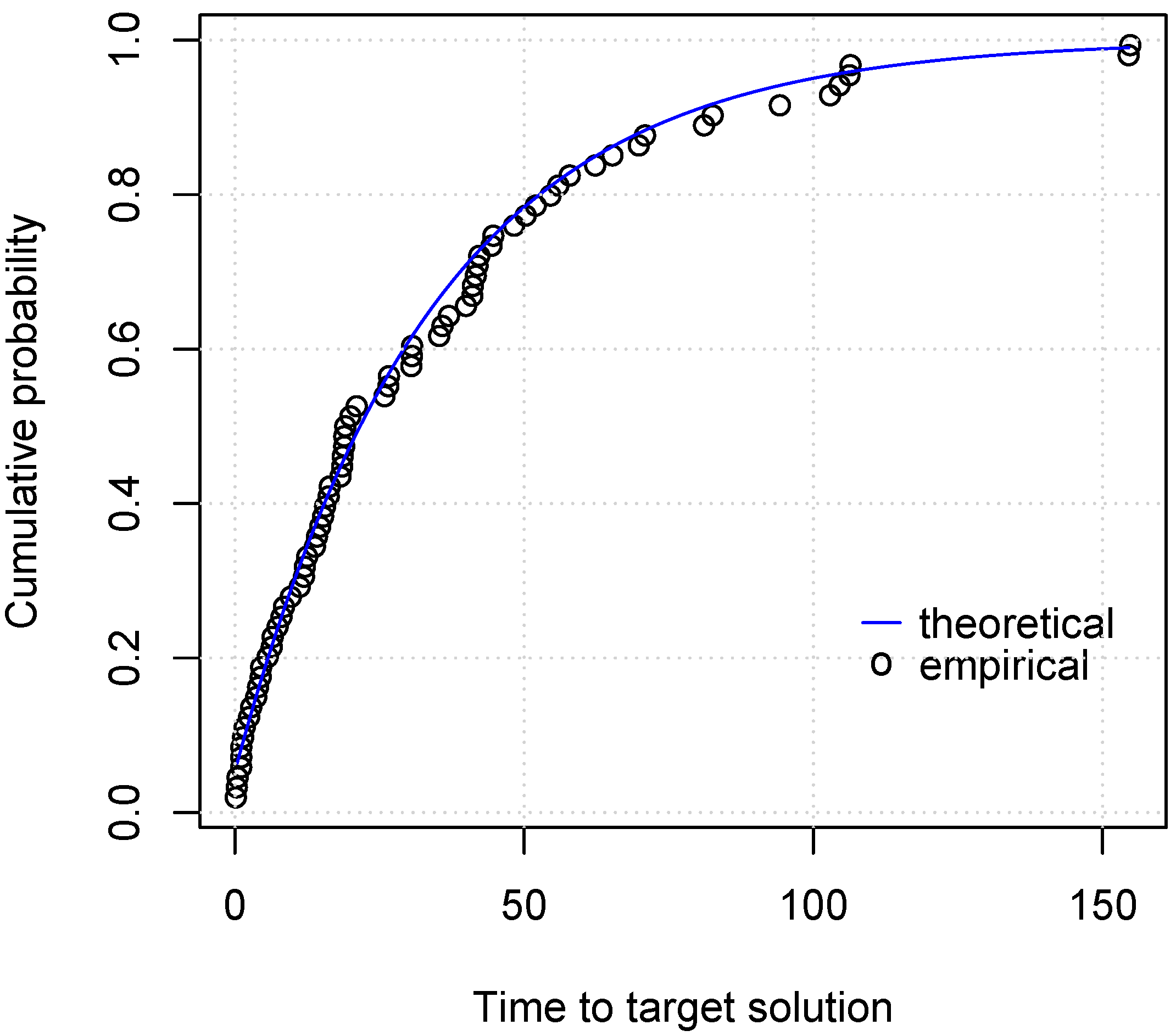
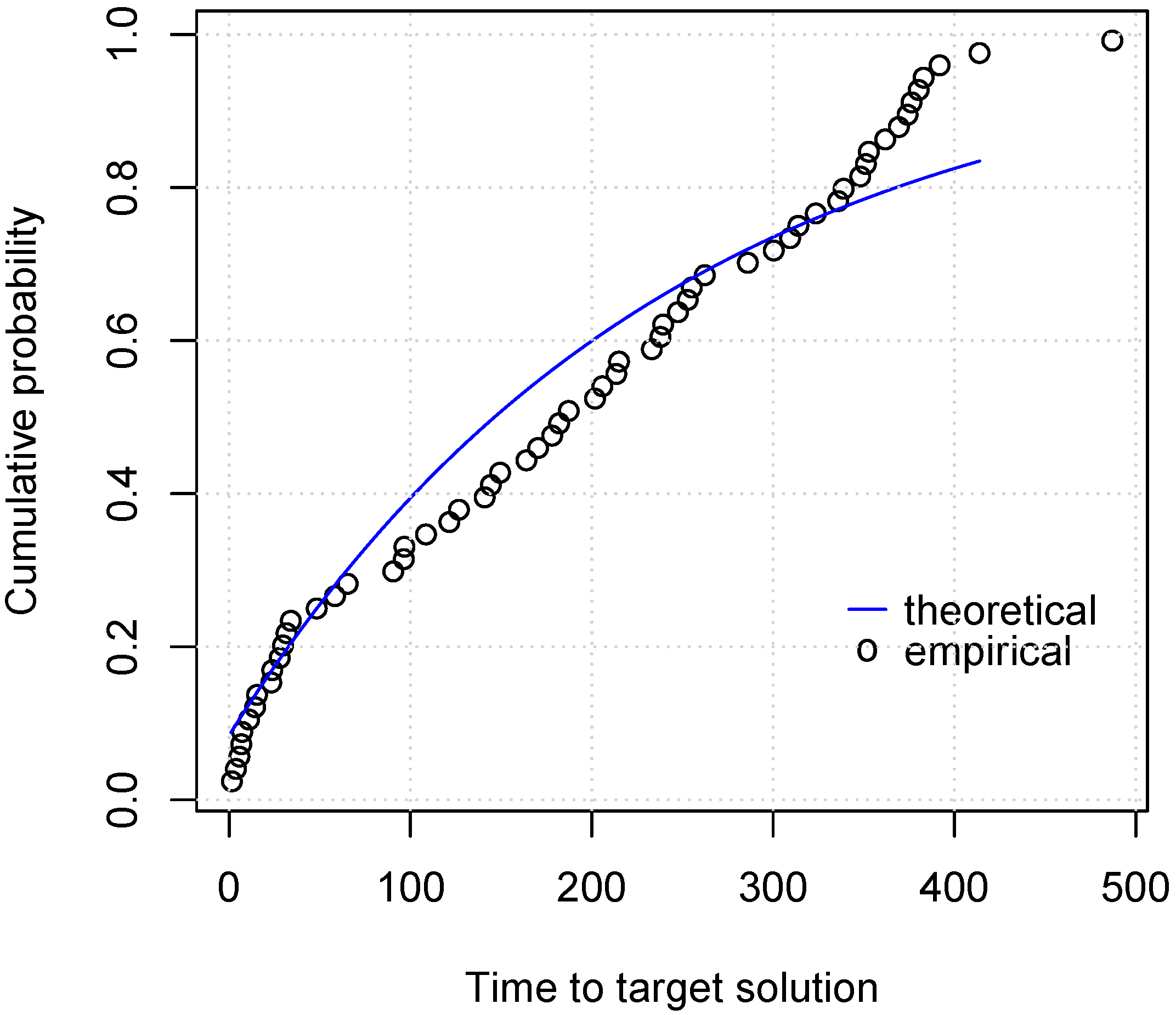
- Aiex, R.M.; Resende, M.G.; Ribeiro, C.C. TTT plots: A perl program to create time-to-target plots. Optim. Lett. 2007, 1, 355–366. [Google Scholar] [CrossRef]
- Reyes, A.; Ribeiro, C.C. Extending time-to-target plots to multiple instances. Int. Trans. Oper. Res. 2018, 25, 1515–1536. [Google Scholar] [CrossRef]
- Gao, Z.; Lin, Z.; LaClair, T.J.; Liu, C.; Li, J.M.; Birky, A.K.; Ward, J. Battery capacity and recharging needs for electric buses in city transit service. Energy 2017, 122, 588–600. [Google Scholar] [CrossRef] [Green Version]
- Conti, V.; Orchi, S.; Valentini, M.P.; Nigro, M.; Calò, R. Design and evaluation of electric solutions for public transport. Transp. Res. Procedia 2017, 27, 117–124. [Google Scholar] [CrossRef]
- Vepsäläinen, J.; Ritari, A.; Lajunen, A.; Kivekäs, K.; Tammi, K. Energy uncertainty analysis of electric buses. Energies 2018, 11, 3267. [Google Scholar] [CrossRef] [Green Version]
- Pamuła, T.; Pamuła, W. Estimation of the energy consumption of battery electric buses for public transport networks using real-world data and deep learning. Energies 2020, 13, 2340. [Google Scholar] [CrossRef]
- SustainableBus. Electric Bus Range, Focus on Electricity Consumption. A Sum-Up. 2021. Available online: https://www.sustainable-bus.com/news/electric-bus-range-focus-on-electricity-consumption-a-sum-up/ (accessed on 9 September 2021).
- Chao, Z.; Xiaohong, C. Optimizing battery electric bus transit vehicle scheduling with battery exchanging: Model and case study. Procedia-Soc. Behav. Sci. 2013, 96, 2725–2736. [Google Scholar] [CrossRef] [Green Version]
- Mahesh, S.; Ramadurai, G. Analysis of driving characteristics and estimation of pollutant emissions from intra-city buses. Transp. Res. Procedia 2017, 27, 1211–1218. [Google Scholar] [CrossRef]
- Ge, L.; Voß, S.; Xie, L. Robustness and Disturbances in Public Transport; Technical Report; Institute of Information Systems, Leuphana University of Lüneburg and Institute of Information Systems (IWI), University of Hamburg: Hamburg, Germany, 2020. [Google Scholar]
- Dekker, M.M.; van Lieshout, R.N.; Ball, R.C.; Bouman, P.C.; Dekker, S.C.; Dijkstra, H.A.; Goverde, R.M.P.; Huisman, D.; Panja, D.; Schaafsma, A.A.M.; et al. A next step in disruption management: Combining operations research and complexity science. Public Transp. 2021. [Google Scholar] [CrossRef]
- Vepsäläinen, J.; Kivekäs, K.; Otto, K.; Lajunen, A.; Tammi, K. Development and validation of energy demand uncertainty model for electric city buses. Transp. Res. D Transp. Environ. 2018, 63, 347–361. [Google Scholar] [CrossRef]
- Jovanovic, R.; Voss, S. The fixed set search applied to the power dominating set problem. Expert Syst. 2020, 37, e12559. [Google Scholar] [CrossRef]

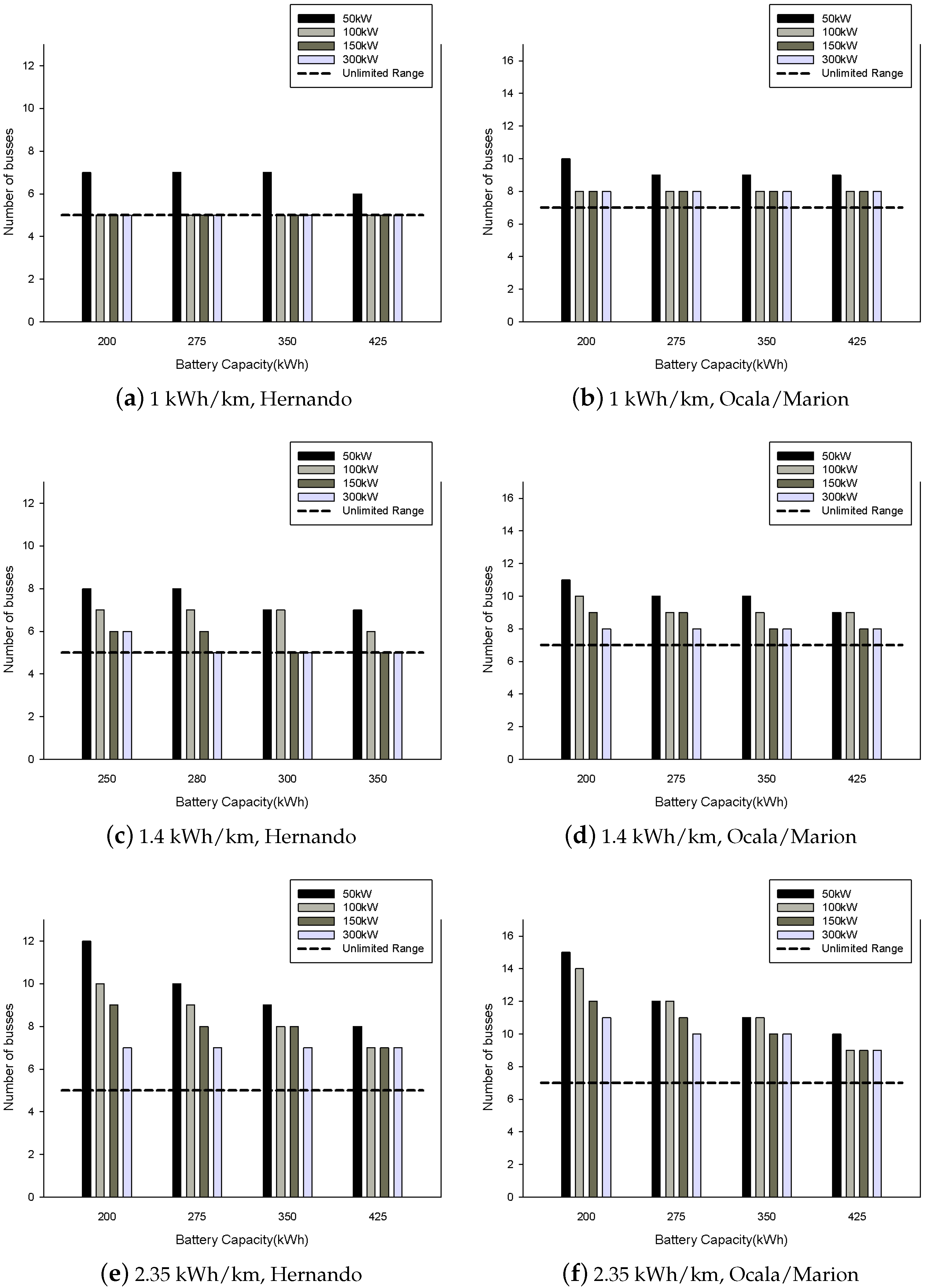
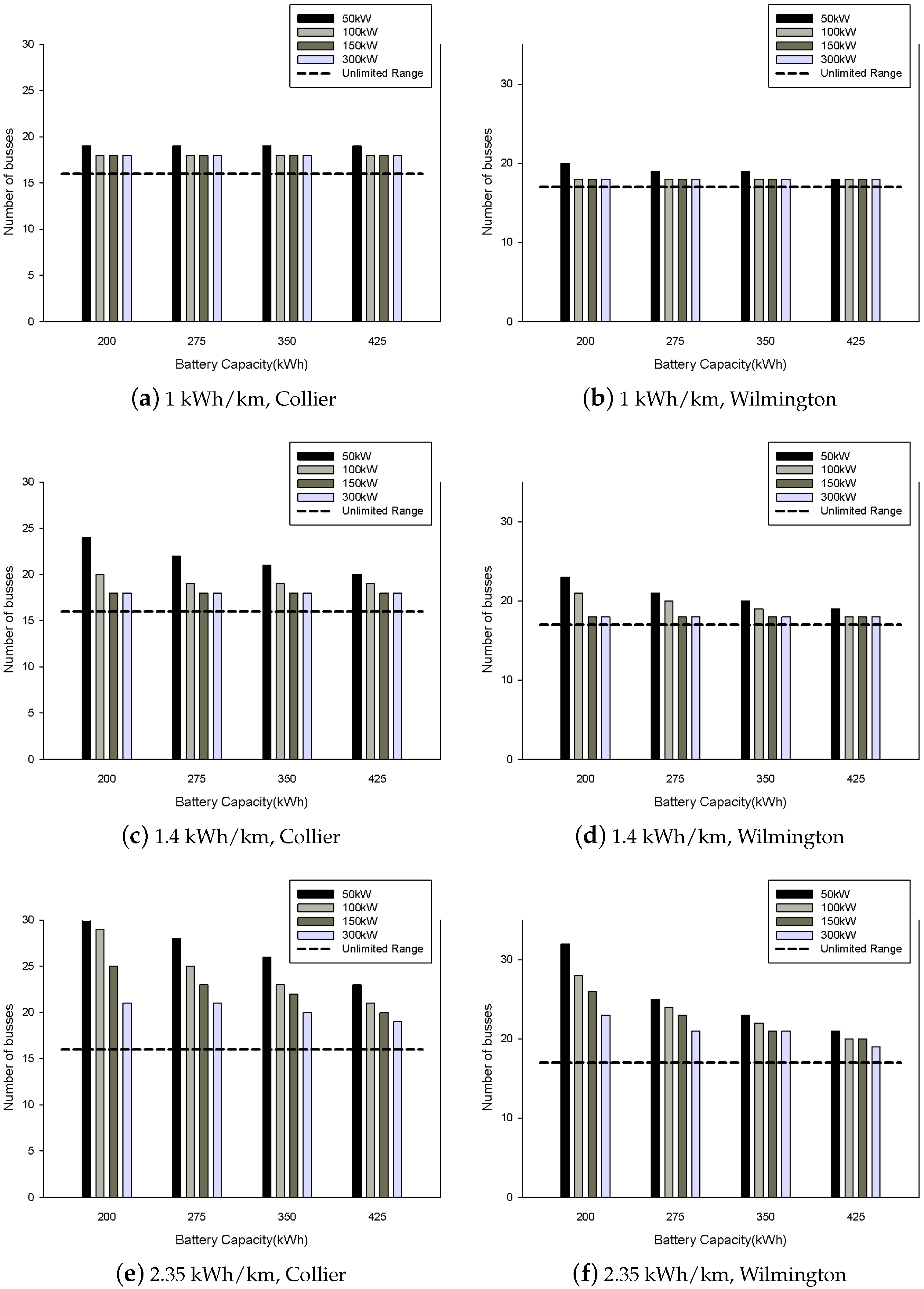
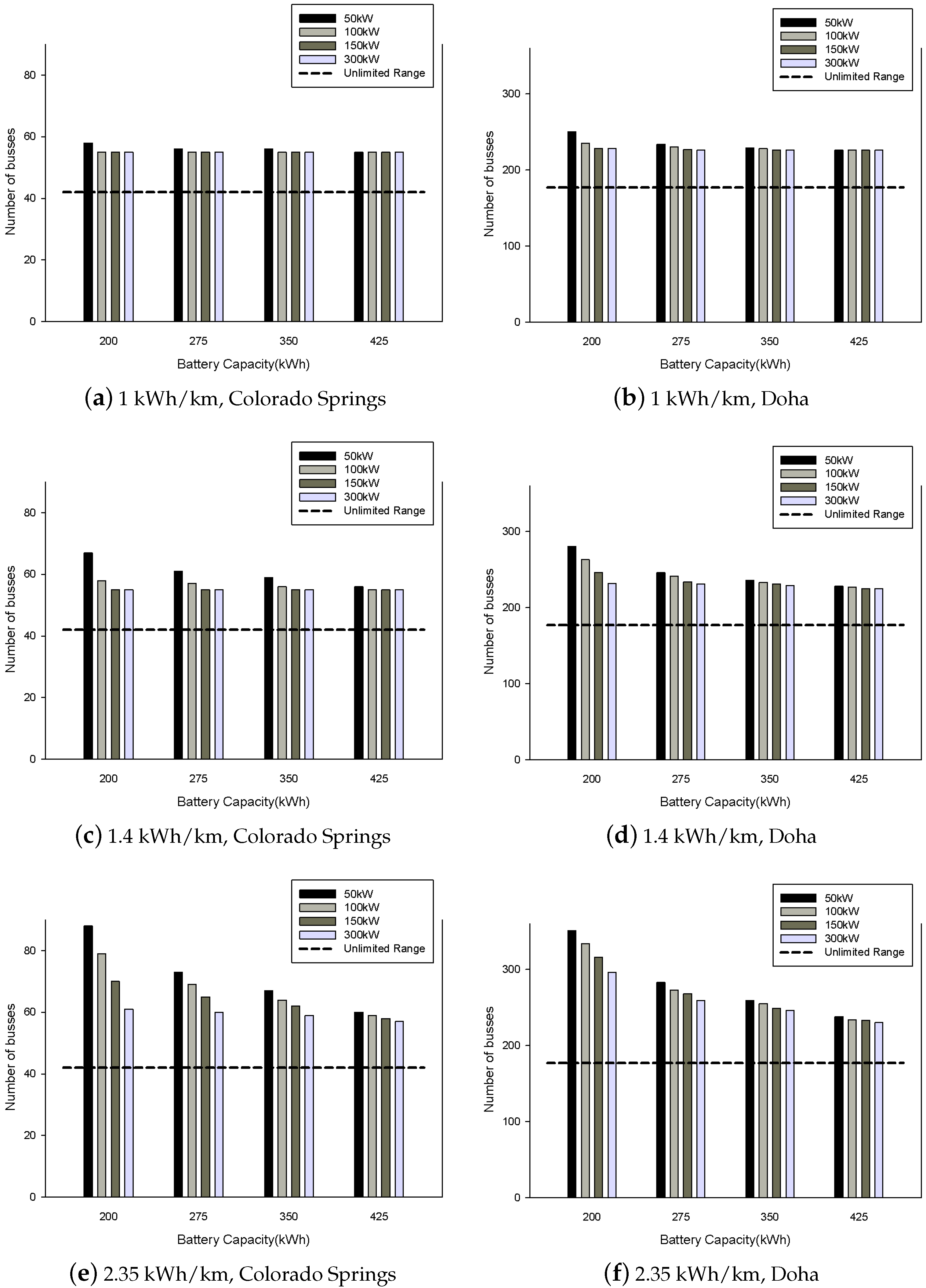
| Parameter | Min Value | Max Value |
|---|---|---|
| 50 | 50 | |
| T | 1400 | 1400 |
| s | 300 | 420 |
| d | 30 | 60 |
| 720 | 900 | |
| f | 60 | 120 |
| Number of Trips | Average Solution | Found Optima | Average Time [s] | ||||
|---|---|---|---|---|---|---|---|
| GRASP | MIP | LB | GRASP | MIP | GRASP | MIP | |
| 20 | 3.60 | 3.60 | 3.60 | 10 | 10 | 0.42 | 0.79 |
| 30 | 5.10 | 4.80 | 4.80 | 7 | 10 | 0.75 | 159.01 |
| 40 | 6.00 | 6.20 | 5.00 | 3 | 3 | 1.15 | 884.53 |
| 50 | 7.20 | 7.70 | 5.61 | 0 | 0 | 1.54 | 1203.15 |
| 100 | 14.10 | 17.30 | 10.05 | 0 | 0 | 5.47 | 1206.40 |
| 200 | 26.60 | 39.30 | 18.50 | 0 | 0 | 20.48 | 1214.17 |
| 400 | 55.20 | - | - | - | - | 84.73 | - |
| 600 | 78.80 | - | - | - | - | 187.95 | - |
| 800 | 103.40 | - | - | - | - | 348.85 | - |
| 1000 | 130.10 | - | - | - | - | 571.24 | - |
| 1500 | 194.10 | - | - | - | - | 1479.20 | - |
| 2000 | 255.80 | - | - | - | - | 2855.66 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jovanovic, R.; Bayram, I.S.; Bayhan, S.; Voß, S. A GRASP Approach for Solving Large-Scale Electric Bus Scheduling Problems. Energies 2021, 14, 6610. https://doi.org/10.3390/en14206610
Jovanovic R, Bayram IS, Bayhan S, Voß S. A GRASP Approach for Solving Large-Scale Electric Bus Scheduling Problems. Energies. 2021; 14(20):6610. https://doi.org/10.3390/en14206610
Chicago/Turabian StyleJovanovic, Raka, Islam Safak Bayram, Sertac Bayhan, and Stefan Voß. 2021. "A GRASP Approach for Solving Large-Scale Electric Bus Scheduling Problems" Energies 14, no. 20: 6610. https://doi.org/10.3390/en14206610
APA StyleJovanovic, R., Bayram, I. S., Bayhan, S., & Voß, S. (2021). A GRASP Approach for Solving Large-Scale Electric Bus Scheduling Problems. Energies, 14(20), 6610. https://doi.org/10.3390/en14206610








