Next Article in Journal
Heating Performance and Ammonia Removal of a Single-Stage Bioscrubber Pilot Plant with Integrated Heat Exchanger under Field Conditions
Next Article in Special Issue
Effective Thermal Conductivity and Borehole Thermal Resistance in Selected Borehole Heat Exchangers for the Same Geology
Previous Article in Journal
Analysis of the Suitability of Signal Features for Individual Sensor Types in the Diagnosis of Gradual Tool Wear in Turning
Previous Article in Special Issue
A Review of the Performance of Minewater Heating and Cooling Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 14
Issue 20
10.3390/en14206483
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Heat Transfer and Bearing Characteristics of Energy Piles: Review

by
Jinli Xie
1 and
Yinghong Qin
1,2,*
1
College of Civil Engineering and Architecture, Guangxi University, 100 University Road, Nanning 530004, China
2
School of Civil Engineering and Architecture, Guangxi University for Nationalities, 188 University Road, Nanning 530006, China
*
Author to whom correspondence should be addressed.
Energies 2021, 14(20), 6483; https://doi.org/10.3390/en14206483
Submission received: 9 September 2021 / Revised: 25 September 2021 / Accepted: 30 September 2021 / Published: 10 October 2021
(This article belongs to the Special Issue Shallow Geothermal Energy 2021)
Browse Figures
Versions Notes

Abstract

:
Energy piles, combined ground source heat pumps (GSHP) with the traditional pile foundation, have the advantages of high heat transfer efficiency, less space occupation and low cost. This paper summarizes the latest research on the heat transfer and bearing capacity of energy piles. It is found that S-shaped tubes have the largest heat transfer area and the best heat transfer efficiency; that energy piles need to be designed conservatively, such as adjusting the safety coefficient, number and spacing of the piles according to the additional temperature loads; and that unbalanced surface temperature has not been resolved, caused by uneven refrigeration/heating demand in one cycle. A composite energy pile applied to water-rich areas is proposed to overcome the decay of bearing and heat transfer performance. Besides, most of the heat transfer models are borehole-oriented and will fit for energy piles effectively if the models support variable ground temperature boundary conditions.

1. Introduction

Traditional fossil fuels such as coal, oil, and natural gas account for most of the energy share. However, these fuels produce large amounts of harmful gases, causing serious environmental pollution. Research on clean energy technologies has received extensive attention to solve this serious problem, and shallow geothermal energy has been advocated as a kind of typical clean energy because of its characteristics of large reserves, wide distribution, and non-polluting. Ground source heat pumps (GSHP) are the main way to utilize shallow geothermal energy and have been widely used in many countries such as South Korea [1], Japan [2], and others [3]. Vertical and horizontal layouts are the two forms of GSHP, in which the horizontal layout requires a large construction area but the vertical one is costly due to borehole drilling. Considering these two shortcomings, energy piles that embed the geothermal heat exchanger in the pile foundation of the building structure offer a new idea for the promotion of GSHP and simultaneously meet the load-bearing and heat exchange requirements. Energy piles are gradually being used in tunnels [4], bridges [5], and other fields [6,7]. As shown in Figure 1, GSHP consists of a main circuit buried in the piles and a secondary circuit in the upper building, both of which are connected by a heat pump to transfer shallow heat energy to upper buildings [8].
Many studies involved in the introduction and analysis of heat transfer for GSHP have been documented. Noorollahi reviewed the previous research and investigations on different ground heat exchanger parameters and their effects [9]. Abuel-Naga investigated the knowledge on the design of energy piles in terms of the geo-structural and heat exchanger functions by [10]. In another study, Fadejev reviewed of available scientific literature, design standards, and guidelines on energy piles [11]. Then, Mohamad explained the knowledge about the thermal and thermo-mechanical behaviors of energy piles [12]. Their works, however, do not address the operational mechanism and optimization of energy piles under thermal-mechanical interactions. The research on energy piles has mainly focused on the heat transfer and bearing characteristics. Heat transfer accompanies heat conduction and heat convection, varying the temperature of the piles and of their surrounding soils. Correspondingly, temperature stresses develop and thus affect the bearing capacity of energy piles. This study systematically summarizes the influencing factors involved in the heat transfer process of energy piles, further presents the heat transfer models adapted to simulate the pile’s performance; then analyzes the structure’s response under temperature loads and proposes a kind of composite energy pile with potential application. The limitations of current research and future research are finally highlighted.

2. Factors Influencing Heat Transfer Performance

2.1. Heat Transfer between Fluid and Tubes

Heat exchange rate Q H = C m ˙ Δ T , W, and relative heat exchange rate Q R = Q H / L , W/m, are usually used to evaluate the heat transfer performance. Heat exchange rate Q H represents the amount of heat transfer between energy piles and soil around the piles over a limited time. The relative heat exchange rate Q R represents the amount of heat transfer per length of tubes and is an index to evaluate the efficiency of heat transfer.
The principle for designing a tube shape is to maximize the area of heat transfer. As shown in Figure 2, the tube shapes include U-shaped, 2U-shaped, 3U-shaped, W-shaped, and S-shaped (spiral-shaped). Their heat performances are illustrated in Table 1. The S-shaped tube has the best heat transfer efficiency because it has the largest heat transfer area [13], shown in Table 1. Furthermore, the selection of tube shapes needs to consider the heat exchange rate, cost, and other factors such as the number of piles, the length of the drilling holes, and the difficulty of construction.
For S-shaped tubes, spiral pitches, are proportional to the heat exchange area. By conducting a thermal performance test using tubes with a pitch of 200 mm and 500 mm, it was found that the heat exchange rate increased with the decrease of the pitch [22]. Figure 3 shows the variation of Q H and Q R under different pitches. The heat flow between the tubes interacts in the case of small pitches, reducing the relative heat exchange rate [23,24]. To subside the interaction, some scholars proposed to add an insulation layer around the fluid outlet [25]. The length of the insulation layer is different for variable operation modes.
Temperature (determined by atmospheric temperature) and velocity of inlet fluid are positively related to the efficiency of heat transfer. The inlet temperature directly affects the temperature difference between the inlet and outlet liquid. According to existing studies [17,18], the heat exchange rate Q H approximately increases linearly with the inlet temperature within a certain temperature range. In addition, high-speed fluid maintains turbulent state, improving the heat exchange rate effectively [26].
The improper arrangement of heat transfer tubes and pile spacing induces thermal interference phenomenon. Furthermore, the quantitative research on their influence of heat transfer efficiency still needs to be explored. The production factors, such as the cost, structural safety, and others, should be considered during design.
The durability of heat exchanger tube material is a subject of concern. The tubes may be damaged by the corrosion of the circulating medium during the cyclic heat transfer. The heat transfer efficiency, load capacity, and durability of energy piles are reduced by damaged tubes. To solve this problem, the maintenance and replacement technology of the tubes must be developed.

2.2. Effects of Materials and Geometry on Heat Transfer

Geometric properties significantly affect the heat transfer performance of energy piles, such as thermal conductivity of concrete, pile length, pile diameter, and others. The heat transfer performance of concrete is evaluated by the thermal conductivity. Studies have shown that the heat exchange rate increases by 42% when the thermal conductivity increases from 1.2 to 2.5 W/(m K) [27]. The thermal conductivity of concrete can be increased by adding admixtures such as steel fiber and graphite. Increasing the pile’s length and diameter can also enlarge the heat transfer area, improving the heat transfer rate [26,27]. Factors including the heat transfer, bearing characteristics, and cost of a pile must be therefore considered in the design.

2.3. Heat Transfer Performance of Soils

2.3.1. Water Content

The pore structure of the soil around the energy piles changes after it is filled by water, varying heat conduction and transfer performance accordingly. Generally, increasing the water content can enlarge the heat storage and heat transfer capacity [28]. When the water content is low, the surface of soil particles is covered with a water film, having little effect on the thermal conductivity [29]; as the water content increases, a “water bridge” forms between soil particles. The thermal conductivity of water is much larger than that of air, resulting in a significant increase in the thermal conductivity of soil [28,30].

2.3.2. Mineral Composition and Dry Density

The thermal conductivity of soil particles can be analyzed through composition and dry density [31]. For different soil minerals, the thermal conductivity is significantly different. The thermal conductivity of quartz is about 7~9 W/(m K), while the thermal conductivity of mica, kaolinite, and feldspar is about 2~3 W/(m K). To quantify the thermal conductivity of soil composed of various mineral components, past studies suggested that the minerals can be divided into quartz and others, then the thermal conductivity of mixed soils can be determined by the quartz content (20% volume fraction as the limit) [32]. However, the calculated thermal conductivity of the same mineral may be different because the impure texture, dry density, and measurement methods are different.
Gases exist in the pores mainly in a free state, while a small part of gases are adsorbed/dissolved on the surface of soil particles. Factors such as shape, structure, and arrangement of soil particles determine the porosity, size, and distribution of soil pores, affecting the thermal conductivity [33,34]. As shown in Figure 4, there is a positive correlation between dry density and thermal conductivity of the soils because the contact area of soil particles increases with the increase of dry density, and the thermal conductivity of mixed soils is closer to the particles [35,36]. The microstructure of soils will also have an influence on the thermal conductivity, and perfect grading has greater thermal conductivity [33,37]. Additionally, previous works showed that the disturbance of the soils have little influence on the thermal conductivity, therefore field tests can be used instead of indoor ones [38].

2.4. Long-Term Service

Within about 10 m under the ground surface, the temperature periodically fluctuates daily and seasonally. Below 10 m depth, the temperature remains relatively constant, which is conducive to continuous heat exchange [39]. In summer, the average temperature of the shallow ground surface is lower than the air temperature and thus the surface buildings can be cooled down. In contrast, the ground temperature in winter is higher than the air temperature, and heat stored underground in summer can be harvested for building heating. However, cooling/heating demand varies seasonally. The heat around energy piles can be correspondingly accumulated or dissipated, leading to the imbalance of soil temperature and further affecting the subsequent periodic thermal cycle [40]. Such an imbalance can be alleviated by integrating solar collectors/cooling equipment to GSHP to compensate for the ground temperature [41] but the costs and long-term performance of this integral have yet to be proven.
Energy piles are mainly adapted in lower buildings and are mostly designed for 5~30 m in length. Heat transfer is concentrated in a certain depth, so the heat transfer range is limited. In most of cold regions, such as Europe and North America, GHSP is successfully used because the temperature where the energy piles are located differs greatly from the atmospheric temperature. The cost of energy piles in warm zones needs to be studied further.
Duration of long-term heat transfer is an urgent issue for energy piles. Seasonal load (unbalanced ground temperature) is the main factor affecting the long-term heat transfer performance of energy piles. In areas where groundwater is rich, the groundwater flow can significantly alleviate the unbalanced ground temperature, while in groundwater-free areas, heat compensation to the soil layer is required but effective forms of the compensation have yet to be designed and improved.

3. Numerical Simulations of GSHP Heat Transfer

In the linear heat source model, the heat transfer process is simplified to a linear and radiating heat flow, and the following assumptions are made [42]: (1) Initial geotechnical temperature is uniform; (2) heat flow is considered to transfer radially and to be constant; (3) geotechnical material is homogeneous and isotropic. The linear heat source model can be categorized into an infinite line heat source model and a finite line heat source model [43]. The solution of an infinite line heat source model is not accurate under long-term conditions, so a finite line heat source model was proposed. The detailed mathematical expressions of each model based on various shapes can be found in Appendix A.
Hollow and solid shapes are two types of cylindrical heat sources [44,45]. The solid cylindrical heat source model is used in S-shaped piles with large diameter and shallow drilling depth. Based on the classical heat source method, Man [44] proposed 1-D and 2-D heat sources for solid cylinders to consider the effect of the geometry of piles. The 1-D method does not consider the heat transfer in the axial direction. For the 2-D method, the finite heat source and surface boundary temperature are considered.
Groundwater is beneficial to enhance the heat transfer efficiency of the energy piles. Water under the groundwater table moves between the particles of the soil layers, creating horizontal flow that alleviates the heat accumulation. Traditional numerical methods based on steady-state are not appropriate to evaluate the transient process with groundwater. While some models for energy piles combined groundwater have been reported, the accurate evaluation of the heat transfer conditions remains unsolved [46,47,48,49,50,51,52,53].
Compared to vertical GSHP, in the line heat source model and cylindrical heat source model, the characteristics of the energy piles are as follows: (1) The buried depth is small, so the ground temperature boundary cannot be ignored; (2) heat transfer of concrete is significant because of the large pile diameter; (3) for a large range of heat transfer, the thermal properties of soils are time dependent. To simplify analysis, these differences are often ignored. The applicable conditions of the above three models are noted in Table 2; it is known that they do not have high adaptability as many parameters are inconsistent in complex environments. In order to get accurate results in a simple way, the models need to be selected regarding the specific application included for the geometric characteristics of the energy piles and the difference in thermal properties of concrete and soil. In the water-rich rock layer, due to groundwater flow thermal convection can mitigate heat accumulation induced by energy piles. However, such a situation is still too complicated to be simulated because of the complex transient coupling for groundwater. Another challenge is that accurate hydrogeological information cannot be obtained due to the high cost and operational difficulties.

4. Response under Thermo-Mechanical Coupling

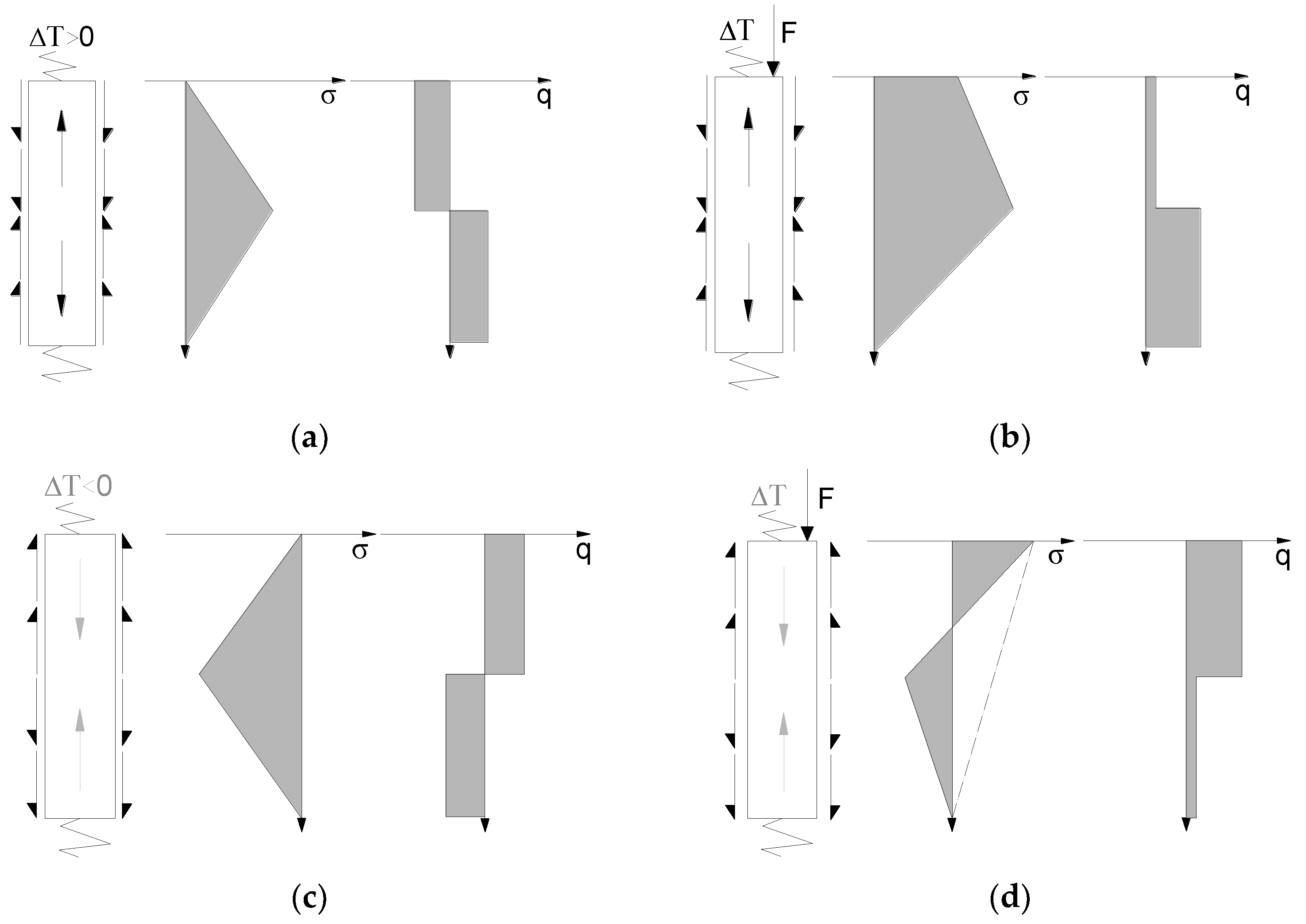
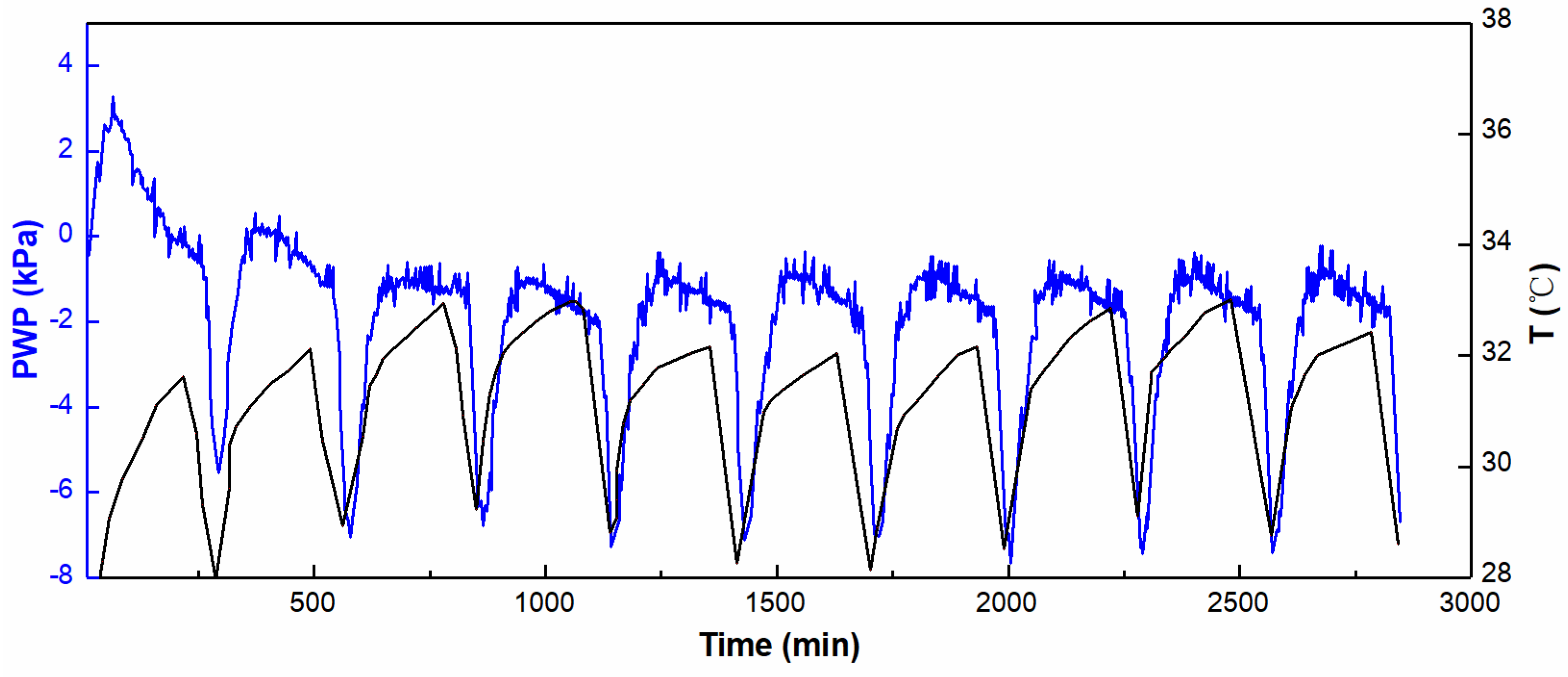
4.1. Pile-Soil Interaction Mechanism

Different from conventional pile foundations, energy piles bear additional temperature loads induced by the continuous heat exchange. The heat transfer changes the temperature distribution, leading to the expansion/contraction of energy piles. Due to the geotechnical constraints, the piles are not free to deform, leading to additional temperature stresses on the piles. Energy piles are commonly frictional piles that are subject to lateral frictional resistance and tip resistance balanced with external forces. To simplify the model, an energy pile is usually assumed to be a rod that deforms thermally [54]. As shown in Figure 5, energy piles are subjected to thermal and mechanical stresses simultaneously. The pile stress is closely related to the temperature. For column piles, the stresses and displacements under temperature loading exhibit thermos-elasticity, indicating that temperature has little effect on mechanical properties [55,56,57].
Existing works show that in case of the small mechanical load, the pile axial stress gradually decreases to zero as the lateral frictional resistance accumulates. The stresses below the zero point are mainly influenced by temperature [57,58,59]. Loading tests found that in the lower and middle parts of the pile, the effect of temperature on the axial force is more significant than the mechanical load [58]. The possibility of tensile stresses the lower and middle parts of the pile during cooling, even under mechanical loads [57].
The main factors affecting the stress and displacement of energy piles include the pile tip restraint and the shape of pipes. As the pile tip restraint increases, the zero point moves downwards [60]. Different tube shapes are subjected to different thermal stresses. The studies show that under the same power of the pump, for different types of heat exchangers the strain and settlement of pile top of the W-shaped and S-shaped piles are more significant than that of the single U-shaped pile [59].Considering the influence of soil, the main factors affecting the bearing capacity of piles include thermal hardening, thermally induced water flow, excess pore water pressure, and volume changes after thermal consolidation [61,62,63,64,65,66,67,68]. For normally consolidated soils, plastic hardening under heating is offset by softening under isostatic drainage conditions. Plastic hardening results in soil compression because compression is much larger than the thermos-elastic expansion of the skeleton (Figure 6). Additionally, the shear strength of the soil increases as the contact between particles becomes tighter after thermal consolidation [67]. For the over-consolidated soils, plastic compression deformation is large enough to offset thermal expansion (Figure 6). The excess pore water pressure caused by temperature rise cannot be dissipated, leading to the decrease of shear strength [69,70].
The thermal properties of the soils around energy piles are changed during the heat transfer process [71,72,73]. By conducting model tests on saturated, normally consolidated clay, Yazdani studied the pore water pressure (PWP) and ultimate bearing capacity of an energy pile under cyclic temperature [74]. The temperature and PWP changed periodically, and the periods were basically the same (Figure 7). The change of pore water pressure is mainly determined by the rate of heating and cooling, permeability, and compressibility of clay [75]. Except for the initial stage, the PWP is basically at a negative value because under the action of the temperature gradient, directional migration of water generates the suction between the soil particles and the pore water. The suction reduces average pore pressure to increase soil skeleton stress and binds the particle surface.
For unconsolidated sand, temperature-induced volumetric expansion/contraction is slight [76]. However, a warning is needed about the stress redistribution induced by thermal expansion/contraction of the energy piles and the differential deformation of the pile-soil interface. Test results showed that the fluctuation of the bearing capacity was small. After one cycle of heating and cooling, the displacement of the pile tip largely recovered, showing thermos-elastic properties [77,78,79]. The bearing capacity of energy piles mainly depends on the amount of settlement when the piles are undamaged. The results of centrifugal tests, as shown in Figure 8, show that the higher the temperature, the smaller the settlement [80]. By monitoring the long-term operating condition of the energy piles, a slight irreversible residual strain was observed under the combined effect of mechanical and temperature loads. Pile-soil calculation methods considering the temperature was subsequently proposed. Additionally, the W-shaped buried tube settlement was 1.8 times that of the single U-shape and 1.6 times that of the S-shaped during heating. During cooling, the displacement of the W-shaped buried tube was mostly significant, which was 1.7 times that of the single U-shaped [59].
The thermal response of clay affects the bearing capacity of pile foundations. Temperature variation can cause periodic expansion/contraction deformation of the energy piles, which changes the pile-soil contact state. The temperature load applied to the soil around the piles can be approximated as a cyclic shear load, which may gradually decay the pile-soil contact stress. The expansion/contraction of clay caused by temperature load can induce the rigid displacement of the energy piles. The directional migration of pore water is the main cause of the expansion/contraction of the clay. As the temperature increases, the clay causes elastic and plastic deformation, while only elastic deformation occurs during cooling. The microstructure of the clay changes. During the early temperature cycle, the expansion/contraction characteristics of clay are sensitive due to the weakened connection between soil particles. After reaching a certain equilibrium state, the expansion/contraction characteristics of the clay tend to stabilize but the expansion/contraction process is not fully reversible for the plastic deformation. Similar to the heat transfer simulations, the errors may be unacceptable in simulating the stress and strain of pile foundations under thermal-mechanical loading. The thermal-stress coupled effect on the pile-soil interface is a long-term and complex process, and thus it is a wise strategy to design energy piles using a conservative approach. There is currently no report of energy pile damage in completed projects. Existing reports showed that compared to conventional piles, the ultimate bearing capacities of energy piles are reduced by 15% [79]. The loss of load-bearing capacity by heat exchange is acceptable and can be solved by improving the safety coefficient.

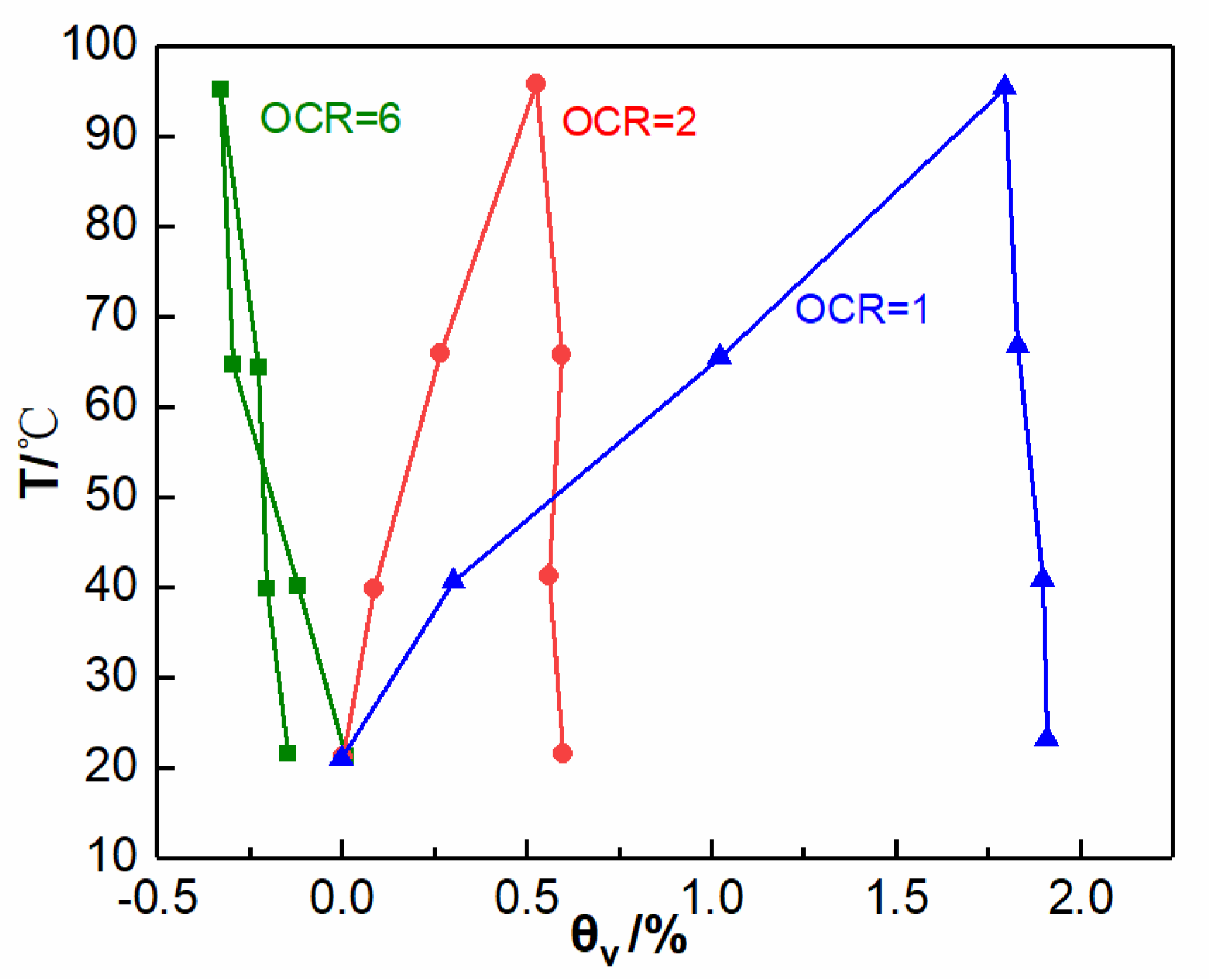
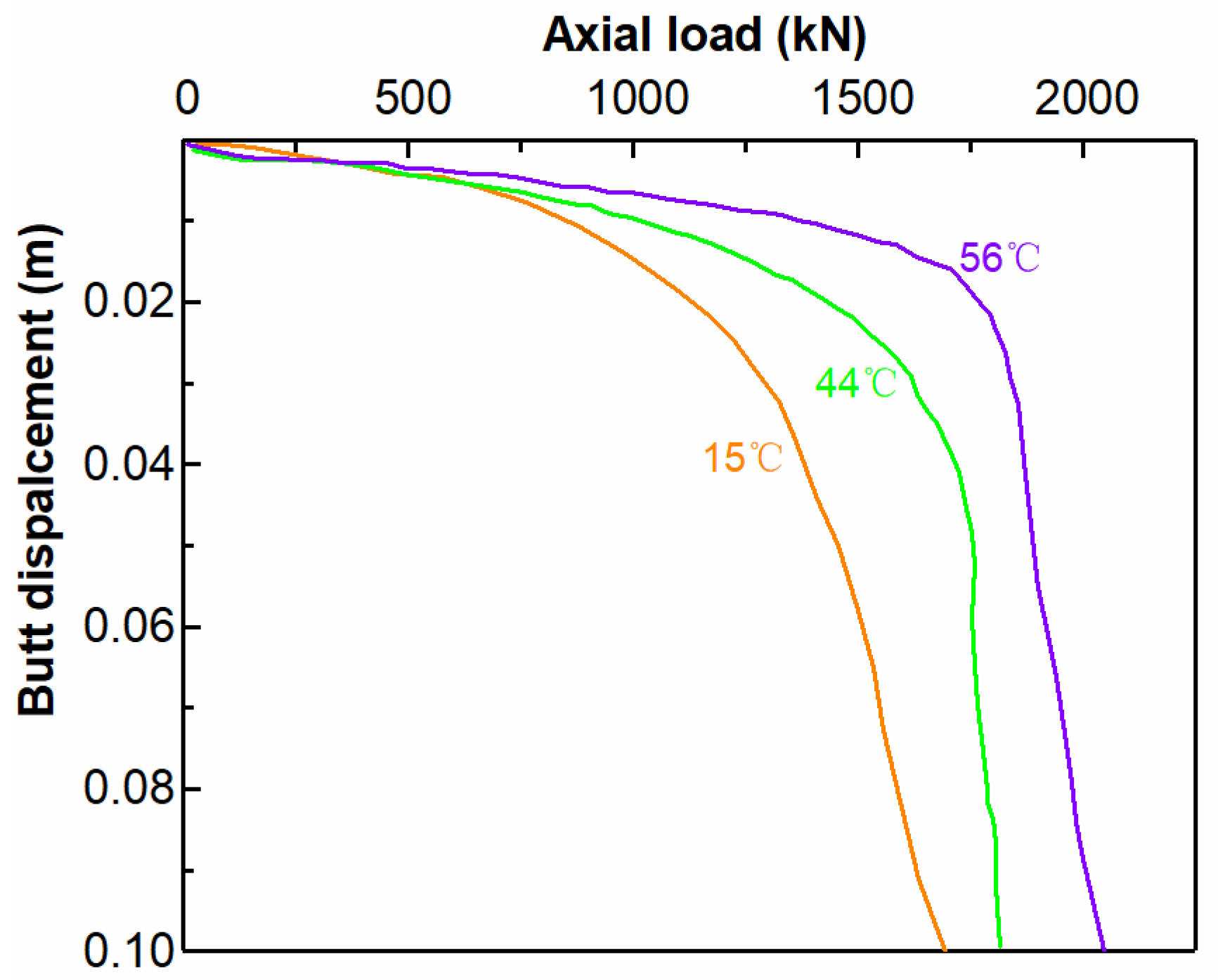
4.2. Bearing Characteristics of Energy Pile Groups

For energy pile groups, internal force redistribution caused by temperature change cannot be ignored [81]. The lateral friction and tip resistance of piles degrade with the accumulation of additional settlement induced by temperature change, resulting in the increase of force or even failure of non-exchange piles [82,83]. Uncoordinated deformation between energy piles and non-exchange piles is the cause of stress redistribution [84]. At the early stage of heat exchange, the difference in stress is the greatest, and then gradually decreases to reach a steady state [82,84]. The main strategy to prevent the negative effect of group piles is to optimize the layout of energy piles and non-exchange piles [85,86,87]. Energy piles showed smaller irreversible pile head displacement in the presence of the adjacent pile than in its absence. Pile cap also restrained the movement of the energy pile [88]. Although group piles are always selected in civil construction for the design of foundations, group piles are rarely studied because of the difficulty in testing and determining the number of pile groups [89].

4.3. Simulations

The finite element method is a good supplement to the experiment. By conducting a thermal-hydraulic-mechanical finite element coupling analysis, Loria [90] proposed the concept of zero temperature displacement, which is also the critical point of additional thermal stress and is consistent with the conclusion by Bourne-Webb [54]. Past studies [91,92,93] simulated the mechanical behavior of the pile-soil interface based on the elastic-plastic principle. The results indicated that the influence degree of the thermal loads on the axial stress and strain is related to the number of energy piles and the relative thermal expansion coefficient of the piles and soils.

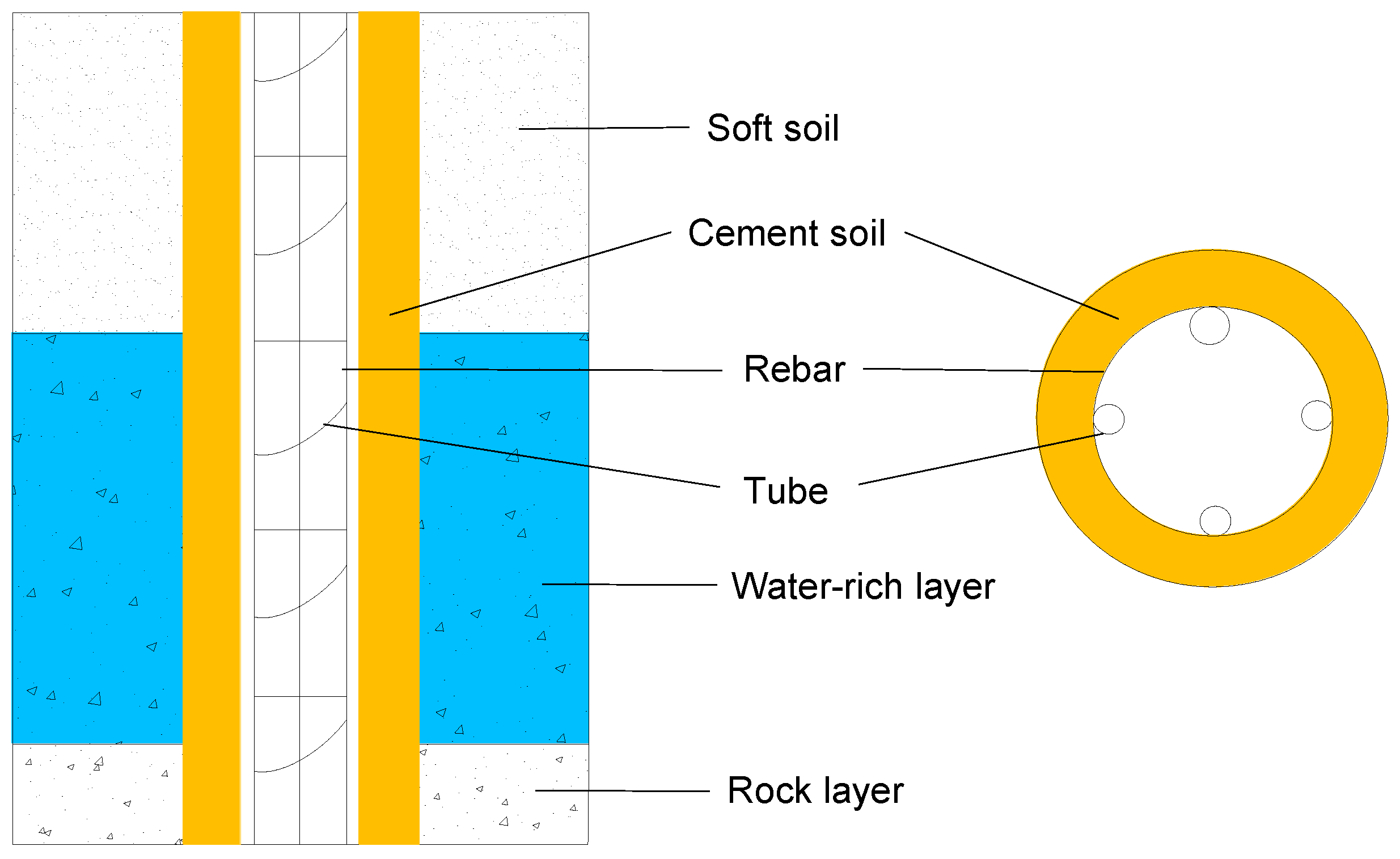
5. Applicability of Composite Energy Piles in Water-Rich Areas

Energy piles have broad prospects in coastal zones with deep soft soil and shallow groundwater. The soft soils are able to be penetrated by groundwater. Piles with large lengths are the main way to solve local geological problems. Energy piles penetrating the groundwater layer have a high heat transfer rate because of the scouring process, but it is uneconomical to use a large amount of concrete to construct reinforced concrete piles in soft ground. Here, a new composite energy pile is proposed, consisting of cement and reinforced concrete piles (Figure 9).
As illustrated in Figure 9, a reinforced concrete core pile encased in cement soil extends to the water-rich layer. With the mixing and rotary spraying equipment, prefabricated cement slurry is injected to first form cement soil. The prefabricated energy piles of reinforced concrete are then placed into the hole and filled with cement paste by lifting equipment. The foundation formed by cement soil and core energy piles will synergistically cause deformation [94].
The advantages of this composite energy pile are significant in terms of load carrying and heat transfer capacity. Soils around energy piles is compacted during the formation of cement soil, and such behavior can enhance the lateral friction resistance of the pile-soil interface [95]. After hydration of cement, cement soil becomes a kind of dense and composite material with higher thermal conductivity than loose soil [96,97,98]. In the soil layers containing abundant pore water, temperature-triggered directional flow is active and will improve the heat transfer efficiency of the energy piles. In addition, cement soil plays a role in preventing the pore water and protecting the core concrete from corrosion.
S-shaped energy piles can be adapted to different soil layers by adjusting the pitch in the water-rich areas. Water content in the strata is unevenly distributed with depth (Figure 9). Below the ground surface, the water content of shallow soft soils depends on climate and rainfall. Rainwater infiltrates to a certain depth and then gathers to form stable water-rich layers, where the water, called pore water, is mainly stored in the pore space between the loose sediment particles. Under the flushing of pore water, the thermal interference between the tubes in energy piles is slight. Therefore, a smaller pitch can be arranged to strengthen the heat transfer performance.

6. Conclusions and Prospects

From the perspective of heat transfer-influencing factors, the current research mainly focuses on macroscopic factors, like tube shape, fluid temperature and velocity, and the thermal conductivity of energy piles and soil. Subsequent studies should consider more microscopic factors, such as the contact state between liquid-pile soil and the thermal properties of concrete. The theoretical and experimental analysis must be carried out to fundamentally understand the influence of factors on the heat transfer performance of energy piles. To describe the complex heat transfer process, simulation methods need to be further optimized. Transient hourly time-step simulation for analysis of energy piles can be performed by applying numerical models in dedicated simulation environments, but these methods are complicated for common engineering. The number of heat exchanger pipes, the mass flow rate, the thermal conductivity of grouting material, and the inlet fluid temperature are the most common decision variables reviewed in previous studies. However, a wide-ranging study on structural parameters is also suggested. In reviewed models, modelling of heat transfer in two regions of energy piles surface boundary in the floor of the building and soil is not realized.
As for the structural response, past studies have shown that the pile bearing capacity will be decayed under temperature loading, but the specific mechanism is unclear. The impact of heat exchange on the bearing capacity should be comprehensively evaluated by considering the nature of pile-soil heat transfer, the pile-soil contact mechanism, and the natural historical conditions of the soil. More evidence is required to confirm the effect of variable temperature for the behavior of energy piles. Another important target that should be investigated is finding the best positions and number of energy piles.

Author Contributions

Writing and editing: J.X.; conceptualization, Y.Q. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the high-level innovation team and outstanding scholar program in Guangxi colleges (to Y. Qin) and the Natural Science Foundation of Guangxi (No. 2018GXNSFAA294070, 2018GXNSFDA138009).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The simulation methods of heat transfer process of energy piles are listed in Table A1, and the meanings of each symbol are listed in Table A2.
Table
Table A1. Mathematical expressions for different simulation methods.
Table A1. Mathematical expressions for different simulation methods.
ModelsMathematical Expression
Infinite line heat source [43] Δ T f = q 4 π k I n t + q [ R b + 1 4 π k I n ( 4 a r b 2 ) − γ 4 π k ]
Finite line heat source [43] Δ T ( r , t ) = q 4 π k r ∫ 0 H { e r f c [ r 2 + ( z − h ) 2 2 a t ] r 2 + ( z − h ) 2 − e r f c [ r 2 + ( z − h ) 2 2 a t ] r 2 + ( z + h ) 2 } d h
Hollow cylindrical heat source [44,45] θ a = ∑ i = 1 n q 4 π k i ∫ H i − 1 H i d h × ∫ 0 2 π { e r f c ( ω 1 2 a i t ) ω 1 − e r f c ( ω 2 2 a i t ) ω 2 } d β
1-D heat source [44] θ 1 , n ( r , t ) = − q 4 π k ∫ 0 π 1 π E i ( − r 2 + r 0 2 − 2 r r 0 cos φ 4 a t ) d φ
1-D heat source [44] θ 2 , n ( r , z , t ) = q ρ c ∫ 0 z ∫ 0 h 1 8 [ π a ( t − t ′ ) ] 3 I 0 [ r r 0 2 a ( t − t ′ ) ] · { exp [ − r 2 + r 0 2 + ( z ′ − z ) 2 4 a ( t − t ′ ) ] − exp [ − r 2 + r 0 2 + ( z ′ + z ) 2 4 a ( t − t ′ ) ] } d z ′ d t ′
Table
Table A2. Nomenclature of each mathematical expression.
Table A2. Nomenclature of each mathematical expression.
Nomenclature
C heat capacity, J/(kg·K) m ˙ flow rate, kg/s
L length of the tubes, m R b thermal resistance, (m·K)/W
Δ T different of fluid temperature, °C γ Euler’s constant
q power per unit length, W/mHdepth, m
kthermal conductivity, W/(m·K)zdimensionless axial coordinate
r b diameter, mrradial coordinate (m)
t Time, sr0cylinder radius (m)
a thermal diffusivity, m / s 2 ω 1 , ω 2 ω 1 = ( R 2 + r 0 2 − 2 R r 0 c cos β + ( h − z ) 2 )
ω 2 = ( R 2 + r 0 2 − 2 R r 0 c cos β + ( h + z ) 2 )
R R = r / r 0

References

  1. Loveridge, F.; Mccartney, J.S.; Narsilio, G.A.; Sanchez, M. Energy geostructures: A review of analysis approaches, in situ testing and model scale experiments. Geomech. Energy Environ. 2020, 22, 100173. [Google Scholar] [CrossRef] [Green Version]
  2. Hamada, Y.; Saitoh, H.; Nakamura, M.; Kubota, H.; Ochifuji, K. Field performance of an energy pile system for space heating. Energy Build. 2006, 39, 517–524. [Google Scholar] [CrossRef]
  3. Liu, H.; Maghoul, P.; Bahari, A.; Kavgic, M. Feasibility study of snow melting system for bridge decks using geothermal energy piles integrated with heat pump in Canada. Renew. Energy. 2019, 136, 1266–1280. [Google Scholar] [CrossRef]
  4. Bidarmaghz, A.; Narsilio, G.A. Heat exchange mechanisms in energy tunnel systems. Géoméch. Energy Environ. 2018, 16, 83–95. [Google Scholar] [CrossRef]
  5. Kong, G.; Wu, D.; Liu, H.; Laloui, L.; Cheng, X.; Zhu, X. Performance of a geothermal energy deicing system for bridge deck using a pile heat exchanger. Int. J. Energy Res. 2018, 43, 596–603. [Google Scholar] [CrossRef] [Green Version]
  6. Buhmann, P.; Moormann, C.; Westrich, B.; Pralle, N.; Friedemann, W. Tunnel geothermics—A German experience with renewable energy concepts in tunnel projects. Géoméch. Energy Environ. 2016, 8, 1–7. [Google Scholar] [CrossRef]
  7. Lai, J.; Wang, X.; Qiu, J.; Zhang, G.; Chen, J.; Xie, Y.; Luo, Y. A state-of-the-art review of sustainable energy based freeze proof technology for cold-region tunnels in China. Renew. Sustain. Energy Rev. 2018, 82, 3554–3569. [Google Scholar] [CrossRef]
  8. Preene, M.; Powrie, W. Ground energy systems: From analysis to geotechnical design. Géotechnique 2009, 59, 261–271. [Google Scholar] [CrossRef]
  9. Noorollahi, Y.; Saeidi, R.; Mohammadi, M.; Amiri, A.; Hosseinzadeh, M. The effects of ground heat exchanger parameters changes on geothermal heat pump performance—A review. Appl. Therm. Eng. 2018, 129, 1645–1658. [Google Scholar] [CrossRef]
  10. Abuel-Naga, H.; Raouf, M.I.N.; Raouf, A.M.I.; Nasser, A.G. Energy piles: Current state of knowledge and design challenges. Environ. Geotech. 2015, 2, 195–210. [Google Scholar] [CrossRef]
  11. Fadejev, J.; Simson, R.; Kurnitski, J.; Haghighat, F. A review on energy piles design, sizing and modelling. Energy 2017, 122, 390–407. [Google Scholar] [CrossRef]
  12. Mohamad, Z.; Fardoun, F.; Meftah, F. A review on energy piles design, evaluation, and optimization. J. Clean. Prod. 2021, 292, 125802. [Google Scholar] [CrossRef]
  13. Yoon, S.; Lee, S.-R.; Xue, J.; Zosseder, K.; Go, G.-H.; Park, H. Evaluation of the thermal efficiency and a cost analysis of different types of ground heat exchangers in energy piles. Energy Convers. Manag. 2015, 105, 393–402. [Google Scholar] [CrossRef]
  14. Miyara, A.; Tsubaki, K.; Inoue, S.; Yoshida, K. Experimental study of several types of ground heat exchanger using a steel pile foundation. Renew. Energy 2011, 36, 764–771. [Google Scholar]
  15. Florides, G.; Christodoulides, P.; Pouloupatis, P. An analysis of heat flow through a borehole heat exchanger validated model. Appl. Energy 2012, 92, 523–533. [Google Scholar] [CrossRef]
  16. Florides, G.A.; Christodoulides, P.; Pouloupatis, P. Single and double U-tube ground heat exchangers in multiple-layer substrates. Appl. Energy 2013, 102, 364–373. [Google Scholar] [CrossRef]
  17. Gao, J.; Zhang, X.; Liu, J.; Li, K.; Yang, J. Numerical and experimental assessment of thermal performance of vertical energy piles: An application. Appl. Energy 2008, 85, 901–910. [Google Scholar] [CrossRef]
  18. Gao, J.; Zhang, X.; Liu, J.; Li, K.S.; Yang, J. Thermal performance and ground temperature of vertical pile-foundation heat exchangers: A case study. Appl. Therm. Eng. 2008, 28, 2295–2304. [Google Scholar] [CrossRef]
  19. Zarrella, A.; De Carli, M.; Galgaro, A. Thermal performance of two types of energy foundation pile: Helical pipe and triple U-tube. Appl. Therm. Eng. 2013, 61, 301–310. [Google Scholar] [CrossRef]
  20. Zarrella, A.; Capozza, A.; Carli, M.D. Analysis of short helical and double U-tube borehole heat exchangers: A simulation-based comparison. Appl. Energy 2013, 112, 358–370. [Google Scholar] [CrossRef]
  21. Luo, J.; Zhao, H.; Gui, S.; Xiang, W.; Rohn, J.; Blum, P. Thermo-economic analysis of four different types of ground heat exchangers in energy piles. Appl. Therm. Eng. 2016, 108, 11–19. [Google Scholar] [CrossRef]
  22. Park, S.; Lee, D.; Choi, H.-J.; Jung, K.; Choi, H. Relative constructability and thermal performance of cast-in-place concrete energy pile: Coil-type GHEX (ground heat exchanger). Energy 2015, 81, 56–66. [Google Scholar] [CrossRef]
  23. Yang, W.; Lu, P.; Chen, Y. Laboratory investigations of the thermal performance of an energy pile with spiral coil ground heat exchanger. Energy Build. 2016, 128, 491–502. [Google Scholar] [CrossRef]
  24. You, T.; Li, X.; Cao, S.; Yang, H. Soil thermal imbalance of ground source heat pump systems with spiral-coil energy pile groups under seepage conditions and various influential factors. Energy Convers. Manag. 2018, 178, 123–136. [Google Scholar] [CrossRef]
  25. Li, X.-Y.; Li, T.-Y.; Qu, D.-Q.; Yu, J.-W. A new solution for thermal interference of vertical U-tube ground heat exchanger for cold area in China. Geothermics 2017, 65, 72–80. [Google Scholar] [CrossRef]
  26. Cecinato, F.; Loveridge, F. Influences on the thermal efficiency of energy piles. Energy 2015, 82, 1021–1033. [Google Scholar] [CrossRef]
  27. Carotenuto, A.; Marotta, P.; Massarotti, N.; Mauro, A.; Normino, G. Energy piles for ground source heat pump applications: Comparison of heat transfer performance for different design and operating parameters. Appl. Therm. Eng. 2017, 124, 1492–1504. [Google Scholar] [CrossRef]
  28. Su, T.; Liu., T.; Li., X.; Yu, J.; Xiao, L. Test and analysis of thermal properties of soil in Nanjing district. Chin. J. Rock Mech. Eng. 2006, 25, 1278–1283. [Google Scholar]
  29. Leong, W.H.; Tarnawski, V.R.; Aittomäki, A. Effect of soil type and moisture content on ground heat pump performance. Int. J. Refrig. 1998, 21, 595–606. [Google Scholar] [CrossRef]
  30. Liu, C.; Zhou, D.; Wu, H. Measurement and prediction of temperature effects of thermal conductivity of soils. Chin. J. Geotech. Eng. 2011, 33, 1877–1886. [Google Scholar]
  31. Barry-Macaulay, D.; Bouazza, A.; Singh, R.M.; Wang, B.; Ranjith, P. Thermal conductivity of soils and rocks from the Melbourne (Australia) region. Eng. Geol. 2013, 164, 131–138. [Google Scholar] [CrossRef] [Green Version]
  32. Zhang, N.; Xia, S.; Hou, X.; Wang, Z. Review on soil thermal conductivity and prediction model. Rock Soil Mech. 2016, 37, 1550–1562. [Google Scholar]
  33. Cai, S.; Zhang, B.; Cui, T.; Guo, H.; Huxford, J. Mesoscopic study of the effective thermal conductivity of dry and moist soil. Int. J. Refrig. 2018, 98, 171–181. [Google Scholar] [CrossRef]
  34. Smits, K.M.; Sakaki, T.; Limsuwat, A.; Illangasekare, T. Thermal Conductivity of Sands under Varying Moisture and Porosity in Drainage–Wetting Cycles. Vadose Zone J. 2010, 9, 172–180. [Google Scholar] [CrossRef]
  35. Abu-Hamdeh, N.H.; Reeder, R.C. Soil Thermal Conductivity: Effects of Density, Moisture, Salt Concentration, and Organic Matter. Soil Sci. Soc. Am. J. 2000, 64, 1285–1290. [Google Scholar] [CrossRef]
  36. Becker, B.R.; Misra, A.; Fricke, B. Development of correlations for soil thermal conductivity. Int. Commun. Heat Mass Transf. 1992, 19, 59–68. [Google Scholar] [CrossRef] [Green Version]
  37. Angelotti, A.; Alberti, L.; La Licata, I.; Antelmi, M. Energy performance and thermal impact of a Borehole Heat Exchanger in a sandy aquifer: Influence of the groundwater velocity. Energy Convers. Manag. 2013, 77, 700–708. [Google Scholar] [CrossRef]
  38. Zhang, Y.-J.; Yu, Z.-W.; Huang, R.; Wu, G.; Hu, J.-H. Measurement of thermal conductivity and temperature effect of geotechnical materials. Chin. J. Geotech. Eng. 2009, 31, 213–217. [Google Scholar]
  39. Florides, G.A.; Kalogirou, S.A. Annual ground temperature measurements at various depths. In Proceedings of the CLIMA 2005, Lausanne, Switzerland, 9–12 October 2005. [Google Scholar]
  40. Bidarmaghz, A.; Narsilio, G.A.; Johnston, I.W.; Colls, S. The importance of surface air temperature fluctuations on long-term performance of vertical ground heat exchangers. Géoméch. Energy Environ. 2016, 6, 35–44. [Google Scholar] [CrossRef]
  41. Faizal, M.; Bouazza, A.; Wuttke, F.; Bauer, S.; Sanchez, M. Effect of forced thermal recharging on the thermal behaviour of a field scale geothermal energy pile. In Proceedings of the International Conference on Energy Geotechnics (ICEGT 2016), Kiel, Germany, 29–31 August 2016; Wuttke, F., Bauer, S., Sánchez, M., Eds.; CRC Press: Boca Rotan, FL, USA; pp. 557–568. [Google Scholar]
  42. Park, S.; Lee, S.; Oh, K.; Kim, D.; Choi, H. Engineering chart for thermal performance of cast-in-place energy pile considering thermal resistance. Appl. Therm. Eng. 2018, 130, 899–921. [Google Scholar] [CrossRef]
  43. Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A finite line-source model for boreholes in geothermal heat exchangers. Heat Transfer-Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
  44. Man, Y.; Yang, H.; Diao, N.; Liu, J.; Fang, Z. A new model and analytical solutions for borehole and pile ground heat exchangers. Int. J. Heat Mass Transf. 2010, 53, 2593–2601. [Google Scholar] [CrossRef]
  45. Wang, Z.; Shao, W.; Zhang, Y. Cylindrical surface model of ground source heat pump considering soil stratification. J. Zhejiang Univ. (Eng. Sci.) 2013, 47, 1338–1345. [Google Scholar]
  46. Adinolfi, M.; Maiorano, R.M.S.; Mauro, A.; Massarotti, N.; Aversa, S. On the influence of thermal cycles on the yearly performance of an energy pile. Géoméch. Energy Environ. 2018, 16, 32–44. [Google Scholar] [CrossRef]
  47. Diao, N.; Li, Q.; Fang, Z. Heat transfer in ground heat exchangers with groundwater advection. Int. J. Therm. Sci. 2004, 43, 1203–1211. [Google Scholar] [CrossRef]
  48. Fan, R.; Jiang, Y.; Yao, Y.; Shiming, D.; Ma, Z. A study on the performance of a geothermal heat exchanger under coupled heat conduction and groundwater advection. Energy 2007, 32, 2199–2209. [Google Scholar] [CrossRef]
  49. Molina-Giraldo, N.; Blum, P.; Zhu, K.; Bayer, P.; Fang, Z. A moving finite line source model to simulate borehole heat exchangers with groundwater advection. Int. J. Therm. Sci. 2011, 50, 2506–2513. [Google Scholar] [CrossRef]
  50. Lee, C.K.; Lam, H. A modified multi-ground-layer model for borehole ground heat exchangers with an inhomogeneous groundwater flow. Energy 2012, 47, 378–387. [Google Scholar] [CrossRef]
  51. Rivera, J.A.; Blum, P.; Bayer, P. Analytical simulation of groundwater flow and land surface effects on thermal plumes of borehole heat exchangers. Appl. Energy 2015, 146, 421–433. [Google Scholar] [CrossRef]
  52. Hu, J. An improved analytical model for vertical borehole ground heat exchanger with multiple-layer substrates and groundwater flow. Appl. Energy 2017, 202, 537–549. [Google Scholar] [CrossRef]
  53. Zhang, W.; Zhang, L.; Cui, P.; Gao, Y.; Liu, J.; Yu, M. The influence of groundwater seepage on the performance of ground source heat pump system with energy pile. Appl. Therm. Eng. 2019, 162, 114217. [Google Scholar] [CrossRef]
  54. Amatya, B.L.; Soga, K.; Bourne-Webb, P.J.; Amis, T.; Laloui, L. Thermo-mechanical behaviour of energy piles. Géotechnique 2012, 62, 503–519. [Google Scholar] [CrossRef]
  55. McCartney, J.S.; Murphy, K.D. Strain Distributions in Full-Scale Energy Foundations (DFI Young Professor Paper Competition 2012). DFI J. 2012, 6, 26–38. [Google Scholar] [CrossRef]
  56. Gashti, E.H.N.; Malaska, M.; Kujala, K. Evaluation of thermo-mechanical behaviour of composite energy piles during heating/cooling operations. Eng. Struct. 2014, 75, 363–373. [Google Scholar] [CrossRef]
  57. Bourne-Webb, P.J.; Amatya, B.; Soga, K.; Amis, T.; Davidson, C.; Payne, C. Energy pile test at Lambeth College, London: Geotechnical and thermodynamic aspects of pile response to heat cycles. Géotechnique 2009, 59, 237–248. [Google Scholar] [CrossRef]
  58. Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of a heat exchanger pile. Int. J. Numer. Anal. Methods Géoméch. 2006, 30, 763–781. [Google Scholar] [CrossRef]
  59. Wang, C.-L.; Liu, H.-L.; Kong, G.-Q.; Wu, D. Model tests on thermal mechanical behavior of energy piles influenced with heat exchangers types. Eng. Mech. 2017, 34, 85–91. [Google Scholar]
  60. Wang, C.; Liu, H.; Kong, G. Influence of different stiffness constraints on stress and displacement of energy piles. Rock Soil Mech. 2018, 39, 4261–4268. [Google Scholar]
  61. Zhou, Y.; Zhao, D.; Li, B.; Tang, Q.; Zhang, Z. Fatigue Damage Mechanism and Deformation Behavior of Granite under Ultrahigh-Frequency Cyclic Loading Conditions. Rock Mech Rock Eng. 2021, 54, 4723–4739. [Google Scholar] [CrossRef]
  62. Laloui, L. Thermo-mechanical behaviour of soils. Rev. Franaise De Génie Civ. 2001, 5, 809–843. [Google Scholar] [CrossRef]
  63. Vardoulakis, I. Dynamic thermo-poro-mechanical analysis of catastrophic landslides. Géotechnique 2002, 52, 157–171. [Google Scholar] [CrossRef]
  64. Zhang, Y.G.; Xie, Y.L.; Zhang, Y.; Qiu, J.B.; Wu, S.X. The adoption of deep neural network (DNN) to the prediction of soil liquefaction based on shear wave velocity. Bull. Eng. Geol. Environ. 2021, 80, 5053–5060. [Google Scholar] [CrossRef]
  65. Yavari, N.; Tang, A.M.; Pereira, J.-M.; Hassen, G. Effect of temperature on the shear strength of soils and the soil–structure interface. Can. Geotech. J. 2016, 53, 1186–1194. [Google Scholar] [CrossRef]
  66. Akrouch, G.A.; Sánchez, M.; Briaud, J.-L. Thermo-mechanical behavior of energy piles in high plasticity clays. Acta Geotech. 2014, 9, 399–412. [Google Scholar] [CrossRef]
  67. Donna, A.D.; Ferrari, A.; Laloui, L. Experimental investigations of the soil–concrete interface: Physical mechanisms, cyclic mobilization, and behaviour at different temperatures. Can. Geotech. J. 2016, 53, 659–672. [Google Scholar] [CrossRef]
  68. Zeng, Z.; Lu, H.; Zhao, Y.; Qin, Y. Analysis of the Mineral Compositions of Swell-Shrink Clays from Guangxi Province, China. Clays Clay Miner. 2020, 68, 161–174. [Google Scholar] [CrossRef]
  69. Goode, J.C.; John, S.M. Centrifuge Modeling of End-Restraint Effects in Energy Foundations. J. Geotech. Geoenviron. Eng. 2015, 141, 04015034. [Google Scholar] [CrossRef] [Green Version]
  70. Kong, L.; Yao, Y. Thermo-visco-elastoplastic constitutive relation for overconsolidated clay. Rock Soil Mech. 2015, 36, 1–8. [Google Scholar]
  71. Hueckel, T.; Borsetto, M. Thermoplasticity of Saturated Soils and Shales: Constitutive Equations. J. Geotech. Eng. 1990, 116, 1765–1777. [Google Scholar] [CrossRef]
  72. Modaressi, H.; Laloui, L. A Thermo-Viscoplastic Constitutive Model for Clays. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 313–335. [Google Scholar] [CrossRef]
  73. Cui, Y.; Sultan, N.; Delage, P. A thermomechanical model for saturated clays. Can. Geotech. J. 2011, 37, 607–620. [Google Scholar] [CrossRef]
  74. Yazdani, S.; Helwany, S.; Olgun, G. Investigation of Thermal Loading Effects on Shaft Resistance of Energy Pile Using Laboratory-Scale Model. J. Geotech. Geoenviron. Eng. 2019, 145, 04019043. [Google Scholar] [CrossRef]
  75. Fuentes, R.; Pinyol, N.; Alonso, E. Effect of temperature induced excess porewater pressures on the shaft bearing capacity of geothermal piles. Géoméch. Energy Environ. 2016, 8, 30–37. [Google Scholar] [CrossRef]
  76. Demars, K.R.; Charles, R.D. Soil volume changes induced by temperature cycling. Can. Geotech. J. 1982, 19, 188–194. [Google Scholar] [CrossRef]
  77. Krämer, C.; Basu, P. Performance of a model geothermal pile in sand. In Proceedings of the 8th International Conference on Physical Modelling in Geotechnics, Perth, Australia, 14–17 January 2014; Gaudin, C., White, D., Eds.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
  78. Olgun, C.G.; Arson, C.F.; Ozudogru, T.Y. Thermo-mechanical radial expansion of heat exchanger piles and possible effects on contact pressures at pile–soil interface. Géotechn. Lett. 2014, 4, 170–178. [Google Scholar] [CrossRef] [Green Version]
  79. Liu, H.-L.; Wang, C.-L.; Kong, G.-Q.; Bouazza, A. Ultimate bearing capacity of energy piles in dry and saturated sand. Acta Geotech. 2018, 14, 869–879. [Google Scholar] [CrossRef]
  80. McCartney, J.S.; Rosenberg, J.E. Impact of Heat Exchange on Side Shear in Thermo-Active Foundations. In Proceedings of the Geo-Frontiers 2011: Advances in Geotechnical Engineering, Dallas, TX, USA, 13–16 March 2011. [Google Scholar]
  81. Loria, A.F.R.; Laloui, L. Thermally induced group effects among energy piles. Géotechnique 2017, 67, 374–393. [Google Scholar] [CrossRef] [Green Version]
  82. Murphy, K.D.; McCartney, J.S. Seasonal Response of Energy Foundations During Building Operation. Geotech. Geol. Eng. 2014, 33, 343–356. [Google Scholar] [CrossRef]
  83. Loria, A.F.R.; Laloui, L. The equivalent pier method for energy pile groups. Géotechnique 2017, 67, 691–702. [Google Scholar] [CrossRef] [Green Version]
  84. Salciarini, D.; Ronchi, F.; Cattoni, E.; Tamagnini, C. Thermomechanical Effects Induced by Energy Piles Operation in a Small Piled Raft. Int. J. Géoméch. 2015, 15, 04014042. [Google Scholar] [CrossRef]
  85. Sanner, B.; Mands, E.; Sauer, M.K. Larger geothermal heat pump plants in the central region of Germany. Geothermics 2003, 32, 589–602. [Google Scholar] [CrossRef]
  86. Ng, C.W.W.; Farivar, A.; Gomaa, S.M.M.H.; Shakeel, M.; Jafarzadeh, F. Performance of elevated energy pile groups with different pile spacing in clay subjected to cyclic non-symmetrical thermal loading. Renew. Energy. 2021, 172, 998–1012. [Google Scholar] [CrossRef]
  87. Saggu, R.; Chakraborty, T. Thermomechanical Response of Geothermal Energy Pile Groups in Sand. Int. J. Géoméch. 2016, 16, 04015100. [Google Scholar] [CrossRef]
  88. Wu, D.; Liu, H.-L.; Kong, G.-Q.; Waing, C.W.; Cheng, X.-H. Displacement response of an energy pile in saturated clay. Proc. Inst. Civ. Eng. Geotech. Eng. 2018, 171, 285–294. [Google Scholar] [CrossRef]
  89. Peng, H.-F.; Kong, G.-Q.; Liu, H.-L.; Abuel-Naga, H.; Hao, Y.-H. Thermo-mechanical behaviour of floating energy pile groups in sand. J. Zhejiang Univ. A 2018, 19, 638–649. [Google Scholar] [CrossRef]
  90. Loria, A.F.R.; Gunawan, A.; Shi, C.; Laloui, L.; Ng, C.W. Numerical modelling of energy piles in saturated sand subjected to thermo-mechanical loads. Géoméch. Energy Environ. 2015, 1, 1–15. [Google Scholar]
  91. Di Donna, A.; Laloui, L. Numerical analysis of the geotechnical behaviour of energy piles. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 861–888. [Google Scholar] [CrossRef]
  92. Wuttke, F.; Bauer, S.; Sanchez, M. Energy Geotechnics||Numerical investigation of the mechanical behaviour of single energy piles and energy pile groups. In Proceedings of the International Conference on Energy Geotechnics, Kiel, Germany, 29–31 August 2016. [Google Scholar]
  93. Sarma, K.; Saggu, R. Implications of Thermal Cyclic Loading on Pile Group Behavior. J. Geotech. Geoenvironmental Eng. 2020, 146, 0420114. [Google Scholar] [CrossRef]
  94. Wonglert, A.; Jongpradist, P. Impact of reinforced core on performance and failure behavior of stiffened deep cement mixing piles. Comput. Geotech. 2015, 69, 93–104. [Google Scholar] [CrossRef]
  95. Voottipruex, P.; Suksawat, T.; Bergado, D.; Jamsawang, P. Numerical simulations and parametric study of SDCM and DCM piles under full scale axial and lateral loads. Comput. Geotech. 2011, 38, 318–329. [Google Scholar] [CrossRef]
  96. Tan, K.; Qin, Y.; Du, T.; Li, L.; Zhang, L.; Wang, J. Biochar from waste biomass as hygroscopic filler for pervious concrete to improve evaporative cooling performance. Constr. Build. Mater. 2021, 287, 123078. [Google Scholar] [CrossRef]
  97. Zhang, L.; Gustavsen, A.; Jelle, B.P.; Yang, L.; Gao, T.; Wang, Y. Thermal conductivity of cement stabilized earth blocks. Constr. Build. Mater. 2017, 151, 504–511. [Google Scholar] [CrossRef]
  98. Ashour, T.; Korjenic, A.; Korjenic, S.; Wu, W. Thermal conductivity of unfired earth bricks reinforced by agricultural wastes with cement and gypsum. Energy Build. 2015, 104, 139–146. [Google Scholar] [CrossRef]
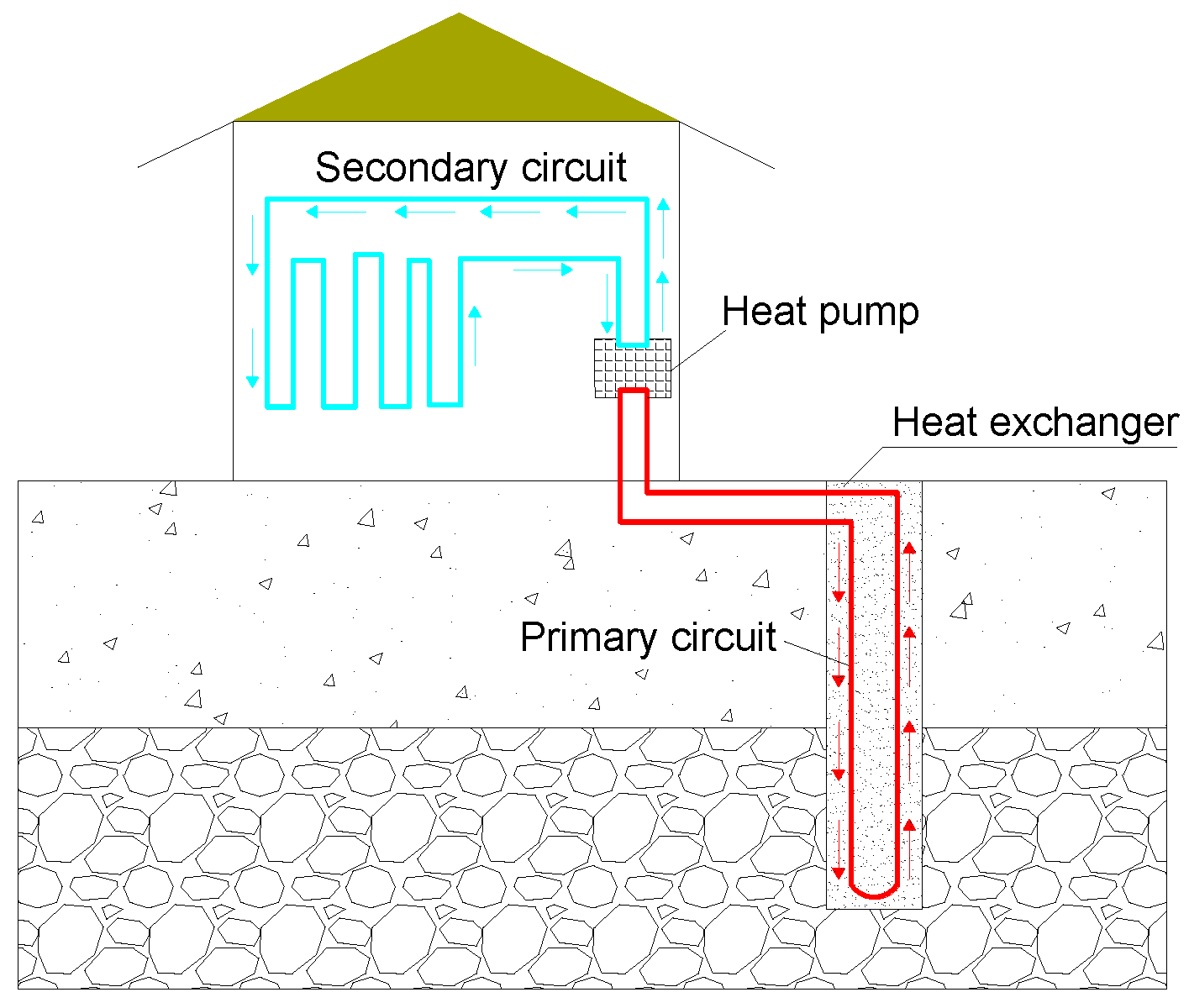
Energies 14 06483 g001 550
Figure 1. Schematic diagram of ground source heat pumps (GSHP).
Figure 1. Schematic diagram of ground source heat pumps (GSHP).
Energies 14 06483 g001
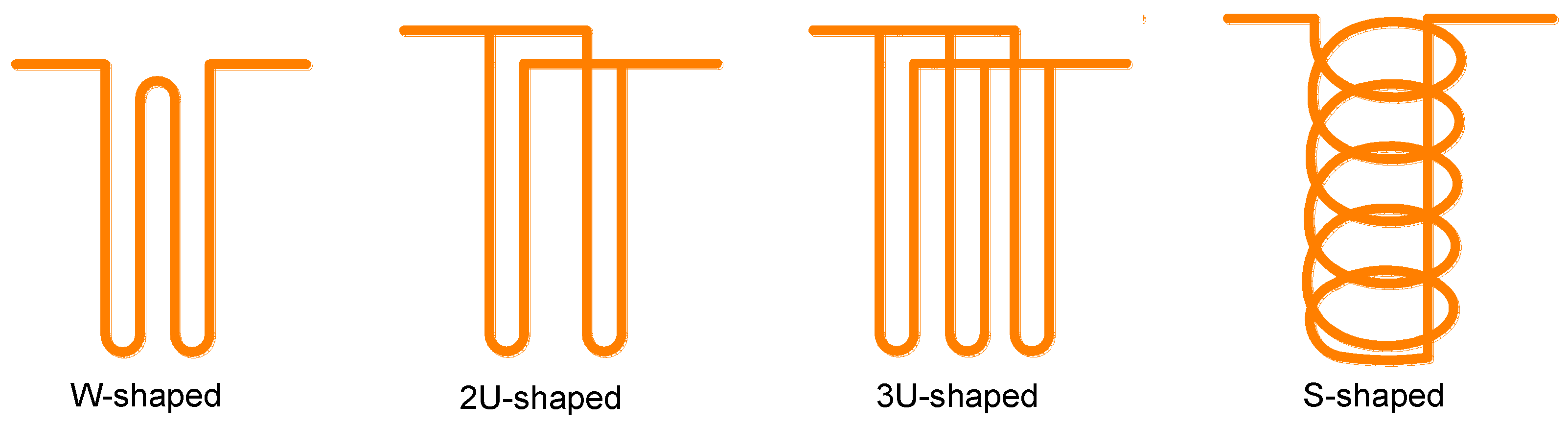
Energies 14 06483 g002 550
Figure 2. The shapes of heat exchange tubes.
Figure 2. The shapes of heat exchange tubes.
Energies 14 06483 g002
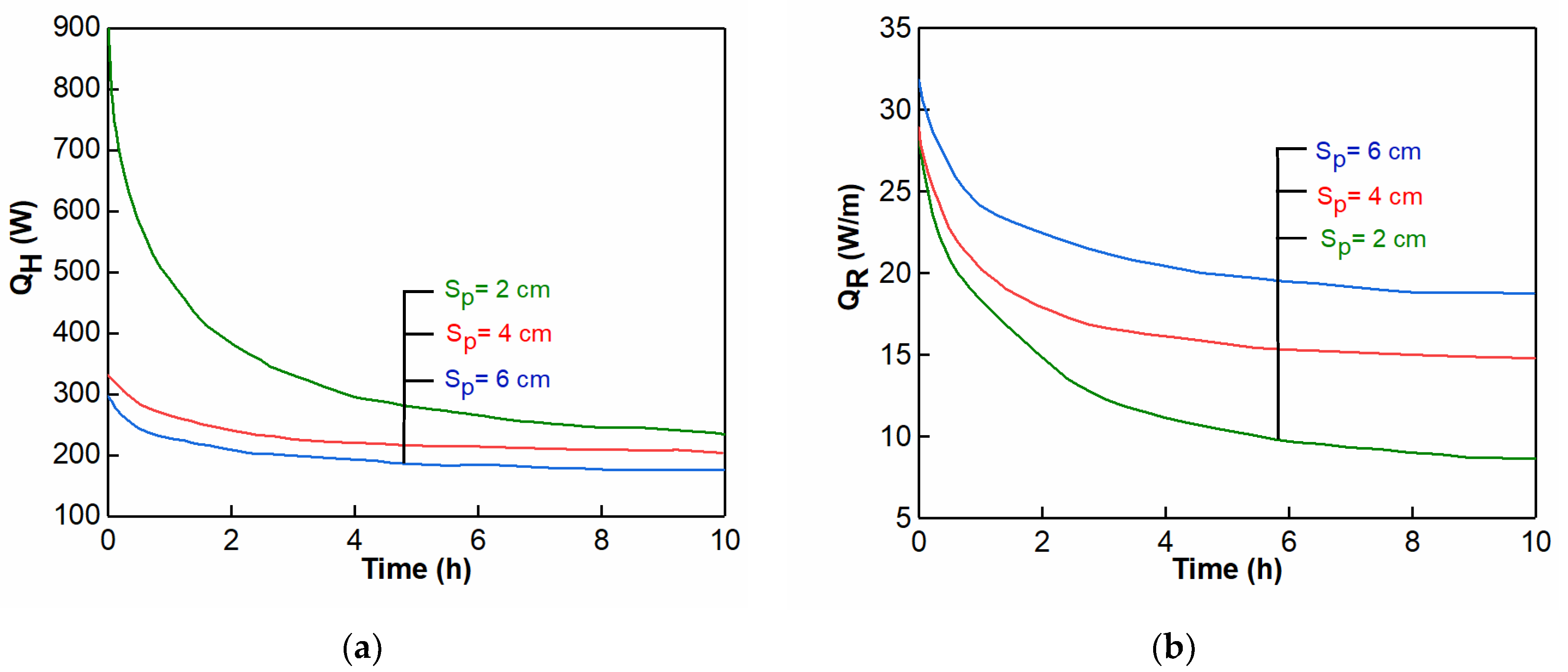
Energies 14 06483 g003 550
Figure 3. Changes of heat exchange rate and relative heat exchange rate with time for different spiral pitches ( S p ), (a) heat exchange rate Q H , (b) relative heat exchange rate Q R .
Figure 3. Changes of heat exchange rate and relative heat exchange rate with time for different spiral pitches ( S p ), (a) heat exchange rate Q H , (b) relative heat exchange rate Q R .
Energies 14 06483 g003
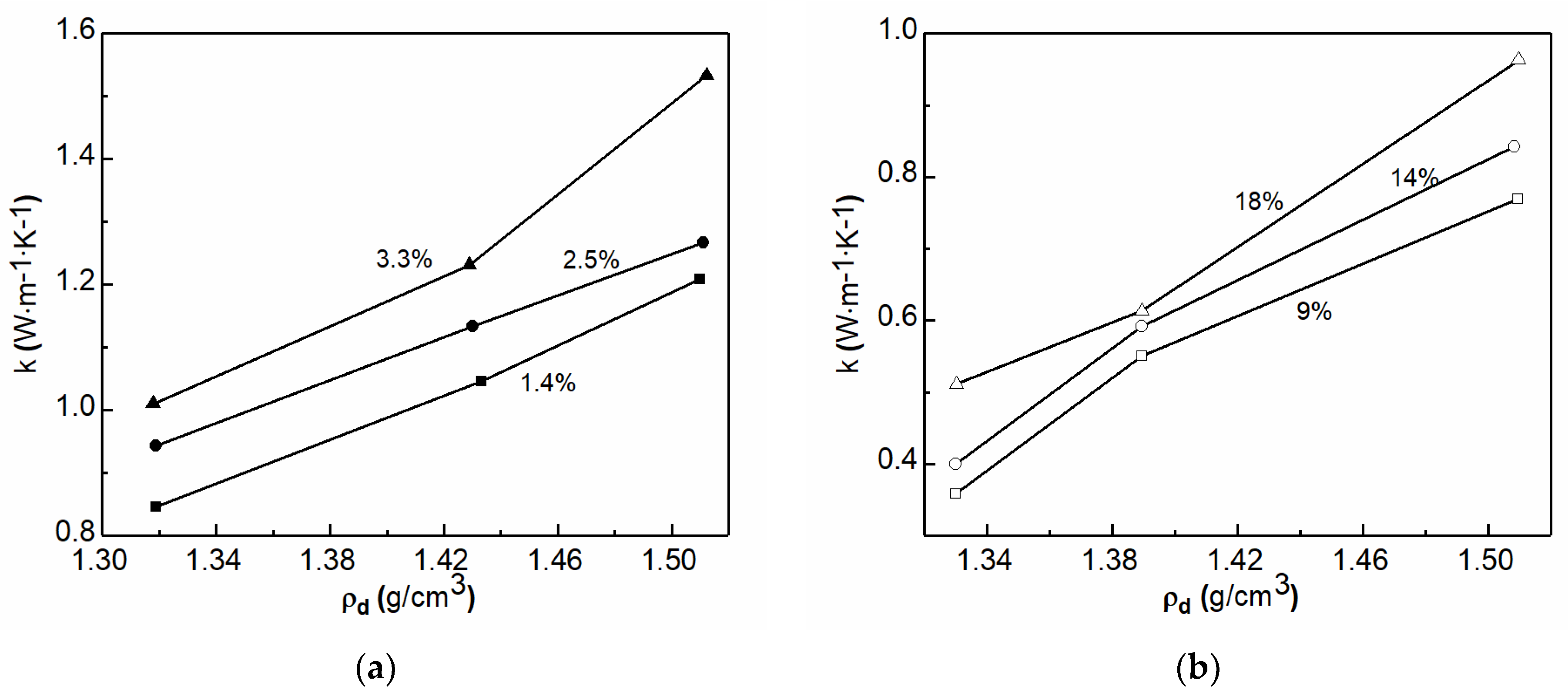
Energies 14 06483 g004 550
Figure 4. Relationship between thermal conductivity and dry density of soil with different water contents, (a) sand; (b) clay.
Figure 4. Relationship between thermal conductivity and dry density of soil with different water contents, (a) sand; (b) clay.
Energies 14 06483 g004
Energies 14 06483 g005 550
Figure 5. Load distribution in energy piles due to thermal, and thermo-mechanical load, (a) heating only, (b) combined load and heating, (c) cooling only, (d) combined load and cooling.
Figure 5. Load distribution in energy piles due to thermal, and thermo-mechanical load, (a) heating only, (b) combined load and heating, (c) cooling only, (d) combined load and cooling.
Energies 14 06483 g005
Energies 14 06483 g006 550
Figure 6. The variationof soil strain ( θ v ) with temperature (T).
Figure 6. The variationof soil strain ( θ v ) with temperature (T).
Energies 14 06483 g006
Energies 14 06483 g007 550
Figure 7. The temperature and pore pressure of soil under the thermal cycling state changes periodically.
Figure 7. The temperature and pore pressure of soil under the thermal cycling state changes periodically.
Energies 14 06483 g007
Energies 14 06483 g008 550
Figure 8. Relationship between pile tip settlement and axial load at different temperatures.
Figure 8. Relationship between pile tip settlement and axial load at different temperatures.
Energies 14 06483 g008
Energies 14 06483 g009 550
Figure 9. Structure diagram of composite energy pile.
Figure 9. Structure diagram of composite energy pile.
Energies 14 06483 g009
Table
Table 1. Comparison of heat transfer performance of different tube shapes.
Table 1. Comparison of heat transfer performance of different tube shapes.
ReferenceTube ShapeConsiderationMethodsPerformance Comparison
Jalaluddin [14]U-shaped, 2U-shaped, 3U-shapedGround temperature, wall temperature, velocity of fluidThermal response experiment2U-shaped > 3U-shaped > U-shaped
Florides [15,16]U-shaped, 2U-shapedPipe size, soil thermal conductivity, soil stratification, costNumerical Simulation2U-shaped > U-shaped
Gao [17,18]U-shaped, 2U-shaped, 3U-shaped, W-shapedCirculating medium flow, inlet temperature, the unbalanced load of cold and heat, ground temperatureThermal response experiment and numerical simulationHigh flow: 2U-shaped > W-shaped > 3U-shaped > U-shaped
Low flow: W-shaped > 2U-shaped > 3U-shaped > U-shaped
Zarrella [19]3U-shaped, S- shapedhelical pitchEquivalent CircuitS-shaped > 3U-shaped
Zarrella [20]2U-shaped, S-shapedAxial heat conduction, drilling length, long-term and short-term heat transfer performanceEquivalent CircuitS-shaped > 2U-shaped
Yoon [13]W-shaped, S-shapedThe intermittent operation, cost, number of pilesThermal response test and numerical simulationS-shaped > W-shaped
Luo [21]2U-shaped, 3U-shaped, 2W-shaped, S-shapedThe intermittent operation, pipe size, costThermal response test and numerical simulation3U-shaped > 2W-shaped, S-shaped > 2U-shaped
Table
Table 2. Applicability evaluation of main heat transfer models of energy piles.
Table 2. Applicability evaluation of main heat transfer models of energy piles.
ModelConsiderationInconsiderationCondition
line heat source modelRadial heat transferGeometry, internal heat transfer, tube shapeConstant heat flow, steady state
Hollow cylindrical heat source modelGeometry, thermal resistanceGeometry, thermal interference between tubesSmall diameter of piles, steady state
Solid cylindrical heat source modelThe transient heat transferThermal properties of concrete and soilsS-shaped tubes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Xie, J.; Qin, Y. Heat Transfer and Bearing Characteristics of Energy Piles: Review. Energies 2021, 14, 6483. https://doi.org/10.3390/en14206483

AMA Style

Xie J, Qin Y. Heat Transfer and Bearing Characteristics of Energy Piles: Review. Energies. 2021; 14(20):6483. https://doi.org/10.3390/en14206483

Chicago/Turabian Style

Xie, Jinli, and Yinghong Qin. 2021. "Heat Transfer and Bearing Characteristics of Energy Piles: Review" Energies 14, no. 20: 6483. https://doi.org/10.3390/en14206483

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop