Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System
Abstract
:1. Introduction
2. Mathematical Background
2.1. FESS
2.2. Nonlinear Systems
2.3. RWFONN
2.4. Filtered Error Training Algorithm
- 1
- , ∈ ( and are uniformly bounded);
- 2
- .
2.5. Nonlinear Block Controllable Form
2.6. Super-Twisting Control Algorithm
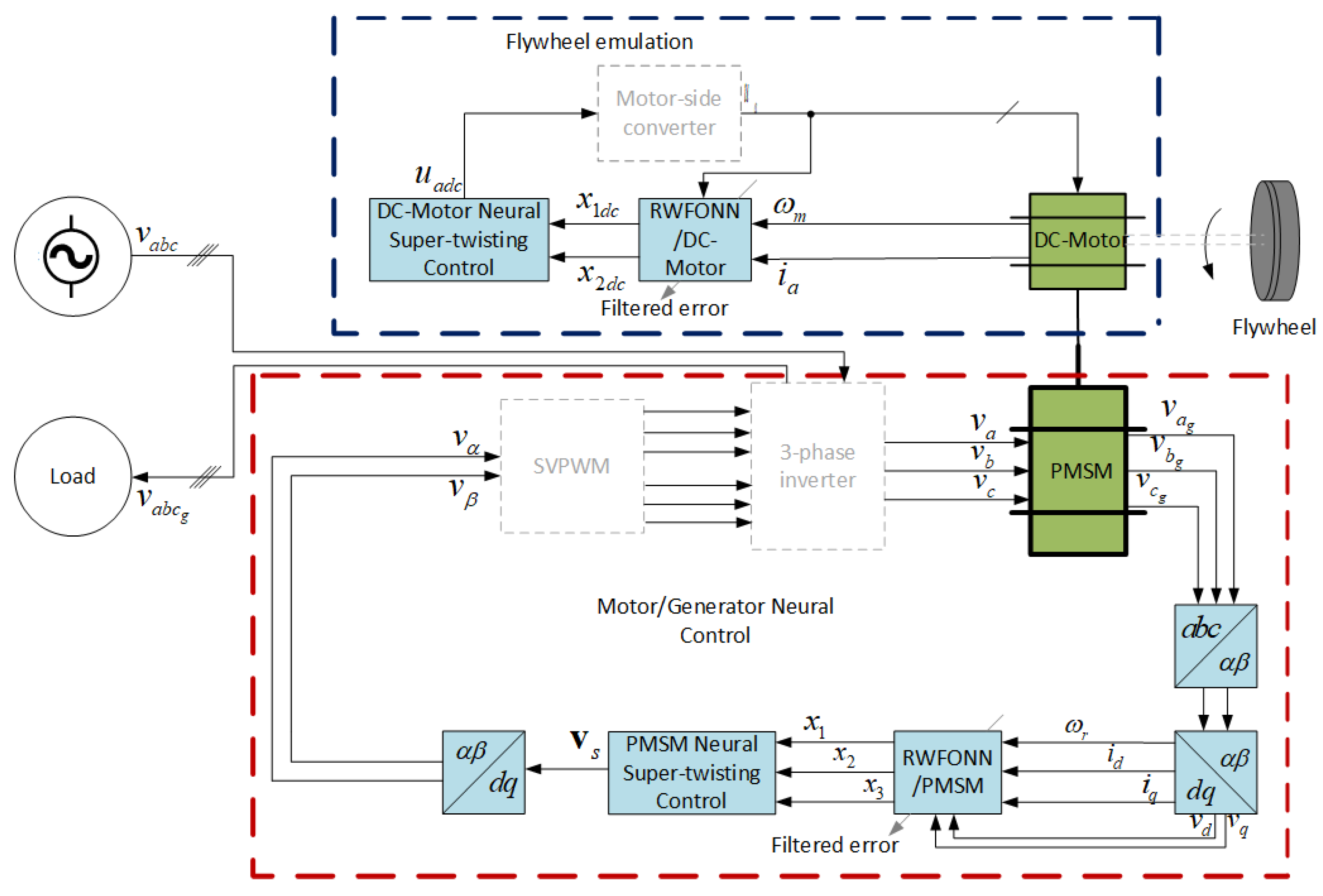
3. Proposed Methodology
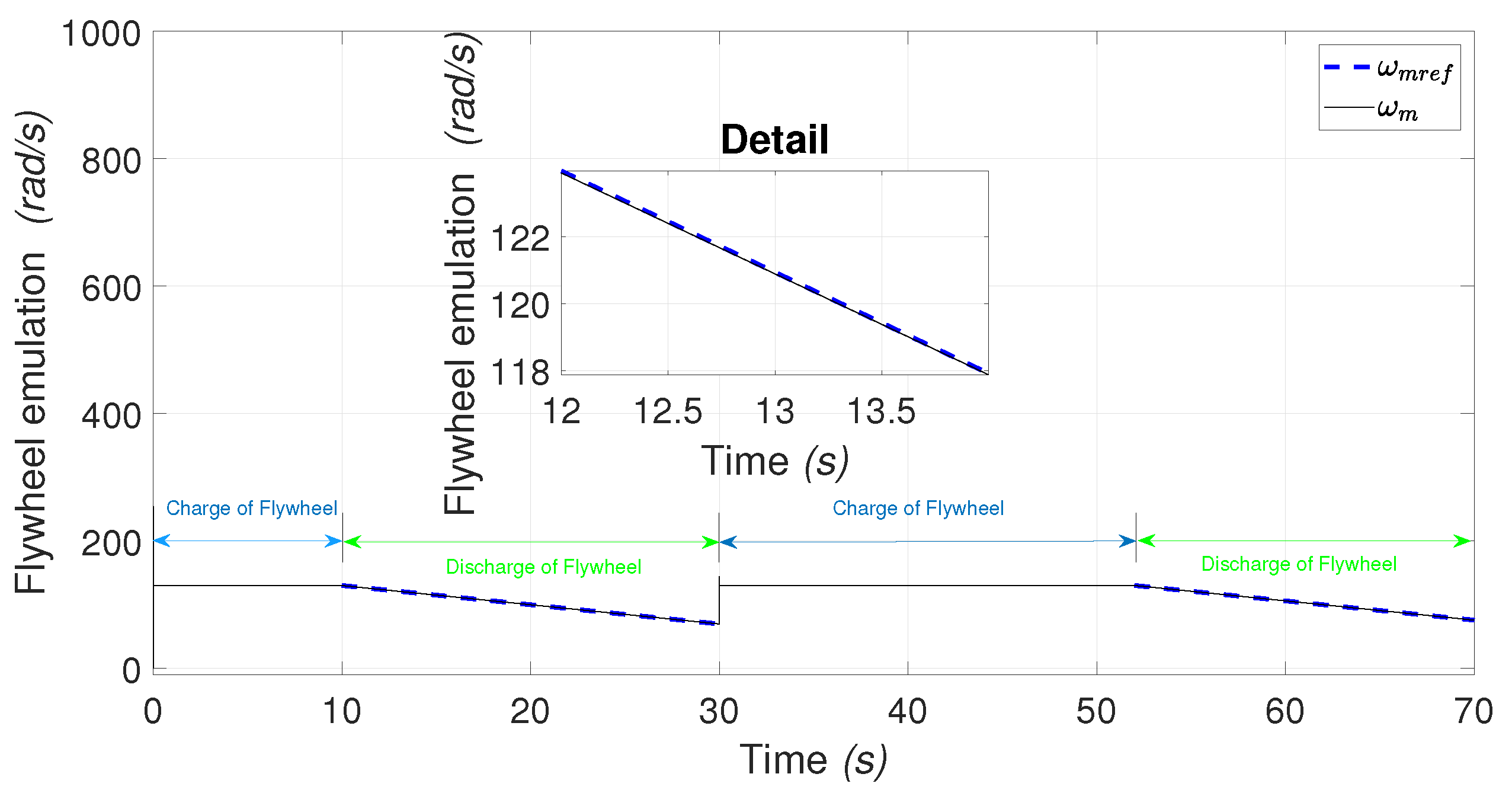
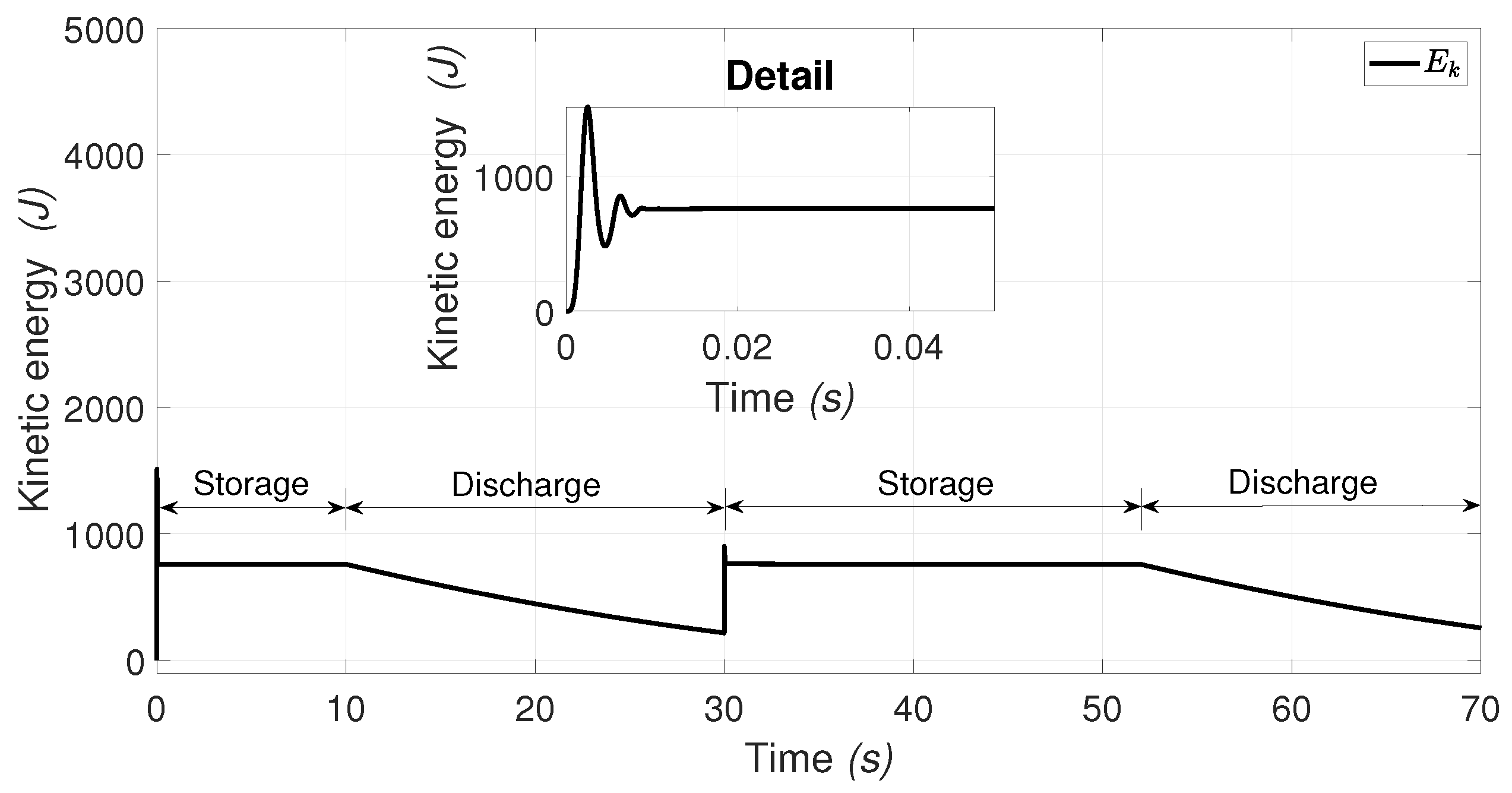
- The charging procedure (storing kinetic energy in the flywheel). This procedure consists of the PMSM in the coordinate frame [30] working in motor mode to the control the angular velocity through the RWFONN using the block control linearization technique. In this scenario, the kinetic energy is stored in the flywheel (dotted red block in Figure 1);
- Discharging procedure (releasing energy). In this stage, the stored energy is now transferred to the PMSM working in generator mode. This scenario is considered in the case when there exists an electrical failure in the utility grid or when the flywheel is required to compensate with active power to the utility grid to solve a problem of the power management office, and the velocity controller for the DC-motor emulates the deceleration of the flywheel through the use of Equation (2). The flywheel energy discharge is emulated by the DC-machine (dotted blue block in Figure 1).
3.1. Flywheel Storage System
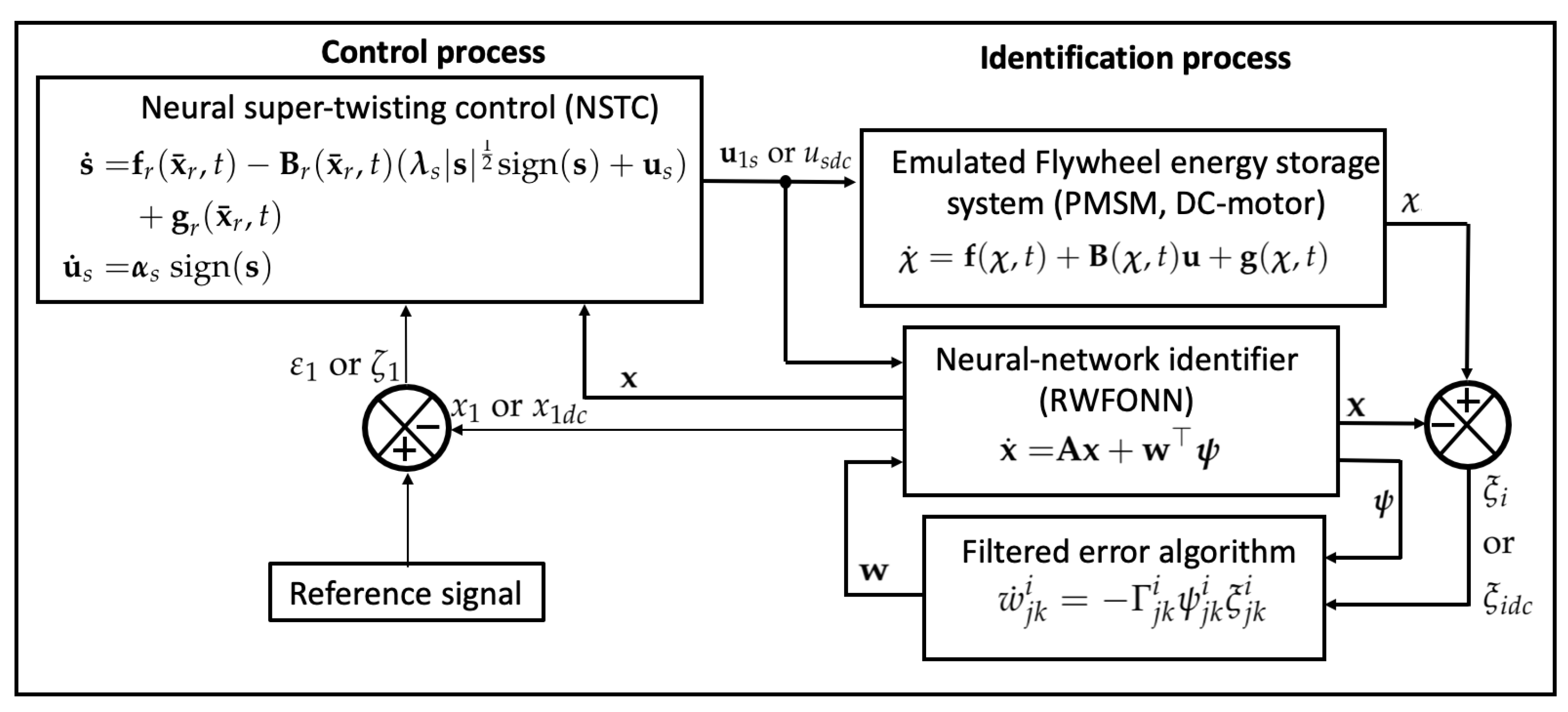
3.2. Nonlinear Identification and NSTC Applied to PMSM
3.2.1. PMSM Neural Identification
3.2.2. NSTC Application to PMSM
3.3. Nonlinear Identification and NSTC Applied to DC-Motor
3.3.1. DC-Motor Neural Identification
3.3.2. NSTC Application to DC-Motor
4. Simulation Results
4.1. Neural Identification
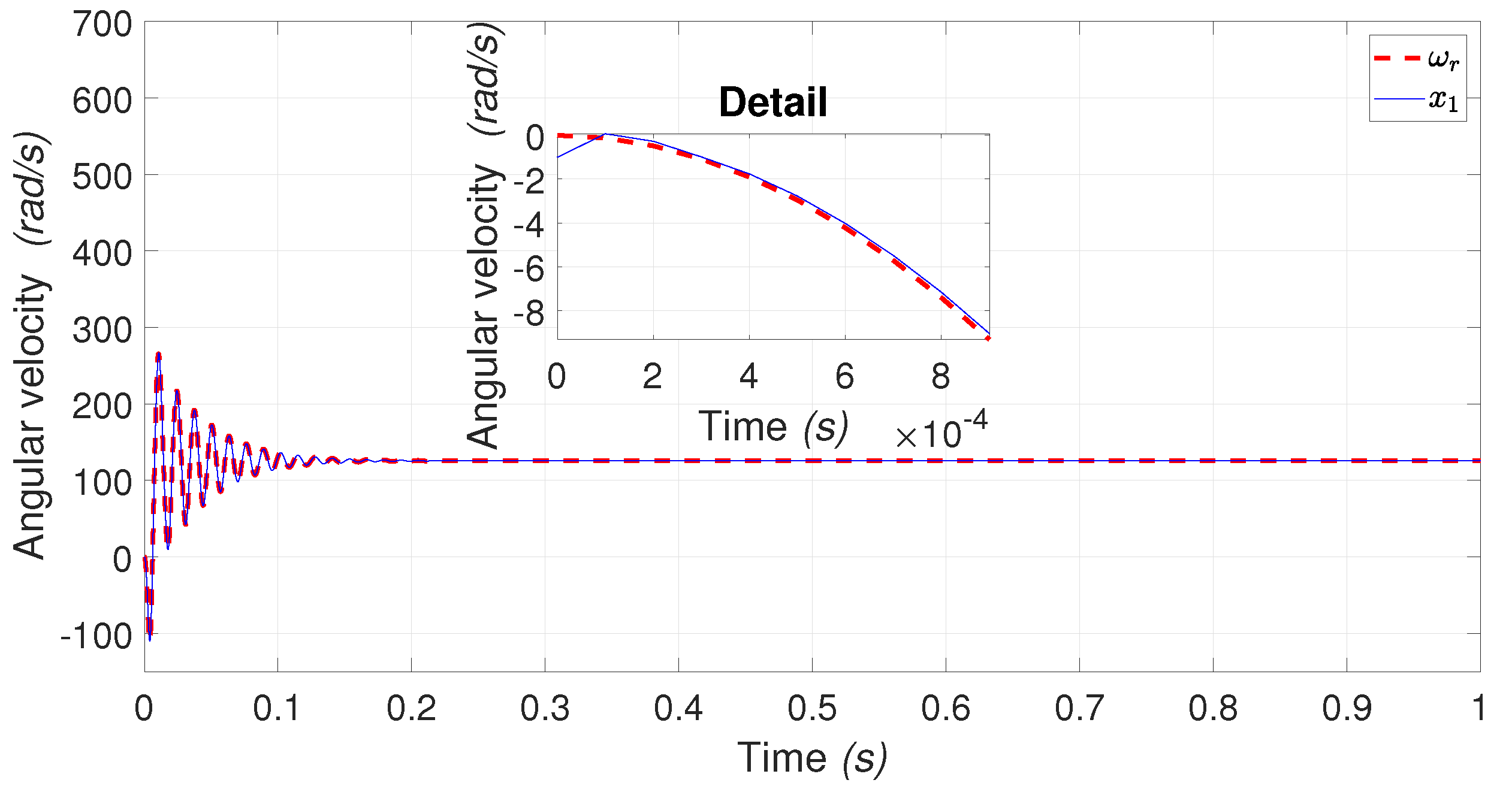
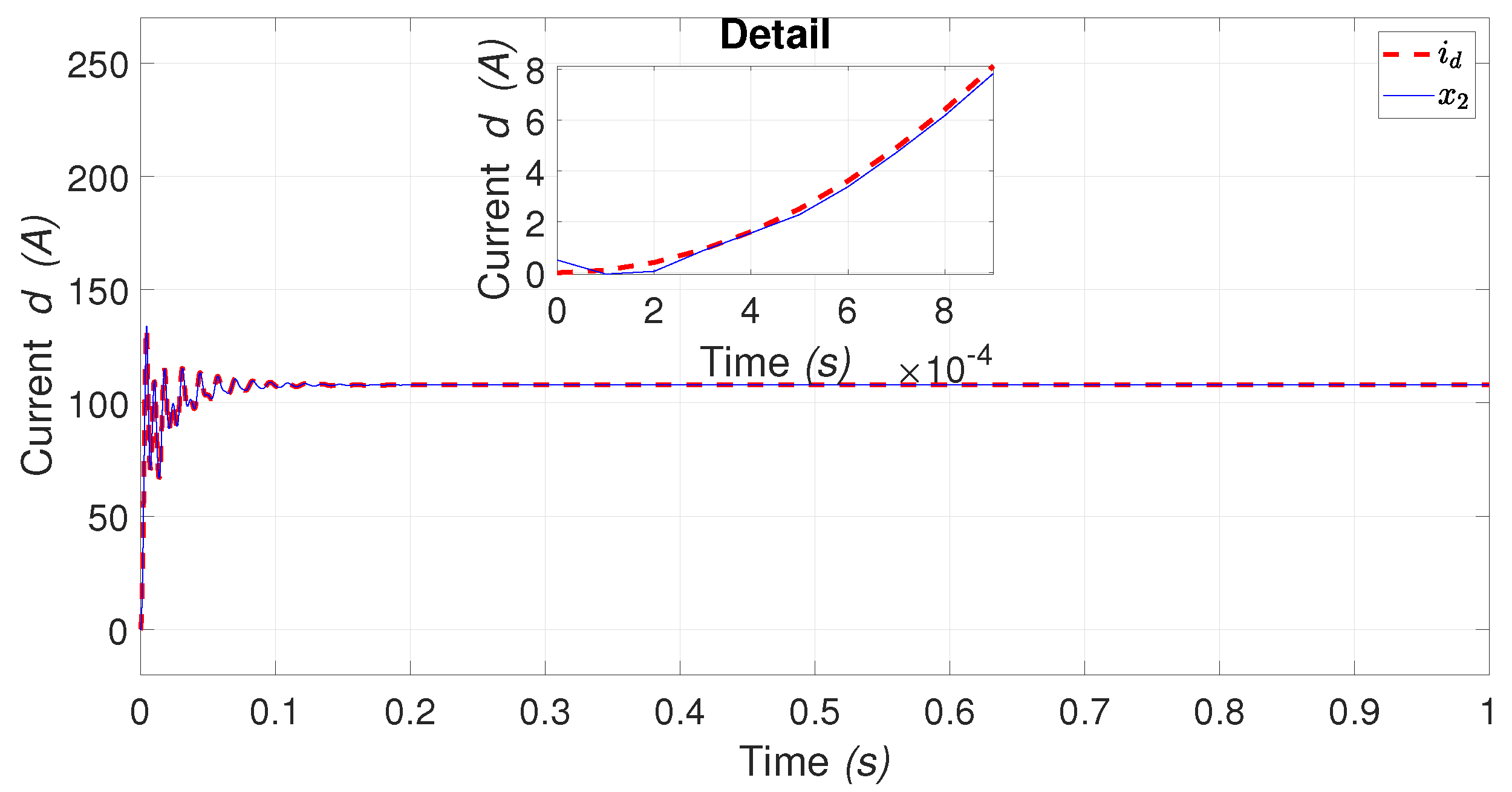
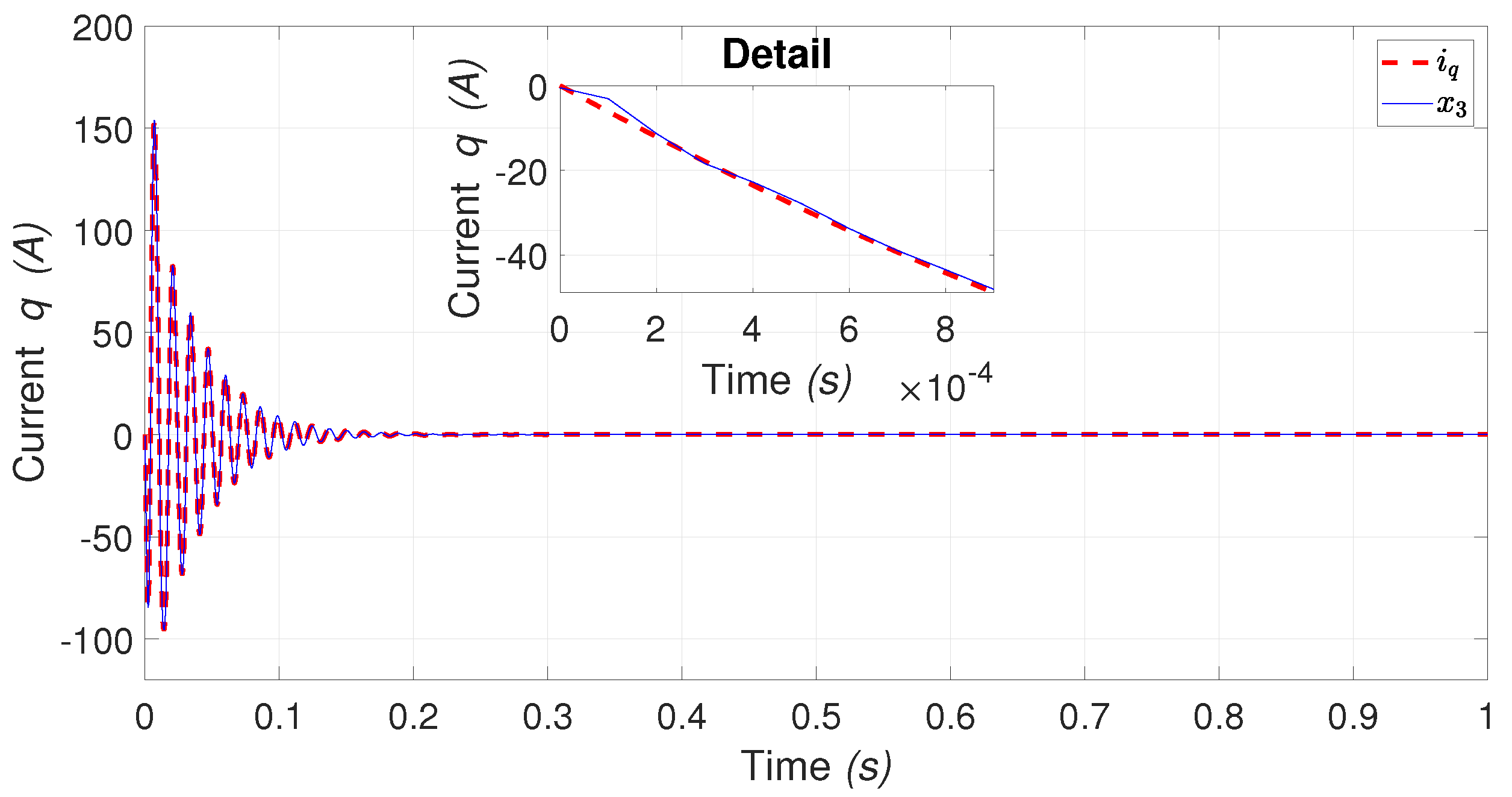
4.1.1. PMSM States Identification
4.1.2. DC-motor States Identification
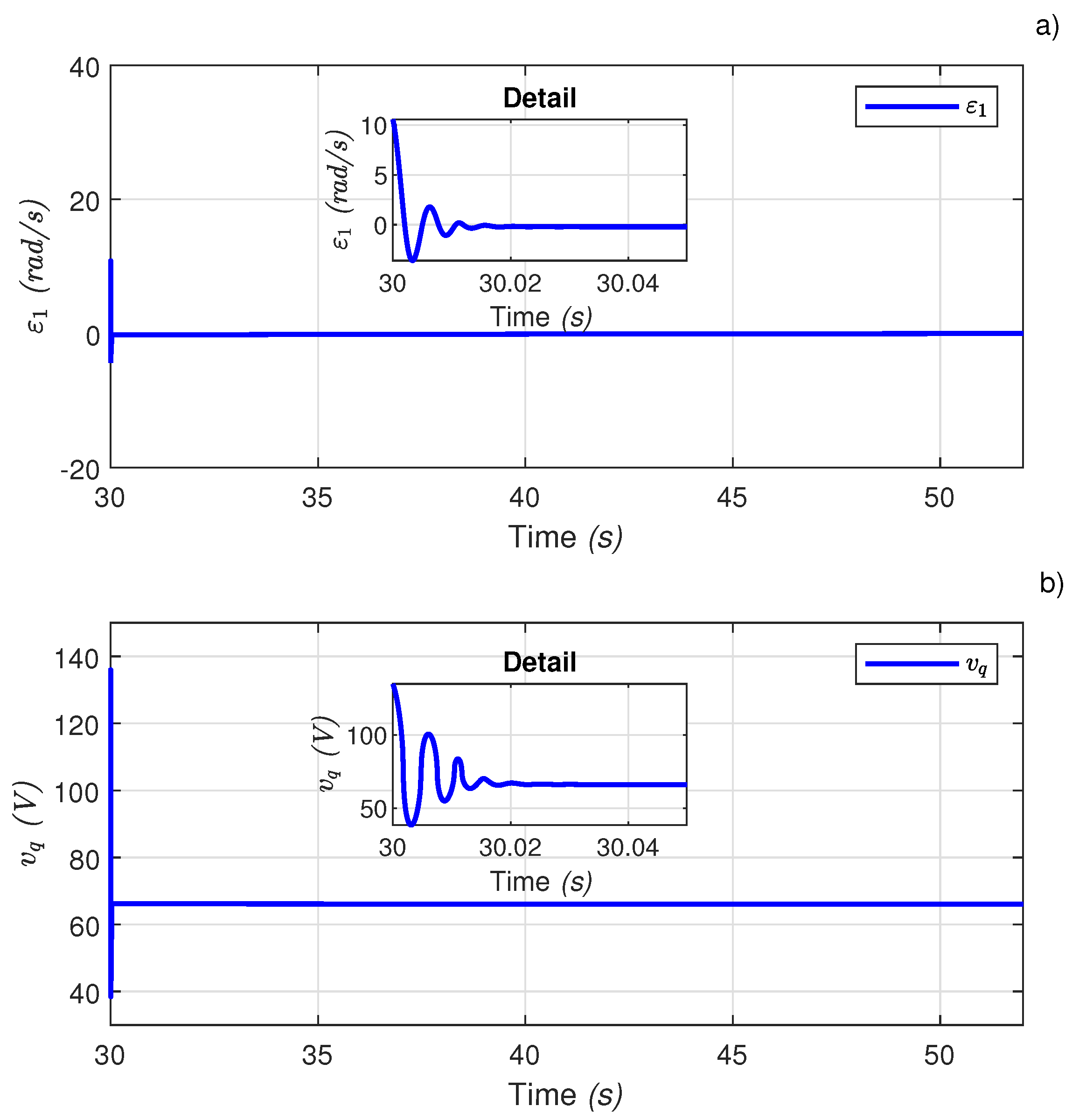
4.2. PMSM and DC-motor Controller-Emulation of Flywheel
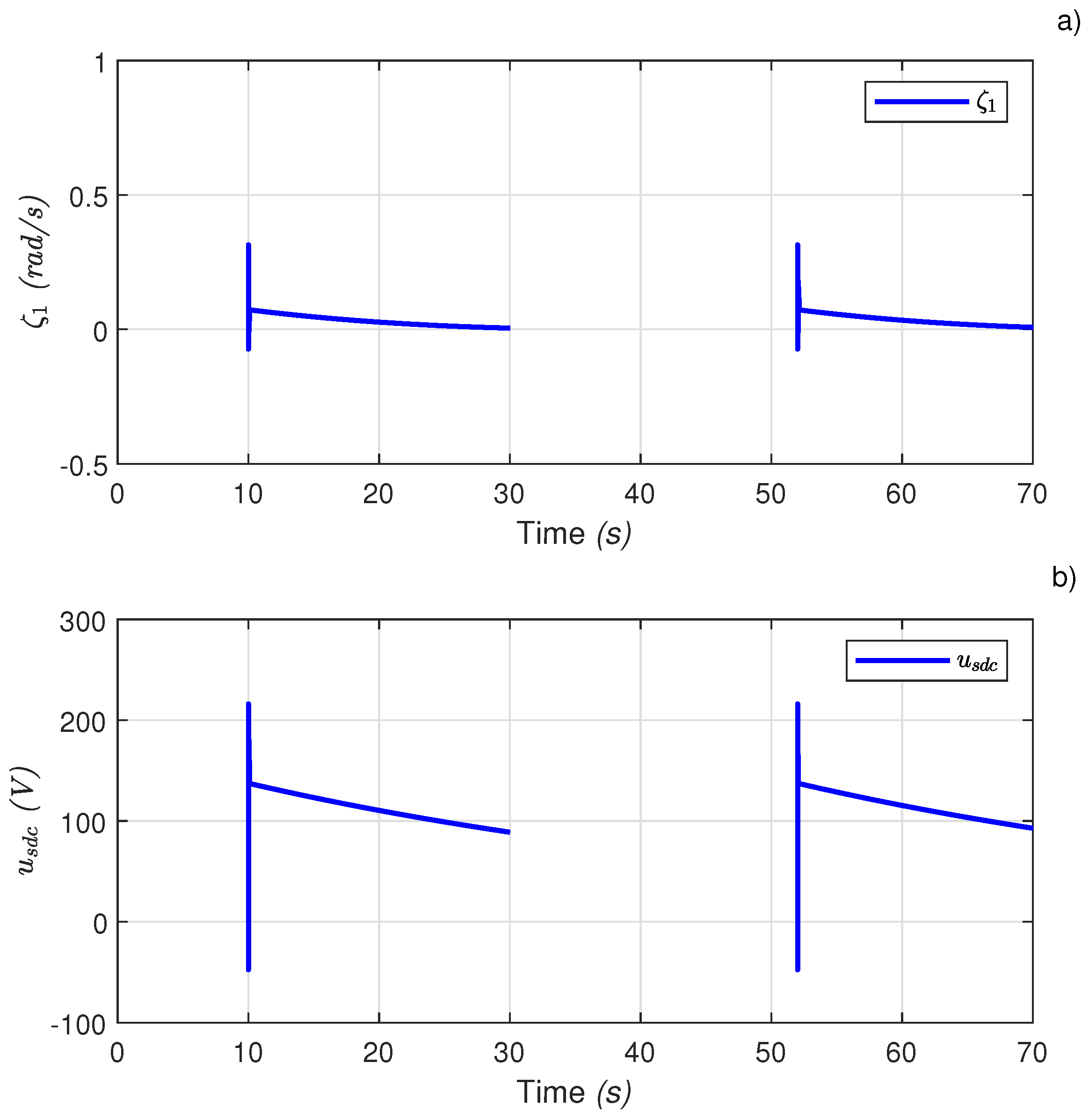
4.3. Power Delivery
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating-Current |
| DC | Direct-Current |
| Direct-Quadrature | |
| FESS | Flywheel Energy Storage System |
| HONN | High Order Neural Network |
| NN | Neural Network |
| NSTC | Neural Super-Twisting Control |
| PMSM | Permanent Magnet Synchronous Machine |
| RMS | Root Mean Square |
| RHONN | Recurrent High Order Neural Network |
| RSFONN | Recurrent Sigmoid First-Order Neural Network |
| RWFONN | Recurrent Wavelet First-Order Neural Network |
| STA | Super-Twisting Algorithm |
| STC | Super-Twisting Control |
| SVPWM | Space Vector Pulse Width Modulation |
| UUB | Uniformly Ultimately Bounded |
Appendix A. Identification Error Boundedness
Appendix B. Closed-Loop Stability Analysis
References
- Bolund, B.; Bernhoff, H.; Leijon, M. Flywheel energy and power storage systems. Renew. Sustain. Energy Rev. 2005, 11, 235–258. [Google Scholar] [CrossRef]
- Soomro, A.; Amiryar, M.E.; Pullen, K.R.; Nankoo, D. Comparison of Performance and Controlling Schemes of Synchronous and Induction Machines Used in Flywheel Energy Storage Systems. Energy Procedia 2018, 151, 100–110. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of Flywheel Energy Storage Systems in the Presence of Uncertainties. IEEE Trans. Sustain. Energy 2019, 10, 36–45. [Google Scholar] [CrossRef]
- Sebastián, R.; Peña-Alzola, R. Control and simulation of a flywheel energy storage for a wind diesel power system. Electr. Power Energy Syst. 2014, 64, 1049–1056. [Google Scholar] [CrossRef]
- Vafakhah, B.; Masiala, M.; Salmon, J.; Knight, A. Emulation of Flywheel Energy Storage Systems With a PMDC Machine. In Proceedings of the 2008 International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2009. [Google Scholar]
- Tria, F.; Srairi, K.; Benchouia, M.; Benbouzid, M.E.H. An integral sliding mode controller with super-twisting algorithm for direct power control of wind generator based on a doubly fed induction generator. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 762–769. [Google Scholar] [CrossRef]
- Wang, J.; Yang, L.; Blalock, C.; Tolbert, L.M. Flywheel Energy Storage Emulation Using Reconfigurable Hardware Test-Bed of Power Converters; Energy Storage Applicatations and Technologies: San Diego, CA, USA, 2013. [Google Scholar]
- Karrari, S.; Baghaee, H.R.; De Carne, G.; Noe, M.; Geisbuesch, J. Adaptive inertia emulation control for high-speed flywheel energy storage systems. IET Gener. Transm. Distrib. 2020, 14, 5047–5059. [Google Scholar] [CrossRef]
- Hedlund, M.; Oliveira, J.G.; Bernhoff, H. Sliding mode 4-quadrant DCDC converter for a flywheel application. Control Eng. Pract. 2013, 21, 473–482. [Google Scholar] [CrossRef]
- Ahsan, H.; Mufti, M.-U.-D. Dynamic performance improvement of a hybrid multimachine system using a flywheel energy storage system. Wind Eng. 2019, 44, 239–252. [Google Scholar] [CrossRef]
- Bowen, C.; Jihua, Z.; Zhang, R. Modeling and Simulation of Permanent Magnet Synchronous Motor Drives. In Proceedings of the Fifth International Conference on Electrical Machines and Systems (ICEMS’2001), Bali, Indonesia, 4–7 August 2001. [Google Scholar]
- He, R.; Han, Q. Dynamics and Stability of Permanent-Magnet Synchronous Motor. Math. Probl. Eng. 2017, 2017, 4923987. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Dong, H.; Ning, B.; Tang, T.; Li, Y. Nonlinear mapping-based feedback technique of dynamic surface control for the chaotic PMSM using neural approximation and parameter identification. IET Control Theory Appl. 2018, 12, 819–827. [Google Scholar] [CrossRef]
- Ewert, P.; Orlowska-Kowalska, T.; Jankowska, K. Effectiveness Analysis of PMSM Motor Rolling Bearing Fault Detectors Based on Vibration Analysis and Shallow Neural Networks. Energies 2021, 14, 712. [Google Scholar] [CrossRef]
- Chapman, S.J. Electric Machines; Mc Graw Hill: New York, NY, USA, 2000. [Google Scholar]
- Castaneda, C.E.; Loukianov, A.G.; Sanchez, E.N.; Castillo-Toledo, B. Discrete-Time Neural Sliding-Mode Block Control for a DC Motor with Controlled Flux. IEEE Trans. Ind. Electron. 2012, 59, 1194–1207. [Google Scholar] [CrossRef]
- Valenzuela, F.A.; Ramírez, R.; Martínez, R.; Morfín, O.A.; Castañeda, C.E. Super-Twisting Algorithm Applied to Velocity Control of DC Motor without Mechanical Sensors Dependence. Energies 2020, 13, 6041. [Google Scholar] [CrossRef]
- Lee, S.-D.; Phuc, B.D.H.; Xu, X.; You, S.S. Roll suppression of marine vessels using adaptive super-twisting sliding mode control synthesis. Ocean Eng. 2019, 195, 106724. [Google Scholar] [CrossRef]
- Amiryar, M.E.; Pullen, K.R. A Review of Flywheel Energy Storage System Technologies and Their Applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Morfín, O.A.; Castañeda, C.E.; Ruiz-Cruz, R.; Valenzuela, F.A.; Murillo, M.A.; Quezada, A.E.; Padilla, N. The Squirrel-Cage Induction Motor Model and Its Parameter Identification Via Steady and Dynamic Tests. Electr. Power Compon. Syst. 2018, 46, 302–315. [Google Scholar] [CrossRef]
- Vázqquez, L.S.; Jurado, F. Continuous-Time Decentralized Wavelet Neural Control for a 2 DOF Robot Manimulator. In Proceedings of the 2014 11th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Ciudad del Carmen, Mexico, 29 September–3 October 2014. [Google Scholar]
- Jurado, F.; Lopez, S. A wavelet neural control scheme for a quadrotor unmanned aerial vehicle. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Magallon, D.A.; Castaneda, C.E.; Jurado, F.; Morfin, O.A. Design of a Morlet wavelet control algorithm using super—Twisting sliding modes applied to an induction machine. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Vázquez, L.A.; Jurado, F.; Alanis, A.Y. Decentralized Identification and Control in Real-Time of a Robot Manipulator via Recurrent Wavelet First-Order Neural Network. Math. Probl. Eng. 2015, 2015, 451049. [Google Scholar] [CrossRef]
- Kosmatopoulos, E.B.; Polycarpou, M.M.; Christodoulou, M.A.; Ioannou, P.A. High-order neural network structures for identication of dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 422–431. [Google Scholar] [CrossRef] [PubMed]
- Loukianov, A.G. Robust Block Decomposition Sliding Mode Control Design. Math. Probl. Eng. 2002, 8, 346–365. [Google Scholar] [CrossRef] [Green Version]
- Utkin, V.; Guldner, J.; Shi, J. Slidin Modes Control in Electromechanical Systems; Taylor & Francis: Abingdon, UK, 1999. [Google Scholar]
- Chalanga, A.; Kamal, S.; Fridman, L.; Bandyopadhyay, B.; Moreno, J.A. Implementation of Super-Twisting Control: Super-Twisting and Higher Order Sliding-Mode Observer-Based Approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Morfin, O.A.; Valenzuela, F.A.; Betancour, R.R.; Castaneda, C.E.; Ruiz-Cruz, R.; Valderrabano-Gonzalez, A. Real-Time SOSM Super-Twisting Combined with Block Control for Regulating Induction Motor Velocity. IEEE Access 2018, 6, 25898–25907. [Google Scholar] [CrossRef]
- Han, Q.; Ham, C.; Phillips, R. PMSM nonlinear robust control for temperature compensation. In Proceedings of the Thirty-Sixth Southeastern Symposium on System Theory, Atlanta, GA, USA, 16 March 2014. [Google Scholar]
- Elbouchikhi, E.; Amirat, Y.; Feld, G.; Benbouzid, M.; Zhou, Z. A Lab-scale Flywheel Energy Storage System: Control Strategy and Domestic Applications. Energies 2020, 13, 653. [Google Scholar] [CrossRef] [Green Version]
- Pillay, P.; Krishnan, R. Modeling, Simulation, and Analysis of Permanent-Magnet Motor Drives, Part I: The Permanent-Magnet Synchronous Motor Drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar] [CrossRef]
- Morfin, O.; Ruiz-Cruz, R.; Hernández, J.; Castañeda, C.; Ramírez-Betancour, R.; Valenzuela-Murillo, F. Real-Time Sensorless Robust Velocity Controller Applied to a DC-motor for Emulating a Wind Turbine. Energies 2021, 14, 868. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, K.H.; Cho, Y.H.; Hong, Y.K. Comparison of harmonic compensation based on wound/squirrel-cage rotor type induction motors with flywheel. In Proceedings of the Third International Power Electronics and Motion Control Conference (IPEMC 2000), Beijing, China, 15–18 August 2000; Volume 2, pp. 531–536. [Google Scholar] [CrossRef]
- Sebastian, R.; Alzola, R.P. Flywheel energy storage systems: Review and simulation for an isolated wind power system. Renew. Sustain. Energy Rev. 2012, 16, 6803–6813. [Google Scholar] [CrossRef]
- Hale, J.K. Ordinary Differential Equations; Wiley InterScience: Hoboken, NJ, USA, 1969. [Google Scholar]
- Rovithakis, G.A.; Christodoulou, M.A. Adaptive Control with Recurrent High-Order Neural Networks, Theory and Industrial Applications; Springer: London, UK, 2000. [Google Scholar]
- Dávila, A.; Moreno, J.A.; Fridman, L. Optimal Lyapunov function selection for reaching time estimation of Super Twisting Algorithm. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009. [Google Scholar]



| PMSM Parameters | Value |
|---|---|
| Stator Resistance R | |
| Inductance | mH |
| Inductance | mH |
| Inertial Moment J | kg·m |
| Damping Coefficient B | N·m ·s/rad |
| Flux Linkage | V·s/rad |
| Pair Poles P | 3 |
| DC-motor Nameplate Data and Parameters | Value |
| Field Voltage | 120 V |
| Field Current | A |
| Armature Voltage | 120 V |
| Armature Current | A |
| Rotor Velocity | 1750 rpm |
| Armature Resistance | |
| Armature Inductance | H |
| Motor Constant | |
| Inertial Moment | N·m·s |
| Frictional Coefficient | N·m·s |
| Neural Network Structure | |||
|---|---|---|---|
| RWFONN | 0.1496 | 0.0311 | 0.0263 |
| RSFONN | 0.0105 | 0.0015 | 0.0286 |
| RHONN | 0.0386 | 0.0032 | 0.0128 |
| Neural Network Structure | ||
|---|---|---|
| RWFONN | 0.0018 | 0.00004 |
| RSFONN | 0.0004 | 0.00005 |
| RHONN | 0.0206 | 0.0009 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magallón, D.A.; Castañeda, C.E.; Jurado, F.; Morfin, O.A. Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System. Energies 2021, 14, 6416. https://doi.org/10.3390/en14196416
Magallón DA, Castañeda CE, Jurado F, Morfin OA. Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System. Energies. 2021; 14(19):6416. https://doi.org/10.3390/en14196416
Chicago/Turabian StyleMagallón, Daniel A., Carlos E. Castañeda, Francisco Jurado, and Onofre A. Morfin. 2021. "Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System" Energies 14, no. 19: 6416. https://doi.org/10.3390/en14196416
APA StyleMagallón, D. A., Castañeda, C. E., Jurado, F., & Morfin, O. A. (2021). Design of a Neural Super-Twisting Controller to Emulate a Flywheel Energy Storage System. Energies, 14(19), 6416. https://doi.org/10.3390/en14196416









