Clustering Methods for Power Quality Measurements in Virtual Power Plant
Abstract
:1. Introduction
- The power quality dataset based on the long-term measurement in a VPP was standardized to cluster analysis.
- The proposed K-means algorithm and agglomerative algorithm were performed to compare the hierarchical and non-hierarchical approach for PQ data, which have different sizes of input data.
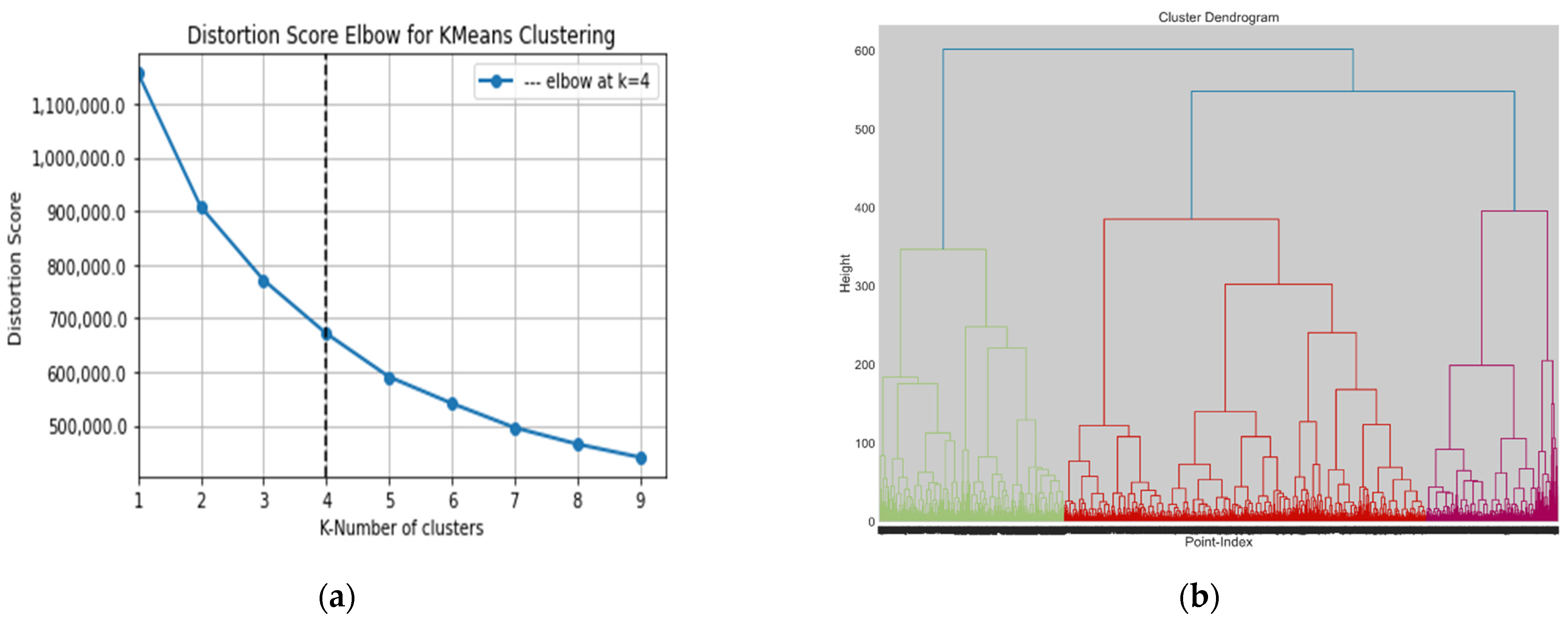
- The elbow method and dendrogram were performed to obtain the optimal number of clusters for PQ data.
- The global index was used for the comparative assessment of PQ parameters between clustering results of the K-means algorithm and agglomerative algorithm.
- The cluster algorithm evaluation and comparison are used to determine which algorithm is suitable for the investigation object.
2. Research Object Description and Methodology
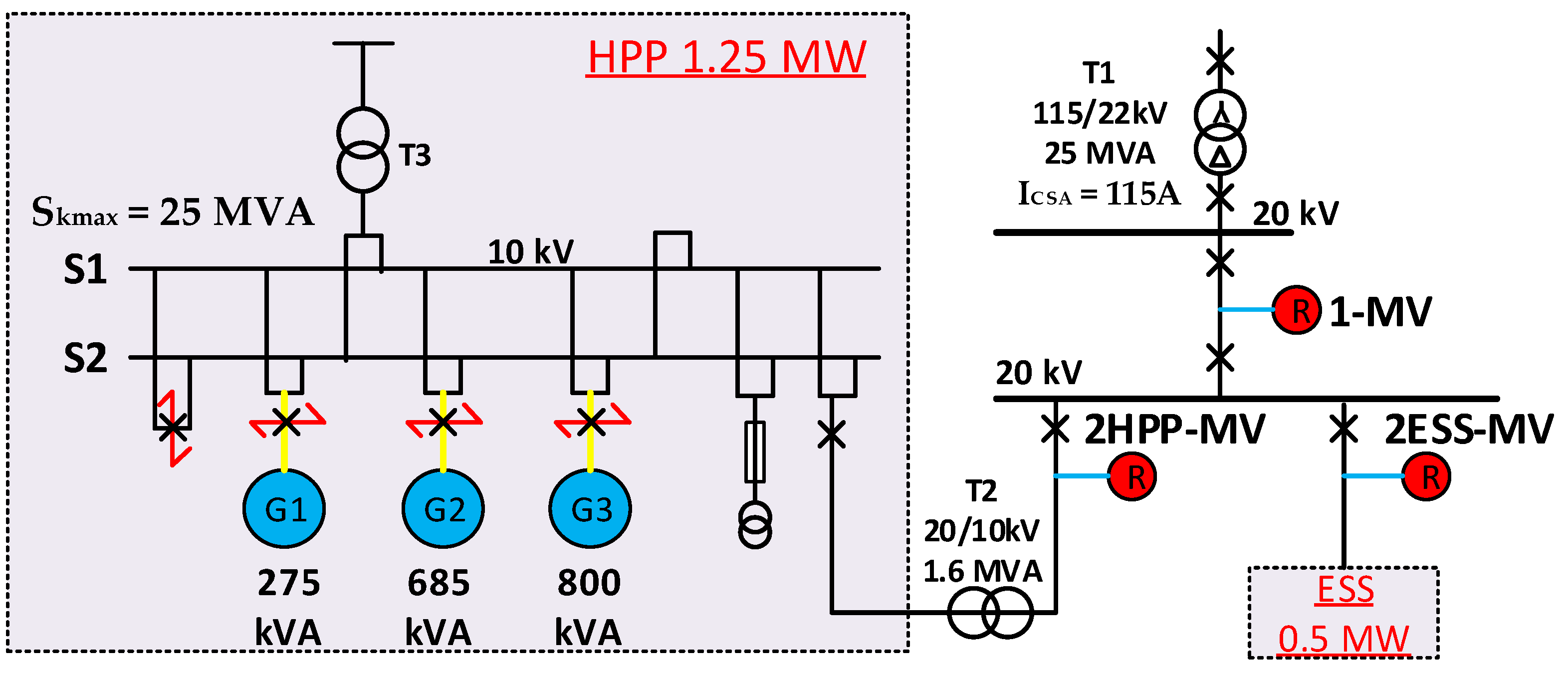
2.1. Object Investigated
2.1.1. First Investigation Object
2.1.2. Second Investigation Object
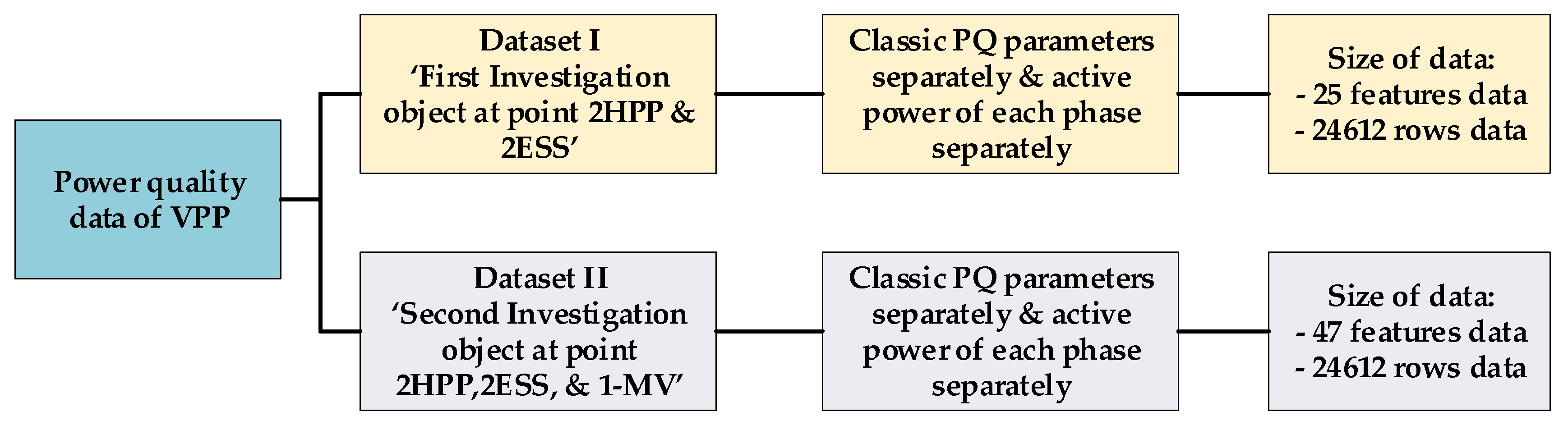
2.2. Parameter of Dataset Description
- Three phases of voltage;
- Three phases of 200 ms minimal voltage;
- Three phases of 200 ms maximal voltage;
- Voltage unbalance;
- Three phases of active power;
- Three phases of total harmonic distortion in voltage;
- Three phases of 200 ms maximum of total harmonic distortion in voltage.
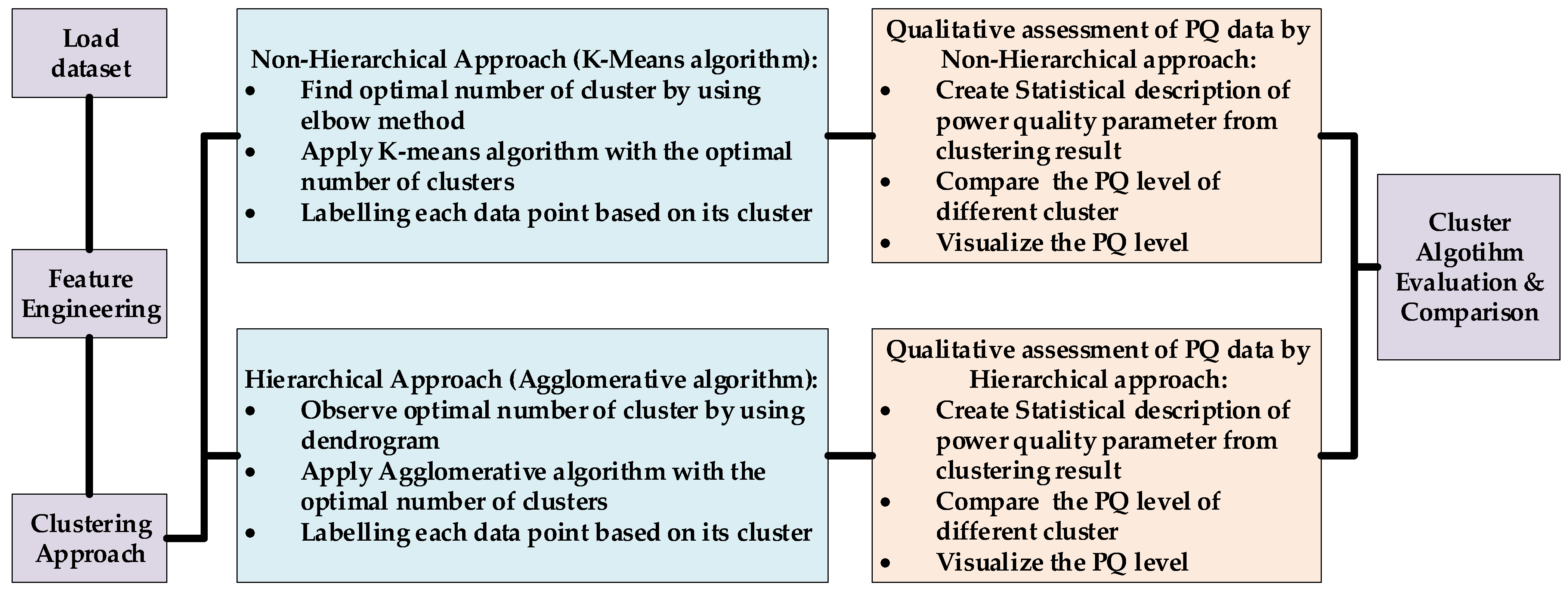
2.3. Proposed Methodology
2.3.1. Load Dataset
2.3.2. Feature Engineering
2.3.3. Clustering Approach
2.3.4. Qualitative Assessment
2.3.5. Cluster Algorithm Evaluation and Comparison
- s: the silhouette coefficient score;
- a: the mean distance between all other points and a sample in the same class;
- b: the mean distance between all other points and a sample in the next closest cluster.
- CH: the Calinski–Harabasz score;
- k: the number of clusters;
- N: the total number of observations (data points);
- SSw: the overall within-cluster variance;
- SSB: the overall between-cluster variance.
3. Result
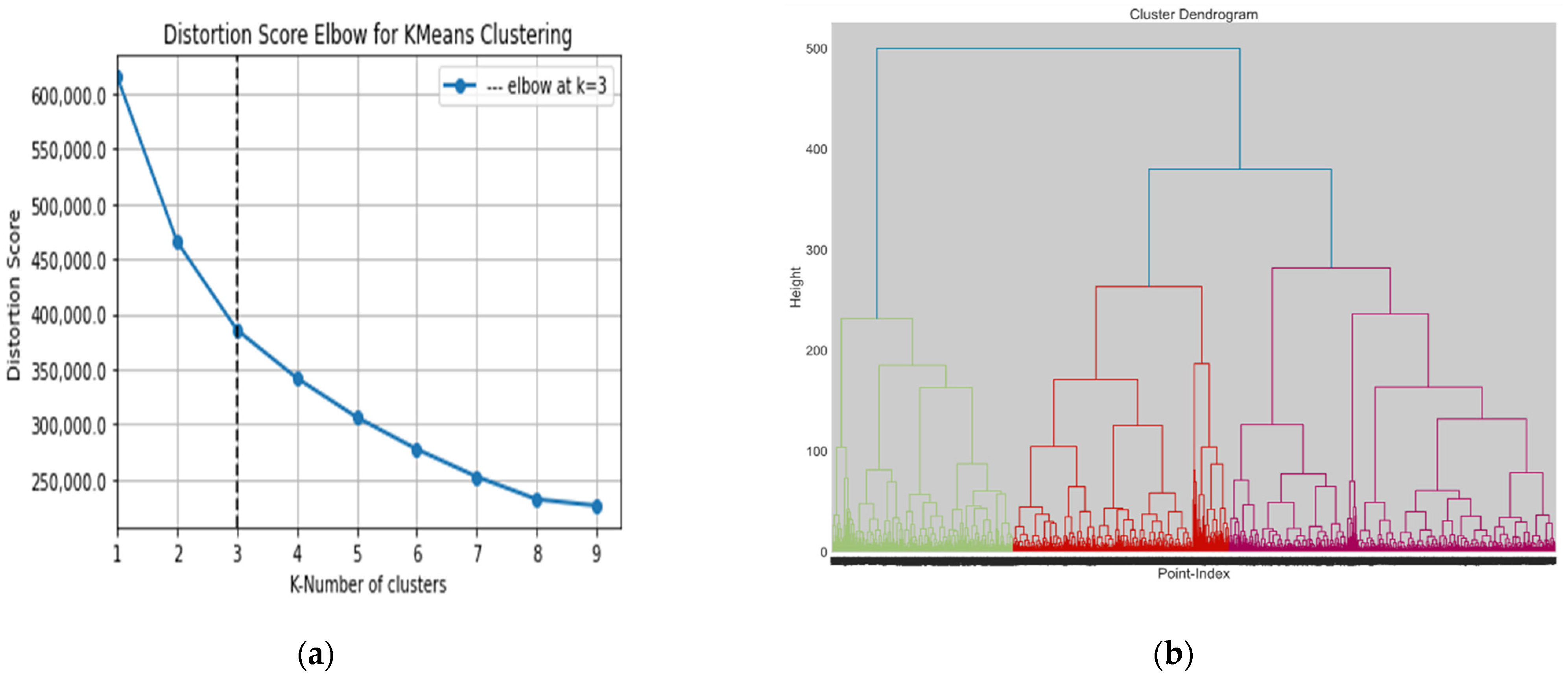
3.1. Optimal Number of Clusters
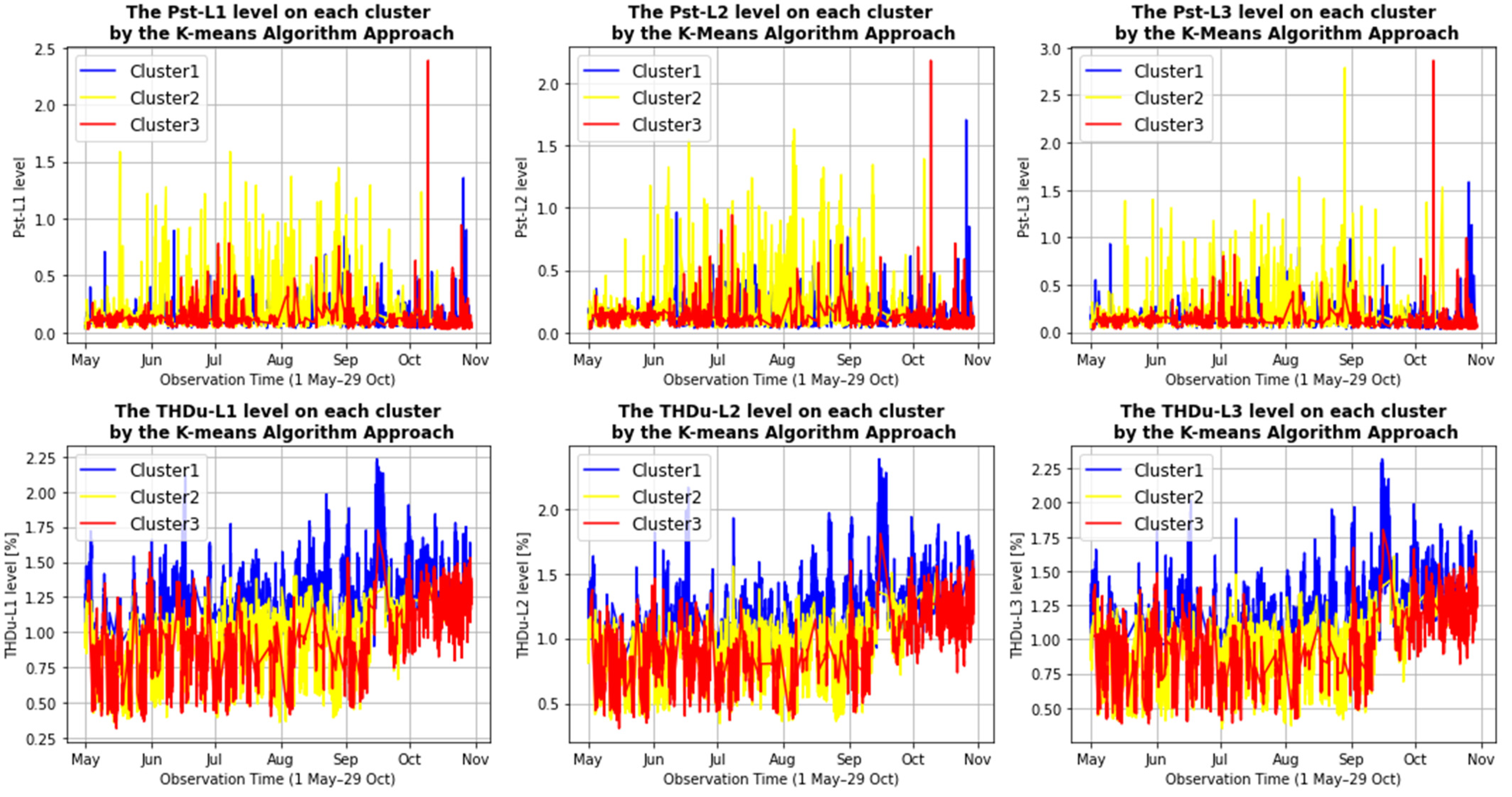
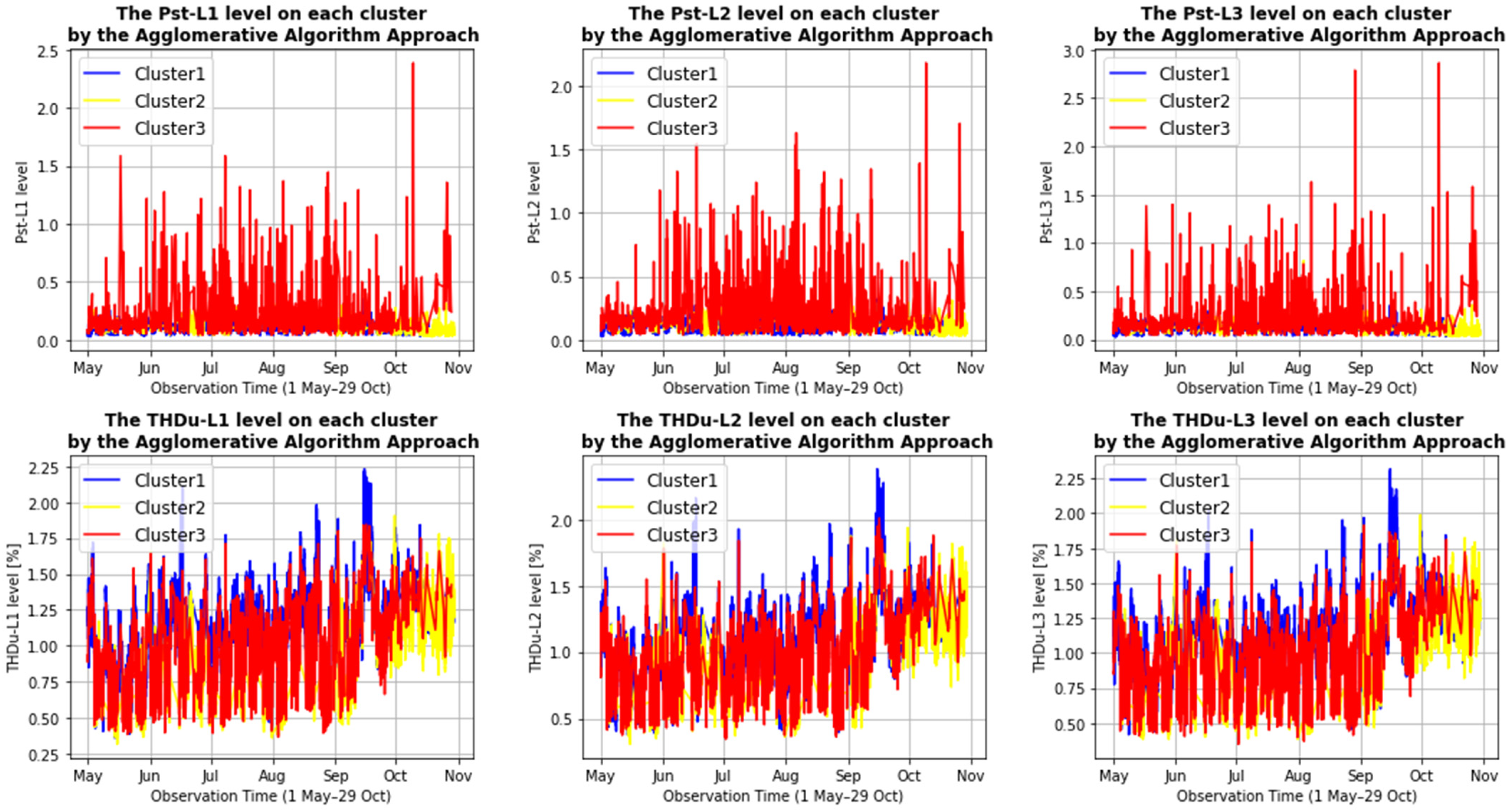
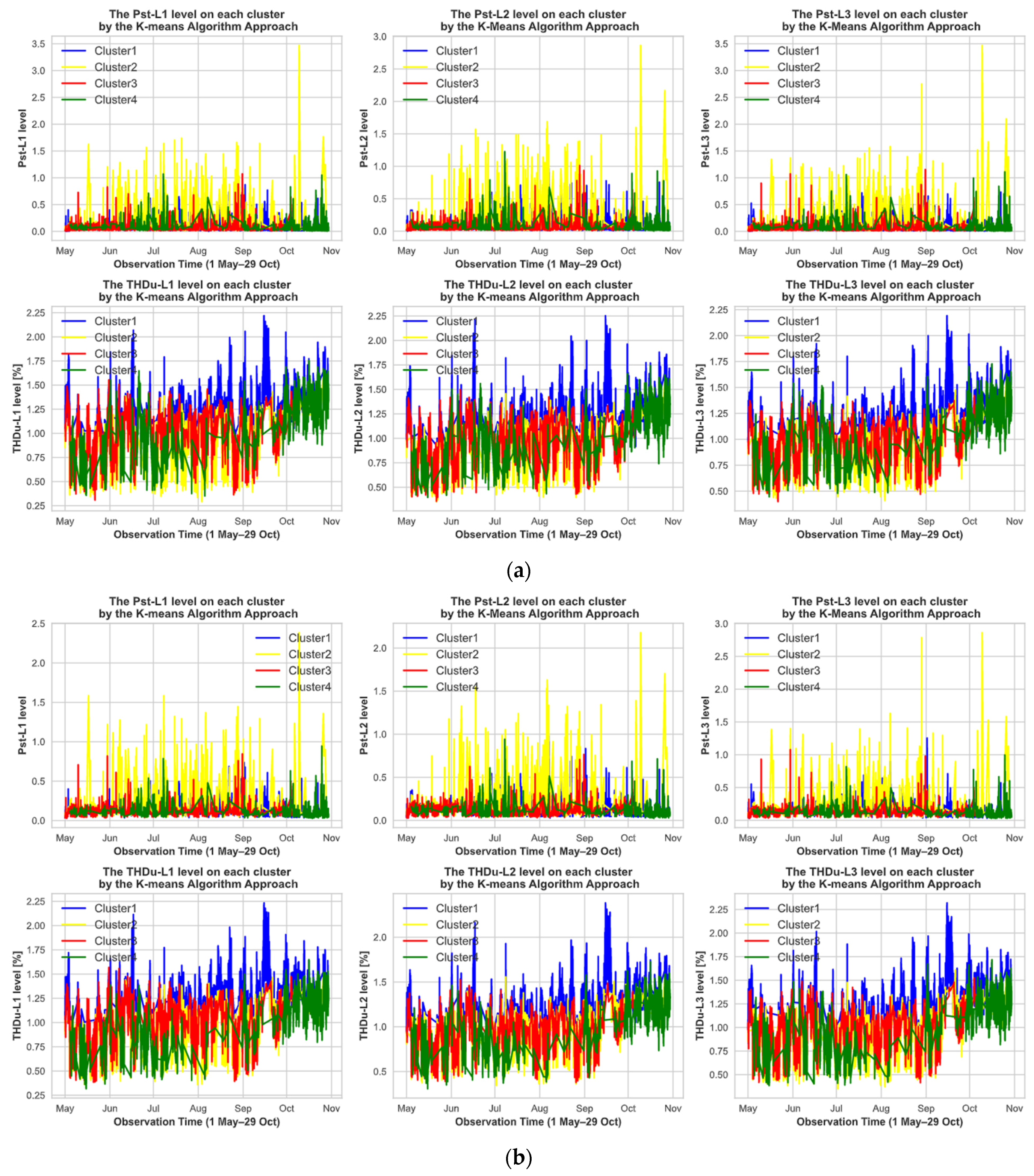
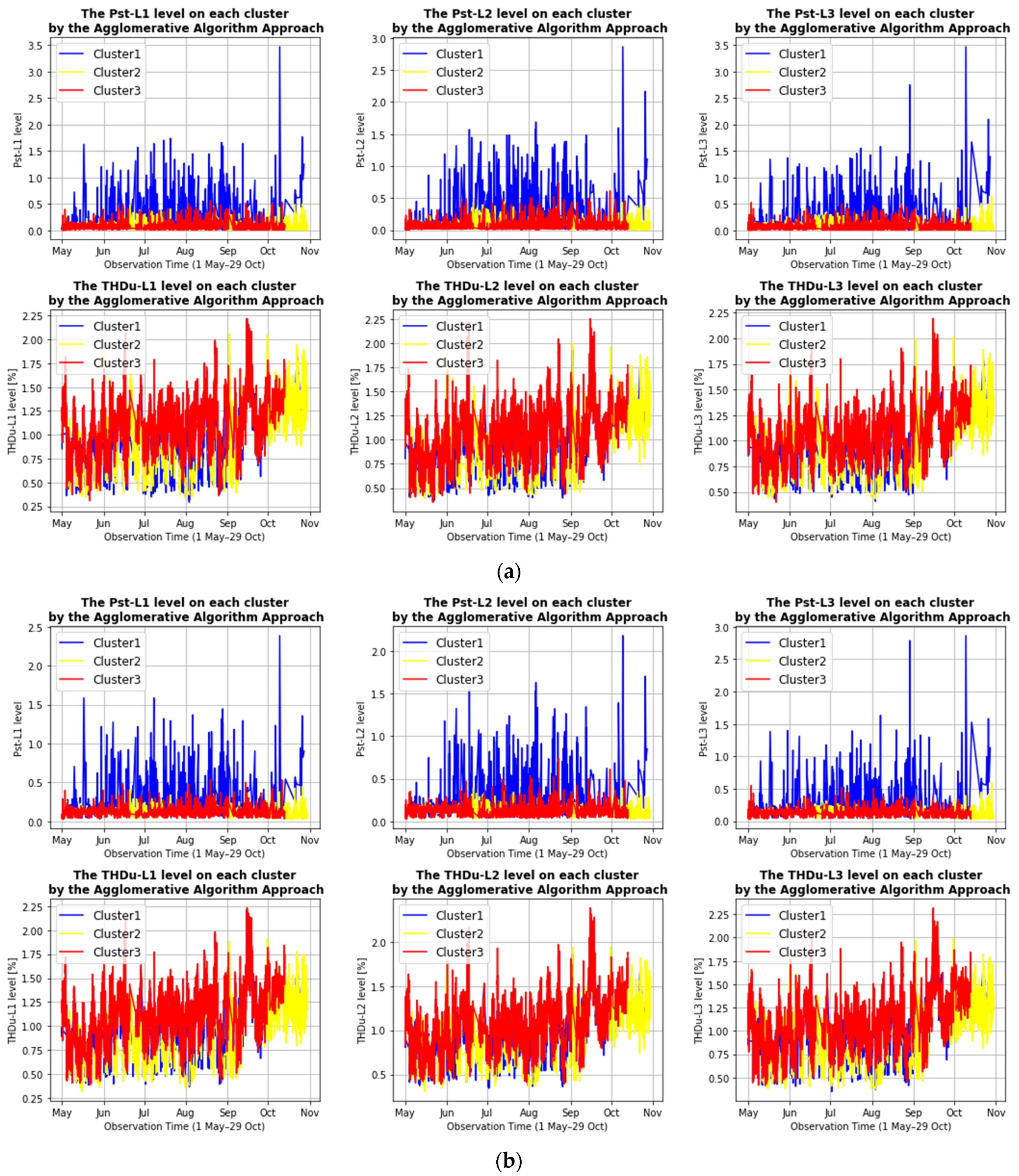
3.2. Qualitative Assessment of Clusters
3.2.1. Qualitative Assessment of the First Investigation Object
3.2.2. Qualitative Assessment of the Second Investigation Object
3.3. Cluster Algorithm Evaluation and Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, Y.-Y. Electric Power Systems Research. Energies 2016, 9, 824. [Google Scholar] [CrossRef] [Green Version]
- Atputharajah, A.; Ramachandaramurthy, V.K.; Pasupuleti, J. Power Quality Problems and Solutions. In Proceedings of the IOP Conference Series Earth and Environmental Science, Putrajaya, Malaysia, 5–6 March 2013; Volume 16, p. 012153. [Google Scholar] [CrossRef] [Green Version]
- Naik, C.A.; Kundu, P. Identification of Short Duration Power Quality Disturbances Employing S-Transform. In Proceedings of the 2011 International Conference on Power and Energy Systems, Chennai, India, 22–24 December 2011; pp. 1–5. [Google Scholar]
- Mekhamer, S.F.; Abdelaziz, A.Y.; Ismael, S.M. Design Practices in Harmonic Analysis Studies Applied to Industrial Electrical Power Systems. Eng. Technol. Appl. Sci. Res. 2013, 3, 467–472. [Google Scholar] [CrossRef]
- More, T.G.; Asabe, P.R.; Chawda, S. Power Quality Issues and It’s Mitigation Techniques. Int. J. Eng. Res. Appl. 2014, 4, 8. [Google Scholar]
- Yadav, J.R.; Vasudevan, K.; Kumar, D.; Shanmugam, P. Power Quality Assessment for Industrial Plants: A Comparative Study. In Proceedings of the 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), IEEE, Sonderborg, Denmark, 23–25 April 2019; pp. 1–6. [Google Scholar]
- Jena, R. Electrical Power Quality. Dep. Electr. Eng. CET BBSR 66. Available online: https://www.cet.edu.in/noticefiles/227_Electrical_Power_Quality-PEEL5403-8th_Sem-Electrical.pdf (accessed on 10 June 2021).
- Crotti, G.; Giordano, D.; D’Avanzo, G.; Femine, A.D.; Gallo, D.; Landi, C.; Luiso, M.; Letizia, P.S.; Barbieri, L.; Mazza, P.; et al. Measurement of Dynamic Voltage Variation Effect on Instrument Transformers for Power Grid Applications. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Barros, J.; Pérez, E.; Diego, R.I. Measurement and Analysis of Voltage Events. In Power Quality; Moreno-Muñoz, A., Ed.; Power Systems; Springer: London, UK, 2007; pp. 73–102. ISBN 978-1-84628-771-8. [Google Scholar]
- Tur, M.R.; Bayindir, R. Comparison of Power Quality Distortion Types and Methods Used in Classification. In Proceedings of the 2020 International Conference on Computational Intelligence for Smart Power System and Sustainable Energy (CISPSSE), Odisha, India, 29–31 July 2020; pp. 1–7. [Google Scholar]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration K-Means Clustering Method and Elbow Method for Identification of the Best Customer Profile Cluster. In Proceedings of the IOP Conference Series Earth and Environmental Science, Banda Aceh, Indonesia, 26–27 September 2018; Volume 336, p. 012017. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Xie, C.; Tang, B.; Liu, R.; Pan, A. The Data Mining Application in the Power Quality Monitoring Data Analysis. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 338–342. [Google Scholar]
- Sangepu, R. Effect of Power Quality Issues in Power System and Its Mitigation by Power Electronics Devices. 2015. Available online: https://www.researchgate.net/publication/325676538_Effect_of_Power_Quality_Issues_in_Power_System_and_Its_Mitigation_by_Power_Electronics_Devices (accessed on 6 June 2021).
- Zakaria, M.F.; Ramachandaramurthy, V.K. Assessment and Mitigation of Power Quality Problems for Puspati Triga Reactor (RTP). J. Appl. Phys. 2017, 020011. [Google Scholar] [CrossRef] [Green Version]
- Gul, O. An Assessment of Power Quality and Electricity Consumer’s Rights in Restructured Electricity Market in Turkey. Electric. Power Qual. Utilis. J. 2008, 14, 29–34. [Google Scholar]
- Mindykowski, J. Fundamentals of Electrical Power Quality Assessment. 2003. Available online: https://www.imeko.org/publications/wc-2003/PWC-2003-TC4-027.pdf (accessed on 20 June 2021).
- Batkiewicz-Pantula, M. The Problem of Selected Parameters of the Power Quality in the Perspective of Tightening Normative Requirements. In Proceedings of the 2019 Modern Electric Power Systems (MEPS), Wroclaw, Poland, 9 September 2019; pp. 1–4. [Google Scholar]
- Legarreta, A.E.; Figueroa, J.H.; Bortolin, J.A. An IEC 61000-4-30 Class a-Power Quality Monitor: Development and Performance Analysis. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2011; pp. 1–6. [Google Scholar]
- What Is the IEC61000-4-30 Standard for Power Quality Analysers? Power Qual. Anal. Available online: https://www.fluke.com/en-gb/learn/blog/power-quality/what-does-the-iec-61000-4-30-class-a-standard-mean-to-me (accessed on 15 June 2021).
- Bollen, M.H.J.; Milanović, J.V.; Čukalevski, N. CIGRE/CIRED JWG C4.112-Power Quality Monitoring. Renew. Energy Power Qual. J. 2014. [Google Scholar] [CrossRef]
- Ferracci, P. Cahier Technique No. 199 Power Quality. Power Qual. 2000. Available online: https://eduscol.education.fr/sti/sites/eduscol.education.fr.sti/files/ressources/techniques/3361/3361-ect199.pdf (accessed on 14 July 2021).
- Karabiber, A. Controllable AC/DC Integration for Power Quality Improvement in Microgrids. Adv. Electr. Comput. Eng. 2019, 19, 97–104. [Google Scholar] [CrossRef]
- Vokas, G.A.; Langouranis, P.A.; Kontaxis, P.A.; Topalis, F.V. Analysis of Power Quality Field Measurements and Considerations on the Power Quality Standard 14. Available online: https://www.researchgate.net/publication/312031589_Analysis_of_power_quality_field_measurements_and_considerations_on_the_power_quality_standard (accessed on 21 June 2021).
- Sezi, I.T.; Zimmer, I.K.; Lang, J. Power Quality Monitoring and Analysis System. In Proceedings of the 18th International Conference and Exhibition on Electricity Distribution (CIRED 2005), Turin, Italy, 15–18 June 2005; Volume 2005, p. v2-62-v2-62. [Google Scholar]
- Nourollah, S.; Moallem, M. A data mining method for obtaining global power quality index. In Proceedings of the 2011 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011. [Google Scholar] [CrossRef]
- Asheibi, A.; Stirling, D.; Robinson, D. Identification of Load Power Quality Characteristics Using Data Mining. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 157–162. [Google Scholar]
- Larose, D.T. Data Mining Methods and Models; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Larose, D.T. Discovering Knowledge in Data: An Introduction to Data Mining; Wiley-Interscience: Hoboken, NJ, USA, 2005; ISBN 978-0-471-66657-8. [Google Scholar]
- Ghavidel, S.; Li, L.; Aghaei, J.; Yu, T.; Zhu, J. A Review on the Virtual Power Plant: Components and Operation Systems. In Proceedings of the 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, Australia, 28 September–1 October 2016; pp. 1–6. [Google Scholar]
- Taylor, K. Oracle Data Mining Concepts 11g Release 2 (11.2). Doc. E1680807 Oracle 2013. Available online: https://docs.oracle.com/cd/E11882_01/datamine.112/e16808/title.htm (accessed on 14 July 2021).
- Ullman, S.; Poggio, T.; Harari, D.; Zysman, D.; Seibert, D. Unsupervised Learn. Slides 2014, Fall 2014 Lecture 13. Available online: http://www.mit.edu/~9.54/fall14/Classes/class13.html (accessed on 24 August 2021).
- Jasiński, M.; Sikorski, T.; Kaczorowska, D.; Rezmer, J.; Suresh, V.; Leonowicz, Z.; Kostyła, P.; Szymańda, J.; Janik, P.; Bieńkowski, J.; et al. A Case Study on Data Mining Application in a Virtual Power Plant: Cluster Analysis of Power Quality Measurements. Energies 2021, 14, 974. [Google Scholar] [CrossRef]
- Dandea, V.; Grigoras, G.; Neagu, B.-C.; Scarlatache, F. K-Means Clustering-Based Data Mining Methodology to Discover the Prosumers’ Energy Features. In Proceedings of the 2021 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25 March 2021; pp. 1–5. [Google Scholar]
- Jasiński, M.; Sikorski, T.; Kaczorowska, D.; Rezmer, J.; Suresh, V.; Leonowicz, Z.; Kostyła, P.; Szymańda, J.; Janik, P.; Bieńkowski, J.; et al. A Case Study on a Hierarchical Clustering Application in a Virtual Power Plant: Detection of Specific Working Conditions from Power Quality Data. Energies 2021, 14, 907. [Google Scholar] [CrossRef]
- Jasiński, M.; Sikorski, T.; Leonowicz, Z.; Borkowski, K.; Jasińska, E. The Application of Hierarchical Clustering to Power Quality Measurements in an Electrical Power Network with Distributed Generation. Energies 2020, 13, 2407. [Google Scholar] [CrossRef]
- Neagu, B.-C.; Grigoras, G. A Fair Load Sharing Approach Based on Microgrid Clusters and Transactive Energy Concept. In Proceedings of the 2020 12th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2020; pp. 1–4. [Google Scholar]
- Jasilski, M.; Borkowski, K.; Sikorski, T.; Kostvla, P. Cluster Analysis for Long-Term Power Quality Data in Mining Electrical Power Network. In Proceedings of the 2018 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 18–22 June 2018; pp. 1–5. [Google Scholar]
- Jureedi, N.V.V. Karunakar.; Rosalina, K.M.; Prema Kumar, N. Clustering Analysis and Its Application in Electrical Distribution System. Int. J. Recent Adv. Eng. Technol. 2020, 8, 38–43. [Google Scholar] [CrossRef]
- Determining the Optimal Number of Clusters: 3 Must Know Methods. Available online: https://www.datanovia.com/en/lessons/determining-the-optimal-number-of-clusters-3-must-know-methods/ (accessed on 22 June 2021).
- Patil, C.; Baidari, I. Estimating the Optimal Number of Clusters k in a Dataset Using Data Depth. Data Sci. Eng. 2019, 4, 132–140. [Google Scholar] [CrossRef] [Green Version]
- Aksan, F.F.; Azizah, A.; Prihastomo, E.D. Prediction of Earthquake Magnitude Based on the Clusters in Sulawesi Island, Indonesia. Int. J. Sci. Res. 2021, 7, 7. [Google Scholar]
- Umargono, E.; Suseno, J.E.; Vincensius Gunawan, S.K. K-Means Clustering Optimization Using the Elbow Method and Early Centroid Determination Based on Mean and Median Formula. In Proceedings of the 2nd International Seminar on Science and Technology (ISSTEC 2019), Yogyakarta, Indonesia, 25 November 2019; Atlantis Press: Yogyakarta, Indonesia, 2020. [Google Scholar]
- EN 50160: Voltage Characteristics of Electricity Supplied by Public Distribution Network. Available online: https://orgalim.eu/position-papers/en-50160-voltage-characteristics-electricity-supplied-public-distribution-system (accessed on 22 June 2021).
- Scikit-Learn: Machine Learning in Python—Scikit-Learn 0.24.2 Documentation. Available online: https://scikit-learn.org/stable/ (accessed on 21 June 2021).
- Welcome to Python.Org. Available online: https://www.python.org/ (accessed on 4 May 2021).
- What Are the Standards for Power Quality Measurements?—Power Quality Analysers. Available online: https://powerqualityanalysers.com/knowledgebase/what-are-the-standards-for-power-quality-measurements/ (accessed on 24 August 2021).
- Kassambara, A. Multivariate Analysis 1: Practical Guide To Cluster Analysis in R, 1st ed.; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2015; Volume 1, ISBN 1542462703. [Google Scholar]
- Rençberoğlu, E. Fundamental Techniques of Feature Engineering for Machine Learning. Available online: https://towardsdatascience.com/feature-engineering-for-machine-learning-3a5e293a5114 (accessed on 19 April 2021).
- Aggarwal, C.C. Data Mining; Springer International Publishing: Cham, Germany, 2015; ISBN 978-3-319-14141-1. [Google Scholar]
- Sklearn Preprocessing StandardScaler—Scikit-Learn 0.24.2 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html (accessed on 16 June 2021).
- Pandas-Python Data Analysis Library. Available online: https://pandas.pydata.org/ (accessed on 16 June 2021).
- Sklearn Cluster KMeans—Scikit-Learn 0.24.2 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html (accessed on 30 April 2021).
- Sklearn Cluster AgglomerativeClustering—Scikit-Learn 0.24.2 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html (accessed on 16 June 2021).
- Manimaran Clustering Evaluation Strategies. Available online: https://towardsdatascience.com/clustering-evaluation-strategies-98a4006fcfc (accessed on 16 June 2021).
- Sklearn Metrics Silhouette_score—Scikit-Learn 0.24.2 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.silhouette_score.html (accessed on 14 June 2021).
- Nanjundan, S.; Sankaran, S.; Arjun, C.R.; Anand, G.P. Identifying the Number of Clusters for K-Means: A Hypersphere Density Based Approach. Available online: https://arxiv.org/abs/1912.00643 (accessed on 22 June 2021).
- Wei, H. How to Measure Clustering Performances When There Are No Ground Truth? Available online: https://medium.com/@haataa/how-to-measure-clustering-performances-when-there-are-no-ground-truth-db027e9a871c (accessed on 14 June 2021).
- Milligan, G.W.; Cooper, M.C. An Examination of Procedures for Determining the Number of Clusters in a Data Set. Available online: https://link.springer.com/article/10.1007/BF02294245 (accessed on 22 June 2021).
- Calinski-Harabasz Index and Boostrap Evaluation with Clustering Methods. Available online: https://ethen8181.github.io/machine-learning/clustering_old/clustering/clustering.html (accessed on 23 June 2021).
- Kutbay, U. Partitional Clustering. In Recent Applications in Data Clustering; Pirim, H., Ed.; InTech: Nappanee, IN, USA, 2018; ISBN 978-1-78923-526-5. [Google Scholar]
- Yellowbrick: Machine Learning Visualization—Yellowbrick v1.3.Post1 Documentation. Available online: https://www.scikit-yb.org/en/latest/ (accessed on 16 June 2021).
- SciPy.Org. Available online: https://www.scipy.org/ (accessed on 16 June 2021).
- Janik, P.; Sikorski, T. Control in Electrical Power Engineering; Wiley: New York, NY, USA, 2009; Volume 168, pp. 1–65. [Google Scholar]
- Markiewicz, H. 5.4.2 Standard EN 50160 Voltage Characteristics in Public Distribution Systems. Available online: http://copperalliance.org.uk/uploads/2018/03/542-standard-en-50160-voltage-characteristics-in.pdf (accessed on 22 June 2021).
- Prabhu, P. Method for Determining Optimum Number of Clusters; Social Science Research Network: Rochester, NY, USA, 2012. [Google Scholar]
- Wang, X.; Xu, Y. An Improved Index for Clustering Validation Based on Silhouette Index and Calinski-Harabasz Index. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 052024. [Google Scholar] [CrossRef] [Green Version]
- Subbalakshmi, C.; Krishna, G.R.; Rao, S.K.M.; Rao, P.V. A Method to Find Optimum Number of Clusters Based on Fuzzy Silhouette on Dynamic Data Set. Procedia Comput. Sci. 2015, 46, 346–353. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Xu, Z.; Liu, F. Method for Determining the Optimal Number of Clusters Based on Agglomerative Hierarchical Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 3007–3017. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Masud, M.d.A.; Mazumder, B. Estimation of the Number of Clusters Based on Simplical Depth. In Proceedings of the 2020 2nd International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 19 December 2020; pp. 1–5. [Google Scholar]
- Visual Studio Code-Code Editing. Redefined. Available online: https://code.visualstudio.com/ (accessed on 15 July 2021).
| Parameter | Voltage Characteristic |
|---|---|
| Voltage | 10% of declared voltage |
| Short-term flicker severity | 1.0 |
| Total harmonic distortion in voltage | 8% |
| Voltage unbalance | 2% |
| The PQ Parameter Level at Measurement Points 2HPP-MV and 2ESS-MV | ||||||||
|---|---|---|---|---|---|---|---|---|
| Clustering Algorithm | Cluster | Value | Pst | THDu (%) | ||||
| L1 | L2 | L3 | L1 | L2 | L3 | |||
| K-means Approach | Cluster 1 | Mean | 0.111 | 0.115 | 0.125 | 1.3 | 1.3 | 1.3 |
| Min | 0.032 | 0.028 | 0.03 | 0.6 | 0.5 | 0.6 | ||
| Max | 1.358 | 1.704 | 1.584 | 2.2 | 2.4 | 2.3 | ||
| Cluster 2 | Mean | 0.138 | 0.143 | 0.147 | 0.8 | 0.8 | 0.8 | |
| Min | 0.034 | 0.032 | 0.04 | 0.4 | 0.3 | 0.4 | ||
| Max | 1.586 | 1.63 | 2.788 | 1.5 | 1.6 | 1.6 | ||
| Cluster 3 | Mean | 0.101 | 0.107 | 0.111 | 1 | 1 | 1 | |
| Min | 0.028 | 0.024 | 0.03 | 0.3 | 0.3 | 0.4 | ||
| Max | 2.386 | 2.18 | 2.864 | 1.7 | 1.8 | 1.8 | ||
| Agglomerative Approach | Cluster 1 | Mean | 0.104 | 0.111 | 0.119 | 1.158 | 1.108 | 1.142 |
| Min | 0.028 | 0.028 | 0.03 | 0.36 | 0.375 | 0.403 | ||
| Max | 0.36 | 0.352 | 0.412 | 2.234 | 2.384 | 2.319 | ||
| Cluster 2 | Mean | 0.096 | 0.1 | 0.104 | 0.994 | 1.007 | 1.031 | |
| Min | 0.028 | 0.024 | 0.03 | 0.317 | 0.308 | 0.378 | ||
| Max | 0.814 | 0.658 | 0.82 | 1.907 | 1.938 | 1.99 | ||
| Cluster 3 | Mean | 0.159 | 0.163 | 0.167 | 0.905 | 0.886 | 0.894 | |
| Min | 0.04 | 0.038 | 0.036 | 0.366 | 0.345 | 0.351 | ||
| Max | 2.386 | 2.18 | 2.864 | 1.846 | 2.011 | 1.914 | ||
| The PQ Parameter Level at Measurement Point 1-MV | ||||||||
|---|---|---|---|---|---|---|---|---|
| Clustering Algorithm | Cluster | Value | Pst | THDu (%) | ||||
| L1 | L2 | L3 | L1 | L2 | L3 | |||
| K-means Approach | Cluster 1 | Mean | 0.064 | 0.06 | 0.058 | 0.933 | 0.878 | 0.913 |
| Min | 0.006 | 0.008 | 0.006 | 0.308 | 0.357 | 0.4 | ||
| Max | 1.074 | 1.012 | 1.154 | 1.553 | 1.498 | 1.422 | ||
| Cluster 2 | Mean | 0.121 | 0.113 | 0.114 | 0.778 | 0.785 | 0.803 | |
| Min | 0.012 | 0.014 | 0.014 | 0.293 | 0.354 | 0.409 | ||
| Max | 3.47 | 2.864 | 3.47 | 1.587 | 1.584 | 1.56 | ||
| Cluster 3 | Mean | 0.065 | 0.064 | 0.061 | 1.382 | 1.338 | 1.33 | |
| Min | 0.004 | 0 | 0.006 | 0.61 | 0.519 | 0.671 | ||
| Max | 0.87 | 0.968 | 0.844 | 2.218 | 2.252 | 2.191 | ||
| Cluster 4 | Mean | 0.07 | 0.068 | 0.066 | 1.121 | 1.082 | 1.112 | |
| Min | 0.006 | 0.002 | 0.004 | 0.351 | 0.397 | 0.446 | ||
| Max | 1.07 | 1.226 | 1.11 | 1.755 | 1.743 | 1.727 | ||
| Agglomerative Approach | Cluster 1 | Mean | 0.148 | 0.138 | 0.14 | 0.758 | 0.764 | 0.784 |
| Min | 0.014 | 0.014 | 0.008 | 0.293 | 0.354 | 0.409 | ||
| Max | 3.47 | 2.864 | 3.47 | 1.953 | 1.929 | 1.944 | ||
| Cluster 2 | Mean | 0.067 | 0.064 | 0.063 | 1.068 | 1.04 | 1.071 | |
| Min | 0.006 | 0.002 | 0.004 | 0.335 | 0.378 | 0.433 | ||
| Max | 0.506 | 0.444 | 0.654 | 2.057 | 1.999 | 2.014 | ||
| Cluster 3 | Mean | 0.061 | 0.06 | 0.057 | 1.147 | 1.096 | 1.108 | |
| Min | 0.004 | 0 | 0.006 | 0.308 | 0.357 | 0.4 | ||
| Max | 0.57 | 0.744 | 0.528 | 2.218 | 2.252 | 2.191 | ||
| The PQ parameter level at measurement points 2HPP-MV and 2ESS-MV | ||||||||
| K-means Approach | Cluster 1 | Mean | 0.111 | 0.119 | 0.124 | 0.934 | 0.874 | 0.919 |
| Min | 0.028 | 0.028 | 0.032 | 0.384 | 0.378 | 0.415 | ||
| Max | 0.846 | 0.766 | 1.078 | 1.569 | 1.526 | 1.526 | ||
| Cluster 2 | Mean | 0.152 | 0.156 | 0.16 | 0.81 | 0.802 | 0.807 | |
| Min | 0.04 | 0.038 | 0.04 | 0.36 | 0.345 | 0.351 | ||
| Max | 2.386 | 2.18 | 2.864 | 1.471 | 1.556 | 1.608 | ||
| Cluster 3 | Mean | 0.111 | 0.116 | 0.125 | 1.392 | 1.366 | 1.383 | |
| Min | 0.032 | 0.028 | 0.03 | 0.552 | 0.537 | 0.613 | ||
| Max | 0.736 | 0.982 | 1.254 | 2.234 | 2.384 | 2.319 | ||
| Cluster 4 | Mean | 0.097 | 0.1 | 0.105 | 1.027 | 1.033 | 1.057 | |
| Min | 0.028 | 0.024 | 0.03 | 0.317 | 0.308 | 0.385 | ||
| Max | 0.944 | 0.942 | 0.996 | 1.648 | 1.727 | 1.718 | ||
| Agglomerative Approach | Cluster 1 | Mean | 0.171 | 0.174 | 0.179 | 0.792 | 0.779 | 0.786 |
| Min | 0.04 | 0.038 | 0.04 | 0.366 | 0.345 | 0.351 | ||
| Max | 2.386 | 2.18 | 2.864 | 1.801 | 1.865 | 1.914 | ||
| Cluster 2 | Mean | 0.097 | 0.101 | 0.105 | 0.991 | 1.004 | 1.026 | |
| Min | 0.028 | 0.024 | 0.03 | 0.317 | 0.308 | 0.378 | ||
| Max | 0.452 | 0.398 | 0.602 | 1.907 | 1.938 | 1.99 | ||
| Cluster 3 | Mean | 0.11 | 0.117 | 0.124 | 1.159 | 1.11 | 1.14 | |
| Min | 0.028 | 0.028 | 0.03 | 0.388 | 0.391 | 0.418 | ||
| Max | 0.54 | 0.742 | 0.552 | 2.234 | 2.384 | 2.319 | ||
| Object Dataset | Cluster Algorithm | Find Optimal Number Method | Optimal Number of Clusters | Clustering Performance Evaluation Metric | |
|---|---|---|---|---|---|
| Silhouette Coefficient | Calinski–Harabasz Index | ||||
| Dataset I | K-Means | Elbow method | 3 | 0.235 | 7336.44 |
| Agglomerative | Dendrogram | 3 | 0.201 | 5811.29 | |
| Dataset II | K-Means | Elbow method | 4 | 0.213 | 5923.020 |
| Agglomerative | Dendrogram | 3 | 0.219 | 4954.945 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksan, F.; Jasiński, M.; Sikorski, T.; Kaczorowska, D.; Rezmer, J.; Suresh, V.; Leonowicz, Z.; Kostyła, P.; Szymańda, J.; Janik, P. Clustering Methods for Power Quality Measurements in Virtual Power Plant. Energies 2021, 14, 5902. https://doi.org/10.3390/en14185902
Aksan F, Jasiński M, Sikorski T, Kaczorowska D, Rezmer J, Suresh V, Leonowicz Z, Kostyła P, Szymańda J, Janik P. Clustering Methods for Power Quality Measurements in Virtual Power Plant. Energies. 2021; 14(18):5902. https://doi.org/10.3390/en14185902
Chicago/Turabian StyleAksan, Fachrizal, Michał Jasiński, Tomasz Sikorski, Dominika Kaczorowska, Jacek Rezmer, Vishnu Suresh, Zbigniew Leonowicz, Paweł Kostyła, Jarosław Szymańda, and Przemysław Janik. 2021. "Clustering Methods for Power Quality Measurements in Virtual Power Plant" Energies 14, no. 18: 5902. https://doi.org/10.3390/en14185902
APA StyleAksan, F., Jasiński, M., Sikorski, T., Kaczorowska, D., Rezmer, J., Suresh, V., Leonowicz, Z., Kostyła, P., Szymańda, J., & Janik, P. (2021). Clustering Methods for Power Quality Measurements in Virtual Power Plant. Energies, 14(18), 5902. https://doi.org/10.3390/en14185902











