Optimal Planning of Remote Area Electricity Supply Systems: Comprehensive Review, Recent Developments and Future Scopes
Abstract
:1. Introduction
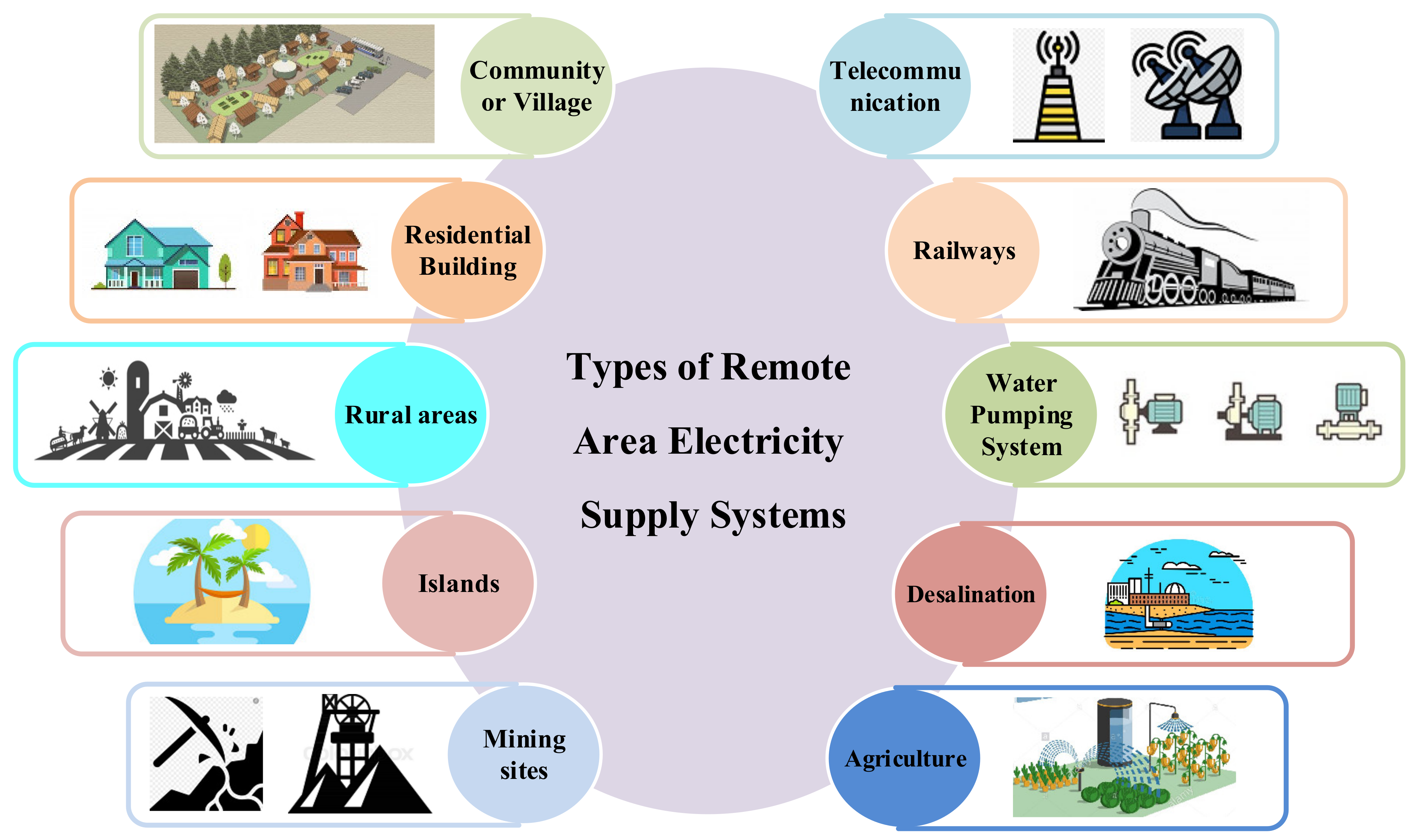
1.1. Background and Motivation
1.2. Critical Literature Review
- The existing studies did not provide a thorough review of optimal planning of RAES systems. This includes the optimization process, input data, methods, objective functions, study based on the country, and design constraints.
- The technical challenges of the existing studies were not found by the review papers.
- The advantages and disadvantages of applied methodologies and data uncertainties for RAES optimal planning were not described by the review studies.
- The potential future directions were not introduced for researchers. Since the optimal planning problem of RAES systems is extremely critical, future perspectives should be identified to develop more significant studies.
1.3. Contribution
- Overviewing the optimization problem of RAES systems’ planning.
- Conducting a review on the state of the art in optimal planning of RAES systems.
- Classifying the existing studies on optimal planning of RAES systems.
- Identifying the current technical challenges on optimal planning of RAES systems.
- Outlooking the future research trends in optimal planning of RAES systems.
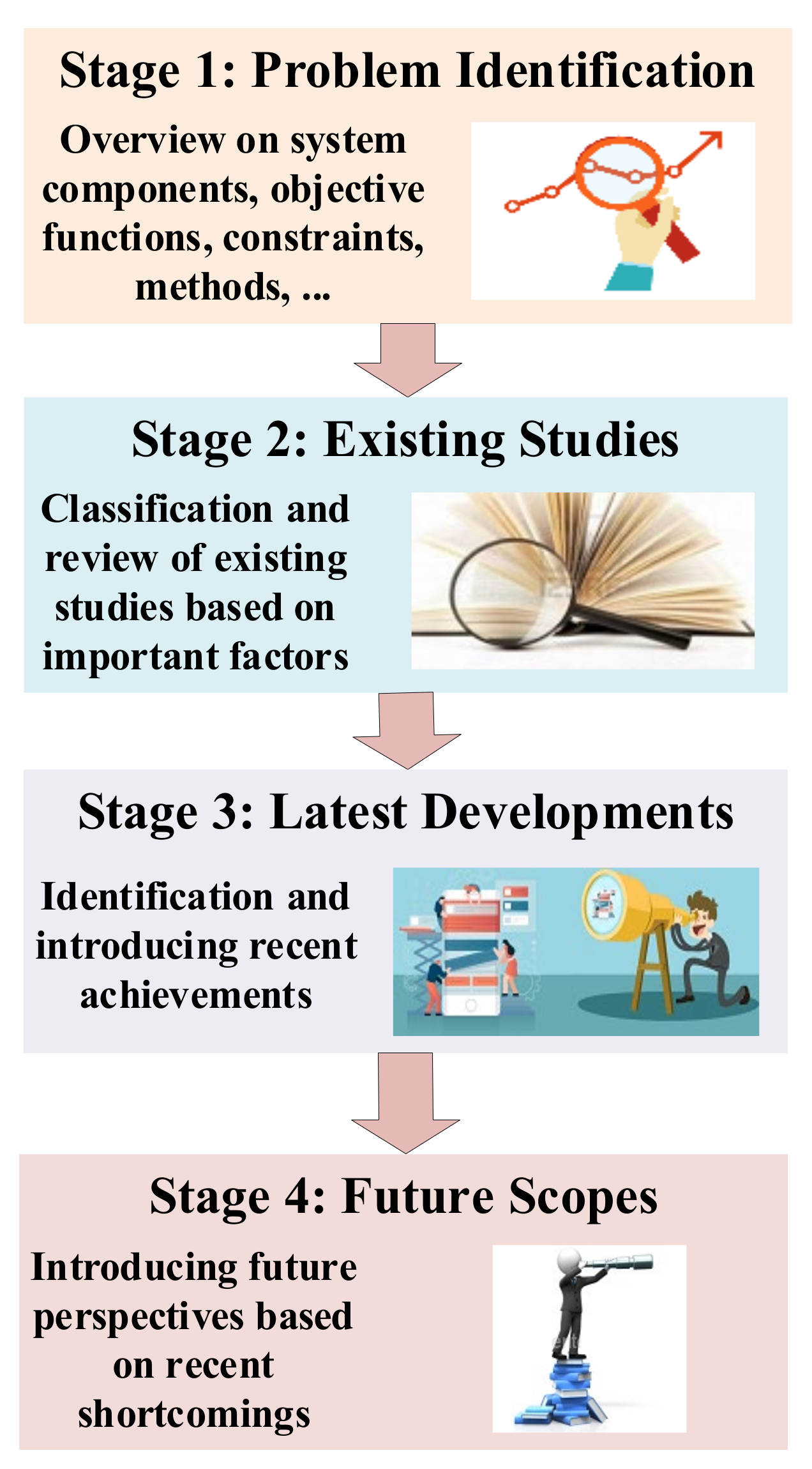
1.4. Article Organization
2. Overview on Optimal Planning of RAES Systems
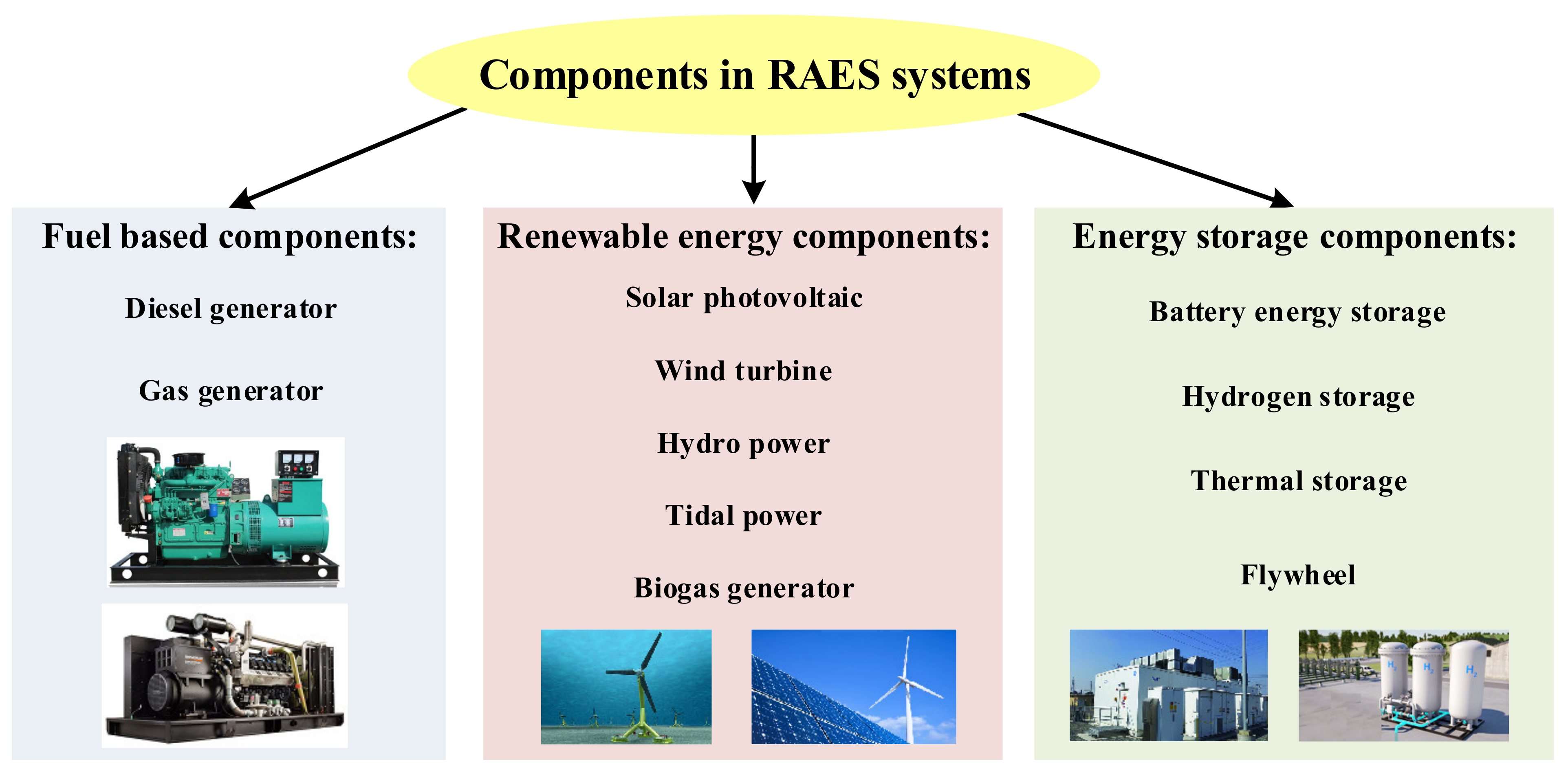
2.1. System Components
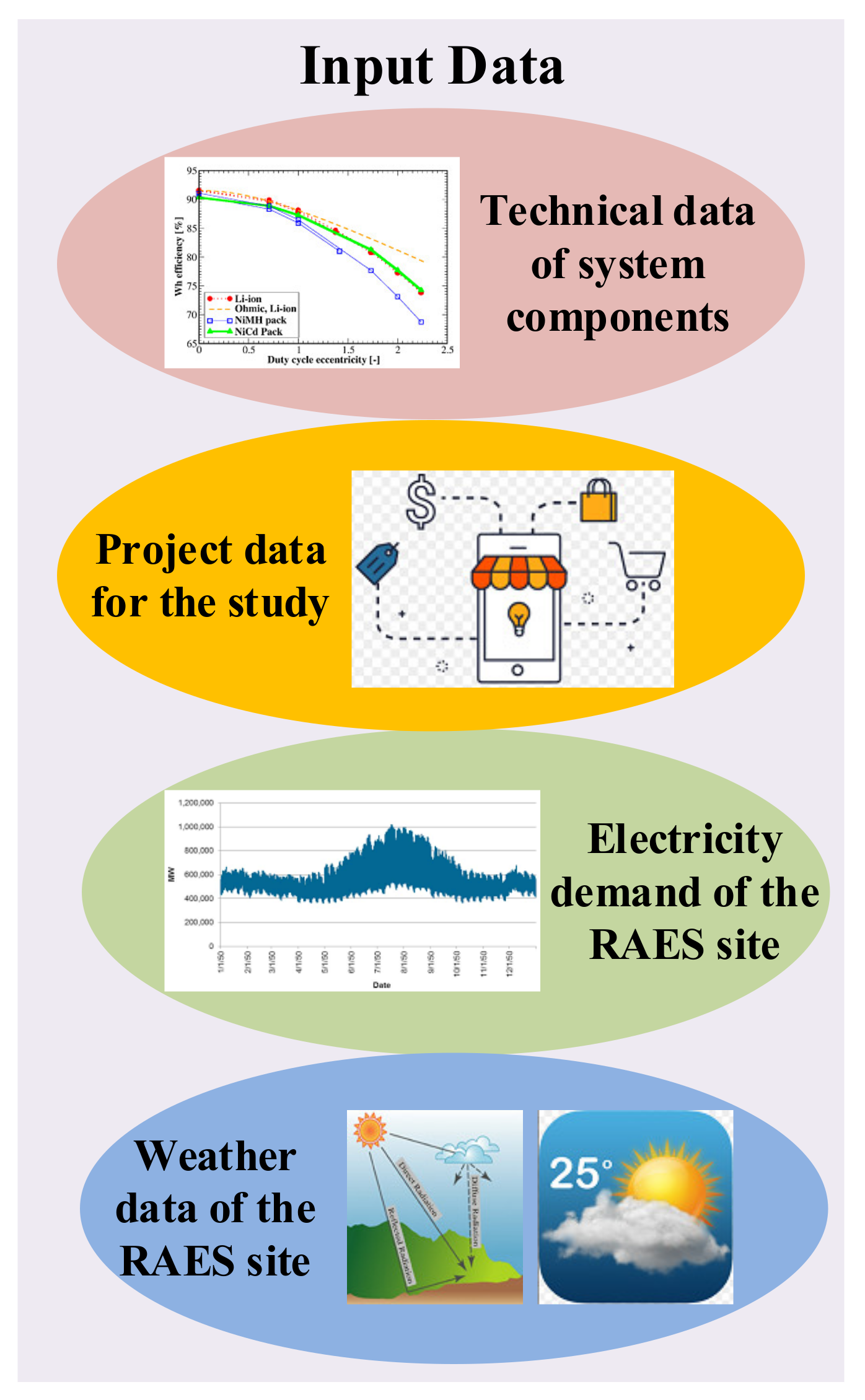
2.2. Input Data
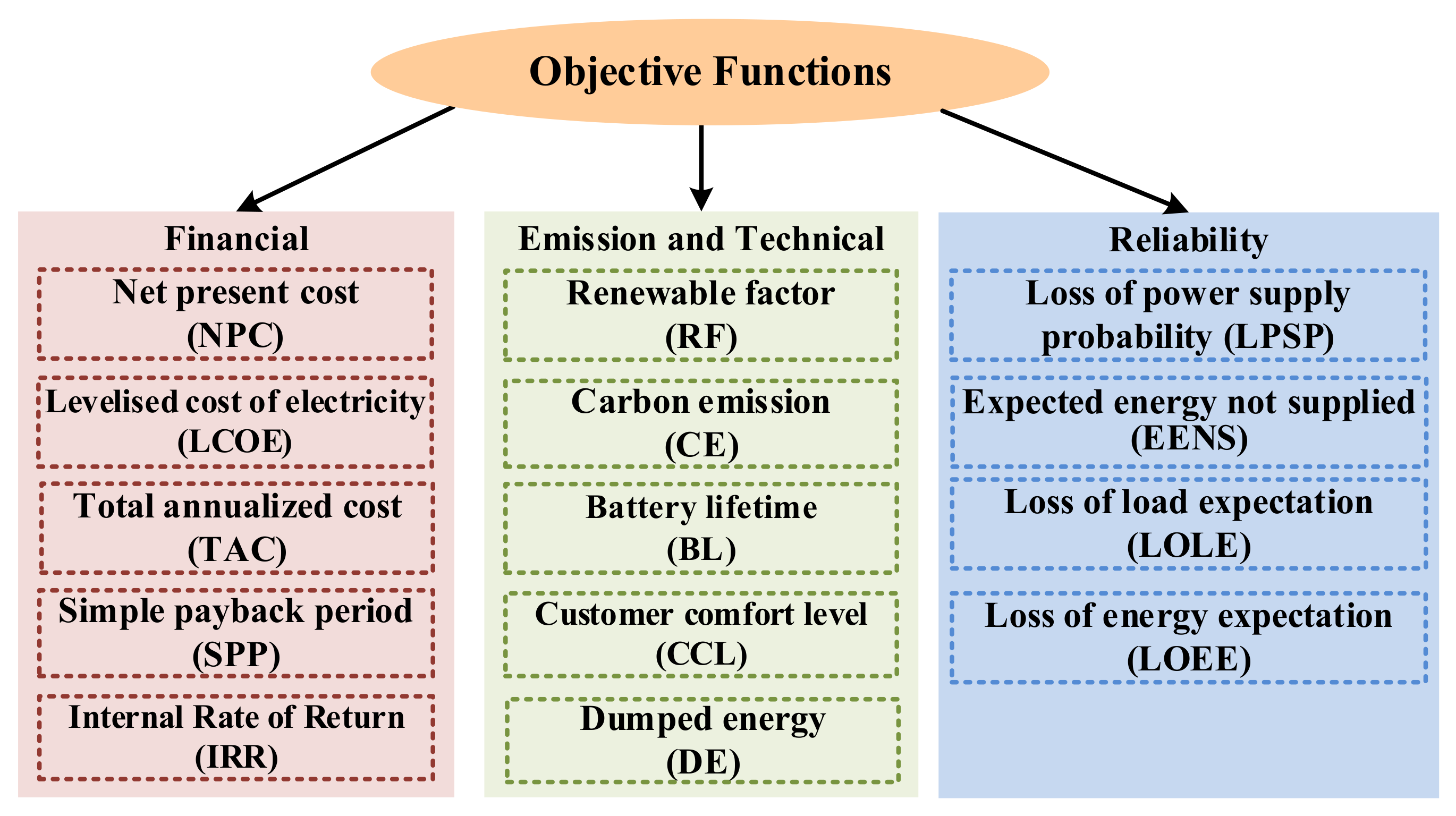
2.3. Objective Functions
2.3.1. Financial Objective Functions
2.3.2. Reliability Objective Functions
2.3.3. Emission and Technical Objective Functions
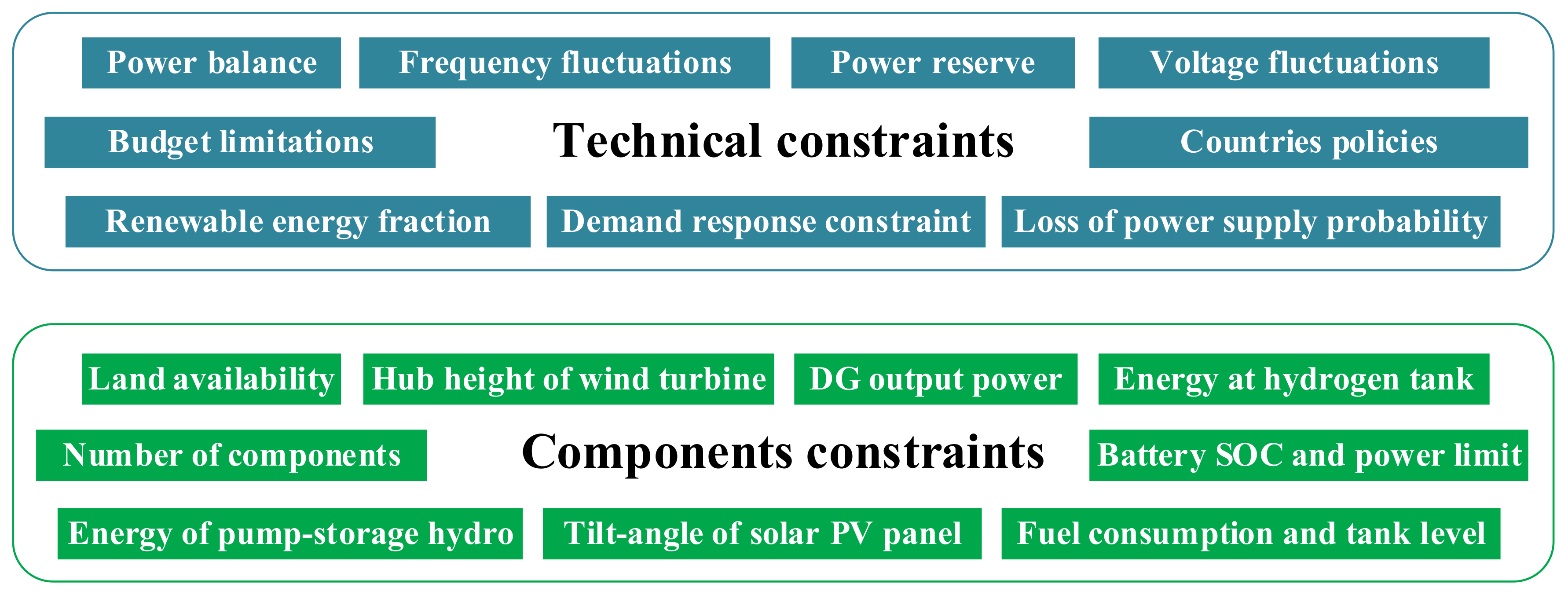
2.4. Feasibility Constraints
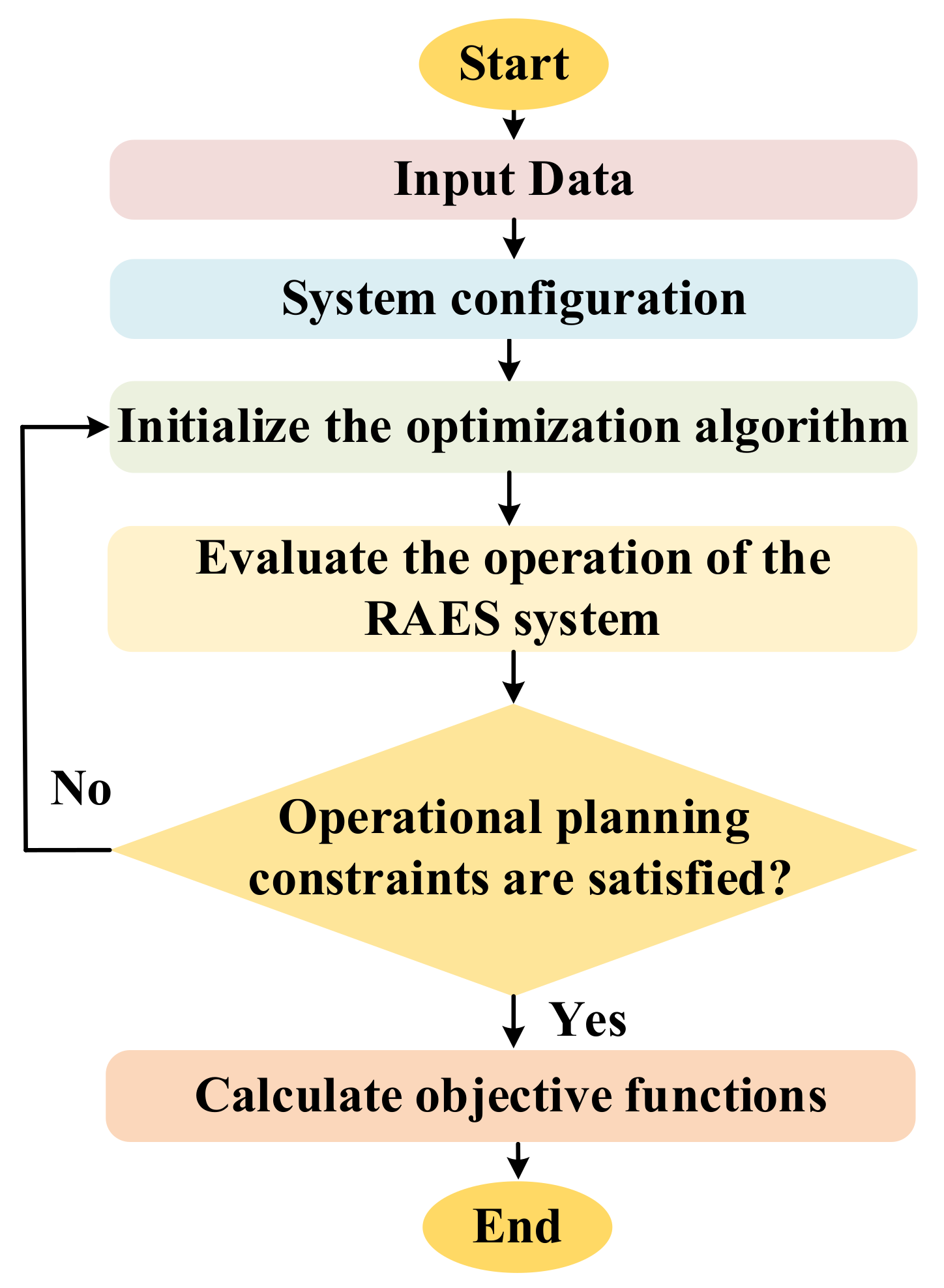
2.5. Operation Strategies
2.6. Solving the RAES Optimal Planning
2.6.1. Metaheuristic Methods
2.6.2. Other Optimization Methods
2.6.3. HOMER Software
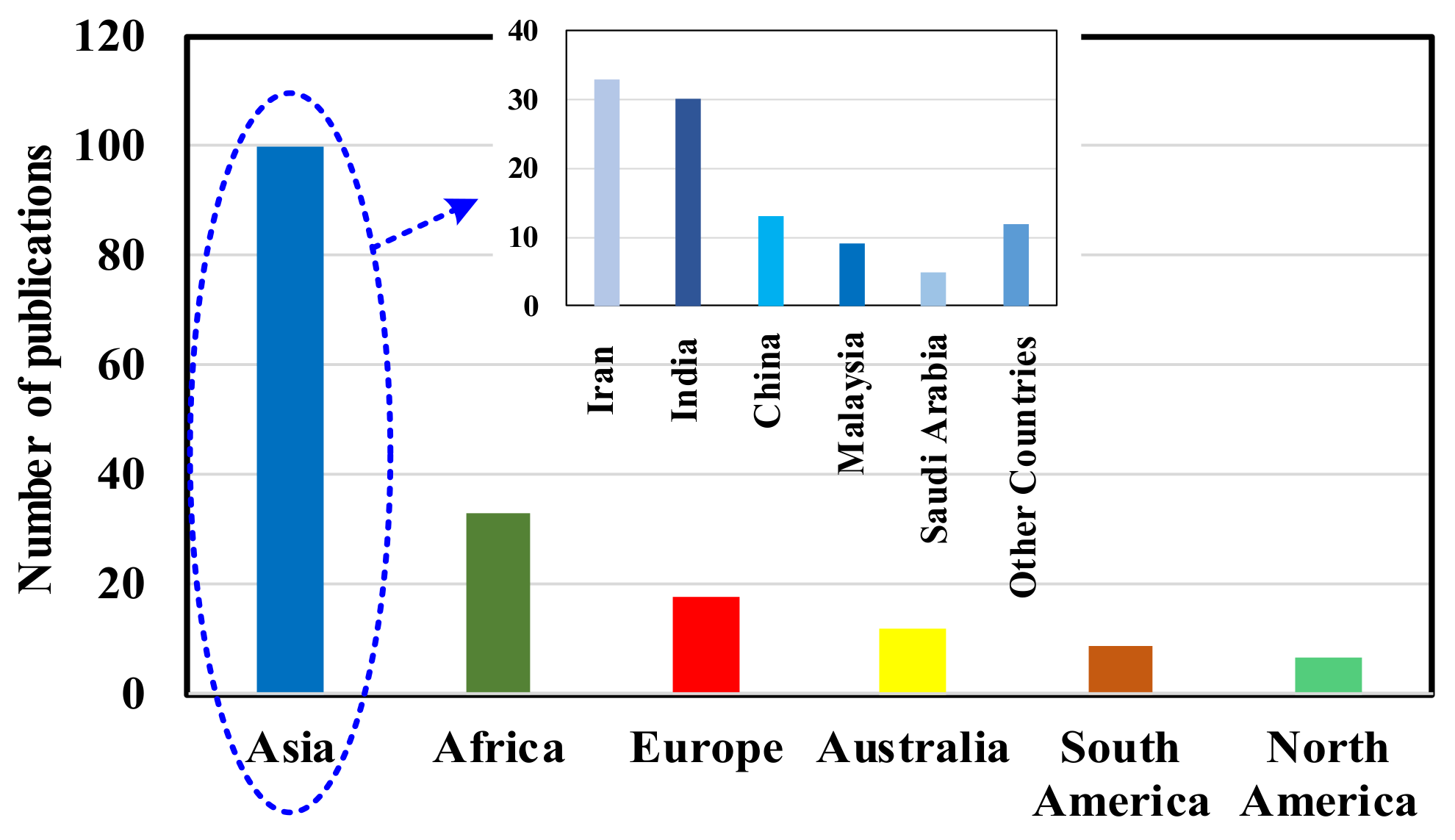
3. Review on Existing Studies and Technical Challenges
3.1. Hybrid RAES Systems with/without ESS
3.1.1. HOMER Software for Hybrid RAES Systems
3.1.2. Metaheuristic Methods for Hybrid RAES Systems
3.1.3. Non-Metaheuristic Optimization Algorithms for Hybrid RAES Systems
3.2. Clean (Renewable-Storage) RAES Systems
3.2.1. HOMER Software for Renewable-Storage RAES Systems
3.2.2. Metaheuristic Methods for Renewable-Storage RAES Systems
3.2.3. Non-Metaheuristic Optimization Algorithms for Renewable-Storage RAES Systems
3.3. Discussion
3.3.1. Electricity Supply Cost for RAES Systems
3.3.2. Discussions on Methods
3.3.3. Technical Challenges
- High capacity of BES in clean remote area energy supply systems.
- Demand response strategies for optimal planning in RAES systems.
- Robust optimal planning of components for clean RAES systems.
- Neglecting guidelines for customers in RAES systems.
- Neglecting distribution network constraints in the optimal planning model.
4. Recent Developments
4.1. EV Charging Stations and Diesel Generator
4.2. Integrated Energy System with Solar PV and Biogas
4.3. Hybrid Energy Storage and PV
4.4. Optimal Configuration
4.5. Accurate Battery Lifetime Estimation and Technology Selection
4.6. Concentrating Solar Power Plant
4.7. Cooperation of a Diesel Generator and Flywheel with Incentive DR
5. Future Scopes
5.1. Incentive Demand Response
5.2. Distribution Network Constraints
5.3. Considering Voltage and Frequency Control
5.4. New Software Tools for Optimal Planning of RAES Systems
5.5. Guidelines for RAES Customers
5.6. Feed-in-Tariff in RAES
5.7. Robust Optimal Planning
5.8. Resilient Optimal Planning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. World Energy Outlook. Available online: https://www.iea.org/reports/world-energy-outlook-2018 (accessed on 15 February 2021).
- Khodayar, M.E. Rural electrification and expansion planning of off-grid microgrids. Electr. J. 2017, 30, 68–74. [Google Scholar] [CrossRef]
- Combe, M.; Mahmoudi, A.; Haque, M.H.; Khezri, R. Cost-effective sizing of an AC mini-grid hybrid power system for a remote area in South Australia. IET Gener. Transm. Distrib. 2019, 13, 277–287. [Google Scholar] [CrossRef]
- Akuru, U.B.; Onukwube, I.E.; Okoro, O.I.; Obe, E.S. Towards 100% renewable energy in Nigeria. Renew. Sustain. Energy Rev. 2017, 71, 943–953. [Google Scholar] [CrossRef]
- Hansen, K.; Mathiesen, B.V.; Skov, I.R. Full energy system transition towards 100% renewable energy in Germany in 2050. Renew. Sustain. Energy Rev. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Child, M.; Kemfert, C.; Bogdanov, D.; Breyer, C. Flexible electricity generation, grid exchange and storage for the transition to a 100% renewable energy system in Europe. Renew. Energy 2019, 139, 80–101. [Google Scholar] [CrossRef]
- Jalilpour, K.; Khezri, R.; Mahmoudi, A.; Oshnoei, A. Optimal sizing of energy storage system. In Variability, Scallability, and Stability of Microgrids; Muyeen, S.M., Islam, S., Blaabjerg, F., Eds.; The Institution of Engineering and Technology (IET): London, UK, 2019; pp. 263–289, Chapter 9. [Google Scholar]
- Mahesh, A.; Sandhu, K.S. Hybrid wind/photovoltaic energy system developments: Critical review and findings. Renew. Sustain. Energy Rev. 2015, 52, 1135–1147. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P. Solar–wind hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of software tools for hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.S.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Singh, R.; Bansal, R.C. Review of HRESs based on storage options, system architecture and optimisation criteria and methodologies. IET Renew. Power Gener. 2018, 12, 747–760. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W. A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. J. Clean. Prod. 2019, 221, 73–88. [Google Scholar] [CrossRef]
- Rojas-Zerpa, J.C.; Yusta, J.M. Methodologies, technologies and applications for electric supply planning in rural remote areas. Energy Sustain. Dev. 2014, 20, 66–76. [Google Scholar] [CrossRef]
- Mohammed, Y.S.; Mustafa, M.W.; Bashir, N. Hybrid renewable energy systems for off-grid electric power: Review of substantial issues. Renew. Sustain. Energy Rev. 2014, 35, 527–539. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. A review on integrated renewable energy system based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Siddaiah, R.; Saini, R.P. A review on planning, configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
- Lahimer, A.A.; Alghoul, M.A.; Yousif, F.; Razykov, T.M.; Amin, N.; Sopian, K. Research and development aspects on decentralized electrification options for rural household. Renew. Sustain. Energy Rev. 2013, 24, 314–324. [Google Scholar] [CrossRef]
- Mandelli, S.; Barbieri, J.; Mereu, R.; Colombo, E. Off-grid systems for rural electrification in developing countries: Definitions, classification and a comprehensive literature review. Renew. Sustain. Energy Rev. 2016, 58, 1621–1646. [Google Scholar] [CrossRef]
- Neves, D.; Silva, C.A.; Connors, S. Design and implementation of hybrid renewable energy systems on micro-communities: A review on case studies. Renew. Sustain. Energy Rev. 2014, 31, 935–946. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.; Jayasinghe, S.D.; Enshaei, H.J. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Faccio, M.; Gamberi, M.; Bortolini, M.; Nedaei, M. State-of-art review of the optimization methods to design the configuration of hybrid renewable energy systems (HRESs). Front. Energy 2018, 12, 591–622. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Bahramara, S.; Moghaddam, M.P.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A. Review on the state-of-the-art multi-objective optimisation of hybrid standalone/grid-connected energy systems. IET Gener. Transm. Distrib. 2020, 14, 4285–4300. [Google Scholar] [CrossRef]
- Tan, Y.; Meegahapola, L.; Muttaqi, K.M. A review of technical challenges in planning and operation of remote area power supply systems. Renew. Sustain. Energy Rev. 2014, 38, 876–889. [Google Scholar] [CrossRef] [Green Version]
- Benedek, J.; Sebestyén, T.T.; Bartók, B. Evaluation of renewable energy sources in peripheral areas and renewable energy-based rural development. Renew. Sustain. Energy Rev. 2018, 90, 516–535. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, D.; Li, C.; Chung, C.Y.; Cao, Y.; Chan, K.W.; Wu, Q. Optimal scheduling of biogas–solar–wind renewable portfolio for multicarrier energy supplies. IEEE Trans. Power Syst. 2018, 33, 6229–6239. [Google Scholar] [CrossRef] [Green Version]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Hussain, A.; Mansor, M.B.; Blaabjerg, F. Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Javeed, I.; Khezri, R.; Mahmoudi, A.; Yazdani, A.; Shafiullah, G.M. Optimal Sizing of Rooftop PV and Battery Storage for Grid-Connected Houses Considering Flat and Time-of-Use Electricity Rates. Energies 2021, 14, 3520. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S. Multi-objective optimization and design of photovoltaic-wind hybrid system for community smart DC microgrid. IEEE Trans. Smart Grid 2014, 5, 2635–2643. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Aki, H. Optimal Planning of Renewable Energy Resources and Battery Storage System for an Educational Campus in South Australia. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3677–3683. [Google Scholar]
- Khezri, R.; Mahmoudi, A.; Aki, H. Multi-Objective Optimization of Solar PV and Battery Storage System for A Grid-Connected Household. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020. [Google Scholar]
- Askarzadeh, A.; Rezazadeh, A. A grouping-based global harmony search algorithm for modeling of proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2011, 36, 5047–5053. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Mouli, G.C.; Qin, Z.; Elizondo, L.R.; Bauer, P. Techno-economical model based optimal sizing of pv-battery systems for microgrids. IEEE Trans. Sustain. Energy 2020, 11, 1657–1668. [Google Scholar] [CrossRef]
- Guo, L.; Wang, N.; Lu, H.; Li, X.; Wang, C. Multi-objective optimal planning of the stand-alone microgrid system based on different benefit subjects. Energy 2016, 116, 353–363. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar–wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Khezri, R.; Muyeen, S.M. Risk-constrained stochastic optimal allocation of energy storage system in virtual power plants. J. Energy Storage 2020, 31, 101732. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Arab, A.H.; Guessoum, A. An adaptive artificial neural network model for sizing stand-alone photovoltaic systems: Application for isolated sites in Algeria. Renew. Energy 2005, 30, 1501–1524. [Google Scholar] [CrossRef] [Green Version]
- Khatod, D.K.; Pant, V.; Sharma, J. Analytical approach for well-being assessment of small autonomous power systems with solar and wind energy sources. IEEE Trans. Energy Convers. 2009, 25, 535–545. [Google Scholar] [CrossRef]
- Abushnaf, J.; Rassau, A. Impact of energy management system on the sizing of a grid-connected PV/Battery system. Electr. J. 2018, 31, 58–66. [Google Scholar] [CrossRef]
- Ramli, M.A.; Hiendro, A.; Sedraoui, K.; Twaha, S. Optimal sizing of grid-connected photovoltaic energy system in Saudi Arabia. Renew. Energy 2015, 75, 489–495. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A. Optimal smart home energy management considering energy saving and a comfortable lifestyle. IEEE Trans. Smart Grid 2014, 6, 324–332. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H. Two-Stage Optimal Sizing of Standalone Hybrid Electricity Systems with Time-of-Use Incentive Demand Response. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 2759–2765. [Google Scholar]
- Pan, X.; Khezri, R.; Mahmoudi, A.; Yazdani, A.; Shafiullah, G.M. Energy Management Systems for Grid-Connected Houses with Solar PV and Battery by Considering Flat and Time-of-Use Electricity Rates. Energies 2021, 14, 5028. [Google Scholar] [CrossRef]
- Cuevas, E.; Espejo, E.B.; Enríquez, A.C. Metaheuristics Algorithms in Power Systems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Atwa, Y.M.; El-Saadany, E.F. Probabilistic approach for optimal allocation of wind-based distributed generation in distribution systems. IET Renew. Power Gener. 2011, 5, 79–88. [Google Scholar] [CrossRef]
- Jordehi, A.R. Allocation of distributed generation units in electric power systems: A review. Renew. Sustain. Energy Rev. 2016, 56, 893–905. [Google Scholar] [CrossRef]
- Tan, W.S.; Hassan, M.Y.; Majid, M.S.; Rahman, H.A. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- Homer Pro Software. Available online: https://www.homerenergy.com/products/pro/index.html (accessed on 15 February 2021).
- Ngan, M.S.; Tan, C.W. Assessment of economic viability for PV/wind/diesel hybrid energy system in southern Peninsular Malaysia. Renew. Sustain. Energy Rev. 2012, 16, 634–647. [Google Scholar] [CrossRef]
- Yilmaz, S.; Dincer, F. Optimal design of hybrid PV-Diesel-Battery systems for isolated lands: A case study for Kilis, Turkey. Renew. Sustain. Energy Rev. 2017, 77, 344–352. [Google Scholar] [CrossRef]
- Olatomiwa, L.J.; Mekhilef, S.; Huda, A.S. Optimal sizing of hybrid energy system for a remote telecom tower: A case study in Nigeria. In Proceedings of the 2014 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 13–14 October 2014; pp. 243–247. [Google Scholar]
- Al-Ammar, E.A.; Habib, H.U.; Kotb, K.M.; Wang, S.; Ko, W.; Elmorshedy, M.F.; Waqar, A. Residential community load management based on optimal design of standalone HRES with model predictive control. IEEE Access 2020, 8, 12542–12572. [Google Scholar] [CrossRef]
- Ali, L.; Shahnia, F. Determination of an economically-suitable and sustainable standalone power system for an off-grid town in Western Australia. Renew. Energy 2017, 106, 243–254. [Google Scholar] [CrossRef] [Green Version]
- Rehman, S.; Natrajan, N.; Mohandes, M.; Alhems, L.M.; Himri, Y.; Allouhi, A. Feasibility Study of Hybrid Power Systems for Remote Dwellings in Tamil Nadu, India. IEEE Access 2020, 8, 143881–143890. [Google Scholar] [CrossRef]
- Ansong, M.; Mensah, L.D.; Adaramola, M.S. Techno-economic analysis of a hybrid system to power a mine in an off-grid area in Ghana. Sustain. Energy Technol. Assess. 2017, 23, 48–56. [Google Scholar] [CrossRef]
- Aziz, A.S.; Tajuddin, M.F.; Adzman, M.R.; Azmi, A.; Ramli, M.A. Optimization and sensitivity analysis of standalone hybrid energy systems for rural electrification: A case study of Iraq. Renew. Energy 2019, 138, 775–792. [Google Scholar] [CrossRef]
- Muh, E.; Tabet, F. Comparative analysis of hybrid renewable energy systems for off-grid applications in Southern Cameroons. Renew. Energy 2019, 135, 41–54. [Google Scholar] [CrossRef]
- Das, B.K.; Hoque, N.; Mandal, S.; Pal, T.K.; Raihan, M.A. A techno-economic feasibility of a stand-alone hybrid power generation for remote area application in Bangladesh. Energy 2017, 134, 775–788. [Google Scholar] [CrossRef]
- Boonbumroong, U.; Pratinthong, N.; Thepa, S.; Jivacate, C.; Pridasawas, W. Particle swarm optimization for AC-coupling stand alone hybrid power systems. Sol. Energy 2011, 85, 560–569. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Askarzadeh, A. Distribution generation by photovoltaic and diesel generator systems: Energy management and size optimization by a new approach for a stand-alone application. Energy 2017, 122, 542–551. [Google Scholar] [CrossRef]
- Fioriti, D.; Giglioli, R.; Poli, D.; Lutzemberger, G.; Micangeli, A.; Del Citto, R.; Perez-Arriaga, I. Stochastic sizing of isolated rural mini-grids, including effects of fuel procurement and operational strategies. Electr. Power Syst. Res. 2018, 160, 419–428. [Google Scholar] [CrossRef] [Green Version]
- Sawle, Y.; Gupta, S.C.; Bohre, A.K. Optimal sizing of standalone PV/Wind/Biomass hybrid energy system using GA and PSO optimization technique. Energy Procedia 2017, 117, 690–698. [Google Scholar] [CrossRef]
- Combe, M.; Mahmoudi, A.; Haque, M.H.; Khezri, R. AC-coupled hybrid power system optimisation for an Australian remote community. Int. Trans. Electr. Energy Syst. 2020, 30, e12503. [Google Scholar] [CrossRef]
- Bansal, A.K.; Kumar, R.; Gupta, R.A. Economic analysis and power management of a small autonomous hybrid power system (SAHPS) using biogeography based optimization (BBO) algorithm. IEEE Trans. Smart Grid 2013, 4, 638–648. [Google Scholar] [CrossRef]
- Diab, A.A.; Sultan, H.M.; Mohamed, I.S.; Kuznetsov, O.N.; Do, T.D. Application of different optimization algorithms for optimal sizing of PV/wind/diesel/battery storage stand-alone hybrid microgrid. IEEE Access 2019, 7, 119223–119245. [Google Scholar] [CrossRef]
- Katsigiannis, Y.A.; Georgilakis, P.S.; Karapidakis, E.S. Hybrid simulated annealing–tabu search method for optimal sizing of autonomous power systems with renewables. IEEE Trans. Sustain. Energy 2012, 3, 330–338. [Google Scholar] [CrossRef]
- Prathapaneni, D.R.; Detroja, K.P. An integrated framework for optimal planning and operation schedule of microgrid under uncertainty. Sustain. Energy Grids Netw. 2019, 19, 100232. [Google Scholar] [CrossRef]
- Ghaffari, A.; Askarzadeh, A. Design optimization of a hybrid system subject to reliability level and renewable energy penetration. Energy 2020, 193, 116754. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV–wind–diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Li, P.; Wang, K.; Xue, M.; Wang, C. Optimal sizing, operating strategy and operational experience of a stand-alone microgrid on Dongfushan Island. Appl. Energy 2014, 113, 1656–1666. [Google Scholar] [CrossRef]
- Wang, R.; Li, G.; Ming, M.; Wu, G.; Wang, L. An efficient multi-objective model and algorithm for sizing a stand-alone hybrid renewable energy system. Energy 2017, 141, 2288–2299. [Google Scholar] [CrossRef]
- Shi, B.; Wu, W.; Yan, L. Size optimization of stand-alone PV/wind/diesel hybrid power generation systems. J. Taiwan Inst. Chem. Eng. 2017, 73, 93–101. [Google Scholar] [CrossRef]
- Jamshidi, M.; Askarzadeh, A. Techno-economic analysis and size optimization of an off-grid hybrid photovoltaic, fuel cell and diesel generator system. Sustain. Cities Soc. 2019, 44, 310–320. [Google Scholar] [CrossRef]
- El-Bidairi, K.S.; Nguyen, H.D.; Jayasinghe, S.D.; Mahmoud, T.S.; Penesis, I. Impact of tidal energy on battery sizing in standalone microgrids: A case study. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering, Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Wang, R. Multi-objective configuration optimization method for a diesel-based hybrid energy system. Energy Rep. 2020, 6, 2146–21452. [Google Scholar] [CrossRef]
- Rodríguez-Gallegos, C.D.; Yang, D.; Gandhi, O.; Bieri, M.; Reindl, T.; Panda, S.K. A multi-objective and robust optimization approach for sizing and placement of PV and batteries in off-grid systems fully operated by diesel generators: An Indonesian case study. Energy 2018, 160, 410–429. [Google Scholar] [CrossRef]
- Belfkira, R.; Zhang, L.; Barakat, G. Optimal sizing study of hybrid wind/PV/diesel power generation unit. Sol. Energy 2011, 85, 100–110. [Google Scholar] [CrossRef]
- Kaabeche, A.; Ibtiouen, R. Techno-economic optimization of hybrid photovoltaic/wind/diesel/battery generation in a stand-alone power system. Sol. Energy 2014, 103, 171–182. [Google Scholar] [CrossRef]
- Tsuanyo, D.; Azoumah, Y.; Aussel, D.; Neveu, P. Modeling and optimization of batteryless hybrid PV (photovoltaic)/Diesel systems for off-grid applications. Energy 2015, 86, 152–163. [Google Scholar] [CrossRef]
- Katti, P.K.; Khedkar, M.K. Alternative energy facilities based on site matching and generation unit sizing for remote area power supply. Renew. Energy 2007, 32, 1346–1362. [Google Scholar] [CrossRef]
- Malheiro, A.; Castro, P.M.; Lima, R.M.; Estanqueiro, A. Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems. Renew. Energy 2015, 83, 646–657. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Li, R.X.; Cao, Y.; Li, D.Y.; Xie, G. Multiobjective sizing optimization for island microgrids using a triangular aggregation model and the levy-harmony algorithm. IEEE Trans. Ind. Inform. 2017, 14, 3495–3505. [Google Scholar] [CrossRef]
- Morsali, R.; Kowalczyk, R. Demand response based day-ahead scheduling and battery sizing in microgrid management in rural areas. IET Renew. Power Gener. 2018, 12, 1651–1658. [Google Scholar] [CrossRef]
- Singh, R.; Bansal, R.C. Optimization of an autonomous hybrid renewable energy system using reformed electric system cascade analysis. IEEE Trans. Ind. Inform. 2018, 15, 399–409. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, S.; Shaaban, M.F.; Ismail, M.; Serpedin, E.; Qaraqe, K.A. An efficient planning algorithm for hybrid remote microgrids. IEEE Trans. Sustain. Energy 2018, 10, 257–267. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L.; Elmore, A.C. Optimal sizing of a vanadium redox battery system for microgrid systems. IEEE Trans. Sustain. Energy 2015, 6, 729–737. [Google Scholar] [CrossRef]
- Alharbi, H.; Bhattacharya, K. Stochastic optimal planning of battery energy storage systems for isolated microgrids. IEEE Trans. Sustain. Energy 2017, 9, 211–227. [Google Scholar] [CrossRef]
- Nurunnabi, M.; Roy, N.K.; Hossain, E.; Pota, H.R. Size Optimization and Sensitivity Analysis of Hybrid Wind/PV Micro-Grids-A Case Study for Bangladesh. IEEE Access 2019, 7, 150120–150140. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Aftab, M.A.; Ali, I.; Hussain, S.M.; Ustun, T.S. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. [Google Scholar] [CrossRef] [Green Version]
- Luta, D.N.; Raji, A.K. Optimal sizing of hybrid fuel cell-supercapacitor storage system for off-grid renewable applications. Energy 2019, 166, 530–540. [Google Scholar] [CrossRef]
- Fazelpour, F.; Soltani, N.; Rosen, M.A. Economic analysis of standalone hybrid energy systems for application in Tehran, Iran. Int. J. Hydrog. Energy 2016, 41, 7732–7743. [Google Scholar] [CrossRef]
- Murugaperumal, K.; Raj, P.A. Feasibility design and techno-economic analysis of hybrid renewable energy system for rural electrification. Sol. Energy 2019, 188, 1068–1083. [Google Scholar] [CrossRef]
- Goel, S.; Sharma, R. Optimal sizing of a biomass–biogas hybrid system for sustainable power supply to a commercial agricultural farm in northern Odisha, India. Environ. Dev. Sustain. 2019, 21, 2297–2319. [Google Scholar] [CrossRef]
- Kumaravel, S.; Ashok, S. An optimal stand-alone biomass/solar-PV/pico-hydel hybrid energy system for remote rural area electrification of isolated village in Western-Ghats region of India. Int. J. Green Energy 2012, 9, 398–408. [Google Scholar] [CrossRef]
- Kaabeche, A.; Diaf, S.; Ibtiouen, R. Firefly-inspired algorithm for optimal sizing of renewable hybrid system considering reliability criteria. Sol. Energy 2017, 155, 727–738. [Google Scholar] [CrossRef]
- Das, M.; Singh, M.A.; Biswas, A. Techno-economic optimization of an off-grid hybrid renewable energy system using metaheuristic optimization approaches–case of a radio transmitter station in India. Energy Convers. Manag. 2019, 185, 339–352. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Comparative study of artificial intelligence techniques for sizing of a hydrogen-based stand-alone photovoltaic/wind hybrid system. Int. J. Hydrog. Energy 2014, 39, 9973–9984. [Google Scholar] [CrossRef]
- Samy, M.M.; Barakat, S.; Ramadan, H.S. Techno-economic analysis for rustic electrification in Egypt using multi-source renewable energy based on PV/wind/FC. Int. J. Hydrog. Energy 2020, 45, 11471–11483. [Google Scholar] [CrossRef]
- Rajanna, S.; Saini, R.P. Development of optimal integrated renewable energy model with battery storage for a remote Indian area. Energy 2016, 111, 803–817. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Size optimization and demand response of a stand-alone integrated renewable energy system. Energy 2017, 124, 59–73. [Google Scholar] [CrossRef]
- Lorestani, A.; Gharehpetian, G.B.; Nazari, M.H. Optimal sizing and techno-economic analysis of energy-and cost-efficient standalone multi-carrier microgrid. Energy 2019, 178, 751–764. [Google Scholar] [CrossRef]
- Guangqian, D.; Bekhrad, K.; Azarikhah, P.; Maleki, A. A hybrid algorithm based optimization on modeling of grid independent biodiesel-based hybrid solar/wind systems. Renew. Energy 2018, 122, 551–560. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M. Particle swarm optimization of a hybrid wind/tidal/PV/battery energy system. Application to a remote area in Bretagne, France. Energy Procedia 2019, 162, 87–96. [Google Scholar] [CrossRef]
- Jahannoosh, M.; Nowdeh, S.A.; Naderipour, A.; Kamyab, H.; Davoodkhani, I.F.; Klemeš, J.J. New Hybrid Meta-Heuristic Algorithm for Reliable and Cost-Effective Designing of Photovoltaic/Wind/Fuel Cell Energy System Considering Load Interruption Probability. J. Clean. Prod. 2021, 278, 123406. [Google Scholar] [CrossRef]
- Maleki, A. Design and optimization of autonomous solar-wind-reverse osmosis desalination systems coupling battery and hydrogen energy storage by an improved bee algorithm. Desalination 2018, 435, 221–234. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H. Optimal WT, PV and BES based energy systems for standalone households in South Australia. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3475–3482. [Google Scholar]
- Lai, C.S.; McCulloch, M.D. Sizing of stand-alone solar PV and storage system with anaerobic digestion biogas power plants. IEEE Trans. Ind. Electron. 2016, 64, 2112–2121. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Nowdeh, S.A.; Kamyab, H.; Ramtin, A.R.; Shahrokhi, S.; Klemeš, J.J. Comparative evaluation of hybrid photovoltaic, wind, tidal and fuel cell clean system design for different regions with remote application considering cost. J. Clean. Prod. 2021, 283, 124207. [Google Scholar] [CrossRef]
- Javed, M.S.; Ma, T.; Jurasz, J.; Ahmed, S.; Mikulik, J. Performance comparison of heuristic algorithms for optimization of hybrid off-grid renewable energy systems. Energy 2020, 210, 118599. [Google Scholar] [CrossRef]
- Nyeche, E.N.; Diemuodeke, E.O. Modelling and optimisation of a hybrid PV-wind turbine-pumped hydro storage energy system for mini-grid application in coastline communities. J. Clean. Prod. 2020, 250, 119578. [Google Scholar] [CrossRef]
- Ma, G.; Xu, G.; Chen, Y.; Ju, R. Multi-objective optimal configuration method for a standalone wind–solar–battery hybrid power system. IET Renew. Power Gener. 2016, 11, 194–202. [Google Scholar] [CrossRef]
- Kaur, R.; Krishnasamy, V.; Kandasamy, N.K.; Kumar, S. Discrete multiobjective grey wolf algorithm based optimal sizing and sensitivity analysis of PV-wind-battery system for rural telecom towers. IEEE Syst. J. 2019, 14, 729–737. [Google Scholar] [CrossRef]
- Guezgouz, M.; Jurasz, J.; Bekkouche, B.; Ma, T.; Javed, M.S.; Kies, A. Optimal hybrid pumped hydro-battery storage scheme for off-grid renewable energy systems. Energy Convers. Manag. 2019, 199, 112046. [Google Scholar] [CrossRef]
- Brka, A.; Al-Abdeli, Y.M.; Kothapalli, G. The interplay between renewables penetration, costing and emissions in the sizing of stand-alone hydrogen systems. Int. J. Hydrog. Energy 2015, 40, 125–135. [Google Scholar] [CrossRef]
- Gharavi, H.; Ardehali, M.M.; Ghanbari-Tichi, S. Imperial competitive algorithm optimization of fuzzy multi-objective design of a hybrid green power system with considerations for economics, reliability, and environmental emissions. Renew. Energy 2015, 78, 427–437. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Abbes, D.; Martinez, A.; Champenois, G. Life cycle cost, embodied energy and loss of power supply probability for the optimal design of hybrid power systems. Math. Comput. Simul. 2014, 98, 46–62. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Reliability/cost-based multi-objective Pareto optimal design of stand-alone wind/PV/FC generation microgrid system. Energy 2016, 115, 1022–1041. [Google Scholar] [CrossRef]
- Huang, Z.; Xie, Z.; Zhang, C.; Chan, S.H.; Milewski, J.; Xie, Y.; Yang, Y.; Hu, X. Modeling and multi-objective optimization of a stand-alone PV-hydrogen-retired EV battery hybrid energy system. Energy Convers. Manag. 2019, 181, 80–92. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hazim, H.; Ahmadipour, M. Sizing and implementing off-grid stand-alone photovoltaic/battery systems based on multi-objective optimization and techno-economic (MADE) analysis. Energy 2020, 207, 118163. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Naghizadeh, R.A. Multi-criteria optimal sizing of hybrid renewable energy systems including wind, photovoltaic, battery, and hydrogen storage with ɛ-constraint method. IET Renew. Power Gener. 2018, 12, 883–892. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Khatib, T.; Abdulabbas, T.E. Sizing of a standalone photovoltaic water pumping system using hybrid multi-criteria decision making methods. Sol. Energy 2018, 159, 1003–1015. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Feasibility study and economic analysis of pumped hydro storage and battery storage for a renewable energy powered island. Energy Convers. Manag. 2014, 79, 387–397. [Google Scholar] [CrossRef]
- Castaneda, M.; Cano, A.; Jurado, F.; Sánchez, H.; Fernández, L.M. Sizing optimization, dynamic modeling and energy management strategies of a stand-alone PV/hydrogen/battery-based hybrid system. Int. J. Hydrog. Energy 2013, 38, 3830–3845. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Sizing optimization of grid-independent hybrid photovoltaic/wind power generation system. Energy 2011, 36, 1214–1222. [Google Scholar] [CrossRef]
- Norbu, S.; Bandyopadhyay, S. Power Pinch Analysis for optimal sizing of renewable-based isolated system with uncertainties. Energy 2017, 135, 466–475. [Google Scholar] [CrossRef]
- Belmili, H.; Haddadi, M.; Bacha, S.; Almi, M.F.; Bendib, B. Sizing stand-alone photovoltaic–wind hybrid system: Techno-economic analysis and optimization. Renew. Sustain. Energy Rev. 2014, 30, 821–832. [Google Scholar] [CrossRef]
- Shrestha, G.B.; Goel, L. A study on optimal sizing of stand-alone photovoltaic stations. IEEE Trans. Energy Convers. 1998, 13, 373–378. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M.; Haddad, S.; Feld, G. Optimal sizing and energy management of hybrid wind/tidal/PV power generation system for remote areas: Application to the Ouessant French Island. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4205–4210. [Google Scholar]
- Astaneh, M.; Roshandel, R.; Dufo-López, R.; Bernal-Agustín, J.L. A novel framework for optimization of size and control strategy of lithium-ion battery based off-grid renewable energy systems. Energy Convers. Manag. 2018, 175, 99–111. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S. Stochastic performance assessment and sizing for a hybrid power system of solar/wind/energy storage. IEEE Trans. Sustain. Energy 2013, 5, 363–371. [Google Scholar] [CrossRef]
- Khiareddine, A.; Salah, C.B.; Rekioua, D.; Mimouni, M.F. Sizing methodology for hybrid photovoltaic/wind/hydrogen/battery integrated to energy management strategy for pumping system. Energy 2018, 153, 743–762. [Google Scholar] [CrossRef]
- Hosseinalizadeh, R.; Shakouri, H.; Amalnick, M.S.; Taghipour, P. Economic sizing of a hybrid (PV–WT–FC) renewable energy system (HRES) for stand-alone usages by an optimization-simulation model: Case study of Iran. Renew. Sustain. Energy Rev. 2016, 54, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Alberizzi, J.C.; Rossi, M.; Renzi, M. A MILP algorithm for the optimal sizing of an off-grid hybrid renewable energy system in South Tyrol. Energy Rep. 2020, 6, 21–26. [Google Scholar] [CrossRef]
- Ahadi, A.; Kang, S.K.; Lee, J.H. A novel approach for optimal combinations of wind, PV, and energy storage system in diesel-free isolated communities. Appl. Energy 2016, 170, 101–115. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Tong, N.; Li, Z.; Sun, S.; Liu, C. Optimal planning of a 100% renewable energy island supply system based on the integration of a concentrating solar power plant and desalination units. Int. J. Electr. Power Energy Syst. 2020, 117, 105707. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Samu, R.; Taylan, O.; Fahrioglu, M. Sizing renewable energy systems with energy storage systems in microgrids for maximum cost-efficient utilization of renewable energy resources. Sustain. Cities Soc. 2020, 55, 102059. [Google Scholar] [CrossRef]
- Fathi, M.; Khezri, R.; Yazdani, A.; Mahmoudi, A. Comparative Study of Metaheuristic Algorithms for Optimal Sizing of Standalone Microgrids in a Remote Area Community. Neural Comput. Appl. 2021, 1–19. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H. A Demand Side Management Approach for Optimal Sizing of Standalone Renewable-Battery Systems. IEEE Trans. Sustain. Energy 2021. early access. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and analysis of renewable energy and battery systems in residential microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Li, J.; Zhang, W.; Liu, Y.; Zhao, B.; Zhang, Y. Optimal sizing for grid-tied microgrids with consideration of joint optimization of planning and operation. IEEE Trans. Sustain. Energy 2017, 9, 237–248. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renewable and sustainable energy Reviews. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Mohamed, S.; Ismail, M.; Qaraqe, K.A.; Serpedin, E. Joint planning of smart EV charging stations and DGs in eco-friendly remote hybrid microgrids. IEEE Trans. Smart Grid 2019, 10, 5819–5830. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Li, C.; Yang, H.; Zhou, B.; Cao, Y.; Zeng, L.; Xu, Z. Optimal Planning of Islanded Integrated Energy System with Solar-Biogas Energy Supply. IEEE Trans. Sustain. Energy 2019, 11, 2437–2448. [Google Scholar] [CrossRef]
- Mohandes, B.; Acharya, S.; El Moursi, M.S.; Al-Sumaiti, A.; Doukas, H.; Sgouridis, S. Optimal Design of an Islanded Microgrid with Load Shifting Mechanism Between Electrical and Thermal Energy Storage Systems. IEEE Trans. Power Syst. 2020, 35, 2642–2657. [Google Scholar] [CrossRef]
- Hamad, A.A.; Nassar, M.E.; El-Saadany, E.F.; Salama, M.M. Optimal configuration of isolated hybrid AC/DC microgrids. IEEE Trans. Smart Grid 2019, 10, 2789–2798. [Google Scholar] [CrossRef]
- Masaud, T.M.; El-Saadany, E. Correlating Optimal Size, Cycle Life Estimation, and Technology Selection of Batteries: A Two-Stage Approach for Microgrid Applications. IEEE Trans. Sustain. Energy 2019, 11, 1257–1267. [Google Scholar] [CrossRef]
- Combe, M.; Mahmoudi, A.; Haque, M.H.; Khezri, R. Optimal sizing of an AC-coupled hybrid power system considering incentive-based demand response. IET Generation. Transm. Distrib. 2019, 13, 3354–3361. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H. Optimal Capacity of Solar PV and Battery Storage for Australian Grid-Connected Households. IEEE Trans. Ind. Appl. 2020, 56, 5319–5329. [Google Scholar] [CrossRef]
- Hayat, M.A.; Shahnia, F.; Shafiullah, G.M. Replacing Flat Rate Feed-In Tariffs for Rooftop Photovoltaic Systems with a Dynamic One to Consider Technical, Environmental, Social, and Geographical Factors. IEEE Trans. Ind. Inform. 2018, 15, 3831–3844. [Google Scholar] [CrossRef]
- Aghamohamadi, M.; Mahmoudi, A.; Haque, M. Two-stage Robust Sizing and Operation Co-optimization for Residential PV-battery Systems Considering the Uncertainty of PV Generation and Load. IEEE Trans. Ind. Inform. 2020, 17, 1005–1017. [Google Scholar] [CrossRef]

| Objective Function | Equation | Equation Number |
|---|---|---|
| NPC | (1) | |
| (2) | ||
| (3) | ||
| LCOE | (4) | |
| TAC | (5) | |
| SPP | (6) | |
| IRR | (7) | |
| (8) | ||
| Parameters and variables | : Total NPC of the RAES system, : NPC of the RAES components, : NPC of the fuel consumption, : Present values of capital, maintenance, replacement, and salvation costs, : Amount of fuel consumption, : Fuel price, : Total time period of the planning project, : Project lifetime, : Interest rate, : Total energy demand of the RAES system, : Discount rate, : Annual cost of components, : Annual payment of the RAES system for the external system, : is the net cash flow in year y. | |
| Objective Function | Equation | Equation Number |
|---|---|---|
| LPSP | (9) | |
| EENS | (10) | |
| LOLE | (11) | |
| LOEE | (12) | |
| SAIFI | (13) | |
| SAIDI | (14) | |
| Parameters and variables | : Total energy generation by renewable energy, : Total energy generation by diesel generators, : Total discharged energy generation by battery, : Total charged energy generation by battery, : Total dumped energy, : Average annual load, : Duration of unmet load, : Probability of meeting state s, : Loss of load duration, : all loss of energy states, : Rate of power interruption, : Duration of power outage, : Number of customers for location i. | |
| Objective Function | Equation | Equation Number |
|---|---|---|
| RF | (15) | |
| CE | (16) | |
| BL | (17) | |
| CCL | (18) | |
| DE | (19) | |
| Parameters and variables | : Approximate emission coefficients, : Generated power by diesel generator, : Battery capacity degradation due to charging/discharging cycles and environmental issues | |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [63] | Particle swarm optimization | Diesel generator-PV-WT-BES | Island village | Life cycle cost | Power balance Diesel generator output power, Battery constraint | Thailand | 2011 |
| [64] | Grasshopper optimization algorithm | Diesel generator-PV-WT-BES | Off-grid community | LCOE | Renewable energy fraction, number of components | Nigeria | 2019 |
| [65] | Harmony search algorithm | Diesel generator-PV | Remote community | NPC | LPSP, number of components | Iran | 2017 |
| [66] | Particle swarm optimization | Diesel generator-PV-BES | Rural mini-grids | NPC | Power balance, fuel consumption and tank level, curtailment of PV, energy of BES | Kenya | 2016 |
| [67] | Particle swarm optimization | Diesel generator-Biomass-PV-WT-BES | Small remote area community | LCOE | LPSP | India | 2017 |
| [68] | Particle swarm optimization | Diesel generator-FT-PV-WT-BES-FW | Remote community | LCOE | Power balance, SOC, number of components, power reserve | Australia | 2020 |
| [69] | Biogeography based optimization | Diesel generator-PV-WT-Hydro-BES | Remote home | Total cost | Number of components, power balance, SOC | India | 2013 |
| [70] | Several algorithms | Diesel generator-PV-WT-BES | Remote village | LCOE | LPSP, power balance, SOC | Egypt | 2019 |
| [71] | Hybrid simulated annealing–tabu search | Diesel generator-Biodiesel-PV-WT-BES-FC | Educational Institute | LCOE | Initial cost, unmet load, capacity shortage, fuel consumption, renewable factor, components’ size | Greece | 2012 |
| [72] | Particle swarm optimization | Diesel generator-PV-BES-EV | Residential | Lifetime cost | Size of components, unit commitment constraints | India | 2019 |
| [73] | Crow search algorithm | Diesel generator-PV-FC | Remote area community | NPC | LPSP, renewable energy portion | Iran | 2020 |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [74] | Multi-objective genetic algorithm | Diesel generator-PV-WT-BES | Not specified | LCOE, CE | Not specified | Spain | 2011 |
| [75] | Multi-objective genetic algorithm | Diesel generator-PV-WT-BES | Residential island | Cycle cost, CE, RF | SOC | China | 2014 |
| [76] | Non-dominated sorting genetic algorithm II | Diesel generator-PV-WT-BES | Island | TAC, LPSP and emission | Number of components, height of WTs, tilt angle of PV, SOC | China | 2017 |
| [77] | Multi-objective line-up competition algorithm | Diesel generator-PV-WT-BES | Residential | Total TAC, total greenhouse gas | Energy of BES, power of Diesel generator, number of components, energy supply constraint | Not specified | 2017 |
| [78] | Multi-objective crow search algorithm | Diesel generator-PV-FC | Not specified | NPC and LPSP | Number of components, tank energy | Iran | 2019 |
| [79] | Multi-objective grey wolf algorithm | Diesel generator-PV-WT-Tidal-BES | Flinders island | LCOE, emission | Number of components, operating reserve | Australia | 2018 |
| [80] | Fuzzy artificial bee colony optimization mechanism | Diesel generator-PV-WT-BES | An edge region | Annualized cost, emission | Number of components, battery’s energy | USA | 2020 |
| [81] | Non-dominated sorting genetic algorithm II | Diesel generator-PV-BES | Island | LCOE, CE, grid voltage deviation | Number of components, battery’s energy | Indonesia | 2018 |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [82] | Deterministic algorithm | Diesel generator-PV-WT-BES | Not specified | NPC | Power balance, SOC, number of components | Senegal | 2011 |
| [83] | Iterative approach | Diesel generator-PV-WT-BES | Residential | Energy cost | Energy of battery | Algeria | 2014 |
| [84] | Developed method | Diesel generator-PV | Campus | LCOE | Not specified | Burkina Faso | 2015 |
| [85] | Decision support technique | Diesel generator-PV-WT-BES | Remote village | NPC | LPSP | India | 2007 |
| [86] | MILP with GAMS/CPLEX | Diesel generator-PV-WT-BES | Not specified | LCOE | Minimum Diesel generator power, battery’s energy, power balance | Portugal | 2015 |
| [87] | Triangular Aggregation Model and the Levy-Harmony Algorithm | Diesel generator-PV-WT-BES | Island village | COE, TAC, loss of renewable energy, LOLP, emission, LPSP | SOC, Diesel generator output power, LPSP | Australia | 2018 |
| [88] | CPLEX optimizer in JAVA | Diesel generator-PV-BES | Ten households in rural area | Capacity of battery | SOC, Diesel generator’s output power | Australia | 2018 |
| [89] | Reformed electric system cascade analysis | Diesel generator-PV-WT-BES | Residential community with 100 homes | Defined based on constraints | Final Excess Energy, Renewable Energy Fraction, LPSP, Annual System Cost | USA | 2019 |
| [90] | MINLP in GAMS using BARON solver | Diesel generator-PV-BES | A remote 38-bus distribution network | Annualized costs | Power flow, active and reactive power mismatch constraints, system frequency | Not specified | 2019 |
| [91] | Dynamic programming algorithm | Diesel generator-PV-BES | Not specified | Total cost per day | Power and energy of BES | USA | 2015 |
| [92] | Stochastic MINLP optimization with GAMS | Diesel generator-PV-WT-BES | Not specified | NPC | Power balance, Diesel generator constraints, operating reserve, BES constraints, budget constraint | Not specified | 2018 |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [100] | Firefly-inspired algorithm | PV-WT-BES | Group of twenty households | COE | Energy of battery, number of components, load dissatisfaction rate | Algeria | 2017 |
| [101] | Water cycle algorithm | Biogas-PHES-PV-BES | Radio transmitter station | NPC | LPSP, number of components, SOC, upper reservoir volume | India | 2019 |
| [102] | Four algorithms | PV-WT-BES PV-WT-FC | Not specified | TAC | Number of components, energy of tank and battery | Iran | 2014 |
| [103] | Flower pollination optimization algorithm | PV-WT-FC | Rustic | NPC | Number of components | Egypt | 2020 |
| [104] | Genetic algorithm | PV-WT-BES | Remote community (2240 home with 4440 population) | NPC | SOC, EENS | India | 2016 |
| [105] | Discrete harmony search | MHP-Biogas-Biomass-PV-WT-BES | Remote rural households (723 homes with 3031 population) | TAC | Unmet load, number of components, energy of BES | India | 2017 |
| [106] | Particle swarm optimization | PV-thermal, WT, microturbine, thermal storage, backup natural gas boiler | Not specified | TAC | LPSP, SOC of energy storage systems, thermal power, number of components | Iran | 2019 |
| [107] | Hybrid harmony search and simulated annealing algorithm | Bio Diesel-PV-WT-BES | Five typical residential building | Life cycle cost | Number of components, power balance, SOC | Iran | 2018 |
| [108] | Particle swarm optimization | PV-WT-Tidal-BES | Remote house | NPC | Number of components, reliability, SOC | France | 2019 |
| [109] | Hybrid grey wolf optimizer-sine cosine algorithm | PV-WT-FC | Residential-commercial center | lifespan cost of hybrid system | Load interruption probability, number of components, energy at tank | Iran | 2020 |
| [110] | Improved bee algorithm | PV-WT-BES-FC-Reverse Osmosis Desalination | Desalination systems and community load | Total life cycle cost | LPSP, energy at hydrogen tank, SOC, number of components | Iran | 2018 |
| [111] | Particle swarm optimization | PV-WT-BES | Single house | NPC | Power balance, number of components | Australia | 2019 |
| [112] | Particle swarm optimization | Biogas-PV-BES | Residential | LCOE | Constraint on deficit power of PV | Kenya | 2017 |
| [113] | Whale optimization algorithm | PV-WT-FC-Tidal | Remote region | NPC | Load deficit probability Size of components | Iran | 2020 |
| [114] | Four algorithms | PV-WT-BES-PHS | Remote island | NPC | Number of components, battery’s energy and SOC | China | 2020 |
| [115] | Genetic algorithm | PV-WT-PHS | Coastline communities | Life cycle cost | Not specified | Nigeria | 2020 |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [116] | Multi-objective particle swarm optimization | PV-WT-BES | Residential | LPSP, LOEP, volatility, life cycle cost | Number of components | China | 2017 |
| [117] | Multi-objective grey wolf algorithm | PV-WT-BES | Rural telecom tower | COE, LPSP, DE | SOC | India | 2020 |
| [118] | Multi-objective grey wolf algorithm | PV-WT-BES-PHS | Isolated farmstead | COE, LPSP | Energy of battery and pump-storage hydro | Algeria | 2019 |
| [119] | Multi-objective genetic algorithm | PV-WT-BES-FC | Not specified | NPC, excess energy, life cycle emission | Number of components, energy of tank | Australia | 2015 |
| [120] | Imperial competitive algorithm | PV-WT-FC | Not specified | Total cost, emission | Equivalent loss factor, angle of PV array, number of components, energy stored at tank | Iran | 2015 |
| [121] | Multi-objective particle swarm optimization | PV-WT-Hydro-PHS | Not specified | LPSP, LCOE, curtailment rate of wind and PV power | Not specified | China | 2020 |
| [122] | Multi-objective genetic algorithm | PV-WT-BES | A residential home with four occupants | Life cycle cost, embodied energy, LPSP | SOC | USA | 2014 |
| [123] | Multi-objective particle swarm optimization | PV-WT-FC | Not specified | TAC, LOEE, LOLE | Energy at tank, number of components, PV tilt angle | Not specified | 2016 |
| [124] | Non-dominated sorting genetic algorithm II | PV-BES-FC | Residential (10 houses) | LPSP, system cost, potential energy waste | Number of components | China | 2019 |
| [125] | Mutation adaptive differential evolution | PV-BES | Rural area | Life cycle cost, LOLP, LCOE | SOC | Malaysia | 2020 |
| Ref. | Applied Method | System Components | RAES Type | Objective Function | Feasibility Constraints | Country | Year |
|---|---|---|---|---|---|---|---|
| [126] | ε-constraint method | PV-WT-BES-FC | Not specified | NPC, LPSP, DE | SOC, energy in hydrogen tank, number of components | Not specified | 2018 |
| [127] | Hybrid multi-criteria decision-making method | PV | Water pumping | Life cycle cost, LOLP, excess water volume | Not specified | Malaysia | 2018 |
| [128] | Sensitivity analysis | PV-WT-BES-PHS | Remote island | Life cycle cost | Not specified | Hong Kong | 2014 |
| [129] | Simulink Design Optimization | PV-BES-FC | Not specified | Cost | Not specified | Spain | 2013 |
| [130] | Iterative technique | PV-WT-BES | Remote residential household | LPSP and LCOE | SOC, number of components | Algeria | 2011 |
| [131] | Power Pinch Analysis | PV-BES | Remote community | Cost | Not specified | Bhutan | 2017 |
| [132] | Object-Oriented Programming | PV-WT-BES | Not specified | NPC | LPSP, SOC | Algeria | 2014 |
| [133] | Probabilistic simulation | PV-BES | A refrigerator used for medical supply in remote area | Loss of load hour, energy not supplied | Not specified | USA | 1998 |
| [134] | Linear programming based on a cascade calculation | PV-WT-Tidal-BES | Island | Equivalent loss Factor | SOC | France | 2016 |
| [135] | Enumerative method | PV-BES | House | LCOE | Unmet load percentage, number of days of autonomy | Spain | 2018 |
| [136] | Pattern search-based optimization | PV-WT-BES | Not specified | Total system cost | SOC, load constraint for DR, EENS, energy index of reliability | USA | 2014 |
| [137] | Iterative method in MATLAB | PV-WT-BES-FC | Pumping system (centrifugal pump) | Deficiency Power Supply, NPC | SOC, tank energy | Tunisia | 2018 |
| [138] | Iterative simulation-optimization | PV-WT-BES-FC | Not specified | LCOE | LOLE | Iran | 2016 |
| [139] | An iterative method | PV-WT-BES | Ten houses in a remote island | NPC | LPSP, COE | China | 2019 |
| [140] | MILP | PV-WT-BES | Remote area mountain lodge | NPC | Energy of BES, power balance | Italy | 2020 |
| [141] | Logical approach | PV-WT-BES | Remote community | NPC | Number of components | South Korea | 2016 |
| [142] | MILP with CPLEX solver in GAMS | PV-WT-BES | Forestry camp | NPC | BES energy and charge/ discharge, demand response constraint | Iran | 2017 |
| [143] | Stochastic optimization | WT-concentrating solar power (CSP) plant-BES | Island | Overall cost | SOC, power balance, output power of components | China | 2020 |
| [144] | Sensitivity based method | PV-WT-FC-PHS | University | RES fraction | Not specified | Cyprus | 2020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khezri, R.; Mahmoudi, A.; Aki, H.; Muyeen, S.M. Optimal Planning of Remote Area Electricity Supply Systems: Comprehensive Review, Recent Developments and Future Scopes. Energies 2021, 14, 5900. https://doi.org/10.3390/en14185900
Khezri R, Mahmoudi A, Aki H, Muyeen SM. Optimal Planning of Remote Area Electricity Supply Systems: Comprehensive Review, Recent Developments and Future Scopes. Energies. 2021; 14(18):5900. https://doi.org/10.3390/en14185900
Chicago/Turabian StyleKhezri, Rahmat, Amin Mahmoudi, Hirohisa Aki, and S. M. Muyeen. 2021. "Optimal Planning of Remote Area Electricity Supply Systems: Comprehensive Review, Recent Developments and Future Scopes" Energies 14, no. 18: 5900. https://doi.org/10.3390/en14185900
APA StyleKhezri, R., Mahmoudi, A., Aki, H., & Muyeen, S. M. (2021). Optimal Planning of Remote Area Electricity Supply Systems: Comprehensive Review, Recent Developments and Future Scopes. Energies, 14(18), 5900. https://doi.org/10.3390/en14185900








