Closed-Form Formulas for Automated Design of SiC-Based Phase-Shifted Full Bridge Converters in Charger Applications
Abstract
:1. Introduction
2. Materials and Methods
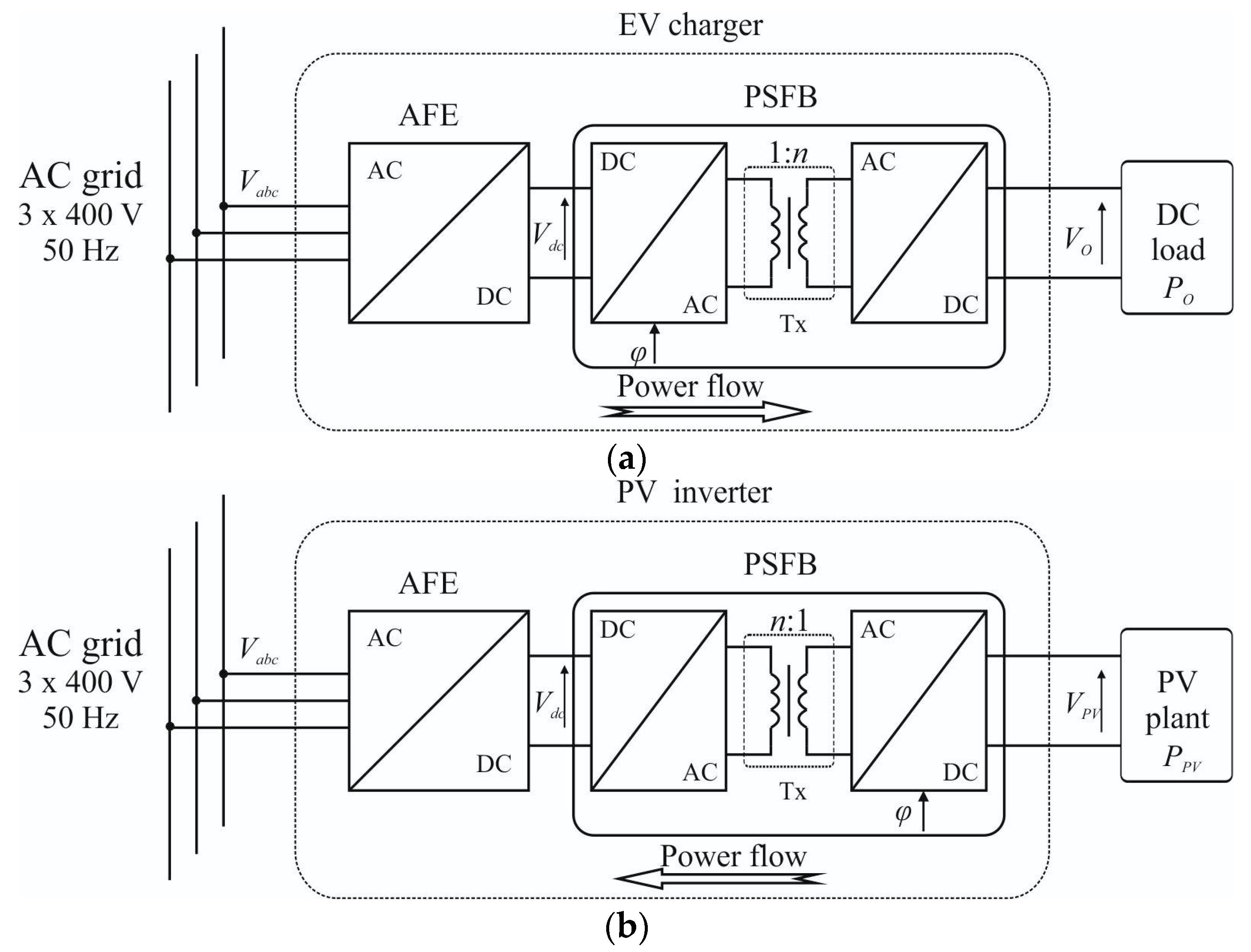
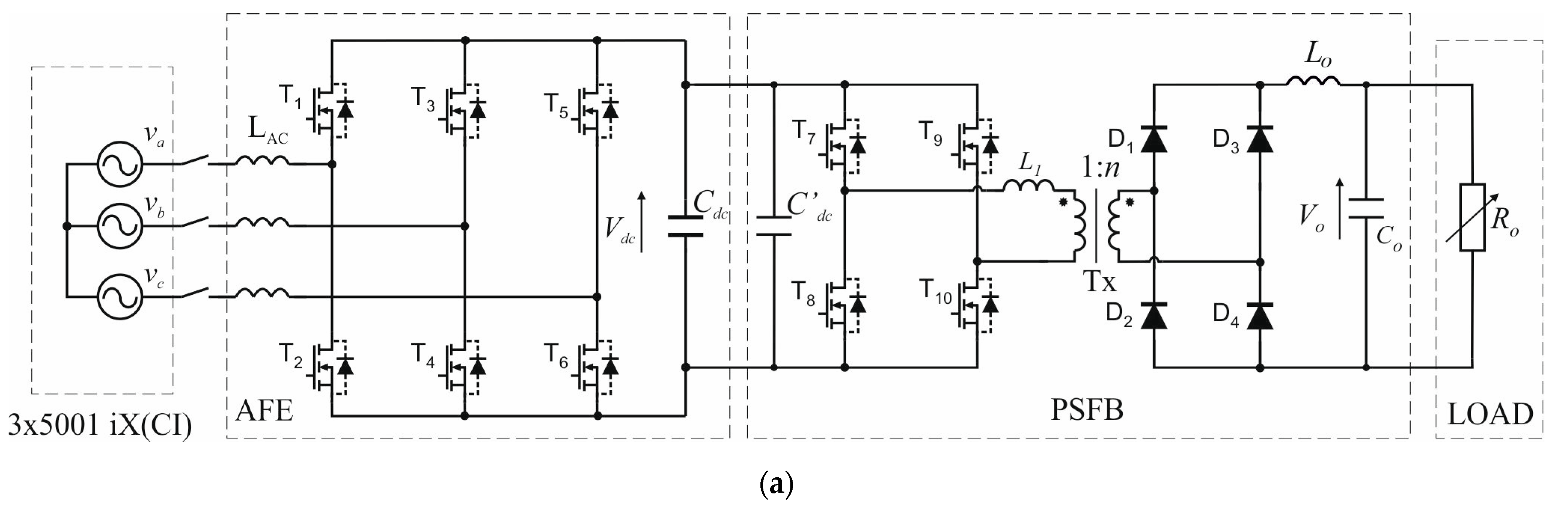
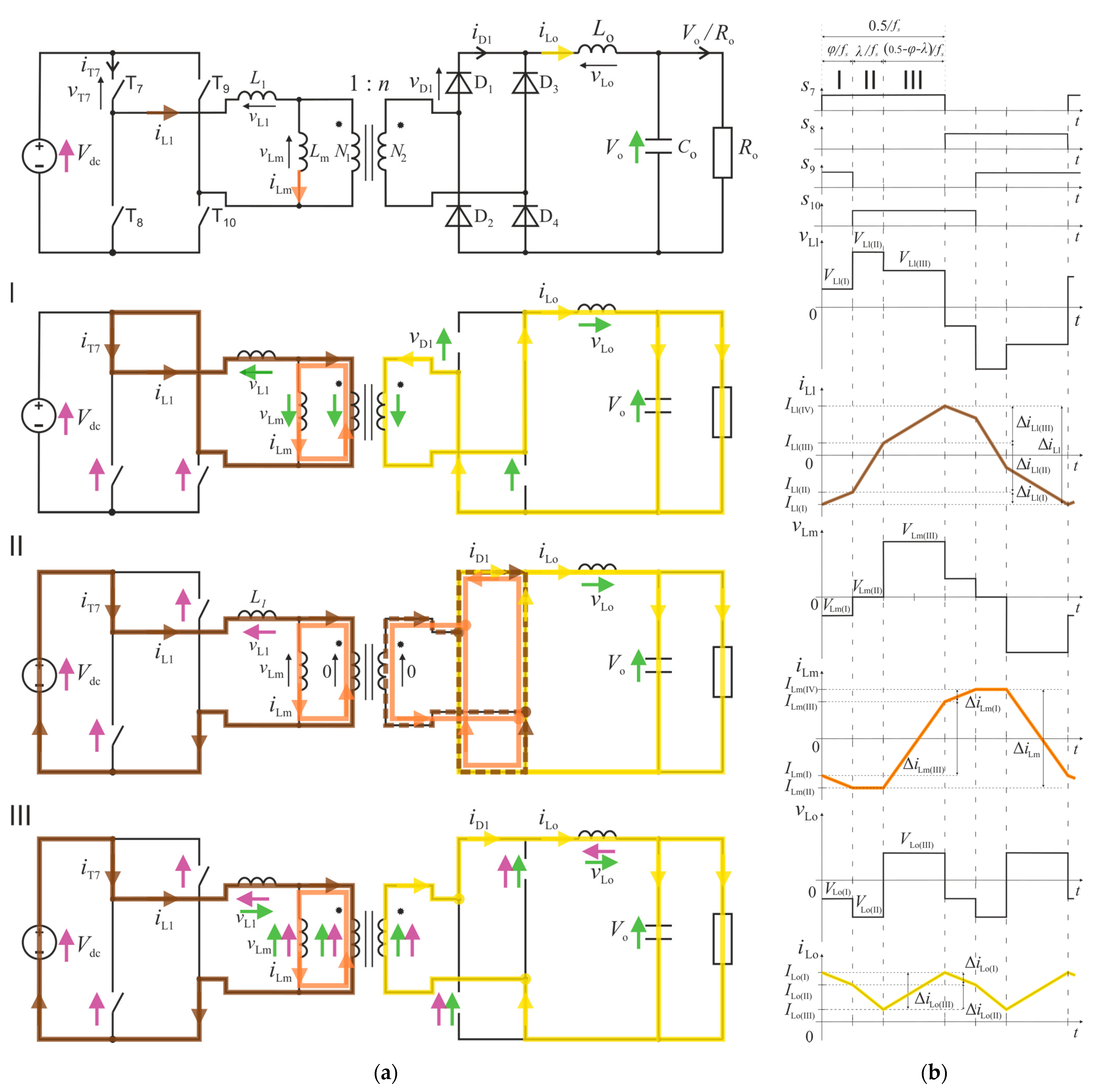
2.1. Topological Details
2.2. Topology Analysis
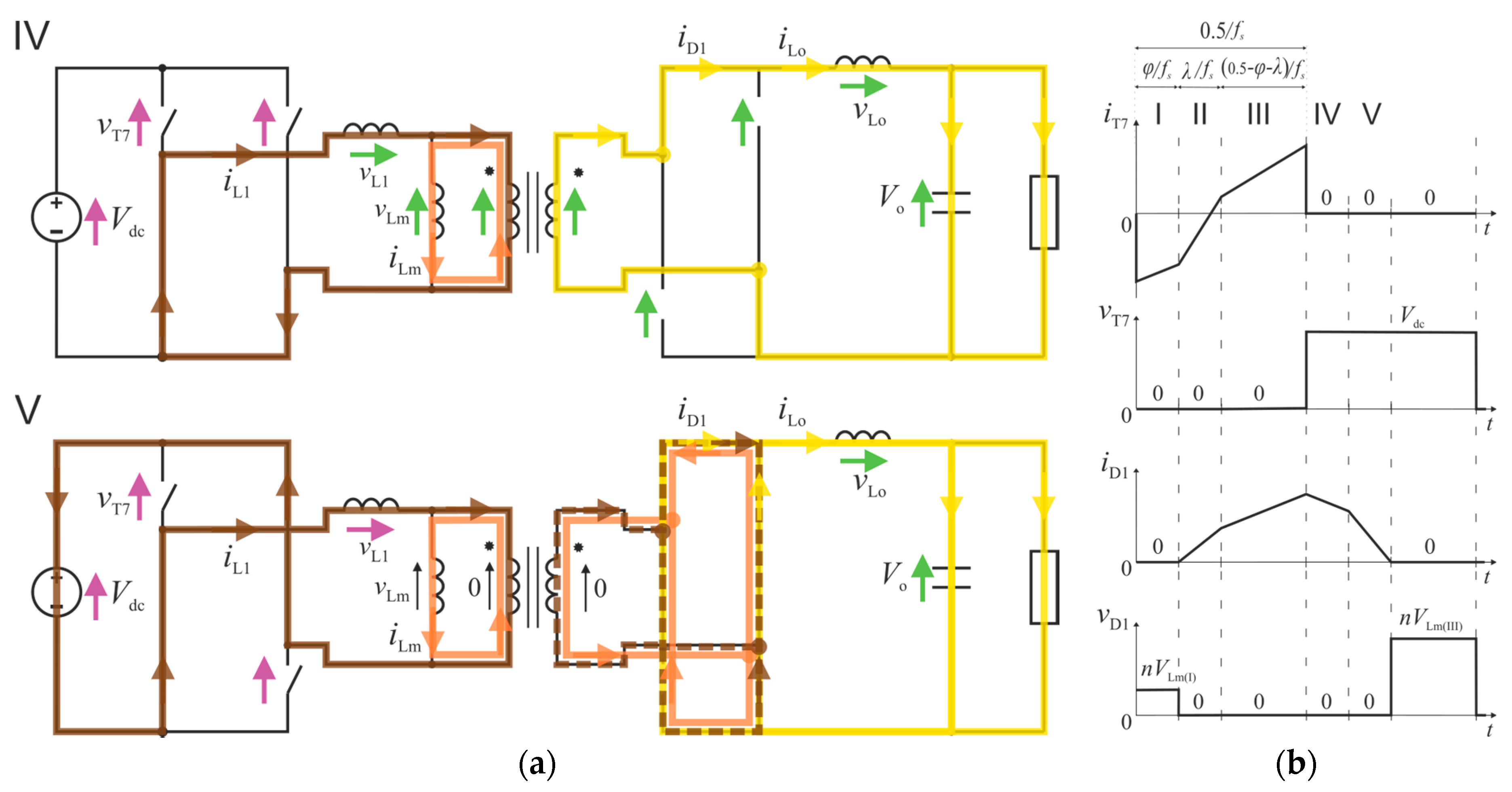
2.2.1. State I Analysis
2.2.2. State II Analysis
2.2.3. State III Analysis
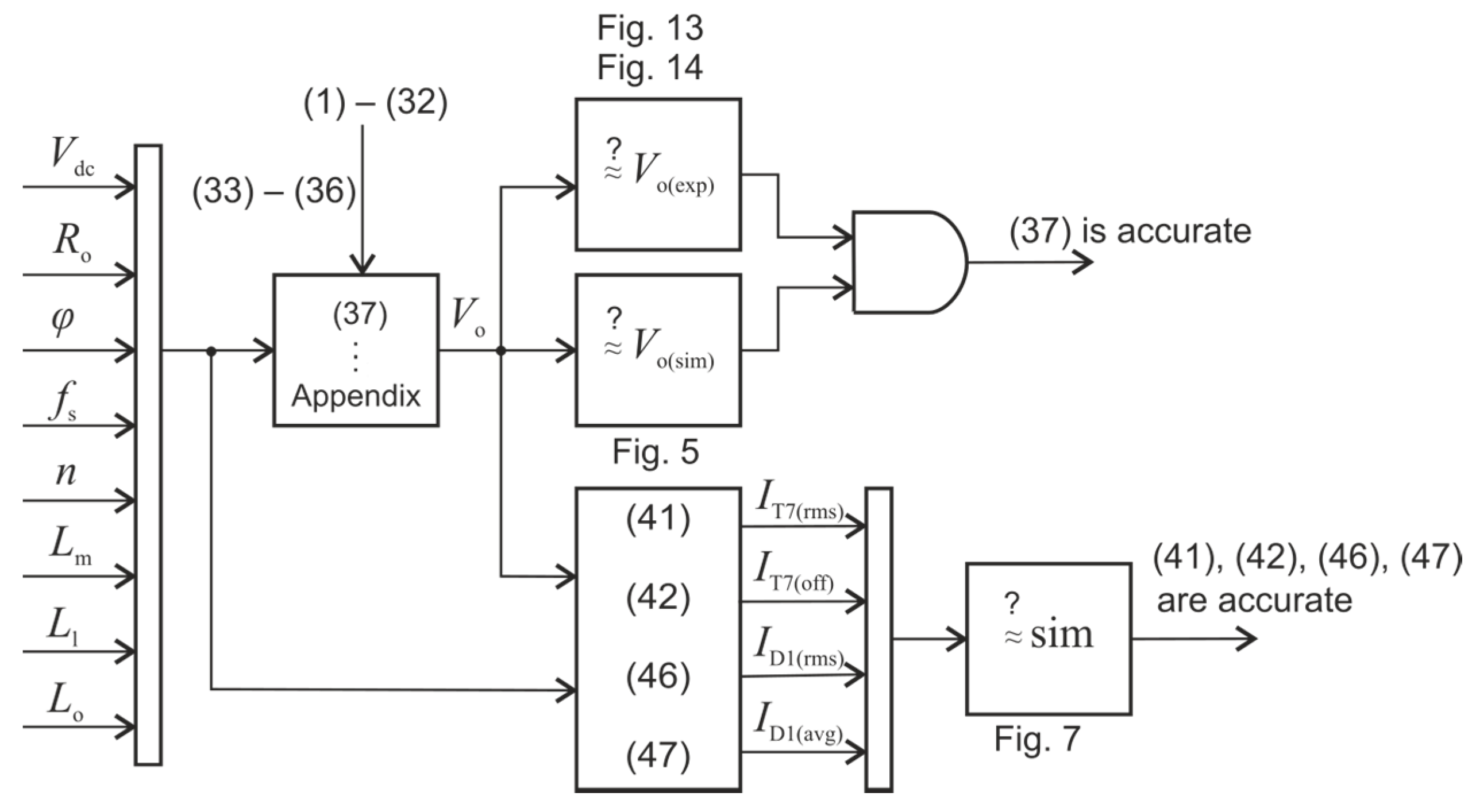
2.2.4. Derivation Results—Output Voltage Expression
2.2.5. Derivation Results—Semiconductor-Loss-Related Parameters
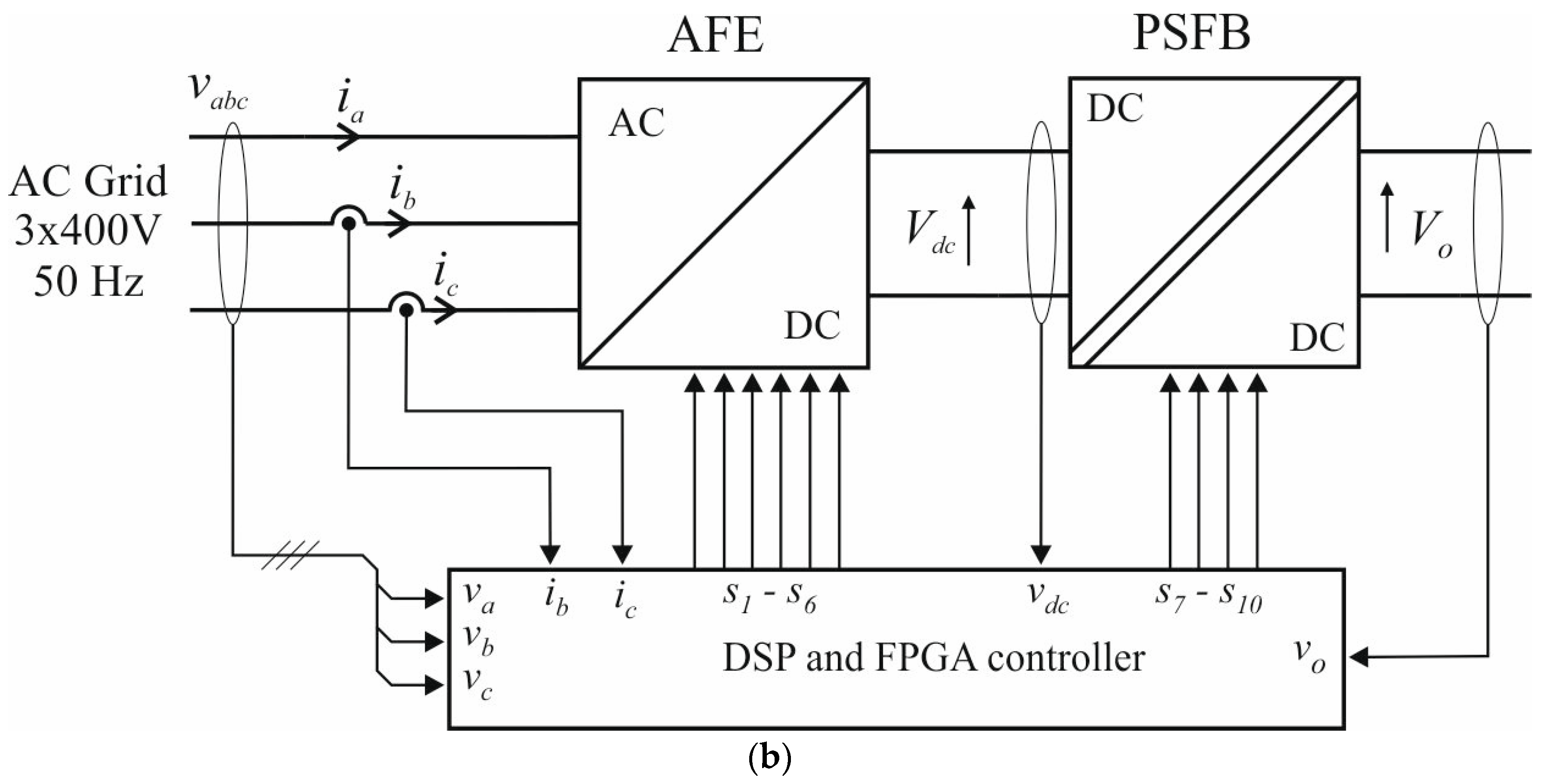
2.3. Control Scheme for Grid-Connected Operation
3. Results
3.1. Laboratory Setup
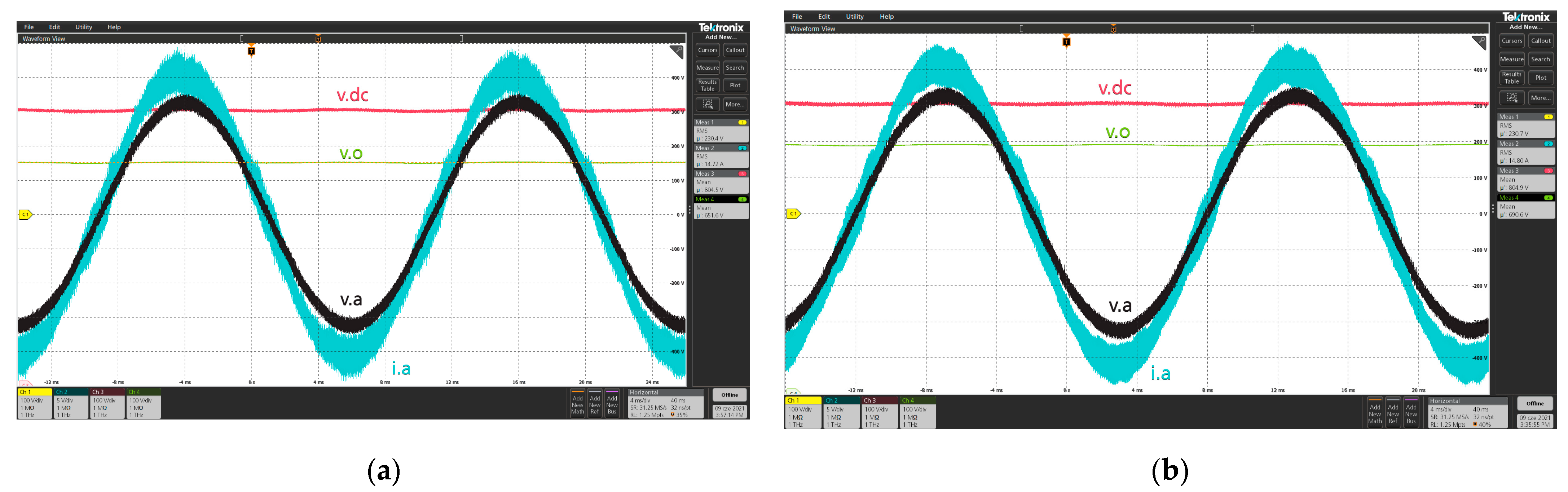
3.2. Laboratory Tests
Steady-State Operation
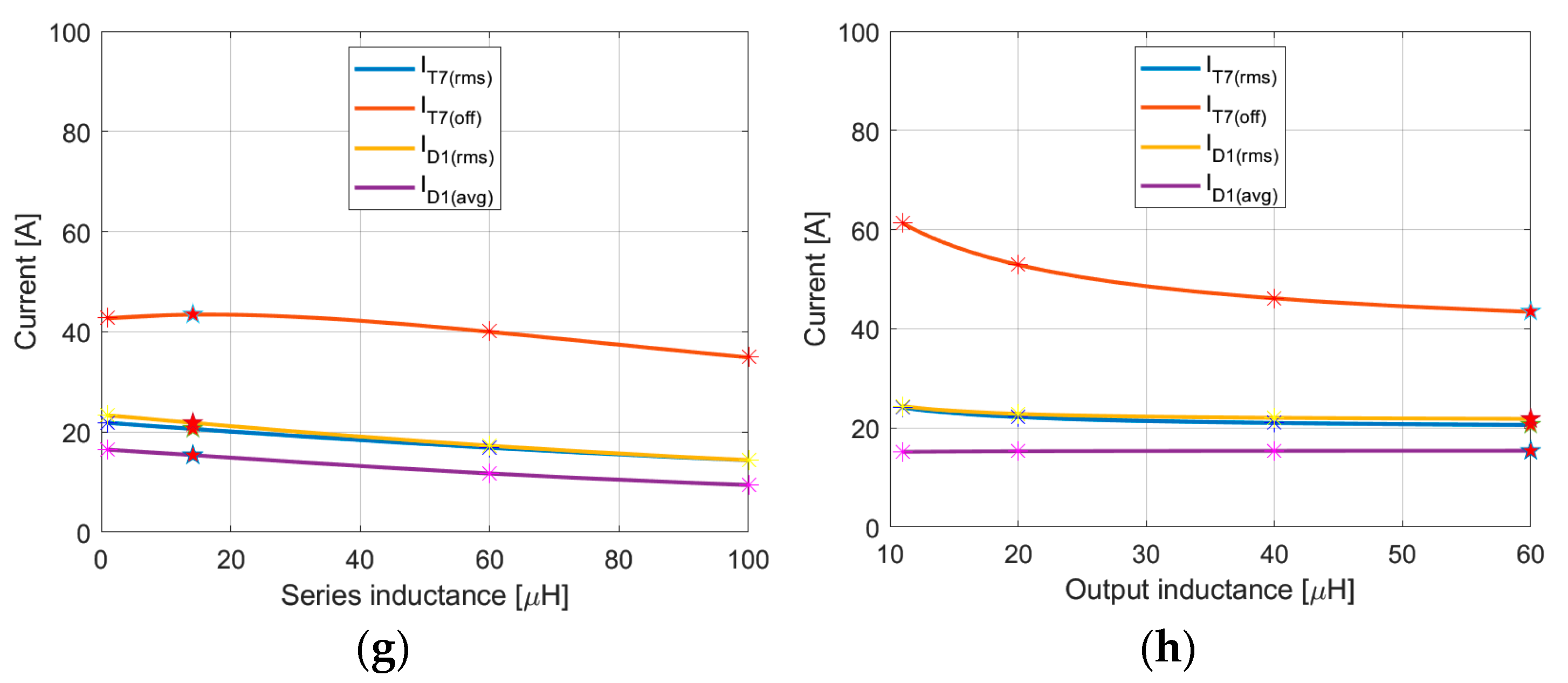
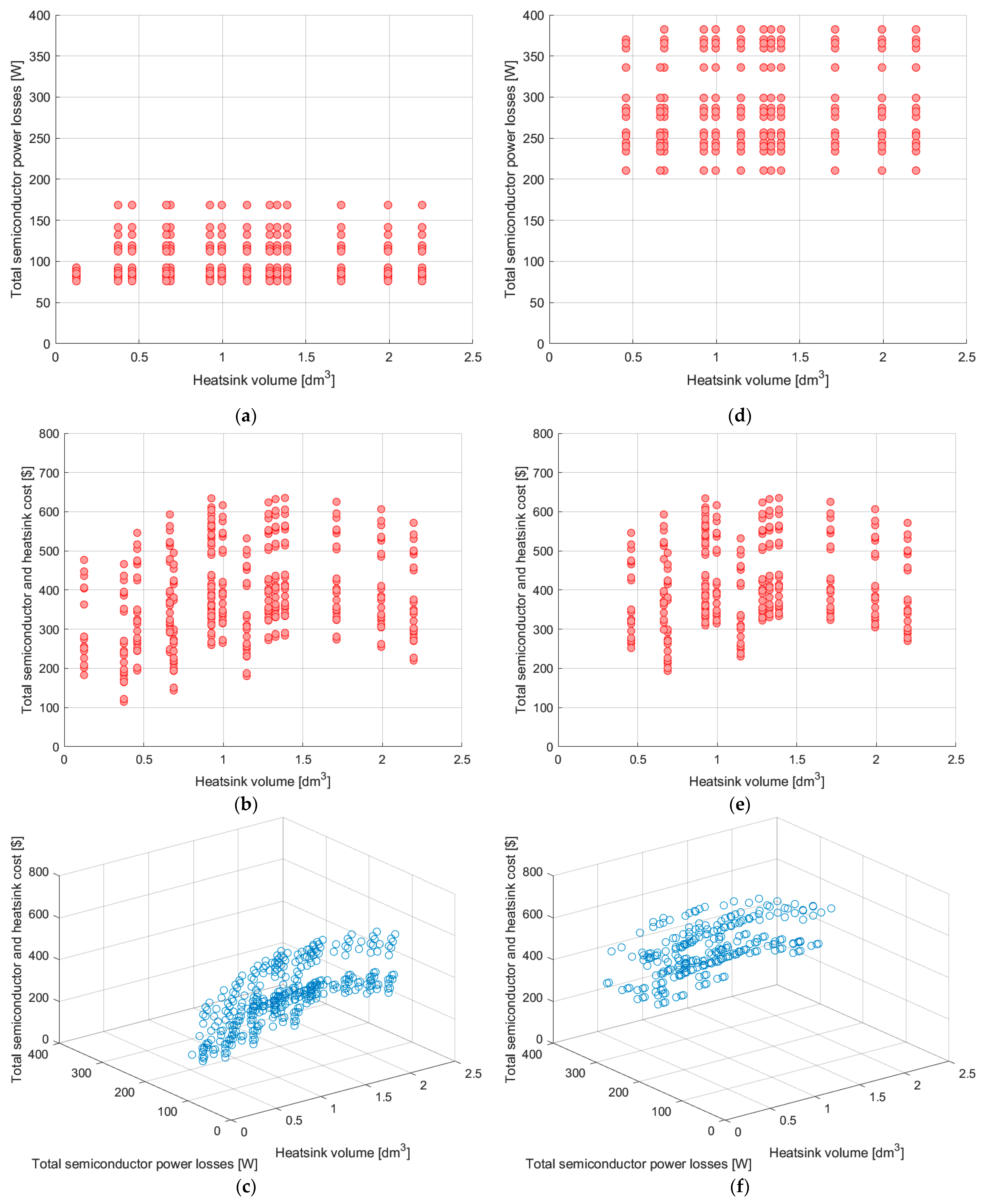
3.3. The Design Procedure
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Burkart, R.M.; Kolar, J.W. Advanced Modeling and Multi-Objective Optimization/Evaluation of SiC Converter Systems. In Proceedings of the Tutorial at the 3rd IEEE Workshop on Wide Bandgap Power Devices and Applications (WiPDA 2015), Blacksburg, VA, USA, 2–5 November 2015. [Google Scholar]
- Sabate, J.A.; Vlatkovic, V.; Ridley, R.B.; Lee, F.C.; Cho, B.H. Design considerations for high-voltage high-power full-bridge zero-voltage-switched PWM converter. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC), Los Angeles, CA, USA, 11–16 March 1990; pp. 275–284. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. Pulse-Width Modulated DC–DC Power Converters, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2016; pp. 330–361. [Google Scholar]
- Whitaker, B.; Barkley, A.; Cole, Z.; Passmore, B.; Martin, D.; McNutt, T.R.; Lostetter, A.B.; Lee, J.S.; Shiozaki, K. A High-Density, High-Efficiency, Isolated On-Board Vehicle Battery Charger Utilizing Silicon Carbide Power Devices. IEEE Trans. Power Electron. 2014, 29, 2606–2617. [Google Scholar] [CrossRef]
- Kanamarlapudi, V.R.K.; Wang, B.; So, P.L.; Wang, Z. Analysis, Design, and Implementation of an APWM ZVZCS Full-Bridge DC–DC Converter for Battery Charging in Electric Vehicles. IEEE Trans. Power Electron. 2017, 32, 6145–6160. [Google Scholar] [CrossRef]
- Ravyts, S.; Vecchia, M.D.; Zwysen, J.; Van den Broeck, G.; Driesen, J. Study on a cascaded DC-DC converter for use in building-integrated photovoltaics. In Proceedings of the IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Piasecki, S.; Jasinski, M.; Wrona, G.; Chmielak, W. Robust control of grid connected AC-DC converter for distributed generation. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5840–5845. [Google Scholar] [CrossRef]
- Rodríguez, P.; Teodorescu, R.; Candela, I.; Timbus, A.V.; Liserre, M.; Blaabjerg, F. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Barlik, R.; Grzejszczak, P.; Leszczyński, B.; Szymczak, M. Investigation of a high-efficiency and high-frequency 10-kW/800-V three-phase PWM converter with direct power factor control. Int. J. Electron. Telecommun. 2019, 65, 619–624. [Google Scholar] [CrossRef]
- Hassanzadeh, N.; Yazdani, F.; Haghbin, S.; Thiringer, T. Design of a 50 kW Phase-Shifted Full-Bridge Converter Used for Fast Charging Applications. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Escudero, M.; Kutschak, M.-A.; Meneses, D.; Rodriguez, N.; Morales, D.P. A Practical Approach to the Design of a Highly Efficient PSFB DC-DC Converter for Server Applications. Energies 2019, 12, 3723. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-M.; Lee, J.; Ryu, K.; Won, C.-Y. Power Device Temperature-Balancing Control Method for a Phase-Shift Full-Bridge Converter. Energies 2020, 13, 1623. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Li, H.; Liu, Y.; Li, Z. High Efficiency Variable-Frequency Full-Bridge Converter with a Load Adaptive Control Method Based on the Loss Model. Energies 2015, 8, 2647–2673. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.; Su, Z.; Chang, Y. Novel Phase-Shift Control Technique for Full-Bridge Converter to Reduce Thermal Imbalance under Light-Load Condition. IEEE Trans. Ind. Appl. 2015, 51, 1651–1659. [Google Scholar] [CrossRef]
- Chen, B.; Lai, Y. Switching Control Technique of Phase-Shift-Controlled Full-Bridge Converter to Improve Efficiency under Light-Load and Standby Conditions Without Additional Auxiliary Components. IEEE Trans. Power Electron. 2010, 25, 1001–1012. [Google Scholar] [CrossRef]
- Lee, W.; Kim, C.; Moon, G.; Han, S. A New Phase-Shifted Full-Bridge Converter with Voltage-Doubler-Type Rectifier for High-Efficiency PDP Sustaining Power Module. IEEE Trans. Ind. Electron. 2008, 55, 2450–2458. [Google Scholar] [CrossRef]
- Shu, L.; Chen, W.; Ma, D.; Ning, G. Analysis of Strategy for Achieving Zero-Current Switching in Full-Bridge Converters. IEEE Trans. Ind. Electron. 2018, 65, 5509–5517. [Google Scholar] [CrossRef]
- Shih, L.; Liu, Y.; Chiu, H. A Novel Hybrid Mode Control for a Phase-Shift Full-Bridge Converter Featuring High Efficiency over a Full-Load Range. IEEE Trans. Power Electron. 2019, 34, 2794–2804. [Google Scholar] [CrossRef]
- Pástor, M.; Dudrik, J.; Vitkovská, A. Soft-Switching DC-DC Converter with SiC Full-Bridge Rectifier. In Proceedings of the International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 347–352. [Google Scholar] [CrossRef]
- Bouvier, Y.E.; Serrano, D.; Borović, U.; Moreno, G.; Vasić, M.; Oliver, J.A.; Alou, P.; Cobos, J.A.; Carmena, J. ZVS Auxiliary Circuit for a 10 kW Unregulated LLC Full-Bridge Operating at Resonant Frequency for Aircraft Application. Energies 2019, 12, 1850. [Google Scholar] [CrossRef] [Green Version]
- Xiaofeng, X. Small-signal model for current mode control full-bridge phase-shifted ZVS converter. In Proceedings of the Third International Power Electronics and Motion Control Conference (IPEMC), Beijing, China, 15–18 August 2000; pp. 514–518. [Google Scholar] [CrossRef]
- Schutten, M.J.; Torrey, D.A. Improved small-signal analysis for the phase-shifted PWM power converter. IEEE Trans. Power Electron. 2003, 18, 659–669. [Google Scholar] [CrossRef]
- Loh, C.K.R.M. Phase Shifted Bridge Converter for a High Voltage Application. Ph.D. Thesis, The University of Edinburgh, Edinburgh, Scotland, December 2003. [Google Scholar]
- Li, P.; Wang, Q.; Zhao, Y.; Lu, S. Power conversion efficiency calculation models for electric vehicle fast charger system. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 316–321. [Google Scholar] [CrossRef]
- Awwad, A.E.; Badawi, N.; Dieckerhoff, S. Efficiency analysis of a high frequency PS-ZVS isolated unidirectional full-bridge DC-DC converter based on SiC MOSFETs. In Proceedings of the 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Petreus, D.; Etz, R.; Patarau, T.; Ciocan, I. Comprehensive Analysis of a High-Power Density Phase-Shift Full Bridge Converter Highlighting the Effects of the Parasitic Capacitances. Energies 2020, 13, 1439. [Google Scholar] [CrossRef] [Green Version]
- Kasper, M.; Burkart, R.M.; Deboy, G.; Kolar, J.W. ZVS of Power MOSFETs Revisited. IEEE Trans. Power Electron. 2016, 31, 8063–8067. [Google Scholar] [CrossRef]
- Roig, J.; Gomez, G.; Bauwens, F.; Vlachakis, B.; Rogina, M.R.; Rodriguez, A.; Lamar, D.G. High-accuracy modelling of ZVS energy loss in advanced power transistors. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 263–269. [Google Scholar] [CrossRef] [Green Version]
- Ayyanar, R.; Mohan, N. Novel soft-switching DC-DC converter with full ZVS-range and reduced filter requirement. I. Regulated-output applications. IEEE Trans. Power Electron. 2001, 16, 184–192. [Google Scholar] [CrossRef]
- Szymczak, M.; Grzejszczak, P.; Barlik, R. Control strategies for isolated high-frequency modular DC/DC converter implemented in programmable logic array. In Proceedings of the Progress in Applied Electrical Engineering Conference, Koscielisko, Poland, 18–22 June 2018. [Google Scholar] [CrossRef]
- Barlik, R.; Grzejszczak, P.; Zdanowski, M. Determination of the Basic parameters of the high-frequency planar transformer. Prz. Elektrotech. 2016, 92, 71–78. [Google Scholar] [CrossRef] [Green Version]





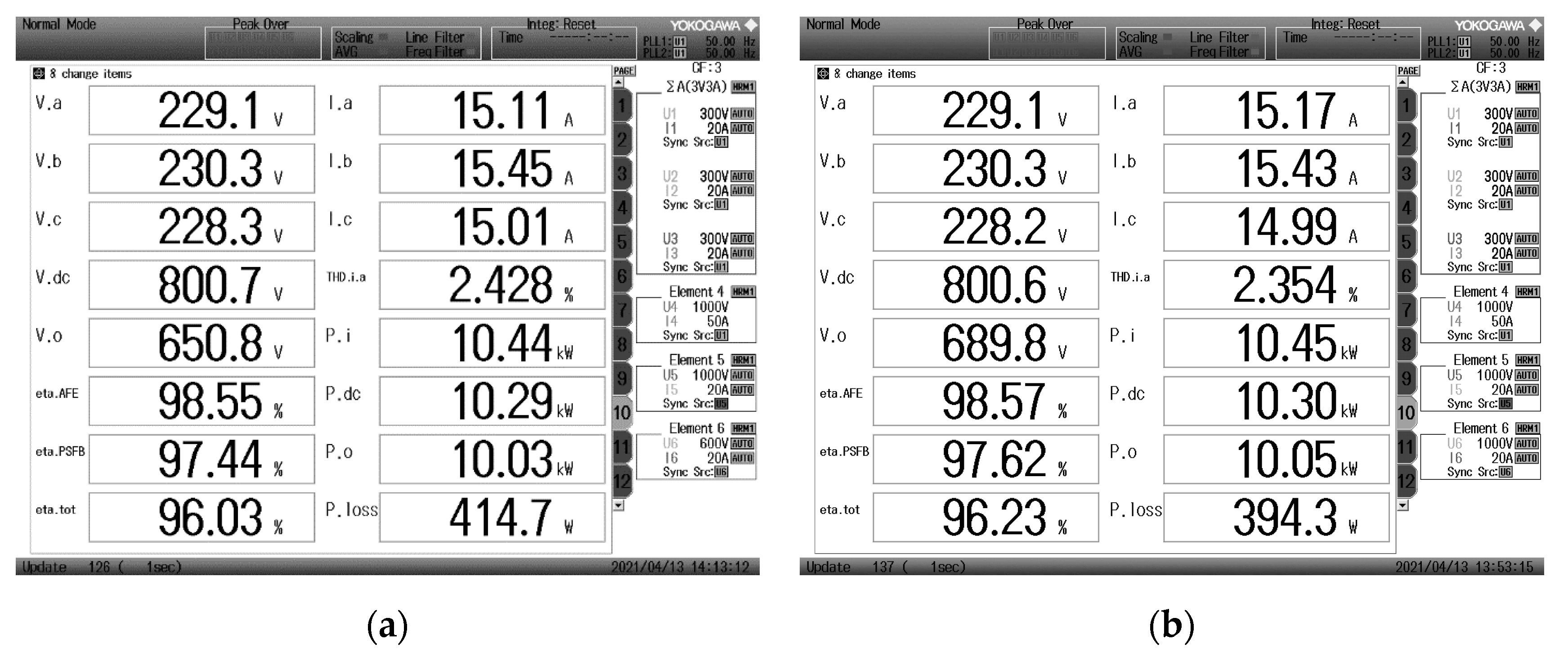
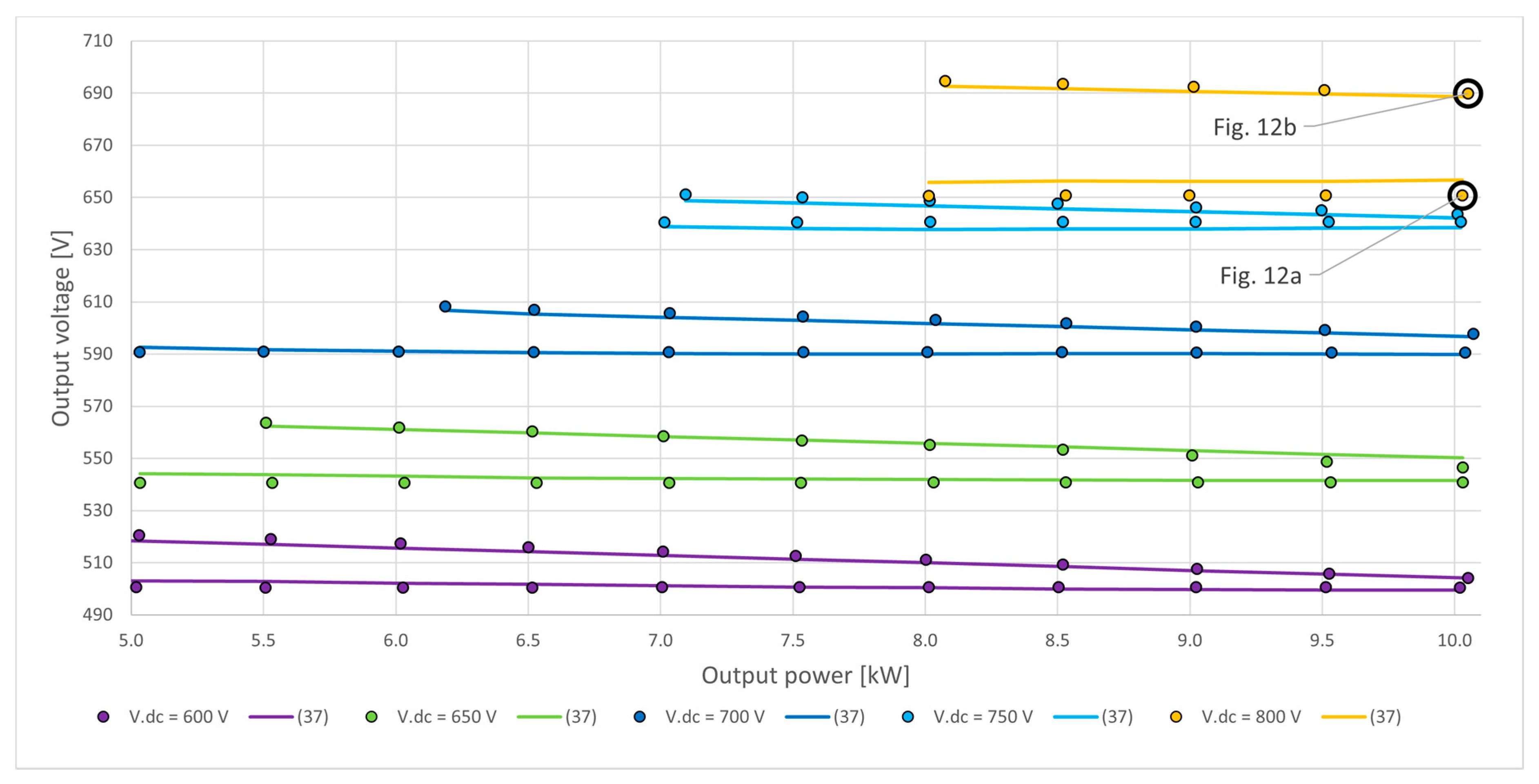
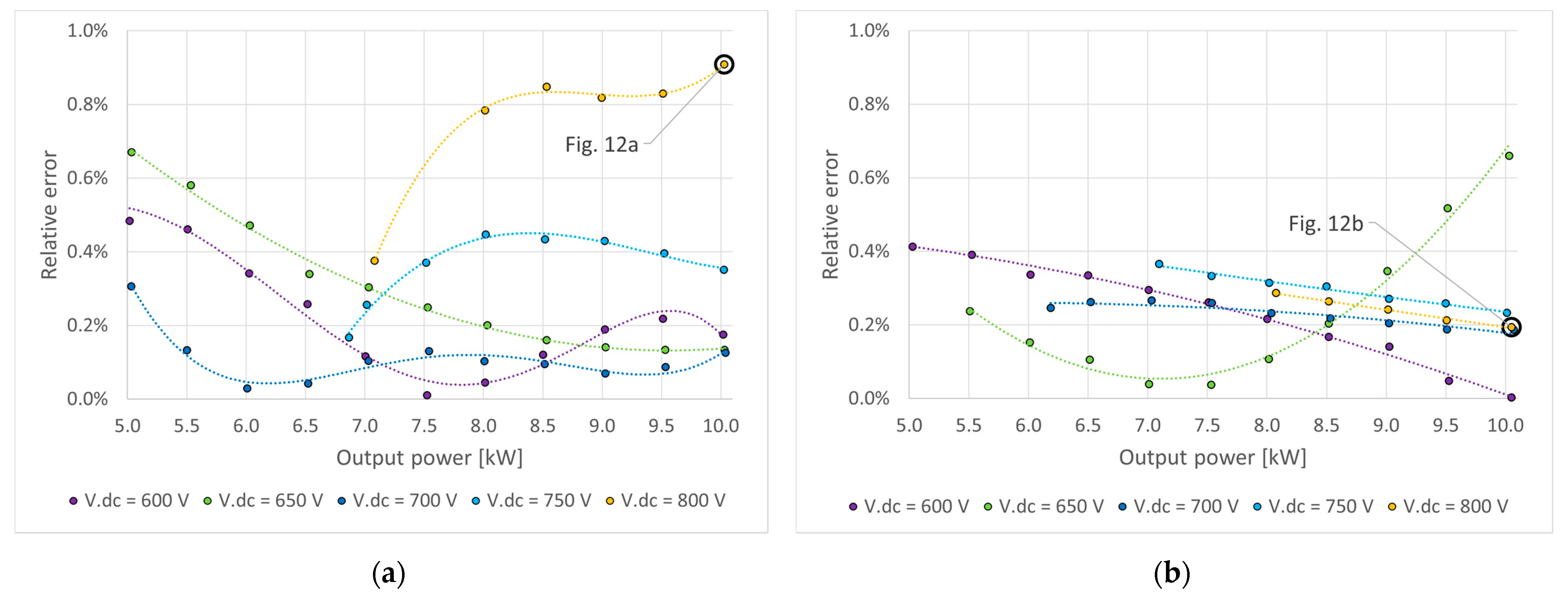
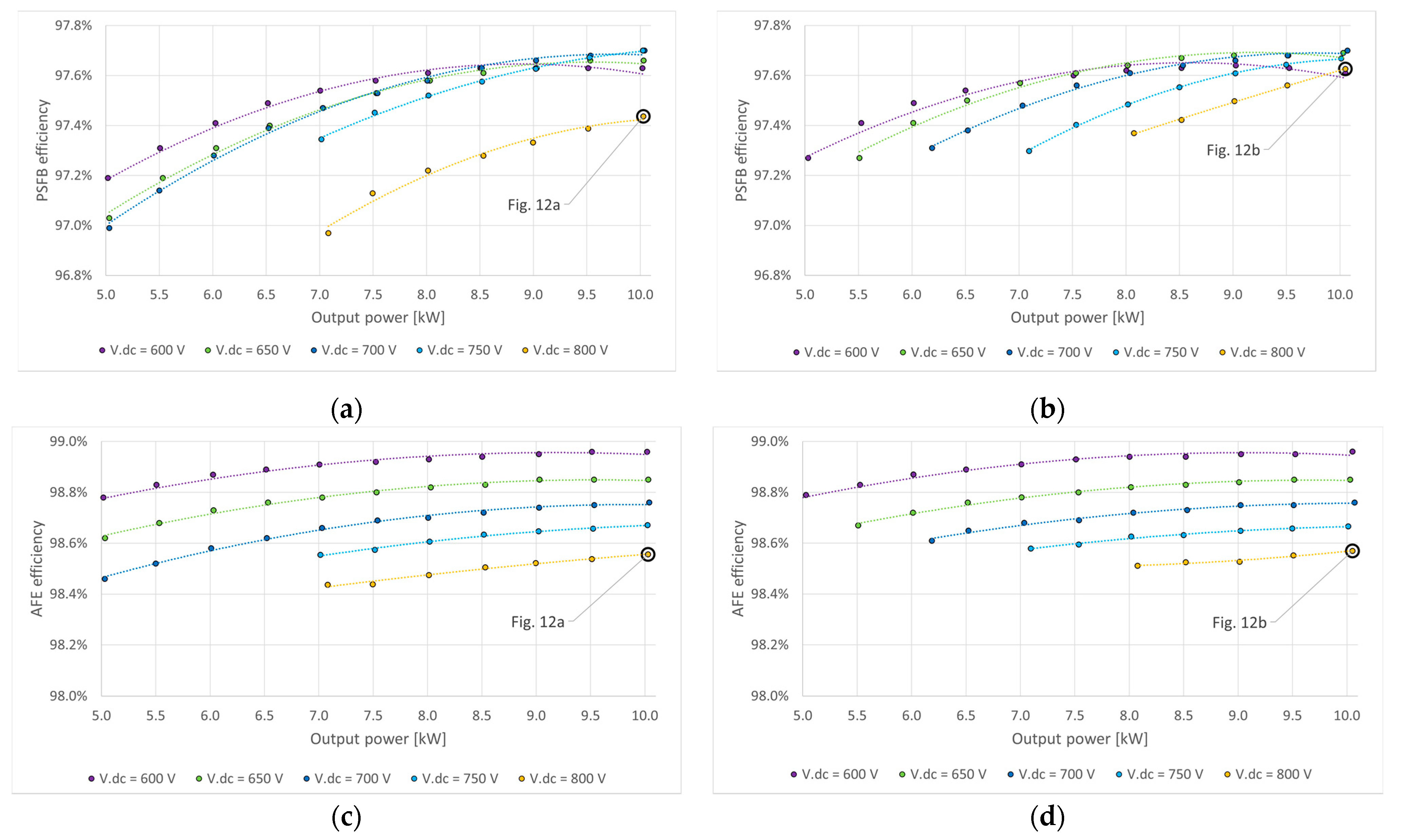

| Parameter | Symbol | Value |
|---|---|---|
| Input voltage | Vabc | 3 × 400 V, 50 Hz |
| DC-link voltage | Vdc | 800 V |
| Output voltage | Vo | 650 V |
| Output power | Po | 20 kW |
| Parameter | Symbol | Value |
|---|---|---|
| DC-link voltage | Vdc | 800 V |
| Load resistance | Ro | 21.125 Ω |
| Phase shift ratio | φ | 1.43% |
| Switching frequency | fs | 25 kHz |
| Turns ratio | n | 0.9 |
| Magnetizing inductance | Lm | 792 μH |
| Series inductance | Ll | 14.15 μH |
| Output inductance | Lo | 60 μH |
| AFE | PSFB | |
|---|---|---|
| Controller | TMS320F28379D DSP | 10CL025 FPGA |
| Control frequency | 60 kHz | 25 kHz |
| Deadtime | 100 ns | 165 ns |
| ADC sampling | 12 bit, 120 kS/s | 12 bit, 250 kS/s |
| Resources used | CPU + CLA | ~20k LE |
| Component | Parameter | Value | Model |
|---|---|---|---|
| PSFB transformer | n | 0.9 | Payton T10000AC-9-10 |
| Lm | 792 μH | ||
| PSFB series inductor | Ll | 14.15 μH (incl. transf. leak.) | Custom-made |
| PSFB output inductor | Lo | 60 μH | Custom-made |
| AFE input inductors | LAC | 210 μH | Custom-made |
| AFE transistors | T1–T6 | - | C3M0021120K |
| PSFB transistor | T7–T8 | - | 2 × SCTH100N120G2-AG |
| PSFB diodes | D1–D4 | - | 2 × STPSC20H12CWL |
| Po | Volume [dm3] | Cost | Ploss(tot) [W] | T7–T10 | D1–D4 | Heatsink | fs [kHz] | n | Lm [mH] | Ll [μH] | Lo [μH] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 kW | 0.375 | $115 | 169 | C3M0120100K | STPSC20H12C | LAM 5 150 12 | 20 | 0.9 | 1.5 | 36 | 130 |
| 0.375 | $466 | 76 | CAB011M12FM3 | C4D40120D | LAM 5 150 12 | 20 | 0.9 | 1.5 | 36 | 130 | |
| 0.125 | $183 | 92 | C3M0032120J1 | C4D15120H | LAM 5 50 12 | 20 | 0.9 | 1.5 | 36 | 130 | |
| 20 kW | 0.688 | $193 | 382 | C3M0032120J1 | STPSC20H12C | LA V 6 150 12 | 20 | 0.9 | 1.5 | 25 | 130 |
| 0.688 | $495 | 211 | CAB011M12FM3 | C4D40120D | LA V 6 150 12 | 20 | 0.9 | 1.5 | 25 | 130 | |
| 0.459 | $252 | 299 | C3M0032120J1 | C4D15120H | LA 6 100 12 | 20 | 0.9 | 1.5 | 25 | 130 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolski, K.; Grzejszczak, P.; Szymczak, M.; Barlik, R. Closed-Form Formulas for Automated Design of SiC-Based Phase-Shifted Full Bridge Converters in Charger Applications. Energies 2021, 14, 5380. https://doi.org/10.3390/en14175380
Wolski K, Grzejszczak P, Szymczak M, Barlik R. Closed-Form Formulas for Automated Design of SiC-Based Phase-Shifted Full Bridge Converters in Charger Applications. Energies. 2021; 14(17):5380. https://doi.org/10.3390/en14175380
Chicago/Turabian StyleWolski, Kornel, Piotr Grzejszczak, Marek Szymczak, and Roman Barlik. 2021. "Closed-Form Formulas for Automated Design of SiC-Based Phase-Shifted Full Bridge Converters in Charger Applications" Energies 14, no. 17: 5380. https://doi.org/10.3390/en14175380
APA StyleWolski, K., Grzejszczak, P., Szymczak, M., & Barlik, R. (2021). Closed-Form Formulas for Automated Design of SiC-Based Phase-Shifted Full Bridge Converters in Charger Applications. Energies, 14(17), 5380. https://doi.org/10.3390/en14175380






