Increasing the Utilization of Existing Infrastructures by Using the Newly Introduced Boundary Voltage Limits

Abstract

The increasing share of distributed generation aggravates voltage limit compliance at customers’ delivery points. Currently, grid operators validate compliance with the voltage limits specified in Grid Codes by conducting load flow simulations at the medium voltage level, considering the connected low voltage grids as ‘loads’ to reduce the modeling effort. This approach does not support the accurate validation of limit compliance, as the voltage drops at the low voltage level are unknown. Nevertheless, to guarantee acceptable voltages even under worst-case conditions, safety margins are involved that impair the utilization of the electricity infrastructure. This study conducts load flows simulations in a test distribution grid, revealing the variable character of the voltage limits at different system boundaries. The conventional load model is extended by new parameters—the boundary voltage limits—to enable the consideration of variable voltage limits in load flow analysis of LINK-based smart grids. The standardized structure of the LINK-architecture allows for the systematic and accurate validation of voltage limit compliance by reducing the required modeling data to the technically necessary minimum. Use cases are specified that allows smart grids to increase the utilization of the electricity infrastructure by day-ahead scheduling and short-term adaptation of boundary voltage limits.

1. Introduction

The power system is the most extensive and complex human-made system existing on earth that is owned, operated, and used by different stakeholders. Its complete analysis as a single entity is impracticable due to the related modeling effort, the required computational resources, and unknown system details. Therefore, power system analysis is restricted to relatively small grid parts considering the neighboring systems by lumped models. The lumped modeling of system parts is challenging as these parts usually include numerous elements with distinct characteristics and complex inter-dependencies.

Historically, power systems comprised power plants and the electricity grid up to the end customers’ Delivery Points (DP) [1]. The grid was divided into the transmission part, including the High Voltage (HV) level, and the distribution part, including the Medium (MV) and Low Voltage (LV) levels. Customer demand was mainly met by the large thermal and hydroelectric power plants connected to the transmission grid. The distribution grids were designed to cope with the resulting unidirectional power flows without requiring extensive secondary technologies for monitoring and automation. Load Flow (LF) analysis is traditionally conducted only at the HV and MV levels, considering the subordinate grid parts as ‘loads’. The term ‘load’ has several meanings in power systems: it may refer to the power consumption of a device, the total power consumed by all devices connected to a power system, the power output of a generator, or a portion of the system that is not explicitly represented in a power system model [2]. The lumped model of the latter is a load in the conventional LF analysis characterized by the active (P) and reactive power (Q) contributions, which are considered as constant, voltage- or frequency-dependent [3,4]. Load profiles are used to analyze the system behavior over time [5].

The current climate change conditions foster the integration of renewable and distributed generation. Their presence challenges the distribution grids’ operation regarding power quality, protection, and stability [6,7,8]. Voltage limit violations at the customers’ DPs are, in many cases, the limiting factor for the Photovoltaic (PV) integration [9]. On the other hand, the ability of distributed energy resources to participate in the Volt/var process [10] and the active role of Customer Plants (CP) [11] introduce new control opportunities. Smart grids are emerging that use automation and ICT to monitor, protect, and automatically optimize the operation of the entire power system, including CPs [12]. They are subject to rigorous data privacy and cyber-security requirements [13] and have to support the execution of various operation processes, such as monitoring, static and dynamic stability, generation load balance, and demand response [14,15]. Maintaining voltage limit compliance belongs to the major concerns of smart grids [16] that requires careful power system analysis. The conventional analysis method, where LF calculations are performed at the MV level and load models represent all LV grids, does not support the validation of voltage limit compliance at the customers’ DPs. Meanwhile, modeling the distribution grid in detail, including the MV and LV levels and the CPs, is inconvenient and requires extensive data sharing between the corresponding stakeholders, impairing data privacy and cyber-security. The inability to accurately verify compliance with voltage limits requires the use of safety margins that reduce the utilization rate of the electricity infrastructure. Because of these shortcomings, the conventional approach to power system analysis is inadequate to meet the requirements of future smart grids and environmental protection, which requires full use of the existing infrastructures.

Meanwhile, holistic smart grid architectures evolve based on their fractal property [17], i.e., the repetition of similar structural details on ever-decreasing sizes. The fractal nature of the vertical power system axis, which includes the HV, MV, LV, and CP levels, paves the way for the systematic validation of voltage limit compliance throughout the entire smart grid: it allows using the same modeling and analysis procedures at each system level.

This paper analyzes the behavior of voltage limits at different system boundaries using the LINK-based holistic architecture [18] to systematize the validation of voltage limit compliance in smart grids. Section 2 overviews the state-of-the-art concerning the voltage limits to be respected and the conventional modeling approach, working out the problem statement in detail. Section 3 provides the materials and methods used in this paper, i.e., the methodology and scope, the test grids, and the calculation procedures. The emergence and behavior of voltage limits on the boundaries of the test grids is discussed in Section 4. Based on the findings, Section 5 develops and discusses the lumped Link-Grid model that allows considering the voltage limits at different system boundaries. New functionalities for state-of-the-art LF programs are suggested. Finally, conclusions are drawn in Section 6.

2. Legal Voltage Limits and Conventional Modeling

2.1. Voltage Limits Specified by Grid Codes

European Distribution System Operators (DSO) are legally obliged to maintain acceptable voltages at the DPs to grid users, such as residential, commercial, and industrial customers, Electricity Producer Operators (EPO), and Electricity Storage Operators (ESO). The German Grid Code [19] stipulates voltage limits of ±10% around the nominal value at all DPs at the MV and LV levels. Transmission System Operators (TSO) and DSOs usually define the voltage limits at the TSO–DSO boundary by contractual arrangements.

Figure 1 shows an overview of the voltage limits specified by European Grid Codes. The TSO operates the HV grid, while the DSO operates the MV and LV grids. Meanwhile, EPOs operate the Producers (Pr), and ESOs operate the Storages (St). The CPs are owned by customers and comprise the CP grid and the connected producers, storages, and Consuming Devices (Dev). Typically, residential CPs are connected to the LV grid, while commercial and industrial ones are connected to the LV or the MV grid. According to the Grid Code, the voltage limits at the DPs to grid users are time-invariant. The DSO has to ensure compliance with these voltage limits in normal operating conditions.

2.2. Conventional Grid Modeling

LF analysis is used to verify compliance with the voltage limits in offline calculations. While the studied grid part is modeled in detail, lumped models represent the connected producers, storages, and neighboring grid parts. Each lumped model corresponds to one of the following node-elements:

• PV node-element: The element’s active power contribution and the voltage magnitude at its boundary node are specified for the regarded instant of time. Additional Q-limits may be defined. Typical examples include producers, such as generators of conventional power plants, and reactive power devices, such as static var compensators and synchronous condensers.
• PQ node-element: The element’s active and reactive power contributions are specified for the regarded instant of time, either independent of the voltage at the boundary node or as a function of it. Typical examples include producers such as PV systems, storages, and neighboring grid parts.
• Slack node-element: The voltage magnitude and angle at its boundary node are specified for the regarded instant of time. The superordinate grid is usually selected as the sole slack node-element in the LF analysis at the MV, LV, and CP levels. Meanwhile, the largest generator may be defined as the slack node-element at the HV level, or the slack node-element may be divided between different large generators.

The specification of the PQ node-elements that represent entire system parts is of great uncertainty. Their active and reactive power contributions vary over time and node voltage. The time dependency mainly results from the behavior of customers and thermostatic controls that switch on and off the consuming devices, from the weather conditions that determine the injection of renewable producers, and from the schedules of storages and thermal power plants. Meanwhile, the voltage dependency inheres the power system hardware itself and may be intensified by control schemes such as Q(U) [20].

Figure 2 shows an overview of the conventional power system modeling. The symbol # represents a wildcard for any system level, i.e., HV, MV, LV, and CP. The study grid part shown in Figure 2a may apply to HV, MV, or LV grids. Neighboring grid parts are conventionally modeled as PQ node-elements specifying their P(U) and Q(U) behavior for each regarded instant of time (t), Figure 2b. They are commonly represented by the “→” symbol in load flow analysis tools.

2.3. Problem Statement

Usually, the DSO conducts LF calculations only at the MV level to verify voltage limit compliance at the MV and LV levels. Detailed modeling and analysis of LV grids are not performed. Figure 3a illustrates the voltage limits to be verified at the MV level. The time-invariant limits at the DPs to customer plants, producers, and storages are known as the Grid Code specifies them. In contrast, the voltage limits at the MV–LV boundaries are unknown (see Figure 1). These limits are estimated based on worst-case assumptions without considering their time-variance to guarantee limit compliance at the LV level at all times, Figure 3b. They are more conservative compared to the DP limits. For example, the DSO operates its MV grids within ±6% around the nominal voltage to allow for voltage variations of ±4% at the LV level.

Using worst-case assumptions to estimate the unknown voltage limits at the MV–LV boundaries does not support the full utilization of the electricity infrastructure.

3. Materials and Methods

3.1. Methodology

This study analyzes the behavior of voltage limits at the distribution and supplying substation levels by conducting LF simulations in real typical test grids. Figure 4 shows the used methodology. After setting the voltage limits at the CP level conform the Grid Code, numerous LF simulations are performed in the LV and MV grids to investigate and identify feasible voltage limits at MV–LV and HV–MV boundaries. Calculations are performed by automating LF simulations within the ‘PSS^®Sincal’ software [21] using ‘MATLAB’ [22] and the corresponding Component Object Model (COM) interface.

Based on the LINK-Architecture [18], the conventional lumped grid model is extended to consider the voltage limits at different system boundaries in LF analysis. Use cases are specified, enabling smart grids to increase the utilization of the existing electricity infrastructure.

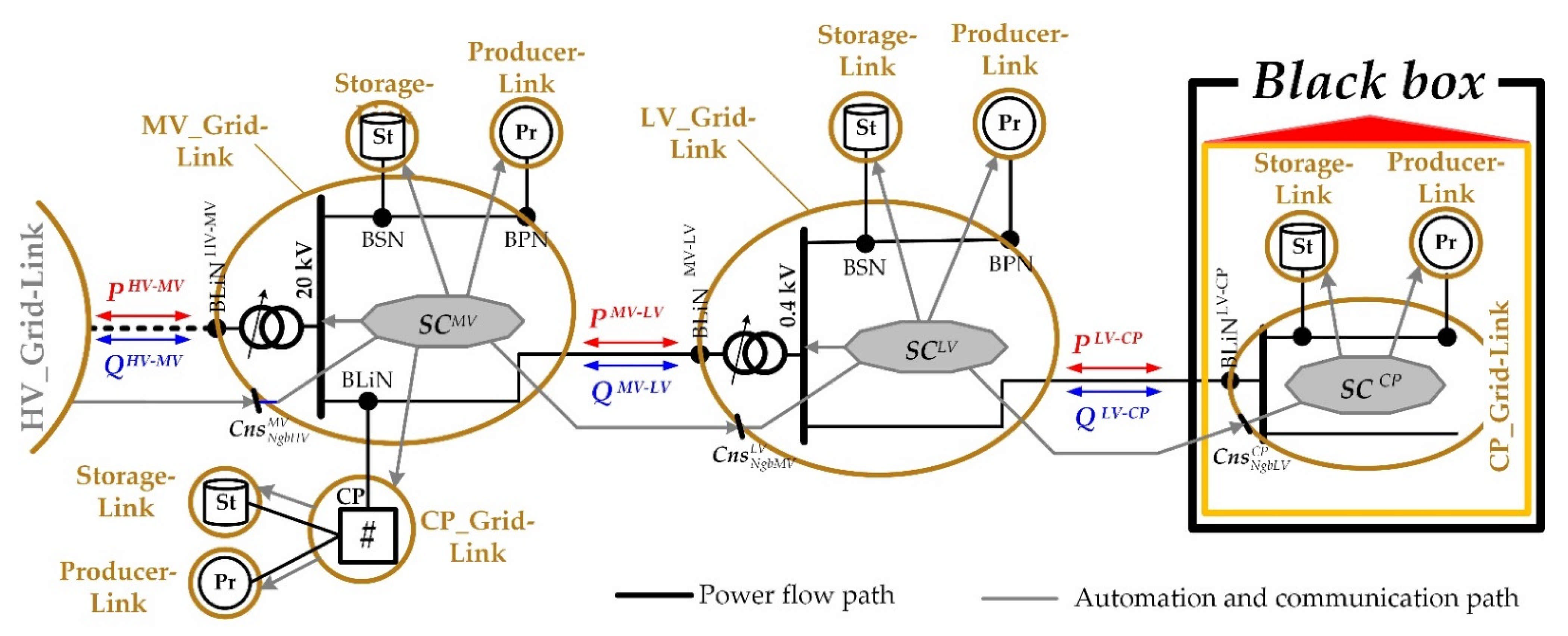
3.2. Structure of the Vertical Link Chain

The LINK-based holistic architecture provides a systematic approach for power system modeling as it relies on the fractal feature of power systems. It divides the entire electricity grid into well-defined Grid-, Producer- and Storage-Links that fit into one another to establish flexible chains over the vertical and horizontal power system axes [23]. Each Link comprises electrical appliances, the corresponding controlling schema, and the interface(s) [18]. Figure 5 shows an exemplary setup of the vertical link chain, where the Grid-Links are set upon three classical smart grid levels: MV, LV, and CP. However, by definition, the Grid-Link size is variable and defined from the area where the corresponding Secondary Control (SC) is set up. It may include one subsystem, e.g., the STR and the feeders supplied from it, or a part of the sub-transmission network, as long as the SC is set up on the respective area. Each Grid-Link consists of electrical appliances, Hertz/Watt, and Volt/var Secondary Control (VvSC), and interfaces to neighboring links. The SCs calculate set points for the available control variables while respecting constraints at the boundaries to neighboring Links. The entirety of all lines and cables, transformers, and reactive power devices included in a Grid-Link is denoted as ‘Link-Grid’. Neighboring Link-Grids, producers, and storages are represented by the , , and symbols, respectively, and are connected to the Link-Grids through Boundary Link Nodes (BLiN), Boundary Producer Nodes (BPN), and Boundary Storage Nodes (BSN). Producer- and Storage-Links include the PV-system, generator, battery, etc., the primary control, and the interface to the corresponding SC. Both MV and LV grids are usually operated with radial structures. The CPs also include radial grids, i.e., the underpinned wires that interconnect the producers, storages, and consuming devices through the sockets and switches in the house. LINK-Solution intends the DSO to operate the STR, so the STR is included in the MV_Link-Grid.

3.3. Description of Simulated Grids

Figure 6 shows the structure of the complete test grid in different levels of detail. The MV grid connects 15 hydroelectric power plants, 45 rural and 11 urban LV grids, as well as 143 commercial and 2 industrial CPs, Figure 6b. LV grids and CPs are considered balanced.

The exact model data of the LV grids are provided in a public data repository [24]. Numerous residential CPs are connected to the LV grids. This section describes the models of the rural residential CP, the rural LV grid, and the MV grid. The models of the urban residential, commercial, and industrial CPs and of the urban LV grid are given in Appendix A.

3.3.1. Rural Residential CP

Figure 7 overviews the model of the rural residential CP. As shown in Figure 7a, the CP is modeled as a single node—i.e., the LV-CP boundary node—that connects an equivalent consuming device model (Dev.-model), a producer model (Pr.-model), and a storage model (St.-model) to the LV grid. Equation (1) determines the active ($P_t^{LV-CP}$) and reactive power ($Q_t^{LV-CP}$) exchange between the LV grid and the rural residential CP for each instant of time (t).

$$P_t^{LV-CP}=P_t^{CP-Dev}+P_t^{CP-Pr}+P_t^{CP-St},$$

(1a)

$$Q_t^{LV-CP}=Q_t^{CP-Dev}+Q_t^{CP-Pr}+Q_t^{CP-St}.$$

(1b)

where $P_t^{CP-Dev}$, $Q_t^{CP-Dev}$ are the active and reactive power contributions of the Dev.-model; $P_t^{CP-Pr}$, $Q_t^{CP-Pr}$ are the active and reactive power contributions of the Pr.-model; $P_t^{CP-St}$, $Q_t^{CP-St}$ are the active and reactive power contributions of the St.-model.

The production and load profiles shown in Figure 7b–d do not consider clouds and the discrete behavior of consuming devices and storages within a single CP, i.e., jumps in consumption when the customer switches on a device or initiates the charging process of its Electric Vehicle (EV). Instead, they represent the appliances’ typical average behavior over many CPs. The Dev.-model represents all consuming devices simultaneously connected to the CP. The voltage-dependent behavior of the consuming devices is modeled by Equation (2), using load profiles and time-variable ZIP-coefficients from [25].

$$\frac{P_t^{CP-Dev}}{P_{nom,t}^{CP-Dev}}=C_t^{Z,P}·{\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)}^2+C_t^{I,P}·\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)+C_t^{P,P},$$

(2a)

$$\frac{Q_t^{CP-Dev}}{Q_{nom,t}^{CP-Dev}}=C_t^{Z,Q}·{\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)}^2+C_t^{I,Q}·\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)+C_t^{P,Q}$$

(2b)

where $C_t^{Z,P}$, $C_t^{I,P}$, $C_t^{P,P}$ and $C_t^{Z,Q}$, $C_t^{I,Q}$, $C_t^{P,Q}$ are the active and reactive power-related ZIP-coefficients; $P_{nom,t}^{CP-Dev}$, $Q_{nom,t}^{CP-Dev}$ are the active and reactive power consumptions of the Dev.-model for nominal voltage; $U_t^{LV-CP}$ is the actual LV–CP boundary voltage; $U_{nom}^{LV}$ is the nominal voltage of the connecting LV grid. The corresponding load profiles are shown in Figure 7b and consider the capacitive behavior of residential CPs with modern consuming devices, such as LED lamps, in the evening [26].

The Pr.-model represents the PV system with a module rating of 5 kW and an inverter rating of 5.56 kVA. Its active power production ($P_t^{CP-Pr}$) is determined by the production profile shown in Figure 7c and is independent of the voltage at the corresponding DP. The reactive power contribution ($Q_t^{CP-Pr}$) of the Pr.-model is set to zero as no Volt/var control is considered. Module and inverter losses are neglected. The St.-model represents an EV battery that is connected to the CP through the EV charger. By analogy with the Dev.-model, the active power absorbed by the charger is specified using ZIP models from [27] and load profiles from [28], see Equation (3a) and Figure 7d. Its reactive power contribution is set to zero.

$$\frac{P_t^{CP-St}}{P_{nom,t}^{CP-St}}=-0.02·{\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)}^2+0.03·\left(\frac{U_t^{LV-CP}}{U_{nom}^{LV}}\right)+0.99,$$

(3a)

$$Q_t^{CP-St}=0.$$

(3b)

where $P_{nom,t}^{CP-St}$ is the St.-model’s active power consumption for nominal voltage.

3.3.2. Rural LV Grid

Figure 8 shows the simplified one-line diagram of the rural LV grid with a nominal voltage of 0.4 kV. It is a real Austrian grid that includes 4 feeders with a total line length of 6.335 km and a cable share of 58.64%. While the shortest feeder is 0.565 km in length, the longest one reaches 1.63 km. The feeders connect 61 rural residential CPs. The 21 kV/0.42 kV distribution transformer is rated with 400 kVA and has a total short circuit voltage of 3.7% with a resistive part of 1%. Its tap changer is fixed in mid-position. The MV–LV boundary node is set to the primary bus bar of the distribution transformer (DTR), and the corresponding active and reactive power flows are designated as $P_t^{MV-\mathrm{LV}}$ and $Q_t^{MV-\mathrm{LV}}$, respectively.

3.3.3. MV Grid

Figure 9 shows the simplified one-line diagram of the MV grid, which is a real Austrian grid that includes 6 feeders with a total line length of 267.151 km and a cable share of 74.66%. While the shortest feeder is 2 km in length, the longest one reaches 46.10 km. It is operated with a nominal voltage of 20 kV. The feeders connect 143 commercial and 2 industrial CPs, as well as 45 rural and 11 urban LV grids. Furthermore, 15 hydroelectric power plants with maximal production capacities between 60 and 400 kW are connected along the feeders. They are simply modeled as PQ node-elements that constantly inject 70% of their maximal active power production with unity power factor. The voltage limits at the corresponding DPs are set to 0.9 and 1.1 p.u. The STR is not included in the model, i.e., the HV–MV boundary node is set to its secondary bus bar, and the corresponding active and reactive power flows are designated as $P_t^{HV-\mathrm{MV}}$ and $Q_t^{HV-\mathrm{MV}}$, respectively.

3.4. Calculation Procedure

The exemplary grid is used to analyze the P(U), Q(U), and voltage limit behavior at the MV–LV and HV–MV boundaries. Firstly, the daily behavior at the distribution substation is calculated by connecting the slack node to the DTR’s primary bus bar and varying the slack voltage between 0.85 and 1.15 p.u. for each instant of time. All slack voltages that provoke voltage limit violations at the LV–CP boundaries are identified, and the corresponding P(U) and Q(U) curves are recorded. Next, the slack node is moved to the HV–MV boundary node, and the calculation procedure is repeated to record the behavior at the supplying substation. Here, all slack voltages that provoke voltage limit violations at the MV–CP, MV–Pr, and LV–CP boundaries are recorded.

4. Results: Emergence of Boundary Voltage Limits

This section discusses the P(U), Q(U), and voltage limits behavior of the MV–LV boundary node of the rural LV grid and at the HV–MV boundary node. The results corresponding to the urban LV grid are documented in Appendix B. The voltage drops within the LV and MV grids significantly deforming the voltage limits at the MV–LV and HV–MV boundaries.

4.1. Voltage Limits Behavior on the MV-LV Boundaries

Figure 10 shows the daily behavior of the rural LV grid for various voltages at the MV–LV boundary node. Voltage limit violations at the DPs occur in the striped zone. The intensity of the colors red and blue indicates the active and reactive power exchanges between the MV and LV grids.

The voltage drops at the LV level deforming the voltage limits at the MV–LV boundary into curved shapes. Strong coupling is observed between the MV–LV active power exchange and the limit curve deformation. In PV production times, the upper voltage limit is strongly tightened, reaching a very low value of 0.9875 p.u. around noontime. The lower limit is tightened almost during the complete time horizon, especially when the rural LV grid consumes active power. This increases the lower voltage limit at the MV–LV boundary up to the maximum value of 0.9525 p.u. in the evening hours. The limits are not violated in cases A, B, and C; however, case $\tilde{\mathrm{B}}$ lies within the upper limit violation zone. A strong time-dependency and weak voltage-dependency characterize the power exchanges. The LV grid consumes 56.62 and 73.85 kW in cases A and C, respectively, and produces 241.99 kW in case B. Meanwhile, 11.21 and 24.78 kvar flow from the MV into the LV level in cases A and B, respectively. In case C, 2.53 kvar are injected into the MV level.

The corresponding voltage profiles are shown in Figure 11a,b for cases B and $\tilde{\mathrm{B}}$, respectively. The LV–CP boundary nodes are marked by black dots. In Figure 11a, no limit violations occur, although the PV injections significantly increase the feeder voltages. Meanwhile, the upper voltage limit is violated in case $\tilde{\mathrm{B}}$, Figure 11b.

4.2. Voltage Limits Behavior on the HV–MV Boundaries

The voltage limits at the HV–MV boundary are drastically deformed, leaving only a small corridor of permissible voltages during the day, Figure 12. Each point (U, t) within the limit violation zones corresponds to limit violations at the connection points of customer plants and hydroelectric power plants. Strong coupling is found between the active power exchange and the limit curve deformation. The injection of active power into the HV level lowers the upper limit to 0.9175 p.u. at mid-day. As a consequence, case B lies far within the upper limit violation zone. When high amounts of active power flow into the MV level, the lower voltage limit increases, reaching 1.0175 p.u. at 18:00. A strong time-dependency and weak voltage-dependency are observed for the power exchanges.

The analyzed test grid can hardly be operated in the traditional way, i.e., with On-Load Tap Changer (OLTC) in supplying substation and without additional Volt/var control strategies applied in LV and/or CP level. The MV grid injects active power into the HV level from 10:15 to 13:59 and absorbs one before and after this interval. In case A and C, 12.22 and 15.21 MW flow from the HV into the MV level, respectively, while in case B, 6.22 MW flow reversely. Meanwhile, the reactive power flows into the HV level at night-time, i.e., before 7:19 and after 20:12, amounting to 2.18 and 2.29 Mvar respective to cases A and C. In case B, the MV grid absorbs 5.32 Mvar from the HV level.

Figure 13 shows the voltage profiles of the MV and LV grids’ feeders for case B. Therein, the profiles of the MV feeders are represented by black lines, and the ones of the LV grids by grey lines. The DPs to the connected residential, commercial, and industrial CPs and the hydroelectric power plants are marked by different symbols and colors: While black bullets represent the DPs to the commercial and industrial CPs, the ones to residential CPs are marked by grey ones. Meanwhile, the DPs at which the hydroelectric power plants are connected are highlighted as red asterisks. The upper voltage limit at the DPs to customer plants, producers, and storages is indicated by a red horizontal line at 1.1 p.u. Due to their lower operating voltage, the profiles of the LV feeders are much steeper than the MV ones. Voltage limit violations occur at the LV level from an electrical distance of 18.92 km from the supplying substation. As a result, case B lies within the upper limit violation zone of the HV–MV boundary node.

4.3. Deformation of Boundary Voltage Limits

The results indicate strong deformations of the voltage limits at distribution and especially supplying substation. This deformation is illustrated in Figure 14. As the STR is not modeled in this study, the HV–MV boundary node is set to its secondary bus bar. The time-invariant voltage limits at the DPs to customers, EPOs, and ESOs provoke time-variant voltage limits at the MV–LV and HV–MV boundaries. In the analyzed example, the deformation degree increases from the MV–LV to the HV–MV boundaries.

5. Discussion

5.1. LINK-Based Grid Modeling

The results presented in Section 4 reveal the variable character of the voltage limits at different system boundaries. Meanwhile, the conventional grid modeling described in Section 2.2 does not support the consideration of variable voltage limits. Therefore, the conventional grid modeling approach must be extended to enable the accurate validation of voltage limit compliance. This section discusses the necessary extensions based on the LINK-Architecture.

5.1.1. Overview of Lumped Link-Grid Model Parameters

The standardized structure of the LINK-Architecture allows for systematic analysis of the vertical link chain. Figure 15 shows an overview of the LINK-based grid modeling. The study Link-Grid may apply to HV, MV, LV, or CP_Link-Grids, Figure 15a. Neighboring Link-Grids are represented by the lumped Link-Grid model shown in Figure 15b, which complements the conventional lumped grid model by two additional variables:

• Upper Boundary Voltage Limit ($\overline{\mathrm{BVL}}$);
• Lower Boundary Voltage Limit ($\underset{¯}{\mathrm{BVL}}$).

Definition 1.

The boundary voltage limits specify the voltage limits that must be respected at a certain boundary link node of a Link-Grid to guarantee voltage limit compliance at all other boundary nodes of the Link-Grid.

5.1.2. Calculation of Lumped Link-Grid Model Parameters

The aggregate behavior of any Link-Grid can be calculated if its structure and the lumped models of the connected elements are known. Figure 16 illustrates the aggregation of the Link-Grid. The BLiN at which the Link-Grid is aggregated is designated as the “BLiN of aggregation”. The Link-Grid to be aggregated connects producers, storages, and neighboring Link-Grids, Figure 16a. Their lumped models include the power contributions as functions of boundary voltage ($U_t^{\#-\#}$) and time and the corresponding boundary voltage limits (see Figure 15b).

Figure 16b shows the lumped Link-Grid model, which is calculated by using the procedures described below.

• Connect the slack node-element to the BLiN of aggregation.
• Define the slack voltage range of interest, e.g., from 0.9 p.u. to 1.1 p.u., and the corresponding resolution, e.g., 0.01 p.u. steps.
• Select one instant of time specified by the lumped models of the connected elements.
• Repeat load flow simulations of the selected instant of time for all defined slack voltages and record the P- and Q-values provided by the slack node-element. Furthermore, document all slack voltage values that provoke violations of the boundary voltage limits of any connected element.
• Repeat steps 1 to 4 for all other instants of time specified by the lumped models of the connected elements.

This procedure yields the following results for each instant of time:

• The power contributions of the Link-Grid to be aggregated as functions of its boundary voltage;
• A set of slack voltage values that provoke violations of upper voltage limits at the boundary node of any connected lumped model. This set of values is denoted as $U_{k,t}^{upper-viol.}$, where k indexes the different values within this set;
• And a set of slack voltage values that provoke violations of lower voltage limits at the boundary node of any connected lumped model. This set of values is denoted as $U_{m,t}^{lower-viol.}$, where m indexes the different values within this set.

Subsequently, the upper and lower boundary voltage limits of the lumped Link-Grid model are calculated using Equation (4).

$${\overline{BVL}}_t^{\#-\#}=\underset{k}{\min }\left(U_{k,t}^{upper-viol.}\right),$$

(4a)

$${\underset{¯}{BVL}}_t^{\#-\#}=\underset{m}{\max }\left(U_{m,t}^{lower-viol.}\right).$$

(4b)

5.1.3. Chain Modeling in the Vertical Power System Axis

The link chain modeling approach allows considering variable boundary voltage limits in the vertical power system axis analysis. Each Link level may be separately simulated using the lumped Link-Grid model for the neighboring grid parts. This approach is illustrated in Figure 17 for the MV, LV, and CP levels. It follows a bottom-up approach with three steps:

• The first step is to define the CP models, i.e., the structures of the CP_Link-Grids; The $P_t\left(U_t\right)$- and $Q_t\left(U_t\right)$-behavior of the connected consuming devices, storages, and producers; the upper and lower LV–CP boundary voltage limits. These specifications allow analyzing the CP level and calculating the lumped CP_Link-Grid models according to the procedure described in Section 5.1.2.
• The next step is to analyze the LV level by representing the connected CPs by their lumped Link-Grid models and specifying the behavior and boundary voltage limits of producers and storages directly connected at the LV level. Again, the procedure described in Section 5.1.2 is used to calculate the lumped LV_Link-Grid models.
• Finally, the MV level is analyzed by representing the connected LV and CP_Link-Grids by their lumped Link-Grid models and by specifying the behavior and boundary voltage limits of the producers and storages directly connected at the MV level. The lumped MV_Link-Grid model can be calculated and provided for the analysis of the HV level.

The link chain modeling approach may be applied in offline and online power system analysis. Section 5.2 presents use cases that allow using the chain modeling process online for the BVL day-ahead scheduling and short-term adaption due to unexpected and sudden changes in consumption and production.

5.1.4. Validating Voltage Limit Compliance at the MV Level

The concept of boundary voltage limits facilitates the validation of voltage limit compliance at the MV level by minimizing the necessary modeling data: no detailed information on the LV grids and the thereto connected elements is necessary for LF analysis at the MV level. Figure 18 illustrates the validation process at the MV level for case B of the simulations (see Figure 12). Different symbols and colors mark the boundary nodes to the connected elements: While black bullets represent the boundary link nodes to the commercial and industrial CPs, the ones to the rural and urban LV grids are marked by yellow and violet asterisks, respectively. The boundary producer nodes at which the hydroelectric power plants are connected are highlighted as red asterisks. Furthermore, the relevant boundary voltage limits are shown in the respective colors. The CPs and the hydroelectric power plants all have an upper boundary voltage limit of 1.1 p.u. throughout the considered time horizon. Meanwhile, the BVLs of the rural and urban LV_Link-Grids vary over time, restricting the maximal MV–LV boundary voltage to 0.9875 and 1.0225 p.u. at 12:10, respectively (see Figure 10 and Figure A4). The voltages increase along the feeders, reaching 1.0161 p.u. close to the end of the longest feeder. In these conditions, some of the BLiN^MV-LV to the rural LV_Link-Grid violate their upper voltage limit. As a result, case B lies within the upper limit violation zone.

5.2. Increasing the Infrastructure Utilization by Considering Boundary Voltage Limits

The lumped Link-Grid model allows formulating use cases for the boundary voltage limits that apply in different timeframes, e.g., in day-ahead and real-time. These use cases allow smart grids to increase the utilization of the electricity infrastructure.

5.2.1. Generalized Use Case

Figure 19 shows the generalized use case for the boundary voltage limits. The study Grid-Link calculates its own lumped Link-Grid model and provides it for the calculation of the neighboring Grid-Link. Additional information concerning the study Grid-Link itself and the thereto connected Grid-, Producer- and Storage-Links are not relevant for the neighboring Grid-Link. The neighboring Grid-Link checks its own limits. When limit compliance is verified, the neighboring Grid-Link sets the constraints of its VvSC, i.e., the voltage limits at the BLiN to the study Link-Grid, according to the BVLs of the study Grid-Link and sends an approval signal.

5.2.2. Day-Ahead BVL Scheduling Chain

Figure 20 shows the LINK-based day-ahead BVL scheduling chain. While the TSO operates the HV_Grid-Link, the Medium (MVSO) and Low Voltage System Operators (LVSO) operate the MV and LV_Grid-Links. Home Management Units (HMU) operate the CPs in real-time and closed-loop. Each CP_Grid-Link estimates the day-ahead schedule for the parameters of its own lumped Link-Grid model at the corresponding BLiN^LV-CP. The CP_Grid-Links send their lumped Link-Grid model parameters to the connecting LV_Grid-Links. Information concerning the CP_Link-Grid structure and the connected appliances are not relevant for the LV_Grid-Links. Each LV_Grid-Link calculates the day-ahead schedule for the parameters of its own lumped Link-Grid model by setting the BLiN of aggregation to the BLiN^MV-LV. The LV_Grid-Links send their lumped Link-Grid model parameters to the connecting MV_Grid-Link. The MV_Grid-Link calculates the day-ahead schedule for the parameters of its own lumped Link-Grid model by setting the BLiN of aggregation to the BLiN^HV-MV. The MV_Grid-Link sends its lumped Link-Grid model parameters to the connecting HV_Grid-Link. The HV_Grid-Link checks its limits: if the HV_Grid-Link is able to maintain the voltages at the BLiN^HV-MV within the requested limits, it sets the constraints of its VvSC^HV accordingly and sends an approval signal to the MV_Grid-Link. The MV_Grid-Link sets the constraints of its VvSC^MV, i.e., the voltage limits at the BLiN^MV-LV, accordingly and sends approval signals to the connected LV_Grid-Links. Again, the LV_Grid-Links set the constraints of their VvSC^LV, i.e., the voltage limits at the BLiN^LV-CP, accordingly, and sends approval signals to the connected CP_Grid-Links. As the Grid Code fixes the voltage limits at the BLiN^LV-CP, the LV_Grid-Link may set the constraints of its VvSC^LV in the beginning of the procedure.

5.2.3. Short-Term BVL Adaptation Chain

Figure 21 shows the LINK-based short-term BVL adaptation chain. Due to any reason, e.g., a forecasting error or a change in consumption due to demand response [29], deviations of the actual lumped CP_Link-Grid model from the scheduled one occur. The corresponding CP_Grid-Link updates its model parameters and sends them to the connecting LV_Grid-Link. The LV_Grid-Link recalculates its own model parameters based on the updated information and sends them to the connecting MV_Grid-Link. Next, the MV_Grid-Link recalculates its own model parameters based on the updated information and sends them to the connecting HV_Grid-Link. The HV_Grid-Link checks its limits: if the HV_Grid-Link is able to maintain the voltages at the BLiN^HV-MV within the requested limits, it updates the constraints of its VvSC^HV accordingly and sends an approval signal to the MV_Grid-Link. The MV_Grid-Link updates the constraints of its VvSC^MV accordingly and sends approval signals to the corresponding LV_Grid-Link. The LV_Grid-Link updates the constraints of its VvSC^LV accordingly and sends approval signals to the corresponding CP_Grid-Link.

5.3. New Functionalities for Load Flow Programs

The standardized structure of the LINK-Architecture allows for the systematic load flow analysis of smart grids. Each grid part—i.e., HV, MV, LV, or CP grid—is aggregated according to a standardized procedure, and the results are provided for the calculations of the neighboring grid parts. The consideration of boundary voltage limits enables the accurate validation of voltage limit compliance at all system levels.

State-of-the-art load flow programs should be upgraded with the following basic functionalities to facilitate the analysis of smart grids:

• Automated calculation of the lumped Link-Grid model parameters
  • The user defines the detailed model of the study Link-Grid and the lumped models (including boundary voltage limits) of the neighboring elements. The LF program automatically calculates the lumped model parameters of the study Link-Grid using the procedure described in Section 5.1.2.
• Automated lumped model creation for the calculation of neighboring Link-Grids
  • The LF program uses the calculated parameters to generate the lumped Link-Grid model that can be used for the analysis of neighboring Link-Grids.

6. Conclusions

The analysis of the radial test grids revealed the variable character of the voltage limits at the MV–LV and HV–MV boundaries, which are deformed by the voltage drops at the LV and MV levels.

The conventional grid modeling approach does not support the consideration of variable boundary voltage limits. Therefore, the compliance with voltage limits specified in Grid Codes should be validated by using worst-case assumptions for the limits at the HV–MV or MV–LV boundaries; by modeling the complete distribution grid, including MV and LV grids and all connected elements. While the former option does not allow for the complete utilization of the electricity infrastructure, the latter one is impracticable due to the high modeling effort and data-sharing issues.

The LINK-based holistic architecture allows validating voltage limit compliance throughout the entire smart grid by reducing the required modeling data to the technically necessary minimum. Its standardized structure enables the systematic chain modeling by extending the conventional lumped grid model with new parameters: the boundary voltage limits. LINK-smart grids can use the concept of boundary voltage limits for day-ahead scheduling and short-term adaptation to increase the utilization of the electricity infrastructure. Data privacy is preserved by exchanging minimal data amounts. While the day-ahead scheduling facilitates the operational planning process, the online calculation allows for the prompt update of boundary voltage limits under unexpected and sudden topology changes and significant fluctuations in consumption and production. Upgrading load flow programs with functionalities that allow for the consideration of boundary voltage limits greatly facilitates the analysis of smart grids.

Quantifying the impact of the proposed process on the electricity infrastructure’s utilization rate in the presented use cases and beyond requires an in-depth investigation of the economic benefits, thus constituting the focus of future research.