A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities
Abstract
:1. Introduction
1.1. Positive Energy District Analysis in Literature
1.2. Annual Energy Balance in Energy System Modelling
1.3. Open-Source Energy Modelling
1.4. Progress beyond the State of the Art
- Is a PED technically and spatially feasible under perfect climatic conditions?
- How is a PED affected by the type of settlement (urban or rural) under these conditions?
- What are the PED’s implications in terms of cost and technology portfolio if the grid impact is kept low?
- How does the renewable share of the grid mix affect the PED economically and technically, if assessed hourly?
2. Materials and Methods
2.1. Model Overview
2.2. Mathematical Model
2.2.1. Objective Function
- , the initial investment cost in year zero of the optimised technology portfolio;
- , the annual revenues from selling excess generated electricity to the grid; specified in Equation (2);
2.2.2. PED Energy Balance
2.2.3. PV Constraints
2.2.4. Battery Constraints
2.3. Case Study Definition
2.3.1. Location
2.3.2. Time Series Data
2.3.3. Initial Scenarios
2.3.4. Sensitivity Scenarios
3. Results
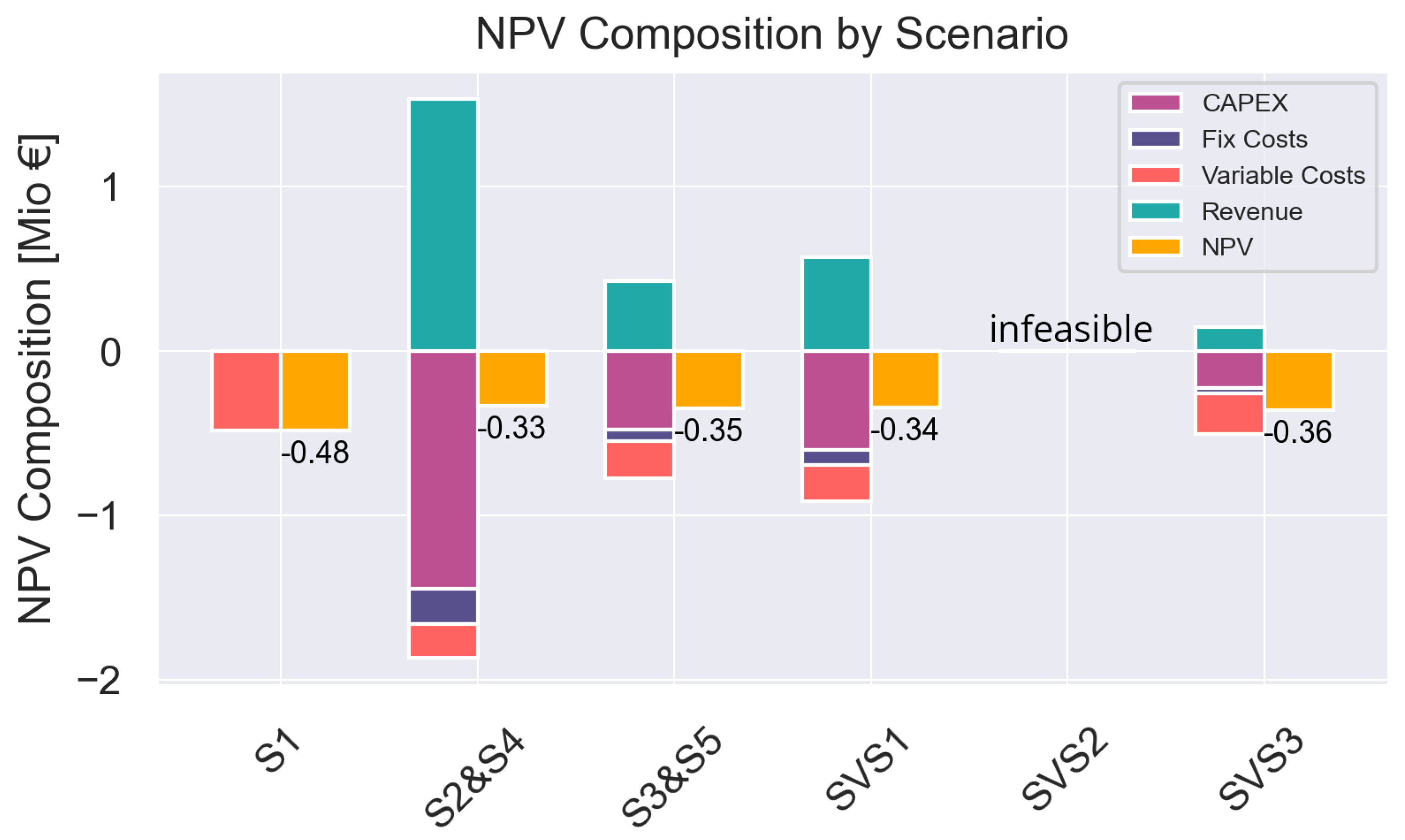
3.1. Rural vs. Urban and Variation of Roof Space Available
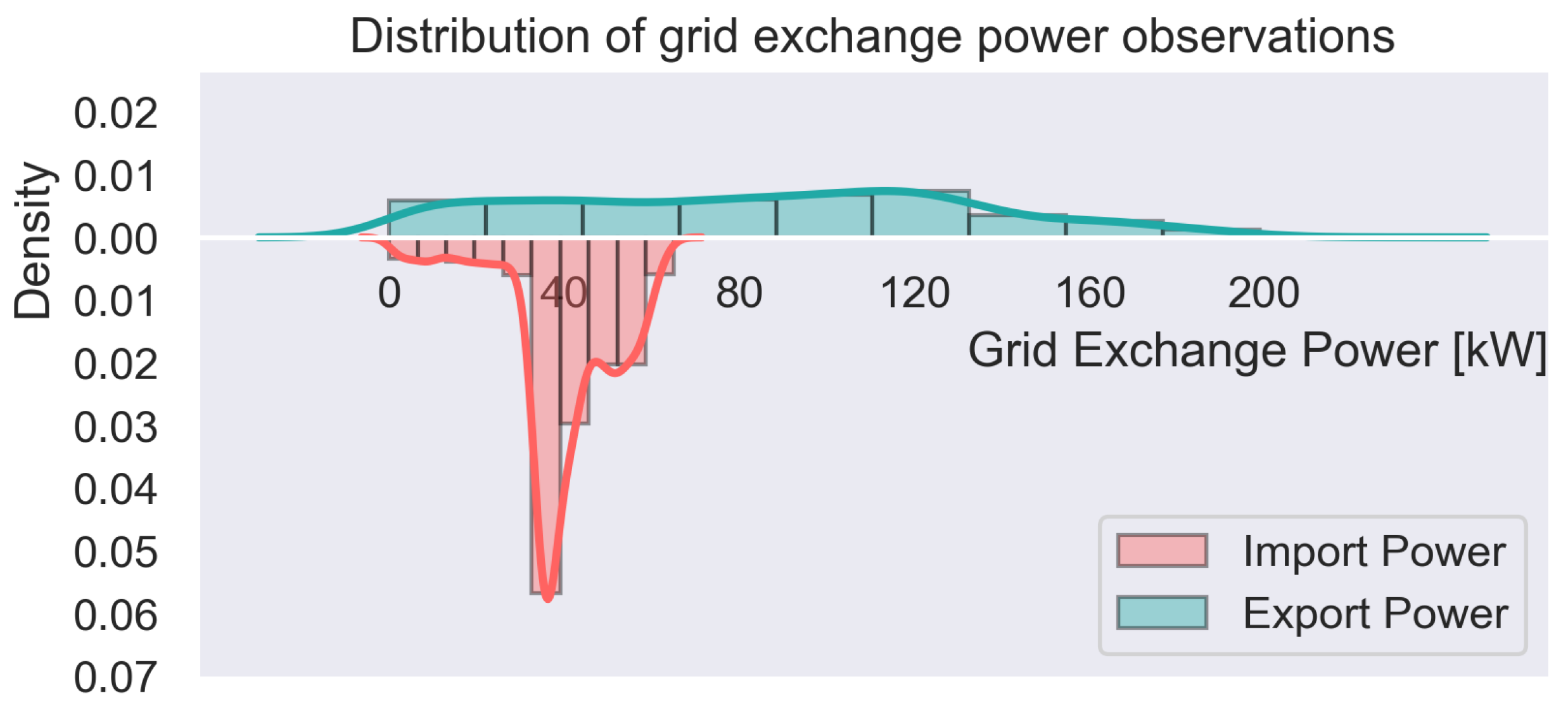
3.2. Variation of Grid Exchange Power
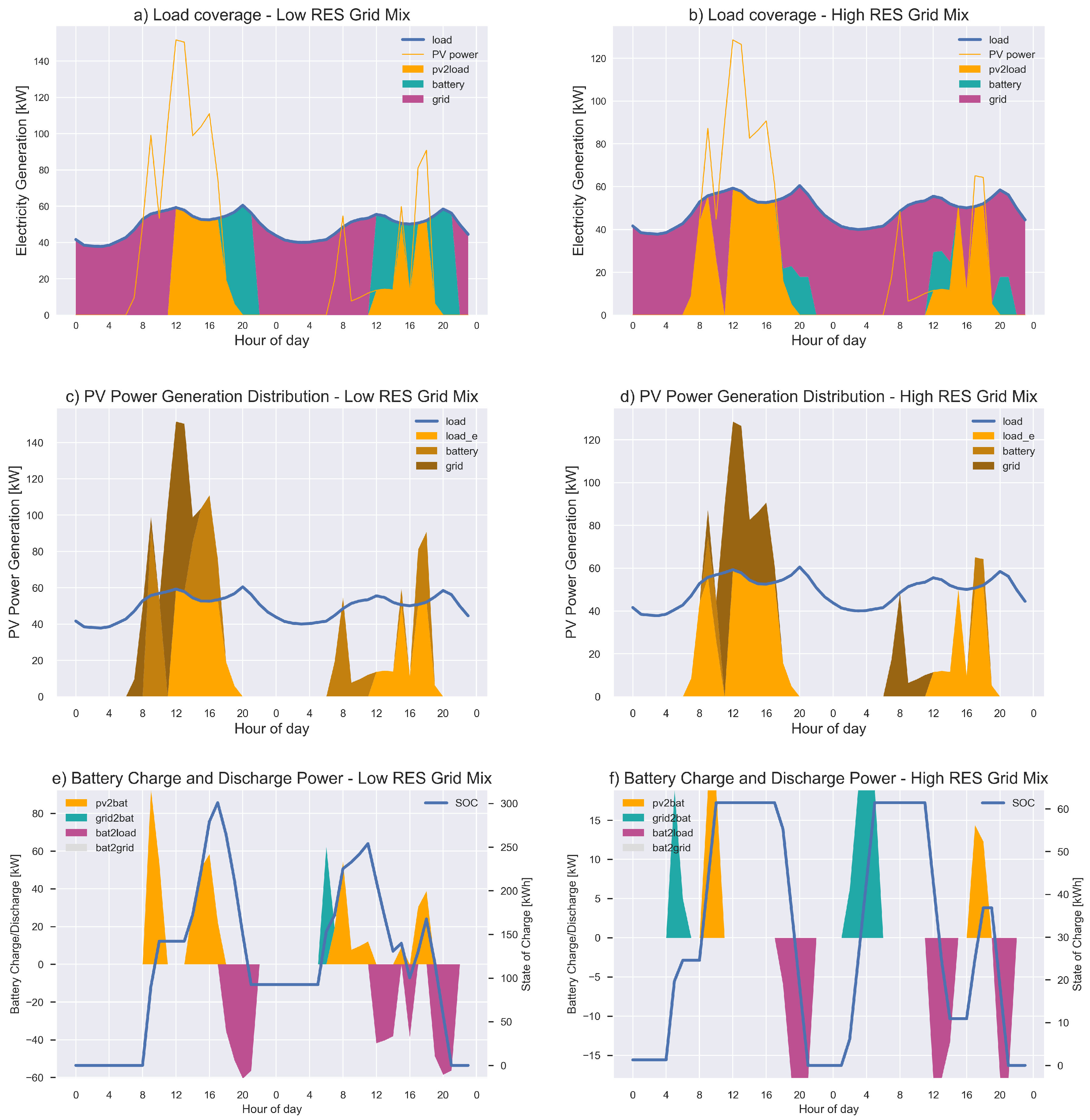
3.3. Variation of Local Generation Mix
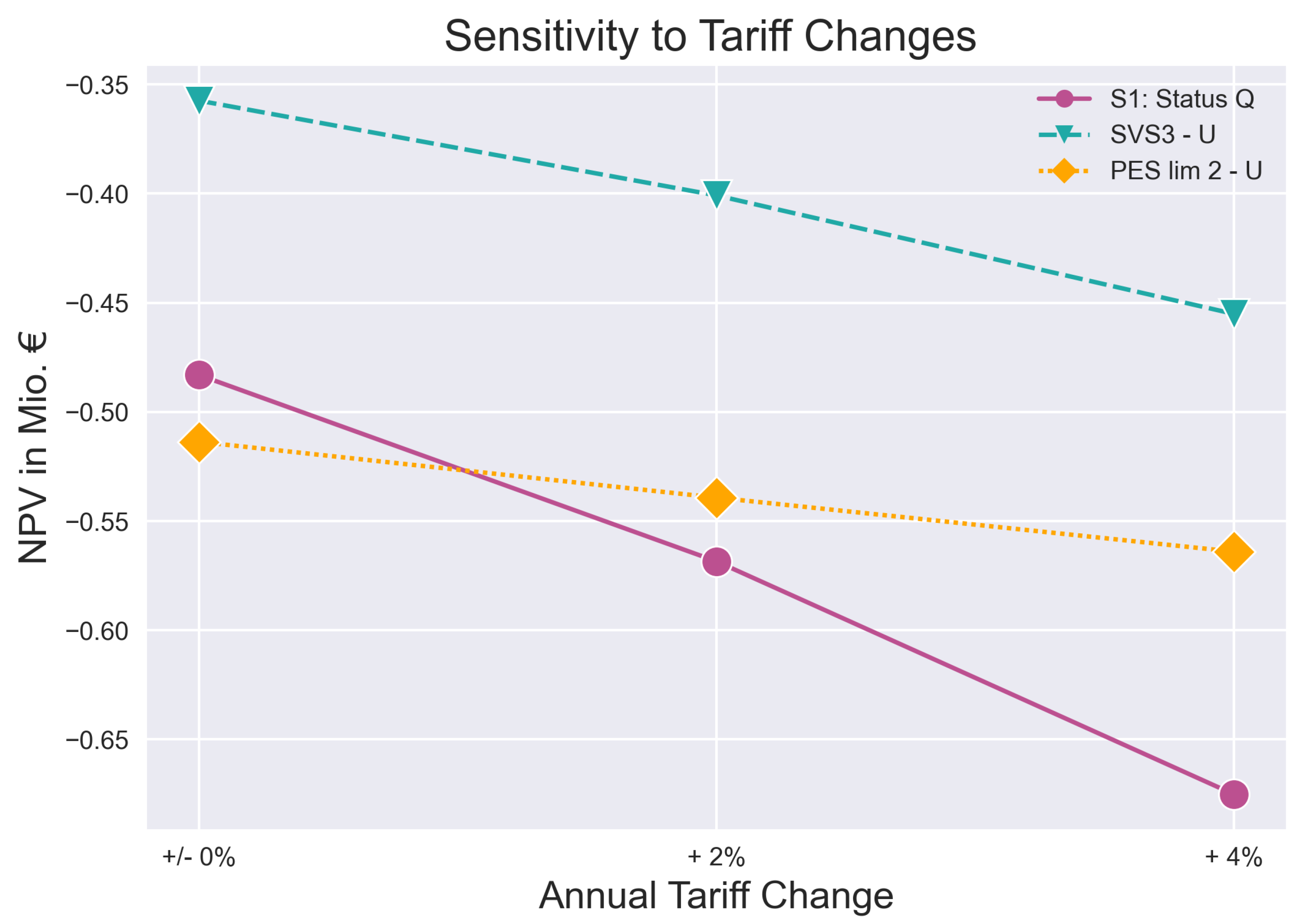
3.4. Variation of the Electricity Price
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Delta | |
| CAPEX | Capital Expenditure |
| Carbon Dioxide | |
| EC | European Commission |
| EPN | Energy Positive Neighbourhood |
| EU | European Union |
| ex | Export |
| FSI | Floor Space Index |
| GFA | Gross Floor Area |
| GGS | Grid Generation Mix Scenario |
| GTS | Grid Tariff Scenario |
| im | Import |
| KPI | Key Performance Indicator |
| LP | Linear Programming |
| MILP | Mixed Integer Linear Programming |
| NPV | Net Present Value |
| PED | Positive Energy District |
| PEF | Primary Energy Factor |
| PES | Power Exchange Scenario |
| PV | Photovoltaic |
| PVPC | Voluntary Price for Small Consumer |
| REE | Red Eléctrica de España |
| ts | Time step |
| R | Rural |
| S | Scenario |
| SET | Strategic Energy Technology |
| SVS | Space Variation Scenario |
| U | Urban |
| Units | |
| ° | Degree |
| € | Euro |
| kW | Kilowatt |
| Kilowatt peak | |
| kWh | Kilowatt hour |
| Square meter | |
| t | Tonnes |
Appendix A. Primary Energy Factor of Import Electricity
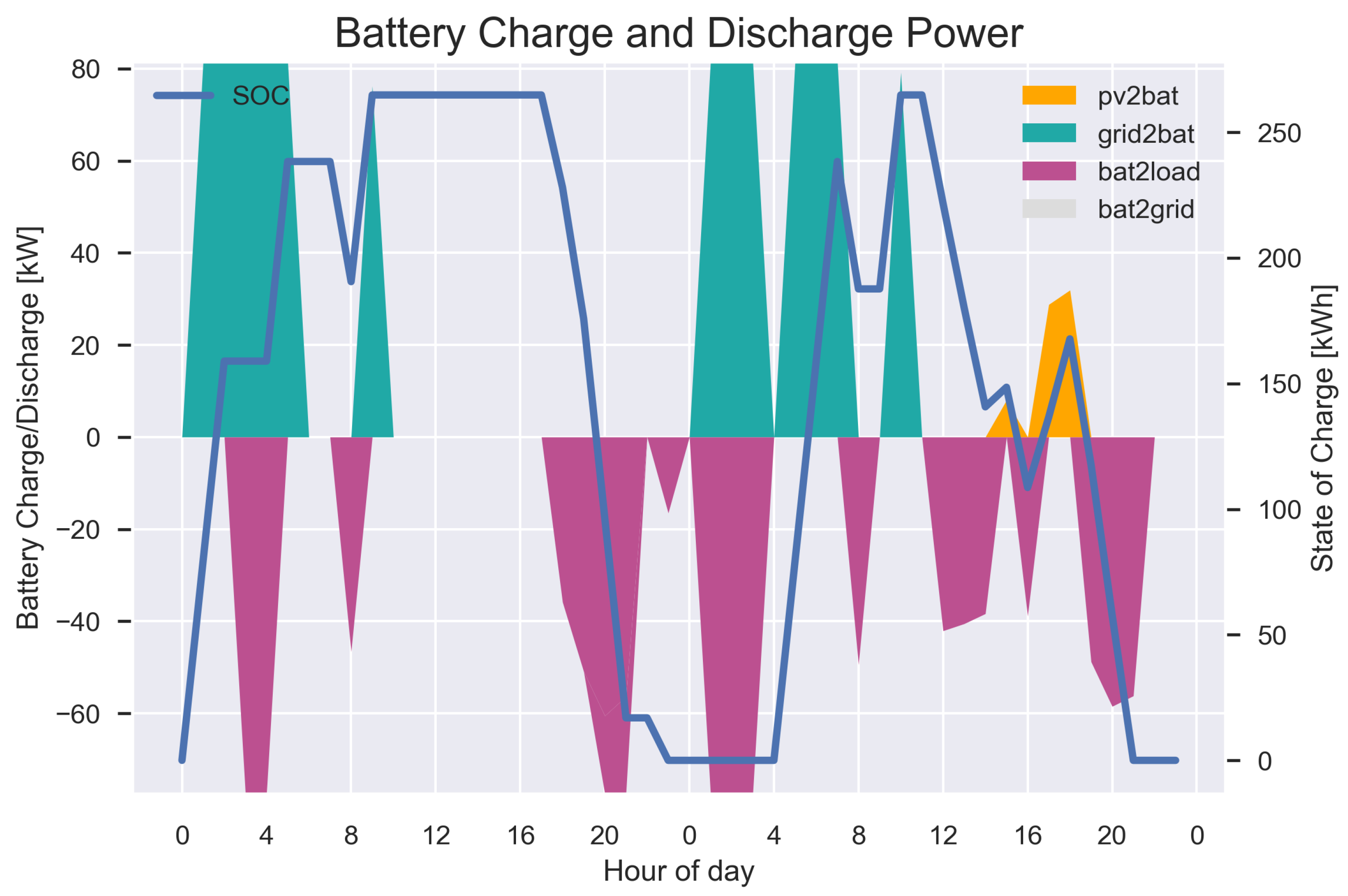
Appendix B. Input data
| Input Variable | Value | Unit |
|---|---|---|
| CAPEX | 1070.0 | EUR/ |
| OPEX fix | 12.8 | EUR/a |
| OPEX var | 0.0 | EUR/kWh |
| 19 | % | |
| PR | 0.84 | - |
| GCR flat | 0.8 | - |
| GCR tilt roof | 1 | - |
| Input Variable | Value | Unit |
|---|---|---|
| CAPEX | 750.0 | EUR/kWh |
| OPEX fix | 0.0 | EUR/a |
| OPEX var | 0.0 | EUR/kWh |
| 95 | % | |
| Cap/Power ratio | 0.3 | - |
| 0 | kWh |
| Input Variable | Value | Unit |
|---|---|---|
| Latitude | 28.803 | - |
| Longitude | −17.774 | - |
| Altitude | 288 | m |
| Albedo | 0.15 | - |
| Average Temperature | 17.8 | °C |
| Input Variable | Value | Unit |
|---|---|---|
| i | 0.05 | - |
| 2.75 | - | |
| Emission factor diesel | 74.1 | t/TJ |
References
- Rosales Carreón, J.; Worrell, E. Urban energy systems within the transition to sustainable development. A research agenda for urban metabolism. Resour. Conserv. Recycl. 2018, 132, 258–266. [Google Scholar] [CrossRef]
- IRENA. Rise of Renewables in Cities: Energy Solutions for the Urban Future; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; ISBN 978-92-9260-271-0. [Google Scholar]
- Groth, N.B.; Fertner, C.; Grosse, J. Urban energy generation and the role of cities. J. Settl. Spat. Plan. 2016, 5–17. [Google Scholar] [CrossRef]
- European Commission. SET-Plan ACTION n°3.2 Implementation Plan: Europe to Become a Global Role Model in Integrated, Innovative Solutions for the Planning, Deployment, and Replication of Positive Energy Districts. Available online: https://jpi-urbaneurope.eu/wp-content/uploads/2018/09/setplan_smartcities_implementationplan.pdf (accessed on 28 February 2020).
- European Commission. SETIS—SET Plan Information System. Available online: https://setis.ec.europa.eu/index_en (accessed on 3 June 2021).
- JPI Urban Europe / SET Plan Action 3.2. White Paper on PED Reference Framework for Positive Energy Districts and Neighbourhoods. Vienna. 2020. Available online: https://jpi-urbaneurope.eu/ped/ (accessed on 5 October 2020).
- Lindholm, O.; Rehman, H.U.; Reda, F. Positioning positive energy districts in European cities. Buildings 2021, 11, 19. [Google Scholar] [CrossRef]
- Cupelli, L.; Schumacher, M.; Monti, A.; Mueller, D.; De Tommasi, L.; Kouramas, K. Simulation Tools and Optimization Algorithms for Efficient Energy Management in Neighborhoods. In Energy Positive Neighborhoods and Smart Energy Districts; Academic Press: London, UK, 2017; pp. 57–100. [Google Scholar] [CrossRef]
- Schöfmann, P.; Zelger, T.; Bartlmä, N.; Schneider, S.; Leibold, J.; Bell, D. Zukunftsquartier—Weg zum Plus-Energie-Quartier in Wien; Federal Ministry for Climate Action, Environment, Energy, Mobility, Innovation and Technology: Vienna, Austria, 2020. [Google Scholar]
- Leibold, J.; Schneider, S.; Tabakovic, M.; Zelger, T.; Bell, D.; Schöfmann, P.; Bartlmä, N. ‘Zukunftsquartier’—On the Path to Plus Energy Neighbourhoods in Vienna. In Sustainability in Energy and Buildings: Proceedings of SEB 2019; Springer: Singapore, 2020; pp. 199–209. [Google Scholar] [CrossRef]
- Moreno, A.G.; Vélez, F.; Alpagut, B.; Hernández, P.; Montalvillo, C.S. How to achieve positive energy districts for sustainable cities: A proposed calculation methodology. Sustainability 2021, 13, 710. [Google Scholar] [CrossRef]
- Sougkakis, V.; Lymperopoulos, K.; Nikolopoulos, N.; Margaritis, N.; Giourka, P.; Angelakoglou, K. An Investigation on the Feasibility of Near-Zero and Positive Energy Communities in the Greek Context. Smart Cities 2020, 3, 19. [Google Scholar] [CrossRef]
- Ala-Juusela, M.; Crosbie, T.; Hukkalainen, M. Defining and operationalising the concept of an energy positive neighbourhood. Energy Convers. Manag. 2016, 125, 133–140. [Google Scholar] [CrossRef] [Green Version]
- ur Rehman, H.; Reda, F.; Paiho, S.; Hasan, A. Towards positive energy communities at high latitudes. Energy Convers. Manag. 2019, 196, 175–195. [Google Scholar] [CrossRef]
- Laitinen, A.; Lindholm, O.; Hasan, A.; Reda, F.; Hedman, Å. A techno-economic analysis of an optimal self-sufficient district. Energy Convers. Manag. 2021, 236. [Google Scholar] [CrossRef]
- IEA EBC. IEA EBC—Annex 83. Available online: https://annex83.iea-ebc.org/subtasks (accessed on 27 July 2021).
- Doubleday, K.; Parker, A.; Hafiz, F.; Irwin, B.; Hancock, S.; Pless, S.; Hodge, B.M. Toward a subhourly net zero energy district design through integrated building and distribution system modeling. J. Renew. Sustain. Energy 2019, 11. [Google Scholar] [CrossRef]
- Bakhtavar, E.; Prabatha, T.; Karunathilake, H.; Sadiq, R.; Hewage, K. Assessment of renewable energy-based strategies for net-zero energy communities: A planning model using multi-objective goal programming. J. Clean. Prod. 2020, 272. [Google Scholar] [CrossRef]
- Gremmelspacher, J.M.; Campamà Pizarro, R.; van Jaarsveld, M.; Davidsson, H.; Johansson, D. Historical building renovation and PV optimisation towards NetZEB in Sweden. Sol. Energy 2021, 223, 248–260. [Google Scholar] [CrossRef]
- Miftahurrahman, F.; Farizal; Dachyar, M. Optimization Model of Power Generation and Load Equipment Selection for near Zero Energy Building with Rooftop PV Integrated. In Proceedings of the 2019 6th IEEE International Conference on Engineering, Technologies and Applied Sciences (ICETAS 2019), Kuala Lumpur, Malaysia, 20–21 December 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Madathil, D.; Nair, M.G.; Jamasb, T.; Thakur, T. Consumer-focused solar-grid net zero energy buildings: A multi-objective weighted sum optimization and application for India. Sustain. Prod. Consum. 2021, 27, 2101–2111. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Doorman, G.; Fischer, D.; Korpås, M.; Ånestad, A.; Sartori, I. Methodology for optimal energy system design of Zero Energy Buildings using mixed-integer linear programming. Energy and Buildings. Energy Build. 2016, 127, 194–205. [Google Scholar] [CrossRef] [Green Version]
- Zwickl-Bernhard, S.; Auer, H. Open-source modeling of a low-carbon urban neighborhood with high shares of local renewable generation. Appl. Energy 2021, 282. [Google Scholar] [CrossRef]
- Kriechbaum, L.; Scheiber, G.; Kienberger, T. Grid-based multi-energy systems-modelling, assessment, open source modelling frameworks and challenges. Energy Sustain. Soc. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Groissböck, M. Are open source energy system optimization tools mature enough for serious use? Renew. Sustain. Energy Rev. 2019, 102, 234–248. [Google Scholar] [CrossRef]
- Openmod. Open Models. Available online: https://wiki.openmod-initiative.org/wiki/Open_Models (accessed on 30 June 2021).
- Bruck, A. PEDSO for MDPI Publication—Model and Data. 2021. Available online: https://github.com/urbLexa/PEDSO_MDPI (accessed on 30 June 2021).
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.W.; da Silva Santos, L.B.; Bourne, P.E.; et al. Comment: The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Energy Efficiency Targets. Available online: https://ec.europa.eu/energy/topics/energy-efficiency/targets-directive-and-rules/eu-targets-energy-efficiency_en (accessed on 30 July 2021).
- Hart, W.E.; Laird, C.; Watson, J.P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python, 2nd ed.; Springer Nature: Cham, Switzerland, 2017; ISBN 978-1-4614-3225-8. [Google Scholar] [CrossRef]
- Hart, W.E.; Watson, J.P.; Woodruff, D.L. Pyomo: Modeling and solving mathematical programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Esser, A.; Sensfuss, F. Evaluation of Primary Energy Factor Calculation Options for Electricity. 2016. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/final_report_pef_eed.pdf (accessed on 11 May 2021).
- Eicker, U. Solare Technologien für Gebäude; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2012; ISBN 978-3-8348-1281-0. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef] [Green Version]
- Gobierno de Canarias. Anuario EnergÉtico de Canarias 2019. 2020. Available online: https://www.gobiernodecanarias.org/cmsweb/export/sites/energia/doc/Publicaciones/AnuarioEnergeticoCanarias/20210219_AnuarioEnergeticoCanarias2019.pdf (accessed on 19 April 2021).
- La Palma Renovable. La Palma Renovable Promueve la primera Comunidad Energética Local de Canarias. Available online: https://lapalmarenovable.es/la-palma-renovable-promueve-la-primera-comunidad-energetica-local-de-canarias/ (accessed on 19 April 2021).
- Red Eléctrica de España. ESIOS Electricity · Data · Transparency. Available online: https://www.esios.ree.es/en (accessed on 20 April 2021).
- Minesterio para la Transición Ecológica. Real Decreto 244/2019, de 5 de abril, por el que se Regulan las Condiciones Administrativas, Técnicas y Económicas del Autoconsumo de Energía Eléctrica. 2019. Available online: https://www.boe.es/diario_boe/txt.php?id=BOE-A-2019-5089 (accessed on 20 April 2021).
- Red Eléctrica de España. Demanda Canaria en Tiempo Real. Available online: https://www.ree.es/es/actividades/sistema-electrico-canario/demanda-de-energia-en-tiempo-real (accessed on 20 April 2021).
- European Commission. TMY Generator|EU Science Hub. Available online: https://ec.europa.eu/jrc/en/PVGIS/tools/tmy (accessed on 20 April 2021).
- Eurostat. Electricity Price Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity\_price\_statistics\#Electricity\_prices\_for\_household\_consumers (accessed on 20 May 2021).
- Red Eléctrica de España. Voluntary Price for the Small Consumer (PVPC). Available online: https://www.ree.es/en/activities/operation-of-the-electricity-systemvoluntary-price-small-consumer-pvpc (accessed on 1 July 2021).
- Danish Energy Agency. Technology Data—Generation of Electricity and District Heating. Available online: https://ens.dk/en/our-services/projections-and-models/technology-data/technology-data-generation-electricity-and (accessed on 12 April 2021).
- Danish Energy Agency. Technology Data–Energy Storage. Available online: https://ens.dk/en/our-services/projections-and-models/technology-data/technology-data-energy-storage (accessed on 12 April 2021).
- Fina, B.; Auer, H.; Friedl, W. Profitability of active retrofitting of multi-apartment buildings: Building-attached/integrated photovoltaics with special consideration of different heating systems. Energy Build. 2019, 190, 86–102. [Google Scholar] [CrossRef]
- Fina, B.; Auer, H.; Friedl, W. Profitability of PV sharing in energy communities: Use cases for different settlement patterns. Energy 2019, 189. [Google Scholar] [CrossRef]
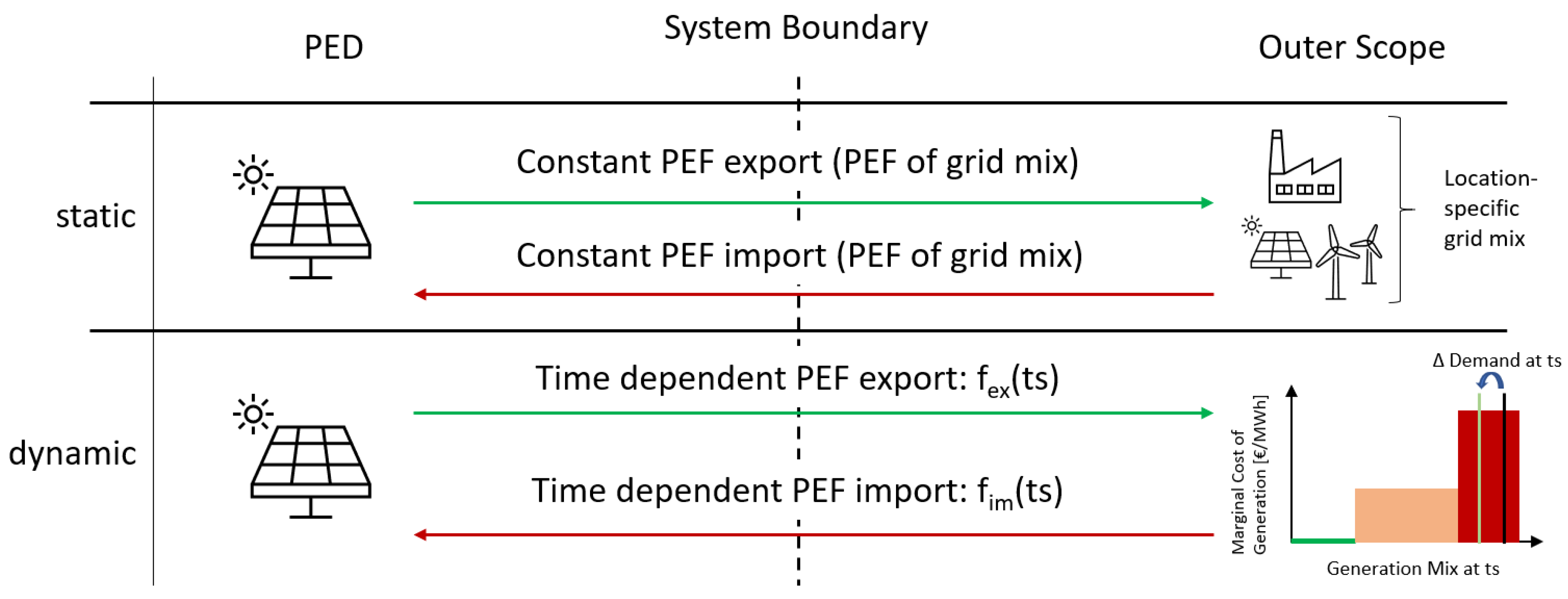

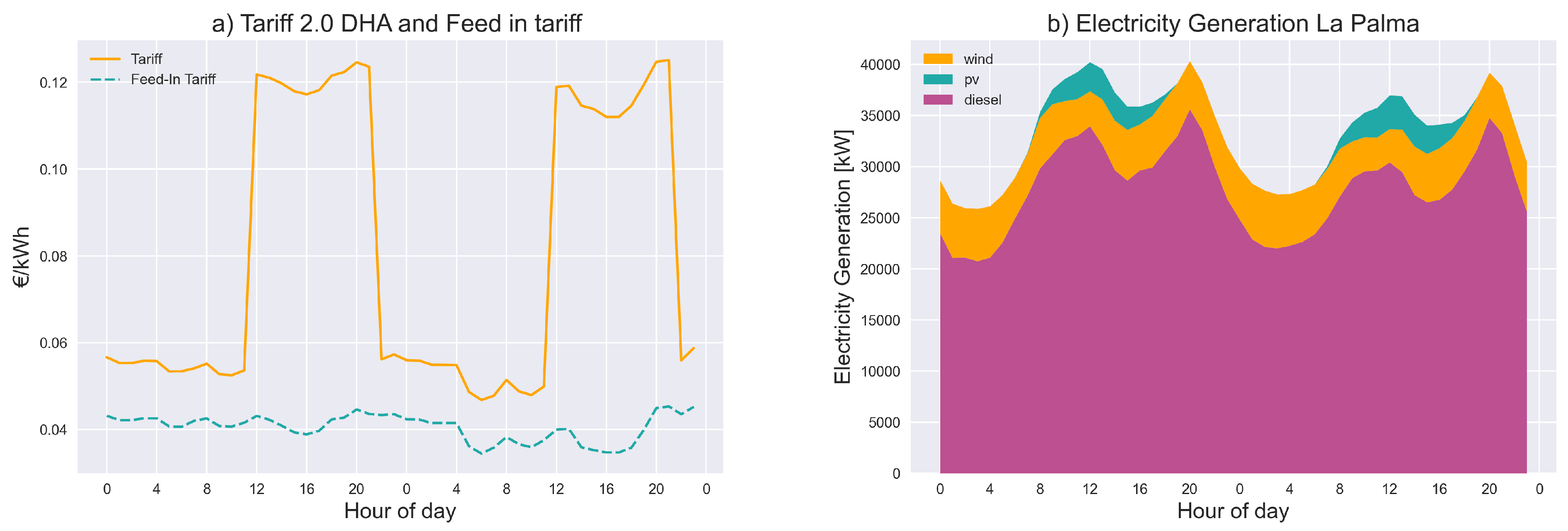


| Model Decision Variables | |
|---|---|
| Capacities of selected technologies | |
| Fuel consumption at each time step each year (not used in this work) | |
| Power flow at each time step in each year depending on source (out) and target (in) | |
| Area used for PV installation for each angle pair | |
| Annual costs | |
| Investment cost at year 0 | |
| Net Present Value - model objective | |
| Annual fix costs | |
| Annual variable costs | |
| Annual Revenues | |
| State of charge of the battery at each time step each year | |
| Other model parameters | |
| Efficiency | |
| Tilt angle | |
| A | Area |
| Azimuth angle | |
| Vector of considered azimuth angles | |
| Feed-in Tariff at each ts | |
| Irradiance | |
| Performance Ratio | |
| Ground Coverage Ratio | |
| Tariff at each ts | |
| Specific technology | |
| Vector over all selected technologies | |
| Vector of tilt angles | |
| Number of time steps in one year | |
| v | Optimisation variable |
| V | Vector of optimisation variables |
| x | Technology with electricity output |
| X | Vector over technologies with electricity output |
| y | Year |
| Y | Time horizon in years |
| z | Technology with electricity input |
| Z | Vector over technologies with electricity input |
| Occupation | Area Urban [m2] | Area Rural [m2] |
|---|---|---|
| Flat roof | 678 | 3138 |
| Terrace | 2150 | 2295 |
| Water Storage | 0 | 2190 |
| Total | 2828 | 8323 |
| Azimuth Angle [°] | Area Urban [m2] | Area Rural [m2] |
|---|---|---|
| 0 | 40 | 235 |
| 45 | 0 | 195 |
| 90 | 29 | 270 |
| 135 | 0 | 170 |
| 180 | 40 | 240 |
| 225 | 0 | 215 |
| 270 | 90 | 250 |
| 315 | 0 | 155 |
| S # | Description |
|---|---|
| 1 | R & U: status quo |
| 2 | R: no PED |
| 3 | U: no PED |
| 4 | R: PED |
| 5 | U: PED |
| SVS # | Description |
| 1 | R: PED; no terrace or water storage for PV generation |
| 2 | U: PED; no terrace for PV generation |
| 3 | U/R: PED; 25% of terrace allowed if no PED possible in SVS 1/2 |
| Scenario | NPV [€Mio] | PV_flat [kW] | PV_tilt roof [kW] | Battery [kWh] | Export/ Import | Emissions [t] |
|---|---|---|---|---|---|---|
| S 1 | −0.483 | 0 | 0 | 0 | - | 1971 |
| S 2 & S 4 | −0.332 | 1265 | 86 | 0 | 12.60 | 978 |
| S 3 & S 5 | −0.346 | 430 | 17 | 0 | 3.29 | 1047 |
| SVS 1 | −0.342 | 477 | 86 | 0 | 4.47 | 1025 |
| SVS 2 | - | - | - | - | - | - |
| SVS 3—urban | −0.357 | 185 | 25 | 0 | 1.04 | 1134 |
| Scenario | NPV [€Mio] | PV_flat [kW] | PV_tilt roof [kW] | Battery [kWh] | Export/ Import | Emissions [t] |
|---|---|---|---|---|---|---|
| PES lim 2—R | −0.385 | 38 | 185 | 0 | 0.942 | 1110 |
| PES lim 1.5—R | −0.445 | 34 | 192 | 148 | 0.937 | 944 |
| PES lim 1—R | −0.631 | 29 | 200 | 424 | 0.928 | 867 |
| PES lim 2—U | −0.514 | 175 | 29 | 301 | 0.932 | 1014 |
| PES lim 1.5—U | −0.698 | 175 | 29 | 551 | 0.930 | 976 |
| PES lim 1—U | −0.907 | 176 | 29 | 842 | 0.926 | 894 |
| Scenario | NPV [€Mio] | PV_flat [kW] | PV_tilt roof [kW] | Battery [kWh] | Export/ Import | Emissions [t] |
|---|---|---|---|---|---|---|
| SVS1—R | −0.342 | 477 | 86 | 0 | 4.467 | 476 |
| PES lim 2—R | −0.370 | 74 | 108 | 0 | 0.727 | 536 |
| PES lim 1.5—R | −0.393 | 19 | 172 | 15 | 0.714 | 567 |
| PES lim 1—R | −0.493 | 8 | 180 | 178 | 0.671 | 529 |
| SVS3—U | −0.357 | 185 | 25 | 0 | 1.036 | 530 |
| PES lim 2—U | −0.392 | 159 | 11 | 61 | 0.696 | 563 |
| PES lim 1.5—U | −0.495 | 132 | 29 | 183 | 0.646 | 586 |
| PES lim 1—U | −0.667 | 130 | 29 | 407 | 0.626 | 592 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruck, A.; Díaz Ruano, S.; Auer, H. A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities. Energies 2021, 14, 4864. https://doi.org/10.3390/en14164864
Bruck A, Díaz Ruano S, Auer H. A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities. Energies. 2021; 14(16):4864. https://doi.org/10.3390/en14164864
Chicago/Turabian StyleBruck, Axel, Santiago Díaz Ruano, and Hans Auer. 2021. "A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities" Energies 14, no. 16: 4864. https://doi.org/10.3390/en14164864
APA StyleBruck, A., Díaz Ruano, S., & Auer, H. (2021). A Critical Perspective on Positive Energy Districts in Climatically Favoured Regions: An Open-Source Modelling Approach Disclosing Implications and Possibilities. Energies, 14(16), 4864. https://doi.org/10.3390/en14164864







