Stability Domain Analysis and Enhancement of Squirrel Cage Induction Generator Wind Turbines in Weak Grids
Abstract
:1. Introduction
- Comprehensive analysis of bifurcations in weak grids and uncovering new modes, which have not been reported in previous research.
- Proposing a new voltage regulator design for the SVC to aid in damping SSR along with a design of a new damping controller.
- Validating the performance of the proposed controller through detailed time domain simulations when the system is subjected to frequency disturbances on the grid side, mimicking the action of speed governors, which has not been documented in the earlier research.
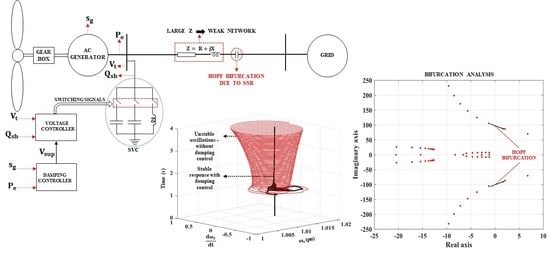
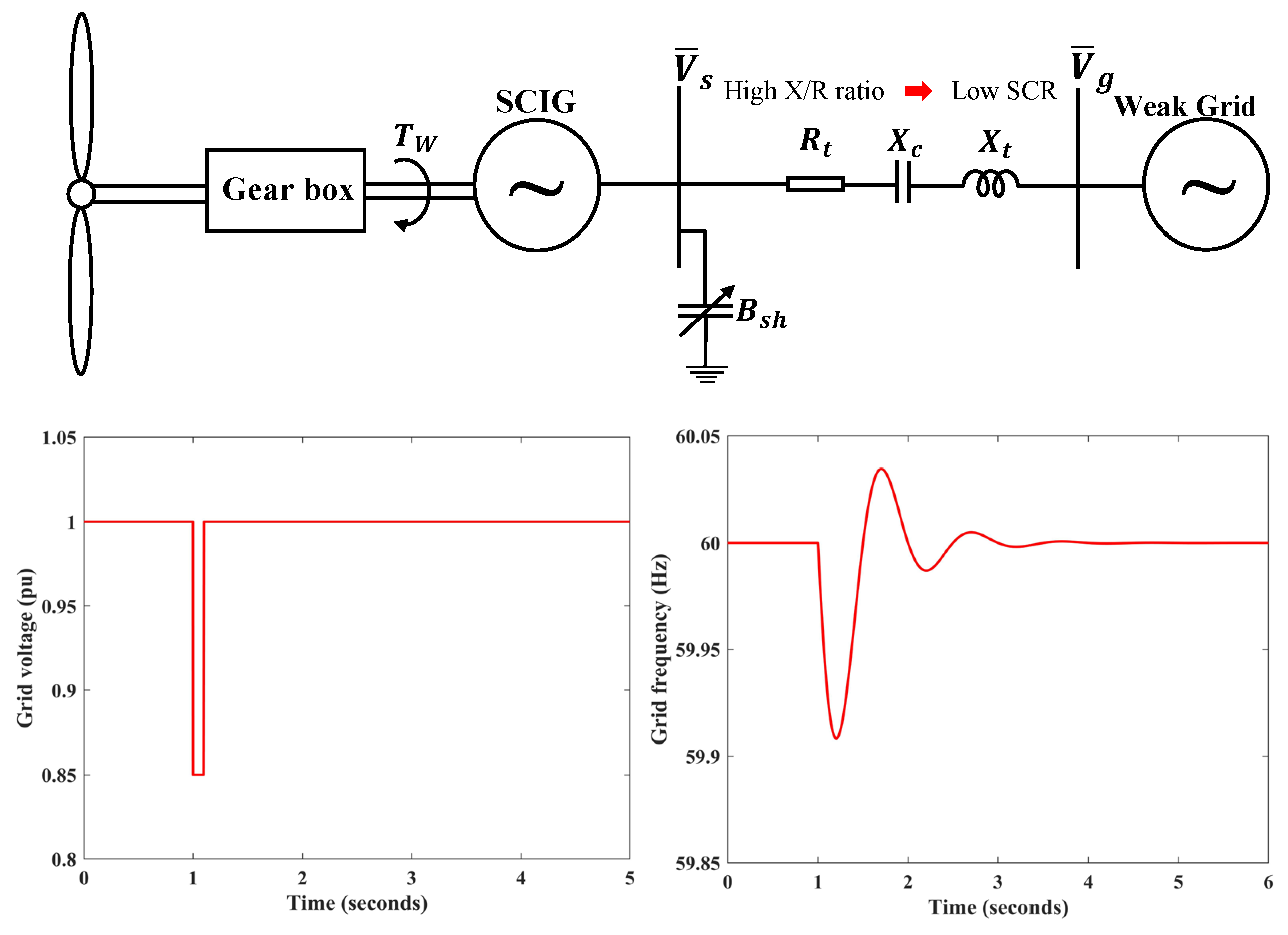
2. Dynamic Modeling of WT-SCIG and Controller
2.1. Dynamics of Induction Generator
2.2. Dynamics of Transmission Line, Shunt and Series Capacitors
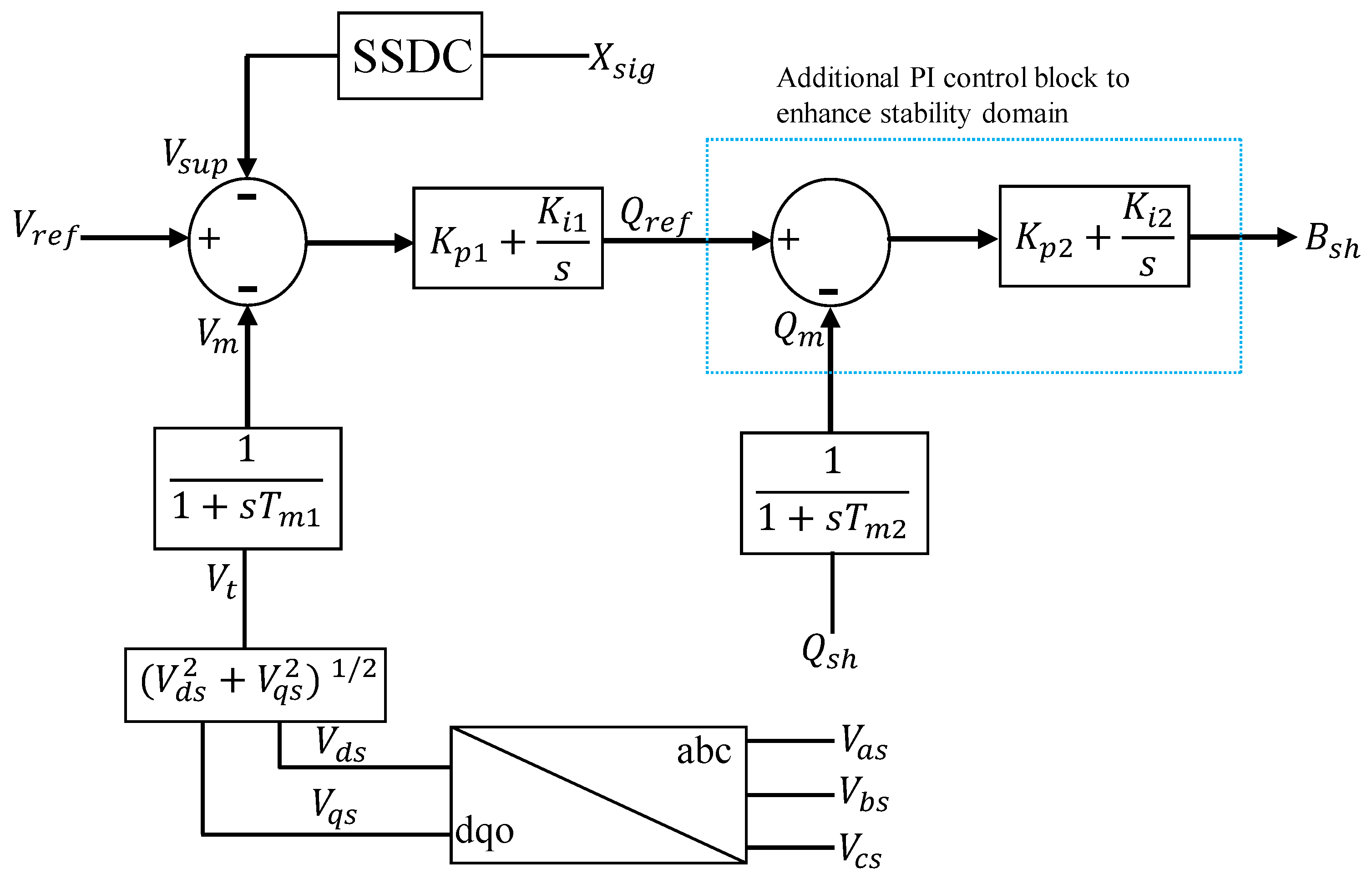
2.3. Design of Voltage Regulator
2.4. Design of the SSDC
3. Results
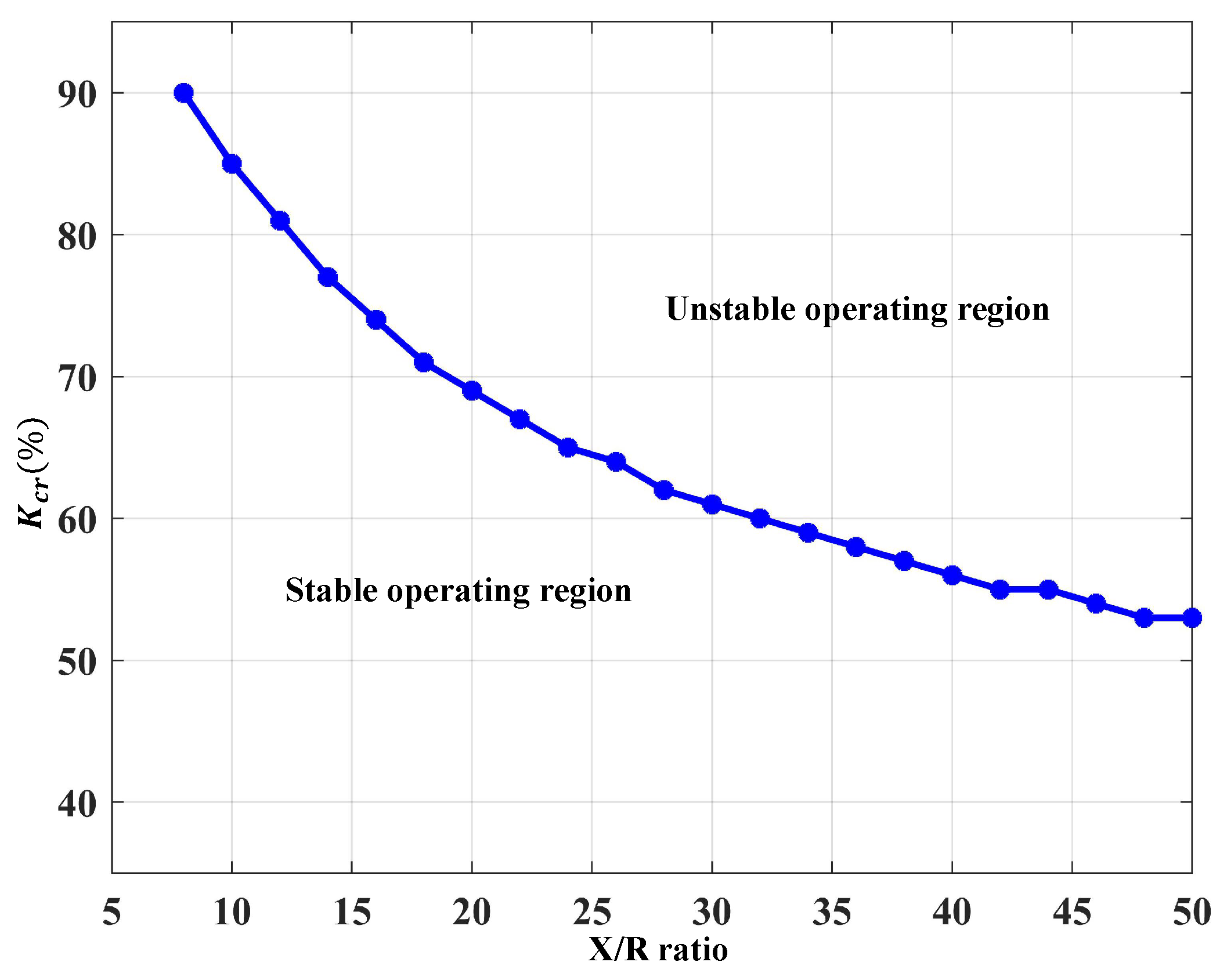
3.1. Stability Domain Analysis of WT-SCIG with Fixed Shunt Capacitor Compensation
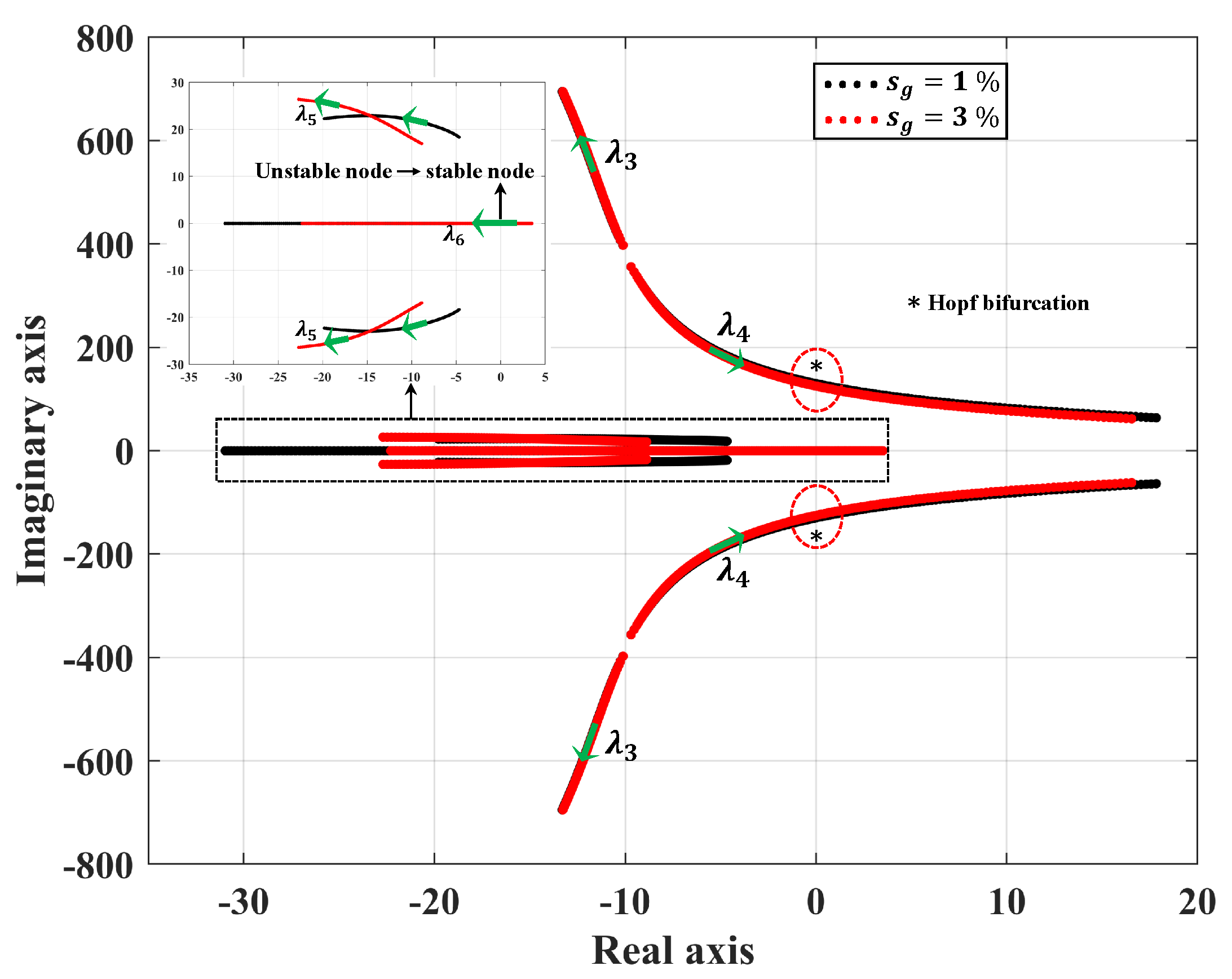
3.1.1. Eigenvalue Trajectories for Different Generator Slips
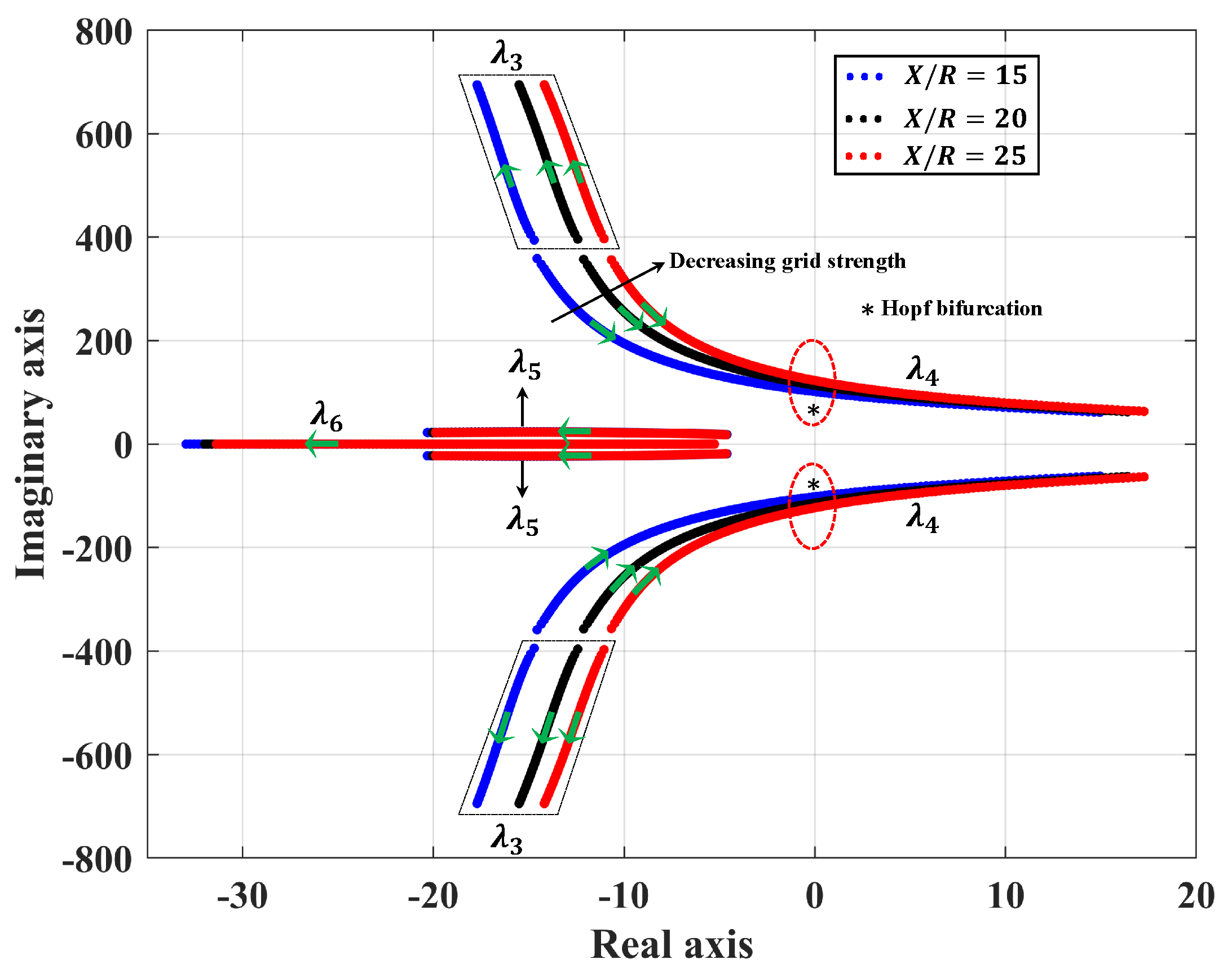
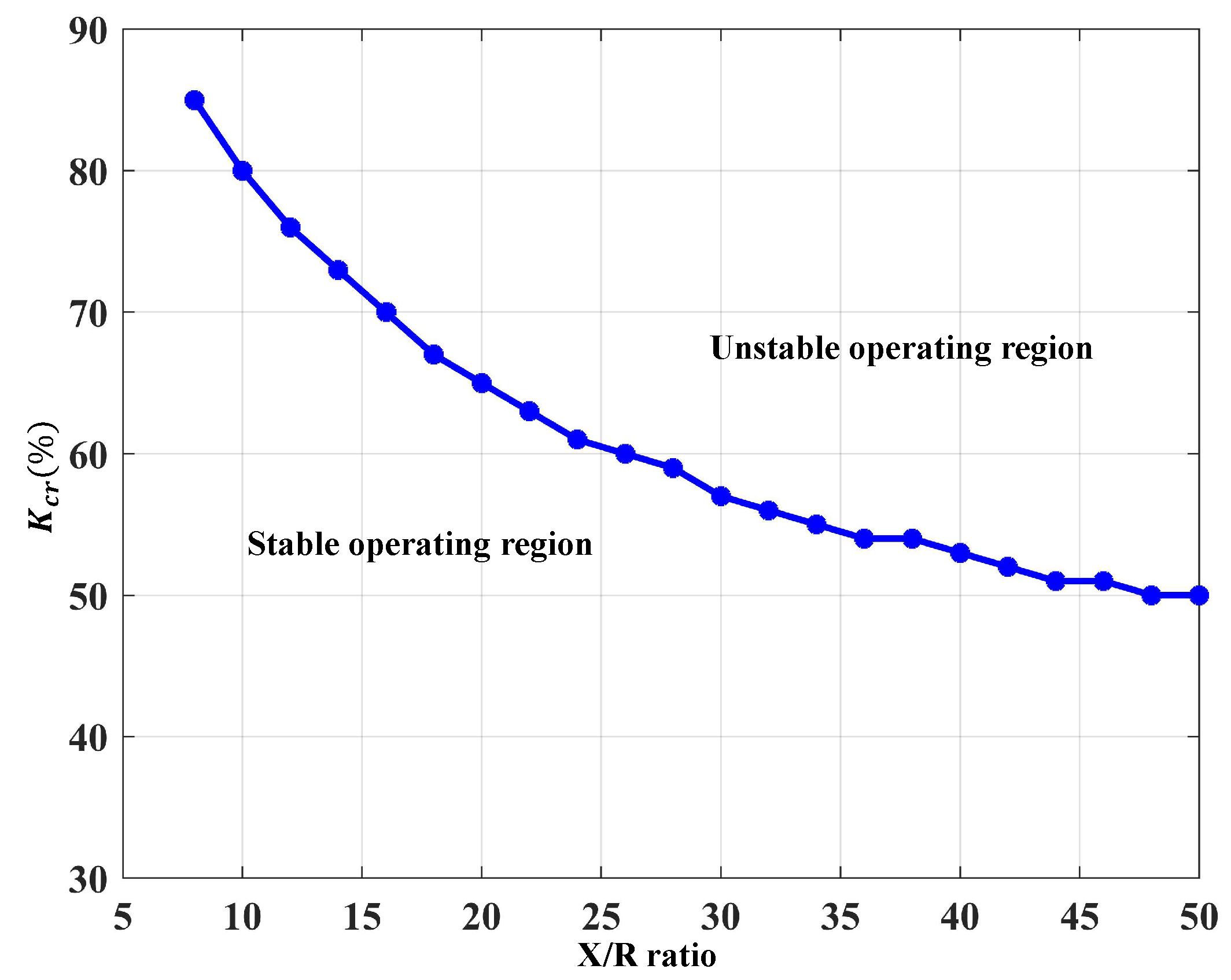
3.1.2. Eigenvalue Trajectories for Different Grid Strengths
3.2. Stability Domain Analysis of WT-SCIG with SVC at the Stator Terminals
3.2.1. Eigenvalues for Low and High Wind Speeds
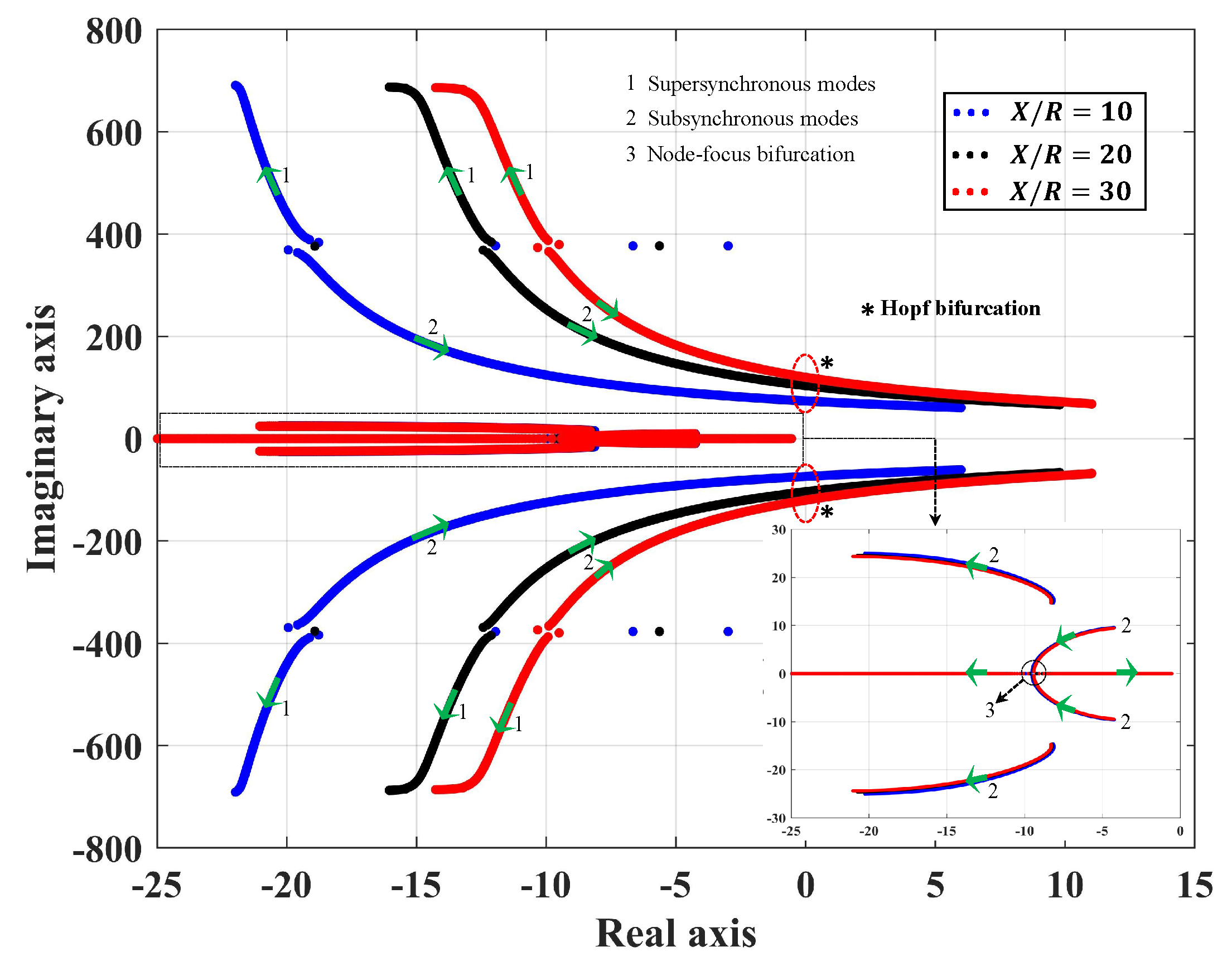
3.2.2. Eigenvalues for Different Grid Strengths
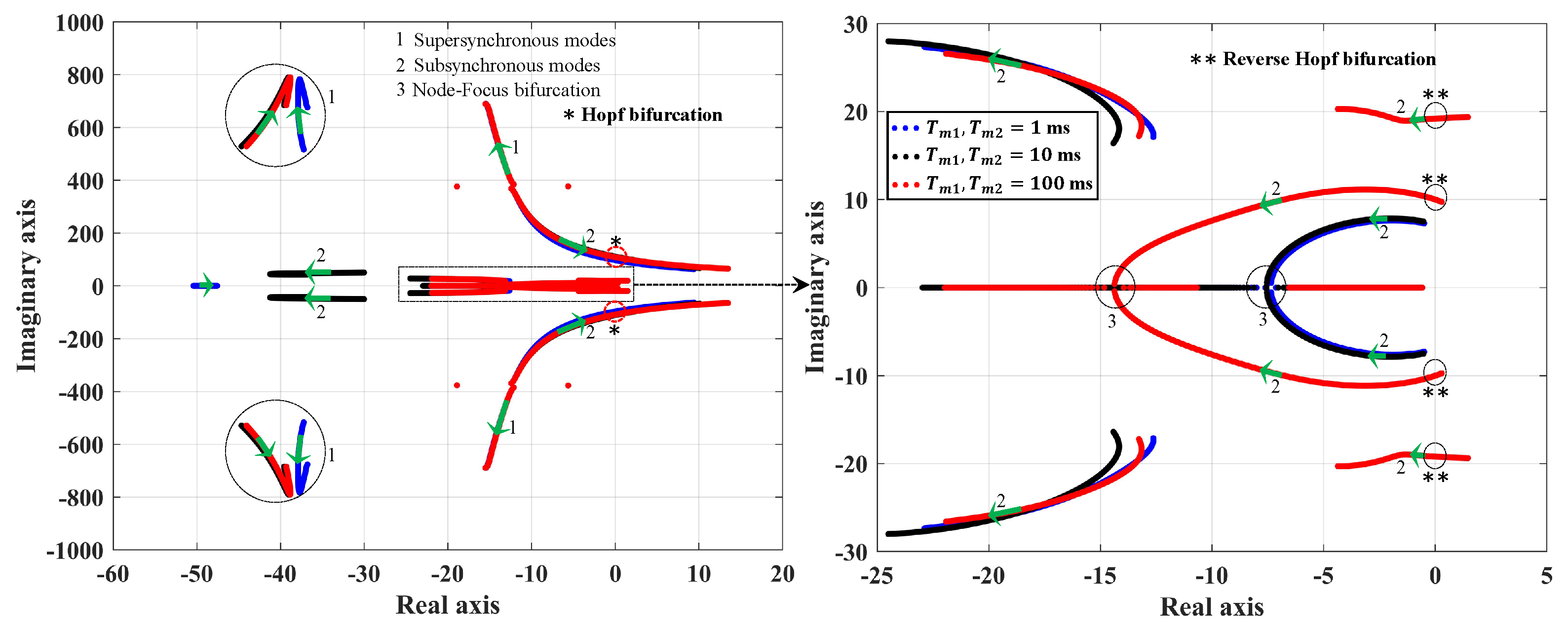
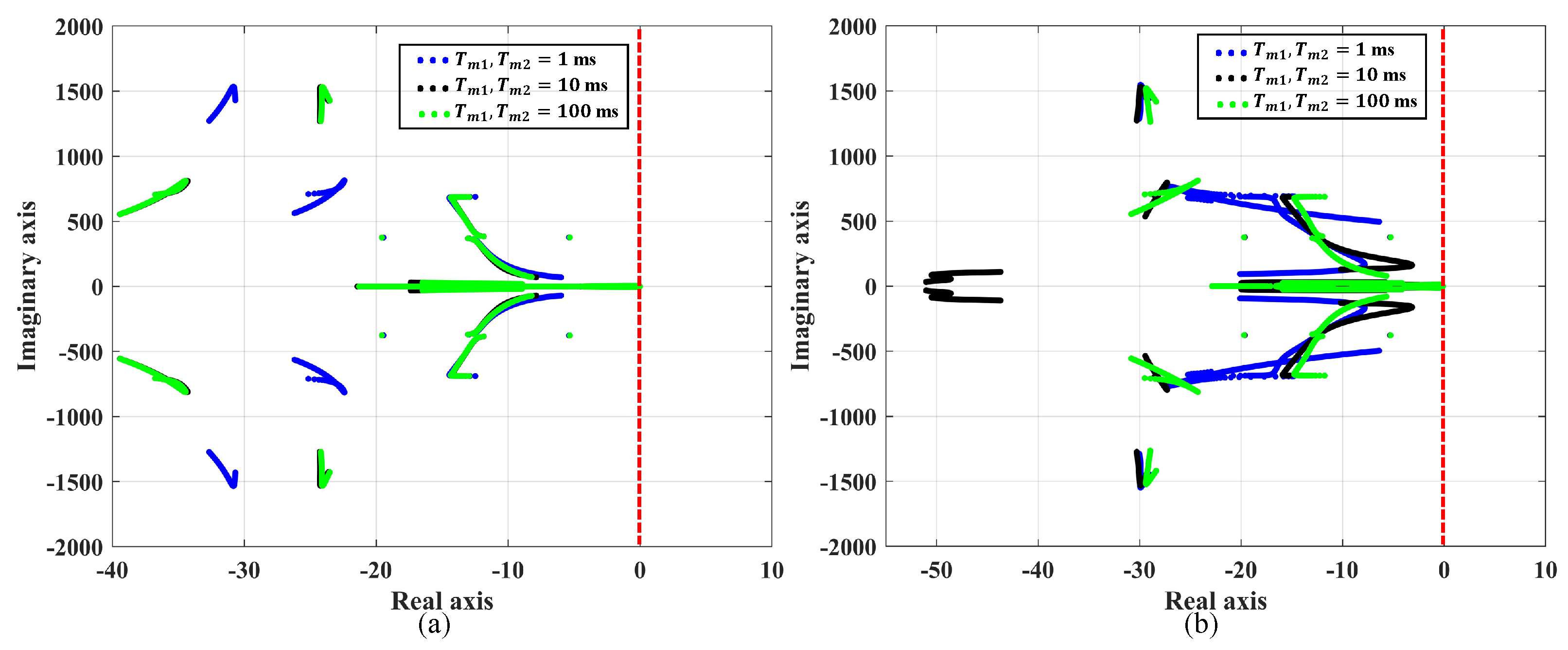
3.2.3. Eigenvalues for Different Measurement Time Delays
3.3. Stability Domain Analysis of WT-SCIG with SVC and SSDC
3.3.1. Eigenvalue Trajectories with SSDC for Low and High Wind Speeds
3.3.2. Eigenvalue Trajectories with SSDC for Varying Grid Strengths
3.3.3. Eigenvalue Trajectories with SSDC for Varying Measurement Time Delays
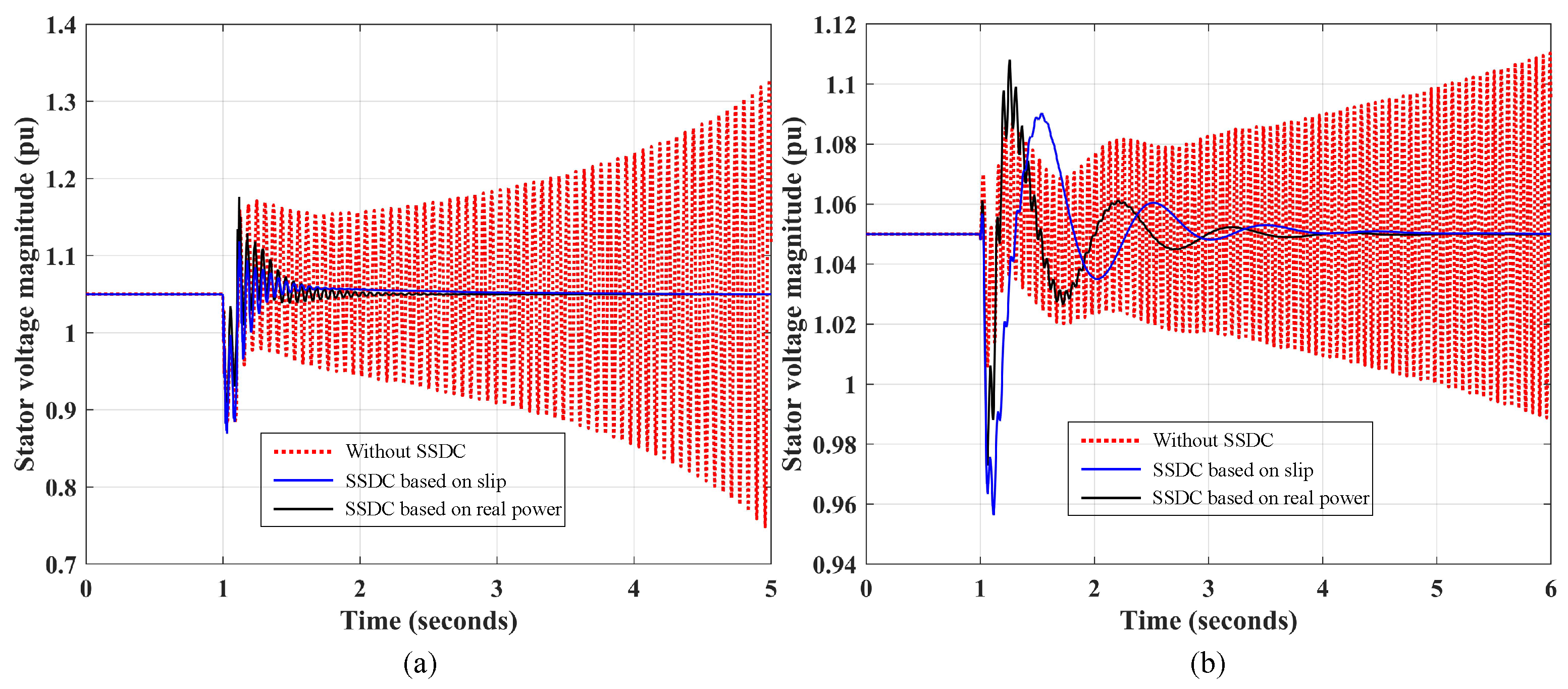
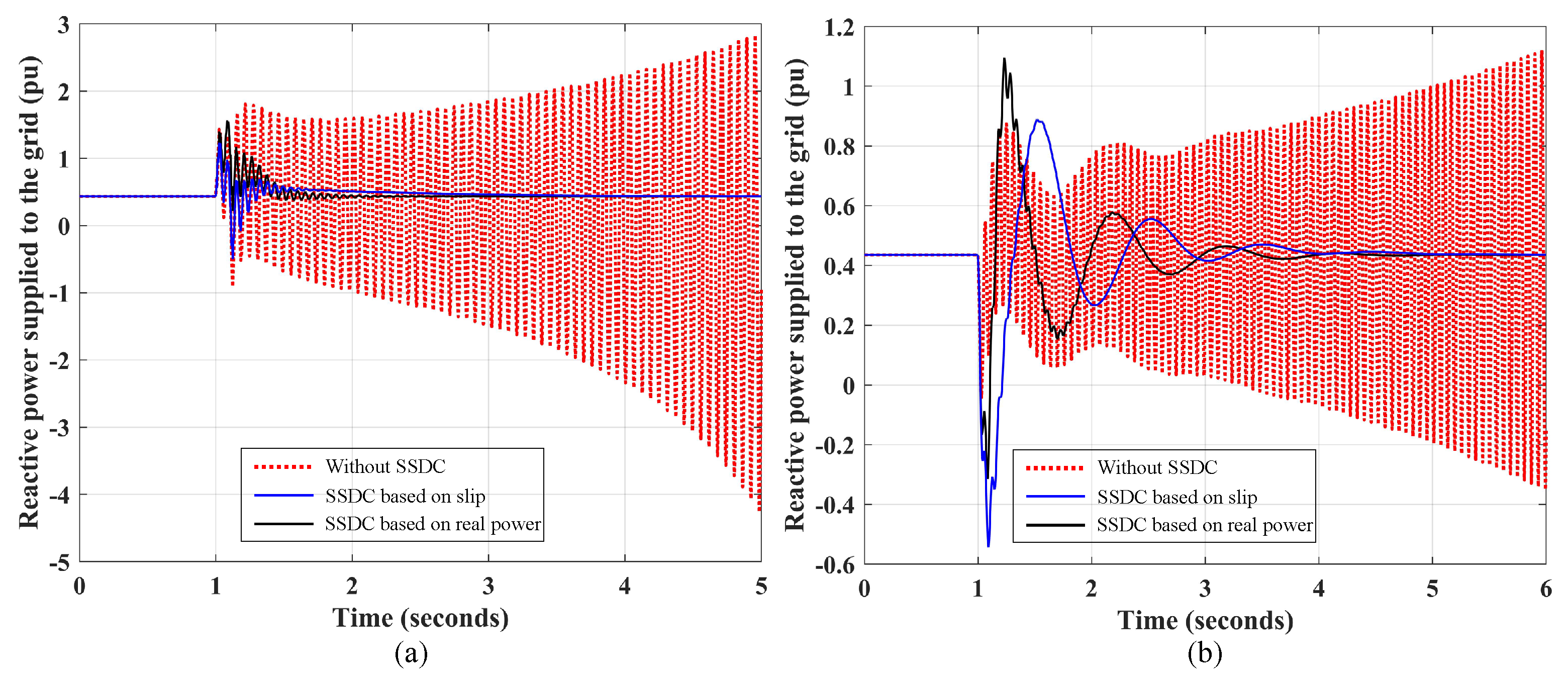
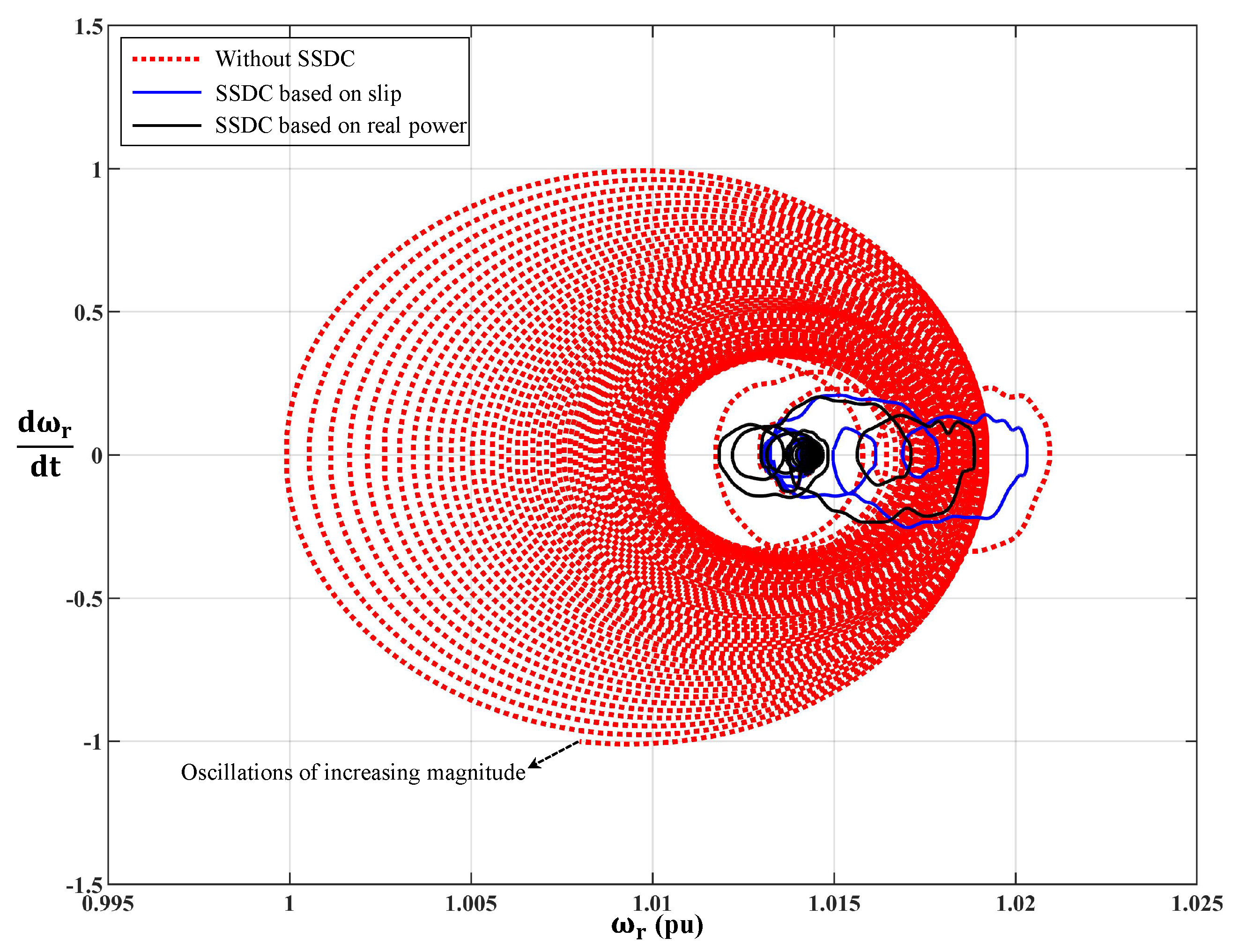
3.4. Time Domain Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WT—SCIG | Wind Turbine—Squirrel Cage Induction Generators |
| SVC | Static Var Compensator |
| SSDC | Subsynchronous Damping Controller |
| SSR | Subsynchronous Resonance |
| IGE | Induction Generator Effect |
| POI | Point of Interconnection |
Appendix A
Parameters of Induction Generator and Network
Parameters of Wind Turbine
References
- Miller, J.; Brunet-Watson, M.; Leighfield, J. Review of series compensation for transmission lines. In PSC North America Specialist Consultant to the Electricity Industry; PSC—Power Systems Consultants: Kirkland, WA, USA, 2014. [Google Scholar]
- Tang, J.; Achilles, R.; Agrawal, B.; Baker, D.; Bowler, C.; Concordia, C.; Cruz, C.; Dorney, J.; Edris, A.; Farmer, D.; et al. Readers Guide To Subsynchronous Resonance-IEEE Committee Report. IEEE Trans. Power Syst. 1992, 7, 150–157. [Google Scholar]
- Lesson Learned: Sub-Synchronous Interaction between Series-Compensated Transmission Lines and Generation. Available online: https://www.nerc.com/pa/rrm/ea/LessonsLearnedDocumentLibrary/LL20110705_Sub-Synchronous_Interaction.pdf (accessed on 26 July 2011).
- He, C.; Sun, D.; Song, L.; Ma, L. Analysis of subsynchronous resonance characteristics and influence factors in a series compensated transmission system. Energies 2019, 12, 3282. [Google Scholar] [CrossRef] [Green Version]
- Moharana, A.; Varma, R.K. Subsynchronous resonance in single-cage self-excited-induction-generator-based wind farm connected to series-compensated lines. IET Gener. Transm. Distrib. 2011, 5, 1221–1232. [Google Scholar] [CrossRef]
- Varma, R.K.; Auddy, S.; Semsedini, Y. Mitigation of Subsynchronous Resonance in a Series-Compensated Wind Farm Using FACTS Controllers. IEEE Trans. Power Deliv. 2008, 23, 1645–1654. [Google Scholar] [CrossRef]
- Varma, R.K.; Auddy, S. Mitigation of subsynchronous oscillations in a series compensated wind farm with static var compensator. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 7. [Google Scholar]
- Varma, R.K.; Moharana, A. SSR in Double-Cage Induction Generator-Based Wind Farm Connected to Series-Compensated Transmission Line. IEEE Trans. Power Syst. 2013, 28, 2573–2583. [Google Scholar] [CrossRef]
- Ackermann, T. Wind Power in Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Camm, E.H.; Behnke, M.R.; Bolado, O.; Bollen, M.; Bradt, M.; Brooks, C.; Dilling, W.; Edds, M.; Hejdak, W.J.; Houseman, D.; et al. Characteristics of wind turbine generators for wind power plants. In Proceedings of the 2009 IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Adib, A.; Mirafzal, B.; Wang, X.; Blaabjerg, F. On Stability of Voltage Source Inverters in Weak Grids. IEEE Access 2018, 6, 4427–4439. [Google Scholar] [CrossRef]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S. Analysis of Electric Machinery and Drive Systems; Wiley Online Library: Hoboken, NJ, USA, 2002; Volume 2. [Google Scholar]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 101. [Google Scholar]
- Kundur, P. Power system stability. In Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 2007; pp. 1–7. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Lerm, A.A.; Cañizares, C.A.; Lemos, F.A.; e Silva, A.S. Multi-parameter bifurcation analysis of power systems. In Proceedings of the North American Power Symposium, Cleveland, OH, USA, 19–20 October 1998; pp. 76–82. [Google Scholar]
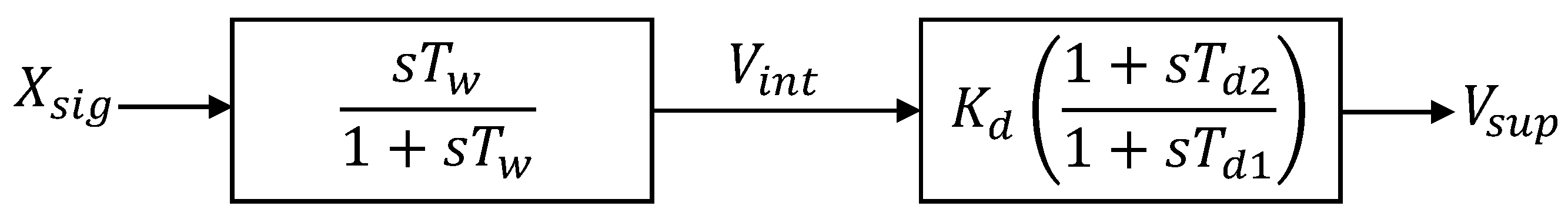





| Participating States | ||
|---|---|---|
| ,,,,,,,,, | ||
| ,,,,,,, | ||
| ,,,,,,,,, | ||
| ,,,,,,, | ||
| ,,,,,,,,, | ||
| ,,,, |
| 0.246 | 0.24 | 0.243 | 0.237 | 0.007 | 0.007 | 0.009 | 0.009 |
| 3.5009 | 0.103 | 0.307 | 0.119 | 0.376 | 0.093 |
| 0.250 | 0.181 | 0.310 | 0.223 | 0.033 |
| 1.05 pu | 1 ms | 1 ms | 0.1 | 0 | 40 | 40 |
| A | 0.5 | 0.1 | 1 | 1 | 450 | 10 ms | 150 ms | 10 s |
| B | 0.1 | 0 | 100 | 100 | 0.1 | 10 ms | 100 ms | 10 s |
| A | 0.55 | 0.1 | 1 | 1 | 450 | 10 ms | 150 ms | 10 s |
| B | 0.1 | 0 | 50 | 50 | 0.7 | 10 ms | 100 ms | 10 s |
| , | ||||
|---|---|---|---|---|
| 1 ms | 0.1 | 0 | 200 | 100 |
| 10 ms | 0.1 | 0.2 | 100 | 100 |
| 100 ms | 0.1 | 0.3 | 300 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devadason, J.; Moses, P.S.; Masoum, M.A.S. Stability Domain Analysis and Enhancement of Squirrel Cage Induction Generator Wind Turbines in Weak Grids. Energies 2021, 14, 4786. https://doi.org/10.3390/en14164786
Devadason J, Moses PS, Masoum MAS. Stability Domain Analysis and Enhancement of Squirrel Cage Induction Generator Wind Turbines in Weak Grids. Energies. 2021; 14(16):4786. https://doi.org/10.3390/en14164786
Chicago/Turabian StyleDevadason, Jonathan, Paul S. Moses, and Mohammad A. S. Masoum. 2021. "Stability Domain Analysis and Enhancement of Squirrel Cage Induction Generator Wind Turbines in Weak Grids" Energies 14, no. 16: 4786. https://doi.org/10.3390/en14164786
APA StyleDevadason, J., Moses, P. S., & Masoum, M. A. S. (2021). Stability Domain Analysis and Enhancement of Squirrel Cage Induction Generator Wind Turbines in Weak Grids. Energies, 14(16), 4786. https://doi.org/10.3390/en14164786