Stochastic Technical Stability Test of a Passenger Railroad Car Crossing a Turnout
Abstract
1. Introduction
2. Materials and Methods
Notion of Stochastic Technical Stability (STS)
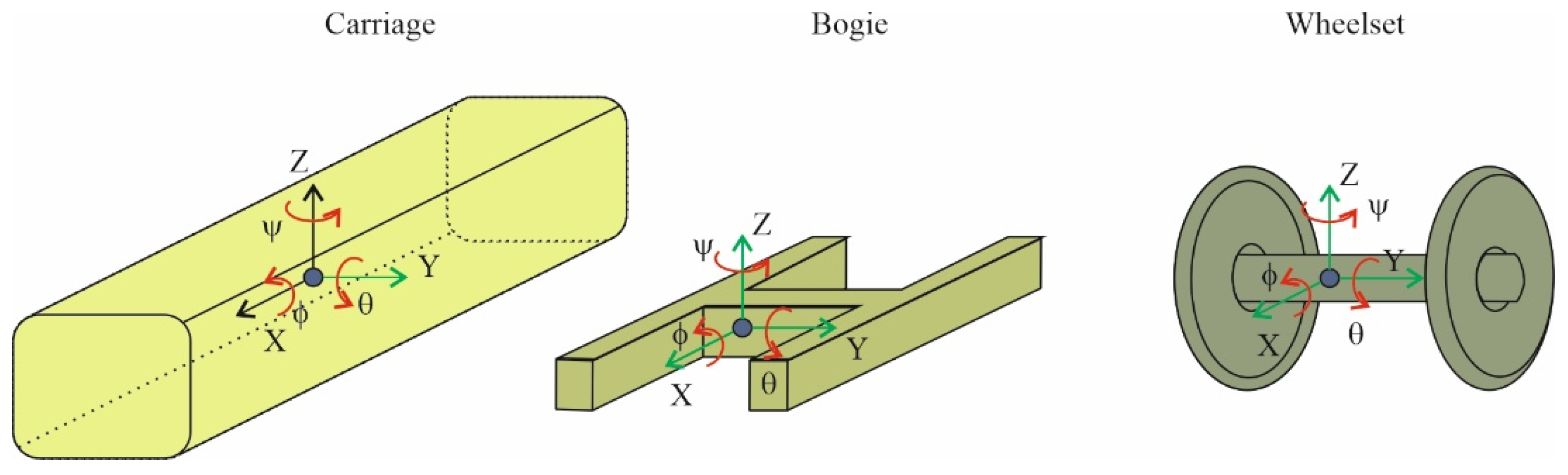
3. Mathematical Model of a Rail Vehicle
- In a mathematical model of rail vehicle-track dynamics, contact occurrence, described in this article as Kalker’s linear theory, must be included. Contact occurrence is determined for two- and three-point contacts between the wheelset and the turnout.
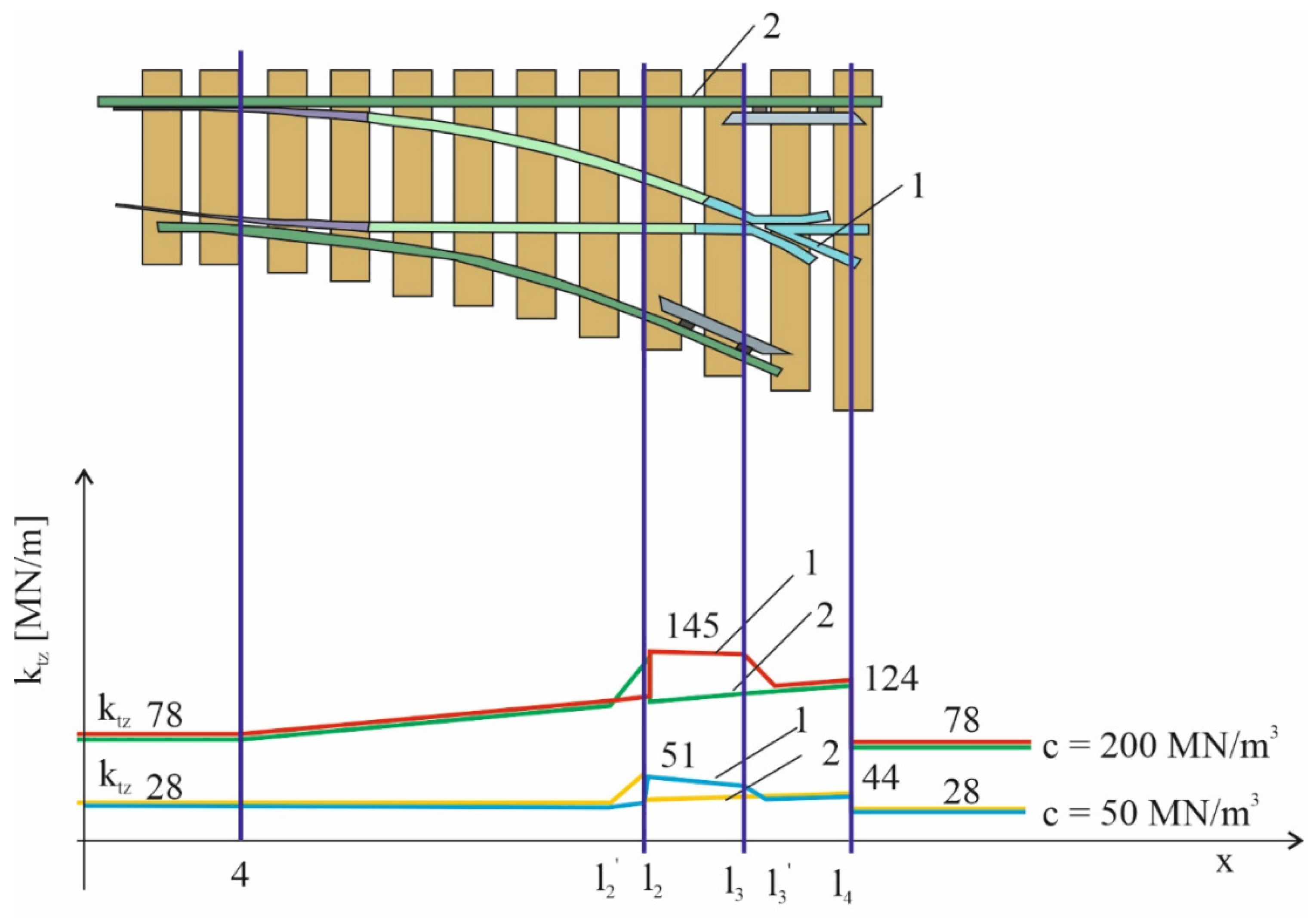
- Normal force on a rail is a variable value and will be determined from a previous series of mathematical calculations completed for specific train parameters (wheelbase of wheelsets and bogies).
- The rail track was modelled as a Euler–Bernoulli beam on which a wheel rolls with v speed and contacts occur (an ellipse is formed of a and b parameters). The beam is supported by a track stiffness variable.
- In the dynamics of vehicle motion along the track, such phenomena as adhesion, microslips and material wear of wheels and rails have to be taken into account.
- A possibility of two contact ellipses occurring as a result of a wheel rolling on the rail and the blade was considered in the described model.
- Flexible elements between solids in the vehicle were assumed to be linear.
- Due to track stiffness, the railway vehicle-track system is nonlinear.
- 2b—the distance between contact points (wheel–rail) in the wheelset middle position,
- r—radius of a wheel being an element of the wheelset measured in the middle position,
- —coefficient that links the angular and transverse displacement of a wheelset.
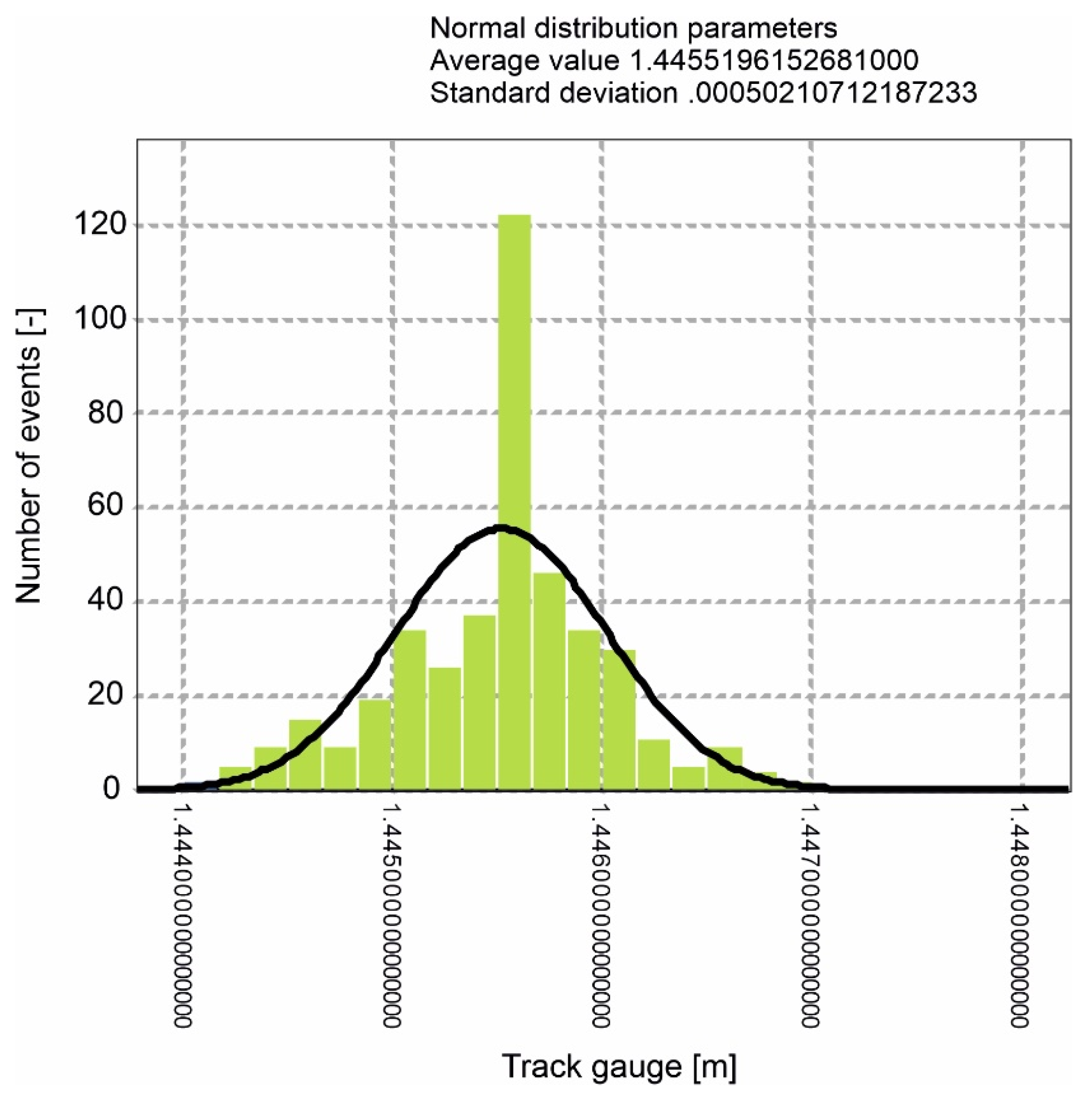
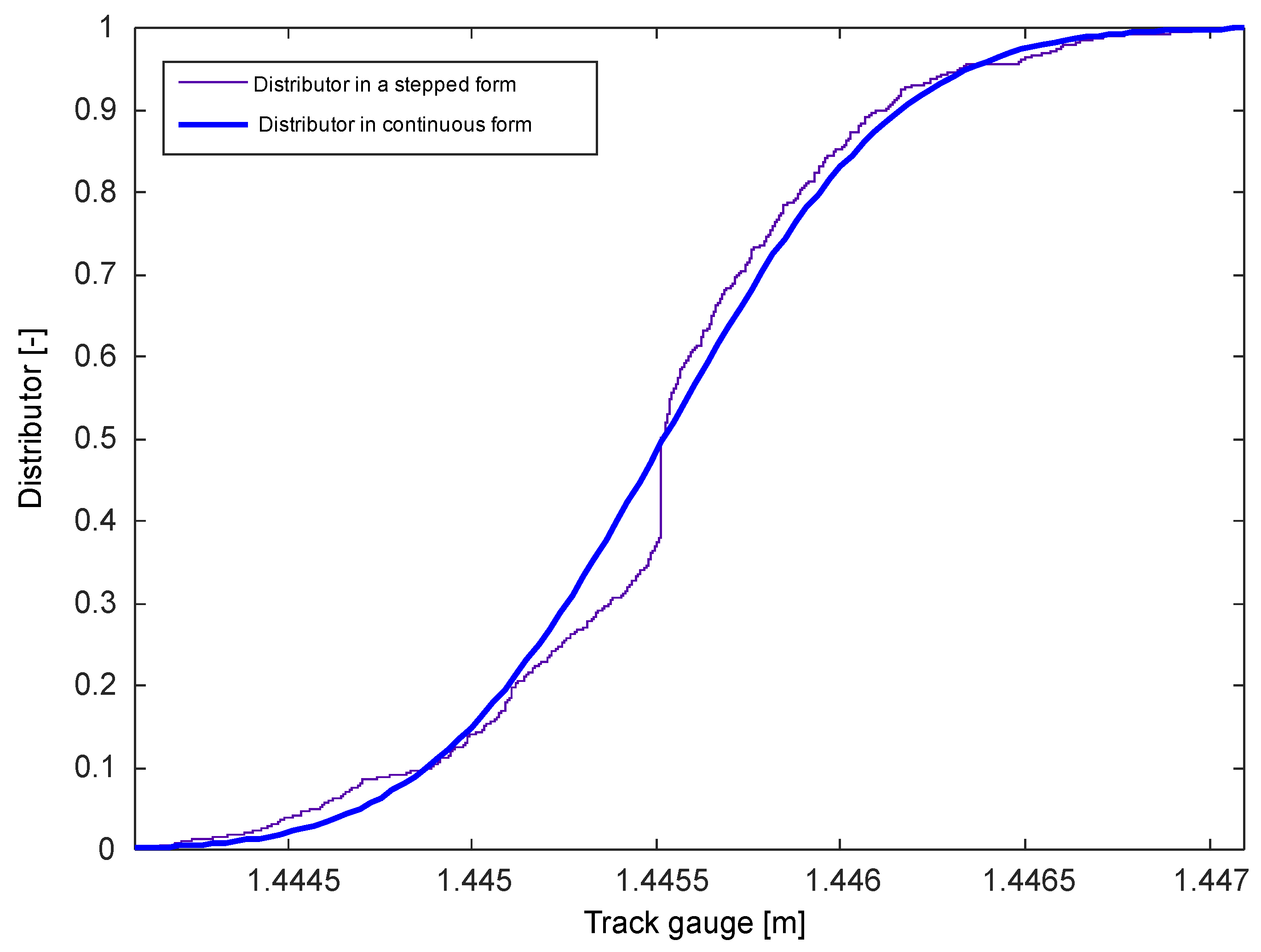
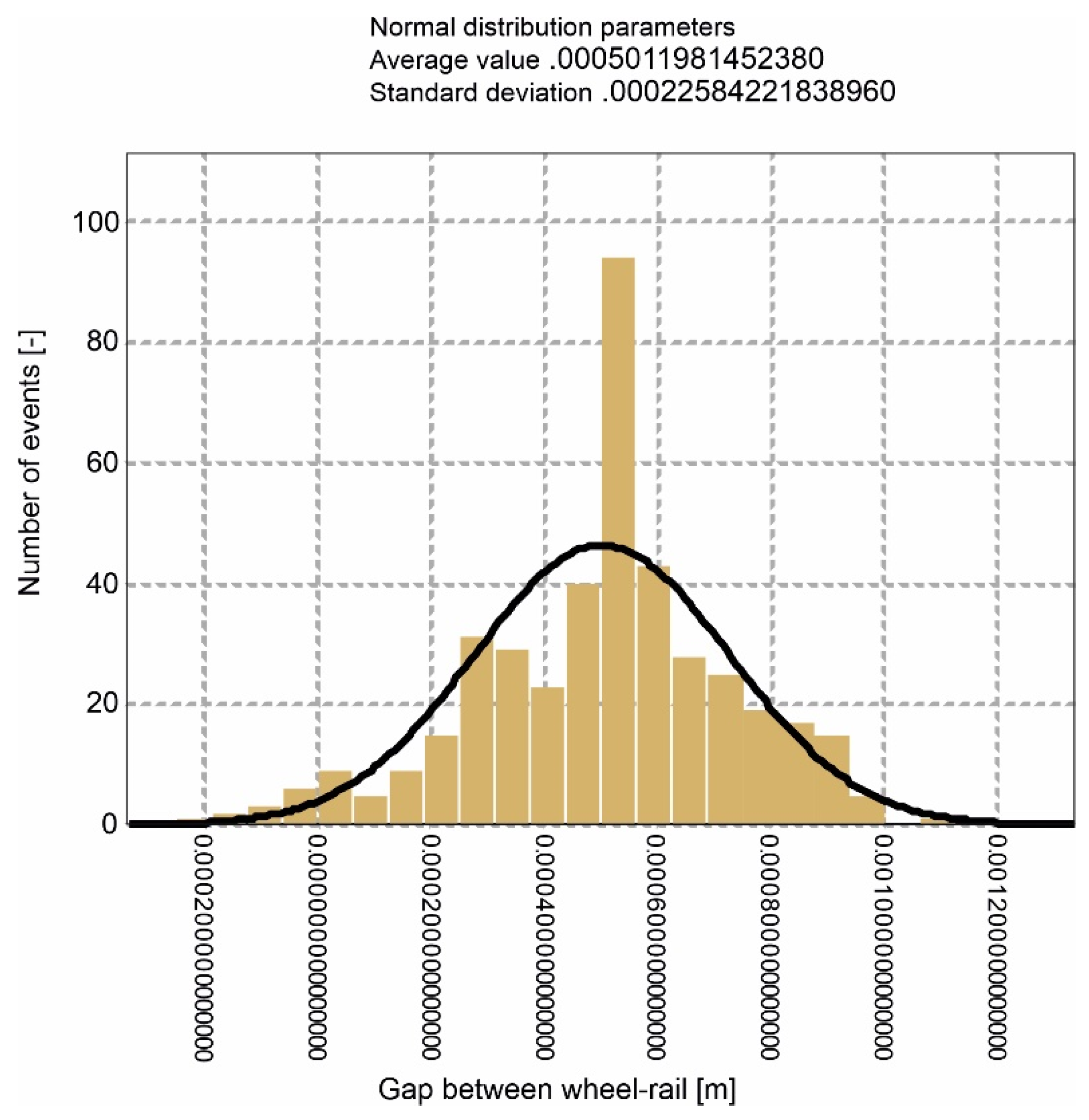
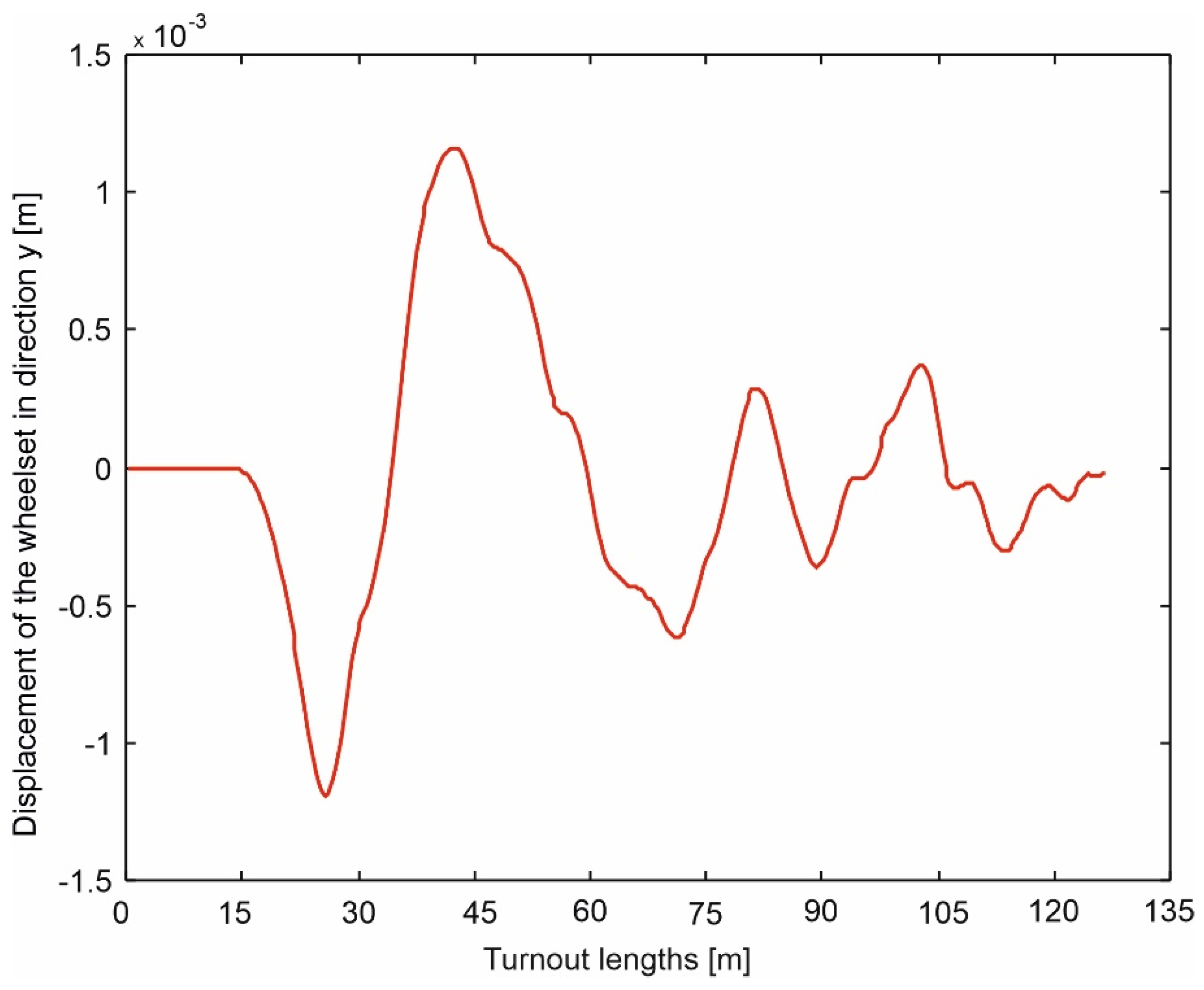
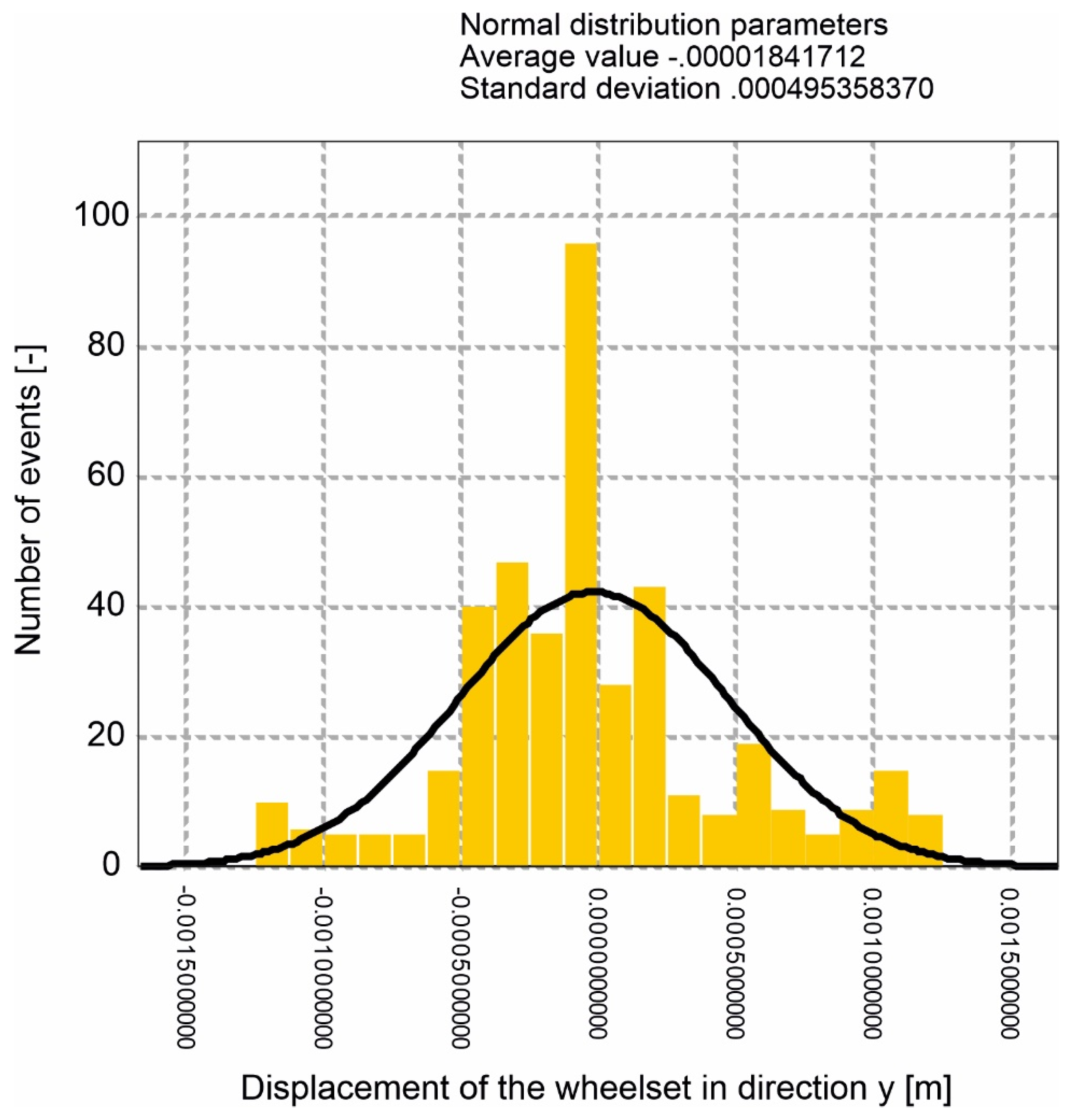
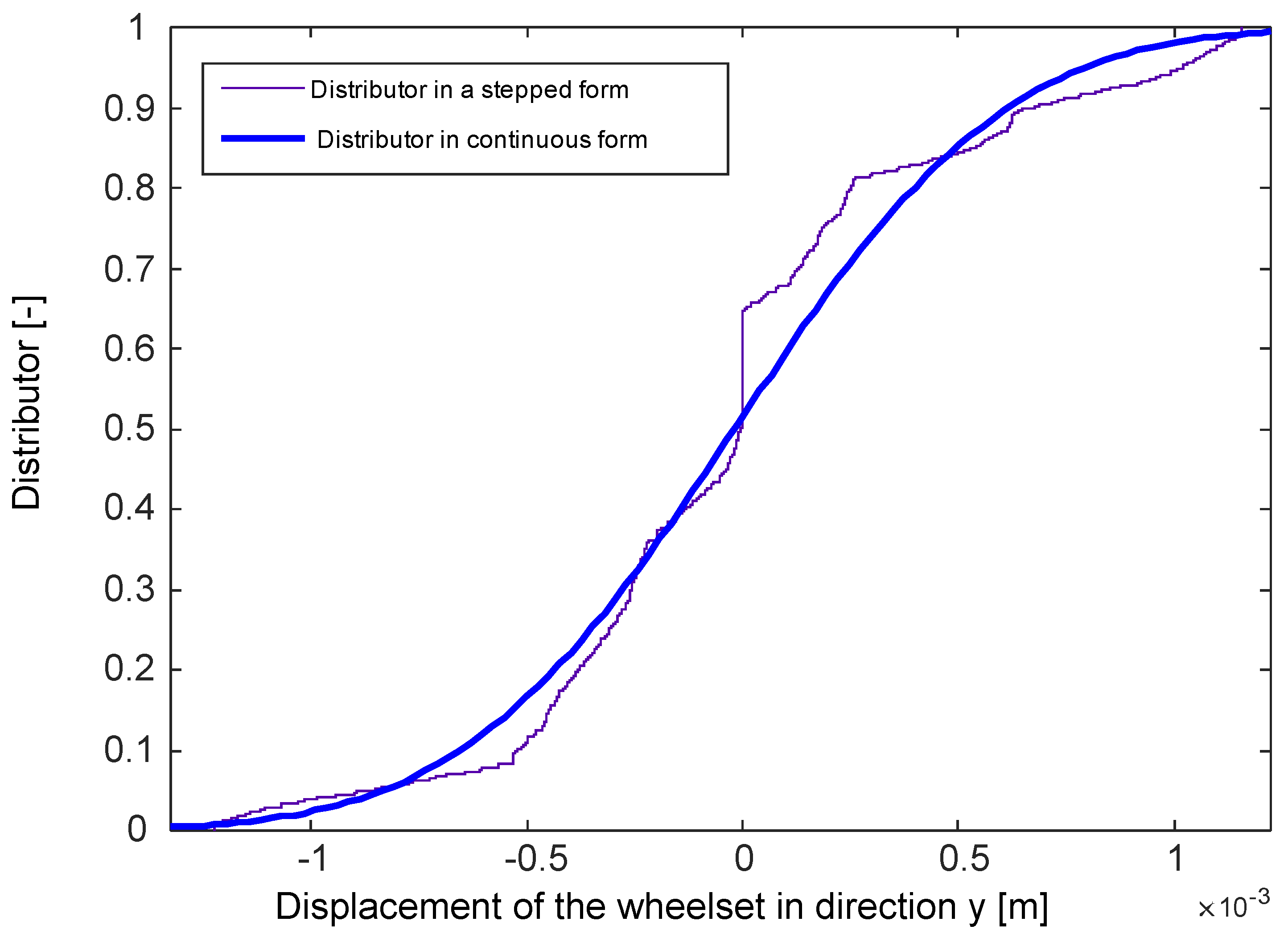
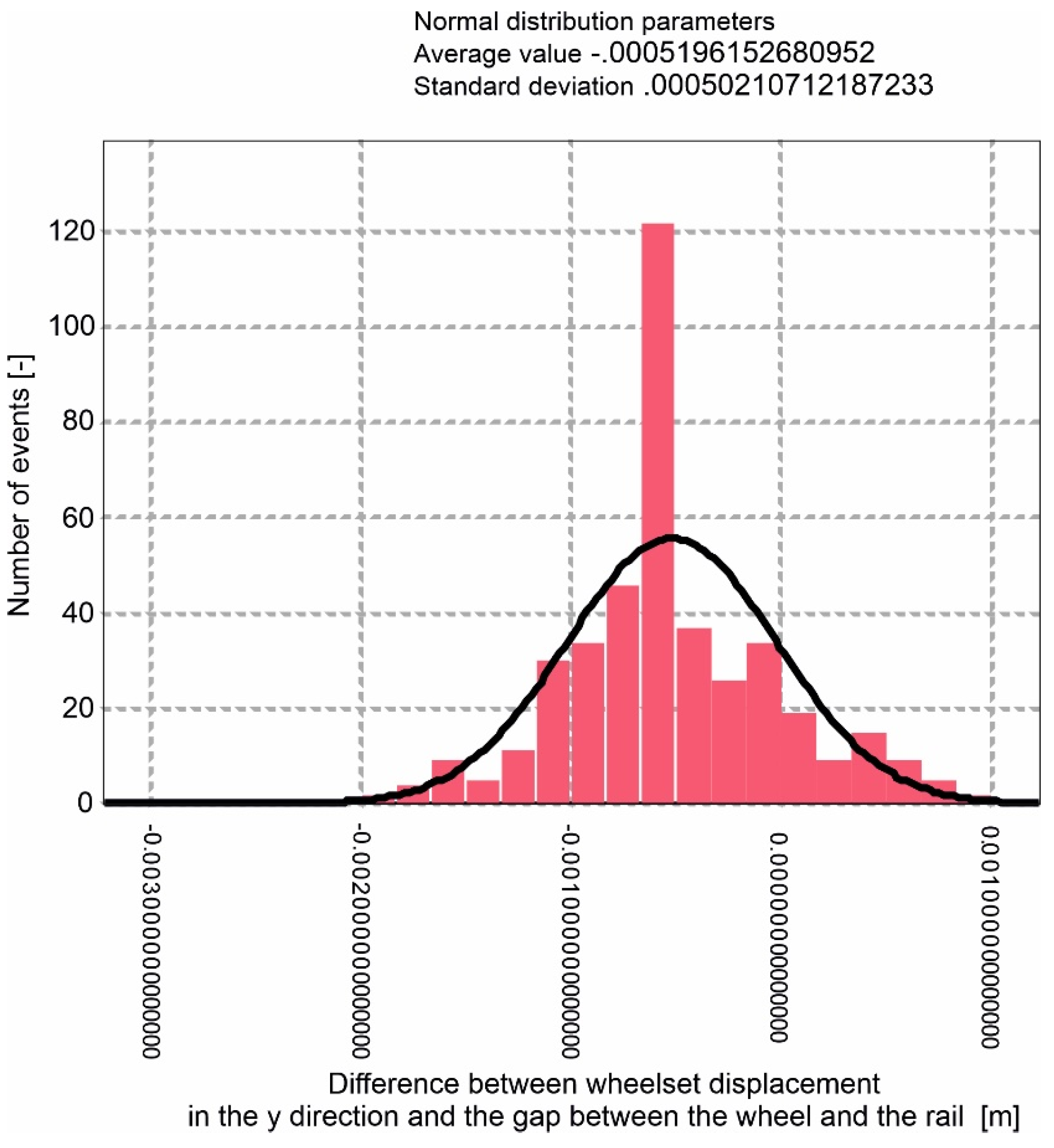
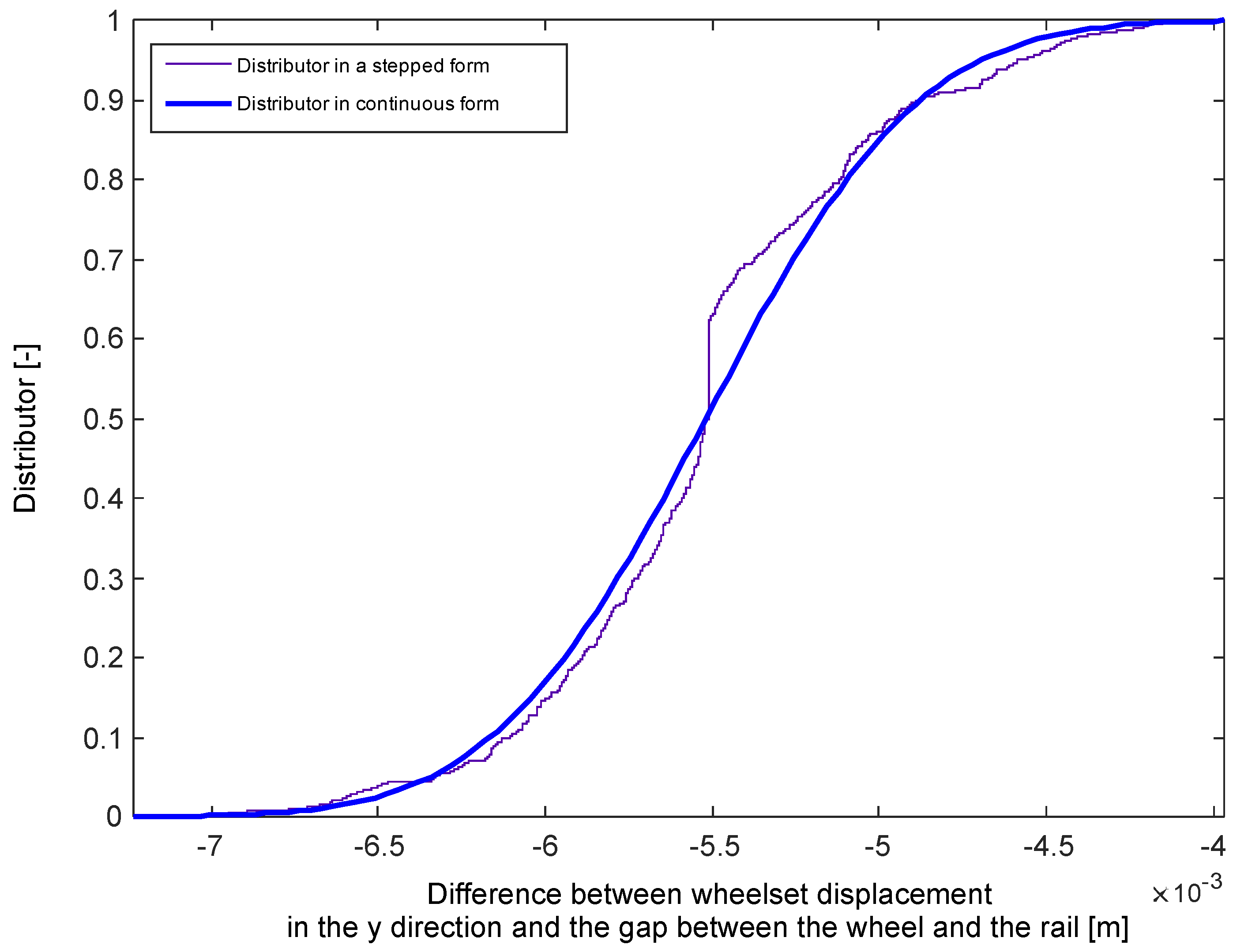
4. Results
- -
- for 250 km/h: average value: −0.000513834692; standard deviation: 0.000485753384
- -
- for 300 km/h: average value: 0.00036598735; standard deviation: 0.000503405022
- -
- for 350 km/h: average value: −0.000385392073; standard deviation: 0.000570222943.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wickens, A.H. Steering and Dynamic Stability of Railway Vehicles. Veh. Syst. Dyn. 1976, 5, 15–46. [Google Scholar] [CrossRef]
- Wickens, A.H. Fundamentals of Rail Vehicle Dynamics, Guidance and Stability; Swets&Zeitlinger, B.V.: Lisse, The Netherlands, 2003. [Google Scholar]
- Wickens, A. The dynamic stability of railway vehicle wheelsets and bogies having profiled wheels. Int. J. Solids Struct. 1965, 1, 319–341. [Google Scholar] [CrossRef]
- Knothe, K.; Stichler, S. Rail Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Popp, K.; Schiehlen, W. System dynamics and Long-Term Behaviour of Railway Vehicles, Track and Subgrade; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dukkipati, R.V.; Amyot, J.R. Simulation in Railway Dynamics Hardcover; North Oxford Academic: Banbury, UK, 1986. [Google Scholar]
- Dukkipati, R.V.; Garg, V.K. Dynamics of Railway Vehicle Systems; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Dukkipati, R.V.; Dong, R. Impact loads due to wheel flats and shells. Veh. Syst. Dyn. 1992, 31, 1–22. [Google Scholar] [CrossRef]
- Dukkipati, R.V.; Garg, V.K. Lateral Stability of Railway Vehicles on Tangent Track. Veh. Syst. Dyn. 1984, 225–262. [Google Scholar]
- Dukkipati, R.V.; Dong, R.G.; Sankar, S. A finite element model of railway track and its application to the wheel flat problem. Proc. Inst. Mech. Engrs. Part F J. Rail Rapid Transit 1994, 208, 61–72. [Google Scholar] [CrossRef]
- de Pater, A.D. Die untersuchung der stabilitat der bewegung eines eisenbahnfahrzeuges mit hilfe der neumarkschen methode. Ing. Arch. 1980, 49, 195–200. [Google Scholar] [CrossRef]
- Elkins, J.; Carter, A. Testing and Analysis Techniques for Safety Assessment of Rail Vehicles: The State-of-the-Art. Veh. Syst. Dyn. 1993, 22, 185–208. [Google Scholar] [CrossRef]
- Andersson, C.; Dahlberg, T. Wheel/rail impacts at a railway turnout crossing. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1998, 212, 123–134. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Lin, B.-H. Vehicle-Bridge Interaction Analysis by Dynamic Condensation Method. J. Struct. Eng. 1995, 121, 1636–1643. [Google Scholar] [CrossRef]
- Dukkipati, R.V. Vehicle Dynamics; Narosa Publishing House: New Delhi, India, 2000. [Google Scholar]
- Hague, I.; Lieh, J. A study of parametric stability of railway vehicles. Int. J. Veh. Des. 1993, 14, 246–260. [Google Scholar] [CrossRef]
- Goldhirsch, I.; Sulem, P.; Orszag, S.A. Stability and Lyapunov stability of dynamical systems: A differential approach and a numerical method. Phys. D 1987, 27, 311–337. [Google Scholar] [CrossRef]
- Goverde, R.M. Railway timetable stability analysis using max-plus system theory. Transp. Res. Part B 2006, 41, 179–201. [Google Scholar] [CrossRef]
- Hannebrink, D.N.; Lee, H.S.H.; Weinstock, H.; Hedrick, J.K. Closure to “Discussion of ‘Influence of Axial Load, Track Gage, and Wheel Profile on Rail Vehicle Hunting’”. J. Eng. Ind. 1977, 99, 926–927. [Google Scholar]
- Newton, S.G.; Clark, R.A. An Investigation into the Dynamic Effects on the Track of Wheelflats on Railway Vehicles. J. Mech. Eng. Sci. 1979, 21, 287–297. [Google Scholar] [CrossRef]
- Polach, O. Application of nonlinear stability analysis in railway vehicle industry. In Non-Smooth Problems in Vehicle Systems Dynamics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 15–27. [Google Scholar]
- True, H. Dynamics of a Rolling Wheelset. Appl. Mech. Rev. 1993, 46, 438–444. [Google Scholar] [CrossRef]
- Kisilowski, J.; Kardas-Cinal, E. On a Certain Method of Examining Stability of Mathematical Models of Railway Vehicles with Disturbances Occurring in Real Objects. Veh. Syst. Dyn. 1994, 23, 262–273. [Google Scholar] [CrossRef]
- Kardas-Cinal, E. Study of the Technical Stability of the Stochastic Mathematical Model of a Rail Vehicle. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 1994. [Google Scholar]
- Fermer, M.; Niesen, J.C.O. Vertical interaction between train and track with soft and stiff railpads–full-scale experiments and theory’. Proc. Inst. Mech. Engrs. Part F J. Rail Rapid Transit 1995, 209, 39–47. [Google Scholar] [CrossRef]
- He, Y.; McPhee, J. Optimization of the Lateral Stability of Rail Vehicles. Veh. Syst. Dyn. 2002, 38, 361–390. [Google Scholar] [CrossRef]
- Horak, D.; Wormley, D.N. Nonlinear Stability and Tracking of Rail Passenger Trucks. J. Dyn. Syst. Meas. Control. 1982, 104, 256–263. [Google Scholar] [CrossRef]
- Ingwerson, D.R. A Modified Lyapunov Method for Nonlinear Stability Problems. IRE Trans. Autom. Control 1961, 6, 199–210. [Google Scholar] [CrossRef]
- Law, E.H.; Karogal, I.; Ayalew, B. An Iterative Approach for Steady State Handling Analysis of Vehicles. In Proceedings of the n International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Brooklyn, NY, USA, 3–6 August 2008; IDETC-CIE2008. pp. 641–649. [Google Scholar] [CrossRef]
- Law, E.H.; Cooperrider, N.K. A Survey of Railway Vehicle Dynamics Research. J. Dyn. Syst. Meas. Control 1974, 96, 132–146. [Google Scholar] [CrossRef]
- Wu, H.; Zeng, X.-H.; Lai, J.; Yu, Y. Nonlinear hunting stability of high-speed railway vehicle on a curved track under steady aerodynamic load. Veh. Syst. Dyn. 2019, 58, 175–197. [Google Scholar] [CrossRef]
- Olusola, O.B.; Likins, P.W. Stability analysis of constant speed transit vehicles. Veh. Syst. Dyn. 1975, 4, 223–248. [Google Scholar] [CrossRef]
- Richard, J.A. Stability of railway-car running at high speed. Veh. Syst. Dyn. 1987, 16, 37–49. [Google Scholar] [CrossRef]
- Walker, J.A. On the Stability of Linear Discrete Dynamic Systems. J. Appl. Mech. 1970, 37, 271–275. [Google Scholar] [CrossRef]
- Bogusz, W. Stateczność Techniczna; IPPT PAN: Warsaw, Poland, 1972; p. 132. [Google Scholar]
- Kisilowski, J.; Skopińska, H. Dynamika Krzyżownicy Rozjazdu Zwyczajnego, Archiwum Inżynierii Lądowej–Tom XXIX 4/83; Warszawa, Poland, 1983. [Google Scholar]
- Kisilowski, J. Dynamika Układu tor- Pojazd, Prace ITPW, Zeszyt 15; Warsaw, Poland, 1978. [Google Scholar]
- Bałuch, H. Optymalizacja Układów Geometrycznych Toru; WKiŁ: Warsaw, Poland, 1983. [Google Scholar]
- Kisilowski, J. Dynamika Układu Mechanicznego Pojazd Szynowy-Tor; PWN: Warsaw, Poland, 1991. [Google Scholar]
- Bell, C.E.; Horak, D.; Hedrick, J.K. Stability and Curving Mechanics of Rail Vehicles. J. Dyn. Syst. Meas. Control 1981, 103, 181–190. [Google Scholar] [CrossRef]
- Bracciali, A.; Cascini, G.; Ciuffi, R. Time Domain Model of the Vertical Dynamics of a Railway Track up to 5 kHz. Veh. Syst. Dyn. 1998, 30, 1–15. [Google Scholar] [CrossRef]
- Chung, W.-J.; Shim, J.-K. Influence Factors on Critical Speed Hysteresis in Railway Vehicles. JSME Int. J. Ser. C 2003, 46, 278–288. [Google Scholar] [CrossRef][Green Version]
- Cox, E.H.; Garg, V.K.; Goodspeed, C.H.; Singh, S.P. Comparative Study of the Linear and Non-Linear Locomotive Response. J. Dyn. Syst. Meas. Control 1979, 101, 263–271. [Google Scholar] [CrossRef]
- Cox, J.J.; Hedrick, J.K.; Cooperrider, N.K. Optimization of Rail Vehicle Operating Speed with Practical Constraints. J. Dyn. Syst. Meas. Control 1978, 100, 260–269. [Google Scholar] [CrossRef]
- Dym, C.L. Stability Theory and Its Applications to Structural Mechanics; Noordhoff International Publishing Co.: Leyden, The Netherlands, 1974. [Google Scholar]
- Goverde, R.M. Punctuality of Railway Operations and Timetable Stability Analysis. Ph.D. Thesis, Delft University of Technology, TRAIL Research School, Delft, The Netherlands, 2005. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Appl. Math. Sci. 1983, 42, 462. [Google Scholar]
- Inozemtsev, V.; Tibilov, T. Lyapunov–Bautin bifurcation and the hunting of a railway wheelset. In Proceedings of the 2nd International Conference Control of Oscillations and Chaos, Scientific Counsil on Transoptation Problems of RAS, Moscow, St. Petersburg, Russia, 5–7 July 2000. [Google Scholar]
- Law, E.H.; Brand, R.S. Analysis of the Nonlinear Dynamics of a Railway Vehicle Wheelset. J. Dyn. Syst. Meas. Control 1973, 95, 28–35. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Cheng, Y.-C. Nonlinear Analysis on Hunting Stability for High-Speed Railway Vehicle Trucks on Curved Tracks. J. Vib. Acoust. 2004, 127, 324–332. [Google Scholar] [CrossRef]
- Lei, X.; Nodab, N.A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vib. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Nath, Y.; Jayadev, K. Influence of yaw stiffness on the nonlinear dynamics of railway wheelset. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 179–190. [Google Scholar] [CrossRef]
- Suda, Y. High Speed Stability and Curving Performance of Longitudinally Unsymmetric Trucks with Semi-active Control. Veh. Syst. Dyn. 1994, 23, 29–52. [Google Scholar] [CrossRef]
- Xu, G.; Troger, H.; Steindl, A. Global analysis of the loss of stability of a special railway bogy. In Nonlinear Dynamics in Engineering Systems; Springer: Berlin/Heidelberg, Germany, 1990; pp. 345–353. [Google Scholar]
- Yang, Y.-R. Limit Cycle Hunting of a Bogie with Flanged Wheels. Veh. Syst. Dyn. 1995, 24, 185–196. [Google Scholar] [CrossRef]
- Young, J.A.; Apparao, T.A.P.S. Lateral Dynamics of a Rail Transit Vehicle: A Comparison of Experimental and Theoretical Results. J. Dyn. Syst. Meas. Control 1981, 103, 39–48. [Google Scholar] [CrossRef]
- Kowalik, R. Wybrane Problemy Dynamiki Rozjazdu Kolejowego Przy Dużych Prędkościach Współczesnych Pociągów; Instytut Naukowo-Wydawniczy Spatium: Radom, Poland, 2020; e-ISBN: 978-83-66550-16-2. [Google Scholar]
- Gou, H.; Yang, L.; Mo, Z.; Guo, W.; Shi, X.; Bao, Y. Effect of Long-Term Bridge Deformations on Safe Operation of High-Speed Railway and Vibration of Vehicle–Bridge Coupled System. Int. J. Struct. Stab. Dyn. 2019, 19. [Google Scholar] [CrossRef]
- Zalewski, J. On a Certain Approach Towards the U-Turn of a Motor Vehicle Maneuver, Communications in Computer and Information Science; Springer: Cham, Switzerland, 2020; 1289 CCIS; pp. 354–367. [Google Scholar] [CrossRef]
- Uyulan, C.; Gokasan, M.; Bogosyan, S. Hunting stability and derailment analysis of the high-speed railway vehicle moving on curved tracks. Int. J. Heavy Veh. Syst. 2019, 26, 824. [Google Scholar] [CrossRef]
- Zalewski, J. Selected Problems of a Motor Vehicle Motion in a Turn after Steering Wheel Release, Communications in Computer and Information Science; Springer: Cham, Switzerland, 2019; Volume 1049, pp. 273–286. [Google Scholar] [CrossRef]
- Kim, H.-W.; Cha, H.-R. Sliding Mode-Based Slip Control of Compact Electric Vehicle Truck for Varying Load and Yaw Rate. Appl. Sci. 2021, 11, 6465. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Rath, J.; Lv, C.; Guerra, T.-M.; Lauber, J. Human-Machine Shared Driving Control for Semi-Autonomous Vehicles Using Level of Cooperativeness. Sensors 2021, 21, 4647. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Dorsch, V.; Gauterin, F. Mass Data Measurement, Approximation and Influence on Vehicle Stability for Ultra-Light Human-Powered Vehicles. Appl. Sci. 2021, 11, 5485. [Google Scholar] [CrossRef]
- Lei, T.; Wang, J.; Yao, Z. Modelling and Stability Analysis of Articulated Vehicles. Appl. Sci. 2021, 11, 3663. [Google Scholar] [CrossRef]
- Yang, K.; Dong, D.; Ma, C.; Tian, Z.; Chang, Y.; Wang, G. Stability Control for Electric Vehicles with Four In-Wheel-Motors Based on Sideslip Angle. World Electr. Veh. J. 2021, 12, 42. [Google Scholar] [CrossRef]
- Xue, X.; Cheng, K.; Chan, W.; Fong, Y.; Kan, K.; Fan, Y. Design, Analysis and Application of Single-Wheel Test Bench for All-Electric Antilock Braking System in Electric Vehicles. Energies 2021, 14, 1294. [Google Scholar] [CrossRef]
- Ni, T.; Li, W.; Zhao, D.; Kong, Z. Road Profile Estimation Using a 3D Sensor and Intelligent Vehicle. Sensors 2020, 20, 3676. [Google Scholar] [CrossRef]
- Che, F.; Niu, Y.; Li, J.; Wu, L. Cooperative Standoff Tracking of Moving Targets Using Modified Lyapunov Vector Field Guidance. Appl. Sci. 2020, 10, 3709. [Google Scholar] [CrossRef]
- Yim, S. Comparison among Active Front, Front Independent, 4-Wheel and 4-Wheel Independent Steering Systems for Vehicle Stability Control. Electronics 2020, 9, 798. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, W.; Hou, B.; Zhong, Y. Analysis of Influencing Mechanism of Subgrade Frost Heave on Vehicle-Track Dynamic System. Appl. Sci. 2020, 10, 8097. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Dunford, W.; Chen, J.; Liu, Z. Integrated Full-Frequency Impedance Modeling and Stability Analysis of the Train-Network Power Supply System for High-Speed Railways. Energies 2018, 11, 1714. [Google Scholar] [CrossRef]







| Parameter | Value | Unit |
|---|---|---|
| Car body weight | 42,400 | [kg] |
| Rotational inertia of the body | 7.06·105 | [kg∙m2] |
| Moment of inertia between the body nodes | 2.27·106 | [kg∙m2] |
| Rotational inertia of the body defined along φ axis | 2.08·106 | [kg∙m2] |
| Bogie weight | 3100 | [kg] |
| Rotational inertia of the bogie | 5045 | [kg∙m2] |
| Moment of inertia between bogie nodes | 2806 | [kg∙m2] |
| Rotational inertia of the bogie defined along φ axis | 2247 | [kg∙m2] |
| Wheelset weight | 1850 | [kg] |
| Rotational inertia of the wheelset | 717 | [kg∙m2] |
| Rotational inertia of wheelset defined along φ axis | 717 | [kg∙m2] |
| Stiffness coefficient along X-axis | 1.45·105 | [N/m] |
| Stiffness coefficient along Y-axis | 2.05·105 | [N/m] |
| Stiffness coefficient along Z-axis | 1.48·105 | [N/m] |
| Damping coefficient of secondary suspension along X-axis | 3.43·105 | [Ns/m] |
| Damping coefficient of secondary suspension along Y-axis | 2.45·104 | [Ns/m] |
| Damping coefficient of secondary suspension along Z-axis | 3.16·104 | [Ns/m] |
| Stiffness coefficient of primary suspension along X-axis | 2.80·107 | [N/m] |
| Stiffness coefficient of primary suspension along Y-axis | 4·106 | [N/m| |
| Stiffness coefficient of primary suspension along Z-axis | 1.2·106 | [N/m] |
| Lateral damping coefficient of primary suspension | 1.77·104 | [Ns/m] |
| Vertical distance between the center of body mass and secondary suspension | 1100 | [m] |
| Vertical distance between the secondary suspension and the gravity center of the bogie | 0.100 | [m] |
| Vertical distance between the gravity center of the bogie and primary suspension | 0.270 | [m] |
| Half the transverse distance between the primary suspension | 0.813 | [m] |
| Half the transverse distance between the secondary suspension | 0.978 | [m] |
| Half distance between the bogie axles | 1350 | [m] |
| Half distance between the gravity centers of the body | 8750 | [m] |
| Nominal wheel rolling radius | 0.430 | [m] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kisilowski, J.; Kowalik-Adamczyk, E. Stochastic Technical Stability Test of a Passenger Railroad Car Crossing a Turnout. Energies 2021, 14, 4569. https://doi.org/10.3390/en14154569
Kisilowski J, Kowalik-Adamczyk E. Stochastic Technical Stability Test of a Passenger Railroad Car Crossing a Turnout. Energies. 2021; 14(15):4569. https://doi.org/10.3390/en14154569
Chicago/Turabian StyleKisilowski, Jerzy, and Elżbieta Kowalik-Adamczyk. 2021. "Stochastic Technical Stability Test of a Passenger Railroad Car Crossing a Turnout" Energies 14, no. 15: 4569. https://doi.org/10.3390/en14154569
APA StyleKisilowski, J., & Kowalik-Adamczyk, E. (2021). Stochastic Technical Stability Test of a Passenger Railroad Car Crossing a Turnout. Energies, 14(15), 4569. https://doi.org/10.3390/en14154569







