The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply
Abstract
:1. Introduction
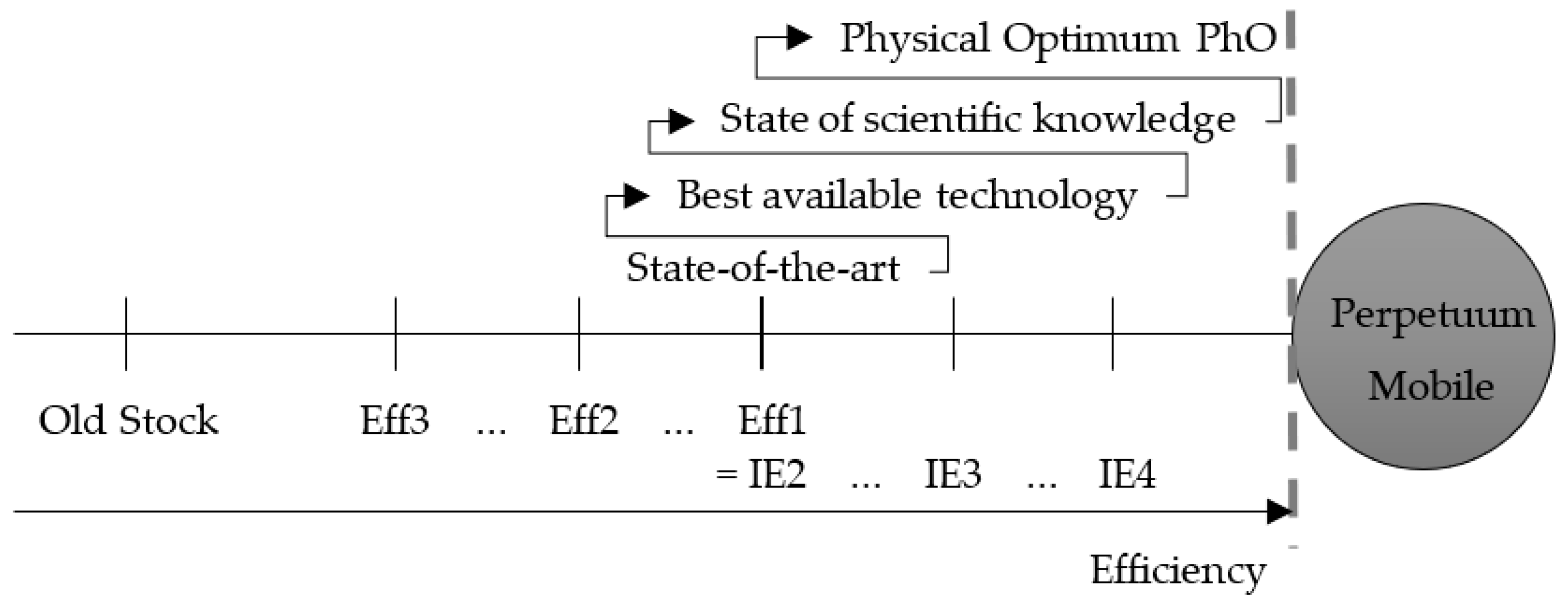
- BDP: best demonstrated practice;
- OEO: operational energy optimum;
- PEO: plant energy optimum;
- TEO: theoretical energy optimum;
- Best practice observed;
- BAT: best available technology;
2. Materials and Methods
2.1. Efficiency
2.2. Exergy Analysis
2.3. Physical Optimum
3. Results
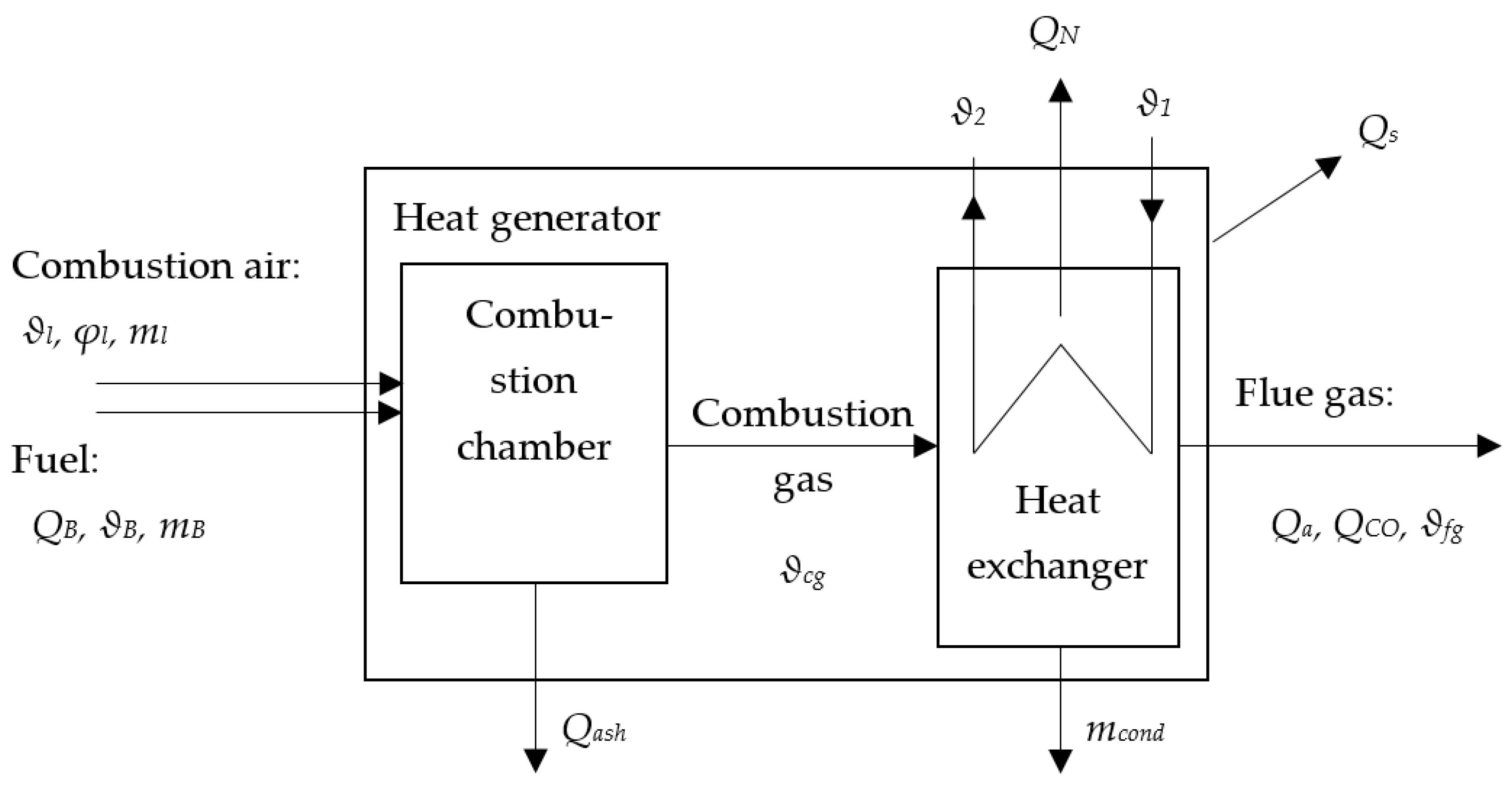
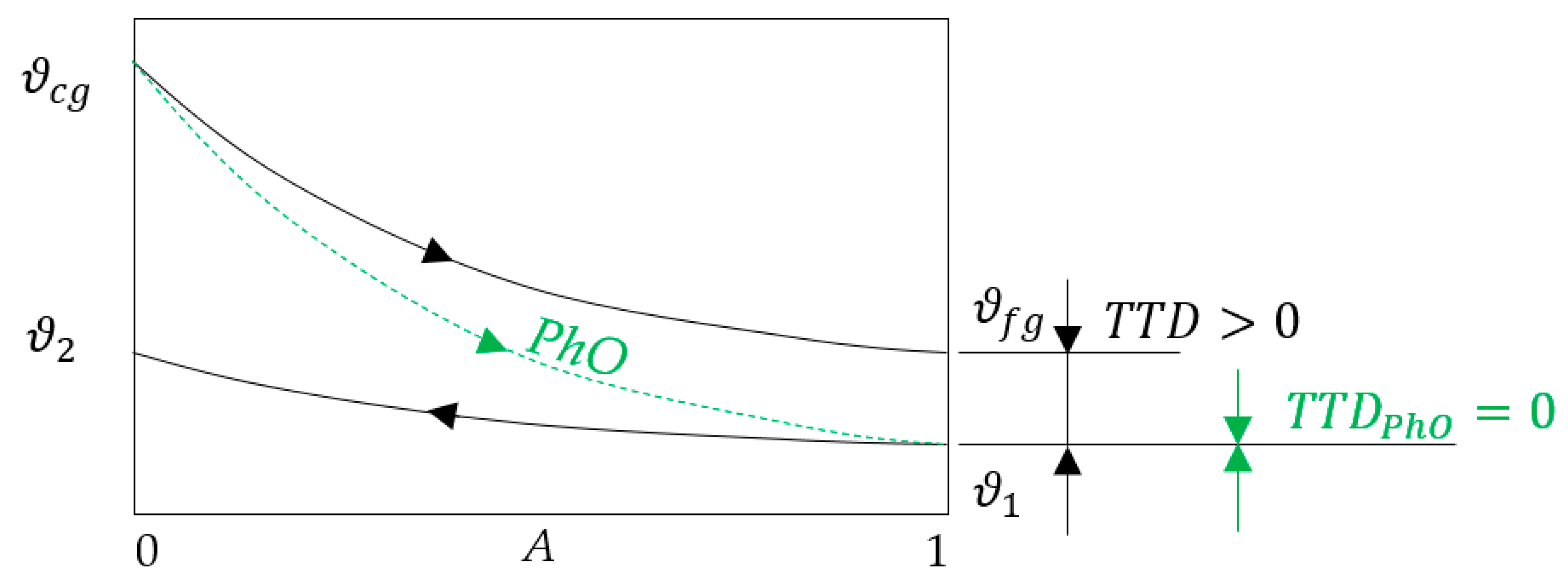
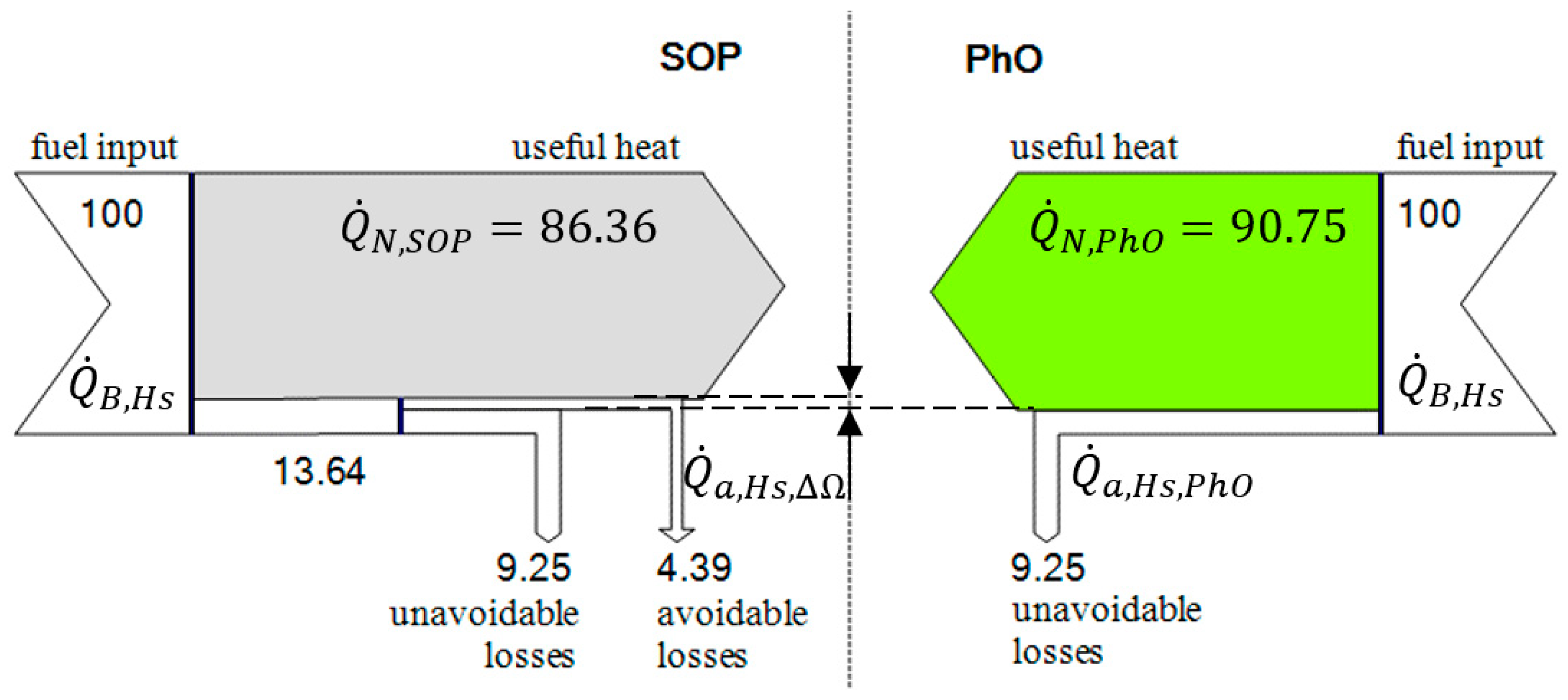
3.1. Application of PhO to Boiler Process
- Qfg exhaust loss;
- Qash ash loss;
- QCO losses by incompletely burned material;
- QS surface loss.
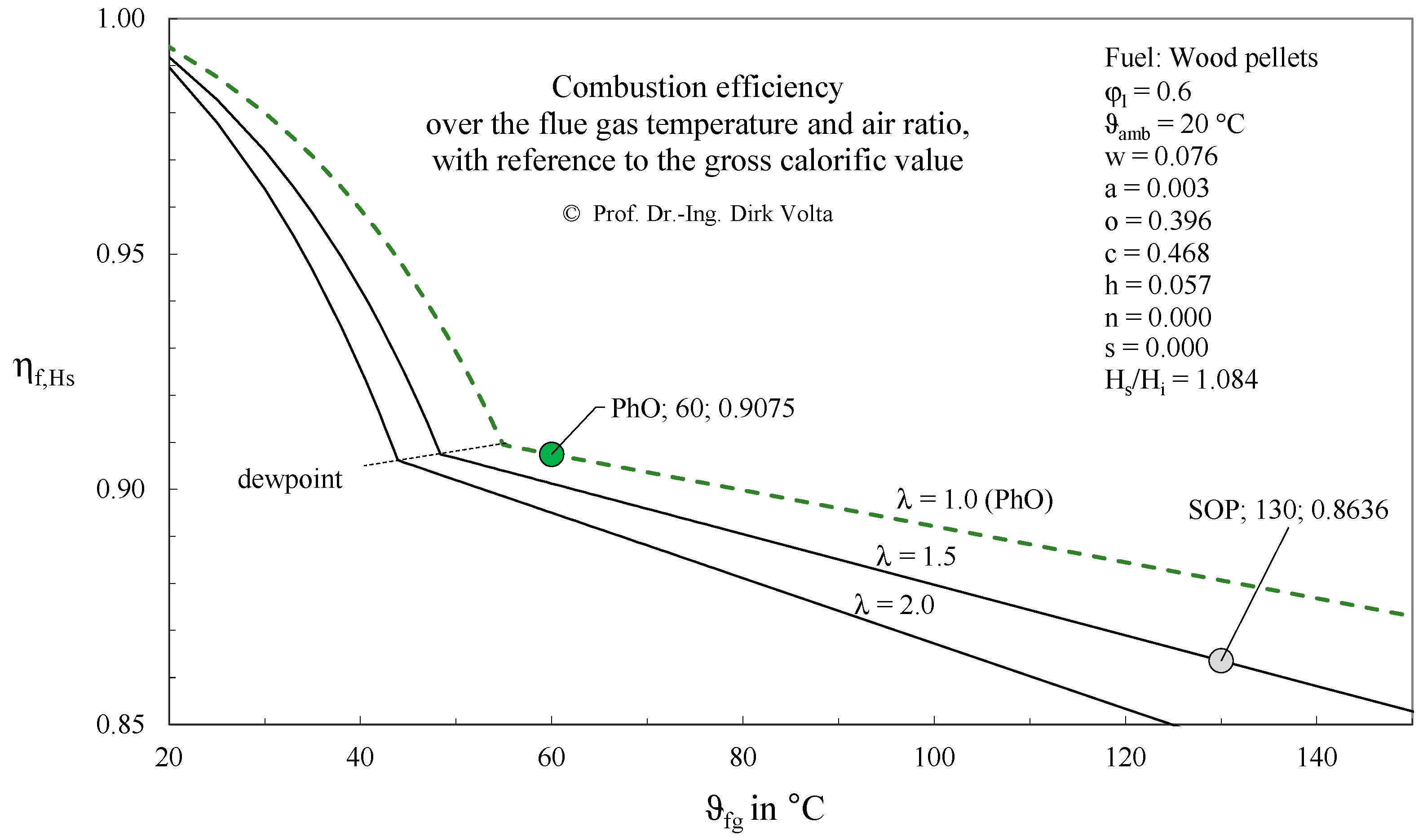
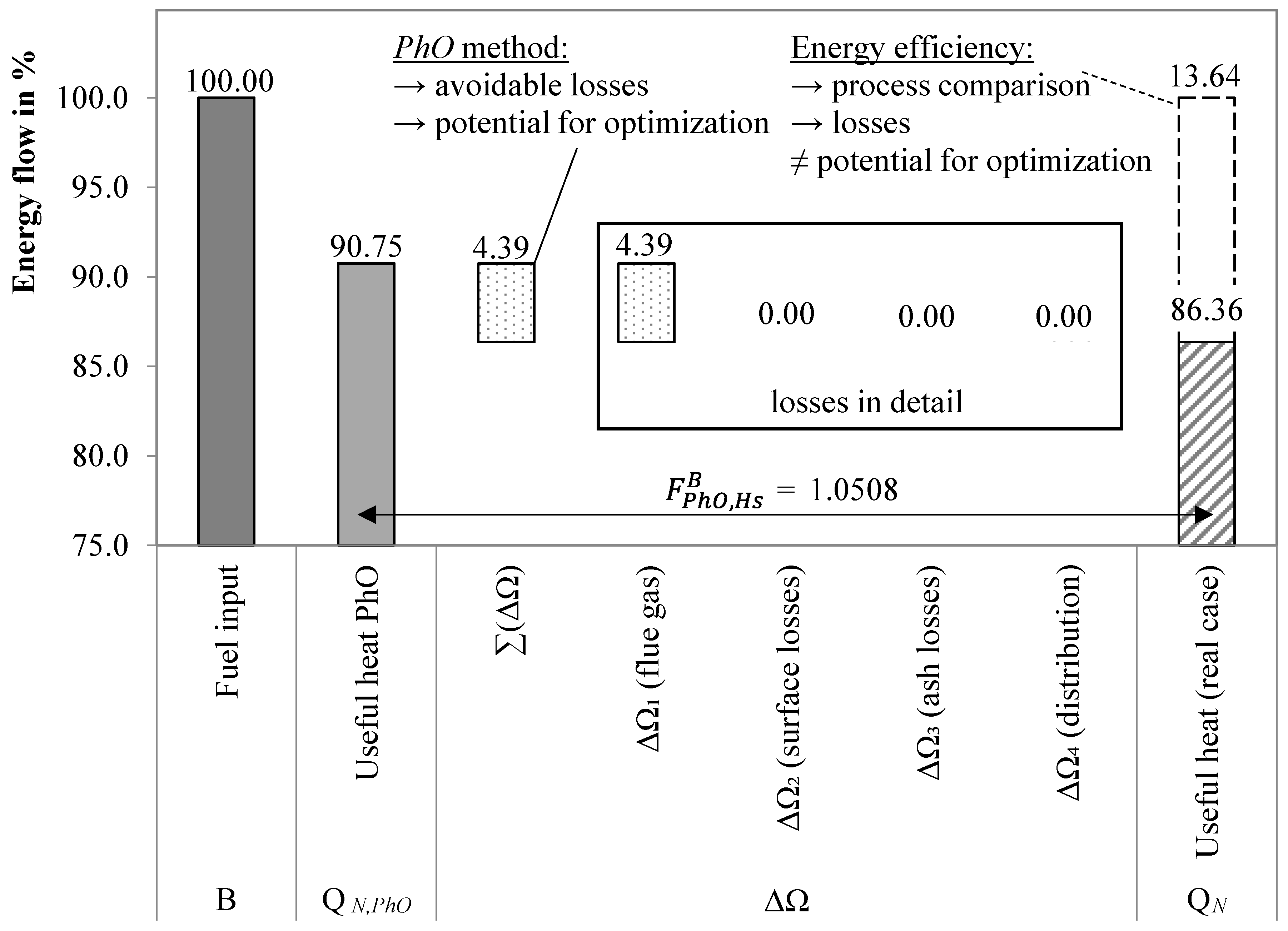
3.1.1. Example
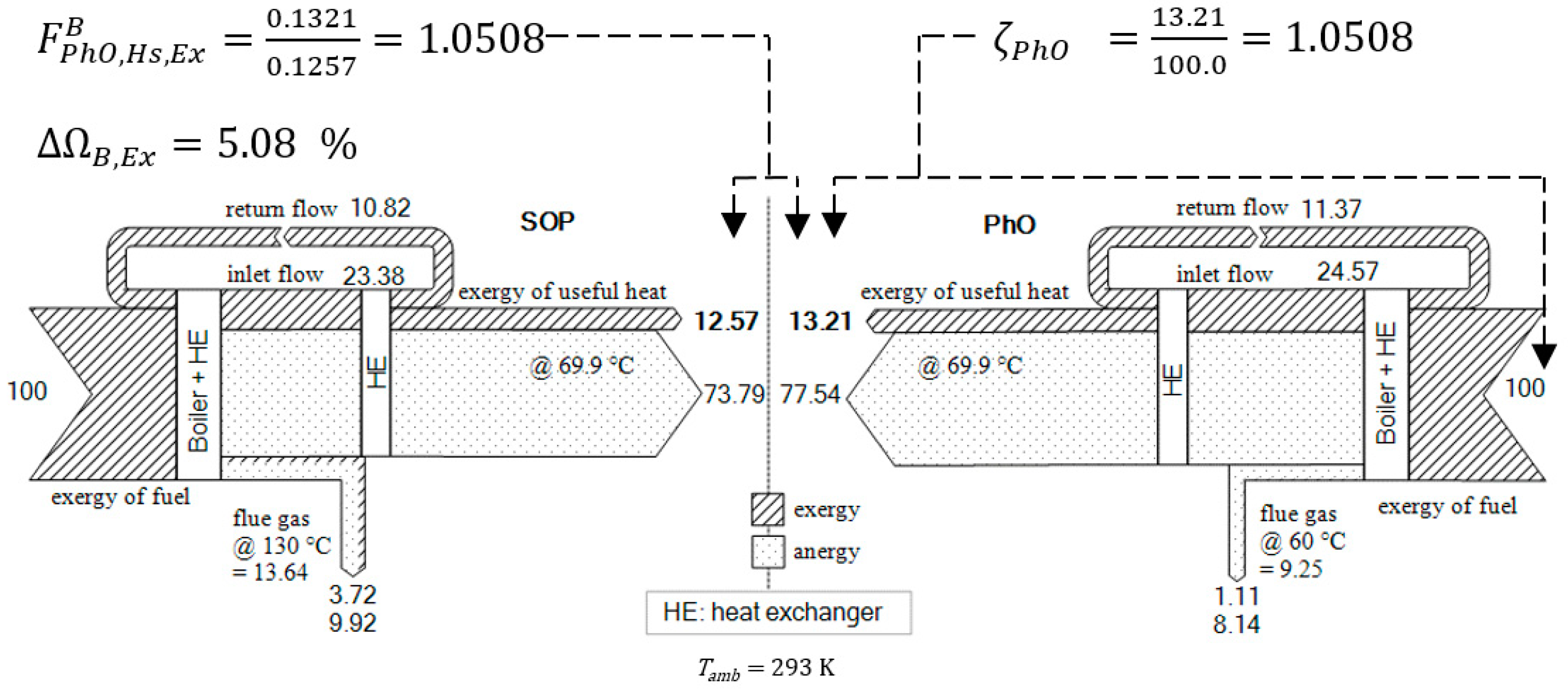
3.1.2. PhO Factor Based on Exergy Analysis
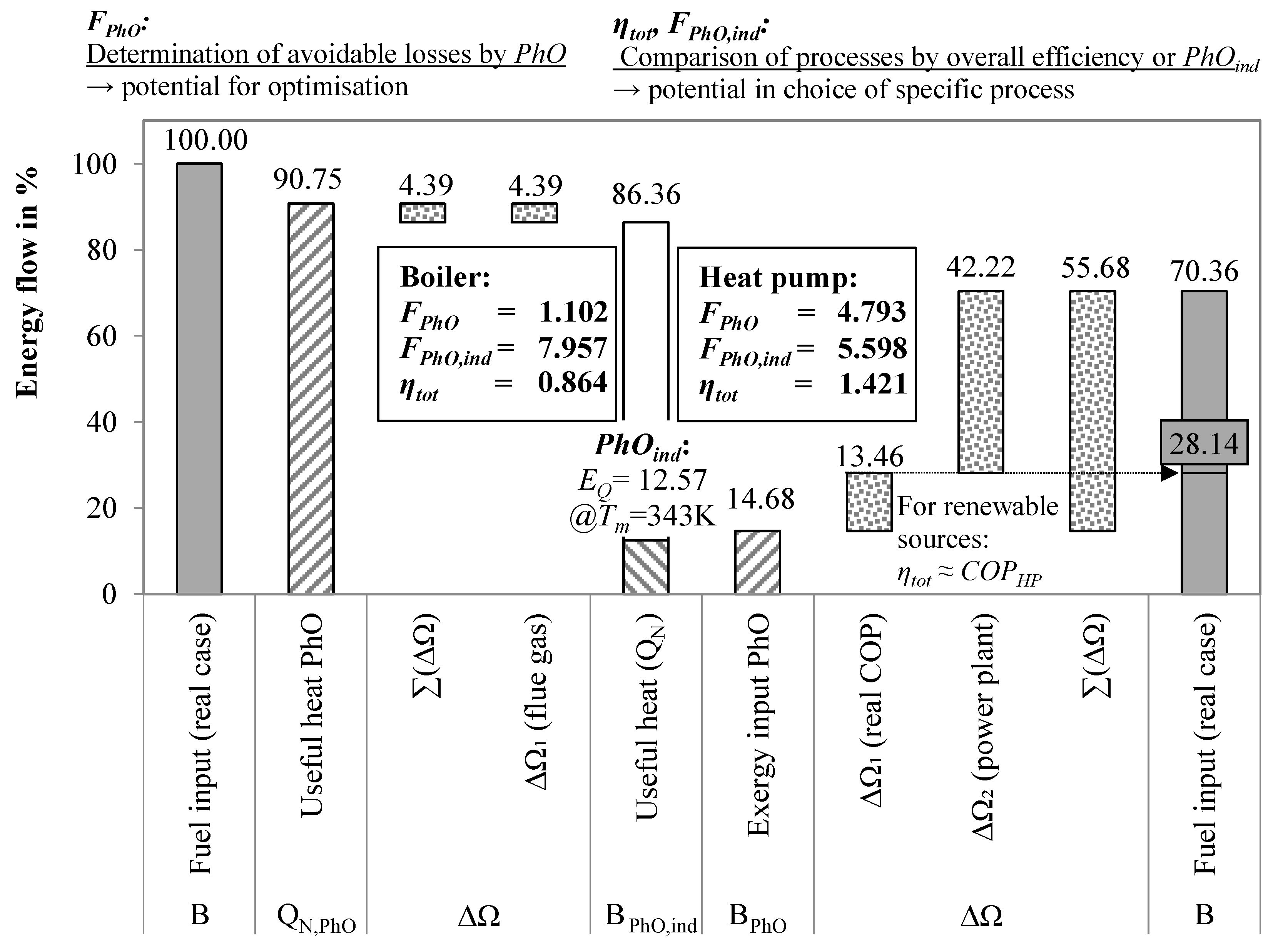
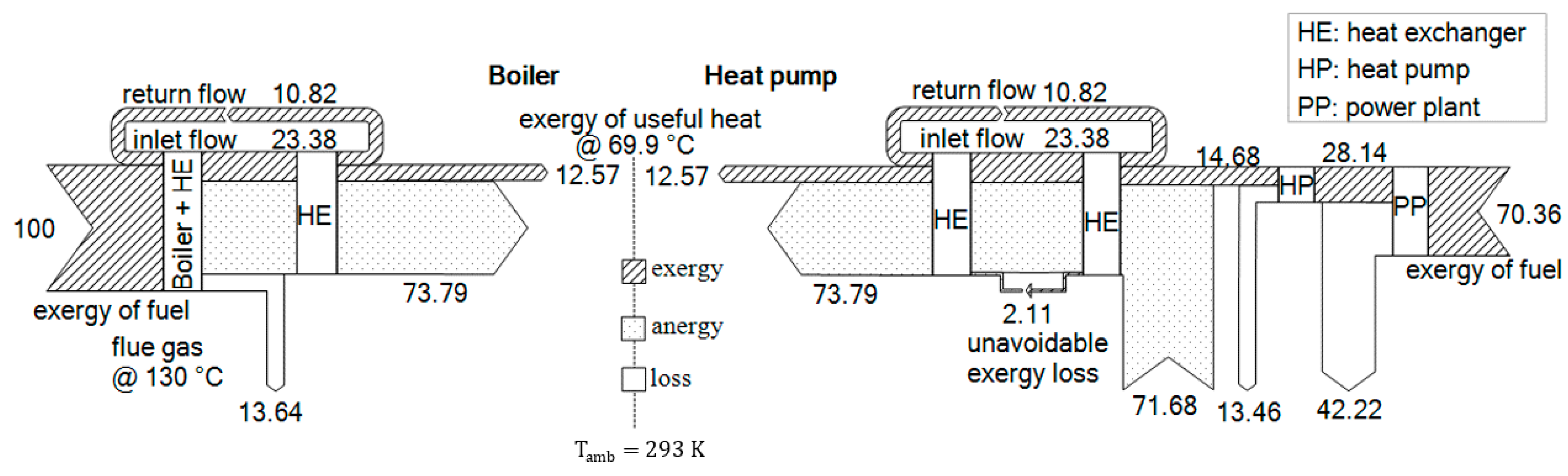
3.2. Comparison of Boiler and Heat Pump with PhO
3.2.1. PhO Factor and Efficiency
- For BPhO: Assuming a TTD of 0 K, the ideal HP operates between 20 and 80 °C, with a COP of 5.88.
- For : For the real HP, the liquefaction temperature is set to 85 °C, and the evaporation temperature is set to 15 °C (TTD = 5 K). With a Carnot grade of approximately 0.6, the COP of the real HP would be 3.07.
- For : Furthermore, the efficiency of the power plant (PP) delivering the electric energy is assumed to be 40%.
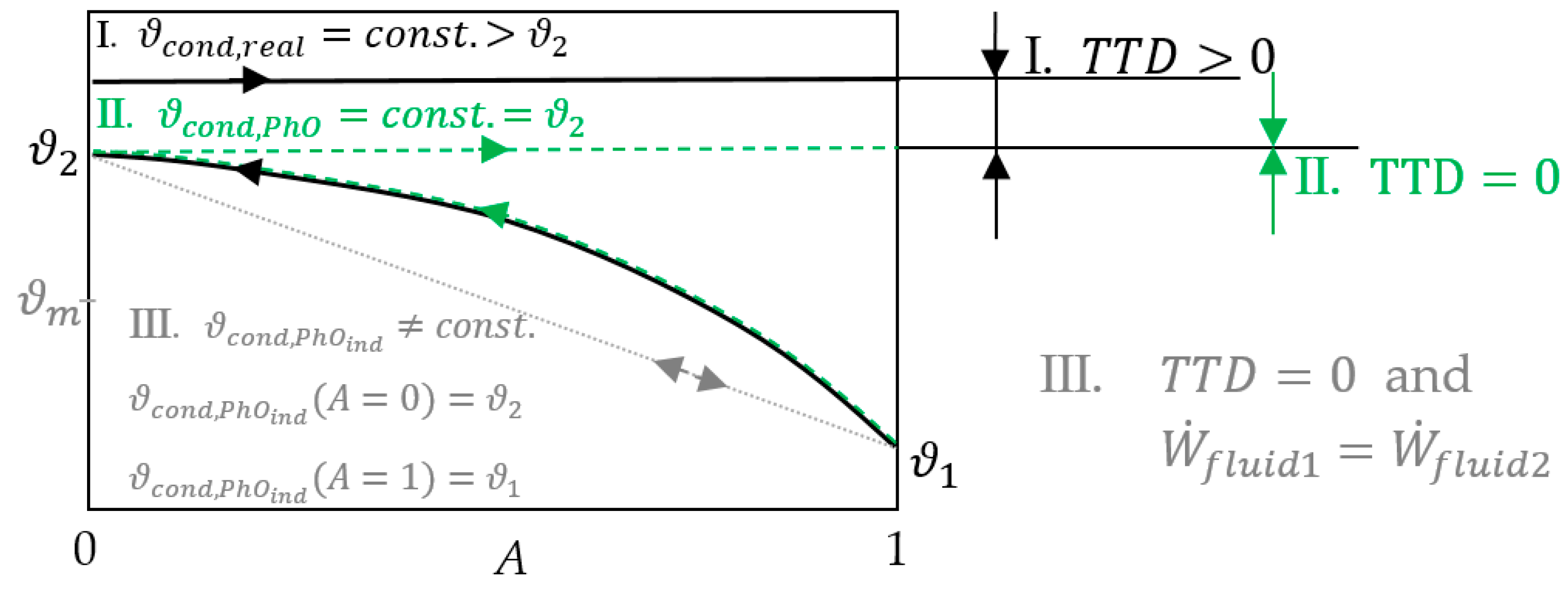
3.2.2. Process-Independent PhO
4. Discussion
4.1. Degree of Idealization
4.2. Description of the Benefit of a Process
4.3. Using Exergy to Describe the PhO
4.4. Research Directions: Change in Load
4.5. Application of the PhO to Other Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman Symbols | ||
| Symbol | Unit | Description |
| B | e.g., J, W | Demand |
| cp | J/(kgK) | Specific isobaric heat capacity |
| E | J | Exergy |
| - | PhO factor, based on demand | |
| H | J | Enthalpy |
| Hi | J/kg | Lower calorific value |
| Hs | J/kg | Gross calorific value |
| m | kg | Mass |
| Q | J | Heat |
| r | J/kg | Specific condensation enthalpy |
| S | J | Entropy |
| T | K | Kelvin temperature |
| TTD | K | Terminal temperature difference |
| Greek Symbols | ||
| - | Exergy efficiency | |
| - | Efficiency | |
| λ | - | Air ratio |
| - | Stoichiometric number | |
| e.g., J, W | Avoidable losses | |
| Sub- and Superscript | ||
| Symbol | Description | |
| amb | Ambient | |
| ash | Ashes | |
| B | Fuel, demand | |
| C | Carnot | |
| cg | Combustion gas | |
| CO | Incompletely burned | |
| cond | Condensate | |
| Ex | Exergy | |
| fg | Flue gas (exhaust) | |
| f | Combustion | |
| HP | Heat pump | |
| ind | Process-independent | |
| irr | Irreversible | |
| l | Loss; for air: dry air | |
| m | Mean, average | |
| N | Useful part (e.g., of heat) | |
| PhO | Physical optimum | |
| q | Heat | |
| S | Surface | |
| SOP | Standard operating point | |
| tot | Total, overall | |
| Differentiation by time | ||
References
- Volta, D. Das Physikalische Optimum als Basis von Systematiken zur Steigerung der Energie- und Stoffeffizienz von Produktionsprozessen. Ph.D. Thesis, TU Clausthal, Clausthal-Zellerfeld, Germany, 5 December 2014. [Google Scholar]
- Keichel, C. Methode der grenzwertorientierten Bewertung—Energie- und Ressourceneffizienz von Gesamtbetriebsweisen. Ph.D. Thesis, TU Clausthal, Clausthal-Zellerfeld, Germany, 24 April 2017. [Google Scholar]
- VDI 4663, Blatt 1. Bewertung von Energie- und Stoffeffizienz—Methodische Anwendung des Physikalischen Optimums; Verein Deutscher Ingenieure (VDI): Düsseldorf, Germany, 2013. [Google Scholar]
- Wenzel, P.; Radgen, P.; Westermeyer, J. Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace. Energies 2021, 14, 1621. [Google Scholar] [CrossRef]
- Kerpen, L.; Schmidt, A.; Sankol, B. Differentiating the Physical Optimum from the Exergetic Evaluation of a Methane Com-bustion Process. Energies 2021, 14, 3419. [Google Scholar] [CrossRef]
- Baehr, H.D. Thermodynamik, 16th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Waide, P.; Brunner, C.U. Energy-Efficiency Policy Opportunities for Electric Motor-Driven Systems—Working Paper; International Energy Agency: Paris, France, 2011. [Google Scholar]
- Cerbe, G.; Lendt, B. Grundlagen der Gastechnik, 8th ed.; Hanser Fachbuchverlag: München, Germany, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volta, D.; Weber, S.A. The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply. Energies 2021, 14, 4426. https://doi.org/10.3390/en14154426
Volta D, Weber SA. The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply. Energies. 2021; 14(15):4426. https://doi.org/10.3390/en14154426
Chicago/Turabian StyleVolta, Dirk, and Samanta A. Weber. 2021. "The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply" Energies 14, no. 15: 4426. https://doi.org/10.3390/en14154426
APA StyleVolta, D., & Weber, S. A. (2021). The Physical Optimum as an Ideal Reference Value for Balancing Thermodynamic Processes Integrating the Exergetic Evaluation by the Example of Heat Supply. Energies, 14(15), 4426. https://doi.org/10.3390/en14154426




