Quantification of Demand-Supply Balancing Capacity among Prosumers and Consumers: Community Self-Sufficiency Assessment for Energy Trading
Abstract
:1. Introduction
2. Research Background
3. Methodology
3.1. Basic Definitions
3.2. Dynamic Energy Use Behavior at the Household Level
3.3. Dynamic Energy Use Behavior and Load Profile Change at the Household Level
3.4. Battery Modeling
4. Results and Discussion
4.1. Case-Study Community Characteristics
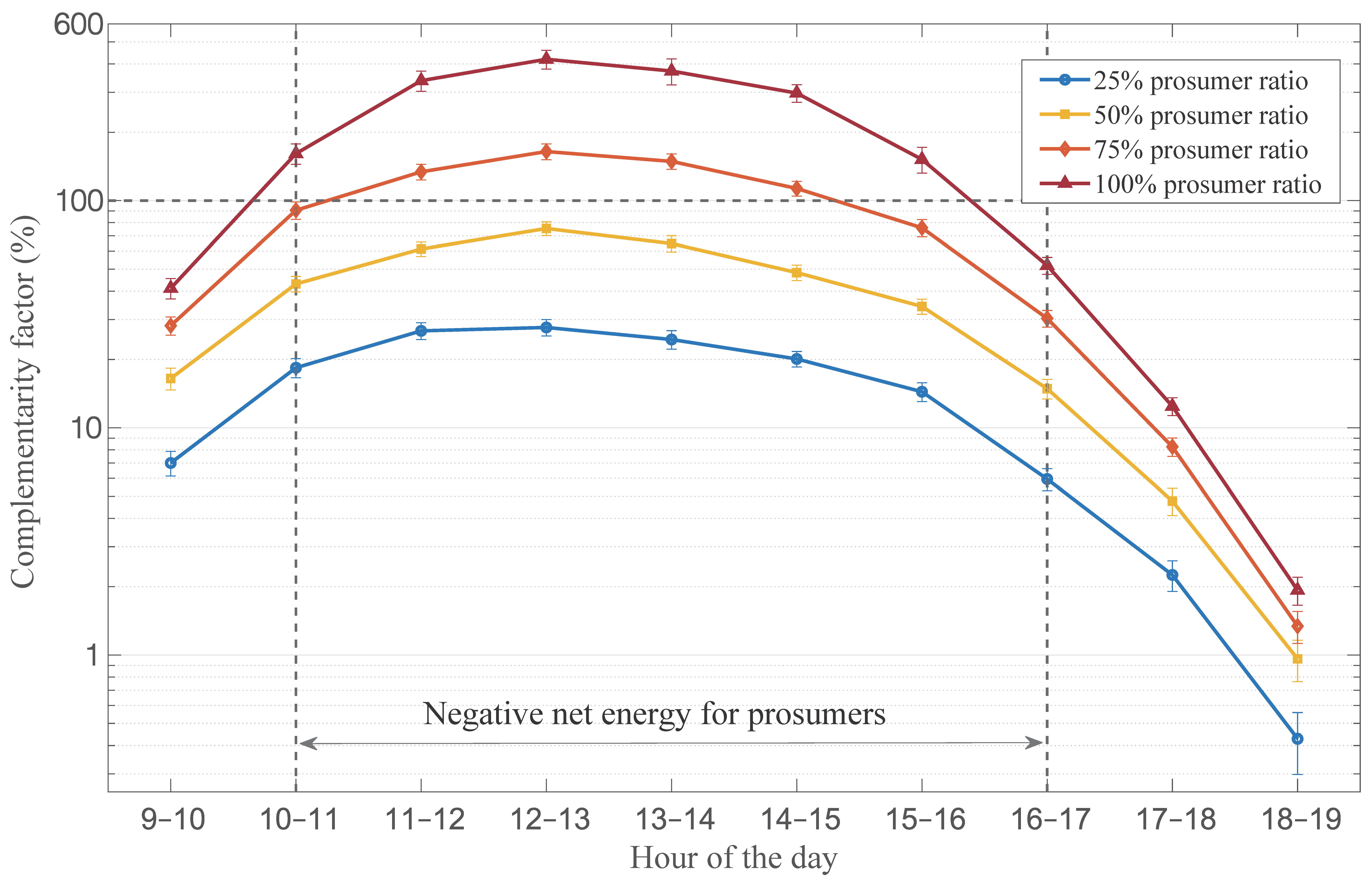
4.2. Baseline Surplus–Deficit Temporal Complementarity Quantification
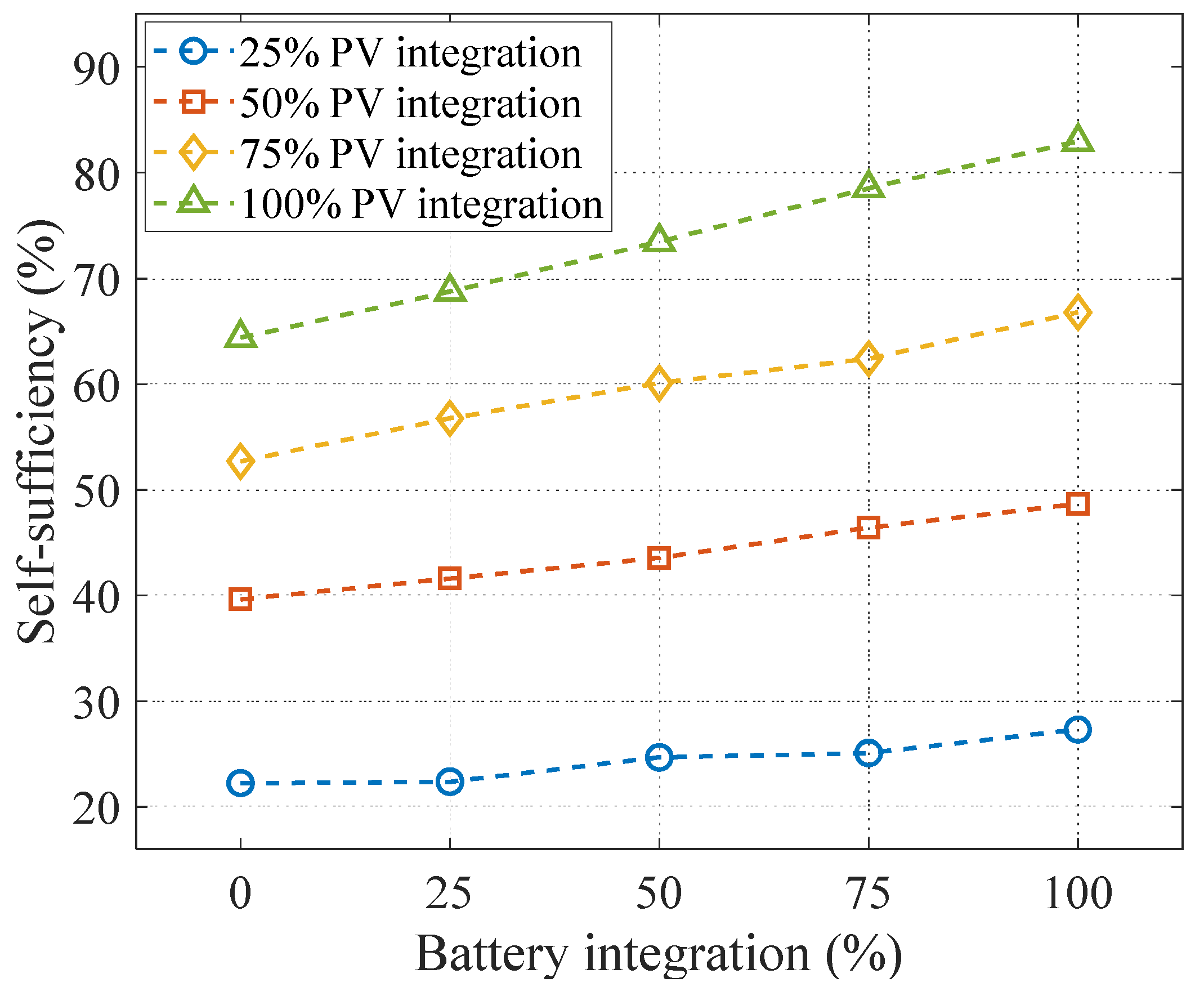
4.3. Energy Storage Integration
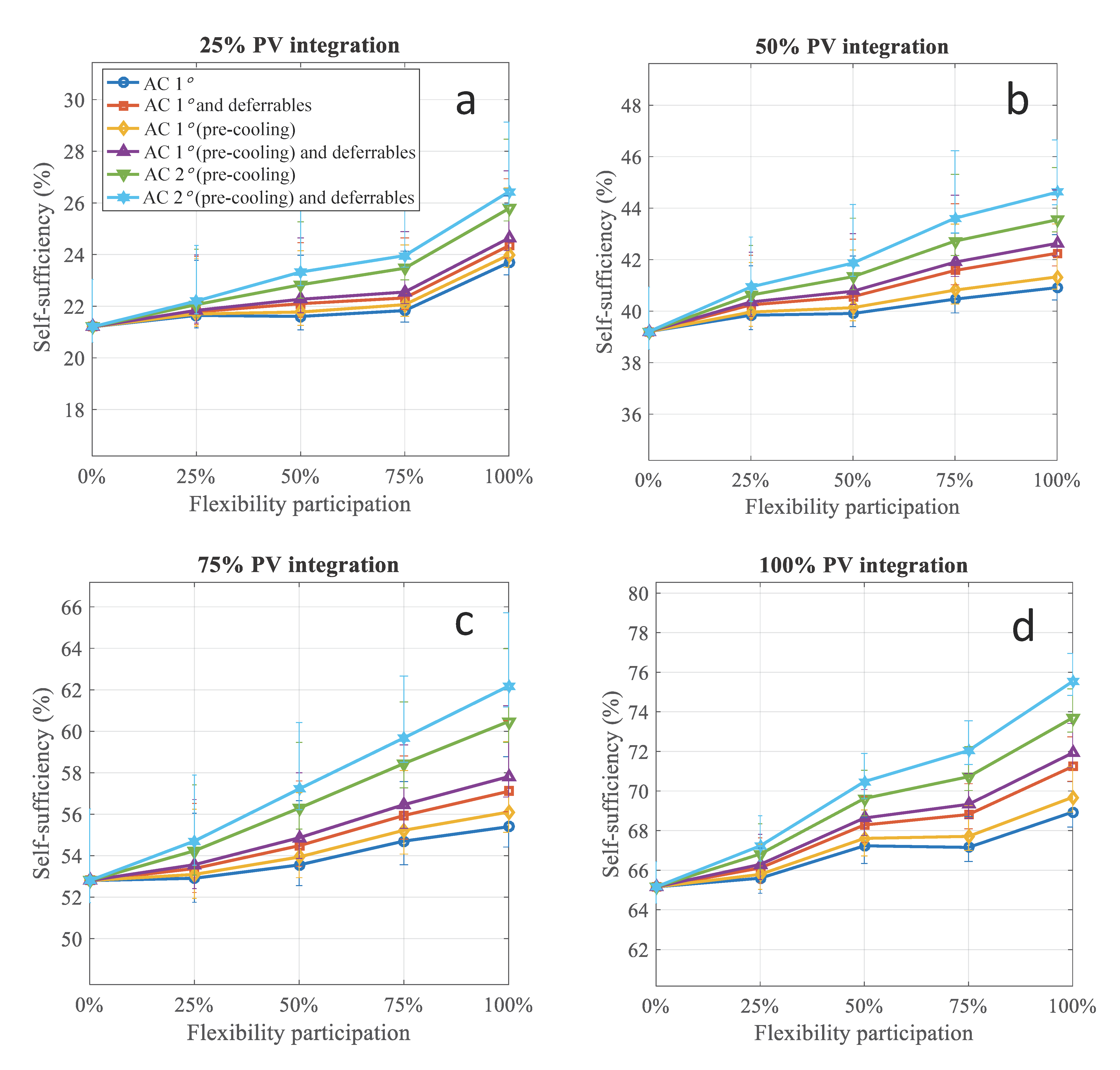
4.4. User Adaptation and Load Profile Change as Complementarity Capacity
4.5. Market Design and User Behavior Dimensions’ Impact on Self-Sufficiency
4.6. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chopra, A.; Kundra, V. A Policy Framework for the 21st Century Grid: Enabling Our Secure Energy Future; CiteSeerX: University Park, PA, USA, 2011. [Google Scholar]
- Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D.; Poor, H.V. Peer-to-peer trading in electricity networks: An overview. IEEE Trans. Smart Grid 2020, 11, 3185–3200. [Google Scholar] [CrossRef] [Green Version]
- German Renewable Energy Sources Act. Available online: https://en.wikipedia.org/wiki/German_Renewable_Energy_Sources_Act (accessed on 13 July 2021).
- Nowak, S. Trends 2013 in Photovoltaic Applications: Survey Report of Selected IEA Countries between 1992 and 2012; Technical Report IEA-PVPS T1-23; Int. Energy Agency (IEA): Paris, France, 2013; Volume 2013. [Google Scholar]
- News, I.C. As Rooftop Solar Grows, What Should the Future of Net Metering Look Like? Available online: https://insideclimatenews.org/news/11062019/rooftop-solar-net-metering-rates-renewable-energy-homeowners-utility-state-law-changes-map (accessed on 13 July 2021).
- Salom, J.; Widén, J.; Candanedo, J.; Lindberg, K.B. Analysis of grid interaction indicators in net zero-energy buildings with sub-hourly collected data. Adv. Build. Energy Res. 2015, 9, 89–106. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Hong, T.; Kang, C. Review of smart meter data analytics: Applications, methodologies, and challenges. IEEE Trans. Smart Grid 2018, 10, 3125–3148. [Google Scholar] [CrossRef] [Green Version]
- Afzalan, M.; Jazizadeh, F. Residential loads flexibility potential for demand response using energy consumption patterns and user segments. Appl. Energy 2019, 254, 113693. [Google Scholar] [CrossRef]
- Afzalan, M.; Jazizadeh, F. A Machine Learning Framework to Infer Time-of-Use of Flexible Loads: Resident Behavior Learning for Demand Response. IEEE Access 2020, 8, 111718–111730. [Google Scholar] [CrossRef]
- Afzalan, M.; Jazizadeh, F. Efficient integration of smart appliances for demand response programs. In Proceedings of the 5th Conference on Systems for Built Environments, Shenzhen, China, 7 November 2018; pp. 29–32. [Google Scholar]
- Zhang, Z.; Li, R.; Li, F. A novel peer-to-peer local electricity market for joint trading of energy and uncertainty. IEEE Trans. Smart Grid 2019, 11, 1205–1215. [Google Scholar] [CrossRef]
- Liu, T.; Tan, X.; Sun, B.; Wu, Y.; Guan, X.; Tsang, D.H. Energy management of cooperative microgrids with p2p energy sharing in distribution networks. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 410–415. [Google Scholar]
- Cui, S.; Wang, Y.-W.; Xiao, J.-W. Peer-to-peer energy sharing among smart energy buildings by distributed transaction. IEEE Trans. Smart Grid 2019, 10, 6491–6501. [Google Scholar] [CrossRef]
- Morstyn, T.; Farrell, N.; Darby, S.J.; McCulloch, M.D. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy 2018, 3, 94–101. [Google Scholar] [CrossRef]
- Andoni, M.; Robu, V.; Flynn, D.; Abram, S.; Geach, D.; Jenkins, D.; Peacock, A. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renew. Sustain. Energy Rev. 2019, 100, 143–174. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wu, J.; Long, C.; Cheng, M. Review of existing peer-to-peer energy trading projects. Energy Proc. 2017, 105, 2563–2568. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Alam, M.R.; St-Hilaire, M.; Kunz, T. Peer-to-peer energy trading among smart homes. Appl. Energy 2019, 238, 1434–1443. [Google Scholar] [CrossRef]
- An, J.; Lee, M.; Yeom, S.; Hong, T. Determining the Peer-to-Peer electricity trading price and strategy for energy prosumers and consumers within a microgrid. Appl. Energy 2020, 261, 114335. [Google Scholar] [CrossRef]
- Hahnel, U.J.; Herberz, M.; Pena-Bello, A.; Parra, D.; Brosch, T. Becoming prosumer: Revealing trading preferences and decision-making strategies in peer-to-peer energy communities. Energy Policy 2020, 137, 111098. [Google Scholar] [CrossRef]
- Morstyn, T.; McCulloch, M.D. Multiclass energy management for peer-to-peer energy trading driven by prosumer preferences. IEEE Trans. Power Syst. 2018, 34, 4005–4014. [Google Scholar] [CrossRef]
- Zepter, J.M.; Lüth, A.; del Granado, P.C.; Egging, R. Prosumer integration in wholesale electricity markets: Synergies of peer-to-peer trade and residential storage. Energy Build. 2019, 184, 163–176. [Google Scholar] [CrossRef]
- Nguyen, S.; Peng, W.; Sokolowski, P.; Alahakoon, D.; Yu, X. Optimizing rooftop photovoltaic distributed generation with battery storage for peer-to-peer energy trading. Appl. Energy 2018, 228, 2567–2580. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Cheng, M.; Al-Wakeel, A. Feasibility of peer-to-peer energy trading in low voltage electrical distribution networks. Energy Proc. 2017, 105, 2227–2232. [Google Scholar] [CrossRef]
- Lopes, R.A.; Martins, J.; Aelenei, D.; Lima, C.P. A cooperative net zero energy community to improve load matching. Renew. Energy 2016, 93, 1–13. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Kwac, J.; Flora, J.; Rajagopal, R. Household energy consumption segmentation using hourly data. IEEE Trans. Smart Grid 2014, 5, 420–430. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Linssen, J.; Stenzel, P.; Fleer, J. Techno-economic analysis of photovoltaic battery systems and the influence of different consumer load profiles. Appl. Energy 2017, 185, 2019–2025. [Google Scholar] [CrossRef]
- Quoilin, S.; Kavvadias, K.; Mercier, A.; Pappone, I.; Zucker, A. Quantifying self-consumption linked to solar home battery systems: Statistical analysis and economic assessment. Appl. Energy 2016, 182, 58–67. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S.; Teklu, Y. Load profiles of selected major household appliances and their demand response opportunities. IEEE Trans. Smart Grid 2013, 5, 742–750. [Google Scholar] [CrossRef]
- Knezović, K.; Marinelli, M.; Codani, P.; Perez, Y. Distribution grid services and flexibility provision by electric vehicles: A review of options. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar]
- Hu, M.; Xiao, F.; Wang, L. Investigation of demand response potentials of residential air conditioners in smart grids using grey-box room thermal model. Appl. Energy 2017, 207, 324–335. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F. Investigation of the demand response potentials of residential air conditioners using grey-box room thermal model. Energy Proc. 2017, 105, 2759–2765. [Google Scholar] [CrossRef]
- Tesla Powerwall. Available online: https://www.tesla.com/support/energy/powerwall/learn/how-powerwall-works (accessed on 13 July 2021).
- Barbour, E.; González, M.C. Projecting battery adoption in the prosumer era. Appl. Energy 2018, 215, 356–370. [Google Scholar] [CrossRef] [Green Version]
- Source: Pecan Street Inc., Dataport. Available online: https://www.pecanstreet.org/dataport/ (accessed on 13 July 2021).
- Afzalan, M.; Jazizadeh, F.; Wang, J. Self-configuring event detection in electricity monitoring for human-building interaction. Energy Build. 2019, 187, 95–109. [Google Scholar] [CrossRef]
- Jazizadeh, F.; Afzalan, M.; Becerik-Gerber, B.; Soibelman, L. EMBED: A dataset for energy monitoring through building electricity disaggregation. In Proceedings of the Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018; pp. 230–235. [Google Scholar]
- Klemperer, P. What really matters in auction design. J. Econ. Perspect. 2002, 16, 169–189. [Google Scholar] [CrossRef] [Green Version]
- Rosen, C.; Reinhard, M. An auction design for local reserve energy markets. Decis. Support Syst. 2013, 56, 168–179. [Google Scholar] [CrossRef]
- Block, C.; Dirk, N.; Christof, W. A market mechanism for energy allocation in micro-chp grids. In Proceedings of the 41st Annual Hawaii International Conference on System Sciences (HICSS 2008), Waikoloa, Big Island, HI, USA, 7–10 January 2008; p. 172. [Google Scholar]
- Griego, D.; Schopfer, S.; Henze, G.; Fleisch, E.; Tiefenbeck, V. Aggregation effects for microgrid communities at varying sizes and prosumer-consumer ratios. Energy Proc. 2019, 159, 346–351. [Google Scholar] [CrossRef]
- Wörner, A.M.; Ableitner, L.; Arne, M.; Felix, W.; Tiefenbeck, V. Peer-to-peer energy trading in the real world: Market design and evaluation of the user value proposition. In Proceedings of the 4th International Conference on Information Systems (ICIS 2019), Munich, Germany, 15–18 December 2019. [Google Scholar]
- Mengelkamp, E.; Johannes, G.; Kerstin, R.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Bichler, M.; Alok, G.; Wolfgang, K. Research commentary—Designing smart markets. Inf. Syst. Res. 2010, 21, 688–699. [Google Scholar] [CrossRef] [Green Version]
- Wolfgang, K.; Collins, J.; Reddy, P. Power TAC: A competitive economic simulation of the smart grid. Energy Econ. 2013, 39, 262–270. [Google Scholar]
- Koolen, D.; Liangfei, Q.; Wolfgang, K.; Alok, G. The sustainability tipping point in electricity markets. In Proceedings of the 38th International Conference on Information Systems: Transforming Society with Digital Innovation, ICIS 2017, Seoul, Korea, 10–13 December 2018. [Google Scholar]
- Mengelkamp, E.; Johannes, G.; Weinhardt, C. Decentralizing energy systems through local energy markets: The LAMP-Project. In Multikonferenz Wirtschaftsinformatik; Verlag: Berlin, Germany, 2018; pp. 924–930. [Google Scholar]
- Lacity, M.C. Addressing key challenges to making enterprise blockchain applications a reality. MIS Q. Exec. 2018, 17, 201–222. [Google Scholar]
- Heydarian, A.; McIlvennie, C.; Arpan, L.; Yousefi, S.; Syndicus, M.; Schweiker, M.; Jazizadeh, F.; Rissetto, R.; Pisello, A.L.; Piselli, C.; et al. What drives our behaviors in buildings? A review on occupant interactions with building systems from the lens of behavioral theories. Build. Environ. 2020, 179, 106928. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). PV Watts. Available online: https://pvwatts.nrel.gov/ (accessed on 13 July 2021).
- Bigerna, S.; Bollino, C.A.; Polinori, P. Renewable energy and market power in the Italian electricity market. Energy J. 2016, 37. [Google Scholar] [CrossRef]

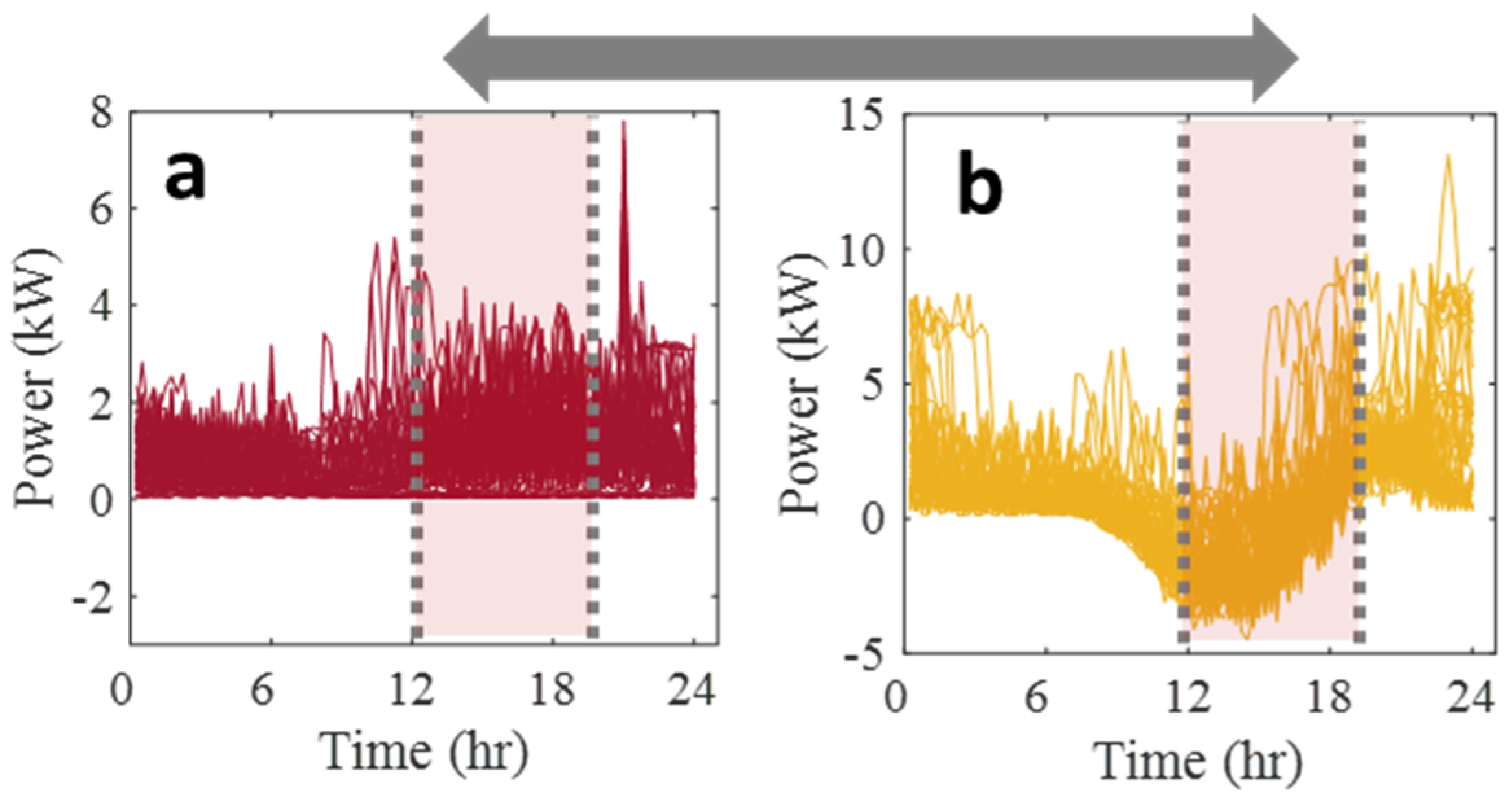
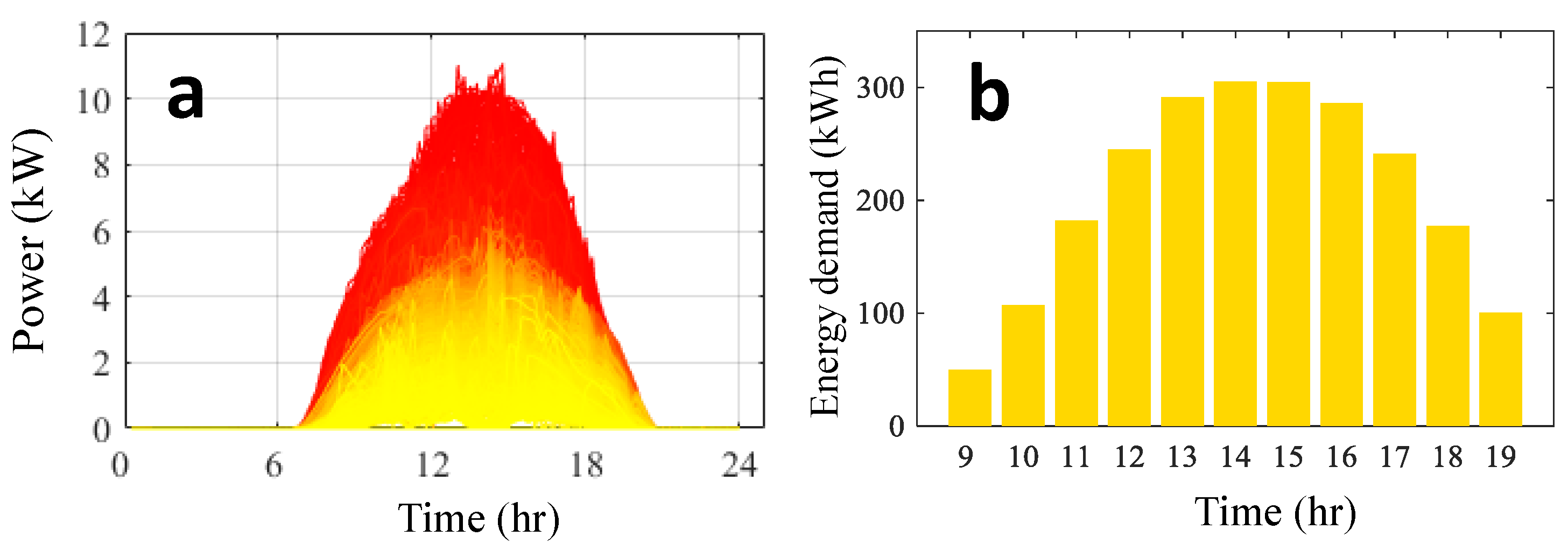
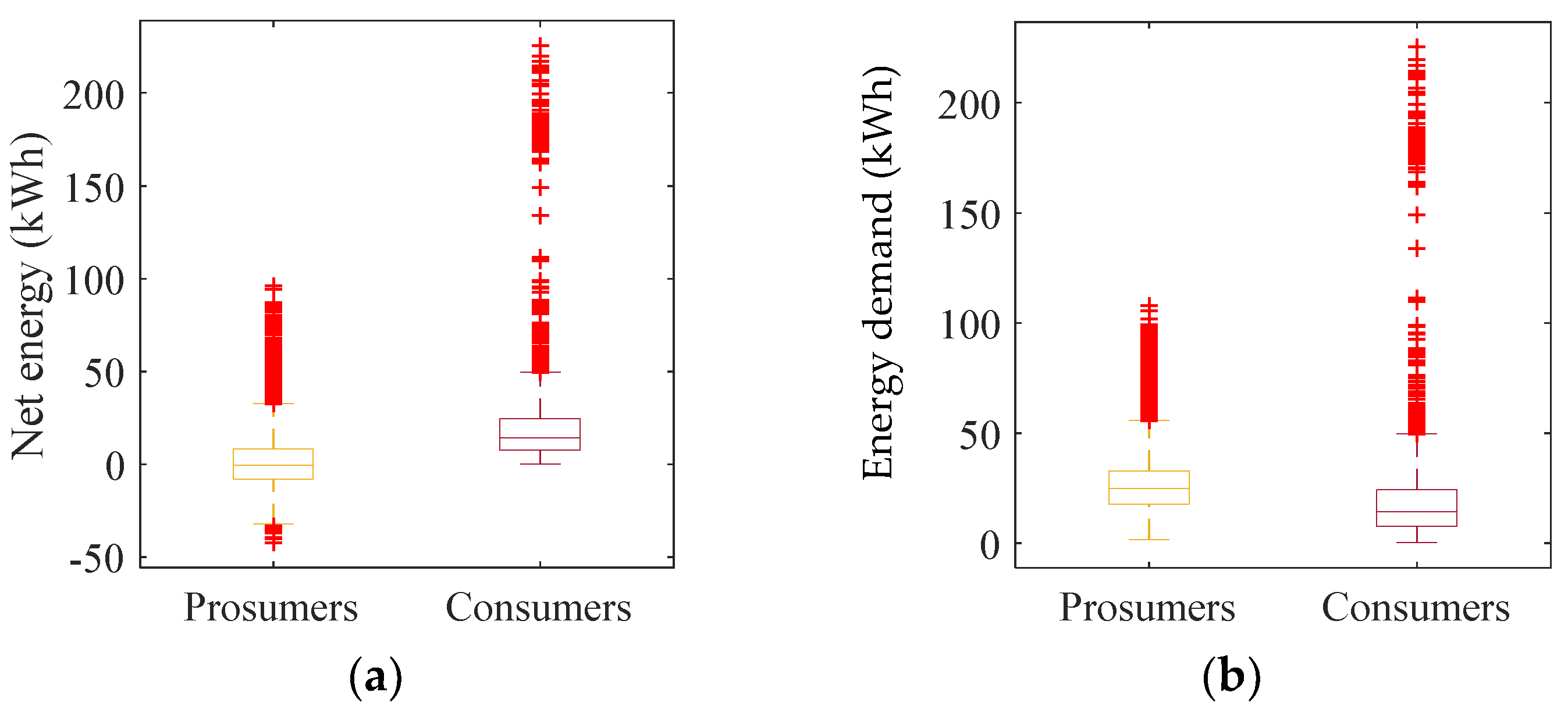
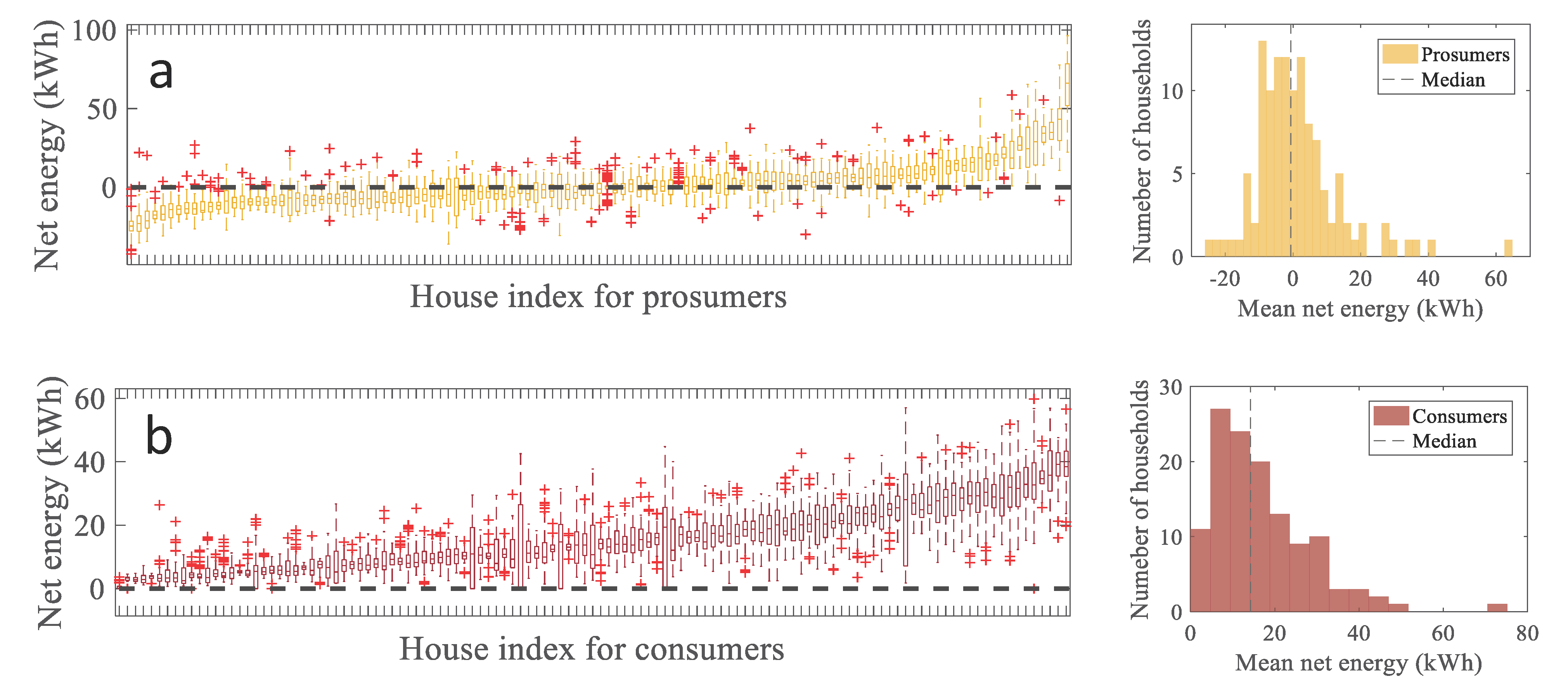
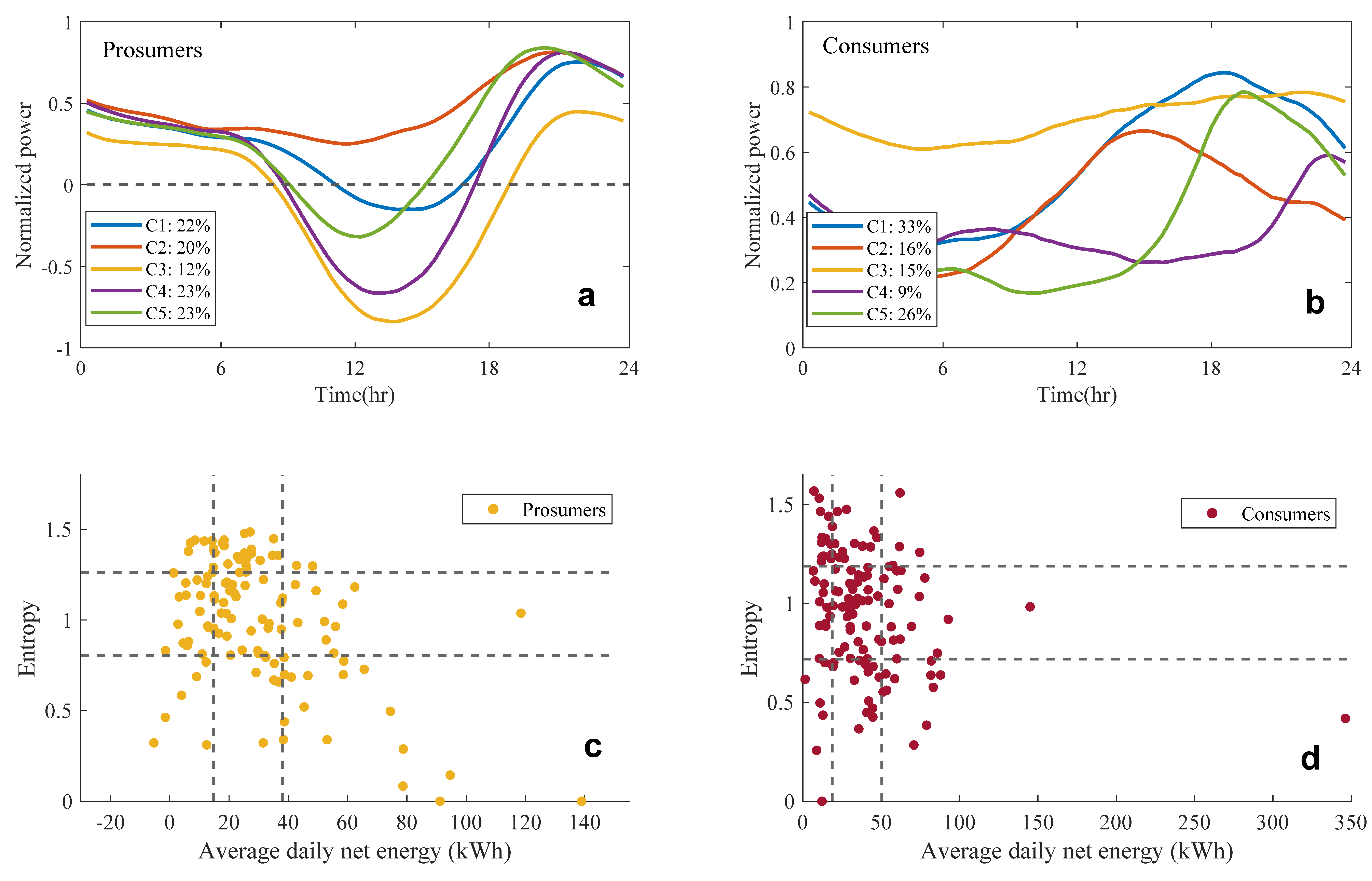
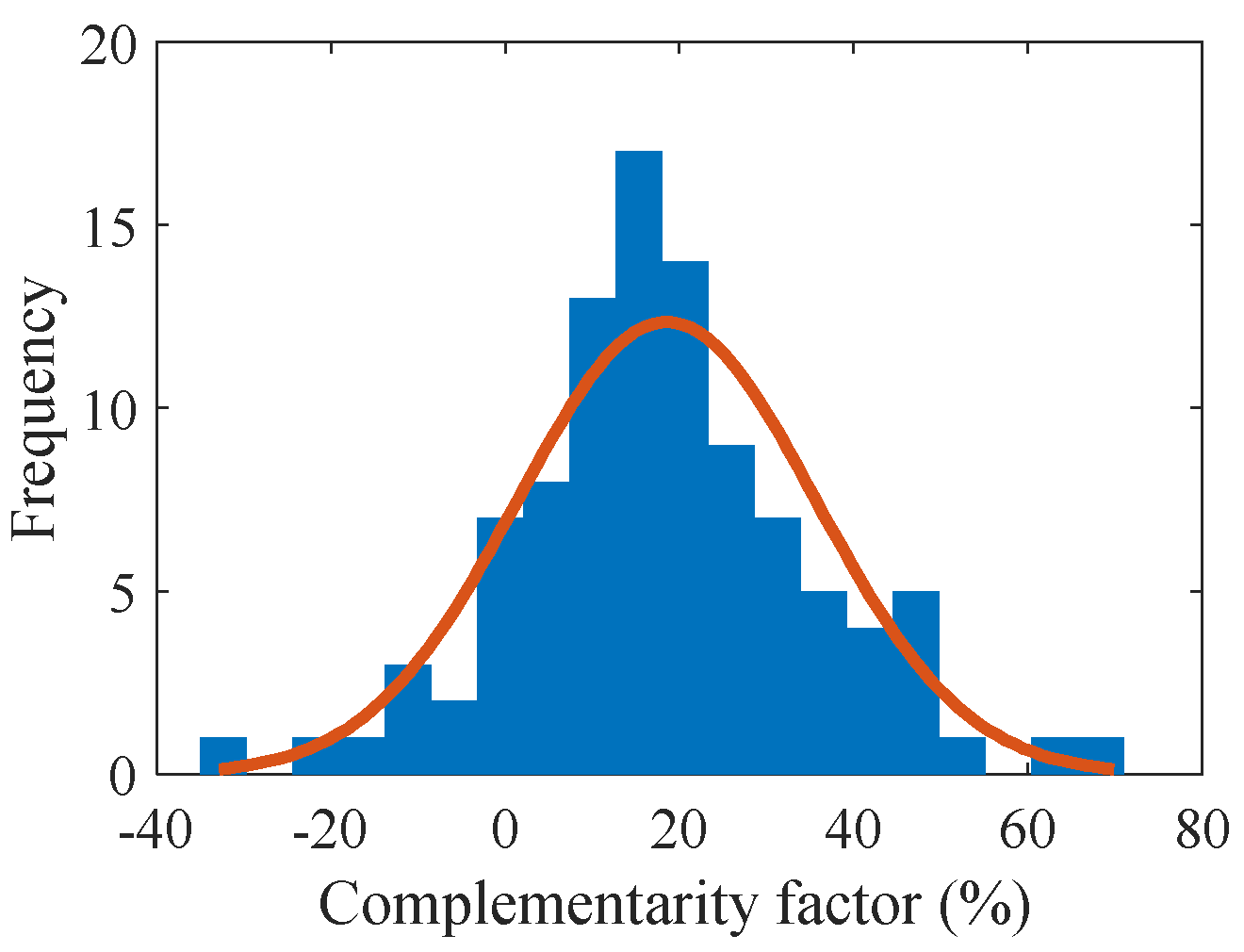

| Time of Day | Community Size | Prosumer Net Energy (kW h) *, ** | Consumer Net Energy (kW h) * | CF (%) * |
|---|---|---|---|---|
| 9 a.m.–10 a.m. | 20 | 3.9 | 10.1 | 17.2 |
| 40 | 8.6 | 22.1 | 14.8 | |
| 60 | 12.0 | 33.0 | 15.3 | |
| 80 | 16.4 | 42.6 | 15.6 | |
| 100 | 20.0 | 54.3 | 15.1 | |
| 10 a.m.–11 a.m. | 20 | −2.6 | 13.0 | 45.7 |
| 40 | −3.8 | 23.5 | 43.1 | |
| 60 | −6.1 | 36.0 | 41.5 | |
| 80 | −9.4 | 48.4 | 42.5 | |
| 100 | −10.1 | 60.3 | 41.2 | |
| 11 a.m.–12 p.m. | 20 | −6.0 | 13.7 | 62.2 |
| 40 | −13.6 | 27.5 | 63.9 | |
| 60 | −21.5 | 41.5 | 64.6 | |
| 80 | −28.2 | 54.8 | 63.7 | |
| 100 | −34.1 | 71.6 | 59.8 | |
| 12 p.m.–1 p.m. | 20 | −10.2 | 15.3 | 79.3 |
| 40 | −19.6 | 33.2 | 69.6 | |
| 60 | −29.4 | 47.1 | 71.7 | |
| 80 | −39.8 | 62.6 | 72.1 | |
| 100 | −48.9 | 78.9 | 69.9 | |
| 1 p.m.–2 p.m. | 20 | −8.5 | 18.8 | 61.4 |
| 40 | −17.3 | 35.2 | 61.8 | |
| 60 | −25.0 | 55.2 | 57.8 | |
| 80 | −32.6 | 72.1 | 57.3 | |
| 100 | −42.3 | 89.4 | 58.4 | |
| 2 p.m.–3 p.m. | 20 | −6.6 | 18.9 | 52.2 |
| 40 | −12.6 | 37.1 | 49.9 | |
| 60 | −21.1 | 58.2 | 50.2 | |
| 80 | −27.0 | 76.4 | 49.6 | |
| 100 | −32.7 | 95.6 | 48.3 | |
| 3 p.m.–4 p.m. | 20 | −1.5 | 20.2 | 32.7 |
| 40 | −3.8 | 41.5 | 31.9 | |
| 60 | −5.3 | 63.2 | 30.8 | |
| 80 | −7.6 | 81.2 | 32.1 | |
| 100 | −10.0 | 103.2 | 31.6 | |
| 4 p.m.–5 p.m. | 20 | 5.6 | 20.7 | 16.2 |
| 40 | 9.0 | 44.8 | 16.1 | |
| 60 | 17.5 | 64.8 | 15.0 | |
| 80 | 22.4 | 86.9 | 15.2 | |
| 100 | 27.4 | 109.1 | 15.2 | |
| 5 p.m.–6 p.m. | 20 | 14.3 | 23.3 | 4.9 |
| 40 | 29.4 | 48.1 | 4.5 | |
| 60 | 42.9 | 70.7 | 4.6 | |
| 80 | 57.8 | 94.9 | 4.6 | |
| 100 | 71.1 | 117.2 | 4.8 | |
| 6 p.m.–7 p.m. | 20 | 23.8 | 25.2 | 0.8 |
| 40 | 48.0 | 51.4 | 0.8 | |
| 60 | 70.0 | 75.6 | 0.9 | |
| 80 | 94.1 | 101.0 | 0.9 | |
| 100 | 117.9 | 125.3 | 0.9 | |
| Average | 35.6 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afzalan, M.; Jazizadeh, F. Quantification of Demand-Supply Balancing Capacity among Prosumers and Consumers: Community Self-Sufficiency Assessment for Energy Trading. Energies 2021, 14, 4318. https://doi.org/10.3390/en14144318
Afzalan M, Jazizadeh F. Quantification of Demand-Supply Balancing Capacity among Prosumers and Consumers: Community Self-Sufficiency Assessment for Energy Trading. Energies. 2021; 14(14):4318. https://doi.org/10.3390/en14144318
Chicago/Turabian StyleAfzalan, Milad, and Farrokh Jazizadeh. 2021. "Quantification of Demand-Supply Balancing Capacity among Prosumers and Consumers: Community Self-Sufficiency Assessment for Energy Trading" Energies 14, no. 14: 4318. https://doi.org/10.3390/en14144318
APA StyleAfzalan, M., & Jazizadeh, F. (2021). Quantification of Demand-Supply Balancing Capacity among Prosumers and Consumers: Community Self-Sufficiency Assessment for Energy Trading. Energies, 14(14), 4318. https://doi.org/10.3390/en14144318






