Drying and Heating Processes in Arbitrarily Shaped Clay Materials Using Lumped Phenomenological Modeling
Abstract
:1. Introduction
2. Methodology
2.1. The Physical Problem and Geometry
2.2. Mathematical Modeling
- (a)
- The solid is homogeneous and with constant thermophysical properties;
- (b)
- Moisture content and temperature distributions inside the brick are uniform along the drying process;
- (c)
- Drying process occurs by heat and mass diffusion inside the solid and heat and mass convection and evaporation occur on its surface;
- (d)
- Dimensions of the brick are constant along the drying process.
2.2.1. Mass Conservation Equation
2.2.2. Thermal Energy Conservation Equation
2.3. Applications to Drying of Industrial Ceramic Bricks
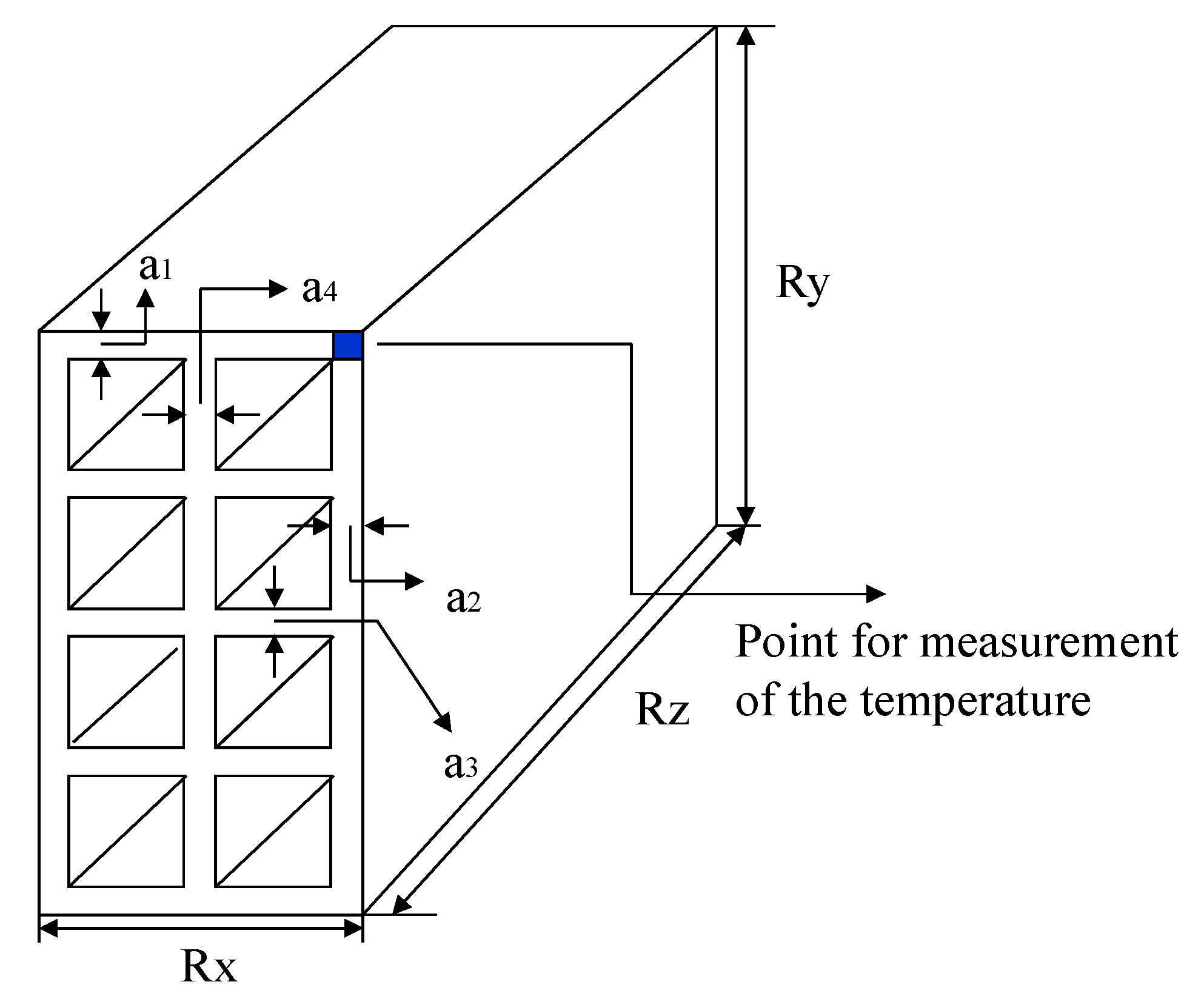
2.3.1. Volume and Surface Area of the Brick
2.3.2. Thermophysical Properties of Air and Water
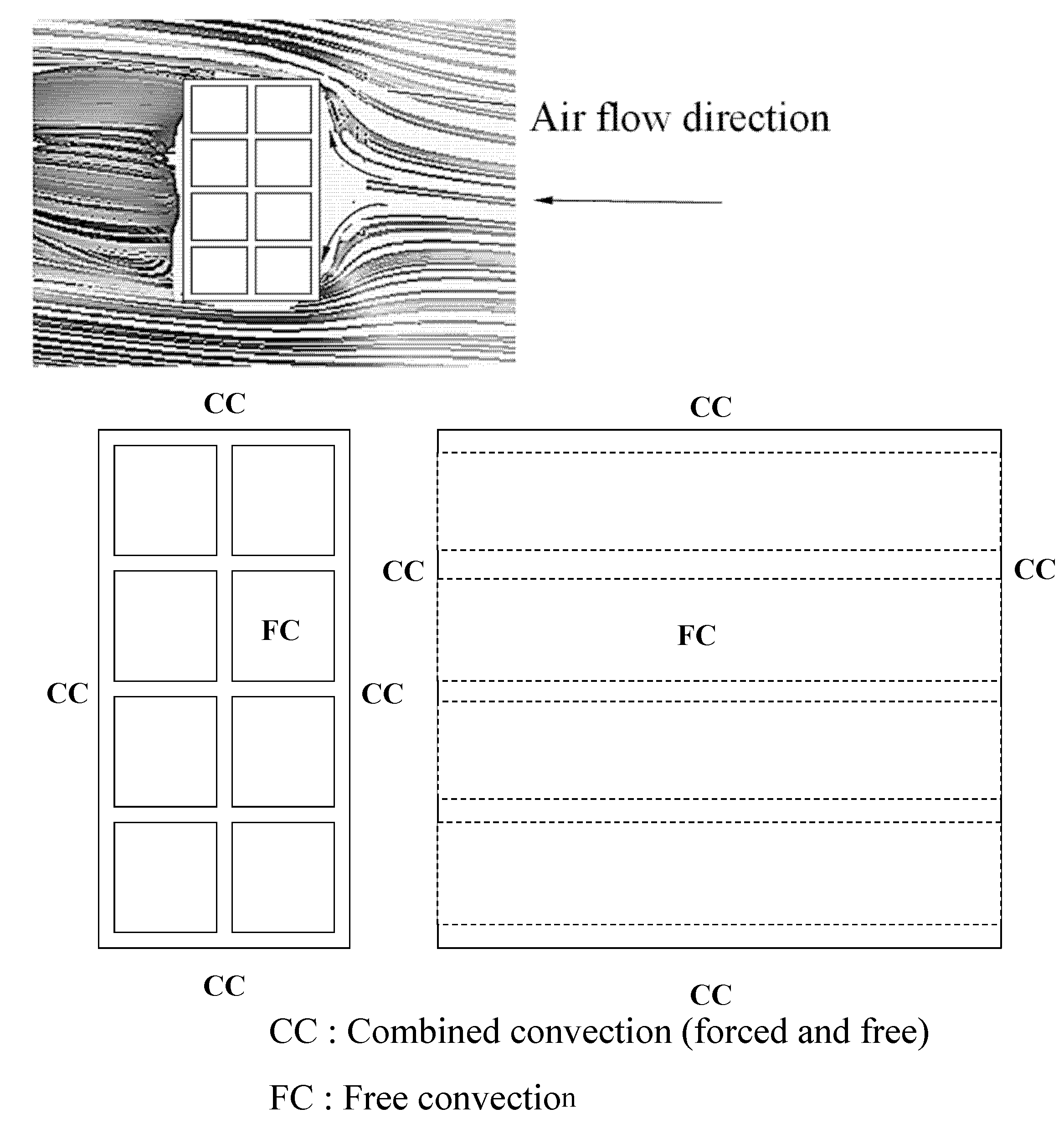
2.3.3. Estimation of Convective Heat and Mass Transfer Coefficients
Natural Convection
Forced Convection
Combined Natural and Forced Convection
2.3.4. Cases Studied
Validation
- Initially, dimensions, mass, brick temperature, ambient temperature and relative humidity were measured.
- Following that, the bricks were placed inside the oven where drying was carried out. In this process, air temperature inside the oven was established at 100°C through the temperature controller.
- At previously established time intervals, the brick was withdrawn from the oven, making it possible to measure its temperature, mass and dimensions. In principle, measurements were made every 10 min for up to 30 min. Then, the measurements were made every 30 min, with the next measurements being made every 60 min until the mass was approximately constant.
- Soon after, the sample was subjected to drying for 24 h to obtain the equilibrium mass, and then for another 24 h, to obtain the dry mass.
Studied Cases
3. Results and Discussion
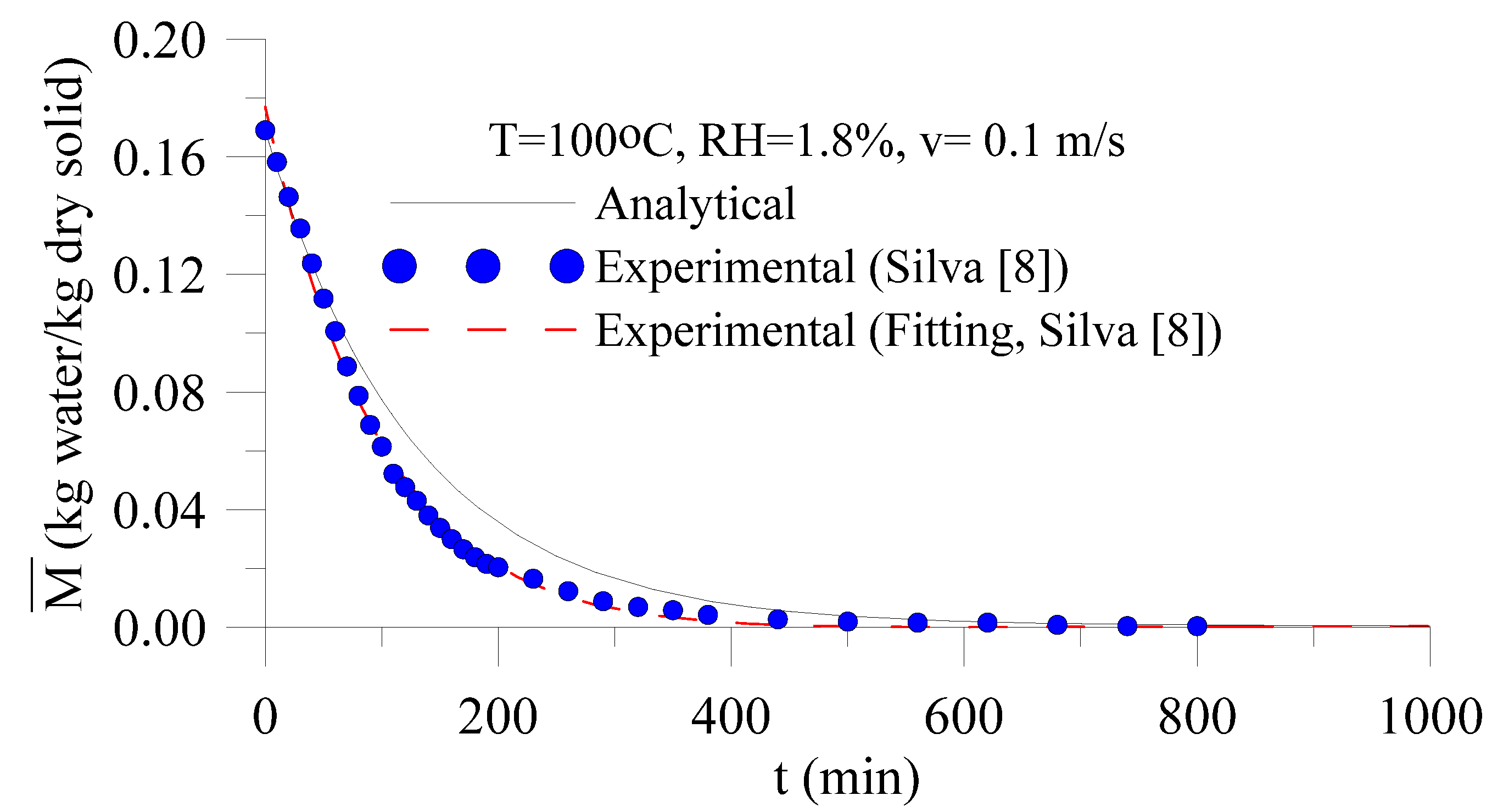
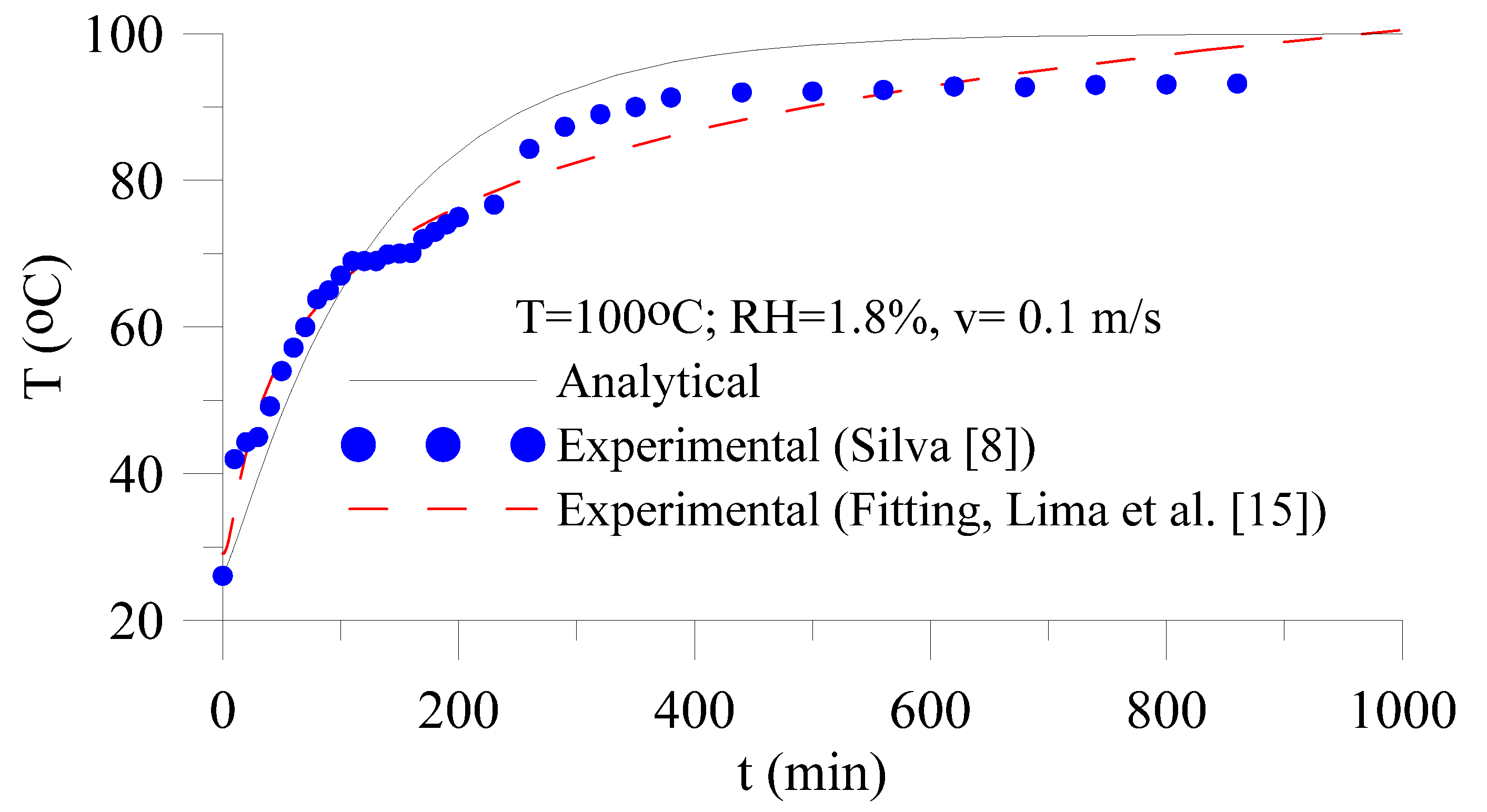
3.1. Validation
3.2. Analysis of the Drying Process
3.2.1. Effect of Relative Humidity of Drying Air
3.2.2. Effect of Drying Air Speed
3.3. Limitations of the Proposed Model
- (a)
- In physical situations involving the effect of moisture removal on solid heating (simultaneous heat and mass transport);
- (b)
- In physical situations involving heterogeneous solids;
- (c)
- It does not allow for the determination of temperature gradients and the moisture content inside the material; therefore, analysis of internal hydric and thermal stresses during the drying process is not possible.
4. Conclusions
- (a)
- The phenomenological mathematical modelling based on a lumped analysis to predict the mass and heat transfers in hollow ceramic bricks, was adequate, with small deviations from the experimental data on the average moisture content and temperature of the product over the process;
- (b)
- The lower the relative humidity is and the higher the speed of the drying air is, the faster the brick loses moisture and raises its temperature, which can cause defects in the post-drying product, reducing its quality for the firing step;
- (c)
- The heat and mass transfer coefficients on the external surface and on the brick hole are different, being higher on the external surface, especially under a forced convection condition;
- (d)
- The convective mass transfer coefficient on the external surface of the brick varied from 1.89 × 10−7 m/s in the drying condition at 100 °C, 70% and 0.1 m/s (natural convection) up to 20.90 × 10−7 m/s at 100 °C, 70% and 8.0 m/s (combined and natural convection). The convective mass transfer coefficient in the brick hole varied from 1.83 × 10−7 m/s in the drying condition at 100 °C, 20% and 0.1 m/s (natural convection) up to 2.30 × 10−7 m/s at 100 °C, 70% and 8.0 m/s (natural convection).
- (e)
- The convective heat transfer coefficient on the external surface of the brick varied from 4.13 W/m2K in the drying condition 100 °C, 70% and 0.1 m/s (natural convection) to 45.55 W/m2K at 100 °C, 70% and 8.0 m/s (combined and natural convection). The convective heat transfer coefficient in the brick hole varied from 3.98 W/m2K in the drying condition 100 °C, 70% and 0.1 m/s (natural convection) to 5.02 W/m2K at 100 °C, 70% and 8.0 m/s (natural convection).
- (f)
- Based on the maximum final moisture content of 3 to 4% (dry basis) after drying, commonly used in the industry, the temperature of the brick, the position of the brick with a hole perpendicular to the air flow, the drying time in these moisture content conditions and the experimental results (in terms of brick quality during drying) presented by the author of [8], T = 100 °C, RH = 50% and v = 0.1 m/s are proposed as the optimal drying conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Letters | ||
| a1, a2, a3, a4 | Dimensions of the brick holes | (m) |
| Total surface area | (m2) | |
| Lateral area | (m2) | |
| AI | Internal surface area | (m2) |
| Height of a hole | (m) | |
| Width of a hole | (m) | |
| Specific heat of the brick | (J/kgK) | |
| specific heat of the vapor phase | (J/kgK) | |
| Specific heat of the air | (J/kgK) | |
| specific heat of water in the liquid phase | (J/kgK) | |
| diffusion coefficient of water vapor in the air | (m2/s) | |
| ERMQM | Quadratic deviations for moisture content | (kg2/kg2) |
| ERMQθ | Quadratic deviations for temperature | (°C2/°C2) |
| Gr | Grashof number | (---) |
| g | Gravitational acceleration | (m/s2) |
| Latent heat of water vaporization | (J/kg) | |
| External convective heat transfer coefficients | (W/m2K) | |
| Internal convective heat transfer coefficients | (W/m2K) | |
| External convective mass transfer coefficients | (m/s) | |
| Internal convective mass transfer coefficients | (m/s) | |
| Lewis number | (---) | |
| Lc | Characteristic length | (m) |
| molecular weight of the water vapor | (kg/kmol) | |
| Generation of moisture | (kg/kg/s) | |
| Equilibrium moisture content | (kg/kg, d.b) | |
| Initial moisture content | (kg/kg, d.b) | |
| Average moisture content | (kg/kg, d.b) | |
| Molecular weight of the gas | (kg/kmol) | |
| n | Number of experimental points | (---) |
| Number of fitted parameters | (---) | |
| Nu | Nusselt number | (---) |
| Pvwb | Vapor pressure in the air at the wet bulb temperature | (Pa) |
| Pr | Prandtl number | (---) |
| Pvs | Saturation vapor pressure | (Pa) |
| Patm | Atmospheric pressure | (Pa) |
| P | pressure | (Pa) |
| Heat generation per unit volume | (W/m³) | |
| Universal constant of the gases | (J/molK) | |
| Ra | Rayleigh number | (---) |
| Re | Reynolds number | (---) |
| Rx | Width | (m] |
| Ry | Height | (m] |
| Rz | Length | (m] |
| RH | Relative humidity | (%] |
| S1 | Internal surface area | (m²] |
| S2 | Enternal surface area | (m²] |
| Variance for moisture content | (kg2/kg2) | |
| Variance for temperature | (°C2/°C2) | |
| t | Time | (s or min) |
| Tabs | Absolute temperature | (K) |
| Film temperature | (K or °C) | |
| Ts | Plate temperature | (K or °C) |
| T∞ | Fluid temperature | (K or °C) |
| Volume of the solid brick (with the holes) | (m³0 | |
| Volume of the holes | (m³) | |
| V | Volume | (m³) |
| xa | Absolute humidity of the air | (kg/kg) |
| xo | Absolute humidity of the air at the drying air temperature | (kg/kg) |
| xbu | Absolute humidity of the air at the wet bulb temperature | (kg/kg) |
| Greek Letters | ||
| Thermal diffusivity of the air | (m2/s) | |
| Thermal expansion coefficient | (K−1) | |
| Kinematic viscosity | (m2/s) | |
| Specific density of the dry solid | (kg/m3) | |
| Air density | (kg/m3) | |
| Specific density of the wet solid | (kg/m3) | |
| Instantaneous temperature | (K or °C) | |
| Temperature of the external medium | (K or °C) | |
| Initial temperature of the solid | (K or °C) | |
References
- Cabral Junior, M.; Motta, J.F.M.; Almeida, A.S.; Tanno, L.C. RMIs: Clay for red ceramic. Rocks and industrial minerals in Brazil: Uses and specifications. CETEM 2008, 2, 747–770. (In Portuguese) [Google Scholar]
- Sahu, K.M.; Singh, L.; Choudhary, S.N. Critical Review on Bricks. Int. J. Eng. Manag. Res. 2016, 6, 80–88. [Google Scholar]
- Andrade, F.A.; Al-Qureshi, H.A.; Hotza, D. Measuring the plasticity of clays: A review. Appl. Clay Sci. 2011, 51, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Brooker, D.B.; Bakker-Arkema, F.W.; Hall, C.W. Drying and Storage of Grains and Oilseeds; AVI Book: New York, NY, USA, 1992. [Google Scholar]
- Yang, J.; Lu, H.; Zhang, X.; Li, J.; Wang, W. An experimental study on solidifying municipal sewage sludge through skeleton building using cement and coal gangue. Adv. Mater. Sci. Eng. 2017, 2017, 5069581. [Google Scholar] [CrossRef] [Green Version]
- Musielak, G.; Śliwa, T. Modeling and Numerical Simulation of Clays Cracking During Drying. Dry Technol. 2015, 33, 1758–1767. [Google Scholar] [CrossRef]
- Itaya, Y.; Taniguchi, S.; Hasatani, M. A numerical study of transient deformation and stress behavior of a clay slab during Drying. Dry Technol. 1997, 15, 1–21. [Google Scholar] [CrossRef]
- Silva, J.B. Simulation and Experimentation of the Holed Ceramic Bricks Drying. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2009. [Google Scholar]
- Silva, J.B.; Almeida, G.S.; Lima, W.M.P.B.; Neves, G.A.; de Barbosa Lima, A.G. Heat and mass diffusion including shrinkage and hygrothermal stress during drying of holed ceramics bricks. Defect Diffus. Forum 2011, 312–315, 971–976. [Google Scholar] [CrossRef]
- Van der Zanden, A.J.J. Modelling and Simulating Simultaneous Liquid and Vapour Transport in Partially Sutured Porous Materials, Mathematical Modeling and Numerical Techniques in Drying Technology; Mareei Dekker Inc.: New York, NY, USA, 1997. [Google Scholar]
- Van der Zanden, A.J.J.; Schoenmakers, A.M.E.; Kerkof, P.J.A.M. Isothermal Vapour and Liquid Transport Inside Clay During Drying. Dry Technol. 1996, 14, 647–676. [Google Scholar] [CrossRef]
- Zaccaron, A.; Souza Nandi, V.; Bernardin, A.M. Fast drying for the manufacturing of clay ceramics using natural clays. J. Build. Eng. 2021, 33, 101877. [Google Scholar] [CrossRef]
- El Ouahabi, M.; El Boudour El Idrissi, H.; Daoudi, L.; El Halim, M.; Fagel, N. Moroccan clay deposits: Physico-chemical properties in view of provenance studies on ancient ceramics. Appl. Clay Sci. 2019, 172, 65–74. [Google Scholar] [CrossRef]
- Kolesnikov, G.; Gavrilov, T. Modeling the Drying of Capillary-Porous Materials in a Thin Layer: Application to the Estimation of Moisture Content in Thin-Walled Building Blocks. Appl. Sci. 2020, 10, 6953. [Google Scholar] [CrossRef]
- De Barbosa Lima, A.G.; Delgado, J.M.P.Q.; Nascimento, L.P.C.; Lima, E.S.; Oliveira, V.A.B.; Silva, A.V.; Silva, J.V. Clay ceramic materials: From fundamentals and manufacturing to drying process predictions. In Transport Processes and Separation Technologies, 1st ed.; Delgado, J.M.P.Q., Lima, A.G.B., Eds.; Springer: Cham, Switzerland, 2021; Volume 133, pp. 1–29. [Google Scholar]
- Yan, M.; Song, X.; Tian, J.; Lv, X.; Zhang, Z.; Yu, X.; Zhang, S. Construction of a New Type of Coal Moisture Control Device Based on the Characteristic of Indirect Drying Process of Coking Coal. Energies 2020, 13, 4162. [Google Scholar] [CrossRef]
- Lima, E.S.; Lima, W.M.P.B.; Lima, A.G.B.; Farias Neto, S.R.; Silva, E.G.; Oliveira, V.A.B. Advanced study to heat and mass transfer in arbitrary shape porous materials: Foundations, phenomenological lumped modeling and applications. In Transport Phenomena in Multiphase Systems, 1st ed.; Delgado, J.M.P.Q., Lima, A.G.B., Eds.; Springer: Cham, Switzerland, 2018; Volume 93, pp. 181–217. [Google Scholar]
- Araújo, M.V.; Correia, B.R.B.; Brandão, V.A.A.; Oliveira, I.R.; Santos, R.S.; Oliveira Neto, G.L.; Silva, L.P.L.; de Barbosa Lima, A.G. Convective Drying of Ceramic Bricks by CFD: Transport Phenomena and Process Parameters Analysis. Energies 2020, 13, 2073. [Google Scholar] [CrossRef] [Green Version]
- Silva, W.P.; Silva, C.M.D.P.S.; Silva, L.D.; Farias, V.S.O. Drying of clay slabs: Experimental determination and prediction by two-dimensional diffusion models. Ceram. Int. 2013, 39, 7911–7919. [Google Scholar] [CrossRef]
- Silva, A.M.V.; Delgado, J.M.P.Q.; Guimarães, A.S.; Lima, W.M.P.B.; Gomez, R.S.; Farias, R.P.; Lima, E.S.; de Barbosa Lima, A.G. Industrial Ceramic Blocks for Buildings: Clay Characterization and Drying Experimental Study. Energies 2020, 13, 2834. [Google Scholar] [CrossRef]
- Lima, W.M.P.B.; Lima, E.S.; Lima, A.R.C.; Oliveira Neto, G.L.; Oliveira, N.G.N.; Farias Neto, S.R.; de Barbosa Lima, A.G. Applying Phenomenological Lumped Models in Drying Process of Hollow Ceramic Materials. Defect Diffus. Forum 2020, 400, 135–145. [Google Scholar] [CrossRef]
- De Lemos, M.J.S. Turbulence in Porous Media: Modeling and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wana, H.; Xua, X.; Gaoa, J.J.; Lia, A. A moisture penetration depth model of building hygroscopic material. Procedia Eng. 2017, 205, 3235–3242. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, M.; Rode, C.; Chen, Z. Moisture buffering phenomenon and its impact on building energy consumption. Appl. Therm. Eng. 2017, 124, 337–345. [Google Scholar] [CrossRef]
- Incropera, F.P.; de Witt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Pakowski, Z.; Bartczak, Z.; Strumillo, C.; Stenstrom, S. Evaluation of equations approximating thermodynamic and transport properties of water, steam and air for use in CAD of drying processes. Dry Technol. 1991, 9, 753–773. [Google Scholar] [CrossRef]
- Jumah, R.Y.; Mujumdar, A.S.; Raghavan, G.S.V. A mathematical model for constantand intermittent batch drying of grains in a novel rotating jet spouted bed. Dry Technol. 1996, 14, 765–802. [Google Scholar]
- Çengel, Y.A. Heat and Mass Transfer: A Practical Approach; McGraw Hill: Boston, MA, USA, 2007. [Google Scholar]
- Figliola, R.S.; Beasley, D.E. Theory and Design for Mechanical Measurements; Wiley: New York, NY, USA, 1995. [Google Scholar]


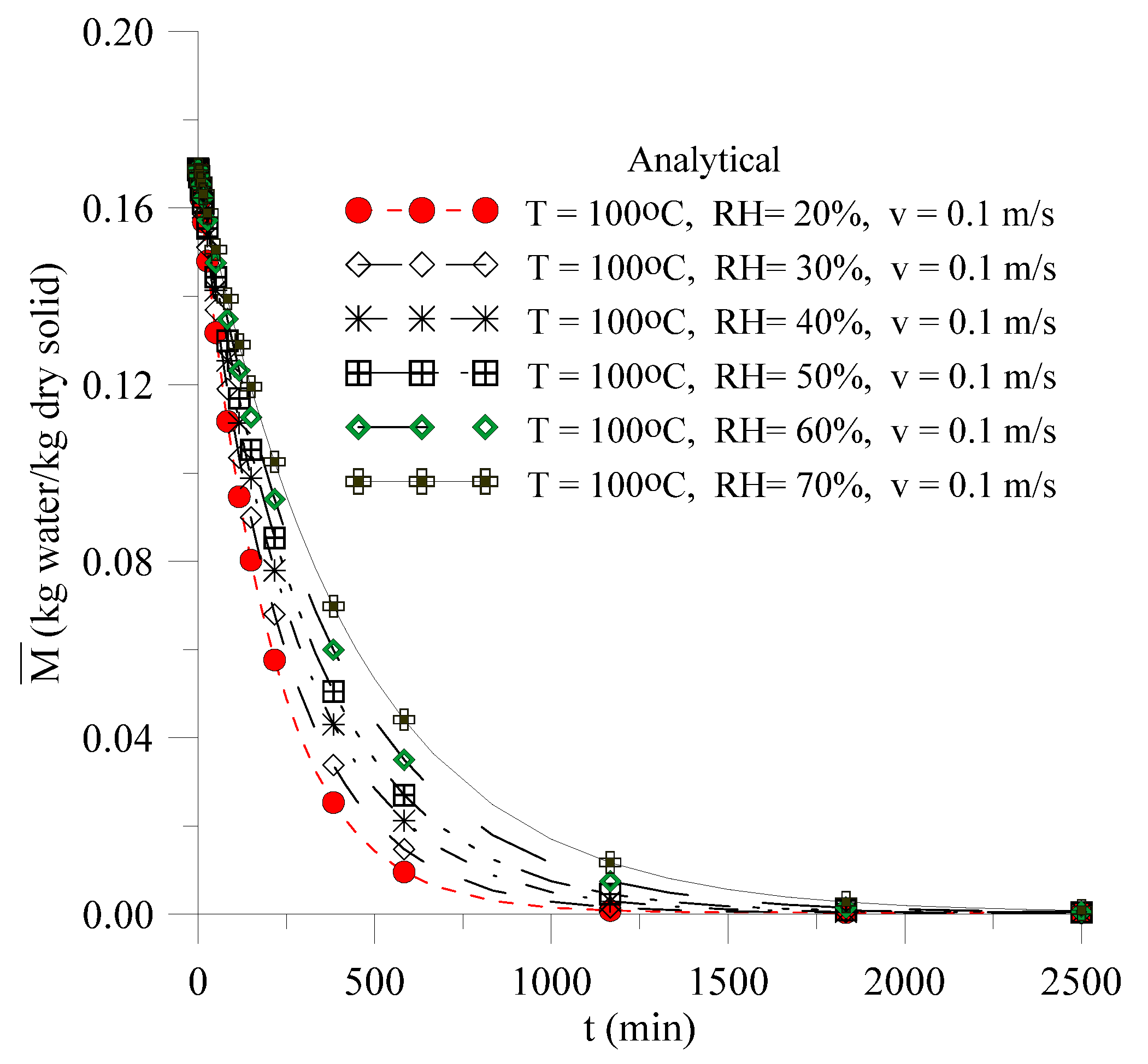
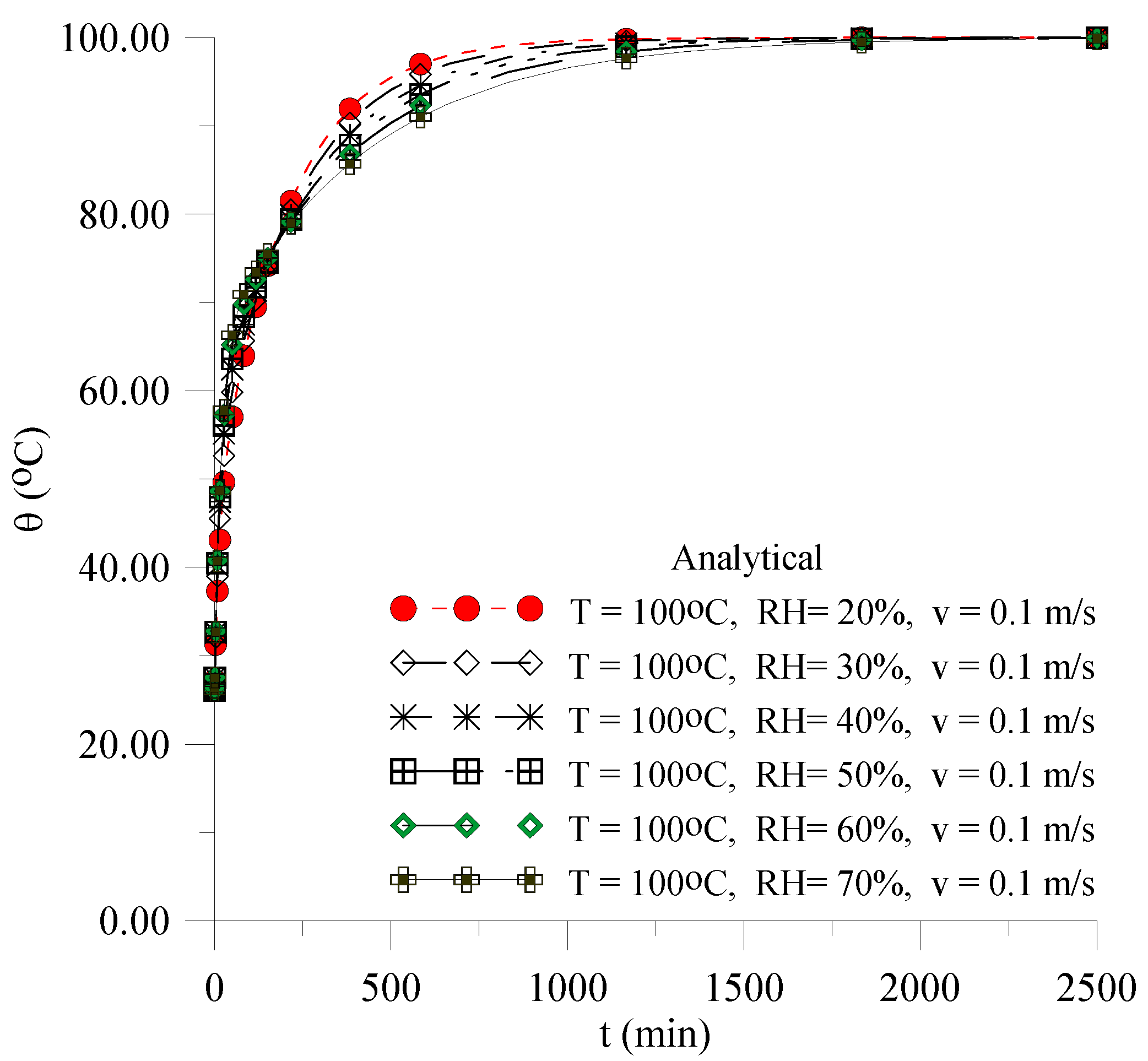
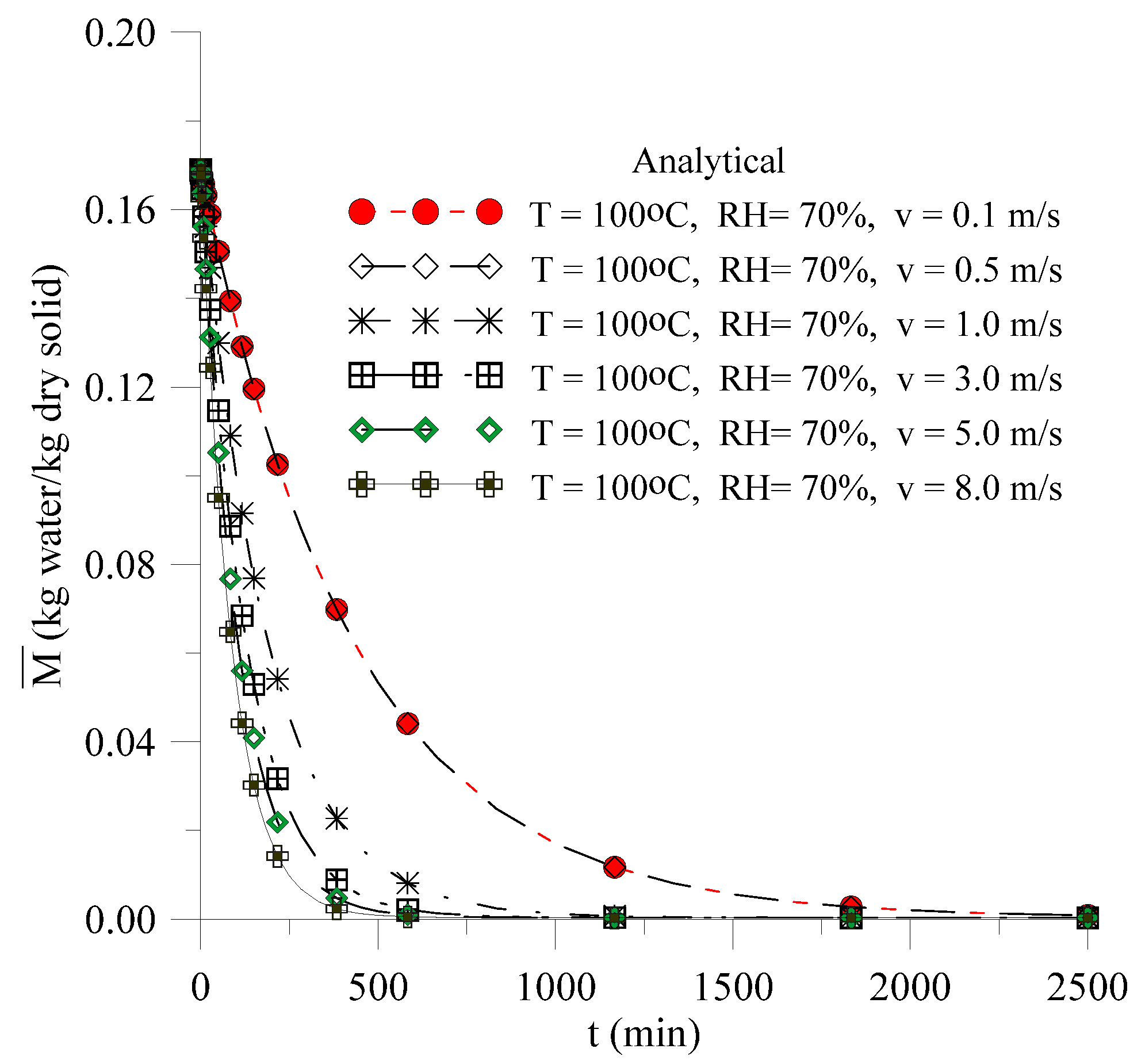

| T (°C) | Parameters | R | Proportion of Variance | |||
|---|---|---|---|---|---|---|
| A1 (-) | k1 (min−1) | A2 (-) | k2 (min−1) | |||
| 100 | 4.875507 | −0.008383 | −3.827964 | −0.007881 | 0.998297496 | 0.996597890 |
| T (°C) | Parameters | R | Proportion of Variance | |||
|---|---|---|---|---|---|---|
| B1 (°C) | B2 (°C/Log10(min)) | B3 (min) | k3 (-) | |||
| 100 | −2.86969 | 15.41788 | 118.38213 | 2.234665 | 0.984632771 | 0.969501694 |
| Air | Brick | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T (°C) | RH (%) | v (m/s) | Rx (mm) | Ry (mm) | Rz (mm) | a1 (mm) | a2 (mm) | a3 (mm) | a4 (mm) |
| 100 | 1.8 | 0.10 | 92.8 | 198.0 | 202.0 | 11.7 | 9.41 | 8.74 | 8.0 |
| Air | Brick | t (h) | ||||
|---|---|---|---|---|---|---|
| T (°C) | Mo (d.b.) | Mf (d.b.) | Me (d.b.) | θ0 (°C) | θf (°C) | |
| 100 | 0.16903 | 0.00038 | 0.00038 | 26.1 | 93.2 | 12.3 |
| Brick | ||||||
|---|---|---|---|---|---|---|
| k (W/mK) | ρu (kg/m3) | ρs (kg/m3) | cp (J/kgK) | S1 (mm2) | S2 (mm2) | V (mm3) |
| 0.833 | 1754.88 | 1889.95 | 545.00 | 134,651.775 | 226,514.720 | 1,734,026.095 |
| Case | Air | ||||
|---|---|---|---|---|---|
| RH (%) | v (m/s) | Twb (°C) | x0 (kg/kg) | ||
| 1 | 100 | 20 | 0.1 | 62.46 | 0.15550 |
| 2 | 100 | 30 | 0.1 | 70.48 | 0.26660 |
| 3 | 100 | 40 | 0.1 | 76.76 | 0.41470 |
| 4 | 100 | 50 | 0.1 | 81.98 | 0.62210 |
| 5 | 100 | 60 | 0.1 | 86.45 | 0.93330 |
| 6 | 100 | 70 | 0.1 | 90.38 | 1.45200 |
| 7 | 100 | 70 | 0.5 | 90.38 | 1.45200 |
| 8 | 100 | 70 | 1.0 | 90.38 | 1.45200 |
| 9 | 100 | 70 | 3.0 | 90.38 | 1.45200 |
| 10 | 100 | 70 | 5.0 | 90.38 | 1.45200 |
| 11 | 100 | 70 | 8.0 | 90.38 | 1.45200 |
| Drying Air Condition | Mass Transfer Coefficient | Heat Transfer Coefficient | Gr/Re2 (-) | ||||
|---|---|---|---|---|---|---|---|
| T (°C) | RH (%) | v (m/s) | hm1 (m/s) | hm2 (m/s) | hc1 (W/m2K) | hc2 (W/m2K) | |
| 100 | 20 | 0.1 | 4.10 × 10−7 | 3.92 × 10−7 | 5.91 | 5.66 | 6037.75 |
| 100 | 30 | 0.1 | 3.46 × 10−7 | 3.32 × 10−7 | 5.53 | 5.31 | 4694.73 |
| 100 | 40 | 0.1 | 2.94 × 10−7 | 2.83 × 10−7 | 5.19 | 4.99 | 3663.88 |
| 100 | 50 | 0.1 | 2.59 × 10−7 | 2.50 × 10−7 | 4.85 | 4.67 | 2820.57 |
| 100 | 60 | 0.1 | 2.22 × 10−7 | 2.14 × 10−7 | 4.50 | 4.34 | 2107.97 |
| 100 | 70 | 0.1 | 1.89 × 10−7 | 1.83 × 10−7 | 4.13 | 3.98 | 1488.59 |
| Drying Air Condition | Mass Transfer Coefficient | Heat Transfer Coefficient | Gr/Re2 (-) | ||||
|---|---|---|---|---|---|---|---|
| T (°C) | RH (%) | v (m/s) | hm1 (m/s) | hm2 (m/s) | hc1 (W/m2K) | hc2 (W/m2K) | |
| 100 | 70 | 0.1 | 1.89 × 10−7 | 1.83 × 10−7 | 4.13 | 3.98 | 1488.59 |
| 100 | 70 | 0.5 | 1.89 × 10−7 | 1.83 × 10−7 | 4.13 | 3.98 | 59.54 |
| 100 | 70 | 1.0 | 7.44 × 10−7 | 2.30 × 10−7 | 16.22 | 5.02 | 14.89 |
| 100 | 70 | 3.0 | 12.81 × 10−7 | 2.30 × 10−7 | 27.93 | 5.02 | 1.65 |
| 100 | 70 | 5.0 | 16.53 × 10−7 | 2.30 × 10−7 | 36.02 | 5.02 | 0.59 |
| 100 | 70 | 8.0 | 20.90 × 10−7 | 2.30 × 10−7 | 45.55 | 5.02 | 0.23 |
| Case | Air | Brick | ||||
|---|---|---|---|---|---|---|
| RH (%) | v (m/s) | M (kg/kg) | θ (°C) | t (min) | ||
| 1 | 100 | 20 | 0.1 | 0.03239 | 89.65 | 333.33 |
| 2 | 100 | 30 | 0.1 | 0.03385 | 90.34 | 383.33 |
| 3 | 100 | 40 | 0.1 | 0.03398 | 91.31 | 450.00 |
| 4 | 100 | 50 | 0.1 | 0.03502 | 91.60 | 500.00 |
| 5 | 100 | 60 | 0.1 | 0.03502 | 92.30 | 583.33 |
| 6 | 100 | 70 | 0.1 | 0.03644 | 92.58 | 666.67 |
| 7 | 100 | 70 | 0.5 | 0.03644 | 92.58 | 666.67 |
| 8 | 100 | 70 | 1.0 | 0.03825 | 92.21 | 283.33 |
| 9 | 100 | 70 | 3.0 | 0.03167 | 93.56 | 216.67 |
| 10 | 100 | 70 | 5.0 | 0.03782 | 92.30 | 158.33 |
| 11 | 100 | 70 | 8.0 | 0.03024 | 93.86 | 150.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lima, E.S.; Delgado, J.M.P.Q.; Guimarães, A.S.; Lima, W.M.P.B.; Santos, I.B.; Gomes, J.P.; Santos, R.S.; Vilela, A.F.; Viana, A.D.; Almeida, G.S.; et al. Drying and Heating Processes in Arbitrarily Shaped Clay Materials Using Lumped Phenomenological Modeling. Energies 2021, 14, 4294. https://doi.org/10.3390/en14144294
Lima ES, Delgado JMPQ, Guimarães AS, Lima WMPB, Santos IB, Gomes JP, Santos RS, Vilela AF, Viana AD, Almeida GS, et al. Drying and Heating Processes in Arbitrarily Shaped Clay Materials Using Lumped Phenomenological Modeling. Energies. 2021; 14(14):4294. https://doi.org/10.3390/en14144294
Chicago/Turabian StyleLima, Elisiane S., João M. P. Q. Delgado, Ana S. Guimarães, Wanderson M. P. B. Lima, Ivonete B. Santos, Josivanda P. Gomes, Rosilda S. Santos, Anderson F. Vilela, Arianne D. Viana, Genival S. Almeida, and et al. 2021. "Drying and Heating Processes in Arbitrarily Shaped Clay Materials Using Lumped Phenomenological Modeling" Energies 14, no. 14: 4294. https://doi.org/10.3390/en14144294
APA StyleLima, E. S., Delgado, J. M. P. Q., Guimarães, A. S., Lima, W. M. P. B., Santos, I. B., Gomes, J. P., Santos, R. S., Vilela, A. F., Viana, A. D., Almeida, G. S., Lima, A. G. B., & Franco, J. E. F. (2021). Drying and Heating Processes in Arbitrarily Shaped Clay Materials Using Lumped Phenomenological Modeling. Energies, 14(14), 4294. https://doi.org/10.3390/en14144294









