A New Chaotic Artificial Bee Colony for the Risk-Constrained Economic Emission Dispatch Problem Incorporating Wind Power

Abstract

Due to the rapid increase in the consumption of electrical energy and the instability of fossil fuel prices, renewable energy, such as wind power (WP), has become increasingly economically competitive compared to other conventional energy production methods. However, the intermittent nature of wind energy creates certain challenges to the power network operation. The combined economic environmental dispatch (CEED) including WP is one of the most fundamental challenges in power system operation. Within this context, this paper presents a new attempt to solve the probabilistic CEED problem with WP penetration. The optimal WP to be incorporated in the grid is determined in such a way that the system security is within acceptable limits. The system security is described by various fuzzy membership functions in terms of the probability that power balance cannot be met. These membership functions are formulated based on the dispatcher’s attitude. This probabilistic and non-convex CEED problem is solved using a new technique combining chaos theory and artificial bee colony (ABC) technique. In this improved version of ABC (IABC), chaotic maps are used to generate initial solutions, and the random numbers involved in the standard ABC are substituted by chaotic sequences. The effectiveness of IABC is tested on two groups of benchmark functions and practical cases. The impacts of dispatcher’s attitude and risk level are investigated in the simulation section.

1. Introduction

1.1. Research Background and Related Works

Economic dispatch problem (EDP) is a static optimization problem that aims to find the optimal combination of power outputs of generating units so as to operate the power network in the most economical way [1]. This optimal distribution must obviously respect the power balance constraint and production limits of the power plants. The decision variables of the EDP are, therefore, power outputs of generating units. Generally, the generation of electricity from fossil fuels is accompanied by emission of harmful gases. Thus, emissions released by thermal units should be taken into account in the power generation scheduling of the power network. Unfortunately, the minimum fuel cost does not necessarily correspond to the minimum emissions and vice-versa [2], which is proved in various research studies [2,3,4,5]. To handle this problem, system operators are called to simultaneously consider both fuel cost and emissions in the load dispatch problem. This problem is called combined economic environmental dispatch (CEED). The purpose of CEED is to exploit thermal units with minimum production cost and minimum emissions while satisfying the total power demand and operational constraints, such as generation capacity and valve point loading effects (VPLEs) [3]. However, when VPLEs are considered, sinusoidal forms are added to the fuel cost function, and the CEED becomes highly nonlinear and non-convex. In the meantime, with the gradual exhaustion of fossil resources worldwide and the increase of the demand for energy, renewable energy, such as wind energy, has been incorporated into the existing power networks. As a matter of fact, wind energy sources have the advantage of reducing polluting gas emissions and conserving irreplaceable fuel reserves. However, this deployment of the wind power (WP) sector is not without technical problems linked to its insertion into the power network. Among other things, the difficulties imposed by the variability of wind power compromise the balance between production and consumption, the quality of energy and the network safety [4]. Therefore, when high WP penetration is included into power networks, impact of WP intermittency has to be considered in the CEED modeling. A conventional strategy based on the average values of WP is used to describe WP availability [5]. Although this method appears easy for implementation, it results in high probabilistic infeasibility coming from describing WP through the average of random variables [6].

Generally, the CEED has been formulated as a conflicting bi-objective optimization problem. Hence, the resolution of this kind of problem leads to a set of optimal solutions, called non-dominated solutions or Pareto solutions, instead of a single solution [7]. Therefore, decision makers should seek suitable strategies for extracting a compromise solution from among the Pareto solutions set. From a mathematical point of view, approaches applied for solving CEED can be classified into three categories. In the first category, fuel cost and emissions have been combined in a single objective function by the linear weighted sum or normalizing fuel cost and emissions by using price penalty factors [8,9,10]. The set of Pareto solutions may be obtained by running the selected optimization algorithm several times. The second category also converts the CEED into a single objective problem but by incorporating the emissions in the system constraints [11,12]. However, decision makers do not have any idea concerning tradeoffs between cost and emissions. The third category involves both functions simultaneously where the Pareto set is generated in one run of the opted optimization algorithm [13].

From the literature review [5,7], it was found that various optimization techniques have been applied to solve the CEED where some works have incorporated renewable energy sources in the problem. Traditional methods, such as quadratic programming [14], linear programming [15], interior point method [16], and ε-constrained technique [17], have been criticized for their sensitivity to the problem constraints and initial solutions. Moreover, these techniques are iterative and may fail to converge to the global optima.

Over the last two decades, various meta-heuristic techniques have been suggested to overcome the drawbacks of conventional methods. Meta-heuristic techniques are usually inspired by nature, whether found in physics, such as simulated annealing; in biology, such as genetic algorithms; or in ethology, such as ant colony algorithms. The most popular meta-heuristics are genetic algorithms (GA), differential evolution (DE), particle swarm optimization (PSO), artificial bee colony (ABC), tabu search (TS), simulated annealing (SA), gravitational search algorithm (GSA), firefly algorithm (FA), and invasive weed optimization (IWO). Without a doubt, various meta-heuristic algorithms have been investigated in the literature to examine the CEED problem. For instance, in [18], a GSA-based method has been proposed for minimizing the production cost. The same method has been implemented by Guvenc et al. [19] for the CEED problem, where cost and emissions have been combined in a single objective function by using price penalty factors. A version of the NSGAII algorithm, modified by adding a dynamic crowding distance, has been used to minimize simultaneously the fuel cost and emissions for static load [20]. The proposed scheme has been evaluated on various test systems. In [21], a flower pollination algorithm-based methodology was suggested for solving the CEED problem incorporating VPLE constraints. The adopted methodology has been executed on various test cases. Mason et al. [22] have proposed three variants of PSO algorithm for the issue of the dynamic economic emission dispatch (DEED). The proposed variants of PSO are the standard PSO, the PSO with avoidance of worst locations (PSO AWL), and the PSO with a gradually increasing directed neighborhood (PSO GIDN). The performances of the adopted algorithms have been tested against the NSGAII. The DEED has been solved also in [23] by using an improved version of the multi-objective evolutionary algorithm where the algorithm has been implemented on the 6-unit, 10-unit, and 14-unit systems.

At present, the incorporation of renewable energy in the CEED has become the fundamental issue in the power dispatch problems. Hence, some formulations of the CEED problem have considered the inclusion of renewable energy, such as WP and photovoltaic (PV) systems [24,25]. Jin et al. [24] have developed a model to include wind farms in the CEED problem where the stochastic output of the farm is described by the overestimation and underestimation cost of available WP. In [5], the effect of WP intermittency on the DEED results is described by a chance constraint, as suggested in a pioneering work by Liu and Xu [6]. In the same way as in [5], a chance-constraint-based model for the dynamic EDP with wind farm was investigated in [25], where the problem was converted into a deterministic optimization problem, and then, an improved version of PSO was used for its solution. Large scale WP penetration in the optimum allocation of real power generation was considered also in [26], where the random characteristics of WP was described by the Weibull distribution function, and multi-objective PSO (MOPSO) was used for the simultaneous minimization of the fuel cost and emissions.

In order to avoid security implications in power grids due to the volatility of WP, another pioneer formulation of the power dispatch with wind plant has been developed in [27]. In [27], the authors added the risk level in the dispatch problem as an objective function to be minimized. The risk level was expressed using fuzzy membership functions in terms of wind power running cost. These membership functions were employed to describe the dispatcher’s attitudes toward WP integration. Wang and Singh [28] have also applied this pioneering formulation for the economic dispatch where the PSO technique has been used for its resolution. In [29], the economic dispatch with WP was solved using a multi-objective PSO-based method, where the operational cost and risk level functions were incorporated in the problem formulation as objective functions. A fuzzy linear membership function has been suggested for the risk calculation. However, the minimization of the risk corresponds to minimum WP penetration. Therefore, it is advised to seek a trade-off between operation cost and system security [30]. In order to keep WP generation within permissible values, the probability of the power balance that cannot be met may also be taken into consideration in the problem constraints. Thus, the problem becomes more complex due to the stochastic variables and the addition of new nonlinear constraints. Moreover, the final solutions will depend on the dispatcher’s attitude. Consequently, the selection of the suitable optimization method that may be used for the resolution of this kind of problem appears to be a critical task.

Recently, the artificial bee colony (ABC) algorithm introduced by Karaboga [31] has been successfully employed for solving many issues in various engineering domains, such as in power system operation, sensor placement, and neural network training [32]. The ABC algorithm is inspired by the food tracking of honey bees. At its core, the ABC algorithm consists of four phases, which are the (i) initialization phase, (ii) employed bee phase, (iii) onlooker bee phase, and (iv) scout bee phase. All of these phases are based on random variables. According to the literature review, the ABC algorithm, similar to other stochastic-based techniques, has been criticized for its slow convergence, and it can be trapped in local optima, especially for multimodal problems with multiple optima [33]. To overcome these drawbacks linked to the ABC algorithm, various variants of ABC have been appearing during recent years [33,34,35]. Although these ABC variants have improved the performance of the standard ABC, the majority of them have failed to solve the slow convergence and the diversity issues addressed in the original algorithm. Recently, chaotic maps have been employed, together with evolutionary algorithms, to improve its performance. For instance, chaos has been inserted in the reproduction operators of GA to enhance the population diversity [36]. In [37], chaos theory has been applied to generate initial populations for DE and GA methods.

As do some other research works [33,34], this paper presents a new attempt to further improve the robustness and performance of the standard ABC algorithm. In the developed optimization technique, chaos theory is integrated into the ABC algorithm in order to improve the exploration and exploitation abilities of the classical ABC and, on the other hand, to avoid the convergence into a local optimum. This improved version of ABC (IABC) is proposed to deal with the multimodal CEED problem including wind farms.

1.2. Contributions

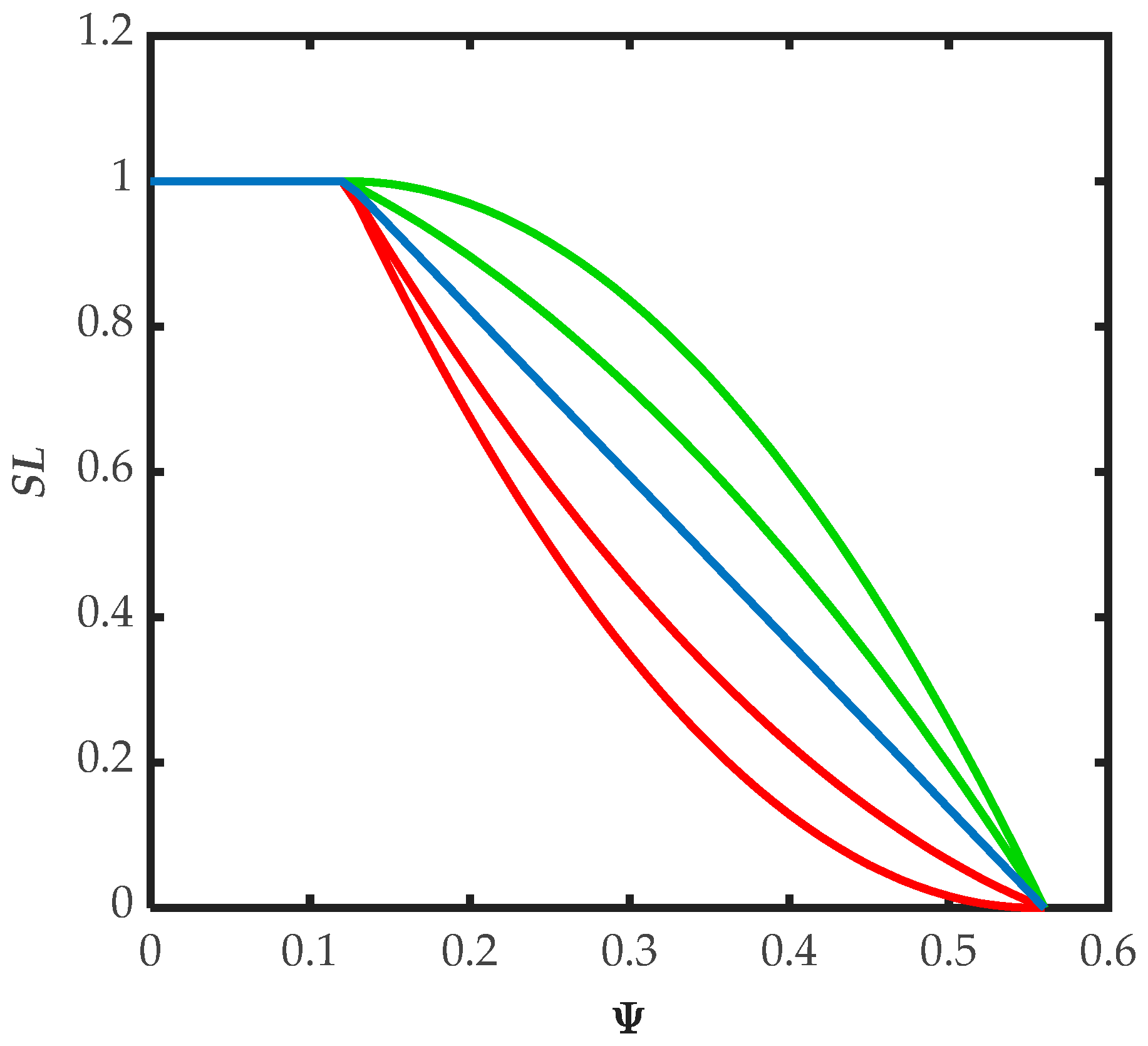
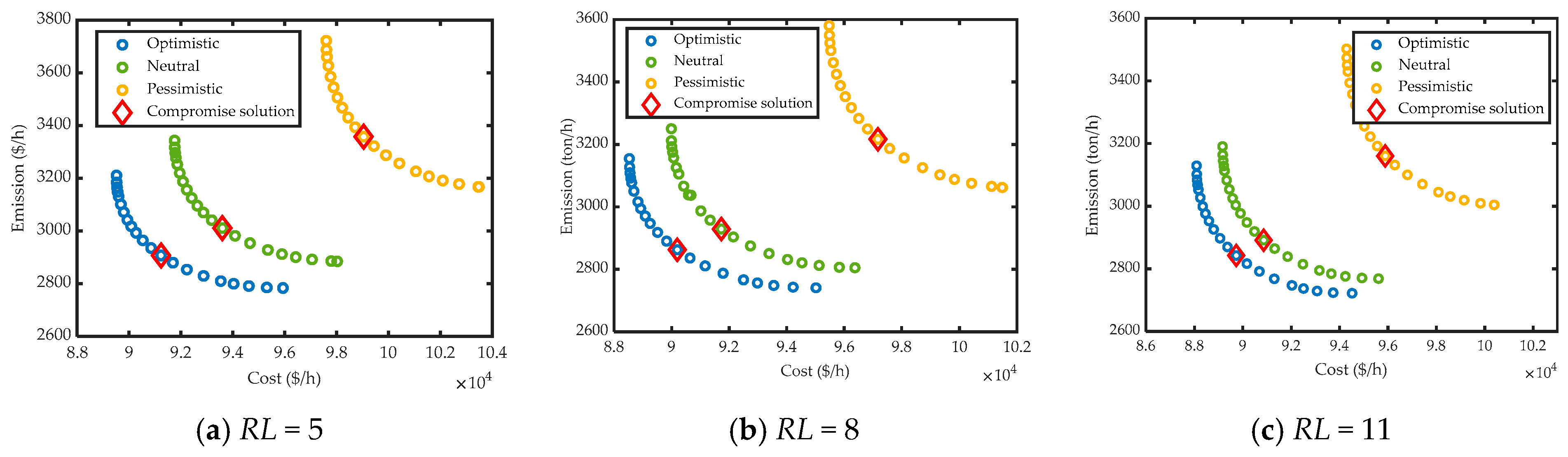
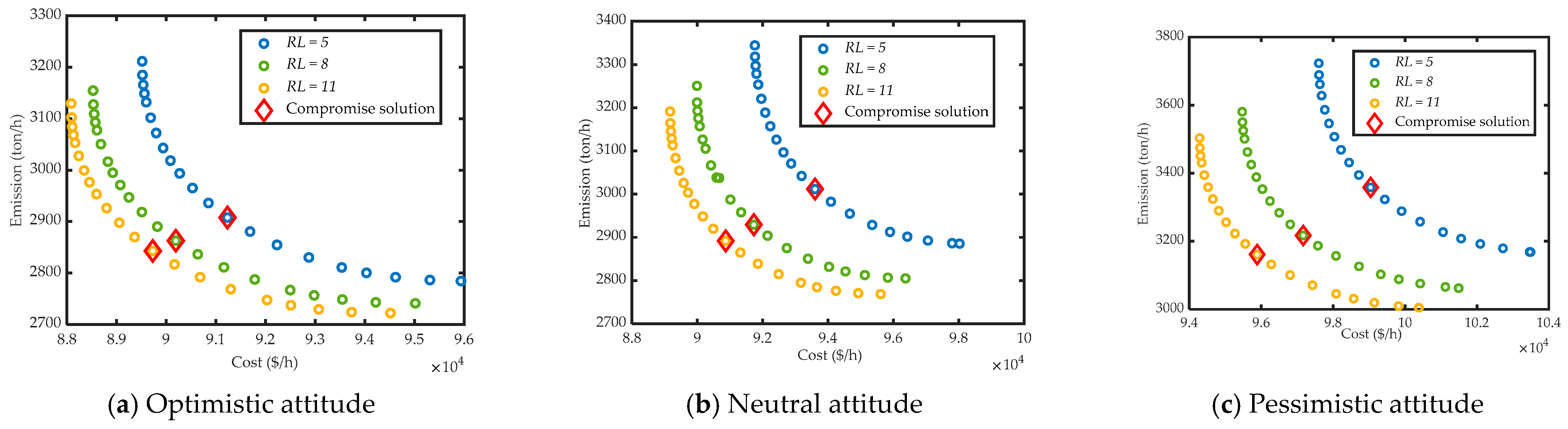
The present study proposes an improved version of the ABC algorithm based on chaos theory to deal with the stochastic CEED problem with WP. In order to take into account the random characteristics of WP, the problem is converted into a chance constraint optimization problem, and fuel cost and emission functions are combined in a single objective function by using the weighted sum method. The optimal WP to be incorporated in the grid is determined in such a way that the system security is kept within certain limits fixed based on the dispatcher’s attitudes. The system security is represented by various fuzzy membership functions in terms of the probability that power balance cannot be met.

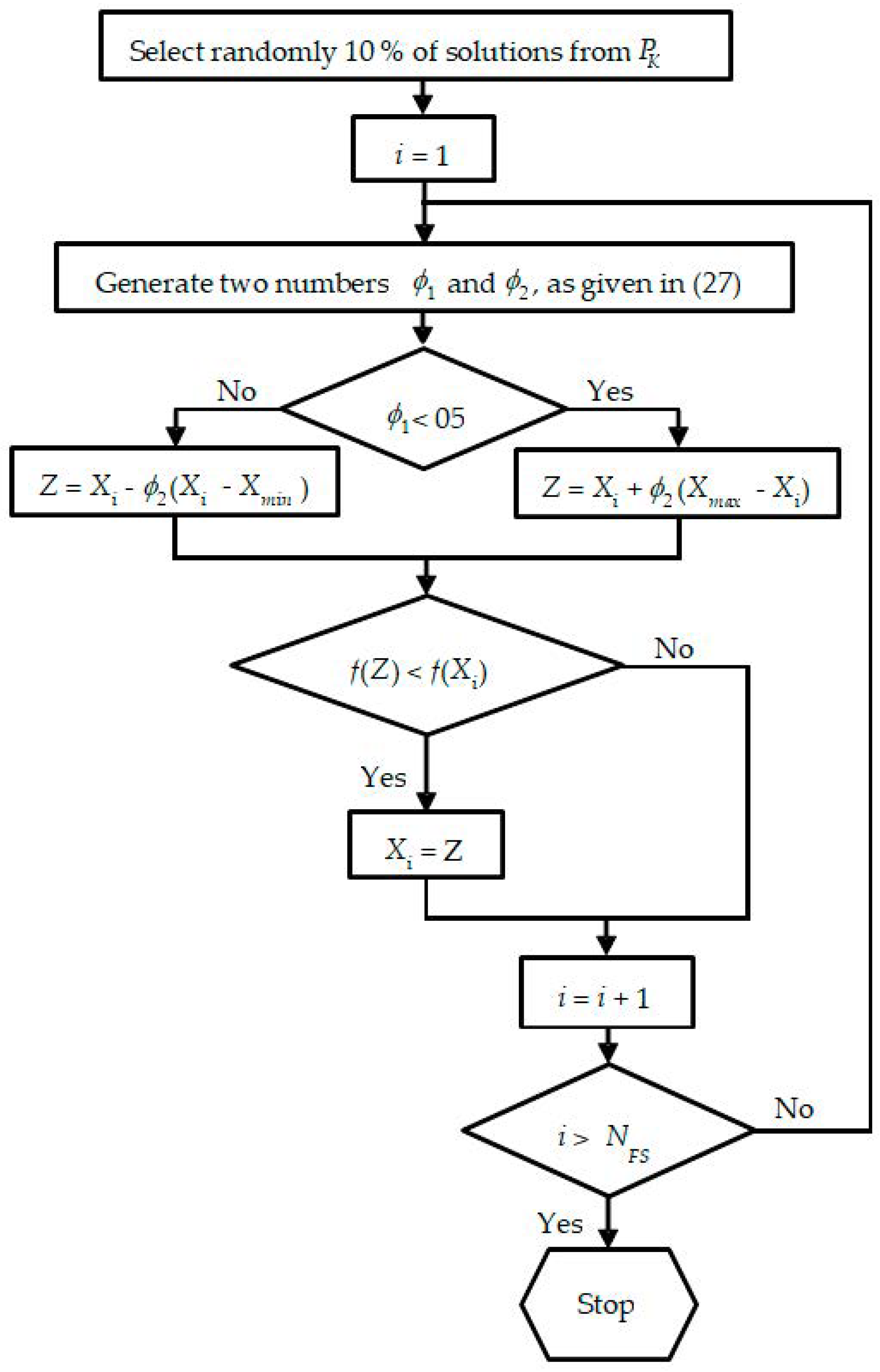
In the suggested IABC method, first, the generation of the initial population was based on chaotic maps. Therefore, initial solutions with high quality could be furnished. Then, all random numbers involved in the employed bee, onlooker bee, and scout bee phases were substituted by chaotic sequences. Note that the Ikeda map [38] was used for these two steps. To provide an appropriate balance between exploration and exploitation abilities and improve the global convergence of the algorithm, a chaotic-based local search was embedded at the end of each cycle of the fundamental ABC. In this step, chaotic sequences were generated using the Zaslavskii map [39]. To the best of our knowledge, the proposed technique has not been used for solving the dispatch problems or any other optimization problems.

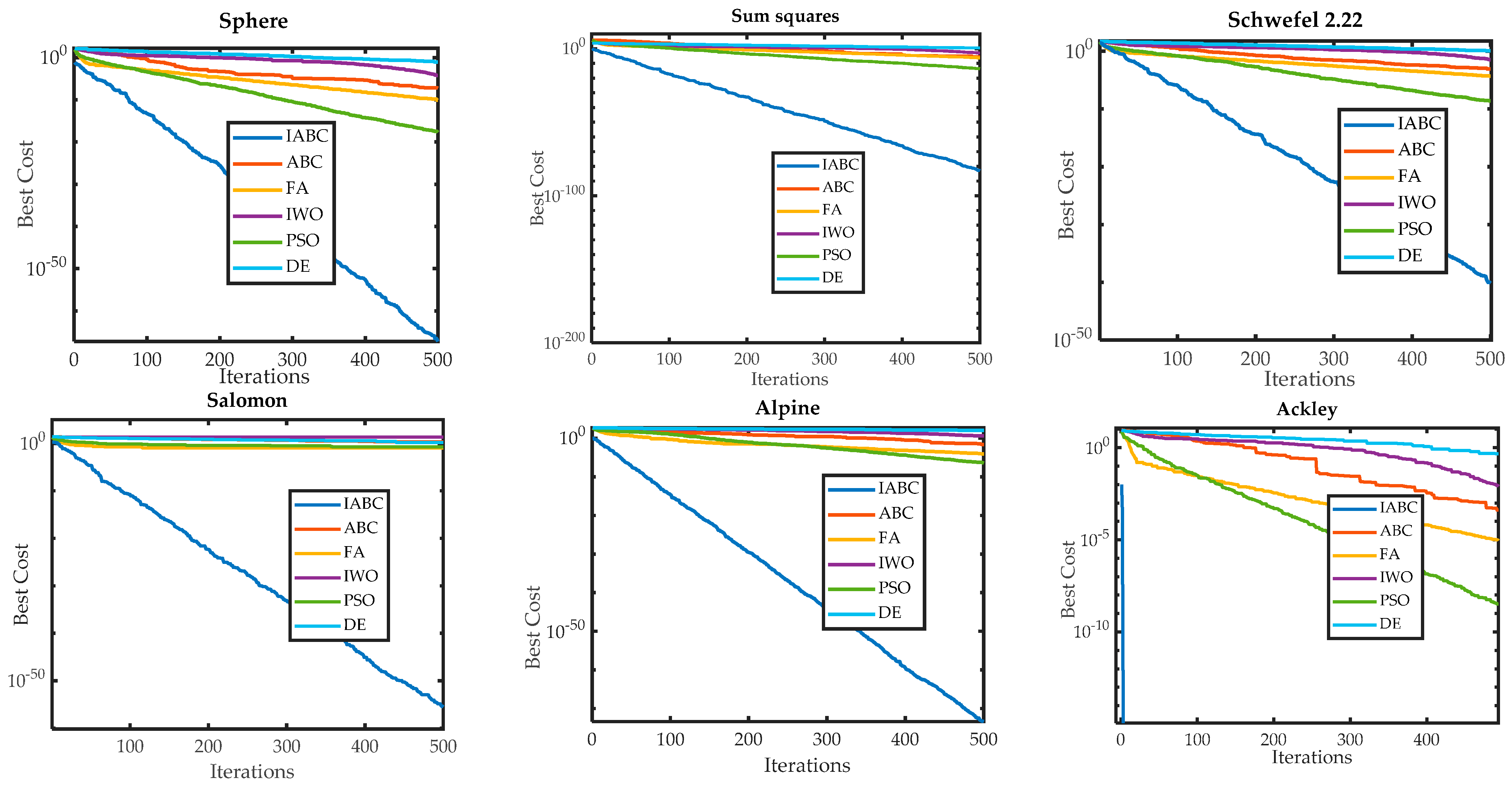
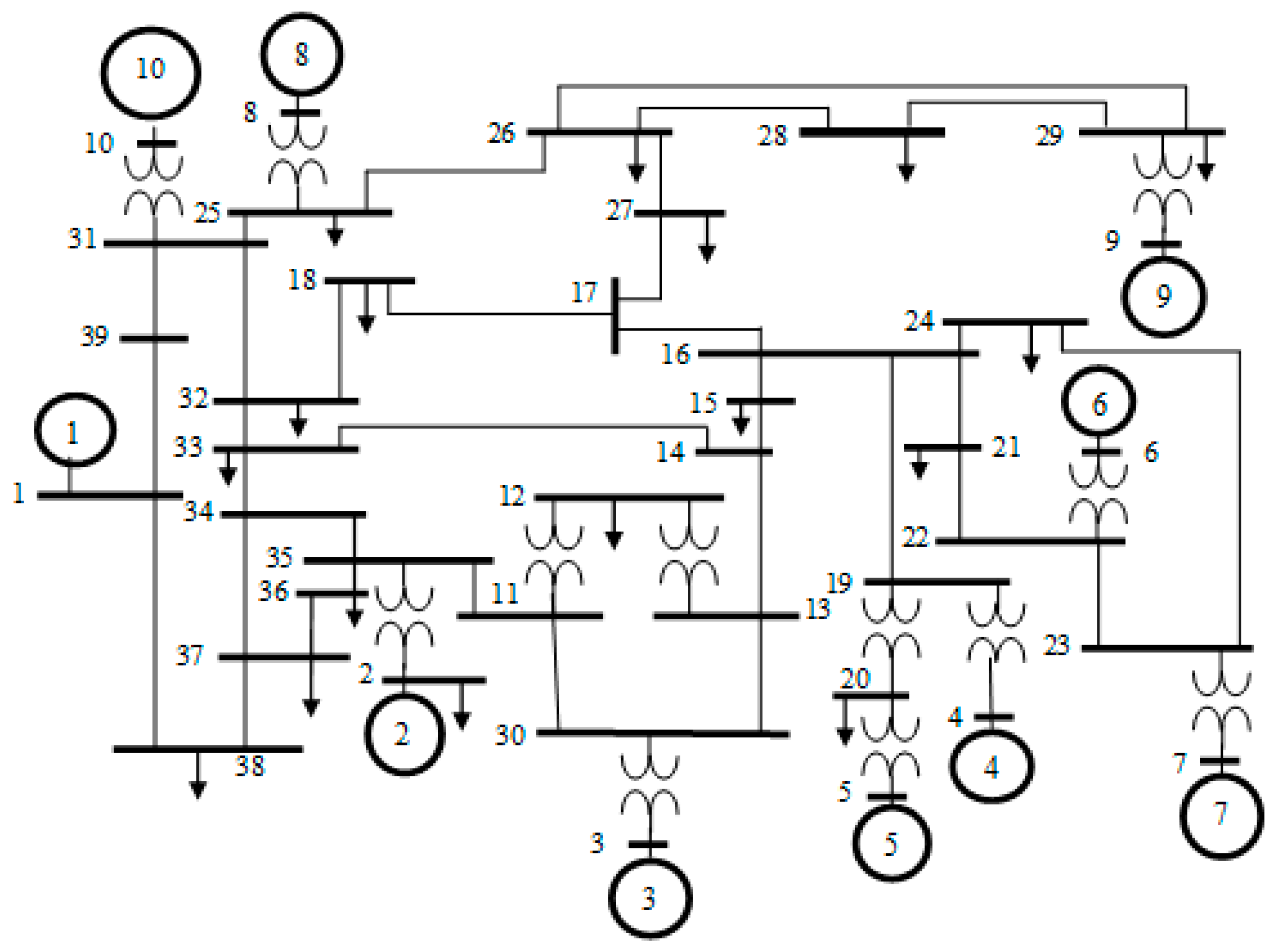
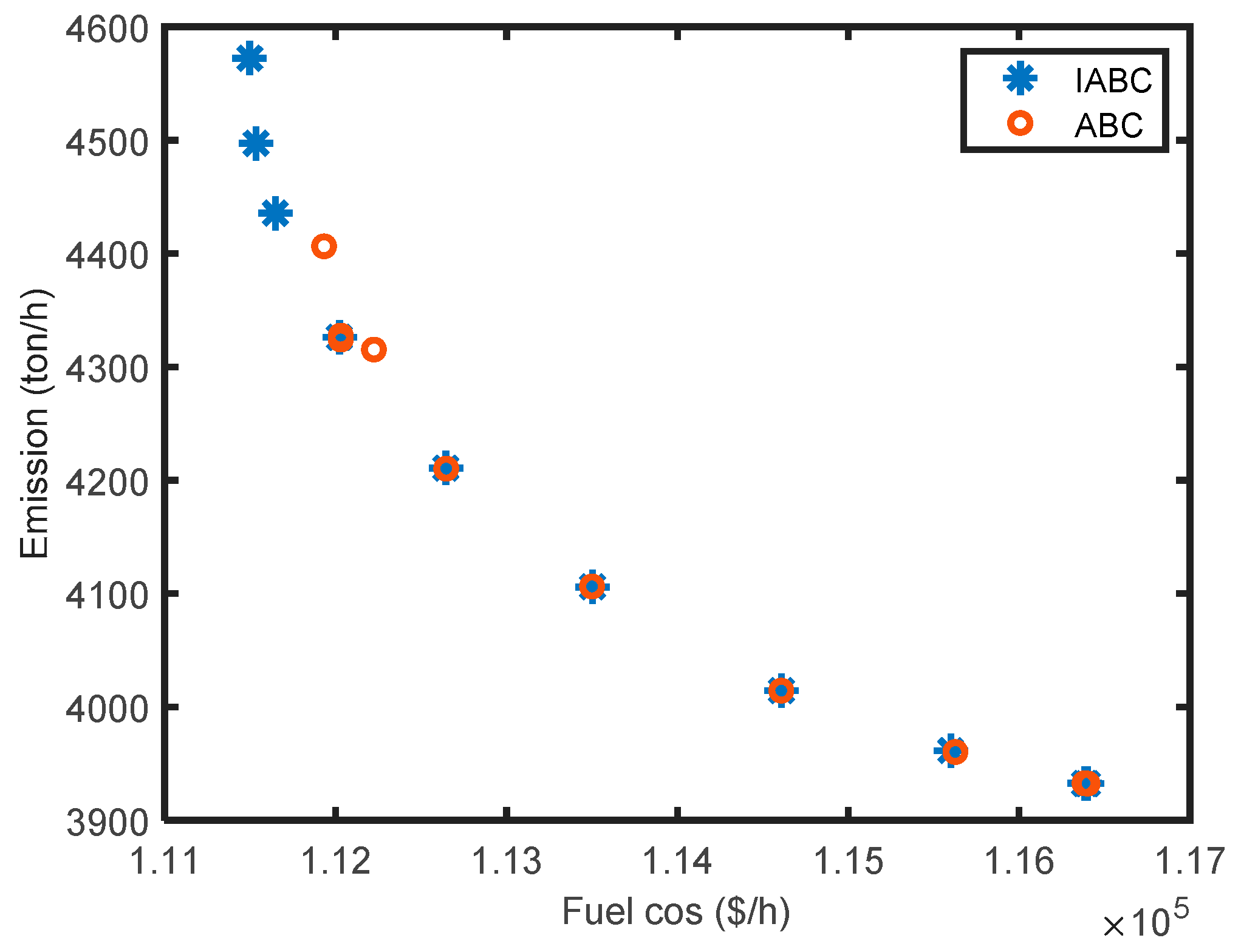
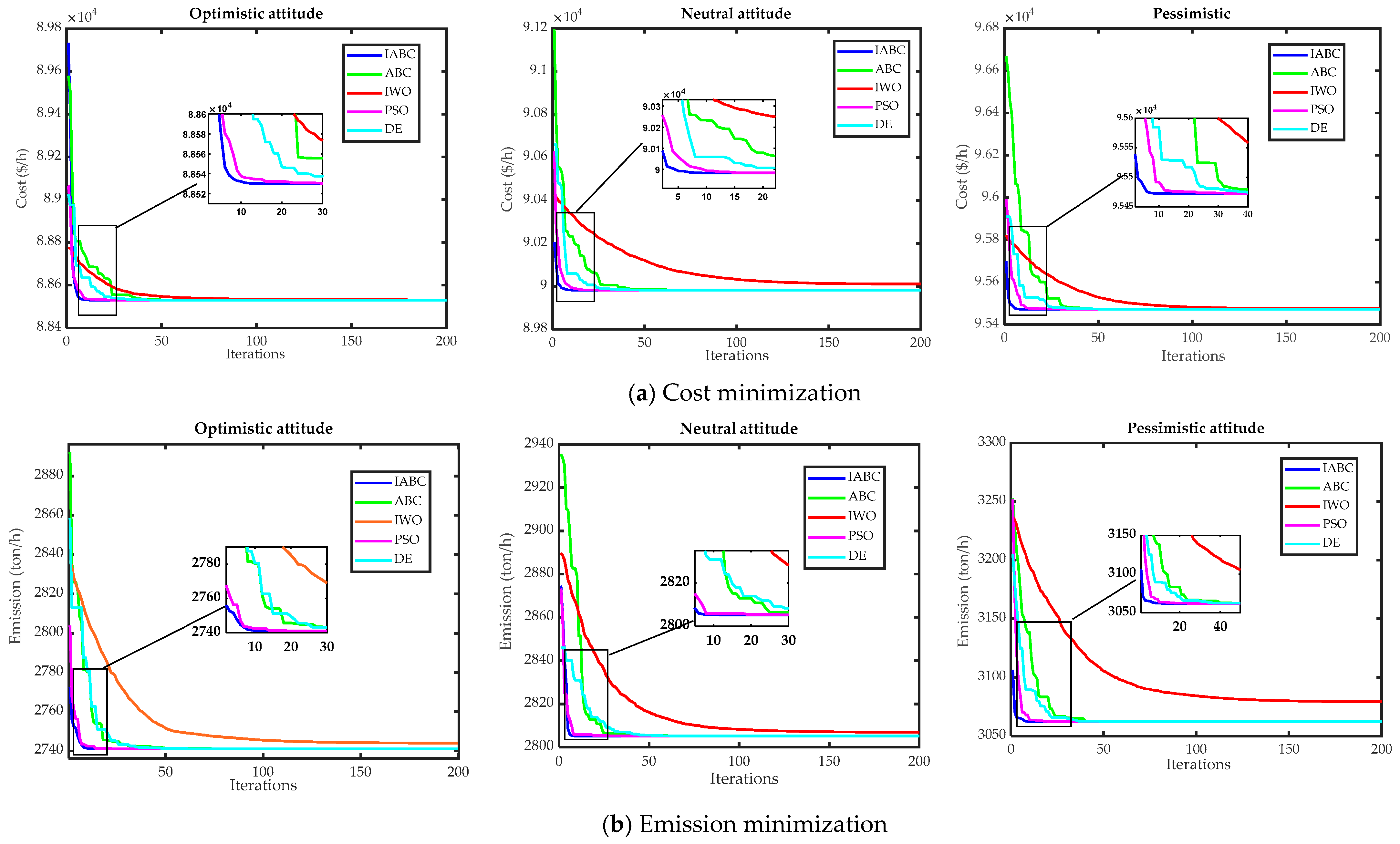
The performance of this new algorithm was first assessed on various unimodal and multimodal benchmark functions, well used in the literature for assessing optimization techniques. To further test the effectiveness and robustness of the proposed IABC for solving the non-convex CEED problem including WP, two practical power systems were used where all systems’ constraints were considered. Simulation results showed that the proposed IABC outperformed other meta-heuristic techniques reported in the literature, such as DE [40], PSO [9], IWO [41], FA [42], ABC [31], kernel search optimization (KSO) [3], OGHS [43], and NGPSO [44].

The remaining sections of this paper are organized as follows. In Section 2, the problem formulation and the research methodology are developed. In Section 3, numerical examples based on benchmark functions and power system tests are investigated to validate the suggested model and the optimization method. Finally, the conclusion is presented in Section 4.

2. Materials and Methods

2.1. Problem Formulation

The main objective of the conventional CEED is to find the optimal power contribution of each generation group of the power network so that the total production cost and emissions are as minimized as possible for any load condition while respecting all system constraints. Therefore, problem decision variables are power outputs of all generating units. For a more practical CEED model, VPLEs are considered in the cost function. Thus, a sinusoidal form is added to the classic cost function. The total fuel cost in $/h including VPLEs can be expressed as given (1). The total emission of harmful gases, such as carbon dioxide (CO2), nitrogen oxides (NOx), and sulfur oxides (SOx), in ton/h is expressed as a combination of quadratic and exponential functions of the output power of thermal units [7,8,9,10]. Therefore, the total emissions can be expressed as follows.

$$C_T={\displaystyle \sum _{i=1}^{NG}{a}_i+b_i{P}_i+c_i{\left(P_i\right)}^2+\left|d_i\sin \left\{e_i\left(P_i^{\min }-P_i\right)\right\}\right|}$$

(1)

$$E_T={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+{\beta }_i{P}_i+{\gamma }_i{\left(P_i\right)}^2+{\eta }_i\exp \left({\lambda }_i{P}_i\right)}$$

(2)

where a_i, b_i, c_i, d_i, and e_i are the fuel cost coefficients of thermal unit i. ${\alpha }_i, {\beta }_i, {\gamma }_i, {\eta }_i, \mathrm{and} {\lambda }_i$ are the emission coefficients of thermal unit i.

Generally, objective functions C_T and E_T are minimized subject to one equality constraint, describing the energy balance constraint given in Equation (3) and N inequality constraints describing the generation limits, as given in (5).

$${\displaystyle \sum _{i=1}^{NG}{P}_i-P_D-P_L}=0$$

(3)

where P_L is the total real power losses that can be approximated by the following expression [26].

$$P_L={\displaystyle \sum _{i=1}^{NG}{\displaystyle \sum _{j=1}^{NG}{P}_i{B}_{ij}{P}_j}}$$

(4)

$$P_i^{\min }\le P_i\le P_i^{\max },\hspace{1em}i=1,2,\dots ,NG$$

(5)

In this study, the CEED was converted into a mono-objective problem by combining the two objective functions in a single objective functionm employing the price penalty factor (PPF) method. This function can be described by the following equation.

$$F_T=\mu C_T+\left(1-\mu \right)\delta E_T$$

(6)

where $\mu \in \left[0,1\right]$ is a weight factor, and $\delta$ is a scaling factor.

In this study, real power outputs of all generators are provided by the optimization algorithm, except for the slack generator, which serves to compensate the system losses. This assumption is suggested in order to maintain the balance between the total generation in the one hand and the demand power and losses on the other hand. For notational simplicity, the N-th generator is considered the slack generator.

In presence of a wind farm, the power balance equation given in (3) becomes as follows.

$${\displaystyle \sum _{i=1}^{NG}{P}_i+P_W-P_D-P_L}=0$$

(7)

Therefore, to take into account the impact of the intermittency of WP, the power balance constraint (3) in the conventional CEED model can be expressed in the form of chance constraint, as given in (8). The chance constraint has been suggested in several works to avoid the high probabilistic infeasibility of employing average WP [5]. In (8), $\Psi$ is the tolerance that power balance constraint cannot be satisfied.

$$\mathrm{Pr}\left({\displaystyle \sum _{i=1}^{NG}{P}_i+P_W\le P_D+P_L}\right)\le \Psi$$

(8)

As given in (9), the randomness of the wind speed (v) can be described by the Weibull distribution function. Moreover, the continuous relationship between wind speed and WP generated by the wind farm can be expressed as given in (10) [6]. It is noteworthy that a wind farm cannot generate power for low wind speeds ($V<v_{in}$) or above the cut-out speed ($V\ge v_{out}$). However, WP is fixed at the rated power ($w_r$) when $v_r\le V<v_{out}$.

$$f_v\left(v\right)=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left[-\left(\frac{v}{c}\right)\right]$$

(9)

$$W=\frac{V-v_{in}}{v_r-v_{in}}{w}_r;\hspace{1em}{v}_{in}\le V<v_r$$

(10)

From Equations (9) and (10), the cumulative distribution function of WP for the continuous domain can be written as follows.

$$F_W\left(w\right)=\mathrm{Pr}\left(W\le w\right)=1-\exp \left\{-\frac{v_{in}^k}{c^k}{\left(1+\frac{h}{w_r}w\right)}^k\right\}+\exp \left(-{\left(\frac{v_{out}}{c}\right)}^k\right)$$

(11)

Based on probability theory, the probability of the power balance that cannot be met can be expressed by the following equation [6].

$$\begin{array}{cc}\mathrm{Pr}\left({\displaystyle \sum _{i=1}^{NG}{P}_i+P_W\le P_D+P_L}\right)& =\mathrm{Pr}\left(P_W\le P_D+P_L-{\displaystyle \sum _{i=1}^{NG}{P}_i}\right)=F_W\left(P_D+P_L-{\displaystyle \sum _{i=1}^{NG}{P}_i}\right)\hfill \\ & =1-\exp \left\{-\frac{v_{in}^k}{c^k}{\left(1+\frac{h}{w_r}\left(P_D+P_L-{\displaystyle \sum _{i=1}^{NG}{P}_i}\right)\right)}^k\right\}+\exp \left(-{\left(\frac{v_{out}}{c}\right)}^k\right)\hfill \end{array}$$

(12)

Therefore, chance constraint given in (12) can be converted into the following deterministic constraint.

$$1-\exp \left\{-\frac{v_{in}^k}{c^k}{\left(1+\frac{h}{w_r}\left(P_D+P_L-{\displaystyle \sum _{i=1}^{NG}{P}_i}\right)\right)}^k\right\}+\exp \left(-{\left(\frac{v_{out}}{c}\right)}^k\right)\le \Psi$$

(13)

Here, $h=\frac{v_r}{v_{in}}-1$.

2.2. Security Level of WP Penetration

The security of the system is the main precaution when a WP resource is incorporated in the power network. As given in [28], the security level (SL) can be described by a fuzzy membership function regarding WP penetration. Mathematically, it can be expressed as follows.

$$SL=\{\begin{array}{cc}1,\hfill & P_W\le P_W^{\min }\hfill \\ \frac{P_W^{\max }-P_W}{P_W^{\max }-P_W^{\min }},\hfill & P_W^{\min }\le P_W\le P_W^{\max }\hfill \\ 0,\hfill & P_W^{\max }\le P_W\hfill \end{array}$$

(14)

The linear fuzzy membership function given by Equation (14) can be substituted by a quadratic membership function, as in Equation (15).

$$SL=\{\begin{array}{cc}1,\hfill & P_W\le P_W^{\min }\hfill \\ {\alpha }_w{P}_W^2+{\beta }_w{P}_W+{\gamma }_w,& P_W^{\min }\le P_W\le P_W^{\max }\hfill \\ 0,\hfill & P_W^{\max }\le P_W\hfill \end{array}$$

(15)

In a similar manner, the security level may be expressed also by a fuzzy membership function regarding the operational cost of WP or the tolerance value $\Psi$. For instance, the security level in terms of the tolerance value is expressed as follows.

$$SL=\{\begin{array}{cc}1,\hfill & \Psi \le {\Psi }^{\min }\hfill \\ {\alpha }_{\psi }{\Psi }^2+{\beta }_{\psi }\Psi +{\gamma }_{\psi },\hfill & {\Psi }^{\min }\le \Psi \le {\Psi }^{\max }\hfill \\ 0,\hfill & {\Psi }^{\max }\le \Psi \hfill \end{array}$$

(16)

From Figure 1, it is clear that the curve shape of the quadratic function given by Equation (16) depends on the values of its coefficients ${\alpha }_{\psi }$, ${\beta }_{\psi }$, and ${\gamma }_{\psi }$. These shapes determine the attitudes of the dispatcher regarding WP penetration. In Figure 1, curves in green reflect the optimistic attitude, curves in red correspond to pessimistic, whilst curves in blue reflect the neutral attitude toward WP penetration.

From Equation (16), it can be seen that if the WP penetration increases, the SL will decrease. Therefore, it is advised to maintain WP penetration under a certain range in order to keep the security of the system security within acceptable limits. From the literature review [28,30], it was found that a risk level function was introduced to measure the system security. As shown in Equation (17), the risk level (RL) is inversely proportional to the SL function.

$$RL=\frac{1}{SL}$$

(17)

The risk level due to the fluctuation nature of WP can be included in the conventional CEED by adding the following constraint.

$$R{L}^{\min }\le RL\le R{L}^{\max }$$

(18)

Finally, the CEED problem with WP penetration can be formulated as an optimization problem, as illustrated in the following equation.

$$\{\begin{array}{c}\mathrm{minimize} F_T=\mu C_T+\left(1-\mu \right)\delta E_T\hfill \\ \mathrm{subject}\mathrm{to}:\hfill \\ 1-\exp \left\{-\frac{v_{in}^k}{c^k}{\left(1+\frac{h}{w_r}\left(P_D+P_L-{\displaystyle \sum _{i=1}^{NG}{P}_i}\right)\right)}^k\right\}+\exp \left(-{\left(\frac{v_{out}}{c}\right)}^k\right)\le \Psi \hfill \\ P_i^{\min }\le P_i\le P_i^{\max },\hspace{1em}i=1,2,\dots ,NG\hfill \\ 0\le P_W\le w_r\hfill \\ R{L}^{\min }\le RL\le R{L}^{\max }\hfill \end{array}$$

(19)

2.3. Proposed Optimization Technique

2.3.1. Original ABC

Population-based algorithms have generated a great deal of research interest in solving optimization problems. Some of these algorithms are based on selecting the best individuals, while others are interested in the behaviors of poorly intelligent but extremely communicative populations. These behaviors have been described mainly through ant colony, particle swarm, and artificial bee colony (ABC) algorithms. The latter algorithm, introduced by Karaboga in 2005 [31], emulates the behavior of different categories of bees in order to explore the optimization search space. This algorithm has proven its efficiency with respect to other population-based algorithms, whether based on selection, such as DE, or swarm intelligence, such as PSO. As in all population-based methods, the ABC algorithm begins by creating random initial population of N_FS solutions or food sources. These food sources are assigned to the employed bees of the hive. N_FS is half of the entire population size (PN). The second half of the population contains the onlooker bees. For a D-dimensional problem, the initial population is generated as given in Equation (20). The fitness function that signifies the nectar quantity estimated by the employed bee at i-th food source $X^i=\left[\begin{array}{cccc}{x}_1^i& x_2^i& \dots & x_D^i\end{array}\right]$ can be calculated as given in (21).

$$x_j^i=X_j^{\min }+rnd\left(0,1\right)\left(X_j^{\max }-X_j^{\min }\right), i=1,\dots ,N_{FS} \mathrm{and} j=1,\dots ,D$$

(20)

where $X_j^{\min }$ and $X_j^{\max }$ are lower and upper limits of the j-th decision variable.

$$fit\left(X^i\right)=\{\begin{array}{c}\frac{1}{1+f\left(X^i\right)}, f\left(X^i\right)\ge 0\hfill \\ 1+\left|f\left(X^i\right)\right|, f\left(X^i\right)<0\hfill \end{array}$$

(21)

where f is the objective function.

Based on nectar amounts, the probability $S{C}_i$ to select the candidate food source $X^i$ by onlooker bees is expressed as given in Equation (22).

$$S{C}_i=\frac{fit\left(X^i\right)}{{\displaystyle \sum _{j=1}^{N_{FS}}fit\left(X^j\right)}}$$

(22)

Once candidate solutions $X^i$ are selected, they will be updated by onlooker bees to discover new ones. The new solution $V^i$ is obtained by changing only one parameter $x_j^i$ of $X^i$, as given in Equation (23).

$$v_j^i=x_j^i+{\delta }_j^i\left(x_j^i-x_j^k\right)$$

(23)

where j and $k\ne i$ are chosen randomly from $\left\{1,2,\dots ,D\right\}$ and $\left\{1,2,\dots ,N_{FS}\right\}$, respectively. ${\delta }_j^i$ is a real number chosen randomly from $\left[0,1\right]$.

If the modified solution $V^i$ is better than $X^i$, solution, $V^i$ will replace $X^i$ in the population, and the abundance counter of $X^i$ is then reset. Otherwise, solution $X^i$ is conserved in the population, and its abundance counter is incremented. The i-th food source is abandoned if it cannot be improved after a predetermined number of trials $T_{LIMIT}$. In this case, the corresponding employed bee becomes a scout bee, and the food source $X^i$ is updated randomly as follows.

$$x_j^i=X_j^{\min }+rand\left(0,1\right)\left(X_j^{\max }-X_j^{\min }\right),j=1,\dots ,D$$

(24)

where $X_j^{\min }$ and $X_j^{\max }$ are bounds of $x_j^i$.

2.3.2. Improved ABC

From literature review of [32,33,34,35], it was found that the ABC algorithm has proven good performance in solving several engineering problems. Unfortunately, it has the disadvantage to be trapped in local optima, as are the majority of population-based methods [36]. In addition, the random variables used in the ABC phases increase its convergence rate. In fact, compared to other variants of ABC and some population-based techniques, such as PSO-based methods, the ABC algorithm has typically the slowest convergence speed [33,34]. In order to overcome these limitations, the ABC algorithm is hybridized with chaos in this study. Indeed, several researchers have proven that the non-repetition and ergodicity of chaos make it more efficient in performing thorough searches with an acceptable convergence rate compared to probabilistic-based searches [37]. Generally, the chaotic structure may be described by a dynamical system where its behavior is sensitive to the initial condition. Mathematically, the chaotic structure is described by chaotic sequences, as given in the following equation.

$$w_{n+1}=h\left(w_n\right);\hspace{1em}0<w_n<1, n=1, 2, \dots$$

(25)

The use of chaotic sequences instead of random sequences has demonstrated good results in several research domains, such as power system operation [45], image processing [46], and communication [47]. In fact, chaos theory is highly sensitive to small changes of initial condition and can lead to a large change in the system behavior. Accordingly, the integration of chaotic maps can avoid the convergence into local optima more easily than random-based optimization algorithms.

From literature review of [34], it was shown that classical ABC is widely criticized for its unbalanced exploration–exploitation abilities. This is due to the fact that the search processes in the employed bee, onlooker bee, and scout bee phases employ the same strategy. In addition, these phases use random variables to update the feasible solutions.

In this study, two chaotic maps are integrated in the classical ABC to escape the convergence into a local optimum and to improve the optimizing algorithm properties. The first chaotic map, which is the Ikeda map, is used to generate the initial population. Ikeda map is suggested also to generate chaotic sequences used to substitute all random numbers used in employed bee, onlooker bee, and scout bee phases. In order to maintain the diversity of the population, a chaos-based local search is embedded at the end of each iteration of the proposed algorithm. The diversity of the population is performed using the Zaslavskii map. The Ikeda map and Zaslavskii map are described by Equations (26) and (27), respectively.

$$\{\begin{array}{c}{x}_{n+1}=1+a\left(x_n\cos t_n-y_n\sin t_n\right)\hfill \\ y_{n+1}=a\left(x_n\sin t_n-y_n\cos t_n\right)\hfill \\ t_n=c-\left(6/\left(1+x_n^2+y_n^2\right)\right)\hfill \end{array}$$

(26)

where μ and c are the system parameters. $x_n,y_n,\mathrm{and}{t}_n$ are the state variables.

$$\{\begin{array}{c}{x}_{n+1}=\mathrm{mod}\left(\left[x_n+v\left(1+b{y}_n\right)+evb\cos \left(2\pi x_n\right)\right],1\right)\hfill \\ y_{n+1}=e^{-r}\left(y_n+e\cos \left(2\pi x_n\right)\right)\hfill \\ b=\frac{1-e^{-r}}{r}\hfill \end{array}$$

(27)

where e, v, r, and a are the system parameters.

The flowchart of the chaotic local search applied at the k-th iteration is illustrated in Figure 2. It starts by randomly selecting 10% of candidate solutions from the population. Then, for each solution $X^i$, two variables ${\varphi }_1$ and ${\varphi }_2$ are generated by the Zaslavskii map. Based on the value of ${\varphi }_1$, a new food source Z is discovered. The updated solution is the solution Z if Z is better than $X^i$, and it is $X^i$, otherwise.

It is worth mentioning that the input parameters of the proposed algorithm are algorithm parameters and power network data such as cost coefficients, emission coefficients and B-loss coefficients. The outputs of the algorithm are the optimum generation of thermal units and wind farms, as well as minimum values of fuel cost and emissions. The pseudo-code of the improved ABC is shown in Algorithm 1.

Algorithm 1. Pseudo-code of the IABC.

1. Input: Power network data

Algorithm parameters

2. Output: Generation of units

Minimum fuel cost

Minimum emission

3. Generate chaotic sequences CK based on Ikeda map

4. Generate chaotic sequences CZ based on Zaslavskii map

5. Generate initial population P0:

while i < NFS do

while j < D do

$x_j^i=X_j^{\min }+C{K}_j^i\left(X_j^{\max }-X_j^{\min }\right)$

end while

Evaluate $fit\left(X^i\right)$ as given in (15)

end while

6. iter = 1

7. while iter < itermax do

Select candidate food source Xi, as given in (16)

count = 0

$j=round\left(D\times C{K}_j^i\right)$

${\left(x_j^i\right)}_{new}=x_j^i+C{K}_j^i\left(x_j^i-x_j^k\right)$

if $f\left({\left(X^i\right)}_{new}\right)<f\left(X^i\right)$ then

$X^i={(X^i)}_{new}$

Else

Count = count + 1

end if

if count > TLIMIT

j = 1

while j < D do

$x_j^i=X_j^{\min }+C{K}_j^i\left(X_j^{\max }-X_j^{\min }\right)$

j = j + 1

end while

Apply local search procedure as in Figure 1

iter = iter + 1

8. end while

3. Results and Discussions

3.1. Experimental Analysis of the Proposed Method

In order to assess the performance of the proposed IABC, various numerical experiments have been investigated. Experiments were based on two groups of benchmark functions, unimodal and multimodal, mostly used in the literature for testing optimization techniques. Names, formula, ranges, type, and accepted global optima of these benchmark functions are shown in

Table 1. Proprieties of the test functions.

Function	Formula	Range	Type	Accepted
Sphere	$f_1(x)={\displaystyle {\sum }_{i=1}^n{x}_i^2}$	[−100,100]	Unimodal	0.00001
Sum Squares	$f_2(x)={\displaystyle {\sum }_{i=1}^{n}i{x}_i^2}$	[−100,100]	Unimodal	0.00001
Schwefel 2.22	$f_3(x)={\displaystyle {\sum }_{i=1}^n\left|x_i\right|}+{\displaystyle {\prod }_{i=1}^n\left|x_i\right|}$	[−100,100]	Unimodal	0.00001
Salomon	$f_4=1-\cos \left(2\pi \sqrt{{\displaystyle \sum _{i=1}^D{x}_i^2}}\right)+0.1\sqrt{{\displaystyle \sum _{i=1}^D{x}_i^2}}$	[−100,100]	Multimodal	0.00001
Alpine	$f_5(x)={\displaystyle {\sum }_{i=1}^n\left|x_i\sin \left(x_i\right)+0.1x_i\right|}$	[−100,100]	Multimodal	0.00001
Ackley	$\begin{array}{cc}{f}_6(x)\hfill & =-20\exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{x}_i^2}}\right)\hfill \\ \hfill & -\exp \left(\frac{1}{n}{\displaystyle {\sum }_{i=1}^n\cos \left(2\pi x_i\right)}\right)+20+e\hfill \end{array}$	[−32.768,32.768]	Multimodal	0.00001

. Experimental results obtained with the IABC are compared with DE, PSO, IWO, FA, and ABC. For fair comparison, all of these algorithms were run with the same common parameters. In this section, the population size, the maximum number of iterations, and the number of the decision variables were fixed as 500, 500, and 30, respectively. All these algorithms were coded in Matlab, and they were run using a personal computer with an Intel Core i7 1.99 GHz and 8 GB of random access memory (RAM).

Figure 3 depicts the convergence characteristics of the chaotic-based ABC method and the aforementioned optimization algorithms. It can be seen that the proposed method is clearly faster than the other techniques since it reaches the accepted optimum values, shown in Table 1, within the lowest number of iterations for all benchmark functions. In addition, the proposed algorithm starts from initial values less than the other optimization techniques, due to the chaotic-based initialization incorporated in the improved ABC algorithm.

The performance of the IABC was assessed through measurements of the best values, mean and standard deviation (SD) values.

Table A2. Experimental results.

Function		DE	PSO	IWO	FA	ABC	IABC
f1	Best	9.69 × 10−2	1.99 × 10−18	5.74 × 10−5	7.76 × 10−11	5.20 × 10−8	6.06 × 10−68
	Mean	1.31 × 101	7.39 × 10−18	6.79 × 10−5	1.02 × 10−10	1.02 × 10−7	1.67 × 10−63
	SD	2.25 × 10−2	7.52 × 10−18	5.45 × 10−6	1.28 × 10−11	5.11 × 10−8	4.89 × 10−63
f2	Best	2.32 × 100	2.20 × 10−14	1.07 × 10−3	5.49 × 10−7	2.64 × 10−6	1.12 × 10−83
	Mean	3.08 × 101	3.20 × 10−13	2.05 × 10−3	6.53 × 10−7	8.72 × 10−6	2.17 × 10−77
	SD	5.79 × 10−1	2.57 × 10−13	7.65 × 10−4	5.51 × 10−8	7.66 × 10−6	6.56 × 10−77
f3	Best	1.15 × 100	2.35 × 10−9	3.27 × 10−2	4.72 × 10−5	8.18 × 10−4	7.23 × 10−41
	Mean	1.34 × 100	3.43 × 10−9	4.02 × 10−2	4.85 × 10−5	1.05 × 10−3	7.62 × 10−38
	SD	1.65 × 101	1.12 × 10−9	1.65 × 10−1	1.05 × 10−6	2.42 × 10−4	1.41 × 10−37
f4	Best	1.60 × 100	2.00 × 10−1	1.95 × 101	9.99 × 10−2	2.10 × 100	3.25 × 10−57
	Mean	2.32 × 100	3.00 × 10−1	2.14 × 101	9.99 × 10−2	2.83 × 100	9.64 × 10−54
	SD	3.20 × 10−1	6.67 × 10−2	8.17 × 10−1	2.62 × 10−14	3.17 × 10−1	2.12 × 10−53
f5	Best	1.05 × 102	3.30 × 10−7	3.73 × 100	8.55 × 10−5	2.44 × 10−2	4.29 × 10−74
	Mean	1.28 × 102	2.14 × 10−5	7.46 × 100	9.43 × 10−5	3.98 × 10−1	1.36 × 10−70
	SD	1.68 × 101	5.97 × 10−5	2.75 × 100	4.80 × 10−6	2.94 × 10−1	4.25 × 10−70
f6	Best	3.84 × 101	2.84 × 10−9	6.08 × 10−3	7.80 × 10−6	4.04 × 10−4	8.88 × 10−16
	Mean	4.98 × 101	5.44 × 10−9	6.72 × 10−3	8.21 × 10−6	6.18 × 10−4	8.88 × 10−16
	SD	7.55 × 102	2.06 × 10−9	6.29 × 10−4	2.71 × 10−7	1.76 × 10−4	0.00 × 100

shows the experimental results, which were furnished after 30 runs for all aforementioned algorithms. For guidance, best results of the best method are marked as bold.

From Table A2, it can be seen clearly that the proposed optimization method furnished the best results for all studied test functions. By examining results illustrated in Table A2, it can be seen that the IABC could preclude bees from trapping into the local optimum. In addition, the standard deviation values when IABC was used were almost zero for the majority of the test functions, which allowed us to conclude that this algorithm was more robust and accurate.

3.2. Test Systems and Discussions

In this study, the 10-unit system shown in Figure 4 and the 40-unit system were used to evaluate the effectiveness of the suggested method for solving the CEED problem without and with wind energy sources. All required data of these two systems, which are widely used for this kind of problems, were taken from [44]. The power demand was set to 2000 MW. Three cases with different scales of complexity were investigated in this section. In case 1, the 10-unit system without WP was used. In contrast, power system losses and VPLEs were considered. In case 2, the proposed optimization algorithm was also tested on a large system known as the 40-unit system. The rated demand power of this system was set to 10,500 MW. In case 3, a wind farm was added to the 10-unit system where the impacts of the dispatcher’s attitudes and the risk level on the final solutions were investigated. For all cases, the scaling factor $\delta$ was chosen as 10 for comparison reasons with the works presented in [3,43,44].

Obtained results for all cases are compared with the original ABC and other algorithms published in recent references.

3.2.1. Case 1: Ten-Unit System without Wind Farm

To test the performance of the proposed optimization technique in solving the bi-objective CEED problem, the 10-unit system was used. The generator’s data and the B-loss matrix are given in

Table A1. Generator’s data (10-unit system).

Unit	${\mathit{P}}^{\mathbf{min}}$	${\mathit{P}}^{\mathbf{max}}$	A	b	c	d	E	A	β	Γ	η	Δ
1	10	55	1000.403	40.5407	0.12951	33	0.0174	360.0012	−3.9864	0.04702	0.25475	0.01234
2	20	80	950.606	39.5804	0.10908	25	0.0178	350.0056	−3.9524	0.04652	0.25475	0.01234
3	47	120	900.705	36.5104	0.12511	32	0.0162	330.0056	−3.9023	0.04652	0.25163	0.01215
4	20	130	800.705	39.5104	0.12111	30	0.0168	330.0056	−3.9023	0.04652	0.25163	0.01215
5	50	160	756.799	38.5390	0.15247	30	0.0148	13.8593	0.3277	0.00420	0.24970	0.01200
6	70	240	451.325	46.1592	0.10587	20	0.0163	13.8593	0.3277	0.00420	0.24970	0.01200
7	60	300	1243.531	38.3055	0.03546	20	0.0152	40.2669	−0.5455	0.00680	0.24800	0.01290
8	70	340	1049.998	40.3965	0.02803	30	0.0128	40.2669	−0.5455	0.00680	0.24990	0.01203
9	135	470	1658.569	36.3278	0.02111	60	0.0136	42.8955	−0.5112	0.00460	0.25470	0.01234
10	150	470	1356.659	38.2704	0.01799	40	0.0141	42.8955	−0.5112	0.00460	0.25470	0.01234

and Equation (A1), respectively. Results obtained using the proposed technique were compared with the classical ABC and other meta-heuristic techniques, such as KSO [3], OGHS [43], and NGPSO [44]. For fair comparison with these algorithms, results of the IABC and ABC were obtained after 30 runs. In addition, IABC and ABC had the same population size, set as 200, and the same maximum number of iterations, set as 100. To compare the accuracy of the proposed method with above techniques, the following criterion was used. This criterion describes the violation of the equality constraint given in Equation (3).

$$\zeta ={\displaystyle \sum _{i=1}^N{P}_i-P_D-P_L}$$

(28)

Optimal solutions for minimum fuel cost and minimum emission are shown in

Table A3. Minimum cost and minimum emission (Case 1).

	Minimum Cost					Minimum Emission
	IABC	ABC	KSO	OGHS	NGPSO	IABC	ABC	KSO	OGHS	NGPSO
P1	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00
P2	80.00	77.31	80.00	80.00	80.00	80.00	80.00	80.00	80.00	80.00
P3	106.94	92.68	106.84	106.99	106.94	81.13	81.16	81.1342	81.11	81.13
P4	100.58	105.12	100.92	100.54	100.58	81.36	81.25	81.3637	81.41	81.36
P5	81.50	93.96	81.32	81.45	81.50	160.00	160.00	160.00	160.00	160.00
P6	83.02	125.56	82.95	83.07	83.02	240.00	240.00	240.00	240.00	240.00
P7	300.00	293.58	300.00	300.00	300.00	294.49	294.46	294.49	294.51	294.49
P8	340.00	302.88	340.00	340.00	340.00	297.27	297.80	297.27	297.26	297.27
P9	470.00	470.00	470.00	470.00	470.00	396.77	396.71	396.77	396.74	396.77
P10	470.00	470.00	470.00	470.00	470.00	395.58	395.22	395.58	395.57	395.58
CT	111,497.6	111,932.7	111,497.2	111,497.6	111,497.6	116,412.4	116,413.3	116,412.4	116,412.7	116,412.4
ET	4572.20	4406.25	4573.24	4572.20	4572.20	3932.24	3932.25	3932.24	3932.24	3932.24
PL	87.04	86.09	87.04	87.04	87.04	81.60	81.60	81.60	81.60	81.60
ζ	0	0	5.68 × 10−3	3.08 × 10−4	2.29 × 10−5	0	0	4.69 × 10−5	2.02 × 10−4	4.69 × 10−5

. It is worth noting that if $\mu =1$, the CEED is equivalent to the economic dispatch problem, and if $\mu =0$ the CEED is equivalent to the emission dispatch problem. It is clear that all techniques give almost the same results, except the ABC algorithm, where it fails to provide good results for the fuel cost function. Nevertheless, it is evident that the proposed method is the most accurate since its error $\zeta$ is nil for both economic and emission dispatch problems.

The diagram of the Pareto solutions for case 1, obtained using IABC and ABC, is shown in Figure 5. The Pareto solutions in Figure 5 were obtained by varying the weight factor from 0 to 1 with a fixed step length of 0.1. Figure 5 confirms clearly that fuel cost and emission are conflicting functions, which means that if fuel cost is minimal (111,497.63 $/h), emission is maximal (4572.20 ton/h), and if the latter is minimal (3932.24 ton/h), the fuel cost is maximal (116,412.44 $/h). Moreover, it is clear that the proposed IABC provides better results compared to the original ABC.

Table A4. Some Pareto solutions for case 1.

	Sol. 1	Sol. 2	Sol. 3	Sol. 4	Sol. 5	Sol. 6	Sol. 7	Sol. 8	Sol. 9	Sol. 10
P1	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00
P2	80.00	80.00	80.00	80.00	80.00	80.00	80.00	80.00	80.00	80.00
P3	82.74	100.17	91.91	84.85	88.88	91.35	81.46	81.09	81.11	93.46
P4	81.93	95.07	88.19	83.50	86.14	87.77	81.00	81.00	81.17	89.42
P5	160.00	86.57	93.45	142.83	106.05	94.84	160.00	160.00	160.00	91.76
P6	196.41	90.21	99.63	163.17	116.67	101.55	229.26	240.00	240.00	97.33
P7	293.90	300.00	300.00	299.84	300.00	300.00	290.11	291.30	292.74	300.00
P8	305.77	340.00	338.77	315.44	328.24	336.40	298.72	296.80	297.02	340.00
P9	413.05	470.00	470.00	428.59	459.87	470.00	403.16	398.55	397.74	470.00
P10	413.86	470.00	470.00	430.62	465.39	470.00	403.24	397.93	396.86	470.00
CT	114,828	111,516	111,598	113,455	111,898	111,621	115,958	116,393	116,402	111,572
ET	4000.54	4517.51	4457.02	4110.68	4356.79	4446.43	3947.10	3932.39	3932.29	4470.40
PL	82.6550	87.0051	86.9515	83.85	86.24	86.90	81.94	81.66	81.63	86.98
ζ	0	0	0	0	0	0	0	0	0	0

shows ten Pareto solutions extracted randomly from the Pareto front. These solutions were obtained using IABC for random values of µ. It can be seen that the error described by Equation (28) was nil, which implies that the power balance constraint given in Equation (3) was met.

Table 2. Statistical results for case 1.

Method	CTmin	CTmax	CTmean	CTstd	ETmin	ETmax	ETmean	ETstd
IABC	111,497.63	111,497.63	111,497.63	1.92 × 10−11	3932.24	3932.24	3932.24	8.91 × 10−12
ABC	111,932.72	113,017.94	112,366.02	3.28 × 102	3932.25	3932.27	3932.25	8.60 × 10−2
KSO	111,497.27	111,497.27	111,497.27	1.63 × 10−8	3932.24	3932.24	3932.24	2.02 × 10−7
GQPSO	112,429.74	113,327.07	113,102.46	2.56 × 102	4011.92	4042.19	4032.93	7.55 × 100
NGPSO	111,497.63	111,497.63	111,497.63	1.00 × 10−7	3932.24	3932.24	3932.24	2.10 × 10−7

gives the statistical results for case 1. Statistical results comprise best results for fuel cost and emission function, worst results, mean and standard deviation calculated over 30 runs. It is obvious that the proposed IABC algorithm provides good results, and it is more accurate than other algorithms since it has the lowest standard deviation.

3.2.2. Case 2: Forty-Unit System

In this case, the 40-unit system was investigated to demonstrate the performance and robustness of the proposed IABC for solving the CEED problem. All system data were taken from [26]. For comparison and validation reasons, ABC, PSO, IWO, and DE methods were also applied in this case. Results for best cost and best emission functions are shown in

Table A5. Minimum cost and minimum emission (Case 2).

	Minimum Cost				Minimum Emission
	IABC	ABC	PSO	IWO	IABC	ABC	PSO	IWO
P1	110.8450	111.3641	110.9010	111.4197	114.0000	113.8285	113.9988	113.9999
P2	112.1858	109.5912	110.8714	110.6162	114.0000	114.0000	113.9972	114.0000
P3	97.7193	98.4941	97.3968	97.5388	120.0000	120.0000	120.0000	119.9989
P4	184.5171	179.1746	179.3874	179.5246	169.3817	169.4321	169.5929	169.6320
P5	87.2357	87.7107	87.8428	87.7873	97.0000	97.0000	96.9987	97.0000
P6	138.1245	137.1576	139.7708	139.9465	124.2279	123.8641	124.0369	123.8395
P7	270.5507	260.3538	259.5705	259.5561	299.6932	299.6624	299.6476	299.9976
P8	286.3837	284.2520	284.6386	286.3124	297.9188	297.7297	298.1975	298.5931
P9	283.5651	284.1212	284.6819	285.1064	297.2383	297.4607	297.3520	297.2260
P10	126.7438	131.4724	130.0277	130.0032	130.0004	130.2870	130.1642	130.1269
P11	166.1594	94.1592	94.3266	94.0056	298.3737	298.5548	298.7272	297.8058
P12	94.2932	96.9285	94.0000	94.4145	298.0197	298.6605	297.7651	298.2772
P13	125.0000	214.7893	214.5878	214.7347	433.5540	434.1361	434.0628	433.9170
P14	392.6837	395.2164	393.9880	393.5015	421.7370	422.2661	421.7389	422.2624
P15	304.6277	393.9762	393.9665	394.3603	422.7375	422.0997	423.2587	422.6111
P16	391.0454	391.9201	394.2508	392.9629	422.7258	423.2121	422.9191	422.8975
P17	488.4008	489.3008	489.4116	488.7496	439.4095	439.4198	439.4145	439.3474
P18	489.5738	491.1833	489.2478	489.5804	439.4171	439.2563	439.1378	439.5659
P19	511.1673	511.3917	511.2494	511.4366	439.4196	438.6266	439.1975	438.4250
P20	509.8529	512.0034	511.3330	511.4017	439.3958	439.4069	439.5349	438.7017
P21	520.9811	523.1079	523.0426	522.8566	439.4513	439.9723	439.2536	439.4745
P22	523.5281	523.8395	523.2598	523.4053	439.4672	439.4037	439.1641	439.5576
P23	523.2782	527.2794	523.4752	523.5002	439.8674	440.5531	439.8990	440.6765
P24	523.2786	523.1660	523.5534	523.6311	439.7652	440.3097	439.7934	438.8849
P25	523.2794	523.0954	523.3525	522.6826	440.2100	439.2480	440.2725	439.6838
P26	536.0372	523.8944	523.2625	523.5993	440.0756	439.8054	439.9108	440.3067
P27	10.7392	10.0000	10.1378	10.1404	28.9865	28.8613	28.6089	28.6591
P28	10.4550	10.0000	10.0656	10.0097	28.9835	28.4855	28.8201	29.2981
P29	10.2878	11.7193	10.1217	10.0817	29.0007	29.1435	29.0521	29.3533
P30	94.5453	88.8525	87.8176	89.7398	97.0000	96.8219	96.9991	97.0000
P31	201.5044	189.5977	189.9171	187.5943	172.2906	171.8171	172.1706	172.3456
P32	201.4599	190.0000	189.7234	189.7889	172.3162	172.1836	172.2623	172.9962
P33	201.0691	187.3032	189.5659	187.4317	172.4265	172.2490	172.4617	171.9107
P34	197.5792	164.6171	164.8130	164.7339	200.0000	200.0000	199.9999	199.9998
P35	167.6128	191.4556	196.0190	197.9058	200.0000	200.0000	200.0000	199.9996
P36	202.0145	200.0000	199.3190	199.3729	200.0000	199.9604	199.9995	200.0000
P37	121.8601	108.4169	110.0000	109.5215	100.8258	101.0213	100.5579	101.0274
P38	116.9887	108.2045	109.8785	109.8297	100.8315	100.7063	100.7956	100.7498
P39	121.1704	109.2600	110.0000	109.9598	100.8625	101.2347	100.8899	100.5919
P40	521.6561	511.6302	511.2252	511.2558	439.3896	439.3197	439.3468	439.2597
CT	121,124	121,672	121,408	121,499	129,954	129,947	129,949	129,957
ET	385,305	361,652	359,737	358,728	176,682	176,717	176,684	176,690
ζ	0	0	0	0	0	0	0	0

. From this table, it is clear that the improved ABC method provides the best results where the minimum fuel cost and emissions, reached using IABC method, are 121,124 $/h and 176,682 ton/h. Statistical results obtained after convergence of IABC and other algorithms published recently are tabulated in

Table 3. Statistical results (Case 2).

Method	CTmin	CTmax	CTmean	CTstd	ETmin	ETmax	ETmean	ETstd
CABC	121,123.82	121,219.81	121,186.25	2.76 × 101	176,682.32	176,682.32	176,682.32	4.69 × 10−11
ABC	121,672.47	121,801.23	121,760.24	2.96 × 101	176,717.52	176,777.98	176,748.37	1.77 × 101
KSO	121,375.87	121,927.12	121,538.12	1.81 × 102	176,682.26	176,682.26	176,682.26	5.82 × 10−11
GQPSO	146,121.50	152,214.35	151,703.04	9.18 × 102	270,191.92	312,560.56	298,292.51	7.40 × 103
NGPSO	121,513.48	122,697.77	122,065.12	2.67 × 102	176,685.2	176,684.83	176,683.40	5.58 × 10−1

. These results were obtained over 30 runs. From Table 3, it is obvious that the proposed IABC is more robust and gives better results than the compared techniques.

3.2.3. Case 3: Ten-Unit System with Wind Farm

In this case, the intermittency of wind farm output is considered in the CEED model of the 10-unit system described in case 1. The actual WP is considered to be 400 MW. The wind parameters are as follows.

$k=1.7$; $c=17$; $v_{in}=5$; $v_{out}=45$; $v_r=15$;

In this study, the minimum and maximum values of WP are 10% and 20% of the total demand power. The parameters of the membership function in terms of the tolerance $\Psi$ are set as follows.

• Optimistic attitude: ${\alpha }_{\psi }=-5.2477$, ${\beta }_{\psi }=1.2959$, and ${\gamma }_{\psi }=0.92$.
• Pessimistic attitude: ${\alpha }_{\psi }=5.3504$, ${\beta }_{\psi }=-5.9427$, and ${\gamma }_{\psi }=1.65$.
• Neutral attitude: ${\Psi }^{\min }=0.123$ and ${\Psi }^{\max }=0.56$.

The aforementioned values of the parameters of the membership function are selected in order to give various curve shapes (optimistic, neutral, and pessimistic) of the SL given in Equation (16). To do this, one parameter can be fixed and the two others can be determined by solving the following system of equations. ${\Psi }^{\min }$ and ${\Psi }^{\max }$ are fixed in such a way that WP output is within its permissible limits.

$$\{\begin{array}{c}{\alpha }_{\psi }{\left({\Psi }^{\min }\right)}^2+{\beta }_{\psi }{\Psi }^{\min }+{\gamma }_{\psi }=1\hfill \\ {\alpha }_{\psi }{\left({\Psi }^{\max }\right)}^2+{\beta }_{\psi }{\Psi }^{\max }+{\gamma }_{\psi }=0\hfill \end{array}$$

(29)

In order to prove the robustness and performance of the IABC, results have been compared with those obtained by using other heuristic techniques, such as standard ABC, DE, PSO, and IWO. For example, Figure 6 shows the convergence characteristics of the aforementioned techniques for RL = 8 and under different dispatcher’s attitudes. It is clear that the IABC method provides high quality initial solutions, and it has the best convergence rate for both fuel cost and emission functions.

The proposed optimization technique IABC is applied to solve the stochastic CEED problem for various values of the RL to investigate the impact of the RL on the final solutions.

In order to investigate the impact of the security level of WP penetration and dispatcher’s attitudes on the final solutions of the studied problem, the CEED problem incorporating WP was solved for different values of RL and dispatcher’s attitudes (optimistic, pessimistic, or neutral). Optimal non-dominated solutions obtained using the proposed IABC method for RL = 5, RL = 8, and RL = 11 are shown in Figure 7. The ranges of the values of the RL were selected in this study based on the results presented in [28]. It is noteworthy that non-dominated solutions are the optimum solutions of the CEED problem obtained for various values of µ ranging from 0 to 1. Figure 7 shows also the compromise solutions for all scenarios. In this, a fuzzy-based method presented in [48] was used to extract the best compromise solutions. As shown in Figure 7, the non-dominated solutions were widely distributed on the trade-off curve thanks to the chaotic maps incorporated in the optimization algorithm. Figure 8 shows also that if the risk level is kept constant, the optimistic attitude corresponds to the lowest cost and emission since it corresponds to the largest WP penetration compared with the two other dispatcher’s attitudes, whilst the largest cost and emission are obtained for the pessimistic case.

In order to study the impact of the risk level on the final optimal solutions, three scenarios were considered where the dispatcher’s attitude was kept unchangeable and the risk level was changed for each scenario. Simulation results corresponding to this experiment are shown in Figure 8. It can be seen that, whatever the dispatcher’s attitude, the more the RL increased, the more the best fuel cost and the best emission decreased, and vice-versa. In other words, if the RL increased, the Pareto fronts moved towards lower cost and emission. This was due to the fact that higher values of the RL implied higher WP penetration and vice-versa. Among all investigated scenarios, the minimum best cost and minimum best emission, which were obtained for RL = 11 and under optimistic attitude, were 88,089.98 $/h and 2722.09 ton/h, respectively. The worst best cost and best emission were 97,601.16 $/h and 3168.41 ton/h, which correspond to the pessimistic attitude and RL = 5. Hence, it can be concluded that the more wind power is used, the less reliable is the system and the more the cost and emission decrease.

Since the CEED problem is a multi-objective problem involving two conflicting objective functions, it is preferable to provide the best compromise solution extracted from set of Pareto solutions. The optimal generation in MW, as well as best cost and best emission corresponding to the compromise solutions, are depicted in

Table 4. Compromise solution in MW (Case 3).

	Optimistic			Neutral			Pessimistic
	RL = 5	RL = 8	RL = 11	RL = 5	RL = 8	RL = 11	RL = 5	RL = 8	RL = 11
P1	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00	55.00
P2	71.33	70.85	70.64	72.42	71.56	71.1610	76.63	75.03	74.28
P3	71.71	71.24	71.02	72.80	71.94	71.5437	77.22	75.51	74.76
P4	70.60	70.11	69.89	71.71	70.83	70.4241	75.72	74.23	73.47
P5	122.20	120.37	119.56	126.37	123.07	121.5528	120.86	125.51	123.01
P6	134.10	131.77	130.72	139.42	135.21	133.2679	134.11	139.28	136.07
P7	235.22	232.54	231.34	241.30	236.49	234.2663	263.66	255.49	251.48
P8	241.30	238.42	237.14	247.83	242.66	240.2768	274.24	264.12	259.79
P9	349.87	346.48	344.96	357.46	351.46	348.6694	383.32	370.48	366.00
P10	348.11	344.63	343.07	355.88	349.74	346.8790	385.11	372.81	372.37
PW	356.11	373.02	380.57	318.04	348.18	362.1258	220.15	255.55	275.38
CT ($/h)	91,235.70	90,195.25	89,732.23	93,598.91	91,725.97	90,865.00	99,044.05	97,169.31	95,887.68
ET (ton/h)	2907.95	2862.89	2842.97	3011.81	2929.323	2891.84	3358.42	3217.07	3161.00
PL (MW)	55.58	54.42	53.91	58.24	56.13	55.17	66.02	63.00	61.61

. It can be clearly seen that the compromise solution corresponding to the optimistic attitude and RL = 11 has the minimum values of cost (89,732.23 $/h), emission (2842.97 ton/h), and total power losses (53.9070 MW). In fact, high value of the RL implies that the system operator can take more risk concerning the WP generation, and therefore, the total generation of real power from thermal units will be decreased. This leads to a decrease in the total cost and total emission.

4. Conclusions

In this paper, a new optimization technique called improved ABC (IABC) algorithm is developed for the CEED problem including wind farm. Due to intermittent characteristics of WP, the amount of WP to be integrated in the power system has been considered an important issue for power system dispatchers. In fact, uncertainty of WP may cause certain problems related to system security. Within this context, a new formulation for the CEED problem is presented in order to take into account the security level of power grids when WP resources are incorporated. The optimal WP to be incorporated in the grid is determined in such a way that the system security is within a certain range. In order to take into account the availability of WP, the system security is described by various fuzzy membership functions in terms of the probability that power balance cannot be met. These membership functions are employed to characterize the dispatcher’s attitude concerning the availability of WP.

In order to apply the proposed optimization method, the probabilistic CEED problem was converted into a deterministic problem where fuel cost and emission were merged in a single objective function by employing the linear weighted sum. The Weibull distribution function was used to describe the randomness of WP output. In the proposed IABC, the random numbers in the various phases of the standard ABC were substituted by chaotic sequences generated by the Ikeda map. Moreover, the Ikeda map was used to generate the initial population instead of the random initialization applied in the classical ABC algorithm. In order to improve the convergence rate of the suggested algorithm and to provide high quality solutions, a chaotic-based local search procedure was run at the end of each iteration. This procedure was based on the Zaslavskii map. In order to test the feasibility and the effectiveness of the suggested optimization technique, six benchmark functions with different complexities were used. Experimental results were compared with those obtained using other meta-heuristics. Practical cases were also used to further assess the performance of the proposed IABC for solving the probabilistic CEED problem with WP. From simulation results, it was observed that the number of iterations to reach the best global optimum was reduced. Moreover, experimental and statistical results showed that the proposed technique outperformed other meta-heuristic techniques reported in the literature.

This research work can be extended by introducing the risk level in the dynamic dispatch and unit commitment problems, as objective function.