Multi-Objective Electrical Power System Design Optimization Using a Modified Bat Algorithm

Abstract

The design of energy systems is very important in order to reduce operating costs and guarantee the reliability of a system. This paper proposes a new algorithm to solve the design problem of optimal multi-objective redundancy of series-parallel power systems. The chosen algorithm is based on the hybridization of two metaheuristics, which are the bat algorithm (BA) and the generalized evolutionary walk algorithm (GEWA), also called BAG (bat algorithm with generalized flight). The approach is combined with the Ushakov method, the universal moment generating function (UMGF), to evaluate the reliability of the multi-state series-parallel system. The multi-objective design aims to minimize the design cost, and to maximize the reliability and the performance of the electric power generation system from solar and gas generators by taking into account the reliability indices. Power subsystem devices are labeled according to their reliabilities, costs and performances. Reliability hangs on an operational system, and implies likewise satisfying customer demand, so it depends on the amassed batch curve. Two different design allocation problems, commonly found in power systems planning, are solved to show the performance of the algorithm. The first is a bi-objective formulation that corresponds to the minimization of system investment cost and maximization of system availability. In the second, the multi-objective formulation seeks to maximize system availability, minimize system investment cost, and maximize the capacity of the system.

1. Introduction

Over the past two decades, many researchers were concerned about multi-state systems dependability, for example, regarding optimization and performance measurement [1], multi-state analysis using a fault tree applied to a satellite-based railway system [2], and a multi-state dependability simulation using Monte Carlo [1]. Moreover, researchers have been practically interested in reliability, non-repairable multi-state reliability [3], and multi-state and multi-level reliability redundancy optimization [4]. Accordingly, this research establishes a review of scientific works about multi-state system reliability [5].

One of the most explored multi-state systems is a series-parallel power system or oneincorporating redundancy, which has several states with various ability levels, alternating from total failure to a perfect process. Conversely, in the conventional binary reliability model, only two situations can appear: thoroughly failed or efficiently purposeful. Degraded functioning states must appear when modeling availability, to reflect manufacturing reality [6].

Our research continues to investigate the optimal design problem of a series-parallel power network. We investigated a memetic algorithm for heterogeneous multi-state series-parallel systems design [7]. The algorithm is based on an improved inter-subsystem local search method hybridized to a quantum evolutionary algorithm, adding to the swarm optimization algorithm a credibility-based fuzzy model of cost and performance constraints in reliability maximization [8]. We used Lagrange multipliers to determine the number of redundant elements in the power system in order to maximize reliability [9].

At this time, the redundancy optimization problem still attracts many researchers, such as a binary matrix to model a multi-type production system with cold standby redundant subsystems [10]. The study introduced a continuous-time Markov chain with a multi-objective evolutionary algorithm for the reliability–redundancy allocation problem through the reliability of a hydraulic system for an entire wind turbine [11]. The Markov-based fuzzy dynamic fault-tree analysis method was developed to model reliability including dynamic failure characteristics, to achieve lower cost and higher reliability with active redundancy of the hybrid modular multilevel converter, consisting of half- and full-bridge submodules (MSS) with DC-fault ride-through capability. To achieve this, the authors used a fuzzy system [12].

As the redundancy optimization problem is one of the NP’s complete combinatory optimization problems, conventional methods are often not suitable for parallel-series network design, due to the required execution time when increasing the number of component types or the number of subsystems. In contrast, an approach using intelligent methods, such as metaheuristic ones, seems to provide a good resolution to such a problem in less time. Accordingly, several intelligent methods have been used in series-parallel systems design, such as particle swarm optimization and local search [13], harmony search [14], ant colony optimization [15], tabu search [16], immune algorithm [17], firefly algorithm and bat algorithm [6,18,19,20].

In the last years, the use of metaheuristics rather than conventional methods became crucial in all redundancy optimization problems (ROP), in particular for power applications. In [21], the authors used a new methodology called boundary-simplified swarm optimization (BSO) for ROP, by integrating a novel self-boundary search (SBS) and a two-variable update mechanism (UM2), to improve simplified swarm optimization (SSO) when solving mixed-integer programming problems that include both discrete and continuous variables. The authors of [22] developed an integrated algorithm to solve the reliability design problem by considering instantaneous availability, repairable components, and the selection of configuration strategies based on Markov processes and the NSGA-II algorithm. In [23], the problem is formulated by considering a cold-standby strategy. The decision-making problems are encountered due to the presence of maximizing system reliability and simultaneously minimizing the total cost, weight or volume of the systems. The authors used a multi-objective evolutionary algorithm (NSGA-II). In order to calculate the exact reliability values for the ROP, a Markov-based approach is used. The authors of [24] proposed an advanced reliability–redundancy problem that considers an optimal redundancy strategy, either active or cold standby, with an imperfect detector/switch. They used a parallel genetic algorithm for solving the allocation problem in a mixed-integer nonlinear programming model. The authors of [25] considered a generalized redundancy allocation problem with a generalized network design. The components are linked with each other, neither in parallel nor in series, but in some logical relationship. The system reliability was estimated through simulation. They proposed a partitioning-based simulation optimization PBSO method to solve the problem.

Thus, our recent work in [26] proposed a deep-reinforcement learning algorithm (DRL) that determines the multi-objective optimization problem of the enabled multiphysics-constrained fast charging of a lithium-ion battery. Furthermore, a soft deep-reinforcement learning (DRL) strategy is innovatively exploited to optimize the energy management for a hybrid electric bus, as was presented in [27]. In [28], the authors proposed a recent approach based on an expert-assistance deep deterministic policy gradient algorithm (EADEPGA) to achieve optimized battery-involved energy management for a hybrid electric bus. The authors of [29] proposed a mathematical model for optimizing multiple redundancy-reliability systems, known as mega-systems. The system components are multi-state, and the universal generating function (UGF) has been simulated to evaluate system availability. The components may have a minor or major failure, which reduces the components’ performance rate. They used a parameter-tuned memetic algorithm (MA) to solve the allocation problem. In [30] a Markov model with a genetic algorithm was used to resolve the problem of ready but inactive devices. The approach proposed in this paper hybrids two relatively recent metaheuristics, the bat algorithm (BA) andthe generalized evolutionary walk algorithm (GEWA), to solve the redundancy optimization problem. The algorithm has to find the optimal design of the series-parallel structure. This structure consists of several subsystems, which can be a power production system incorporating solar and gas generators, and a power transmission one.

The optimal solution corresponds to minimizing the required cost, maximizing reliability, and maximizing the performance of the parallel-serial system, while satisfying the customer demand and guaranteeing the reliability of the system. To evaluate the reliability of multi-state series-parallel systems, a rapid reliability estimation function was developed. This procedure is based on the mathematical technique of the Laplace transform. The universal moment generator function (UMGF) developed by Ushakov has been revealed as an efficient technique for many problems [31,32].

To present an energy system design resolution approach, the redundancy optimization problem, as well as the mathematical formulation, are described in the next section. Here, many objectives are combined. In the third section of this paper, the hybridized metaheuristic, which is the bat algorithm with generalized evolutionary flight (BAG) is described, and next, the reliability estimation technique is detailed. In the last section, the proposed approach regarding the distinctive multi-objective problems is investigated, based on an industrial system of electro-energy production.

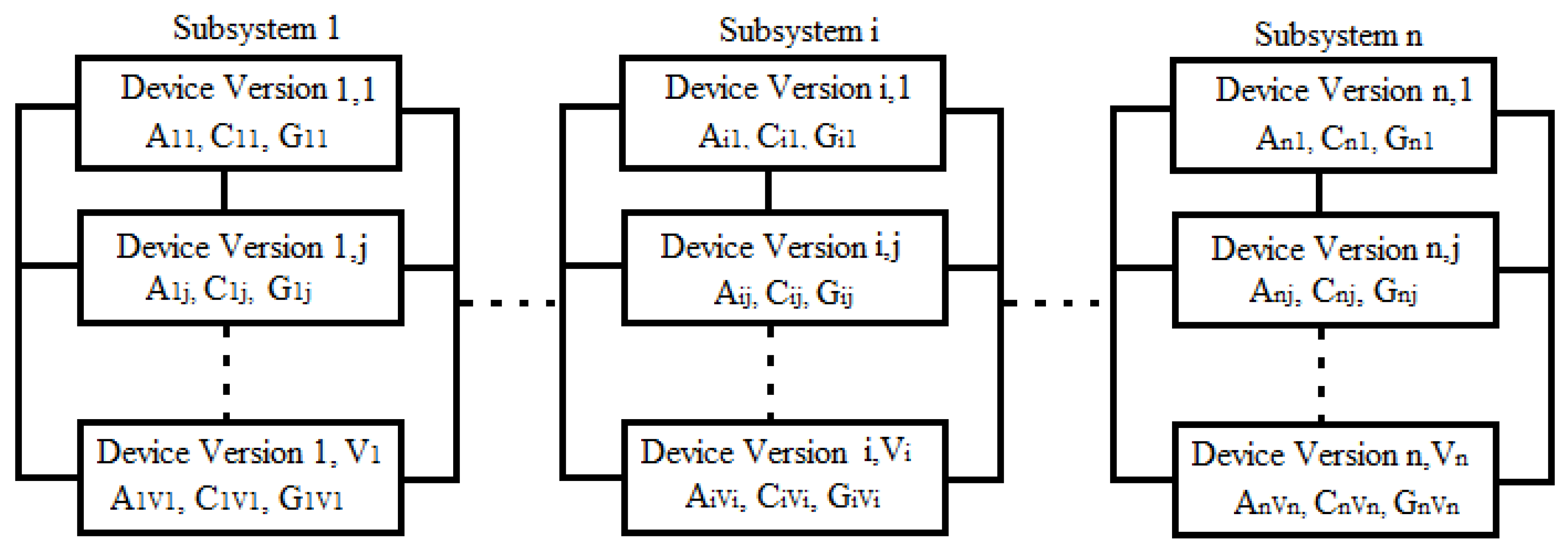
2. Redundancy Energy System Design Optimization Problems

Consider an electrical System enclosing n electrical subsystems (generators, transformers and lines) linked in series. Each subsystem i represents a component and contains a variety of device versions linked in parallel. Device j from subsystem i is described by its availability or reliability (A_ij) or (R_ij), its price (C_ij) and its load capacity (G_ij). The structure of subsystem i can be defined by the number of parallel identical components k_ij for 1≤ j ≤ V_i, where V_i is the number of available versions of type i components, as presented in Figure 1.

The multi-objective optimization of the series-parallel multi-state electrical power network refers to the resolution of two or more objectives to be satisfied simultaneously, with a number of inequality constraints. As with the objectives, many multi-objective design problems can be expressed mathematically. Below, two optimization problems are distinguished: a bi-objective design and a multi-objective one, depending on reliability maximization, cost minimization and performance.

2.1. Bi-Objective Optimization (First Problem)

The first formulation aims to maximize system reliability R, and minimize the total cost C, as given by Equation (1) for a series-parallel system with some cost-constraint, and reliability requirement R₀ is given by Equation (2).

$$\begin{array}{c}\mathrm{Minimize}C={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{V_i}{k}_{ij}{c}_{ij}}}\\ \mathrm{Maximize}R={\displaystyle \prod _{i=1}^n}\left[{\displaystyle \prod _j^{ji}p,q(z){{\displaystyle \min }}_{i=1}^n{\displaystyle \sum _{i=1}^j{{\displaystyle G}}_{ij}}}\right]\end{array}$$

(1)

Under constraints:

$$\begin{array}{c}C={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{V_i}{k}_{ij}{c}_{ij}}}\le {{\displaystyle C}}_{{}_0}\\ {\displaystyle \prod _{i=1}^n}\left[{\displaystyle \prod _j^{ji}p,q(z){{\displaystyle \min }}_{i=1}^n{\displaystyle \sum _{i=1}^j{{\displaystyle G}}_{ij}}}\right]\ge {{\displaystyle R}}_0\end{array}$$

(2)

2.2. Multi-Objective Optimization (Second Problem)

In the second multi-objective formulation, in addition to minimizing the total cost, maximizing the system reliability and the maximization of the system performance as given in Equation (3) for a series-parallel system under cost, reliability and performance constraints, as given in Equation(4).

$$\begin{array}{c}\mathrm{Minimize}C={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{V_i}{k}_{ij}{c}_{ij}}}\\ \mathrm{Maximize} R={\displaystyle \prod _{i=1}^n}\left[{\displaystyle \prod _j^{ji}p,q(z){{\displaystyle \min }}_{i=1}^n{\displaystyle \sum _{i=1}^j{{\displaystyle G}}_{ij}}}\right]\\ \mathrm{Maximize}{{\displaystyle G}}^{\min \{{{\displaystyle a}}_i,{{\displaystyle b}}_j\}}\end{array}$$

(3)

Under constraints:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{V_i}{k}_{ij}{c}_{ij}}}\le {{\displaystyle C}}_{{}_0}\\ {\displaystyle \prod _{i=1}^n}\left[{\displaystyle \prod _j^{ji}p,q(z){{\displaystyle \min }}_{i=1}^n{\displaystyle \sum _{i=1}^j{{\displaystyle G}}_{ij}}}\right]\ge {{\displaystyle R}}_0\\ {{\displaystyle G}}^{\min \{{{\displaystyle a}}_i,{{\displaystyle b}}_j\}}\ge {{\displaystyle G}}_0\end{array}$$

(4)

3. Combined Approaches

In this section, two techniques are described: first, how to evaluate the power system reliability with the universal moment generator function (UMGF); second, the metaheuristic chosen to resolve the optimization of the system design. In this last technique, the standard bat algorithm (BA) and the generalized evolutionary walk algorithm (GEWA) are detailed, to explain adequately why the improved version is used.

3.1. Reliability Estimation Technique

The problem of series-parallel multi-state systems reliability was diagnosed in the 1970s, and revealed as complex [33,34]. The behavior of multi-state systems and their constituents is displayed in many states, with various performances related to each state. In the literature, the structural designs are varied. Several works study series-parallel, multi-state and bridge configurations [32,35,36]. The probability that the electrical system’s total ability satisfies thoroughly the load request level W is estimated in Equation (5):

$$R\left(W\right)=P\left\{G\succ W\right\}=1-P\left\{G\le W\right\}$$

(5)

The Ushakov technique (UMGF: universal moment generator function) developed in 1986 has been explained and appraised in detail in [35]. Therefore, the Ushakov method is corroborated as a rapid technique for numerical applications. A variable G denotes performance and can yield J potential states.Thus, the UMGF of a random performance G is a polynomial is given by Equation (6):

$$u\left(z\right)={\displaystyle \sum _{j=1}^J{{\displaystyle P_j^{}}}_{} {{\displaystyle z}}^{G_j^{}}}$$

(6)

P_j are the state probabilities.

The probabilistic characteristics of the random variable G can be found using the function u(z). In particular, if the discrete random variable G is the stationary output performance of the MSS, availability A is given by the probability (G ≥ W) which can be defined as follows:

$$proba\left(G\ge W\right)=\mathsf{\Phi }\left(u\left(z\right){{\displaystyle z}}^{-w}\right)$$

(7)

When Φ is a distributive operator defined by Expressions (8) and (9) [36]:

$$\mathsf{\Phi }\left({{\displaystyle p_j}}_{} {{\displaystyle z^{\sigma -W}}}^{}\right)=\{\begin{array}{c}p,if \sigma \ge W\\ 0,if \sigma \langle W\end{array}$$

(8)

$$\mathsf{\Phi }\left({\displaystyle \sum _{j=1}^J{{\displaystyle p}}_j{{\displaystyle z}}^{{{\displaystyle G}}_{{}_j}-W}}\right)={\displaystyle \sum _{j=1}^J\mathsf{\Phi }\left({{\displaystyle p}}_j{{\displaystyle z}}^{{{\displaystyle G}}_j-W}\right)}$$

(9)

Moreover, to assess availabilities, two basic operators are brought together. These operators define the polynomial u(z) for a set of elements.

3.1.1. Parallel Elements

The universal moment generator function of a multi-state system linking redundant devices is estimated using the $\Im$ operator is defined as:

$${{\displaystyle u}}_s\left(z\right)=\Im \left({{\displaystyle u}}_1\left(z\right),{{\displaystyle u}}_2\left(z\right),\dots {{\displaystyle u}}_m\left(z\right)\right),$$

(10)

In agreement, the application of the operator in a simple two-redundant device system is displayed in Equation (11):

$$\Im \left({\displaystyle \sum _{j=1}^J{{\displaystyle P}}_j{{\displaystyle z}}^{{{\displaystyle G}}_j-W}}\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{{\displaystyle P}}_i{{\displaystyle Q}}_i{{\displaystyle z}}^{{{\displaystyle a}}_i+{{\displaystyle b}}_j}}}$$

(11)

The parameters a_i and b_j are physically interpreted as the performance of both devices. The variables n and m are the number of possible performance levels for these devices. P_i and Q_j are the probabilities of possible performance levels for the devices.

3.1.2. Series Device

For a multi-state system covering m elements in series, the operator $\delta$ defines its universal function, as given by Equation (12) [31]:

$${{\displaystyle u}}_s\left(z\right)=\delta \left({{\displaystyle u}}_1\left(z\right),{{\displaystyle u}}_2\left(z\right),\dots {{\displaystyle u}}_m\left(z\right)\right),$$

(12)

Therefore, a simple application on two elements is defined as:

$$\delta \left({{\displaystyle u}}_{{}_1}\left(z\right),{{\displaystyle u}}_{{}_2}\left(z\right)\right)={\displaystyle \sum _{i=1}^n{P}_i{{\displaystyle z}}^{{{\displaystyle a}}_i},{\displaystyle \sum _{j=1}^m}}{{\displaystyle Q}}_{{}_j}{{\displaystyle z}}^{{{\displaystyle b_j}}_{}}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{P}_i{{\displaystyle Q_j}}_{}z{{\displaystyle {}^{{{\displaystyle \min (a_i}}_{},b_j)}}}^{}}}$$

(13)

Consequently, the universal moment function of a series-parallel system is attained by consecutively applying the two operators.

3.1.3. Reliability of the Demand Model

In the field of electrical systems, availability or reliability is defined as the degree of the system’s capacity to fulfill the load request (W), in order to offer sufficient energy (G). This definition of reliability is usually used in the power system design. This index (loss of load probability (LOLP)) is often used to evaluate reliability.

3.2. Redundancy Optimization Method

A bat algorithm with generalized flight (BAG) is a hybridization of the bat algorithm and the GEWA algorithm. It was first introduced by [37] and then applied to manufacturing system scheduling in [38], and to a green economic power dispatch problem in [39]. Our improvement lies in adding a global search function to the classical BA, which is the global flight of the worst bats. Bats with a bad position fly according to a probability αg (explained further in the GEWA algorithm) around the best bat, whereas the other artificial bats follow the principles of the original algorithm, as explained below.

3.2.1. The Bat Algorithm (BA)

The bat algorithm is a swarm metaheuristic that was first developed by [40]. It is inspired by the echolocation of small bats that generate sound waves with given frequencies and pulse rates. The bat algorithm has been feasible to apply in various combinatory and continuous optimization areas, such as environmental economic power dispatch problems [41], datascience [42], medical goods dispatching [43], and operating-room scheduling [44]. One can also see its application in robotics [45] and in energy modeling [46]. In the field of power systems design, the authors of [47] investigated the standard algorithm in a mono optimization version. Researchers continue to explore possible meaningful improvement, and then propose modified versions [48,49,50,51,52].

The frequencies vector f contains integers or real numbers, depending on the selectedminimal and maximal values of frequency, which can be given as:

$$f_i=f_{min}+\left(f_{max}-f_{min}\right) rand (), rand \in \left[0,1\right]$$

(14)

The velocities V of bats is represented by positive double numbers. Velocities suggest the flight of bats, which should be changed at a certain moment. A bat communicates with other bats via the best global solution, g_best, as given by Equation (15):

$${{\displaystyle V}}_i={{\displaystyle V}}_i+\left({{\displaystyle X}}_i-{{\displaystyle g}}_{best}\right){{\displaystyle f}}_i$$

(15)

The location can be either updated with velocity using Equation (16), or via the best overall solution, using the intensity defined by Equation (17):

$${{\displaystyle X}}_i={{\displaystyle best}}_i+{{\displaystyle V}}_i$$

(16)

$${{\displaystyle X}}_i={{\displaystyle g}}_{best}+random(-1,1).{{\displaystyle A}}_{moy}$$

(17)

Or randomly:

$${{\displaystyle X}}_i={{\displaystyle best}}_i+random(-1,1).{{\displaystyle A}}_{moy}$$

(18)

A is the average sound level of bats, which can be given as:

$${{\displaystyle A}}_i={{\displaystyle \alpha A}}_i,\alpha \in \left[0,1\right]$$

(19)

r_i are the pulsation rate values, as defined by Equation (20):

$${\mathrm{r}}_{\mathrm{i}}={\mathrm{r}}_{\mathrm{i}}^0\left(1-{\mathrm{e}}^{\left(-\mathsf{\gamma }\mathrm{t}\right)}\right)$$

(20)

With r_i⁰ as a starting pulsation rate, γ > 0, and t is the rank of the current algorithm generation.

3.2.2. The Generalized Evolutionary Walk Algorithm

GEWA is an algorithm based on a generic optimization principle [53], which has been investigated in [37,41,54]. It is based on a random global search that replaces the poor positions of a population of walkers. The random worst walkers’ steps that are made, using step length d, are given by Equation (21):

d as a length vector follows the solutions definition dimension.

$${{\displaystyle w}}^{{{\displaystyle t}}_{}}={{\displaystyle \epsilon }}^{t}d$$

(21)

The new position of the wrong walkers is generated according to Equation (22):

$${{\displaystyle x}}_{worst}^t={{\displaystyle g}}_{Best}^{t-1}+{{\displaystyle w}}^t$$

(22)

where ε^t is Gaussian distribution or normal distribution N (0, δ). δ can be taken as 1. Additionally, the worst walkers can also move respectively to the solution; the definitions of upper and lower boundaries w_max and w_min are given in Equation (23):

$${{\displaystyle x}}_{worst}^t={{\displaystyle w}}_{\min }+\left({{\displaystyle w}}_{\max }-{{\displaystyle w}}_{\min }\right){{\displaystyle \epsilon }}^t$$

(23)

The GEWA algorithm depends on only two parameters: the size of the walker population and α for control. Typically, α = 0.9 is used.

Most of the generalized evolutionary search of GEWA algorithm was included in the improved BAG algorithm so as to benefit from the advantages of both algorithms described in this subsection.

3.2.3. Bat Algorithm with Evolutionary Generalized Flight (BAG)

The authors of [37] improved the standard bat algorithm with a global flight of the worst bat, as with the principle of the generalized evolutionary walker algorithm. The wrong bat, and eventually many bats, exclusively flyaccording to a global search function following Equations (21) and (23). Simultaneously, the other bats follow the bat algorithm principles, see Algorithm 1 below.

Algorithm 1: Hybridization of the GEWA and BAT in the BAG algorithm.

1 BAG(Nbr_iter: generations number, nb:number of bats) 2 Wmin,wmax, δ, d, αG: GEWA coefficients to be initialized 3 Define objective function f(x), x = (x1…,xnb) 4 Generate a bat population xiand speedsvi, 0 < α < 1; γ > 0 5 Set fmin = 0; fmax = 100; 6 Initialize pulse frequenciesfi: fmin + (fmax − fmin)rand() 7 Initializes pulse: ri0[0.1] and intensities: Ai[1.2]. 8 Evaluate objective function:Fitness(i) ←f(xi), besti←xi 9 Determine the best overall fitnessfgbest←min(fi) and itsgbestpositionand bad fitness 10 fgworst←max(fi) 11 While (index < Nbr_generation) do 12 εiter← uniform(0,δ) 13 Fori←1tonb do 14 if(f (xi) == fgworst) 15 if(rand < αG) 16 w←εindex*d//Flight depends on thestep 17 xi←gbest + w//dependentontheglobalbest 18 else 19 x←wmin + (wmax − wmin)εindex//randomflightin the field 20 End if Else 21 else 22 fi←fmin + (fmax − fmin)rand()//rand [0,1],Adjustedfrequencies 23 vi←vi + (xi − gbest)fi//velocitiesupdate 24 xi←besti + vi//Generate new bats 25 if(rand > ri) 26 xi←gbest+ random(−1,1).Amoy otherwise 27 xi←besti+random(−1,1).Amoy 28 End if 29 if rand < Aiand f(xi) < fitness(i) 30 besti←xi//Accept new solutions 31 ri←ri0(1-exp(-γ.index))//Incrementri 32 Ai←αAi//α] 0, 1[, reduce Ai 33 End if 34 End if else 35 End For 36 Sort bats and save the current bestgbestsolutionandUpdatefgworst 37 index++ 38 End While 39 End

4. Computational Experimentation and Results

4.1. Data

The purpose is to properly pick the optimal combination so as to maximize the reliability and performance, and also to minimize the total budget of a series-parallel power network. This structure has been previously introduced by [55].

The two examples presented afterward are composed of the five main subsystems described below. Two different objective function formulations are considered. In the first example [56], the bi-objective formulation considered was the maximization of system availability and the minimization of system investment cost. The second example in [57] considers a multi-objective formulation that seeks the maximization of system availability, the minimization of system investment cost, and the maximization of the performance system.

The systems considered in the two problems are electrical network systems. The electricity networks that provide energy to users are designed with five basic subsystems, as shown in Figure 2. The entire set of devices in the system are considered as a unit, with a total breakdown. The electricity is delivered by the first column (subsystem 1) and then the transformation by the HVB transformers (Subsystem 2), and thenrouted by the HVB lines (subsystem 3). A second transformation is effected by the HVB/HVA transformers (subsystem 4), where the load is fed through HVA lines (subsystem 5). Each device is characterized by its reliability R_ij, cost C_ij (mls $), and installed capacity G_ij (MW). This supplies energy to users.

To achieve the optimum system, it is necessary to choose the parameters of the algorithms used in this study. Several simulations were done based on increasing or decreasing the parameters mostfound in the literature, as per the following formula:

Parameter r0 = most literature_known_parameter

Parameter _i+1 = Parameter _i±

(24)

Rand() x (max literature_known_parameter− min literature_ known_parameter)

The retained parameters values are:

For GEWA part: αgewa = 0.7, δgewa = 1;

And for BAT part: A_max = 30, A_min = 0.01, α = γ = 0.02.

In addition, for each of the examples, the algorithm BAG was run assuming a population size of 15 and 40 generations.

The metaheuristic chosen in this article was programmed in C++ on a computer with the following characteristics: i5-SSD 256 @ 3.00 GHz 12 GB RAM.

4.1.1. First Example

First, we consider the design of a hybrid gas solar power plant, The data for the various versions of all subsystems are defined in

Table 1. Characteristics of the system elements available [56].

Sub-System	Version	Reliability R [%]	Cost C [mln $]	Performance G [MW]
Power Units	1	0.994	77	65
	2	0.988	64	60
	3	0.996	45	25
HVB Transformers	1	0.996	2.805	120
	2	0.992	2.272	100
	3	0.997	2.594	120
	4	0.993	2.569	100
	5	0.997	1.857	100
HVB Lines	1	0.975	1.985	150
	2	0.987	1.983	140
	3	0.971	1.842	140
	4	0.986	1.318	130
HVB/HVA Transformers	1	0.992	0.842	60
	2	0.982	0.875	80
	3	0.984	0.745	60
	4	0.983	0.654	40
	5	0.957	0.625	30
	6	0.968	0.608	40
	7	0.969	0.492	60
	8	0.979	0.415	30
HVA Lines	1	0.988	0.456	30
	2	0.959	0.432	40
	3	0.989	0.364	20
	4	0.981	0. 283	20
	5	0.968	0.242	10

, as has already been used in [53].

Five subsystems are connected in series, and for all of the subsystems, 3 to 8 various device types, connected in parallel, are available. This table shows that all equipment is represented by reliability R, performance (capacity) G, and cost C.

Table 2. Parameters of the cumulative load [56].

Wm [MW]	140	125	100	60
Tm [h]	1752	1752	3504	1752

shows thecumulative load demand curve, demand level Wm, and the time interval Tm. Reliability is obtained by the probability that its performance is more than or equal to consumption.

4.1.2. Second Example

Second, we take the model of a gas unit; the data for the various versions of all subsystems are shown in

Table 3. Characteristics of the system elements available [57].

Subsystems	Versions	Reliability A [%]	Cost C [mln $]	Capacity Ξ [MW]
Power Units	1	0.980	0.590	120
	2	0.977	0.535	100
	3	0.982	0.470	85
	4	0.978	0.420	85
	5	0.983	0.400	48
	6	0.920	0.180	31
	7	0.984	0.220	26
HVB Transformers	1	0.995	0.205	100
	2	0.996	0.189	92
	3	0.997	0.091	53
	4	0.997	0.056	28
	5	0.998	0.042	21
HVB Lines	1	0.971	7.525	100
	2	0.973	4.720	60
	3	0.971	3.590	40
	4	0.976	2.420	20
HVB/HVA Transformers	1	0.977	0.180	115
	2	0.978	0.160	100
	3	0.978	0.150	91
	4	0.983	0.121	72
	5	0.981	0.102	72
	6	0.971	0.096	72
	7	0.983	0.071	55
	8	0.982	0.049	25
	9	0.977	0.044	25
HVA Lines	1	0.984	0.986	128
	2	0.983	0.825	100
	3	0.987	0.490	60
	4	0.981	0. 475	51

, as has already been modeled by [57].

Five subsystems are connected in series, and for all the subsystems, 4 to 9 various types of components connected in parallel are available.This table indicates that all equipment is represented by reliability R, performance (capacity) G, and cost C.

Table 4. Parameters of the cumulative load [57].

Wm [MW]	100	80	50	200
Tm [h]	4208	788	1228	2536

shows the cumulative load demand curve, demand level Wm, and the time interval Tm. Reliability is obtained using the probability that its performance is more than or equal to consumption.

4.2. Results and Discussion

In order to solve the multi-objective optimization, for each example, different arithmetic Pareto factors were retained in order to put the three objectives (cost, performance, and reliability) in the same scale and to avoid favoring one objective over another. The choice was based essentially on the known middle global cost of each scenario.

Table 5. Optimal design configurations for bi-objective optimization (first problem).

Bi-Objective Optimization: System Availability Maximization and System Cost Minimization
Data	Optimal Configuration	Reliability [%]	Cost [mln $]
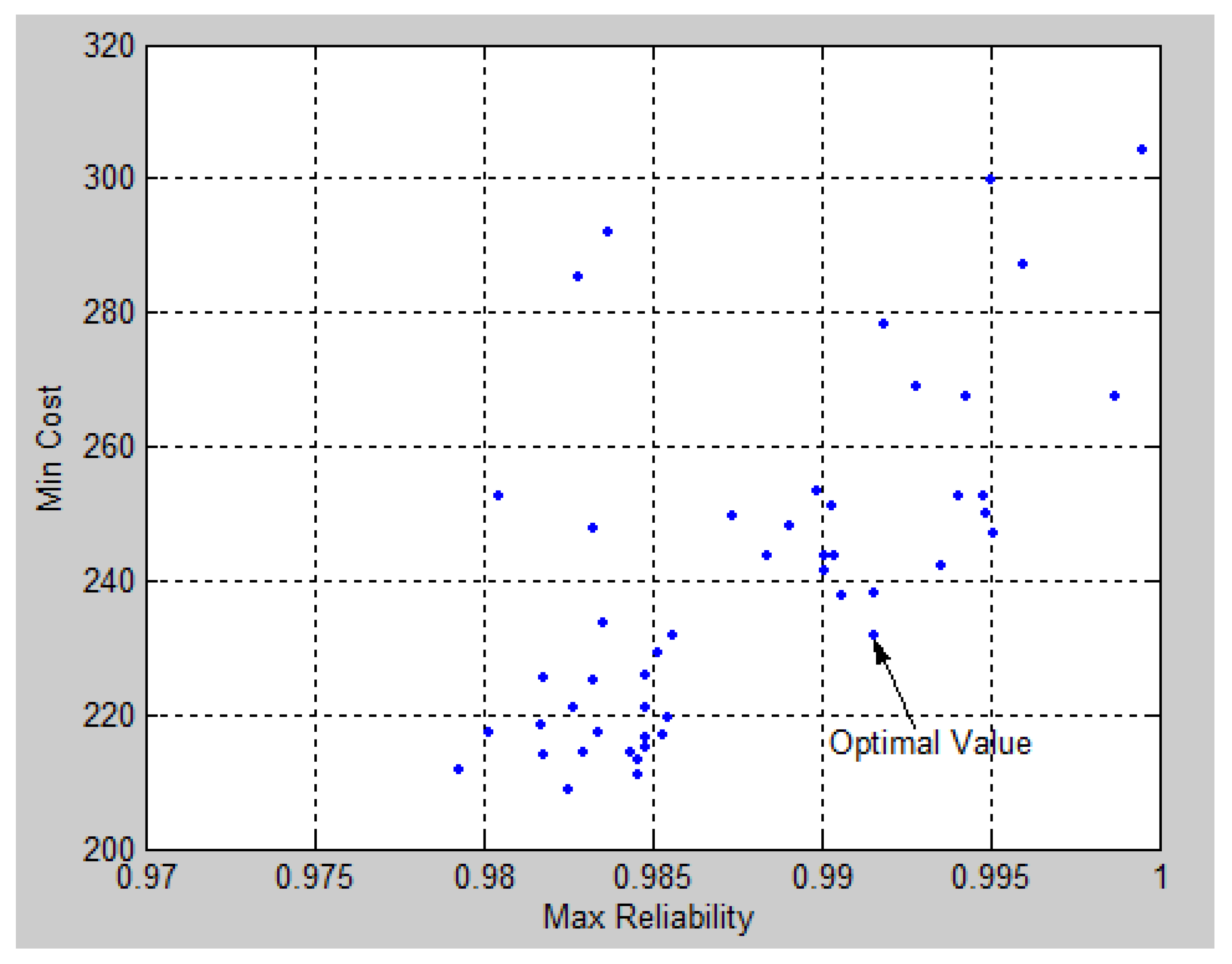
Example 1	Subsystem 1: 1(1)–2(2)	99.16	231.6
	Subsystem 2: 1(1)–3(2)–1(5)
	Subsystem 3: 2(2)–2(3)–1(4)
	Subsystem 4: 2 (2)–1(4)–1(5)
	Subsystem 5: 5(1)–2(2)
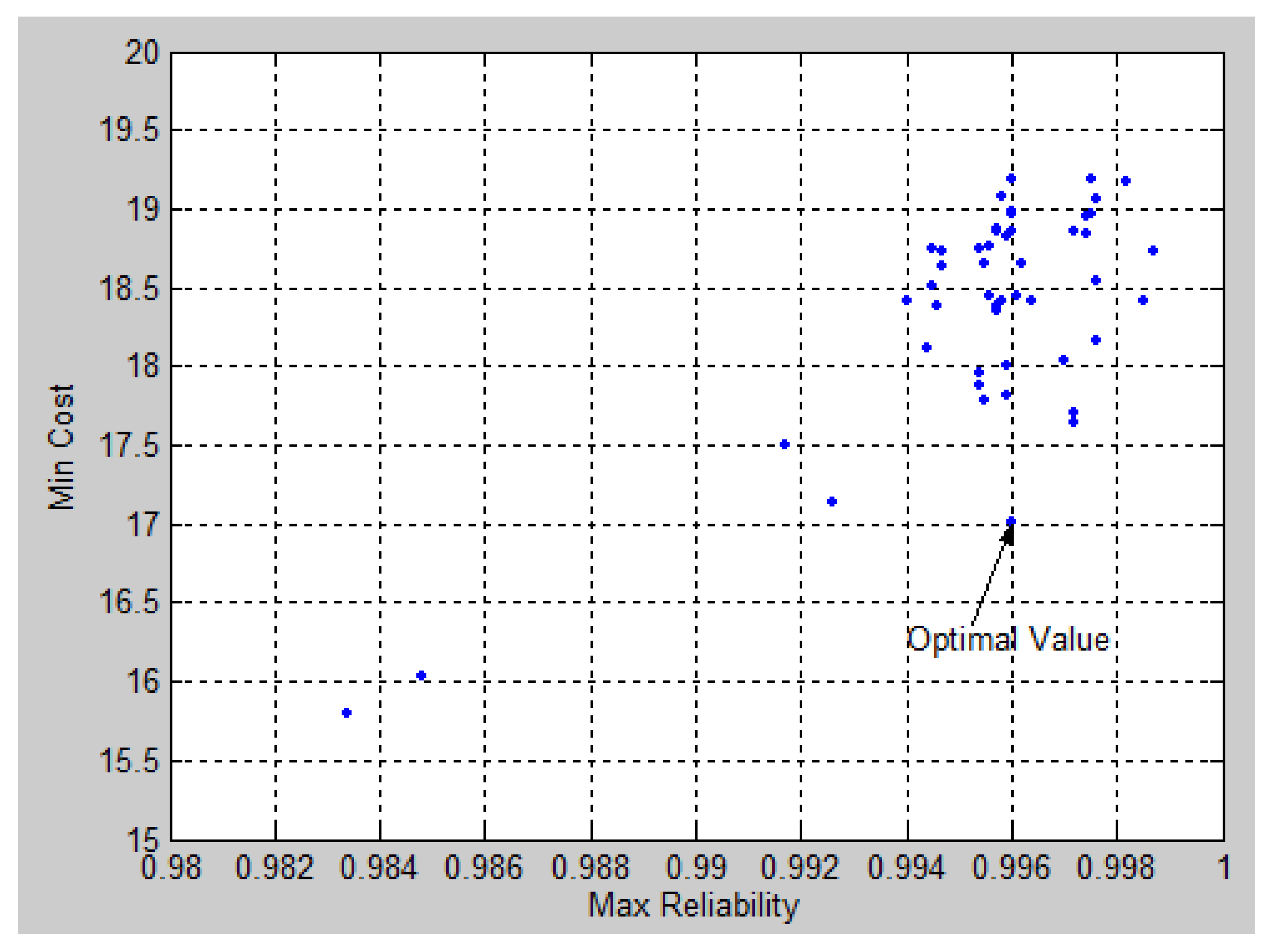
Example 2	Subsystem 1: 5(7)	99.6	17.01
	Subsystem 2: 3(3)–2(4)–1(5)
	Subsystem 3: 3(3)–1(4)
	Subsystem 4: 2(8)–4(9)–1(5)
	Subsystem 5: 2(1)

illustrates the structure of the optimal or approximately optimal system configurations. The purpose is to select the optimal combination of elements used in theseries-parallel electrical power system, which must correspond to the maximization of system availability and the minimization of system investment cost.

The designs shown in Table 5 have good reliability that exceeds 99% and costs that meet those known to be good for the dataset (about USD 231 million for the first example and USD 17million for the second example).

After using BAG to solve this problem, 49 solutions for example 1 were found in the Pareto front, as shown in Figure 3, and 45 solutions for example 2 were found in the Pareto front, as shown in Figure 4. As is shown with an arrow on the values cloud in Figure 3, the optimal value found (USD 231 million with a reliability of 99.1%) through generation and simulations using the multi-objective optimization program meets perfectly the minimum cost with the right reliability, inasmuch as the perfect reliability cost is considerably more (from USD 260 million to more than USD 300 million).

In the fourth figure, it is more obvious how the multi-objective optimization program reaches the best bi-objective solutions (USD 17 million and a reliability of 99.6%) and how there is not any better cost that could be found under that value (USD 17 million) without a loss in system reliability, since a design of one million less (USD 16 million) cannot even reach a reliability of 98.5%.

Table 6. Optimal design configurations for multi-objective optimization (second problem).

Multi-Objective Optimization: Maximization of System Availability, Minimization of System Cost and Maximization of System Performance
Data	Optimal Configuration	Reliability [%]	Performance [MW]	Cost [mln $]
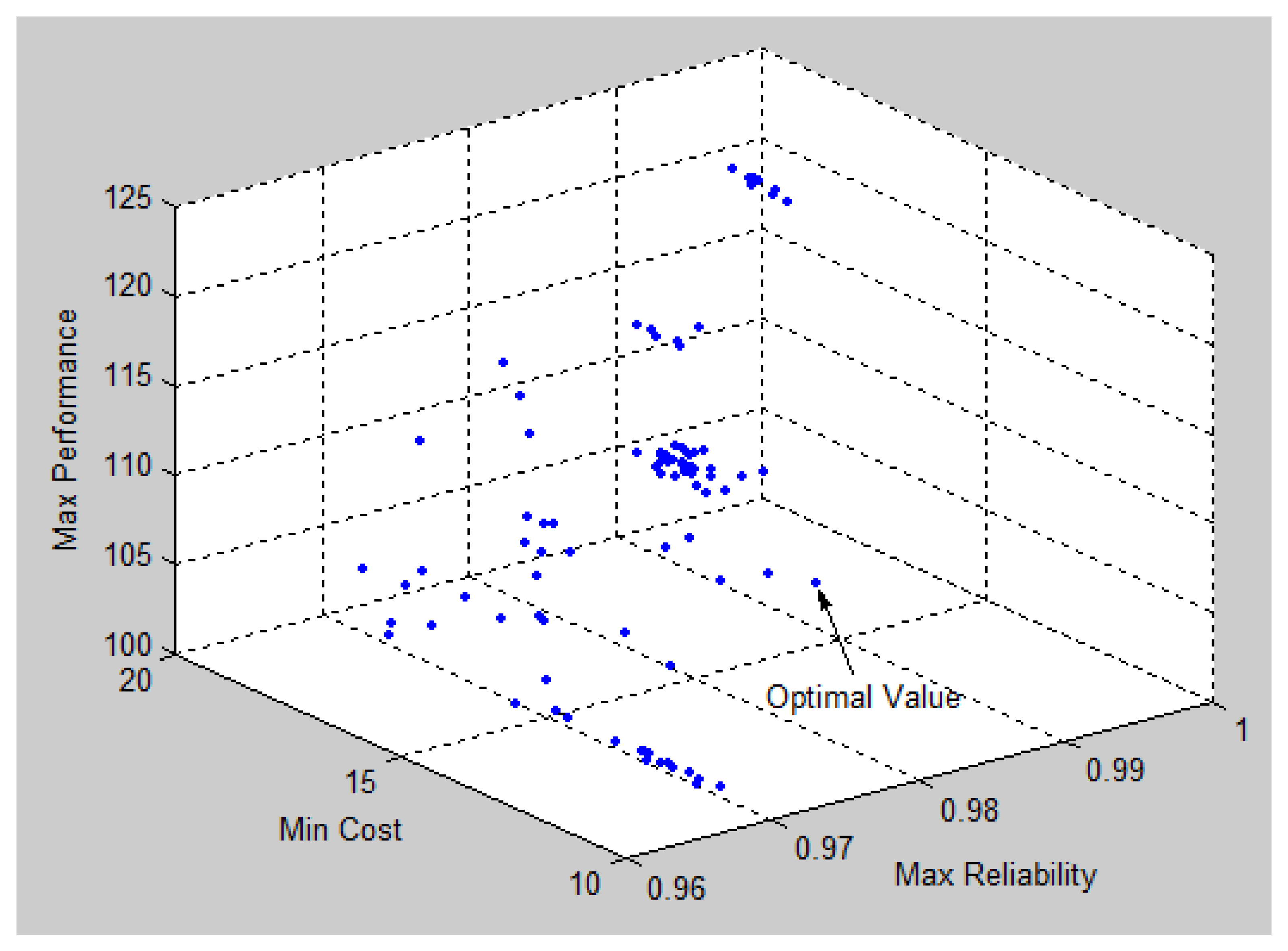
Example 1	Subsystem 1: 1(1)–2(2)	99.21	180	235.5
	Subsystem 2: 4(2)–2(3)–1(5)
	Subsystem 3: 4(4)
	Subsystem 4: 4(2)–1(3)–1(4)
	Subsystem 5: 4(1)–3(3)
Example 2	Subsystem 1: 1(2)	99.42	100	16.88
	Subsystem 2: 6(5)
	Subsystem 3: 4(3)
	Subsystem 4: 6(9)
	Subsystem 5: 3(3)

shows the result of multi-objective optimization, which seeks to maximize system reliability, maximize performance, and minimize series-parallel electrical power system design cost. The designs keep the best reliabilities (99.21% for the first example and 99.42 for the second example) and the best costs (USD 235 million for the first example and USD 16.88 million for the second example) despite seeking good performance (180 for the first example and 100 for the second).

After using BAG to solve this problem, 48 solutions for example 1 were found in the Pareto front, as shown in Figure 5, and81 solutions for example 2 were found in the Pareto front, as shown in Figure 6.

As is presented in the 3-dimensional Pareto values clouds, better performances could be reached if reliability or cost purposes are neglected. This is why the multi-objective design optimization program promotes correct multi-objective solutions with the most suitable cost, performance and reliability values, especially due to the choice of equitable Pareto and scale factors.

Multi-objective and bi-objective designs satisfy cost and reliability constraints. To illustrate this, the best bi- and multi-objective solutions for the second example are compared to the figures from the literatureas the known best cost, individually optimized, in

Table 7. Comparison between bi- and multi-objective design values, and individually optimized cost.

Subsystem		Bi-Objective	Multi-Objective	Best Cost Individually
		Best Solution	Best Solution	Optimized [20]
System Design	Subsystem 1	5(7)	1(2)	2(1)
	Subsystem 2	3(3)–2(4)–1(5)	6(5)	3(2)
	Subsystem 3	3(3)–1(4)	4(3)	2(2) 3(1)
	Subsystem 4	2(8)–4(9)–1(5)	6(9)	6(1) 7(2)
	Subsystem 5	2(1)	3(3)	3(1) 4(2)
Cost [mlm $]	17.01		16.88	15.425
Reliability [%]	99.66		99.42	99.1

. Our compromised costs (16.88 and 17.01) are still in the range of the known best cost found in the literature (15.425), whereas their corresponding reliabilities (99.42% and 99.6%) topped the corresponding reliability found in the cost for the mono-optimization design (99.1%).

5. Conclusions

In this article, we have proposed a resolution for the multi-state heterogeneousseries- parallel electrical power system design multi-objective problem, considering the necessity of high reliability and a lower budget. Two variants of multi-objective redundancy optimization were mathematically formulated. For the purpose of minimizing investment cost and maximizing reliability and performance, some constraints were added, to findthe best range of solutions. The multi-objective functions of cost, reliability and performance were formulated as a Pareto function, taking into account the penalty of constraints abuse.

The optimization methodology was based on an improved hybrid algorithm, based overall on the bat algorithm (BA) and a global search function similar to the generalized evolutionary walk algorithm (GEWA). The power of the chosen method lies in adding a global search function, or the flight of the worst bat. As the performance and the reliability of an electrical system are implicitly dependent, the universal general function (UMGF), also known as the Ushakov technique, was used.

Two different power system design allocation examples are presented, to illustrate the performance of the developed algorithm. The choice of value was based on a middle budget and cost of each system, and also the performance of components. First, the design of a hybrid gas solar power plant was considered, with five subsystems connected in series, and for all of the subsystems, three to eightassorteddevices. Second, the design of the gasunit was considered asfive subsystems connected in series, and for all the subsystems, four to nine various types of components. Each device is characterized by its reliability R_ij (%), cost C_ij (mls $), and installed capacity G_ij (MW).

Pareto and scale factors were customized for each dataset according to the known interval of system cost, as the multi-objective function is also based on a probability that ranges from 0 to 1.

As shown in the paper, the setting of parameters of the bat algorithm with generalized flight (BAG) were not easily determined, due to the number of parameters of GEWA and BAT metaheuristics. The known used parameter values of each algorithm can be found separately in the literature for continuous optimization rather than highly complex combinatorial problems. Thatia why intensive experimentation was needed for this combinatorial redundancy problem.

Regarding time efficiency, the proposed improved metaheuristic for multi-objective optimization, using the Ushakov approach for objective function evaluation, ensured a rapid execution time.

After using a bat algorithm with generalized flight to solve a bi-objective problem that aimed to maximize reliability and minimize cost under constraints, 49 solutions for example 1 and 45 solutions for example 2 were found in the Pareto front. The optimalvalues found through generation and simulations using the bi-objective optimization design meet perfectly the minimum cost with the right reliability, inasmuch as the perfect reliability cost was considerably more.

The result of multi-objective optimization that seeks to maximize system reliability, maximize performance and minimize design cost, showed that the design kept the best reliabilities and the best costs despite the fact of searching for good performances. After using the bat algorithm with generalized flight to solve this problem, 48 solutions for the first example and 81 solutions for the second example were found in the Pareto front.

However, in addition to confirming how multi-objective and bi-objective designs satisfy either cost or reliability constraints, the compromised value had to be compared to theliterature’s known best value. In the bat algorithm with generalized flight, compromised costs are still in the range of the known best cost found in the literature, whereas their corresponding reliabilities conquered the corresponding reliability found in the cost mono-optimization design. If the goal is to design an efficient power system, the proposed improved approach can at least seek an optimum design for a gas system and for a solar plant system.

The actual work might reveal the power of the proposed metaheuristic to solve such high-complexity combinatorial multi-objective problems. The premature problem of convergence could be avoided through the use of various global search parts in the improved bat algorithm with generalized flight, good discretization and finally the careful choice of parameter values.

Currently, work is ongoing to extensively study the non-heterogenous networks and preventive maintenance of a multi-state power system.