Towards Scalable Economic Photovoltaic Potential Analysis Using Aerial Images and Deep Learning
Abstract
:1. Introduction
1.1. Existing PV Potential Analysis with Respect to Potential Type
1.2. Existing PV Potential Analysis with Respect to Method
1.3. Contributions of the Paper
- A methodology for scalable, bottom-up, economic PV potential analysis using aerial images and deep learning as well as publicly available data;
- The application of CNNs for semantic segmentation of roof segments and roof superstructure. Initial results are discussed to point out the advantages and disadvantages of the methodology;
- A comprehensive summary of research challenges and opportunities for this novel approach.
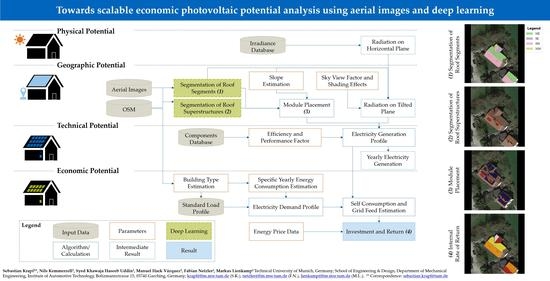
2. Materials and Methods
2.1. Physical Potential
2.2. Geographic Potential
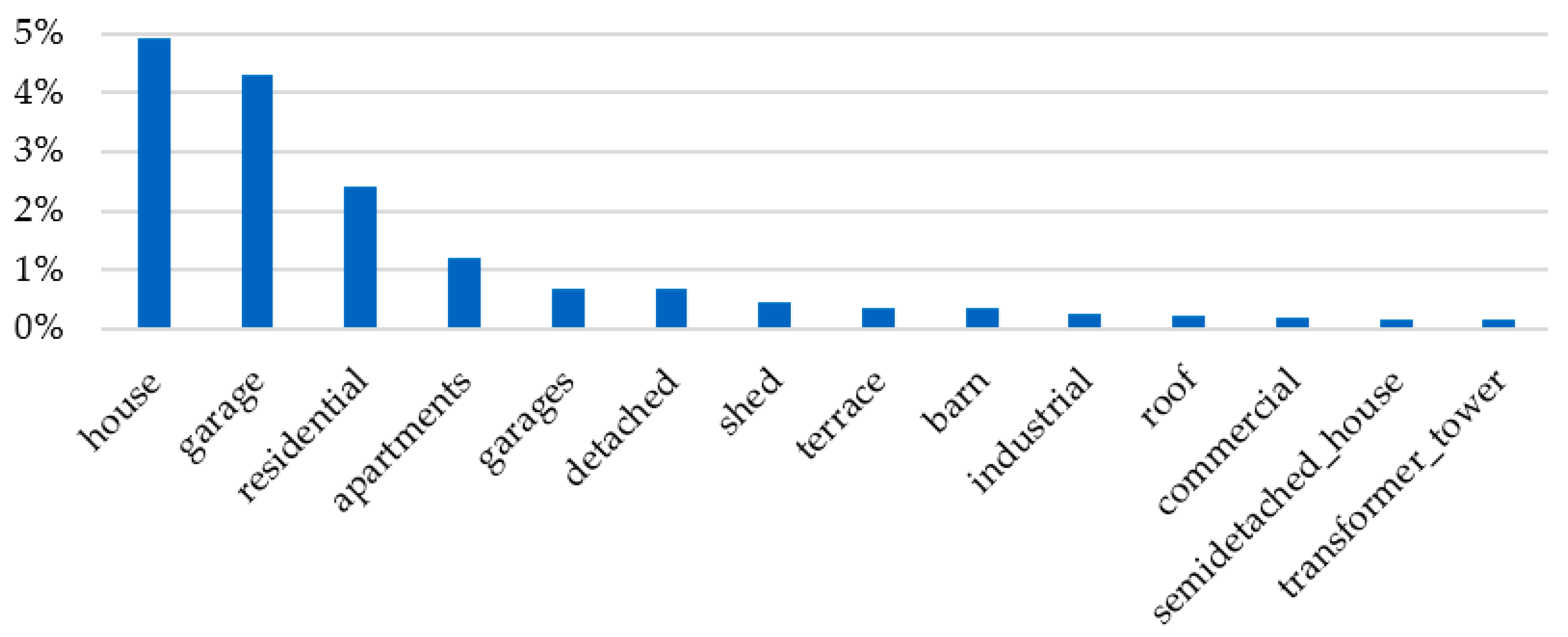
2.2.1. Datasets for Semantic Segmentation
2.2.2. Performance Evaluation of Semantic Segmentation
2.2.3. Semantic Segmentation for Roof Segments
2.2.4. Semantic Segmentation for Roof Superstructures
2.3. Technical Potential
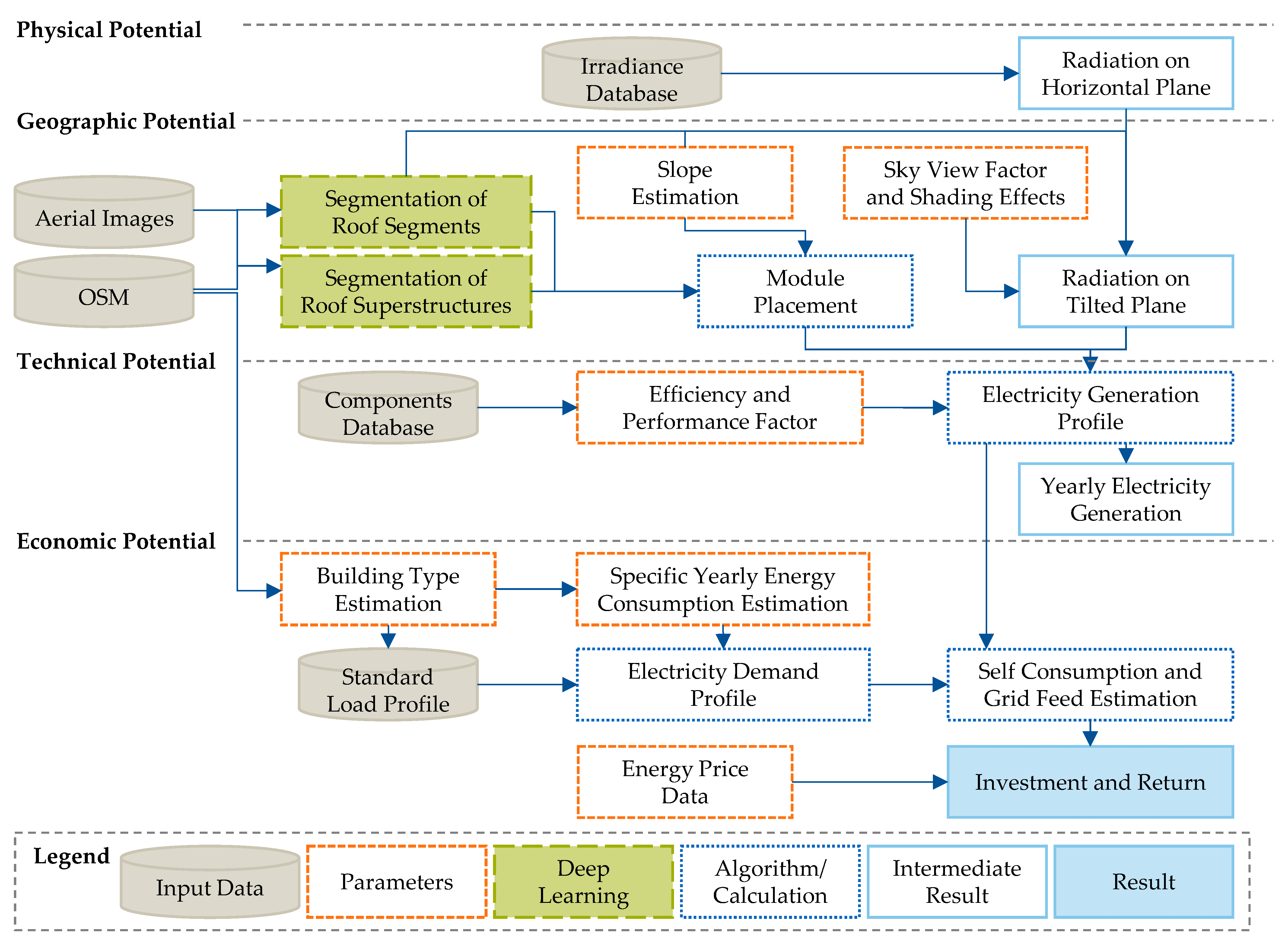
2.4. Economic Potential
2.5. Case Study and Parameterization
3. Results and Discussion
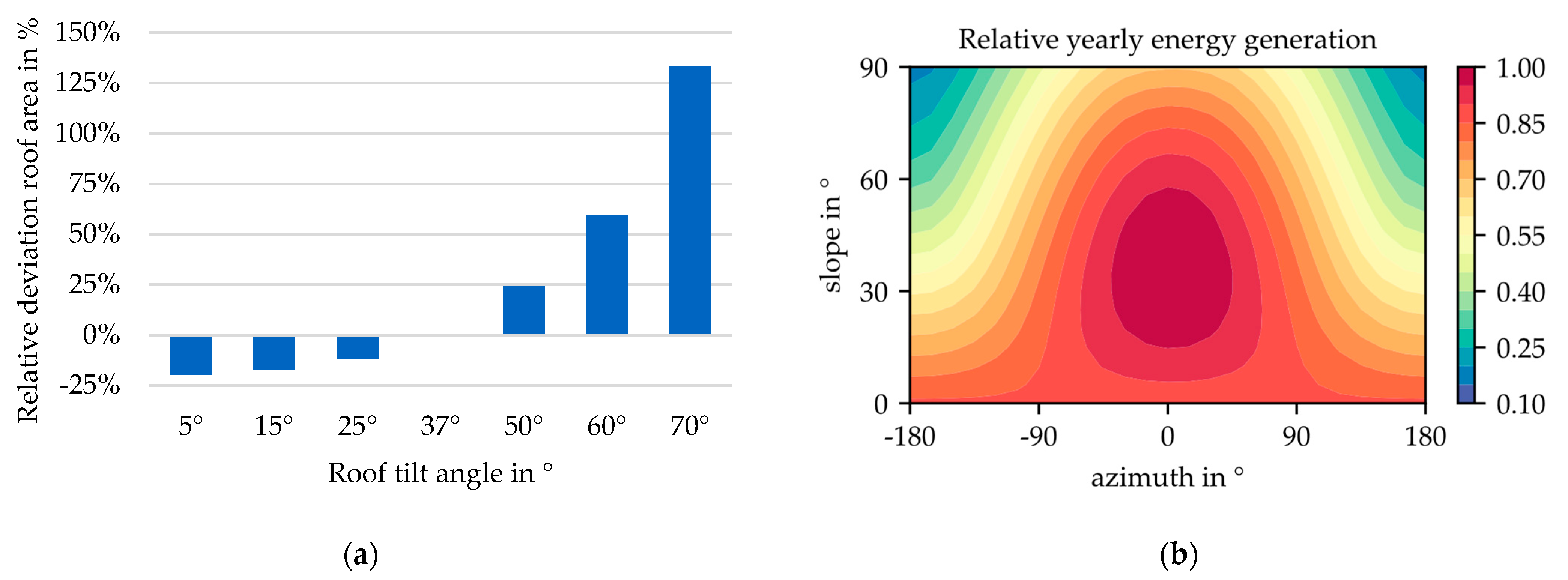
3.1. Results Convolutional Neural Networks
3.2. Results Economic Potential
3.3. Comparison of Aerial Image and LiDAR Based Approach
4. Research Opportunities
4.1. Deep Learning for Extraction of Roof Information
4.2. Improving Economic PV Potential Estimation Based on Aerial Images
4.3. Using Economic PV Potential for Energy System Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Calculations
| Calculation of the Technical Potential | |
| Physical Potential | |
| Geographic Potential | |
| Global Irradiation on Tilted Surface | |
| Effective Irradiation on Tilted Surface | |
| Module Area on a Tilted Surface | |
| Technical Potential | |
| Calculation of the Economic Potential | |
| Investment Costs | |
| Maintenance Costs | |
| Weighted Average Cost of Capital | |
| Self-Consumption Ratio | |
| Fed-In Electricity Within One Year | |
| Self-Consumed Electricity Within One Year | |
| Net Present Value | |
| Revenues from Feed-In | |
| Revenues from Self-Consumption | |
| EEG-levy (Levy for self-consumption in Germany) | |
| Variable | Unit | Description | Variable | Unit | Description |
|---|---|---|---|---|---|
| m² | Projected Horizontal Module | - | Self-Consumption Rate | ||
| m² | Area all Modules on Segment | € | Debt | ||
| - | Degradation Rate | - | Hurdle Rate | ||
| m | Module Width | kWh/m² | Ground-Reflected Irradiation on a Tilted Surface | ||
| € | Maintenance Costs | kWh/m² | Diffuse Irradiation on a Tilted Surface | ||
| € | Fix maintenance Costs | kWh/m² | Direct Irradiation on a Tilted Surface | ||
| €/kWp | Variable maintenance Costs | kWh/m² | Effective Irradiation on a Tilted Surface | ||
| € | Costs from EEG Levy | kWh/m² | Global Irradiation on a Tilted Surface | ||
| € | Investment Costs | kWh/m² | Diffuse Irradiation on a Horizontal Surface | ||
| €/kWh | EEG Levy | kWh/m² | Direct Irradiation on a Horizontal Surface | ||
| - | Yearly Change EEG Levy | kWh/m² | Global Irradiation on a Horizontal Surface | ||
| €/kWp | Specific Investment Costs | - | Internal Rate of Return | ||
| kWh | Self-Consumption | Interest Rate (Equity) | |||
| kWh | Feed-In Electricity | Interest Rate (Debt) | |||
| kWh | Geographic Potential | - | Inflation Rate | ||
| kWh | Economic Potential | € | Net Present Value | ||
| kWh/m² | Physical Potential | m | Length of pv Module | ||
| kWh | Technical Potential | - | Value Added Tax | ||
| kWh | Electricity Consumption | - | Utilization Factor Irradiation | ||
| € | Equity | kWp | Plant Size | ||
| €/kWh | Feed-In Tariff |
Appendix B. Technical and Economic Assumptions
| Factor | Variable | Value |
|---|---|---|
| Module Placement on Flat Roofs | South-Orientation | |
| Area Usage on Flat Roofs | F | 1:2 |
| Module Slope on Flat Roofs | - | 36° |
| Shadow Utilization Factor | 0.85 | |
| Performance Ratio | 0.80 | |
| Module Peak Power | 300 Wp | |
| Efficiency | 20.0% | |
| Module Length | 1650 mm | |
| Module Width | 992 mm |
| Factor | Variable | Value | Source |
|---|---|---|---|
| Specific Investment Costs (incl. Value-added tax, VAT) | 1071 €/kWp | [3] + VAT | |
| Maintenance Costs Variable | 22.50 €/kWp | [3,100] | |
| Maintenance Cost Fix | 100.00 € | [3,100] | |
| Electricity Price | 30 ct/kWh | Assumption | |
| Yearly Change of Electricity Price | 2.0% | Assumption | |
| Feed-In Tariff up to 10 kWp | 7.81 ct/kWh | [101] | |
| Feed-In Tariff up to 40 kWp | 7.59 ct/kWh | [101] | |
| Feed-In Tariff up to 100 kWp | 5.95 ct/kWh | [101] | |
| EEG-Levy | 6.50 ct/kWh | [102] | |
| Interest Rate Equity | 6.0% | [103] (p 159) | |
| Interest Rate Debt | 2.0% | [104] | |
| Debt Ratio | 80.0% | [3] | |
| Inflation Rate | 1.5% | Assumption | |
| Degradation | 0.25% | [105,106] | |
| Time Horizon | 20a | [3,107,108] |
References
- Apostoleris, H.; Sgouridis, S.; Stefancich, M.; Chiesa, M. Evaluating the factors that led to low-priced solar electricity projects in the Middle East. Nat. Energy 2018, 3, 1109–1114. [Google Scholar] [CrossRef]
- Apostoleris, H.; Al Ghaferi, A.; Chiesa, M. What is going on with Middle Eastern solar prices, and what does it mean for the rest of us? Prog. Photovolt. Res. Appl. 2021, 29, 638–648. [Google Scholar] [CrossRef]
- Kost, C.; Shammugam, S.; Jülch, V.; Nguyen, H.-T.; Schlegl, T. Levelized cost of electricity renewable energy. Fraunhofer Inst. Sol. Energy Syst. ISE 2013, 144, 1–40. [Google Scholar]
- Mavsar, P.; Sredenšek, K.; Štumberger, B.; Hadžiselimović, M.; Seme, S. Simplified Method for Analyzing the Availability of Rooftop Photovoltaic Potential. Energies 2019, 12, 4233. [Google Scholar] [CrossRef] [Green Version]
- Walch, A.; Castello, R.; Mohajeri, N.; Scartezzini, J.-L. Big data mining for the estimation of hourly rooftop photovoltaic potential and its uncertainty. Appl. Energy 2020, 262, 114404. [Google Scholar] [CrossRef]
- Martín-Chivelet, N. Photovoltaic potential and land-use estimation methodology. Energy 2016, 94, 233–242. [Google Scholar] [CrossRef]
- Mainzer, K.; Killinger, S.; McKenna, R.; Fichtner, W. Assessment of rooftop photovoltaic potentials at the urban level using publicly available geodata and image recognition techniques. Sol. Energy 2017, 155, 561–573. [Google Scholar] [CrossRef] [Green Version]
- Izquierdo, S.; Rodrigues, M.; Fueyo, N. A method for estimating the geographical distribution of the available roof surface area for large-scale photovoltaic energy-potential evaluations. Sol. Energy 2008, 82, 929–939. [Google Scholar] [CrossRef]
- Suri, M.; Hofierka, J. A New GIS-based Solar Radiation Model and Its Application to Photovoltaic Assessments. Trans. GIS 2004, 8, 175–190. [Google Scholar] [CrossRef]
- European Commission. Photovoltaic Geographical Information System. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/#PVP (accessed on 8 June 2021).
- Copernicus Atmosphere Monitoring Service. Available online: https://ads.atmosphere.copernicus.eu/cdsapp#!/home (accessed on 8 June 2021).
- Tiwari, A.; Meir, I.A.; Karnieli, A. Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto. Remote Sens. 2020, 12, 223. [Google Scholar] [CrossRef] [Green Version]
- Jochem, A.; Höfle, B.; Rutzinger, M.; Pfeifer, N. Automatic roof plane detection and analysis in airborne lidar point clouds for solar potential assessment. Sensors 2009, 9, 5241–5262. [Google Scholar] [CrossRef]
- Brito, M.C.; Gomes, N.; Santos, T.; Tenedório, J.A. Photovoltaic potential in a Lisbon suburb using LiDAR data. Sol. Energy 2012, 86, 283–288. [Google Scholar] [CrossRef]
- Hofierka, J.; Kaňuk, J. Assessment of photovoltaic potential in urban areas using open-source solar radiation tools. Renew. Energy 2009, 34, 2206–2214. [Google Scholar] [CrossRef]
- Margolis, R.; Gagnon, P.; Melius, J.; Phillips, C.; Elmore, R. Using GIS-based methods and lidar data to estimate rooftop solar technical potential in US cities. Environ. Res. Lett. 2017, 12, 74013. [Google Scholar] [CrossRef]
- Hong, T.; Lee, M.; Koo, C.; Jeong, K.; Kim, J. Development of a method for estimating the rooftop solar photovoltaic (PV) potential by analyzing the available rooftop area using Hillshade analysis. Appl. Energy 2017, 194, 320–332. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Scartezzini, J.-L. Quantifying rooftop photovoltaic solar energy potential: A machine learning approach. Sol. Energy 2017, 141, 278–296. [Google Scholar] [CrossRef]
- Bergamasco, L.; Asinari, P. Scalable methodology for the photovoltaic solar energy potential assessment based on available roof surface area: Further improvements by ortho-image analysis and application to Turin (Italy). Sol. Energy 2011, 85, 2741–2756. [Google Scholar] [CrossRef] [Green Version]
- Lingfors, D.; Bright, J.M.; Engerer, N.A.; Ahlberg, J.; Killinger, S.; Widén, J. Comparing the capability of low- and high-resolution LiDAR data with application to solar resource assessment, roof type classification and shading analysis. Appl. Energy 2017, 205, 1216–1230. [Google Scholar] [CrossRef]
- Defaix, P.R.; van Sark, W.G.J.H.M.; Worrell, E.; de Visser, E. Technical potential for photovoltaics on buildings in the EU-27. Sol. Energy 2012, 86, 2644–2653. [Google Scholar] [CrossRef] [Green Version]
- Schallenberg-Rodríguez, J. Photovoltaic techno-economical potential on roofs in regions and islands: The case of the Canary Islands. Methodological review and methodology proposal. Renew. Sustain. Energy Rev. 2013, 20, 219–239. [Google Scholar] [CrossRef]
- Miranda, R.F.C.; Szklo, A.; Schaeffer, R. Technical-economic potential of PV systems on Brazilian rooftops. Renew. Energy 2015, 75, 694–713. [Google Scholar] [CrossRef]
- Sun, Y.-W.; Hof, A.; Wang, R.; Liu, J.; Lin, Y.-J.; Yang, D.-W. GIS-based approach for potential analysis of solar PV generation at the regional scale: A case study of Fujian Province. Energy Policy 2013, 58, 248–259. [Google Scholar] [CrossRef]
- Lee, M.; Hong, T.; Jeong, K.; Kim, J. A bottom-up approach for estimating the economic potential of the rooftop solar photovoltaic system considering the spatial and temporal diversity. Appl. Energy 2018, 232, 640–656. [Google Scholar] [CrossRef]
- Lee, M.; Hong, T.; Jeong, J.; Jeong, K. Development of a rooftop solar photovoltaic rating system considering the technical and economic suitability criteria at the building level. Energy 2018, 160, 213–224. [Google Scholar] [CrossRef]
- Brito, M.C.; Freitas, S.; Guimarães, S.; Catita, C.; Redweik, P. The importance of facades for the solar PV potential of a Mediterranean city using LiDAR data. Renew. Energy 2017, 111, 85–94. [Google Scholar] [CrossRef]
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef] [Green Version]
- Weniger, J.; Tjaden, T.; Quaschning, V. Sizing of Residential PV Battery Systems. Energy Procedia 2014, 46, 78–87. [Google Scholar] [CrossRef] [Green Version]
- O’Shaughnessy, E.; Cutler, D.; Ardani, K.; Margolis, R. Solar plus: Optimization of distributed solar PV through battery storage and dispatchable load in residential buildings. Appl. Energy 2018, 213, 11–21. [Google Scholar] [CrossRef]
- Mariaud, A.; Acha, S.; Ekins-Daukes, N.; Shah, N.; Markides, C.N. Integrated optimisation of photovoltaic and battery storage systems for UK commercial buildings. Appl. Energy 2017, 199, 466–478. [Google Scholar] [CrossRef]
- Melius, J.; Margolis, R.; Ong, S. Estimating Rooftop Suitability for PV: A Review of Methods, Patents, and Validation Techniques; NREL/TP-6A20-60593; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2013.
- Freitas, S.; Catita, C.; Redweik, P.; Brito, M.C. Modelling solar potential in the urban environment: State-of-the-art review. Renew. Sustain. Energy Rev. 2015, 41, 915–931. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Scartezzini, J.-L. Estimation of Large-Scale Solar Rooftop PV Potential for Smart Grid Integration: A Methodological Review. In Sustainable Interdependent Networks; Amini, M.H., Boroojeni, K.G., Iyengar, S.S., Pardalos, P.M., Blaabjerg, F., Madni, A.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 173–219. ISBN 978-3-319-74411-7. [Google Scholar]
- Lehmann, H.; Peter, S. Assessment of Roof & Façade Potentials for Solar Use in Europe; Institute for Sustainable Solutions and Innovations (ISUSI): Aachen, Germany, 2003. [Google Scholar]
- Kolbe, T.H. Representing and Exchanging 3D City Models with CityGML. In 3D Geo-Information Sciences; Cartwright, W., Gartner, G., Meng, L., Peterson, M.P., Lee, J., Zlatanova, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 15–31. ISBN 978-3-540-87394-5. [Google Scholar]
- Willenborg, B.; Pültz, M.; Kolbe, T.H. Integration of Semantic 3d City Models and 3d Mesh Models for Accuracy Improvements of Solar Potential Analyses. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, XLII-4/W10, 223–230. [Google Scholar] [CrossRef] [Green Version]
- Romero Rodríguez, L.; Duminil, E.; Sánchez Ramos, J.; Eicker, U. Assessment of the photovoltaic potential at urban level based on 3D city models: A case study and new methodological approach. Sol. Energy 2017, 146, 264–275. [Google Scholar] [CrossRef]
- Jakubiec, J.A.; Reinhart, C.F. A method for predicting city-wide electricity gains from photovoltaic panels based on LiDAR and GIS data combined with hourly Daysim simulations. Sol. Energy 2013, 93, 127–143. [Google Scholar] [CrossRef]
- Song, X.; Huang, Y.; Zhao, C.; Liu, Y.; Lu, Y.; Chang, Y.; Yang, J. An Approach for Estimating Solar Photovoltaic Potential Based on Rooftop Retrieval from Remote Sensing Images. Energies 2018, 11, 3172. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, P.; Margolis, R.; Melius, J.; Phillips, C.; Elmore, R. Estimating rooftop solar technical potential across the US using a combination of GIS-based methods, lidar data, and statistical modeling. Environ. Res. Lett. 2018, 13, 24027. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Scartezzini, J.-L. Large-scale rooftop solar photovoltaic technical potential estimation using Random Forests. Appl. Energy 2018, 217, 189–211. [Google Scholar] [CrossRef]
- Mapdwell. Solar System Cambridge. Available online: https://mapdwell.com/en/solar/cambridge (accessed on 28 April 2021).
- Google. Project Sunroof. Available online: https://www.google.com/get/sunroof/data-explorer/ (accessed on 8 June 2021).
- Tetraeder.solar gmbh. Solar Potential Maps for Municipalities. Available online: https://solar.tetraeder.com/en_v2/municipalities/spm/ (accessed on 28 April 2021).
- Hazelhoff, L.; With, P.N. Localization of buildings with a gable roof in very-high-resolution aerial images. In Proceedings of the IS&T/SPIE Electronic Imaging, Visual Information Processing and Communication II, San Francisco, CA, USA, 31 January 2011; Volume 7882, p. 788208. [Google Scholar] [CrossRef]
- Guru, D.S.; Shekar, B.H.; Nagabhushan, P. A simple and robust line detection algorithm based on small eigenvalue analysis. Pattern Recognit. Lett. 2004, 25, 1–13. [Google Scholar] [CrossRef]
- Fan, H.; Yao, W.; Fu, Q. Segmentation of Sloped Roofs from Airborne LiDAR Point Clouds Using Ridge-Based Hierarchical Decomposition. Remote Sens. 2014, 6, 3284–3301. [Google Scholar] [CrossRef] [Green Version]
- El Merabet, Y.; Meurie, C.; Ruichek, Y.; Sbihi, A.; Touahni, R. Building roof segmentation from aerial images using a lineand region-based watershed segmentation technique. Sensors 2015, 15, 3172–3203. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Be, K. Topological structural analysis of digitized binary images by border following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Nvidia: Santa Clara, CA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Shi, Y.; Auer, S.; Roschlaub, R.; Möst, K.; Schmitt, M.; Glock, C.; Zhu, X. Detection of Undocumented Building Constructions from Official Geodata Using a Convolutional Neural Network. Remote Sens. 2020, 12, 3537. [Google Scholar] [CrossRef]
- Wei, S.; Ji, S.; Lu, M. Toward Automatic Building Footprint Delineation From Aerial Images Using CNN and Regularization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2178–2189. [Google Scholar] [CrossRef]
- Yu, J.; Wang, Z.; Majumdar, A.; Rajagopal, R. DeepSolar: A Machine Learning Framework to Efficiently Construct a Solar Deployment Database in the United States. Joule 2018, 2, 2605–2617. [Google Scholar] [CrossRef] [Green Version]
- Mayer, K.; Wang, Z.; Arlt, M.-L.; Neumann, D.; Rajagopal, R. DeepSolar for Germany: A deep learning framework for PV system mapping from aerial imagery. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), 2020/09, Istanbul, Turkey, 7–9 September 2020; IEEE: Piscataway, NJ, USA, 2020. ISBN 9781728147017. [Google Scholar]
- Castello, R.; Roquette, S.; Esguerra, M.; Guerra, A.; Scartezzini, J.-L. Deep learning in the built environment: Automatic detection of rooftop solar panels using Convolutional Neural Networks. J. Phys. Conf. Ser. 2019, 1343, 12034. [Google Scholar] [CrossRef]
- Huang, Z.; Mendis, T.; Xu, S. Urban solar utilization potential mapping via deep learning technology: A case study of Wuhan, China. Appl. Energy 2019, 250, 283–291. [Google Scholar] [CrossRef]
- Lee, S.; Iyengar, S.; Feng, M.; Shenoy, P.; Maji, S. Deeproof: A data-driven approach for solar potential estimation using rooftop imagery. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Teredesai, A., Kumar, V., Li, Y., Rosales, R., Terzi, E., Karypis, G., Eds.; ACM: New York, NY, USA, 2019; pp. 2105–2113, ISBN 9781450362016. [Google Scholar]
- OpenStreetMap Contributors. OpenStreetMap. Available online: https://www.openstreetmap.org (accessed on 23 June 2021).
- Google Maps. Google Maps. Available online: https://www.google.de/maps (accessed on 8 June 2021).
- Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Killius, N.; Betcke, J.; Lefèvre, M.; Wald, L.; Wey, E.; Saboret, L. User’s Guide to the CAMS Radiation Service (CRS): Status December 2018. Available online: http://www.soda-pro.com/documents/10157/326332/CAMS72_2015SC3_D72.1.3.1_2018_UserGuide_v1_201812.pdf/95ca8325-71f6-49ea-b5a6-8ae4557242bd (accessed on 23 June 2021).
- Brovelli, M.; Zamboni, G. A New Method for the Assessment of Spatial Accuracy and Completeness of OpenStreetMap Building Footprints. ISPRS Int. J. Geo Inf. 2018, 7, 289. [Google Scholar] [CrossRef] [Green Version]
- Google. Google Maps Static API. Available online: https://developers.google.com/maps/documentation/maps-static/overview (accessed on 23 June 2021).
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef] [Green Version]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. JOSS 2018, 3, 884. [Google Scholar] [CrossRef] [Green Version]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef] [Green Version]
- Walch, A.; Castello, R.; Mohajeri, N.; Guignard, F.; Kanevski, M.; Scartezzini, J.-L. Spatio-temporal modelling and uncertainty estimation of hourly global solar irradiance using Extreme Learning Machines. Energy Procedia 2019, 158, 6378–6383. [Google Scholar] [CrossRef]
- Brito, M.C.; Redweik, P.; Catita, C.; Freitas, S.; Santos, M. 3D Solar Potential in the Urban Environment: A Case Study in Lisbon. Energies 2019, 12, 3457. [Google Scholar] [CrossRef] [Green Version]
- Gutschner, M.; Nowak, S.; Ruoss, D.; Toggweiler, P.; Schoen, T. Potential for building integrated photovoltaics. In IEA-PVPS Task; International Energy Agency: Paris, France, 2002; Volume 7. [Google Scholar]
- Takebayashi, H.; Ishii, E.; Moriyama, M.; Sakaki, A.; Nakajima, S.; Ueda, H. Study to examine the potential for solar energy utilization based on the relationship between urban morphology and solar radiation gain on building rooftops and wall surfaces. Sol. Energy 2015, 119, 362–369. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Pearce, J.M. Incorporating shading losses in solar photovoltaic potential assessment at the municipal scale. Solar Energy 2012, 86, 1245–1260. [Google Scholar] [CrossRef] [Green Version]
- Mainzer, K. Analyse und Optimierung urbaner Energiesysteme—Entwicklung und Anwendung eines übertragbaren Modellierungswerkzeugs zur Nachhaltigen Systemgestaltung. Ph.D. Dissertation, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2019. [Google Scholar]
- Chen, Q.; Wang, L.; Wu, Y.; Wu, G.; Guo, Z.; Waslander, S.L. Aerial Imagery for Roof Segmentation: A Large-Scale Dataset towards Automatic Mapping of Buildings. ISPRS J. Photogramm. Remote. Sens. 2019, 147, 42–55. [Google Scholar] [CrossRef] [Green Version]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can semantic labeling methods generalize to any city? The inria aerial image labeling benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3226–3229, ISBN 978-1-5090-4951-6. [Google Scholar]
- Bradbury, K.; Saboo, R.; Johnson, T.L.; Malof, J.M.; Devarajan, A.; Zhang, W.; Collins, L.M.; Newell, R.G. Distributed solar photovoltaic array location and extent dataset for remote sensing object identification. Sci. Data 2016, 3, 160106. [Google Scholar] [CrossRef] [Green Version]
- Csurka, G.; Larlus, D.; Perronnin, F. What is a good evaluation measure for semantic segmentation? In Proceedings of the British Machine Vision Conference 2013, Bristol, UK, 9–13 September 2013; Burghardt, T., Damen, D., Mayol-Cuevas, W., Mirmehdi, M., Eds.; British Machine Vision Association: Guildford, UK, 2013; pp. 32.1–32.11, ISBN 1-901725-49-9. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. Available online: http://arxiv.org/pdf/1505.04597v1 (accessed on 23 June 2021).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. Available online: https://arxiv.org/pdf/1512.03385 (accessed on 23 June 2021).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. Available online: https://arxiv.org/pdf/1412.6980 (accessed on 23 June 2021).
- Perez, L.; Wang, J. The Effectiveness of Data Augmentation in Image Classification using Deep Learning. arXiv 2017, arXiv:1712.04621. Available online: https://arxiv.org/pdf/1712.04621 (accessed on 23 June 2021).
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; Chaudhuri, K., Salakhutdinov, R., Eds.; 2019; pp. 6105–6114. Available online: https://arxiv.org/abs/1905.11946 (accessed on 23 June 2021).
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. (Eds.) Inception-V4, Inception-Resnet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Available online: https://arxiv.org/abs/1602.07261 (accessed on 23 June 2021).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; IEEE: Piscataway, NJ, USA; pp. 1026–1034. [Google Scholar]
- Jadon, S. A survey of loss functions for semantic segmentation. In 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Via del Mar, Chile, 27–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. ISBN 978-1-7281-9468-4. [Google Scholar]
- Quaschning, V. Regenerative Energiesysteme: Technologie—Berechnung—Klimaschutz; Aktualisierte und Erweiterte Auflage; Hanser Fachbuchverlag: Munich, Germany, 2019; ISBN 3446461132. [Google Scholar]
- Fünfgeld, C.; Remo, T. Anwendung derRepräsentativen VDEW-Lastprofile: Step-by-Step. Available online: https://www.bdew.de/media/documents/2000131_Anwendung-repraesentativen_Lastprofile-Step-by-step.pdf (accessed on 22 September 2020).
- Alhamwi, A.; Medjroubi, W.; Vogt, T.; Agert, C. OpenStreetMap data in modelling the urban energy infrastructure: A first assessment and analysis. Energy Procedia 2017, 142, 1968–1976. [Google Scholar] [CrossRef]
- Bertsch, V.; Geldermann, J.; Lühn, T. What drives the profitability of household PV investments, self-consumption and self-sufficiency? Appl. Energy 2017, 204, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Tetraeder.Solar. Solarpotenzialkataster Kreis Ebersberg. Available online: https://www.solare-stadt.de/kreis-ebersberg/Solarpotenzialkataster?s=13 (accessed on 23 June 2021).
- De Hoog, J.; Maetschke, S.; Ilfrich, P.; Kolluri, R.R. Using Satellite and Aerial Imagery for Identification of Solar PV. In Proceedings of the e-Energy ’20: The Eleventh ACM International Conference on Future Energy Systems, Melbourne, Australia, 22–26 June 2020; ACM: New York, NY, USA, 2020; pp. 308–313, ISBN 9781450380096. [Google Scholar]
- Shepero, M.; Munkhammar, J.; Widén, J.; Bishop, J.D.K.; Boström, T. Modeling of photovoltaic power generation and electric vehicles charging on city-scale: A review. Renew. Sustain. Energy Rev. 2018, 89, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Rausch, B.; Mayer, K.; Arlt, M.-L.; Gust, G.; Staudt, P.; Weinhardt, C.; Neumann, D.; Rajagopal, R. An Enriched Automated PV Registry: Combining Image Recognition and 3D Building Data. arXiv 2020, arXiv:2012.03690. [Google Scholar]
- Bastani, F.; He, S.; Abbar, S.; Alizadeh, M.; Balakrishnan, H.; Chawla, S.; Madden, S. Machine-assisted map editing. In Proceedings of the SIGSPATIAL ’18: 26th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 6–9 November 2018; Banaei-Kashani, F., Hoel, E., Güting, R.H., Tamassia, R., Xiong, L., Eds.; ACM: New York, NY, USA, 2018; pp. 23–32, ISBN 9781450358897. [Google Scholar]
- van Coillie, F.M.B.; Gardin, S.; Anseel, F.; Duyck, W.; Verbeke, L.P.C.; de Wulf, R.R. Variability of operator performance in remote-sensing image interpretation: The importance of human and external factors. Int. J. Remote Sens. 2014, 35, 754–778. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S.; Emery, W.J. Object-Based Convolutional Neural Network for High-Resolution Imagery Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3386–3396. [Google Scholar] [CrossRef]
- Du, S.; Zhang, F.; Zhang, X. Semantic classification of urban buildings combining VHR image and GIS data: An improved random forest approach. ISPRS J. Photogramm. Remote Sens. 2015, 105, 107–119. [Google Scholar] [CrossRef]
- Robinius, M.; Otto, A.; Heuser, P.; Welder, L.; Syranidis, K.; Ryberg, D.; Grube, T.; Markewitz, P.; Peters, R.; Stolten, D. Linking the Power and Transport Sectors—Part 1: The Principle of Sector Coupling. Energies 2017, 10, 956. [Google Scholar] [CrossRef] [Green Version]
- Bergner, J.; Quaschning, V. Zehn Kilowatt, Hürde oder Grenze? Dimensionierungsempfehlung für Prosumer. In Proceedings of the PV Symposium, Albuquerque, NM, USA, 14–16 May 2019. [Google Scholar]
- Bundesnetzagentur. Archivierte EEG-Vergütungssätze und Datenmeldungen. Available online: https://www.bundesnetzagentur.de/DE/Sachgebiete/ElektrizitaetundGas/Unternehmen_Institutionen/ErneuerbareEnergien/ZahlenDatenInformationen/EEG_Registerdaten/ArchivDatenMeldgn/ArchivDatenMeldgn_node.html;jsessionid=25CAADA929ED9360D0078A857DC5C100 (accessed on 23 June 2021).
- Bundesnetzagentur. Entwicklung der EEG-Umlage. Available online: https://www.bundesnetzagentur.de/SharedDocs/A_Z/E/EEG_Umlage.html (accessed on 23 June 2021).
- Quaschning, V. Erneuerbare Energien und Klimaschutz: Hintergründe—Techniken und Planung—Ökonomie und Ökologie—Energiewende; Aktualisierte Auflage; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2020; ISBN 3446462937. [Google Scholar]
- KfW-Bank. Merkblatt KfW-Programm Erneuerbare Energien “Standard”. Available online: https://www.kfw.de/Download-Center/F%C3%B6rderprogramme-(Inlandsf%C3%B6rderung)/PDF-Dokumente/6000000178-Merkblatt-270-274.pdf (accessed on 17 October 2020).
- Kiefer, K.; Farnung, B.; Müller, B.; Reinartz, K.; Rauschen, I.; Klünter, C. Degradation in PV Power Plants: Theory and Practice. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019; pp. 1331–1335. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R.; VanSant, K.; Newmiller, J. Compendium of photovoltaic degradation rates. Prog. Photovolt. Res. Appl. 2016, 24, 978–989. [Google Scholar] [CrossRef]
- § 48 Solare Strahlungsenergie. Erneuerbare-Energien-Gesetz—EEG 2017; Bundesministerium für Wirtschaft und Energie: Berlin, Germany, 2017; Available online: http://www.gesetze-im-internet.de/eeg_2014/ (accessed on 23 June 2021).
- Hsu, D.D.; O’Donoughue, P.; Fthenakis, V.; Heath, G.A.; Kim, H.C.; Sawyer, P.; Choi, J.-K.; Turney, D.E. Life Cycle Greenhouse Gas Emissions of Crystalline Silicon Photovoltaic Electricity Generation. J. Ind. Ecol. 2012, 16, S122–S135. [Google Scholar] [CrossRef]




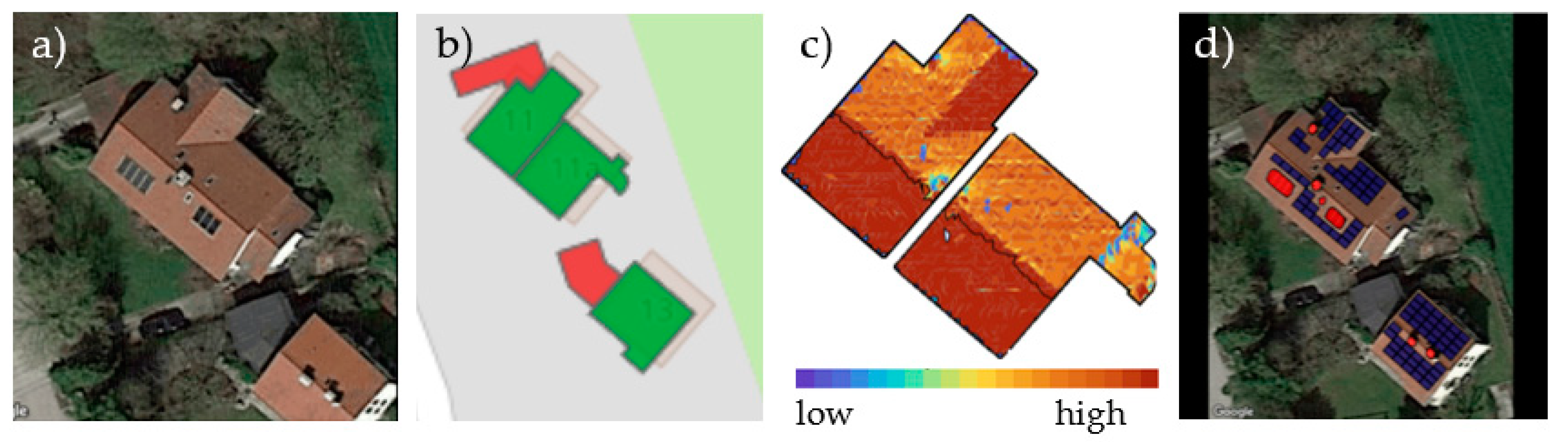

| Value | This Paper | LiDAR | Difference | Diff. in% |
|---|---|---|---|---|
| Total Area in m2 | 9188.97 | 10,185.4 | −996.43 | −10.84 |
| Total Modules | 3211 | 5637 | −2426 | −75.55 |
| Mean Modules | 45.22 | 79.39 | −34.17 | −75.55 |
| Total Potential in MWh/Year | 625.18 | 1364.57 | −739.39 | −118.27 |
| Mean Potential in kWh/Year | 8805.35 | 19,219.27 | −10,413.92 | −118.27 |
| Mean Slope in Deg | 30.94 | 21.51 | 9.43 | 30.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krapf, S.; Kemmerzell, N.; Khawaja Haseeb Uddin, S.; Hack Vázquez, M.; Netzler, F.; Lienkamp, M. Towards Scalable Economic Photovoltaic Potential Analysis Using Aerial Images and Deep Learning. Energies 2021, 14, 3800. https://doi.org/10.3390/en14133800
Krapf S, Kemmerzell N, Khawaja Haseeb Uddin S, Hack Vázquez M, Netzler F, Lienkamp M. Towards Scalable Economic Photovoltaic Potential Analysis Using Aerial Images and Deep Learning. Energies. 2021; 14(13):3800. https://doi.org/10.3390/en14133800
Chicago/Turabian StyleKrapf, Sebastian, Nils Kemmerzell, Syed Khawaja Haseeb Uddin, Manuel Hack Vázquez, Fabian Netzler, and Markus Lienkamp. 2021. "Towards Scalable Economic Photovoltaic Potential Analysis Using Aerial Images and Deep Learning" Energies 14, no. 13: 3800. https://doi.org/10.3390/en14133800
APA StyleKrapf, S., Kemmerzell, N., Khawaja Haseeb Uddin, S., Hack Vázquez, M., Netzler, F., & Lienkamp, M. (2021). Towards Scalable Economic Photovoltaic Potential Analysis Using Aerial Images and Deep Learning. Energies, 14(13), 3800. https://doi.org/10.3390/en14133800