Trefftz Method of Solving a 1D Coupled Thermoelasticity Problem for One- and Two-Layered Media
Abstract
1. Introduction
2. Basic Equations
2.1. Heat Conduction Equation
2.2. Equations of Motion and Constitutive Equations
3. Formulation of the Problem
3.1. Case I: One Layer
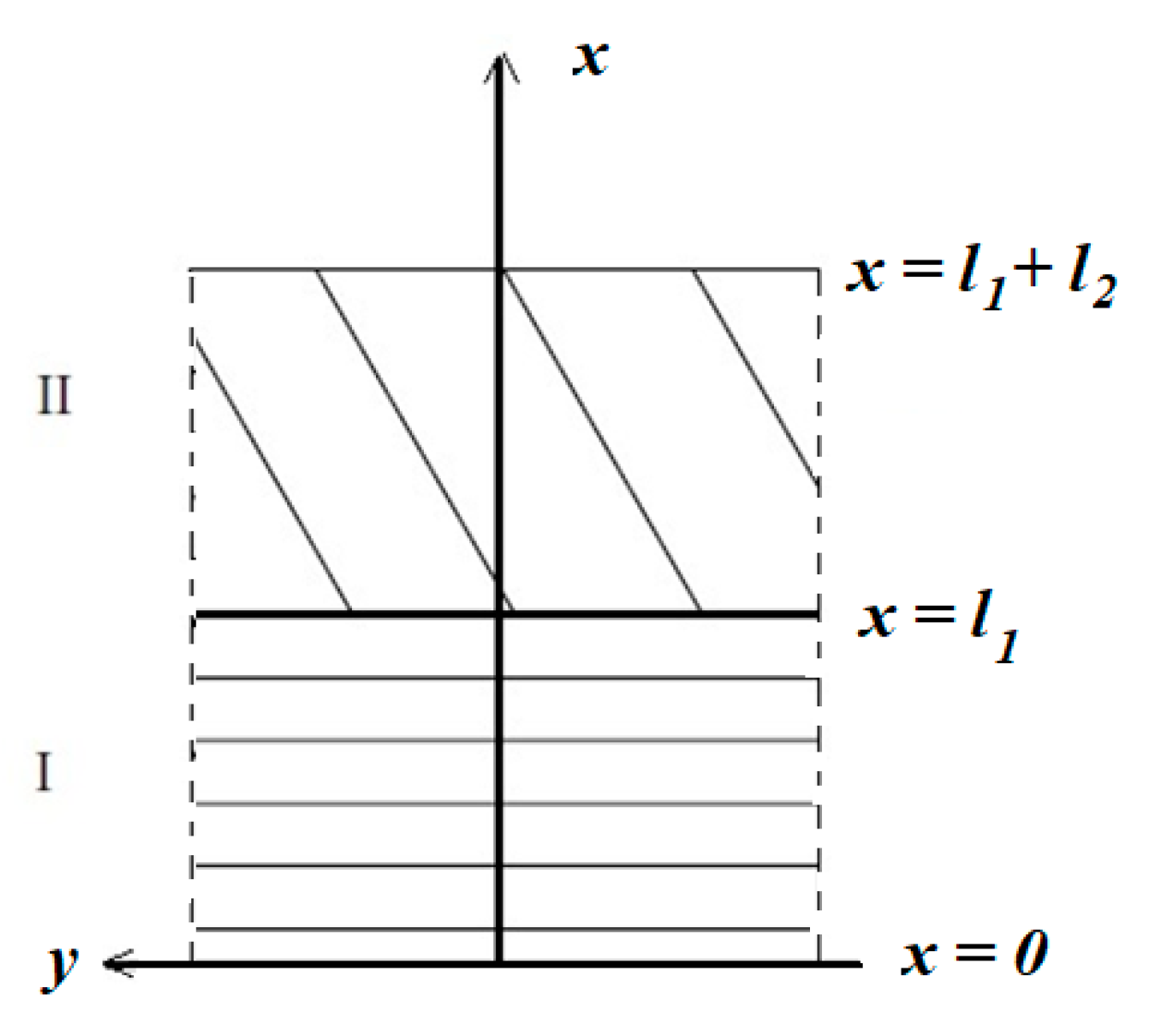
3.2. Case II: Two Layers
4. Trefftz Functions and Inverse Operators
4.1. Trefftz Functions for Cases I and II
4.2. Inverse Operator for Operators (24) and (25)
4.3. Solution of Nonhomogeneous System of Equations
5. Objective Functionals
5.1. The Objective Functional for the Case I
5.2. The Objective Functional for the Case II
6. Numerical Results and Discussion
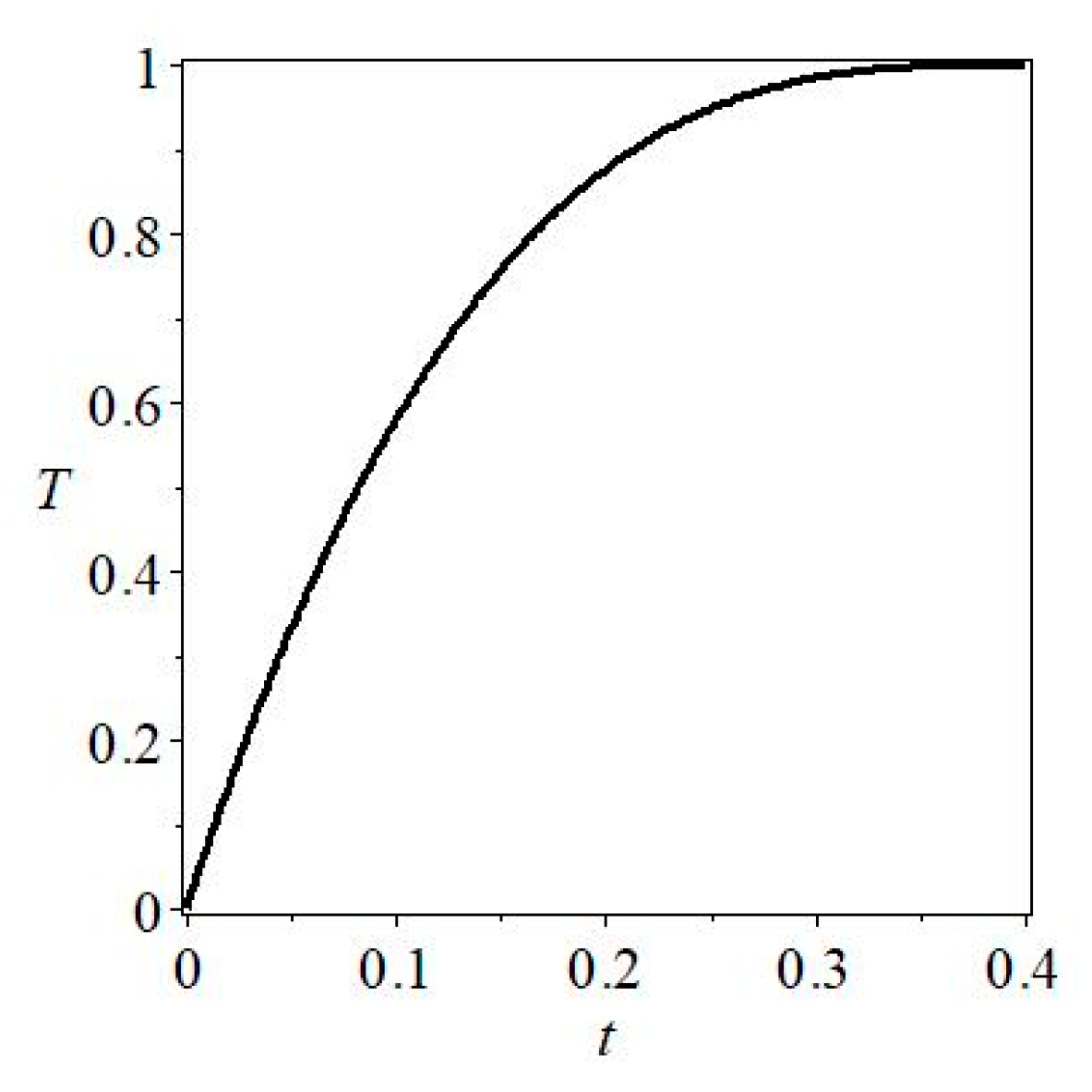
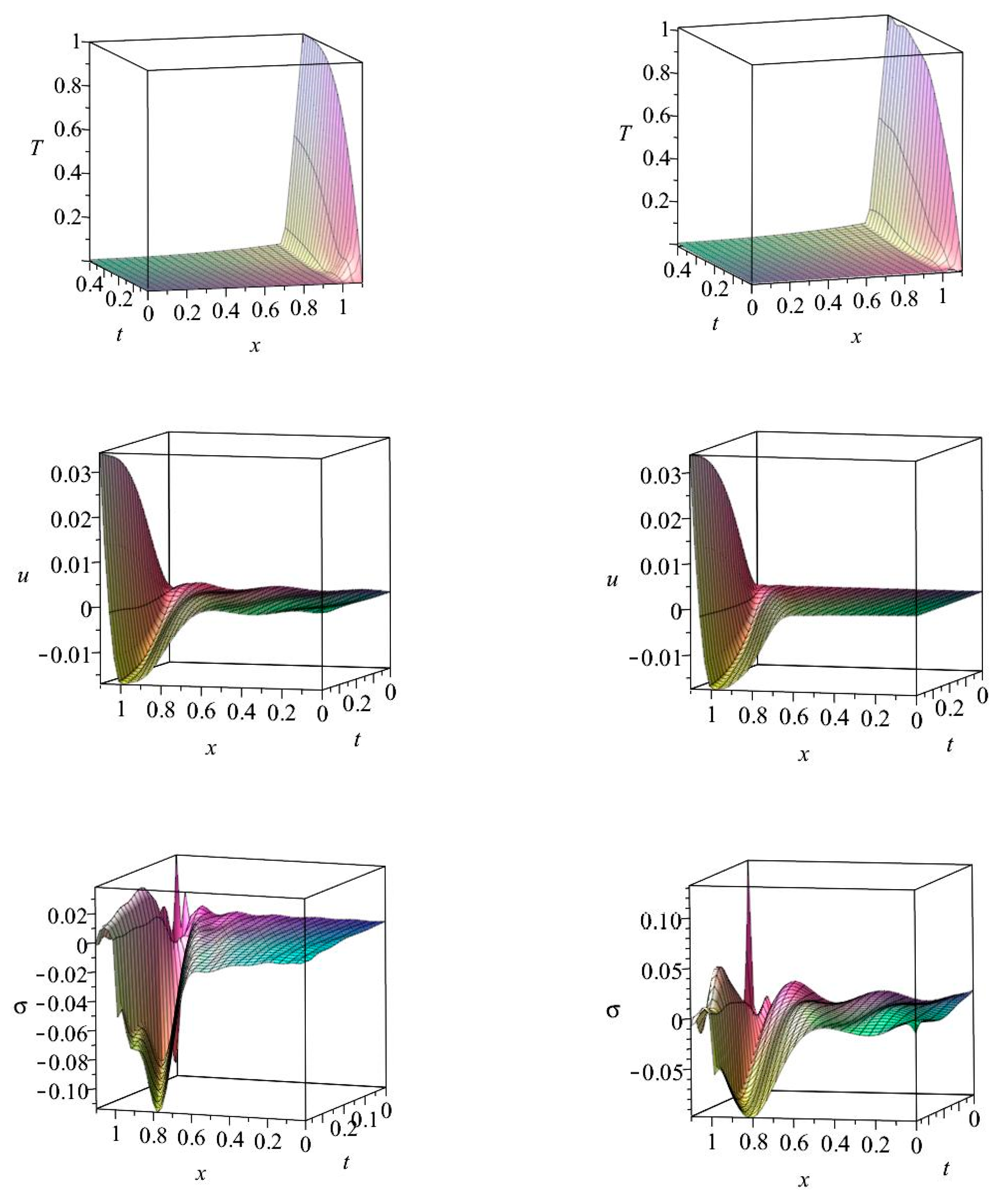
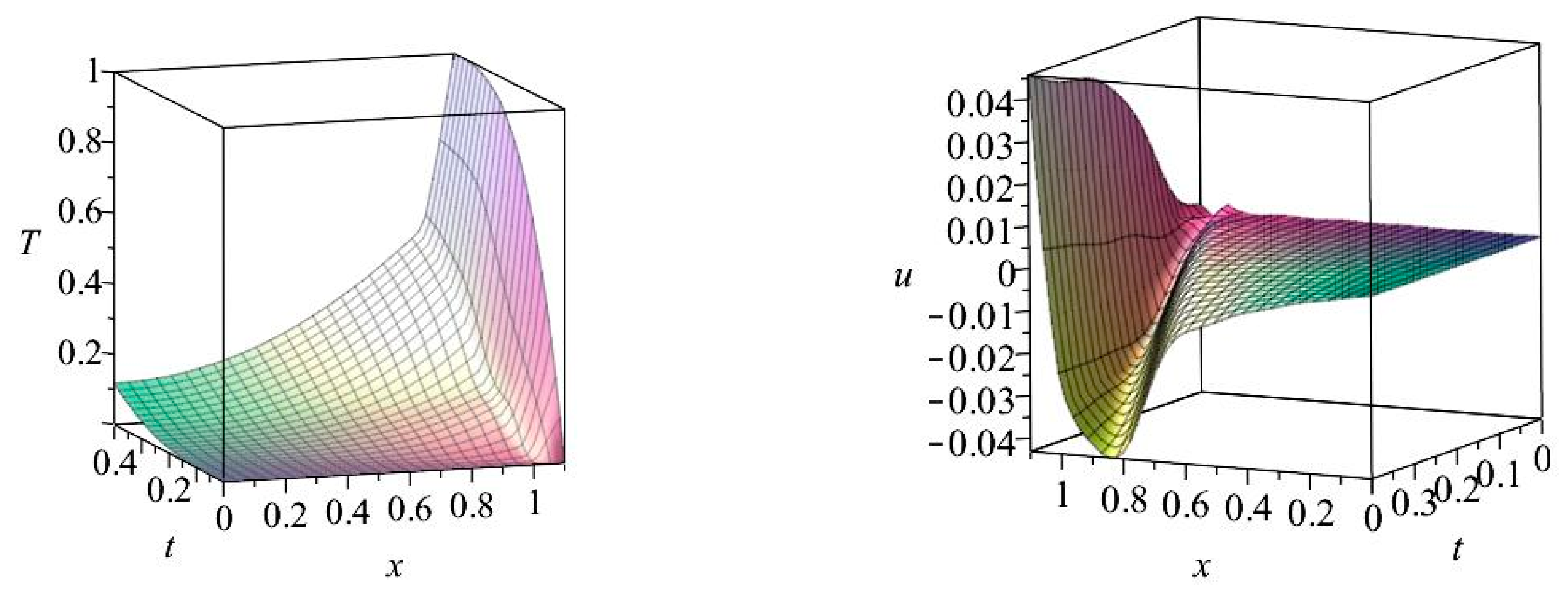
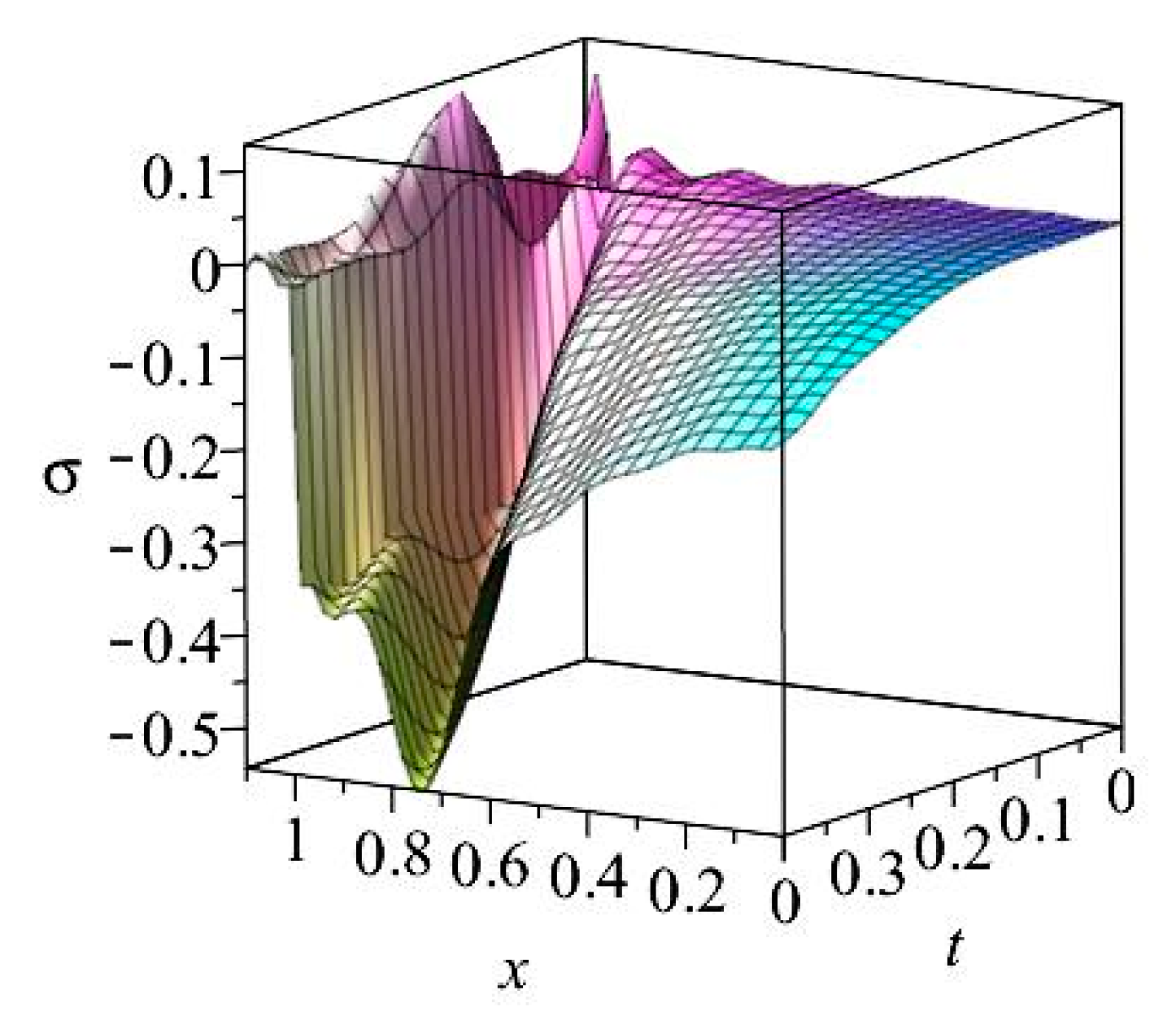
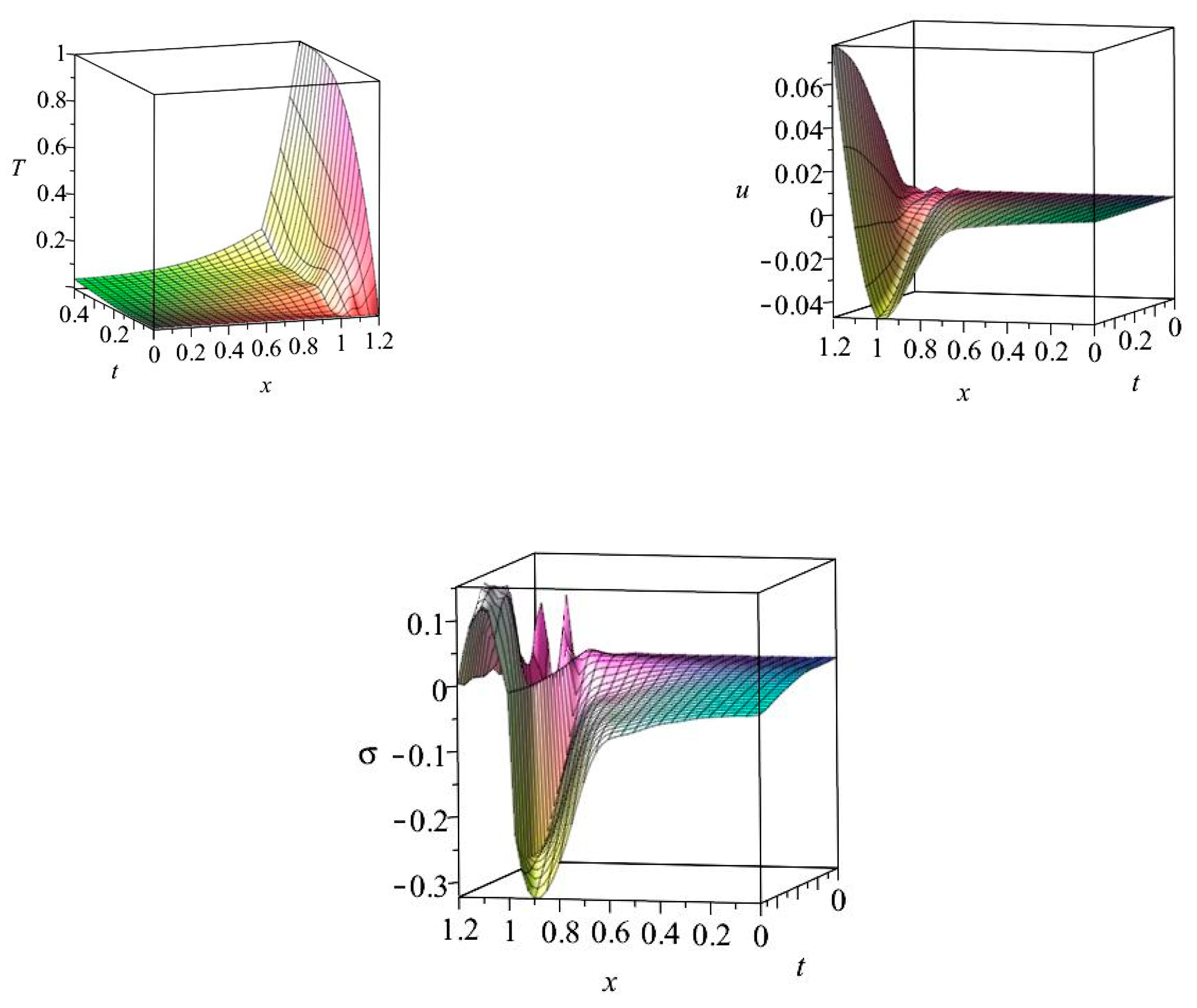
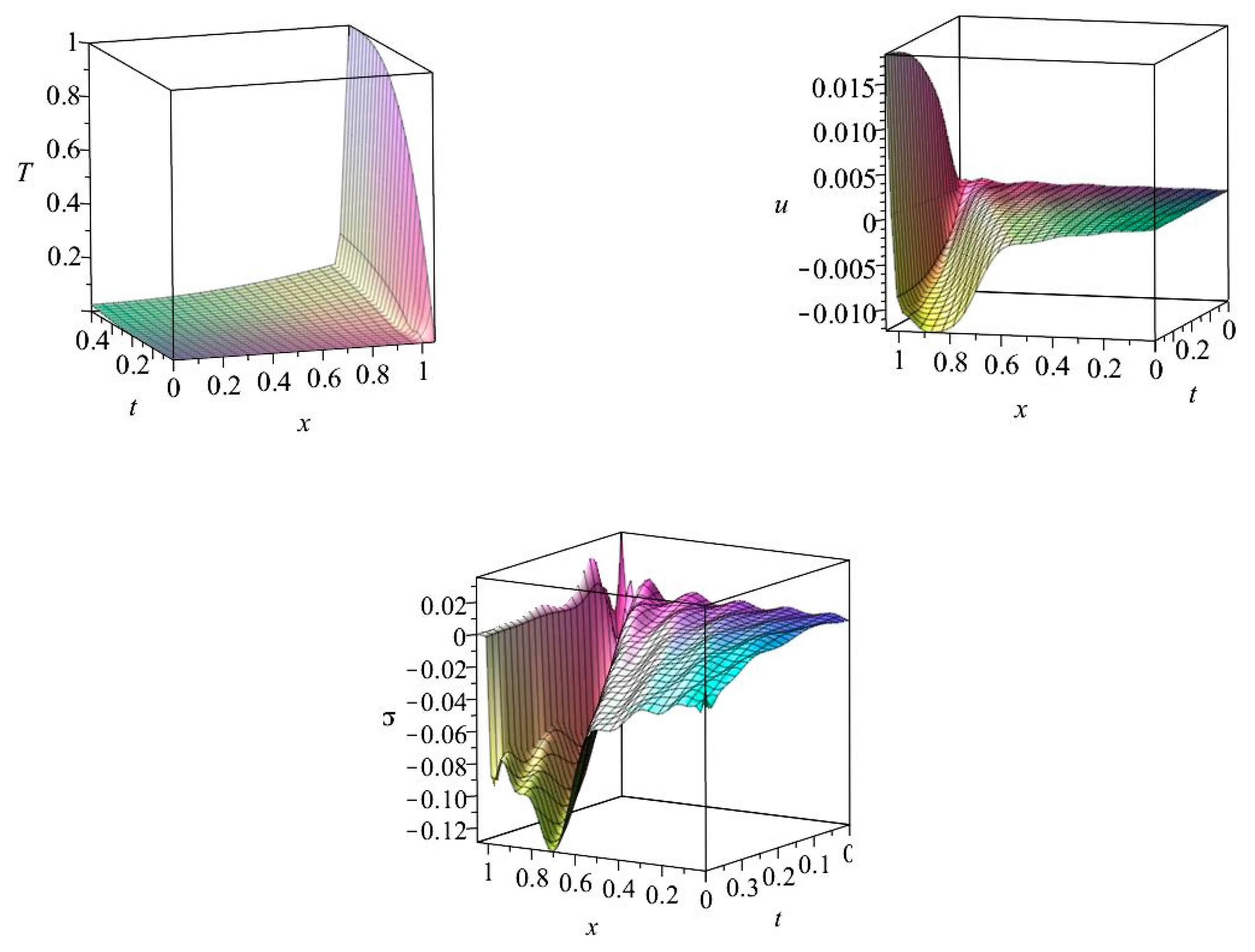
6.1. Results for Case I
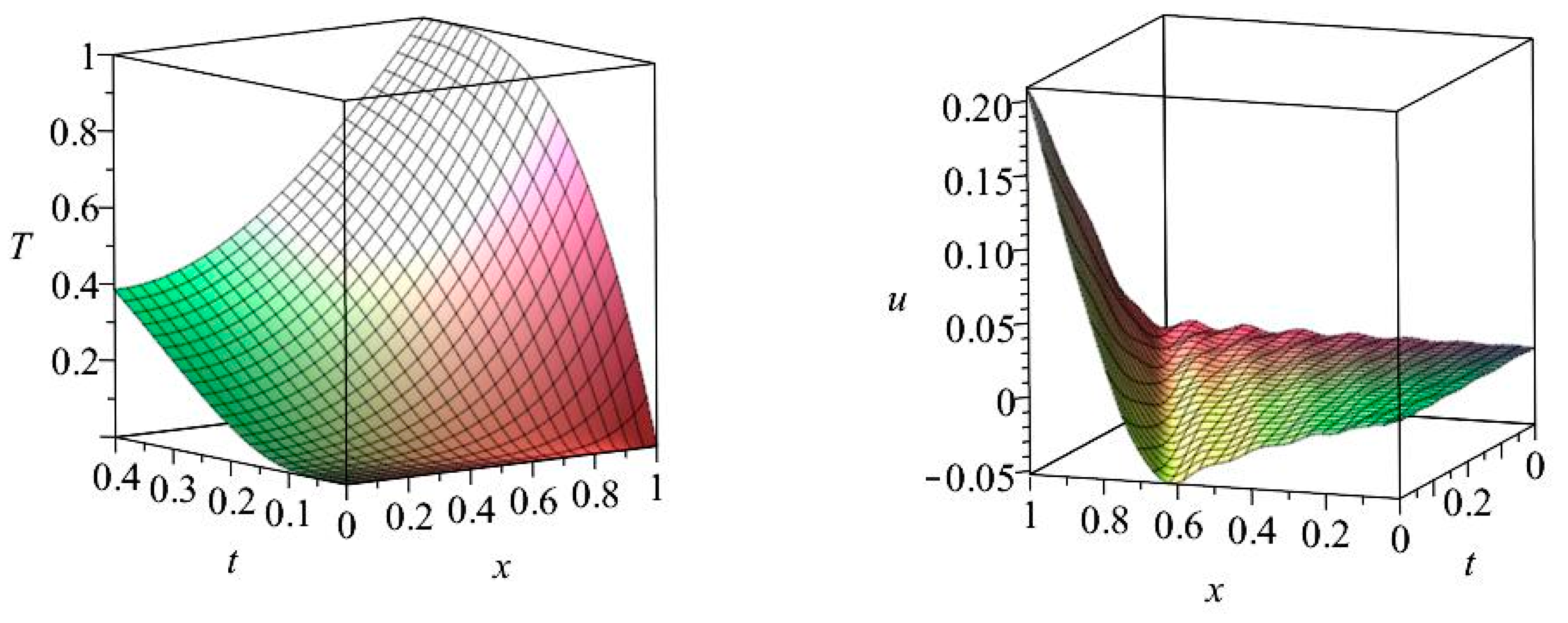
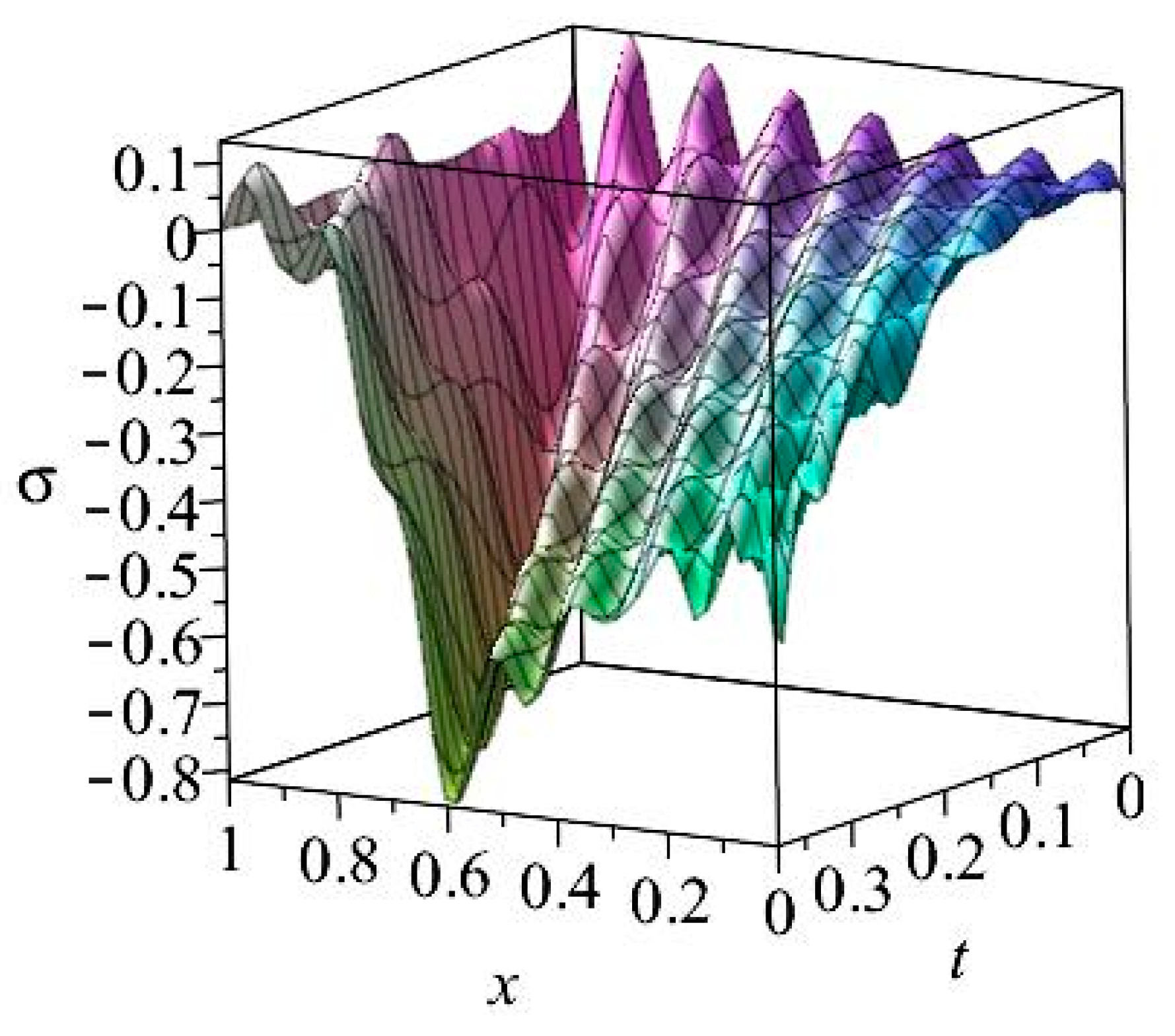
6.2. Results for Case II
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bufler, H. Theory of Elasticity of a Multilayered Medium. J. Elast. 1971, 1, 125–143. [Google Scholar] [CrossRef]
- Bahar, L.Y. Transfer Matrix Approach to Layered Systems. J. Eng. Mech. Div. 1972, 98, 1159–1172. [Google Scholar] [CrossRef]
- Bahar, L.Y.; Hetnarski, R.B. Coupled Thermoelasticity of a Layered Medium. J. Therm. Stress. 1980, 3, 141–152. [Google Scholar] [CrossRef]
- Thangjitham, S.; Choi, H.J. Thermal Stresses in a Multilayered Anisotropic Medium. ASME J. Appl. Mech. 1991, 58, 1021–1027. [Google Scholar] [CrossRef]
- Chen, T.; Jang, H.; Tseng, A.A. Transient Thermal Stresses in a Multilayered Anisotropic Medium. ASME J. Appl. Mech. 1995, 117, 1067–1069. [Google Scholar] [CrossRef]
- Cetinkaya, C.; Li, C. Propagation and Localization of Longitudinal Thermoelastic Waves in Layered Structures. J. Vib. Acoust. 2000, 122, 263–271. [Google Scholar] [CrossRef]
- Lee, Z.-Y. Coupled Problem of Thermoelasticity for Multilayered Spheres with Time-Dependent Boundary Conditions. J. Mar. Sci. Tech. 2004, 12, 93–101. [Google Scholar]
- Hosseini Zad, S.K.; Komeili, A.; Eslami, M.R.; Fariborz, S. Classical and Generalized Coupled Thermoelasticity Analysis in One-Dimensional Layered Media. Arch. Appl. Mech. 2012, 82, 267–282. [Google Scholar] [CrossRef]
- Koo, J.; Valgur, J. Analysis of Thermoelastic Stresses in a Layered Plates. In Proceedings of the 6th International DAAAM Baltic Conference. Industrial Engineering, Tallinn, Estonia, 24–26 April 2008. [Google Scholar]
- Zamani Nejad, M.; Rastgoo, A.; Hadi, A. Effect of Exponentially-Varying Properties on Displacements and Stresses in Pressurized Functionally Graded Thick Spherical Shells with Using Iterative Technique. J. Solid Mech. 2014, 6, 366–377. [Google Scholar]
- Vatulyan, A.; Nesterov, S.; Nedin, R. Regarding some Thermoelastic Models of “Coating-Substrate” System Deformation. Contin. Mech. Thermodyn. 2020, 32, 1173–1186. [Google Scholar] [CrossRef]
- Durbin, F. Numerical Inversion of Laplace Transforms: An Efficient Improvement to Dubner and Abate’s Method. Comput. J. 1974, 17, 371–376. [Google Scholar] [CrossRef]
- Pawar, S.P.; Bikram, J.J.; Kedar, G.D. Thermoelastic Behaviour in a Multilayer Composite Hollow Sphere with Heat Source. J. Solid Mech. 2020, 12, 883–901. [Google Scholar] [CrossRef]
- Serpilli, M.; Dumont, S.; Rizzoni, R.; Lebon, F. Interface Models in Coupled Thermoelasticity. Technologies 2021, 9, 17. [Google Scholar] [CrossRef]
- Qin, Q.H. The Trefftz Finite and Boundary Element Method; WIT Press: Southampton, UK; Boston, MA, USA, 2000. [Google Scholar]
- Li, Z.C.; Lu, T.T.; Hu, H.Y.; Cheng, A. The Trefftz and Collocation Methods; WIT Press: Southampton, UK, 2008. [Google Scholar]
- Maciąg, A. Trefftz Functions for Some Direct and Inverse Problems of Mechanics; Kielce University of Technology Publishers: Kielce, Poland, 2009. (In Polish) [Google Scholar]
- Grysa, K. Trefftz Functions and Their Applications in Solving the Inverse Problems; Kielce University of Technology Publishers: Kielce, Poland, 2010. (In Polish) [Google Scholar]
- Maciąg, A. Trefftz Function for a Plate Vibration Problem. J. Theor. Appl. Mech. 2011, 49, 97–116. [Google Scholar]
- Grysa, K.; Maciąg, A. Solving Direct and Inverse Thermoelasticity Problems by Means of Trefftz Base Functions for Finite Element Method. J. Therm. Stress 2011, 34, 78–93. [Google Scholar] [CrossRef]
- Grysa, K.; Maciąg, A.; Adamczyk-Krasa, J. Trefftz Functions Applied to Direct and Inverse Non-Fourier Heat Conduction Problems. J. Heat Transf. 2014, 136, 091302. [Google Scholar] [CrossRef]
- Maciejewska, B.; Piasecka, M. An Application of the Non-Continuous Trefftz Method to the Determination of Heat Transfer Coefficient for Flow Boiling in a Minichannel. Heat Mass Transf. 2016, 53, 1211–1224. [Google Scholar] [CrossRef]
- Frackowiak, A.; Cialkowski, M. Application of Discrete Fourier Transform to Inverse Heat Conduction Problem Regularization. Int. J. Numer. Meth. Heat Fluid Flow 2018, 28, 239–253. [Google Scholar] [CrossRef]
- Grysa, K.; Maciąg, A. Identifying Heat Source Intensity in Treatment of Cancerous Tumor Using Therapy Based on Local Hyper-thermia—The Trefftz method approachs. J. Therm. Biol. 2019, 84, 16–25. [Google Scholar] [CrossRef]
- Ciałkowski, M.J. Trefftz Functions as Basic Functions of FEM in Application to Solution of Inverse Heat Conduction Problem. Comp. Ass. Mech. Eng. Sci. CAMES 2001, 8, 247–260. [Google Scholar]
- Cialkowski, M.J.; Frackowiak, A. Thermal and related functions used in solving certain problems of mechanics, Part I. Solving some differential equations with the use of inverse operator. In Modern Problems of Technics; University of Zielona Góra Publishers: Zielona Góra, Poland, 2003; Volume 3, pp. 7–70. [Google Scholar]
- Maciąg, A. The Usage of Wave Polynomials in Solving Direct and Inverse Problems for Two-Dimensional Wave Equation. Commun. Numer. Meth. Eng. 2011. [Google Scholar] [CrossRef]
- Sharma, J.N.; Pal, M.; Chand, D. Three-Dimensional Vibration Analysis of a Piezothermoelastic Cylindrical Panel. Int. J. Eng. Sci. 2004, 42, 1655–1673. [Google Scholar] [CrossRef]
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, MA, USA, 1998; p. 289. [Google Scholar]
- Sfarra, S.; López, F.; Sarasini, F.; Tirillò, J.; Ferrante, L.; Perilli, S.; Ibarra-Castanedo, C.; Paoletti, D.; Lampani, L.; Barbero, E.; et al. Analysis of damage in hybrid composites subjected to ballistic impacts: An integrated non-destructive approach. In Handbook of Composites from Renewable Materials; Scrivener Publishing: Beverly, MA, USA, 2017; Chapter 8; pp. 175–210. [Google Scholar] [CrossRef]
| The Parameter | Stainless Steel | PZT-5A |
|---|---|---|
| ρ ] | 7970 | 7750 |
| C [] | 561 | 420 |
| [K] | 293 | 293 |
| k [] | 19.5 | 1.5 |
| λ [] | 105.5 × | 7.54 × |
| μ [] | 74 × | 2.56 × |
| 17.7 × | 352 × |
| 12–10 | 14–12 | 16–14 | 18–16 | 20–18 | 22–20 | 24–22 | 26–24 | 28–26 | 30–28 | 32–30 | 34–32 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BC | 0.012 | 0.007 | 0.006 | 0.008 | 0.0065 | 0.0025 | 0.0045 | 0.004 | 0.0012 | 0.001 | 0.0015 | 0.0008 |
| T | 0.012 | 0.007 | 0.007 | 0.008 | 0.0065 | 0.0025 | 0.0045 | 0.004 | 0.0012 | 0.001 | 0.0015 | 0.0008 |
| U | 0.025 | 0.027 | 0.009 | 0.005 | 0.006 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.002 | 0.002 |
| σ | 0.4 | 0.5 | 0.2 | 0.3 | 0.14 | 0.08 | 0.11 | 0.1 | 0.11 | 0.15 | 0.07 | 0.07 |
| N = | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BC—Tn | 0.035 | 0.028 | 0.021 | 0.015 | 0.015 | 0.011 | 0.009 | 0.009 | 0.007 | 0.006 | 0.005 | 0.004 | 0.0037 |
| 11–9 | 13–11 | 15–13 | 17–15 | 19–17 | 21–19 | 23–21 | 25–23 | |
|---|---|---|---|---|---|---|---|---|
| T | 0.071 | 0.037 | 0.011 | 0.01 | 0.014 | 0.005 | 0.004 | 0.004 |
| u | 0.0028 | 0.00095 | 0.0012 | 0.00022 | 0.0004 | 0.00019 | 0.00035 | 0.00025 |
| σ | 0.08 | 0.034 | 0.035 | 0.016 | 0.03 | 0.013 | 0.022 | 0.008 |
| 13–9 | 17–13 | 21–17 | 25–21 | |
|---|---|---|---|---|
| T | 0.085 | 0.011 | 0.015 | 0.0055 |
| u | 0.0032 | 0.0011 | 0.00045 | 0.0004 |
| σ | 0.11 | 0.045 | 0.035 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciąg, A.; Grysa, K. Trefftz Method of Solving a 1D Coupled Thermoelasticity Problem for One- and Two-Layered Media. Energies 2021, 14, 3637. https://doi.org/10.3390/en14123637
Maciąg A, Grysa K. Trefftz Method of Solving a 1D Coupled Thermoelasticity Problem for One- and Two-Layered Media. Energies. 2021; 14(12):3637. https://doi.org/10.3390/en14123637
Chicago/Turabian StyleMaciąg, Artur, and Krzysztof Grysa. 2021. "Trefftz Method of Solving a 1D Coupled Thermoelasticity Problem for One- and Two-Layered Media" Energies 14, no. 12: 3637. https://doi.org/10.3390/en14123637
APA StyleMaciąg, A., & Grysa, K. (2021). Trefftz Method of Solving a 1D Coupled Thermoelasticity Problem for One- and Two-Layered Media. Energies, 14(12), 3637. https://doi.org/10.3390/en14123637







