Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles
Abstract
1. Introduction
2. Overview of BEV LIB SoC Modelling Approaches
2.1. Physical Electrochemical Models
2.2. Electrical Equivalent Circuit Models
2.2.1. Integral-Order Models
2.2.2. Fractional-Order Models
2.3. Data-Driven Models
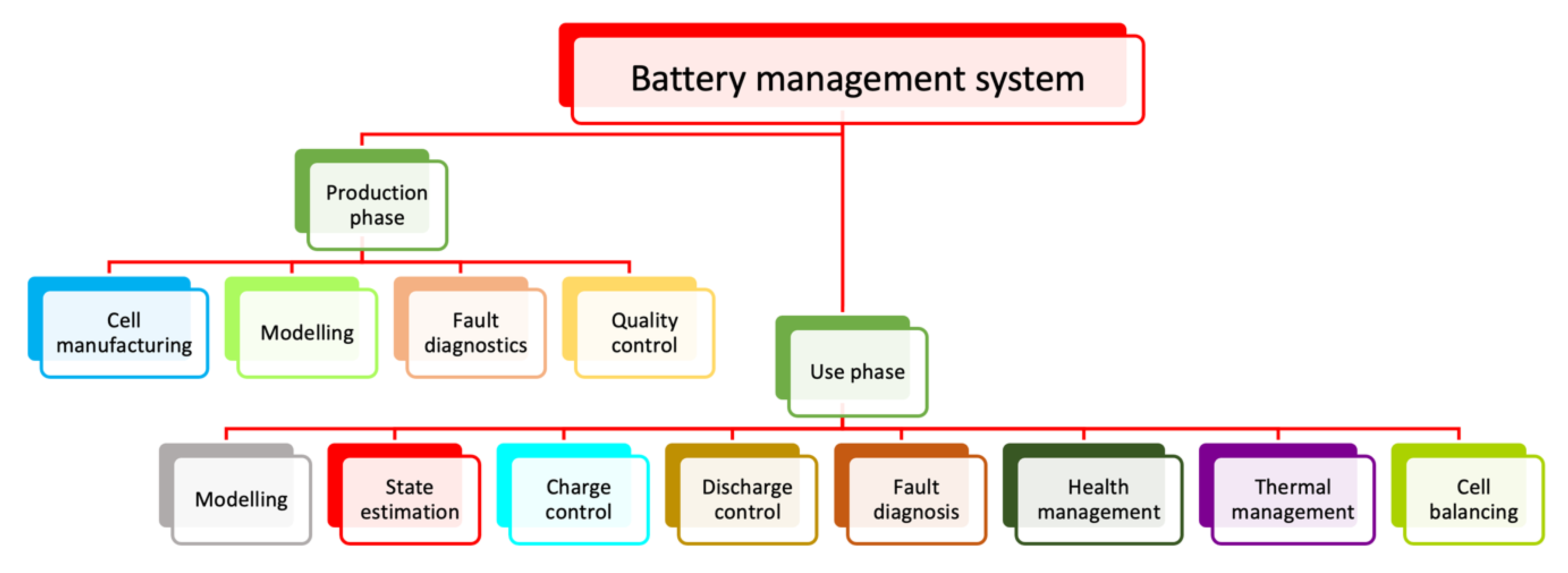
3. State Estimation in BEV LIBs
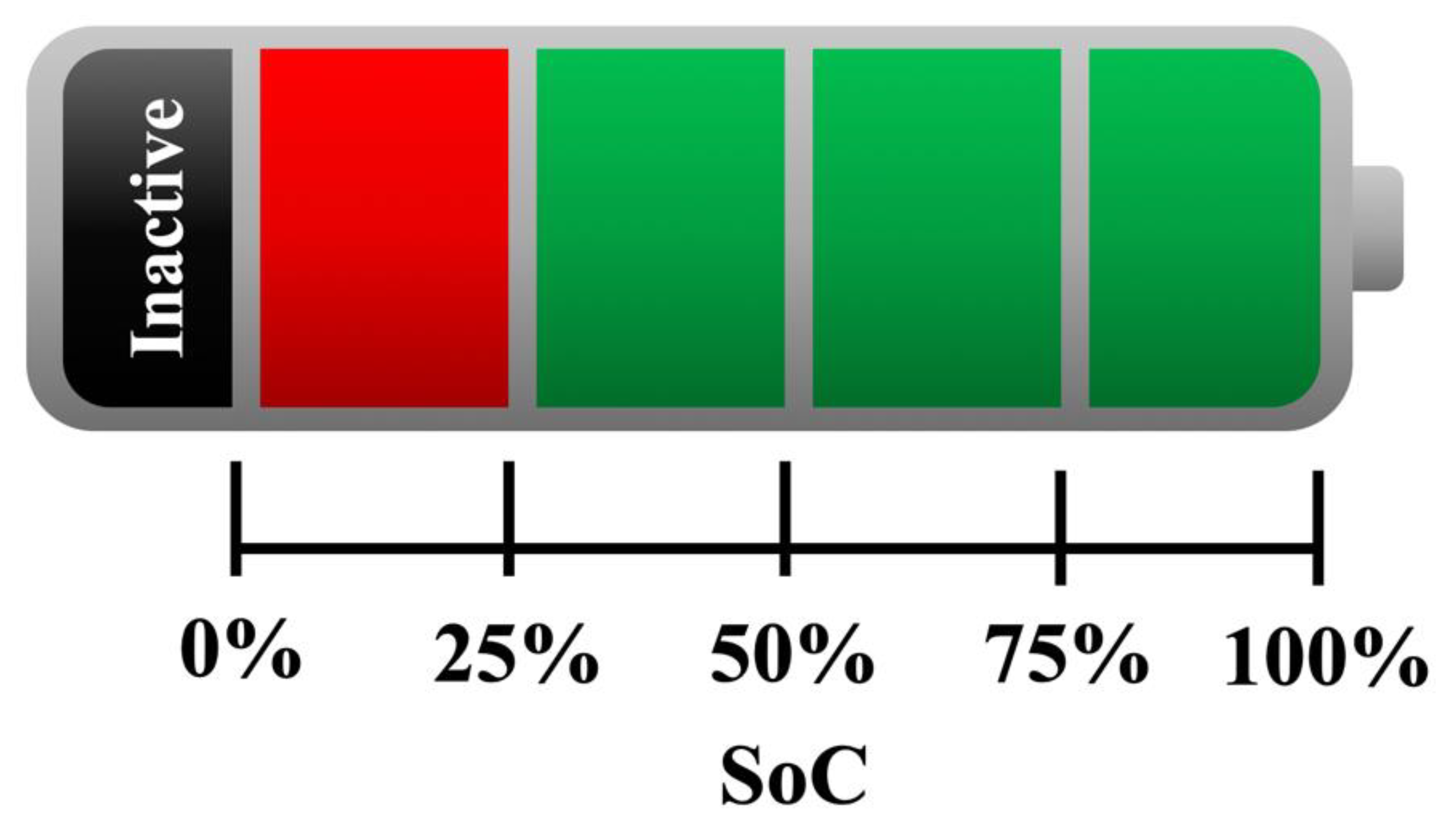
3.1. SoC in LIBs
3.1.1. Coulomb Counting
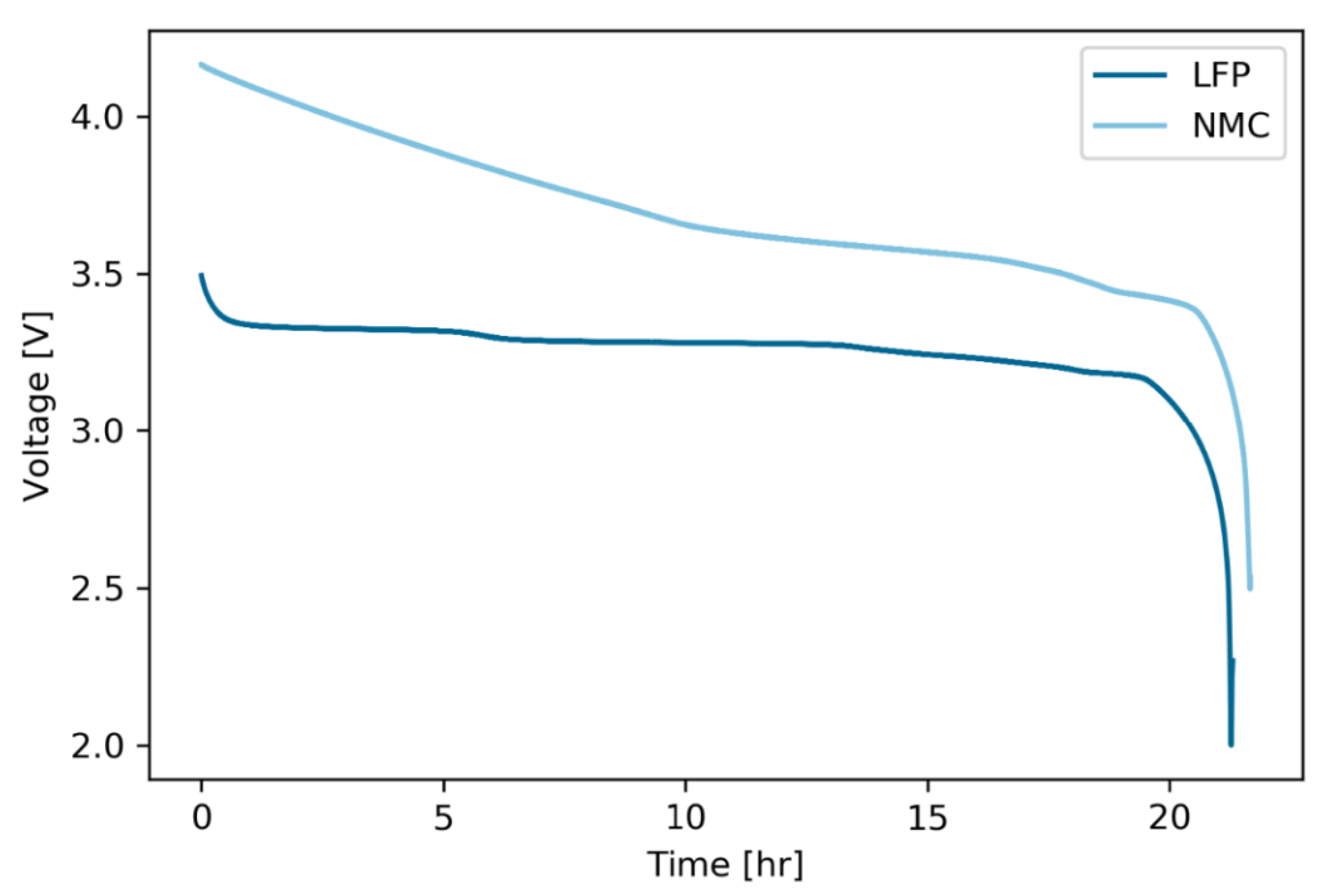
3.1.2. Open Circuit Voltage
3.1.3. State of Health
3.2. Estimation of Energy and Remaining Capacity
3.2.1. Look-Up Tables
Open-Circuit Voltage
Impedance
3.2.2. Ampere-Hour Integral
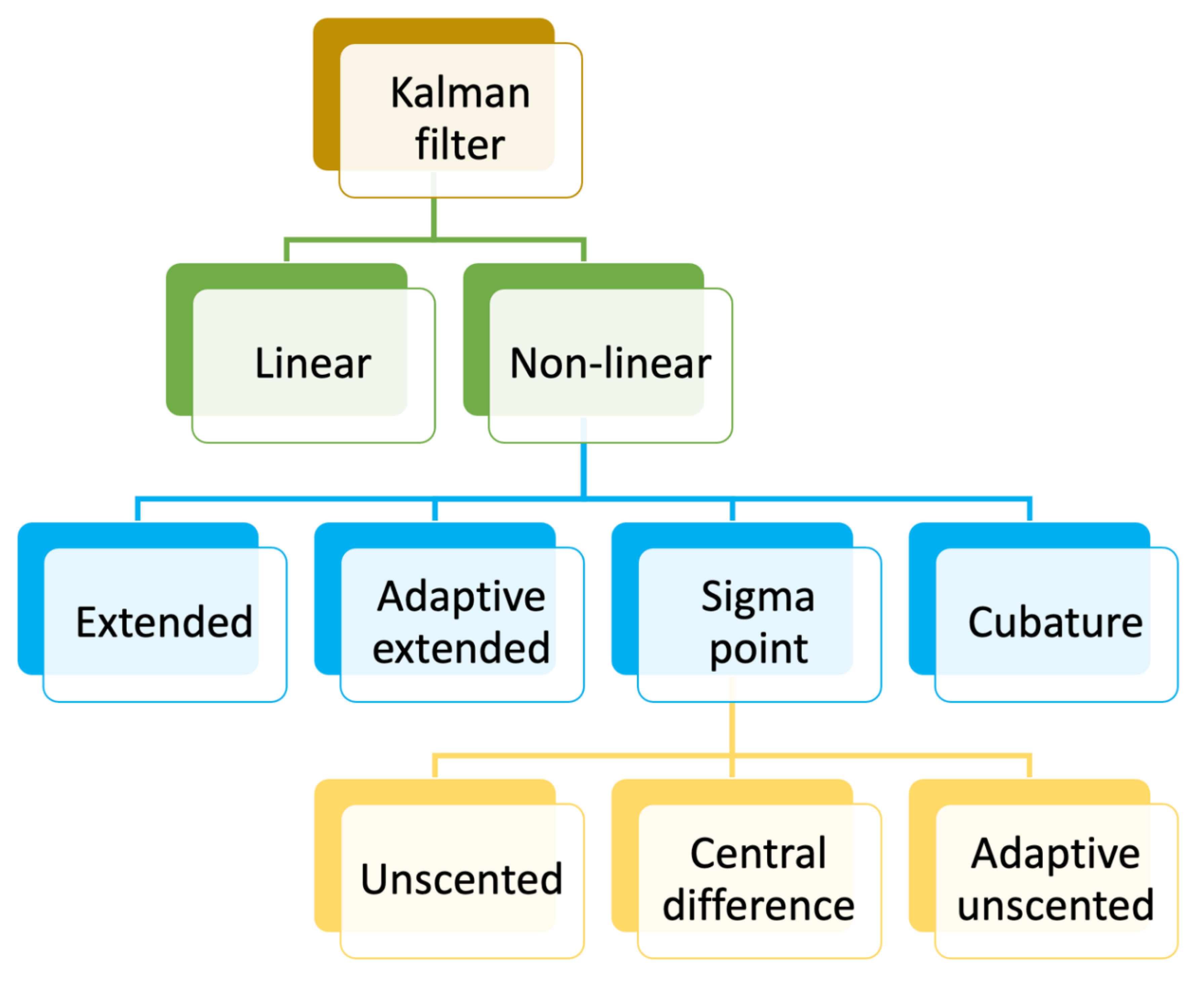
3.2.3. Filter-Based
Linear Kalman Filter
Extended Kalman Filter
Adaptive Extended Kalman Filter
Sigma-Point Kalman Filter
Unscented Kalman Filter
Adaptive Unscented Kalman Filter
Central Difference Kalman Filter
Cubature Difference Kalman Filter
Particle Filter
Unscented Particle Filter
Cubature Particle Filter
3.2.4. Observer-Based
Luenberger
Sliding Mode
Proportional Integral
H-Infinity
3.2.5. Data-Driven
Genetic Algorithm
Support Vector Machines
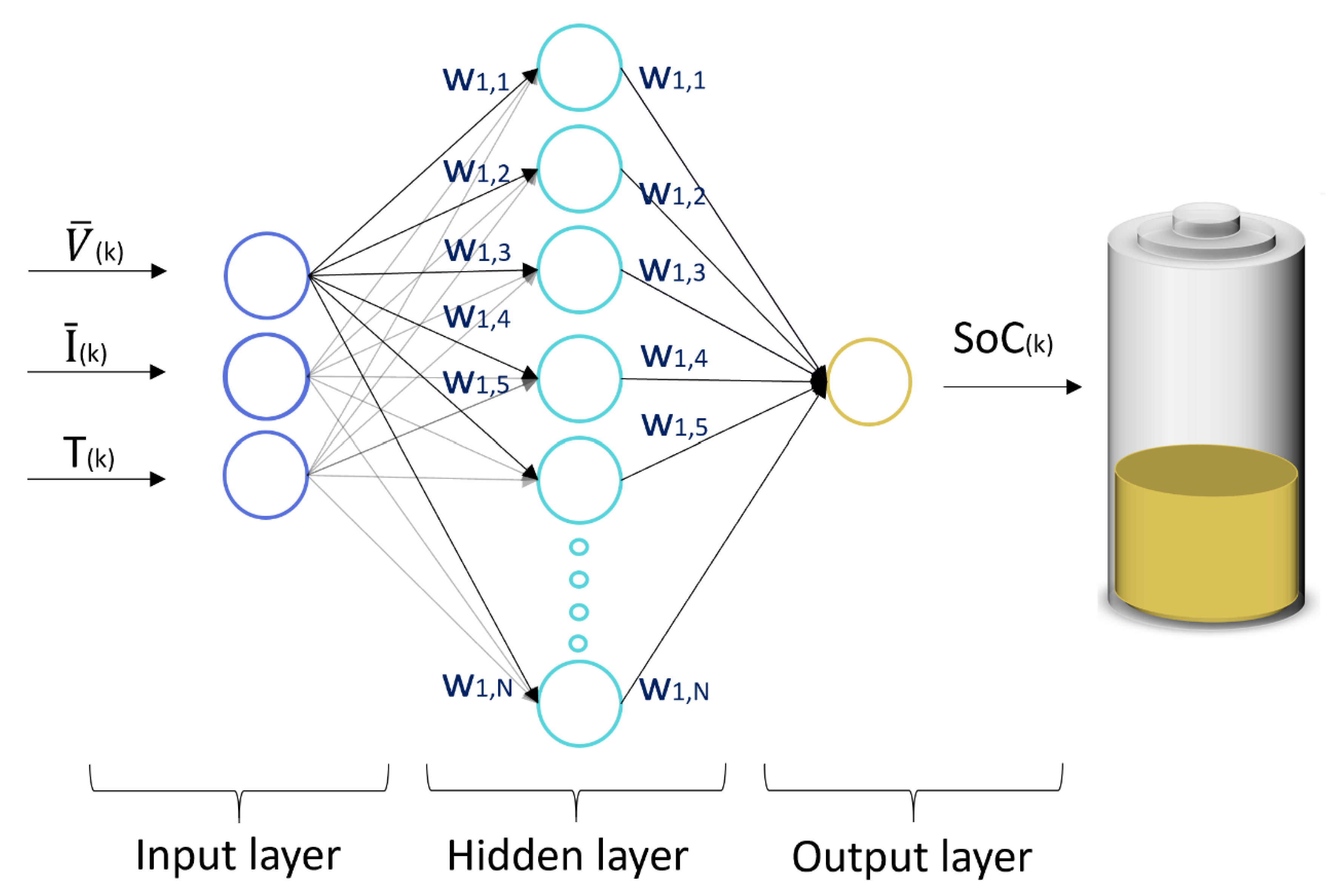
Artificial Neural Networks
3.3. Comparison of Approaches
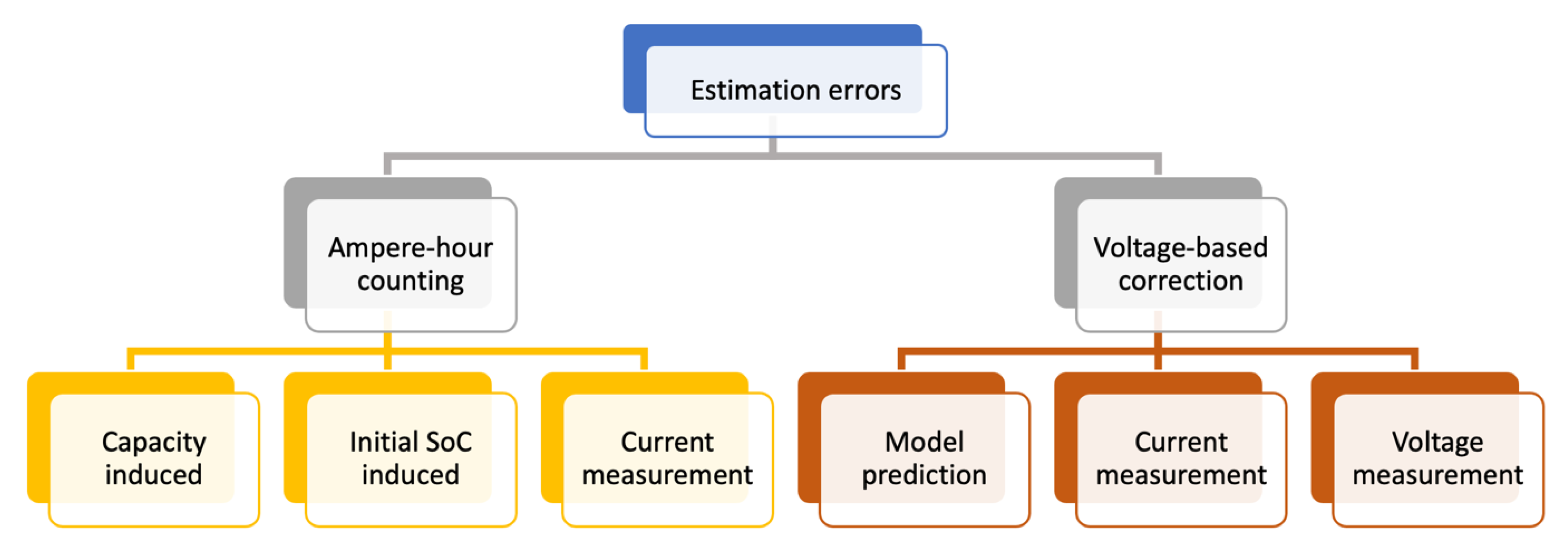
3.4. Errors in Modeling
3.4.1. Capacity Induced Errors
3.4.2. Initial SoC Error
3.4.3. Current Measurement Error
3.4.4. Model Prediction Error
3.4.5. Voltage Measurement Error
4. Challenges in SoC Estimation in LiBs
4.1. Advanced Optical Fiber Sensing
4.2. Multi-State Estimation
4.3. Battery Model Selection and Estimated Parameter Accuracy
4.4. Operating Conditions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery management system: An overview of its application in the smart grid and electric vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Felius, L.C.; Lamb, J.J.; Hrynyszyn, B.D.; Dessen, F. Smart components and systems. In Energy-Smart Buildings: Design, Construction and Monitoring of Buildings for Improved Energy Efficiency; IOP Publishing: Bristol, UK, 2020; Volume 1, pp. 1–16. [Google Scholar]
- Lamb, J.J.; Pollet, B.G.; Burheim, O.S. Energy storage. In Energy-Smart Buildings Design: Construction and Monitoring of Buildings for Improved Energy Efficiency; IOP Publishing: Bristol, UK, 2020; Volume 1, pp. 1–14. [Google Scholar]
- Hamre, B.; Bracchi, T.; Felius, L.C.; Burheim, O.S.; Pollet, B.G.; Lamb, J.J. Energy production in buildings. In Energy-Smart Buildings: Design, Construction and Monitoring of Buildings for Improved Energy Efficiency; IOP Publishing: Bristol, UK, 2020; Volume 1, pp. 1–13. [Google Scholar]
- Aaldering, L.J.; Leker, J.; Song, C.H. Analysis of technological knowledge stock and prediction of its future development potential: The case of lithium-ion batteries. J. Clean. Prod. 2019, 223, 301–311. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Hu, X.; Cao, D.; Egardt, B. Condition monitoring in advanced battery management systems: Moving horizon estimation using a reduced electrochemical model. IEEE/ASME Trans. Mechatron. 2017, 23, 167–178. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Klein, R.; Christensen, J.; Ahmed, J.; Kojic, A. Algorithms for advanced battery-management systems. IEEE Control Syst. Mag. 2010, 30, 49–68. [Google Scholar]
- Wang, Y.; Chen, Z.; Zhang, C. On-line remaining energy prediction: A case study in embedded battery management system. Appl. Energy 2017, 194, 688–695. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Yang, B.; Cui, X.; Li, X. Electrochemical model of lithium-ion battery for wide frequency range applications. Electrochim. Acta 2020, 34, 136094. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2017, 65, 5634–5643. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, D.; Zhang, X.; Chen, Z. Probability based remaining capacity estimation using data-driven and neural network model. J. Power Sources 2016, 315, 199–208. [Google Scholar] [CrossRef]
- Romero-Becerril, A.; Alvarez-Icaza, L. Comparison of discretization methods applied to the single-particle model of lithium-ion batteries. J. Power Sources 2011, 196, 10267–10279. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; Li, L.; Odio, M.X.; Widanage, W.D. Global Sensitivity Analysis of the Single Particle Lithium-Ion Battery Model with Electrolyte. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Dao, T.-S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation. J. Power Sources 2015, 278, 814–825. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the Kalman filter algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Nagasubramanian, G.; Jungst, R.G.; Doughty, D.H. Modeling of lithium ion cells—A simple equivalent-circuit model approach. Solid State Ion. 2004, 175, 835–839. [Google Scholar]
- Verbrugge, M.; Tate, E. Adaptive state of charge algorithm for nickel metal hydride batteries including hysteresis phenomena. J. Power Sources 2004, 126, 236–249. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Pan, R.; Chen, Z. Modeling and state-of-charge prediction of lithium-ion battery and ultracapacitor hybrids with a co-estimator. Energy 2017, 121, 739–750. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Yuan, S.; Yang, J.; Zhou, X. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties. J. Power Sources 2017, 345, 21–29. [Google Scholar] [CrossRef]
- Brand, J.; Zhang, Z.; Agarwal, R.K. Extraction of battery parameters of the equivalent circuit model using a multi-objective genetic algorithm. J. Power Sources 2014, 247, 729–737. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, C.; Wen, G. Equivalent circuit model analysis on electrochemical impedance spectroscopy of lithium metal batteries. J. Power Sources 2015, 294, 67–74. [Google Scholar] [CrossRef]
- Jang, J.; Yoo, J. Equivalent circuit evaluation method of lithium polymer battery using bode plot and numerical analysis. IEEE Trans. Energy Convers. 2011, 26, 290–298. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, J.; Cao, B.; Li, X. A simplified fractional order impedance model and parameter identification method for lithium-ion batteries. PLoS ONE 2017, 12, e0172424. [Google Scholar] [CrossRef]
- Zou, Y.; Li, S.E.; Shao, B.; Wang, B. State-space model with non-integer order derivatives for lithium-ion battery. Appl. Energy 2016, 161, 330–336. [Google Scholar] [CrossRef]
- Mu, H.; Xiong, R.; Zheng, H.; Chang, Y.; Chen, Z. A novel fractional order model based state-of-charge estimation method for lithium-ion battery. Appl. Energy 2017, 207, 384–393. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A novel fractional order model for state of charge estimation in lithium ion batteries. IEEE Trans. Veh. Technol. 2018, 68, 4130–4139. [Google Scholar] [CrossRef]
- Wang, Q.-K.; He, Y.-J.; Shen, J.-N.; Ma, Z.-F.; Zhong, G.-B. A unified modeling framework for lithium-ion batteries: An artificial neural network based thermal coupled equivalent circuit model approach. Energy 2017, 138, 118–132. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Y.; Dong, G.; Wei, J. Data-driven lithium-ion battery states estimation using neural networks and particle filtering. Int. J. Energy Res. 2019, 43, 8230–8241. [Google Scholar] [CrossRef]
- Thangavel, V.; Guerrero, O.X.; Quiroga, M.; Mikala, A.M.; Rucci, A.; Franco, A.A. A three dimensional kinetic Monte Carlo model for simulating the carbon/sulfur mesostructural evolutions of discharging lithium sulfur batteries. Energy Storage Mater. 2020, 24, 472–485. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Kim, I.-S. Nonlinear state of charge estimator for hybrid electric vehicle battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Zhu, C. A combined state of charge estimation method for lithium-ion batteries used in a wide ambient temperature range. Energies 2014, 7, 3004–3032. [Google Scholar] [CrossRef]
- Meissner, E.; Richter, G. Battery monitoring and electrical energy management: Precondition for future vehicle electric power systems. J. Power Sources 2003, 116, 79–98. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Del Olmo, D.; Pavelka, M.; Kosek, J. Open-Circuit Voltage Comes from Non-Equilibrium Thermodynamics. J. Non-Equilib. Thermodyn. 2020, 46, 91–108. [Google Scholar] [CrossRef]
- Vágner, P.; Kodým, R.; Bouzek, K. Thermodynamic analysis of high temperature steam and carbon dioxide systems in solid oxide cells. Sustain. Energy Fuels 2019, 3, 2076–2086. [Google Scholar] [CrossRef]
- Pavelka, M.; Wandschneider, F.; Mazur, P. Thermodynamic derivation of open circuit voltage in vanadium redox flow batteries. J. Power Sources 2015, 293, 400–408. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Cuma, M.U.; Koroglu, T. A comprehensive review on estimation strategies used in hybrid and battery electric vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Waag, W.; Sauer, D.U. Adaptive estimation of the electromotive force of the lithium-ion battery after current interruption for an accurate state-of-charge and capacity determination. Appl. Energy 2013, 111, 416–427. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Yazami, R.; Le, M.D. A practical framework of electrical based online state-of-charge estimation of lithium ion batteries. J. Power Sources 2014, 255, 423–430. [Google Scholar] [CrossRef]
- Dincer, I.; Hamut, H.S.; Javani, N. Thermal Management of Electric Vehicle Battery Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 1118900219. [Google Scholar]
- Andrea, D. Battery Management Systems for Large Lithium Ion Battery Packs; Artech House: Norwood, MA, USA, 2010; ISBN 1608071057. [Google Scholar]
- Rahn, C.D.; Wang, C.-Y. Battery Systems Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 1118517059. [Google Scholar]
- Lillehei, C.W.; Cruz, A.B.; Johnsrude, I.; Sellers, R.D. A new method of assessing the state of charge of implanted cardiac pacemaker batteries. Am. J. Cardiol. 1965, 16, 717–721. [Google Scholar] [CrossRef]
- Tan, X. Electric Vehicle Power Battery Management System Design; Sun Yat-sen University Press: Guangzhou, China, 2011. [Google Scholar]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Pop, V.; Bergveld, H.J.; het Veld, J.H.G.O.; Regtien, P.P.L.; Danilov, D.; Notten, P.H.L. Modeling battery behavior for accurate state-of-charge indication. J. Electrochem. Soc. 2006, 153, A2013. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Junaid Alvi, M.; Kim, H.-J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Klintberg, A.; Zou, C.; Fridholm, B.; Wik, T. Kalman filter for adaptive learning of two-dimensional look-up tables applied to OCV-curves for aged battery cells. Control Eng. Pract. 2019, 84, 230–237. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Zhang, C.; Chen, Z. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar] [CrossRef]
- Ovejas, V.J.; Cuadras, A. Effects of cycling on lithium-ion battery hysteresis and overvoltage. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rashid, M.; Pathan, T.S.; McGordon, A.; Kendrick, E.; Widanage, W.D. Investigation of hysteresis and relaxation behaviour in graphite and LiNi0. 33Mn0. 33Co0. 33O2 electrodes. J. Power Sources 2019, 440, 227153. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online internal resistance measurement application in lithium ion battery capacity and state of charge estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Huet, F.; Nogueira, R.P.; Lailler, P.; Torcheux, L. Investigation of the high-frequency resistance of a lead-acid battery. J. Power Sources 2006, 158, 1012–1018. [Google Scholar] [CrossRef]
- Huang, W.; Qahouq, J.A.A. An online battery impedance measurement method using DC–DC power converter control. IEEE Trans. Ind. Electron. 2014, 61, 5987–5995. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, W.; Lin, S.; Feng, Z. A novel model of the initial state of charge estimation for LiFePO4 batteries. J. Power Sources 2014, 248, 1028–1033. [Google Scholar] [CrossRef]
- Xu, L.; Wang, J.; Chen, Q. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Convers. Manag. 2012, 53, 33–39. [Google Scholar] [CrossRef]
- Mastali, M.; Vazquez-Arenas, J.; Fraser, R.; Fowler, M.; Afshar, S.; Stevens, M. Battery state of the charge estimation using Kalman filtering. J. Power Sources 2013, 239, 294–307. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Chen, Z. Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries. J. Power Sources 2016, 328, 615–626. [Google Scholar] [CrossRef]
- Yu, Z.; Huai, R.; Xiao, L. State-of-charge estimation for lithium-ion batteries using a kalman filter based on local linearization. Energies 2015, 8, 7854–7873. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Mi, C.C. State of charge estimation of lithium-ion batteries in electric drive vehicles using extended Kalman filtering. IEEE Trans. Veh. Technol. 2012, 62, 1020–1030. [Google Scholar] [CrossRef]
- Lee, J.; Nam, O.; Cho, B.H. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering. J. Power Sources 2007, 174, 9–15. [Google Scholar] [CrossRef]
- Dai, H.; Wei, X.; Sun, Z.; Wang, J.; Gu, W. Online cell SOC estimation of Li-ion battery packs using a dual time-scale Kalman filtering for EV applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Lee, K.-T.; Dai, M.-J.; Chuang, C.-C. Temperature-compensated model for lithium-ion polymer batteries with extended Kalman filter state-of-charge estimation for an implantable charger. IEEE Trans. Ind. Electron. 2017, 65, 589–596. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on state of charge estimation of batteries with adaptive extended Kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2012, 62, 108–117. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Seo, B.-H.; Nguyen, T.H.; Lee, D.-C.; Lee, K.-B.; Kim, J.-M. Condition monitoring of lithium polymer batteries based on a sigma-point Kalman filter. J. Power Electron. 2012, 12, 778–786. [Google Scholar] [CrossRef]
- Bi, Y.; Choe, S.-Y. An adaptive sigma-point Kalman filter with state equality constraints for online state-of-charge estimation of a Li (NiMnCo) O2/Carbon battery using a reduced-order electrochemical model. Appl. Energy 2020, 258, 113925. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, C. State-of-charge estimation of valve regulated lead acid battery based on multi-state Unscented Kalman Filter. Int. J. Electr. Power Energy Syst. 2011, 33, 472–476. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl. Math. Model. 2019, 70, 532–544. [Google Scholar] [CrossRef]
- Gholizade-Narm, H.; Charkhgard, M. Lithium-ion battery state of charge estimation based on square-root unscented Kalman filter. IET Power Electron. 2013, 6, 1833–1841. [Google Scholar] [CrossRef]
- Aung, H.; Low, K.S.; Goh, S.T. State-of-charge estimation of lithium-ion battery using square root spherical unscented Kalman filter (Sqrt-UKFST) in nanosatellite. IEEE Trans. Power Electron. 2014, 30, 4774–4783. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, P.; Yang, Y.; Xie, C.; Shi, Y. SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm. Energies 2019, 12, 3122. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Liu, G.; Xu, C.; Li, H.; Jiang, K.; Wang, K. State of charge and online model parameters co-estimation for liquid metal batteries. Appl. Energy 2019, 250, 677–684. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2014, 23, 357–363. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Qiu, X.; Guo, Y.; Zhang, J.; Zhao, H.; Peng, X.; Wu, Z.; Tian, R.; Yang, J. State of Charge Estimation of Lithium Battery Energy Storage Systems Based on Adaptive Correntropy Unscented Kalman Filter. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 851–857. [Google Scholar]
- Lim, J. CDKF approach for estimating a static parameter of carrier frequency offset based on nonlinear measurement equations in OFDM systems. Nonlinear Dyn. 2014, 78, 703–711. [Google Scholar] [CrossRef]
- Xuan, D.-J.; Shi, Z.; Chen, J.; Zhang, C.; Wang, Y.-X. Real-time estimation of state-of-charge in lithium-ion batteries using improved central difference transform method. J. Clean. Prod. 2020, 252, 119787. [Google Scholar] [CrossRef]
- Sangwan, V.; Kumar, R.; Rathore, A.K. State-of-charge estimation for li-ion battery using extended Kalman filter (EKF) and central difference Kalman filter (CDKF). In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 14 March 2018; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature kalman filters. IEEE Trans. Automat. Contr. 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Nummiaro, K.; Koller-Meier, E.; Van Gool, L. An adaptive color-based particle filter. Image Vis. Comput. 2003, 21, 99–110. [Google Scholar] [CrossRef]
- Tulsyan, A.; Tsai, Y.; Gopaluni, R.B.; Braatz, R.D. State-of-charge estimation in lithium-ion batteries: A particle filter approach. J. Power Sources 2016, 331, 208–223. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, H.; Dong, G.; Wei, J.; Wu, J.I. Particle filter-based state-of-charge estimation and remaining-dischargeable-time prediction method for lithium-ion batteries. J. Power Sources 2019, 414, 158–166. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter. J. Power Sources 2015, 279, 306–311. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Zhang, C.; Wu, J. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation. Appl. Energy 2014, 123, 263–272. [Google Scholar] [CrossRef]
- Van Der Merwe, R.; Doucet, A.; De Freitas, N.; Wan, E. The unscented particle filter. Adv. Neural Inf. Process. Syst. 2000, 13, 584–590. [Google Scholar]
- He, Y.; Liu, X.; Zhang, C.; Chen, Z. A new model for State-of-Charge (SOC) estimation for high-power Li-ion batteries. Appl. Energy 2013, 101, 808–814. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z. A framework for state-of-charge and remaining discharge time prediction using unscented particle filter. Appl. Energy 2020, 260, 114324. [Google Scholar] [CrossRef]
- Shen, Y. Hybrid unscented particle filter based state-of-charge determination for lead-acid batteries. Energy 2014, 74, 795–803. [Google Scholar] [CrossRef]
- Wang, D.; Yang, F.; Tsui, K.-L.; Zhou, Q.; Bae, S.J. Remaining useful life prediction of lithium-ion batteries based on spherical cubature particle filter. IEEE Trans. Instrum. Meas. 2016, 65, 1282–1291. [Google Scholar] [CrossRef]
- Guo, R.; Gan, Q.; Zhang, J.; Guo, K.; Dong, J. Huber cubature particle filter and online state estimation. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2017, 231, 158–167. [Google Scholar] [CrossRef]
- Xia, B.; Sun, Z.; Zhang, R.; Cui, D.; Lao, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A comparative study of three improved algorithms based on particle filter algorithms in soc estimation of lithium ion batteries. Energies 2017, 10, 1149. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, J.; Zhao, X.; Zhang, D.; He, Y. State of Charge Estimation for Lithium Battery Based on Adaptively Weighting Cubature Particle Filter. IEEE Access 2019, 7, 166657–166666. [Google Scholar] [CrossRef]
- Luenberger, D. An introduction to observers. IEEE Trans. Automat. Contr. 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Luenberger, D. Observers for multivariable systems. IEEE Trans. Automat. Contr. 1966, 11, 190–197. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive Luenberger observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, S.E.; Moura, S.J.; Peng, H. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional model. IEEE Trans. Control Syst. Technol. 2016, 25, 3–11. [Google Scholar] [CrossRef]
- Huangfu, Y.; Xu, J.; Zhao, D.; Liu, Y.; Gao, F. A novel battery state of charge estimation method based on a super-twisting sliding mode observer. Energies 2018, 11, 1211. [Google Scholar] [CrossRef]
- Kim, D.; Koo, K.; Jeong, J.J.; Goh, T.; Kim, S.W. Second-order discrete-time sliding mode observer for state of charge determination based on a dynamic resistance li-ion battery model. Energies 2013, 6, 5538–5551. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. Adaptive gain sliding mode observer for state of charge estimation based on combined battery equivalent circuit model. Comput. Chem. Eng. 2014, 64, 114–123. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Kim, D.; Goh, T.; Park, M.; Kim, S.W. Fuzzy sliding mode observer with grey prediction for the estimation of the state-of-charge of a lithium-ion battery. Energies 2015, 8, 12409–12428. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Dai, M.; Cao, Z.; Jin, J.; Kapoor, A. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles. IEEE Trans. Veh. Technol. 2015, 65, 1936–1947. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries based on a dual-circuit state observer. J. Power Sources 2015, 296, 23–29. [Google Scholar] [CrossRef]
- Xie, J.; Ma, J.; Sun, Y.; Li, Z. Estimating the state-of-charge of lithium-ion batteries using an H-infinity observer with consideration of the hysteresis characteristic. J. Power Electron. 2016, 16, 643–653. [Google Scholar] [CrossRef]
- Zhu, Q.; Xiong, N.; Yang, M.-L.; Huang, R.-S.; Hu, G.-D. State of charge estimation for lithium-ion battery based on nonlinear observer: An H∞ method. Energies 2017, 10, 679. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, L.; Hu, X.; Xiong, N.; Hu, G.-D. H∞-Based Nonlinear Observer Design for State of Charge Estimation of Lithium-Ion Battery With Polynomial Parameters. IEEE Trans. Veh. Technol. 2017, 66, 10853–10865. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.M.; Karim, T.F.; How, D.N.T. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine Learning Applied to Electrified Vehicle Battery State of Charge and State of Health Estimation: State-of-the-Art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman filter parameters via genetic algorithm for state-of-charge estimation in battery management system. Sci. World J. 2014, 2014, 176052. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, Z.; Lü, Z.; Li, J.; Ji, B.; Wei, H.; Pan, H. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms. IEEE Trans. Power Electron. 2017, 33, 8797–8807. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilán, J.A.V. Support vector machines used to estimate the battery state of charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented Kalman filter and support vector machine. IEEE Trans. Power Electron. 2015, 31, 2226–2238. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion battery using dual neural network fusion battery model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Hannan, M.A.; Hussain, A.; Saad, M.H.M. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection. J. Renew. Sustain. Energy 2017, 9, 64102. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Chen, J.; Ouyang, Q.; Xu, C.; Su, H. Neural network-based state of charge observer design for lithium-ion batteries. IEEE Trans. Control Syst. Technol. 2017, 26, 313–320. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.M.; Ayob, A.; Blaabjerg, F. State of charge estimation for lithium-ion battery using recurrent NARX neural network model based lighting search algorithm. IEEE Access 2018, 6, 28150–28161. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Ker, P.J.; Mahlia, T.M.I.; Mansor, M.; Ayob, A.; Saad, M.H.; Dong, Z.Y. Toward enhanced State of charge estimation of Lithium-ion Batteries Using optimized Machine Learning techniques. Sci. Rep. 2020, 10, 1–15. [Google Scholar]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Yang, F.; Song, X.; Xu, F.; Tsui, K.-L. State-of-charge estimation of lithium-ion batteries via long short-term memory network. IEEE Access 2019, 7, 53792–53799. [Google Scholar] [CrossRef]
- Liu, Y.; Shu, X.; Yu, H.; Shen, J.; Zhang, Y.; Liu, Y.; Chen, Z. State of charge prediction framework for lithium-ion batteries incorporating long short-term memory network and transfer learning. J. Energy Storage 2021, 37, 102494. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Chen, S.; Ren, H.; Gao, Z. A combined robust approach based on auto-regressive long short-term memory network and moving horizon estimation for state-of-charge estimation of lithium-ion batteries. Int. J. Energy Res. 2021. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Han, X.; Feng, X.; Lu, L.; Li, J. Error analysis of the model-based state-of-charge observer for lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 8055–8064. [Google Scholar] [CrossRef]
- Wahl, M.S.; Lamb, J.J.; Muri, H.I.; Snilsberg, R.K.; Hjelme, D.R. Light properties and sensors. In Micro-Optics and Energy: Sensors for Energy Devices.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Muri, H.I.; Wahl, M.S.; Lamb, J.J.; Snilsberg, R.K.; Hjelme, D.R. Sensor fusion. In Micro-Optics and Energy: Sensors for Energy Devices; Springer International Publishing: New York, NY, USA, 2020. [Google Scholar]
- Spitthoff, L.; Lamb, J.J.; Pollet, B.; Burheim, O.S. Lifetime expectancy of lithium-ion batteries. In Micro-Optics and Energy: Sensors for Energy Devices; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Spitthoff, L.; Øyre, E.S.; Muri, H.I.; Wahl, M.S.; Gunnarshaug, A.F.; Pollet, B.; Lamb, J.J.; Burheim, O.S. Thermal management of Lithium ion batteries. In Micro-Optics and Energy: Sensors for Energy Devices; Springer International Publishing: New York, NY, USA, 2020. [Google Scholar]
- Wahl, M.S.; Muri, H.I.; Snilsberg, R.K.; Lamb, J.J.; Hjelme, D.R. Temperature and humidity measurements. In Micro-Optics and Energy: Sensors for Energy Devices; Springer International Publishing: New York, NY, USA, 2020. [Google Scholar]
- Lamb, J.J.; Burheim, O.S.; Pollet, B. Hydrogen fuel cells and water electrolysers. In Micro-Optics and Energy: Sensors for Energy Devices; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yang, G.; Leitão, C.; Li, Y.; Pinto, J.; Jiang, X. Real-time temperature measurement with fiber Bragg sensors in lithium batteries for safety usage. Measurement 2013, 46, 3166–3172. [Google Scholar] [CrossRef]
- David, N.A.; Wild, P.M.; Hu, J.; Djilali, N. In-fibre Bragg grating sensors for distributed temperature measurement in a polymer electrolyte membrane fuel cell. J. Power Sources 2009, 192, 376–380. [Google Scholar] [CrossRef]
- Nascimento, M.; Novais, S.; Leitão, C.; Domingues, M.F.; Alberto, N.; Antunes, P.; Pinto, J.L. Lithium batteries temperature and strain fiber monitoring. In Proceedings of the 24th International Conference on Optical Fibre Sensors, Curitiba, Brazil, 28 September–2 October 2015; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9634, p. 96347V. [Google Scholar]
- Sommer, L.W.; Raghavan, A.; Kiesel, P.; Saha, B.; Schwartz, J.; Lochbaum, A.; Ganguli, A.; Bae, C.-J.; Alamgir, M. Monitoring of intercalation stages in lithium-ion cells over charge-discharge cycles with fiber optic sensors. J. Electrochem. Soc. 2015, 162, A2664. [Google Scholar] [CrossRef]
- Sommer, L.W.; Kiesel, P.; Ganguli, A.; Lochbaum, A.; Saha, B.; Schwartz, J.; Bae, C.-J.; Alamgir, M.; Raghavan, A. Fast and slow ion diffusion processes in lithium ion pouch cells during cycling observed with fiber optic strain sensors. J. Power Sources 2015, 296, 46–52. [Google Scholar] [CrossRef]
- Bae, C.; Manandhar, A.; Kiesel, P.; Raghavan, A. Monitoring the strain evolution of lithium-ion battery electrodes using an optical fiber Bragg grating sensor. Energy Technol. 2016, 4, 851–855. [Google Scholar] [CrossRef]
- Raghavan, A.; Kiesel, P.; Sommer, L.W.; Schwartz, J.; Lochbaum, A.; Hegyi, A.; Schuh, A.; Arakaki, K.; Saha, B.; Ganguli, A. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 1: Cell embedding method and performance. J. Power Sources 2017, 341, 466–473. [Google Scholar] [CrossRef]
- Ganguli, A.; Saha, B.; Raghavan, A.; Kiesel, P.; Arakaki, K.; Schuh, A.; Schwartz, J.; Hegyi, A.; Sommer, L.W.; Lochbaum, A. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 2: Internal cell signals and utility for state estimation. J. Power Sources 2017, 341, 474–482. [Google Scholar] [CrossRef]
- Song, Y.; Liu, D.; Liao, H.; Peng, Y. A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries. Appl. Energy 2020, 261, 114408. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, H.; Feng, F.; Liu, B. An enhanced multi-state estimation hierarchy for advanced lithium-ion battery management. Appl. Energy 2020, 257, 114019. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness evaluation of extended and unscented Kalman filter for battery state of charge estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Yang, S.; Deng, C.; Zhang, Y.; He, Y. State of charge estimation for lithium-ion battery with a temperature-compensated model. Energies 2017, 10, 1560. [Google Scholar] [CrossRef]
- Zhang, Y.; Shang, Y.; Cui, N.; Zhang, C. Parameters identification and sensitive characteristics analysis for lithium-ion batteries of electric vehicles. Energies 2018, 11, 19. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-ion battery parameters and state-of-charge joint estimation based on H-infinity and unscented Kalman filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Wang, Q.; Kang, J.; Tan, Z.; Luo, M. An online method to simultaneously identify the parameters and estimate states for lithium ion batteries. Electrochim. Acta 2018, 289, 376–388. [Google Scholar] [CrossRef]
- CALCE Battery Research Group. CALCE Battery Group. Available online: https://web.calce.umd.edu/batteries/index.html# (accessed on 3 May 2021).

| Method | Maximum Error | |
|---|---|---|
| Look-up tables | OCV | 1.2% [58] |
| Impedance | 1.4% [66] | |
| Ampere-hour integral | Current integration | 4% [69] |
| Filter | Linear Kalman | 2% [72] |
| Extended Kalman | 1.4% [74] | |
| Adaptive Kalman | 2% [80] | |
| Sigma-point Kalman | 1.2% [85] | |
| Unscented Kalman | 0.12% [87] | |
| Adaptive unscented Kalman | 0.1% [94] | |
| Central difference Kalman | 1.4% [98] | |
| Cubature Kalman | 2.7% [101] | |
| Particle | 0.86% [106] | |
| Unscented particle | 0.9% [114] | |
| Cubature particle | 1.1% [114] | |
| Observer | Luenberger | 0.88% [118] |
| Sliding mode | 2% [120] | |
| Proportional integral | 2.5% [126] | |
| H-infinity | 3.36% [128] | |
| Data-driven | Genetic algorithm | 2.98% [33] |
| Support vector machine | 6% [134] | |
| Neural network | 3.8% [137] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espedal, I.B.; Jinasena, A.; Burheim, O.S.; Lamb, J.J. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies 2021, 14, 3284. https://doi.org/10.3390/en14113284
Espedal IB, Jinasena A, Burheim OS, Lamb JJ. Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies. 2021; 14(11):3284. https://doi.org/10.3390/en14113284
Chicago/Turabian StyleEspedal, Ingvild B., Asanthi Jinasena, Odne S. Burheim, and Jacob J. Lamb. 2021. "Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles" Energies 14, no. 11: 3284. https://doi.org/10.3390/en14113284
APA StyleEspedal, I. B., Jinasena, A., Burheim, O. S., & Lamb, J. J. (2021). Current Trends for State-of-Charge (SoC) Estimation in Lithium-Ion Battery Electric Vehicles. Energies, 14(11), 3284. https://doi.org/10.3390/en14113284









