Improvement Dependability of Offshore Horizontal-Axis Wind Turbines by Applying New Mathematical Methods for Calculation the Excess Speed in Case of Wind Gusts
Abstract
:1. Introduction
1.1. Relevance of the Research Topic
1.2. Solving a Scientific Problem
1.3. Theoretical Purpose of the Developed Methodology
1.4. Application of the Developed Methodology
1.5. Review of Scientific Investigations
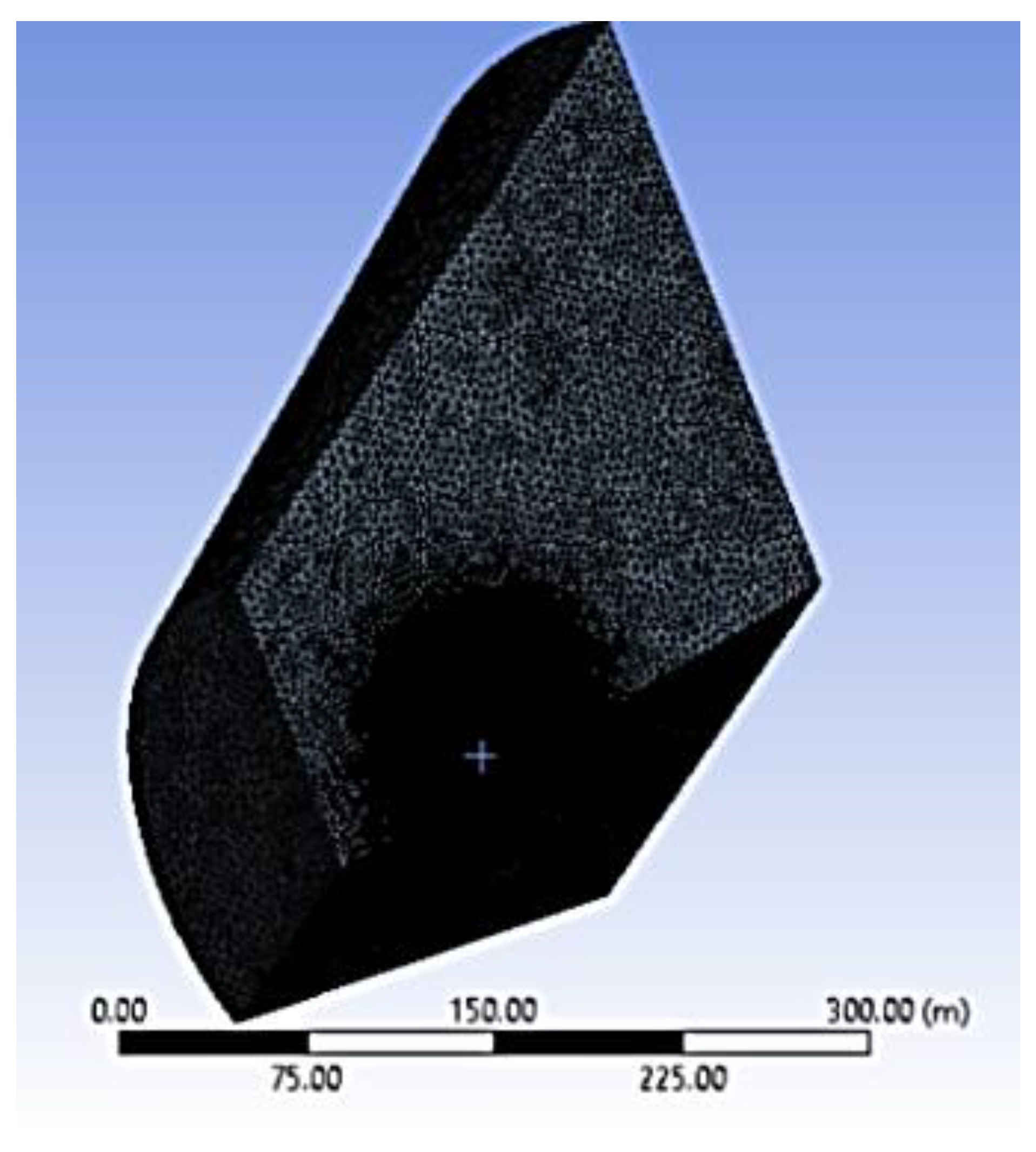
2. Experimental Unit
2.1. Experimental Investigations of Gas Dynamics of Air Flows
2.2. Reliability and Uncertainty of Measurement Device Data
3. Mathematical Part
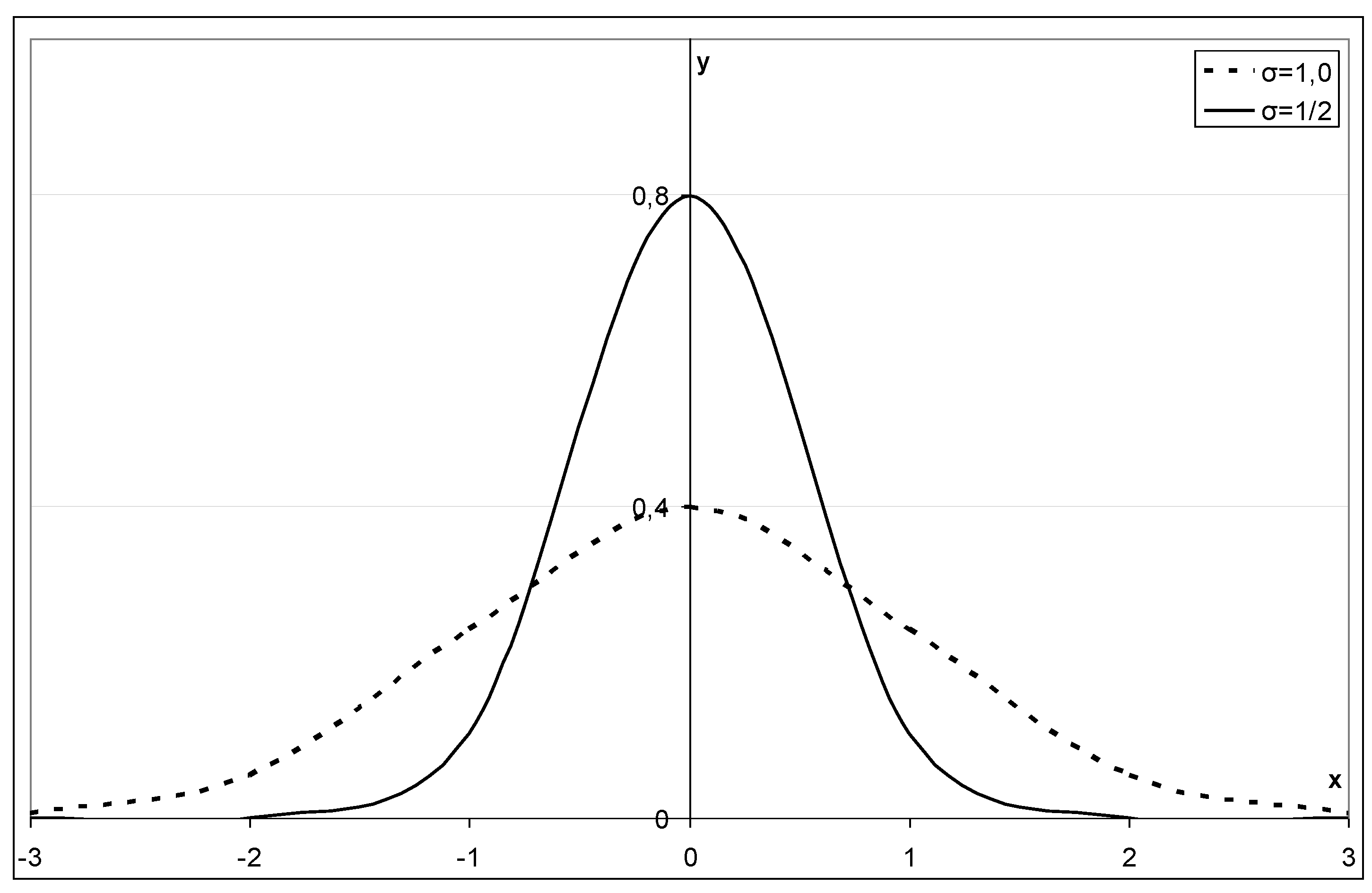
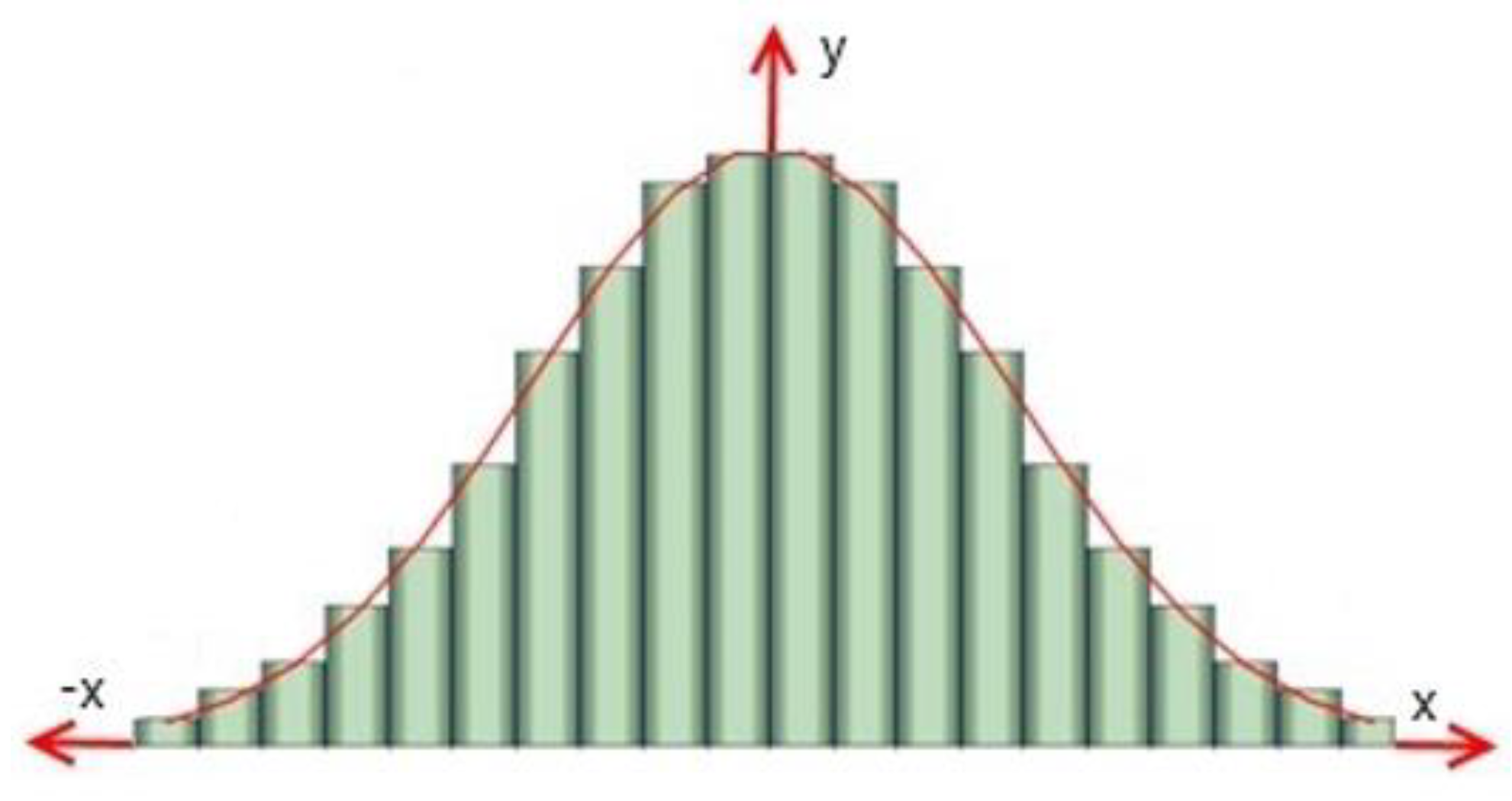
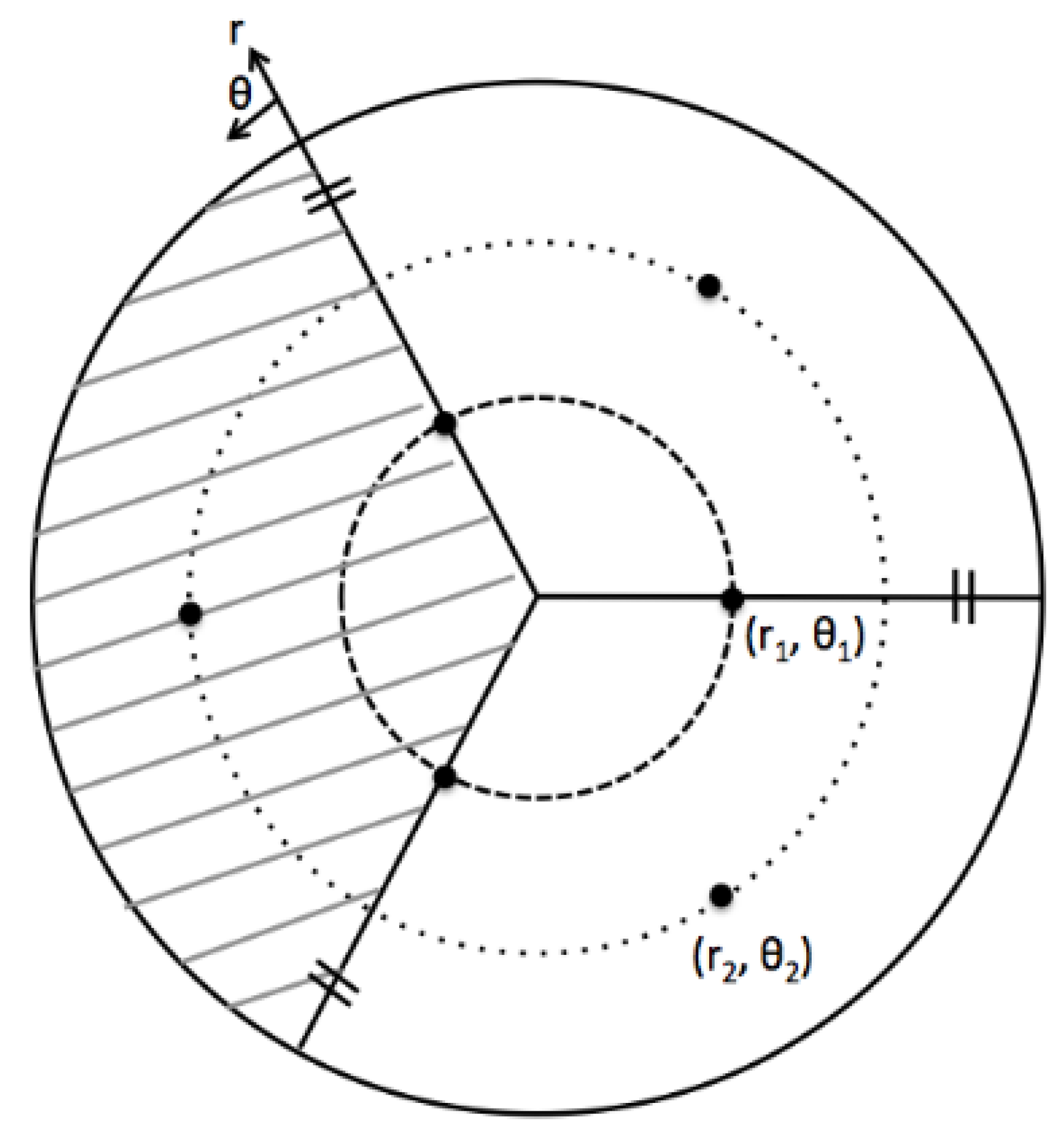
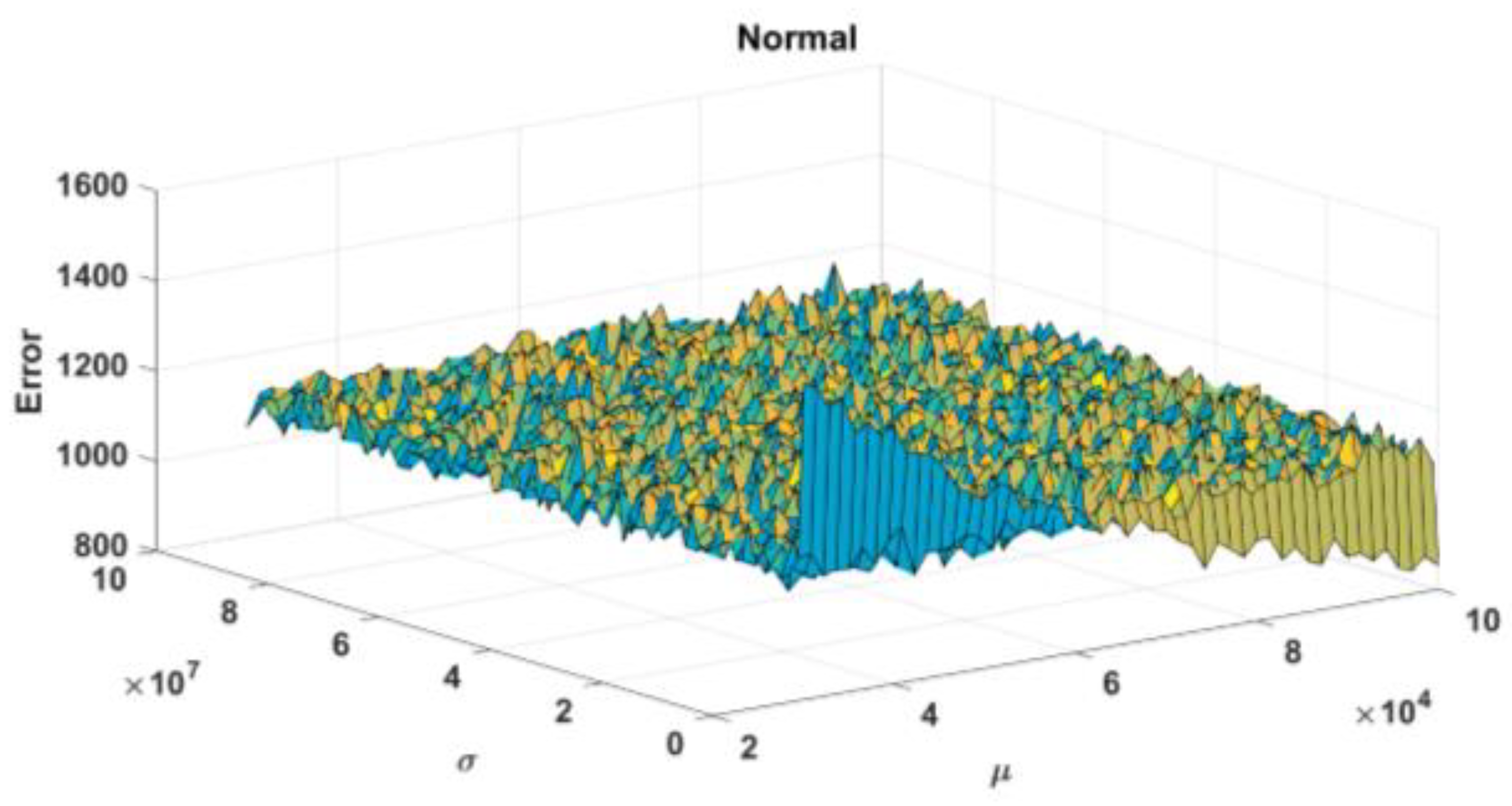
3.1. Application of the Normal Probability Distribution of Wind Velocity Deviation from the Mean Value
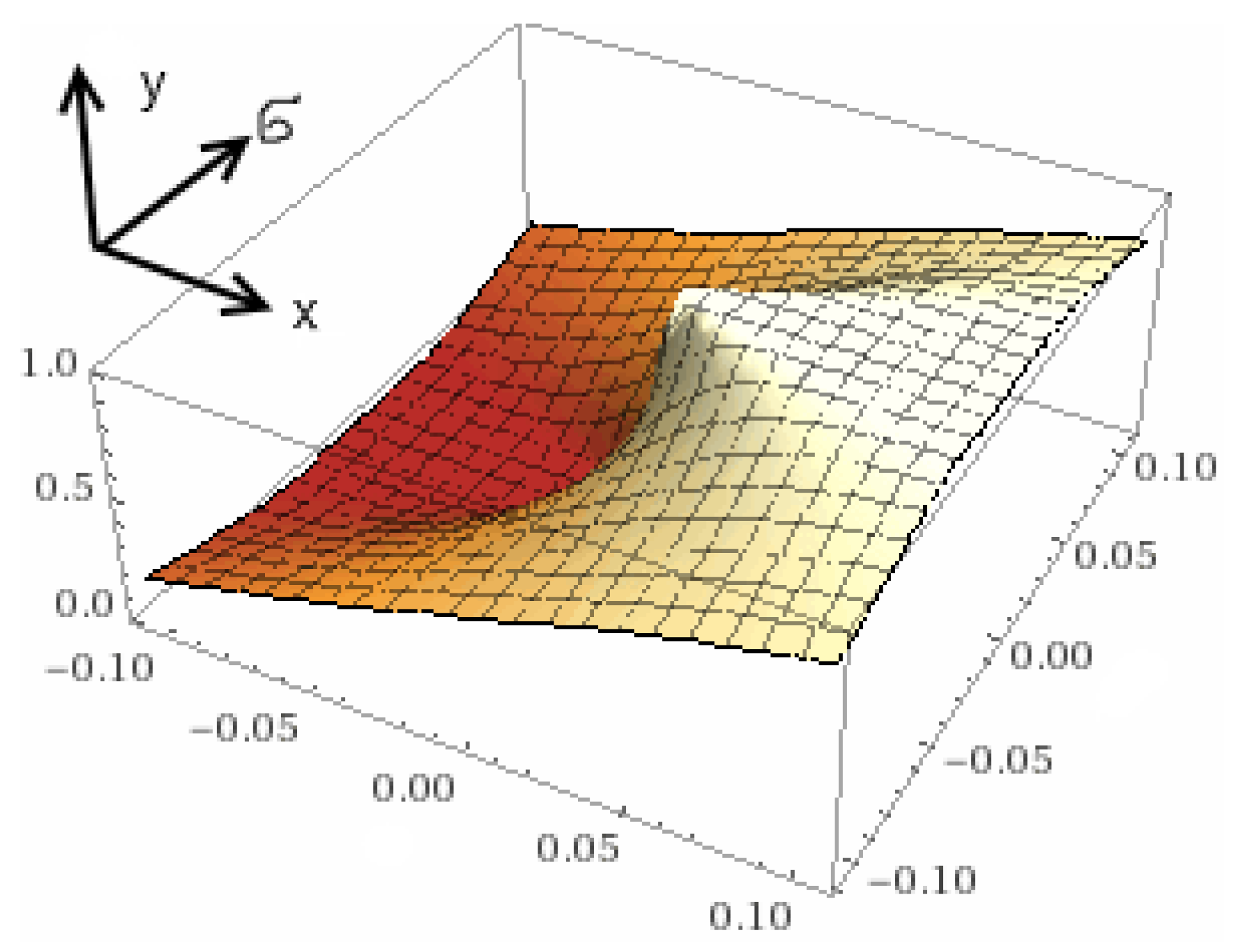
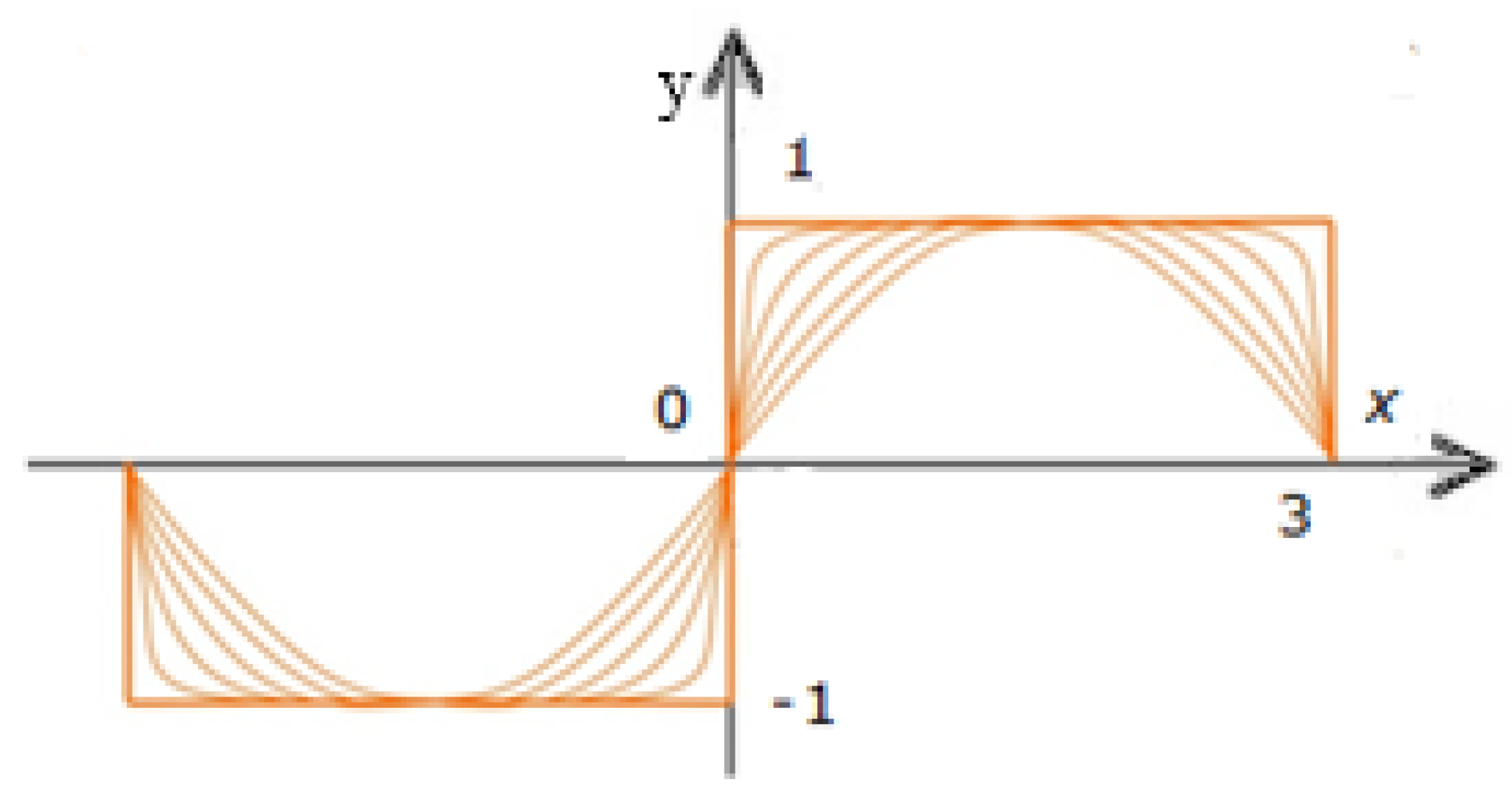
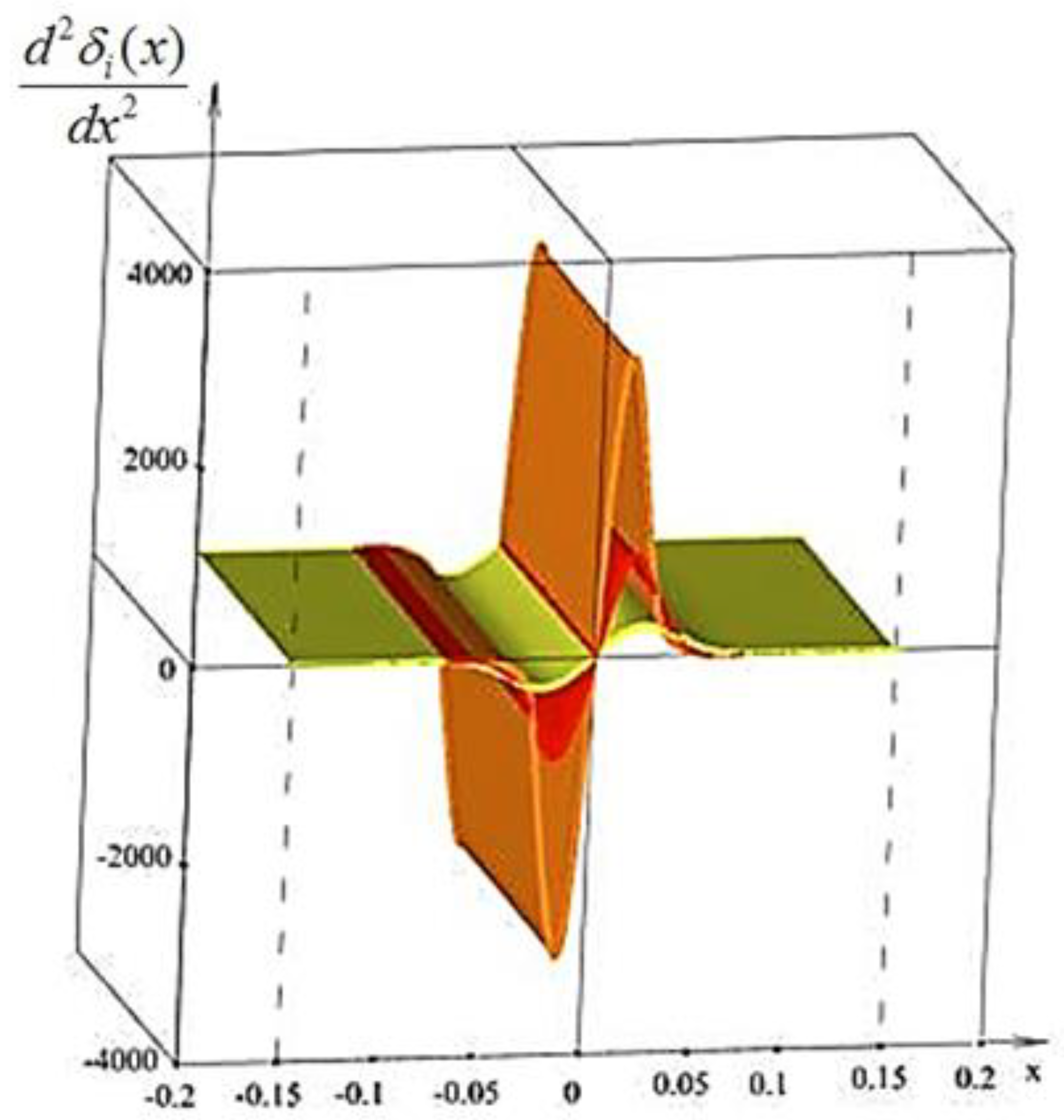
3.2. Approximation Methods. Application of Differential Curves to Describe the Velocity Distribution
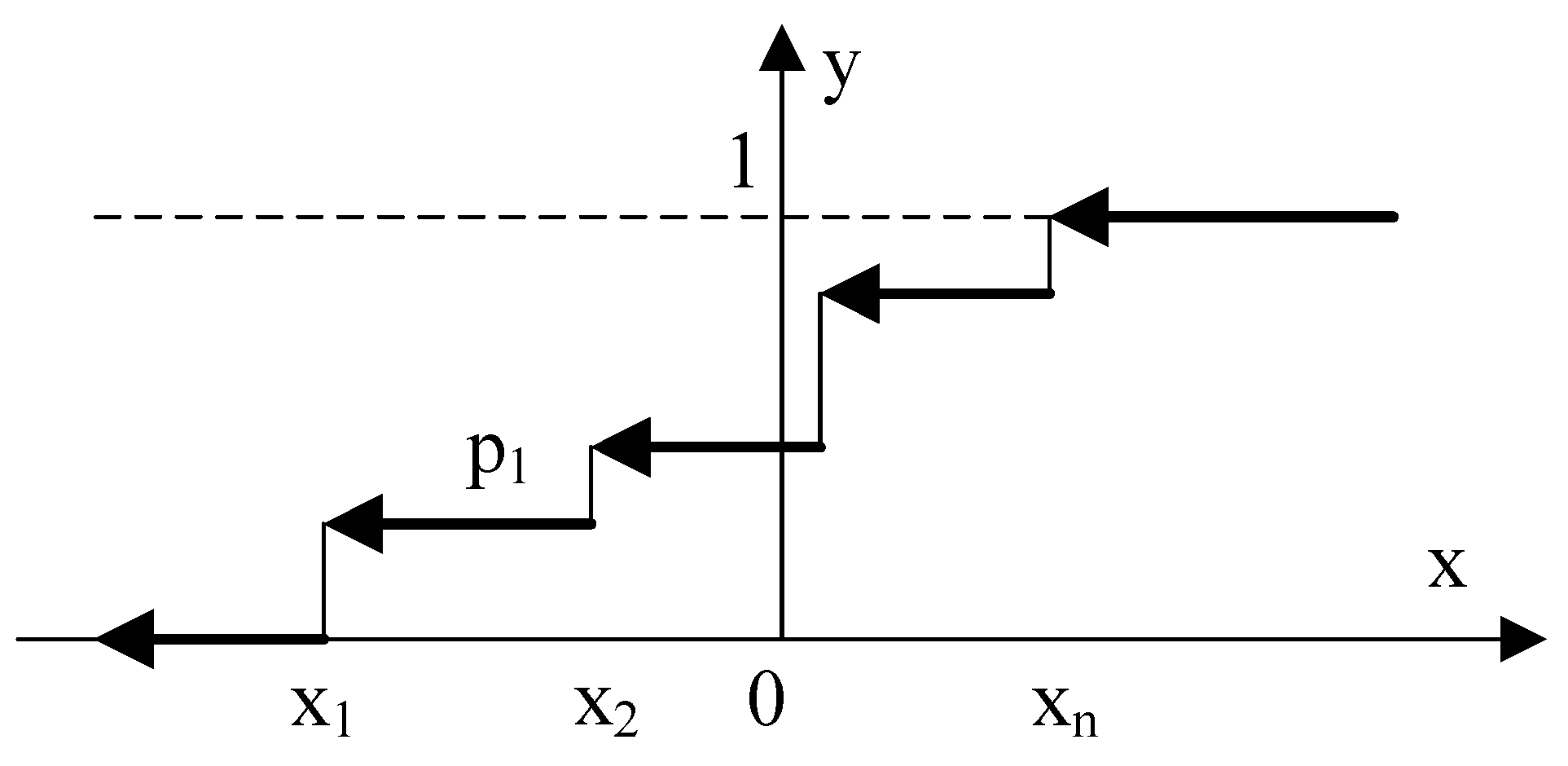
3.3. Application of Piecewise Linear Functions and Recursive Function Approximations for the Mathematical Description of the Coal Dust Sieving Process
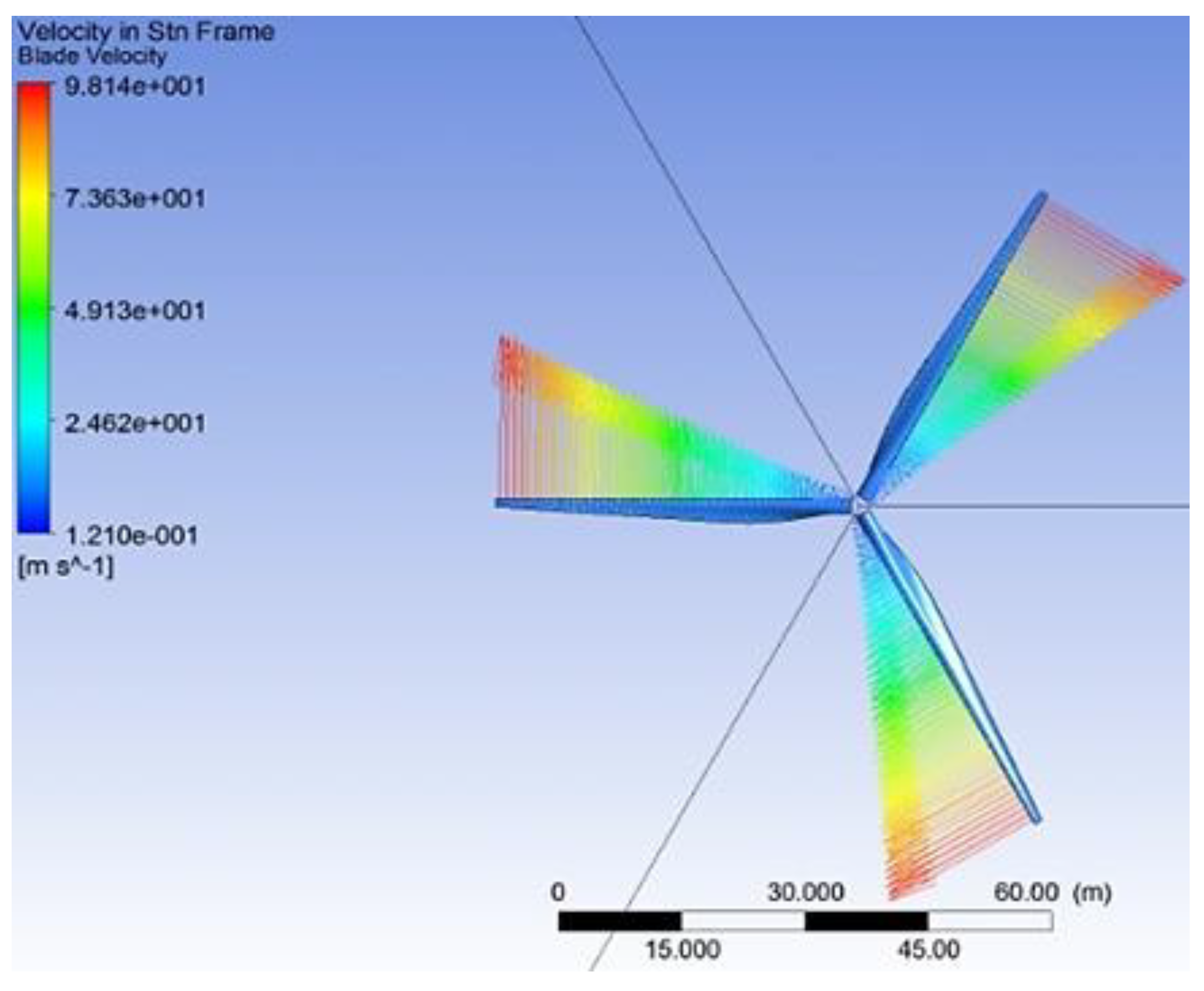
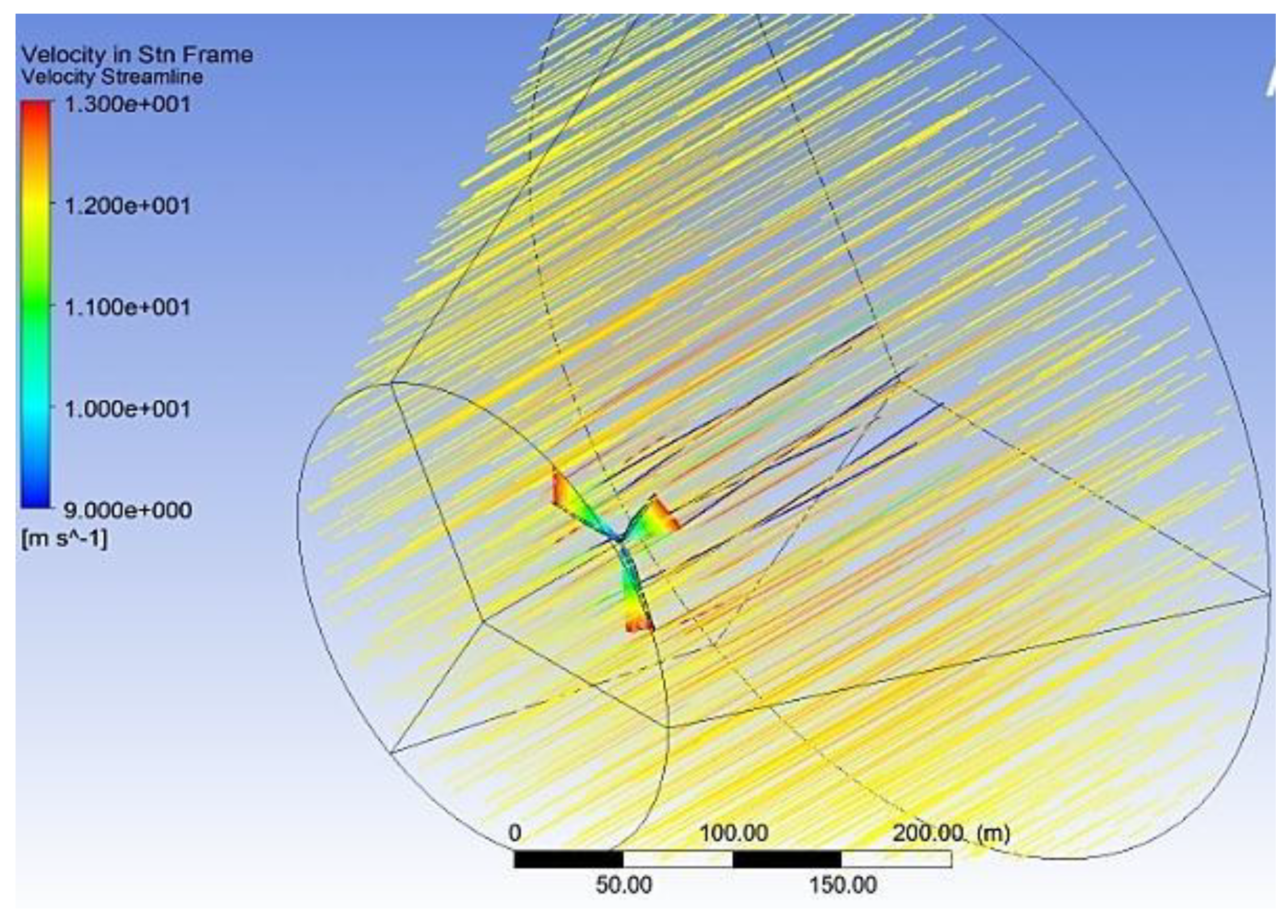
3.4. Computer Modeling of the Gas Dynamics of Air Flow
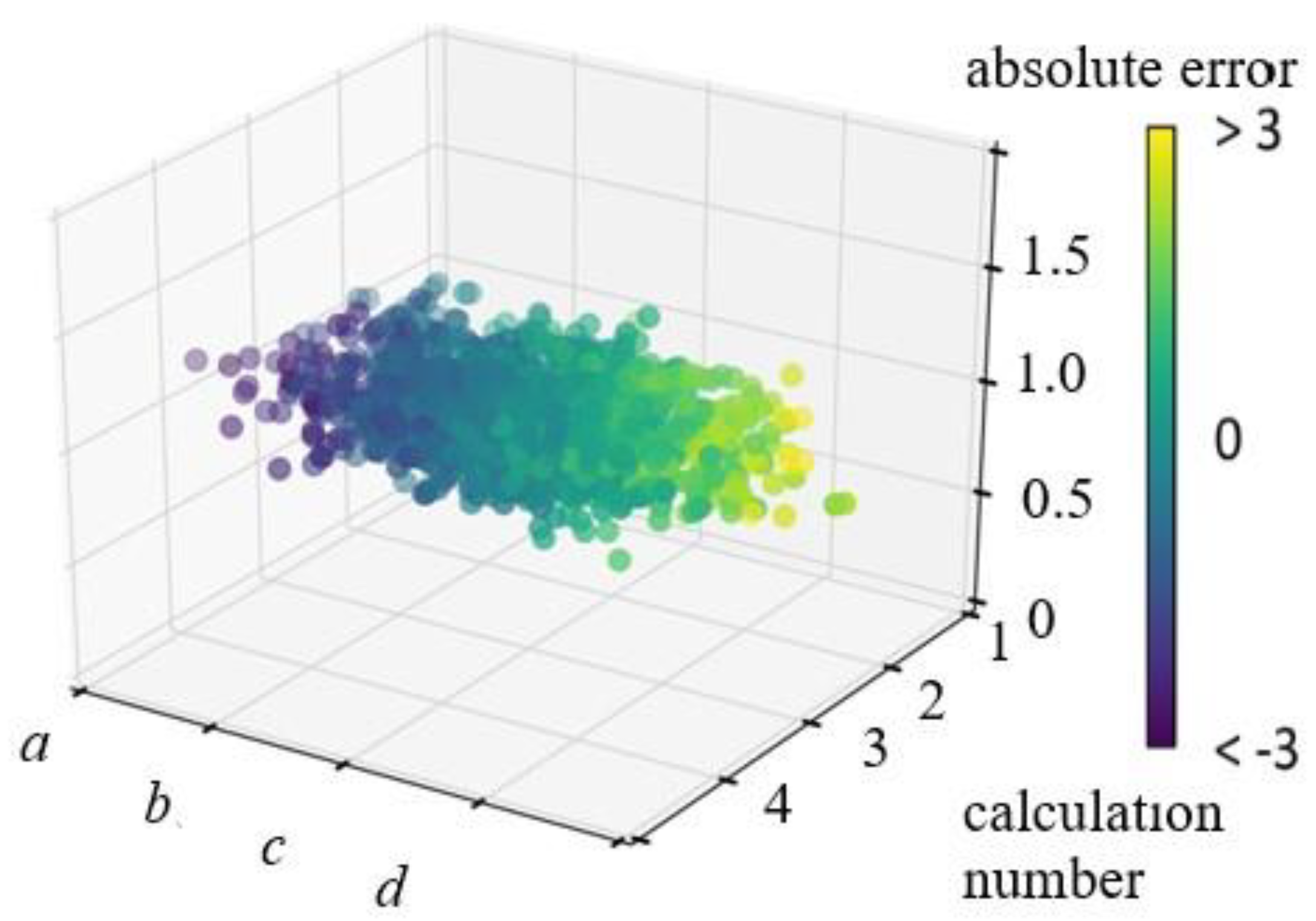
3.5. Estimation of Errors in the Processing of Experimental Data and Computer Simulation Results
4. Calculation of Measurement Uncertainty on a Laboratory Bench
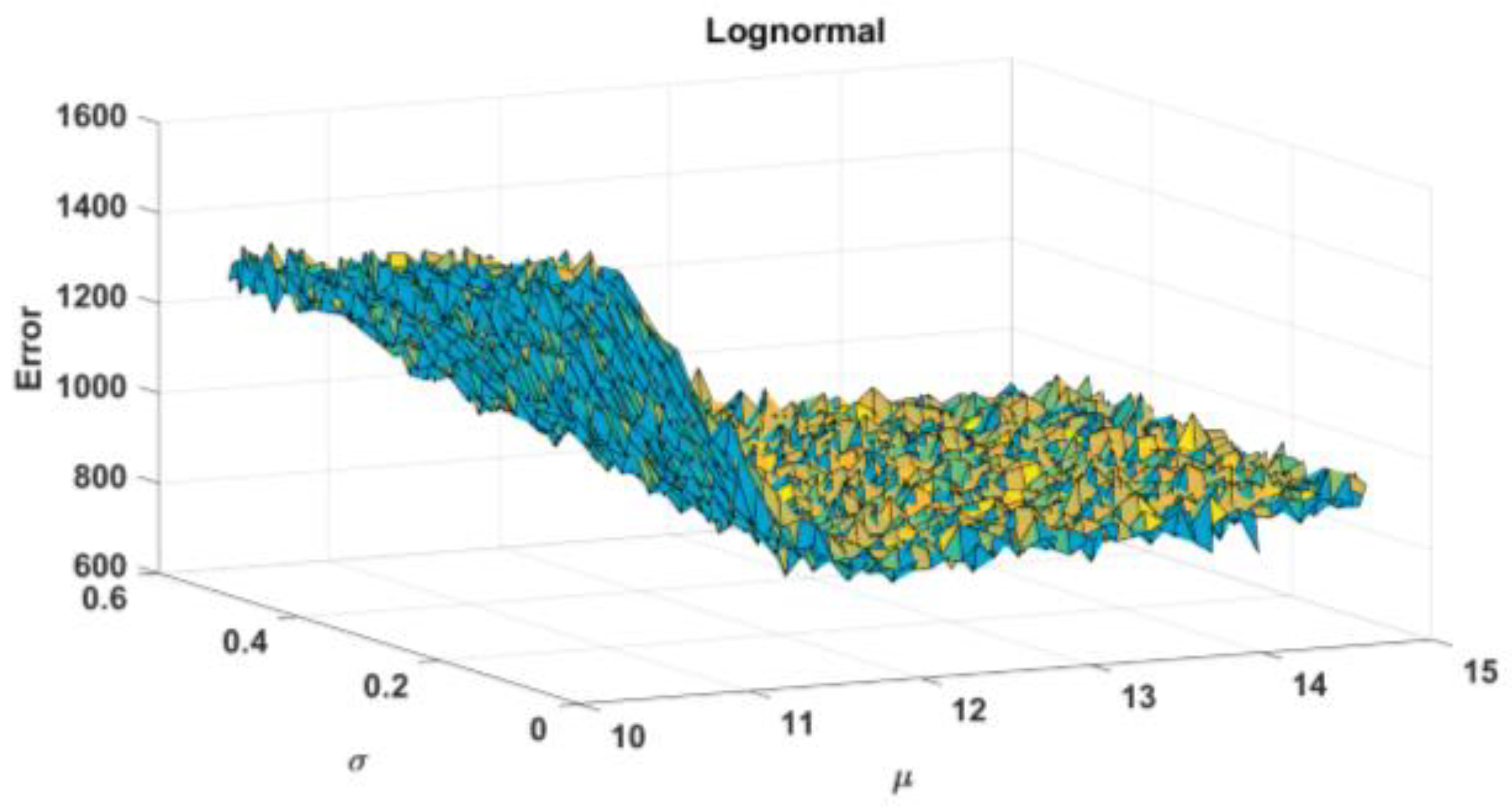
5. Sensitivity Analysis and Validation of Research Results
6. Results and Discussion
7. Conclusions
- Based on the new methods for approximating piece linear functions by recursive functions, we developed a methodological approach to solve the problems of the gas dynamics of flows during their mathematical modeling and the use of difference schemes.
- During the preliminary mathematical modeling of dynamic processes in technological devices, the new approximation methods reduce the calculation time and the calculation error.
- The approximation is performed by the generalized functions, which can be differentiated and their derivatives of any order can be found. Thus, the main functions of the parameters for k-omega computer modeling of the airflow can be approximated using the new method.
- The obtained approximations more accurately describe the initial function. The proposals for improving the mathematical apparatus of the standard k-omega model will help researchers to develop the theory of approximation by recursive functions of Professor S.V. Aliukov. The obtained results will allow us to solve one of the essential problems of modeling at this stage of its development, namely: to reduce the calculation time and the adequacy of the model built for similar installations and devices.
- In the present investigation, the aerodynamic efficiency of the horizontal axis wind turbine using computational methods of fluid dynamics is studied. The obtained CFD results are compared with the mathematical calculation and experimental data of the GE1.5 axle turbine. This study has demonstrated that the CFD methods confirm the experimental results and can be used to optimize and confirm the shape specifications of the turbine. According to the results of this research, it can be concluded that the power coefficient of the turbine is actually matched to the theoretical results as demonstrated.
- It should be taken into account that discontinuous gas-dynamic flows occur in stormy conditions on offshore wind turbines. In this case, the wind speeds can significantly exceed the permissible ones in terms of the stability and reliability of the wind turbine. However, you can choose the operating modes of the wind turbine in stormy conditions, but only when building a mathematical model. The authors of the article have developed new approximation methods for discontinuous gas-dynamic functions, which allow us to describe the processes in storm conditions at offshore wind turbines with a sufficient degree of confidence.
- The scientific problem of increasing the reliability of wind turbines is becoming relevant in the development of new offshore oil and natural gas fields in connection with the autonomous operation of drilling rigs and bulk seaports in the subarctic and Arctic climate. The inability to use centralized energy supply systems has led to the use of renewable energy sources as the main sources of energy supply. In this regard, failures and emergencies at such power plants are minimized. The scientific solution to this problem is to optimize the operating modes of wind turbines in the event of strong wind gusts. Modes of operation at supercritical speeds without emergency shutdown are worked out. The possibility of such work is justified by the application of new optimization methods, in particular, mathematical transformations associated with the approximation of piecewise linear functions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuik, G.A.M. The Lanchester-Betz-Joukowsky Limit. Wind Energy 2007, 10, 289–291. [Google Scholar] [CrossRef]
- Ragheb, M.; Ragheb, A.M. Wind Turbines Theory-The Betz Equation and Optimal Rotor Tip Speed Ratio. Fundam. Adv. Top. Wind Power 2011, 1, 19–38. [Google Scholar]
- Acker, T.; Hand, M. Aerodynamic Performance of the NREL Unsteady Aerodynamics Experiment (Phase IV) Twisted Rotor. In Proceedings of the Prepared for the 37th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; pp. 211–221. [Google Scholar]
- Phelps, C.; Singleton, J. Wind Turbine Blade Design; Cornell University, Sibley School of Engineering: Ithaca, NY, USA, 2013; pp. 2–14. [Google Scholar]
- Thakur, T.S.; Patel, B. Structural Analysis of a Composite Wind Turbine Blade to optimize its Constructional Parameters using a FEA Software. Int. J. Sci. Res. Dev. 2016, 3, 572–576. [Google Scholar]
- James, P.A.B.; Bahaj, A.S. Small-Scale Wind Turbines. Wind Energy Engineering. In A Handbook for Onshore and Offshore Wind Turbines; Academic Press: Cambridge, MA, USA, 2017; pp. 389–418. Available online: https://www.pdfdrive.com/wind-energy-engineering-a-handbook-for-onshore-and-offshore-wind-turbines-e187538163.html (accessed on 12 March 2021). [CrossRef]
- Sargsyan, A. Simulation and Modeling of Flow Field around a Horizontal Axis Wind Turbine (HAWT) Using RANS Method; Florida Atlantic University: Boca Raton, FL, USA, 2010; pp. 7–15. [Google Scholar]
- Manual, U.D.F. Fluent, ANSYS FLUENT 12.0 Theory Guide; Sections 18.1.1 and 18.1.2; ANSYS Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Fluent, Ansys Fluent 12.0, Tutorial 9-11-12-23-28-29. Turbulence and Discrete Phase Modeling. Available online: http://ansys.fem.ir/ansys_fluent_tutorial.pdf (accessed on 10 March 2021).
- GE Energy 1.5xle-Manufacturers and Turbines-Online Access-the Wind Power; RMT, Inc.; North Coast Wind & Power LLC. Available online: https://www.thewindpower.net/turbine_en_58_ge-energy_1.5xle.php (accessed on 11 February 2021).
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Chichester, UK, 2001; pp. 45–47. [Google Scholar]
- Zheng, Y.; Zhao, R.Z.; Liu, H. Mode Analysis of Horizontal Axis Wind Turbine Blades. Telkomnika Indones. J. Electr. Eng. 2014, 12, 1212–1216. [Google Scholar] [CrossRef]
- Kurniawati, D.M.; Tjahjana, D.D.D.P.; Santoso, B. Experimental investigation on performance of crossflow wind turbine as effect of blades number. In Proceedings of the 1st international conference and exhibition on powder technology Indonesia (ICePTi) 2017, Bandung, Indonesia, 8–9 August 2017. [Google Scholar] [CrossRef]
- Sheng, S.; O’Connor, R. Reliability of Wind Turbines. In Wind Energy Engineering; International Journal of Power Electronics and Drive Systems: Melaka, Malaysia, 2017. [Google Scholar] [CrossRef]
- Mahdy, M.; Alghamdi, A.S.; Bahaj, A.S. Offshore wind energy potential around the east coast of the Red Sea. In Proceedings of the KSAISES Solar World Congress 2017-IEA SHC International Conference on Solar Heating and Cooling for Buildings and Industry 2017, Abu Dhabi, United Arab Emirates, 29 October–2 November 2017. [Google Scholar] [CrossRef]
- Helmberg, G. The Gibbs phenomenon for Fourier interpolation. J. Approx. Theory 1994, 78, 41–63. [Google Scholar] [CrossRef] [Green Version]
- Utomo, I.S.; Tjahjana, D.D.D.P.; Hadi, S. Experimental studies of Savonius wind turbines with variations sizes and fin numbers towards performance. In Proceedings of the 1st International Conference and Exhibition on Powder Technology Indonesia (ICePTi) 2017, Bandung, Indonesia, 8–9 August 2017. [Google Scholar] [CrossRef]
- Beetle, V.V.; Nathanson, G.I. Trigonometricheskie riady Fur’e i elementy teorii approksimatsii. In Trigonometric Fourier Series and Elements of Approximation Theory; Leningrad Publishing House: Leningrad, Russia, 1983. [Google Scholar]
- Aliukov, S.V. Approximation of step functions in mathematical modeling problems. Math. Model. 2011, 23, 75–88. [Google Scholar] [CrossRef]
- Coles, D.S.; Blunden, L.S.; Bahaj, A.S. Experimental validation of the distributed drag method for simulating large marine current turbine arrays using porous fences. Int. J. Mar. Energy 2016, 16, 298–316. [Google Scholar] [CrossRef] [Green Version]
- Mahdy, M.; Bahaj, A.S. Multi criteria decision analysis for offshore wind energy potential in Egypt. Renew. Energy 2018, 118, 278–289. [Google Scholar] [CrossRef]
- Harper, M.; Anderson, B.; James, P.A.; Bahaj, A.S. Onshore wind and the likelihood of planning acceptance: Learning from a Great Britain context. Energy Policy 2019, 128, 954–966. [Google Scholar] [CrossRef]
- Toropov, E.; Osintsev, K.; Aliukov, S. New theoretical and methodological approaches to the study of heat transfer in coal dust combustion. Energies 2019, 12, 136. [Google Scholar] [CrossRef] [Green Version]
- Toropov, E.V.; Osintsev, K.V.; Aliukov, S.V. Analysis of the calculated and experimental dependencies of the combustion of coal dust on the basis of a new methodological base of theoretical studies of heat exchange processes. Int. J. Heat Technol. 2018, 36, 1240–1248. [Google Scholar] [CrossRef]
- Osintsev, K.; Aliukov, S.; Prikhodko, Y. New Methods for Control System Signal Sampling in Neural Networks of Power Facilities. IEEE Access 2020, 8, 192857–192866. [Google Scholar] [CrossRef]
- Aliukov, S.; Osintsev, K. Mathematical modeling of coal dust screening by means of sieve analysis and coal dust combustion based on new methods of piece-linear function approximation. Appl. Sci. 2021, 11, 1609. [Google Scholar] [CrossRef]
- Osintsev, K.; Aliukov, S.; Kuskarbekova, S. Experimental Study of a Coil Type Steam Boiler Operated on an Oil Field in the Subarctic Continental Climate. Energies 2021, 14, 1004. [Google Scholar] [CrossRef]





| Speed (u) m/s | 11.2 | 11.4 | 11.7 |
| Deviation (δ) m/s | 0.02 | 0.05 | 0.09 |
| Speed (u) m/s | 6.8 | 7.06 | 7.3 |
| Deviation (δ) m/s | 0.013 | 0.016 | 0.018 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osintsev, K.; Aliukov, S.; Shishkov, A. Improvement Dependability of Offshore Horizontal-Axis Wind Turbines by Applying New Mathematical Methods for Calculation the Excess Speed in Case of Wind Gusts. Energies 2021, 14, 3085. https://doi.org/10.3390/en14113085
Osintsev K, Aliukov S, Shishkov A. Improvement Dependability of Offshore Horizontal-Axis Wind Turbines by Applying New Mathematical Methods for Calculation the Excess Speed in Case of Wind Gusts. Energies. 2021; 14(11):3085. https://doi.org/10.3390/en14113085
Chicago/Turabian StyleOsintsev, Konstantin, Seregei Aliukov, and Alexander Shishkov. 2021. "Improvement Dependability of Offshore Horizontal-Axis Wind Turbines by Applying New Mathematical Methods for Calculation the Excess Speed in Case of Wind Gusts" Energies 14, no. 11: 3085. https://doi.org/10.3390/en14113085






