Cost-Effective Increase of Photovoltaic Electricity Feed-In on Congested Transmission Lines: A Case Study of The Netherlands

Abstract

In many areas in the world, the high voltage (HV) electricity grid is saturated, which makes it difficult to accommodate additional solar photovoltaic (PV) systems connection requests. In this paper, different scenarios to increase the installed PV capacity in a saturated grid are assessed on the basis of the net present value (NPV). The developed scenarios compare an increase of grid capacity, PV system azimuth variation, curtailment, and battery storage. For each scenario the net present value (NPV) is assessed using an optimization model as a function of the overbuild capacity factor, which is defined as the relative amount of PV capacity added beyond the available capacity. The scenarios are applied on a case study of the Netherlands, and the analysis shows that, by optimising curtailment, a PV system’s capacity can be increased to 120% overbuild capacity. For larger overbuild capacity investments in the electricity-grid are preferred when these costs are taken into account. However, the optimum NPV lies at 40% overbuild, thus the societal and NPV optimum are not always aligned. Furthermore, the use of a battery system as an alternative to an infrastructure upgrade was not found to be a cost-effective solution. Thus, applying curtailment could be cost-efficient to a certain extent to allow for additional PV capacity to be connected to a saturated grid. Furthermore, the inverter size compared to the installed PV capacity should be significantly reduced. For a connection request that exceeds 120% overbuild increasing network capacity should be considered.

1. Introduction

The reduction of greenhouse gas (GHG) emissions is an essential part of combating climate change as a large portion of GHG emissions are attributed to fossil-fueled electricity generation [1]. A possible way to reduce these emissions is by integrating more renewable energy sources (RES) in the national electricity generation mix, with solar photovoltaic (PV) energy, next to wind energy being an important technology in this context [2]. By taking governmental subsidies into account, PV energy is an economically attractive option for investors on both large and small scales, while it should be noted that their costs have been decreasing significantly in the past decades. In this paper, for consistency in terminology, the following conventions are followed. A PV system consists of a number of PV modules connected to a single inverter with a capacity within the range of kWp, whereas the focus in this paper is on large-scale PV power plants within the range of MWp, which are referred to as PV plants in the remaining of the paper and consist of several PV systems operated together. With growing amounts of large-scale (multi-MWp) PV plants, connectivity to existing medium or high voltage electricity grids may cause problems, especially when these PV plants are planned in the least densely populated areas. For instance, in the Netherlands, it became clear in 2019 that, for specific areas in the north of the country, the capacity of the existing electricity network was insufficient to meet the transport requirements of new solar PV projects [3]. This is mainly caused by capacity needs to be reserved for peak generation moments for the planned PV systems, in conjunction with the rural transmission grids that presently are not designed to accommodate large scale electricity production sites [4]. According to the Dutch Transmission System Operator (TSO), TenneT, such areas of concern are especially the provinces of Groningen, Drenthe and Overijssel [5], where the relatively low land costs as well as lower societal opposition are leading to significant investments in PV projects [6]. The areas of concern are expanding to Zeeland, Brabant and Limburg [7,8]. In this context, a saturated or congested grid is defined when “at some point in time” the maximum power transport capacity is reached. Solar PV generated energy is a varying resource and therefore would require more capacity than would be expected when observing the average solar PV production [2], whereas, certainly for the Netherlands, peak power generation is rarely observed. Nevertheless, the power capacity limits of transmission lines may hamper further development of large scale PV plants.

The most obvious solution for this problem is to increase transmission grid capacity. However, this is costly and time-consuming, since it can take up to 10 years due to long legislative and administration procedures [9]. These investment costs are also currently not taken into account by PV investors. Nevertheless, to reach the targets set by the European Commission for the year 2030, it would be most beneficial to install additional PV systems, not only in the residential sector where a significant increase of installations is observed over the past years in the form of Building Integrated PV (BiPV) and roof-top PV systems [10], but also as large-scale PV plants before that time, as the Dutch government has committed to these targets [11]. Both investors, the TSO and the electricity consumers would benefit when this is addressed in a fast and cost-effective way while maintaining security of supply. It is clear that an alternative solution to resolve the grid capacity issue is a key priority for many stakeholders.

On the short term, another solution is to alleviate the N-1 principle [12], which ensures the security of supply in case that any disturbances (e.g., malfunctions, maintenance) in connections occur. This reliability measure has now been lifted temporarily by the Dutch national regulator from 1 January 2021 onwards in the Northern provinces [13]. This would allow an additional 500 MWp to be connected [14].

Other solutions are the curtailment of power [15,16], actively or passively (by undersizing inverters, or variation of azimuths of the PV system), or the addition of local demand, such as charging stations for electric vehicles, or adding battery-based energy storage systems.

Curtailed energy is defined as generated energy that is not exported or used [17]. Its annual amount can be calculated by using the difference between the maximum annual energy that is fed back to the grid with and without a certain feed-in limitation. A common way to curtail is by using an inverter with a capacity that is lower than the capacity of the connected PV system. Therefore, the peaks are curtailed in the inverter of the system, which changes the energy injection of the PV system to the network. Theoretically, electricity production becomes more stable; then again, it is less efficient since not all produced electricity is used. It has also been argued that high amounts of dynamic curtailment in combination with overbuilding capacity is favorable for mitigation of intermittency of PV systems [18].

Curtailment can be a cost-beneficial option for the investor, since a smaller inverter is less costly, whereas the energy losses are not significant [19]. The energy losses due to curtailment are not very significant compared to the annual energy production since it is reported that a 6% curtailment loss occurs at a system size 1.6 times the feed-in limitation [20]. Other studies corroborate that, for instance, Ochoa et al. [21] demonstrated in the UK that generation capacity can be doubled if 2% curtailment is applied. Similarly, Litjens [22] showed for PV systems in the Netherlands, that curtailment, in the form of a normalized feed-in limit, of 80% would lead to an annual energy loss of only 0.81%. This is based on an analysis of an average annual load curve, see Figure 1. in this figure note that the hours on the horizontal axis are shown using a log scale. The percentage of PV electricity production that can be exported to the grid and the percentage of energy that is curtailed (in red) are shown on the right side of the plot. The PV yield was modelled with an orientation of 185 surface azimuth, a 36 tilt, a high performance ratio of 91% and with weather data of The Netherlands from 2010 until 2016 [23] Doubling generation capacity and applying a 50% feed-in limitation would lead to 14% curtailed energy. This demonstrates that the effects of curtailment depend on the load curve, and hence on solar irradiance levels at the specific location of a PV system. As a further consequence, the relative connection cost is decreased.

The orientation and tilt of a PV system can play an important role in addressing the mismatch between electricity consumption and production. It is generally known that by changing the azimuth of a PV system, from South to East or West, the generation peak can shift to approximately 2.5 h earlier or later than noon [24], while its level is also lower. It has been shown that this can decrease the re-dispatch cost of electricity due to the timing of the production [25], whereas the reduction in annual yield with a different optimization angle is only about 10% [26].

Litjens et al. suggest that electricity market prices have a minor effect on optimal PV orientation [17]. As curtailment can be decreased by changing the module orientation and/or tilt angles, both the market prices and the module angles can be determined by adapting the PV supply curve to the available demand. The demand has an impact on the optimal azimuth angle; therefore, future changes in electricity demand should be considered in the design of the solar PV system [17]. Perez et al. found, using a case study in Minnesota (USA), that PV system’s curtailment can be a cost-effective alternative to energy storage costs, specifically when looking at larger regions [18].

Li et al. showed that the combination of different renewable energy sources (RES) was essential to create an optimized grid with optimum output when installed wind capacity is double the installed PV capacity, as demonstrated for different regions in China [27]. Curtailment at a large scale is only necessary when the level of RES in the system is extremely high. For moderate RES deployment scenarios, Cebeci et al. found that there is almost no need for curtailment [28], while Conlon et al. suggested that high curtailment is necessary for deep penetration targets on renewable energy resources mostly due to the imbalances in supply and demand [29]. In the research by Conlon, energy storage capacity is rapidly increasing its value to 65% renewable energy penetration, a result quite different from the apparent importance of energy storage in the study by Cebeci et al. [28]. The difference in importance of energy storage can be explained as it was not owned and operated by the market party, but rather operated by the TSO, which lead to significant variation in re-dispatch costs. Another study demonstrated that proper management of battery energy storage can reduce curtailment losses, also for high penetration of PV electricity [30].

It is clear that by decreasing the maximum power output of a PV system actively or passively, the pressure on the transmission or distribution grid will decrease [31]. Batteries can be used to temporarily store the electricity at peak generation moments [23,30,32]. In this study Li-ion batteries are considered as they can be considered a mature technology [33,34,35].

The above solutions come with additional cost. In this research, this is addressed by providing insight on how solar PV investors could determine their strategies in the future, especially considering the limitations that a high voltage (HV) network may have. In this paper, a specific case study concerning an HV grid in the North of the Netherlands is considered, where the following scenarios are studied: adjusting the azimuth angle, curtailment through decreasing inverter size and adding battery storage. The main findings are twofold. First, with increasing overbuild PV capacity, curtailment is the most cost-effective solution, whereas after a certain overbuild factor investments in infrastructure become more cost-effective. Second, the optimal overbuild factor varies with different azimuth angles, electricity prices, battery integration, or different forms of compensation. This paper is further organized as follows. In Section 2 the models in detail, including various assumptions, are described, as well as the case study. Section 3 presents results for all scenarios, which are discussed in Section 4. In Section 5 conclusions are drawn.

2. Methods

An optimization model was developed to determine the most cost-effective way to increase PV installed capacity in a capacity-limited grid. As input to the model electricity prices are needed as well as revenues from subsidy schemes. Four different investor scenarios have been used, which are further detailed in Section 2.4:

• Infrastructure cost scenario (denoted as INFRA)
• Azimuth variation scenario (AV)
• Curtailment scenario (CUR)
• Battery storage scenario (BAT)

The results of the four scenarios and some scenario combinations are compared by using three different electricity price profiles as inputs. These price profiles were chosen to represent three different situations: (a) the current situation; (b) the situation where the current subsidy scheme would not be present anymore; and (c) the predicted electricity prices in 2030. Through this paper, hourly time resolution is used.

The PV system is modelled to be connected to a congested transmission line. Due to a lack of actual output data of large-scale PV systems in the area of the case study, solar irradiation data in that area were used to simulate the PV power output. A Five-year period on an hourly basis is simulated, using 2014–2018 as the reference years. A time frame of five years was chosen since 2018 was exceptionally sunny, thus not being representative for the Netherlands.

2.1. Case Study

Stadskanaal, an area in the province of Groningen in the northeast of the Netherlands, is chosen as a case study, due to the urgent need for additional grid capacity in that area. Specifically, it is one of the areas where the planned PV systems exceed the available transport capacity of the network. The demand data of the Stadskanaal area was provided by TenneT which, as TSO of the Netherlands, is responsible for the connection of large-scale electricity producers to the electricity grid. Data was provided at 5 min time resolution for the years 2016 and 2018 and the average hourly values of these two years are calculated and used for all five years of the model output. However, the demand values (hourly) are small compared to the PV plant production, as they vary between 0–17 MWh only, whereas the limit on the grid is 300 MWh. Therefore the assumed peak hourly energy generation of the PV plant is 300 MWh. In order to model the weather conditions at Stadskanaal, data from the KNMI weather station at Eelde [36] was used, which is at about 30 km distance from the Stadskanaal area.

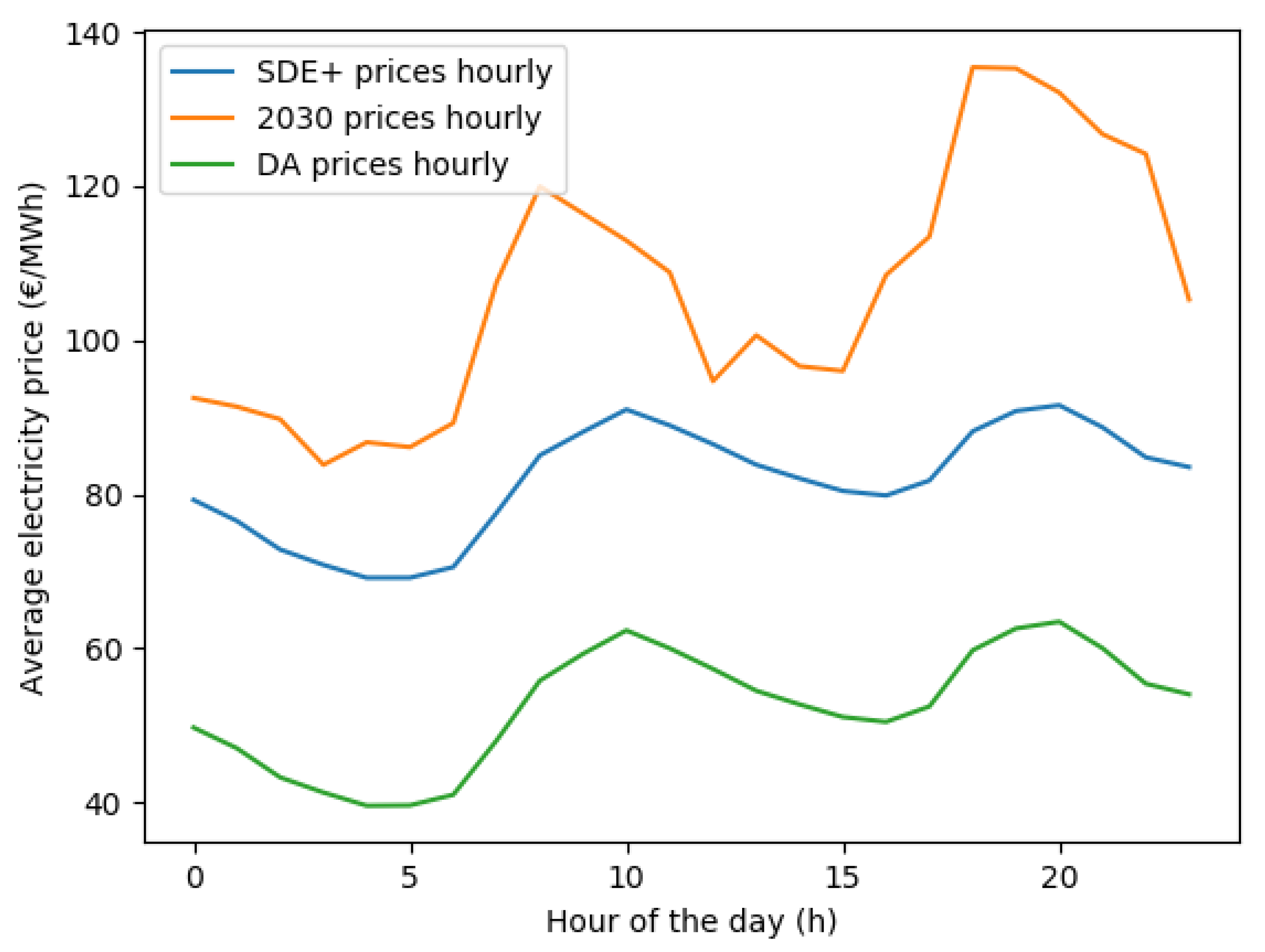
2.2. Electricity Prices

A large part of the revenue for PV investors in the Netherlands comes from the governmental SDE++ (in Dutch: Stimulering Duurzame Energieproductie) subsidy scheme, and it is received per generated electrical energy unit (kWh), either fed to the grid or self-consumed [37]. In this way the PV system is optimized on maximum energy output [17]. The SDE++ scheme is in force per 1 January 2021. Its predecessor SDE+ has been reformed, as was announced by the former minister Wiebes of Economic Affairs and Climate [38]. It can be expected that the SDE++ subsidy scheme will be reformed in future, and this insecurity of subsidy could cause the value of PV electricity to be optimised by the market price instead of volume. The market prices often reflect the electricity demand, due to the present merit order based dispatch, and are highest when demand is peaking [39]. However, a PV system itself is not a flexible asset and cannot produce when prices are high, thus a different electricity price might affect the way in which design of large-scale PV systems are optimized in economical terms in the future.

For each of the four scenarios, three different electricity prices are compared. Firstly, the 2018 day-ahead (DA) market prices for electricity are used. The DA market is chosen due to the as of yet inaccurate predictability of PV production [40] and the variability that is clearly reflected in this price. Secondly, the SDE++ subsidy is used to estimate the revenue from PV systems. Thirdly, the estimated electricity prices for 2030 are used (see below). The average hourly prices for the different price scenarios used are shown in Figure 2. Note that hourly prices for one year were used as input to the model, however, due to confidentiality reasons only the average hourly prices are illustrated in this figure. For the electricity prices a time period of one year was used. These electricity prices were used for all the five climate years for which PV production was modelled. Another key point to note is that potential electricity price changes over the lifetime of the PV system are not taken into account.

The prices that are used to estimate the SDE+ values are the intraday prices of 2018. When hourly intraday prices were zero, it was assumed that no trading took place on the intraday market and the day-ahead price was used. The calculation scheme is detailed in Equations (1)–(3). The strikeprice ($SP$) is the maximum price the investor receives for the electricity with subsidy, thus it is the only price received in case that the market price ($STp$) is larger than the $SP$. If $STp$ is lower than the floor price ($FP$), the subsidy given is sum of the $SP$ and $STP$ subtracted with the $FP$.

$$IfSTp<FP:ReturnSP-FP+STp$$

(1)

$$IfSTp<SP:ReturnSP$$

(2)

$$IfSTp>SP:ReturnSTp.$$

(3)

The values of $SP$ and $FP$ are determined by The Netherlands Enterprise Agency (RVO) for the SDE+ subsidy each year [41]. The subsidy is capped on the maximum amount of full load hours per year. The $FP$ is fixed at 0.08 €/kWh [41]. Note that during the analysis 2019 values are used. Each year these are modified, that is, typically lowered. For the calculation of $SP$, there are three phases to determine the subsidy level. In the first phase projects that would have a maximum price of 0.09 €/kWh can apply for subsidy. In the last (third) round more expensive projects up to 0.13 €/kWh can also request subsidy. It is therefore estimated that $SP$ for the case study is 0.11 €/kWh on average.

For the 2030 price scenario marginal cost values on an hourly basis that are simulated by TenneT for 2030 are used. These are based on simulations reported in the ‘kwaliteits en capaciteitsdocument’ [quality and capacity document] for the climate action scenario [42]. This scenario is characterised by high CO${}_2$ prices. Note that marginal cost values are not equal to actual electricity prices, as they do not include scarcity pricing which happens in real markets, nor do they include capital costs.

2.3. PV System Model

As mentioned above, PV electricity generation is simulated for a five-year period on an hourly basis, with meteorological data for 2014–2018 as the reference years. The energy output was modeled by using the Python library PVlib [43]. The orientation of the PV system was kept constant during the time frame of the model (except for the azimuth variation scenario, see below). PV power was calculated using Equation (4) [24]:

$$P_{dc}=\frac{G_{POA}}{1000}{P}_{dc0}(1+{\gamma }_{pdc}(T_{cell}-T_{ref})),$$

(4)

in which $P_{dc}$ is the generated PV power, $G_{POA}$ the irradiance that the PV modules receive (POA: plane-of-array), which depends on azimuth and tilt angles of the system, $P_{dc0}$ the installed capacity (determined at standard test conditions (STC), or rated capacity), ${\gamma }_{pdc}$ is the temperature coefficient of the used PV technology, $T_{cell}$ is the cell temperature, and $T_{ref}$ is the cell reference temperature (25 °C). Cell temperature was calculated using PVlib’s pvsystem.sapm_celltemp routine, assuming that the PV system is an open rack installation. ${\gamma }_{pdc}=-0.0047$, is used, which is common for silicon PV technology [44].

For the Stadskanaal case study (52.98947° N, 6.9504° E) irradiance data was used measured at the closest KNMI station, that is, Eelde (station #280). From the provided global horizontal irradiance (GHI), direct normal (DNI) and diffuse horizontal (DHI) irradiance are calculated using the DIRINT model, since it is the most accurate model for the Netherlands [45]. Further, wind speed and air temperature data was taken from KNMI [36].

2.4. Scenarios

2.4.1. Infrastructure Cost (INFRA) Scenario

The PV system output of this scenario was used to estimate the amount of grid capacity increase needed to export the produced energy. The maximum constraint, applicable to a saturated grid, is not included in this simulation, since it is a business as usual scenario. For the INFRA scenario the maximum power output (as shown in Equation (5) was simulated using an azimuth angle $\gamma$ of 210°. This was based on earlier work by Litjens et al. on optimization of azimuth angles in relation to electricity demand and price [17].

$$max\sum _T{P}_{PV,\gamma }\left(t\right),$$

(5)

with ${\sum }_T{P}_{PV,\gamma }\left(t\right)$ the sum of the energy output of the PV system in kWh for t in range (T), t is time interval in hours (limited due to KNMI data resolution), and $\gamma$ is the azimuth angle in degrees. Note, an azimuth angle of 180° corresponds to South (on the Northern hemisphere).

Simulations for solar parks with capacity within the range of 300–900 MWp have been performed, that consist of several PV systems, in order to determine the effect of larger installed capacity on the transmission line. Cable capacity was 300 MW, and it is assumed that only a solar park would supply power to this cable. This capacity was tested for an overbuild factor of 0–200%, using an interval of 10%. The percentage overbuild reflects the amount of solar installed capacity added to the grid compared to the maximum grid capacity. Furthermore, it suggests that there is more solar added to the grid than there is capacity available. This overbuild factor disregarded the initial 15% overbuild that is considered standard for large-scale PV plants, as it was assumed that the base-case was overbuild by that amount [46].

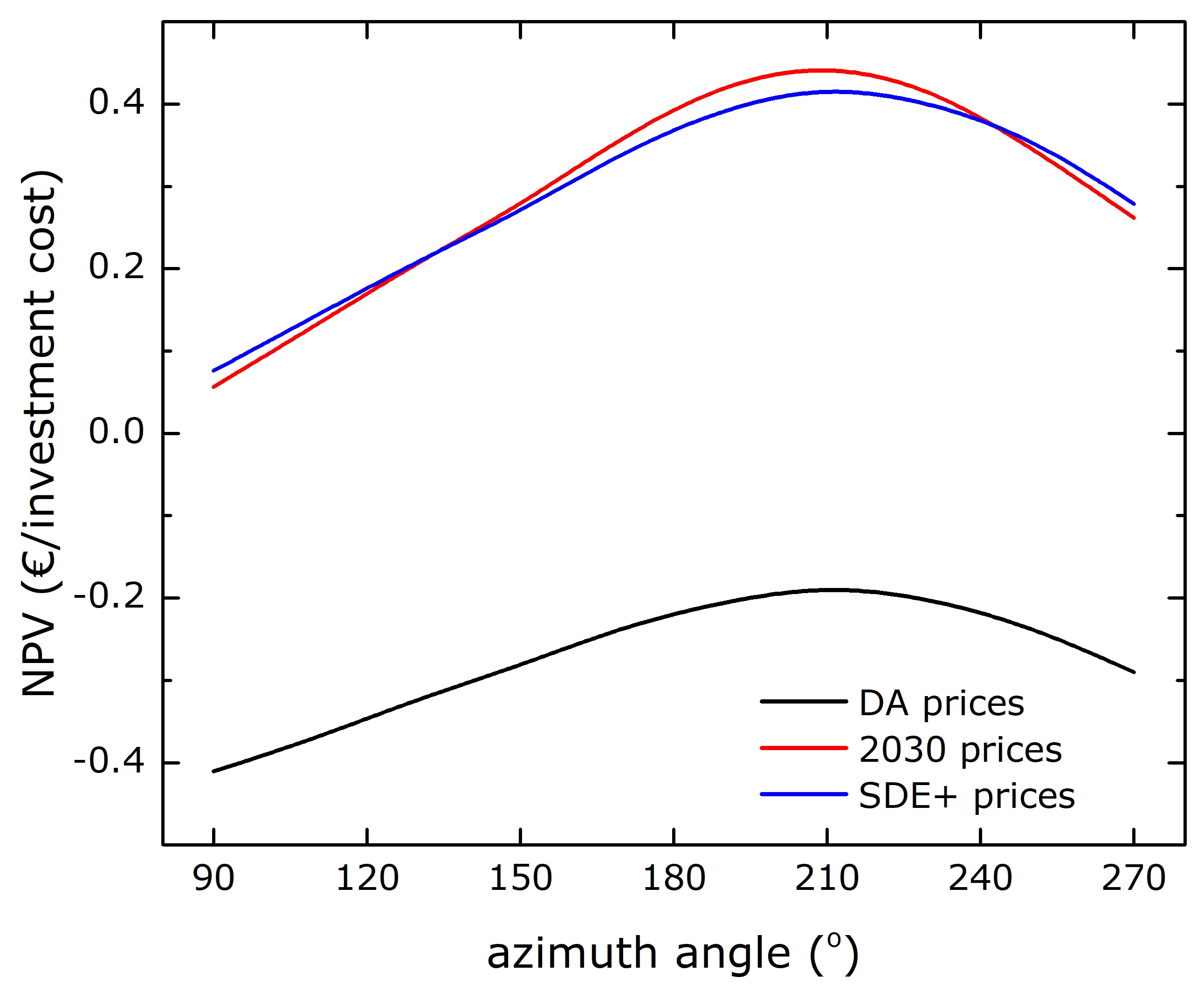
2.4.2. Azimuth Variation Scenario (AV)

In this scenario the azimuth angle was varied. For each azimuth the optimum tilt $\beta$ was determined, by modeling every azimuth-tilt combination in order to find the one with the maximum net present value ($NPV$). Limitations on the grid capacity cause the installed capacity to differ for each azimuth angle and tilt combination. Therefore, for each azimuth angle in the range of 90–270° a specific capacity was calculated. This was done by determining for each hour the maximum limit of the grid and the maximum capacity that could be used without violating this limit. The optimization problem is formulated as follows:

$$max\sum _T{P}_{PV}\left(t\right)$$

(6)

subject to

$$P_{PV,\gamma ,\beta }\left(t\right)\le P_{max}\left(t\right),$$

(7)

where

$$P_{PV,\gamma ,\beta }\left(t\right)=C_{max}-max\left(D\left(t\right)\right)$$

(8)

$$CF=\sum _t^{T=1year}\left(P_{PV,\gamma ,\beta }\left(t\right)\ast c\left(t\right)\right)-O\&M$$

(9)

$$NPV=\sum _y^n\frac{C{F}_y}{{(1+r)}^y}$$

(10)

$$PI=\frac{NPV}{I},$$

(11)

where: $C_{max}$ [kW] is the limiting capacity on the transmission grid, $P_{max}$ [kW] the maximum power allowed to be injected into the grid, $D\left(t\right)$ [kWh] the demand on that transmission line at time t, $c\left(t\right)$ [€/kWh] electricity prices at time t, $CF$ [€/yr] cash flow per year generated from the electricity production, O&M [€/kW/yr] operation and management costs, $NPV$ [€] net present value of electricity, y [years] time period in years, n [years] the lifetime, r discount rate, $PI$ [-] the profitability index [47], I [€]: investment costs. The optimal point (solution) is the azimuth angle that results in the largest value of the profitability index ($NPV/I$). A project is considered profitable for $PI>0$ [47].

The following input was used next to the information from the INFRA scenario:

• demand on the transmission line at t in range (T), provided by the TSO
• limiting capacity on the transmission grid: 300 MW
• discount rate. Cost guidelines suggest a discount rate of 7% for OECD countries, however note that this is just an estimated value which could vary for each unique project [48]. For infrastructure cost a discount rate of 3% is estimated by TenneT [49], resulting from the stability in income for such investments.
• electricity price, provided by TSO/EPEX [50], see Section 2.2
• lifetime, assumed to be 20 years
• investment and O&M costs, from a market study, see Section 2.6

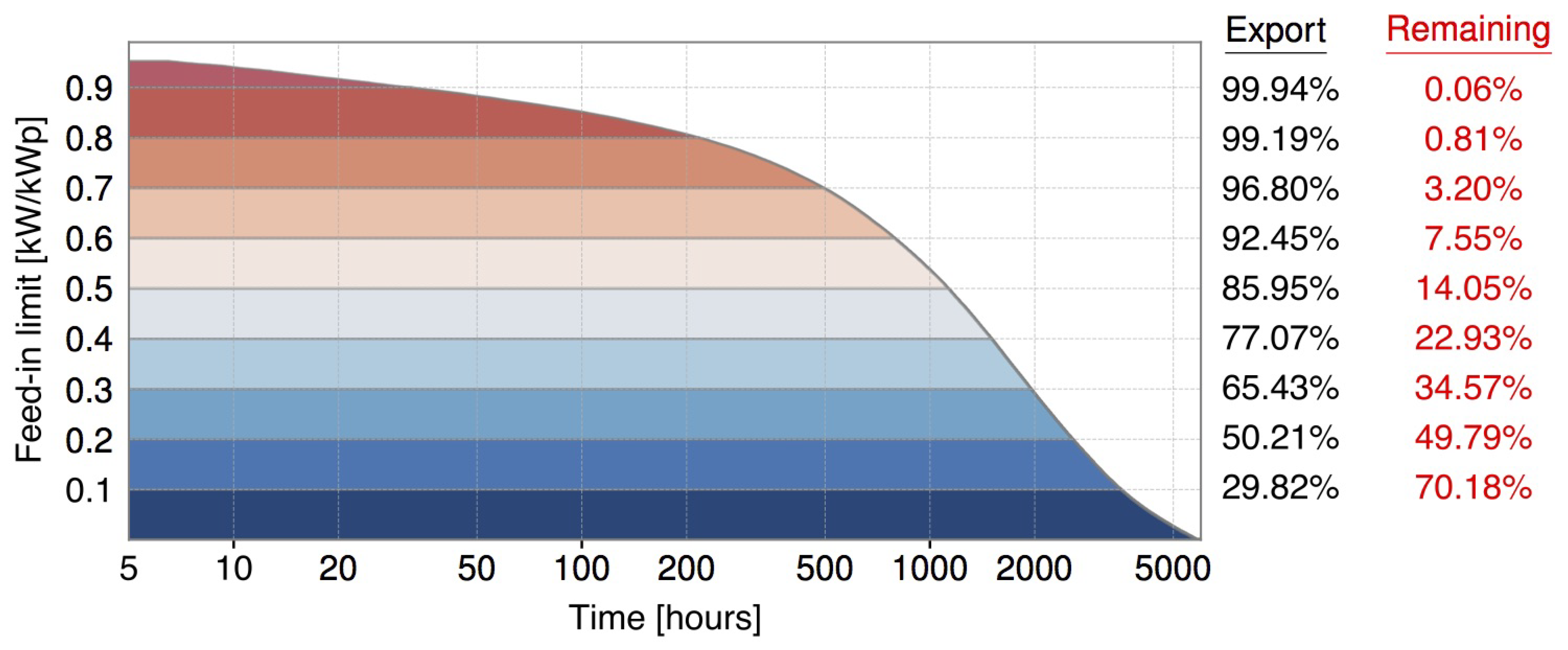
2.4.3. Curtailment Scenario (CUR)

In the curtailment scenario it is assumed that the PV investors increase the number of panels further than can be accommodated on the grid. The optimal azimuth angle of 210 degrees, determined in the AV scenario calculations, was used and the maximum electricity production was assumed to be curtailed using the inverter power clipping method, as shown in Equation (12). Therefore, the inverter size is kept constant while the number of PV modules (thus total PV capacity) increases, or % overbuild was increased. In this scenario, Equations (8)–(10) were also applied, but they are subject to

$$When{P}_{PV,\gamma ,\beta }\left(t\right)>P_{max}\left(t\right):P_{PV,\gamma ,\beta }\left(t\right)=P_{max}\left(t\right).$$

(12)

The optimal point (solution) has the largest value for $NPV/I$ for each % overbuild.

2.4.4. Battery Storage Scenario (BAT)

In the battery storage scenario, it was assumed that, instead of curtailing electricity, the surplus electricity is used to charge a battery system. The battery system size was determined by the maximum sum of the curtailed energy during one day for all 5 years studied. The battery was assumed to discharge completely in the evening using the average price between 18h00–22h00. The capacity that was not needed during the day for investment deferral of infrastructure (replacement) was sold as frequency containment reserve (FCR). This is a way for the TSO to maintain frequency deviations close to the nominal value of 50 Hz if something unexpected happens. This is an additional function, utilised to create extra revenue from using the battery. An overview of the operating reserves for balancing that are currently traded in the Netherlands, including FCR, can be found in [51]. To calculate the capacity available for FCR, the capacity is halved, since FCR provision requires a symmetrical product in terms of (capacity) bids [51], see Equation (15). For FCR services, the service should be able to absorb or deliver electricity at any point in time [52]. The battery capacity is calculated using Equation (13), which is needed to calculate the battery cost in Equation (14). The total revenue of the battery is calculated in Equation (16). In this scenario, Equations (7)–(10) were also used. Equations (17) and (18) are used to calculate the average revenue associated with battery usage.

$$C{P}_{batt}=ma{x}_{yearly}(P_{PV}\left(d\right)-P_{max}\left(d\right))\times \frac{1}{1-(1-So{C}_{max}+So{C}_{min})}$$

(13)

$$F_{batt}=f_{batt}\times C{P}_{batt}$$

(14)

$$R_{FCR}=\left(C{P}_{batt}-\left(P_{PV,\gamma ,\beta }\left(t\right)\times (1-So{C}_{max}+So{C}_{min})\times \eta )/2\right)\right)\times {\pi }_{fcr}$$

(15)

$$R_{batt}=sum(P_{PV}-P_{max})\times {\pi }_{bat}\times \eta +\sum \left(R_{FCR}\right)$$

(16)

$$C_h=\frac{{\sum }_{hourly}c\left(t\right)}{nofhours}$$

(17)

$$ba{t}_{price}=\frac{{\sum }_{yearlyaverage18:00-22:00}{C}_h}{4},$$

(18)

where $C{P}_{batt}$ is battery capacity in kWh, $P_{PV}\left(d\right)$ daily PV power [kW], d time period, in days, $P_{max}\left(d\right)$ the maximum power allowed to be injected into the grid [kW] $So{C}_{min}$ battery minimum state of charge [%], $So{C}_{max}$ battery max state of charge [%], $F_{batt}$ battery cost [€], $f_{batt}$ battery cost per kWh capacity [€/kWh], $C{P}_{batt}$ battery capacity [kWh], $R_{FCR}$ revenue from the frequency containment reserve function of the battery [€], $\eta$ the round-trip efficiency of the battery [%], ${\pi }_{fcr}$ FCR price that is paid by TenneT [€/kWh], $R_{batt}$ revenue made by the battery per year [€/a], ${\pi }_{bat}$ average price used to calculate the revenue made by the battery [€/kWh], and $C_h$ hourly electricity price [€/kWh].

The $NPV$ was calculated as a function of the overbuild factor. For this specific scenario the following input was needed:

• state of charge: the minimum $SoC$ was 10% and the maximum $SoC$ was 90% of the total installed capacity [53],
• round trip efficiency: 82.5% [53],
• cost per kWh capacity Li-ion battery: 156 €/kWh [54].
• FCR prices (TenneT): 20 €/MWh [55].

2.5. NPV

Equation (11) for the profitability index shows that annualized cash flow is divided by the initial investment costs to avoid any scaling factors. The cash flow calculation is calculated for each year separately, where the initial year (0) includes only the investment costs, whereas the following years are a combination of all power sales and the O&M cost. At year 10, the re-investment of the inverter is taken into account. The following input values have been used:

• Cable and plant investments costs that are paid to TenneT for the connection
• Land costs
• Investment costs for the inverter
• Investment costs for the PV modules
• Infrastructure costs

The O&M costs are a combination of cable and plant O&M costs that are paid to TenneT for the connection, and O&M costs of the PV plants, depending on its capacity (in kWp).

2.6. Investment and O&M Cost

The land costs in the area of Stadskanaal fluctuated from €42,002/ha to €69,197/ha over the time-period of March 2018–March 2019 [56]. A 90 MWp PV plant was planned to be located on an area of around 70 ha including landscaping, fence, modules and stations [46]. Assuming a low price for land (55,000 €/ha) the land costs for the PV plant is 43 €/kWp. In the model a PV module price of 310 €/kWp was used [57], and 0.22 €/Wp [58] for large central inverters (around 1 MW). Due to the lifetime of the inverter, the model assumed the purchase of new inverter after 10 years using half the price (i.e., 0.11 €/Wp). A realistic O&M cost value to cover the maintenance, cleaning and insurance of the PVplant of 13.1 €/kWp was used [59].

2.7. Network Costs

There are two types of network costs. The connection costs for the PV investor and the congestion or network investment costs for the TSO. The network costs for the PV investor are the connection costs as defined by the Netherlands Authority for Consumers and Markets (ACM) in the directive ‘Tarievencode Elektriciteit’ (article 2) [60], which are divided between plant and cable costs. For larger fields, the cable length is assumed to be 5 km and the cost is estimated by TenneT at 1 million €/km [61]. Therefore the estimated cost for the cable is 5 million €, regardless of the exact PV plant size, of which the cost is estimated to be 2 million €. Annually, the connection O&M costs are 0.6% and 0.2% of the investment costs for the PV plant and the cable, respectively. Thus the annual O&M is estimated to be 12,000 € for the plant and 10,000 € for the cable [61].

For the TSO, congestion costs are levied by network tariffs for transport and system services and are exclusively paid by the electricity consumers. Long-term solutions to congestion costs are building or reinforcing interconnection lines, however, these are costly endeavors. Therefore, if network investments are necessary for the connection of the PV plant that will have an effect on the overall cost of electricity without having any impact on the investor. Optimising network investments would therefore be beneficial for society. Legally, TenneT is obligated to connect everyone that wants to participate in the electricity market and cannot restrict investors without compensation [62]. A current paradigm in network regulation in the Netherlands is that the TSO is to expand network capacity in a way that it can accommodate all transport requests from connected parties. However, for the variable renewable feed-in it may not be cost effective for society to built a network for infrequently occurring production peaks. Alternative ideas such as peak management costs can be considered as well, however they are rarely used over re-dispatch. To estimate the social impact of the investment costs for solar parks, the network costs paid by the TSO were estimated in €/MWp, as a yardstick value. In practice, the cost for each network expansion differs, thus to estimate the infrastructure costs, ten previous investments by TenneT have been compared and analysed. The analysis showed a range of 0.08–0.35 €/MW for reinforcement of the grid and the average cost of 0.22 €/MW was used in this study.

2.8. Sensitivity Analysis

A sensitivity analysis was conducted to investigate the impact of the investment cost on the outcome of the $NPV$, since the investment costs can significantly change in the future, whereas the infrastructure investment decisions are made for a 40 year lifetime. The following ranges were used: investment cost for the inverter [150–220 €/kWp], investment cost for the solar modules [260–310 €/kWp], and battery investment cost [100–156 €/kWh]. The elasticity ${\eta }_E$ is calculated to show the sensitivity to price increases. It gives a percentage change in quantity demanded when there is a one percent increase in price, keeping everything else constant [63]. To perform a sensitivity analysis, the elasticity of the variable prices ($\pi$) were determined using the following equation:

$${\eta }_E=\frac{(NP{V}_1-NP{V}_0)÷(NP{V}_1+NP{V}_0)}{({\pi }_1-{\pi }_0)÷({\pi }_1+{\pi }_0)}.$$

(19)

3. Results

3.1. Azimuth Variation (AV) Scenario

In Figure 3 $NPV/I$ for all different azimuth angles is presented. As can be seen, without subsidy, the PV plant would currently not be profitable, as the $NPV/I$ is negative using the DA prices as input. Moreover, in this and the following scenarios, the DA price results into negative $NPV/i$ for all azimuth angles. Therefore, in the rest of the paper the DA prices are excluded from the results in the analysis. As can be seen from Figure 3, the optimal $NPV/I$ is at an azimuth angle of 210° (tilt angle was 40°). The higher volatility of future electricity prices (see Figure 2) seems to have little effect on the optimal azimuth angle. Differences in price values also lead only to minimal differences in $NPV/I$ for the various orientations.

In order to design a PV plant with panels oriented in two different azimuth angles, several azimuth angle combinations were analysed. This was inspired by the fact that price peaks exist in the morning and afternoon such that a combination of eastern and western oriented panels would be leading to potentially large $NPV$. However, a single orientation still leads to the largest $NPV/I$ value.

It is observed that the irradiance for different azimuth angles has a larger effect on $NPV/I$ than the electricity prices used. This can result from the higher investment costs that are necessary for the different azimuth angles due to the capacity factor calculated at that angle. Furthermore, results show that the angle with the highest total irradiance (which is 180°) does not have the highest revenue: electricity prices do influence the optimal angle for the revenue, as was also shown by Litjens et al. [17]. Interestingly, the different price schemes used do not affect the optimal azimuth angle when optimizing for $NPV/I$, which is due to the fact that the hourly profiles are quite similar (see Figure 2).

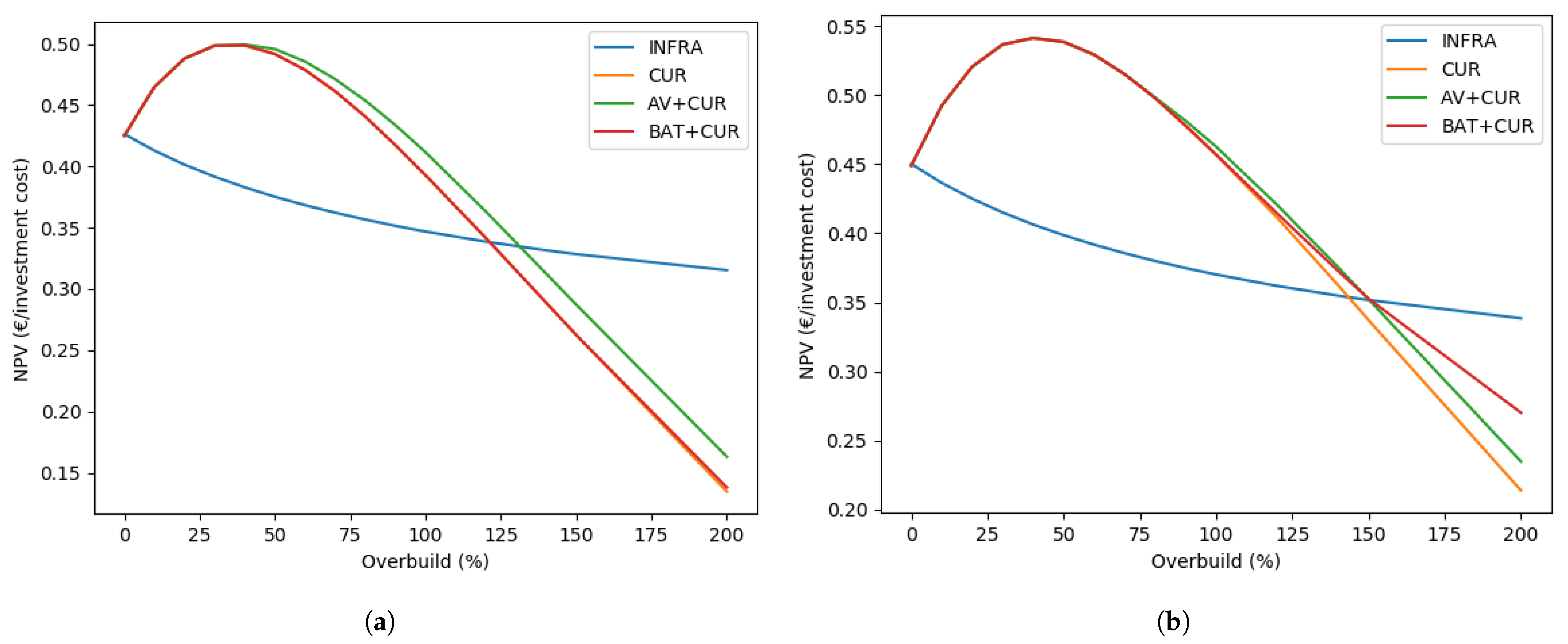
3.2. Infrastructure (INFRA), Curtailment (CUR) & Battery (BAT) Scenarios

In these scenarios, the modeled PV plant is oriented at 210° to have the largest $NPV/I$. The INFRA, CUR and BAT scenario are combined in the same graphs to show the difference in the calculated $NPV/I$ for each value of overbuild factor (in %) to the congested transmission network. In Figure 4, the results are shown using the current SDE+ subsidy and 2030 electricity prices. For the INFRA scenario, $NPV/I$ decreases in a near-linear fashion. The BAT scenario never results into a higher $NPV/I$ compared to the other scenarios, mostly due to the large investment costs for the battery as the battery size scales with the overbuild percentage. The CUR scenario clearly leads to the highest $NPV/I$ compared to the other scenarios, with a maximum at 40% overbuild for both price values inputs. The cross-over point of the CUR scenario with the INFRA scenario lies at 120% overbuild for the SDE+ price and at 140% for the 2030 price. Comparing Figure 4a,b, the curves are very similar. Using 2030 prices, the NPV increases at a higher rate, which changes the CUR curve and due to this change, the crossover point of the INFRA $NPV/I$ curve and the CUR curve increases by about 25% overbuild using more volatile prices.

Sensitivity Analysis

The effect of the investment costs on $NPV/I$ is linear for all variables assessed. Obviously, $NPV/I$ increases with decreasing investment for the PV modules. The maximum $NPV/I$ changes from 40% to 50% overbuild using 2030 electricity prices in the CUR scenario, when lowering investment costs. This shows that the decrease in PV module investment costs increases the possibility of curtailment. The decrease in investment cost increases the gap between the maximum $NPV/I$ and the INFRA and CUR curves cross-over point as well. The overbuild factor has an inverse correlation to the investment cost of the PV module and the inverter. When the PV module investment is lower, the maximum $NPV/I$ occurs at a higher overbuild factor. With lower inverter investment prices, the maximum $NPV/I$ occurs at a lower overbuild factor. Therefore, it can be expected that the overbuild factor at which the highest $NPV/I$ occurs would not change drastically in the future.

In

Table 1. Price elasticity of selected variables.

Price Elasticity	SDE+ Prices	2030 Prices
Battery investment cost (€/kWp)	−0.0018	−0.0016
Inverter investment cost (€/MWp)	−0.0005	−0.0005
Solar panels investment cost (€/MWp)	−0.0005	−0.0005

, the elasticity of the investment costs of the battery, inverter and the PV modules are presented. Of these variables, the battery cost has the largest effect on $NPV/I$ of the BAT scenario, while the PV modules and the inverter investment costs have the same elasticity. The difference between the SDE+ and the 2030 electricity price elasticities show that the effect of the electricity prices is non-linear.

The sensitivity analysis showed that downward trends in investment cost for various technologies could also have a large effect on the overbuild percentage for optimal $NPV/I$. This is due to the opposite drivers of both panel and inverter investment cost on $NPV/I$. This leads to the conclusion that the curves shown in Figure 4 are quite robust. Neither the electricity prices nor the investment cost did have a large effect on the pattern or the position of the maximum $NPV/I$. Moreover, not only the effect of the electricity prices, but also the effect of the azimuth variation on the $NPV/I$ is limited.

3.3. AV & CUR Scenario

In this scenario, the $NPV/I$ was compared at each overbuild factor with each possible azimuth angle combination. The ideal azimuth angle changed at an overbuild of 40%, from 210° to 230° using SDE+ subsidy prices in the calculation. Using the 2030 prices, the same change in optimum azimuth occurred but at 80%. The optimal angle changes when more electricity is curtailed. This has an effect on the production profile of the PV plant, namely that it somewhat changes the time of production during the day. The panel direction (a lower irradiance on the panel) and curtailment are both a form of efficient use of available solar energy.

3.4. BAT & CUR Scenario

An optimisation was used for the CUR scenario, to determine the optimal size of the battery system with the aim to increase $NPV/I$. The considered range of battery system sizes was 0–1200 MWh. Figure 5 shows the optimum size as a function of overbuild ratio. Adding a battery in the CUR scenario becomes interesting starting at 100% overbuild considering 2030 prices and starting at 150% considering SDE+ prices. Above all, the BAT & CUR scenario demonstrates that the volatility in electricity prices does determine at which value of the overbuild factor the integration of battery storage becomes profitable.

To visualise the effect of the AV & CUR and BAT & CUR scenarios, $NPV/I$ was plotted in comparison to the original CUR and INFRA curves in Figure 6a,b and it shows that Considering the current SDE+ subsidy, the azimuth angle change does affect the CUR curve. Note the curves for the CUR and BAT & CUR overlap. In Figure 6a the cross-over point with the INFRA $NPV/I$ curve changes from 120% to 130% due to the change in azimuth angle. Moreover, the effect of the additional battery only shows a slight change in $NPV/I$ from 150%. The trends in Figure 6b show that the significance of the azimuth change is smaller using 2030 prices compared to the effect using the SDE+ prices. The azimuth angle can change the cross-over with the INFRA $NPV/I$ curve from 143% to 150%, while the battery integration affects the $NPV/I$ compared to the CUR scenario significantly beyond 140% overbuild. These effects however do not change the cross-over point with the INFRA curve significantly.

From Figure 4 and Figure 6 it follows that the highest $NPV/I$ is determining the optimum solution for society as societal costs are included in these graphs. The infrastructure costs were added to analyze if the investment would benefit society and would decrease, or at least not increase, the electricity costs. The overall downward trend of the INFRA curve suggests that the costs of the infrastructure are not an optimal investment when solely looking at PV energy transportation.

4. Discussion

4.1. Model Limitations

The developed model only applies when PV generated electricity solely results into the need to increase the grid infrastructure capacity. If any other technology would be addressed to produce electricity then the model outcomes obviously would differ. Furthermore, the imbalance cost, and the engineering and installation cost are not taken into account in the model. The $NPV$ would be negative when these cost would be included in the calculations. It would also reflect a similar investment for all different scenarios and is therefore not deemed essential, due to the fact that it is a comparative study between scenarios. The revenue is likely underestimated since the model does not assume yearly inflation of electricity prices. The 2030 prices are marginal prices and can therefore never drop below zero. Actual market prices can drop below zero in 2030. This is witnessed already a few times recently in the Netherlands but occurred more often in Germany due to the increase of renewable energy generation feed-in to the grid [64]. Such situations could create an even more volatile electricity profile than is presented here. This is a limitation, due to the possibility of active curtailment when the electricity price drops.

Another limitation is that the SDE++ price is changing the spike price each year which is not taken into account. It is therefore most likely that the model overestimates the SDE++ subsidy. A price change over time is also not applied for these 2030 prices, due to the uncertainty in these developments. The SDE++ subsidy at the same time is underestimated due to the fact that the actual SDE++ subsidy is modeled per hour while the average yearly DA price is used to estimate the correction value per kWh.

4.1.1. Energy Curtailment

The energy that is curtailed is actually wasted [18]. Thus, it can be suggested that this amount of electricity should be better put into use. However, this is complicated since there is relatively little demand in the area of the case study. When one would decide to use the electricity close to the location of generation the PV plant would require a larger inverter, which then would result reduce the $NPV$. Extra demand may be a solution to bridge the gap before investing in additional infrastructure, such as locating a fast-charging facility for electrical vehicles or a data center close to the solar park. This requires the demand to be adjusted to the maximum of the PV electricity production, which in turn creates inefficiency in that process. Therefore, some sort of energy waste is preferred, as it can be argued that it is not as valuable as the placement of larger inverters, cables, and additional production plants. The wasted electricity is transformed to heat in the inverter. This heat could be used for other functions and potentially even be sold.

When looking at the marginal energy that is created with the added PV panels and a curtailment strategy, the additional production occurs in the early morning and late afternoon hours. This is favorable as it matches the normal electricity consumption pattern.

There are possible downsides to curtailment. Over-power and over-voltage situations occur when there is a high power output combined with lower temperatures (causing voltage rise). When an over-power condition occurs, the inverter will increase the voltage, which will cause the modules to move away from their maximum power point. The excess power will then be curtailed as heat. Over-voltage situations lead to a disruption of the energy production. This occurs when the inverter voltage design is too narrow for the power curtailment. At high curtailment values, the inverter manufacturer needs to be consulted to ensure the inverter is compatible with the required voltage range [65]. Since this is very difficult to predict and the impact on the overall $NPV$ is limited, this has not been taken into account. In order to avoid the over-voltage situations, one solution found in the literature could be the utilization of micro-inverters [66]. Micro-inverters can be used as well for active curtailment as each panel can be switched off individually. However, micro-inverters are said to increase the investment costs of the solar plant [67].

For passive curtailment, the inverter is used, as is also done in the model. However, it is said that passive curtailment can only be used up to 100% overbuild, whereafter active curtailment is required [46]. This is not included in the scenario, and would require additional circuit breakers and software to accomplish that.

4.1.2. Grid Requirements

Due to grid requirements proposed by TenneT, such as the reactive power capability and voltage requirements, a buffer is needed on the connection [68]. This buffer was not taken into account. It has not been investigated how this would have an effect on the curtailment ability. However, it can also be assumed that the effect could be similar for all different scenarios.

4.1.3. Battery System

In all price scenarios studied, the battery system is the least attractive solution as replacement of infrastructure from an $NPV$ perspective, even though the battery integration can increase the revenue of the PV plant. However, battery-based energy storage systems can be employed in multi-revenue business models for the provision of multiple services such as market optimization [69], in combination with system balancing [70], and for the provision of peak shaving services in distribution grids [71], compared to simply curtailing the electricity. Furthermore, in this work a pure economic optimization approach is followed, whereas recent work in battery multi-objective optimization, by considering both economic and environmental objectives, has shown that costs and emissions can simultaneously be decreased [72]. Therefore, it is recommended that future research also considers the utilization of battery-based storage systems for multiple purposes in increasing its value, as well as the use of second-life Li-ion batteries from electric vehicles.

In the model, only a Li-ion battery system was modeled. This technology is known for large compatibility but also for high investment costs. There are of course other forms of electricity storage, such as hydrogen production which could be transported through the gas network [73] or other type of batteries such as the vanadium redox battery [74]. A combination of multiple technologies when looking at large peak capacities could also be beneficial. This has not been taken into consideration in the study.

Model limitations are that the lifetime of the battery is not included, which is depending on the usage of the battery [53]. Furthermore, the battery system is not ‘smart’. It is assumed to not be able to predict the electricity prices and therefore, only average electricity prices are used. However one day in advance, the production output can be relatively accurately predicted and also the DA prices are available. These prices can then be used to determine when the battery will release or store its energy. Such a predictive method could potentially improve the revenue.

4.1.4. Infrastructure Connection Cost

The infrastructure connection cost in the model is assumed to be independent of the power capacity of the PV plant. This is true to a certain extent. The estimated cost given is only for a 110 kV cable. If the solar plant would increase in size, it eventually has to move up to the 150 kV network or the 220 kV network that is present in the Netherlands. The 220 kV network can take up about 900 MVA but this would increase the investment and O&M costs significantly [61]. The O&M cost (expressed in percentage of the investment cost) would remain at the same percentage as for the 110 kV network. The connection cost of the PV plant to the 220 kV network is about three times higher than for the 110 kV cable. The cable cost for a 220 kV cable are about 4 times more expensive [61]. The MWp dependent network and related cable cost were not taken into account due to the dependence on the location of the PV plant. If TenneT TSO would change the infrastructure connection cost to be more MWp dependent in the future, then the incentive to decrease the maximum power output of the power plant might be more clear, and part of the other deep network investments could be paid from these extra charges. Creating such incentive for the PV energy producer could be beneficial for the overall infrastructure cost and consumer electricity prices.

4.2. Impact TSOs

In this research, a case study in the Netherlands was considered. However, the findings of this study can be useful for other TSOs as well. For the current connections and for future connections, data should become available not only on the connection size, but also on the DC/AC ratio (the ratio of panel size and inverter size). This could determine the amount of curtailment that will take place, and through this data, a more accurate prediction of the production profile could be found. The business case for PV plants for which the grid has to be expanded is also not attractive and may therefore not be implemented, because it would result in higher electricity prices for the consumer. The overbuild fraction also creates a more stable production throughout the entire year [18,75]. To create a more cost-effective electricity system, the design of PV plants should already be altered, rather than waiting until after the construction is completed.

It can be recommended to TenneT that when the capacity of the local electricity grid is insufficient to meet the transport requirements of new PV connection requests, changing the plant design of these PV plants could be sufficient to connect additional PV plants to the electricity grid. The inverter size compared to the solar panel capacity should be significantly reduced. This can create a more cost-effective electricity system. If the PV connection requests exceeds a 120% overbuild of the electricity network, increasing network capacity should be considered. As the market parties have to alter the design of the PV plant, careful communication is necessary as well as more information on the PV module capacity related to the connection request.

4.3. Recommendations for Further Research

This study was performed to provide insights on how PV investors could determine their strategies. In future research it could be interesting to further model a curtailed production profile for a PV plant and determine the impact on grid congestion and grid associated investments. The developed model considers only PV energy on the transmission line and a more complex transmission system which includes wind and other forms of energy on the same grid would be an interesting option for expanding this research. The technical limitations of curtailment and its impact on the energy output and $NPV$ could be researched to establish the impact. It would be interesting to apply this model to a grid that has a higher demand and determine the impact on the azimuth angle and revenue. Furthermore, not all forms of congestion management have been studied, and the model could be expanded to add different forms to compare and contrast these, such as hydrogen production or re-dispatch. Ultimately, the goal is to translate these results into a cost effective and sustainable electricity system for society. To achieve this, further research has to be performed on how to change the behavior of the investor and subsequently how that has an effect on the electricity prices in the Netherlands. From an environmental perspective, it can also be questioned whether extra solar panels still create environmentally friendly electricity when there is large-scale curtailment. To make a judgement on this, the environmental footprint of an inverter should be compared to the footprint of the additional infrastructure [76].

Finally, we recognize that traditional methods that are based on the net present value do not take into account the fact that PV (and wind) energy is intermittent which requires conventional operators to accommodate their output [77]. However, as an example, the US Department of Energy has introduced a Levelized Avoided Cost model in relation to renewables investments [78] in their recent energy outlook. Future research should thus also take into account the dispatch priority of PV energy in liberalized electricity markets and the value of flexibility.

5. Conclusions

In this work, the cost effectiveness of various options is studied, which would allow connecting large PV plants in areas with limited grid capacity. For this purpose, a generic methodology is proposed and applied to a case study focusing on an HV grid in the North of the Netherlands. The methodology is generic in the sense that it can be applied to different contexts, however, the input data such as irradiation data, cost of land, cost of installation, electricity prices, subsidy schemes, and so forth are case-specific, and as such the results cannot be generalized. The main findings of the analysis are twofold:

• with increasing overbuild PV capacity, curtailment is the most cost-effective solution, whereas after a certain overbuild factor investments in infrastructure become more cost-effective.
• the optimal overbuild factor varies with different azimuth angles, electricity prices, battery integration, or different forms of compensation.

Curtailment can significantly increase the $NPV/I$ of a PV system. The installed capacity of the PV system can be increased by 130% using a combination of curtailment and azimuth angle changes without investing in infrastructure before it becomes less cost-effective compared to increasing grid capacity. The market parties will optimise curtailment to overbuild their PV plant by 40%. At the location of the case study (Stadskanaal), more curtailment would increase the cost-effectiveness of the electricity system. It can therefore be concluded that using the constraints mentioned in the research, the PV investor’s optimum and the societal optimum are not always aligned. If market parties would be remunerated for increasing the curtailment of the PV plant, the added cost would decrease the optimum overbuild using curtailment to 85% (SDE+ prices). Furthermore, the analysis showed that the use of a Li-ion battery system as a means of deferring infrastructure investments was not cost-effective. However, when a battery system was added after large-scale curtailment, it did have a positive effect on the $NPV/I$ of the electricity system. This was specifically after 100% overbuild (2030 prices) and after 150% overbuild (SDE+ prices). The optimal azimuth angle is also affected by the level of curtailment. It changes from 210 to 230° at 40% overbuild (SDE+ prices) and 80% overbuild (2030 prices) on the curtailment curve.

Overall, large-scale PV plants in rural areas, such as in the case study of Stadskanaal, requires curtailment for a more cost-effective transmission system. High curtailment results into the need for different azimuth angles in the design, whereas in the future integration of battery-based energy storage systems in multi-revenue business models shall be considered prior to infrastructure investments.