Study on Spectral Radiative Heat Transfer Characteristics of a Windowed Receiver with Particle Curtain
Abstract
1. Introduction
- Solid particles can directly absorb the concentrated solar radiation without additional fluid pipes;
- Solid particles can reach a higher working temperature;
- Solid particles can also be used as the heat exchange medium and heat storage medium at the same time, without additional pipes and heat exchange equipment;
- The cost of using particles as a medium is lower;
- The system can reach a high degree of stability at high temperatures.
2. Model Analysis
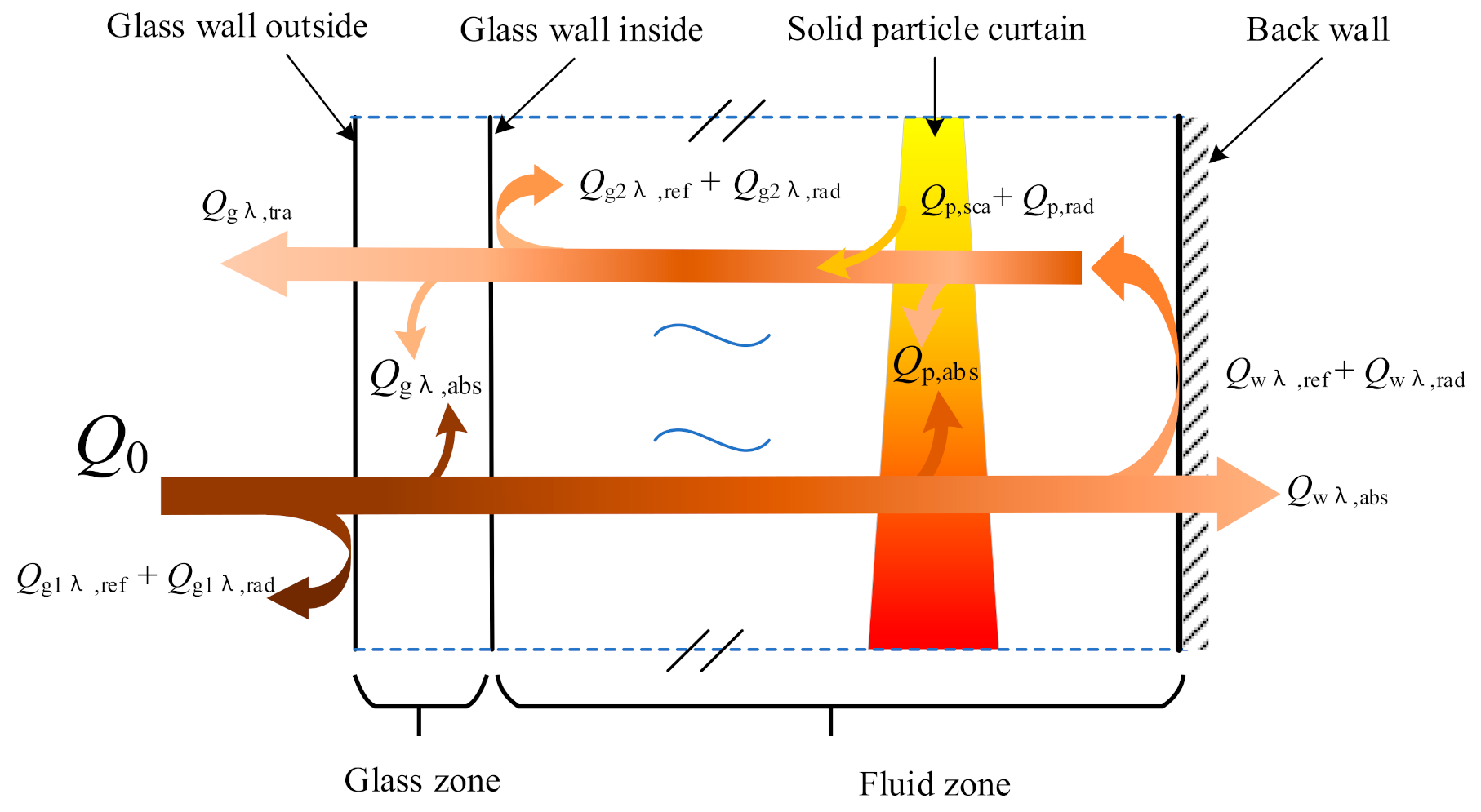
2.1. Physical Model and Boundary Conditions
2.2. Numerical Model
2.2.1. Gas-Phase Equation
2.2.2. Particle Phase Equation
2.2.3. Particle Radiation Model
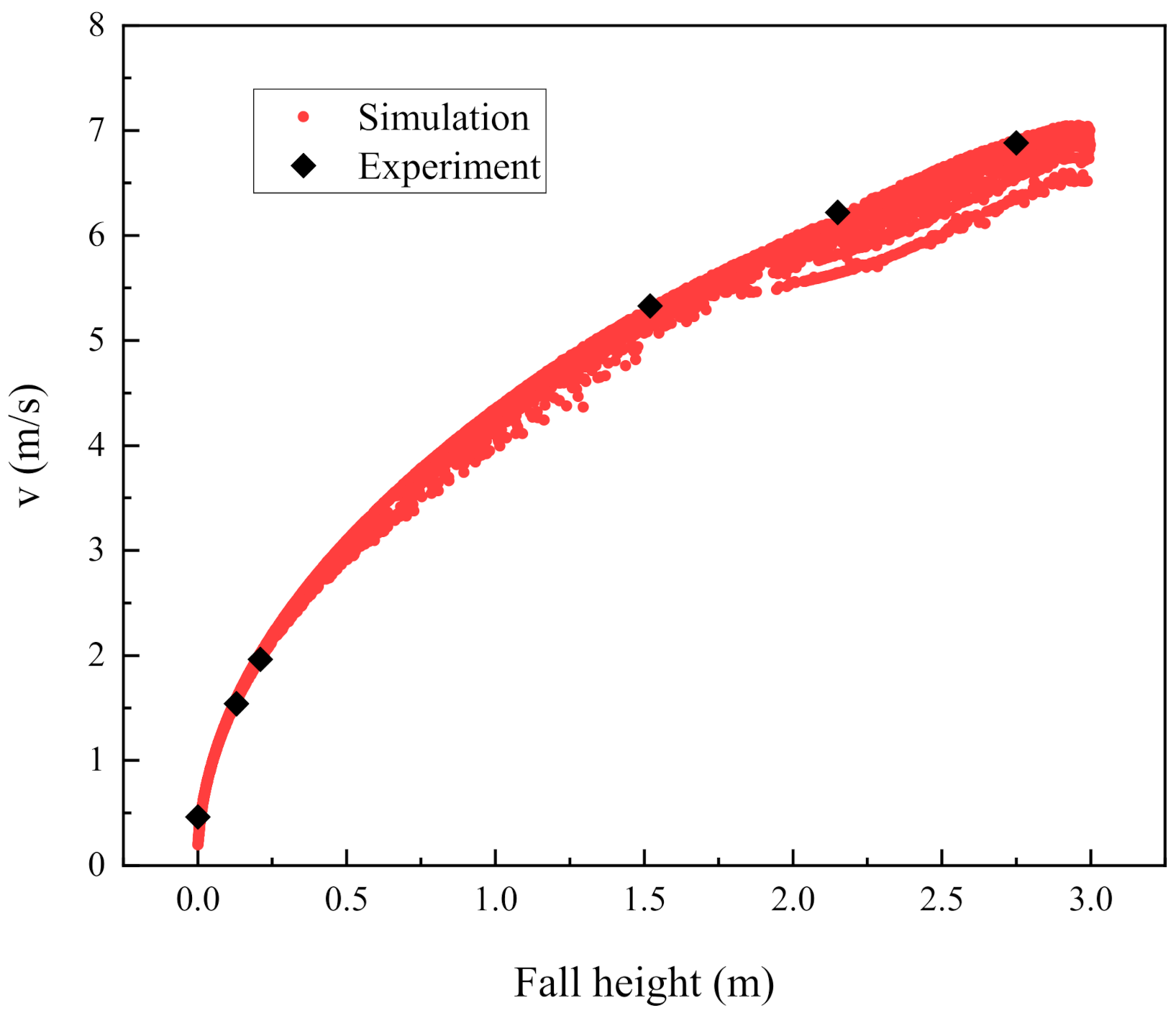
3. Simulation Method
4. Discussion
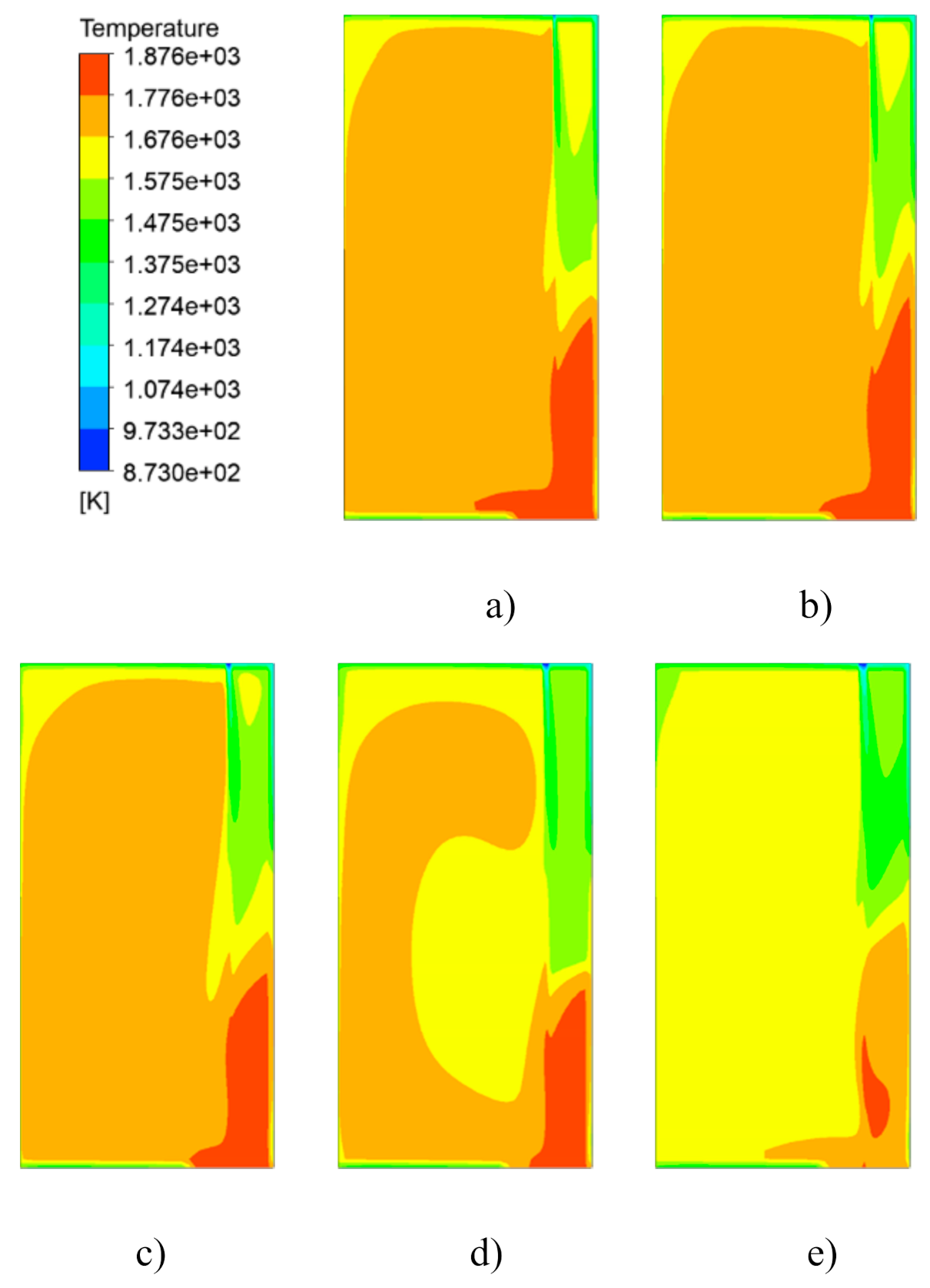
4.1. Comparative Analysis with Aerowindow Receiver
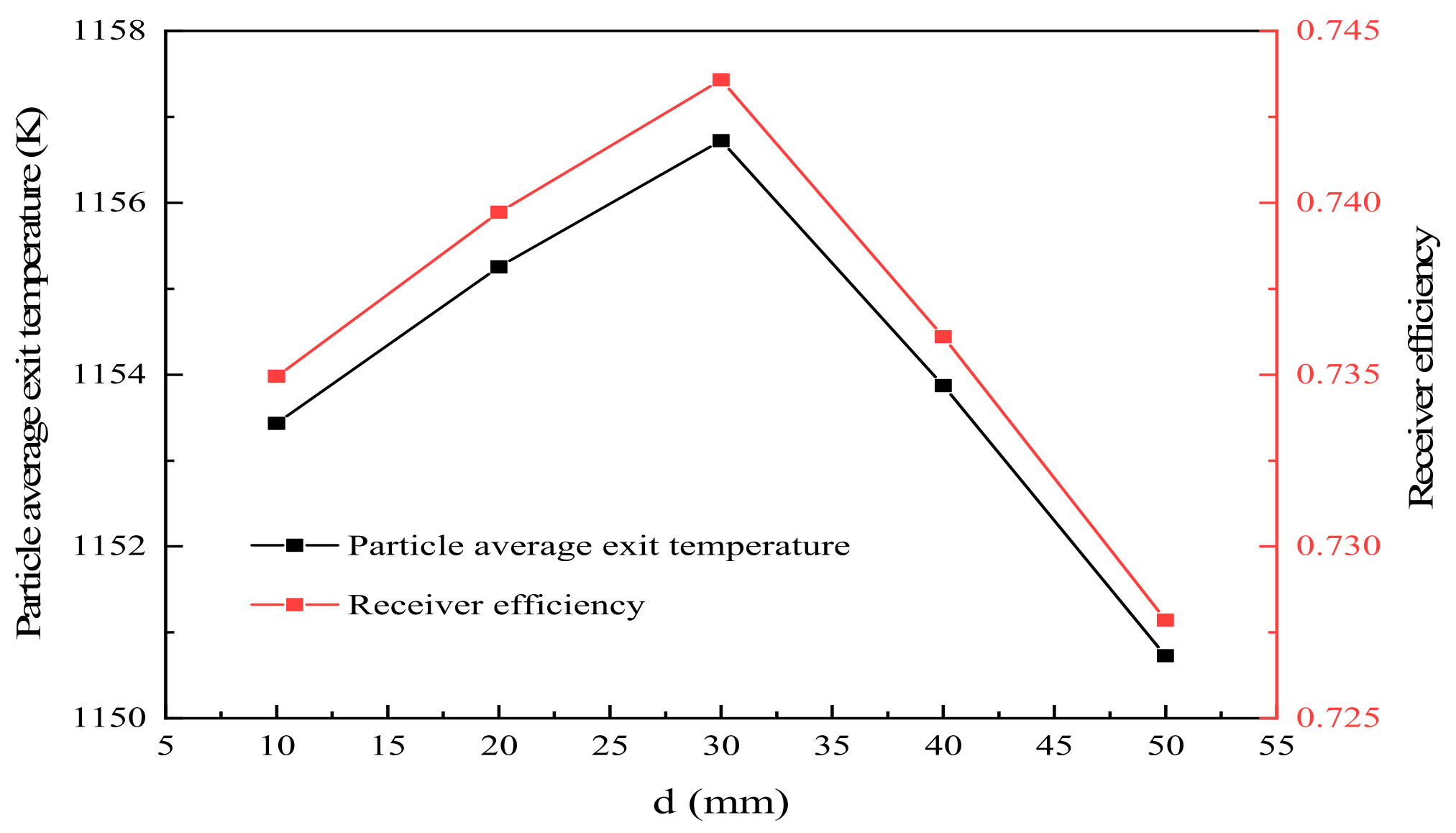
4.2. Influence of Different Particle Curtain Thickness
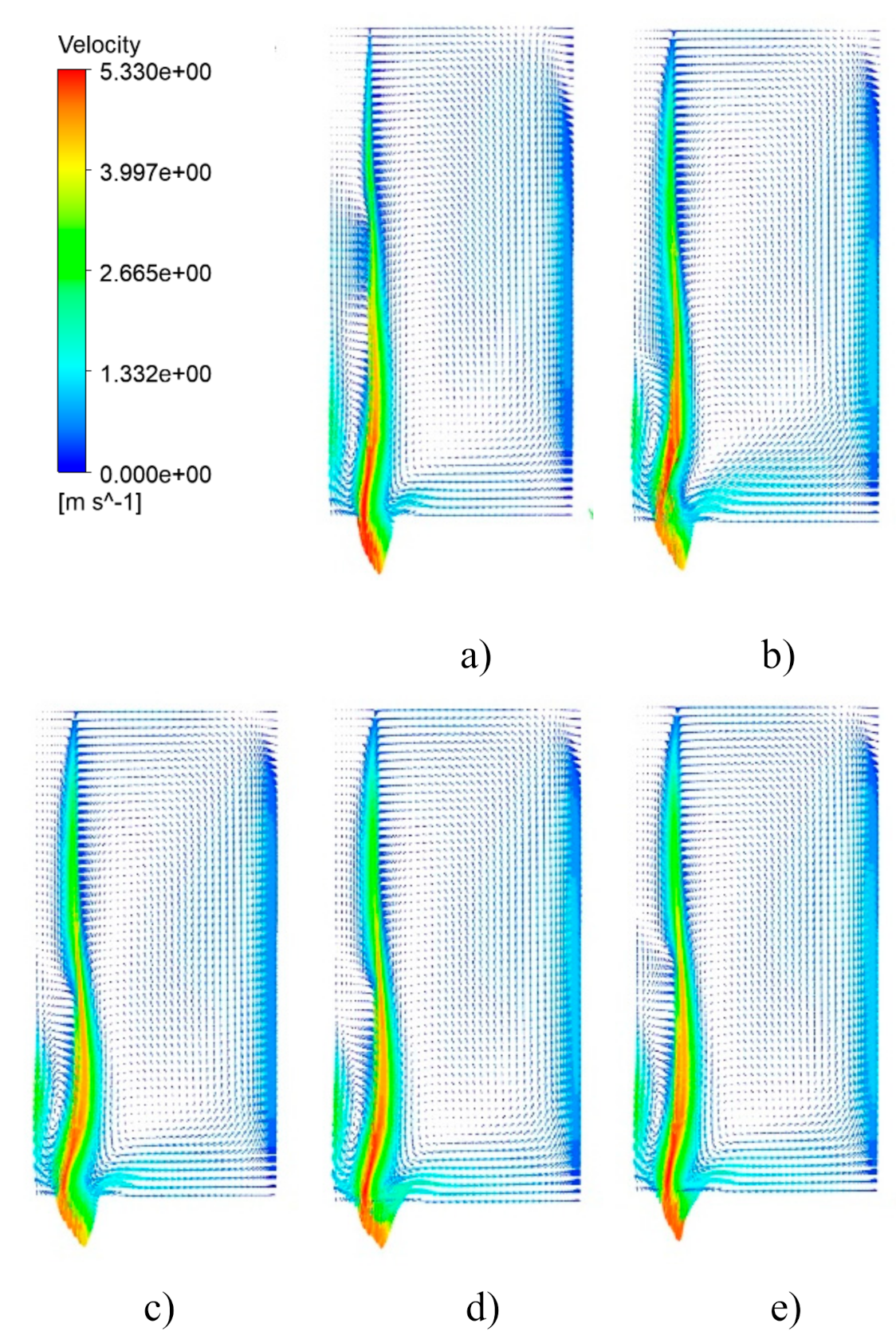
4.2.1. Analysis of Flow Characteristics
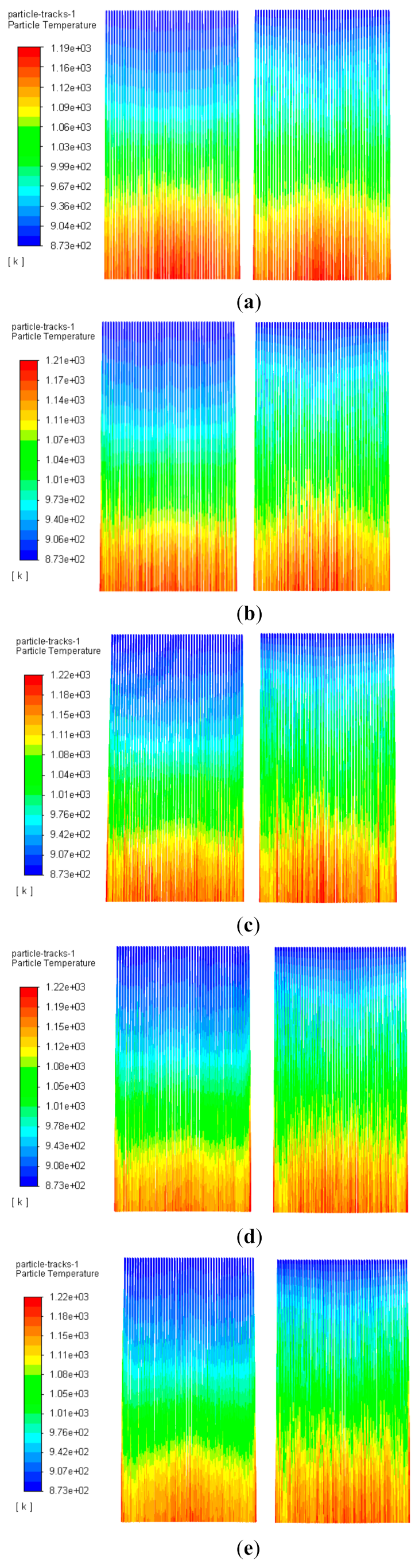
4.2.2. Analysis of the Temperature Distribution Characteristics
4.2.3. Radiation Field Analysis
4.2.4. Receiver Efficiency
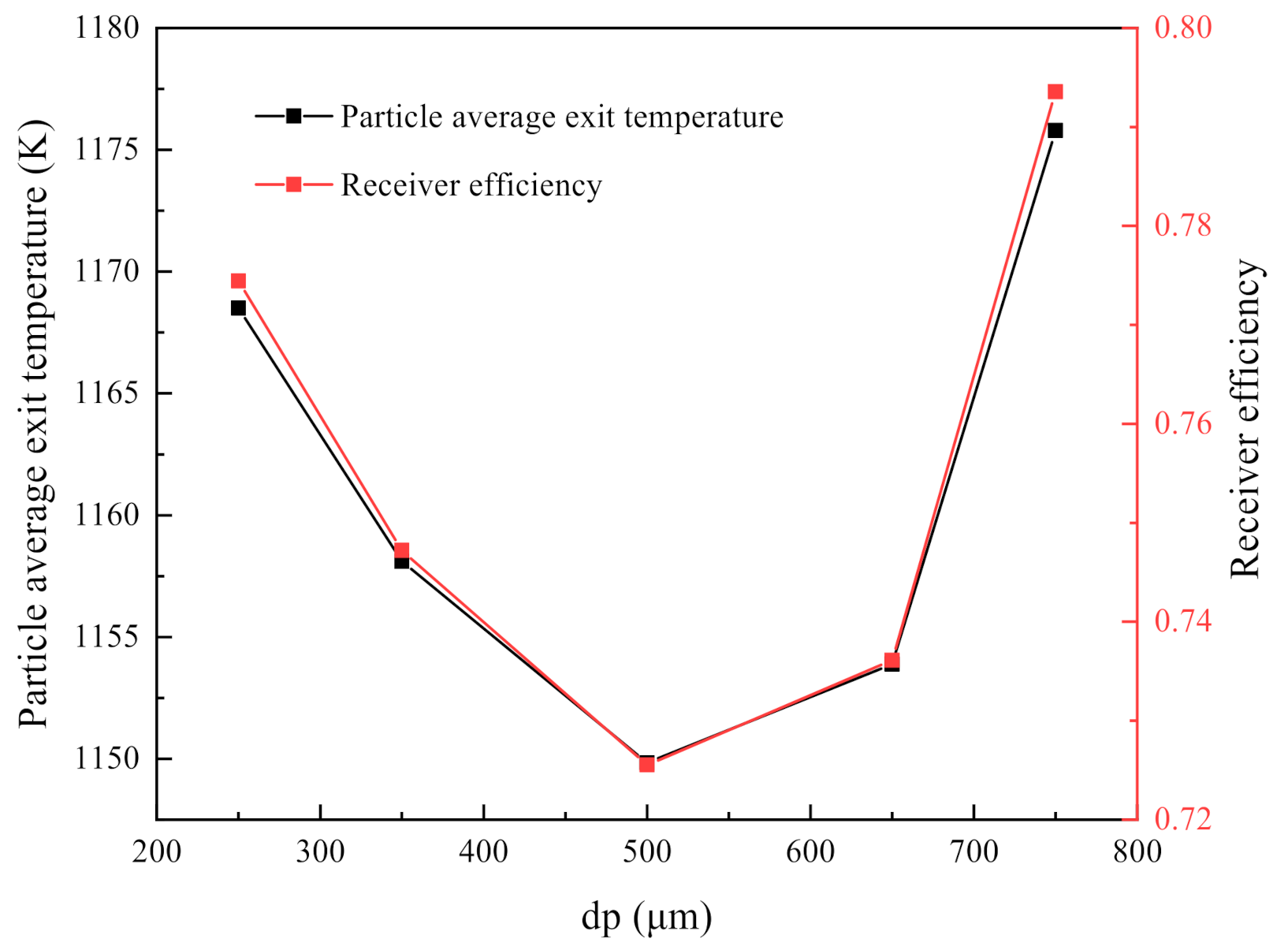
4.3. Influence of Different Particle Size
5. Conclusions
- With the advantage of selective transmission, the heat loss of convection and re-radiation in the cavity can be reduced, and the particle average exit temperature and the receiver efficiency can be noticeably improved.
- When the mass flow rate is the same, the influence of the inlet thickness of particles on the flow pattern and temperature distribution of the particle curtain cannot be ignored. The volume fraction and flow stability of the particle curtain decrease with the increase in the thickness of the particle curtain. When the thickness of the particle inlet is 10–50 mm, with the increase in particle entrance thickness, the particle average exit temperature and the receiver efficiency first increase and then decrease.
- The particle size also has a significant effect on the flow pattern and the radiation distribution inside the curtain. The exit temperature of particles with different particle sizes presents a trend of high in the middle and low on both sides along the width. The particle size is small, and the influence of vortices on the two sides of the curtain is strong when the particles fall freely, resulting in the obvious dispersion of particles in a thickness distribution. The particle temperature in the front of the curtain is significantly higher than that in the back wall side. When the particle size is between 250 and 750 μm, the particle average exit temperature and the receiver efficiency first decrease and then increase with the increase in the particle size.
Author Contributions
Funding
Conflicts of Interest
References
- Behar, O.; Khellaf, A.; Mohammedi, K. A review of studies on central receiver solar thermal power plants. Renew. Sustain. Energy Rev. 2013, 23, 12–39. [Google Scholar] [CrossRef]
- Benoit, H.; Spreafico, L.; Gauthier, D.; Flamant, G. Review of heat transfer fluids in tube-receivers used in concentrating solar thermal systems: Properties and heat transfer coefficients. Renew. Sustain. Energy Rev. 2016, 55, 298–315. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Islam, T.; Huda, N.; Abdullah, A.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2018, 91, 987–1018. [Google Scholar] [CrossRef]
- Ju, X.; Xu, C.; Hu, Y.; Han, X.; Wei, G.; Du, X. A review on the development of photovoltaic/concentrated solar power (PV-CSP) hybrid systems. Sol. Energy Mater. Sol. Cells 2017, 161, 305–327. [Google Scholar] [CrossRef]
- Tan, T.; Chen, Y. Review of study on solid particle solar receivers. Renew. Sustain. Energy Rev. 2010, 14, 265–276. [Google Scholar] [CrossRef]
- Tang, N.; Zhang, Y.; Niu, Y.; Du, X. Solar energy curtailment in China: Status quo, reasons and solutions. Renew. Sustain. Energy Rev. 2018, 97, 509–528. [Google Scholar] [CrossRef]
- Calderón, A.; Palacios, A.; Barreneche, C.; Segarra, M.; Prieto, C.; Rodriguez-Sanchez, A.; Fernández, A.I. High temperature systems using solid particles as TES and HTF material: A review. Appl. Energy 2018, 213, 100–111. [Google Scholar] [CrossRef]
- Gobereit, B.; Amsbeck, L.; Buck, R.; Pitz-Paal, R.; Röger, M.; Müller-Steinhagen, H. Assessment of a falling solid particle receiver with numerical simulation. Sol. Energy 2015, 115, 505–517. [Google Scholar] [CrossRef][Green Version]
- Ho, C.; Christian, J.; Gill, D.; Moya, A.; Jeter, S.; Abdel-Khalik, S.; Sadowski, D.; Siegel, N.; Al-Ansary, H.; Amsbeck, L.; et al. Technology Advancements for Next Generation Falling Particle Receivers. Energy Procedia 2014, 49, 398–407. [Google Scholar] [CrossRef]
- Ho, C.K. A review of high-temperature particle receivers for concentrating solar power. Appl. Therm. Eng. 2016, 109, 958–969. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, J.-S.; Lipiński, W. Radiation absorption in a particle curtain exposed to direct high-flux solar irradiation. J. Sol. Energy Eng. 2018, 140, 061007. [Google Scholar] [CrossRef]
- Knott, R.C.; Sadowski, D.L.; Jeter, S.M.; Abdel-Khalik, S.I.; Al-Ansary, H.A.; El-Leathy, A. Sintering of Solid Particulates Under Elevated Temperature and Pressure in Large Storage Bins for Thermal Energy Storage. In Proceedings of the ASME 2014 8th International Conference on Energy Sustainability Collocated with the ASME 2014 12th International Conference on Fuel Cell Science, Engineering and Technology, Boston, MA, USA, 30 June–2 July 2014. [Google Scholar] [CrossRef]
- Siegel, N.P.; Gross, M.D.; Coury, R. The Development of Direct Absorption and Storage Media for Falling Particle Solar Central Receivers. J. Sol. Energy Eng. 2015, 137, 041003. [Google Scholar] [CrossRef]
- Zhao, W.; Sun, Z.; Alwahabi, Z.T. Emissivity and absorption function measurements of Al2O3 and SiC particles at elevated temperature for the utilization in concentrated solar receivers. Sol. Energy 2020, 207, 183–191. [Google Scholar] [CrossRef]
- Nie, F.; Bai, F.; Cui, Z.; Zhao, Z.; Wang, Z. Cold-state experimental study on discharge characteristics of solid particles in a gravity driven moving bed solar receiver. Sol. Energy. 2020, 195, 14–26. [Google Scholar] [CrossRef]
- Nie, F.; Bai, F.; Cui, Z.; Wang, Z. Properties of solid particles as heat transfer fluid in a gravity driven moving bed solar receiver. Sol. Energy Mater. Sol. Cells 2019, 200, 110007. [Google Scholar] [CrossRef]
- Kang, Q.; Flamant, G.; Dewil, R.; Baeyens, J.; Zhang, H.; Deng, Y. Particles in a circulation loop for solar energy capture and storage. Particuology 2019, 43, 149–156. [Google Scholar] [CrossRef]
- Jiang, K.; Du, X.; Kong, Y.; Xu, C.; Ju, X. A comprehensive review on solid particle receivers of concentrated solar power. Renew. Sustain. Energy Rev. 2019, 116, 109463. [Google Scholar] [CrossRef]
- Martin, J.; Vitko, J., Jr. ASCUAS: A Solar Central Receiver Utilizing a Solid Thermal Carrier. 1982. Available online: https://www.osti.gov/biblio/5663779-ascuas-solar-central-receiver-utilizing-solid-thermal-carrier (accessed on 20 November 2020).
- Falcone, P.K.; Noring, J.E.; Hruby, J.M. Assessment of a Solid Particle Receiver for a High Temperature Solar Central Receiver System. 1985. Available online: https://www.osti.gov/biblio/6023191-assessment-solid-particle-receiver-high-temperature-solar-central-receiver-system (accessed on 12 December 2020).
- Chen, H.; Chen, Y.; Hsieh, H.-T.; Siegel, N.P. CFD Modeling of Gas Particle Flow within a Solid Particle Solar Receiver. In Proceedings of the Solar Energy; ASME International, Denver, CO, USA, 8–13 July 2006; pp. 37–48. [Google Scholar]
- Siegel, N.P.; Ho, C.K.; Khalsa, S.S.; Kolb, G.J. Development and Evaluation of a Prototype Solid Particle Receiver: On-Sun Testing and Model Validation. J. Sol. Energy Eng. 2010, 132, 021008. [Google Scholar] [CrossRef]
- Gobereit, B.; Amsbeck, L.; Happich, C.; Schmücker, M. Assessment and improvement of optical properties of particles for solid particle receiver. Sol. Energy 2020, 199, 844–851. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, J.-S.; Lipiński, W. Radiation Characteristics of a Particle Curtain in a Free-Falling Particle Solar Receiver. In Proceedings of the ASME 2017 Heat Transfer Summer Conference, Bellevue, WA, USA, 9–12 July 2017. [Google Scholar]
- Siegel, N.; Gross, M.; Ho, C.; Phan, T.; Yuan, J. Physical Properties of Solid Particle Thermal Energy Storage Media for Concentrating Solar Power Applications. Energy Procedia 2014, 49, 1015–1023. [Google Scholar] [CrossRef]
- Kim, K.; Moujaes, S.F.; Kolb, G.J. Experimental and simulation study on wind affecting particle flow in a solar receiver. Sol. Energy 2010, 84, 263–270. [Google Scholar] [CrossRef]
- Kim, K.; Siegel, N.; Kolb, G.; Rangaswamy, V.; Moujaes, S.F. A study of solid particle flow characterization in solar particle receiver. Sol. Energy 2009, 83, 1784–1793. [Google Scholar] [CrossRef]
- Tan, T.; Chen, Y.; Chen, Z. Performance of Solid Particle Receivers with or Without the Protection of an Aerowindow. In Proceedings of the ASME 2008 2nd International Conference on Energy Sustainability, Jacksonville, FL, USA, 10–14 August 2008; pp. 95–104. [Google Scholar]
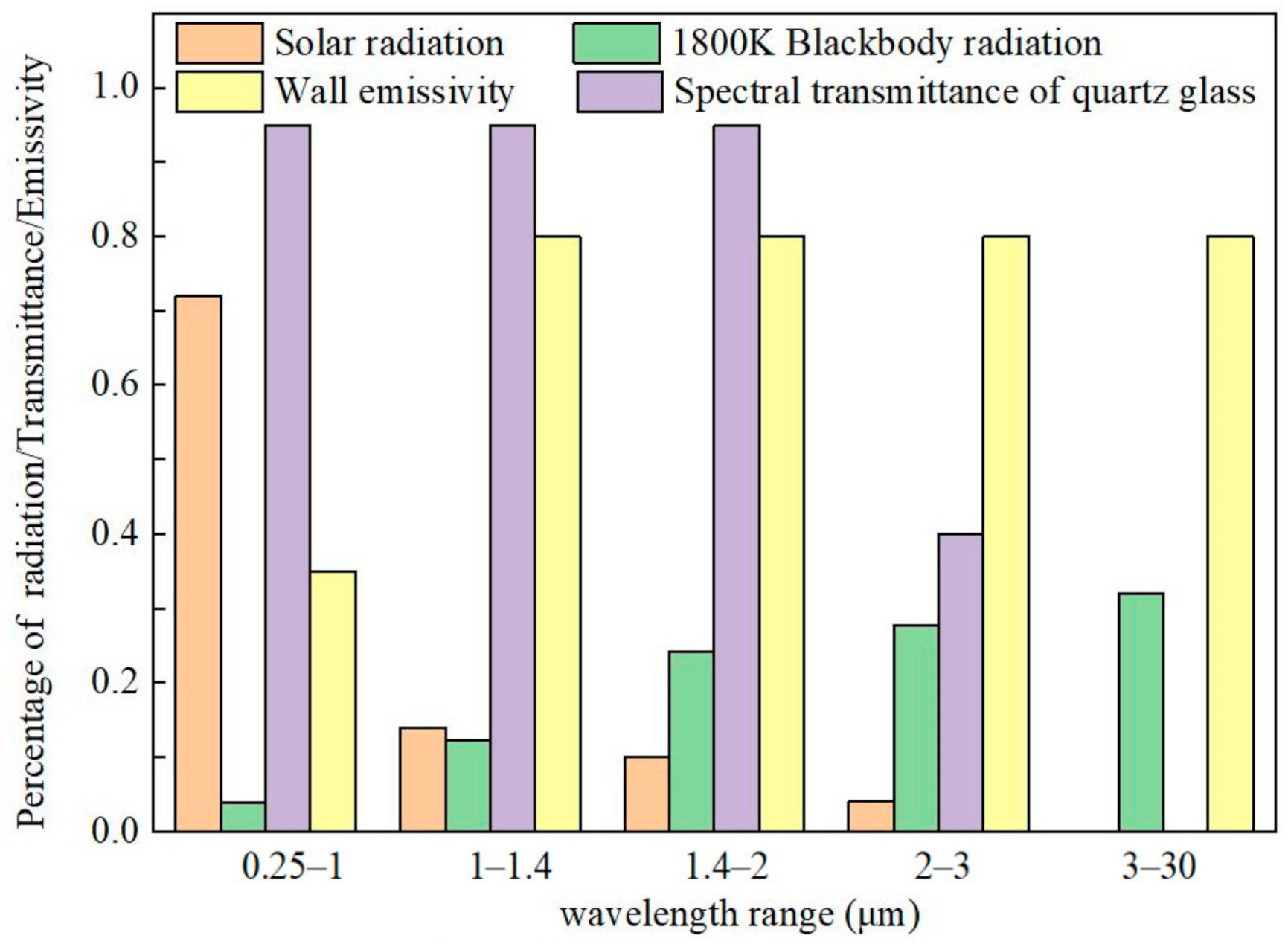
- Hang, T.; Ping, X.H. Study on spectral properties and energy conversion mechanism of glass. J. Inorg. Mater. 2013, 28, 696–700. [Google Scholar]
- Xi, G.F. Optical and Spectral Properties of Glass; Shanghai Scientific and Technical: Shanghai, China, 1992. [Google Scholar]
- Wang, P.; Liu, D.; Xu, C.; Xia, L.; Zhou, L. A unified heat transfer model in a pressurized volumetric solar receivers. Renew. Energy 2016, 99, 663–672. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Bai, F.; Liu, D.; Xu, C.; Zhao, L.; Wang, Z. Experimental and theoretical evaluation on the thermal performance of a windowed volumetric solar receiver. Energy 2017, 119, 652–661. [Google Scholar] [CrossRef]
- Hruby, J.; Steele, B.; Burolla, V. Solid particle receiver experiments: Radiant heat test. Solid Part. Receiv. Exp. Radiant Heat Test 1984, A05, 1. [Google Scholar] [CrossRef]
- Thomasson, P.G.; Cheng, P. Two-dimensional radiating gas flow by a moment method. AIAA J. 1964, 2, 1662–1664. [Google Scholar]
- Raithby, G.D.; Chui, E.H. A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media. J. Heat Transf. 1990, 112, 415–423. [Google Scholar] [CrossRef]
- Chui, E.H.; Raithby, G.D. Implicit Solution Scheme to Improve Convergence Rate in Radiative Transfer Problems. Numer. Heat Transf. Part B Fundam. 1992, 22, 251–272. [Google Scholar] [CrossRef]
- Tan, T.; Chen, Y. Protection of an Aerowindow, One Scheme to Enhance the Cavity Efficiency of a Solid Particle Solar Receiver. In Proceedings of the Volume 1: Heat Transfer in Energy Systems; Thermophysical Properties; Heat Transfer Equipment; Heat Transfer in Electronic Equipment; ASME International, San Francisco, CA, USA, 19–23 July 2009; pp. 611–618. [Google Scholar]





| Types | Value |
|---|---|
| Density (kg/m3) | 3200 |
| Specific heat (J/kg-K) | 1085 |
| Solar radiation absorption rate | 0.9 |
| Thermal conductivity (W/m-K) | 6.67 |
| Types | Aerowindow | Quartz Window |
|---|---|---|
| Particle average exit temperature K | 1108 | 1154 |
| The receiver efficiency | 61.7% | 73.6% |
| Convection heat loss | 4.8% | 1.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yang, L.; Liu, J.; Wang, P. Study on Spectral Radiative Heat Transfer Characteristics of a Windowed Receiver with Particle Curtain. Energies 2021, 14, 2801. https://doi.org/10.3390/en14102801
Wang L, Yang L, Liu J, Wang P. Study on Spectral Radiative Heat Transfer Characteristics of a Windowed Receiver with Particle Curtain. Energies. 2021; 14(10):2801. https://doi.org/10.3390/en14102801
Chicago/Turabian StyleWang, Li, Long Yang, Junjie Liu, and Pei Wang. 2021. "Study on Spectral Radiative Heat Transfer Characteristics of a Windowed Receiver with Particle Curtain" Energies 14, no. 10: 2801. https://doi.org/10.3390/en14102801
APA StyleWang, L., Yang, L., Liu, J., & Wang, P. (2021). Study on Spectral Radiative Heat Transfer Characteristics of a Windowed Receiver with Particle Curtain. Energies, 14(10), 2801. https://doi.org/10.3390/en14102801







