Abstract
An abundance of research has been performed to understand the physics of latent thermal energy storage with phase change material. Some analytical and numerical findings have been validated by experiments, but there are few free and open-source models available to the general public for use in systems simulation and analysis. The Modelica programming language is a good avenue to make such models available, because it is object-oriented, equation-based, declarative, and acausal. These characteristics have enabling the creation of component model libraries that can be used to build larger system simulations for design analysis. The authors have previously developed a numerical framework to model phase change thermal storage and have validated model predictions with experiments. The objectives of this paper are to describe the transfer of the numerical framework to an implementation in a Modelica component model and to validate the Modelica model with data from the experiment and the original numerical framework.
1. Introduction
Numerous research investigations have been conducted over the past four decades to understand the physics of latent thermal energy storage (TES) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Many are either strictly analytical and numerical or analytical and experimental [1,2,3,4,5,6,7,8]. Some combine computational research techniques with lab testing by using experimental data from the literature [9,10,11]. While these studies are valuable, they are subject to unintentional discrepancies between physical devices and the models that aim to represent them. Other researchers have in-house experimental data available with which to validate detailed numerical models [12,13,14,15,16,17,18,19,20]. In order to have confidence in physically representative thermal storage models, experimental tests should be performed whenever possible to validate computational model predictions. A key aspect that stands out from these studies is that there are few to no thermal storage models available to the general public, particularly heating, ventilation, and air conditioning (HVAC) designers, for system simulation and analysis [4]. This dearth makes the creation and dissemination of easy-to-use, physically accurate models of phase change material (PCM) heat exchangers for latent thermal energy storage particularly important.
The Modelica programming language is a good avenue to make such models available because it is object-oriented, equation-based, declarative, and acausal [21]. These characteristics have enabled the creation of component model libraries that can be used to build larger system simulations for design analysis. One such library that has gained traction in the building industry is called the Modelica Buildings Library and is made available free and open source [22]. The Modelica Buildings Library offers flexible modeling and dynamic simulation of building envelopes, HVAC equipment, and more. It was created, in part, to design and analyze non-conventional energy systems and develop and deploy energy-minimizing controls. Such functionality is ideal for rapid prototyping of innovative building energy solutions, including those that achieve load shifting with thermal storage systems.
In previous works, we established a dimensionless first-principles framework to model transient heat transfer in a TES device, similar to effectiveness–NTU analysis methods for compact heat exchangers. We began by deriving a non-dimensional framework in order to analyze thermal energy storage and characterize its performance [23]. During that examination, we found that we would need to focus our efforts on quantifying the space- and time-varying conductance inherent in the transient melting and freezing processes of latent thermal storage. Similar to steady-state effectiveness–NTU predictions, we found that the effectiveness of high performance devices is not sensitive to variations in conductance [24]. Those findings justified the use of a space—and time—averaged conductance, which we determined from a simple thermal resistance network as a function of the phase change material melt fraction [25]. In tandem, the TES device was examined in the context of a larger subsystem, consisting of external heat exchangers used to transfer energy to and from the storage. This problem was mathematically challenging by introducing spatially varying initial conditions (due to the nature of cyclic melting and freezing processes), as well as a transient boundary condition (for the varying working fluid temperature from the heat exchangers) [26]. The culmination of previous work provided a great basis for comparison with experimental testing of a TES device and validation of our first-principle numerical framework [27].
Since then, we have been working to develop new models of thermal energy storage in Modelica. The objectives of this paper are to describe the transfer of the numerical framework to an implementation in a Modelica component model that will be made available free and open source and to validate the Modelica model with data from the experiment and the original numerical framework. This modeling effort is one piece of a so-called “hybrid” HVAC project that is integrating thermal storage, heat pump, and evaporative cooling components to shift thermal loads and enable the decarbonization of space and water heating. The benefits of integrating PCM TES in HVAC systems are numerous, providing opportunities to use smaller heat pumps, avoid electric resistance backup heating, reduce the spatial footprint for domestic hot water storage, improve heat pump performance, “store cold” from overnight evaporative cooling, and recover waste heat. By pairing this technology with on-site renewable generation (e.g., photovoltaics), PCM TES could be charged when energy is available and later discharged when needed. To support the implementation of TES for load shifting applications, we have developed PCM heat exchanger models that others will be able to incorporate in simulation of system designs. It is important to note that most load shifting applications are highly dependent on weather and climate and thus require annual simulations to evaluate system performance in different seasons. Computational time must remain manageable, giving further support to the use of Modelica over more complex computational fluid dynamics (CFD) approaches.
The structure of this paper is as follows: In Section 2, we provide a literature review of Modelica-based implementations of PCM heat exchangers. In Section 3, we describe the experimental setup for a TES prototype. In Section 4, we summarize the first-principle modeling approach developed in previous work. In Section 5, we describe the Modelica implementation. In Section 6, we compare results and discuss. In Section 7, we conclude.
2. Literature Review
Early into its inception, De Coninck et al. used the Modelica Buildings Library to model the sensible thermal energy storage of a hot water tank for a residential building equipped with photovoltaic panels [28]. The system used an air-to-water heat pump to transfer energy into and out of the tank for six weeks in winter. To simulate the system, the authors created a Modelica model based on an early hydronic heating example from the Buildings Library [29]. The finite volume model of the storage tank includes conduction between layers of water in the tank as well as losses from the metal walls to the surroundings. The paper describes and analyzes three control strategies: optimizing the heat pump heating curve only, daytime use priority to maximize solar energy input, and grid load based on minimizing power peaks. The authors recommend aligning the heat pump with PV while looking carefully at how storage impacts heat pump power consumption over the entire year. Meanwhile, similar research using Modelica was conducted at the E.ON Energy Research Center in Aachen, Germany. In contrast to De Coninck’s work, people at E.ON wanted to model latent thermal energy storage using phase change material (PCM). While water is readily available, PCM offers a greater storage density and lower heat losses, making it a viable alternative. However, heat transfer in PCM is challenging to model for three major reasons: conductance changes with distance from the heat flux boundary, natural convection may occur, and freezing is often different from melting.
At E.ON, Leonhardt and Müller created and analyzed a model of a latent storage system [30]. Their Modelica model of the phase change material heat exchanger includes pipes to transfer energy into or out of slabs of PCM. In their model, heat is transferred into the pipe via convection from the working fluid and conduction through a thin massless wall into a finite volume of storage material. The PCM slab consists of four cardinal heat conduction blocks and one central capacitor. The conductivity is calculated based on the liquid fraction in each discrete element. The central capacitor is implemented as a modification to the thermal capacitance component model of the Modelica Standard Library [31].The modified basic capacitor block is a very valuable feature of this model. The authors note that this initial latent heat storage component model could be improved by adding mass and conduction to the plate walls that separate the working fluid from the PCM.
Using their internal Modelica Library from the Institute for Energy Efficient Buildings and Indoor Climate, Leonhardt and Müller modified their fairly simple model consisting of two fluid volumes, sandwiching a PCM block (described above) to include conduction through the steel frame of the storage container. The authors also expanded beyond the cold storage studied in their previous work to evaluate the combination of hot storage, a heat pump, and solar thermal for residential buildings [32]. The PCM heat exchanger model employs the assumption that the working fluid is evenly distributed around all slabs, though there may be preferential paths in reality. Additionally, the model uses a fixed melt temperature for heating and cooling. To validate the model, the researchers developed a test bench to measure the behavior of a storage prototype. The experimental test bench measures water flow rates and heat exchanger inlet and exit temperatures. They tested two phase change materials: a salt hydrate with a melt temperature of 29 C and a paraffin with a melt temperature at 35 C. The validation shows that the mean relative deviation in fluid temperature prediction is about 3% for the salt hydrate PCM and 4% for the paraffin PCM. However, this model validation relies on several free parameters: amount of bypass flow, melt temperature value, width of the specific heat capacity range, and baseline specific heat capacity value. As such, the model is tuned to achieve the lowest mean relative deviation of 3–4% reported here.
In the decade since that work was conducted, simulation technology and software development companies have become increasingly interested in using Modelica to model dynamic systems. TLK-Thermo GmbH developed an internal library, the TIL Suite, with add-ons for PCM heat exchangers. Researchers at SINTEF used this commercial library to conduct a study of a cold storage installation at the University College of Bergen in Norway. Jokiel created a detailed model to represent the cold storage tanks and validated this model with measurement data from the the plant [33]. The installation consists of four PCM cold storage tanks with a 10 C transition point integrated into a chilled water distribution loop to reduce the capacity of the chiller by ∼50%. Jokiel uses the TIL Suite to represent the thermal components in the chilled water system and investigate storage charging and discharging dynamics. Inside the cylindrical tanks, PCM slabs are stacked to occupy as much of the volume as possible. Jokiel represents this configuration as a rectangular finned-tube heat exchanger in Modelica. The heat exchanger model consists of working fluid, channel wall, and PCM sections, neglecting the steel wall of the tank. It is discretized in both the axial flow and perpendicular directions. The model transfers heat via forced convection with the working fluid and pure conduction through the HDPE wall encapsulating the PCM through to its centerline. The heat transfer rate for one layer is calculated and subsequently multiplied by the number of layers to determine the total energy transferred to or from the storage tank, thus neglecting the difference between different cells. Three tests are conducted to validate estimations for freezing and melting times: constant mass flow rate and inlet temperature, variable inlet temperature, and variable mass flow rate and inlet temperature. In the paper, the working fluid outlet temperature and the heat flow rate are recorded to compare to experiments and validate the model [33]. While the total amount of energy absorbed or released was predicted fairly accurately, the model outlet temperature did not match experiments very well. Jokiel suggests greater care in considering how the heat transfer coefficient changes with progressing melting or freezing within the PCM containers.
Researchers at the Norwegian University of Science and Technology also used the TIL Suite to model cold storage within an ammonia/carbon dioxide cascade refrigeration system for a poultry processing plant in Norway, with the goal of shifting refrigeration load and reducing peak electricity use [34]. Selvnes et al. used Modelica to model latent thermal energy storage at −11 C with carbon dioxide as the refrigerant through the PCM heat exchanger, thus introducing an additional phase change process. The heat exchanger is a steel tank with a stack of steel heat exchanger plates through which carbon dioxide is condensed to melt the PCM or evaporated to freeze the PCM depending on the mode of operation. Two models were developed, one with a tube-based thermal storage model and one without. This paper does not include a detailed description of either of these Modelica models, though it can be assumed that they resemble those described by Jokiel with the addition of liquid-vapor phase change on the working fluid side.
A similar study on supermarket refrigeration coupled with cold storage was conducted at the University of Maryland. Bush et al. proposed adding latent thermal storage to a mechanical carbon dioxide refrigerant subcooling loop for supermarket refrigeration [35]. The system PCM heat exchanger consists of a cylindrical tank with multiple nodes, representing finite volumes. At each node, the enthalpy changes with time via heat transfer between the channel wall and PCM, losses between the PCM and ambient environment outside the tank, and conduction between adjacent PCM nodes. The authors took a lumped-parameter approach in which convection and mass transfer are lumped into conductive heat transfer in the phase change material. Additionally, an average of the solid and liquid density are used in order to neglect volume change. Four phase change materials with melt temperatures between −5 and 10 C were evaluated. The model assumes a constant heat transfer coefficient of 65 W/mK, thereby avoiding the complication of time and space varying conductance. This paper validates the TES model with previous results from the literature, both of which included storage geometry and material properties that could be used as model inputs [36,37]. The simulation predicted time to freeze and working fluid outlet temperature are slightly off from experimental data from those previous papers, perhaps due to the assumption of constant values for various parameters.
Dhumane, another researcher at University of Maryland’s Center for Environmental Energy Engineering (CEE), continues to iterate on the in-house CEE Modelica library, and the latent storage component in particular. The roving comforter, RoCo, was imagined as a system that could provide localized space cooling using refrigerant as a working fluid through a PCM heat exchanger. In 2017, Dhumane et al. introduced their Modelica model for RoCo [38]. The PCM is represented as a combined conductor and capacitor which interacts with the tube and container walls. The heat transfer coefficient is determined via correlation for refrigerant in helical coils. This first paper compared preliminary experimental data and model temperature predictions. Several years later, Dhumane et al. were able to compare their Modelica model to a compact prototype of RoCo. Using the prototype performance as feedback, they have improved models of various system components and focused on using a heat pump to solidify the PCM. Dhumane et al. provided a thorough documentation of their implemention of a refrigerant PCM heat exchanger in Modelica, though their models are not publicly available [39].
Similar to the results summarized above, our new TES model captures unit cell heat transfer within the storage device in addition to the component scale time-varying temperature of the working fluid that travels through it. The remainder of this work begins with a description of experimental prototype testing followed by an overview of the first-principles numerical framework and development of the PCM heat exchanger model in Modelica. With experimental data available through the development process, we validated the Modelica model with the previous numerical and experimental findings as we built it. With this valid, open-source model, we intend to make a suite of component-level building blocks of thermal storage for incorporation into space conditioning and hot water systems for residential, commercial, and industrial applications. This paper describes the numerical implementation and validation for the first of the models in this proposed suite: a white-box PCM heat exchanger model with one inlet and one outlet port for a working fluid that can be divided into any number of parallel rectangular flow channels within the device. Though we are not the first researchers to pursue this endeavor, we hope that adding a suite of PCM heat exchanger models to the open-source Modelica Buildings Library will make thermal load shifting simulations easier for HVAC designers, facility operators, and energy researchers around the world.
3. Experiment Design
The experiment we used to validate our two models entailed measuring the performance of a 100 kJ TES device shown in Figure 1. Though this prototype was commissioned for the purposes of research, its design could be viable for commercial endeavors. One possibility is to scale this device up and couple it with a water-to-air heat exchanger for condenser pre-cooling. Other applications could integrate PCM TES with hydronic heat pumps to serve building loads. For either of these systems, energy would be used to charge the device when it is most economically and environmentally advantageous. It would subsequently be discharged to meet thermal loads on demand.

Figure 1.
Photograph and schematic (not to scale) illustrating heat flux (q″) from hot heat transfer fluid (HTF) flow passages into phase change material (PCM) storage sections during melting process.
The PCM heat exchanger we tested was fabricated and assembled by a commercial vendor (Allcomp Inc., Industry, CA, USA) and subsequently filled with phase change material. Water was used as a heat transfer fluid (HTF) to melt and solidify the PCM in repeated thermal cycles of solidification and melting. The TES device has an offset fin configuration on the working fluid side and aluminum porous fins in the storage matrix. The device has five flow channels and four hermetically sealed storage sections filled with PCM. Experimental testing of this prototype was performed at Texas A&M. The experimental apparatus and procedure are explained in greater detail in previous work [27]. Here, we’ll only summarize the major pieces.
3.1. Device Geometry
The TES prototype consists of stacked rectangular sections, alternating between flow passages and storage matrix sections. Specific details of the design are summarized in Table 1. Of particular interest is the void fraction, which greatly impacts the effective properties that form the dimensionless parameters in the governing equations.

Table 1.
Thermal Energy Storage Prototype Geometry.
3.2. Thermophysical Properties
There are four types of phase change materials that might be used in this type of application: organic paraffins, organic non-paraffins, inorganic salt hydrates, and inorganic metal eutectics [40]. Our collaborators at Texas A&M considered various materials for this prototype, including organic PCMS-like wax hydrocarbon (PureTemp 29) and poly ethylene glycol (MPEG 750), as well as inorganic PCMs like lithium nitrate, calcium chloride, and sodium sulphate salt hydrates. All displayed a similar melt temperature range (27–32 C) but differed in the latent heat, subcooling, phase segregation, nucleating agents, and additives required. The five PCMs were ranked in terms of cost, reliability, volumetric storage capacity, and ease of application. The material selected for the prototype was lithium nitrate trihydrate (LNT), a salt hydrate that has been optimized to better handle transient cycling. Anhydrous lithium nitrate salt powders were procured commercially from Beantown Chemical, NH, with purity greater than 99%. Thermophysical properties shown in Table 2 are consistent with the literature [41].

Table 2.
PCM Properties: Lithium Nitrate Trihydrate.
The melt temperature often experimentally deviates from a single value, , due to the subcooling or superheating required to initiate phase change [42]. The liquidus temperature, , was taken to be C and the solidus temperature, , was taken to be C. These values used in the numerical models are well within the range predicted by experiments, though they differ from the single value of C reported in the table. The amount of PCM inserted into the TES prototype was 474 g. The latent heat of LNT was measured in this study to be 278 kJ/kg using the T-History method [43]. The theoretical latent energy storage capacity of the device was found to be 132 kJ, which differs from the rated capacity of 100 kJ. For context, the latent heat of fusion of water is 334 kJ/kg. The cooling that this device can provide through phase change is equivalent to ∼14 ice cubes. While an ice tray might be enough to keep a beverage in a pitcher cold through a party, this device would have to be significantly scaled up to prove useful for power and refrigeration systems.
Phase change materials, including LNT, suffer from low thermal conductivity, making heat exchanger design all the more critical to facilitate good heat transfer. For the prototype, we considered several configurations, including shell and tube, metal foam matrix, chevron plate frame, rectangular channel, and plate-fin geometries. The design we ultimately selected consisted of offset fins within larger rectangular sections, alternating between fluid flow and PCM storage sections. Thermal properties were improved by using a metal mesh in the PCM, enabling effective heat conduction through the storage matrix. Many high conductivity materials, like copper and aluminum, are well suited for enhancing heat exchange. Considering all factors, the low cost and chemical compatibility of aluminum made it ideal for the metal mesh in our prototype. Its properties are shown in Table 3.

Table 3.
Metal Mesh Properties: Aluminum 5056.
Metal pathways are ideal for transporting the thermal energy away from the channel wall towards the melt front. They enhance the effective properties (conductivity, density, specific heat) of the storage matrix which are calculated according to Equation (1) and summarized in Table 4.

Table 4.
Effective Properties: Storage Matrix.
The thermophysical properties of the working fluid are also necessary in order to solve the governing equations. The experiments were conducted with pure de-ionized water. Its properties were taken at the average inlet temperatures for melting and freezing respectively. The ranges in Table 5 reflect the values associated with the cold and hot fluid inlet temperatures.

Table 5.
Working Fluid Properties: Water.
3.3. Transport Parameters
Mass flow rates for melting and freezing were provided with the experimental data. The total mass flow rate, given in Table 6, is assumed to be distributed equally among the five flow passages in the device.

Table 6.
Thermal Energy Storage Experimental Conditions.
The working fluid was controlled to achieve a relatively constant inlet temperature for the duration of each test. The properties of the working fluid were assumed to be constant throughout a given process and determined based on the average water inlet temperature.
3.4. Heat Transfer Coefficient
With the device geometry, thermophysical properties, and transport parameters specified, a convective heat transfer coefficient was determined via empirical correlation. The Colburn analogy can be used to characterize convective heat transfer for flow geometry with transport mechanisms that are difficult to analytically simplify. The flow passages consist of offset fins, giving the following Colburn-j type relation from the literature [44]:
where is the Reynolds number of the flow, s is the spacing between fins, is the height of the fins, is the thickness of the fins, and is the length of the fins.
The Colburn-j factor is used to calculate the Stanton number, , which relates the magnitude of heat transfer into a fluid to the thermal capacity of the fluid. This is subsequently used to calculate the Nusselt number, , which describes the relative magnitudes of convective and conductive heat transfer at a fluid boundary. From there, we solved for the convective heat transfer coefficient, h:
With h, the overall heat transfer coefficient, U, can be found for the first-principles model. The Modelica model does not require an explicit definition of U, though it does use the correlation for h described above.
Based on geometry, a stability analysis is performed for the PCM matrix enclosure to determine whether or not natural convection occurs. A fluid heated from the bottom is stable provided that its Rayleigh number is below a critical value. The Rayleigh number has a cubic dependence on the characteristic length. For the geometry given in Table 1, natural convection is not present. As noted in the introduction, previous work has been used to derive U [24,25]. The more elegant of these results will be used, namely that the overall heat transfer coefficient, U, can be found from the device geometry (), thermophysical properties (), convective coefficient, h, and the melt fraction, , which is a function of position in the device as well as time:
where includes the offset fin efficiency and is the height of the storage matrix sections.
A key finding from both studies of conductance was that an average U could be used in place of a spatially and temporally varying one for high performance devices. To be sure that this was also the case for the prototype experiments, we applied a quasi-steady treatment of the variation of U with and compared our results to constant conductance. As the conductance is quite high, we see no measurable difference in the fluid outlet temperature predicted. Thus, an average conductance is suitable for modelling the TES. In order to average Equation (4), we integrate over the range of encountered during the melting process.
After integrating over melt fraction and normalizing by the final value, we find that:
This gives a value for that falls between the convective heat transfer coefficient, h, and the steady state value reached at the end of melting that U asymptotes to when the PCM melt front reaches the adiabat between flow passages. The key term in the variable U expression, , can be interpreted as a proxy for the growing distance between the channel wall and the melt front. This term is the dominant thermal resistance in the problem due to the high efficiency of the working fluid side heat transfer. By extrapolating this simple model to freezing, we predicted the values given in Table 7 for conductance in the experimental prototype.

Table 7.
Averaged Overall Heat Transfer Coefficient, .
This average overall heat transfer coefficient is subsequently used to calculate , the number of transfer units required to solve the non-dimensionalized set of equations that comprise the first-principles numerical framework.
4. First-Principles Framework
Three differential equations govern the temperature and melt fraction fields within a thermal energy storage device [26]. Thermal energy is advected by the working fluid (w) and enters or leaves the storage matrix element (e) through the channel wall.
for (sensible heat transfer) and or .
for (latent heat transfer) and .
These equations are converted to a non-dimensional framework, as is typically done for effectiveness–NTU heat exchanger analysis. Due to the complex nature of phase change physics, we require several dimensionless groups to predict performance. The differential equations within the TES device are non-dimensionalized using the following definitions:
These non-dimensional equations scale the , , and variables to values between 0 and 1.
for and or .
for and .
Relevant dimensionless parameters are formed to concisely write the governing equations. Two of the non-dimensional groups are similar to those that result from compact heat exchanger analysis, with the addition of a third that accounts for latent heat transfer. The number of transfer units, , relates the heat transfer into the matrix to that advected along the flow. It is critical for design because it encapsulates the conductance, , which is inherently dependent on the device configuration. The second parameter, , is the ratio of thermal capacities between the working fluid and matrix element and thus is dependent on the materials selected. The third parameter, the Stefan number, , relates the relative importance of sensible heat transfer to latent heat transfer between the inlet and outlet. This captures the operating conditions, namely the temperature range in which the thermal energy storage is used. For the previously outlined purpose to transfer energy via latent heat transfer, the Stefan number will be quite small. These dimensionless groups are defined as:
Typical values of the dimensionless numbers for low temperature energy applications are:
These are calculated from TES device geometry, thermophysical properties, and transport parameters. For the experiment considered here, the complete set of parameters in the three governing equations were non-dimensionalized according to Equation (15) to give the values shown in Table 8.

Table 8.
Thermal Energy Storage Prototype Dimensionless Variable Values.
The three coupled differential equations each have slightly different forms. Equation (12) is an inhomogeneous first order partial differential equation, while Equations (13) and (14) are inhomogeneous first order ordinary differential equations. Many numerical methods for heat transfer problems employ symmetric approximations to derivatives because the diffusion equation is parabolic and requires spatial information on both sides of each node. In earlier iterations of analyzing the TES device, a central difference approximation was used to account for diffusion. However, in comparing the coefficients for advective and diffusive terms, we found that advection was significantly more important than diffusion. This means that energy transfer via flow through the device greatly outweighs the potential for energy transfer through axial conduction. The advection equation is hyperbolic and requires spatial information on the upstream side of each node. By employing one-sided approximations to derivatives in the differential equations, we can achieve first order accuracy in time and space. This method matches the asymmetry in the equations; Equation (12) models translation in space and all three equations march forward in time. Thus, in order to solve the differential equations numerically, we use a first order accurate finite difference approximation, employing the upwind and forward Euler discretization methods respectively. The temperature and melt fraction fields in the storage matrix are determined using these equations. This working fluid temperature, , is dictated by:
This equation is first order in time and space, necessitating a boundary and an initial condition. The working fluid exchanges heat with phase change material in the storage matrix, which undergoes both sensible and latent heat transfer depending on the temperature of each discrete node. Sensible energy storage occurs when a cell containing PCM at position and time is not at its melt temperature, . The storage matrix temperature at the next time step can be determined via:
for and or .
If Equation (18) would result in the element temperature at the next time step, , passing the PCM melt temperature, then is set to and latent heat transfer begins, with melt fraction change calculated from Equation (19):
for and .
The grid size used to solve Equations (17)–(19) for the first-principles model results presented in this paper are and .
The equations governing the storage matrix temperature and melt fraction are first order in time but have no spatial derivative. As such, only one boundary condition is required to solve these coupled first order differential equations. In , we non-dimensionalize the time varying working fluid inlet temperature, , to write the boundary condition in its dimensionless form:
for .
Initial conditions on temperatures, and , and melt fraction, , are also required for the entire domain. At the beginning of the heating process, we might expect the PCM in the device to be completely frozen at the cold system temperature, corresponding to dimensionless values of 0 for , , and . Conversely, after a complete melting process ending at the hot system temperature, the initial conditions for re-freezing the device should correspond to dimensionless values of 1. These can represent any distribution desired, as in Equation (21):
for .
Table 8 enables us to proceed with the solution of the differential Equations (17)–(19), with boundary condition given by Equation (20) and initial conditions from Equation (21) for the first-principles model. Solving the differential equations with specified initial and boundary conditions provides spatially and temporally resolved temperature and melt fraction fields.
These initial and boundary conditions can be spatially uniform and temporally steady if desired. To capture charge and discharge cycles, the initial conditions can be modified to match the end and beginning of subsequent processes and the boundary condition can be adjusted to capture time-varying conditions. The temperature and melt fraction fields should be resolved spatially and temporally until the melting or freezing process end time, , is reached. In order to determine device performance at , the following equation should be used to evaluate effectiveness, , for a PCM heat exchanger:
for the melting process.
for the freezing process.
The storage process, which may occur between melting and freezing processes, is not characterized as having an effectiveness (because no energy is added or removed from the device). For the experimental testing of the prototype, freezing immediately followed melting; no storage took place. The effectiveness for either energy transfer process has the functional relationship:
In addition, the latent energy capacity of the TES can be calculated according to:
The results of using this numerical first-principles framework to predict performance of the TES prototype will be compared to those generated by an object-oriented approach with Modelica.
5. Modelica Implementation
5.1. Preliminary Modelica Model
Before constructing complex system models, it was necessary to verify Modelica’s capability to effectively capture phase change physics in the thermal storage component. The preliminary model test setup, shown in Figure 2, was composed of a connected series of unit cells of finite volume. On one side of these, the primary pump delivered working fluid to the heat exchanger at a specified inlet temperature. The working fluid traveled through the series of PCM heat exchanger elements before reaching the outlet.
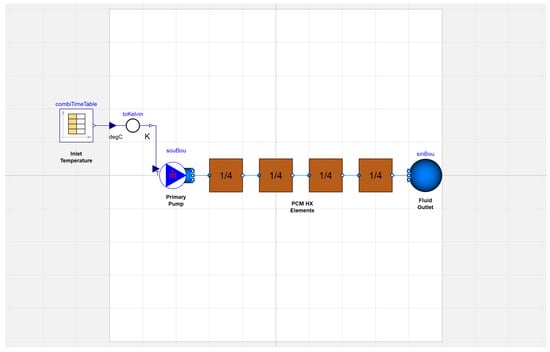
Figure 2.
Preliminary model of the thermal energy storage test rig in Modelica.
The preliminary model for a PCM heat exchanger element of the TES device is shown in Figure 3. This included two ports on either side that served as inlets and outlets for the working fluid. There were also two temperature sensors, one before and one after energy transfer. On the working fluid side, the convective heat transfer coefficient was computed by a function that determines its value based on the Reynolds number, consistent with Equation (2). The heat transfer area in the conductance term mirrored that of the experimental prototype, though it could be updated for different designs.
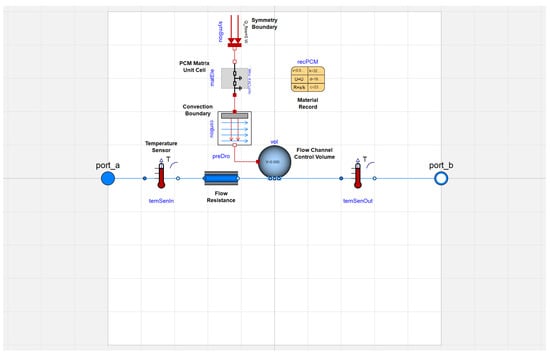
Figure 3.
Preliminary model of a single PCM heat exchanger element in Modelica.
The PCM was exposed to a convection boundary, with the flow channel control volume on one side () and a symmetry boundary at the centerline of the storage section between flow passages (). The thickness of the slab, x, between these two boundaries is defined in the PCM material record. In Modelica, we have the freedom to spatially resolve the PCM matrix unit cell via the parameter which dictates the number of states or nodes. can be automatically determined by an algorithm based on the thickness and thermal diffusivity of a material slab and the number of states, , in a defined reference material layer. The PCM matrix unit cell in the thermal energy storage model used the Modelica Buildings Library Buildings.HeatTransfer.Conduction.SingleLayer component [45]. The algorithm behind this object is the heat diffusion equation with specific internal energy, u, replacing temperature, T, as the independent variable to be determined:
Temperature is then modeled as a function of internal energy with a constitutive equation including , , , c, and . This function is represented by a cubic hermite spline interpolation with linear extrapolation. The required PCM properties were set to those of the effective properties described in the experiment design section.
5.2. Full Modelica Model
Following preliminary model validation, we developed a full Modelica model of the experimental prototype with parameters that could be easily extended to other PCM heat exchanger designs. The full TES model is composed of a series of finite volumes and uses the Modelica Buildings.Fluid.HeatExchangers.DryCoilDiscretized heat exchanger as a basis of design [29]. Our full model, similar to the preliminary model, discretizes the TES into a number of heat exchanger elements that capture the most basic heat transfer phenomena between the working fluid and PCM. There were a few simplifications in the preliminary model that we improved with three major enhancements.
5.2.1. Metal Frame Capacitance and Conductance
The prototype TES unit has five working fluid passages that sandwich four PCM matrix sections. We are able to capture this geometry by differentiating between perimeter and core elements, essentially dividing the model shown in Figure 3 into two separate classes of PCM heat exchanger elements. The core elements contain a flow channel control volume that exchanges heat with a PCM matrix unit cell on both sides, whereas the perimeter elements only exchange heat with a PCM matrix unit cell on one side. For perimeter elements, the other side of the flow channel control volume exchanges heat with the metal case unit cell, that also provides structural support for the PCM heat exchanger.
In the full model, we accounted for the additional thermal mass in the heat exchanger core due to the metal casing that contains the PCM. This mass is most significant around the perimeter of the core. On the top, bottom, and sides, there are aluminum plates that are 5 mm thick. Considering the perimeter casing around the length of the prototype device, this is 0.86 kg of metal, with a capacitance of 769 J/K. To account for this capacitance, the metal case was added to a perimeter heat exchanger element in the Modelica model as in Figure 4. The thermophysical properties of this metal case are specified in a material record. As the material is significantly more conductive than PCM, the metal case unit cell undergoes axial conduction with neighboring nodes in the PCM heat exchanger. It has an insulation boundary with ambience to prevent environmental heat losses.
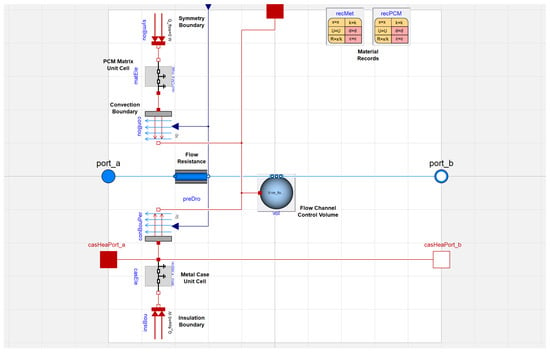
Figure 4.
Full model of a perimeter element in Modelica.
5.2.2. Flow Channel Discretization
The flow channel is divided axially into pipe segments that are specified as a parameter rather than hard-coded. The full model also accounted for manifolds to divide the flow into parallel elements with a common convection coefficient, as shown in Figure 5. There are two outer flow channels and any number of inner flow channels, which is consistent with most rectangular stack PCM heat exchanger designs. The model user can specify the number of sequential and parallel pipes as parameters.
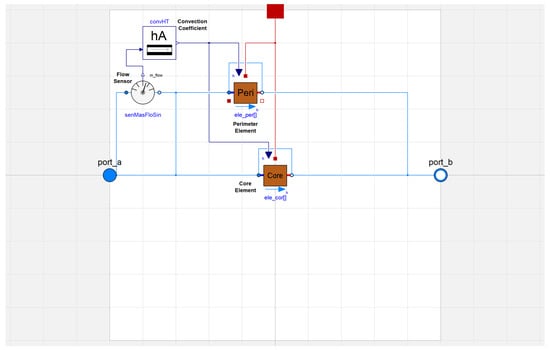
Figure 5.
Full model of the PCM heat exchanger in Modelica with core and perimeter elements.
5.2.3. Working Fluid Residence Time
We determined the residence time within the prototype to be 51 s, on average, and incorporated an existing Buildings.Fluid.Delays.DelayFirstOrder block from the Modelica Buildings Library into our full TES model [29]. Figure 6 shows this delay block to the right of the PCM heat exchanger in the updated model of the thermal energy storage system.
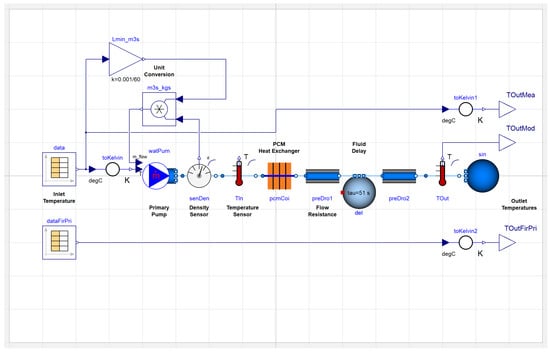
Figure 6.
Full model of the thermal energy storage test rig in Modelica.
6. Results and Discussion
Figure 6 shows a representation of the test rig in Modelica. This setup enables easier comparison to both the measured data and first-principles model prediction of outlet temperature. Figure 7 presents the comparison of experimental, first-principal numerical model, and Modelica model inlet and outlet temperature measurements. Prior to simulation of the melting process, we initialized the TES device models to 25.5 C, consistent with experiments. For the duration of the test, we used the experimental time-varying inlet temperature, shown in red, as a boundary condition for both of the models. It first increases to melt the PCM and then decreases to initiate freezing of the PCM, thereby producing a complete energy transfer cycle. The dashed blue line is the TES working fluid outlet temperature from experimental data. The solid blue line is the exit temperature variation predicted by the previously developed first-principles computational model, and the solid black line is the exit temperature predicted by the Modelica model.
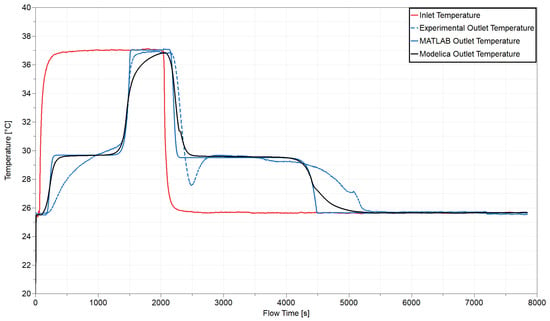
Figure 7.
Comparison of experimental data with model predictions of prototype outlet temperature.
In this experiment, melting is immediately followed by freezing, with no storage period between the two processes. Given a temperature gradient between the PCM and surrounding environment, additional energy losses would occur through the exposed sides of the heat exchanger throughout the cycle. If the device were properly insulated, as the prototype is, thermal energy could be stored for hours. A larger device, with a lower surface area to volume ratio, could likely retain much of its thermal energy for days if needed. The models assume perfect insulation from the surroundings, which is a reasonable approximation for this device. Future model iterations could explore this further.
There are some discrepancies to note between the experimental data and first-principles and Modelica model predictions. Some of this has to do with additional dynamics that neither of the models account for. The highest discrepancy is observed during freezing. There, the models are not designed to capture the poor nucleation rates that necessitate subcooling before the phase change material can start freezing. The dip in the dashed blue line at ∼2500 s reflects this phenomenon. We’ve discussed this for the first-principles model in previous work [27].
Aside from subcooling, the greatest disagreement appears between the curves below the melt temperature for both melting and freezing. We note that both model slopes differ from experiments while the PCM is solid for both processes, but that slopes match well while the PCM is liquid for both processes. This inconsistency could be attributed to a difference in thermophysical properties (, , ) which impact both conductance (heat transfer) and capacitance (energy storage). The models currently use constant average values for each of these thermophysical properties and do not account for the variation between liquid and solid PCM. That said, the difference in thermophysical properties between the two PCM states is fairly minimal. Instead, we believe that there is most likely a major contact resistance between the flow channel and PCM when the salt hydrate is dehydrated.
Noting our inability to capture subcooling and contact resistance, we can see a limitation of our modeling approaches. By creating white box (physics-based) models based on first principles equations, we neglect secondary dynamics that have a measurable impact on heat transfer. To address this, we could instead create grey box (mixed) or black box (data-based) models of thermal energy storage. Such a technique would likely involve nonlinear (least squares) regression to determine a set of coefficients that fit the experimental data. While there is utility in this method, data-based models are often bounded by their inability to make accurate predictions outside of the training data set.
Beyond temperature predictions, we can also explore other comparative metrics, including the amount of energy accumulation in the TES prototype for the melting and freezing cycle. In order to determine this, we performed a water-side integration of the transient heat transfer rate and collected results in Table 9. For the calculation, we used constant thermophysical properties (,) associated with the fluid inlet temperature for each process. Previously, we estimated that the latent energy storage capacity of the TES prototype was 132 kJ. The higher storage capacities in the table below reflect additional sensible energy storage.

Table 9.
Water-Side Energy Balance of Full Cycle.
To understand the meaning of the values in this table, we need to understand the signs associated with the energy difference, . A negative sign indicates that more energy was removed by the working fluid than put into the TES. We see that for the experimental data, this was the case. We suspect that there was more energy initially in the thermal storage than estimated, as the initial conditions of the prototype were not included in this simple calculation. A positive sign for indicates that more energy was put into the TES than was removed by the working fluid. For the first-principles model, this means that some energy accumulated in the battery over the duration of the cycle. This makes sense, given that we specify a heat transfer effectiveness of 95%. We cannot fully remove all of the energy stored in the battery. In a perfect melt and freeze cycle with identical initial and final conditions, the water-side energy balance would show 0 kJ, indicating that all energy input into the storage was removed. Our Modelica model nearly predicts a perfect energy balance and we believe that the energy difference shown is due to simplifications made to perform this water-side calculation. This indicates that all energy input into the Modelica model is extracted at the end of the cycle.
Another metric that we can use to determine whether or not the models effectively capture the physics is the process end time (e.g., heating time, cooling time), which includes both sensible and latent energy transfer. For the experimental run shown here, the completion times summarized in Table 10 were observed. The times indicate when the outlet temperature reaches the inlet temperature for both the heating and cooling processes. These can serve as proxies for rate of charge and discharge.

Table 10.
Times to Complete Heating and Cooling Processes.
The process completion times are close, with the model prediction error ranging from 3–25%. For the melting process, we see 3.9% error in the first-principles prediction, while we see 24.7% error in the Modelica prediction. For the freezing process, we see 16.4% error in the first-principles prediction and 3.9% error in the Modelica prediction. While these are promising, they indicate further work to be done to better characterize the conductance which dictates process completion times. In particular, we recommend further research to determine the potential impact of contact resistance for solid salt hydrate phase change materials. We expect that cavities form as the phase change material solidifies and shrinks, reducing conductance in the device below the transition temperature.
It will be challenging to represent exact heat transfer physics with the models without a careful inclusion of additional dynamics. However, in the models presented here, the average absolute difference between experimental measurement and numerical prediction of outlet fluid temperature is one to two degrees celsius. In addition to the energy comparison and process completion time metrics, this small temperature difference lends significant support to the accuracy of the first-principles and Modelica predictions and meets our intended goal of developing and validating models that designers can use for the simulation and analysis of thermal storage systems.
7. Conclusions
In previous works, we established a dimensionless first-principles framework to model transient heat transfer in a TES device [26]. We also presented a summary of experimental tests of a TES prototype using lithium nitrate trihydrate phase change material as a storage medium [27]. The experimental design and numerical framework were summarized in this paper, to be used as benchmarks to validate the performance of a new TES model in Modelica. Modelica is an object-oriented language that gives us the freedom to develop models, simulate performance, test controls, iterate on system designs, and make all of this available as part of larger component libraries.
Our new TES model captures unit cell heat transfer within the storage device in addition to component scale time-varying temperature of the working fluid that travels through it. We validated its performance with our previous experimental data and first-principles predictions. Using energy accumulation, heat transfer rates, and outlet temperature differences as metrics, we found that the model meets our expectations. There are a few sources of discrepancies that could be explored in future work to improve this model further. In particular, we note that subcooling and solid-phase PCM contact resistances appear to be the primary physics driving differences between measured data and model predictions. Those secondary dynamics should be considered when evaluating whether a model is good enough to represent phase change thermal storage for the application at hand. For our purposes of modeling innovative HVAC systems with load shifting capabilities, we believe it is.
We are in the process of creating a free and open-source thermal storage suite in Modelica that contains this PCM heat exchanger model and others. We intend to make the models available to other researchers by including them in the Modelica Buildings Library package. With this contribution, we aim to make load shifting with active thermal storage easier to simulate and ultimately incorporate into building heating and cooling systems.
Author Contributions
Conceptualization, D.H. and V.P.C.; methodology, D.H. and D.H.B.; software, S.M.D.; validation, D.H. and D.H.B.; formal analysis, D.H.; investigation, D.H.; resources, D.H.B.; data curation, D.H.; writing—original draft preparation, D.H.; writing—review and editing, D.H.B. and S.M.D.; visualization, D.H.; supervision, V.P.C. and S.M.D.; project administration, V.P.C. and S.M.D.; funding acquisition, V.P.C. and S.M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Advanced Research In Dry Cooling (ARID) program of the Advanced Research Projects Agency-Energy (ARPA-E) grant number DE-AR-0000577 and the U.S. Department of Energy (DOE) grant number DE-LC-000L048.
Acknowledgments
We would like to acknowledge Jianping (Gene) Tu of Allcomp Inc. for the design and fabrication of the 100 kJ TES device used in this study to validate the first-principles and Modelica models.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| Cross-sectional area of the working fluid flow passage | |
| Effective specific heat of the storage matrix | |
| Specific heat of the working fluid | |
| Latent heat of fusion of the PCM in the storage matrix | |
| Effective thermal conductivity of the storage matrix | |
| Thermal conductivity of the working fluid | |
| L | Length of the TES device |
| Working fluid mass flow rate per passage | |
| Wetted perimeter of the working fluid flow passage | |
| Temperature of a discrete element in the storage matrix | |
| Liquidus temperature of the PCM in the storage matrix | |
| Melt temperature of the PCM in the storage matrix | |
| Maximum temperature encountered in the TES device | |
| Minimum temperature encountered in the TES device | |
| Solidus temperature of the PCM in the storage matrix | |
| Temperature of a discrete parcel of working fluid | |
| U | Overall heat transfer coefficient |
| Melt fraction of a discrete element in the storage matrix | |
| Non-dimensional temporal discretization | |
| Non-dimensional spatial discretization | |
| Fraction of the storage matrix occupied by PCM | |
| Dimensionless temperature of a discrete element in the storage matrix | |
| Storage matrix volume per unit length of the device | |
| Effective density of the storage matrix | |
| Density of the working fluid | |
| Dimensionless temperature of a discrete parcel of working fluid |
References
- Smith, R.; Ebersole, T.; Griffin, F. Heat Exchanger Performance in Latent Heat Thermal Energy Storage. J. Sol. Energy Eng. 1980, 102, 112–118. [Google Scholar] [CrossRef]
- Fath, H.E. Heat Exchanger Performance for Latent Heat Thermal Energy Storage System. Energy Convers. Manag. 1991, 31, 149–155. [Google Scholar] [CrossRef]
- Bellecci, C.; Conti, M. Transient Behaviour Analysis of a Latent Heat Thermal Storage Module. Int. J. Heat Mass Transf. 1993, 36, 3851–3857. [Google Scholar] [CrossRef]
- Ihm, P.; Krarti, M.; Henze, G.P. Development of a thermal energy storage model for EnergyPlus. Energy Build. 2004, 36, 807–814. [Google Scholar] [CrossRef]
- Oró, E.; Gil, A.; Miró, L.; Peiró, G.; Álvarez, S.; Cabeza, L.F. Thermal energy storage implementation using phase change materials for solar cooling and refrigeration applications. Energy Procedia 2012, 30, 947–956. [Google Scholar] [CrossRef]
- Moreno, P.; Castell, A.; Solé, C.; Zsembinszki, G.; Cabeza, L.F. PCM thermal energy storage tanks in heat pump system for space cooling. Energy Build. 2014, 82, 399–405. [Google Scholar] [CrossRef]
- Pakzad, K.; Ajarostaghi, S.S.M.; Sedighi, K. Numerical simulation of solidification process in an ice-on-coil ice storage system with serpentine tubes. SN Appl. Sci. 2019, 1, 1258. [Google Scholar] [CrossRef]
- Sun, X.; Mo, Y.; Li, J.; Chu, Y.; Liu, L.; Liao, S. Study on the energy charging process of a plate-type latent heat thermal energy storage unit and optimization using Taguchi method. Appl. Therm. Eng. 2020, 164, 114528. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, Y.; Zhu, Y.; Hu, X. A General Model for Analyzing the Thermal Performance of the Heat Charging and Discharging Processes of Latent Heat Thermal Energy Storage Systems. J. Sol. Energy Eng. 2001, 123, 232–236. [Google Scholar] [CrossRef]
- Elbahjaoui, R.; El Qarnia, H. Numerical study of a shell-and-tube latent thermal energy storage unit heated by laminar pulsed fluid flow. Heat Transf. Eng. 2017, 38, 1466–1480. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Poncet, S.; Sedighi, K.; Aghajani Delavar, M. Numerical modeling of the melting process in a shell and coil tube ice storage system for air-conditioning application. Appl. Sci. 2019, 9, 2726. [Google Scholar] [CrossRef]
- Saitoh, T.; Hirose, K. High-performance phase-change thermal energy storage using spherical capsules. Chem. Eng. Commun. 1986, 41, 39–58. [Google Scholar] [CrossRef]
- Drees, K.H.; Braun, J.E. Modeling of area-constrained ice storage tanks. HVAC&R Res. 1995, 1, 143–158. [Google Scholar]
- Cheralathan, M.; Velraj, R.; Renganarayanan, S. Heat transfer and parametric studies of an encapsulated phase change material based cool thermal energy storage system. J. Zhejiang Univ. Sci. A 2006, 7, 1886–1895. [Google Scholar] [CrossRef]
- Bony, J.; Citherlet, S. Numerical Model and Experimental Validation of Heat Storage with Phase Change Materials. Energy Build. 2007, 39, 1065–1072. [Google Scholar] [CrossRef]
- Fan, J.; Furbo, S.; Andersen, E.; Chen, Z.; Perers, B.; Dannemand, M. Thermal behavior of a heat exchanger module for seasonal heat storage. Energy Procedia 2012, 30, 244–254. [Google Scholar] [CrossRef]
- Hosseini, M.; Rahimi, M.; Bahrampoury, R. Thermal analysis of PCM containing heat exchanger enhanced with normal annular fines. Mech. Sci. 2015, 6, 221. [Google Scholar] [CrossRef]
- Wu, J.; Tremeac, B.; Terrier, M.F.; Charni, M.; Gagnière, E.; Couenne, F.; Hamroun, B.; Jallut, C. Experimental investigation of the dynamic behavior of a large-scale refrigeration–PCM energy storage system. Validation of a complete model. Energy 2016, 116, 32–42. [Google Scholar] [CrossRef]
- Ghani, F.; Waser, R.; O’Donovan, T.; Schuetz, P.; Zaglio, M.; Wortischek, J. Non-linear system identification of a latent heat thermal energy storage system. Appl. Therm. Eng. 2018, 134, 585–593. [Google Scholar] [CrossRef]
- Waser, R.; Ghani, F.; Maranda, S.; O’Donovan, T.; Schuetz, P.; Zaglio, M.; Worlitschek, J. Fast and experimentally validated model of a latent thermal energy storage device for system level simulations. Appl. Energy 2018, 231, 116–126. [Google Scholar] [CrossRef]
- Mattsson, S.E.; Elmqvist, H. Modelica-An international effort to design the next generation modeling language. IFAC Proc. Vol. 1997, 30, 151–155. [Google Scholar] [CrossRef]
- Wetter, M.; Zuo, W.; Nouidui, T.S.; Pang, X. Modelica buildings library. J. Build. Perform. Simul. 2014, 7, 253–270. [Google Scholar] [CrossRef]
- Helmns, A.; Carey, V.P. Modeling of heat transfer and energy efficiency performance of transient cold storage in phase change thermal storage components. In Proceedings of the ASME 2016 Heat Transfer Summer Conference, Washington, DC, USA, 10–14 July 2016; p. V001T05A009. [Google Scholar]
- Helmns, A.; Carey, V.P. Modeling of intramatrix heat transfer in thermal energy storage for asynchronous cooling. In Proceedings of the ASME 2017 Heat Transfer Summer Conference, Bellevue, WA, USA, 9–12 July 2017; p. V001T09A006. [Google Scholar]
- Theroff, Z.M.; Helmns, D.; Carey, V.P. Exploration of Variable Conductance Effects During Input and Extraction of Heat from Phase Change Thermal Storage. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar]
- Helmns, A.; Carey, V.P. Multiscale Transient Modeling of Latent Energy Storage for Asynchronous Cooling. J. Therm. Sci. Eng. Appl. 2018, 10, 051004. [Google Scholar] [CrossRef]
- Helmns, D.; Carey, V.P.; Kumar, N.; Banerjee, D.; Muley, A.; Stoia, M. Comparison of Model Predictions and Performance Test Data for a Prototype Thermal Energy Storage Module. In Proceedings of the ASME 2019 Heat Transfer Summer Conference collocated with the ASME 2019 13th International Conference on Energy Sustainability, Bellevue, WA, USA, 14–17 July 2019. [Google Scholar]
- De Coninck, R.; Baetens, R.; Verbruggen, B.; Saelens, D.; Driesen, J.; Helsen, L. Modelling and simulation of a grid connected photovoltaic heat pump system with thermal energy storage using Modelica. In Proceedings of the 8th International Conference on System Simulation, Liege, Belgium, 13–15 December 2010; p. 21. [Google Scholar]
- Wetter, M. Modelica Library for Building Heating, Ventilation and Air-Conditioning Systems; Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2009.
- Leonhardt, C.; Müller, D. Modelling of Residential Heating Systems using a Phase Change Material Storage System. In Proceedings of the 7th International Modelica Conference, Como, Italy, 20–22 September 2009; Number 043. pp. 507–512. [Google Scholar]
- Elmqvist, H.; Dynasim, A.; Tummescheit, H.M. Tiller: Modelica Thermal Library. Modelica Workshop 2000 Proceedings. In Proceedings of the Modelica Workshop, Lund, Sweden, 23–24 October 2000; pp. 137–144. [Google Scholar]
- Leonhardt, C.; Müller, D. Latent Heat Storage Devices for Heat Pump and Solar Heating Systems; ON Energy Research Center Series; E. ON ERC: Cambridge, UK, 2011; Volume 3. [Google Scholar]
- Jokiel, M. Development and Performance Analysis of an Object Oriented Model for Phase Change Material Thermal Storage; SINTEF Energy Research: Trondheim, Norway, 2016. [Google Scholar]
- Selvnes, H.; Hafner, A.; Kauko, H. Cold thermal storage integration in a large industrial refrigeration system. In Proceedings of the 13th IIR Gustav Lorentzen Conference, Valencia, Spain, 18–20 June 2018. [Google Scholar]
- Bush, J.; Aute, V.; Radermacher, R. Thermal storage subcooling for CO2 booster refrigeration systems. Sci. Technol. Built Environ. 2019, 25, 570–587. [Google Scholar] [CrossRef]
- Tay, N.; Belusko, M.; Bruno, F. Experimental investigation of tubes in a phase change thermal energy storage system. Appl. Energy 2012, 90, 288–297. [Google Scholar] [CrossRef]
- López-Navarro, A.; Biosca-Taronger, J.; Corberán, J.; Peñalosa, C.; Lázaro, A.; Dolado, P.; Payá, J. Performance characterization of a PCM storage tank. Appl. Energy 2014, 119, 151–162. [Google Scholar] [CrossRef]
- Dhumane, R.; Ling, J.; Aute, V.; Radermacher, R. Modeling of a thermosiphon to recharge phase change material based thermal battery for a portable air conditioning device. In Proceedings of the 12th International Modelica Conference, Prague, Czech Republic, 15–17 May 2017; Number 132. pp. 459–465. [Google Scholar]
- Dhumane, R.; Ling, J.; Aute, V.; Radermacher, R. Modeling Heat Pump Recharge of a Personal Conditioning System with Latent Heat Storage. In Proceedings of the 13th International Modelica Conference, Regensburg, Germany, 4–6 March 2019. Number 157. [Google Scholar]
- Kumar, N.; Banerjee, D. Phase Change Materials. In Handbook of Thermal Science and Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 2213–2275. [Google Scholar]
- Shamberger, P.J.; Reid, T. Thermophysical Properties of Lithium Nitrate Trihydrate from (253 to 353) K. J. Chem. Eng. Data 2012, 57, 1404–1411. [Google Scholar] [CrossRef]
- Mandilaras, I.; Kontogeorgos, D.; Founti, M. A hybrid methodology for the determination of the effective heat capacity of PCM enhanced building components. Renew. Energy 2015, 76, 790–804. [Google Scholar] [CrossRef]
- Kumar, N.; Banerjee, D. Characterization Phase Change Materials (PCM) Using T-History Method. In Proceedings of the ASME 2016 Heat Transfer Summer Conference Collocated with the ASME 2016 Fluids Engineering Division Summer Meeting and the ASME 2016 14th International Conference on Nanochannels, Microchannels, and Minichannels, Washington, DC, USA, 10–14 July 2016. [Google Scholar]
- Manglik, R.M.; Bergles, A.E. Heat transfer and pressure drop correlations for the rectangular offset strip fin compact heat exchanger. Exp. Therm. Fluid Sci. 1995, 10, 171–180. [Google Scholar] [CrossRef]
- Wetter, M.; Zuo, W.; Nouidui, T.S. Recent Developments of the Modelica “Buildings” Library for Building Energy and Control Systems; Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2011.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).