Techno-Economic Feasibility Analysis of Grid-Connected Microgrid Design by Using a Modified Multi-Strategy Fusion Artificial Bee Colony Algorithm
Abstract
1. Introduction
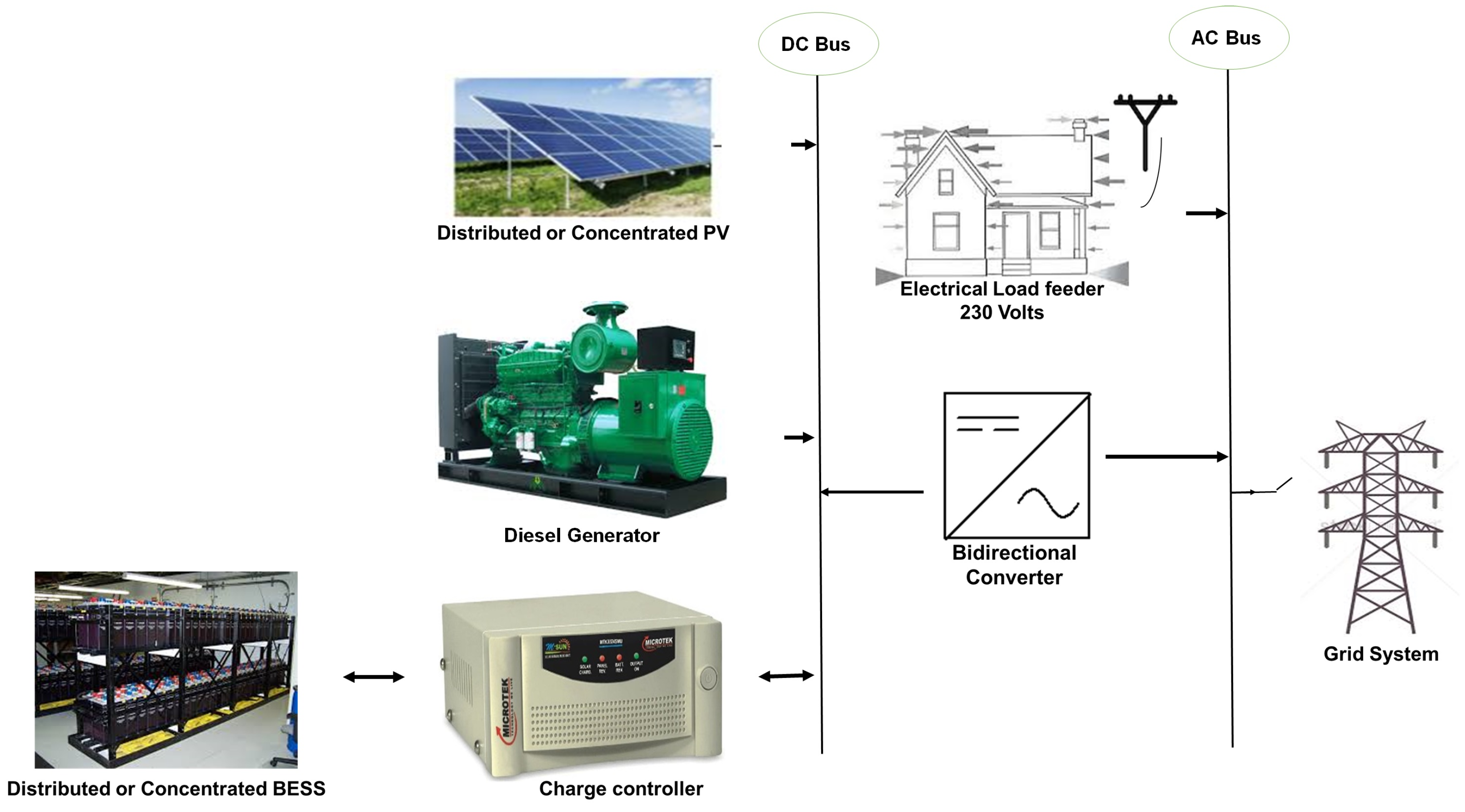
- Hybrid system design is proposed for rural electrification in a rural village that comprises of SPV system with limited grid power supply and BESS.
- The modified multi-strategy fusion artificial bee colony (MFABC+) algorithm is proposed and its feasibility and superiority demonstrated in comparison to MFABC and other optimization method.
- The optimal capacity of the system components is determined using the proposed MFABC+ algorithm.
- An integrated renewable energy-based microgrid system is proposed for lowest possible LCOE.
2. Study Area
2.1. Load Estimation
2.2. Estimation of Resources
3. Mathematical Modeling
3.1. SPV Panel
3.2. Power Converter
3.3. Battery Bank
3.4. Diesel Generator (DG)
4. Problem Formulation
4.1. Operational Strategy
4.2. Objective Function
4.3. Constraints
4.3.1. Economic Criteria
4.3.2. Power Balance Criteria
4.3.3. Power Output Limit
4.3.4. Battery Constraints
4.4. Optimization Methodology
| Algorithm 1 Pseudo-code of proposed MFABC+ method |
 |
5. Results and Discussion
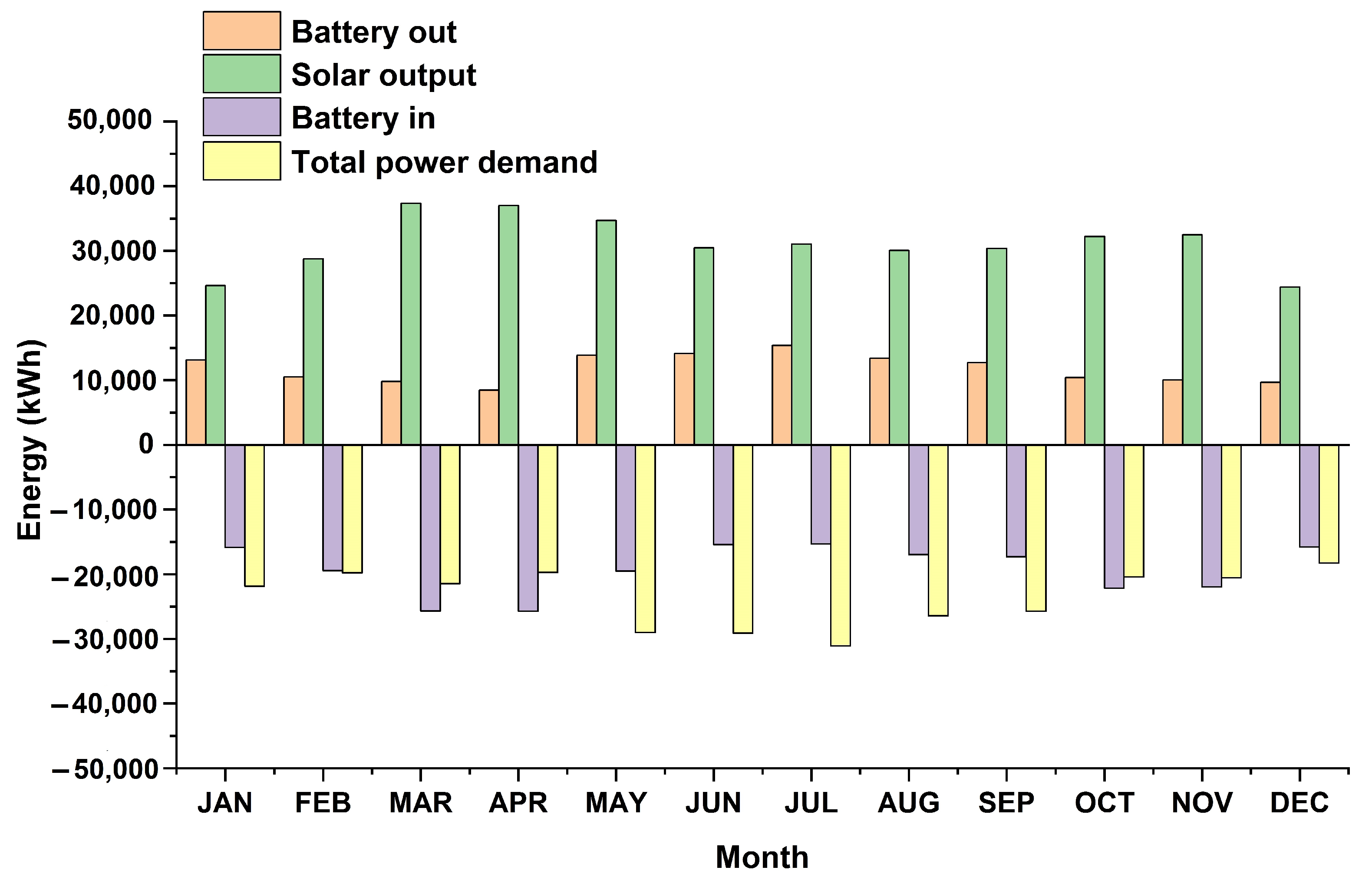
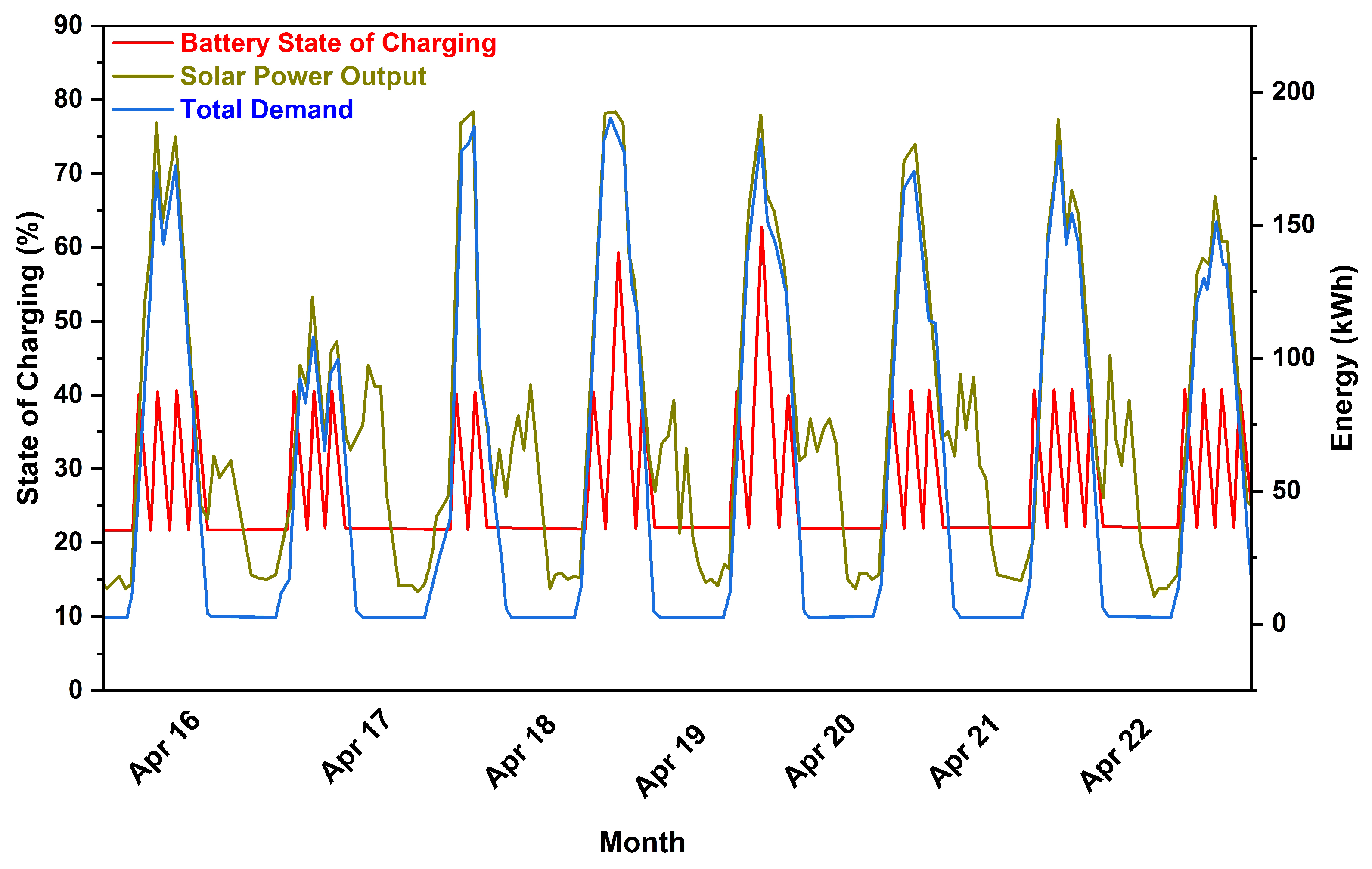
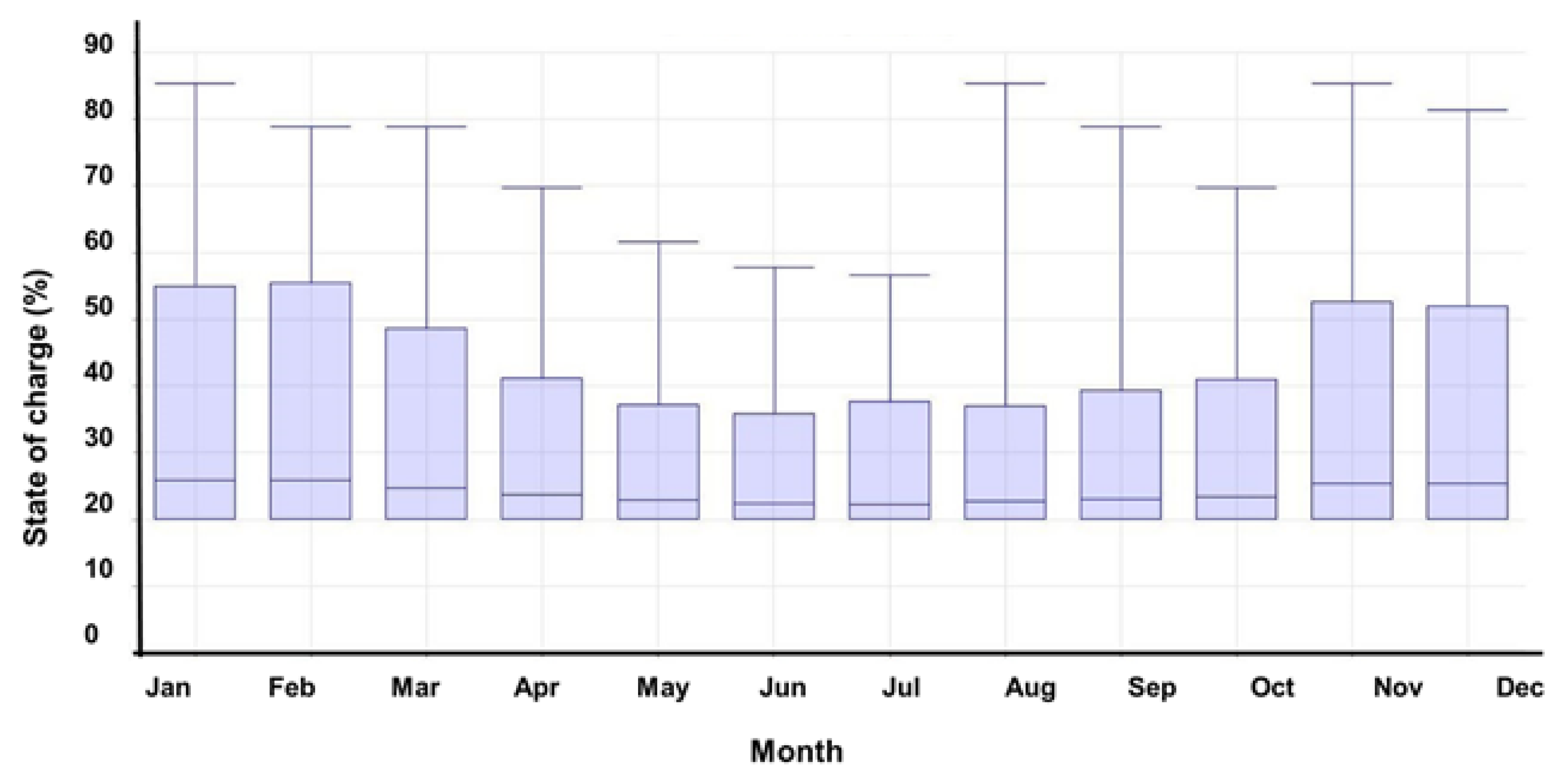
5.1. Analysis of Results
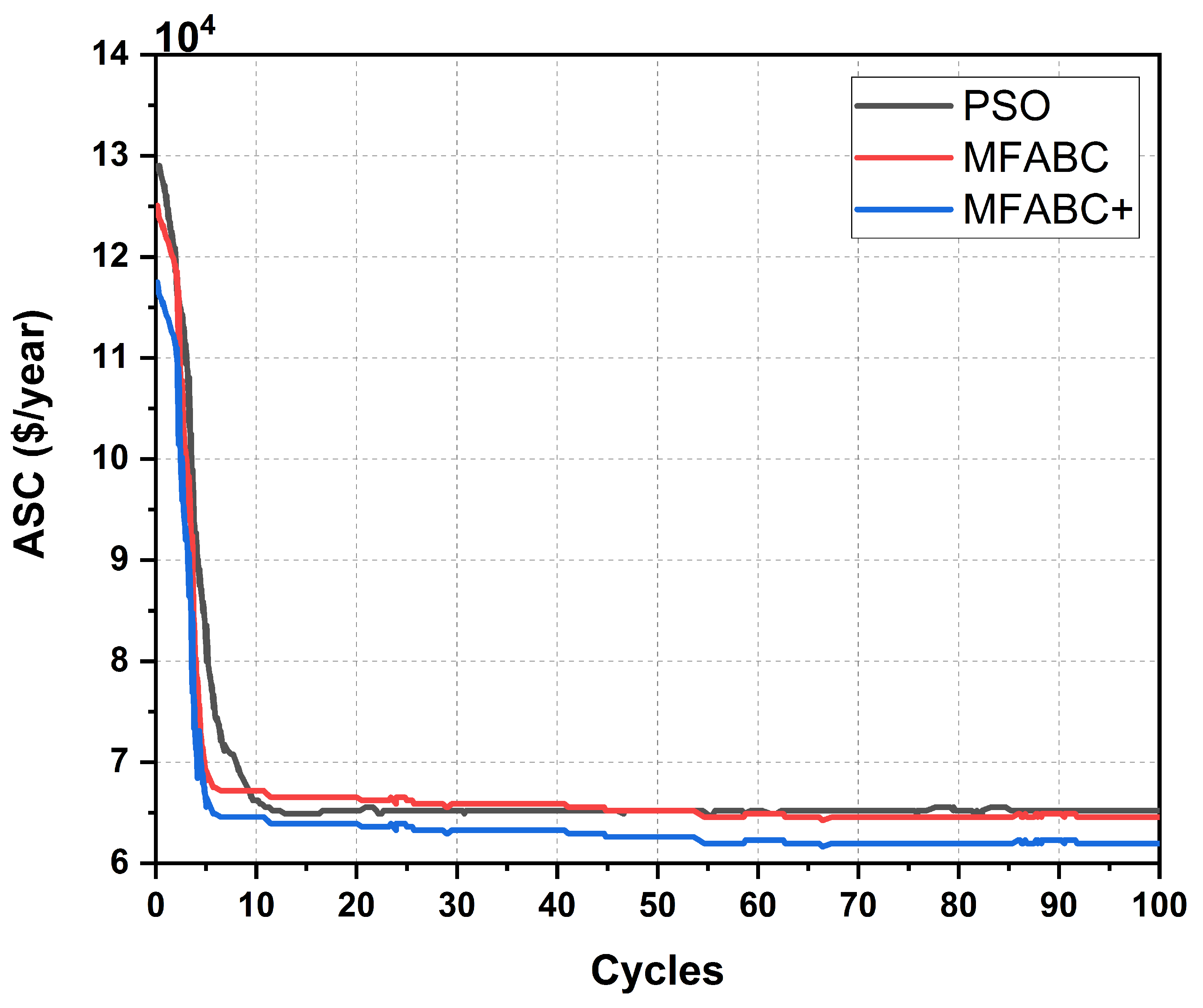
5.2. Effectiveness of MFABC+ Algorithm
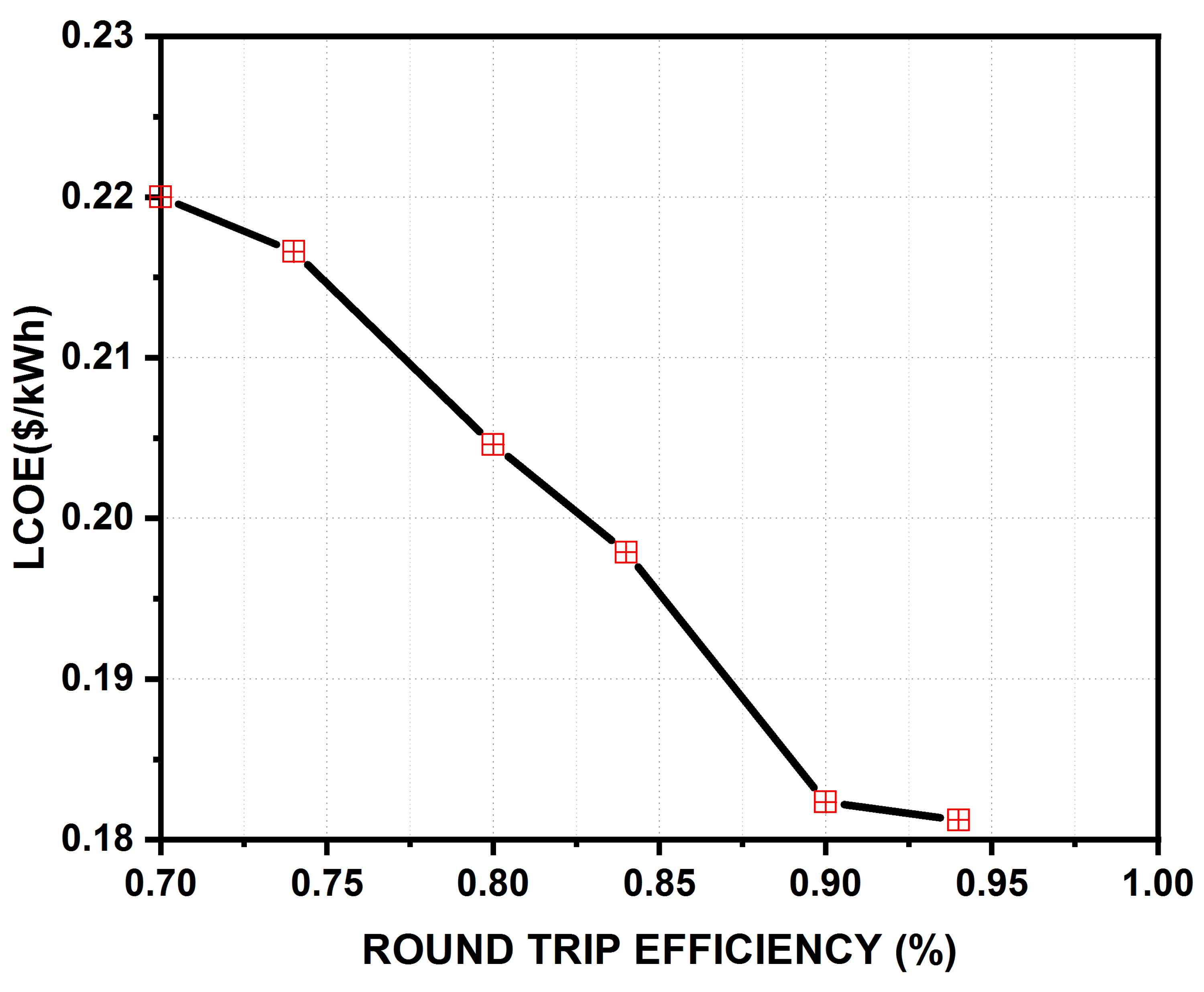
5.3. Battery’s Efficiency and LCOE
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Capital and installment cost ($/yr) | |
| Replacement cost ($/yr) | |
| Cost of battery (per unit) ($/yr) | |
| The capacity of a single battery (kW) | |
| Cost of solar PV panel ($) | |
| Capital and installation cost of solar PV panel ($/yr) | |
| The replacement cost of solar PV panel ($/yr) | |
| The operational cost of solar PV panel ($/yr) | |
| The annual maintenance cost of the solar PV panel ($/yr) | |
| Salvage cost of solar PV panel ($/yr) | |
| The capacity of a single battery (kW) | |
| Salvage cost of the battery (per unit) ($/yr) | |
| Capital and installation cost of battery (per unit) ($/yr) | |
| the replacement cost of the battery (per unit) ($/yr) | |
| The operational cost of the battery (per unit) ($/yr) | |
| The annual maintenance cost of the battery (per unit) ($/yr) | |
| Cost of converter ($/yr) | |
| Capital and installation cost of converter ($/yr) | |
| The replacement cost of the converter ($/yr) | |
| The operational cost of the converter ($/yr) | |
| The annual maintenance cost of the converter ($/yr) | |
| Salvage cost of converter ($/yr) | |
| Salvage cost ($) | |
| D | Number of dimensions to be optimized |
| Energy generated by the integrated renewable energy system in t-th hour (kWh) | |
| Diesel fuel coefficient | |
| Number of food sources | |
| Derating factor | |
| Solar radiation (w/m) | |
| Solar radiations incident hourly onto the solar panel (w/m) | |
| Standard incident radiation (w/m) | |
| Standard radiation for environment (w/m) | |
| Maximum battery charging current (A) | |
| Maximum number of function evaluations | |
| Population size | |
| Number of batteries | |
| Batteries connected in series | |
| Solar photovoltaic system concerning total no of solution | |
| Maximum number of batteries | |
| Maximum number of solar PV panels | |
| Battery input/output power | |
| Minimum generated battery capacity range (kW) | |
| Maximum generated battery capacity range (kW) | |
| Power conversion function associated with the SPV system | |
| Size of the converter | |
| Diesel fuel is consumed by diesel generator | |
| Excess or dump energy | |
| Power output from grid | |
| Energy not supplied | |
| Peak power demand with respect to the time (kW) | |
| Total power produced by SPV system (kW) | |
| Conversion function associated with the SPV | |
| SPV panel rating (kW) | |
| Peak load (kW) | |
| Rated capacity of the DG (kW) | |
| Output power from DG (kW) | |
| Power output from solar PV (kW) | |
| Probability function | |
| Cut in radiation point (w/m) | |
| Minimum value associated with the state of charge of the battery system | |
| Maximum value associated with the state of charge of the battery system | |
| The SOC of the battery at any given tth hour. | |
| Bus voltage (V) | |
| Voltage associated with a single battery (V) | |
| Round trip efficiency associated with a single battery | |
| Charging efficiency of the battery | |
| Discharging efficiency | |
| Inverter efficiency | |
| Fuel curve intercept coefficient (L/h/) | |
| Diesel curve intercept coefficient (L/h/) | |
| Annual discount rate ($) | |
| Life of the plant (year) |
References
- Mamaghani, A.H.; Escandon, S.A.A.; Najafi, B.; Shirazi, A.; Rinaldi, F. Techno-economic feasibility of photovoltaic, wind, diesel and hybrid electrification systems for off-grid rural electrification in Colombia. Renew. Energy 2016, 97, 293–305. [Google Scholar] [CrossRef]
- Entering, A.; Gas, A.G.A.O. World Energy Outlook; International Energy Agency: Paris, France, 2011. [Google Scholar]
- Bhatt, A.; Sharma, M.P.; Saini, R.P. Feasibility and sensitivity analysis of an off-grid micro hydro-photovoltaic-biomass and biogas-diesel-battery hybrid energy system for a remote area in Uttarakhand state, India. Renew. Sustain. Energy Rev. 2016, 61, 53–69. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Discrete harmony search based size optimization of integrated renewable energy system for remote rural areas of Uttarakhand state in India. Renew. Energy 2016, 94, 587–604. [Google Scholar] [CrossRef]
- Castellanos, J.G.; Walker, M.; Poggio, D.; Pourkashanian, M.; Nimmo, W. Modelling an off-grid integrated renewable energy system for rural electrification in India using photovoltaics and anaerobic digestion. Renew. Energy 2015, 74, 390–398. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S. Flexible hybrid renewable energy system design for a typical remote village located in tropical climate. J. Clean. Prod. 2018, 177, 908–924. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Olatomiwa, L.; Hazelton, J. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia. Energy Convers. Manag. 2017, 144, 322–339. [Google Scholar] [CrossRef]
- Shezan, S.A.; Julai, S.; Kibria, M.A.; Ullah, K.R.; Saidur, R.; Chong, W.T.; Akikur, R.K. Performance analysis of an off-grid wind-PV (photovoltaic)-diesel-battery hybrid energy system feasible for remote areas. J. Clean. Prod. 2016, 125, 121–132. [Google Scholar] [CrossRef]
- Rajanna, S.; Saini, R.P. Modeling of integrated renewable energy system for electrification of a remote area in India. Renew. Energy 2016, 90, 175–187. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Mandelli, S.; Merlo, M.; Colombo, E. Novel procedure to formulate load profiles for off-grid rural areas. Energy Sustain. Dev. 2016, 31, 130–142. [Google Scholar] [CrossRef]
- Ramchandran, N.; Pai, R.; Parihar, A.K.S. Feasibility assessment of Anchor-Business-Community model for off-grid rural electrification in India. Renew. Energy 2016, 97, 197–209. [Google Scholar] [CrossRef]
- Li, B.; Roche, R.; Miraoui, A. Microgrid sizing with combined evolutionary algorithm and MILP unit commitment. Appl. Energy 2017, 188, 547–562. [Google Scholar] [CrossRef]
- Singh, S.; Singh, M.; Kaushik, S.C. Feasibility study of an islanded microgrid in rural area consisting of PV, wind, biomass and battery energy storage system. Energy Convers. Manag. 2016, 128, 178–190. [Google Scholar] [CrossRef]
- Kim, H.; Jung, T.Y. Independent solar photovoltaic with Energy Storage Systems (ESS) for rural electrification in Myanmar. Renew. Sustain. Energy Rev. 2018, 82, 1187–1194. [Google Scholar] [CrossRef]
- Mazzola, S.; Astolfi, M.; Macchi, E. The potential role of solid biomass for rural electrification: A techno economic analysis for a hybrid microgrid in India. Appl. Energy 2016, 169, 370–383. [Google Scholar] [CrossRef]
- Upadhyay, S.; Sharma, M.P. Selection of a suitable energy management strategy for a hybrid energy system in a remote rural area of India. Energy 2016, 94, 352–366. [Google Scholar] [CrossRef]
- Maleki, A.; Pourfayaz, F.; Rosen, M.A. A novel framework for optimal design of hybrid renewable energy-based autonomous energy systems: A case study for Namin, Iran. Energy 2016, 98, 168–180. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.S.O.; Ayodele, T.R.; Akinola, O.A. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Appl. Energy 2016, 171, 153–171. [Google Scholar] [CrossRef]
- Ramli, M.A.; Hiendro, A.; Twaha, S. Economic analysis of PV/diesel hybrid system with flywheel energy storage. Renew. Energy 2015, 78, 398–405. [Google Scholar] [CrossRef]
- Kolhe, M.L.; Ranaweera, K.I.U.; Gunawardana, A.S. Techno-economic sizing of off-grid hybrid renewable energy system for rural electrification in Sri Lanka. Sustain. Energy Technol. Assess. 2015, 11, 53–64. [Google Scholar] [CrossRef]
- Singh, S.S.; Fernandez, E. Modeling, size optimization and sensitivity analysis of a remote hybrid renewable energy system. Energy 2018, 143, 719–731. [Google Scholar] [CrossRef]
- Bordin, C.; Anuta, H.O.; Crossland, A.; Gutierrez, I.L.; Dent, C.J.; Vigo, D. A linear programming approach for battery degradation analysis and optimization in offgrid power systems with solar energy integration. Renew. Energy 2017, 101, 417–430. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; Xu, Z.; Lai, L.L.; Li, X.; Cao, J.; McCulloch, M.D. Levelized cost of electricity for photovoltaic/biogas power plant hybrid system with electrical energy storage degradation costs. Energy Convers. Manag. 2017, 153, 34–47. [Google Scholar] [CrossRef]
- Rajbongshi, R.; Borgohain, D.; Mahapatra, S. Optimization of PV-biomass-diesel and grid base hybrid energy systems for rural electrification by using HOMER. Energy 2017, 126, 461–474. [Google Scholar] [CrossRef]
- Ahmadi, S.; Abdi, S. Application of the Hybrid Big Bang–Big Crunch algorithm for optimal sizing of a stand-alone hybrid PV/wind/battery system. Sol. Energy 2016, 134, 366–374. [Google Scholar] [CrossRef]
- Ahmad, J.; Imran, M.; Khalid, A.; Iqbal, W.; Ashraf, S.R.; Adnan, M.; Khokhar, K.S. Techno economic analysis of a wind-photovoltaic-biomass hybrid renewable energy system for rural electrification: A case study of Kallar. Energy 2018, 148, 208–234. [Google Scholar] [CrossRef]
- Sandwell, P.; Chan, N.L.A.; Foster, S.; Nagpal, D.; Emmott, C.J.; Candelise, C.; Nelson, J. Off-grid solar photovoltaic systems for rural electrification and emissions mitigation in India. Sol. Energy Mater. Sol. Cells 2016, 156, 147–156. [Google Scholar] [CrossRef]
- Nacer, T.; Hamidat, A.; Nadjemi, O.; Bey, M. Feasibility study of grid connected photovoltaic system in family farms for electricity generation in rural areas. Renew. Energy 2016, 96, 305–318. [Google Scholar] [CrossRef]
- Maisanam, A.K.S.; Podder, B.; Biswas, A.; Sharma, K.K. Site-specific tailoring of an optimal design of renewable energy system for remote water supply station in Silchar, India. Sustain. Energy Technol. Assess. 2019, 36, 100558. [Google Scholar] [CrossRef]
- Song, X.; Zhao, M.; Xing, S. A multi-strategy fusion artificial bee colony algorithm with small population. Expert Syst. Appl. 2020, 142, 112921. [Google Scholar] [CrossRef]
- Chen, Y.; Roux, B. Generalized Metropolis acceptance criterion for hybrid non-equilibrium molecular dynamics-Monte Carlo simulations. J. Chem. Phys. 2015, 142, 024101. [Google Scholar] [CrossRef] [PubMed]
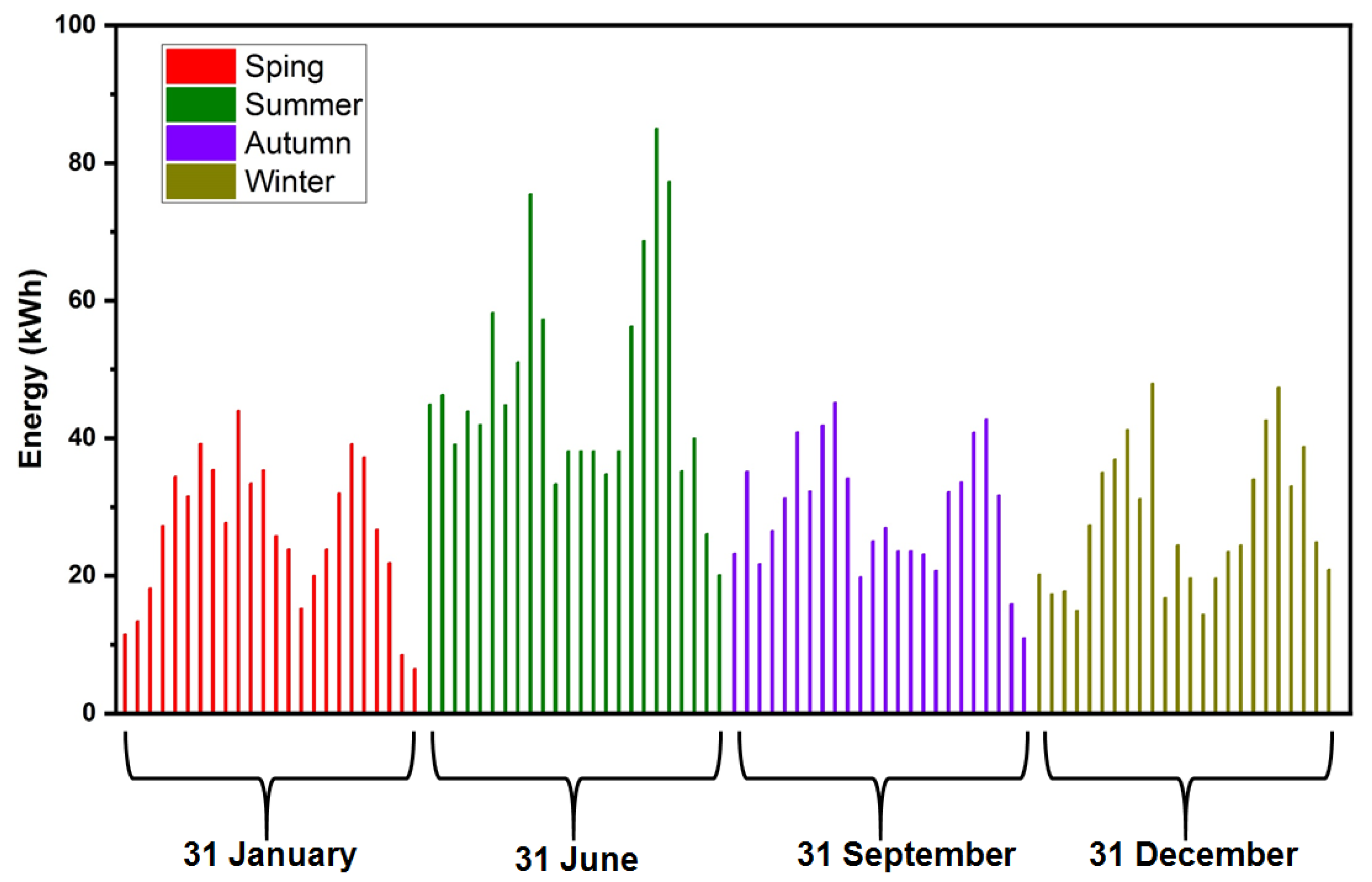
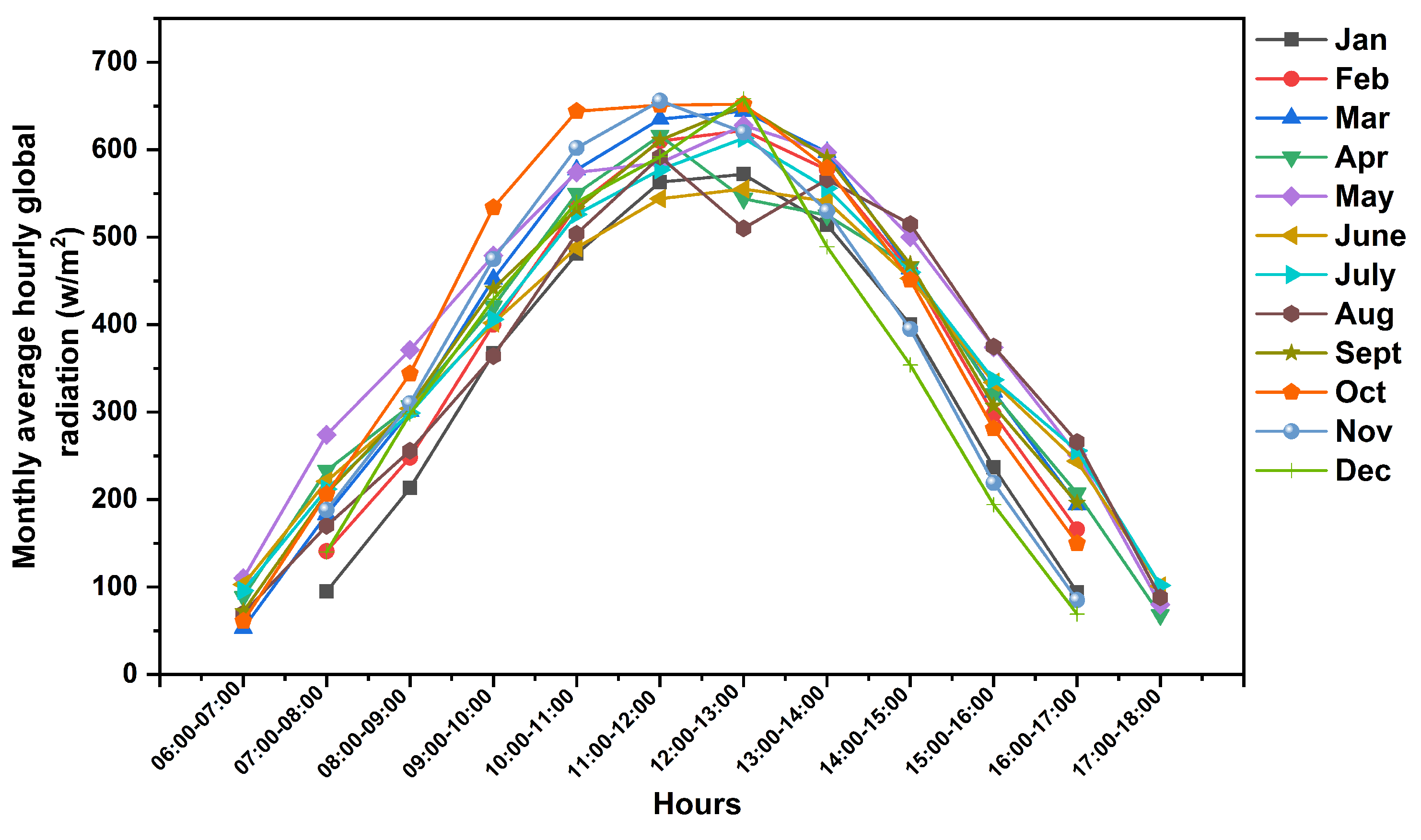
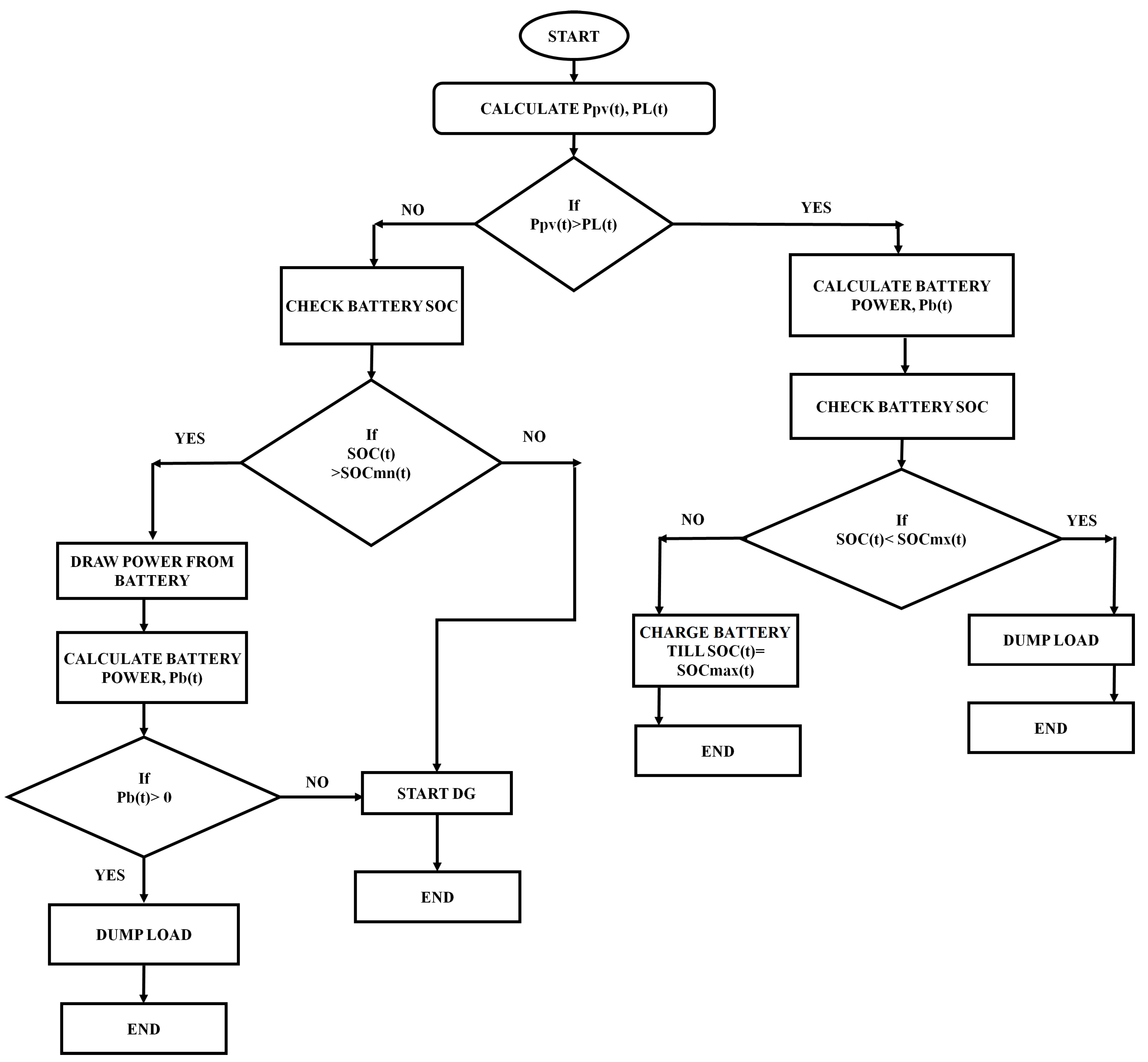


| SN | Domestic Electrical Load | No of Load | Power (W) | Summer (May–August) | Autumn (September–October) | Winter (November–Feburary) | Spring (Feburary–April) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| h/day | Watt-h/day | h/day | Watt-h/day | h/day | Watt-h/day | h/day | Watt-h/day | ||||
| 1 | CFL-I | 4 | 23 | 8 | 736 | 8 | 736 | 8 | 736 | 8 | 736 |
| 2 | CFL-II | 1 | 11 | 8 | 88 | 8 | 88 | 8 | 88 | 8 | 88 |
| 3 | Ceiling Fan | 1 | 120 | 20 | 2400 | 2 | 240 | 0 | 0 | 8 | 960 |
| 4 | Kitchen fan | 1 | 100 | 6 | 600 | 2 | 200 | 0 | 0 | 6 | 600 |
| 5 | Cooler | 2 | 120 | 10 | 2400 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | Television | 1 | 100 | 8 | 800 | 8 | 800 | 8 | 800 | 8 | 800 |
| 7 | Computer | 1 | 300 | 4 | 1200 | 4 | 1200 | 4 | 1200 | 4 | 1200 |
| 8 | Exhaust | 1 | 15 | 5 | 75 | 5 | 75 | 5 | 75 | 5 | 75 |
| 9 | Table fan | 1 | 15 | 8 | 120 | 0 | 0 | 0 | 0 | 5 | 75 |
| 10 | Room Heater | 1 | 120 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | Bulb | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 |
| 6119 | 3439 | 2999 | 4634 | ||||||||
| S.No. | Objective Components | Objective Parameters | Value | Unit |
|---|---|---|---|---|
| 1 | SPV | Photovoltaic Power Rating | 1 | kW |
| PV Capital Expenses | 933.33 | $ | ||
| PV Replacement Cost | 800.00 | $ | ||
| Operation and Maintenance Cost | 13.33 | $/kW | ||
| Derating Factor | 88 | % | ||
| Photovoltaic Life | 20 | years | ||
| 2 | Converter | Converter Power Rating | 1 | kW |
| Capital cost of the converter | 133.33 | $ | ||
| Replacement Cost of the converter | 106.67 | $ | ||
| Operation and Maintenance Cost | 160 | yr | ||
| Overall Converter Efficiency | 90 | % | ||
| Converter Life | 20 | Years | ||
| 3 | BESS | Battery Capital-Cost | 133.33 | $ |
| Replacement Cost | 56.00 | $ | ||
| Operation and Maintenance Cost | 1.33 | $ | ||
| Size of the unit battery | 2.1 | kW | ||
| Battery Rated voltage | 6 | Volt | ||
| Minimum SOC | 30 | % | ||
| Maximum SOC | 100 | % | ||
| Efficiency | 95 | % | ||
| Life of Battery | 5 | Year | ||
| 4 | DGs | Capital Expenses | 9467 | $ |
| Replacement Cost | 28.35 | $ | ||
| Operation and Maintenance Cost | 2449.5 | $/kw | ||
| Efficiency | 80 | % | ||
| Life | 25 | year | ||
| 4 | Grid | Supply Cost | 10 | $ |
| 5 | Other | Rate for discount | 6 | % |
| Life of Project | 20 | Year |
| PSO Algorithm | MFABC Algorithm | MFABC+ Algorithm |
|---|---|---|
| Dimension (D): 4 | Dimension (D1): 4 | Dimension (D2): 4 |
| Propulsion size (N): 20 | Employed Bees = Onlooker bees:10 | Employed bees (ABC/best) = Onlooker bees(CABC):12 |
| Initial weight (): 0.3 | Colony size (NP): 20 | Colony size (NP1): 40 |
| Final weight (): 0.8 | Food Number: NP/2 | Food number: NP1/4 |
| Maximum Iteration (): 100 | Maximum cycle: 100 | Maximum Iteration: 100 |
| Weighting factor: (C1 and C2):2 | Limit: 100 | Limit: 100 |
| Parameters | PSO | HOMER | MFABC | MFABC+ |
|---|---|---|---|---|
| PV units | 235 | 244 | 232 | 230 |
| Battery units | 800 | 1000 | 1000 | 800 |
| Inverter sizing (kW) | 110 | 110 | 110 | 110 |
| ASC($/yr) | 61,584 | 63,573 | 61,006 | 56,002 |
| TNPC ($) | 730,011 | 739,980 | 723,378 | 700,000 |
| LCOE ($/kWh) | 0.198 | 0.201 | 0.196 | 0.195 |
| Components | HOMER (kWh/yr) | PSO (kWh/yr) | MFABC (kWh/yr) | MFABC+ (kWh/yr) |
|---|---|---|---|---|
| Solar | 492,134 | 410,024 | 400,201 | 421,257 |
| Battery in | 178,840 | 241,580 | 287,348 | 280,243 |
| Battery out | 158,470 | 121,542 | 145,203 | 160,232 |
| Total demand served | 291,678 | 345,167 | 321,450 | 355,230 |
| Excess electricity | 128,087 | 7540 | 6897 | 5320 |
| Components | Capital Cost ($/yr) | Replacement Cost ($/yr) | Maintenance Cost ($/yr) | Salvage Cost ($/yr) | Total Cost ($/yr) |
|---|---|---|---|---|---|
| PV | 51,014 | - | 3716 | 464 | 55,194 |
| Batteries | 33,765 | 9876 | 176 | - | 43,817 |
| Inverter | 10,925 | 1012 | 862 | - | 12,799 |
| Total | 95,704 | 10,888 | 4,754 | 464 | 111,810 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Slowik, A.; Kanwar, N.; Meena, N.K. Techno-Economic Feasibility Analysis of Grid-Connected Microgrid Design by Using a Modified Multi-Strategy Fusion Artificial Bee Colony Algorithm. Energies 2021, 14, 190. https://doi.org/10.3390/en14010190
Singh S, Slowik A, Kanwar N, Meena NK. Techno-Economic Feasibility Analysis of Grid-Connected Microgrid Design by Using a Modified Multi-Strategy Fusion Artificial Bee Colony Algorithm. Energies. 2021; 14(1):190. https://doi.org/10.3390/en14010190
Chicago/Turabian StyleSingh, Sweta, Adam Slowik, Neeraj Kanwar, and Nand K. Meena. 2021. "Techno-Economic Feasibility Analysis of Grid-Connected Microgrid Design by Using a Modified Multi-Strategy Fusion Artificial Bee Colony Algorithm" Energies 14, no. 1: 190. https://doi.org/10.3390/en14010190
APA StyleSingh, S., Slowik, A., Kanwar, N., & Meena, N. K. (2021). Techno-Economic Feasibility Analysis of Grid-Connected Microgrid Design by Using a Modified Multi-Strategy Fusion Artificial Bee Colony Algorithm. Energies, 14(1), 190. https://doi.org/10.3390/en14010190






