Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform
Abstract
1. Introduction
2. Models
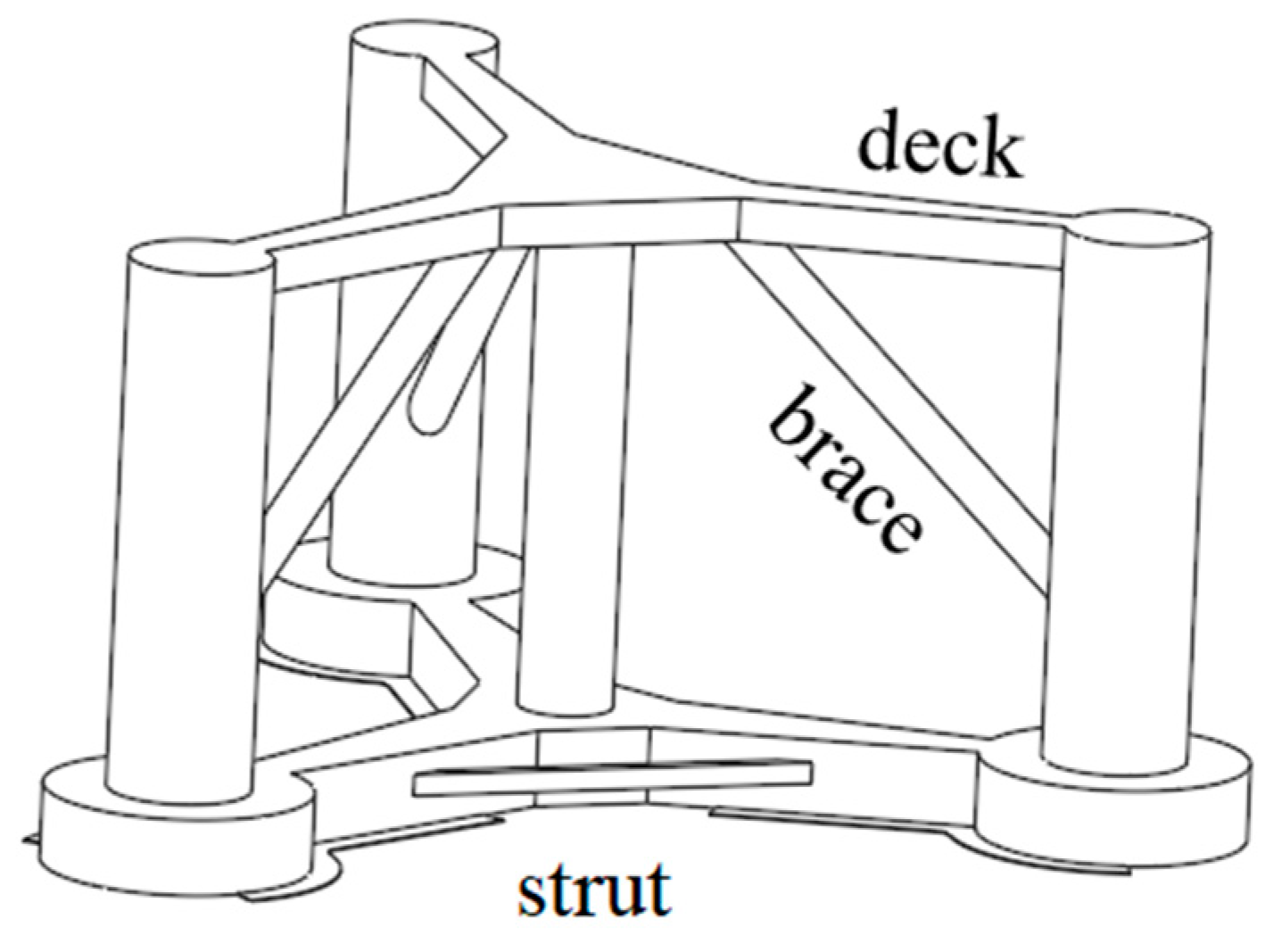
2.1. Description of a 1:60 Scale Elastic Platform Model
2.2. Hydrodynamic Coefficient Models for the Multibody
2.3. Numerical Model for the Dynamic Analysis
3. Results and Discussion
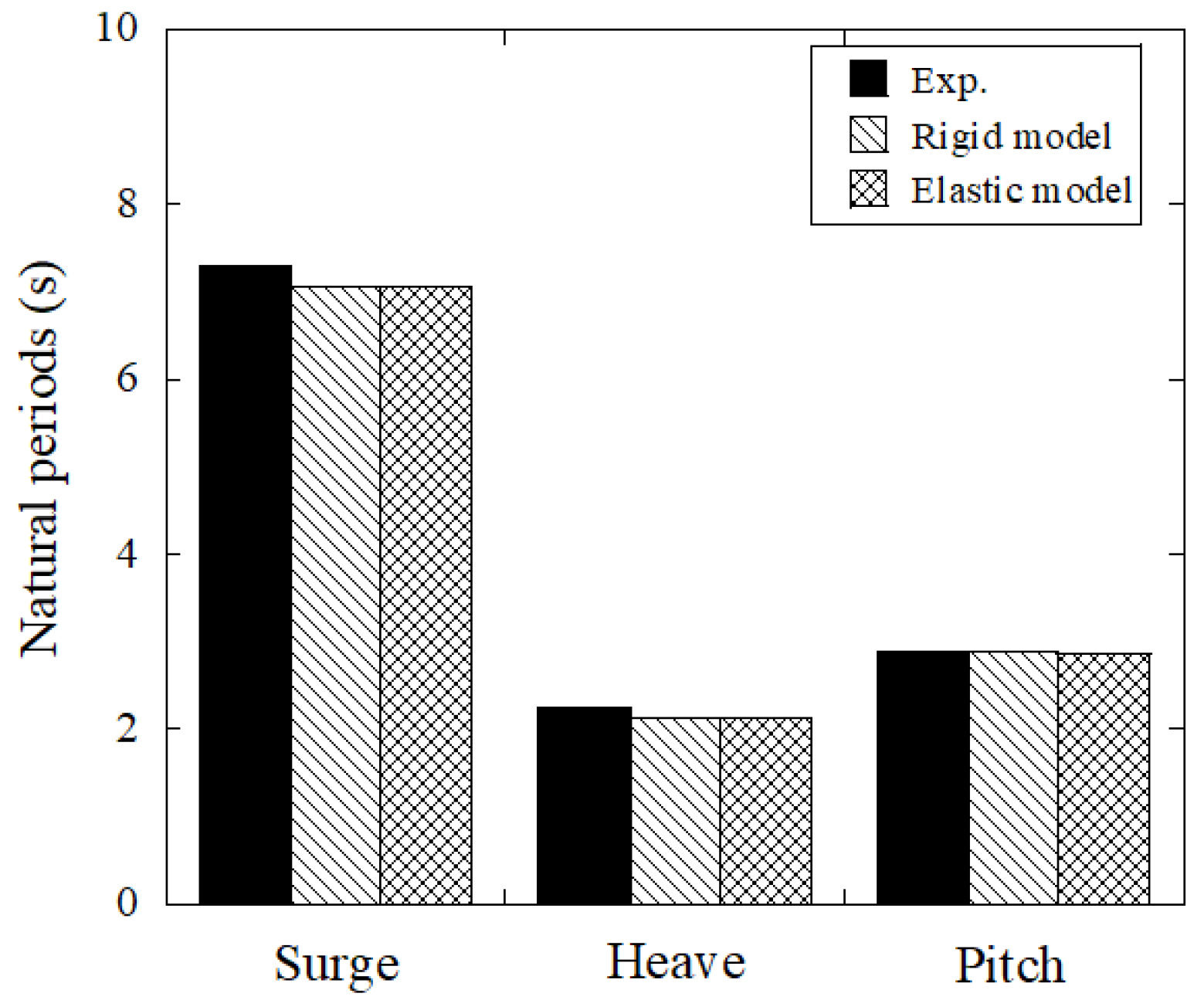
3.1. Water Tank Test with an Elastic Platform
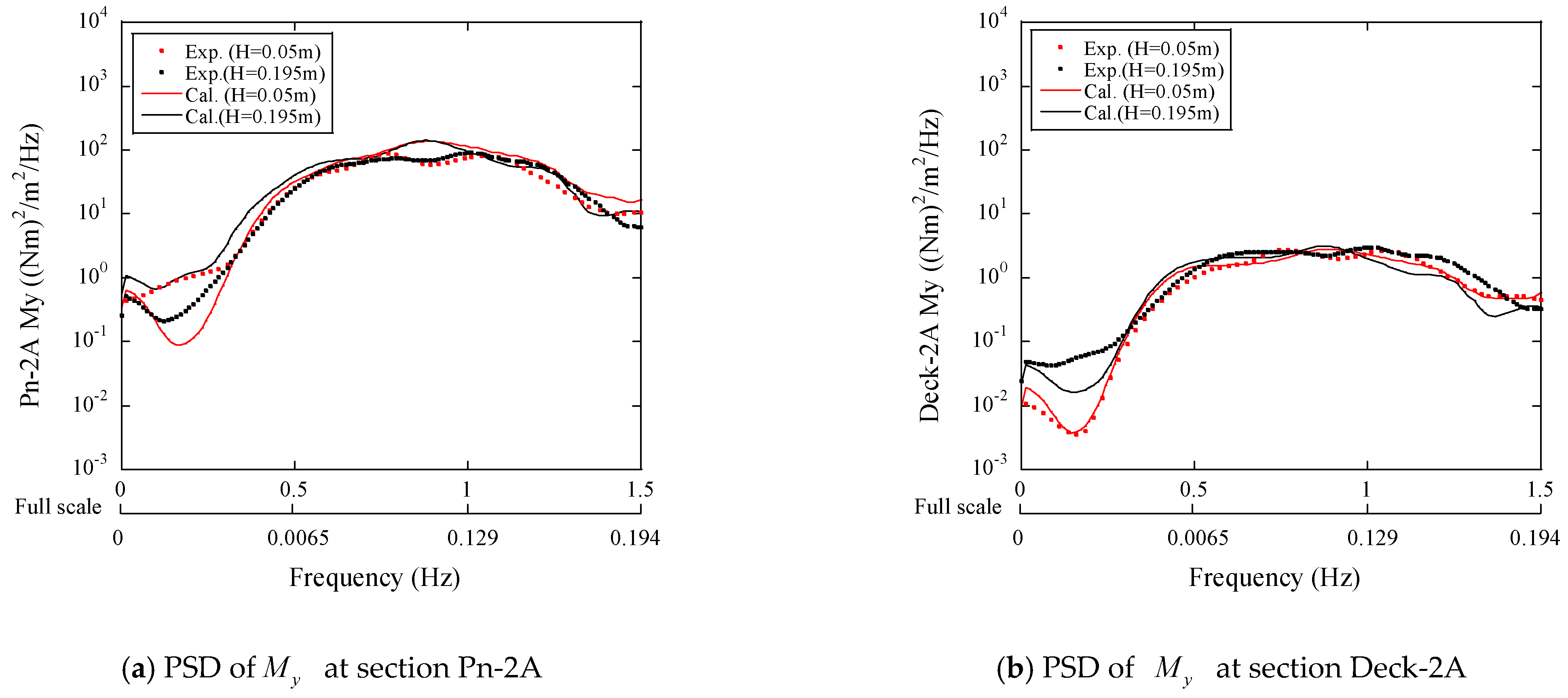
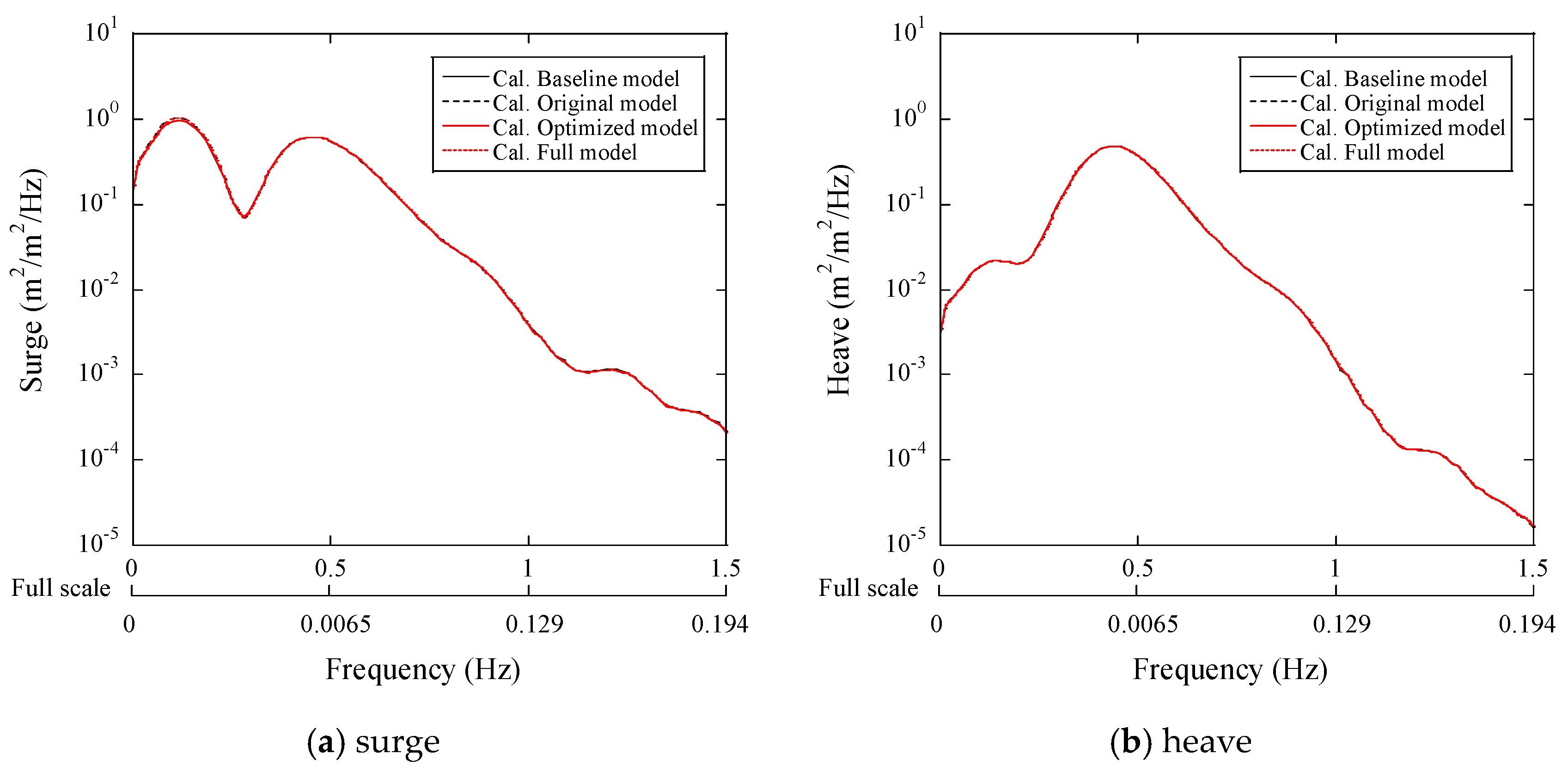
3.2. Dynamic Response of the Platform and Mooring Lines
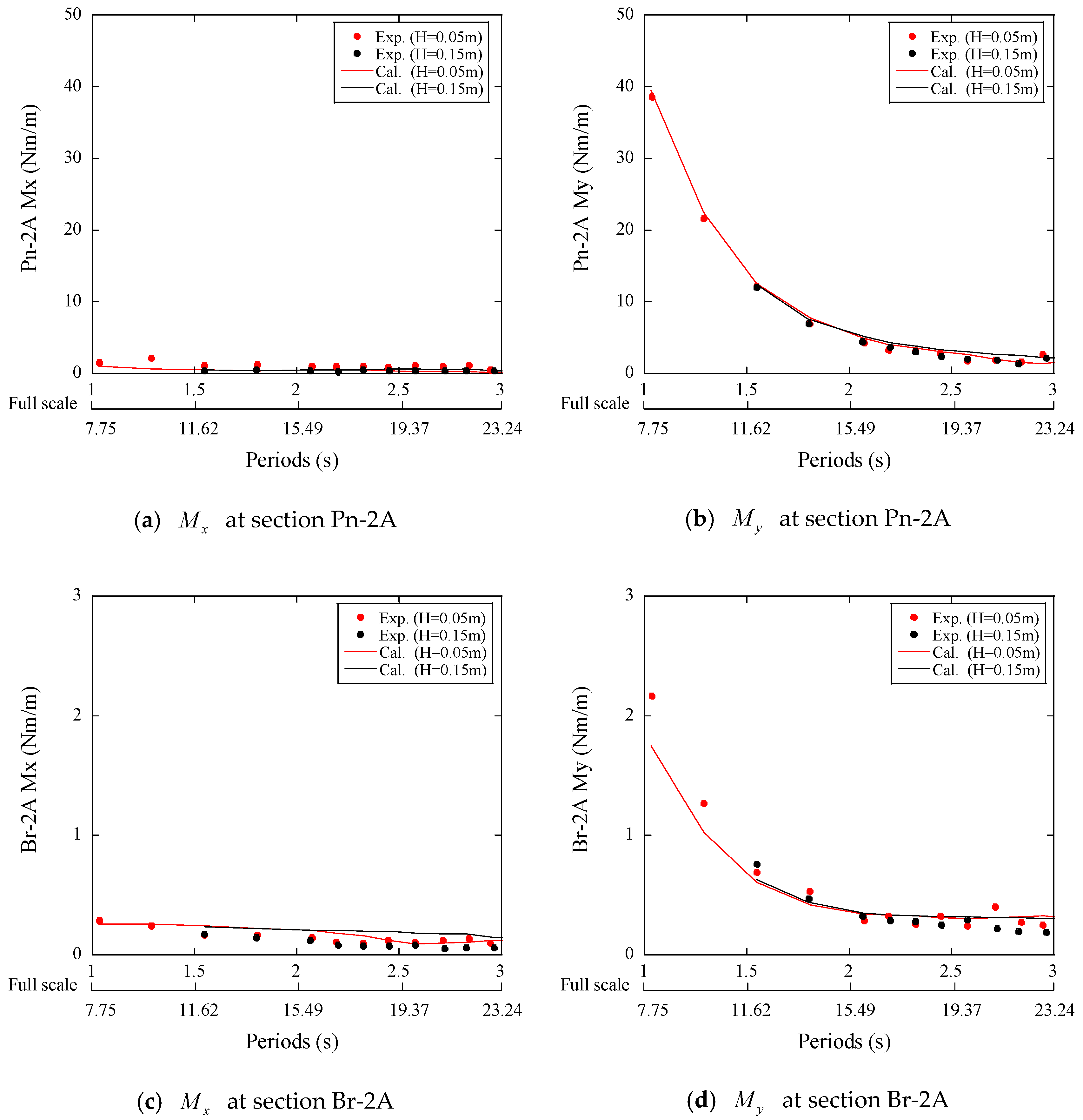
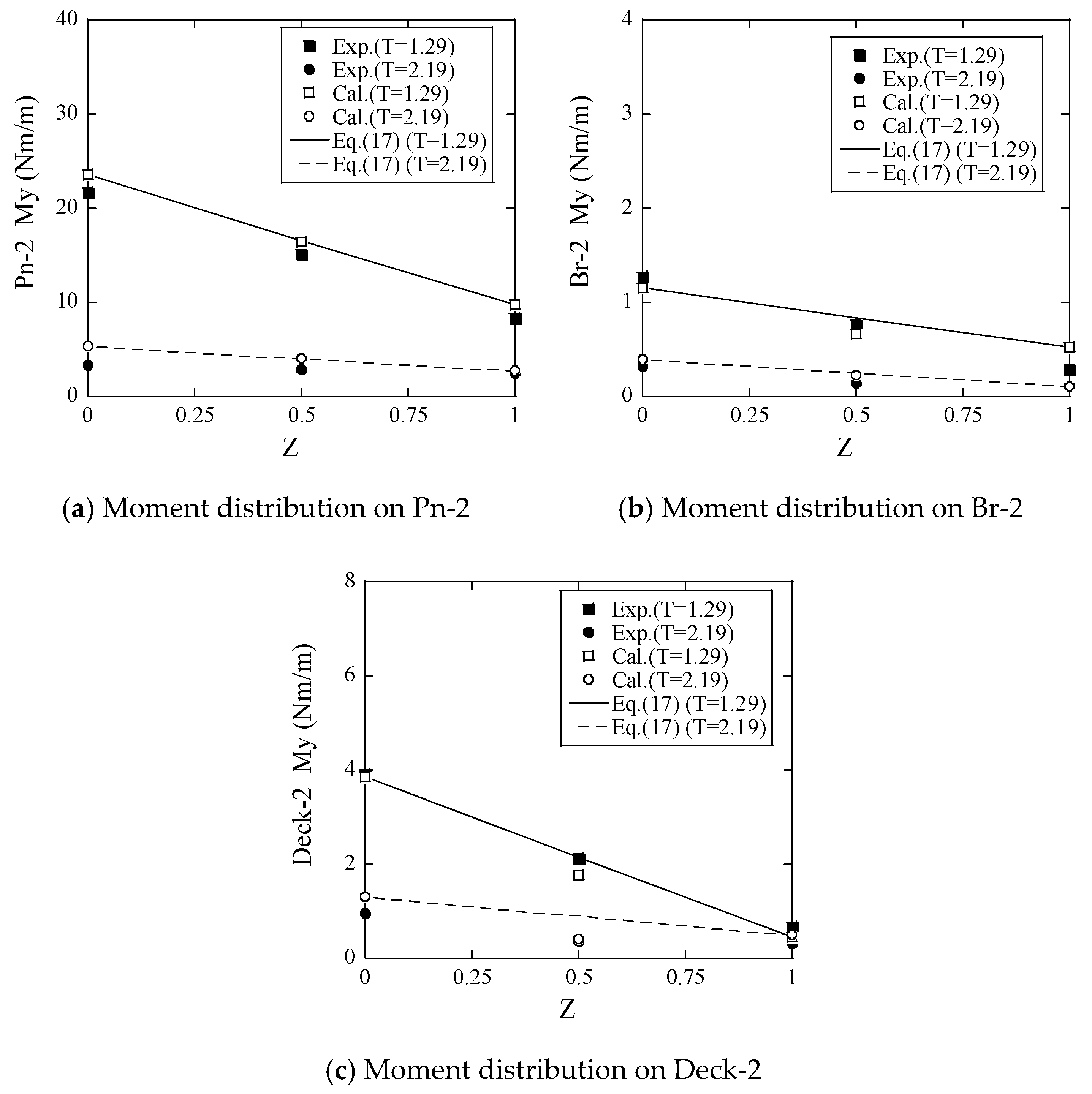
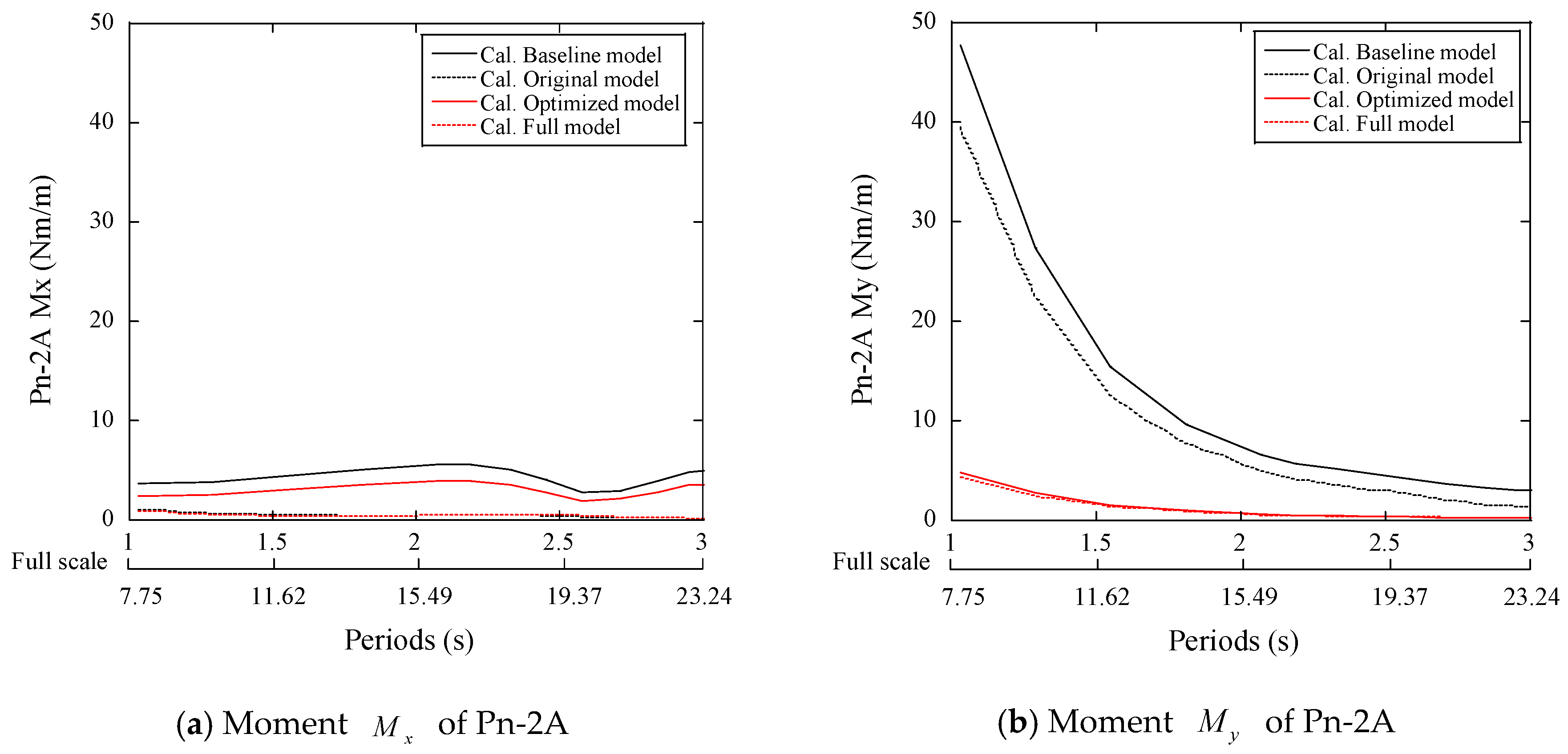
3.3. Sectional Loads on the Platform
3.4. Structural Optimization
4. Conclusions
- The nonlinear hydrodynamic coefficient models for the multibody are proposed considering the effects of Reynolds and KC numbers on the added mass and drag coefficients. The predicted dynamic response and mooring tension of the elastic platform by the proposed model show good agreement with the experimental data obtained from the water tank test. The influence of structural stiffness on the dynamic response of the platform is negligible since the stiffness of the platform used in the demonstration is quite high.
- The sectional loads on the deck, brace and pontoon were investigated using multiple hydrodynamic bodies. The bending moments due to horizontal hydrodynamic loads are much larger than those caused by the vertical hydrodynamic loads. A linear formula is proposed to predict the distribution of the sectional loads on the connection element.
- The sectional load on the pontoon was analyzed by the four platforms with and without the braces, decks and struts. The largest contribution to the fatigue load of the pontoon comes from the horizontal loads and the struts significantly reduce the stress on the pontoon, while the contributions from the decks and braces are limited.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kikuchi, Y.; Ishihara, T. Upscaling and levelized cost of energy for offshore wind turbines supported by semi-submersible floating platforms, Comparison of dynamic response and levelized cost of energy on three platform concepts of floating offshore wind turbine systems. J. Phys. Conf. Ser. 2019, 1356, 012033. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Ishihara, T. Comparison of dynamic response and levelized cost of energy on three platform concepts of floating offshore wind turbine systems. J. Phys. Conf. Ser. 2020, 1452, 012035. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Vorpahl, F.; Popko, W.; Qvist, J.; Frøyd, L.; Chen, X.; Azcona, J.; Uzunoglu, E.; Soares, C.G.; et al. Offshore code comparison collaboration continuation within IEA wind task 30: Phase II results regarding a floating semisubmersible wind system. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar] [CrossRef]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 Project Phase II: Validation of Global Loads of the DeepCwind Floating Semisubmersible Wind Turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
- Borg, M.; Hansen, A.M.; Bredmose, H. Floating substructure flexibility of large-volume 10MW offshore wind turbine platforms in dynamic calculations. J. Phys. Conf. Ser. 2016. [Google Scholar] [CrossRef]
- Borg, M.; Bredmose, H.; Hansen, A.M. Elastic deformations of floaters for offshore wind turbines: Dynamic modelling and sectional load calculations. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Trondheim, Norway, 25–30 June 2017. [Google Scholar] [CrossRef]
- Silva de Souza, C.E.; Bachynski, E.E. Effects of hull flexibility on the structural dynamics of a tension leg platform floating wind turbine. J. Offshore Mech. Arct. Eng. 2020, 142, 011903. [Google Scholar] [CrossRef]
- Ishihara, T.; Van Phuc, P.; Sukegawa, H. A numerical study on the dynamic response of a floating offshore wind turbine system due to resonance and nonlinear wave. In Proceedings of the European Offshore Wind Conference (EOW2007), Berlin, Germany, 4–6 December 2007; pp. 1–9. [Google Scholar]
- Suzuki, H.; Xiong, J.; do Carmo, L.H.S.; Vieira, D.P.; de Mello, P.C.; Malta, E.B.; Simos, A.N.; Hirabayashi, S.; Gonçalves, R.T. Elastic response of a light-weight floating support structure of FOWT with guywire supported tower. J. Mar. Sci. Technol. 2018, 24, 1015–1028. [Google Scholar] [CrossRef]
- Suzuki, H.; Shiohara, H.; Schnepf, A.; Houtani, H.; Carmo, L.H.S.; Hirabayashi, S.; Haneda, K.; Chujo, T.; Nihei, Y.; Malta, E.B.; et al. Wave and wind responses of a very-light fowt with guy-wired-supported tower: Numerical and experimental studies. J. Mar. Sci. Eng. 2020, 8, 841. [Google Scholar] [CrossRef]
- Xiong, J.; Do Carmo, L.H.S.; Vieira, D.P.; De Mello, P.C.; Malta, E.B.; Simos, A.N.; Suzuki, H.; Gonçalves, R.T. Experimental and numerical comparison of the wave dynamics and guy wire forces of a very light FOWT considering hydroelastic behavior. In Proceedings of the ASME 2018 1st International Offshore Wind Technical Conference, IOWTC 2018, San Francisco, CA, USA, 4–7 November 2018. [Google Scholar]
- Campos, A.; Molins, C.; Trubat, P.; Alarcón, D. A 3D FEM model for floating wind turbines support structures. Energy Procedia 2017, 137, 177–185. [Google Scholar] [CrossRef]
- Faltinsen, O.M.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; ISBN 0-521-45870-6. [Google Scholar]
- Beyer, F.; Choisnet, T.; Kretschmer, M.; Cheng, P.W. Coupled MBS-CFD simulation of the IDEOL floating offshore wind turbine foundation compared to wave tank model test data. In Proceedings of the International Offshore and Polar Engineering Conference, Big Island, HI, USA, 21–26 June 2015; pp. 367–374, ISBN 978-1-880653-89-0. [Google Scholar]
- Yoshimoto, H.; Kamizawa, K. Validation of the motion analysis method of floating offshore wind turbines using observation data acquired by full scale demonstration project. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Glasgow, Scotland, 9–14 June 2019. [Google Scholar] [CrossRef]
- Lamei, A.; Hayatdavoodi, M. On motion analysis and elastic response of floating offshore wind turbines. J. Ocean Eng. Mar. Energy 2020, 6, 71–90. [Google Scholar] [CrossRef]
- Zhang, S.; Ishihara, T. Effects of multidirectional sea states and flexible foundation on dynamic response of floating offshore wind turbine system. In Proceedings of the First International Symposium on Flutter and its Application, Tokyo, Japan, 15–17 May 2016; pp. 729–738. [Google Scholar]
- Guignier, L.; Courbois, A.; Mariani, R.; Choisnet, T. Multibody modelling of floating offshore wind turbine foundation for global loads analysis. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016; pp. 333–339, ISBN 978-1-880653-88-3. [Google Scholar]
- Kvittem, M.I.; Moan, T. Time domain analysis procedures for fatigue assessment of a semi-submersible wind turbine. Mar. Struct. 2015, 40, 38–59. [Google Scholar] [CrossRef]
- Luan, C.; Gao, Z.; Moan, T. Development and verification of a time-domain approach for determining forces and moments in structural components of floaters with an application to floating wind turbines. Mar. Struct. 2017, 51, 87–109. [Google Scholar] [CrossRef]
- Luan, C.; Chabaud, V.; Bachynski, E.E.; Gao, Z.; Moan, T. Experimental validation of a time-domain approach for determining sectional loads in a floating wind turbine hull subjected to moderate waves. Energy Procedia 2017, 137, 366–381. [Google Scholar] [CrossRef]
- Luan, C.; Gao, Z.; Moan, T. Comparative analysis of numerically simulated and experimentally measured motions and sectional forces and moments in a floating wind turbine hull structure subjected to combined wind and wave loads. Eng. Struct. 2018, 177, 210–233. [Google Scholar] [CrossRef]
- Urbano, R.B.; Alexandre, A.; Urbano, R.B.; Roadnight, J.; Harries, R. Methodology for calculating floating offshore wind foundation internal loads using bladed and a finite element analysis software. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Madrid, Spain, 17–22 June 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Oh, S.; Ishii, K.; Iijima, K.; Suzuki, H. Implementation of potential flow hydrodynamics to time-domain analysis of flexible platforms of floating offshore wind turbines. J. Phys. Conf. Ser. 2019. [Google Scholar] [CrossRef]
- Fukushima FORWARD. Available online: http://www.fukushima-forward.jp/english/index.html (accessed on 1 November 2020).
- Roddier, D.; Cermelli, C.; Aubault, A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2, 033104. [Google Scholar] [CrossRef]
- Ohta, M.; Komatsu, M.; Ito, H.; Kumamoto, H. Development of a V-shaped Semi-submersible Floating Structure for 7MW Offshore Wind Turbine. In Proceedings of the International Symposium on Marine and Offshore Renewable Energy, Tokyo, Japan, 28–30 October 2013; pp. 1–5. [Google Scholar]
- OrcaFlex—Dynamic Analysis Software for Offshore Marine Systems. Available online: https://www.orcina.com/orcaflex/ (accessed on 20 December 2020).
- Yamaguchi, A.; Danupon, S.; Ishihara, T. Load estimation and wind measurement considering full scale floater motion. In Proceedings of the EERA DeepWind 2020, Trondheim, Norway, 15–17 January 2020. [Google Scholar]
- ANSYS Inc. Ansys Aqwa: Hydrodynamics Simulation & Diffraction Analysis|Ansys. Available online: https://www.ansys.com/products/structures/ansys-aqwa (accessed on 17 December 2019).
- Liu, Y.; Ishihara, T. Prediction of dynamic response of semi-submersible floating offshore wind turbines by a novel hydrodynamic coefficient model. J. Phys. Conf. Ser. 2019, 1356, 012035. [Google Scholar] [CrossRef]
- Ishihara, T.; Liu, Y. Dynamic Response Analysis of a Semi-Submersible Floating Wind Turbine in Combined Wave and Current Conditions Using Advanced Hydrodynamic. Models. Energies 2020, 13, 5820. [Google Scholar] [CrossRef]
- Ishihara, T.; Zhang, S. Prediction of dynamic response of semi-submersible floating offshore wind turbine using augmented Morison’s equation with frequency dependent hydrodynamic coefficients. Renew. Energy 2019, 131, 1186–1207. [Google Scholar] [CrossRef]
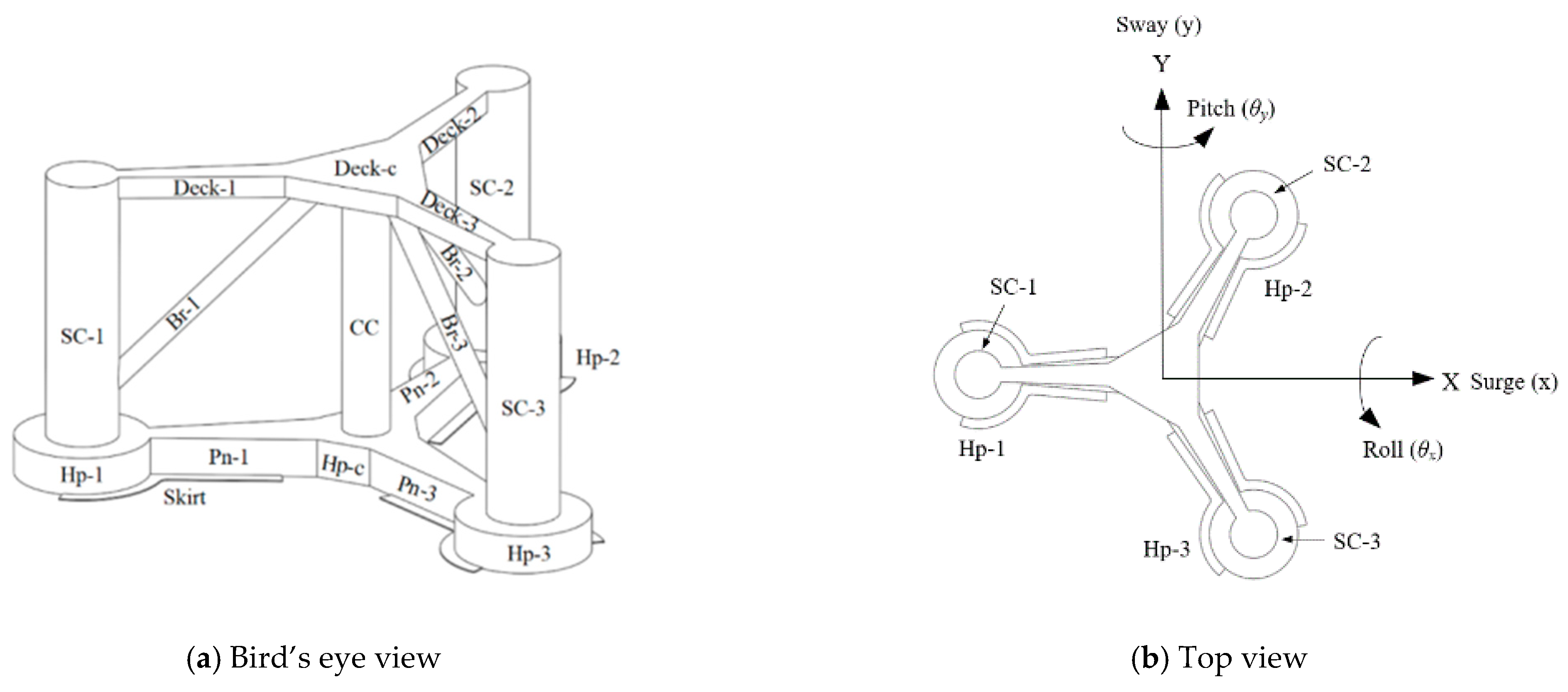
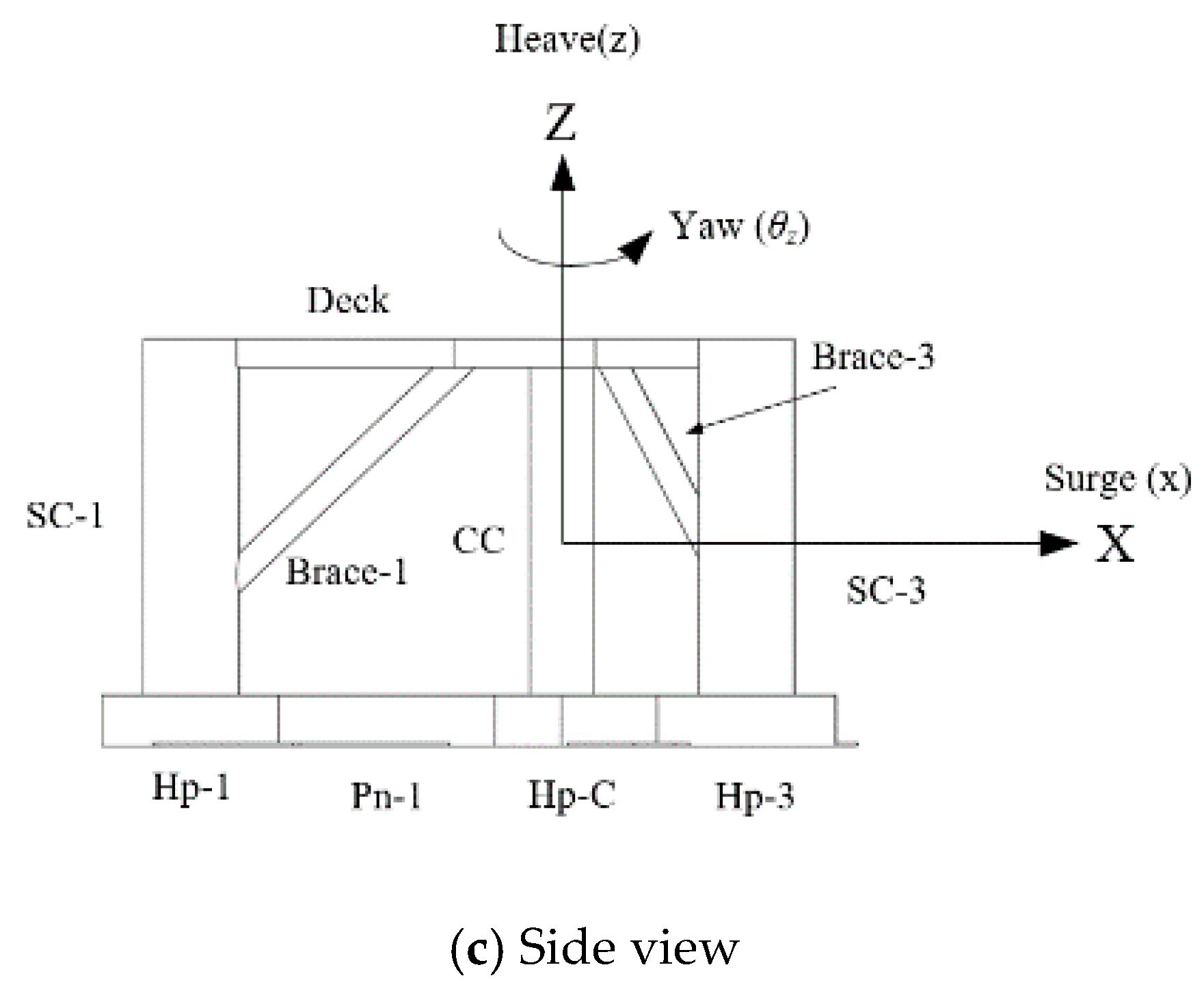










| Elements | Dimension (m) |
|---|---|
| Draft of the platform | 0.2667 |
| Height of central column (Hcc) and side columns (Hsc) | 0.4667 |
| Diameter of central column (Dcc) | 0.0823 |
| Diameter of side columns (Dsc) | 0.1250 |
| Height of heave plate (HHp) and pontoon (HHp) | 0.0667 |
| Diameter of heave plate (DHp) | 0.2333 |
| Width of pontoon | 0.05~0.10 |
| Length of pontoon (LPn) | 0.2827 |
| Diameter of brace (Dbrace) | 0.0375 |
| Length of brace (Lbrace) | 0.3887 |
| Height of deck | 0.0375 |
| Width of deck | 0.0375~0.0608 |
| Center of gravity below still water level | −0.0687 |
| Radius of gyration Kxx | 0.370 |
| Radius of gyration Kyy | 0.374 |
| EIxx (Nm2) | EIyy (Nm2) | EA (N) | GJ (Nm2/rad) | |
|---|---|---|---|---|
| Pontoon | 193.00 | 277.92 | 2.32 × 107 | 213.08 |
| Brace | 20.80 | 20.84 | 6.95 × 106 | 13.52 |
| Deck | 31.10 | 33.10 | 8.11 × 106 | 24.78 |
| Mass (kg) | Center of Gravity (m) | Moment of Inertia (kg m2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | Ixx | Iyy | Izz | Ixy | Iyz | Izx | ||
| Body1 | 14.972 | −0.074 | −0.147 | −0.045 | 1.452 | 2.196 | 1.917 | 0.671 | −0.040 | −0.108 |
| Body2 | 4.239 | 0.237 | 0.411 | −0.098 | 0.188 | 0.186 | 0.019 | −0.002 | 0.000 | 0.000 |
| Body3 (Pn-2) | 1.732 | 0.102 | 0.177 | −0.233 | 0.007 | 0.002 | 0.009 | −0.004 | 0.000 | 0.000 |
| Body4 (Br-2) | 0.271 | 0.128 | 0.221 | 0.069 | 0.004 | 0.002 | 0.002 | −0.001 | 0.001 | 0.002 |
| Body4 (Deck-2) | 0.420 | 0.153 | 0.265 | 0.248 | 0.002 | 0.001 | 0.002 | −0.001 | 0.000 | 0.000 |
| No. | Case | Wave Height (m) | Wave Periods (s) | Note |
|---|---|---|---|---|
| 1 | Free decay | - | - | Stillwater |
| 2 | Regular waves | 0.05, 0.15 | 1.03~3.10 | |
| 3 | Irregular waves | 0.05, 0.195 | 2.16 | PM spectrum |
| Model | Deck and Brace | Strut | Description of Model |
|---|---|---|---|
| Baseline model | ✕ | ✕ | Platform without deck, brace and strut |
| Original model | ◯ | ✕ | Platform with deck and brace, but without strut |
| Optimized model | ✕ | ◯ | Platform with strut, but without deck and brace |
| Full model | ◯ | ◯ | Platform with deck, brace and strut |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ishihara, T. Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform. Energies 2021, 14, 182. https://doi.org/10.3390/en14010182
Liu Y, Ishihara T. Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform. Energies. 2021; 14(1):182. https://doi.org/10.3390/en14010182
Chicago/Turabian StyleLiu, Yuliang, and Takeshi Ishihara. 2021. "Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform" Energies 14, no. 1: 182. https://doi.org/10.3390/en14010182
APA StyleLiu, Y., & Ishihara, T. (2021). Numerical Study on Sectional Loads and Structural Optimization of an Elastic Semi-Submersible Floating Platform. Energies, 14(1), 182. https://doi.org/10.3390/en14010182





