A Novel Moment of Inertia Identification Strategy for Permanent Magnet Motor System Based on Integral Chain Differentiator and Kalman Filter
Abstract
1. Introduction
2. Error Analysis of Existing Methods and the Identification Strategy Proposed in This Paper
2.1. Error Analysis of Existing Acceleration Deceleration Moment of Inertia Identification Methods
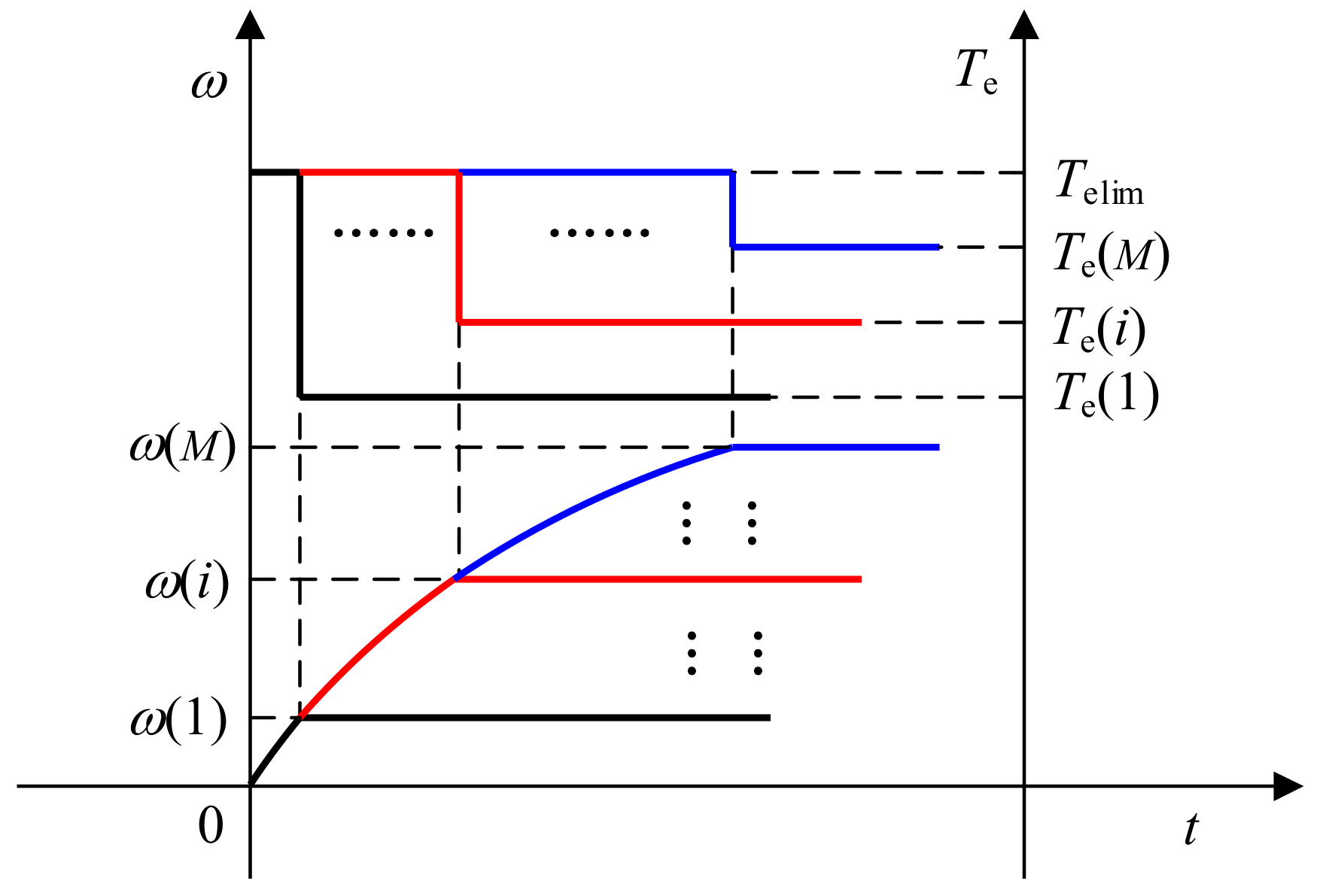
2.1.1. Traditional Acceleration Deceleration Moment of Inertia Identification Method
2.1.2. Improved Acceleration Deceleration Moment of Inertia Identification Method
2.1.3. Simulation Verification of Error Analysis
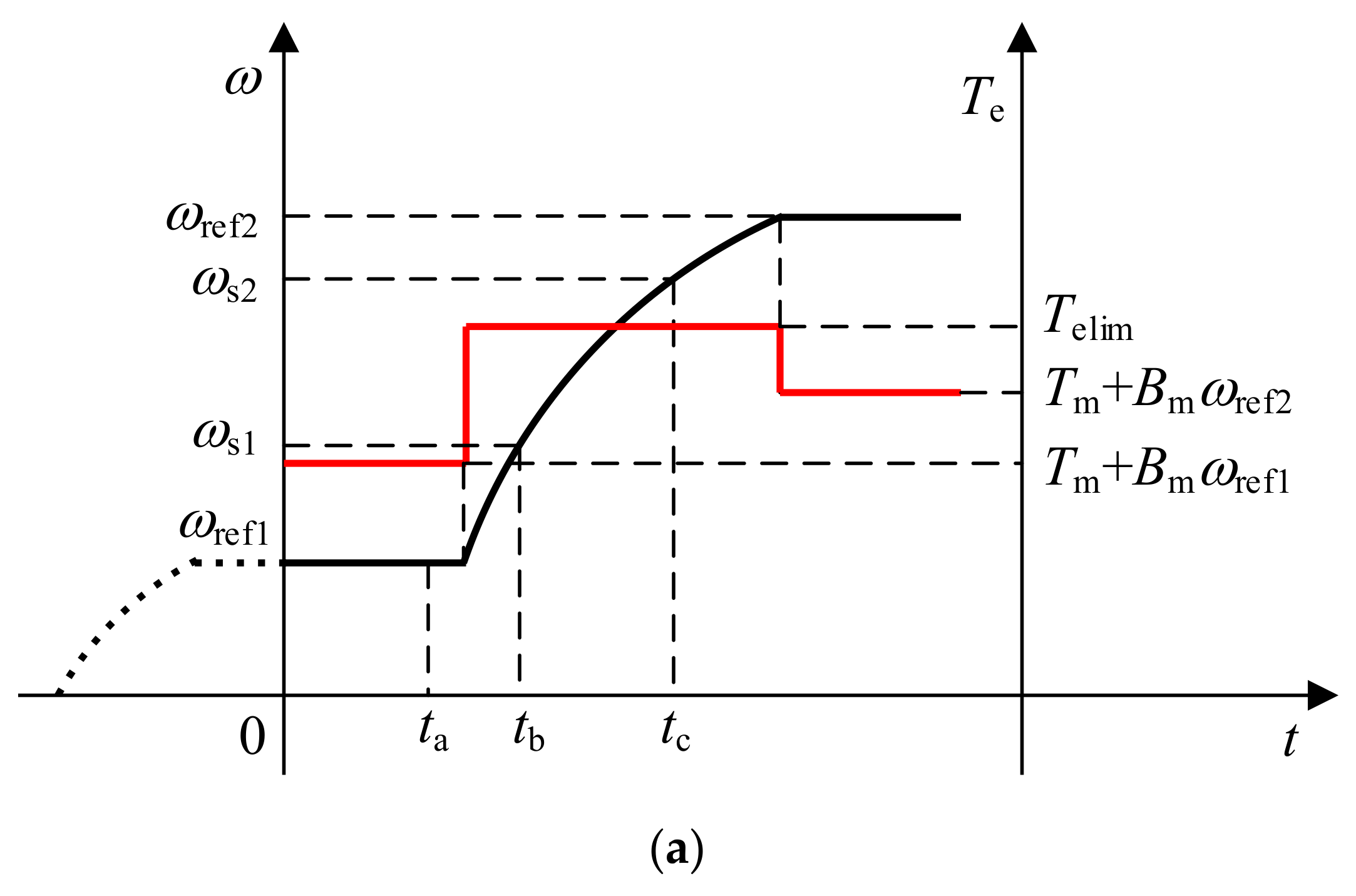
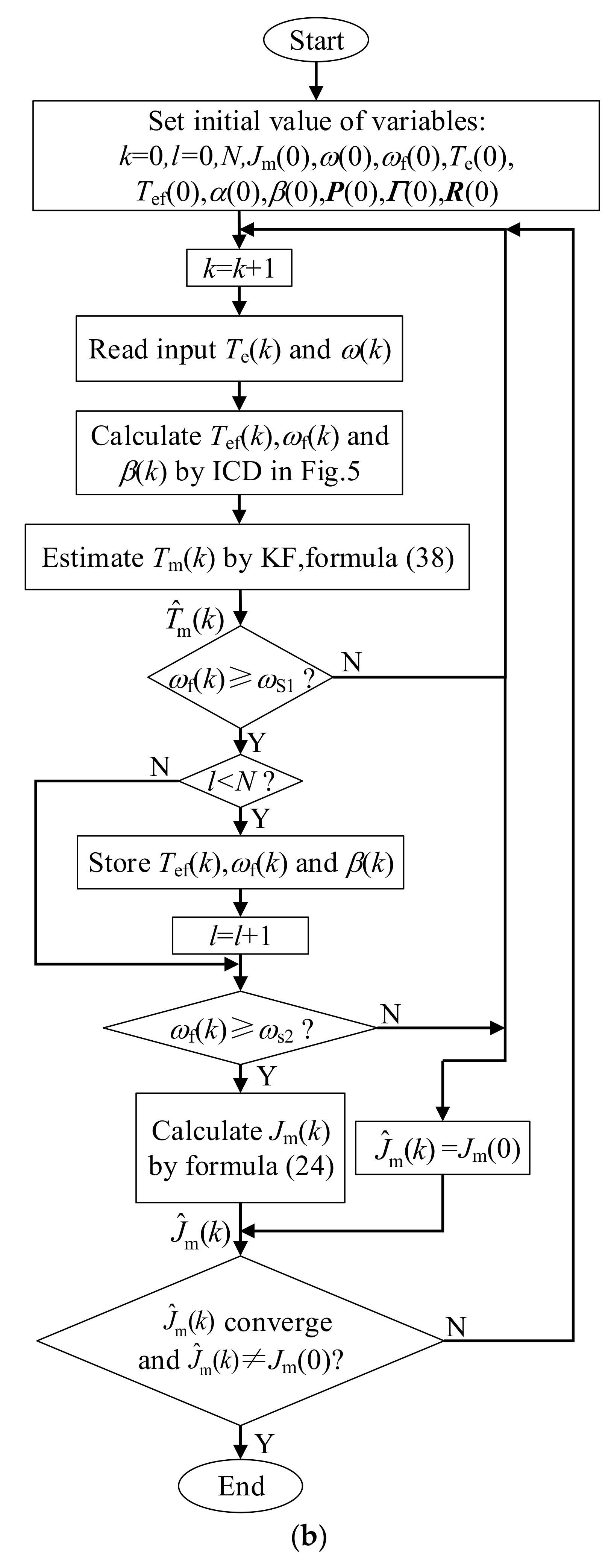
2.2. Moment of Inertia Identification Based on ICD and KF
2.2.1. Method Principle
- (1)
- The viscous friction torque is not considered when solving the inertia torque at a certain moment, which leads to the error in the calculation value of the inertia torque;
- (2)
- The angular acceleration is not constant when the motor speeds up. However, in (8), the angular acceleration corresponding to the inertia torque at a certain moment is not the instantaneous angular acceleration at that moment but the average angular acceleration in ΔT/n. This will also bring error to the identification of the moment of inertia. Combined with (1), why the identification error of this method in Section 2.1 is related to Bm and ΔT can be realized, intuitively;
- (3)
- In the experiment of the moment of inertia identification, there is a lot of noise in the sampling signal, which will affect the result of moment of inertia identification.
2.2.2. Estimation of Viscous Friction Coefficient and Coulomb Friction Torque
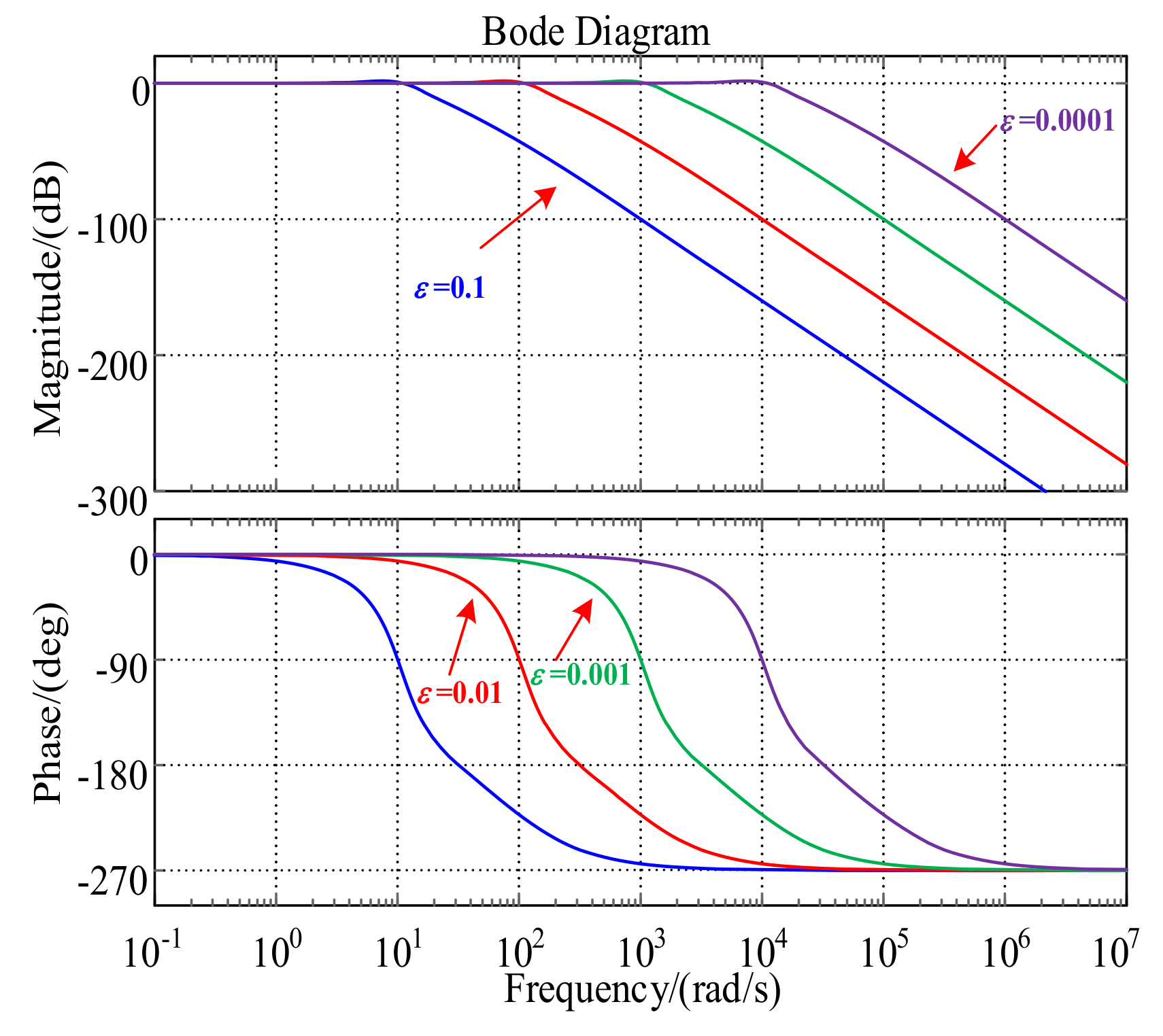
2.2.3. Sampling Noise Suppression and Instantaneous Angular Acceleration Solution
- (1)
- It can be obtained that A(υ) ≈ 1 and ϕ(υ) ≈ 0, when ε→0 and the frequency of the input signal is not large enough. Therefore, ωf(t) can track the original signal ω(t) accurately. Therefore, combined with (28), it can be considered that ωf(t) and β(t) approximately equal the angular velocity and its differential signal, respectively;
- (2)
- In general, the frequency of noise in the input signal is far greater than that of the ideal input signal. From (33), when the input signal frequency is very high, there is A(υ) << 1, indicating that the integrator chain differentiator can suppress the high-frequency noise in the input signal;
- (3)
- According to (33), when the parameters a1, a2, and a3 are determined, the tracking performance and noise suppression performance of the integral chain differentiator are only related to ε and the parameter adjustment is convenient. The smaller the value of ε, the better the tracking effect, but the ability of suppressing high-frequency noise will become worse; the larger the value of ε, the worse the tracking performance of ωf(t) will be, but the ability to resist high-frequency interference will be stronger. Therefore, it is necessary to select a suitable ε value to balance the tracking performance and anti-interference performance of the differentiator.
2.2.4. Estimation of Total Load Torque
2.2.5. Simulation Results
3. Experimental Results
3.1. Identification of Viscous Friction Coefficient and Coulomb Friction Torque
3.2. Experimental Results of Moment of Inertia and Total Load Torque Identification When TL = 50 Nm, TL = 100 Nm
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a1, a2, a3 | system parameters of Integral Chain Differentiator |
| Bm | viscous friction coefficient |
| Cm | Coulomb friction torque |
| eJ | moment of inertia identification error |
| eT | total load torque identification error |
| id | current of d-axis |
| iq | current of q-axis |
| Jm | moment of inertia |
| identification value of moment of inertia | |
| k | iteration times of Kalman Filter |
| Ld | inductance of d-axis |
| Lq | inductance of q-axis |
| n | number of segments in each ΔT |
| nr | motor speed |
| p | number of pole-pairs of the motor |
| R | covariance matrix of measurement noise |
| t | time variable |
| t1 | starting time of Δt |
| t2 | ending time of Δt |
| t20 | starting moment of the second ΔT |
| t2n | ending moment of the second ΔT |
| Te | electromagnetic torque |
| Te1 | electromagnetic torques corresponding to the first ΔT |
| Te2 | electromagnetic torques corresponding to the second ΔT |
| Te1(i) | electromagnetic torque of the i-th sampling point in the first ΔT |
| Te2(i) | electromagnetic torque of the i-th sampling point in the second ΔT |
| TL | load torque |
| Tm | total load torque |
| estimated value of total load torque | |
| Ts | sampling period |
| u | inertia torque |
| α(t) | differential signal of β |
| β | angular acceleration |
| ε | a sufficiently small positive value |
| Γ | covariance matrix of system noise |
| ω | angular velocity |
| ω10 | starting angular velocity of the first ΔT |
| ω20 | starting angular velocity of the second ΔT |
| ω1n | ending angular velocity of the first ΔT |
| ω2n | ending angular velocity of the second ΔT |
| ω2 | angular velocity in the second ΔT |
| ω2i | angular velocity of the i-th sampling point in the second ΔT |
| ω(t) | input signal of Integral Chain Differentiator |
| ωf(t) | angular velocity after noise suppression |
| ω(s) | Laplace transform form of ω(t) |
| ωf(s) | Laplace transform form of ωf(t) |
| ωξ | angular velocity at time ξ |
| ψd | flux linkage of d-axis |
| ψf | rotor flux linkage |
| ψq | flux linkage of q-axis |
| Δt | time length of the calculation interval in traditional acceleration deceleration method |
| ΔT | time length of the calculation interval in improved acceleration deceleration method |
| Δω | angular velocity variation within Δt |
| Δω1 | angular velocity variation within the first ΔT |
| Δω2 | angular velocity variation within the second ΔT |
References
- Yang, M.; Liu, Z.; Long, J.; Qu, W.; Xu, D. An Algorithm for Online Inertia Identification and Load Torque Observation via Adaptive Kalman Observer-Recursive Least Squares. Energies 2018, 11, 778. [Google Scholar] [CrossRef]
- Niu, L.; Xu, D.; Yang, M.; Gui, X.; Liu, Z. On-line Inertia Identification Algorithm for PI Parameters Optimization in Speed Loop. IEEE Trans. Power Electron. 2015, 30, 849–859. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z. Adaptive Speed Control for Permanent-Magnet Synchronous Motor System with Variations of Load Inertia. IEEE Trans. Ind. Electron. 2009, 56, 3050–3059. [Google Scholar]
- Lee, K.B.; Yoo, J.Y.; Song, J.H.; Choy, I. Improvement of low speed operation of electric machine with an inertia identification using ROELO. IEE Proc. Electr. Power Appl. 2004, 151, 116–120. [Google Scholar] [CrossRef]
- Hong, S.J.; Kim, H.W.; Sul, S.K. A novel inertia identification method for speed control of electric machine. In Proceedings of the Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–9 August 1996. [Google Scholar]
- Wei, C.; Zhaosheng, G.; Changliang, X.; Xin, G. Design of Adaptive Disturbance Observer for AC Servo System with Inertia Identification. Trans. China Electrotech. Soc. 2016, 31, 32–42. [Google Scholar]
- Xun, Q.; Wang, P.L.; Li, Z.X.; Cai, Z.D.; Qin, H.H. PMSM Parameters Identification Based on Recursive Least Square Method. Trans. China Electrotech. Soc. 2016, 31, 161–169. [Google Scholar]
- Choi, J.W.; Lee, S.C.; Kim, H.G. Inertia identification algorithm for high-performance speed control of electric motors. IEE Proc. Part B Electr. Power Appl. 2006, 153, 379–386. [Google Scholar] [CrossRef]
- Kim, S. Moment of Inertia and Friction Torque Coefficient Identification in a Servo Drive System. IEEE Trans. Ind. Electron. 2019, 66, 60–70. [Google Scholar] [CrossRef]
- Yao, L.; Qiu, X.; Wang, H.; Yan, Y. Methods of Inertia Identification for Permanent Magnet AC Servo System. Electr. Mach. Control Appl. 2013, 32, 29–35. [Google Scholar]
- Xu, H.; Zhu, X.; Li, Q.; Zhao, D.; Wang, L. Inertia Identification of Servo System Based on Improved Acceleration Deceleration Method. In Proceedings of the International Conference on Intelligent Human-machine Systems & Cybernetics, Hangzhou, China, 27–28 August 2016. [Google Scholar]
- Andoh, F. Moment of Inertia Identification Using the Time Average of the Product of Torque Reference Input and Motor Position. IEEE Trans. Power Electron. 2007, 22, 2534–2542. [Google Scholar] [CrossRef]
- Huynh, D.C.; Dunnigan, M.W. Parameter estimation of an induction machine using advanced particle swarm optimisation algorithms. IET Electr. Power Appl. 2010, 4, 748–760. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wei, H.L.; Zhong, Q.C.; Liu, K.; Xiao, X.S.; Wu, L.H. Parameter Estimation for VSI-Fed PMSM Based on a Dynamic PSO With Learning Strategies. IEEE Trans. Power Electron. 2017, 32, 3154–3165. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Arce-Santana, E.R.; Espinoza-Trejo, D.R. Edge optimisation for parameter identification of induction motors. IET Electr. Power Appl. 2011, 5, 668–675. [Google Scholar] [CrossRef]
- Ciampolini, M.; Fazzini, L.; Berzi, L.; Ferrara, G.; Pugi, L. Simplified Approach for Developing Efficiency Maps of High-Speed PMSM Machines for Use in EAT Systems Starting from Single-Point Data. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Allotta, B.; Costanzi, R.; Gelli, J.; Pugi, L.; Ridolfi, A. Design of a modular propulsion system for MARTA AUV. In Proceedings of the OCEANS 2015—Genova, Genoa, Italy, 18–21 May 2015. [Google Scholar]
- Pugi, L.; Berzi, L.; Savi, R.; Vita, V.; Grasso, F.; Delogu, M.; Boni, E. Electrification of an Innovative Directional Drilling Machine: Sizing and Design Models. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020. [Google Scholar]
- Wang, X.; Liu, J. Differentiator Design and Application—Signal Filtering and Differentiation, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2010; pp. 157–159. [Google Scholar]



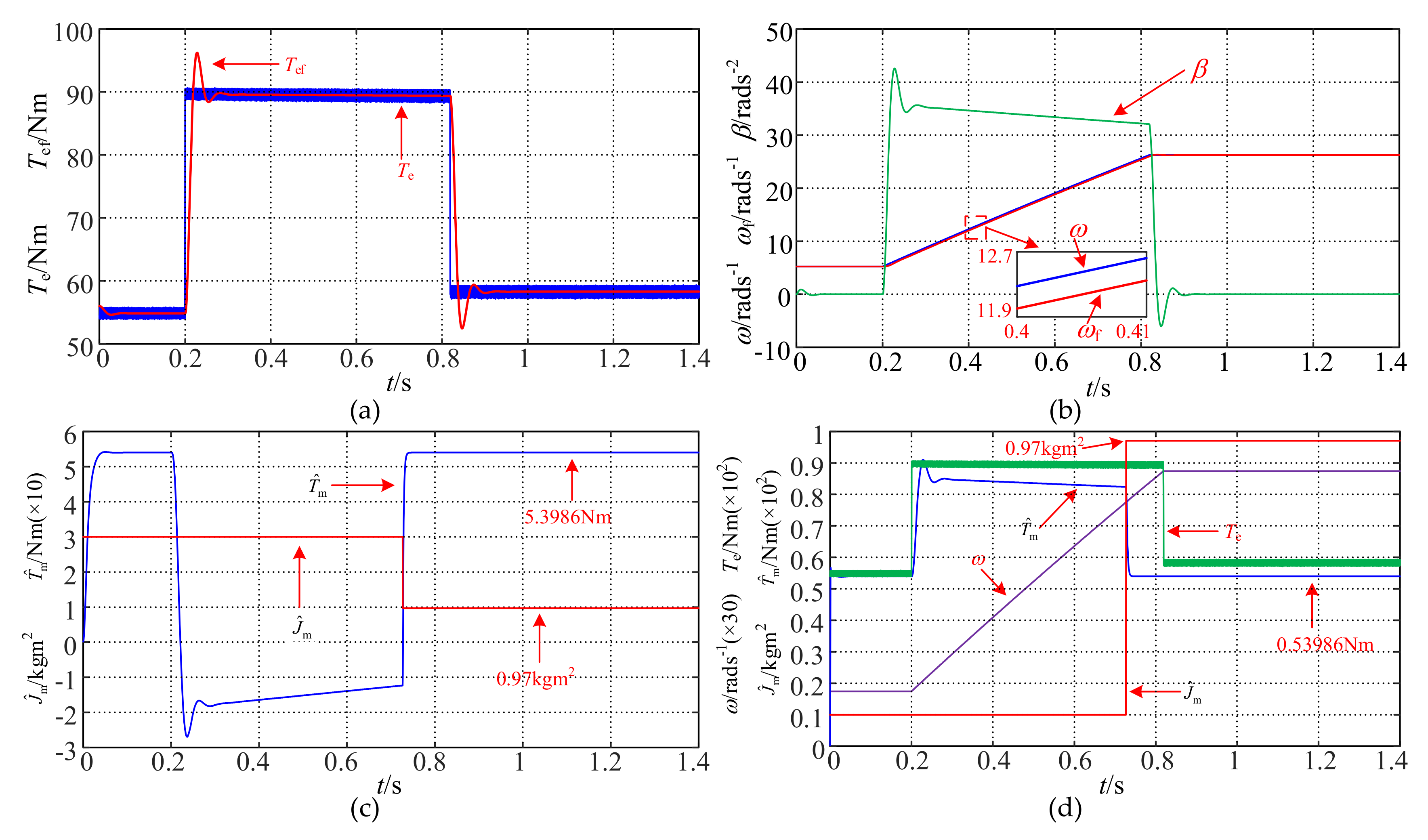

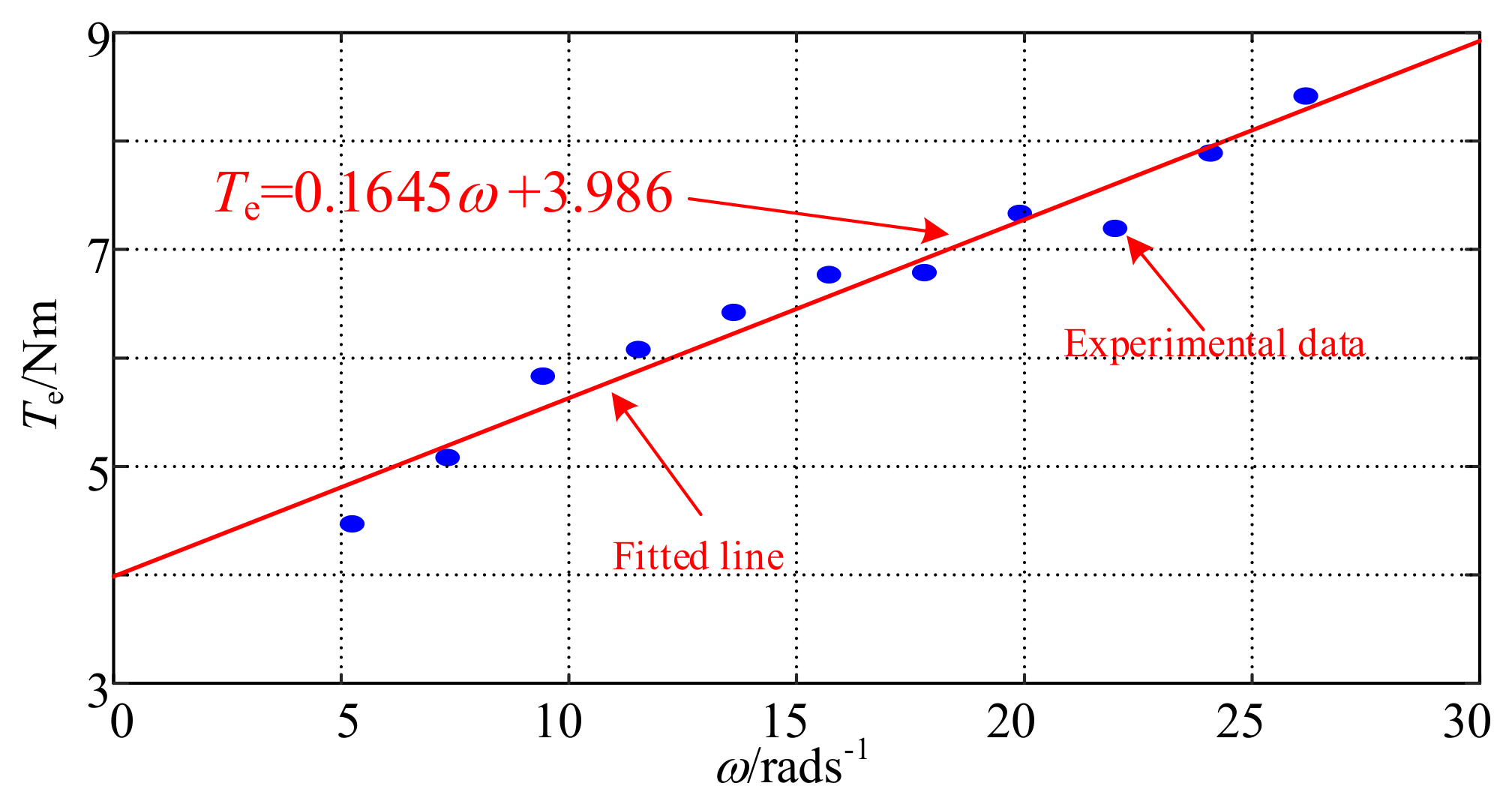


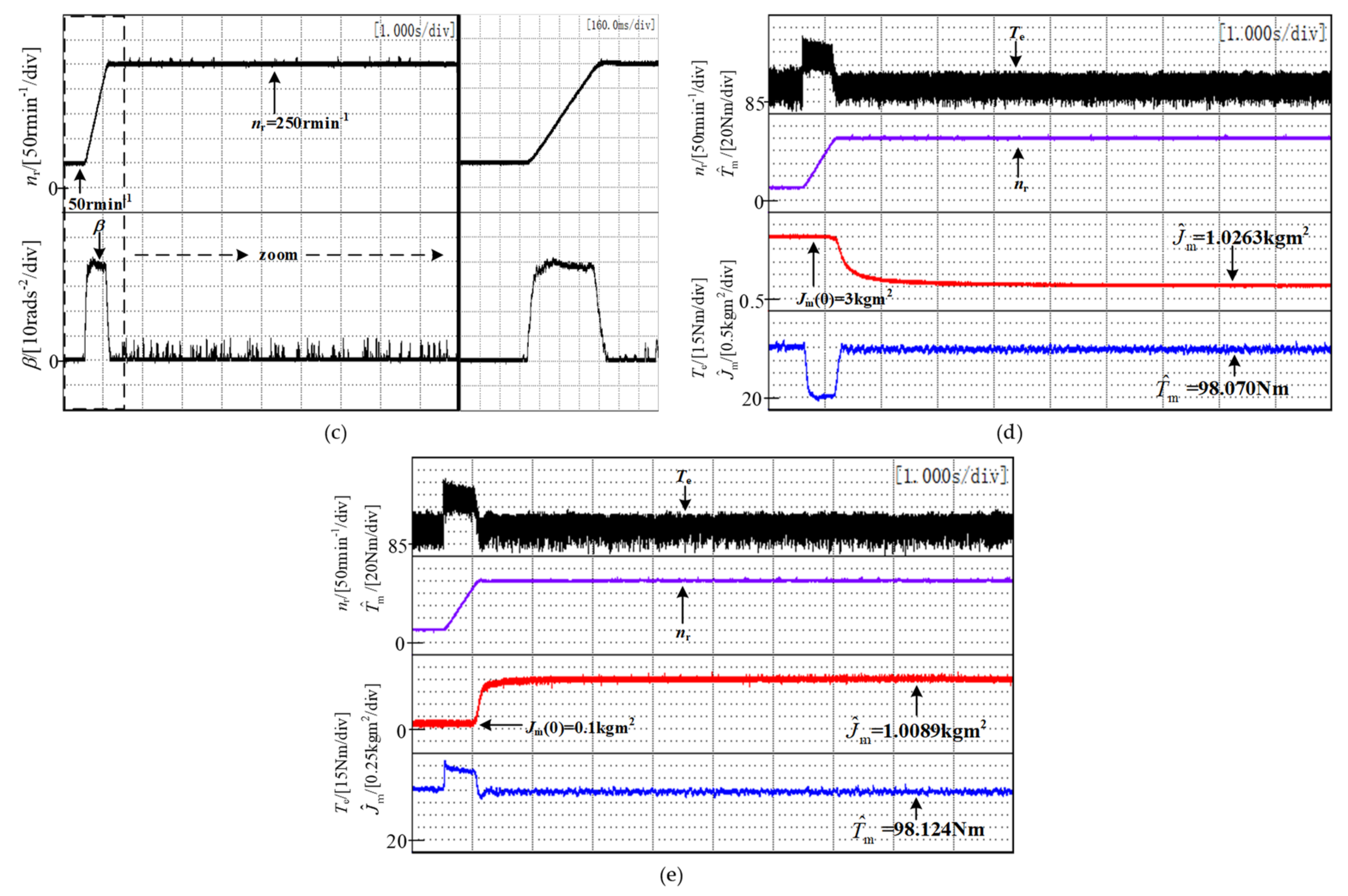
| Parameter | Quantity |
|---|---|
| Rated Power | 6 kW |
| Rated Torque | 192 Nm |
| Rated Speed | 300 r/min |
| Rated Current | 11.8 A |
| Number of pole-pairs | 8 |
| Stator resistance | 0.76 Ω |
| Stator inductance | 13 mH |
| Moment of inertia (with loading motor) | 0.97 kg m2 |
| Parameter Value | Method | Δt(ΔT)/s | ||
|---|---|---|---|---|
| Bm = 0.1645 | Conventional | 0.1 | 1.1461 | 18.15 |
| 0.2 | 1.1564 | 19.22 | ||
| Cm = 3.986 | Improved | 0.02 | 0.9817 | 1.21 |
| 0.1 | 0.9902 | 2.08 | ||
| Bm = 0 | Conventional | 0.1 | 0.9806 | 1.09 |
| Cm = 0 | Improved | 0.02 | 0.9666 | 0.35 |
| Bm = 0 | Conventional | 0.1 | 1.0905 | 12.42 |
| Cm = 3.986 | Improved | 0.02 | 0.9639 | 0.63 |
| Method | Moment of Inertia | Total Load Torque | ||
|---|---|---|---|---|
| Conventional | 1.1547 | 19.04 | - | - |
| Improved | 0.9980 | 2.89 | - | - |
| Proposed in this paper | 0.9700 | 0 | 53.9860 | 0 |
| Tm/Nm | Method | Moment of Inertia | Total Load Torque | ||
|---|---|---|---|---|---|
| 53.986 | Conventional | 1.1558 | 19.15 | - | - |
| Improved | 1.0452 | 7.75 | - | - | |
| Proposed in this paper | 1.0103 | 4.15 | 51.353 | 4.88 | |
| 103.986 | Conventional | 1.0756 | 10.89 | - | - |
| Improved | 0.9131 | 5.87 | - | - | |
| Proposed in this paper | 1.0176 | 4.91 | 98.097 | 5.66 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, C.; Yan, Y.; Lin, S.; Gao, L.; Wang, Z.; Shi, T. A Novel Moment of Inertia Identification Strategy for Permanent Magnet Motor System Based on Integral Chain Differentiator and Kalman Filter. Energies 2021, 14, 166. https://doi.org/10.3390/en14010166
Jing C, Yan Y, Lin S, Gao L, Wang Z, Shi T. A Novel Moment of Inertia Identification Strategy for Permanent Magnet Motor System Based on Integral Chain Differentiator and Kalman Filter. Energies. 2021; 14(1):166. https://doi.org/10.3390/en14010166
Chicago/Turabian StyleJing, Chenchen, Yan Yan, Shiyu Lin, Le Gao, Zhixin Wang, and Tingna Shi. 2021. "A Novel Moment of Inertia Identification Strategy for Permanent Magnet Motor System Based on Integral Chain Differentiator and Kalman Filter" Energies 14, no. 1: 166. https://doi.org/10.3390/en14010166
APA StyleJing, C., Yan, Y., Lin, S., Gao, L., Wang, Z., & Shi, T. (2021). A Novel Moment of Inertia Identification Strategy for Permanent Magnet Motor System Based on Integral Chain Differentiator and Kalman Filter. Energies, 14(1), 166. https://doi.org/10.3390/en14010166







