A Frequency Estimation Method Based on a Revised 3-Level Discrete Fourier Transform with an Estimation Delay Reduction Technique
Abstract
1. Introduction
- The revised 3LDFT can improve harmonic and inter-harmonic suppression performance.
- The proposed frequency estimation method by adding four orthogonal components helps to suppress harmonics and inter-harmonics, which increases the frequency estimation accuracy. However, a potential weakness of the proposed method is the estimation delay error caused by three cycles and three samples.
- Therefore, as a final step, the estimation delay error would be decreased tremendously using the estimation delay reduction technique, compensating for the phase delay of the phasor.
2. The Proposed Frequency Estimation Technique
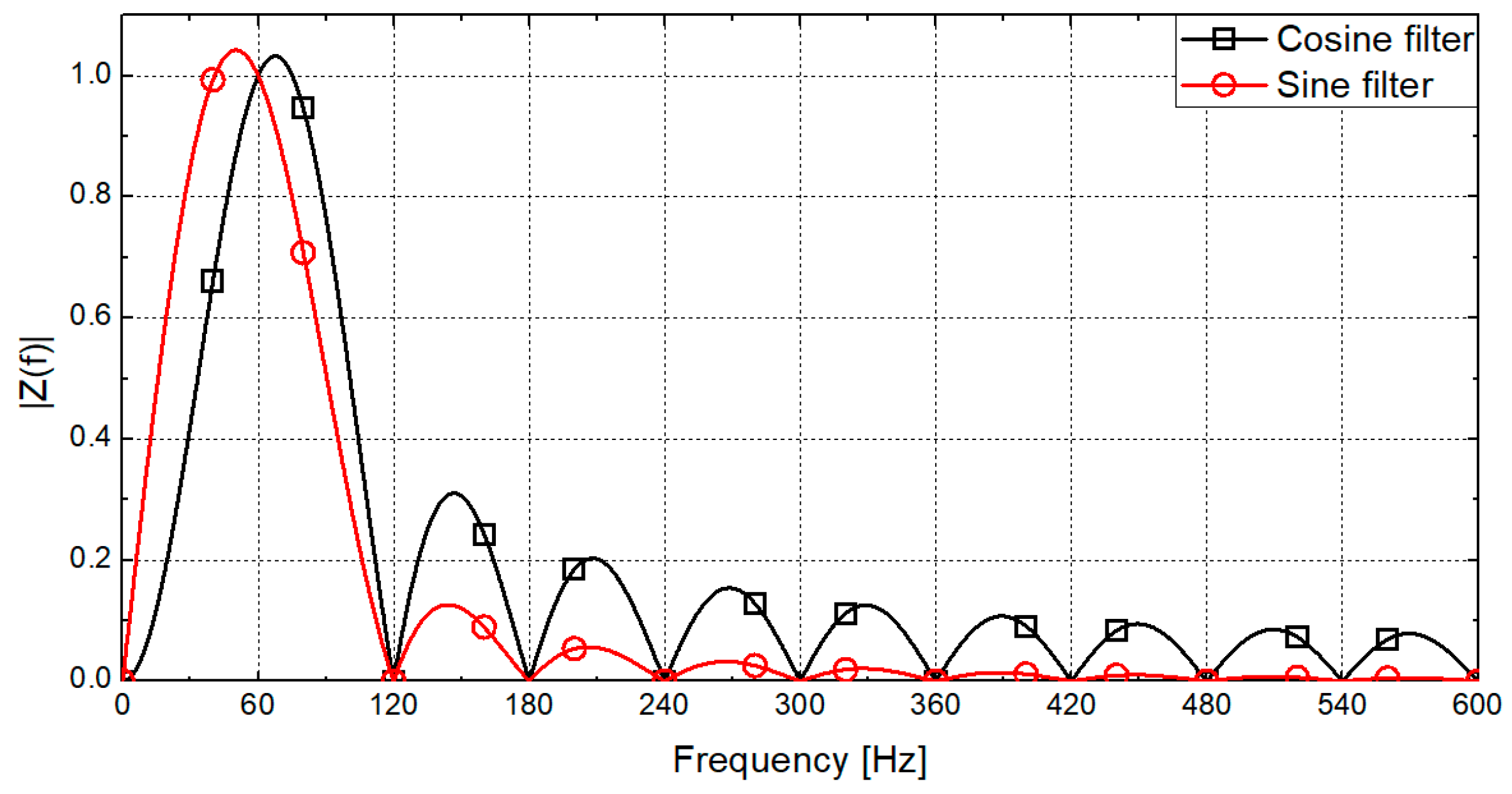
2.1. Sine-Filtered Signals
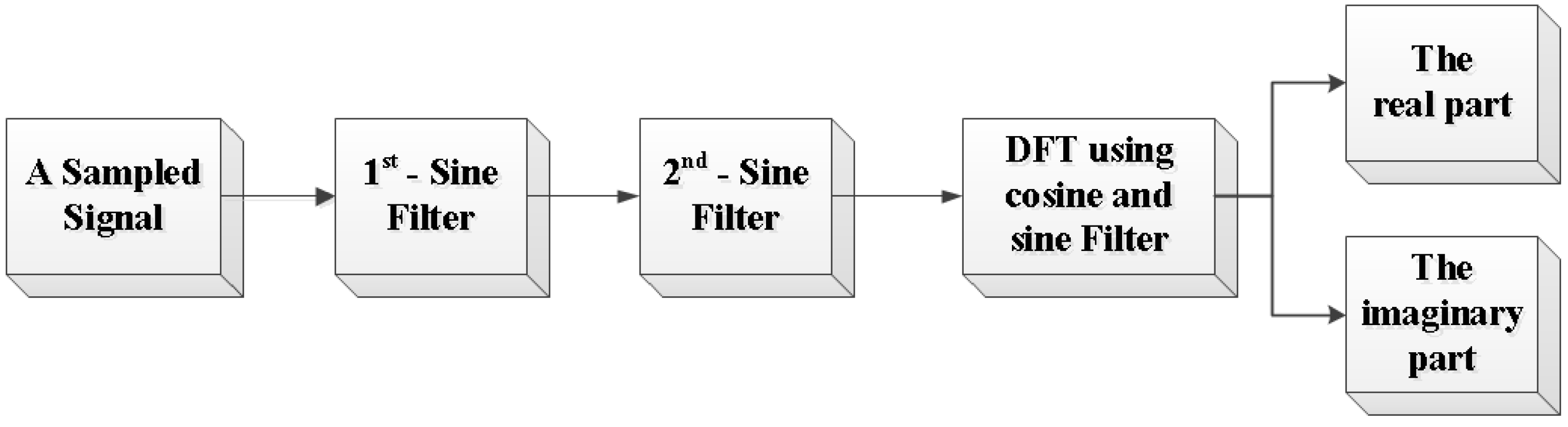
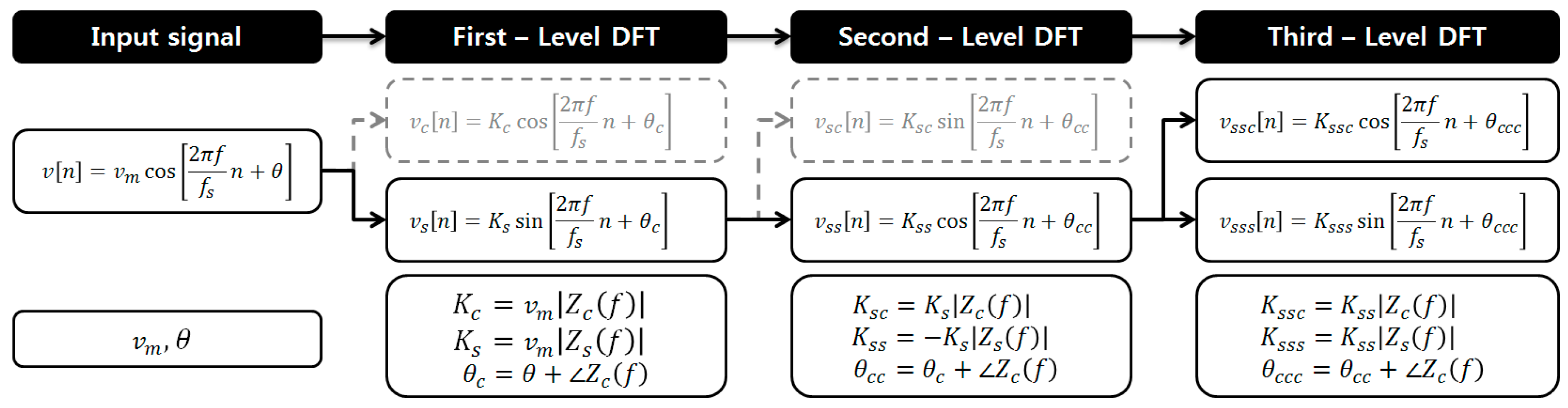
2.2. The Novel Frequency Estimation Method
2.3. The Estimation Delay Reduction Technique
2.4. A Flowchart of the Proposed Method
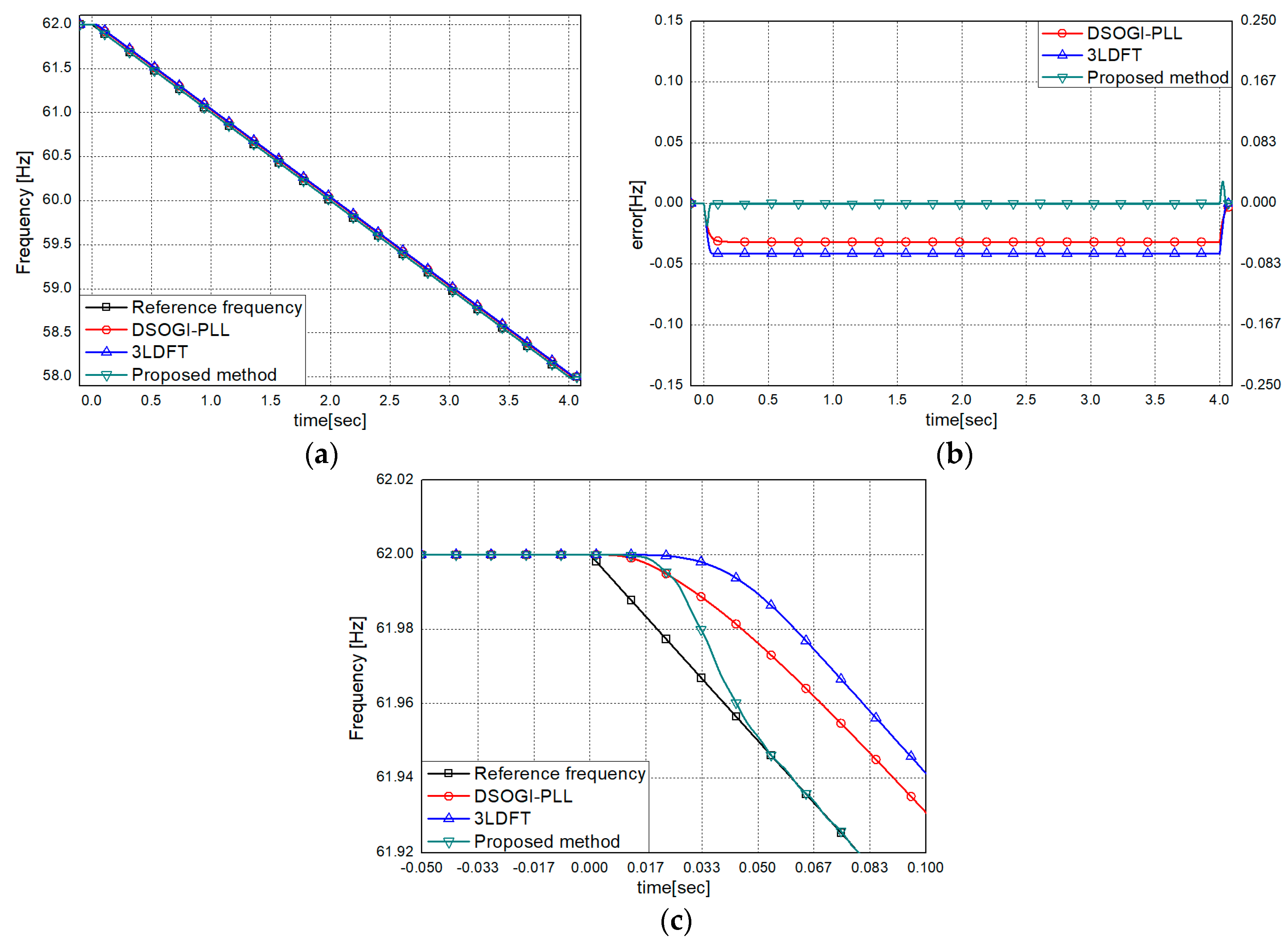
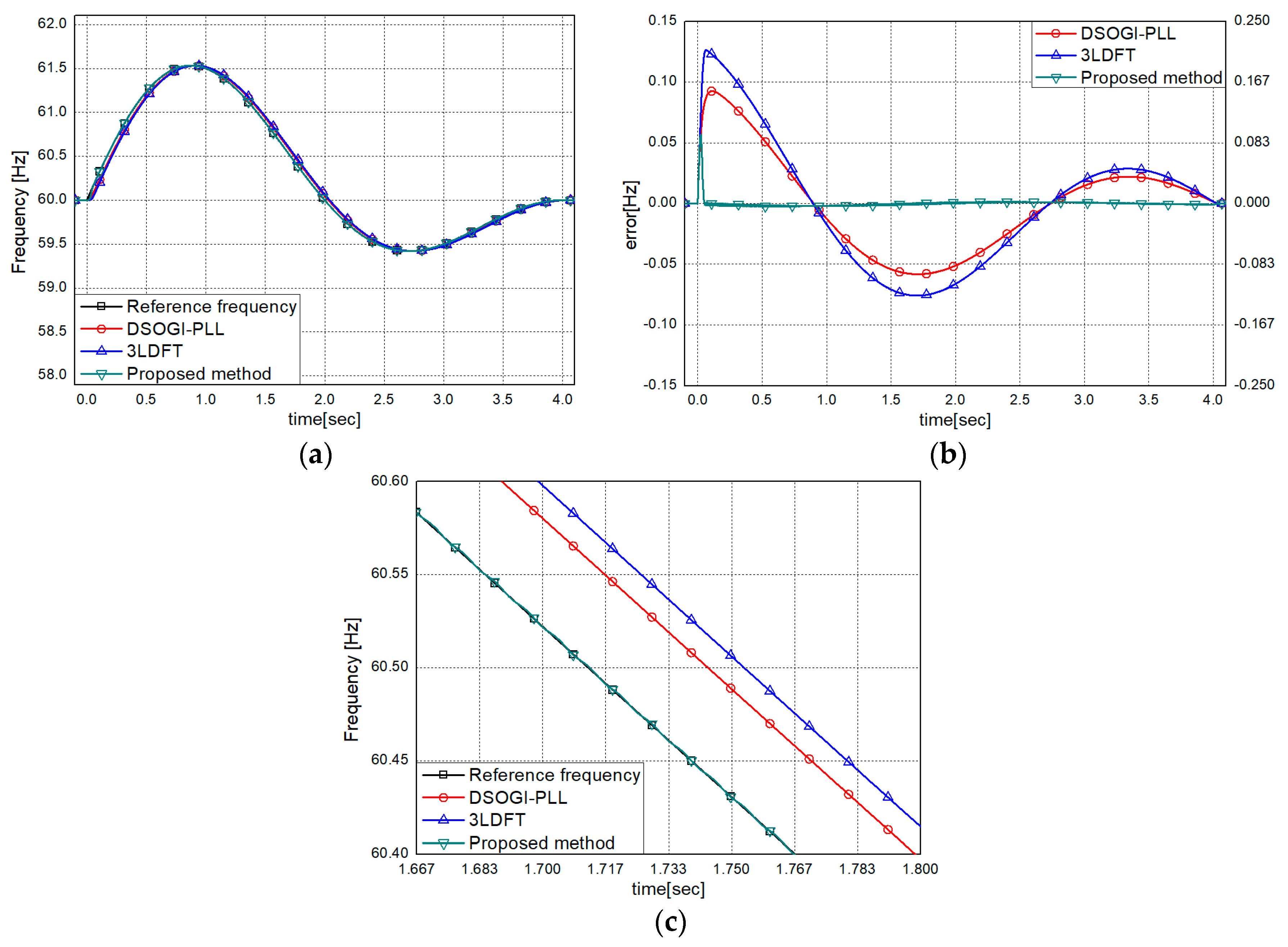
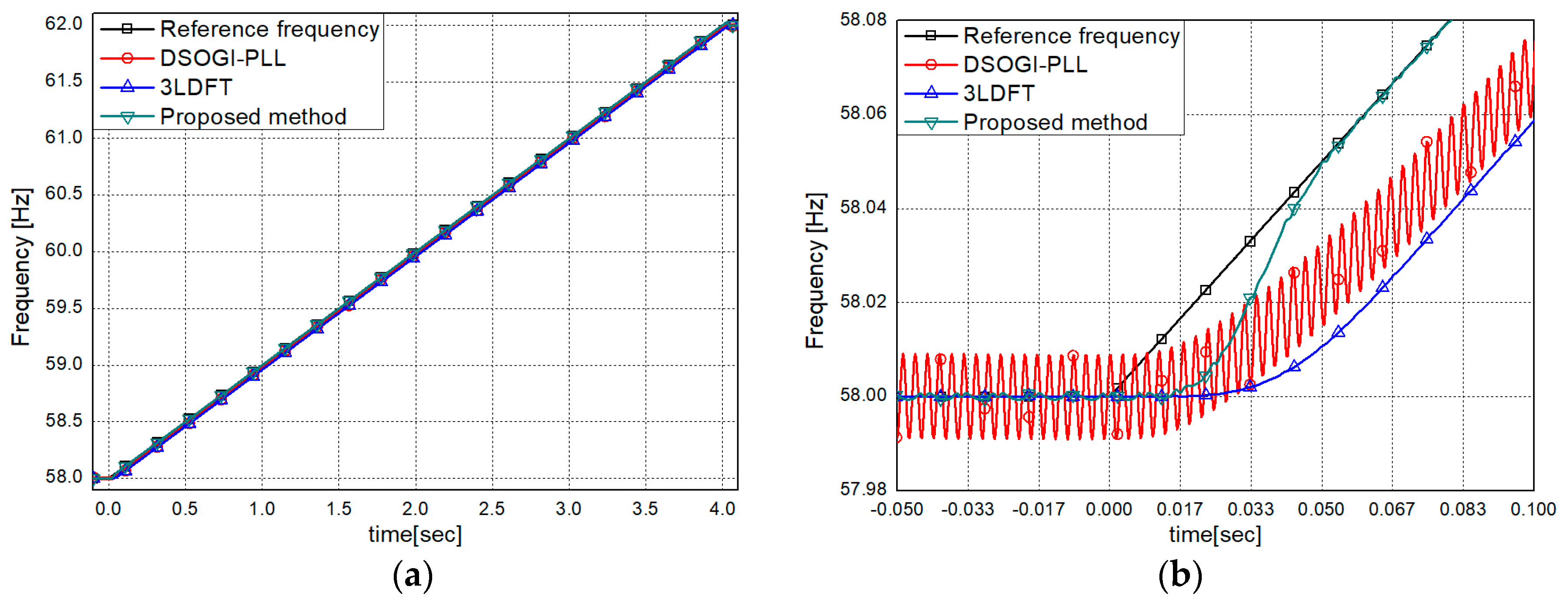
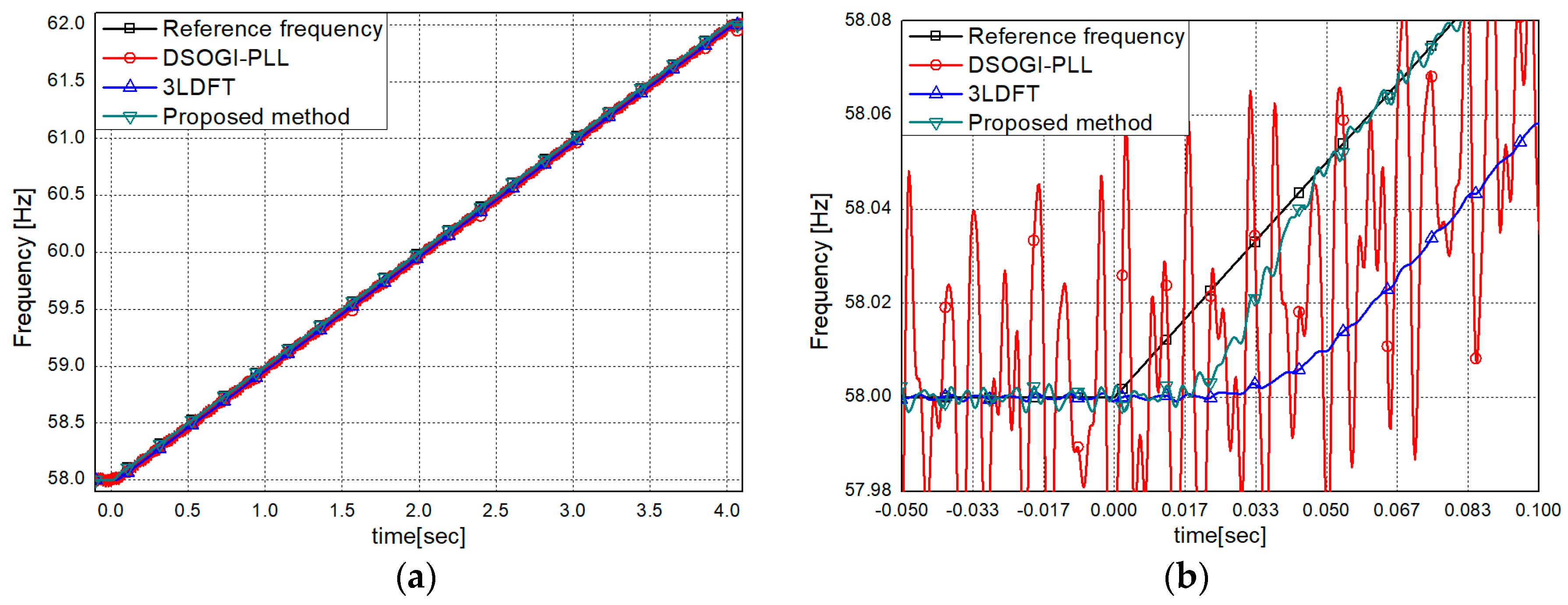
3. Performance Evaluation
3.1. Using Computer Generated Signals
3.1.1. Tests for Basic Signals
3.1.2. Tests for Harmonics and Inter-Harmonics
3.2. Using the PSCAD/EMTDC-Generated Signals
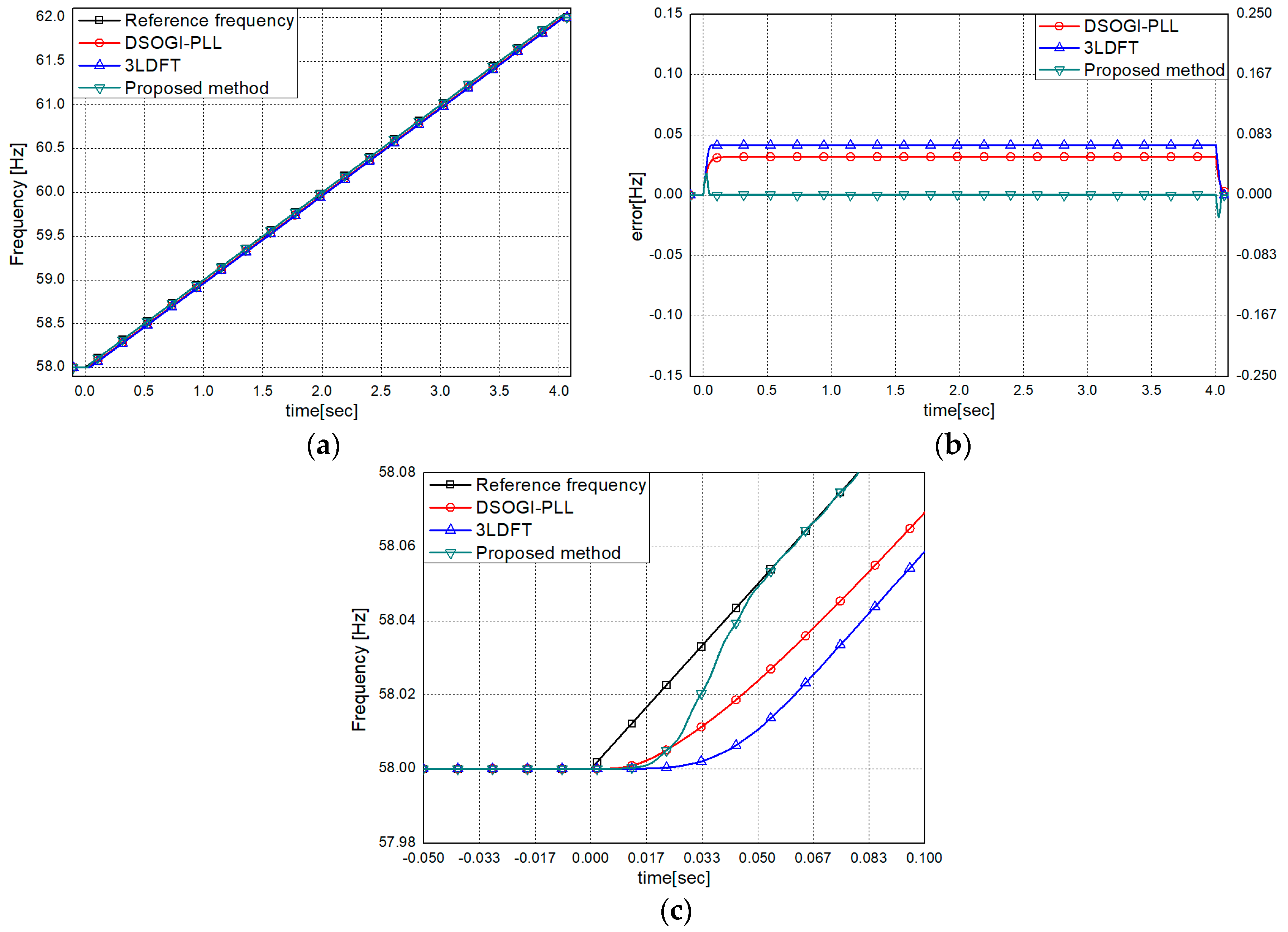
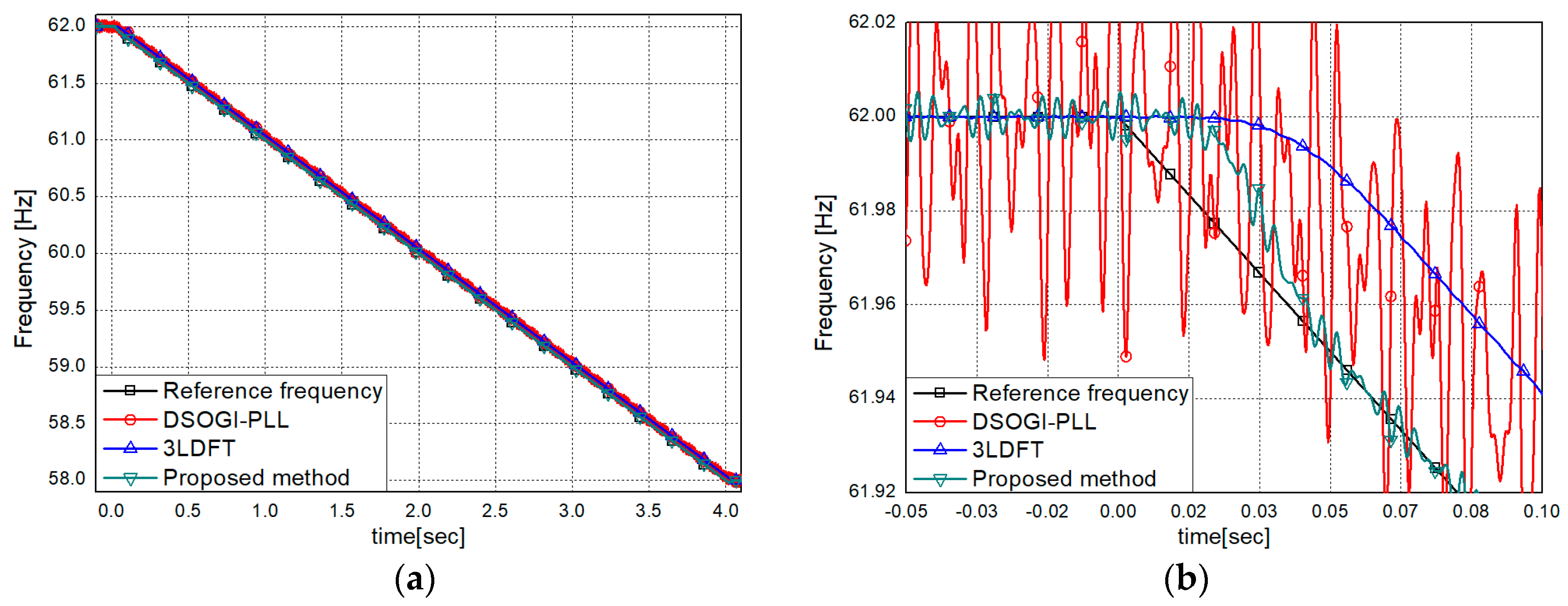
3.2.1. Dynamic Condition
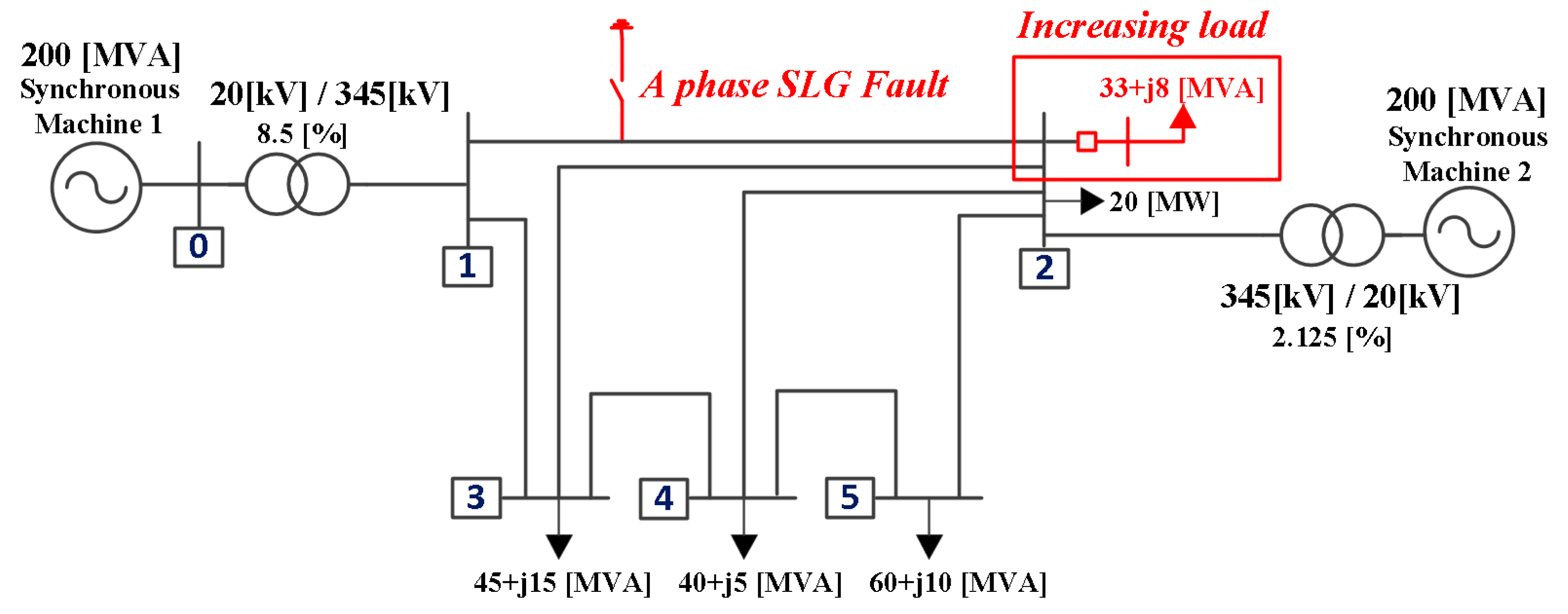
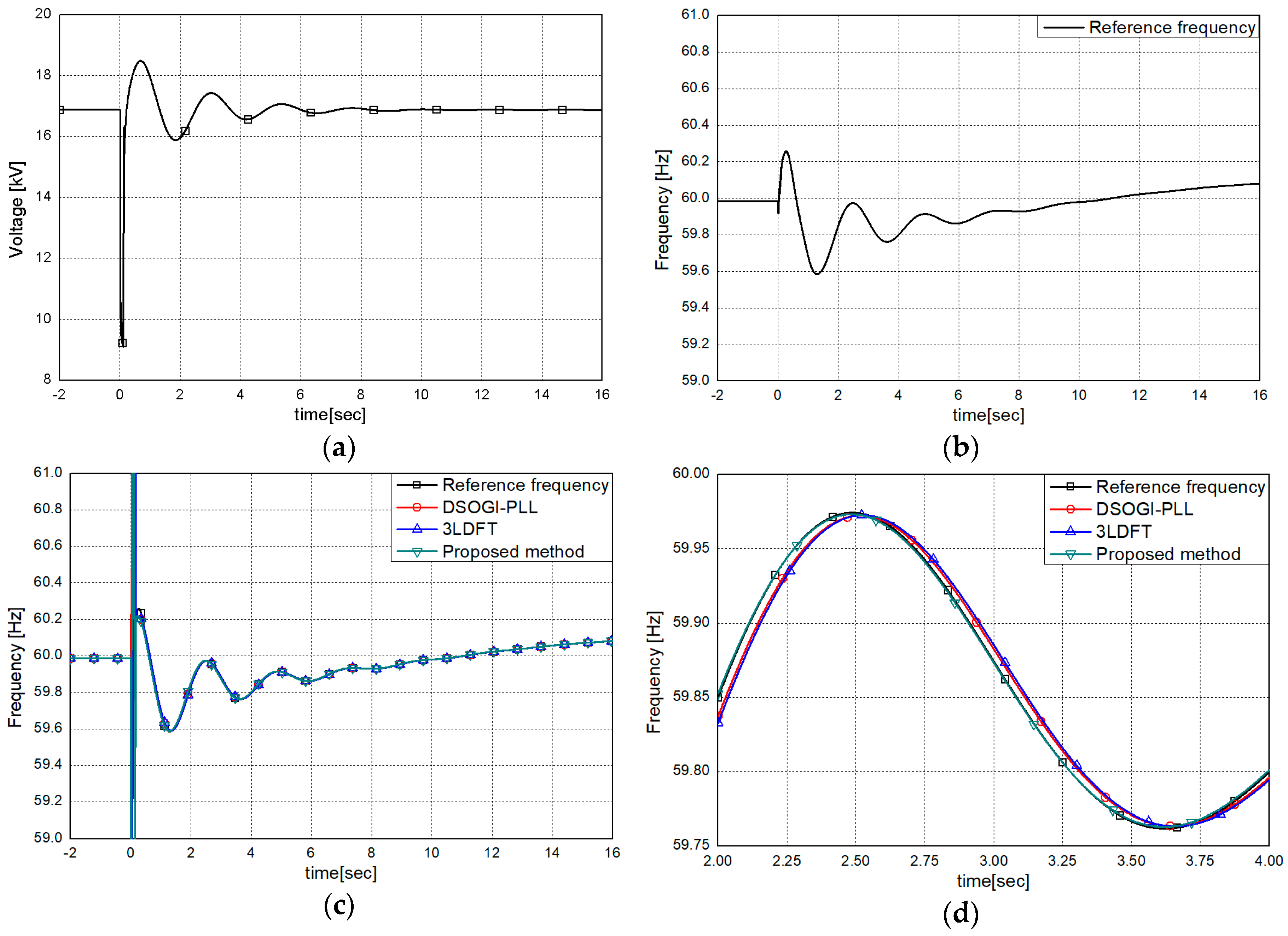
3.2.2. The Single Line-to-Ground Fault
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reza, A.; Kutluyıl, D.; Stefan, W. Recursive Total Least-Square Estimation of Frequency in Three-Phase Power Systems. In Proceedings of the 22nd European Signal Processing Conference, Lisbon, Portugal, 1–5 September 2014. [Google Scholar]
- Thomas, D.W.P.; Woolfson, M.S. Evaluation of Frequency Tracking Methods. IEEE Trans. Power Deliv. 2001, 16, 367–371. [Google Scholar] [CrossRef]
- Aghazadeh, R.; Lesani, H.; Pasand, S.M.; Ganji, B. New Technique for Frequency and Amplitude Estimation of Power System Signals. IEE Proc. Gener. Transm. Distrib. 2005, 152, 435–440. [Google Scholar] [CrossRef]
- Djuric, M.B.; Djurisic, Z.R. Frequency Measurement of Distorted Signals Using Fourier and Zero Crossing Techniques. Electr. Power Syst. Res. 2008, 78, 1407–1415. [Google Scholar] [CrossRef]
- Zheng, L.; Geng, H.; Yang, G. Fast and robust phase estimation algorithm for heavily distorted grid conditions. IEEE Trans. Ind. Electron. 2016, 63, 6845–6855. [Google Scholar] [CrossRef]
- Kaura, V.; Blasko, V. Operation of a Phase Locked Loop System under Distorted Utility Conditions. IEEE Trans. Ind. Appl. 1997, 33, 58–63. [Google Scholar] [CrossRef]
- Chung, S.K. A Phase Tracking System for Three Phase Utility Interface Inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Muñoz-Aguilar, R.S.; Etxeberria-Otadui, I.; Teodorescu, R.; Blaabjerg, F. A Stationary Reference Frame Grid Synchronization System for Three-Phase Grid-Connected Power Converters under Adverse Grid Conditions. IEEE Trans. Power Electron. 2012, 27, 99–112. [Google Scholar] [CrossRef]
- Ahmed, H.; Amamra, S.; Salgado, I. Fast Estimation of Phase and Frequency for Single-Phase Grid Signal. IEEE Trans. Ind. Electron. 2019, 66, 6408–6411. [Google Scholar] [CrossRef]
- Terzija, V.; Cai, D.; Stanojevic, V.; Strbac, G. Frequency and Power Components Estimation from Instantaneous Power Signal. IEEE Trans. Instrum. Meas. 2011, 60, 3640–3649. [Google Scholar] [CrossRef]
- Kusljevic, M.D. A Simple Recursive Algorithm for Simultaneous Magnitude and Frequency Estimation. IEEE Trans. Instrum. Meas. 2008, 57, 1207–1214. [Google Scholar] [CrossRef]
- Routray, A.; Pradhan, A.K.; Rao, K.P. A Novel Kalman Filter for Frequency Estimation of Distorted Signals in Power Systems. IEEE Trans. Instrum. Meas. 2002, 51, 469–479. [Google Scholar] [CrossRef]
- Dash, P.K.; Pardhan, A.K.; Panda, G. Frequency Estimation of Distorted Power System Signals Using Extended Complex Kalman Filter. IEEE Trans. Power Deliv. 1999, 14, 761–766. [Google Scholar] [CrossRef]
- Giray, M.M.; Sachdev, M.S. Off-Nominal Frequency Measurement in Electric Power Systems. IEEE Trans. Power Deliv. 1989, 4, 1573–1578. [Google Scholar] [CrossRef]
- Chudamani, R.; Vasudevan, K.; Ramalingam, C.S. Real-Time Estimation of Power System Frequency Using Nonlinear Least Squares. IEEE Trans. Power Deliv. 2009, 24, 1021–1028. [Google Scholar] [CrossRef]
- Rao, A.V.K.; Soni, K.M.; Sinha, S.K.; Nasiruddin, I. Accurate phasor and frequency estimation during power system oscillations using least squares. IET Sci. Meas. Technol. 2019, 13, 989–994. [Google Scholar]
- Dash, P.K.; Swain, D.P.; Routray, A.; Liew, A.C. An Adaptive Neural Network Approach for the Estimation of Power System Frequency. Electr. Power Syst. Res. 1997, 41, 203–210. [Google Scholar] [CrossRef]
- Lai, L.L.; Chan, W.L.; Tse, C.T.; So, A.T.P. Real-Time Frequency and Harmonic Evaluation Using Artificial Neural Networks. IEEE Trans. Power Deliv. 1999, 14, 52–59. [Google Scholar] [CrossRef]
- Lobos, T.; Rezmer, J. Real-Time Determination of Power System Frequency. IEEE Trans. Instrum. Meas. 1997, 46, 877–881. [Google Scholar] [CrossRef]
- Nam, S.R.; Lee, D.G.; Kang, S.H.; Ahn, S.J.; Choi, J.H. Fundamental Frequency Estimation in Power Systems Using Complex Prony Analysis. J. Electr. Eng. Technol. 2011, 6, 154–160. [Google Scholar] [CrossRef]
- Vladimir, V.T.; Milenko, B.D.; Branko, D.K. Voltage Phasor and Local System Frequency Estimation Using Newton Type Algorithm. IEEE Trans. Power Deliv. 1994, 9, 1368–1374. [Google Scholar]
- Vladimir, V.T.; Dragan, M. Symmetrical Components Estimation through Nonrecursive Newton-Type Numerical Algorithm. IEEE Trans. Power Deliv. 2003, 18, 359–363. [Google Scholar]
- Moore, P.J.; Carranza, R.D.; Johns, A.T. A New Numeric Technique for High-Speed Evaluation of Power System Frequency. IEE Proc. Gener. Transm. Distrib. 1994, 141, 529–536. [Google Scholar] [CrossRef]
- Frigo, G.; Derviškadić, A.; Paolone, M. Reduced Leakage Synchrophasor Estimation: Hilbert Transform Plus Interpolated DFT. IEEE Trans. Instrum. Meas. 2019, 68, 3468–3483. [Google Scholar] [CrossRef]
- Park, S.Y.; Song, Y.S.; Kim, J.H.; Park, J.S. Improved Method for Frequency Estimation of Sampled Sinusoidal Signals without Iteration. IEEE Trans. Instrum. Meas. 2011, 60, 2828–2834. [Google Scholar] [CrossRef]
- Nam, S.R.; Kang, S.H.; Kang, S.H. Real-Time Estimation of Power System Frequency Using a Three-Level Discrete Fourier Transform Method. Energies 2015, 8, 79–93. [Google Scholar] [CrossRef]
- Seo, W.S.; Kang, S.H.; Nam, S.R. Non-recursive Discrete Fourier Transform-Based Frequency Estimation of the Power System. J. Electr. Eng. Technol. 2019, 14, 1505–1515. [Google Scholar] [CrossRef]
- IEEE Standard for Synchrophasor Measurements for Power Systems. IEEE Standard C.37.118.1a-2014; IEEE Standard for Synchrophasor Measurements for Power Systems: Piscataway, NJ, USA, 2014. [Google Scholar]





| Harmonics order | 1 | 3 | 5 | 7 | 9 |
| Percentage | 100 | 20 | 20 | 10 | 10 |
| Harmonics order | 1 | 3 | 3.4 | 4.4 | 5 | 7 | 9 |
| Percentage | 100 | 20 | 10 | 10 | 20 | 10 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.-H.; Seo, W.-S.; Nam, S.-R. A Frequency Estimation Method Based on a Revised 3-Level Discrete Fourier Transform with an Estimation Delay Reduction Technique. Energies 2020, 13, 2256. https://doi.org/10.3390/en13092256
Kang S-H, Seo W-S, Nam S-R. A Frequency Estimation Method Based on a Revised 3-Level Discrete Fourier Transform with an Estimation Delay Reduction Technique. Energies. 2020; 13(9):2256. https://doi.org/10.3390/en13092256
Chicago/Turabian StyleKang, Sang-Hee, Woo-Seok Seo, and Soon-Ryul Nam. 2020. "A Frequency Estimation Method Based on a Revised 3-Level Discrete Fourier Transform with an Estimation Delay Reduction Technique" Energies 13, no. 9: 2256. https://doi.org/10.3390/en13092256
APA StyleKang, S.-H., Seo, W.-S., & Nam, S.-R. (2020). A Frequency Estimation Method Based on a Revised 3-Level Discrete Fourier Transform with an Estimation Delay Reduction Technique. Energies, 13(9), 2256. https://doi.org/10.3390/en13092256





