1. Introduction
The worldwide installed wind capacity has increased rapidly over recent years and decades [
1,
2]. This has resulted in an ever increasing number of older industrial wind farms, on a global scale, reaching an age where major component replacements and re-powering are on the horizon.
It is remarkable that most of the attention about wind turbines aging regards the reliability [
3,
4,
5] and the failure rates [
6], instead of the performance decline. This in some senses is a bit surprising for at least two reasons: all technical systems are subjected to deterioration and there is no theoretical model about wind turbine performance deterioration with time, which is not due only to increasing failure rates but as well to aerodynamic performance and conversion efficiency decline. Therefore, it is necessary to learn from the experience and in particular from the widespread diffusion of Supervisory Control And Data Acquisition (SCADA) data. There is an impressive amount of scientific literature about the use of wind turbine SCADA data for condition monitoring [
7], fault diagnosis [
8] and also performance monitoring [
9,
10,
11], but operation data, to date, has not been well exploited for the assessment of wind turbine performance deterioration with age.
On these grounds, the present study aims to make a contribution to the objective of a data-driven comprehension of how the performance of wind turbines deteriorate with age.
At present, at the best of authors knowledge, there are three main studies about the subject. In [
12], the public data from 282 wind farms sited in United Kingdom are elaborated, covering 1686 farm-years of operation. In this study, wind speed data with high temporal and spatial resolution are used to measure the performance of wind farms by estimating their theoretical potential output over the course of a month and comparing this with the actual reported load factors. The estimate is that the load factor declines by 1.57% per year: over a 20-year lifetime, this corresponds to a 12% reduction and a 9% increase of the electricity cost. Another important consideration from the study in [
12] is that this order of magnitude for the performance decline is remarkable but it is not disastrous because it is in line, for example, with gas turbine technology [
13]. The study in [
14] refers to wind turbines operating in Sweden, constructed before 2007. The methods and the results are different with respect to [
12]: it arises that there is a 0.15 capacity factor percentage points per year decline, corresponding to a lifetime energy loss of 6%; this estimate is lower with respect to [
12]. In [
15], four SCADA-based wind turbine ageing assessment criteria are proposed for measuring the ageing resultant performance degradation of the turbine: they are based on monitoring the power output, the power coefficient, the nacelle vibration and the temperature of key components. The method is applied on data sets from 2015 and 2016 and it is shown to be effective for estimating the aging effect; however, no lifetime estimate of the performance deterioration is proposed.
This work is a collaboration between the Dundalk Institute of Technology and the University of Perugia and it is based on the fact that the Dundalk Institute of Technology installed a 850 kW rated Vestas V52 wind turbine on its campus in October 2005 and this wind turbine is still operating. As discussed in detail in
Section 2, in October 2018 the gearbox of the wind turbine reached the end of life and has been replaced after thirteen years of operation. Therefore, the rationale of this study is employing the operation data of the wind turbine for investigating the performance deterioration with age. In addition, since the gearbox has been replaced, a data set is available describing the operation of the wind turbine with a new gearbox installed with no other modifications made to any of the other original principal components.
The objective of this study has been pursued through the use of the most innovative wind turbine performance monitoring techniques. A benchmark data set of one year, describing the wind turbine running in its first years of operation, has been selected for training a Support Vector Machine Regression with Gaussian Kernel [
16], whose target is the power output of the wind turbine. Doing this, a reference model is obtained and the performance deterioration is estimated by studying how the residuals between measurements and model estimates change from earlier to later data sets. These kinds of methods have been applied in the wind energy literature for test cases conceptually similar, despite having opposite outcomes (performance improvements, instead of ageing deterioration): wind turbine aerodynamic and-or control technology optimization [
17,
18,
19]. The effective use of these kind of methods for detecting performance changes of the order of few percents of Annual Energy Production has inspired their application for the test case of the present study. The regression method and the data sets available are described in
Section 3.
A further study has been included in this work, with a twofold objective: corroborating the results from the Support Vector Regression and providing some indication about the economic impact of the performance degradation and possible strategies for the wind turbine maintenance. A power curve analysis, based on the binning method recommended by the International Electrotechnical Commission (IEC) [
20], has been included in this study: its application is briefly described in
Section 3.3 and the results are reported in
Section 4.3.
Taking into account the different methodologies, the results obtained with the two approaches are substantially consistent: ten years later with respect to the reference data set, the performance and energy degradation is of the order of 5%.
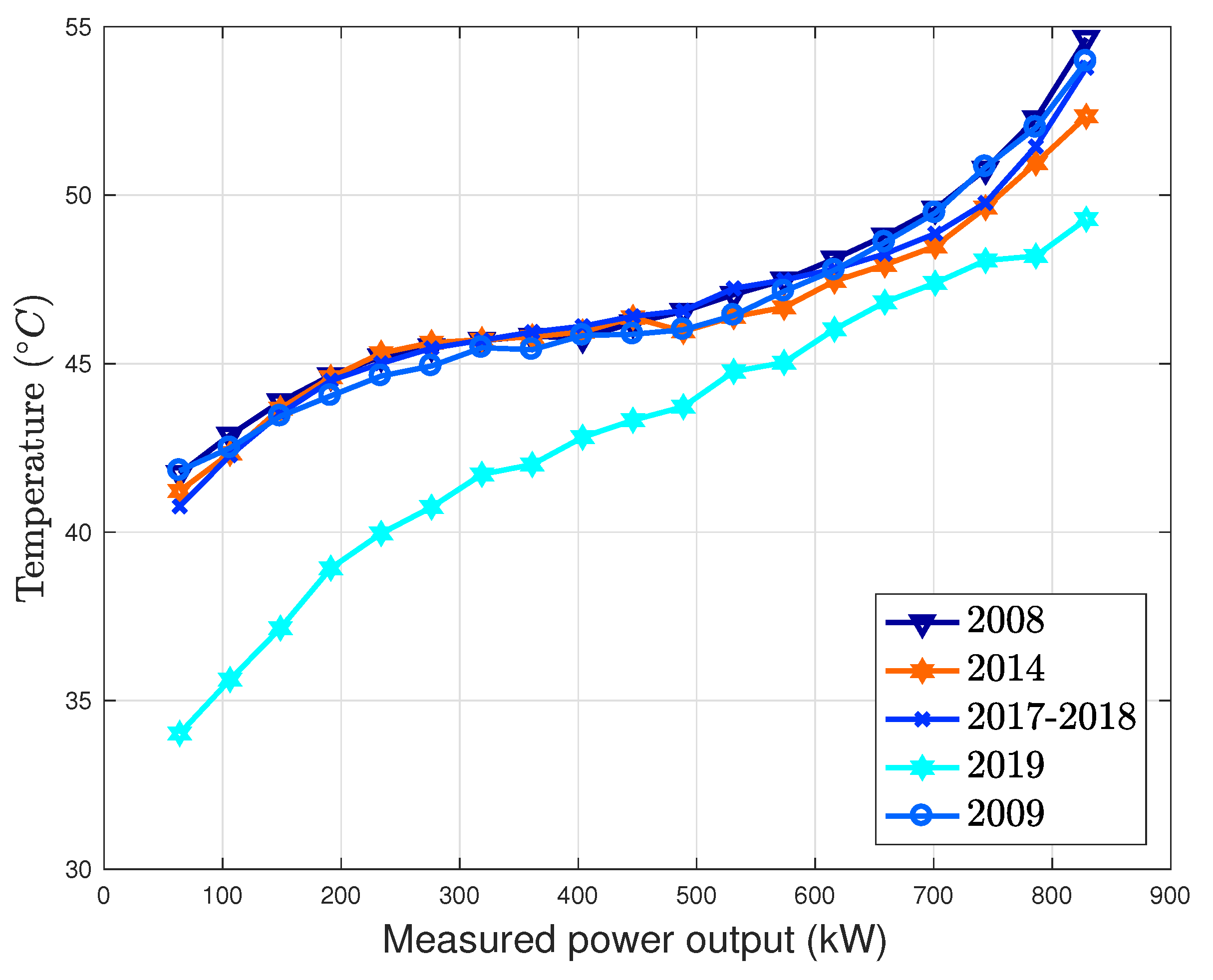
Furthermore, the data sets immediately before and immediately after the gearbox replacement have been compared: it arises that the performance improvement due to the replacement is clear, but of course it accounts for only part of the degradation that occurred as the rest of the machine also aged over the same time frame. Furthermore, an analysis about the gear oil temperature trend in time as a function of the power output has been included, motivated by the fact that there are arguments [
21] supporting that heating increase can be a meaningful indicator of gearbox efficiency and therefore of performance degradation.
The structure of the manuscript is the following:
Section 2 is devoted to the test case description; in
Section 3 the data analysis methods are discussed;
Section 4 is devoted to the results and, finally, in
Section 5 conclusions are drawn and some further direction of the present work is indicated.
2. The Test Case
Dundalk Institute of Technology (DkIT) is a tertiary educational establishment located on the northeast coast of Ireland. In October 2005 DkIT installed a single 850 kW rated Vestas V52 wind turbine on its campus. The turbine has a hub height of 60 m and at a rotor diameter of 52 m. The wind turbine location, as shown on the map in
Figure 1 can be described as a peri-urban coastal site. The site elevation is 13 m above sea level. The wind turbine operates as a wind autoproducer in that it is grid connected behind the main campus electricity meter. The produced electricity is primarily consumed onsite, while electricity exports to the national grid occur only when turbine generation exceeds campus demand [
22]. The economic value of the turbine is realised in avoided electricity purchases from the grid at retail electricity prices.
The Vestas V52 wind turbine is a semi-variable speed system doubly fed induction generator (DFIG). It has an active pitching system: the blade pitch angles of all three rotor blades are controlled simultaneously by a hydraulic pitch control system using the Vestas Opti-tipTM and Opti-speedTM control mechanisms. The control mechanisms aim to maximise energy capture at wind speeds below the rated power wind speed and to fix the power output to rated power at wind speeds above the rated power wind speed. In normal turbine operation the blade pitch angle is always below 20 degrees. In a fault condition or a pause/stop state, the blade pitch angle is fixed to approximately 86 degrees. Time series data of a number of turbine parameters are logged by the wind turbine SCADA system in 10-minute mean values. These parameters include: wind speed, wind speed standard deviation, absolute wind direction, relative wind direction, rotor RPM, generator RPM, blade pitch angle and power output. A number of 10-minute mean temperature parameters are also logged and include: gearbox oil temperature, gearbox bearing temperatures, generator bearing temperatures, internal nacelle temperature and external ambient air temperature at hub height.
In October 2018, the wind turbine gearbox, shown in
Figure 2 and principal specifications in
Table 1, reached the end of life, after thirteen years of operation. Based on a gearbox boroscope inspection and oil sample tests, it was recommended by service provider that the gearbox be replaced. Impact marks and indentation on planetary bearing roller were observed along with wear marks on teeth flanks. The oil sample test results showed an elevated copper particle count that was well in excess of the its recommended limit. The gearbox was replaced with brand new gearbox of the same model and specifications in July 2019.
The 10-minute multi-annual SCADA data from the turbine control system is used in this study to examine the impact of gearbox replacement with the aim of assessing gearbox aging on the power and energy performance over the gearbox lifespan. The data used in
Table 2 are based on availability and sufficient time apart to examine the aging trends.
3. Methods
The objective of this part of the work is detecting and quantifying the performance degradation of the wind turbine, due to the gearbox aging, through operation data analysis.
In general, it is complex to monitor reliably wind turbine performance because of the multivariate dependence of wind turbine power on ambient conditions and working parameters.
The power of a wind turbine, below its rated speed, is defined as in Equation (
1):
where
is the air density,
A is the area swept by the rotor,
is the power factor which is function of the tip speed ratio
and of the blade pitch angle
. Not only
is a non-linear function of
and
, but the actual power factor can differ from the theoretical one due to environmental effects (like wind shear and turbulence) and due to wind turbine functioning (aging, malfunctioning and so on).
The simplest possible approach for monitoring the power P is to compare the observed power against a benchmark for the power curve, i.e., the relation between the wind speed and the power output. Despite the simplicity of this idea, selecting appropriately a data-driven benchmark power curve is questionable as well, for several reasons:
Wind turbines are typically equipped with cup anemometers mounted behind the rotor and the undisturbed wind speed is ex-post reconstructed through a nacelle transfer function;
The power curve has non-trivial seasonal and ambient conditions dependence.
For this reason, therefore, in the wind energy literature, the idea of employing the rotor as wind speed measurement probe has been recently gaining interest: this is the concept of rotor equivalent wind speed [
23,
24]. Thus, the performance monitoring task can translate into the monitoring of appropriate operation curves (alternative to the power curve), like the rotor speed–power curve [
25] and the blade pitch–power curve [
25,
26].
The idea of this work has been to generalize this concept by formulating a multivariate data-driven model, whose output
y is the power of the wind turbine and whose input variables are the most relevant ambient conditions and operation parameters measurements. This kind of approaches has been recently developing in the wind energy literature for performance monitoring and condition monitoring purposes. For some examples, refer to [
27,
28,
29,
30]. For a comprehensive point of view about the use of operation data in wind energy and about data-driven power curve models, refer to [
31]. In order to test the consistency of the proposed method and to provide as well a more intuitive benchmark, also the binned power curve analysis (as dictated by IEC guidelines [
20]) has been adopted (
Section 3.3) and the results are qualitatively compared and discussed.
3.1. Support Vector Machine Regression
For the purposes of the present work, a Support Vector Machine Regression with Gaussian kernel has been selected. As a premise, it should be noted that the consistency of this kind of regression for the objectives of the present work has been crosschecked by comparing the results against other kinds of regression, as for example Principal Component Regression (PCR) and Least Absolute Shrinkage and Selection Operator (LASSO) Regression. It arises that the Support Vector Machine Regression outperforms PCR and LASSO regression in terms of mean error, mean absolute error and root mean square error and furthermore the results are more stable from one model run to the other. These have been considered good arguments for considering the Support Vector Machine Regression an adequate method for this study.
The procedure goes as follows: first, let be the matrix of covariates and be the vector of the target (power output). The number of observations is N and we label a generic observation as n-th. Basing on the disposal of operation and ambient data for the present test case, the column vectors of contain the following regressors:
Undisturbed wind speed average, estimated by the control system through the nacelle transfer function;
Turbulence intensity, estimated as the ratio between the standard deviation and the average of the undisturbed wind speed;
Yaw angle;
Blade pitch angle;
Rotor speed;
Generator speed.
The wind speed
v has been renormalized (
) taking into account the external temperature measurement at disposal, as indicated for example in [
32] and in the IEC guidelines [
33], according to Equations (
2) and (
3):
with
being the air density in standard conditions (
),
being the standard temperature 288.15 K and
T being the external temperature measured on site in Kelvin units.
In order to understand the principles of Support Vector Regression [
34], consider at first a linear model (Equation (
4)):
The objective is finding
with the minimum norm value
subject to the residuals being lower than a threshold
for each observation (Equation (14)):
The optimization of the model is basically a trade-off between the flatness of
and the amount up to which residuals higher than
are tolerated. This can be better formulated in mathematical terms through the Lagrange dual formulation: the function to be minimized is
(Equation (
6)):
with the constraints (Equation (
7))
where
C is the box constraint.
The
parameters can then be rewritten as indicated in Equation (
8):
If either or is different from 0, the corresponding observation is called a support vector.
The model can then be used for predicting new values, given the input observation, through the function (Equation (
9)):
A nonlinear Support Vector Regression is obtained by replacing in the above formulas the dot products between observations matrix with a nonlinear Kernel function (Equation (
10)):
where
is a transformation mapping the
observations into a high-dimensional feature space.
A typical selection of the Kernel function has been adopted in this work, i.e., a Gaussian Kernel (Equation (
11)):
Then, for the nonlinear case, Equation (
6) rewrites as in Equation (
12):
and Equation (
9) for predicting rewrites as in Equation (
13):
3.2. The Data Sets Arrangement and the Performance Monitoring
The data sets before gearbox replacement, at disposal to the authors, have been organized in yearly packets:
;
;
;
;
;
.
Notice that with the data sets at disposal, it is possible to set the standards for the performance basing on the oldest data set at disposal (2008, when the wind turbine and the gearbox were less than 2 years old) and then it is possible to trace the performance evolution (or, better, degradation) from 2012 up to when the gearbox has been replaced (2018).
The data sets are subsequently employed as follows for the regression:
is randomly divided in two subsets: D0 (a random selection of of the data set) and D1 (the remainder of the data set). D0 is used for training the regression, D1 is used for testing the regression. The convergence of model training is obtained through the MATLAB® routine.
A data set posterior to is named as D2 and is used to quantify the performance deviation with respect to 2008.
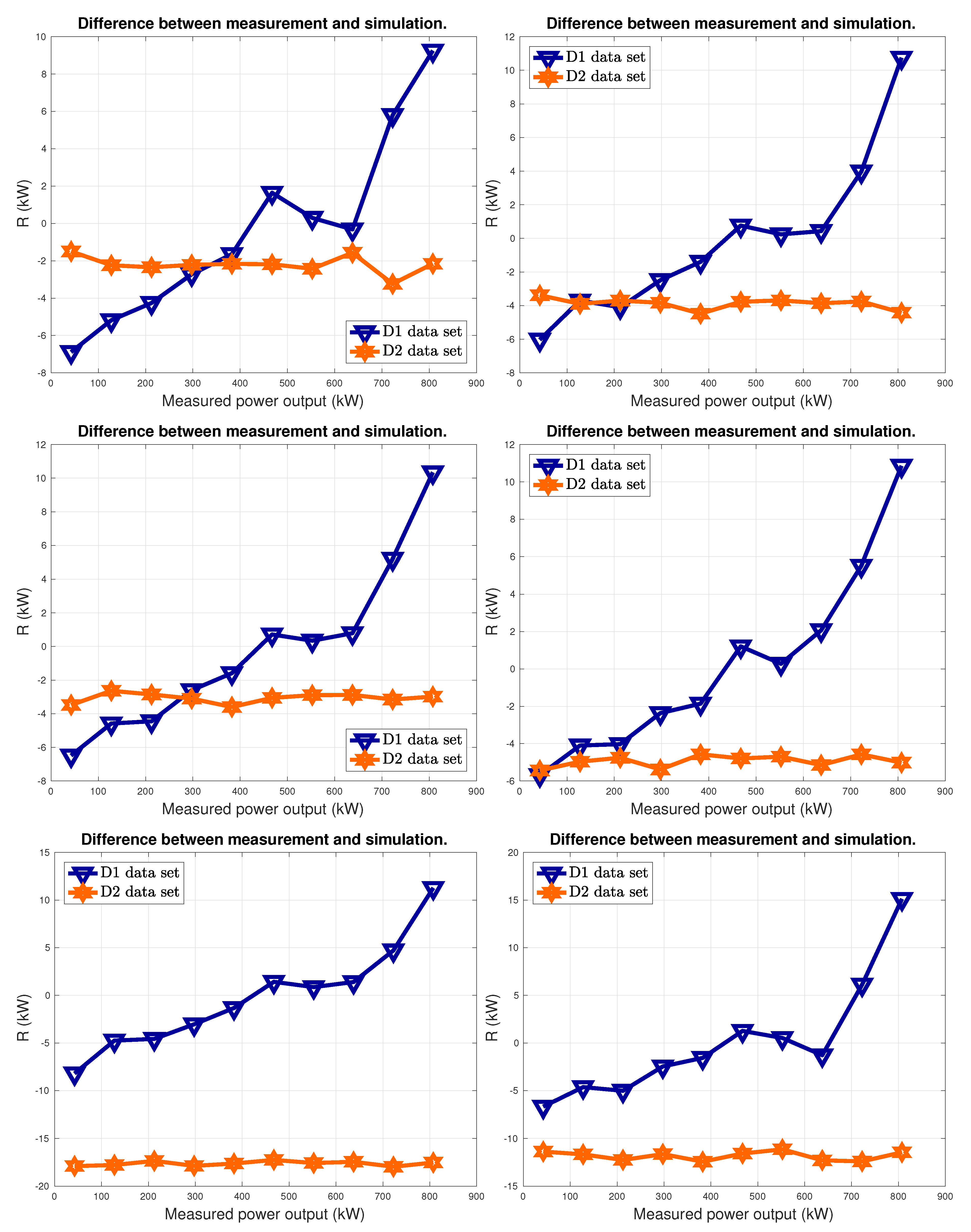
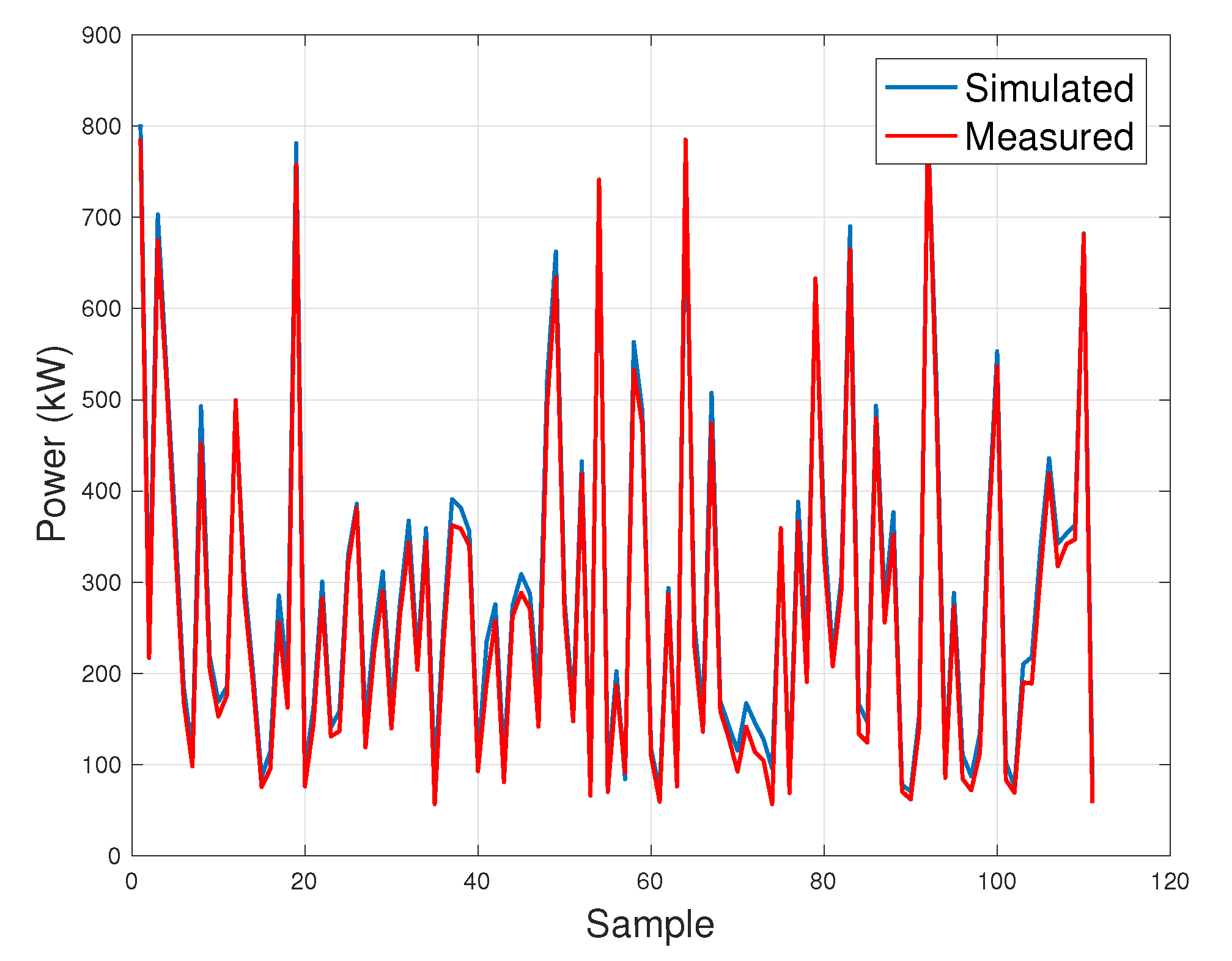
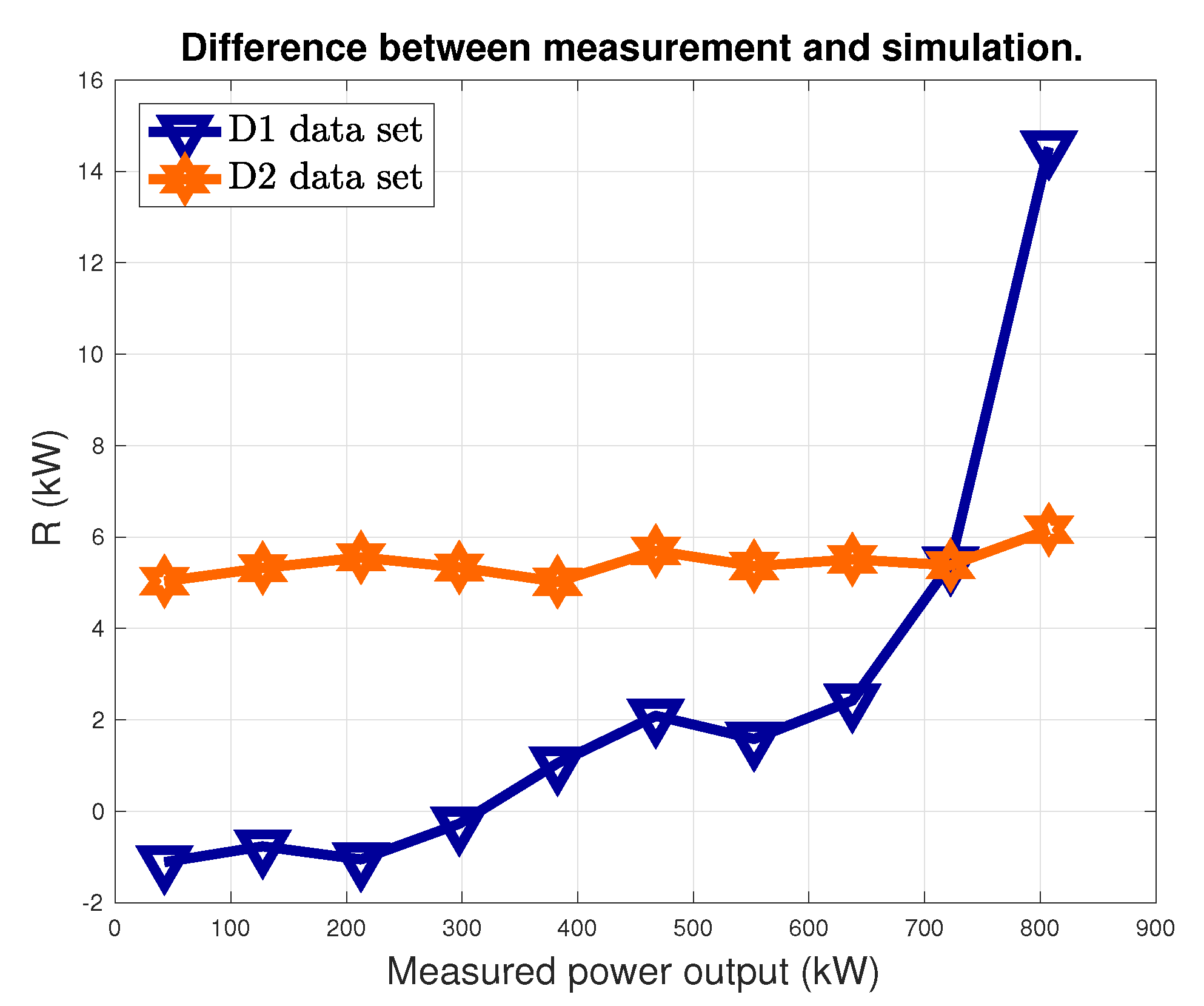
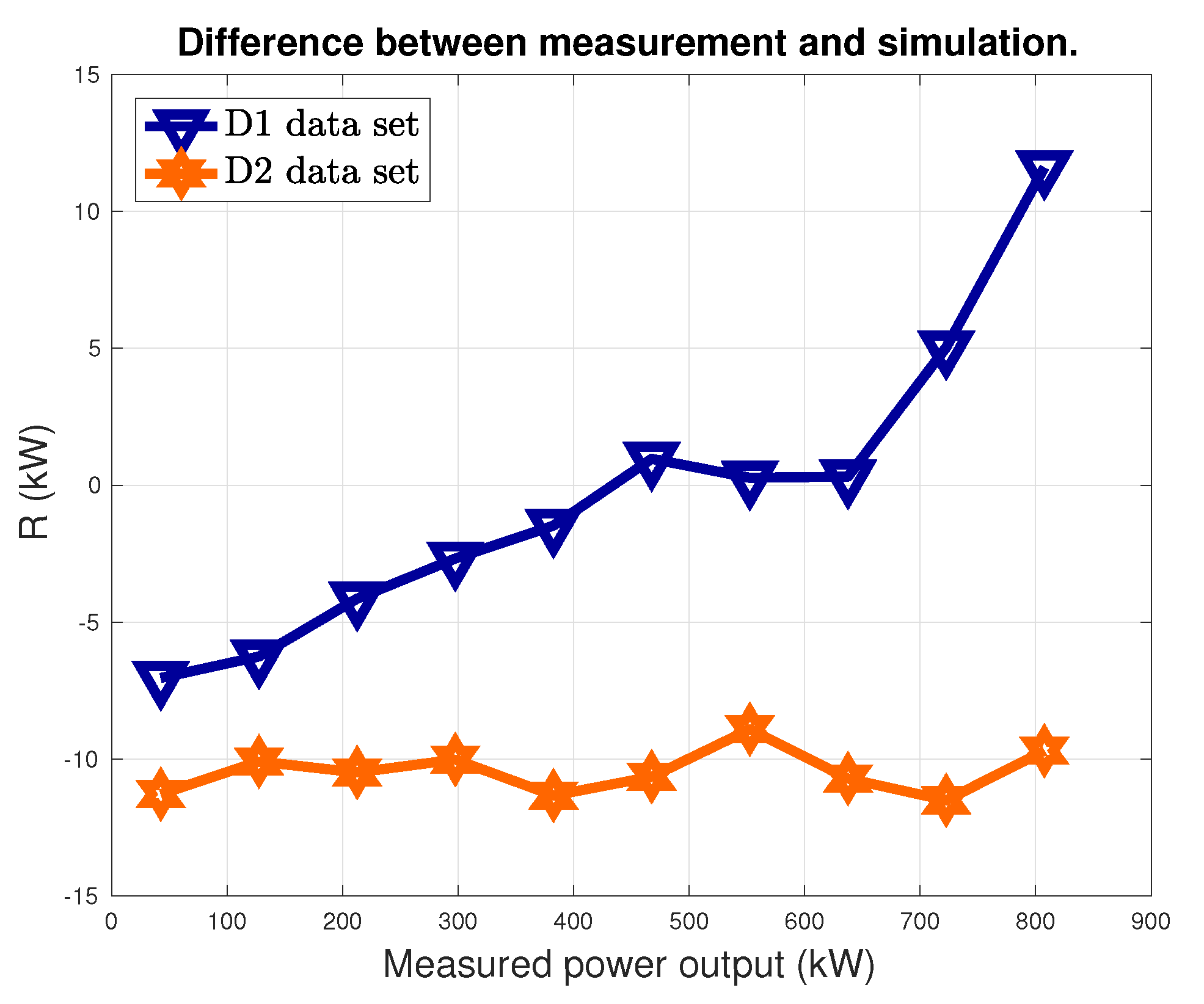
Once the Support Vector Machine Regression has been trained with the D0 data set, the output is simulated (basing on the input variables observations) for data sets D1 and D2. Since D1 belongs to the baseline data set (i.e., 2008), and D2 is a posterior data set, if the performance of the wind turbine has worsened, it should be possible to quantify this phenomenon by observing how the residuals between measurements
Y and simulations
vary from D1 to D2. This method has been shown to be effective for performance control and monitoring and has been applied for different, albeit conceptually similar, test cases: the assessment of wind turbine technology optimization, which is expected to result in improved performance [
17,
18,
19,
35].
Therefore, consider Equation (14) with
.
For
, one computes (Equation (
15))
and the quantity
provides an estimate of the performance deviation from data set D1 to D2.
3.3. Power Curve Analysis
The binning method [
36], as dictated by IEC guidelines [
20], has been employed for power curve analysis.
Once the wind speed measurements are renormalized according to Equations (
2) and (
3), power data are grouped in wind speed bins. The typical selection of bin amplitude is 1 or 0.5 m/s, depending on the size of the data set at disposal. For the objectives of the present work, it has been considered appropriate to select 0.5 m/s wind speed bins.
Given the
i-th wind speed bin, the average wind speed for the bin is computed as in Equation (
16):
and the average power for the bin is computed as in Equation (
17):
where
is the normalised measured wind speed of the
j-th data set in the
i-th wind speed bin,
is the normalised measured power output of the
j-th data set in the
i-th wind speed bin and
is the population of the
i-th wind speed bin.
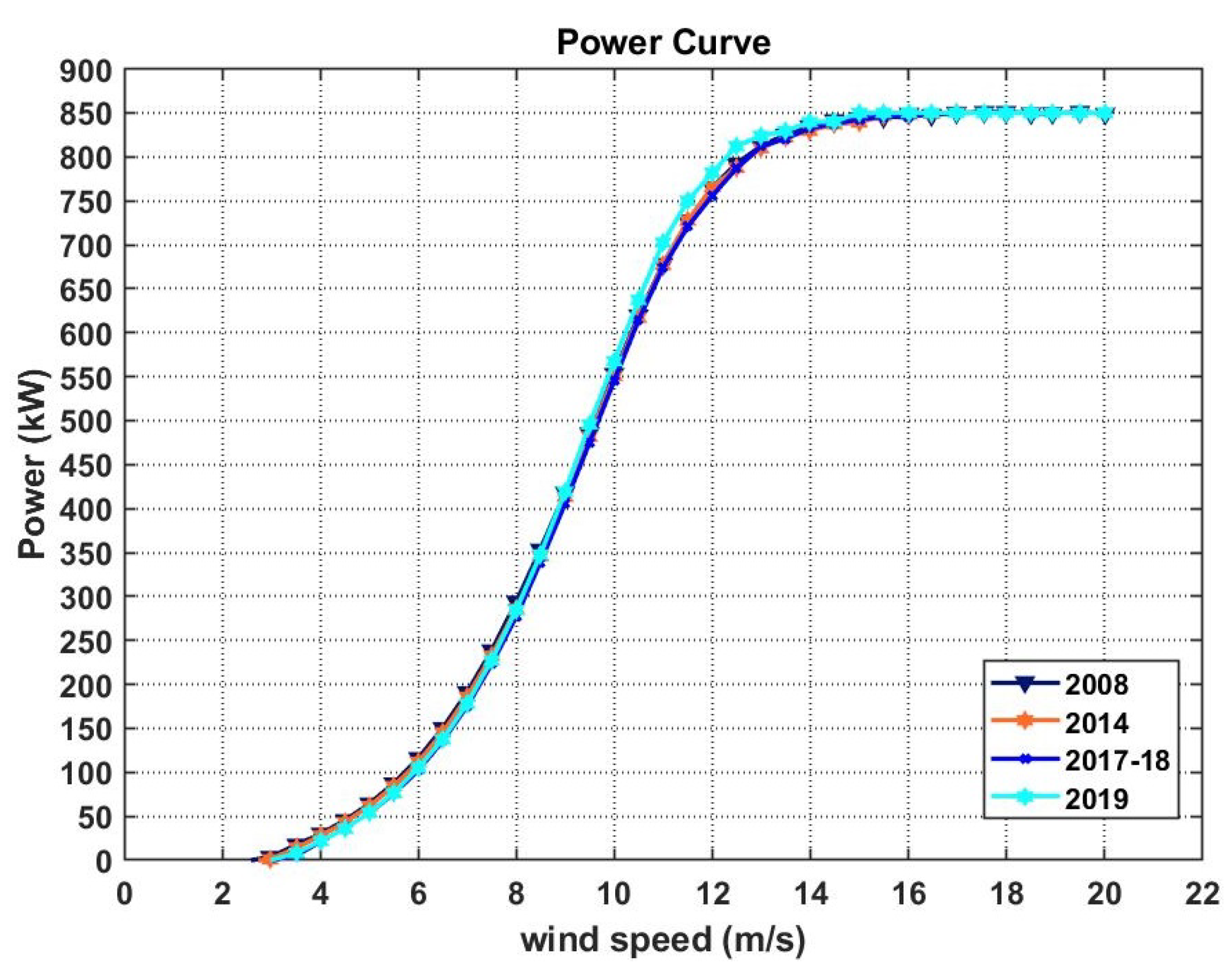
The power curves have been calculated in this way for the data sets listed in
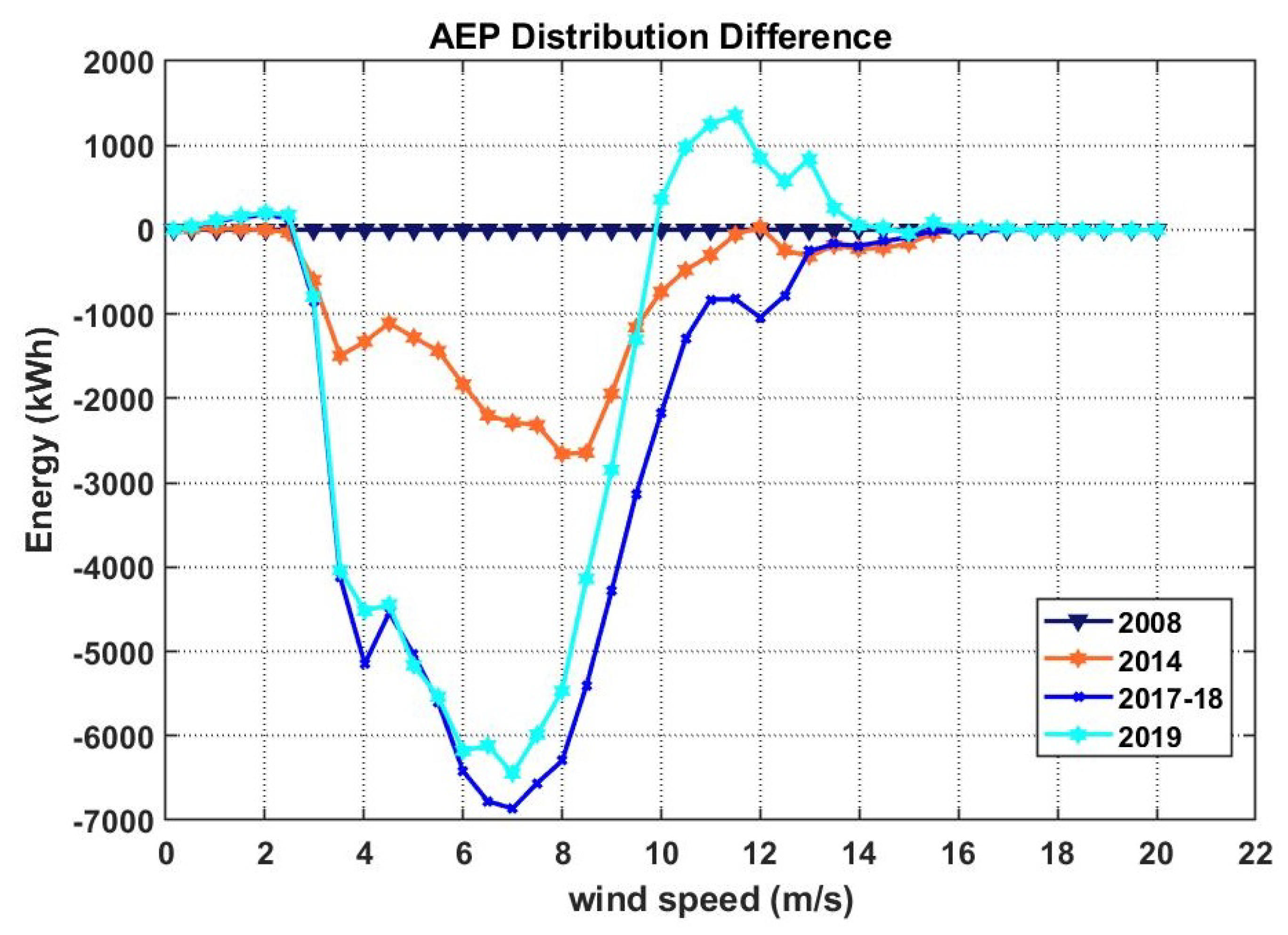
Section 3.2. Having at hand different power curves measured in different periods allows estimating the Annual Energy Production (AEP) trend, if one weights the binned power curves against the same reference wind speed distribution. The data set
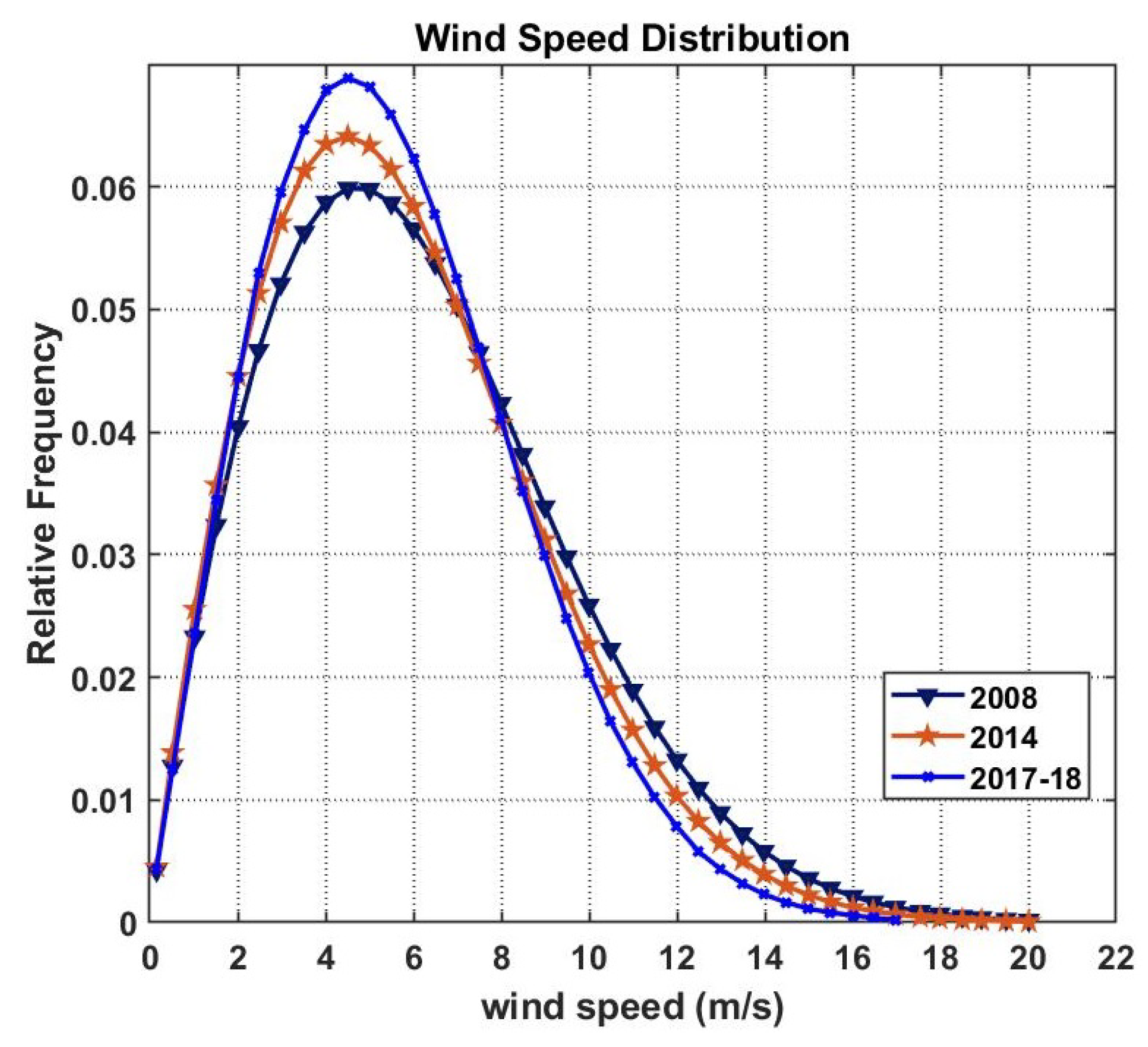
has been selected as reference for the AEP analysis because it is the data set at disposal corresponding to the lower gearbox and wind turbine aging.
The 2008 reference wind speed distribution is characterised by the well-known Weibull probability function (Equation (
18)).
where
A is the scale factor and
k is the is the shape factor.
This scale and shape factors are determined from the MATLAB® function that is based on the statistical method of moments.
The AEP for a given power curve in the reference wind year can be computed from (Equation (
19))
where
is the number of hours in a year.
5. Conclusions
This study has been devoted to a data-driven analysis of wind turbine performance decline with age. Operation data from 2008 to 2019 from a Vestas V52 installed at the Dundalk Institute of Technology have been employed. An important added value of the present test case is that the gearbox of the wind turbine reached its end of life in October 2018 and has been substituted: therefore, it has been possible to draw interesting considerations about the aging of the entire system and about the contribution of the gearbox to wind turbine aging and performance degradation.
This study highlights the potential value of machine learning, in particular Support Vector Regression with Gaussian Kernel, in analysing SCADA data on an ongoing bases to monitor wind turbine performance degradation. This can improve logistical and financial planning for large component replacements, thereby minimising wind turbine down-times at times of large component replacements. Separate approaches to power and energy degradation analysis, in this case, draw similar conclusions. Specifically, an overall wind turbine power and energy degradation in the order of 5% has been determined over the 13-year lifetime of the wind turbine, with the gearbox contributing approximately a 30% share to the degradation. These two main results have been shown not to depend remarkably on the energy density contained in the reference data set. Replacing the gearbox shows best improvement in energy output above wind speeds of 6 m/s suggesting that the gearbox aging has a smaller influence at lower wind class sites. Allowing the gearbox to run to failure is indicated to be economically justified, showing that the gearbox has been quite robust and not the dominant factor in performance degradation. Finally, the results of the present work about wind turbine aging are more in line with those in [
12] than in [
14]: actually, if one extrapolates the present results to a twenty years period, the estimate agrees with [
12]. It should be noted that, differently with respect to what observed in [
12], the results of this study do not conform well to the hypothesis that the aging degradation is linear in time: actually, up to 7 years after the reference data set, the performance worsening is estimated to be of the order of 1%, while 10 years later the worsening reaches the 5%.
The findings add to the broader debate on whether direct-drive gearless wind turbine technology is a significantly better option compared with gear based technology. This may have broader implications for ever increasing number of older wind turbines and wind farms around the world are nearing the end of operational life in the context of turbine re-powering options. Further research in these techniques, using operational data from a broader range of sites and turbine technologies to improve decision making processes in the operation and re-powering of wind farms, would be of great benefit to the industry.