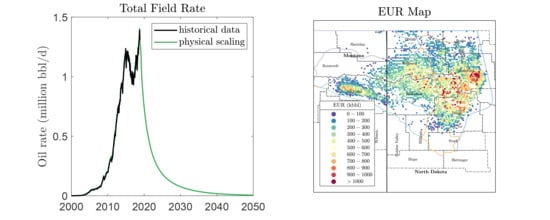
Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale
Abstract
1. Introduction
2. Materials and Methods
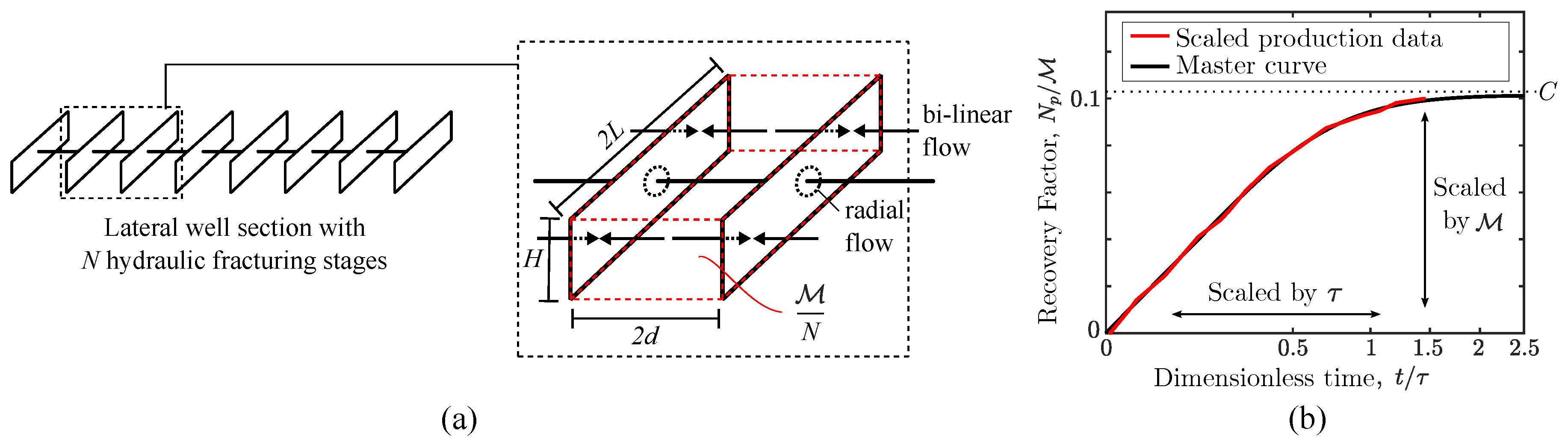
2.1. Physical Scaling
2.1.1. Physical Scaling of Natural Depletion
2.1.2. Physical Scaling of Well Refracturing
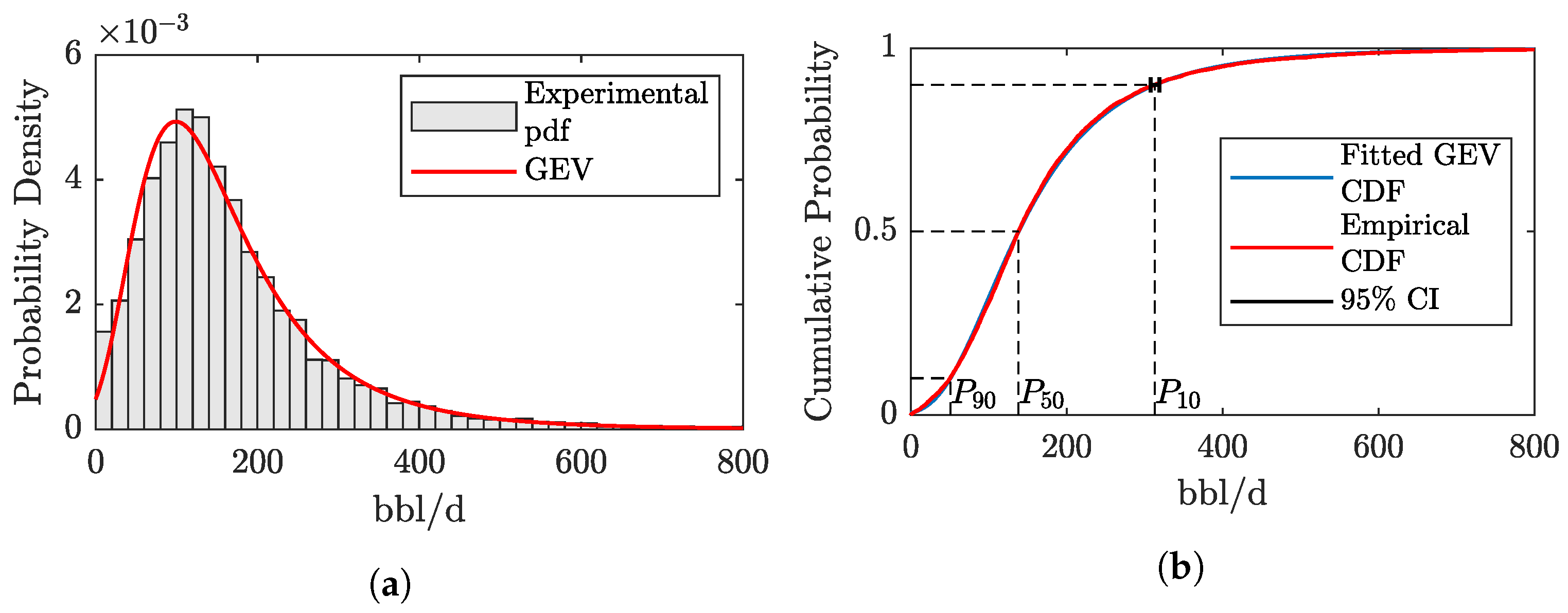
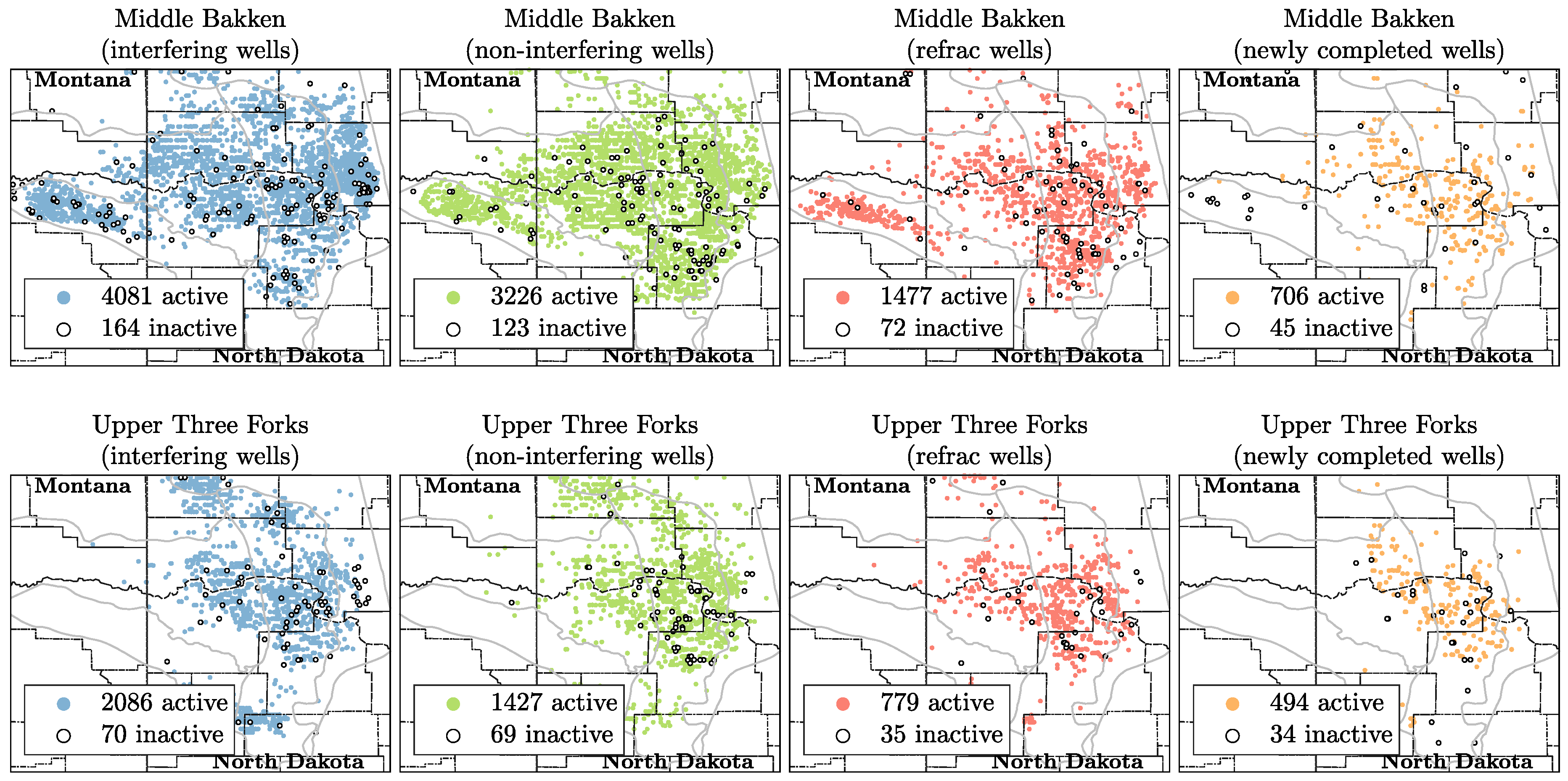
2.2. Data Collection and Scaling Procedure
- Exclude all newly completed wells with less than 12 months of production.
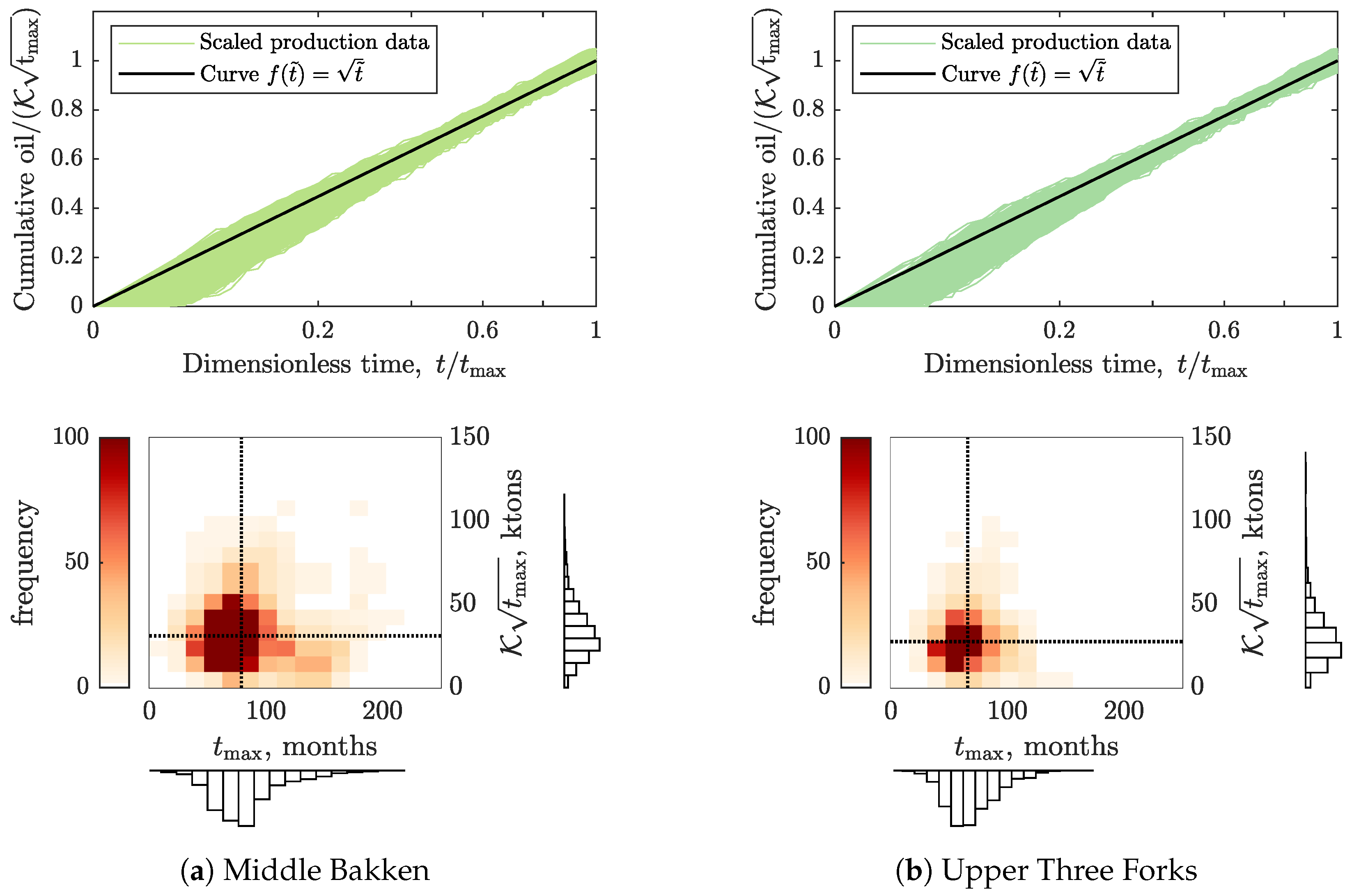
- For each remaining well, plot its cumulative production vs. square root of time on production. Classify these wells as:
- (a)
- Non-interfering wells, if the plot shows a straight line (with, e.g., ).
- (b)
- Interfering wells, if the plot shows a deviation from a straight line (with, e.g., )
- (c)
- Refrac wells, if production jumps are detected.
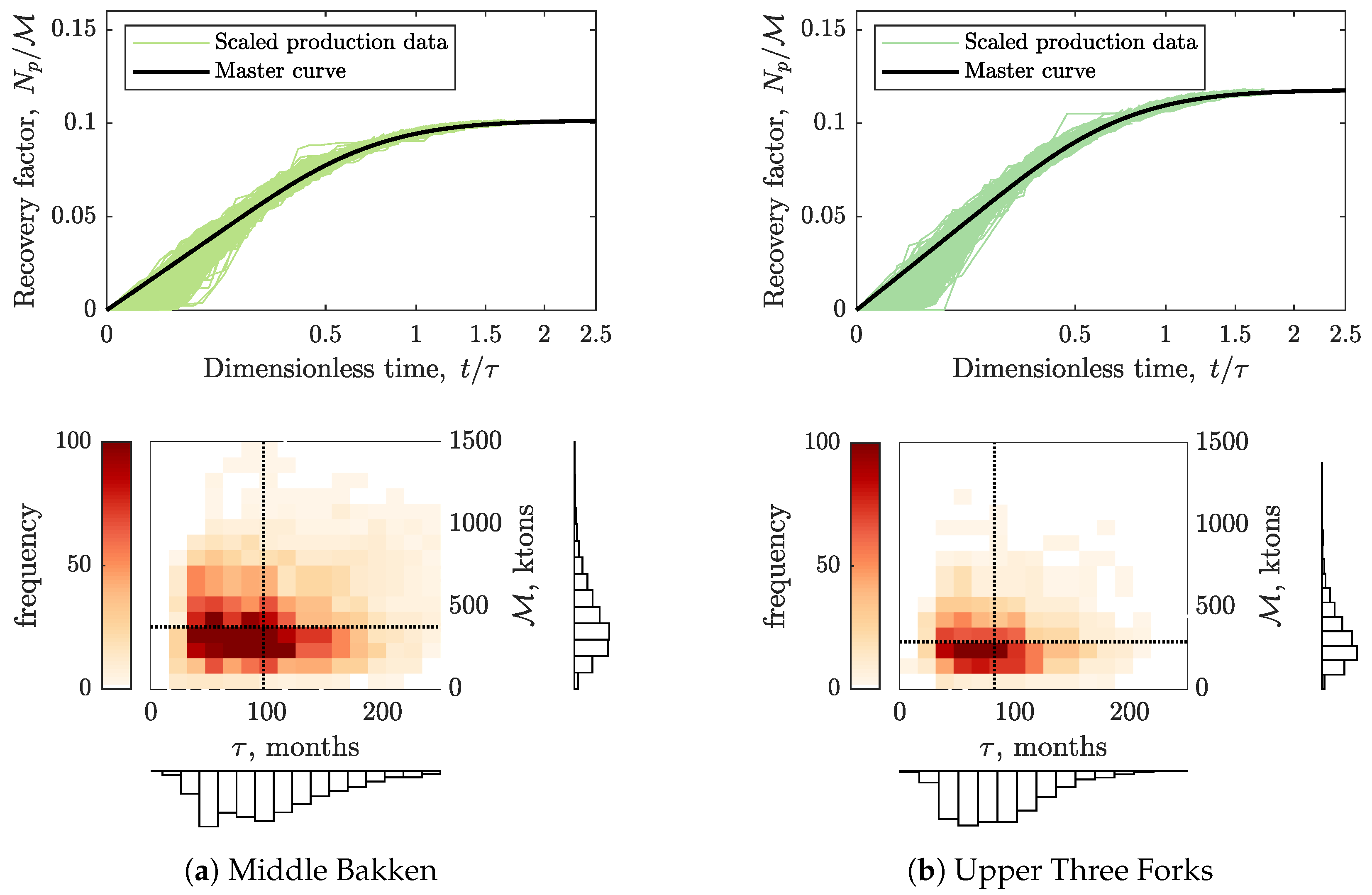
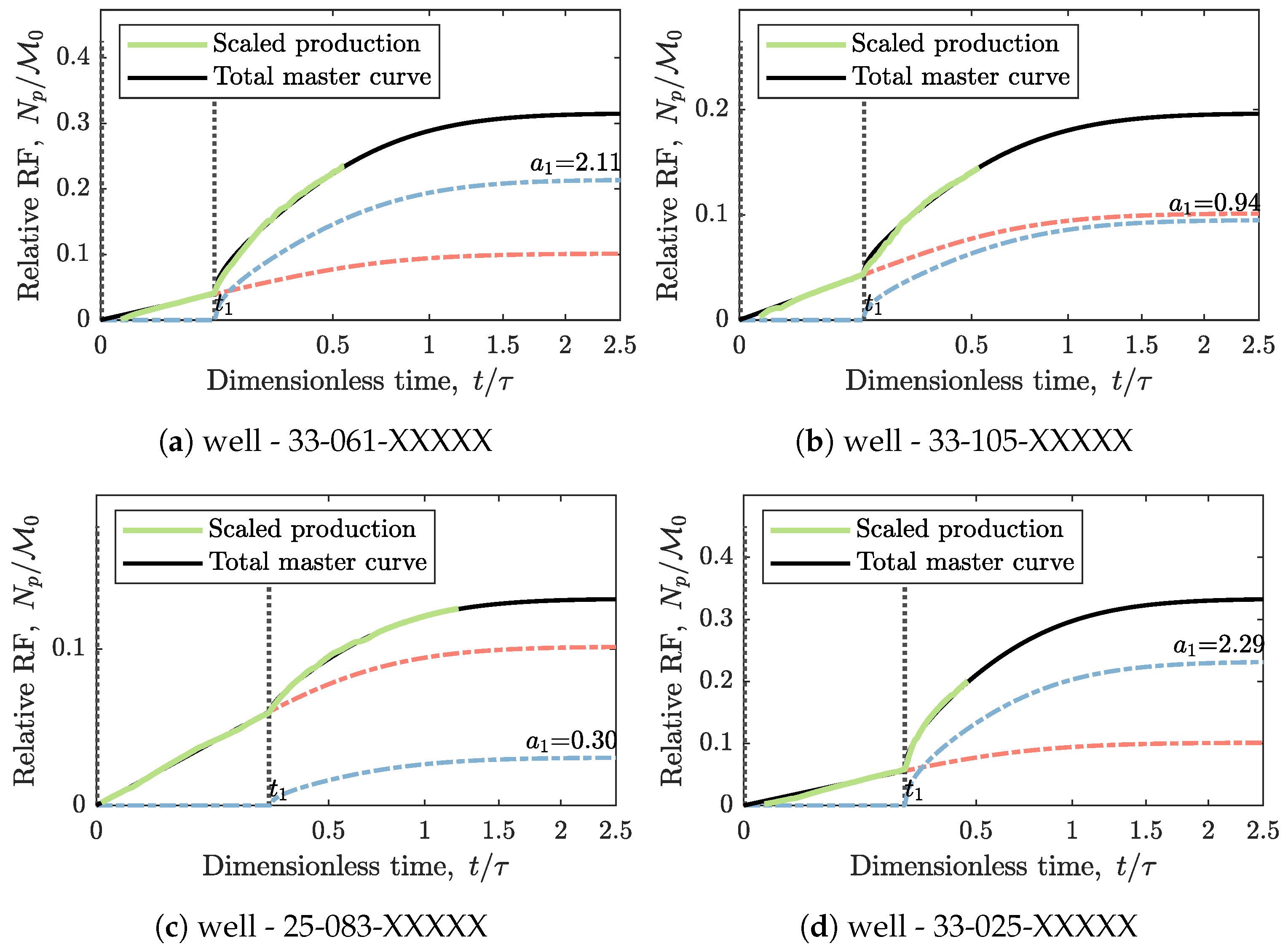
- For each non-interfering well, scale its cumulative production by , on the axis and the elapsed time on production by on the axis to match the line . To predict EUR, assume that deviation from the line starts at . Thus, the corresponding can be calculated as , where is calculated from Equation (8). Finally, is calculated from Equation (11).
- For each newly completed well, calculate its EUR using expected values of and from comparable interfering wells that were completed between 2017 and 2019. Use Equation (11).
3. Results and Discussion
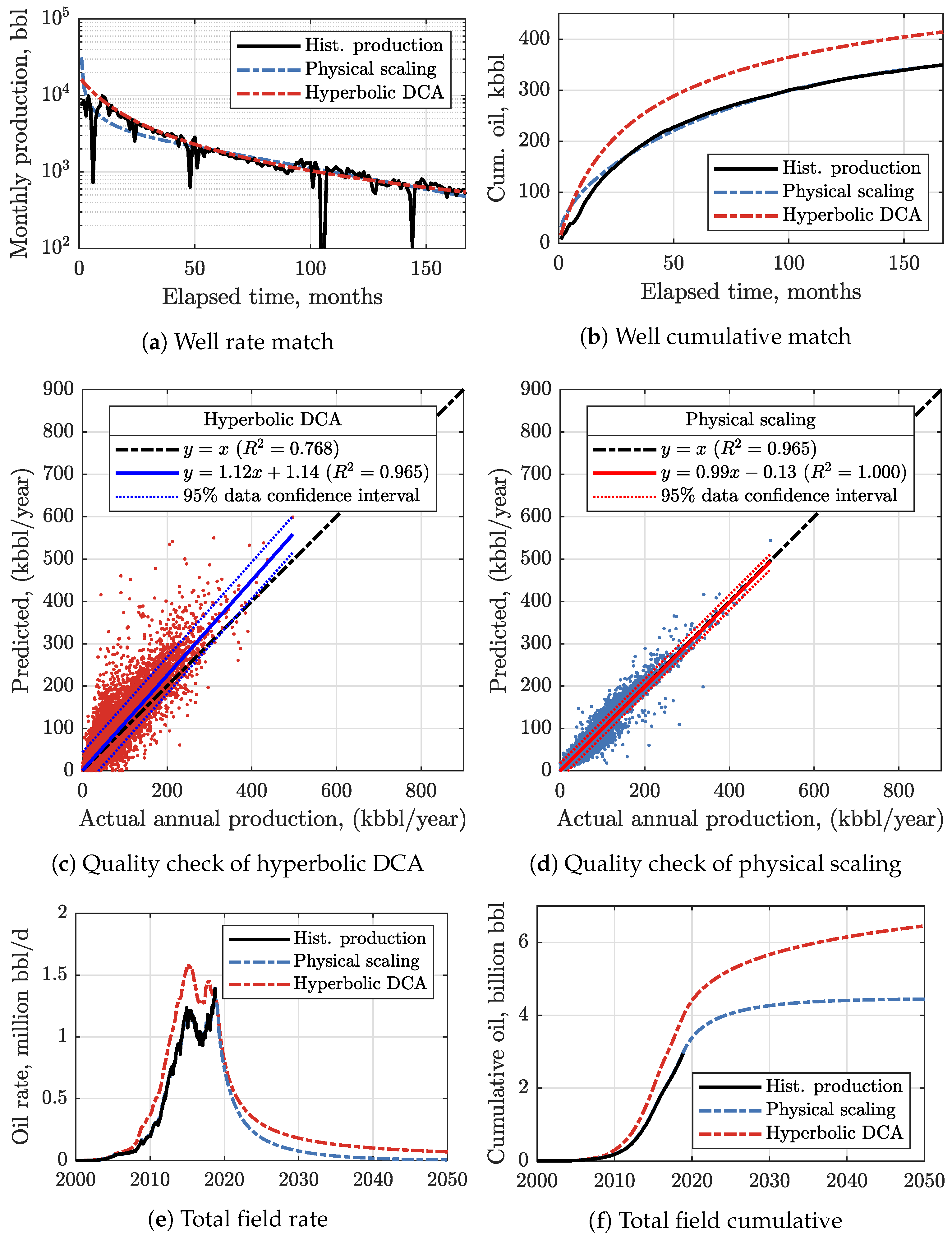
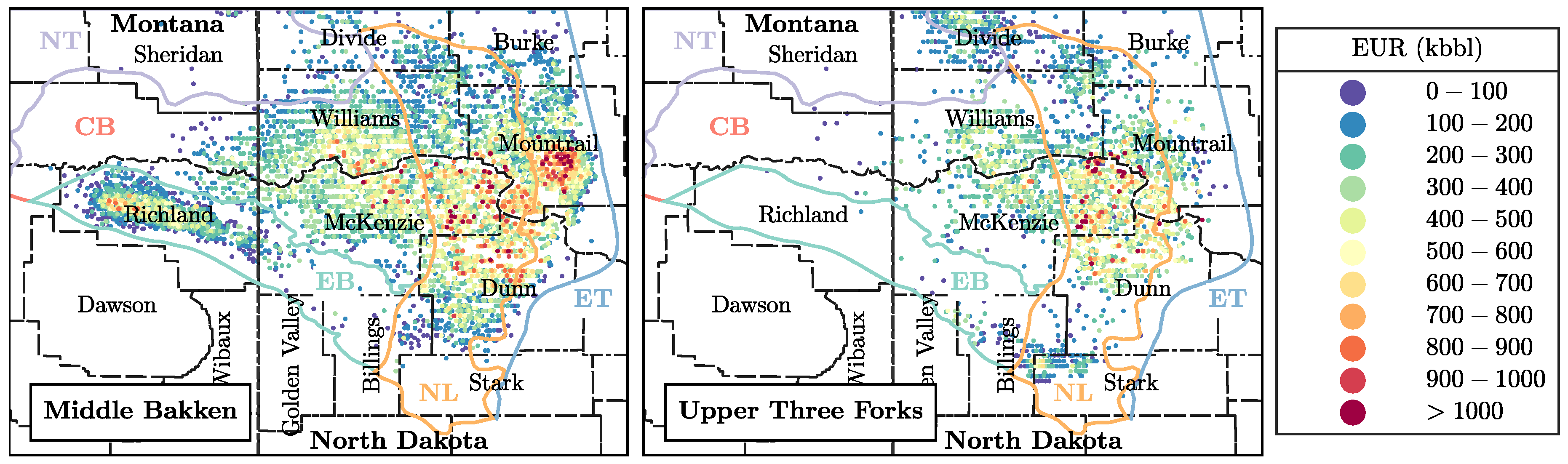
3.1. Physical Scaling Matches
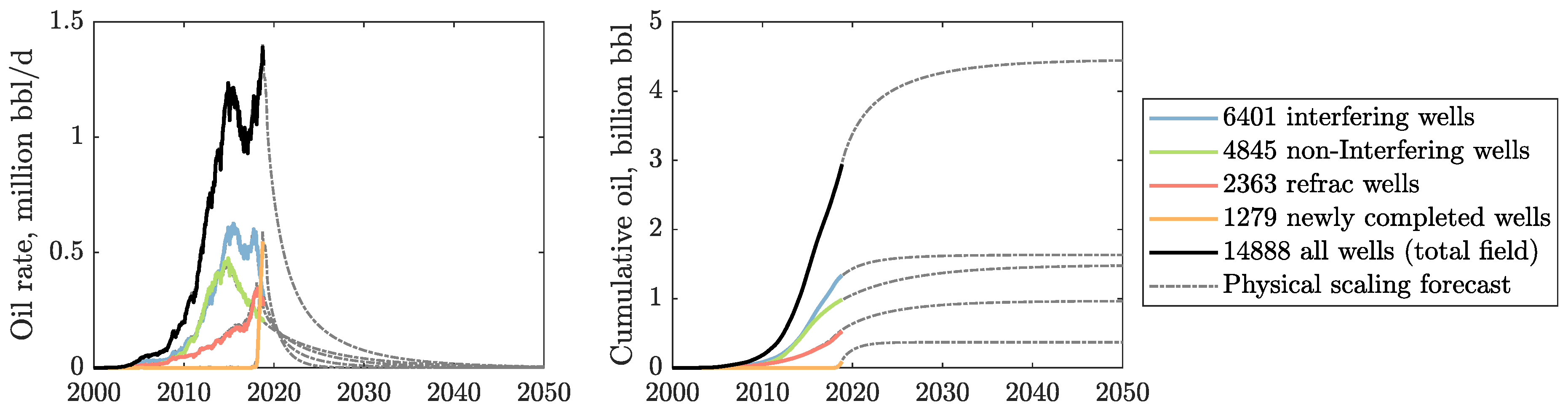
3.2. EUR Predictions
4. Conclusions
- The current 14,888 active oil wells in the Bakken shale will ultimately produce 715 million m (4.5 billion barrels) of oil, with 493 million m (3.1 billion barrels) from 9894 wells in the Middle Bakken and 222 million m (1.4 billion barrels) from 4994 wells in the Upper Three Forks.
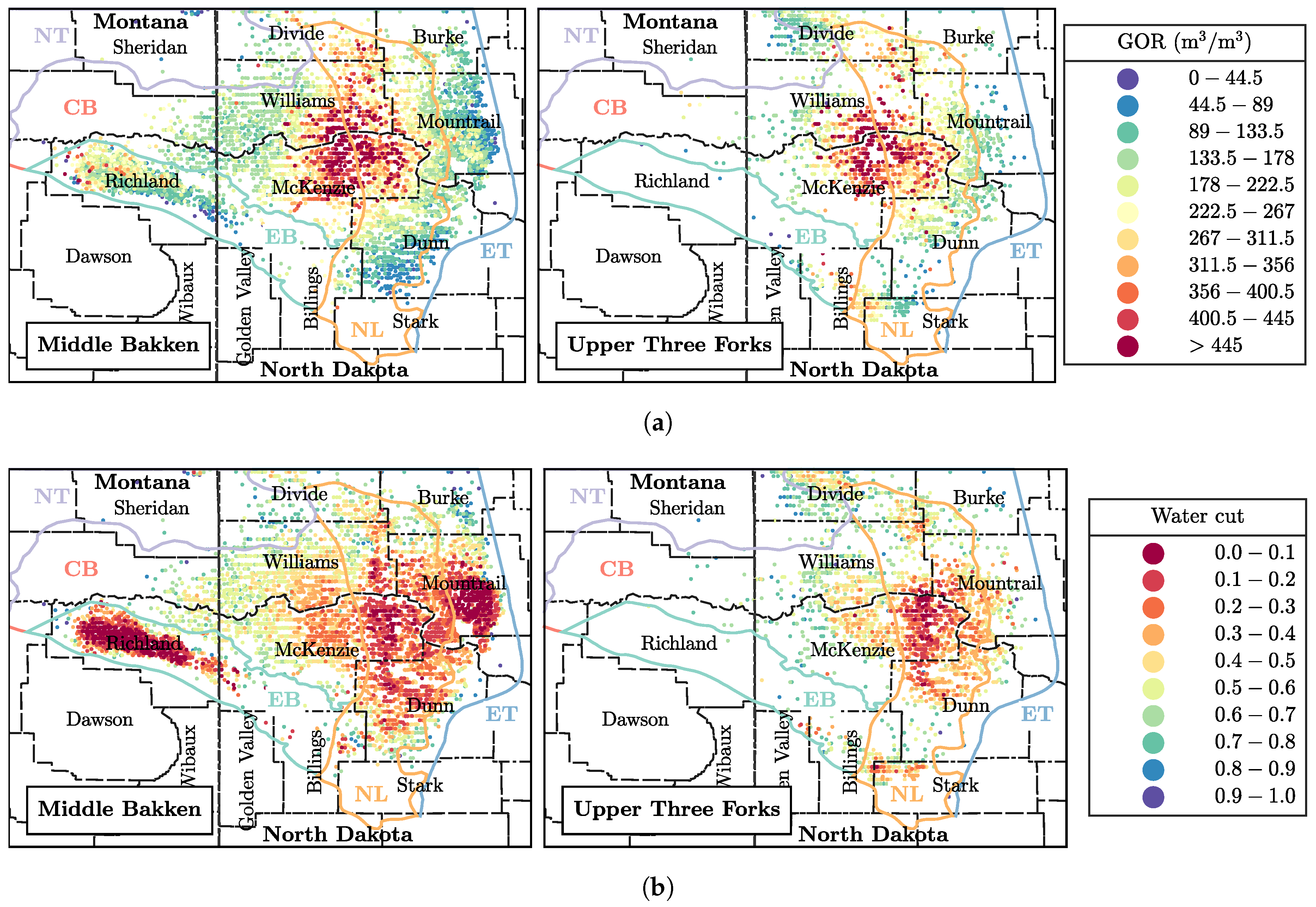
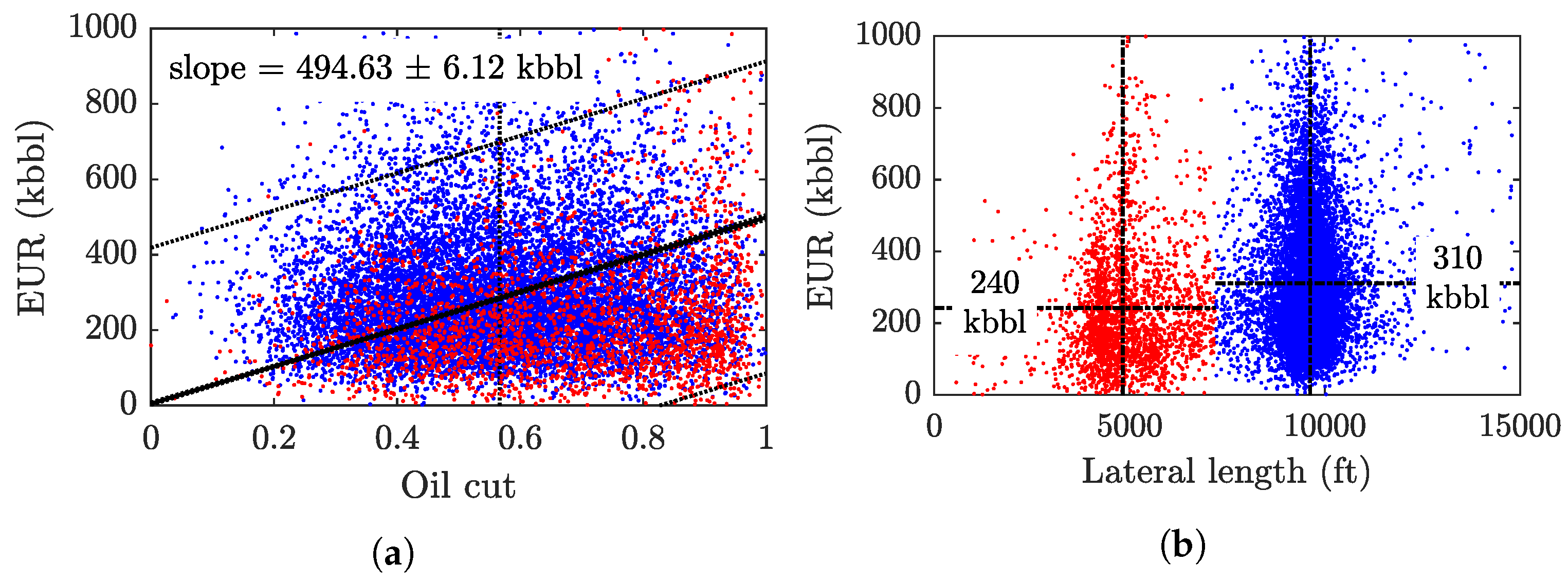
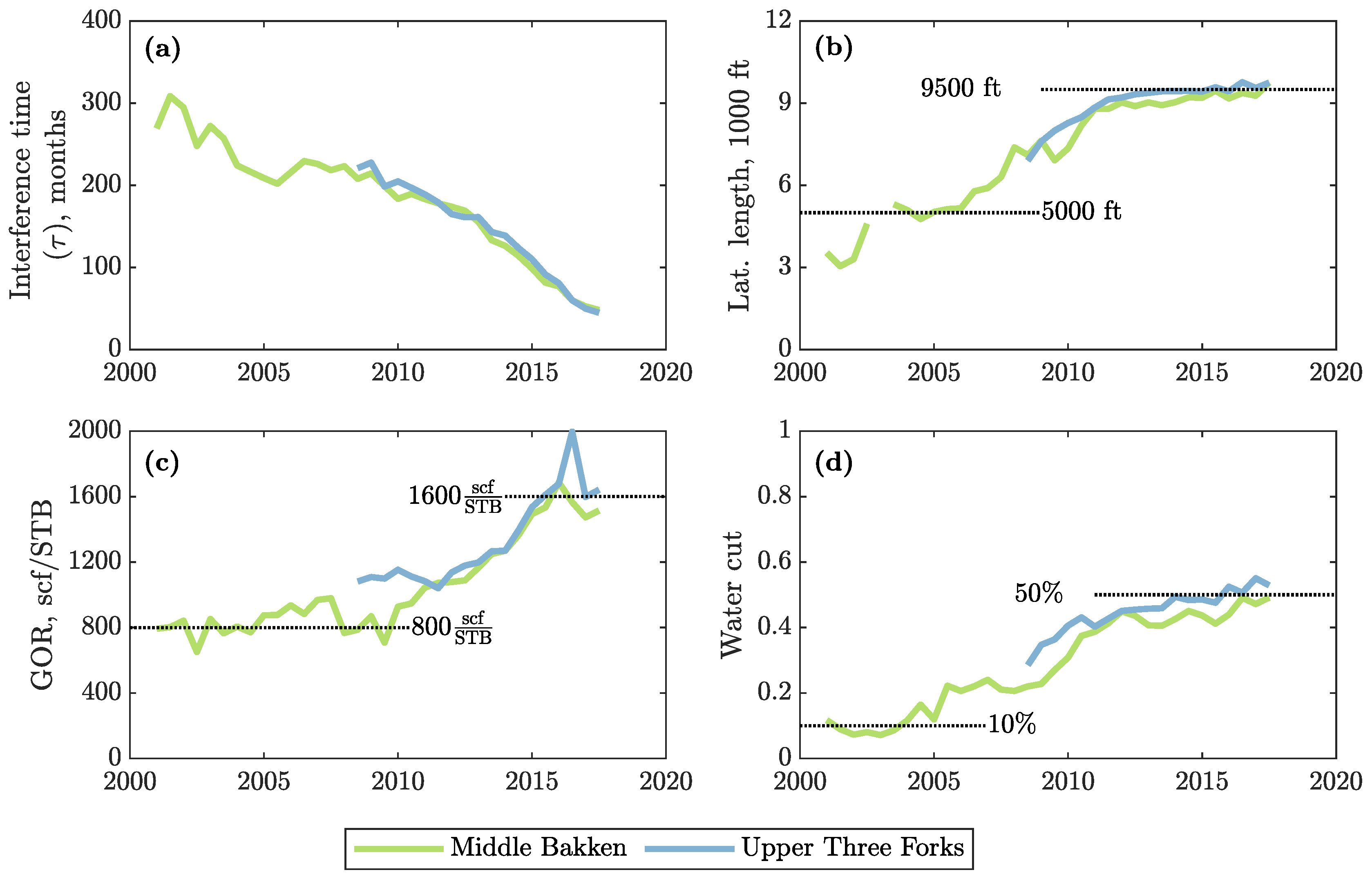
- In general, wells completed in the Middle Bakken produce more oil than those in the Upper Three Forks due to: (1) lower water saturation and water cut, (2) slower decline rate (longer pressure interference times, ), and (3) higher initial oil in place (larger ).
- Newly completed wells start from very high initial oil rates but in general decline faster than the pre-2010 wells. Still, we predict higher EURs for the newly completed wells.
- The more productive newer wells result from recent advancements in completion technology: longer laterals, larger hydrofractures, bigger stimulated reservoir volumes, and more fracture stages.
- Operators have also learned to drill new wells only in the most prolific area of the Bakken region at the center of the Williston Basin.
- With time, negative trends in oil production have amplified in the Bakken. We observe higher GOR values (reservoir degassing); higher water cuts (contacting water-bearing formations and drilling in regions with lower oil saturations); faster decline rates; and excessive well density, especially in the most prolific areas.
- When all most productive areas in the Bakken are extensively drilled, the poor immature areas with high water production will be the only targets left for infill drilling. In this case, technology will not enhance much performance of the future wells.
- We encourage practitioners to adopt our fast and accurate method of predicting oil production in shales that is a viable alternative to the hyperbolic DCA which yields an ‘illusory picture’ of shale oil resources.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| effectiveness of a refrac job | |
| one-sided area of hydrofracture, ft [m] | |
| oil compressibility, psi [Mpa] | |
| water compressibility, psi [Mpa] | |
| pore space compressibility, psi [Mpa] | |
| total compressibility, psi [Mpa] | |
| C | maximum recovery factor before refracturing, fraction |
| d | half-distance between two consecutive hydrofractures, ft [m] |
| estimated ultimate recovery of oil, million bbl, Mbbl | |
| total estimated ultimate recovery of oil from a refractured well, million bbl, Mbbl | |
| dissolved gas–oil ratio, scf/stb [sm/m] | |
| H | fracture height, assumed equal to formation thickness, ft [m] |
| Heaviside unit step function | |
| i | the month on production |
| j | the discontinuity of production rate from a refracturing event |
| k | average permeability of the matrix, d [m] |
| dimensional scaling constant, kton/ | |
| L | hydrofracture half-length, ft [m] |
| mass of saturated oil inside stimulated reservoir volume, kton | |
| mass of saturated oil inside stimulated reservoir volume before refracturing, kton | |
| mass of saturated oil inside stimulated reservoir volume after jth refracturing, kton | |
| N | total number of parallel vertical hydrofractures in a well |
| cumulative mass production of oil, kton | |
| p | pressure, psi [Mpa] |
| estimated initial formation pressure, psi [Mpa] | |
| average bubble point pressure, psi [Mpa] | |
| constant pressure in hydrofractures, psi [Mpa] | |
| a number such that there is an likelihood that true value exceeds | |
| q | oil production rate at downhole conditions, bbl/day [m/s] |
| oil production rate at stock tank conditions, bbl/day [m/s] | |
| a statistical measure of how close the data are to the fitted regression curve | |
| volume of oil produced in month i by a horizontal well, stb/month | |
| recovery factor, fraction | |
| recovery factor for an imaginary well due to jth refracturing event, fraction | |
| total recovery factor for a refractured well, fraction | |
| solution gas–oil ratio, scf/stb [sm/m] | |
| initial oil saturation | |
| connate water saturation | |
| t | elapsed time on production, months [s] |
| elapsed time when jth refracturing event occurs, months [s] | |
| dimensionless time | |
| x | distance, ft [m] |
| pressure diffusivity coefficient, m/s | |
| pressure diffusivity coefficient at initial conditions, m/s | |
| exponent constant in simplified master curve equation | |
| Conway’s constant ≈ 1.30357 | |
| oil viscosity, cp [Pa s] | |
| oil viscosity at initial conditions, cp [Pa s] | |
| fluid density at initial conditions, lb/ft [kg/m] | |
| gas density at stock tank conditions, lb/ft [kg/m] | |
| oil density, lb/ft [kg/m] | |
| oil density at initial conditions, lb/ft [kg/m] | |
| oil density at stock tank (dead oil) conditions, lb/ft [kg/m] | |
| water density, lb/ft [kg/m] | |
| porosity, fraction | |
| characteristic pressure interference time, months |
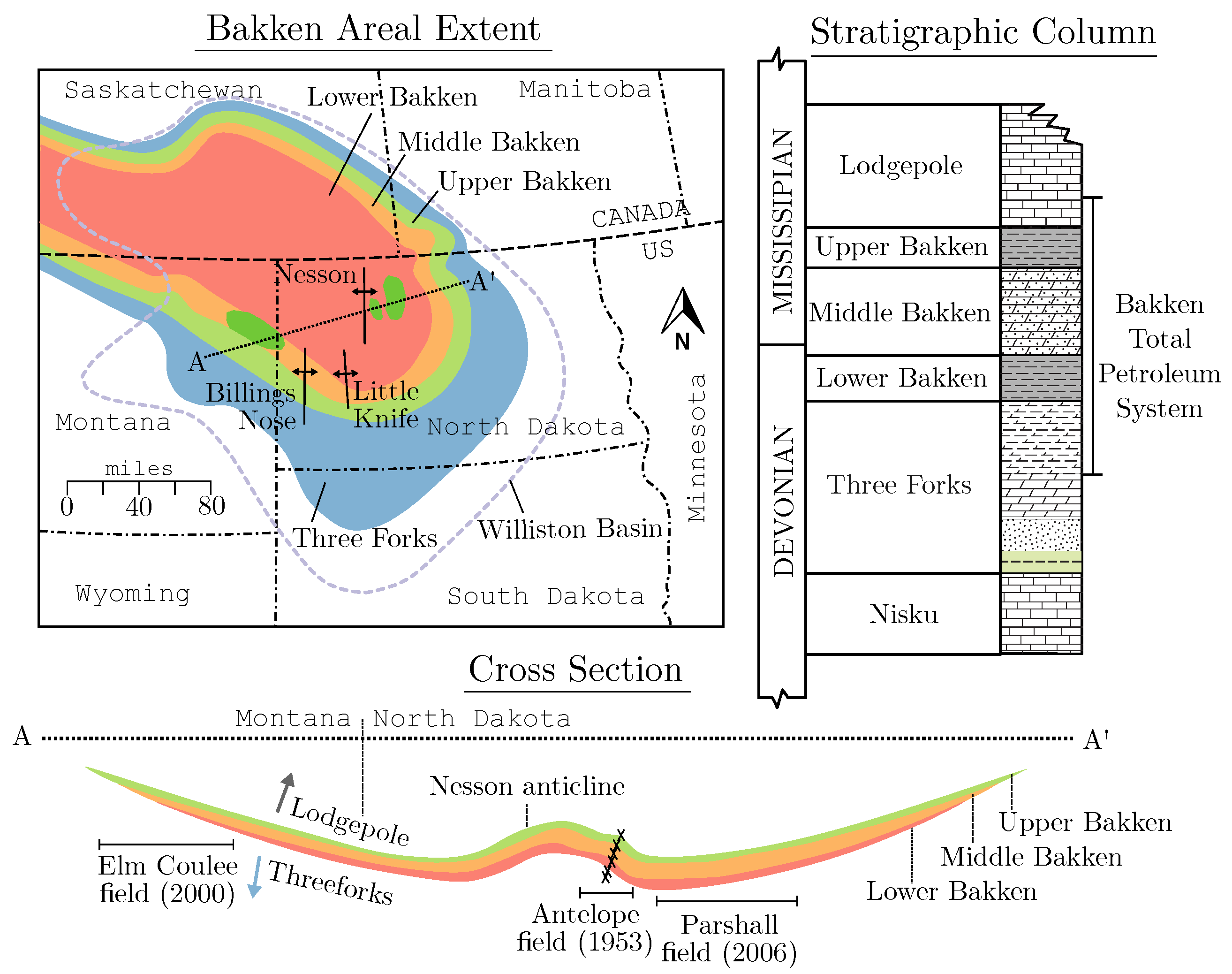
Appendix A. Overview of the Bakken Shale Play
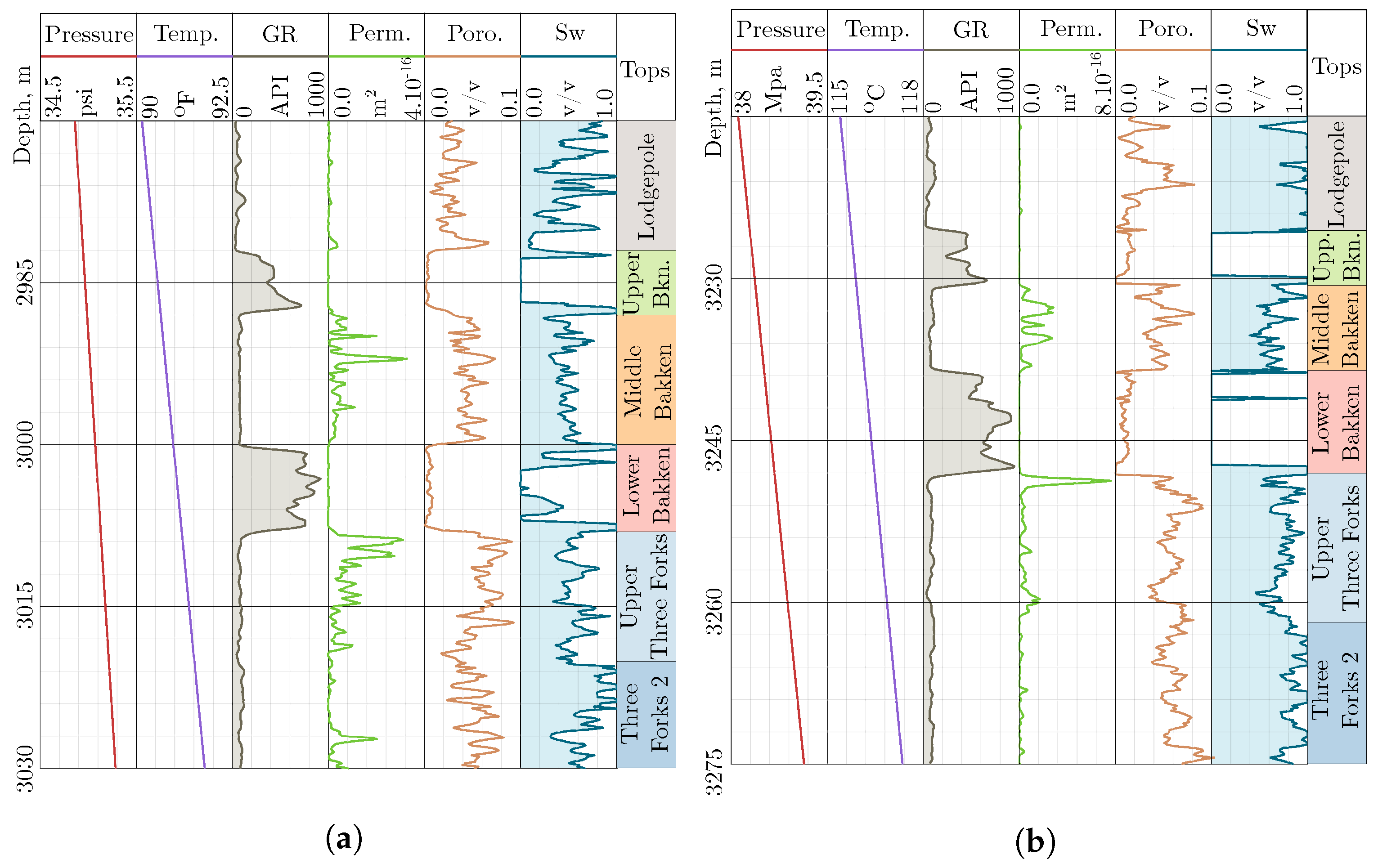
| Formation | Upper Bakken | Middle Bakken | Lower Bakken | Upper Three Forks |
|---|---|---|---|---|
| Depth (m) | 3108 | 3116 | 3125 | 3136 |
| Pressure (Mpa) | 36.7 | 36.8 | 36.9 | 37.0 |
| Temperature (C) | 103 | 103 | 104 | 104 |
| Gamma-Ray ( API) | 431 | 83 | 690 | 81 |
| Permeability (m) | 1.4 | 4.5 | 2.0 | 4.7 |
| Porosity | 0.008 | 0.046 | 0.008 | 0.058 |
| Water Saturation | 0.20 | 0.57 | 0.22 | 0.65 |
| Thickness (m) | 5.8 | 10 | 9.1 | 12 |
Appendix B. Bakken Reservoir Properties, Summary of Matching Parameters, and Details of EURs
| Parameter | Middle Bakken | Upper Three Forks | Data Source | ||
|---|---|---|---|---|---|
| SI Units | Field Units | SI Units | Field Units | ||
| Horizontal well length, | 2900 m | 9500 ft | 2900 m | 9500 ft | DrillingInfo |
| Number of fracture stages, N | 30 | 30 | 30 | 30 | DrillingInfo |
| Fracture height, H | 10 m | 33 ft | 12 m | 40 ft | well log |
| Tip-to-tip fracture length, | 360 m | 1200 ft | 360 m | 1200 ft | DrillingInfo |
| Reservoir temperature, T | 113 C | 237 F | 115 C | 239 F | [65] |
| Initial pressure, | 36.8 Mpa | 5340 psia | 37.1 Mpa | 5380 psia | well log |
| Saturation pressure, | 17.4 Mpa | 2530 psia | 12.1 Mpa | 1753 psia | [65] |
| Fracture pressure, | 3.4 Mpa | 500 psia | 3.4 Mpa | 500 psia | DrillingInfo |
| Connate water saturation, | 0.57 | 0.57 | 0.65 | 0.65 | well log |
| Initial oil saturation, | 0.43 | 0.43 | 0.35 | 0.35 | well log |
| Rock porosity, | 0.046 | 0.046 | 0.058 | 0.058 | well log |
| Rock permeability, k | 4.4 m | 0.045 md | 4.6 m | 0.047 md | well log |
| Rock compressibility, | 4.3 Pa | 3.0 microsip | 4.3 Pa | 3 microsip | [66] |
| Water compressibility, | 4.3 Pa | 3 microsip | 4.3 Pa | 3 microsip | [66] |
| Oil compressibility, | 1.4 Pa | 1 microsip | 1.4 Pa | 1 microsip | [66] |
| Oil viscosity, | 3.9 Pa s | 0.392 cp | 2.8 Pa s | 0.276 cp | [65] |
| Oil formation volume factor, | 1.61 m/sm | 1.61 rbbl/stb | 1.48 m/sm | 1.48 rbbl/stb | [65] |
| API gravity | 42 API | 42 API | 39 API | 39 API | [65] |
| GOR | 1.48 sm/sm | 125 scf/stb | 110 sm/sm | 620 scf/stb | [65] |
| Well Class | Middle Bakken | Upper Three Forks | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (months) | (ktons) | Number | (months) | (ktons) | Number | |||||||||
| of Wells | of Wells | |||||||||||||
| Interfering | 170 | 100 | 50 | 720 | 420 | 190 | 4245 | 140 | 90 | 40 | 540 | 320 | 150 | 2156 |
| Non-Interfering | 250 | 220 | 180 | 860 | 480 | 250 | 3349 | 250 | 210 | 160 | 680 | 400 | 170 | 1496 |
| Refracs | 230 | 150 | 70 | 1210 | 660 | 230 | 1549 | 230 | 140 | 70 | 980 | 540 | 200 | 814 |
| Newly completed | 60 | 50 | 30 | 800 | 520 | 270 | 751 | 60 | 40 | 30 | 620 | 400 | 200 | 528 |
| All wells | 200 | 150 | 90 | 850 | 490 | 220 | 9894 | 180 | 130 | 80 | 660 | 390 | 170 | 4994 |
| AU | State | County | EIA 2019 | Physical Scaling | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bakken | Three Forks | Bakken | Three Forks | |||||||||||
| EUR | Potential | EUR | Potential | P10 | P50 | P90 | Existing | P10 | P50 | P90 | Existing | |||
| (Mb/well) | wells | (Mb/well) | wells | (Mb/well) | (Mb/well) | (Mb/well) | wells | (Mb/well) | (Mb/well) | (Mb/well) | wells | |||
| Central Basin | MT | Daniels | 60 | 189 | 177 | 35,870 | - | - | - | - | - | - | - | - |
| Central Basin | MT | McCone | 60 | 528 | 196 | 196 | 196 | 1 | - | - | - | - | ||
| Central Basin | MT | Richland | 232 | 1083 | 318 | 210 | 103 | 102 | 234 | 118 | 44 | 3 | ||
| Central Basin | MT | Roosevelt | 263 | 4985 | 330 | 212 | 103 | 138 | 228 | 129 | 38 | 11 | ||
| Central Basin | MT | Sheridan | 49 | 753 | 359 | 163 | 37 | 4 | 64 | 59 | 53 | 2 | ||
| Central Basin | ND | Divide | 241 | 12 | - | - | - | - | 99 | -307 | 27 | 3 | ||
| Central Basin | ND | Dunn | 184 | 73 | 459 | 301 | 156 | 41 | 375 | 254 | 160 | 14 | ||
| Central Basin | ND | McKenzie | 263 | 3749 | 465 | 298 | 158 | 1540 | 399 | 250 | 125 | 669 | ||
| Central Basin | ND | Williams | 262 | 3070 | 463 | 300 | 162 | 1261 | 376 | 250 | 143 | 524 | ||
| Eastern Transitional | ND | Burke | 7 | 2706 | 267 | 153 | 62 | 117 | 235 | 148 | 81 | 24 | ||
| Eastern Transitional | ND | Divide | 140 | 658 | 237 | 140 | 64 | 96 | 311 | 182 | 78 | 206 | ||
| Eastern Transitional | ND | Dunn | 423 | 1099 | 620 | 354 | 125 | 248 | 554 | 335 | 208 | 111 | ||
| Eastern Transitional | ND | Hettinger | 169 | 7 | - | - | - | - | - | - | - | - | ||
| Eastern Transitional | ND | McLean | 623 | 245 | 523 | 310 | 144 | 40 | 1198 | 501 | 193 | 4 | ||
| Eastern Transitional | ND | Mercer | 13 | 144 | - | - | - | - | - | - | - | - | ||
| Eastern Transitional | ND | Mountrail | 232 | 2679 | 683 | 388 | 155 | 1163 | 464 | 274 | 114 | 201 | ||
| Eastern Transitional | ND | Stark | 169 | 371 | 177 | 177 | 177 | 1 | 125 | 21 | 11 | 2 | ||
| Eastern Transitional | ND | Ward | 80 | 111 | 209 | 209 | 209 | 1 | - | - | - | - | ||
| Elm Coulee–Billings Nose | MT | McCone | 80 | 116 | - | - | - | - | - | - | - | - | ||
| Elm Coulee–Billings Nose | MT | Richland | 183 | 3421 | 423 | 230 | 75 | 935 | 112 | 64 | 15 | 2 | ||
| Elm Coulee–Billings Nose | ND | Billings | 60 | 828 | 263 | 192 | 17 | 10 | 265 | 149 | 59 | 37 | ||
| Elm Coulee–Billings Nose | ND | Golden Valley | 476 | 130 | 70 | 70 | 70 | 1 | 502 | 337 | 172 | 12 | ||
| Elm Coulee–Billings Nose | ND | McKenzie | 184 | 2449 | 269 | 157 | 62 | 79 | 291 | 134 | 9 | 8 | ||
| Nesson–Little Knife | ND | Billings | 167 | 586 | 268 | 135 | 31 | 49 | 280 | 165 | 76 | 82 | ||
| Nesson–Little Knife | ND | Burke | 188 | 680 | 258 | 174 | 95 | 65 | 265 | 173 | 91 | 68 | ||
| Nesson–Little Knife | ND | Divide | 115 | 603 | 246 | 159 | 82 | 128 | 236 | 151 | 77 | 149 | ||
| Nesson–Little Knife | ND | Dunn | 324 | 2685 | 615 | 358 | 185 | 1258 | 569 | 345 | 181 | 608 | ||
| Nesson–Little Knife | ND | Hettinger | 223 | 106 | - | - | - | - | - | - | - | - | ||
| Nesson–Little Knife | ND | McKenzie | 329 | 1520 | 651 | 397 | 200 | 1072 | 610 | 362 | 164 | 1006 | ||
| Nesson–Little Knife | ND | Mountrail | 312 | 530 | 545 | 326 | 147 | 975 | 503 | 304 | 146 | 655 | ||
| Nesson–Little Knife | ND | Slope | 120 | 167 | - | - | - | - | - | - | - | - | ||
| Nesson–Little Knife | ND | Stark | 156 | 2164 | 199 | 167 | 134 | 2 | 343 | 203 | 93 | 219 | ||
| Nesson–Little Knife | ND | Williams | 178 | 1828 | 365 | 213 | 96 | 410 | 349 | 211 | 100 | 243 | ||
| Northwest–Transitional | MT | Daniels | 82 | 2584 | - | - | - | - | - | - | - | - | ||
| Northwest–Transitional | MT | McCone | 82 | 161 | - | - | - | - | - | - | - | - | ||
| Northwest–Transitional | MT | Roosevelt | 82 | 1312 | - | - | - | - | - | - | - | - | ||
| Northwest–Transitional | MT | Sheridan | 50 | 2857 | 195 | 100 | 24 | 27 | 67 | 67 | 67 | 1 | ||
| Northwest–Transitional | MT | Valley | 1 | 1005 | - | - | - | - | - | - | - | - | ||
| Northwest–Transitional | ND | Divide | 180 | 601 | 248 | 158 | 87 | 41 | 239 | 153 | 77 | 110 | ||
| Northwest–Transitional | ND | Williams | 212 | 669 | 311 | 185 | 81 | 89 | 317 | 224 | 85 | 20 | ||
| AVERAGE EUR (thousand bbl) | 189 | 177 | 515 | 309 | 146 | 456 | 278 | 136 | ||||||
| TOTAL WELL | 49,464 | 35,870 | 9894 | 4994 | ||||||||||
| TOTAL EUR (billion bbl) | 9.3 | 6.3 | 5.1 | 3.1 | 1.4 | 2.3 | 1.4 | 0.7 | ||||||
References
- Medeiros, F.; Ozkan, E.; Kazemi, H. Productivity and Drainage Area of Fractured Horizontal Wells in Tight Gas Reservoirs. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 April 2007. [Google Scholar]
- Ikonnikova, S.; Browning, J.; Horvath, S.C.; Tinker, S. Well Recovery, Drainage Area, and Future Drill-Well Inventory: Empirical Study of the Barnett Shale Gas Play. SPE Res. Eval. Eng. 2014, 17, 484–496. [Google Scholar] [CrossRef]
- Arps, J. Analysis of Decline Curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Gaswirth, S.B.; Marra, K.R.; Cook, T.A.; Charpentier, R.R.; Gautier, D.L.; Higley, D.K.; Klett, T.R.; Lewan, M.D.; Lillis, P.G.; Schenk, C.J. Assessment of undiscovered oil resources in the bakken and three forks formations, Williston Basin Province, Montana, North Dakota, and South Dakota, 2013. US Geol. Surv. Fact Sheet 2013, 3013, 1–4. [Google Scholar]
- Cook, T.A. Procedure for Calculating Estimated Ultimate Recoveries of Bakken and Three Forks Formations Horizontal Wells in the Williston Basin; US Geol. Surv. Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2013; pp. 1–14. [Google Scholar]
- EIA. Assumptions to the Annual Energy Outlook 2019: Oil and Gas Supply Module. US Energy Inf. Adm. Ann. Energy Outlook 2019, 7, 4–7. [Google Scholar]
- Kanfar, M.; Wattenbarger, R. Comparison of Empirical Decline Curve Methods for Shale Wells. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]
- Tan, L.; Zuo, L.; Wang, B. Methods of Decline Curve Analysis for Shale Gas Reservoirs. Energies 2018, 11, 552. [Google Scholar] [CrossRef]
- Olson, B.; Elliott, R.; Mathhews, C.M. Fracking’s Secret Problem–Oil Wells Aren’t Producing as Much as Forecast. The Wall Street Journal, 2 January 2019. Available online: https://www.wsj.com/articles/frackings-secret-problemoil-wells-arent-producing-as-much-as-forecast-11546450162 (accessed on 27 October 2019).
- Lapierre, S. On the Nature and Character of the Widespread Oil Production Shortfalls Reported by the Wall Street Journal. Linkedin Pulse, 11 September 2019. Available online: https://www.linkedin.com/pulse/nature-character-widespread-oil-production-shortfalls-scott-lapierre (accessed on 27 October 2019).
- Ilk, D.; Rushing, J.A.; Perego, A.D.; Blasingame, T.A. Exponential vs. Hyperbolic Decline in Tight Gas Sands: Understanding the Origin and Implications for Reserve Estimates Using Arps & Decline Curves. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Valko, P.P. Assigning value to stimulation in the Barnett Shale: A simultaneous analysis of 7000 plus production hystories and well completion records. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19-21 January 2009. [Google Scholar]
- Valko, P.P.; Lee, W.J. A Better Way To Forecast Production From Unconventional Gas Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Clark, A.J.; Lake, L.W.; Patzek, T.W. Production Forecasting with Logistic Growth Models. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Gong, X.; Gonzalez, R.; McVay, D.A.; Hart, J.D. Bayesian Probabilistic Decline-Curve Analysis Reliably Quantifies Uncertainty in Shale-Well-Production Forecasts. SPE J. 2014, 19, 1047–1057. [Google Scholar] [CrossRef]
- Paryani, M.; Awoleke, O.O.; Ahmadi, M.; Hanks, C.; Barry, R. Approximate Bayesian Computation for Probabilistic Decline-Curve Analysis in Unconventional Reservoirs. SPE Res. Eval. Eng. 2017, 20, 478–485. [Google Scholar] [CrossRef]
- Zhang, H.; Rietz, D.; Cagle, A.; Cocco, M.; Lee, J. Extended exponential decline curve analysis. J. Nat. Gas Sci. Eng. 2016, 36, 402–413. [Google Scholar] [CrossRef]
- Yu, S. A Comprehensive Study of b-Values for Proven Reserve Estimation Using Hyperbolic Decline for Vertical Commingled Gas Producers in Deep Basin Area of WCSB. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 20–22 October 2015. [Google Scholar]
- Stumpf, T.N.; Ayala, L.F. Rigorous and Explicit Determination of Reserves and Hyperbolic Exponents in Gas-Well Decline Analysis. SPE J. 2016, 21, 1843–1857. [Google Scholar] [CrossRef]
- Sharma, P.; Salman, M.; Reza, Z.; Kabir, C. Probing the roots of Arps hyperbolic relation and assessing variable-drive mechanisms for improved DCA. J. Pet. Sci. Eng. 2019, 182, 106288. [Google Scholar] [CrossRef]
- Ogunyomi, B.A.; Patzek, T.W.; Lake, L.W.; Kabir, C.S. History Matching and Rate Forecasting in Unconventional Oil Reservoirs With an Approximate Analytical Solution to the Double-Porosity Model. SPE Res. Eval. Eng. 2016, 19, 070–082. [Google Scholar] [CrossRef]
- Aybar, U.; Eshkalak, M.O.; Sepehrnoori, K.; Patzek, T.W. The effect of natural fractures closure on long-term gas production from unconventional resources. J. Nat. Gas Sci. Eng. 2014, 21, 1205–1213. [Google Scholar] [CrossRef]
- Aybar, U.; Yu, W.; Eshkalak, M.O.; Sepehrnoori, K.; Patzek, T. Evaluation of production losses from unconventional shale reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 509–516. [Google Scholar] [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. From the Cover: Cozzarelli Prize Winner: Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl. Acad. Sci. USA 2013, 110, 19731–19736. [Google Scholar] [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. A simple model of gas production from hydrofractured horizontal wells in shales. AAPG Bull. 2014, 98, 2507–2529. [Google Scholar] [CrossRef]
- Eftekhari, B.; Marder, M.; Patzek, T.W. Field data provide estimates of effective permeability, fracture spacing, well drainage area and incremental production in gas shales. J. Nat. Gas Sci. Eng. 2018, 56, 141–151. [Google Scholar] [CrossRef]
- Patzek, T.; Saputra, W.; Kirati, W.; Marder, M. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Gas Production in the Barnett Shale. Energy Fuels 2019, 33, 12154–12169. [Google Scholar] [CrossRef]
- Patzek, T.W.; Saputra, W.; Kirati, W. A Simple Physics-Based Model Predicts Oil Production from Thousands of Horizontal Wells in Shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Saputra, W.; Albinali, A.A. Validation of the Generalized Scaling Curve Method for EUR Prediction in Fractured Shale Oil Wells. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018. [Google Scholar]
- Conway, J. The Weird and Wonderful Chemistry of Audioactive Decay. In Open Problems in Communication and Computation; Springer: New York, NY, USA, 1987; pp. 173–188. [Google Scholar]
- Ekhad, S.B.; Zeilberger, D. Proof of Conway’s Lost Cosmological Theorem. arXiv 1998, arXiv:math.CO/ math/9808077. [Google Scholar]
- Finch, S.R. Mathematical Constants; Cambridge University Press: Cambridge, UK, 2003; pp. 452–454. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Saputra, W.; Kirati, W.; Patzek, T. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production in the Bakken Shale. Energies 2019, 12, 3641. [Google Scholar] [CrossRef]
- Lantz, T.G.; Greene, D.T.; Eberhard, M.J.; Norrid, R.S.; Pershall, R.A. Refracture Treatments Proving Successful In Horizontal Bakken Wells. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 April 2007. [Google Scholar]
- Oruganti, Y.; Mittal, R.; McBurney, C.J.; Garza, A.R. Re-Fracturing in Eagle Ford and Bakken to Increase Reserves and Generate Incremental NPV: Field Study. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Ruhle, W. Refracturing: Empirical Results in the Bakken Formation. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Li, C.; Han, J.; LaFollette, R.; Kotov, S. Lessons Learned From Refractured Wells: Using Data to Develop an Engineered Approach to Rejuvenation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016. [Google Scholar]
- Gullickson, G.; Ruhle, W.; Cook, P.F. The Lexicon of Recompletion: Empirical Justification for Refrac, Reentry, or Remediation in the Bakken/Three Forks Play. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 23–26 May 2016. [Google Scholar]
- Lane, W.; Chokshi, R. Considerations for Optimizing Artificial Lift in Unconventionals. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Orji, E.; Lissanon, J.; Omole, O. Sucker Rod Lift System Optimization of an Unconventional Well. In Proceedings of the SPE North America Artificial Lift Conference and Exhibition, The Woodlands, TX, USA, 25–27 October 2016. [Google Scholar]
- Oyewole, P. Artificial Lift Selection Strategy to Maximize Unconventional Oil and Gas Assets Value. In Proceedings of the SPE North America Artificial Lift Conference and Exhibition, The Woodlands, TX, USA, 25–27 October 2016. [Google Scholar]
- Sickle, S.V.; Shelly, G.; Snyder, D. Optimizing Completions and Artificial Lift in an Unconventional Play in the United States. In Proceedings of the SPE Artificial Lift Conference ó Latin America and Caribbean, Salvador, Bahia, Brazil, 27–28 May 2015. [Google Scholar]
- Male, F.; Marder, M.; Browning, J.; Gherabati, A.; Ikonnikova, S. Production Decline Analysis in the Eagle Ford. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Male, F.; Gherabati, A.; Browning, J.R.; Marder, M. Forecasting Production From Bakken and Three Forks Wells Using a Segregated Flow Model. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017. [Google Scholar]
- Kondash, A.J.; Albright, E.; Vengosh, A. Quantity of flowback and produced waters from unconventional oil and gas exploration. Sci. Total Environ. 2017, 574, 314–321. [Google Scholar] [CrossRef]
- Cheng, Y. Impact of Water Dynamics in Fractures on the Performance of Hydraulically Fractured Wells in Gas-Shale Reservoirs. J. Can. Pet. Technol. 2012, 51, 143–151. [Google Scholar] [CrossRef]
- Abualfaraj, N.; Gurian, P.L.; Olson, M.S. Characterization of Marcellus Shale Flowback Water. Environ. Eng. Sci. 2014, 31, 514–524. [Google Scholar] [CrossRef]
- Hughes, J.D. 2016 Tight Oil Reality Check; Post Carbon Institude: Santa Rosa, CA, USA, 2016. [Google Scholar]
- Hughes, J.D. Shale Reality Check; Post Carbon Institude: Santa Rosa, CA, USA, 2018. [Google Scholar]
- Hughes, J.D. How Long Will the Shale Revolution Last?: Technology versus Geology and the Lifecycle of Shale Plays; Post Carbon Institude: Santa Rosa, CA, USA, 2019. [Google Scholar]
- Paneitz, J. Evolution of the Bakken Completions in Sanish Field, Williston Basin, North Dakota. In Proceedings of the SPE Applied Technology Workshop (ATW), Keystone, CO, USA, 6 August 2010. [Google Scholar]
- Buffington, N.; Kellner, J.; King, J.G.; David, B.L.; Demarchos, A.S.; Shepard, L.R. New Technology in the Bakken Play Increases the Number of Stages in Packer/Sleeve Completions. In Proceedings of the SPE Western Regional Meeting, Anaheim, CA, USA, 27–29 May 2010. [Google Scholar]
- Weddle, P.; Griffin, L.; Pearson, C.M. Mining the Bakken: Driving Cluster Efficiency Higher Using Particulate Diverters. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017. [Google Scholar]
- Martin, E. United States Tight Oil Production 2018. Available online: https://www.allaboutshale.com/united-states-tight-oil-production-2018-emanuel-omar-martin/ (accessed on 1 September 2019).
- Ahmed, T. Reservoir Engineering Handbook: Fourth Edition; Gulf Professional Publishing: Cambridge, MA, USA, 2010; pp. 1250–1255. [Google Scholar]
- Meissner, F.F. Petroleum geology of the Bakken Formation Williston Basin, North Dakota and Montana. In 1991 Guidebook to Geology and Horizontal Drilling of the Bakken Formation; Montana Geological Society: Butte, MT, USA, 1991. [Google Scholar]
- Sonnenberg, S.A.; Pramudito, A. Petroleum geology of the giant Elm Coulee field, Williston Basin. AAPG Bull. 2009, 93, 1127–1153. [Google Scholar] [CrossRef]
- Jin, H.; Sonnenberg, S.A. Characterization for Source Rock Potential of the Bakken Shales in the Williston Basin, North Dakota and Montana. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013. [Google Scholar]
- Han, Y.; Misra, S.; Simpson, G. Dielectric dispersion log interpretation in Bakken petroleum system. In Proceedings of the SPWLA 58th Annual Logging Symposium, Oklahoma City, OK, USA, 17–21 June 2017. [Google Scholar]
- Han, Y.; Misra, S. Bakken Petroleum System Characterization Using Dielectric-Dispersion Logs. Petrophys. SPWLA J. Form. Eval. Res. Des. 2018, 59, 201–217. [Google Scholar] [CrossRef]
- Alvarez, D.; Joseph, A.; Gulewicz, D. Optimizing Well Completions in the Canadian Bakken: Case History of Different Techniques to Achieve Full ID Wellbores. In Proceedings of the SPE Unconventional Resources Conference, Calgary, AB, Canada, 5–7 November 2013. [Google Scholar]
- LeFever, J.A. History of oil production from the Bakken Formation, North Dakota. In 1991 Guidebook to Geology and Horizontal Drilling of the Bakken Formation; Montana Geological Society: Butte, MT, USA, 1991. [Google Scholar]
- Nordeng, S.H. A brief history of oil production from the Bakken formation in the Williston Basin. Geo News 2010, 37, 5–9. [Google Scholar]
- Kurtoglu, B. Integrated Reservoir Characterization and Modeling in Support of Enhanced Oil Recovery for Bakken; Colorado School of Mines: Golden, CO, USA, 2013. [Google Scholar]
- Tran, T.; Sinurat, P.D.; Wattenbarger, B.A. Production Characteristics of the Bakken Shale Oil. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saputra, W.; Kirati, W.; Patzek, T. Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale. Energies 2020, 13, 2052. https://doi.org/10.3390/en13082052
Saputra W, Kirati W, Patzek T. Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale. Energies. 2020; 13(8):2052. https://doi.org/10.3390/en13082052
Chicago/Turabian StyleSaputra, Wardana, Wissem Kirati, and Tadeusz Patzek. 2020. "Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale" Energies 13, no. 8: 2052. https://doi.org/10.3390/en13082052
APA StyleSaputra, W., Kirati, W., & Patzek, T. (2020). Physical Scaling of Oil Production Rates and Ultimate Recovery from All Horizontal Wells in the Bakken Shale. Energies, 13(8), 2052. https://doi.org/10.3390/en13082052