Improving Accessible Capacity Tracking at Low Ambient Temperatures for Range Estimation of Battery Electric Vehicles
Abstract
1. Introduction
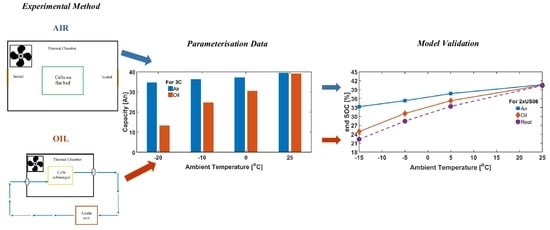
2. Materials and Methods
2.1. Experimental Setup
2.1.1. Galvanostatic Cycling Performance
2.1.2. Open Circuit Voltage (OCV) versus State-of-Charge (SOC) Characterisation
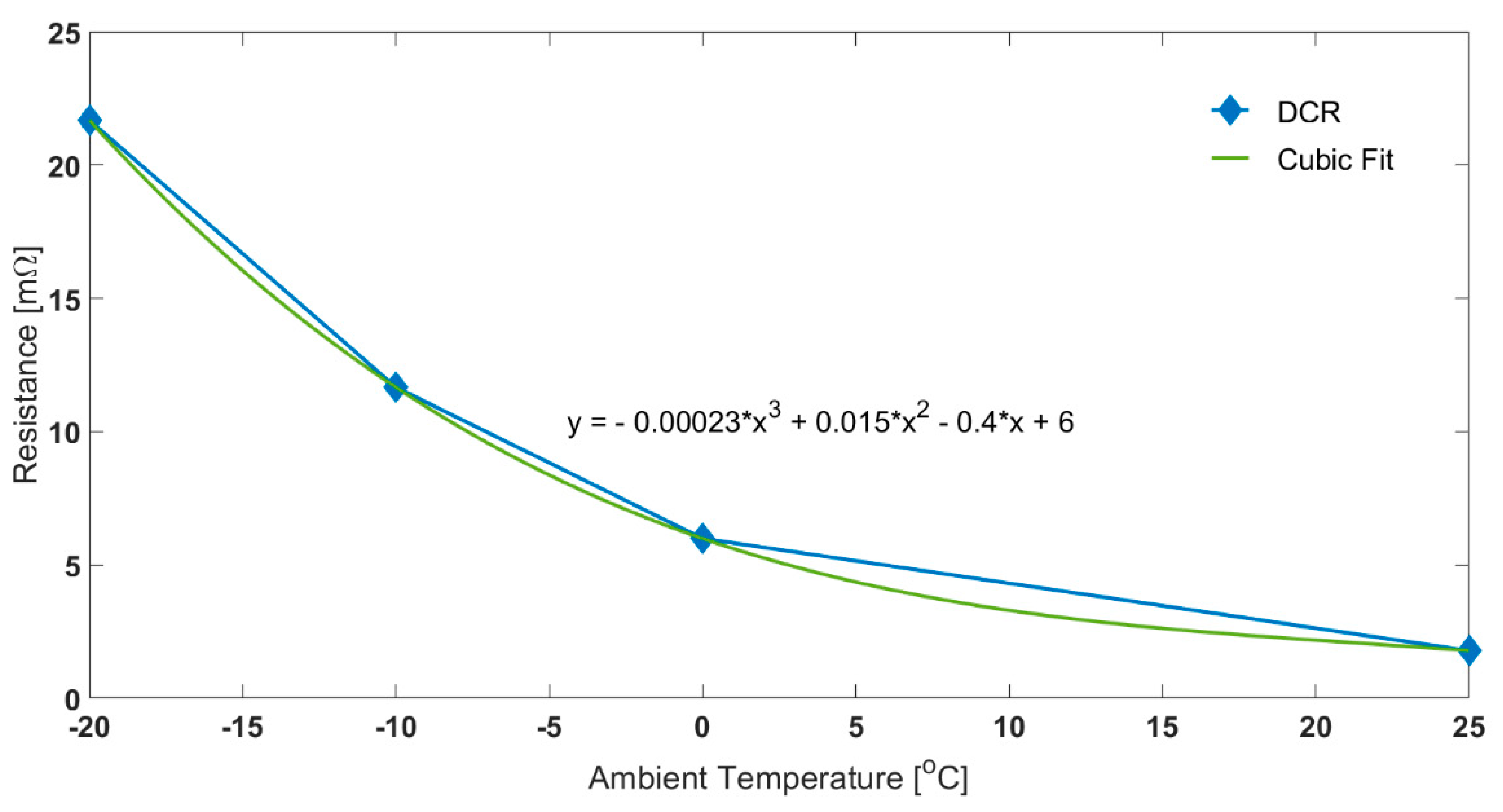
2.2. Modelling Methodology
3. Results and Discussion
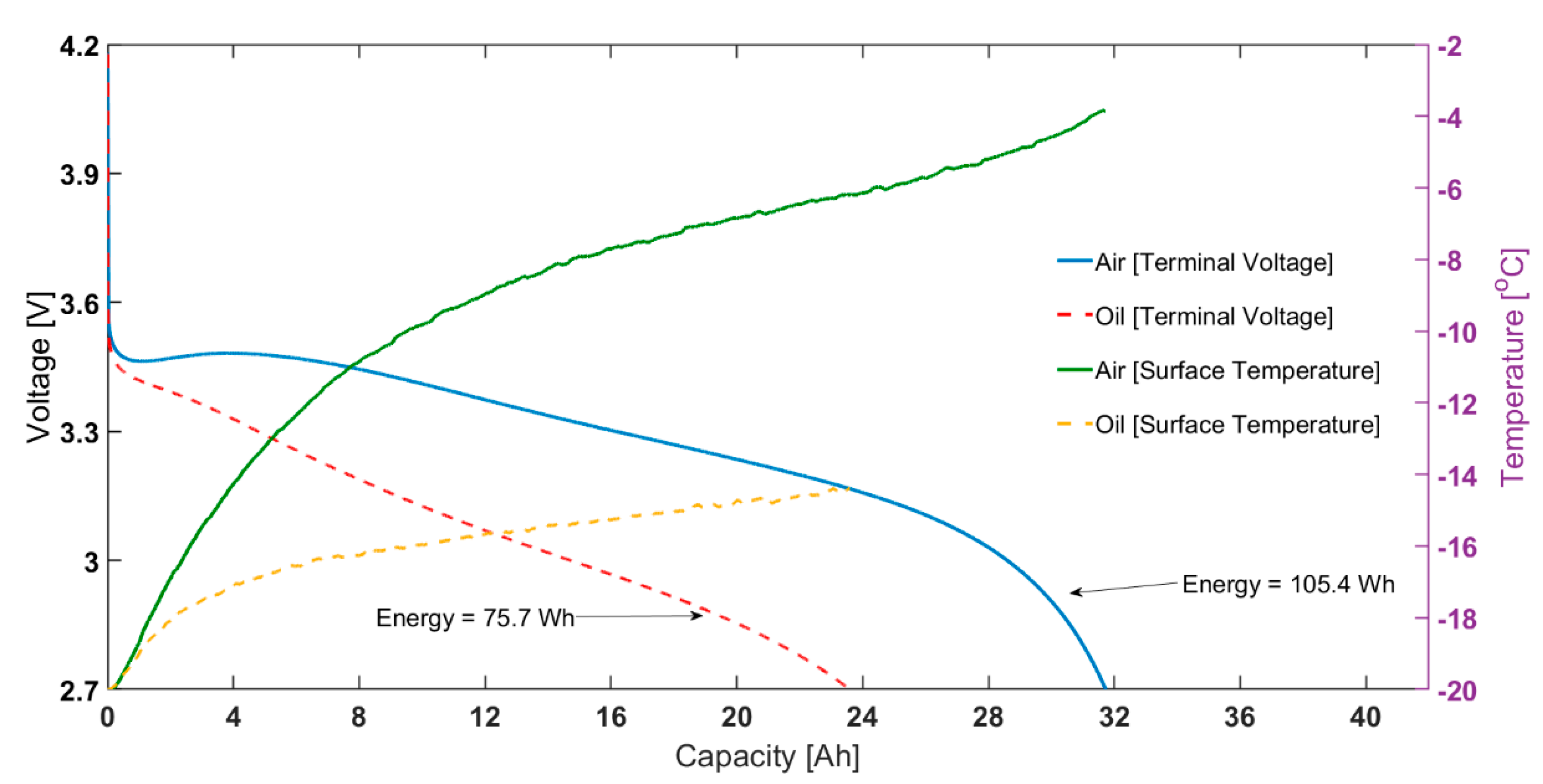
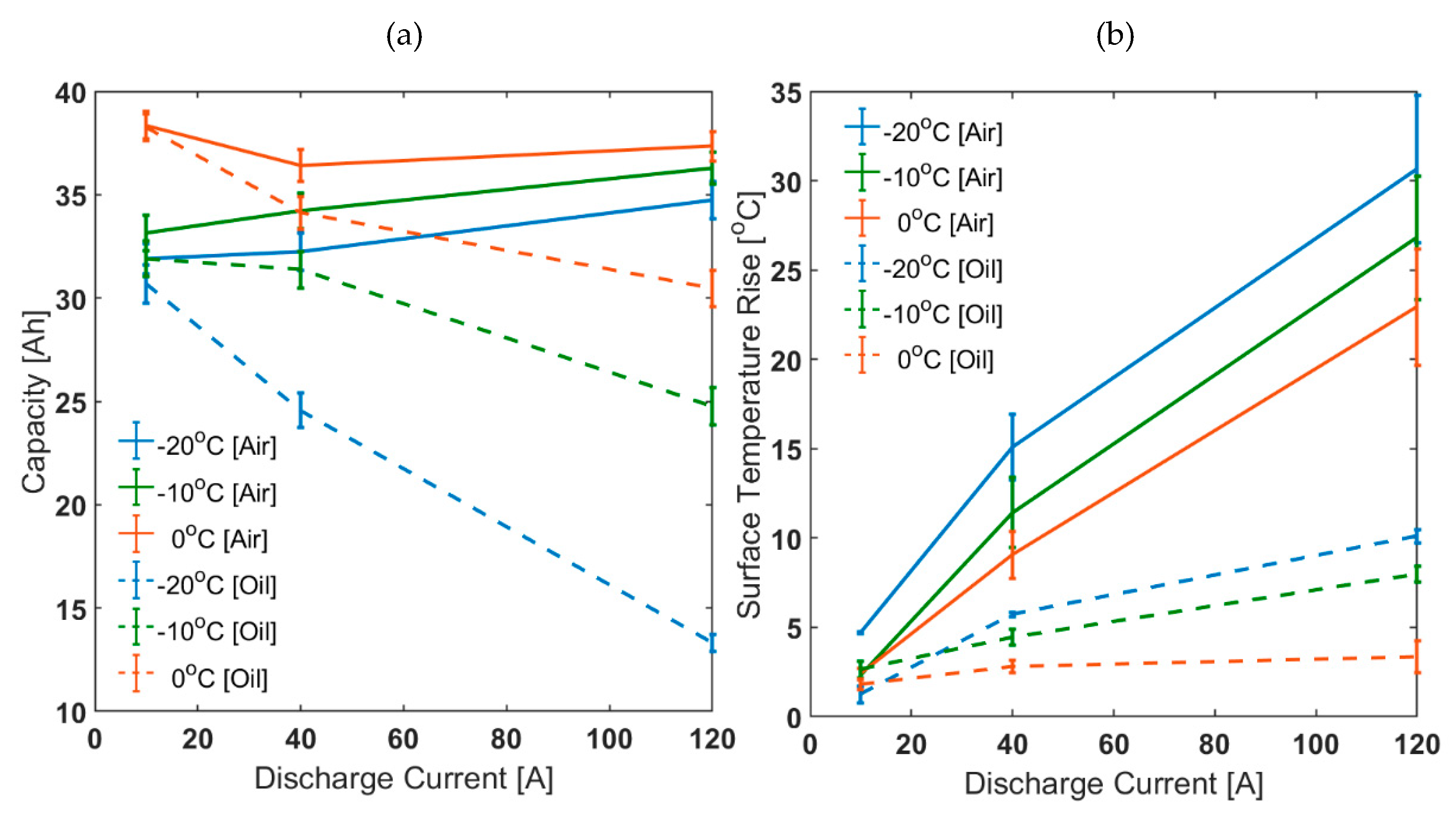
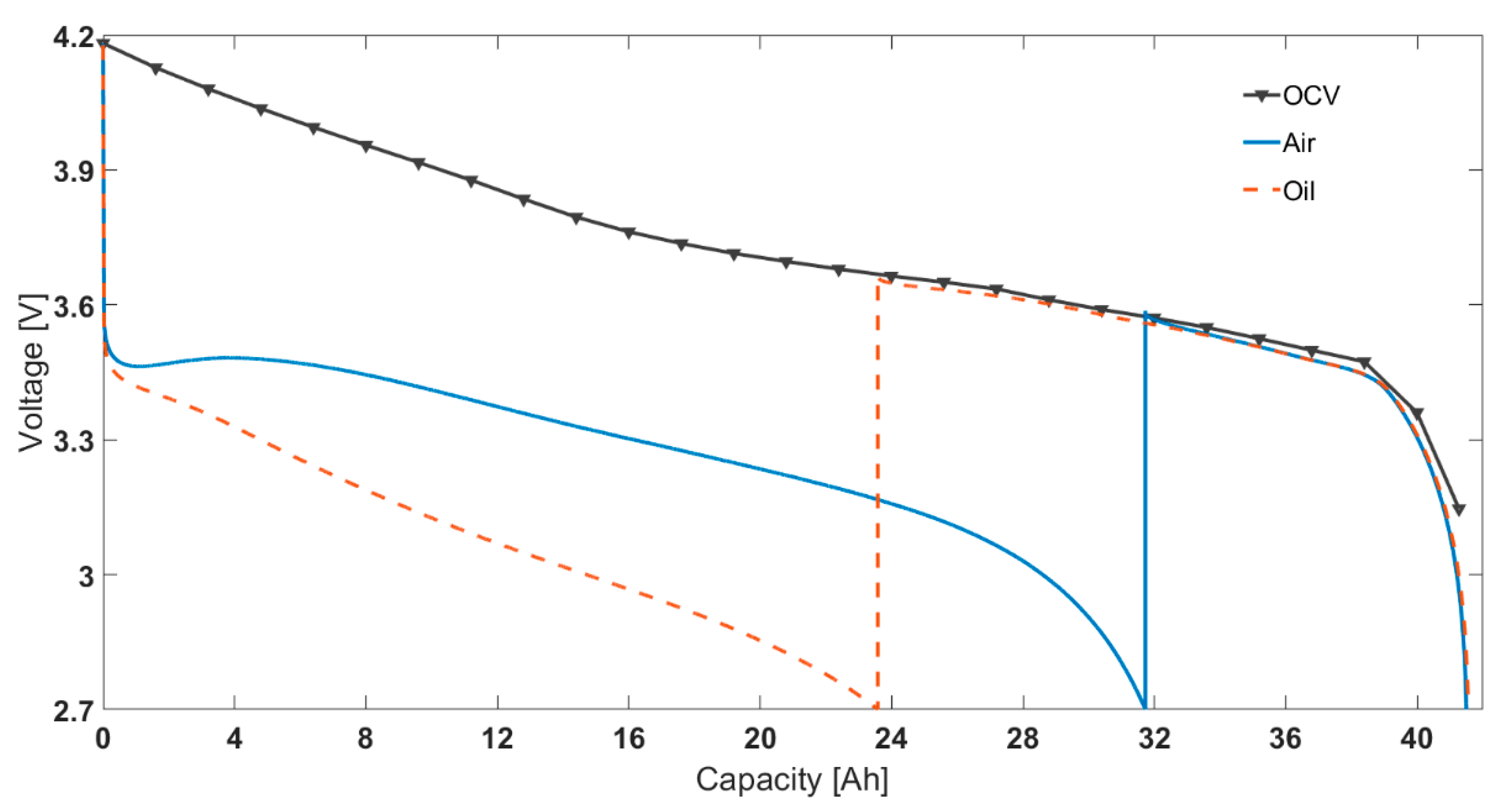
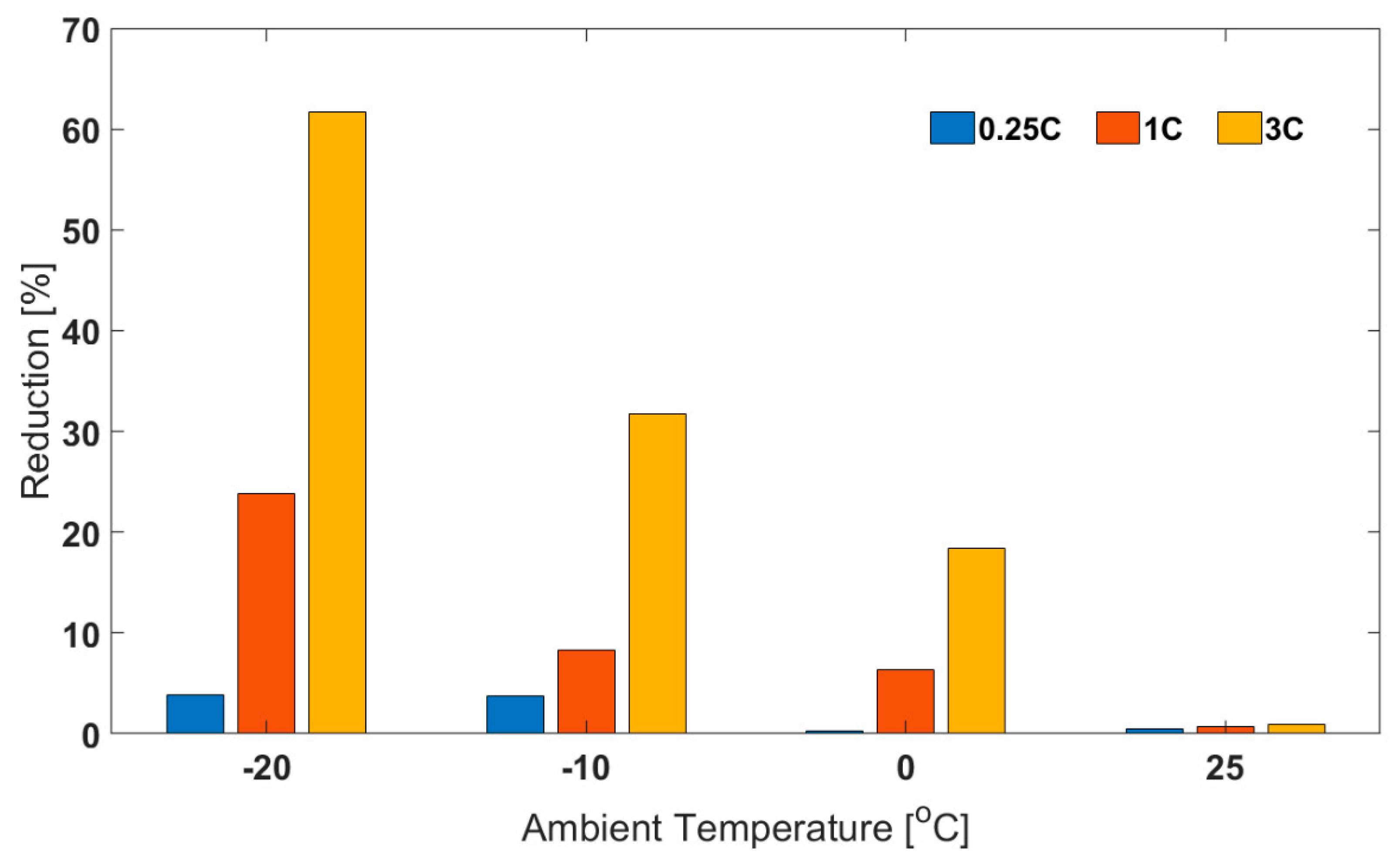
3.1. Comparison between Air and Oil Based Thermal Control System for Low Ambient Temperatures and High Load Currents
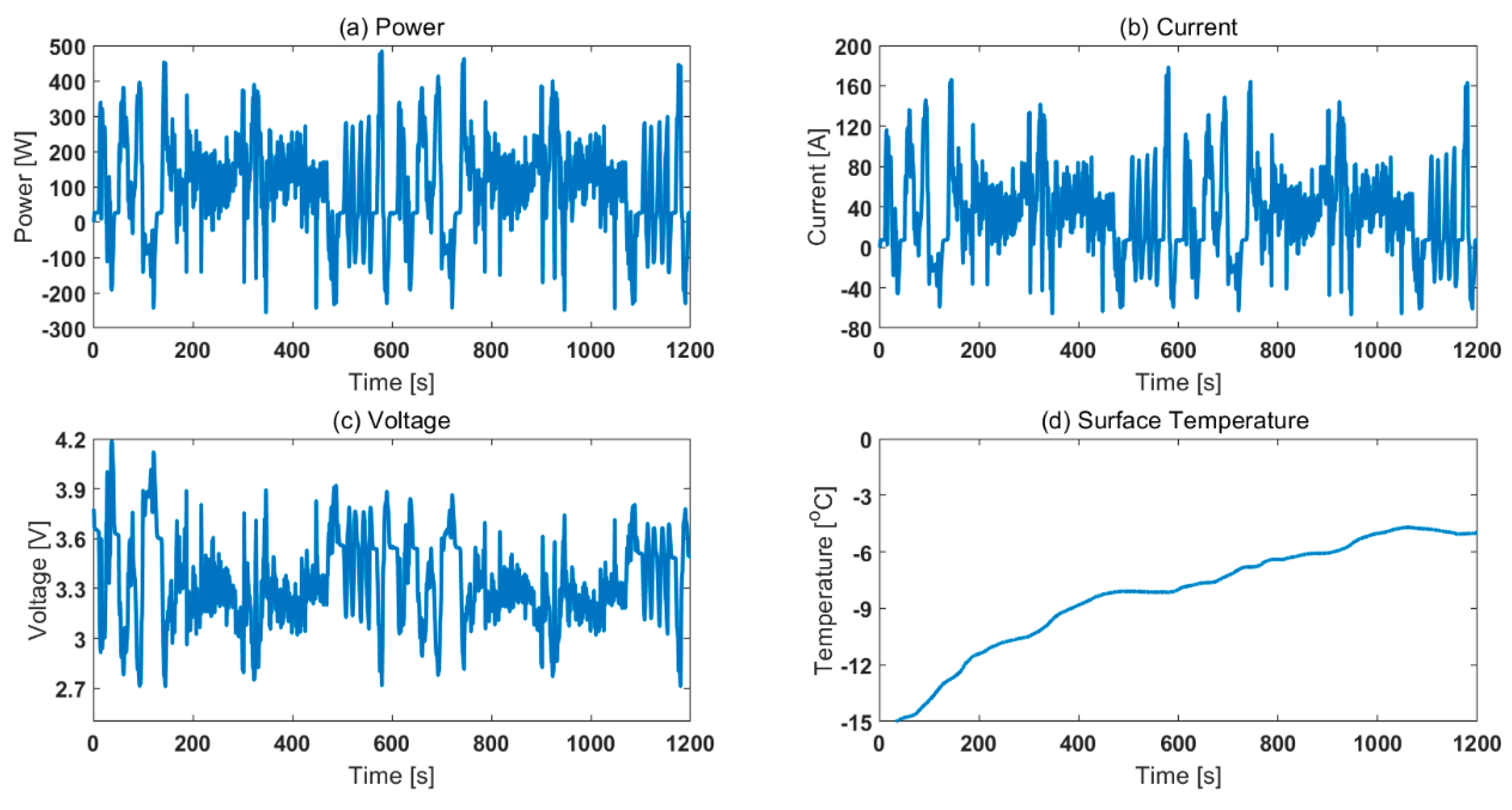
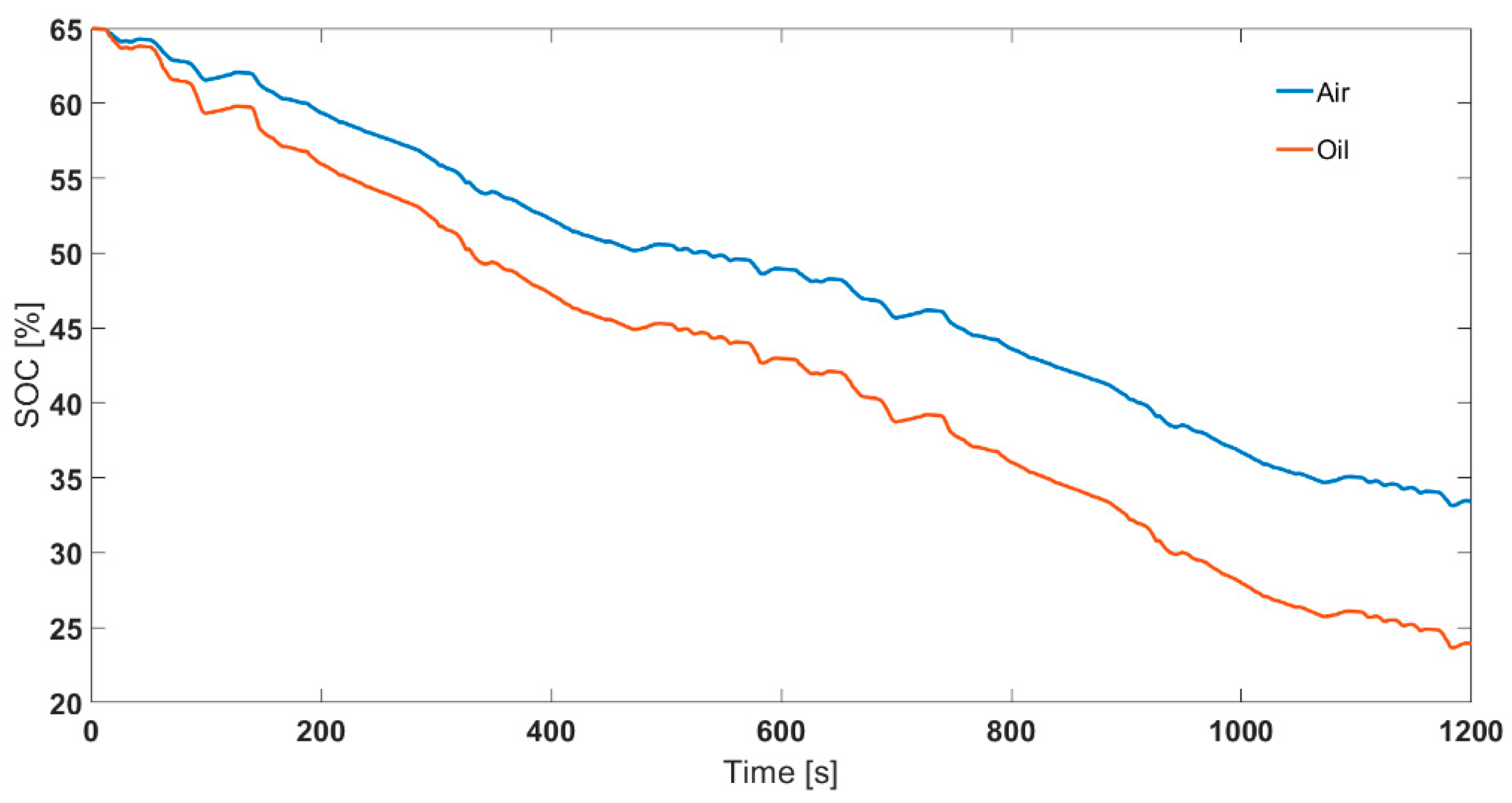
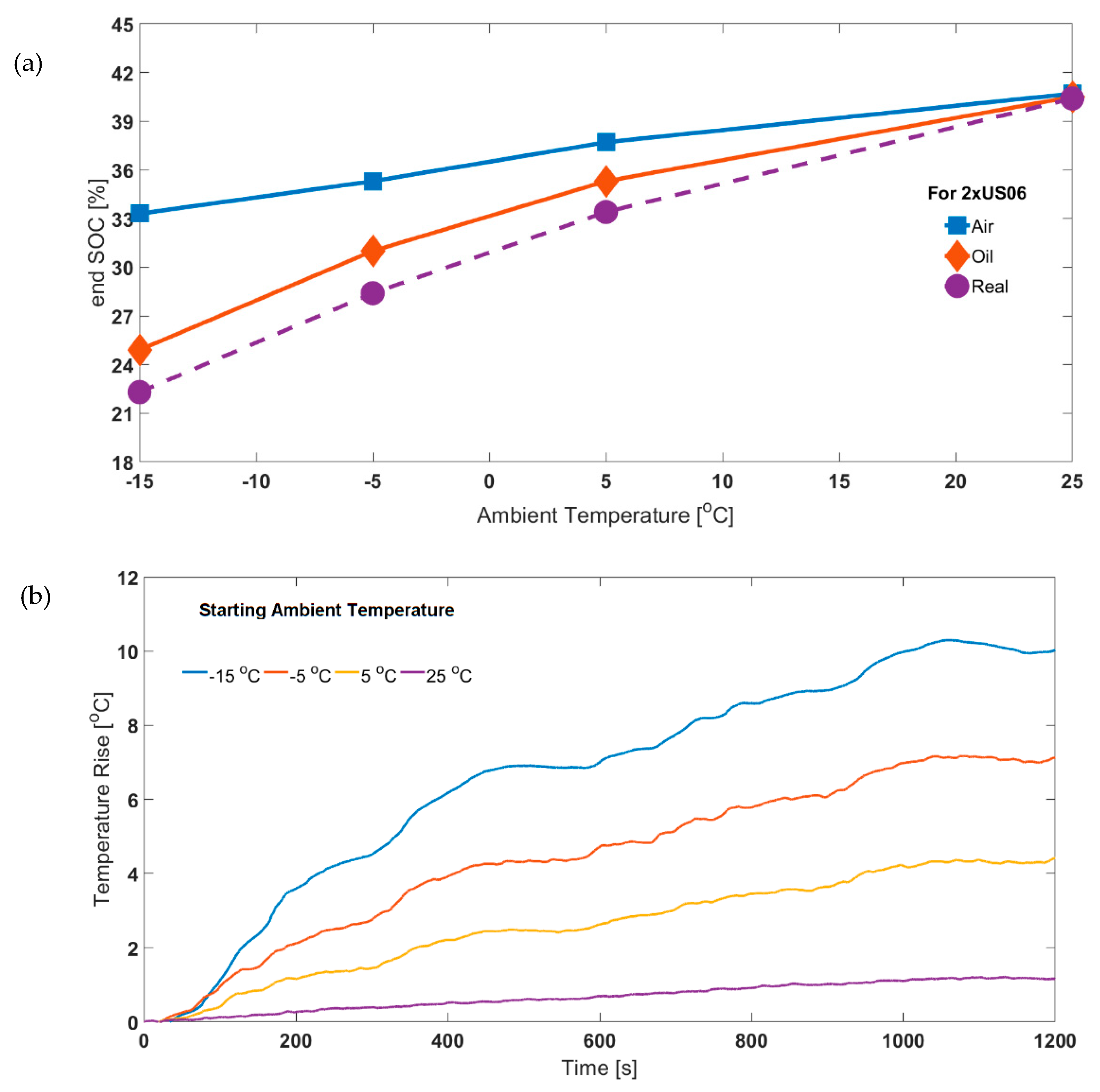
3.2. Validation Using SOC Estimation: Effect of Legislative Drive Cycles
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, H.; Hosoi, K.; Amine, K.; Howell, D.; Passerini, S.; Zeisel, H.; Bresser, D. Perspectives of automotive battery R&D in China, Germany, Japan, and the USA. J. Power Sources 2018, 382, 176–178. [Google Scholar]
- Emadi, A.; Rajashekara, K.; Williamson, S.S.; Lukic, S.M. Topological overview of hybrid electric and fuel cell vehicular power system architectures and configurations. IEEE Trans. Veh. Technol. 2005, 54, 763–770. [Google Scholar] [CrossRef]
- Lithium and Cobalt: A Tale of Two Commodities|McKinsey. Available online: https://www.mckinsey.com/industries/metals-and-mining/our-insights/lithium-and-cobalt-a-tale-of-two-commodities (accessed on 2 February 2020).
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Miller, P. Automotive lithium-ion batteries. Johns. Matthey Technol. Rev. 2015, 59, 4–13. [Google Scholar] [CrossRef]
- World’s First Fully Electric Commercial Aircraft Takes Flight in Canada|World News|The Guardian. Available online: https://www.theguardian.com/world/2019/dec/11/worlds-first-fully-electric-commercial-aircraft-takes-flight-in-canada (accessed on 11 February 2020).
- Green Flyway: Norway, Sweden Create Airspace For Electric Plane Tests. Available online: https://www.forbes.com/sites/davidnikel/2020/01/30/green-flyway-norway-sweden-create-airspace-for-electric-plane-tests/#28ea997541b9 (accessed on 11 February 2020).
- Zahabi, S.A.H.; Miranda-Moreno, L.; Barla, P.; Vincent, B. Fuel economy of hybrid-electric versus conventional gasoline vehicles in real-world conditions: A case study of cold cities in Quebec, Canada. Transp. Res. Part D Transp. Environ. 2014, 32, 184–192. [Google Scholar] [CrossRef]
- Tripathy, Y.; Mcgordon, A.; Low, J.; Marco, J. Low temperature performance of lithium-ion batteries for different drive cycles. In Proceedings of the Electric Vehicle Symposium (EVS 29), Montréal, QC, Canada, 19–21 Junary 2016; pp. 1–12. [Google Scholar]
- Singer, J.P.; Birke, K.P. Kinetic study of low temperature capacity fading in Li-ion cells. J. Energy Storage 2017, 13, 129–136. [Google Scholar] [CrossRef]
- Zhu, G.; Wen, K.; Lv, W.; Zhou, X.; Liang, Y.; Yang, F.; Chen, Z.; Zou, M.; Li, J.; Zhang, Y.; et al. Materials insights into low-temperature performances of lithium-ion batteries. J. Power Sources 2015, 300, 29–40. [Google Scholar] [CrossRef]
- Rizalino, J.; Reyes, M.D.; Member, A.; Parsons, R.V.; Hoemsen, R. Winter happens: The effect of ambient temperature on the travel range of electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4016–4022. [Google Scholar]
- Jeffs, J.; McGordon, A.; Picarelli, A.; Robinson, S.; Tripathy, Y.; Widanage, W. Complex heat pump operational mode identification and comparison for use in electric vehicles. Energies 2018, 11, 2000. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Zhang, C.; Chen, J. Climate control loads prediction of electric vehicles. Appl. Therm. Eng. 2017, 110, 1183–1188. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- We Drove These Electric Cars Until They DIED!—YouTube. Available online: https://www.youtube.com/watch?v=ZH7V2tU3iFc (accessed on 8 April 2020).
- Varga, B.; Sagoian, A.; Mariasiu, F. Prediction of electric vehicle range: A comprehensive review of current issues and challenges. Energies 2019, 12, 946. [Google Scholar] [CrossRef]
- Biggest Winter Range Test Ever Reveals Best EVs For Cold Weather. Available online: https://insideevs.com/news/404632/winter-range-test-best-evs-cold-weather/ (accessed on 28 March 2020).
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Dubarry, M.; Somerville, L.; McGordon, A.; Jennings, P.; Bloom, I. A comparison of methodologies for the non-invasive characterisation of commercial Li-ion cells. Prog. Energy Combust. Sci. 2019, 72, 1–31. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, C.Y. Heating strategies for Li-ion batteries operated from subzero temperatures. Electrochim. Acta 2013, 107, 664–674. [Google Scholar] [CrossRef]
- Grandjean, T.; McGordon, A.; Jennings, P. Structural identifiability of equivalent circuit models for li-ion batteries. Energies 2017, 10, 90. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dube, Y. Characterization and modeling of a hybrid-electric-vehicle lithium-ion battery pack at low temperatures. IEEE Trans. Veh. Technol. 2016, 65, 1–14. [Google Scholar] [CrossRef]
- Silva, L.I.; Jaguemont, J.; De Angelo, C.H. Modeling an Electric Vehicle Lithium-Ion Battery Pack Considering Low Temperature behavior. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016. [Google Scholar]
- Watrin, N.; Roche, R.; Ostermann, H.; Blunier, B.; Miraoui, A. Multiphysical lithium-based battery model for use in state-of-charge determination. IEEE Trans. Veh. Technol. 2012, 61, 3420–3429. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Von Srbik, M.T.; Marinescu, M.; Martinez-Botas, R.F.; Offer, G.J. A physically meaningful equivalent circuit network model of a lithium-ion battery accounting for local electrochemical and thermal behaviour, variable double layer capacitance and degradation. J. Power Sources 2016, 325, 171–184. [Google Scholar] [CrossRef]
- Ardani, M.I.; Patel, Y.; Siddiq, A.; Offer, G.J.; Martinez-Botas, R.F. Combined experimental and numerical evaluation of the differences between convective and conductive thermal control on the performance of a lithium ion cell. Energy 2018, 144, 81–97. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Bolsinger, C.; Birke, K.P. Effect of different cooling configurations on thermal gradients inside cylindrical battery cells. J. Energy Storage 2019, 21, 222–230. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; E, J.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 262–281. [Google Scholar] [CrossRef]
- Nissan LEAF Charger|Pod Point. Available online: https://pod-point.com/landing-pages/nissan-leaf-charging (accessed on 17 January 2019).
- Barai, A.; Uddin, K.; Chevalier, J.; Chouchelamane, G.H.; McGordon, A.; Low, J.; Jennings, P. Transportation safety of lithium iron phosphate batteries—A feasibility study of storing at very low states of charge. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Tripathy, Y.; McGordon, A.; Low, C.T.J. A new consideration for validating battery performance at low ambient temperatures. Energies 2018, 11, 2439. [Google Scholar] [CrossRef]
- Birrell, S.A.; McGordon, A.; Jennings, P.A. Defining the accuracy of real-world range estimations of an electric vehicle. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 2590–2595. [Google Scholar]
- Gao, Z.; LaClair, T.; Ou, S.; Huff, S.; Wu, G.; Hao, P.; Boriboonsomsin, K.; Barth, M. Evaluation of electric vehicle component performance over eco-driving cycles. Energy 2019, 172, 823–839. [Google Scholar] [CrossRef]
- Doucette, R.T.; Mcculloch, M.D. Modeling the CO 2 emissions from battery electric vehicles given the power generation mixes of different countries. Energy Policy 2010, 39, 803–811. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Kambly, K.; Bradley, T.H. Geographical and temporal differences in electric vehicle range due to cabin conditioning energy consumption. J. Power Sources 2015, 275, 468–475. [Google Scholar] [CrossRef]
- Myall, D.; Ivanov, D.; Larason, W.; Nixon, M.; Moller, H. Accelerated reported battery capacity loss in 30 kWh variants of the nissan leaf. Preprints 2018, 2018, 2018030122. [Google Scholar]
- Nikolian, A.; Jaguemont, J.; de Hoog, J.; Goutam, S.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Complete cell-level lithium-ion electrical ECM model for different chemistries (NMC, LFP, LTO) and temperatures (−5 °C to 45 °C)—Optimized modelling techniques. Int. J. Electr. Power Energy Syst. 2018, 98, 133–146. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Venet, P.; Dube, Y.; Sari, A. Lithium-ion battery aging experiments at subzero temperatures and model development for capacity fade estimation. IEEE Trans. Veh. Technol. 2016, 65, 4328–4343. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Y.; Wang, C.-Y. Li-ion cell operation at low temperatures. J. Electrochem. Soc. 2013, 160, A636–A649. [Google Scholar] [CrossRef]
- Grandjean, T.; Barai, A.; Hosseinzadeh, E.; Guo, Y.; Mcgordon, A.; Marco, J. Large format lithium ion pouch cell full thermal characterisation for improved electric vehicle thermal management. J. Power Sources 2017, 359, 215–225. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Capacity loss in rechargeable lithium cells during cycle life testing: The importance of determining state-of-charge. J. Power Sources 2007, 174, 1121–1125. [Google Scholar] [CrossRef]
- Veth, C.; Dragicevic, D.; Merten, C. Thermal characterizations of a large-format lithium ion cell focused on high current discharges. J. Power Sources 2014, 267, 760–769. [Google Scholar] [CrossRef]
- Osswald, P.J.; Del Rosario, M.; Garche, J.; Jossen, A.; Hoster, H.E. Fast and accurate measurement of entropy profiles of commercial lithium-ion cells. Electrochim. Acta 2015, 177, 270–276. [Google Scholar] [CrossRef]
- Everson, J.; Tripathy, Y.; Barai, A.; Amor-Segan, M. Thermal runaway suppression capability of state-of-the-art coolant fluids for lithium-ion battery applications. In Proceedings of the ECS Meeting Abstracts, Atlanta, GA, USA, 13–17 October 2019. [Google Scholar]


| Physical Property | Air | Mineral Oil | Silicone Oil | Water/Glycol |
|---|---|---|---|---|
| Specific Heat Capacity [J/kgK] | 1006 | 1900 | 1370 | 1069 |
| Thermal Conductivity [W/mK] | 0.0242 | 0.13 | 0.15 | 0.3892 |
| Characteristic | Range/Value |
|---|---|
| Supplier | XALT Energy |
| Chemistry | NMC/Graphite |
| Capacity, Ah (Rated at 0.5C) | 40 |
| Nominal Voltage, V | 3.7 |
| Energy, Wh (Rated at 0.5C) | 148 |
| Weight, kg | 0.97 |
| Specific Energy, Wh/kg | 153 |
| Volumetric Energy Density, Wh/L | 350 |
| Direct Current Resistance (10 s at 50% SOC), mΩ | 1.35 |
| Max C-rate Continuous (Charge) | 3C |
| Max C-rate Continuous (Discharge) | 8C |
| Max C-rate Pulse (Discharge) (10 s) | 10C |
| Peak Power, kW | 2.6 |
| Specific Power, W/kg | 2600 |
| Volumetric Power Density, W/L | 5900 |
| Upper Voltage Limit, V | 4.2 |
| Lower Voltage Limit, V | 2.7 |
| Charge Temperature Range, °C | 0 to 45 |
| Discharge Temperature Range, °C | −20 to 60 |
| Characteristic | Range/Value |
|---|---|
| Operating Temperature Range, °C | −95 to 60 |
| Chemical Characterisation | Polydimethylsiloxane |
| Colour | Colourless |
| Kinematic Viscosity, mm2/s (at 20 °C) | 1.6 |
| Density, kg/m3 (at 20 °C) | 855 |
| Specific Heat Capacity, kJ/kgK | 1.8 |
| Pour Point, °C | ≤−111 |
| Boiling Point, °C | ≥190 |
| Ambient Temperature | −20 °C | −10 °C | 0 °C | 25 °C | |
|---|---|---|---|---|---|
| Capacity [Ah] | 0.25C | 31.9 ± 0.7 | 33.2 ± 0.9 | 38.4 ± 0.7 | 42.3 ± 0.2 |
| 1C | 32.2 ± 0.9 | 34.2 ± 0.9 | 36.4 ± 0.8 | 40.6 ± 0.2 | |
| 3C | 34.7 ± 0.9 | 36.3 ± 0.8 | 37.3 ± 0.7 | 39.5 ± 0.4 | |
| Energy [Wh] | 0.25C | 108.9 ± 2.0 | 113.2 ± 2.6 | 138.7 ± 2.1 | 156.4 ± 0.5 |
| 1C | 105.4 ± 2.7 | 115.8 ± 2.7 | 126.9 ± 2.4 | 148.0 ± 0.5 | |
| 3C | 109.9 ± 2.8 | 118.0 ± 2.4 | 124.5 ± 2.1 | 140.2 ± 1.1 | |
| Surface Temperature Rise [°C] | 0.25C | 4.7 ± 0.1 | 2.3 ± 0.8 | 2.4 ± 0.3 | 1.4 ± 0.0 |
| 1C | 15.1 ± 1.8 | 11.4 ± 2.0 | 9.1 ± 1.3 | 4.4 ± 0.1 | |
| 3C | 30.7 ± 4.1 | 26.8 ± 3.4 | 22.9 ± 3.2 | 12.0 ± 0.7 | |
| Oil Bath Temperature [°C] | −20 °C | −10 °C | 0 °C | 25 °C | |
|---|---|---|---|---|---|
| Capacity [Ah] | 0.25C | 30.7 ± 0.9 | 31.9 ± 0.9 | 38.2 ± 0.6 | 41.7 ± 0.3 |
| 1C | 24.6 ± 0.8 | 31.4 ± 0.9 | 34.1 ± 0.8 | 40.3 ± 0.5 | |
| 3C | 13.3 ± 0.4 | 24.8 ± 0.9 | 30.5 ± 0.9 | 39.2 ± 0.2 | |
| Energy [Wh] | 0.25C | 102.6 ± 2.7 | 109.4 ± 2.5 | 138.1 ± 2.0 | 153.7 ± 1.0 |
| 1C | 75.7 ± 2.5 | 103.8 ± 2.5 | 117.0 ± 2.3 | 145.9 ± 1.6 | |
| 3C | 38.0 ± 1.2 | 75.7 ± 2.8 | 101.6 ± 2.6 | 136.7 ± 1.8 | |
| Surface Temperature Rise [°C] | 0.25C | 1.2 ± 0.5 | 1.6 ± 0.4 | 1.8 ± 0.3 | 0.8 ± 0.1 |
| 1C | 5.7 ± 0.1 | 4.4 ± 0.4 | 2.8 ± 0.3 | 1.7 ± 0.5 | |
| 3C | 10.1 ± 0.4 | 8.0 ± 0.4 | 3.3 ± 0.9 | 2.4 ± 0.1 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tripathy, Y.; McGordon, A.; Barai, A. Improving Accessible Capacity Tracking at Low Ambient Temperatures for Range Estimation of Battery Electric Vehicles. Energies 2020, 13, 2021. https://doi.org/10.3390/en13082021
Tripathy Y, McGordon A, Barai A. Improving Accessible Capacity Tracking at Low Ambient Temperatures for Range Estimation of Battery Electric Vehicles. Energies. 2020; 13(8):2021. https://doi.org/10.3390/en13082021
Chicago/Turabian StyleTripathy, Yashraj, Andrew McGordon, and Anup Barai. 2020. "Improving Accessible Capacity Tracking at Low Ambient Temperatures for Range Estimation of Battery Electric Vehicles" Energies 13, no. 8: 2021. https://doi.org/10.3390/en13082021
APA StyleTripathy, Y., McGordon, A., & Barai, A. (2020). Improving Accessible Capacity Tracking at Low Ambient Temperatures for Range Estimation of Battery Electric Vehicles. Energies, 13(8), 2021. https://doi.org/10.3390/en13082021