Analysis of Energy Consumption of the Reduction of Fe₂O₃ by Hydrogen and Carbon Monoxide Mixtures

Abstract

Energy consumption is directly related to the energy supply and production costs of gas-based direct reduction ironmaking, which is an effective choice to reduce the energy consumption of iron making. In this paper, the minimum Gibbs free energy principle was used to calculate the equilibrium composition under the conditions of reduction gas consisting of hydrogen and carbon monoxide (hydrogen concentration of 0–100%, reduction gas amount of 0–6.0 mol, reduction temperature of 790–1100 °C, and 0.5 mol Fe₂O₃). According to the enthalpy change, a simplified energy consumption model of a gas-based direct reduction ironmaking process was established, and the energy consumption per mole of metallic iron produced was calculated in detail. The following conclusions were drawn: at the stage when the reduction reaction occurred, the utilization rate of hydrogen or carbon monoxide remained unchanged with the increase in the amount of reduction gas or the increase in the hydrogen concentration of initial gas. The direct energy consumption increased with the increase in the hydrogen concentration at 790–980 °C and the opposite was true at 980–1100 °C. At 790–980 °C, the total energy consumption per ton of iron was greater than 0 and increased with the increase in initial hydrogen concentration from 40% to 100%, and it was less than 0 and increased with the increase in initial hydrogen concentration from 0% to 30%. It was possible to achieve zero total energy consumption with a hydrogen concentration of 30% and a 973 °C reduction.

1. Introduction

The iron and steel industry were regarded as the largest energy consumption manufacturing sector [1]. The conventional coke-based blast furnace consumes a large amount of energy [2,3], such as coke, oxygen, pulverized coal, etc., so non-blast furnace technologies are expected to reduce energy consumption and carbon emission [4].

Due to technological progress, the consumption of natural resources for ironmaking continuously decreases, but still, there is a lot of potential for further savings [5]. The energy savings can be obtained by reducing energy consumption and improving energy recovery [6,7]. Any modification leading to improvement of energy utilization needs to be emphatic. Gas utilization rate is an important indicator reflecting the operating state and energy consumption of blast furnaces [8] and non-blast furnaces [9]. Energy consumption could be reduced, with sufficient recovery of gas, heat and surplus energy during the iron and steel manufacturing process [10].

However, little progress has been made on decreasing energy consumption through the modification of conventional gas-based ironmaking processes. So, it is an urgent need for researchers and workers to recognize the necessity and feasibility to further lower the energy consumption for gas-based ironmaking.

In the present paper, a simple ironmaking system, just composed only of reduction gas and hematite, is proposed for consideration. The composition and amount of reduction gas and reduction temperature are selected as key factors affecting the energy consumption of ironmaking. Additionally, the temperature change of the system is taken into account, because of the large percentage in all energy demand. The purpose of this paper is to investigate the possibility of minimum energy consumption for gas-based direct reduction iron.

2. Methods

2.1. Energy Consumption Model

To formulate the thermodynamic model of energy consumption of the reduction of Fe₂O₃ by hydrogen and carbon monoxide mixtures with counter-current gas and solid, the following assumptions are made:

(a) The heat of the reactions is released to the external environment, so the temperature of substances before and after the reduction reaction is unchanged.

(b) The kinetic of reaction and heat transfer is neglected.

(c) Some specific aspects, like gangue in iron ore, inert gas in reduction gas, the heat loss of the furnace, etc., have not been considered.

The energy consumption model can show the processes from iron ore and reduction gas at initial temperature to metalized iron and exhaust gas at given temperatures, as is presented in Figure 1. The processes are set as:

(1) Fe₂O₃ and reduction gas are heated by the respective preheat process from 25 °C to the given reduction temperature, and the sensible heat input of solid Fe₂O₃ and reduction gas are calculated by Formula (1).

(2) Fe₂O₃ and reduction gas reach thermodynamic equilibrium in the reduction process. The temperature before and after the reactions does not change, and the reaction heat of the system is calculated by Formula (1), which is also contained in the heat input.

(3) The product metalized iron and exhaust gas are respectively cooled to 50 °C and 150 °C by heat exchange process, and the possible released heat is calculated by Formula (1). These released heats can be recycled, and contained in the heat output.

In a closed system under an equal pressure condition, the energy change equals enthalpy change, so the energy consumption is studied by the enthalpy change between the one state and another state. The enthalpy change is shown in Formula (1).

$$\mathsf{\Delta }H={\displaystyle \sum _{i=1}^N{n}_i}{H}_{i,T_i}^{Ɵ}-{\displaystyle \sum _{j=1}^M{n}_j}{H}_{j,T_j}$$

(1)

where ΔH, represents the enthalpy change and also energy change, J, and negative value is exothermic, positive value is endothermic; i, j, signify the components after and before the state change, respectively; N, M, represent the number of components after and before the state change, respectively; n_i, n_j, represent the amount of components after and before the state change, respectively, mol; T_i, T_j, represent the thermodynamic temperature of components after and before the state change, respectively, K; $H_{i,T_i}^{Ɵ}$, $H_{j,T_j}^{Ɵ}$, represent the standard molar enthalpy of the component i at the thermodynamic temperature T_i and the component j at the thermodynamic temperature T_j, respectively, J·mol⁻¹, are derived from the specific heat capacity data [11] measured by the predecessors.

The temperature increasing or decreasing and chemical reactions, all indicate the changes of the system state, so the sensible heat and chemical reaction heat, heat input and heat output can be calculated by Formula (1).

The heat input is defined to express the heat from outside, such as heating system, and contains the sensible heat input and reaction heat, and indicates the direct energy consumption. The heat output expresses the released heat into the outside, which can be used in total product processes. According to energy balance principles and overall considerations, the total energy consumption is the sum of heat input and heat output. The calculation formulas of sensible heat input, heat input, heat output and total heat are shown in Formulas (2)–(5).

$$\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{input}}=\mathsf{\Delta }{H}_{{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{Fe}}_2{\mathrm{O}}_3}+\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{reduction}\mathrm{gas}}$$

(2)

$$\begin{array}{cc}\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{input}}\hfill & =\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{input}}+\mathsf{\Delta }{H}_{\mathrm{reaction}\mathrm{heat}}\hfill \\ \hfill & =\mathsf{\Delta }{H}_{{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{Fe}}_2{\mathrm{O}}_3}+\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{reduction}\mathrm{gas}}+\mathsf{\Delta }{H}_{\mathrm{reaction}\mathrm{heat}}\hfill \end{array}$$

(3)

$$\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{output}}=\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{output}\mathrm{of}\mathrm{Fe}}+\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{output}\mathrm{of}\mathrm{eahaust}\mathrm{gas}}$$

(4)

$$\begin{array}{cc}\mathsf{\Delta }{H}_{\mathrm{total}\mathrm{heat}}\hfill & =\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{input}}+\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{output}}\hfill \\ \hfill & =\mathsf{\Delta }{H}_{{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{Fe}}_2{\mathrm{O}}_3}+\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{input}\mathrm{of}\mathrm{reduction}\mathrm{gas}}+\mathsf{\Delta }{H}_{\mathrm{reaction}\mathrm{heat}}\hfill \\ \hfill & +\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{output}\mathrm{of}\mathrm{Fe}}+\mathsf{\Delta }{H}_{\mathrm{sensible}\mathrm{heat}\mathrm{output}\mathrm{of}\mathrm{eahaust}\mathrm{gas}}\hfill \end{array}$$

(5)

The units of $\mathsf{\Delta }H$ are J or kece, and the heat of 1 kgce equals the heat of 29,288 kJ, namely 1 GJ equals 34.144 kgce.

In addition, the heat recovery rate is the ratio of heat output to heat input, as shown in Formula (6), and evaluate the energy utilization limit of solid and gas after reduction equilibrium.

$$\mathrm{heat}\mathrm{recovery}\mathrm{rate}=\frac{\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{output}}}{\mathsf{\Delta }{H}_{\mathrm{heat}\mathrm{input}}}\times 100\%$$

(6)

2.2. Equilibrium Composition

The minimum Gibbs free energy method is used to calculate the equilibrium state composition in the reducer [12]. The initial state conditions (amount, temperature, and pressure) can be used to calculate the amount of component in the equilibrium state, ignoring the specific reaction process. The initial conditions and equilibrium components set are shown in Figure 2.

Based on the principle of minimum free energy, that is, the sum of Gibbs free energy of each component in the equilibrium state is the smallest, a calculation model is established, as shown in Formulas (7) and (8). The non-linear equation is solved using constraints to obtain the mass of each component of the equilibrium state at different temperatures and different initial amounts of reduction gas.

$$\min ·G_{\mathrm{all}}={\displaystyle \sum _{i=1}^N{n}_i{G}_i}={\displaystyle \sum _{i=1}^N{n}_i(G_i^{Ɵ}+RT\ln a_i)}$$

(7)

$$\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{i=1}^N{\alpha }_{ie}{n}_i=n_e}(e=1,2,\cdots ,M)$$

(8)

In the formula, i, e, represent the components and elements in the equilibrium state, respectively; N, M, represent the number of components and the number of elements in the equilibrium state, respectively; n_i, n_e, are the amounts of the components i and elements e in the equilibrium state, respectively, mol; $G_i$, $G_i^{Ɵ}$, represent the Gibbs free energy and the standard Gibbs free energy of the components i, respectively, J·mol⁻¹; $p_i$, $p_{\mathrm{total}}$, $p^{Ɵ}$, represent the partial pressure of the components i, the total pressure of all gas, and the standard atmospheric pressure, respectively, Pa, and $p^{Ɵ}=\mathrm{101,325}\mathrm{Pa}$; ${\alpha }_{ie}$ represents the number of atoms in the element; T, represents the thermodynamic temperature of the system, K; R, is the ideal gas constant, which is equal to 8.314, J·mol⁻¹·K⁻¹; $a_i$ represents the activity, when i is a gaseous state $a_i=\frac{p_i}{p^{Ɵ}}=\frac{n_i}{{\displaystyle \sum n_i}}·\frac{p_{\mathrm{total}}}{p^{Ɵ}}$, when i is a solid state $a_i=1$. It should be noted that the real gas can be treated as an ideal gas under high temperature and low pressure.

The utilization rates of H₂, CO, CO + H₂ are defined as the ratio of the changed amount of reduction gas to corresponding initial amount of reduction gas, are shown in Formulas (9)–(11).

$${\eta }_{{\mathrm{H}}_2}^{}=\frac{n_{{\mathrm{H}}_2}^{in}-n_{{\mathrm{H}}_2}^{out}}{n_{{\mathrm{H}}_2}^{in}}=\frac{n_{{\mathrm{H}}_2\mathrm{O}}^{out}-n_{{\mathrm{H}}_2\mathrm{O}}^{in}}{n_{{\mathrm{H}}_2}^{in}}$$

(9)

$${\eta }_{\mathrm{CO}}^{}=\frac{n_{\mathrm{CO}}^{in}-n_{\mathrm{CO}}^{out}}{n_{\mathrm{CO}}^{in}}=\frac{n_{\mathrm{C}{\mathrm{O}}_2}^{out}-n_{\mathrm{C}{\mathrm{O}}_2}^{in}}{n_{\mathrm{CO}}^{in}}$$

(10)

$${\eta }_{{\mathrm{H}}_2+\mathrm{CO}}^{}=\frac{(n_{{\mathrm{H}}_2}^{in}-n_{{\mathrm{H}}_2}^{out})+(n_{\mathrm{CO}}^{in}-n_{\mathrm{CO}}^{out})}{n_{{\mathrm{H}}_2}^{in}+n_{\mathrm{CO}}^{in}}=\frac{(n_{{\mathrm{H}}_2\mathrm{O}}^{out}-n_{{\mathrm{H}}_2\mathrm{O}}^{in})+(n_{\mathrm{C}{\mathrm{O}}_2}^{out}-n_{\mathrm{C}{\mathrm{O}}_2}^{in})}{n_{{\mathrm{H}}_2}^{in}+n_{\mathrm{CO}}^{in}}$$

(11)

where in, out, represent the initial intake gas and equilibrium exhaust gas, respectively; ${\eta }_{{\mathrm{H}}_2}^{}$, ${\eta }_{\mathrm{CO}}^{}$, ${\eta }_{{\mathrm{H}}_2+\mathrm{CO}}^{}$, are the utilization rate of H₂, CO, H₂ + CO, respectively; $n_{{\mathrm{H}}_2}^{}$, $n_{\mathrm{CO}}^{}$, $n_{{\mathrm{H}}_2\mathrm{O}}^{}$, $n_{\mathrm{C}{\mathrm{O}}_2}^{}$, are the amount of H₂, CO, H₂O, and CO₂, respectively.

Energy consumption per mole of Fe or per ton of Fe means the energy consumption of the production of 1 mol Fe and 1 t Fe under sufficient material conditions and with certain temperature conditions. When the reduction gas is not enough, metalized Fe cannot be produced fully, namely the energy consumption is not 1 mol or 1 t Fe. When the amount of reduction gas is more than is needed, unnecessary energy is wasted, in particular, needless sensible heat input of reduction gas is not 1mol or 1 t Fe. These problems need to be calculated precisely.

3. Results and Discussion

Different amounts of reduction gas and different reduction temperatures were set to investigate the effects on the reduction products, gas utilization, and energy consumption.

3.1. Effect of Amount of Reduction Gas

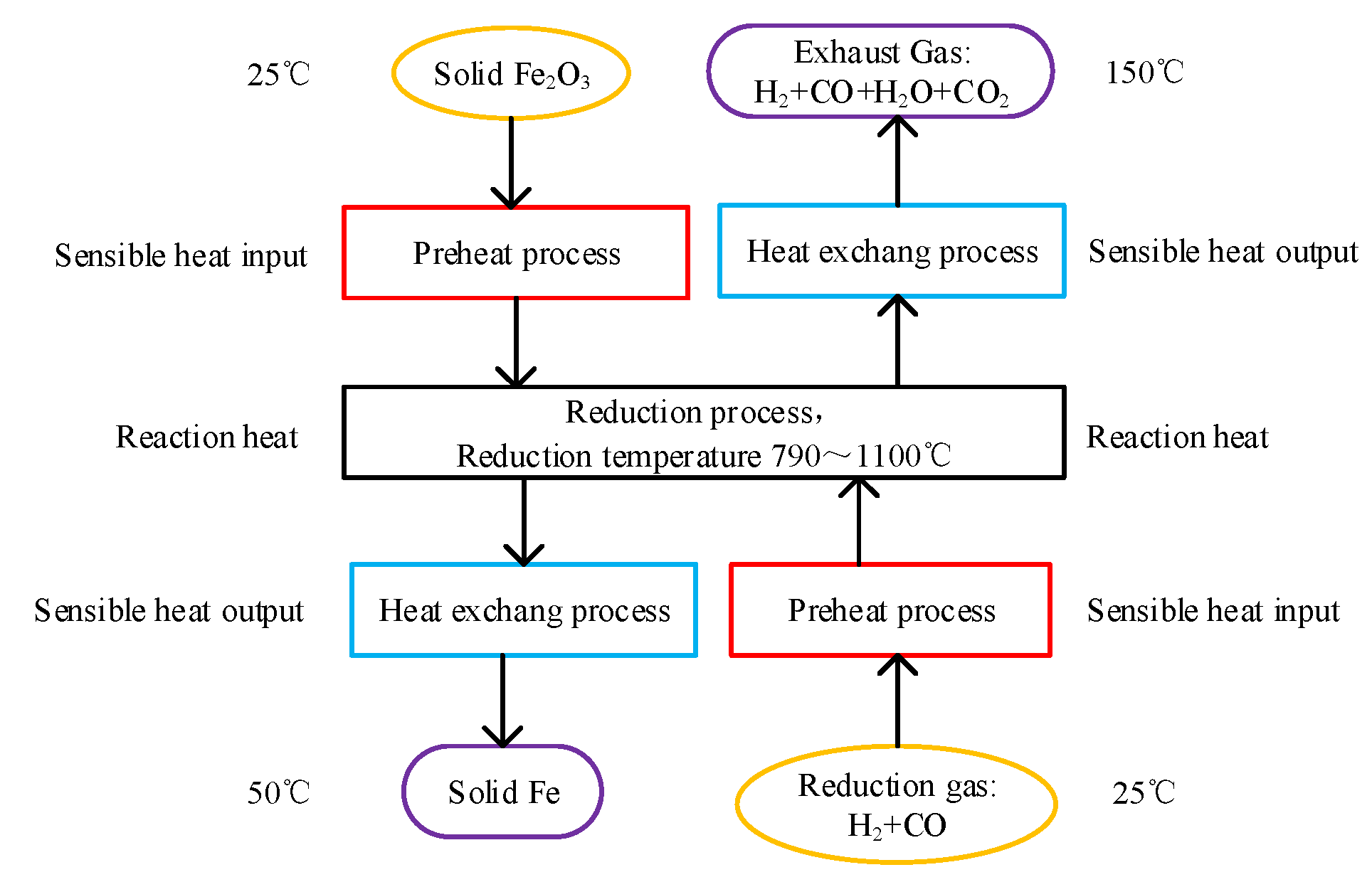
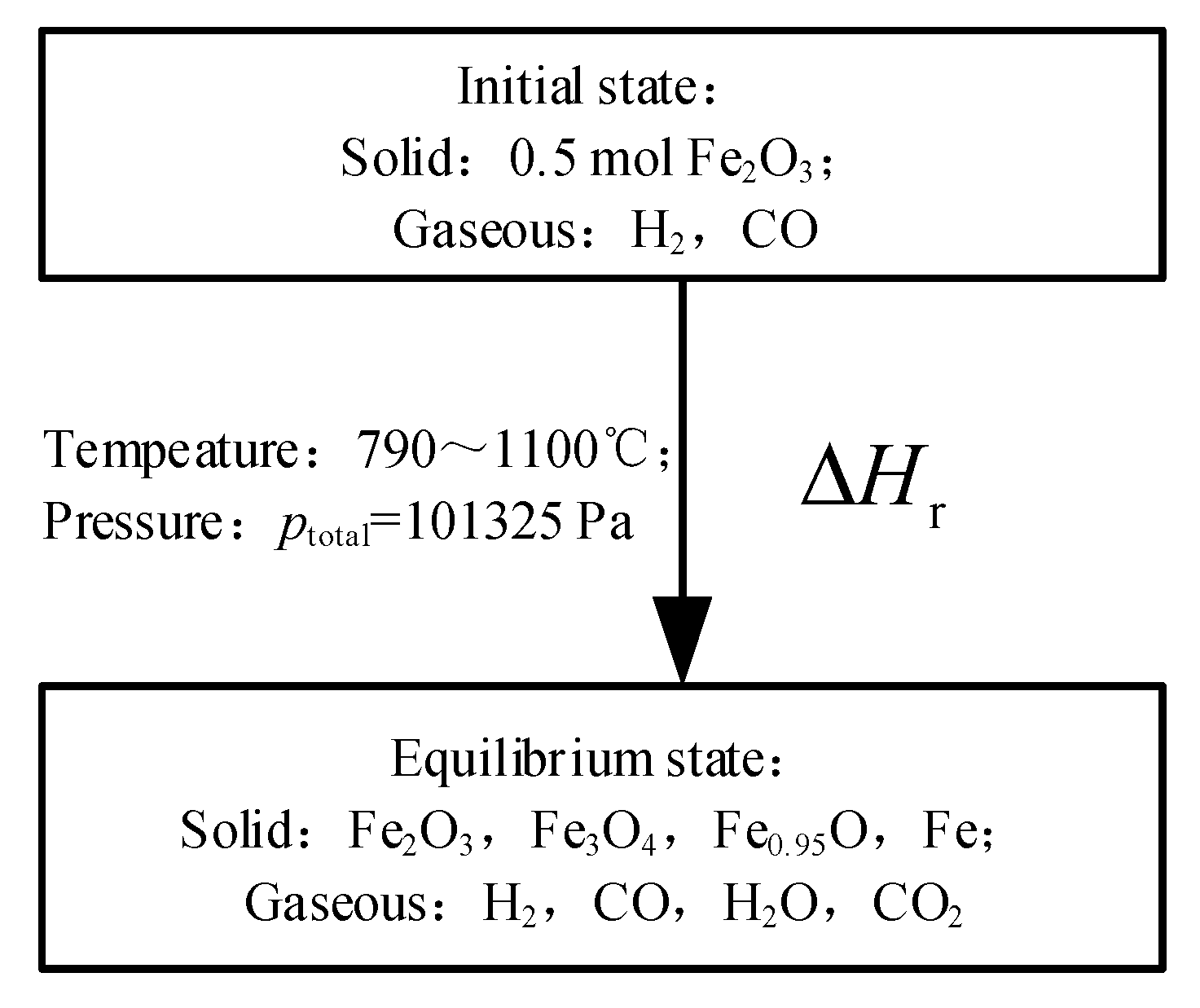
The conditions were set as follows: the initial reduction gas amount was 0.005–0.2 mol (increment 0.005 mol), 0.2–6.0 mol (increment 0.1 mol); the reduction temperature was 900 °C; the initial gas was composed of H₂ and CO, and the H₂ volume fraction was 0–100% (increment 10%); the total pressure was 101,325 Pa; the initial solid was 0.5mol Fe₂O₃, and the maximum Fe output was 1mol. It should be noted that the reduction reactions and water-gas shift reaction are heterogeneous reactions, as shown in in Formulas (12)–(18), and other carbonization reactions and carbon decomposition reaction are not considered in this study.

Reduction reactions:

$$3{\mathrm{Fe}}_2{\mathrm{O}}_3\left(\mathrm{solid}\right)+{\mathrm{H}}_2\left(\mathrm{gas}\right)=2{\mathrm{Fe}}_3{\mathrm{O}}_4\left(\mathrm{solid}\right)+{\mathrm{H}}_2\mathrm{O}\left(\mathrm{gas}\right)$$

(12)

$$3{\mathrm{Fe}}_2{\mathrm{O}}_3\left(\mathrm{solid}\right)+\mathrm{CO}\left(\mathrm{gas}\right)=2{\mathrm{Fe}}_3{\mathrm{O}}_4\left(\mathrm{solid}\right)+{\mathrm{CO}}_2\left(\mathrm{gas}\right)$$

(13)

$${\mathrm{Fe}}_3{\mathrm{O}}_4\left(\mathrm{solid}\right)+{\mathrm{H}}_2\left(\mathrm{gas}\right)=\frac{3}{0.95}{\mathrm{Fe}}_{0.95}\mathrm{O}\left(\mathrm{solid}\right)+{\mathrm{H}}_2\mathrm{O}\left(\mathrm{gas}\right)$$

(14)

$${\mathrm{Fe}}_3{\mathrm{O}}_4\left(\mathrm{solid}\right)+\mathrm{CO}\left(\mathrm{gas}\right)=\frac{3}{0.95}{\mathrm{Fe}}_{0.95}\mathrm{O}\left(\mathrm{solid}\right)+{\mathrm{CO}}_2\left(\mathrm{gas}\right)$$

(15)

$${\mathrm{Fe}}_{0.95}\mathrm{O}\left(\mathrm{solid}\right)+{\mathrm{H}}_2\left(\mathrm{gas}\right)=0.95\mathrm{Fe}\left(\mathrm{solid}\right)+{\mathrm{H}}_2\mathrm{O}\left(\mathrm{gas}\right)$$

(16)

$${\mathrm{Fe}}_{0.95}\mathrm{O}\left(\mathrm{solid}\right)+\mathrm{CO}\left(\mathrm{gas}\right)=0.95\mathrm{Fe}\left(\mathrm{solid}\right)+{\mathrm{CO}}_2\left(\mathrm{gas}\right)$$

(17)

Water-gas shift reaction:

$${\mathrm{H}}_2{\mathrm{O}\left(\mathrm{gas}\right)+\mathrm{CO}\left(\mathrm{gas}\right)=\mathrm{H}}_2{\left(\mathrm{gas}\right)+\mathrm{CO}}_2(\mathrm{gas})$$

(18)

3.1.1. Equilibrium Products and Gas Utilization

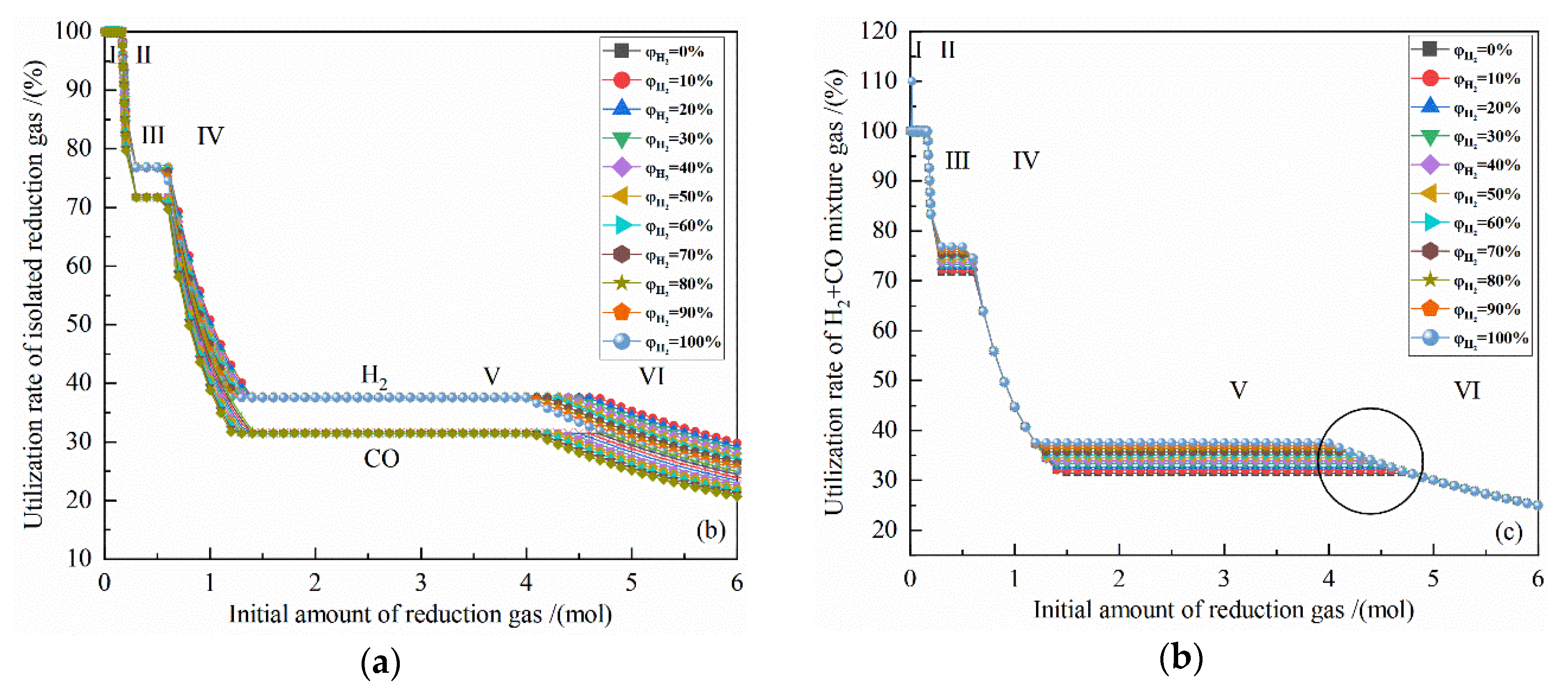
Figure 3 shows the relationship between the initial amount of reduction gas and the amount of equilibrium products in the reduction of 0.5 mol Fe₂O₃ by 50% H₂ and 50% CO concentration at 900 °C. According to the trend of the product type and the amount of the material, the reduction process can be divided into six stages in sequence.

I, the iron-containing products have Fe₂O₃ and Fe₃O₄ at the same time. As the amount of reduction gas increases, Fe₂O₃ gradually decreases to zero, and Fe₃O₄ gradually increases to the maximum amount; the chemical reactions can be expressed as Formulas (12) and (13).

II, the iron-containing products only have Fe₃O₄. As the amount of reduction gas increases, the amount of Fe₃O₄ remains unchanged.

III, the iron-containing products have Fe₃O₄ and Fe_0.95O at the same time, as the amount of reduction gas increases, Fe₃O₄ gradually decreases to zero, and Fe_0.95O gradually increases to the maximum amount; the chemical reactions can be expressed as Formulas (14) and (15).

IV, the iron-containing products only have Fe_0.95O, and as the amount of reduction gas increases, Fe_0.95O content remains unchanged.

V, the iron-containing products have Fe_0.95O and Fe at the same time, and as the amount of reduction gas increases, Fe_0.95O content gradually decreases to zero, and Fe gradually increases to the maximum amount; the chemical reactions can be expressed as Formulas (16) and (17).

VI, iron-containing products only have Fe, as the amount of reduction gas increases, the amount of Fe remains unchanged.

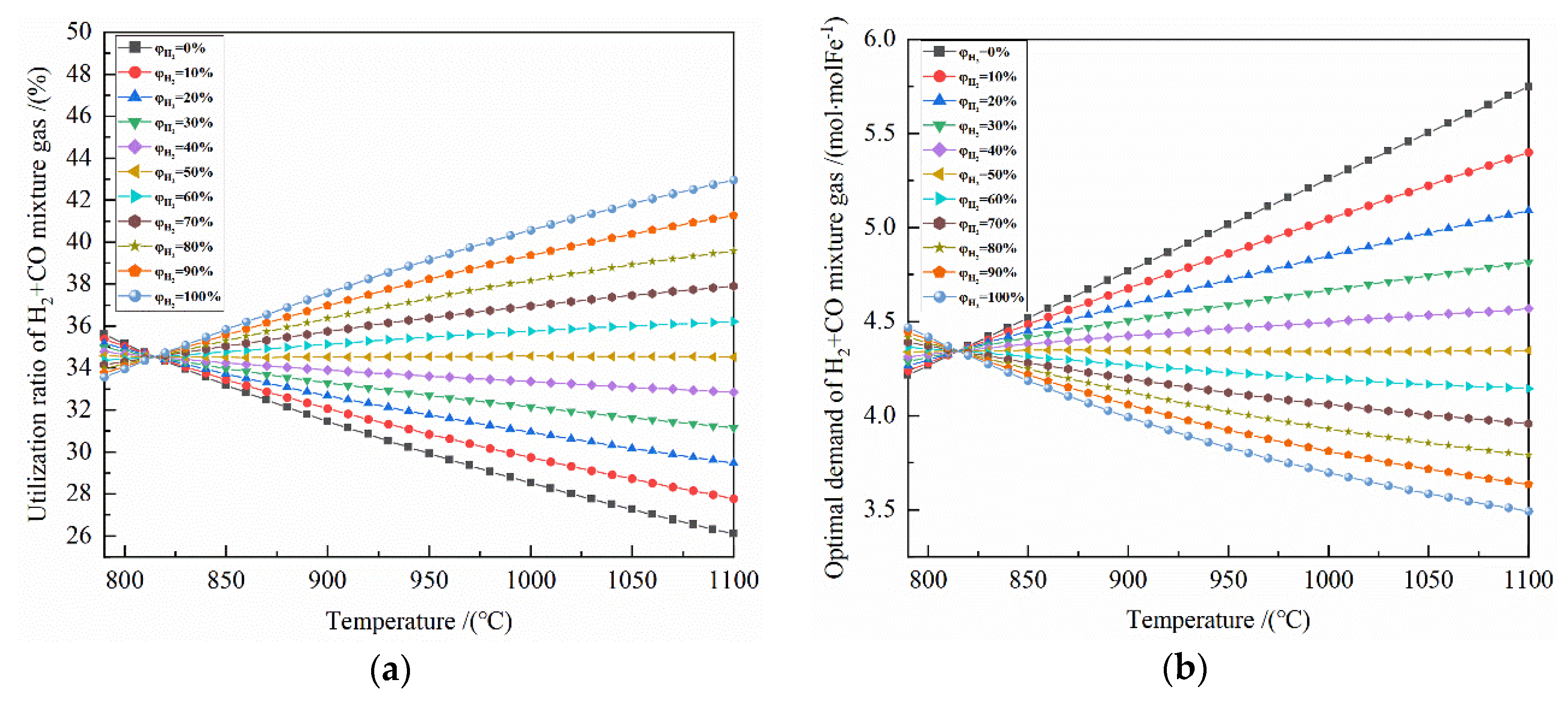
Figure 4a shows the relationship between the gas utilization rate of isolated reduction gas and the initial amount of reduction gas at 900 °C with varied H₂ concentrations. It can be seen from Figure 4a that at 900 °C, as the amount of reduction gas increases, the gas utilization rate of isolated H₂ and isolated CO are 100% at the I stage. The utilization rates of H₂ and CO at the II stage drop to 76.87% and 71.71%, respectively. The utilization rates of H₂ and CO at the III stage remain unchanged. The utilization rate of H₂ and CO at the IV stage decreases to 37.58% and 31.46%. The gas utilization rate at the V stage remains unchanged, and at the VI stage continues to decline. The increase of the amount of reduction gas in the I, III, and V stages is used for the reduction reaction, so the utilization rate remains unchanged, and the initial H₂ concentration does not affect the utilization rate of H₂ and CO in these three stages. In the II, IV, and VI stages, no reduction reaction occurs, as the initial gas amount increases, the H₂ and CO utilization rates decrease. Meanwhile, the higher the initial H₂ concentration is, the smaller the H₂ utilization rate is, and the greater the CO utilization rate is.

The coincident points can be observed in Figure 4a at the reduction reaction occurring stages, which means that the initial concertation of H₂ or CO does not affect the utilization rate of isolated gas, namely the water-gas shift reaction does not affect the utilization rate of isolated gas in gas-based direct ironmaking.

It can be seen from Figure 4b that at the II, IV, and VI stages in which no reduction reaction has occurred and at the I stage in which Fe₂O₃ are reduced to Fe₃O₄, the points of the H₂ + CO mixture utilization rate overlap, indicating that the H₂ concentration and the amount of reduction gas have no effect on H₂ + CO mixture utilization rate of reduction gas in these four stages. In the III and V stage, the 11 lines of the H₂ + CO mixture utilization rate level are displayed in parallel, indicating that the H₂ concentration has a linear effect on the H₂ + CO mixture utilization rate. Since the initial reduction gas is composed of H₂ and CO, namely ${\phi }_{{\mathrm{H}}_2}^{in}+{\phi }_{{\mathrm{H}}_2}^{in}=100\%$, so

$${\eta }_{{\mathrm{H}}_2+\mathrm{CO}}^{}={\phi }_{\mathrm{CO}}^{in}{\eta }_{\mathrm{CO}}^{}+{\phi }_{{\mathrm{H}}_2}^{in}{\eta }_{{\mathrm{H}}_2}^{}={\eta }_{\mathrm{CO}}^{}+{\phi }_{{\mathrm{H}}_2}^{in}({\eta }_{{\mathrm{H}}_2}^{}-{\eta }_{\mathrm{CO}}^{})$$

(19)

It is known from Figure 4a that the gas utilization rate of isolated reduction gas in the III and V stage is independent of the amount of reduction gas and the reduction gas concentration. From Formula (19), it can be observed that the H₂ + CO mixture utilization rate is proportional to the initial H₂ concentration of the reduction gas. The H₂ + CO mixture utilization rate at 900 °C is positively related to the initial H₂ concentration, as shown in the circle in Figure 4b.

3.1.2. Energy Consumption

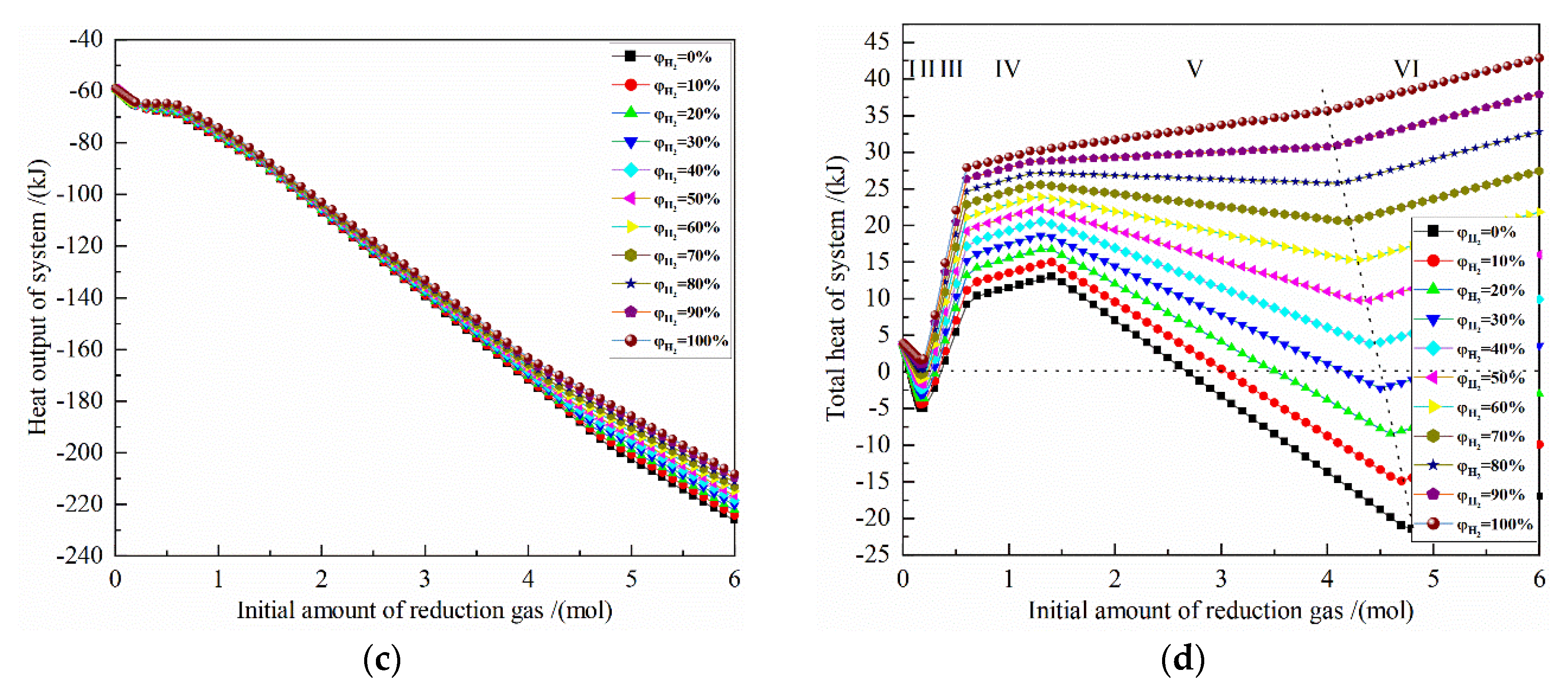
Figure 5 shows the effect of the initial amount of reduction gas on the energy consumption for the reduction of 0.5 mol Fe₂O₃ at 900 °C with varied H₂ concentrations. The X-axis is the increasing reduction gas, and the Y-axis is the energy consumption for the corresponding definition. The horizontal dashed line is 0, ΔH < 0 is exothermic, and ΔH > 0 is endothermic; the oblique dashed line is shown as the energy consumption of the system when 0.5 mol Fe₂O₃ is completely reduced.

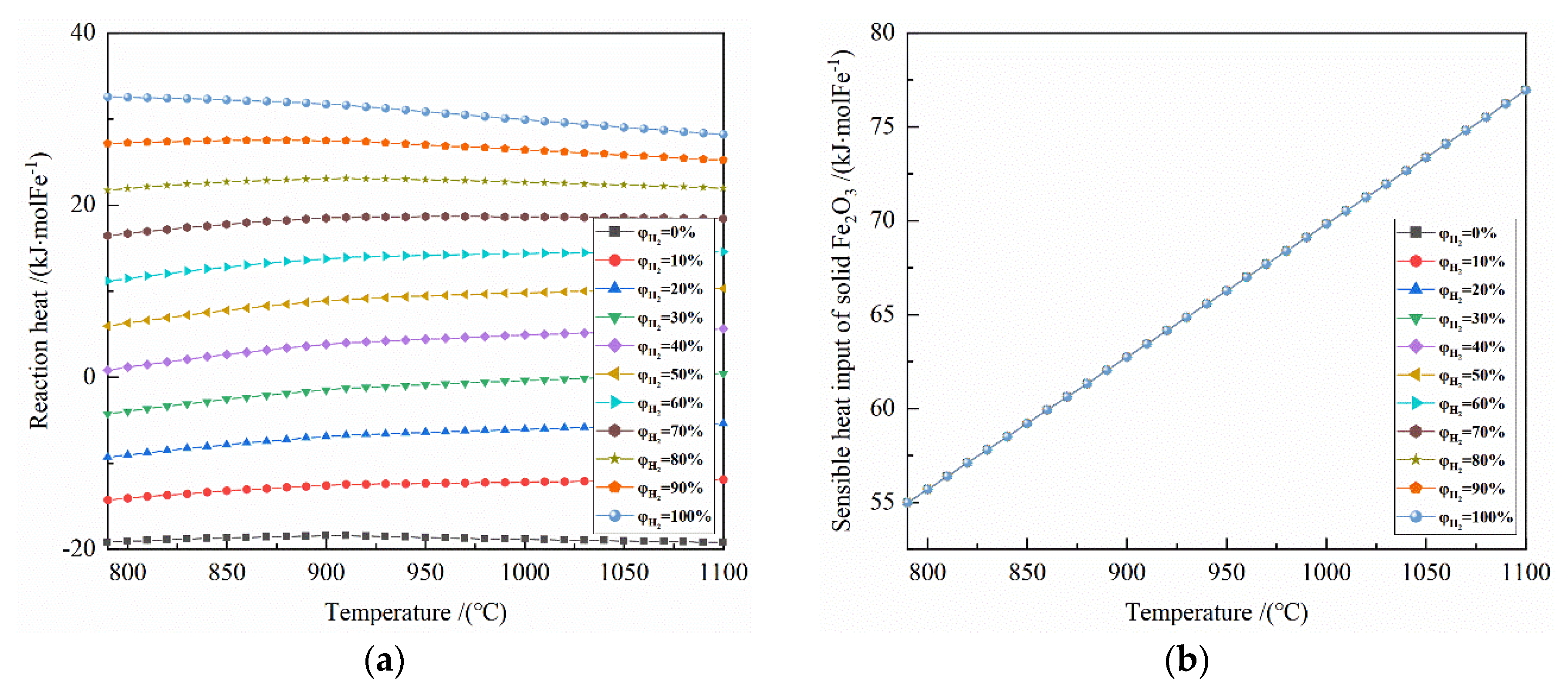
It can be seen from Figure 5a that the change of the reaction heat of the system occurs in the reduction reaction stages I, III and V. According to the calculation principle, the reaction heat of the latter stage includes the reaction heat of all the previous stages, that is, the reaction heat of stage III includes the stages I, II and III, and the reaction heat of stage V includes the stages I, II, III, IV and V. The reaction heat of the I stage is an exothermic reaction, and the larger the initial H₂ concentration is, the smaller the exothermic amount is. At the III stage, as the amount of reduction gas increases, the reaction heat changes from an exothermic reaction to an endothermic reaction for an H₂ concentration of 10% to 100%, and the larger the initial H₂ concentration is, the greater the reaction heat is. In the V stage, for H₂ concentration of 50–100%, the reaction heat gradually increases with the growth of the amount of reduction gas, and the larger the initial H₂ concentration, the greater the reaction heat, and the maximum reaction heat is 31.747 kJ by pure H₂ reduction. For H₂ concentration of 50%, the reaction heat increases very slowly as the amount of reduction gas raises, and the maximum reaction heat is 8.874 kJ. For H₂ concentration of 0% to 40%, the reaction heat increases with the growth of the amount of reduction gas. The increase gradually decreases, and the larger the initial H₂ concentration is, the greater the endothermic energy is. The maximum reaction heat occurs at pure CO reduction and is −18.445 kJ, and the minimum reaction energy occurs at 30% H₂ concentration and is 1.452 kJ.

The sensible heat input of 0.5 mol Fe₂O₃ from 25 °C to 900 °C is 62.737 kJ. When the amount of reduction gas is 4 mol and 5 mol, the sensible heat inputs of pure CO from 25 °C to 900 °C and from 25 °C to 900 °C are 109.944 kJ and 137.43 kJ, respectively, and the sensible heat inputs of pure H₂ gas from 25 °C to 900 °C are 104.384 kJ and 130.480 kJ, respectively.

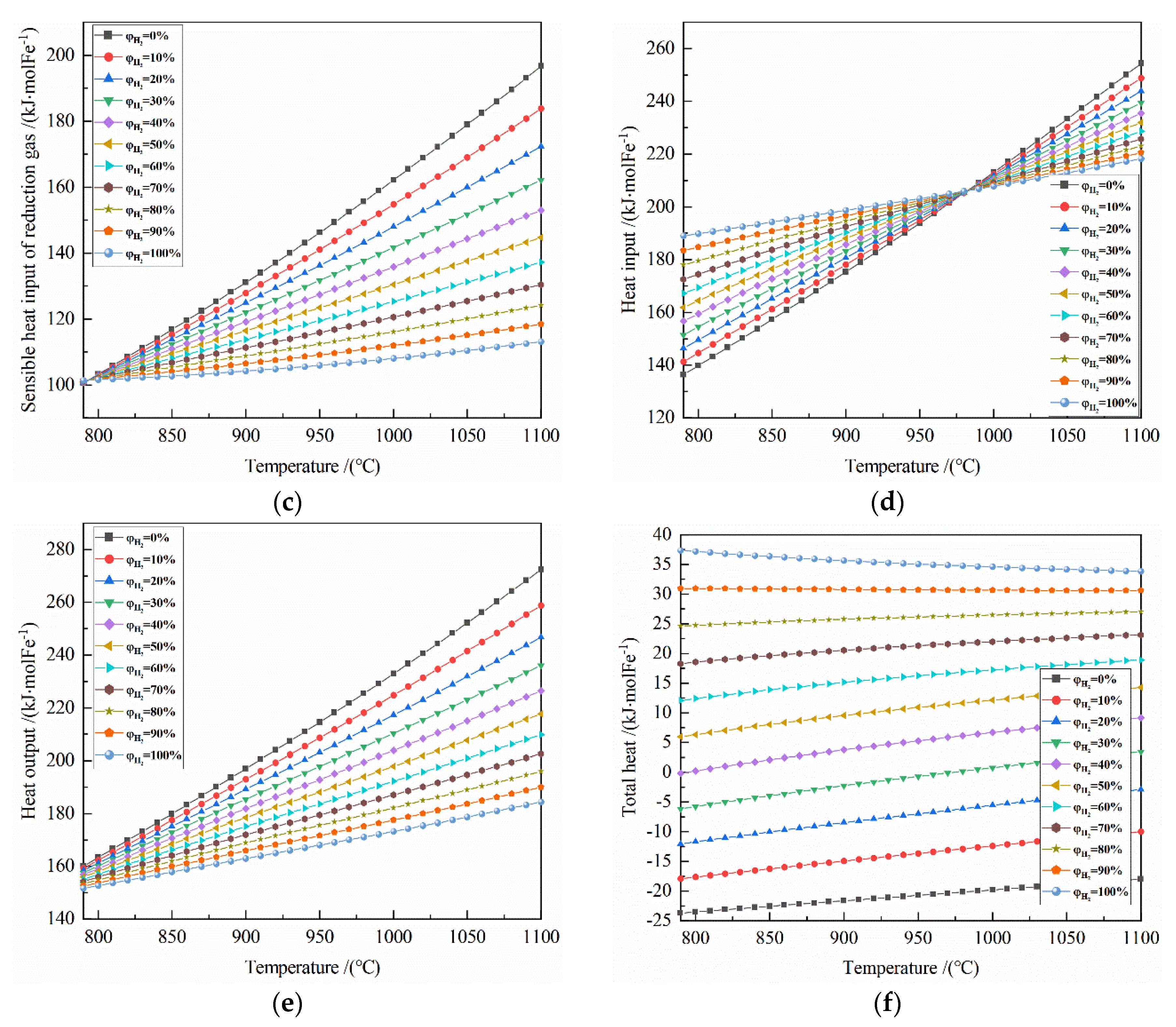
Figure 5b shows that the larger the amount of reduction gas, the greater the heat input of system. Under the same reduction gas condition, the greater the initial H₂ concentration, the greater the heat input of system. When the amount of reduction gas is greater than 4 mol, the heat input of the reduction system by each H₂ concentration is approximately parallel, because the sensible heat of gas and solid are much larger than the reaction heat of the system. When the amount of reduction gas is 4 mol, the maximum value of heat input is 198.869 kJ with pure H₂ reduction, and the minimum value of heat input is 158.387 kJ with pure CO reduction. When the amount of reduction gas is 5 mol, the maximum value of heat input is 222.355 kJ with pure H₂ reduction, and the minimum value of heat input is 181.722 kJ with pure CO reduction. The difference between the maximum and the minimum values are 40.482 kJ and 40.633 kJ, respectively, which are approximately the same.

It can be seen from Figure 5c that the more reduction gas there is, the greater the recovery heat output will be. Under the same reduction gas amount condition, the larger the initial H₂ concentration is, the smaller the system recoverable heat is. When the amount of reduction gas is 4 mol, the maximum absolute value of heat output is −172.066 kJ with pure CO reduction, and the minimum absolute value of heat output is −163.189 kJ with pure H₂ reduction. When the amount of reduction gas is 5 mol, the maximum absolute value of heat output is −202.503 kJ with pure CO reduction, and the minimum absolute value of heat output is −185.678 kJ with pure H₂ reduction. The difference between the maximum and the minimum values are −8.877 kJ and 16.825 kJ, respectively.

From Figure 5d, it can be seen that for the H₂ concentration of 40–100%, the total heat of the system increases as the initial H₂ concentration increases. For the H₂ concentration of 0–30%, the smaller the initial H₂ concentration is, the larger the system total heat is. For the H₂ concentrations of 30% and 40%, the optimal amount of reduction gas is 4.4 mol and 4.5 mol, respectively, and the system total heat is −1.545 kJ and 4.056 kJ, respectively. If the linear difference method is used, when the system total heat is 0, the H₂ concentration is about 32.8%. In addition, after metalized Fe is fully obtained, increasing the amount of reduction gas will greatly increase the total energy consumption, which is not worthwhile. At 900 °C, 0.5 mol Fe₂O₃ is reduced to 1 mol Fe. The system total heat is 35.680 kJ for pure H₂ reduction and −21.527 kJ for pure CO reduction. For other initial concentrations, the system total heat is in between.

3.2. Effect of Reaction Temperature

3.2.1. Optimal Demand of Reduction Gas

Because the initial concentration and the amount of reduction gas have no effect on the utilization rate of H₂ and CO at the V stage, the amount of reduction gas was set, which was used to calculate the utilization rate of total gas in the temperature range 790–1100 °C. The conditions were set as follows: the reduction temperature was 790–1100 °C, and the increment was 10 °C; the initial amount of reduction gas was 3 mol; the initial gas was composed of H₂ and CO, and H₂ volume fraction was 0–100%, and the increment was 10%; the total pressure was 101325 Pa; initial amount of solid was 0.5 mol Fe₂O₃.

From the gas utilization rate of H₂ and CO, according to the material conservation and enthalpy change formulas, the optimal demand of reduction gas, reaction heat of the system, heat input of the system, and heat output of the system can be calculated in turn, as shown in Figure 6 and Figure 7.

Obviously, after the metalized iron was completely gained, increasing the amount of reduction gas cannot increase the production, so the amount of reduction gas just enough for full reduction was defined as the optimal demand of reduction gas.

It can be seen from Figure 6a that under the same temperature conditions, the greater the H₂ concentration is, the greater the utilization rate of total gas is; at 790–810 °C, the opposite is true. At 820–1100 °C, for the H₂ concentration of 60–100%, a higher temperature corresponds with a greater the utilization rate of total gas, and a smaller increased amplitude of the utilization rate of total gas. For the H₂ concentration of 0–40%, the higher the temperature is, the smaller the utilization rate of total gas, and the smaller the effect of temperature on the utilization rate of total gas. The minimum and maximum utilization rates of total gas are 33.184% (pure CO reduction) and 35.832% (pure H₂ reduction) at 850 °C, 31.460% (pure CO reduction) and 37.575% (pure H₂ reduction) at 900 °C, and 29.923% (pure CO reduction) and 39.159% (pure H₂ reduction) at 950 °C, respectively.

It can be seen from Figure 6b that at 820–1100 °C, for H₂ concentration of 60–100%, the higher the temperature is, the lower the optimal demand for reduction gas is. For the H₂ concentration of 0–40%, the optimal demand for reduction gas is greater as the temperature increases. For the H₂ concentration of 50%, the temperature has little effect on the optimal demand for reduction gas. At 790–820 °C, the opposite is true. The optimal demand of reduction gas for 0.5 mol Fe₂O₃ is 4.186 mol (pure H₂ reduction) and 4.520 mol (pure CO reduction) at 850 °C, 3.992 mol (pure H₂ reduction) and 4.768 (pure CO reduction) mol at 900 °C, and 3.831 mol (pure H₂ reduction) and 5.013 mol (pure CO reduction) at 950 °C.

3.2.2. Energy Consumption

Figure 7 shows the effect of reduction temperature on the energy consumption of 0.5 mol Fe₂O₃ reduction under the conditions of 790–1100 °C and varied H₂ concentrations.

It can be seen from Figure 7a that the temperature has a small effect on the reaction heat of the system at 790–1100 °C. For the H₂ concentration of 0% to 30%, the reaction heat is exothermic; for the H₂ concentration of 40% to 100%, the reaction heat is endothermic. Taking 50% H₂ concentration as an example, the reaction heat per mole of Fe is 5.956 to 10.297 kJ at 790–1100 °C.

It can be seen from Figure 7b that the sensible heat input of solid Fe₂O₃ per mole of Fe is 54.988–76.943 kJ at 790–1100 °C.

It can be seen from Figure 7c that at 790–1100 °C, the larger the initial H₂ concentration correlates to the smaller sensible heat input of reduction gas. Taking 900 °C as an example, for every 10% increase in H₂ concentration, the sensible heat input of reduction gas per mole of Fe decreases by 2.3–3.0 kJ.

It can be seen from Figure 7d that at 790–980 °C, the larger the initial H₂ concentration is, the greater the heat input is; at 990–1100 °C, the opposite is true. Taking 50% H₂ concentration as an example, the minimum and maximum of the heat input per mole of Fe are 161.920 kJ at 790 °C reduction and 231.927 kJ at 1100 °C reduction, respectively.

It can be seen from Figure 7e that at 790–980 °C, the higher the temperature is, the greater the heat output is; the greater the initial H₂ concentration, the smaller heat output is. Taking 50% H₂ concentration as an example, the minimum and maximum of the heat input per mole of Fe are 155.982 kJ at 790 °C reduction and 217.666 kJ at 1100 °C reduction, respectively.

From Figure 7f, it can be seen that at 790–1100 °C, for the H₂ concentration of 90–100%, the total heat is more than 0 and it decreases as the temperature increases; for H₂ concentration of 40–80%, the total heat is also greater than 0 and it increases with the increasing temperature. For the H₂ concentration of 30%, the total energy consumption per ton of iron at 790–980 °C is less than 0, and it is more than 0 at 980–1100 °C.

When the H₂ concentration is 100%, the heat input per ton of iron is 115.551 kgce at 790 °C reduction and 133.439 kgce at 1100 °C reduction, the total heat per ton of iron is 22.850 kgce at 790 °C reduction and 20.694 kgce at 1100 °C reduction.

When the CO concentration is 100%, the heat input per ton of iron is 83.380 kgce at 790 °C reduction and 155.553 kgce at 1100 °C reduction, the total heat input per ton of iron is −14.495 kgce at 790 °C reduction and −10.996 kgce at 1100 °C reduction.

When the H₂ concentration is 30%, the heat input per ton of iron is 92.640 kgce at 790 °C reduction and 146.405 kgce at 1100 °C reduction, the total heat input per ton of iron is −3.746 kgce at 790 °C reduction and 2.113 kgce at 1100°C reduction. So, when the H₂ concentration is 30% at 973 °C reduction, the total heat input per ton of iron is zero.

It can be seen from Figure 8 that at 790–1100 °C, the larger the initial H₂ concentration is, the lower the heat recoverable rate is. For the H₂ concentration of 0–30%, the heat recoverable rate is greater than 100%. For the H₂ concentration of 40–100%, the heat recoverable rate is less than 100%. For the H₂ concentration of 0–60%, the higher the temperature is, the smaller the heat recoverable rate is. For the H₂ concentration of 80–100%, the higher the temperature corresponds with the higher heat recoverable rate. For the H₂ concentration of 70%, the effect of the temperature on the heat recovery rate is small.

4. Conclusions

Through the analysis of the energy consumption of the reduction of Fe₂O₃ by CO and H₂, the following conclusions are drawn:

(1) In the stage of the reduction reaction, the utilization rates of H₂ and CO do not change with the increase in the amount of reduction gas or the increase in the initial H₂ concentration.

(2) At 790–980 °C, the heat input per ton of iron increases with the increase in the initial H₂ concentration; at 980–1100 °C, the opposite is true.

(3) At 790–1100 °C, for the H₂ concentration of 40–100%, the total heat per ton of iron increases with the increase in the initial H₂ concentration; for the H₂ concentration of 0–30%, the total heat per ton of iron is negative, and the absolute value increases with the increase of the initial H₂ concentration.