A Multi-Agent Reinforcement Learning Framework for Lithium-ion Battery Scheduling Problems

Abstract

This paper presents a reinforcement learning framework for solving battery scheduling problems in order to extend the lifetime of batteries used in electrical vehicles (EVs), cellular phones, and embedded systems. Battery pack lifetime has often been the limiting factor in many of today’s smart systems, from mobile devices and wireless sensor networks to EVs. Smart charge-discharge scheduling of battery packs is essential to obtain super linear gain of overall system lifetime, due to the recovery effect and nonlinearity in the battery characteristics. Additionally, smart scheduling has also been shown to be beneficial for optimizing the system’s thermal profile and minimizing chances of irreversible battery damage. The recent rapidly-growing community and development infrastructure have added deep reinforcement learning (DRL) to the available tools for designing battery management systems. Through leveraging the representation powers of deep neural networks and the flexibility and versatility of reinforcement learning, DRL offers a powerful solution to both roofline analysis and real-world deployment on complicated use cases. This work presents a DRL-based battery scheduling framework to solve battery scheduling problems, with high flexibility to fit various battery models and application scenarios. Through the discussion of this framework, comparisons have also been made between conventional heuristics-based methods and DRL. The experiments demonstrate that DRL-based scheduling framework achieves battery lifetime comparable to the best weighted-k round-robin (kRR) heuristic scheduling algorithm. In the meantime, the framework offers much greater flexibility in accommodating a wide range of battery models and use cases, including thermal control and imbalanced battery.

1. Introduction

In recent years, many advanced autonomous systems rely on portable and eco-friendly energy supplies. From mobile devices and sensors to drones and electrical vehicles (EVs), the demand for energy supply with long lifetime and stability keeps increasing. The lithium-ion battery holds the advantages of being eco-friendly, lightweight and compact in size, with high energy density. Figure 1a shows the principle of a typical lithium battery. During discharge, the positive Li-ions are released from anode and travel to cathode, which provides an electron current through the load. During charge, the opposite happens, and the anode receives the Li-ions. The capacity of lithium-ion batteries (packs) spans from a few mAh (ampere hour) to kAh, based on application scenarios. Figure 1b shows a diagram of the lithium battery capacity scale for various applications, in order from low to high.

In many cases, the lithium-ion battery appears in packs connected in series and parallel, which are also designed with controllable switches to be connected/disconnected from the load. The smart scheduling of parallel-connected battery packs (charge, discharge, and rest) can enhance the battery utility and extend the battery-pack lifetime. The reason lies in the fact that the lithium-ion battery has two unique characteristics: rate-capacity effect and recovery effect [1,2,3,4]. The rate-capacity effect is the behavior in which the battery shows smaller overall capacity when discharged with higher current. The recovery effect is the behavior in which the battery’s voltage can be slowly recovered during rest, after a continuous discharge process. Due to these properties, the smart scheduling of the battery pack can optimize the discharge current for rate-capacity effect, and make full use of the recovery effect, thus increasing the system’s lifetime. Furthermore, a smart scheduling agent can prevent the battery from over-charge or deep discharge, which could damage the battery’s internal chemistries, and heavily degrade the battery’s lifetime.

Research has been performed on solving the battery management problem using heuristics. The traditional round-robin (RR) can easily out-perform the sequential scheduling, due to the battery recovery effect. There are reported lithium-ion battery scheduling algorithms, including weighted-k round-robin (kRR) scheduling [1], scheduling based on dynamic programming [2], and using analytical approaches such as linear priced timed automata [3,4]. Similar battery scheduling problems have also been solved for wireless sensor network battery usage [5], battery scheduling considering electricity price [6], and situations where the lithium-ion battery is in combined use with a photovoltaic (PV) rooftop [7]. These algorithms are typically formulated as solutions to constraint optimization problems, and derived using heuristics, sometimes borrowing ideas from areas with similar abstractions, such as operating systems.

Reinforcement learning (RL) has been a novel method in scheduling for applications such as job scheduling in clusters [8] and smart grids [9]. Compared with conventional heuristics-based scheduling policies, reinforcement learning has multiple advantages. Firstly, the training process of designed reinforcement learning agents involves exploration and exploitation at the same time, and thus the exact environment parameters (battery recovery effect, etc.) do not need to be pre-determined nor fixed. Instead, one can let the agent learn the optimal strategy through a large number of experiments. Secondly, with the representation power of neural networks [10], RL agents have the potential of discovering better solutions than human intuition, as well as more closely fitting the actual environment than rule-based models. Thirdly, neural network (NN)-based RL models are adaptive and versatile, thanks to differentiability. Numerous works, including transfer learning [11] and model-agnostic meta-learning (MAML) [12], have showcased that a well-trained NN agent can later be used to adapt incrementally to new use cases, or just to further optimize for specific domains. Last, but not least, embedded RL agents can be readily deployed in a wide range of software/hardware platforms, thanks to the large eco-system brought by the deep learning community. Recently, the advancement of both software and hardware technology has made it possible to fit very powerful models into tight power and delay envelopes, with successes in computer vision [13] and speech recognition [14]; thus the design space for the scheduling agent can be quite wide while still maintaining low resource consumption.

Although heuristics-based schedule algorithms already achieve good results in terms of extended battery lifetime, they are limited from requirements for solving constraint optimization problems. Meanwhile, each heuristic scheduling algorithm is developed for certain battery models and use cases and needs to be adjusted when those parameters change. Using RL agents for battery management can overcome these difficulties. By developing a universal RL training framework, the optimized scheduling algorithm can be obtained for any battery model and environment settings, considering many factors, including the load current, temperature, battery balance requirement, and so on. Compared with heuristic scheduling algorithms, the RL scheduling framework can therefore be more flexible towards application scenarios. Due to the time and resource limitations, a computer-simulated battery model can be utilized to develop the RL framework and train the RL scheduling agent.

This paper proposes a reinforcement learning framework to solve the traditional lithium-ion battery scheduling problem. A Python-based battery model incorporating capacity charge/discharge and thermal transfer physics is established. A multi-agent actor-critic method is used to train the battery scheduling agent. The trained RL agent achieves battery lifetime close to the best heuristic scheduling algorithm, protects the battery from overheating, and manages the battery imbalance conditions.

2. Battery Model

Obtaining an accurate analytical model of the lithium-ion battery is critical for training the battery scheduling agent. As described before, two types of effect have been reported for lithium-ion batteries: rate capacity effect and recovery effect. The kinetic battery model (KiBaM), first proposed in [15], is a widely used battery model to explain the two effects and estimate the battery state of charge (SOC). In the KiBaM model (Figure 2), two charge tanks, separated by a tunnel with flow rate k, are used to model the total capacity of the battery. The right tank (direct available tank), which has a capacity ratio c, represents the direct available capacity of the battery; the left tank (bound tank), which has a capacity ratio 1-c, represents the charge temporarily stored and partially being used to supplement the direct available tank. The volume of the charge in two tanks, q₁ and q₂, represents the amount of charge in each tank. The height of the direct available tank, h₁, is directly related to the measured open circuit voltage (OCV) of the battery. During discharge, the electrical load will first drain charge from the direct available tank. Due to the height difference between the two tanks (h₁–h₂), the charge in the left tank will flow into the right tank through the tunnel. The flow rate k is proportional to the conductance and height difference.

Variations of KiBaM have been proposed to improve battery modeling accuracy while incorporating additional environmental parameters, such as temperature dependency [16]. In this work, the fractional-order KiBaM (FO-KiBaM) proposed in [17] is applied, which includes an additional fractional order, α, to further fit the nonlinear battery capacity versus discharge current. The equation below shows the battery charge/discharge dynamic behavior described in this work:

$$\frac{d^{\mathsf{\alpha }}{y}_1}{d{t}^{\mathsf{\alpha }}}=-i\left(t\right)+k {\delta }_h\left(t\right)=-i\left(t\right)+k \left(\frac{y_2\left(t\right)}{1-c}-\frac{y_1\left(t\right)}{c}\right)$$

(1)

$$\frac{d^{\mathsf{\alpha }}{y}_2}{d{t}^{\mathsf{\alpha }}}=-k {\delta }_h\left(t\right)=-k \left(\frac{y_2\left(t\right)}{1-c}-\frac{y_1\left(t\right)}{c}\right)$$

(2)

in which i(t) is the discharge current from the load, k is the conductance between the two tanks, and α is the exponential term between load current and charge change (0 < α < 1). An α closer to 1 indicates the battery has higher linearity in capacity, and a smaller α indicates a higher rate-capacity effect. In [17], the estimated α is 0.99, but simulation for α = 0.9 is also performed to show that the RL agents can perform close to the best heuristic scheduling algorithm for high non-linear battery models.

The heat generated during battery charge/discharge could cause the battery temperature to exceed the maximum allowed, thus causing hazardous battery degradation. For efficient and safe battery operation, the overheated battery should be cooled down before further usage. To model the lithium-ion battery temperature, the model proposed in [18,19] was applied. The governing equations are:

$$C_{cell}\frac{d{T}_{cell}}{dt}=Q_P+Q_S-Q_B$$

(3)

$$Q_P=I\left(V-V_0\right)=I^2{R}_{\eta }$$

(4)

$$Q_S=T_{cell} \mathsf{\Delta }S \frac{I}{nF}$$

(5)

$$Q_B=Ah\left(T_{cell}-T_{amb}\right)$$

(6)

in which C_cell is the heat capacity of the battery, T_cell is the battery temperature, Q_P is the resistive heat, Q_S is heat from system entropy change, and Q_B is the heat transfer between the battery and ambient environment. In the first equation, R_η is the battery’s internal resistance. In the second equation, ΔS is the entropy change of the battery, I is the load current (positive for charging and negative for discharging), n is 1 for lithium-ion battery, and F is the Faraday constant. In the third equation, A is the battery surface area, h is the heat transfer coefficient, and T_amb is the ambient temperature. As can be seen from the equation, T_cell increases quadratically with load current at the beginning, and stabilizes when the T_cell − T_amb reaches certain threshold.

A Murata VTC6 18650 3000 mAh lithium-ion battery was selected as the base model in our experiment [20], and the parameters of this model are listed in

Table 1. The parameters of the lithium-ion battery model used in the work.

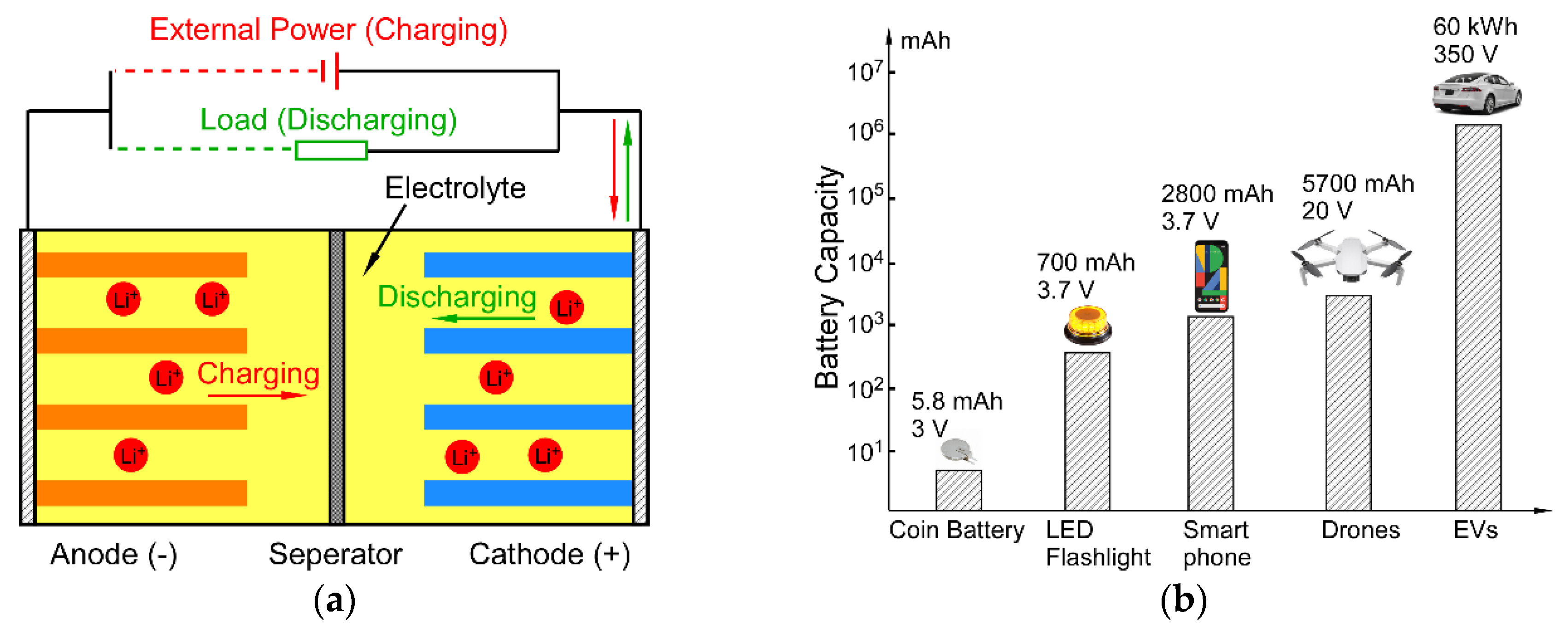
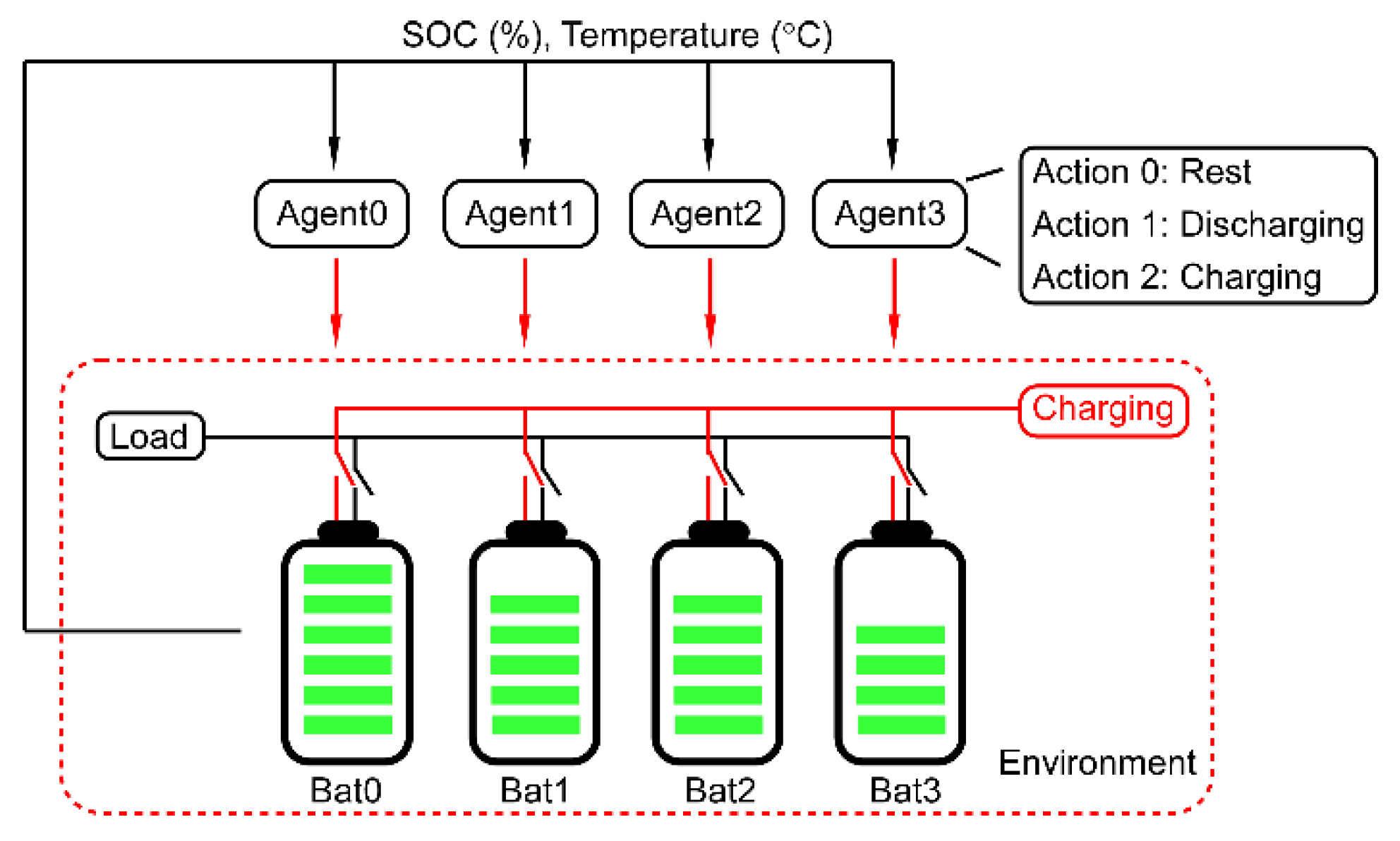
Parameter	Value
Base model	Murata VTC6 18650
Electrical Parameters
Capacity	3000 mAh
Nominal voltage	3.7 V
Capacity ratio c	0.5
Fractional order α	0.9 or 0.99
Recovery flow rate	0.001
Discharge current	4 A
Charge current	0.3 A
Step time duration	1 min
Physical & Thermal Parameters
Battery dimension	18 mm Ø × 65 mm
Battery mass	~45 g
Max operating temp.	60 °C
Battery specific heat capacity	~0.96 ± 0.02 J /g K
Internal resistance	0.1 Ohm
Entropy change ΔS	−30 J/mol·K
Heat transfer coeff. h	13 Wm−2K−1

. The battery model has a cylindrical shape with diameter of 18 mm and height of 65 mm, and a total weight of 46.6 g. The c was set to be 0.5, and k was set to be 0.001; both are within reasonable range for computation precision. The thermal parameters were approximated based on literature on similar battery models [21,22].

The numerical 18650 battery model with thermal behavior was established, based on the above information, for developing the RL battery scheduling framework. Python was selected as the developing language, since it has the feature of fast prototyping, and has a rich developer community which supports many open source libraries. These libraries include circuit simulation packages as PySpice [23] and PySerDes [24], and machine learning packages such as Tensorflow [25] and Pytorch [26]. These packages can help develop the AI-assisted full battery management system simulation framework.

The rate-capacity effect and recovery effect were observed in the simulation plotted in Figure 3a and Figure 3b. In these plots, the SOC in the direct available tank, which is indeed h₁, was selected as the y-axis. This quantity, which is directly related to the battery’s measured OCV, is used to represent battery capacity status in later sections of this paper. The actual interpretation of the battery’s direct available SOC from the battery’s OCV, which forms the classical problem of battery SOC estimation, is beyond the scope of this paper. The temperature of the battery under various discharge currents was also simulated and plotted in Figure 4. As indicated in the plot, the battery’s steady state temperature increased quadratically with discharge current.

3. Reinforcement Learning Algorithm

The architecture of the multi-agent RL battery scheduling framework is shown in Figure 5. The framework consists of an environment for battery pack operation and measurement, and a group of RL agents to control the batteries. The environment in this work consisted of four identical batteries in parallel, each controlled by one RL agent. The state of the environment was defined as the direct available SOC and temperature of each battery. During each step, the state of the environment was first measured and passed to the four battery agents. Each agent then picked an action for the battery, based on the input environment state. Three action values existed, including 0 for rest, 1 for discharge, and 2 for charge with a constant charging current. For all the batteries with discharge action, they were discharged with equal current to supply a total load current, I_load. If any battery’s direct available SOC dropped below a threshold (0.5 in this work), the battery was considered deeply discharged and was disabled in the current episode. After all batteries’ SOC dropped below that threshold value, the episode was considered completed, and the batteries’ states were reinitialized for the next episode. In this work, 1 minute was used as the step duration for each action pair.

During the RL agent training, the environment took the actions from the battery agents, processed the batteries, and generated the reward. The reward for each step was defined as:

$$Reward=1+R_T$$

(7)

$$R_T=A{e}^{\frac{-E_a}{RT}}$$

(8)

in which R_T is the negative reward from temperature effect, A is a pre-exponential constant factor, E_a is the activation energy for lithium-ion battery [22], R is the gas constant, and T is the ambient temperature. During the discharge, each successful discharge step would add reward by 1. Agents that could manage the batteries for longer lifetimes got higher rewards. At elevated temperatures, a negative reward, R_T, would be added to the step reward, to indicate the high temperature degradation of the battery. Equation (8), which is indeed the Arrhenius equation, served as a normal estimation of reaction rate under different temperatures, which indicated battery health condition degradation [27]. This reaction rate was used as an estimation of the battery degradation, and A was arbitrarily picked so that the reward reduced to zero when the battery temperature increased above ~60 °C, which is a nominal upper operating temperature for lithium-ion batteries. Under such environment reward settings, the agents were trained to maximize the number of steps for discharging, while maintaining the battery temperature within safe margins.

A multi-agent actor-critic method was used for training the battery agents, which is a training method used in cooperative tasks such as desktop gaming [28,29] and microgrid energy scheduling [30]. Figure 6 shows the proposed neural network structure for training the battery agents. The battery agents generated the action from the measured environment states and sent to the environment. The environment processed the battery, calculated rewards, and took measurements to generate the new state. The step reward and the new state were then sent to the central critic, which calculated the td-target and then tuned the critic and agent networks. The centralized training was used since all agents shared the same environment states, which could be used by one value function approximator. The actor network was composed of two ResNet layers [31] followed by a fully connected layer, and the critic was composed of three fully connected layers.

4. Experiment

4.1. Electrical Only

The RL battery scheduling framework was first tested under the electrical-only setting, and the battery thermal model was temporarily disabled, as well as the thermal reward, R_T. Two separate scenarios under electrical-only settings were tested: one without charging current (so effectively only discharge and rest action), and the other with a constant charging current.

Table 2. Battery scheduling results using various scheduling algorithms under the simulation setup in this work, electrical-only environment. Unit: minutes.

Experiment	Sequential	RR	2RR	All-Way (4RR)	RL Agent
Discharge only (α = 0.99)	84	92	92	92	92
Discharge only (α = 0.9)	112	124	136	145	145
Charge enabled (α = 0.99)	84	116	108	92	116
Charge enabled (α = 0.9)	112	152	154	145	154

summarizes the battery scheduling results (minutes) for the two scenarios, using both an RL scheduling agent and heuristic scheduling. According to the table, the RL agent achieved the best results for all experiment setups, while other heuristic scheduling algorithms only achieved good results under one or a few circumstances.

In the discharge-only scenario, the constant load current, I_load, was set to be 4 A. Figure 7a shows the reward during the RL agent training, Figure 7b shows the battery’s available SOC curve using the RL agents before training, and Figure 7c shows the battery’s available SOC curve using the RL agents after training, with α as 0.9. The total reward converged after ~50,000 training episodes. Before the RL agents were trained, they generated rather random actions, and some batteries depleted fast with high instant current, losing the opportunity to recover capacity. After training, the batteries were discharged evenly with smaller instant currents, and maintained longer lifetimes. Figure 7c also shows the discharge curves using RR and all-way (4RR) scheduling. Due to the high rate-capacity effect in the FO-KiBaM model, a lower instant discharge current for each individual battery can save the battery capacity. Meanwhile, as long as the battery’s available SOC was above 50% in the experiment setup, the charge in the direct available tank could be supplemented from the storage tank. As a result, the all-way scheduling performed superior to the RR scheduling. The RL agents trained in the experiment behaved close to the all-way scheduling.

In the scenario with a constant charging current, the constant charging current was arbitrarily set to be 0.3 A. The charging action could supply additional charge into the direct available tank, thus could be the optimized action for batteries with low available SOC. Figure 7d shows the battery’s available SOC curve using the 2RR, all-way, and RL agent scheduling. The 2RR scheduling performed superior to the all-way scheduling under constant charging enabled, and the trained RL agents performed close to the 2RR scheduling. The intuition is that 2RR allowed certain cycles of charging, rather than completely discharging in all-way scheduling, and maintained the instant discharge current lower than 1RR. The trained RL agents behaved close to 2RR scheduling.

4.2. Thermal Effect

The framework was then tested with battery temperature effect, and the temperature reward, R_T, was enabled. An increased constant load current, I_load, of 16 A was used, so the battery temperature could easily exceed the safety margin. Figure 8a shows the rewards during training. The total reward converged after ~6000 training episodes. Figure 8b shows the battery’s available SOC and temperature curve before the training, and Figure 8c shows the curves after training. Before the RL agents were trained, certain batteries got discharged more than others, and the temperature of these batteries increased over the maximum allowed value, such as battery 4, which increased to over 100 °C. After training, the RL agents learned to discharge the batteries evenly to reduce the instant current, thus reducing the generated heat quadratically, as indicated in Equations (3)–(6). The RL agents thus maintained the battery temperature under 60 °C before depletion. With a higher instant current, the RL agents could also be trained to shut down the whole battery system (pick all action as 0) to ensure safety.

4.3. Imbalanced Battery

The imbalanced battery is a condition in which the SOC of the batteries inside a battery pack differ from each other. Causes of imbalanced battery include manufacture variation of battery capacity, variation of battery internal resistance, and variation of the battery discharge/charge current [32]. Active and passive cell balancing methods have been developed, in which passive methods dissipate energy for high voltage cells, and active methods use techniques such as switched capacitors to transport charges between imbalanced batteries [33,34]. With the support of a battery management system, the imbalance of the battery should be observed in advance and balanced via the scheduling policy.

In the proposed RL scheduling framework, it is also demonstrated that the RL battery agents can be trained to observe the imbalanced batteries and smartly schedule the battery activity to gradually balanced the battery packs. In the experimental setup, one of the four batteries was randomly picked to have an 80% initial SOC of the other cells. To train the RL agents to balance the batteries, a negative battery imbalance reward, R_imb, was added into the reward equation:

$$Reward=1+R_T+R_{imb}$$

(9)

$$R_{imb}=k ·\sigma \left(SOC\right)$$

(10)

in which $\sigma \left(SOC\right)$ is the standard deviation between the battery’s available SOC, and k is a scale factor, which was selected as −10 so that a standard deviation of 0.1 between battery SOC would cause the R_imb to be −1. R_T was ignored in the experiment for simplifications. Figure 9a shows the battery’s available SOC curves using the traditional RR scheduling, and Figure 9b shows the SOC curves using the trained RL agents. The RL agents learned to first balance the battery pack by discharging the stronger batteries with higher priority, so that the SOC gap between batteries were reduced. After the SOC of the four batteries were close, the RL agents then discharged all batteries evenly to maintain the balanced condition until depletion.

5. Discussion

The experiment results demonstrate that the trained RL agents can smart schedule the battery activity under different scenarios. For electrical-only environment settings, this RL agent achieved comparable results to the best heuristic kRR scheduling algorithm. For heuristic kRR scheduling, as the number of battery n increases, there exists an optimized value k (1 ≤ k ≤ n) for longest battery pack lifetime, which can be obtained using analytical equations from exact battery capacity models. The RL agents can be trained to approximate the optimized kRR algorithm for any battery model and environment settings, without needing information on the battery’s electrical model and exact charge/discharge current, and without solving complicated analytical equations. This feature of RL scheduling allows the on-demand modification of the scheduling algorithm according to the specific battery model and environment settings, without changing the agent training framework. In certain cases, battery and environment physical parameters could also be unavailable for users to access directly.

For environment settings with thermal effect, there is no exact temperature reward, R_T, generated in each training step in real application scenarios, but the battery temperature affects the battery state of health (SOH), which is directly related to the battery capacity. By obtaining the battery SOH model with temperature degradation, the RL agents can be trained to maximize the battery’s total lifetime for a fixed number of deployment cycles. This can involve a decision tradeoff that involves either discharging the batteries for the current deployment cycle as much as possible or stopping the discharge and let the battery cool down for future use.

This work developed an open-source Python-based lithium-ion battery model and scheduling architecture. Based on this battery mode, an open-source benchmark for battery scheduling algorithm comparisons could be further established. Although much research has been performed to enhance battery scheduling efficiency, the battery models in those works are distinct from each other, and the algorithm implementation details are not accessible. By maintaining this open-source Python library and adding additional battery models and use cases, the development of battery scheduling algorithms could be driven forward.

6. Conclusions and Future Work

In conclusion, this work demonstrates the promise of using multi-agent reinforcement learning frameworks to solve lithium-ion battery scheduling problems. A FO-KiBaM-based lithium-ion battery model with thermal effect is implemented in Python and used for simulation. A multi-agent reinforcement learning framework is implemented, and the RL agents are trained using the simulated battery data. The trained RL agents learn to charge/discharge the battery intelligently, and the performance matches the best heuristic scheduling algorithm for various battery model parameters and environmental settings. The RL agents also learn to maintain the battery temperature under safety margins and balance the battery pack’s SOC as needed.

Under purely electrical settings, the RL agent learns to schedule the battery after ~50,000 training episodes. The agent for α = 0.9 battery achieves a lifetime of 145 cycles in discharge-only environment, and 154 cycles in charge-enabled environment, which are both same as the best kRR scheduling results. Under thermal effect enabled settings, the RL agent learns to discharge the batteries evenly after ~6000 training episodes, to keep all batteries’ temperatures under 60 °C during discharge. Under imbalanced battery settings, the RL agent learns to balance the battery’s SOC and stop further discharging the weaker battery, until SOCs for all batteries are balanced.

As future work, more accurate and complete lithium-ion battery models, including OCV measurement and SOC/SOH estimation, can be used for simulation. Such models can be obtained by measuring the real battery charge/discharge curves and extracting the battery physical parameters. The proposed RL-based battery scheduling algorithm could be implemented and used in real-time embedded systems, with the assistance of modern embedded AI platforms, such as Nvidia Jetson Nano [35], for neural network acceleration.