On the Sensitivity of Local Flexibility Markets to Forecast Error: A Bi-Level Optimization Approach
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.2.1. Harnessing Demand Side Flexibility in the Distribution Network
1.2.2. Pricing Flexibility in Distribution Network
1.2.3. Second-Order Cone Relaxation Error
1.2.4. Research Gap
1.3. Contributions
- proposes a new formulation for the SOC-OFD problem that seeks to find an optimal flexibility schedule (i.e., amount and price of flexibility to be dispatched at each bus) with zero relaxation error. This is done by formulating a bi-level optimization model that seeks to solve the SOC-OFD problem while minimizing the SOC-relaxation error,
- introduces an effective reduction/relaxation technique that makes the bi-level problem tractable both analytically and numerically, and
- provides an analytical framework for performing local sensitivity analysis on the reduced OFD problem, which determines the robustness of the resulted optimal flexibility dispatch against imperfect forecasts of input data.
1.4. Outline
2. Problem Formulation
2.1. Assumptions
2.2. Second-Order Cone Relaxed OFD (SOC-OFD)
2.3. Bi-Level Model for the OFD Problem
2.4. Reformulation of the Bi-Level OFD Problem to NLP-OFD
2.5. Derivation of the Sensitivity Matrix in the OFD Problem
3. Numerical Results
3.1. Case Study
3.2. Assumptions
- Each bus represents a cluster of aggregated end users which can be either a net flexible generator or net flexible load.
- The OFD problem is solved per single time-step. Inter-temporal linkages are neglected.
- A fixed cost for curtailing DER production is considered, and .
- Cost of load curtailment is assumed to be zero.
- Load is modelled as negative generation, i.e., negative flexibility for a net flexible load bus indicates an increase in the total consumption of that bus.
3.3. Simulation Results
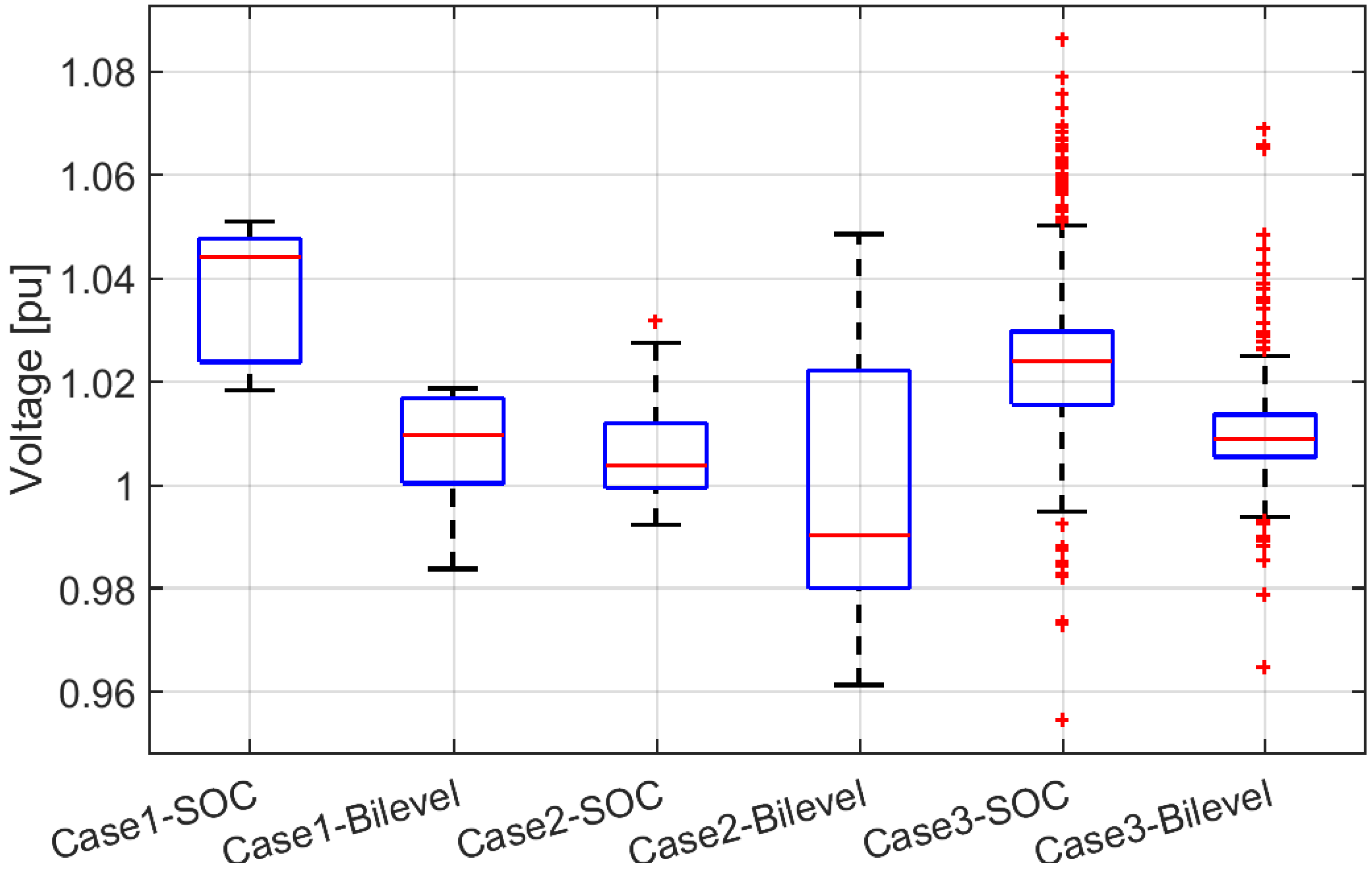
3.3.1. SOC-Relaxation Error ()
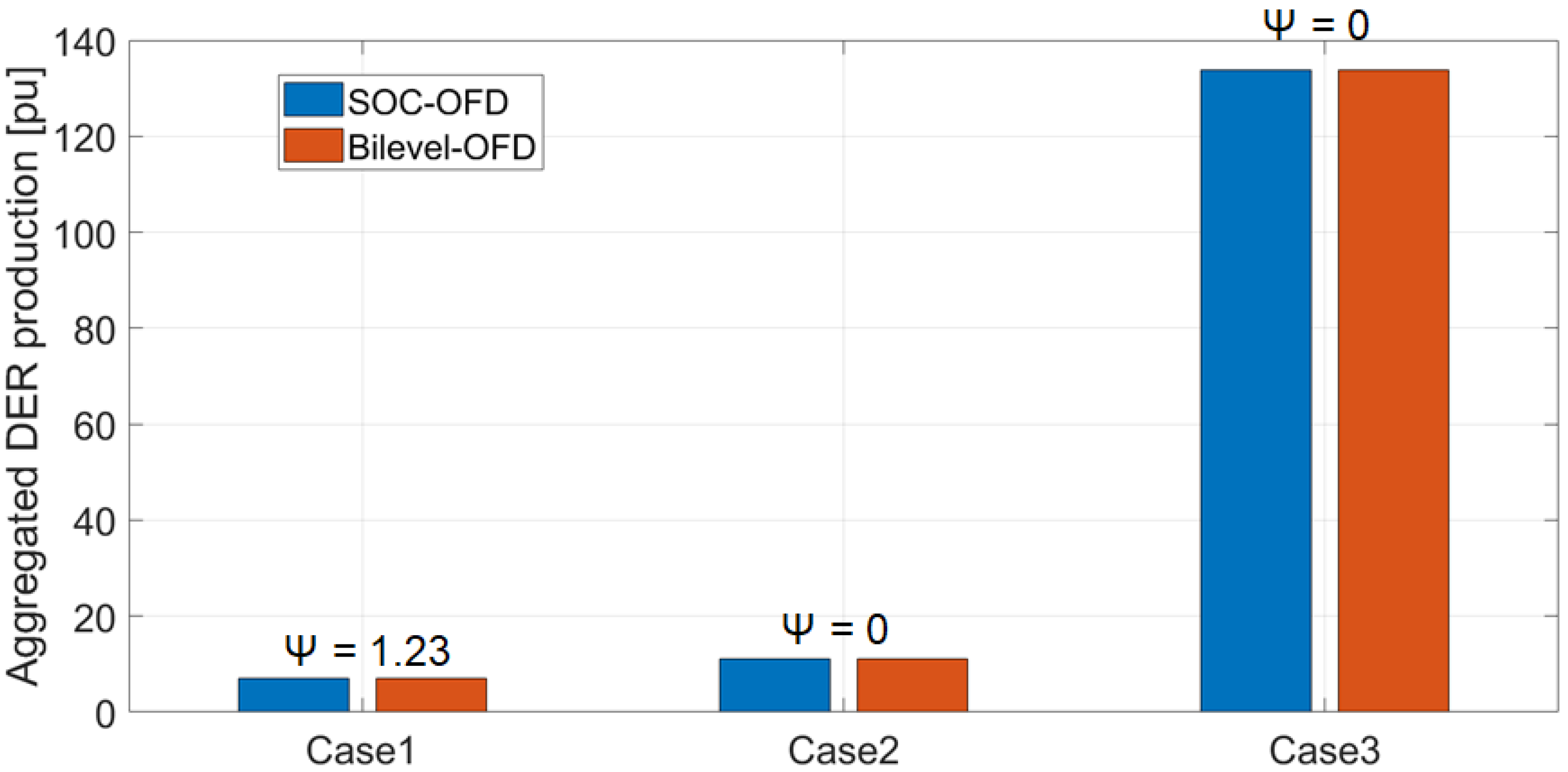
3.3.2. DER Curtailment ()
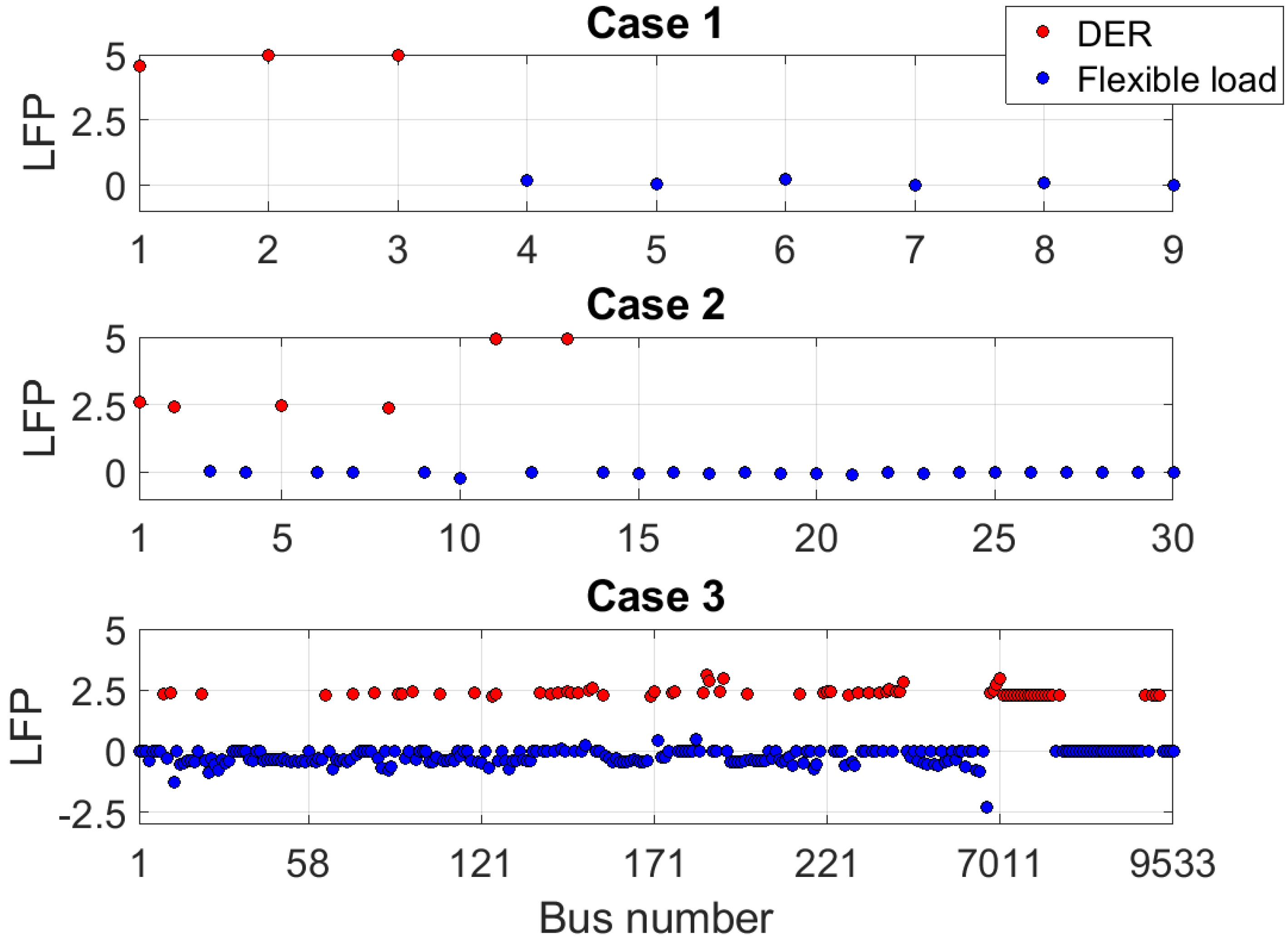
3.3.3. Locational Flexibility Prices (LFPs)
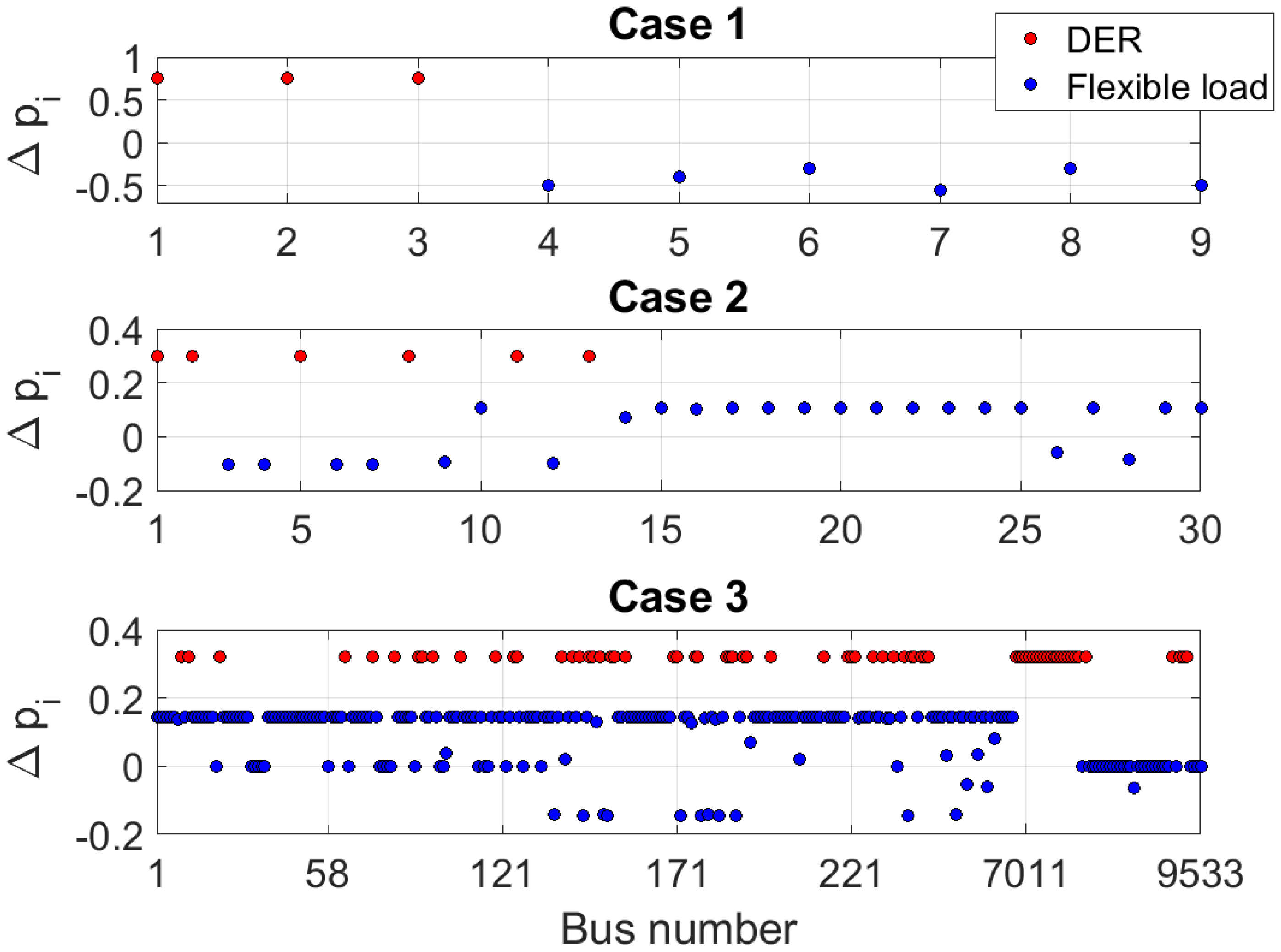
3.3.4. Sensitivity of LFP to Data Perturbation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inf. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Azari, D.; Torbaghan, S.S.; Cappon, H.; Keesman, K.J.; Rijnaarts, H.; Gibescu, M. Exploring the impact of data uncertainty on the performance of a demand response program. Sustain. Energy Grids Netw. 2019, 20, 100262. [Google Scholar] [CrossRef]
- Azari, D.; Torbaghan, S.S.; Cappon, H.; Gibescu, M.; Keesman, K.; Rijnaarts, H. Assessing the flexibility potential of the residential load in smart electricity grids; A data-driven approach. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Morales González, R.; Shariat Torbaghan, S.; Gibescu, M.; Cobben, S. Harnessing the flexibility of thermostatic loads in microgrids with Solar Power Generation. Energies 2016, 9, 547. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Occupancy-based demand response and thermal comfort optimization in microgrids with renewable energy sources and energy storage. Appl. Energy 2016, 163, 93–104. [Google Scholar] [CrossRef]
- Ayón, X.; Gruber, J.; Hayes, B.; Usaola, J.; Prodanović, M. An optimal day-ahead load scheduling approach based on the flexibility of aggregate demands. Appl. Energy 2017, 198, 1–11. [Google Scholar] [CrossRef]
- Kara, E.C.; Tabone, M.D.; MacDonald, J.S.; Callaway, D.S.; Kiliccote, S. Quantifying flexibility of residential thermostatically controlled loads for demand response: A data-driven approach. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings; ACM: New York, NY, USA, 2014; pp. 140–147. [Google Scholar]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M. Energy disaggregation for real-time building flexibility detection. In Power and Energy Society General Meeting (PESGM) 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Good, N.; Zhang, L.; Navarro-Espinosa, A.; Mancarella, P. High resolution modelling of multi-energy domestic demand profiles. Appl. Energy 2015, 137, 193–210. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Zhu, H.; Giannakis, G.B. Distributed optimal power flow for smart microgrids. IEEE Trans. Smart Grid 2013, 4, 1464–1475. [Google Scholar] [CrossRef]
- Forner, D.; Erseghe, T.; Tomasin, S.; Tenti, P. On efficient use of local sources in smart grids with power quality constraints. In 2010 First IEEE International Conference on Smart Grid Communications; IEEE: Piscataway, NJ, USA, 2010; pp. 555–560. [Google Scholar]
- Bhattarai, B.P.; Kouzelis, K.; Mendaza, I.D.D.C.; Bak-Jensen, B.; Pillai, J.R.; Myers, K.S. Smart grid constraint violation management for balancing and regulating purposes. IEEE Trans. Ind. Inf. 2017, 13, 2864–2875. [Google Scholar] [CrossRef]
- Capitanescu, F.; Bilibin, I.; Ramos, E.R. A comprehensive centralized approach for voltage constraints management in active distribution grid. IEEE Trans. Power Syst. 2013, 29, 933–942. [Google Scholar] [CrossRef]
- Dent, C.J.; Ochoa, L.F.; Harrison, G.P. Network distributed generation capacity analysis using OPF with voltage step constraints. IEEE Trans. Power Syst. 2010, 25, 296–304. [Google Scholar] [CrossRef]
- Robertson, J.G.; Harrison, G.P.; Wallace, A.R. OPF techniques for real-time active management of distribution networks. IEEE Trans. Power Syst. 2016, 32, 3529–3537. [Google Scholar] [CrossRef]
- Sansawatt, T.; Ochoa, L.F.; Harrison, G.P. Smart decentralized control of DG for voltage and thermal constraint management. IEEE Trans. Power Syst. 2012, 27, 1637–1645. [Google Scholar] [CrossRef]
- Caramanis, M.; Ntakou, E.; Hogan, W.W.; Chakrabortty, A.; Schoene, J. Co-optimization of power and reserves in dynamic T&D power markets with nondispatchable renewable generation and distributed energy resources. Proc. IEEE 2016, 104, 807–836. [Google Scholar]
- Li, R.; Wu, Q.; Oren, S.S. Distribution locational marginal pricing for optimal electric vehicle charging management. IEEE Trans. Power Syst. 2013, 29, 203–211. [Google Scholar] [CrossRef]
- Yuan, H.; Li, F.; Wei, Y.; Zhu, J. Novel linearized power flow and linearized OPF models for active distribution networks with application in distribution LMP. IEEE Trans. Smart Grid 2016, 9, 438–448. [Google Scholar] [CrossRef]
- Papavasiliou, A. Analysis of distribution locational marginal prices. IEEE Trans. Smart Grid 2017, 9, 4872–4882. [Google Scholar] [CrossRef]
- Mandatova, P.; Mikhailova, O. Flexibility and Aggregation: Requirements for Their Interaction in the Market; Eurelectric: Brussels, Belgium, 2014. [Google Scholar]
- Torbaghan, S.S.; Blaauwbroek, N.; Nguyen, P.; Gibescu, M. Local market framework for exploiting flexibility from the end users. In European Energy Market (EEM), 2016 13th International Conference; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Ramos, A.; De Jonghe, C.; Gómez, V.; Belmans, R. Realizing the smart grid’s potential: Defining local markets for flexibility. Util. Policy 2016, 40, 26–35. [Google Scholar] [CrossRef]
- Minniti, S.; Haque, N.; Nguyen, P.; Pemen, G. Local markets for flexibility trading: Key stages and enablers. Energies 2018, 11, 3074. [Google Scholar] [CrossRef]
- Olivella-Rosell, P.; Lloret-Gallego, P.; Munné-Collado, Í.; Villafafila-Robles, R.; Sumper, A.; Ottessen, S.; Rajasekharan, J.; Bremdal, B. Local flexibility market design for aggregators providing multiple flexibility services at distribution network level. Energies 2018, 11, 822. [Google Scholar] [CrossRef]
- Torbaghan, S.S.; Blaauwbroek, N.; Kuiken, D.; Gibescu, M.; Hajighasemi, M.; Nguyen, P.; Smit, G.J.; Roggenkamp, M.; Hurink, J. A market-based framework for demand side flexibility scheduling and dispatching. Sustain. Energy Grids Netw. 2018, 14, 47–61. [Google Scholar] [CrossRef]
- Torbaghan, S.S.; Suryanarayana, G.; Hoschle, H.; D’hulst, R.; Geth, F.; Chris, C.; Van Hertem, D. Optimal Flexibility Dispatch Problem Using Second-Order Cone Relaxation of AC Power Flow. IEEE Trans. Power Syst. 2019, 35, 98–108. [Google Scholar] [CrossRef]
- Christakou, K.; Tomozei, D.C.; Le Boudec, J.Y.; Paolone, M. AC OPF in radial distribution networks–Part I: On the limits of the branch flow convexification and the alternating direction method of multipliers. Electr. Power Syst. Res. 2017, 143, 438–450. [Google Scholar] [CrossRef]
- Christakou, K.; Tomozei, D.C.; Le Boudec, J.Y.; Paolone, M. AC OPF in radial distribution networks–Part II: An augmented Lagrangian-based OPF algorithm, distributable via primal decomposition. Electr. Power Syst. Res. 2017, 150, 24–35. [Google Scholar] [CrossRef]
- Madani, R.; Ashraphijuo, M.; Lavaei, J. Promises of conic relaxation for contingency-constrained optimal power flow problem. IEEE Trans. Power Syst. 2015, 31, 1297–1307. [Google Scholar] [CrossRef]
- Madani, R.; Sojoudi, S.; Lavaei, J. Convex relaxation for optimal power flow problem: Mesh networks. IEEE Trans. Power Syst. 2014, 30, 199–211. [Google Scholar] [CrossRef]
- Fazel, M.; Hindi, H.; Boyd, S.P. A rank minimization heuristic with application to minimum order system approximation. In Proceedings of the 2001 American Control Conference.(Cat. No. 01CH37148); IEEE: Piscataway, NJ, USA, 2001; Volume 6, pp. 4734–4739. [Google Scholar]
- Venzke, A.; Chatzivasileiadis, S.; Molzahn, D.K. Inexact convex relaxations for AC optimal power flow: Towards AC feasibility. arXiv 2019, arXiv:1902.04815. [Google Scholar]
- Gabriel, S.A.; Conejo, A.J.; Fuller, J.D.; Hobbs, B.F.; Ruiz, C. Complementarity Modeling in Energy Markets; Springer Science & Business Media: Berlin, Germany, 2012; Volume 180. [Google Scholar]
- Conejo, A.J.; Castillo, E.; Minguez, R.; Garcia-Bertrand, R. Decomposition Techniques in Mathematical Programming: Engineering and Science Applications; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Gabriel, S.A.; Conejo, A.J.; Ruiz, C.; Siddiqui, S. Solving discretely constrained, mixed linear complementarity problems with applications in energy. Comput. Oper. Res. 2013, 40, 1339–1350. [Google Scholar] [CrossRef]
- Ruiz, C.; Conejo, A.J.; Gabriel, S.A. Pricing non-convexities in an electricity pool. IEEE Trans. Power Syst. 2012, 27, 1334–1342. [Google Scholar] [CrossRef]
- Brotcorne, L.; Labbé, M.; Marcotte, P.; Savard, G. Joint design and pricing on a network. Oper. Res. 2008, 56, 1104–1115. [Google Scholar] [CrossRef]
- Schneider, K.P.; Fuller, J.C. Voltage control devices on the IEEE 8500 node test feeder. In IEEE PES T&D 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- W3Techs. Available online: https://matpower.org/ (accessed on 25 August 2019).
- Zimmerman, R.D.; Murillo-Sánchez, C.E. Matpower 4.1 user’s manual. In Power Systems Engineering Research Center; Cornell University: Ithaca, NY, USA, 2011. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E. MATPOWER User’s Manual; Technical Report; Power Systems Engineering Research Center (PSerc): Tempe, AR, USA, 2019. [Google Scholar]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the 2004 CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Abdella, J.; Shuaib, K. Peer to peer distributed energy trading in smart grids: A survey. Energies 2018, 11, 1560. [Google Scholar] [CrossRef]
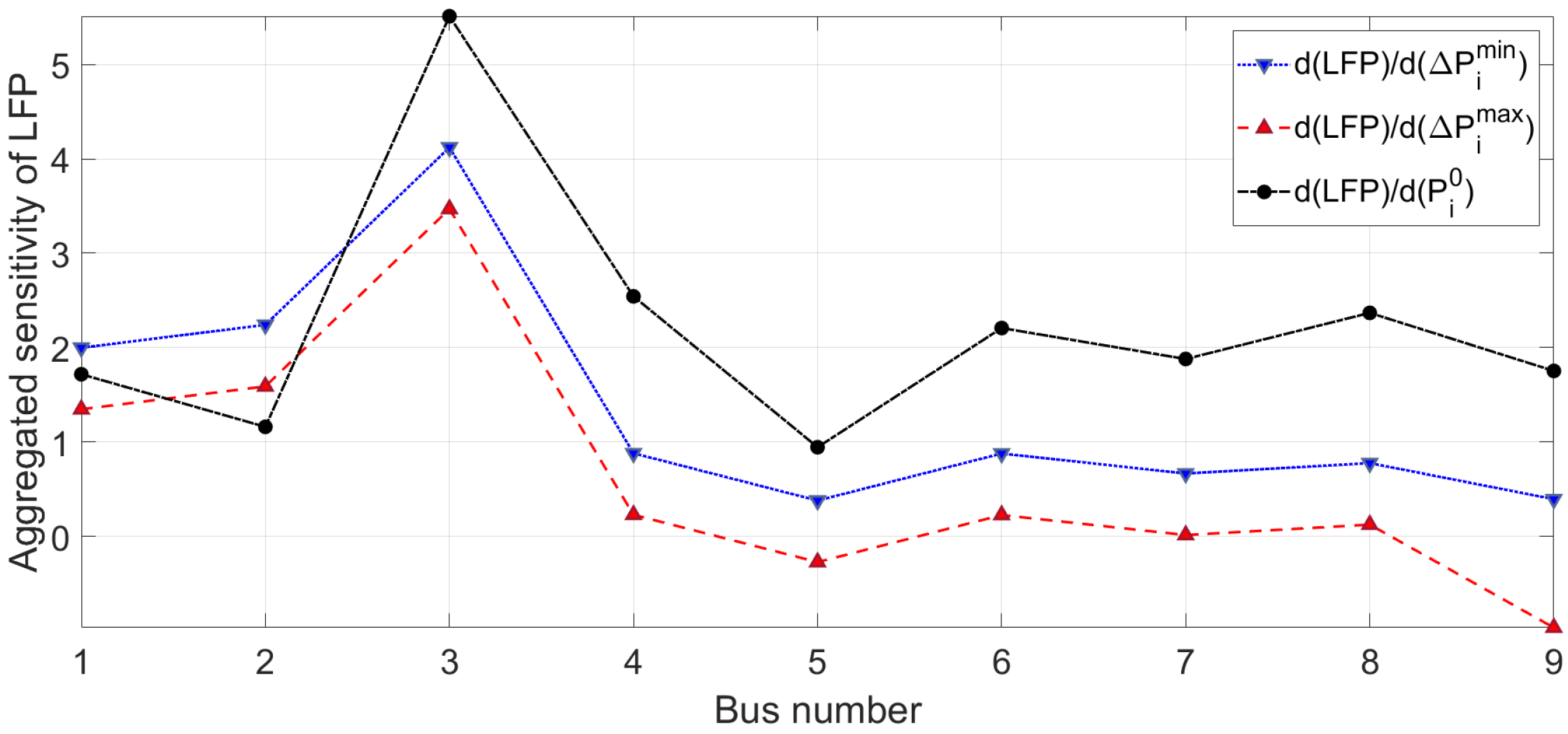
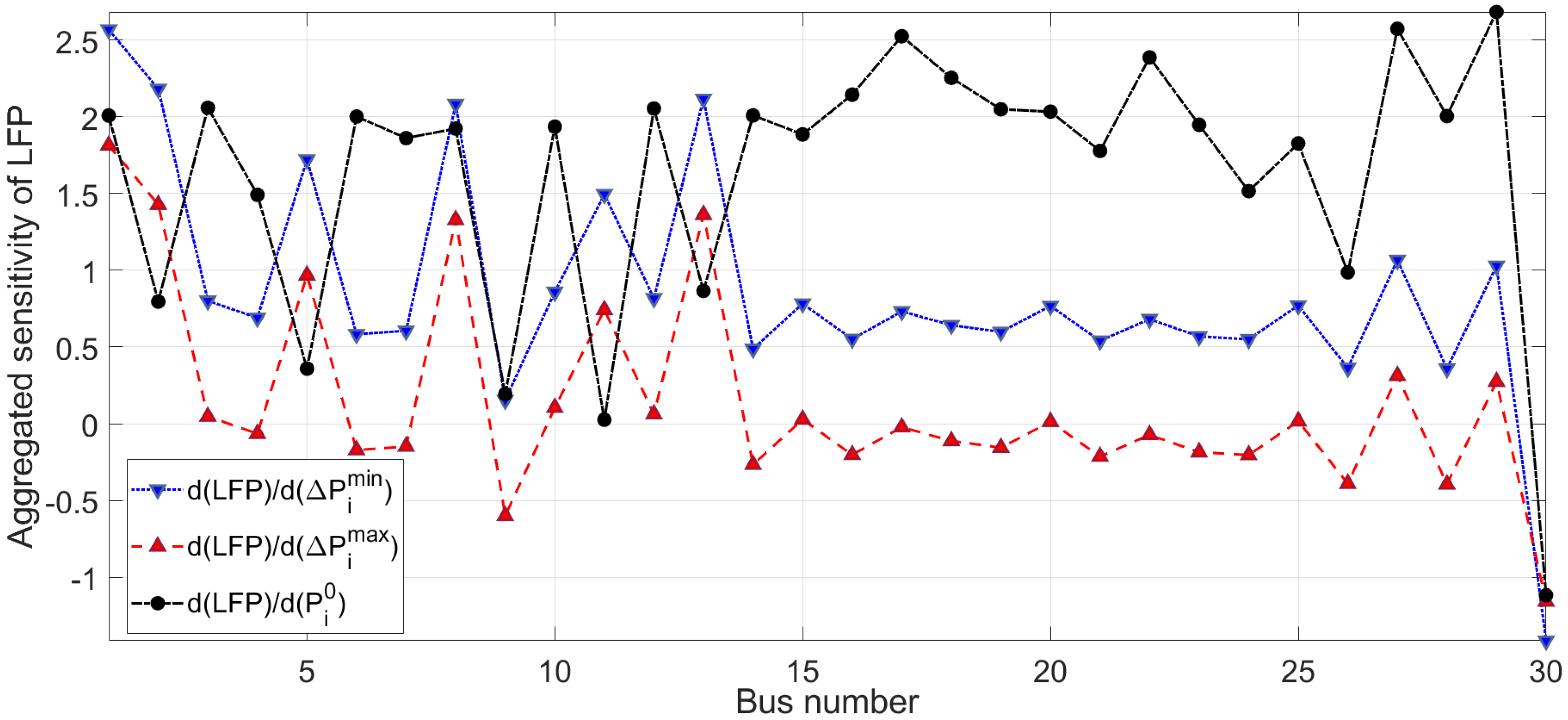
| Case | No. Buses | No. DERs | No. Branches | |||
|---|---|---|---|---|---|---|
| Case 1 | 9 | 3 | 9 | 0.040 | 0.096 | 10.990 |
| Case 2 | 30 | 6 | 41 | 0.076 | 0.200 | 7.498 |
| Case 3 | 300 | 69 | 411 | 0.046 | 0.117 | 88.392 |
| Case | Aggregated Supply | Aggregated Demand | Aggregated Available DER Flexibility | Aggregated Available Demand Flexibility |
|---|---|---|---|---|
| Case 1 | 4.9 | 4.7 | 2.25 | 2.7 |
| Case 2 | 4.14 | 10.67 | 4.66 | 9.40 |
| Case 3 | 5.24 | 50.78 | 8.76 | 38.1 |
| SOC-OFD | Bi-Level OFD | |||||
|---|---|---|---|---|---|---|
| min | max | avg | min | max | avg | |
| Case1 | 0.00 | 0.64 | 0.25 | 0.00 | 0.00 | 0.00 |
| Case2 | 0.01 | 0.24 | 0.07 | 0.00 | 0.00 | 0.00 |
| Case3 | 0.00 | 0.61 | 0.09 | 0.00 | 0.25 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azari, D.; Shariat Torbaghan, S.; Cappon, H.; Keesman, K.J.; Gibescu, M.; Rijnaarts, H. On the Sensitivity of Local Flexibility Markets to Forecast Error: A Bi-Level Optimization Approach. Energies 2020, 13, 1959. https://doi.org/10.3390/en13081959
Azari D, Shariat Torbaghan S, Cappon H, Keesman KJ, Gibescu M, Rijnaarts H. On the Sensitivity of Local Flexibility Markets to Forecast Error: A Bi-Level Optimization Approach. Energies. 2020; 13(8):1959. https://doi.org/10.3390/en13081959
Chicago/Turabian StyleAzari, Delaram, Shahab Shariat Torbaghan, Hans Cappon, Karel J. Keesman, Madeleine Gibescu, and Huub Rijnaarts. 2020. "On the Sensitivity of Local Flexibility Markets to Forecast Error: A Bi-Level Optimization Approach" Energies 13, no. 8: 1959. https://doi.org/10.3390/en13081959
APA StyleAzari, D., Shariat Torbaghan, S., Cappon, H., Keesman, K. J., Gibescu, M., & Rijnaarts, H. (2020). On the Sensitivity of Local Flexibility Markets to Forecast Error: A Bi-Level Optimization Approach. Energies, 13(8), 1959. https://doi.org/10.3390/en13081959






