A Non-Adaptive Single-Phase PLL Based on Discrete Half-Band Filtering to Suppress Severe Frequency Disturbances
Abstract
1. Introduction
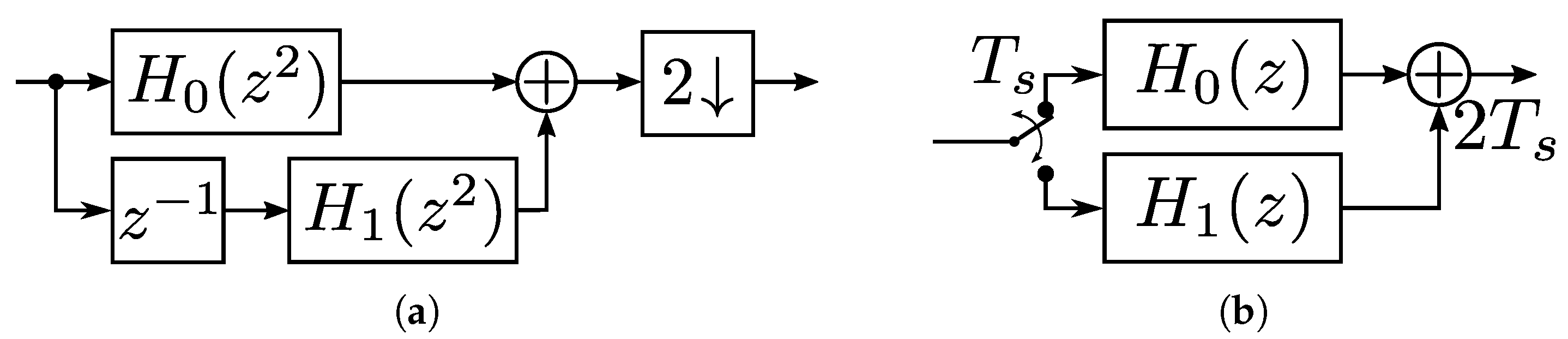
2. Discrete Half-Band Elliptical Filters
2.1. Foundations
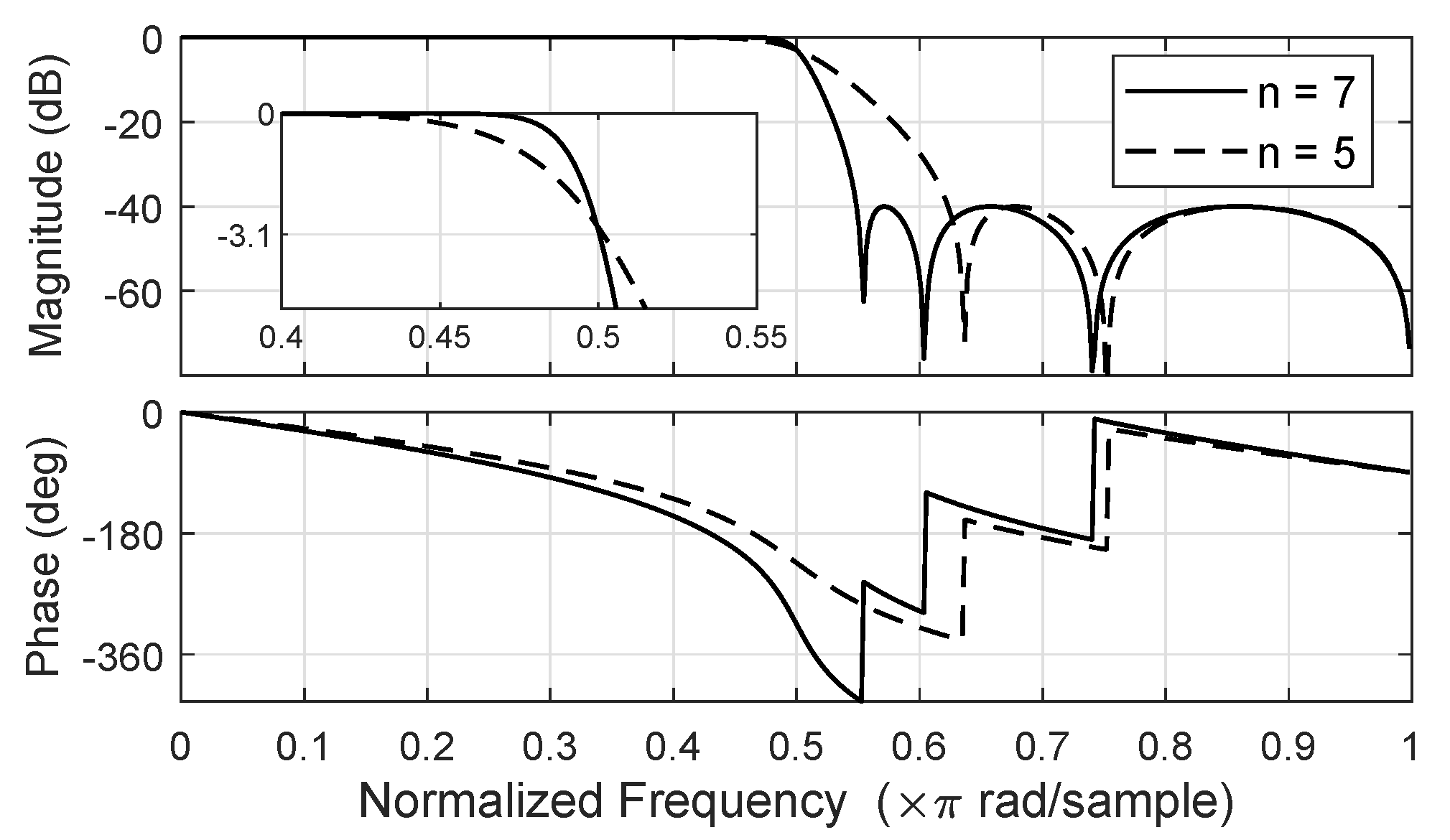
2.2. Design Process
2.3. Case-Study
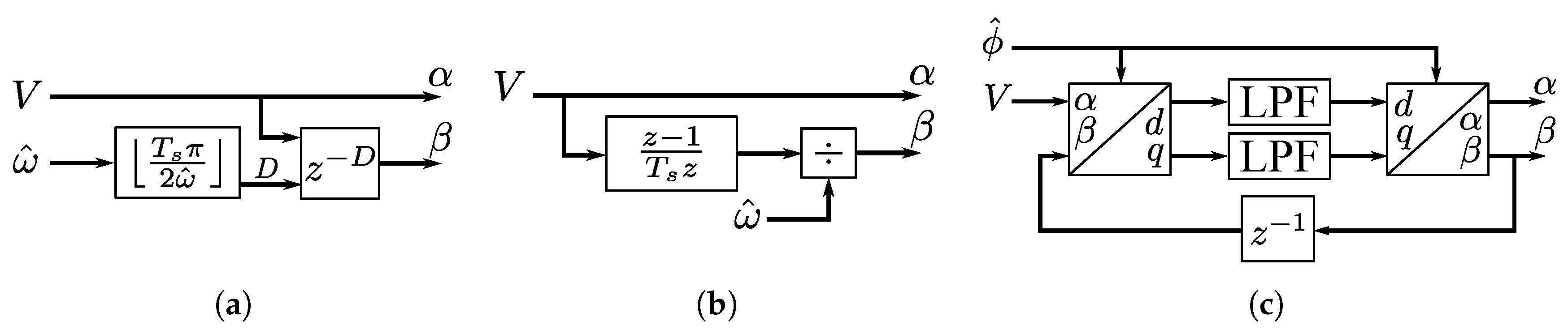
3. PLL Proposal
3.1. MAFs’ Background
3.2. Filtering Proposal
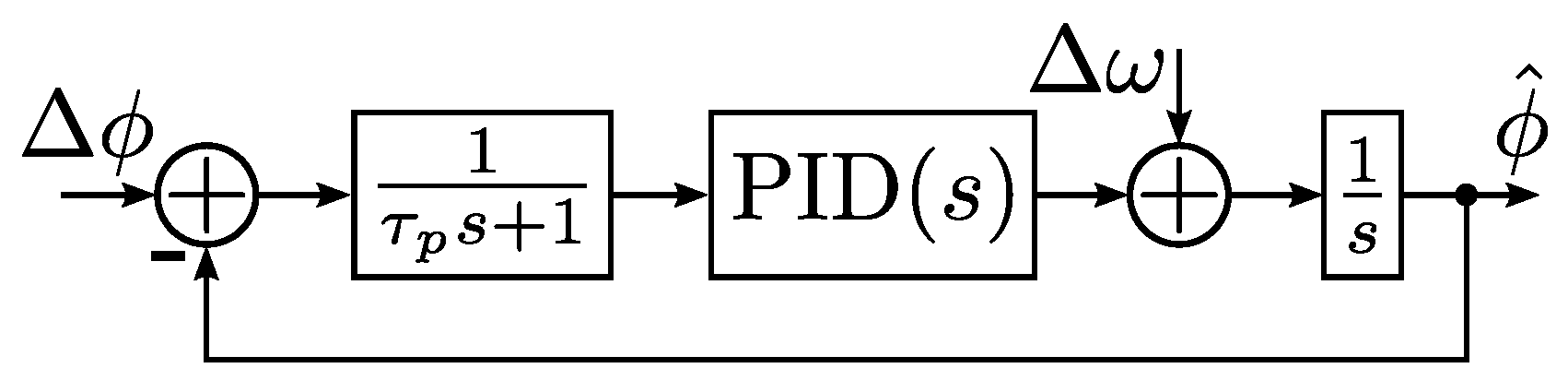
3.3. PID Tuning
4. Testing Protocol
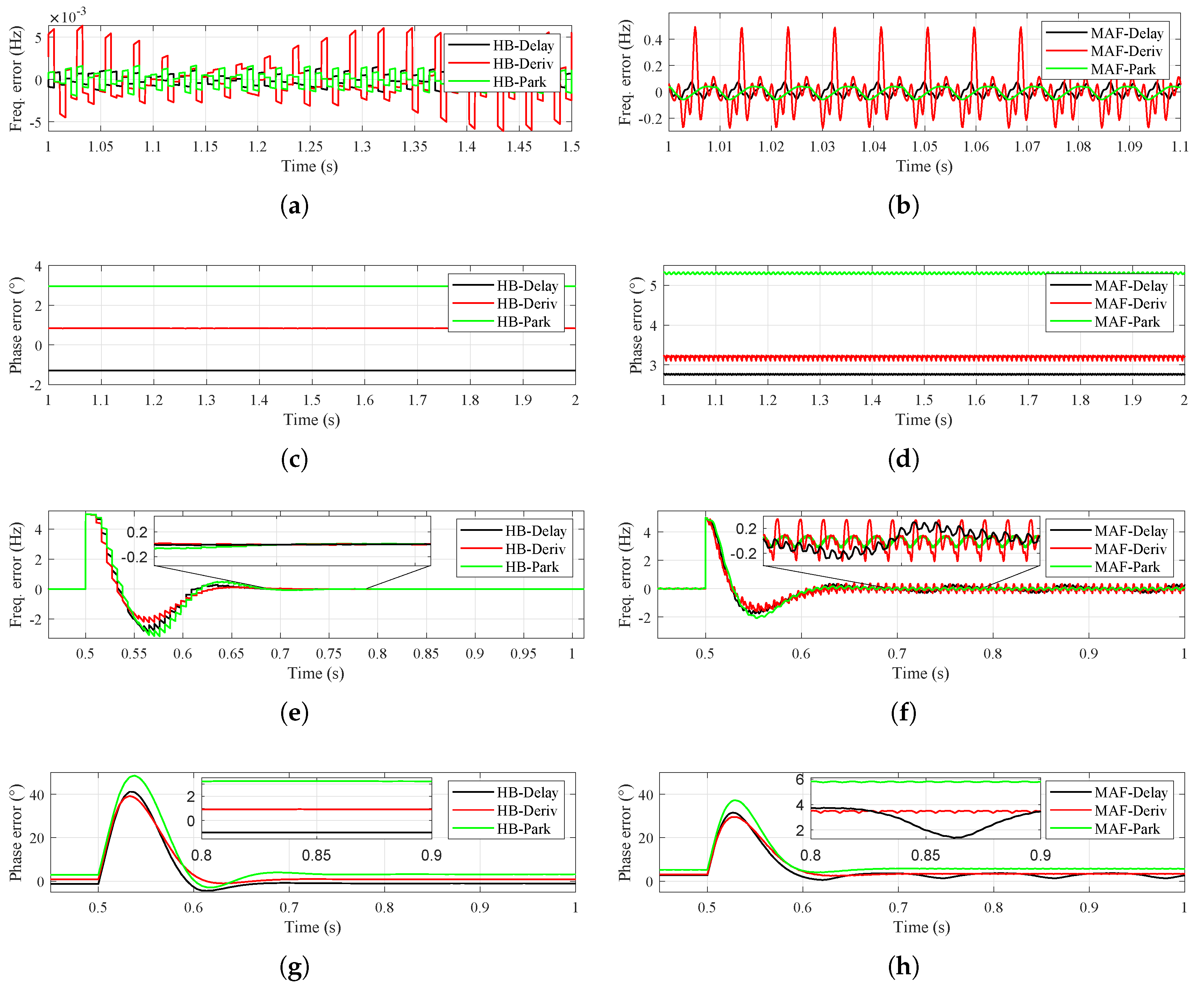
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ADC | Analog to digital converter |
| CDSC | Cascaded delayed signal cancellation blocks |
| DSP | Digital signal processor |
| EN | Energy during steady-state |
| HB | Half-band elliptical filter |
| IIR | Infinite-impulse response |
| LOH | Low-order harmonics |
| LPF | Low-pass filter |
| MAF | Moving average filter |
| MR | Multi-rate |
| OS | Overshoot |
| OSG | Orthogonal signal generator |
| PI | Proportional-integral controller |
| PID | Proportional-integral-derivative controller |
| PK | Peak-to-peak amplitude during steady-state |
| PLL | Phase-locked loop |
| SR | Sampling rate |
| SRF | Synchronous reference frame |
| ST | Settling time |
| THD | Total harmonic distortion |
| ZOH | Zero-order hold |
References
- Alliance, G. The Future of the Grid Evolving to Meet America’s Needs—Final Report: An Industry-Driven Vision of the 2030 Grid and Recommendations for a Path Forward. 2014. Available online: https://www.smartgrid.gov/document/future_grid_evolving_meet_americas_needs_final_report_industry_driven_vision_2030_grid_and.html (accessed on 16 March 2017).
- Al Abri, R.S.; El-Saadany, E.F.; Atwa, Y.M. Optimal Placement and Sizing Method to Improve the Voltage Stability Margin in a Distribution System Using Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 326–334. [Google Scholar] [CrossRef]
- Lima, F.K.d.A.; Araujo, R.G.; Tofoli, F.L.; Branco, C.G.C. A Phase-Locked Loop Algorithm for Single-Phase Systems With Inherent Disturbance Rejection. IEEE Trans. Ind. Electron. 2019, 66, 9260–9267. [Google Scholar] [CrossRef]
- Mellouli, M.; Hamouda, M.; Slama, J.B.H. A comparative Study And Evaluation of Improved MAF- PLL Algorithms. Int. J. Renew. Energy Res. 2017, 7, 88–95. [Google Scholar]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative Performance Evaluation of Orthogonal-Signal-Generators-Based Single-Phase PLL Algorithms—A Survey. IEEE Trans. Power Electron. 2016, 31, 3932–3944. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Chen, C.; Jiang, A.; Zhao, X.; Guerrero, J.M. Performance Evaluations of Four MAF-Based PLL Algorithms for Grid-Synchronization of Three-Phase Grid-Connected PWM Inverters and DGs. J. Power Electron. 2016, 16, 1904–1917. [Google Scholar] [CrossRef]
- Ghoshal, A.; John, V. Performance evaluation of three phase SRF-PLL and MAF-SRF-PLL. Turk. J. Electron. Eng. Comput. Sci. 2015, 23, 1781–1804. [Google Scholar] [CrossRef]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving Average Filter Based Phase-Locked Loops: Performance Analysis and Design Guidelines. IEEE Trans. Power Electron. 2014, 29, 2750–2763. [Google Scholar] [CrossRef]
- Arya, S.R.; Patel, M.M.; Alam, S.J.; Srikakolapu, J.; Giri, A.K. Phase lock loop–based algorithms for DSTATCOM to mitigate load created power quality problems. Int. Trans. Electr. Energy Syst. 2020, 30, e12161. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. A Nonadaptive Window-Based PLL for Single-Phase Applications. IEEE Trans. Power Electron. 2018, 33, 24–31. [Google Scholar] [CrossRef]
- Ahn, C.K.; Shi, P.; You, S.H. Optimal Memory Size Formula for Moving-Average Digital Phase-Locked Loop. IEEE Signal Process. Lett. 2016, 23, 1844–1847. [Google Scholar] [CrossRef]
- He, X.; Geng, H.; Yang, G. A Generalized Design Framework of Notch Filter Based Frequency-Locked Loop for Three-Phase Grid Voltage. IEEE Trans. Ind. Electron. 2018, 65, 7072–7084. [Google Scholar] [CrossRef]
- Jovanovic-Dolecek, G. (Ed.) Multirate Systems: Design and Applications; Idea Group Pub: Hershey, PA, USA, 2002. [Google Scholar]
- Ulloa Rojas, R.A. Filtros: (Aproximacion y SíNtesis); Universidad Iberoamericana: Mexico City, Mexico, 2005. [Google Scholar]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Monfared, M. dq-Frame Cascaded Delayed Signal Cancellation- Based PLL: Analysis, Design, and Comparison With Moving Average Filter-Based PLL. IEEE Trans. Power Electron. 2015, 30, 1618–1632. [Google Scholar] [CrossRef]
- Huang, Q.; Rajashekara, K. An Improved Delayed Signal Cancellation PLL for Fast Grid Synchronization Under Distorted and Unbalanced Grid Condition. IEEE Trans. Ind. Appl. 2017, 53, 4985–4997. [Google Scholar] [CrossRef]
- Li, Y.; Wang, D.; Han, W.; Sun, Z.; Yuan, T. A Hybrid Filtering Stage Based Quasi-type-1 PLL under Distorted Grid Conditions. J. Power Electron. 2017, 17, 704–715. [Google Scholar] [CrossRef]
- Gude, S.; Chu, C.C. Dynamic Performance Improvement of Multiple Delayed Signal Cancelation Filters Based Three-Phase Enhanced-PLL. IEEE Trans. Ind. Appl. 2018, 54, 5293–5305. [Google Scholar] [CrossRef]
- Mathworks. Signal Processing Toolbox Documentation. 2019. Available online: https://www.mathworks.com/help/signal/index.html (accessed on 11 October 2019).
- Ansari, R. Elliptic filter design for a class of generalized halfband filters. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 1146–1150. [Google Scholar] [CrossRef]
- Guo, X.Q.; Wu, W.Y.; Gu, H.R. Phase locked loop and synchronization methods for grid-interfaced converters: A review. Prz. Elektrotechniczny 2011, 87, 182–187. [Google Scholar]
- Pavljaevic, S.; Dawson, F. Synchronization to Disturbed Utility-Network Signals Using a Multirate Phase-Locked Loop. IEEE Trans. Ind. Electron. 2006, 53, 1410–1417. [Google Scholar] [CrossRef]
- Mathworks. DSP System Toolbox Documentation. 2019. Available online: https://www.mathworks.com/help/dsp/ (accessed on 28 January 2020).
- Ali, Z.; Christofides, N.; Saleem, K.; Polycarpou, A.; Mehran, K. Performance evaluation and benchmarking of PLL algorithms for grid-connected RES applications. IET Renew. Power Gener. 2020, 14, 52–62. [Google Scholar] [CrossRef]
- Zarei, M.; Karimadini, M. PLL with frequency and initial-phase-angle detectors: Performance analysis and speed/robustness trade-off improvement. IET Power Electron. 2019, 12, 2761–2770. [Google Scholar] [CrossRef]
- Vukadinović, D.; Nguyen, T.D.; Nguyen, C.H.; Vu, N.L.; Bašić, M.; Grgić, I. Hedge-Algebra-Based Phase-Locked Loop for Distorted Utility Conditions. J. Control Sci. Eng. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Xie, M.; Zhu, C.; Shi, B.; Yang, Y. Power Based Phase-Locked Loop Under Adverse Conditions with Moving Average Filter for Single-Phase System. J. Electr. Syst. 2017, 13, 332–347. [Google Scholar]
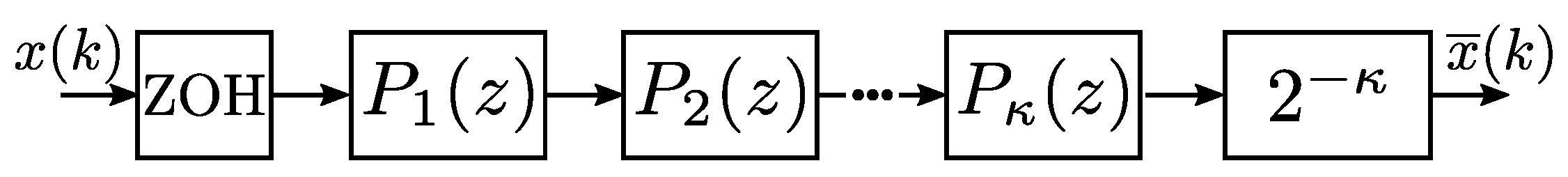
| Ph | () | (Hz) | LOH (seq. - p.u.) | Noise | Sag (p.u.) | |
|---|---|---|---|---|---|---|
| [10] | 1 | THD = 8% @50, 49, | – | – | ||
| [4] | 3 | +3 | , , , , | – | (3) @ | |
| [5] | 1 | – | +5 | 0.05, 0.05, | 0.01 | – |
| [6] | 3 | +5 | , , , | 0.01 | (1) (2) (3) | |
| [15] | 3 | +3 | , , , @47, | – | (1) @ @ | |
| [8] | 3 | +5 | , , | 0.05 | – |
| MAF-Delay | MAF-Deriv | MAF-Park | HB-Delay | HB-Deriv | HB-Park | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | ||
| 3.06E+00 | 9.65E-02 | 2.35E-13 | 9.59E-27 | 2.99E+00 | 9.29E-02 | 2.62E-13 | 1.07E-26 | 2.87E+00 | 9.88E-02 | 2.80E-13 | 1.57E-26 | 3.07E+00 | 1.14E-01 | 5.30E-04 | 2.28E-08 | 3.35E+00 | 1.19E-01 | 7.67E-04 | 3.59E-08 | 2.95E+00 | 1.19E-01 | 1.78E-03 | 3.18E-07 | ||
| 9.16E+00 | 1.05E-01 | 6.20E-12 | 1.49E-24 | 8.19E+00 | 1.08E-01 | 6.55E-12 | 1.48E-24 | 1.13E+01 | 9.98E-02 | 6.11E-12 | 1.61E-24 | 1.07E+01 | 1.03E-01 | 4.97E-04 | 7.69E-09 | 9.63E+00 | 1.13E-01 | 7.71E-04 | 1.43E-08 | 1.42E+01 | 1.49E-01 | 1.76E-03 | 1.19E-07 | ||
| −1.05E+01 | 1.31E-01 | 2.17E-13 | 1.17E-26 | −9.48E+00 | 1.38E-01 | 2.62E-13 | 1.30E-26 | −1.11E+01 | 1.34E-01 | 2.80E-13 | 1.05E-26 | −1.00E+01 | 1.85E-01 | 1.06E-03 | 6.94E-08 | −9.82E+00 | 1.52E-01 | 6.92E-04 | 3.57E-08 | −1.02E+01 | 2.06E-01 | 1.74E-03 | 3.20E-07 | ||
| −2.67E+01 | 1.22E-01 | 6.56E-12 | 1.55E-24 | −2.14E+01 | 1.31E-01 | 6.56E-12 | 1.55E-24 | −2.93E+01 | 1.71E-01 | 6.41E-12 | 1.61E-24 | −4.30E+01 | 1.82E-01 | 1.04E-03 | 2.28E-08 | −3.42E+01 | 1.86E-01 | 7.46E-04 | 1.51E-08 | −4.44E+01 | 1.97E-01 | 1.72E-03 | 1.19E-07 | ||
| 1.04E+00 | 9.73E-02 | 3.06E-03 | 1.17E-06 | 8.77E-01 | 9.77E-02 | 7.98E-03 | 7.97E-06 | 1.12E+00 | 9.35E-02 | 3.19E-02 | 1.27E-04 | 2.05E+00 | 9.77E-02 | 7.58E-04 | 6.54E-08 | 1.57E+00 | 1.09E-01 | 1.33E-03 | 1.84E-07 | 1.83E+00 | 1.52E-01 | 4.68E-03 | 2.47E-06 | ||
| Hz | −1.55E+01 | 8.61E-02 | 1.86E-03 | 4.34E-07 | −1.35E+01 | 9.54E-02 | 4.87E-03 | 2.96E-06 | −1.47E+01 | 8.71E-02 | 1.94E-02 | 4.73E-05 | −2.65E+01 | 1.29E-01 | 7.05E-04 | 2.10E-08 | −2.30E+01 | 9.66E-02 | 1.25E-03 | 7.56E-08 | −2.40E+01 | 1.46E-01 | 4.96E-03 | 1.02E-06 | |
| −1.81E+00 | 1.03E-01 | 1.20E-02 | 1.80E-05 | −1.40E+00 | 1.10E-01 | 1.32E-02 | 2.17E-05 | −2.06E+00 | 9.84E-02 | 4.50E-02 | 2.53E-04 | −3.04E+00 | 1.36E-01 | 1.06E-03 | 1.22E-07 | −2.26E+00 | 1.19E-01 | 7.46E-04 | 5.53E-08 | −3.20E+00 | 1.63E-01 | 2.33E-03 | 6.04E-07 | ||
| Hz | 3.16E+01 | 9.46E-02 | 6.24E-03 | 4.87E-06 | 2.91E+01 | 1.01E-01 | 6.87E-03 | 5.90E-06 | 3.58E+01 | 1.34E-01 | 2.34E-02 | 6.87E-05 | 4.23E+01 | 1.51E-01 | 1.05E-03 | 5.08E-08 | 3.94E+01 | 1.59E-01 | 7.30E-04 | 2.28E-08 | 4.88E+01 | 1.55E-01 | 2.26E-03 | 2.54E-07 | |
| −1.01E+00 | 1.50E+00 | 1.24E+00 | 6.50E-02 | −2.28E+00 | 1.50E+00 | 3.16E+00 | 1.97E-01 | −1.02E+00 | 1.50E+00 | 1.26E+00 | 8.67E-02 | −1.19E+00 | 1.50E+00 | 1.66E+00 | 1.26E-01 | −1.56E+00 | 1.49E+00 | 2.21E+00 | 2.71E-01 | −1.20E+00 | 1.50E+00 | 1.84E+00 | 1.61E-01 | ||
| 5.70E+00 | 1.50E+00 | 4.34E+00 | 1.19E+00 | 5.67E+00 | 1.50E+00 | 4.82E+00 | 1.30E+00 | 7.40E+00 | 1.50E+00 | 4.72E+00 | 1.48E+00 | −4.91E+00 | 1.50E+00 | 6.84E+00 | 3.31E+00 | −3.30E+00 | 1.50E+00 | 7.02E+00 | 3.28E+00 | −1.45E+00 | 1.50E+00 | 7.71E+00 | 4.14E+00 | ||
| −3.99E-01 | 1.47E+00 | 5.26E-01 | 1.21E-02 | −1.02E+00 | 1.50E+00 | 1.41E+00 | 3.95E-02 | −4.57E-01 | 1.47E+00 | 5.66E-01 | 1.74E-02 | −5.40E-01 | 1.46E+00 | 7.39E-01 | 2.50E-02 | −6.99E-01 | 1.48E+00 | 9.75E-01 | 5.40E-02 | −5.36E-01 | 1.46E+00 | 8.30E-01 | 3.22E-02 | ||
| 3.48E+00 | 1.20E+00 | 1.86E+00 | 2.31E-01 | 4.05E+00 | 1.46E+00 | 2.14E+00 | 2.60E-01 | 5.41E+00 | 1.46E+00 | 2.11E+00 | 2.93E-01 | −2.34E+00 | 1.49E+00 | 3.04E+00 | 6.53E-01 | −1.05E+00 | 1.49E+00 | 3.09E+00 | 6.41E-01 | 8.38E-01 | 1.50E+00 | 3.42E+00 | 8.27E-01 | ||
| p.u. | 1.05E+00 | 1.41E-02 | 1.22E-03 | 1.87E-07 | −6.01E-03 | 0.00E+00 | 3.19E-03 | 1.27E-06 | 2.11E+00 | 9.69E-02 | 1.28E-02 | 2.03E-05 | 9.79E-01 | 3.24E-02 | 3.36E-04 | 7.28E-09 | −1.72E-02 | 0.00E+00 | 4.55E-04 | 2.44E-08 | 2.17E+00 | 1.14E-01 | 1.90E-03 | 4.04E-07 | |
| @ | 5.68E+00 | 8.39E-02 | 7.53E-04 | 6.94E-08 | 2.45E+00 | 0.00E+00 | 1.95E-03 | 4.73E-07 | 1.14E+01 | 2.06E-01 | 7.83E-03 | 7.57E-06 | 2.99E+00 | 9.60E-02 | 3.25E-04 | 3.71E-09 | 7.35E-01 | 0.00E+00 | 4.89E-04 | 9.92E-09 | 9.38E+00 | 2.48E-01 | 2.15E-03 | 2.53E-07 | |
| p.u. | 9.90E-01 | 1.39E-02 | 9.22E-07 | 4.79E-14 | 7.36E-03 | 0.00E+00 | 6.48E-10 | 2.09E-20 | 1.95E+00 | 9.37E-02 | 3.02E-06 | 8.21E-13 | 9.41E-01 | 3.24E-02 | 2.85E-04 | 5.36E-09 | −1.19E-02 | 0.00E+00 | 1.99E-04 | 4.20E-09 | 2.02E+00 | 8.68E-02 | 7.01E-04 | 5.14E-08 | |
| @ | 5.73E+00 | 8.24E-02 | 6.82E-06 | 6.33E-12 | 2.61E+00 | 0.00E+00 | 6.33E-09 | 5.58E-18 | 1.10E+01 | 2.04E-01 | 5.10E-05 | 3.26E-10 | 2.56E+00 | 9.51E-02 | 2.96E-04 | 2.99E-09 | 7.75E-01 | 0.00E+00 | 1.87E-04 | 1.43E-09 | 8.96E+00 | 2.46E-01 | 1.29E-03 | 7.99E-08 | |
| p.u. | 9.20E-01 | 1.35E-02 | 4.79E-03 | 2.87E-06 | 8.64E-03 | 0.00E+00 | 5.27E-03 | 3.47E-06 | 1.71E+00 | 8.64E-02 | 1.80E-02 | 4.04E-05 | 8.82E-01 | 3.24E-02 | 5.37E-04 | 2.07E-08 | −1.11E-02 | 0.00E+00 | 2.68E-04 | 8.51E-09 | 1.80E+00 | 8.68E-02 | 9.53E-04 | 9.32E-08 | |
| @ | 5.36E+00 | 8.23E-02 | 2.50E-03 | 7.77E-07 | 2.87E+00 | 0.00E+00 | 2.74E-03 | 9.41E-07 | 1.06E+01 | 2.01E-01 | 9.41E-03 | 1.10E-05 | 1.88E+00 | 9.65E-02 | 5.62E-04 | 9.98E-09 | 8.50E-01 | 0.00E+00 | 2.68E-04 | 3.54E-09 | 8.68E+00 | 2.44E-01 | 1.50E-03 | 9.24E-08 | |
| THD ≈ 8% | THD ≈ 16% | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HB-Delay | HB-Deriv | HB-Park | HB-Delay | HB-Deriv | HB-Park | ||||||||||||||||||||
| OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | ||
| @47 | −1.56E-01 | 0.00E+00 | 1.47E-03 | 1.63E-07 | −2.52E-01 | 1.61E-02 | 1.34E-02 | 1.21E-05 | −1.30E-01 | 0.00E+00 | 6.31E-03 | 4.37E-06 | −3.86E-01 | 1.61E-02 | 2.83E-03 | 6.05E-07 | −6.79E-01 | 1.30E-01 | 2.78E-02 | 9.62E-05 | −3.33E-01 | 1.61E-02 | 1.02E-02 | 1.15E-05 | |
| Hz | −9.49E-01 | 0.00E+00 | 1.16E-02 | 1.52E-05 | 1.51E-01 | 0.00E+00 | 4.27E-02 | 1.23E-04 | 2.05E+00 | 0.00E+00 | 8.10E-03 | 3.17E-06 | −1.67E+00 | 2.67E-02 | 2.81E-02 | 9.58E-05 | −7.75E-01 | 3.33E-02 | 7.74E-02 | 4.14E-04 | 1.37E+00 | 3.48E-02 | 1.30E-02 | 9.87E-06 | |
| @50 | −1.52E-01 | 0.00E+00 | 3.81E-03 | 1.41E-06 | −2.32E-01 | 0.00E+00 | 1.17E-02 | 9.25E-06 | −1.17E-01 | 0.00E+00 | 2.39E-03 | 6.15E-07 | −3.73E-01 | 1.61E-02 | 9.15E-03 | 8.78E-06 | −6.14E-01 | 7.05E-02 | 2.22E-02 | 3.60E-05 | −3.09E-01 | 1.61E-02 | 3.95E-03 | 1.77E-06 | |
| Hz | −1.14E+00 | 0.00E+00 | 1.24E-02 | 1.73E-05 | 2.34E-01 | 0.00E+00 | 3.15E-02 | 9.93E-05 | 2.24E+00 | 0.00E+00 | 3.59E-03 | 6.94E-07 | −1.81E+00 | 2.51E-02 | 3.06E-02 | 1.09E-04 | −6.13E-01 | 2.06E-02 | 5.67E-02 | 3.13E-04 | 1.61E+00 | 3.35E-02 | 7.89E-03 | 4.00E-06 | |
| @55 | −1.41E-01 | 0.00E+00 | 2.68E-03 | 5.76E-07 | −1.97E-01 | 0.00E+00 | 1.22E-02 | 1.00E-05 | −1.11E-01 | 0.00E+00 | 3.05E-03 | 9.77E-07 | −3.47E-01 | 1.61E-02 | 2.54E-03 | 4.29E-07 | −5.13E-01 | 4.87E-02 | 1.65E-02 | 2.81E-05 | −2.84E-01 | 1.61E-02 | 4.82E-03 | 2.52E-06 | |
| Hz | −1.71E+00 | 0.00E+00 | 2.67E-03 | 2.87E-07 | 3.73E-01 | 0.00E+00 | 1.34E-02 | 1.11E-05 | 2.55E+00 | 0.00E+00 | 3.04E-03 | 4.14E-07 | −2.32E+00 | 2.26E-02 | 2.85E-03 | 5.58E-07 | −3.56E-01 | 1.95E-02 | 2.16E-02 | 2.63E-05 | 1.98E+00 | 0.00E+00 | 4.87E-03 | 1.06E-06 | |
| 2.08E+00 | 9.77E-02 | 1.46E-03 | 1.60E-07 | 1.80E+00 | 1.09E-01 | 1.34E-02 | 1.22E-05 | 1.85E+00 | 1.41E-01 | 6.30E-03 | 4.35E-06 | 2.15E+00 | 9.77E-02 | 2.82E-03 | 5.99E-07 | 2.31E+00 | 1.03E-01 | 2.77E-02 | 9.55E-05 | 1.86E+00 | 1.41E-01 | 1.02E-02 | 1.15E-05 | ||
| Hz | −2.69E+01 | 1.29E-01 | 1.16E-02 | 1.52E-05 | −2.35E+01 | 9.63E-02 | 4.28E-02 | 1.23E-04 | −2.44E+01 | 1.46E-01 | 8.09E-03 | 3.17E-06 | −2.75E+01 | 1.29E-01 | 2.81E-02 | 9.58E-05 | −2.43E+01 | 9.49E-02 | 7.73E-02 | 4.13E-04 | −2.51E+01 | 1.46E-01 | 1.30E-02 | 9.91E-06 | |
| −3.02E+00 | 1.36E-01 | 2.68E-03 | 5.75E-07 | −2.21E+00 | 1.19E-01 | 1.23E-02 | 1.00E-05 | −3.18E+00 | 1.63E-01 | 3.05E-03 | 9.77E-07 | −2.99E+00 | 1.36E-01 | 2.48E-03 | 4.27E-07 | −2.27E+00 | 1.19E-01 | 1.65E-02 | 2.81E-05 | −3.15E+00 | 1.63E-01 | 4.83E-03 | 2.52E-06 | ||
| Hz | 4.20E+01 | 1.50E-01 | 2.66E-03 | 2.86E-07 | 3.91E+01 | 1.59E-01 | 1.34E-02 | 1.11E-05 | 4.85E+01 | 1.55E-01 | 3.04E-03 | 4.14E-07 | 4.16E+01 | 1.50E-01 | 2.82E-03 | 5.57E-07 | 3.86E+01 | 1.59E-01 | 2.16E-02 | 2.63E-05 | 4.80E+01 | 1.55E-01 | 4.88E-03 | 1.06E-06 | |
| MAF-Delay | MAF-Deriv | MAF-Park | HB-Delay | HB-Deriv | HB-Park | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | ||
| 3.14E+00 | 9.94E-02 | 4.06E-04 | 2.06E-08 | 3.00E+00 | 9.29E-02 | 4.62E-04 | 2.66E-08 | 2.80E+00 | 1.00E-01 | 1.66E-03 | 3.46E-07 | 3.07E+00 | 1.14E-01 | 5.30E-04 | 2.28E-08 | 3.35E+00 | 1.19E-01 | 7.67E-04 | 3.59E-08 | 2.95E+00 | 1.19E-01 | 1.78E-03 | 3.18E-07 | ||
| 9.57E+00 | 1.03E-01 | 2.33E-04 | 6.78E-09 | 8.52E+00 | 1.08E-01 | 2.65E-04 | 8.76E-09 | 1.22E+01 | 1.02E-01 | 9.54E-04 | 1.14E-07 | 1.07E+01 | 1.03E-01 | 4.97E-04 | 7.69E-09 | 9.63E+00 | 1.13E-01 | 7.71E-04 | 1.43E-08 | 1.42E+01 | 1.49E-01 | 1.76E-03 | 1.19E-07 | ||
| −1.05E+01 | 1.37E-01 | 4.06E-04 | 2.07E-08 | −9.49E+00 | 1.38E-01 | 4.62E-04 | 2.67E-08 | −1.09E+01 | 1.37E-01 | 1.66E-03 | 3.46E-07 | −1.00E+01 | 1.85E-01 | 1.06E-03 | 6.94E-08 | −9.82E+00 | 1.52E-01 | 6.92E-04 | 3.57E-08 | −1.02E+01 | 2.06E-01 | 1.74E-03 | 3.20E-07 | ||
| −2.66E+01 | 1.73E-01 | 2.33E-04 | 6.78E-09 | −2.11E+01 | 1.31E-01 | 2.65E-04 | 8.75E-09 | −2.78E+01 | 1.76E-01 | 9.54E-04 | 1.14E-07 | −4.30E+01 | 1.82E-01 | 1.04E-03 | 2.28E-08 | −3.42E+01 | 1.86E-01 | 7.46E-04 | 1.51E-08 | −4.44E+01 | 1.97E-01 | 1.72E-03 | 1.19E-07 | ||
| 1.10E+00 | 9.68E-02 | 8.36E-03 | 8.74E-06 | 8.82E-01 | 9.77E-02 | 1.31E-02 | 2.15E-05 | 1.12E+00 | 9.82E-02 | 5.01E-02 | 3.14E-04 | 2.05E+00 | 9.77E-02 | 7.58E-04 | 6.54E-08 | 1.57E+00 | 1.09E-01 | 1.33E-03 | 1.84E-07 | 1.83E+00 | 1.52E-01 | 4.68E-03 | 2.47E-06 | ||
| Hz | −1.57E+01 | 1.13E-01 | 5.10E-03 | 3.25E-06 | −1.33E+01 | 9.53E-02 | 7.99E-03 | 7.96E-06 | −1.39E+01 | 8.83E-02 | 3.06E-02 | 1.17E-04 | −2.65E+01 | 1.29E-01 | 7.05E-04 | 2.10E-08 | −2.30E+01 | 9.66E-02 | 1.25E-03 | 7.56E-08 | −2.40E+01 | 1.46E-01 | 4.96E-03 | 1.02E-06 | |
| −1.75E+00 | 9.77E-02 | 1.08E-02 | 1.46E-05 | −1.41E+00 | 1.10E-01 | 2.28E-02 | 6.51E-05 | −2.05E+00 | 1.03E-01 | 7.46E-02 | 6.96E-04 | −3.04E+00 | 1.36E-01 | 1.06E-03 | 1.22E-07 | −2.26E+00 | 1.19E-01 | 7.46E-04 | 5.53E-08 | −3.20E+00 | 1.63E-01 | 2.33E-03 | 6.04E-07 | ||
| Hz | 3.13E+01 | 1.18E-01 | 5.62E-03 | 3.95E-06 | 2.95E+01 | 1.00E-01 | 1.19E-02 | 1.77E-05 | 3.72E+01 | 1.40E-01 | 3.89E-02 | 1.89E-04 | 4.23E+01 | 1.51E-01 | 1.05E-03 | 5.08E-08 | 3.94E+01 | 1.59E-01 | 7.30E-04 | 2.28E-08 | 4.88E+01 | 1.55E-01 | 2.26E-03 | 2.54E-07 | |
| −1.39E+00 | 1.49E+00 | 1.97E+00 | 1.85E-01 | −2.25E+00 | 1.50E+00 | 4.04E+00 | 3.24E-01 | −1.33E+00 | 1.49E+00 | 1.77E+00 | 1.47E-01 | −1.19E+00 | 1.50E+00 | 1.66E+00 | 1.26E-01 | −1.56E+00 | 1.49E+00 | 2.21E+00 | 2.71E-01 | −1.20E+00 | 1.50E+00 | 1.84E+00 | 1.61E-01 | ||
| −2.11E+00 | 1.50E+00 | 7.88E+00 | 4.65E+00 | −1.31E+00 | 1.50E+00 | 6.84E+00 | 2.81E+00 | 1.10E+00 | 1.50E+00 | 6.65E+00 | 3.55E+00 | −4.91E+00 | 1.50E+00 | 6.84E+00 | 3.31E+00 | −3.30E+00 | 1.50E+00 | 7.02E+00 | 3.28E+00 | −1.45E+00 | 1.50E+00 | 7.71E+00 | 4.14E+00 | ||
| −6.08E-01 | 1.49E+00 | 1.10E+00 | 6.16E-02 | −1.01E+00 | 1.50E+00 | 1.78E+00 | 6.39E-02 | −5.96E-01 | 1.45E+00 | 7.92E-01 | 2.92E-02 | −5.40E-01 | 1.46E+00 | 7.39E-01 | 2.50E-02 | −6.99E-01 | 1.48E+00 | 9.75E-01 | 5.40E-02 | −5.36E-01 | 1.46E+00 | 8.30E-01 | 3.22E-02 | ||
| −2.12E-01 | 1.47E+00 | 4.57E+00 | 1.41E+00 | 1.16E+00 | 1.48E+00 | 2.98E+00 | 5.36E-01 | 3.14E+00 | 1.49E+00 | 2.92E+00 | 6.96E-01 | −2.34E+00 | 1.49E+00 | 3.04E+00 | 6.53E-01 | −1.05E+00 | 1.49E+00 | 3.09E+00 | 6.41E-01 | 8.38E-01 | 1.50E+00 | 3.42E+00 | 8.27E-01 | ||
| 1.11E+00 | 1.43E-02 | 3.34E-03 | 1.40E-06 | −1.08E-02 | 0.00E+00 | 5.24E-03 | 3.43E-06 | 2.09E+00 | 9.65E-02 | 2.01E-02 | 5.03E-05 | 9.79E-01 | 3.24E-02 | 3.36E-04 | 7.28E-09 | −1.72E-02 | 0.00E+00 | 4.55E-04 | 2.44E-08 | 2.17E+00 | 1.14E-01 | 1.90E-03 | 4.04E-07 | ||
| @ | 5.63E+00 | 8.54E-02 | 2.05E-03 | 5.19E-07 | 2.75E+00 | 0.00E+00 | 3.19E-03 | 1.27E-06 | 1.23E+01 | 2.09E-01 | 1.23E-02 | 1.87E-05 | 2.99E+00 | 9.60E-02 | 3.25E-04 | 3.71E-09 | 7.35E-01 | 0.00E+00 | 4.89E-04 | 9.92E-09 | 9.38E+00 | 2.48E-01 | 2.15E-03 | 2.53E-07 | |
| 1.06E+00 | 1.41E-02 | 1.64E-04 | 3.30E-09 | 1.18E-02 | 0.00E+00 | 1.85E-04 | 4.27E-09 | 1.93E+00 | 9.32E-02 | 6.70E-04 | 5.53E-08 | 9.41E-01 | 3.24E-02 | 2.85E-04 | 5.36E-09 | −1.19E-02 | 0.00E+00 | 1.99E-04 | 4.20E-09 | 2.02E+00 | 8.68E-02 | 7.01E-04 | 5.14E-08 | ||
| @ | 5.54E+00 | 8.64E-02 | 1.01E-04 | 1.09E-09 | 2.93E+00 | 0.00E+00 | 1.06E-04 | 1.40E-09 | 1.20E+01 | 2.07E-01 | 4.39E-04 | 1.86E-08 | 2.56E+00 | 9.51E-02 | 2.96E-04 | 2.99E-09 | 7.75E-01 | 0.00E+00 | 1.87E-04 | 1.43E-09 | 8.96E+00 | 2.46E-01 | 1.29E-03 | 7.99E-08 | |
| 8.28E-01 | 1.31E-02 | 4.31E-03 | 2.32E-06 | 1.40E-02 | 0.00E+00 | 9.12E-03 | 1.04E-05 | 1.69E+00 | 8.64E-02 | 2.98E-02 | 1.11E-04 | 8.82E-01 | 3.24E-02 | 5.37E-04 | 2.07E-08 | −1.11E-02 | 0.00E+00 | 2.68E-04 | 8.51E-09 | 1.80E+00 | 8.68E-02 | 9.53E-04 | 9.32E-08 | ||
| @ | 5.75E+00 | 7.78E-02 | 2.25E-03 | 6.30E-07 | 3.22E+00 | 0.00E+00 | 4.75E-03 | 2.82E-06 | 1.16E+01 | 2.04E-01 | 1.56E-02 | 3.02E-05 | 1.88E+00 | 9.65E-02 | 5.62E-04 | 9.98E-09 | 8.50E-01 | 0.00E+00 | 2.68E-04 | 3.54E-09 | 8.68E+00 | 2.44E-01 | 1.50E-03 | 9.24E-08 | |
| THD % | THD % | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HB-Delay | HB-Deriv | HB-Park | HB-Delay | HB-Deriv | HB-Park | ||||||||||||||||||||
| OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | OS | ST | PK | EN | ||
| @47 | −1.56E-01 | 0.00E+00 | 1.47E-03 | 1.63E-07 | −2.52E-01 | 1.61E-02 | 1.34E-02 | 1.21E-05 | −1.30E-01 | 0.00E+00 | 6.31E-03 | 4.37E-06 | −3.86E-01 | 1.61E-02 | 2.83E-03 | 6.05E-07 | −6.79E-01 | 1.30E-01 | 2.78E-02 | 9.62E-05 | −3.33E-01 | 1.61E-02 | 1.02E-02 | 1.15E-05 | |
| Hz | −9.49E-01 | 0.00E+00 | 1.16E-02 | 1.52E-05 | 1.51E-01 | 0.00E+00 | 4.27E-02 | 1.23E-04 | 2.05E+00 | 0.00E+00 | 8.10E-03 | 3.17E-06 | −1.67E+00 | 2.67E-02 | 2.81E-02 | 9.58E-05 | −7.75E-01 | 3.33E-02 | 7.74E-02 | 4.14E-04 | 1.37E+00 | 3.48E-02 | 1.30E-02 | 9.87E-06 | |
| @50 | −1.52E-01 | 0.00E+00 | 3.81E-03 | 1.41E-06 | −2.32E-01 | 0.00E+00 | 1.17E-02 | 9.25E-06 | −1.17E-01 | 0.00E+00 | 2.39E-03 | 6.15E-07 | −3.73E-01 | 1.61E-02 | 9.15E-03 | 8.78E-06 | −6.14E-01 | 7.05E-02 | 2.22E-02 | 3.60E-05 | −3.09E-01 | 1.61E-02 | 3.95E-03 | 1.77E-06 | |
| Hz | −1.14E+00 | 0.00E+00 | 1.24E-02 | 1.73E-05 | 2.34E-01 | 0.00E+00 | 3.15E-02 | 9.93E-05 | 2.24E+00 | 0.00E+00 | 3.59E-03 | 6.94E-07 | −1.81E+00 | 2.51E-02 | 3.06E-02 | 1.09E-04 | −6.13E-01 | 2.06E-02 | 5.67E-02 | 3.13E-04 | 1.61E+00 | 3.35E-02 | 7.89E-03 | 4.00E-06 | |
| @55 | −1.41E-01 | 0.00E+00 | 2.68E-03 | 5.76E-07 | −1.97E-01 | 0.00E+00 | 1.22E-02 | 1.00E-05 | −1.11E-01 | 0.00E+00 | 3.05E-03 | 9.77E-07 | −3.47E-01 | 1.61E-02 | 2.54E-03 | 4.29E-07 | −5.13E-01 | 4.87E-02 | 1.65E-02 | 2.81E-05 | −2.84E-01 | 1.61E-02 | 4.82E-03 | 2.52E-06 | |
| Hz | −1.71E+00 | 0.00E+00 | 2.67E-03 | 2.87E-07 | 3.73E-01 | 0.00E+00 | 1.34E-02 | 1.11E-05 | 2.55E+00 | 0.00E+00 | 3.04E-03 | 4.14E-07 | −2.32E+00 | 2.26E-02 | 2.85E-03 | 5.58E-07 | −3.56E-01 | 1.95E-02 | 2.16E-02 | 2.63E-05 | 1.98E+00 | 0.00E+00 | 4.87E-03 | 1.06E-06 | |
| 2.08E+00 | 9.77E-02 | 1.46E-03 | 1.60E-07 | 1.80E+00 | 1.09E-01 | 1.34E-02 | 1.22E-05 | 1.85E+00 | 1.41E-01 | 6.30E-03 | 4.35E-06 | 2.15E+00 | 9.77E-02 | 2.82E-03 | 5.99E-07 | 2.31E+00 | 1.03E-01 | 2.77E-02 | 9.55E-05 | 1.86E+00 | 1.41E-01 | 1.02E-02 | 1.15E-05 | ||
| Hz | −2.69E+01 | 1.29E-01 | 1.16E-02 | 1.52E-05 | −2.35E+01 | 9.63E-02 | 4.28E-02 | 1.23E-04 | −2.44E+01 | 1.46E-01 | 8.09E-03 | 3.17E-06 | −2.75E+01 | 1.29E-01 | 2.81E-02 | 9.58E-05 | −2.43E+01 | 9.49E-02 | 7.73E-02 | 4.13E-04 | −2.51E+01 | 1.46E-01 | 1.30E-02 | 9.91E-06 | |
| −3.02E+00 | 1.36E-01 | 2.68E-03 | 5.75E-07 | −2.21E+00 | 1.19E-01 | 1.23E-02 | 1.00E-05 | −3.18E+00 | 1.63E-01 | 3.05E-03 | 9.77E-07 | −2.99E+00 | 1.36E-01 | 2.48E-03 | 4.27E-07 | −2.27E+00 | 1.19E-01 | 1.65E-02 | 2.81E-05 | −3.15E+00 | 1.63E-01 | 4.83E-03 | 2.52E-06 | ||
| Hz | 4.20E+01 | 1.50E-01 | 2.66E-03 | 2.86E-07 | 3.91E+01 | 1.59E-01 | 1.34E-02 | 1.11E-05 | 4.85E+01 | 1.55E-01 | 3.04E-03 | 4.14E-07 | 4.16E+01 | 1.50E-01 | 2.82E-03 | 5.57E-07 | 3.86E+01 | 1.59E-01 | 2.16E-02 | 2.63E-05 | 4.80E+01 | 1.55E-01 | 4.88E-03 | 1.06E-06 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibarra, L.; Ponce, P.; Ayyanar, R.; Molina, A. A Non-Adaptive Single-Phase PLL Based on Discrete Half-Band Filtering to Suppress Severe Frequency Disturbances. Energies 2020, 13, 1730. https://doi.org/10.3390/en13071730
Ibarra L, Ponce P, Ayyanar R, Molina A. A Non-Adaptive Single-Phase PLL Based on Discrete Half-Band Filtering to Suppress Severe Frequency Disturbances. Energies. 2020; 13(7):1730. https://doi.org/10.3390/en13071730
Chicago/Turabian StyleIbarra, Luis, Pedro Ponce, Raja Ayyanar, and Arturo Molina. 2020. "A Non-Adaptive Single-Phase PLL Based on Discrete Half-Band Filtering to Suppress Severe Frequency Disturbances" Energies 13, no. 7: 1730. https://doi.org/10.3390/en13071730
APA StyleIbarra, L., Ponce, P., Ayyanar, R., & Molina, A. (2020). A Non-Adaptive Single-Phase PLL Based on Discrete Half-Band Filtering to Suppress Severe Frequency Disturbances. Energies, 13(7), 1730. https://doi.org/10.3390/en13071730








