A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids
Abstract
1. Introduction
- A multi-objective optimization problem is formulated for the grid-connected microgrid to realize the appropriate grid-integration of renewable resources, EV charging stations, and energy storage systems.
- A two-layer optimization framework is developed to obtain optimal site and size of DERs, simultaneously, and coordinate DERs operation with the grid.
- A Fuzzy-based ICM is developed for optimal scheduling of charging and discharging of EVs and ESS.
- A time-of-use based demand response program is implemented to investigate how customers behave in response to changes in electricity prices.
- A comprehensive comparison between our proposed algorithm with other algorithms reported in the literature has been reported in this work.
2. Modeling System Components
2.1. Solar Cell
2.2. Wind Turbine
2.3. Energy Storage System
2.4. Probabilistic Model of Parking Lot Hourly Electricity Demand
3. The Formulation and Solution
3.1. Objective Function
3.1.1. Power Losses
3.1.2. Voltage Fluctuations
3.1.3. Electricity Supply Costs
3.2. Constraints
3.2.1. Demand-Supply Balance
3.2.2. Bus Voltage Limitations
3.2.3. Line Current Constraint
3.2.4. Pricing Constraints
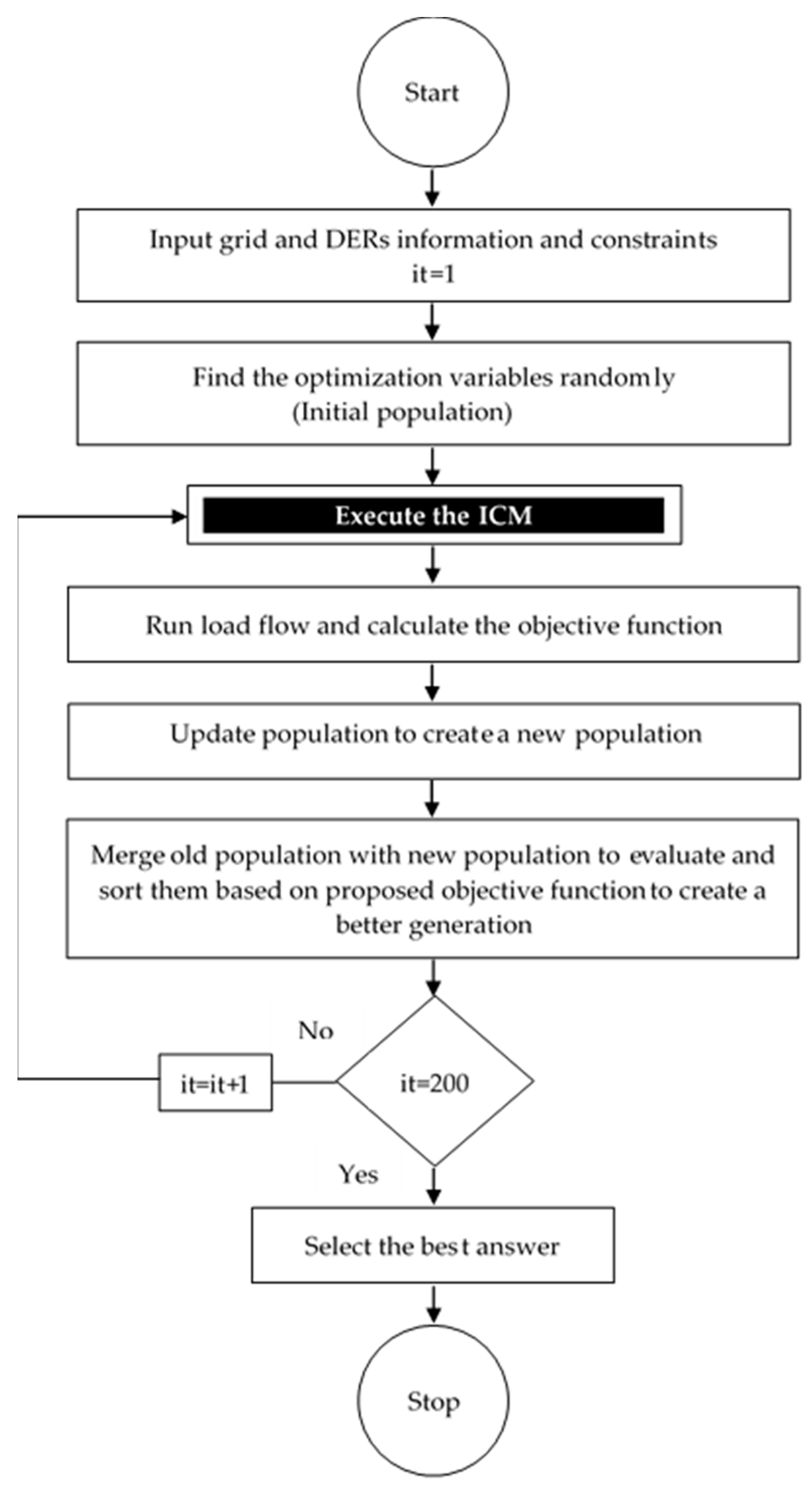
3.3. Methodology
3.3.1. GA
3.3.2. PSO
3.3.3. GA-PSO Optimization Algorithm
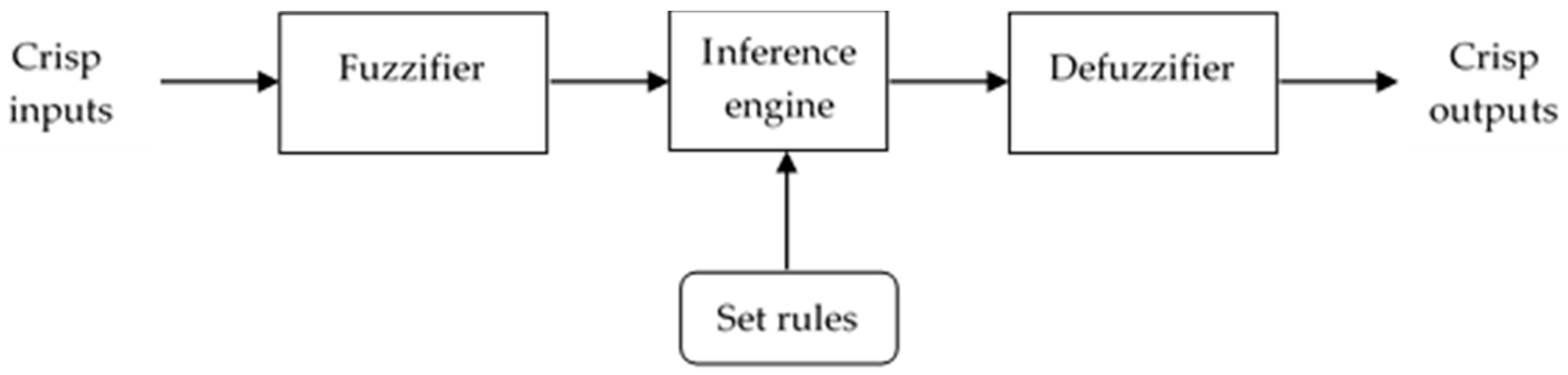
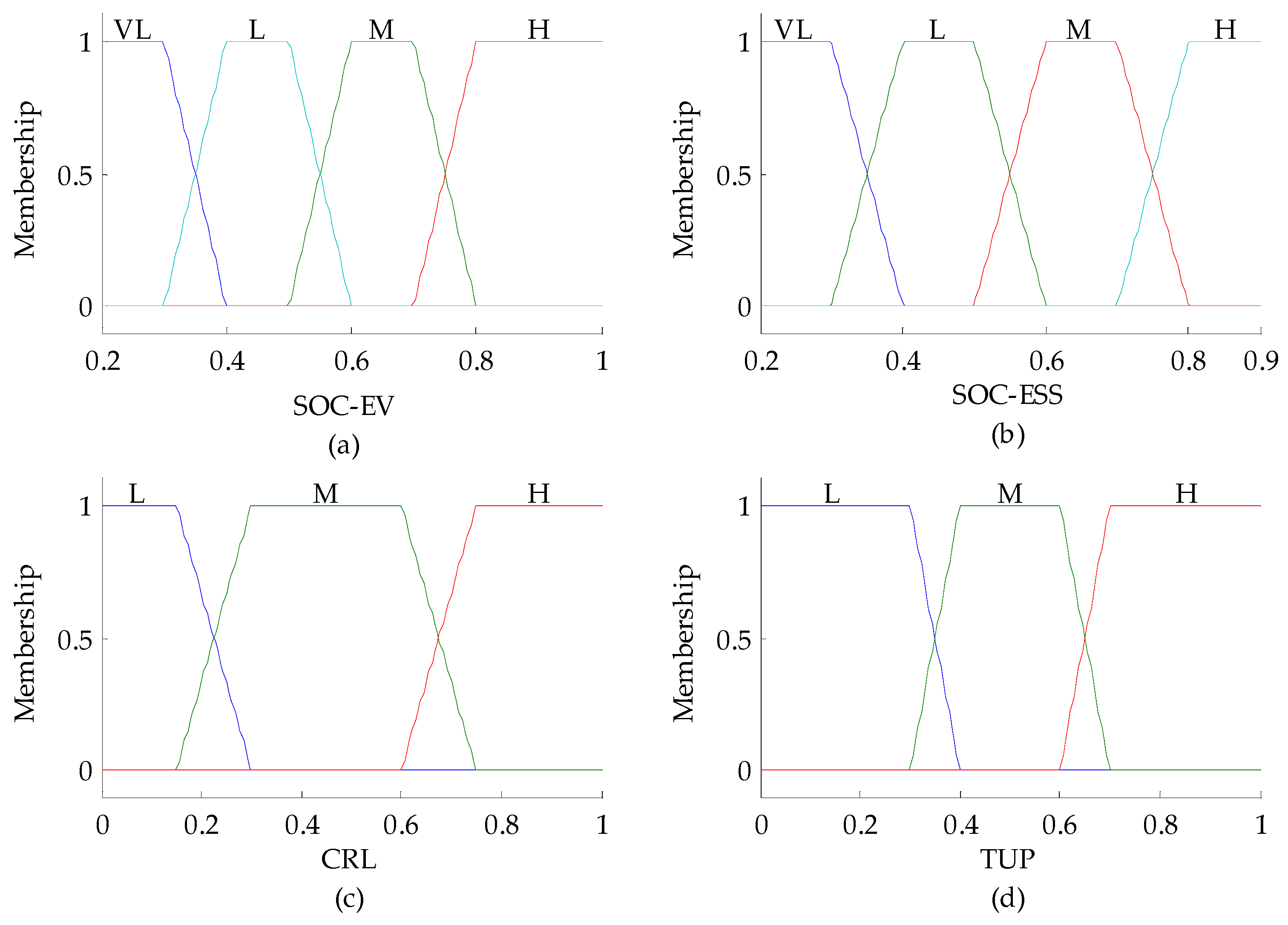
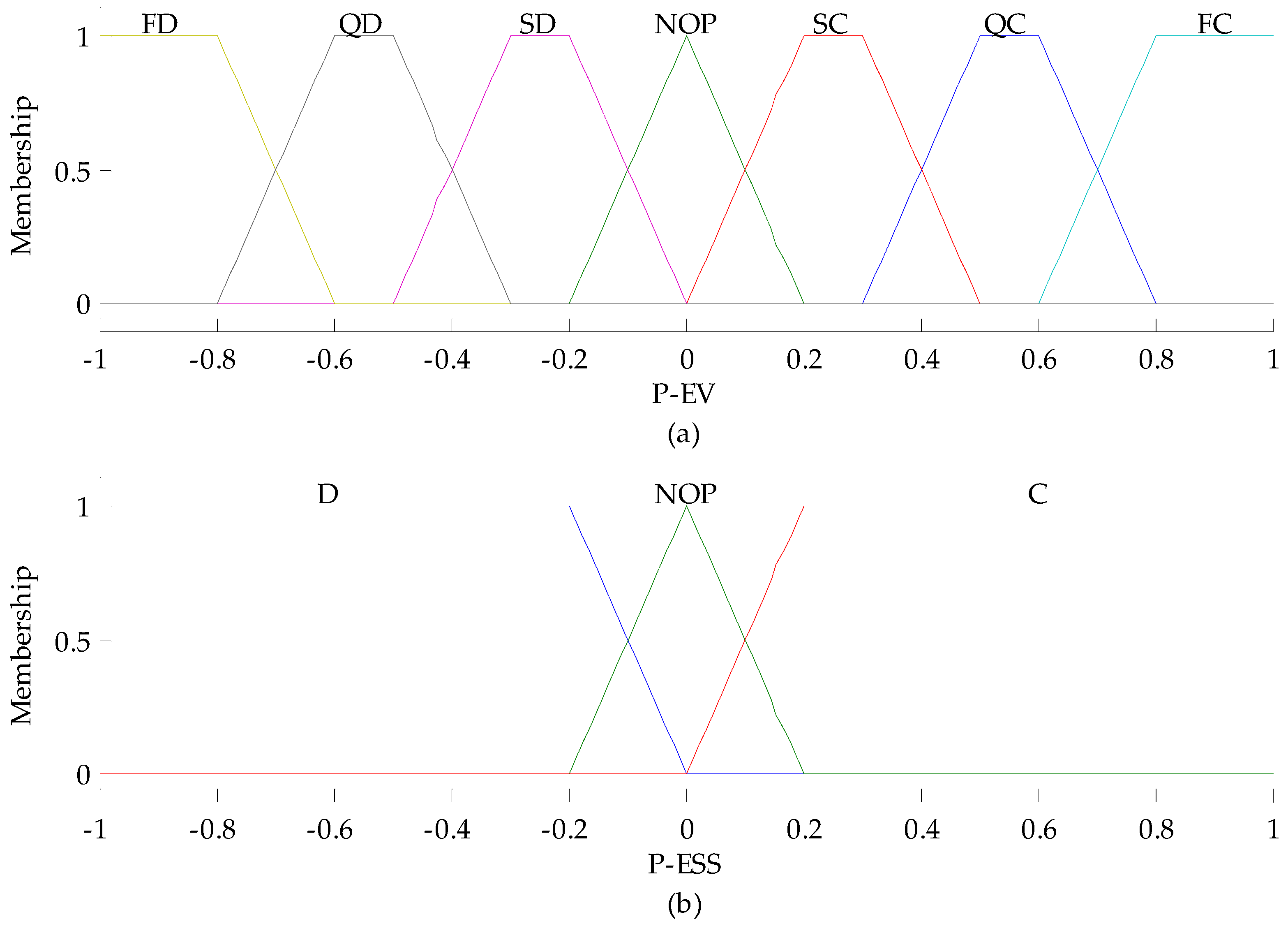
3.3.4. Fuzzy Membership Rule
3.3.5. Demand Response Program
3.3.6. ICM
Set Rules
Fuzzifier
Inference Engine
Defuzzifier
3.3.7. Backward-Forward Sweep Power Flow
- Calculating the apparent power for each bus based on the input parameters;
- Calculating the current of each bus using Equation (48), assuming that the voltage and phase angle at each bus is equal to one and zero, respectively;
- Calculating the line currents based on Equation (49) considering the values obtained for the current of each bus moving from the end nodes to the slack bus:
- Calculating the bus voltages according to Equation (50), taking into account the voltage drop moving from the first bus to the last bus. It has to be mentioned that for 1st bus as it is a slack bus, the voltage magnitude and phase angle are considered to be one and zero, respectively:
- Controlling the convergence criteria (continue if the difference between the newly calculated value for the voltage amount and the previous one is higher than the convergence condition. Otherwise, stop the load flow calculation);
- Calculating the bus currents using new values obtained for the bus voltages;
- Return to the first step of the backward sweep stage.
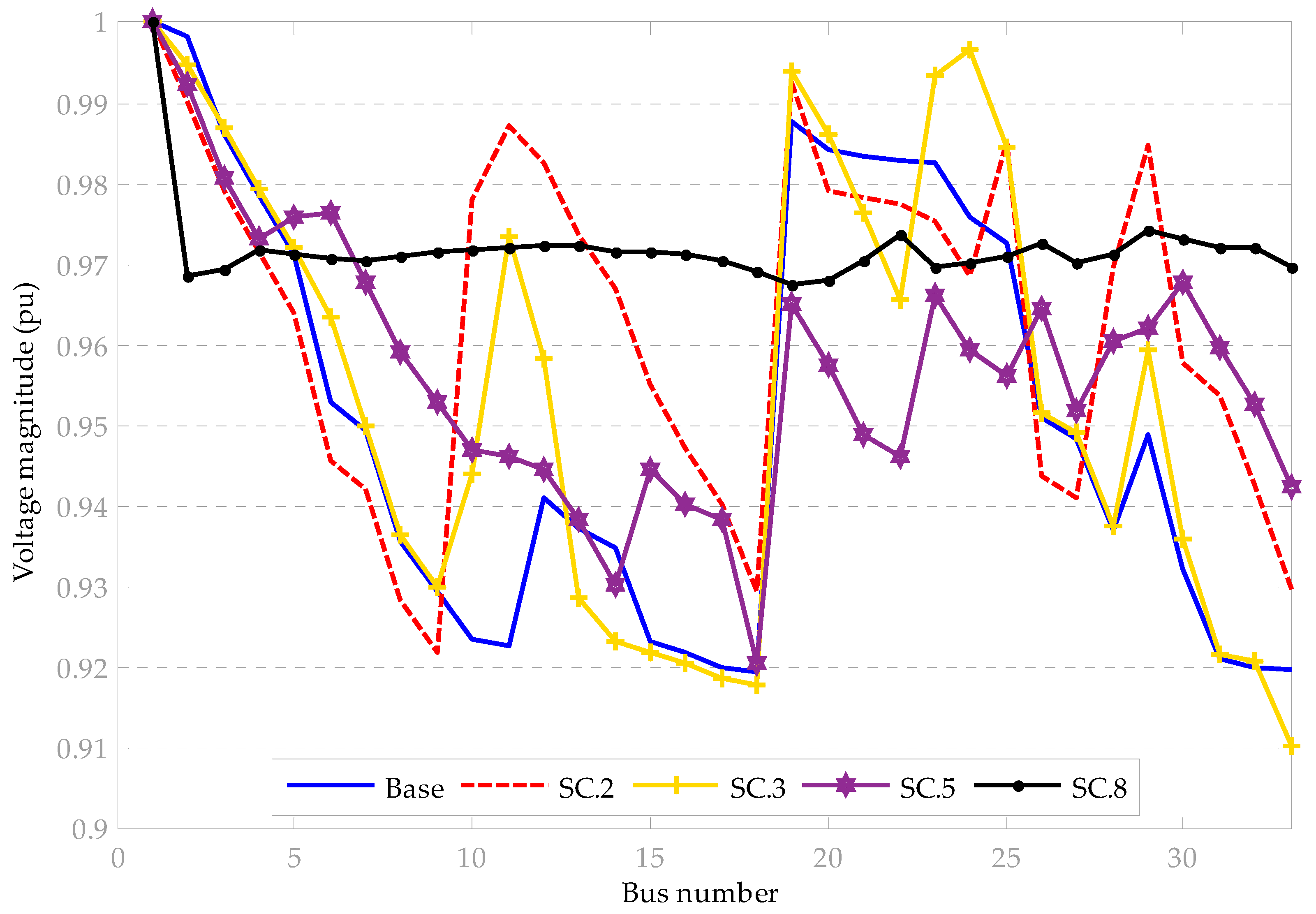
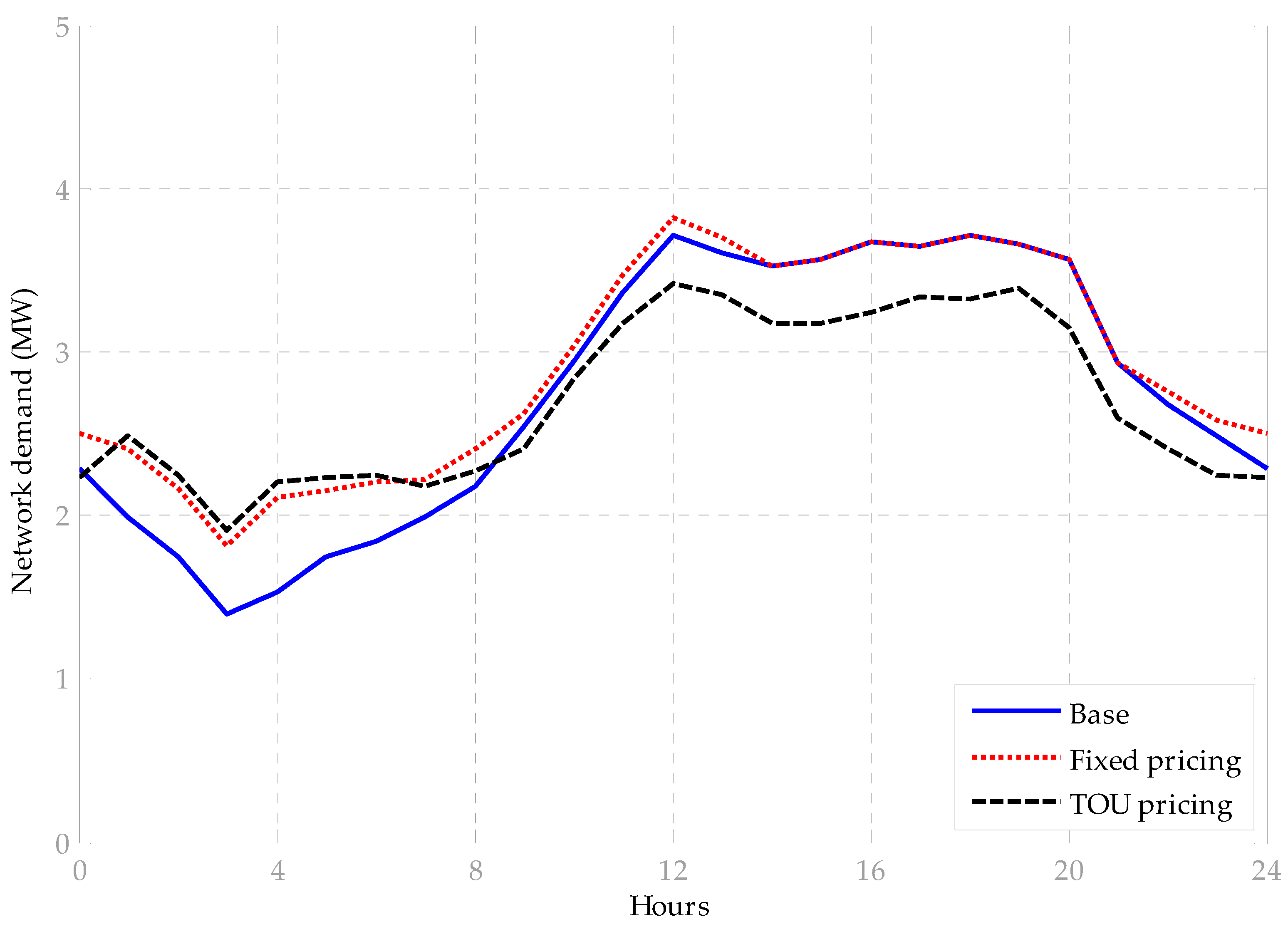
4. Results and Discussion
Sample Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| VL, L, M, H | Very low, low, medium, high |
| FC, QC, SC | Fast, quick, slow charging |
| NOCT | Nominal operating cell temperature (C) |
| TUP | Time-of-use price |
| SOC | State of charge |
| FD, QD, SD | Fast, quick, slow discharging |
| NOP | No operation |
| NOFE | Number of function evaluation |
| CRL | Calculated remaining load |
| DOD | Depth of discharge |
| Aggregated demand in response to price changes (MWh) | |
| Active power generated/demand (MW) | |
| Active power supplied by centralized power plant (MW) | |
| Apparent power flow (MVA) | |
| Arrival/Departure time of EVs to/from parking (h) | |
| Cost of charging/Benefit of discharging ($/MWh) | |
| Duration of the EV availability in the parking (h) | |
| Energy stored in ESS (MWh) | |
| ESS level of charge (%) | |
| EV average demand (MW) | |
| Aggregated demand in response to fixed pricing (MWh) | |
| Max distance traveled by EVs (mile) | |
| Max/Min value of objective function | |
| Distance traveled by EVs (mile) | |
| Time-of-use price of electricity ($/MWh) | |
| Output power of solar cell (MW) | |
| Output power of parking lot (MW) | |
| Output power of wind plant (MW) | |
| Phase angle of voltage at bus -th | |
| Phase angle of the -th element of admittance matrix | |
| Reactive power generated/demand (MVar) | |
| Total EV demand (MW) | |
| System power losses (MW) | |
| Voltage magnitude at bus -th (kV) | |
| Charging/Discharging power of ESS (MW) | |
| Objective function of optimization process | |
| Ambient temperature (C) | |
| Area covered by the wind turbine blades (m2) | |
| AC/DC converter efficiency (%) | |
| , | Beta distribution parameters |
| Charging/discharging power of EVs (MW) | |
| Coefficient of inertia | |
| Base price of electricity ($/MWh) | |
| ESS efficiency (%) | |
| ESS Self-discharge rate (%energy/day) | |
| EV battery capacity (kWh) | |
| EV energy consumption per mile (kWh/mile) | |
| Fuzzy membership value | |
| Global best position of PSO particles | |
| th element of admittance matrix | |
| Z | Impedance of transmission line |
| EV Initial level of charge (kWh) | |
| Kinetic energy of the air | |
| Learning coefficients | |
| Max/Min of bus voltage (kV) | |
| Length of the wind turbine blade (m) | |
| Mass, speed and bulk density of the air | |
| Max apparent power flow (MVA) | |
| Mean and standard deviation of statistical data | |
| Number of charging stations | |
| Number of EVs at each time interval | |
| Number of network buses | |
| Number of objective functions | |
| Number of Pareto front points | |
| Nominal output power of solar cell (MW) | |
| Payment factor | |
| Personal best position of each PSO particle | |
| Position vector of PSO particles | |
| Random variables | |
| Solar cell efficiency (%) | |
| Solar cell temperature (C) | |
| Solar radiation (W/m2) | |
| Velocity vector of PSO particles | |
| , | Weibull distribution parameters |
References
- Hosseini, S.; Sarder, M. Development of a Bayesian network model for optimal site selection of electric vehicle charging station. Int. J. Electr. Power Energy Syst. 2019, 105, 110–122. [Google Scholar] [CrossRef]
- de Melo, H.N.; Trovao, J.P.F.; Pereirinha, P.G.; Jorge, H.M.; Antunes, C.H. A controllable bidirectional battery charger for electric vehicles with vehicle-to-grid capability. IEEE Trans. Veh. Technol. 2017, 67, 114–123. [Google Scholar] [CrossRef]
- Jacob, A.S.; Banerjee, R.; Ghosh, P.C. Sizing of hybrid energy storage system for a PV based microgrid through design space approach. Appl. Energy 2018, 212, 640–653. [Google Scholar] [CrossRef]
- Golshannavaz, S. Cooperation of electric vehicle and energy storage in reactive power compensation: An optimal home energy management system considering PV presence. Sustain. Cities Soc. 2018, 39, 317–325. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Heydarian-Forushani, E.; Golshan, M.; Siano, P.; Moghaddam, M.; Sheikh-El-Eslami, M.; Catalão, J. Optimal trading of plug-in electric vehicle aggregation agents in a market environment for sustainability. Appl. Energy 2016, 162, 601–612. [Google Scholar] [CrossRef]
- Yang, F.; Feng, X.; Li, Z. Advanced microgrid energy management system for future sustainable and resilient power grid. IEEE Trans. Ind. Appl. 2019, 55, 7251–7260. [Google Scholar] [CrossRef]
- Dou, C.; An, X.; Yue, D.; Li, F. Two-level decentralized optimization power dispatch control strategies for an islanded microgrid without communication network. Int. Trans. Electr. Energy Syst. 2017, 27, e2244. [Google Scholar] [CrossRef]
- Faddel, S.; Elsayed, A.T.; Mohammed, O.A. Bilayer multi-objective optimal allocation and sizing of electric vehicle parking garage. IEEE Trans. Ind. Appl. 2018, 54, 1992–2001. [Google Scholar] [CrossRef]
- Marzband, M.; Alavi, H.; Ghazimirsaeid, S.S.; Uppal, H.; Fernando, T. Optimal energy management system based on stochastic approach for a home Microgrid with integrated responsive load demand and energy storage. Sustain. Cities Soc. 2017, 28, 256–264. [Google Scholar] [CrossRef]
- Amini, M.H.; Karabasoglu, O. Optimal operation of interdependent power systems and electrified transportation networks. Energies 2018, 11, 196. [Google Scholar] [CrossRef]
- Gonçalves, J.; Martins, A.; Neves, L. Methodology for real impact assessment of the best location of distributed electric energy storage. Sustain. Cities Soc. 2016, 26, 531–542. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L. Hierarchical energy management of microgrids including storage and demand response. Energies 2018, 11, 1111. [Google Scholar] [CrossRef]
- Maulik, A.; Das, D. Optimal power dispatch considering load and renewable generation uncertainties in an AC–DC hybrid microgrid. IET Gener. Transm. Distrib. 2019, 13, 1164–1176. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and analysis of renewable energy and battery systems in residential microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Amini, M.H.; McNamara, P.; Weng, P.; Karabasoglu, O.; Xu, Y. Hierarchical electric vehicle charging aggregator strategy using Dantzig-Wolfe decomposition. IEEE Des. Test 2017, 35, 25–36. [Google Scholar] [CrossRef]
- Liu, R.-S.; Hsu, Y.-F. A scalable and robust approach to demand side management for smart grids with uncertain renewable power generation and bi-directional energy trading. Int. J. Electr. Power Energy Syst. 2018, 97, 396–407. [Google Scholar] [CrossRef]
- Moradi, H.; Esfahanian, M.; Abtahi, A.; Zilouchian, A. Optimization and energy management of a standalone hybrid microgrid in the presence of battery storage system. Energy 2018, 147, 226–238. [Google Scholar] [CrossRef]
- Asgher, U.; Babar Rasheed, M.; Al-Sumaiti, A.S.; Ur-Rahman, A.; Ali, I.; Alzaidi, A.; Alamri, A. Smart energy optimization using heuristic algorithm in smart grid with integration of solar energy sources. Energies 2018, 11, 3494. [Google Scholar] [CrossRef]
- Rahbari, O.; Vafaeipour, M.; Omar, N.; Rosen, M.A.; Hegazy, O.; Timmermans, J.-M.; Heibati, S.; Van Den Bossche, P. An optimal versatile control approach for plug-in electric vehicles to integrate renewable energy sources and smart grids. Energy 2017, 134, 1053–1067. [Google Scholar] [CrossRef]
- Khalid, Z.; Abbas, G.; Awais, M.; Alquthami, T.; Rasheed, M.B. A Novel Load Scheduling Mechanism Using Artificial Neural Network Based Customer Profiles in Smart Grid. Energies 2020, 13, 1062. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M.; Tousi, S.R.; Hosseinian, S.M. Optimal siting and sizing of renewable energy sources and charging stations simultaneously based on Differential Evolution algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 1015–1024. [Google Scholar] [CrossRef]
- Mozafar, M.R.; Moradi, M.H.; Amini, M.H. A simultaneous approach for optimal allocation of renewable energy sources and electric vehicle charging stations in smart grids based on improved GA-PSO algorithm. Sustain. Cities Soc. 2017, 32, 627–637. [Google Scholar] [CrossRef]
- Abedini, M.; Moradi, M.H.; Hosseinian, S.M. Optimal management of microgrids including renewable energy scources using GPSO-GM algorithm. Renew. Energy 2016, 90, 430–439. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M.; Shen, H.; Fotuhi-Firuzabad, M. Planning and operation of parking lots considering system, traffic, and drivers behavioral model. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1879–1892. [Google Scholar] [CrossRef]
- Grande, L.S.A.; Yahyaoui, I.; Gómez, S.A. Energetic, economic and environmental viability of off-grid PV-BESS for charging electric vehicles: Case study of Spain. Sustain. Cities Soc. 2018, 37, 519–529. [Google Scholar] [CrossRef]
- Domínguez-Navarro, J.; Dufo-López, R.; Yusta-Loyo, J.; Artal-Sevil, J.; Bernal-Agustín, J. Design of an electric vehicle fast-charging station with integration of renewable energy and storage systems. Int. J. Electr. Power Energy Syst. 2019, 105, 46–58. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, C. Optimal mix of solar and wind distributed generations considering performance improvement of electrical distribution network. Renew. Energy 2015, 75, 173–186. [Google Scholar] [CrossRef]
- Delfino, F.; Ferro, G.; Minciardi, R.; Robba, M.; Rossi, M.; Rossi, M. Identification and optimal control of an electrical storage system for microgrids with renewables. Sustain. Energy Grids Netw. 2019, 17, 100183. [Google Scholar] [CrossRef]
- Jarraya, I.; Masmoudi, F.; Chabchoub, M.H.; Trabelsi, H. An online state of charge estimation for Lithium-ion and supercapacitor in hybrid electric drive vehicle. J. Energy Storage 2019, 26, 100946. [Google Scholar] [CrossRef]
- Amini, M.; Moghaddam, M.P. Probabilistic modelling of electric vehicles’ parking lots charging demand. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013; pp. 1–4. [Google Scholar]
- Mozafar, M.R.; Amini, M.H.; Moradi, M.H. Innovative appraisement of smart grid operation considering large-scale integration of electric vehicles enabling V2G and G2V systems. Electric Power Syst. Res. 2018, 154, 245–256. [Google Scholar] [CrossRef]
- Domínguez-García, A.; Heydt, G.; Suryanarayanan, S. Implications of the smart grid initiative on distribution engineering (final project report-part2). PSERC Doc. 2011, 11–50. Available online: https://pserc.wisc.edu/document_search.aspx (accessed on 20 February 2017).
- Meliopoulos, S.; Meiselrge, J.; Overbye, T. Power system level impacts of plug-In hybrid vehicles (final project report). PSERC Doc. 2009, 14–38. Available online: https://pserc.wisc.edu/document_search.aspx (accessed on 20 February 2017).
- Pasaoglu, G.; Fiorello, D.; Martino, A.; Scarcella, G.; Alemanno, A.; Zubaryeva, A.; Thiel, C. Driving and parking patterns of European car drivers-a mobility survey. Luxemb. Eur. Comm. Joint Res. Centre 2012. Available online: https://ec.europa.eu/jrc/en/publication/eur-scientific-and-technical-research-reports/driving-and-parking-patterns-european-car-drivers-mobility-survey (accessed on 18 May 2017).
- Pasaoglu, G.; Fiorello, D.; Zani, L.; Martino, A.; Zubaryeva, A.; Thiel, C. Projections for electric vehicle load profiles in Europe based on travel survey data. Joint Res. Cent. Eur. Comm. Petten Neth. 2013. Available online: https://ec.europa.eu/jrc/en/publication/eur-scientific-and-technical-research-reports/projections-electric-vehicle-load-profiles-europe-based-travel-survey-data (accessed on 18 May 2017).
- Letendre, S.; Denholm, P.; Lilienthal, P. New load, or new resource? The industry must join a growing chorus in calling for new technology. Public Util. Fortn. 2006, 144, 28–37. [Google Scholar]
- Beasley, D.; Bull, D.R.; Martin, R.R. An overview of genetic algorithms: Part 2, research topics. Univ. Comput. 1993, 15, 170–181. [Google Scholar]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence (Morgan Kaufmann Series in Evolutionary Computation); Morgan Kaufmann Publishers: Burlington, MA, USA, 2001. [Google Scholar]
- Benegiamo, A.; Loiseau, P.; Neglia, G. Dissecting demand response mechanisms: The role of consumption forecasts and personalized offers. Sustain. Energy Grids Netw. 2018, 16, 156–166. [Google Scholar] [CrossRef]
- Aalami, H.; Moghaddam, M.P.; Yousefi, G. Demand response modeling considering interruptible/curtailable loads and capacity market programs. Appl. Energy 2010, 87, 243–250. [Google Scholar] [CrossRef]
- Board, O.E. Regulated Price Plan Manual. 2005. Available online: http://www.ontla.on.ca/library/repository/mon/11000/255532.pdf (accessed on 16 May 2018).
- Rana, A.; Darji, J.; Pandya, M. Backward/forward sweep load flow algorithm for radial distribution system. Int. J. Sci. Res. Dev. 2014, 2, 398–400. [Google Scholar]
- H.O.E. Independent Electricity System Operator (IESO). Available online: http://reports.ieso.ca/public/DemandZonal/ (accessed on 16 May 2018).
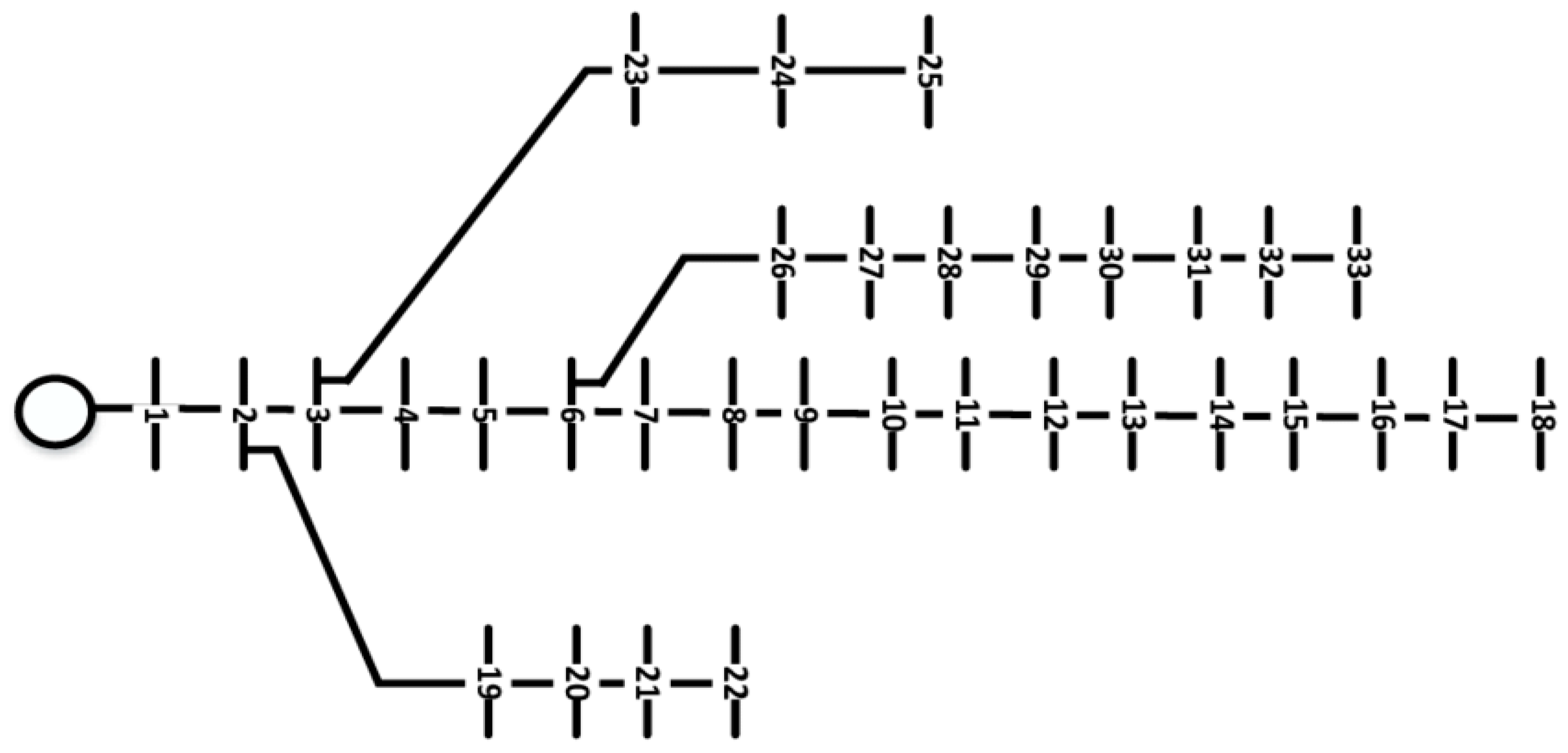
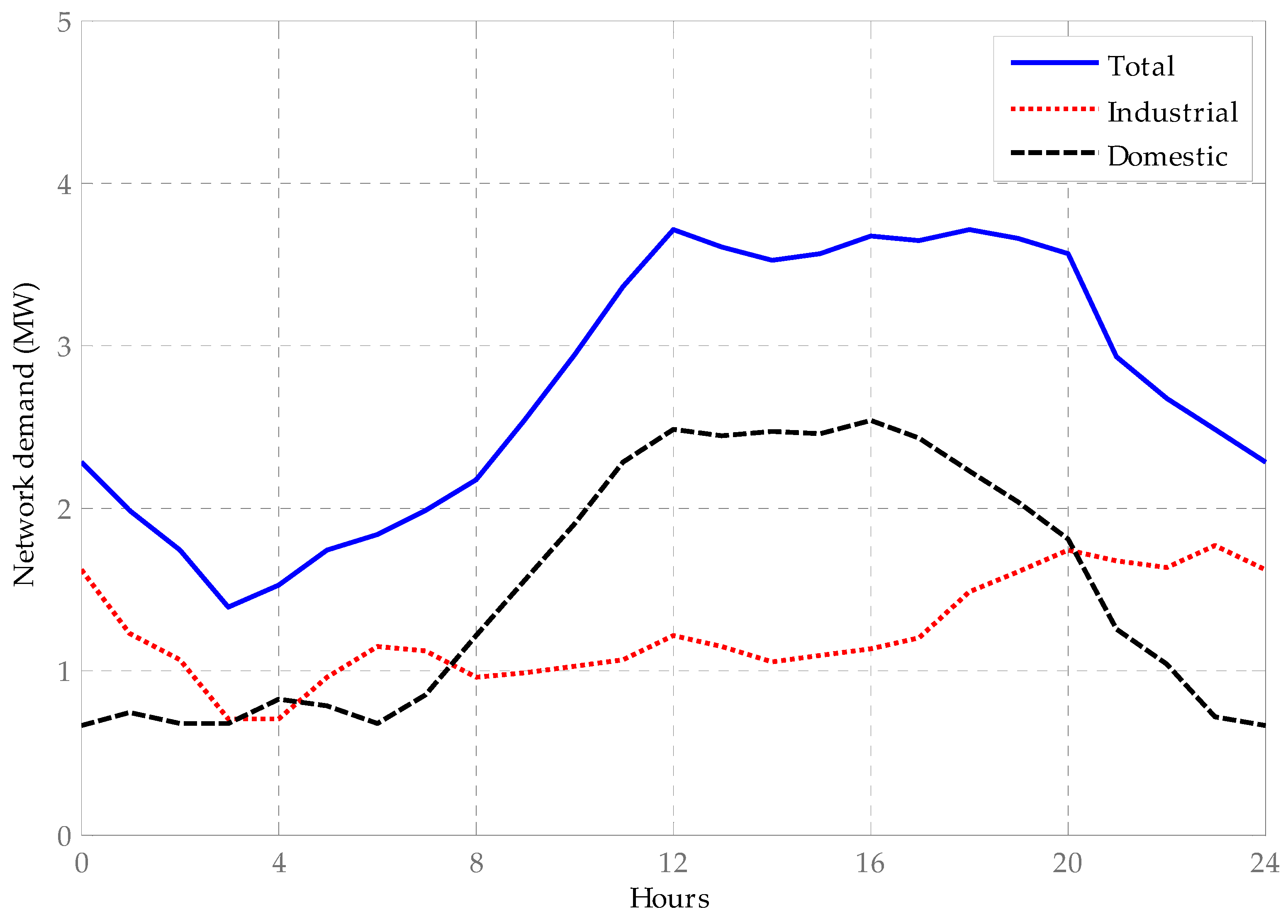
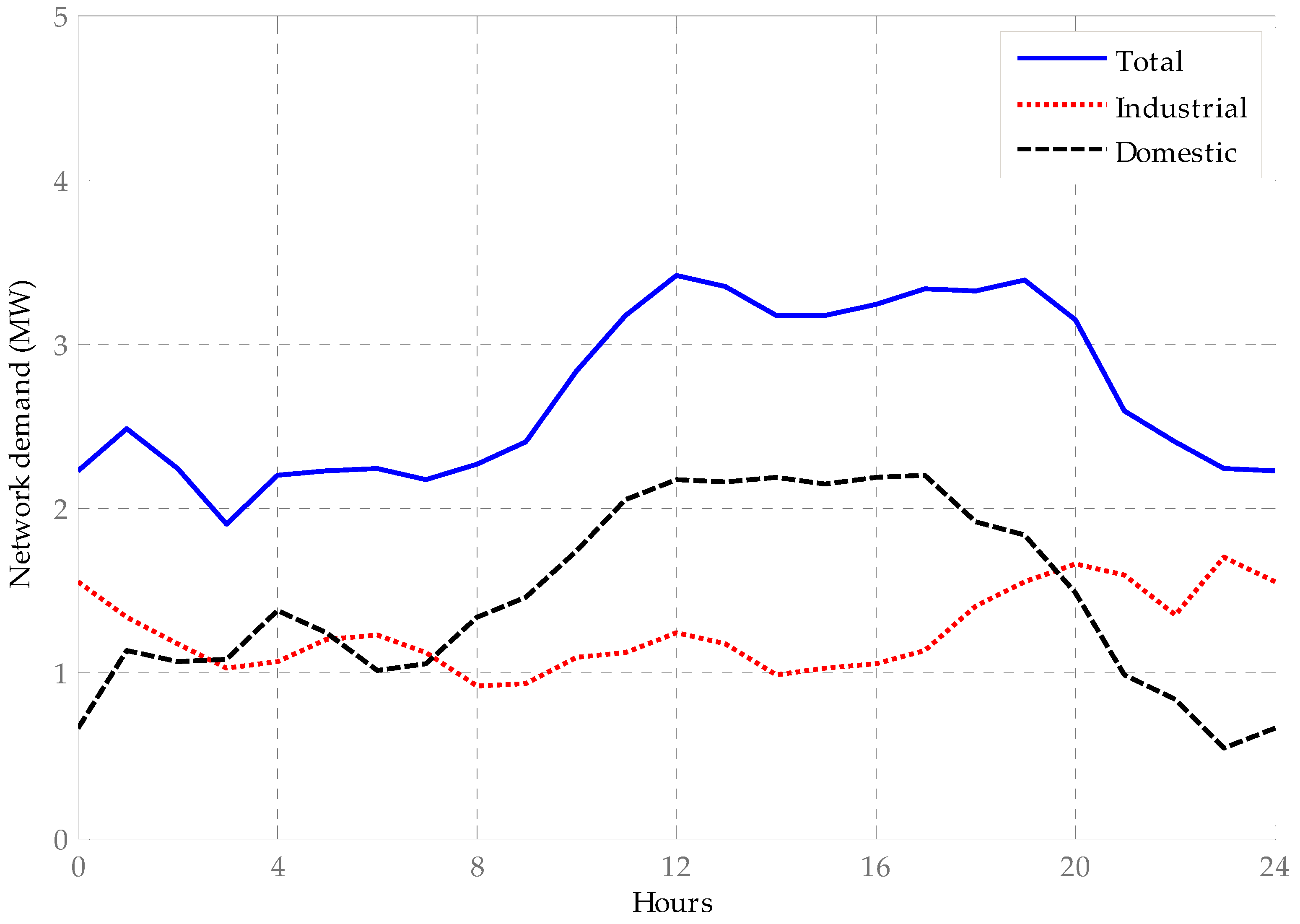
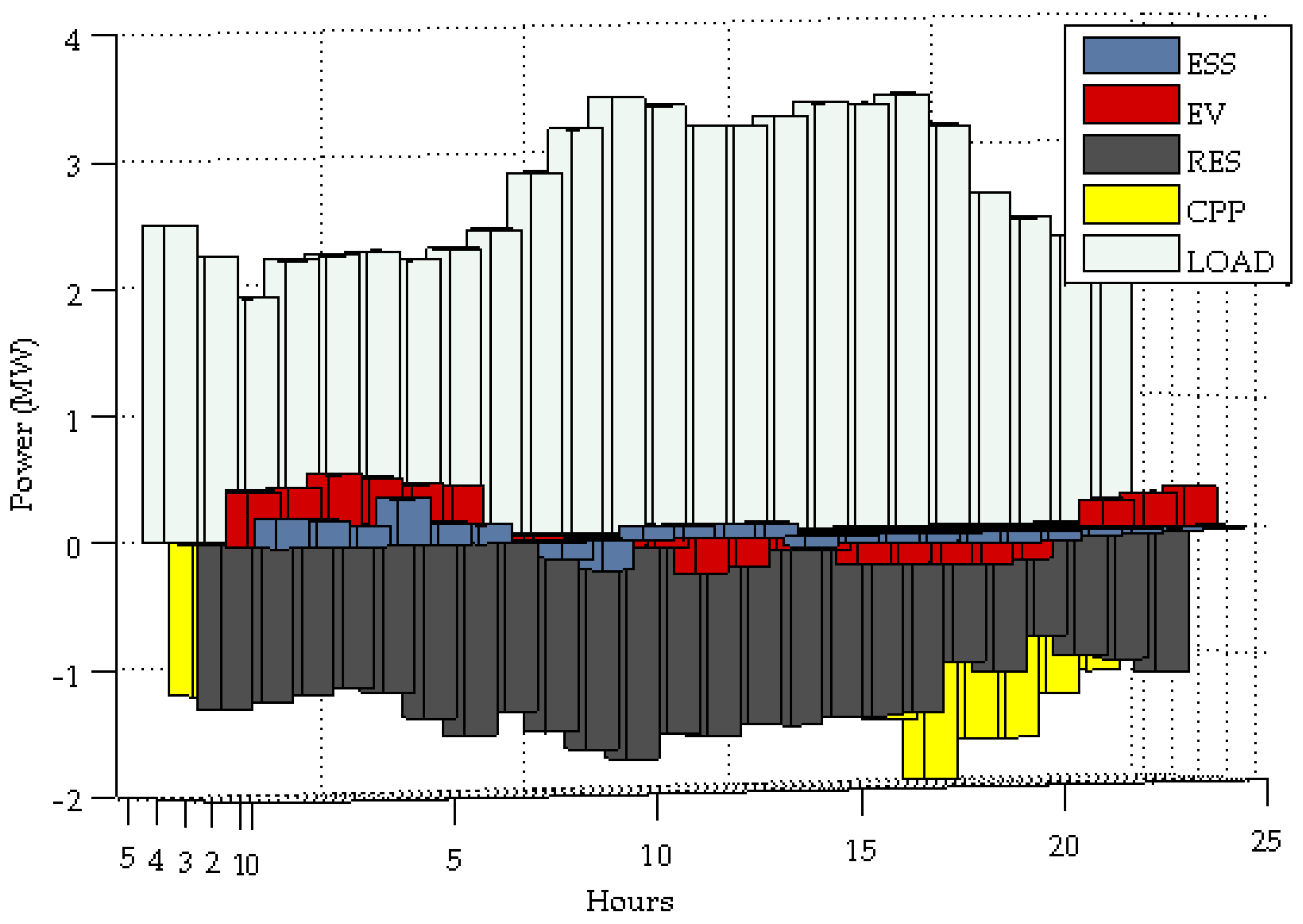
| SOC1 Upper Limit (%) | SOC Lower Limit (%) | Self-discharge Rate (%Energy/month) | Efficiency (%) |
|---|---|---|---|
| 90 | 20 | 5 | 95 |
| EV Type | Battery Cap (kWh) | Energy Consumption (kWh/mile) | Market Share (%) | |||
|---|---|---|---|---|---|---|
| Road | City | Freeway | High Traffic | |||
| A | 35 | 0.14 | 0.182 | 0.210 | 0.213 | 38 |
| B | 16 | 0.13 | 0.168 | 0.194 | 0.196 | 9 |
| C | 18 | 0.16 | 0.210 | 0.242 | 0.245 | 25.5 |
| D | 12 | 0.16 | 0.210 | 0.242 | 0.245 | 27.5 |
| Mean value | 18.54 | 0.1397 | 0.1945 | 0.2245 | 0.2274 | |
| Charging/Discharging Power (kW) | Charging Mode |
|---|---|
| 0.1 | Slow charging |
| 0.3 | Quick charging |
| 1.0 | Fast charging |
| Load Type | IMP |
|---|---|
| Domestic | 0.1 |
| Industrial | 0.5 |
| INP-1 | VL | VL | VL | VL | VL | VL | VL | VL | VL | |
| INP-2 | VL | VL | VL | VL | VL | VL | VL | VL | VL | |
| INP-3 | CRL | L | L | L | M | M | M | H | H | H |
| INP-4 | TUP | L | M | H | L | M | H | L | M | H |
| OUT-1 | ESS C/D | C | C | C | C | C | C | C | C | C |
| OUT-2 | EV C/D | FC | FC | FC | FC | QC | QC | FC | QC | SC |
| INP-1 | L | L | L | L | L | L | L | L | L | |
| INP-2 | L | L | L | L | L | L | L | L | L | |
| INP-3 | CRL | L | L | L | M | M | M | H | H | H |
| INP-4 | TUP | L | M | H | L | M | H | L | M | H |
| OUT-1 | ESS C/D | C | C | C | C | C | NOP | C | C | NOP |
| OUT-2 | EV C/D | FC | QC | QC | QC | SC | NOP | QC | SC | NOP |
| INP-1 | M | M | M | M | M | M | M | M | M | |
| INP-2 | M | M | M | M | M | M | M | M | M | |
| INP-3 | CRL | L | L | L | M | M | M | H | H | H |
| INP-4 | TUP | L | M | H | L | M | H | L | M | H |
| OUT-1 | ESS C/D | C | C | D | C | NOP | SD | NOP | D | D |
| OUT-2 | EV C/D | SC | SC | SD | SC | NOP | SD | NOP | SD | QD |
| INP-1 | H | H | H | H | H | H | H | H | H | |
| INP-2 | H | H | H | H | H | H | H | H | H | |
| INP-3 | CRL | L | L | L | M | M | M | H | H | H |
| INP-4 | TUP | L | M | H | L | M | H | L | M | H |
| OUT-1 | ESS C/D | NOP | D | D | D | D | D | D | D | D |
| OUT-2 | EV C/D | NOP | SD | QD | QD | QD | FD | QD | FD | FD |
| Scenario | Description | Scenario | Description |
|---|---|---|---|
| 1 | Base case | 2 | Only RES |
| 3 | Only ESS | 4 | RES and ESS |
| 5 | Only parking lot | 6 | RES and Parking lot |
| 7 | ESS and Parking lot | 8 | RES and ESS and Parking lot |
| Target Variables | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| PV loc. | − | 29 | − | 12 | − | 33 | − | 12 |
| PV cap. | − | 715.26 | − | 603.99 | − | 868.19 | 704.5 | |
| Wind loc. | − | 11 | − | 31 | − | 22 | 29 | |
| Wind cap. | − | 956.26 | − | 1196.01 | − | 1108.72 | − | 1308.4 |
| ESS loc. | − | − | 11 24 | 25 22 | − | − | 10 31 | 10 25 |
| ESS cap. | − | − | 350.04 271.88 | 314.62 388.27 | − | − | 295.65 403.04 | 375 625 |
| Parking loc. | − | − | − | − | 6 30 | 23 12 | 22 25 | 4 27 |
| Parking cap. | − | − | − | − | 847.91 515.37 | 881.26 1004.79 | 756.21 843.79 | 1200.32 1254.58 |
| Scenario | Processing Time (sec) | |||
|---|---|---|---|---|
| 1 | 82 | 4.04 | 38.05 | 16,431,256.00 |
| 2 | 149 | 3.01 | 29.2 | 09,416,752.81 |
| 3 | 125 | 3.75 | 36.98 | 16,209,434.04 |
| 4 | 199 | 2.79 | 27.77 | 08,743,071.31 |
| 5 | 187 | 3.27 | 34.16 | 16,027,047.10 |
| 6 | 263 | 2.44 | 24.99 | 07,952,727.90 |
| 7 | 240 | 3.35 | 33.67 | 15,843,017.04 |
| 8 | 317 | 1.98 | 22.54 | 07,360,217.66 |
| Demand Supplied by Other Resources (%) | |||||
|---|---|---|---|---|---|
| Scenario | Total System Load (MW) | RES | V2G | ESS | CPP (%) |
| 1 | 66.280 | − | − | − | 100 |
| 2 | 66.280 | 40.65 | − | − | 59.35 |
| 3 | 67.190 | − | − | 1.27 | 98.73 |
| 4 | 67.309 | 43.57 | − | 1.44 | 54.99 |
| 5 | 68.133 | − | 2.46 | − | 97.54 |
| 6 | 68.166 | 47.91 | 2.50 | − | 49.59 |
| 7 | 68.902 | − | 2.10 | 1.39 | 96.51 |
| 8 | 70.238 | 49.27 | 3.42 | 1.63 | 45.68 |
| Scenario | Total DSO Profit ($) | Peak Hours Profit ($) | Low Load Hours Profit ($) |
|---|---|---|---|
| 2 | 6,926,503.47 | 3,869,185.11 | 3,057,318.36 |
| 3 | 0311,911.95 | 0276,199.37 | 0035,712.58 |
| 4 | 7,185,884.93 | 4791,212.64 | 3,946,720.29 |
| 5 | 0394,297.27 | 0244,049.55 | 0150,247.72 |
| 6 | 8,378,418.19 | 5,570,857.10 | 2,807,561.09 |
| 7 | 0683,438.52 | 0295,294.17 | 0388,144.35 |
| 8 | 9,071,038.34 | 6,170,581.26 | 2,900,457.08 |
| Scenario | Total System Loss (MW) | Total System Load (MW) | Peak Shaving (MW) | Peak to Valley Distance (MW) | Load Factor (%) |
|---|---|---|---|---|---|
| Base case | 4.04 | 66.280 | − | 2.326 | 85.1 |
| Fixed pricing | 2.11 | 70.238 | −0.1 | 1.997 | 88.5 |
| Online pricing | 1.98 | 65.248 | 0.295 | 1.506 | 90.2 |
| Algorithm | Iteration | Pop Size | NOFE | Processing Time (sec) | |||
|---|---|---|---|---|---|---|---|
| Adaptive GA-PSO | 200 | 50 | 72,480 | 317 | 1.98 | 22.54 | 07,360,217.66 |
| NSGA-II | 200 | 50 | 99,667 | 436 | 3.00 | 23.81 | 10,109,490.86 |
| DE | 200 | 50 | 83,516 | 374 | − | − | − |
| GA | 200 | 50 | 96,860 | 428 | − | − | − |
| E-PSO | 200 | 50 | 114,127 | 495 | 2.09 | 22.90 | 07,582,571.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaeimozafar, M.; Eskandari, M.; Amini, M.H.; Moradi, M.H.; Siano, P. A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids. Energies 2020, 13, 1706. https://doi.org/10.3390/en13071706
Rezaeimozafar M, Eskandari M, Amini MH, Moradi MH, Siano P. A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids. Energies. 2020; 13(7):1706. https://doi.org/10.3390/en13071706
Chicago/Turabian StyleRezaeimozafar, Mostafa, Mohsen Eskandari, Mohammad Hadi Amini, Mohammad Hasan Moradi, and Pierluigi Siano. 2020. "A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids" Energies 13, no. 7: 1706. https://doi.org/10.3390/en13071706
APA StyleRezaeimozafar, M., Eskandari, M., Amini, M. H., Moradi, M. H., & Siano, P. (2020). A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids. Energies, 13(7), 1706. https://doi.org/10.3390/en13071706







