Techno-Economic Optimization of an Off-Grid Solar/Wind/Battery Hybrid System with a Novel Multi-Objective Differential Evolution Algorithm
Abstract
1. Introduction
2. Component Models and Energy Management Strategy
2.1. Wind turbine
2.2. PV Panel
2.3. Battery System
2.4. Load Profile
2.5. Economic Model
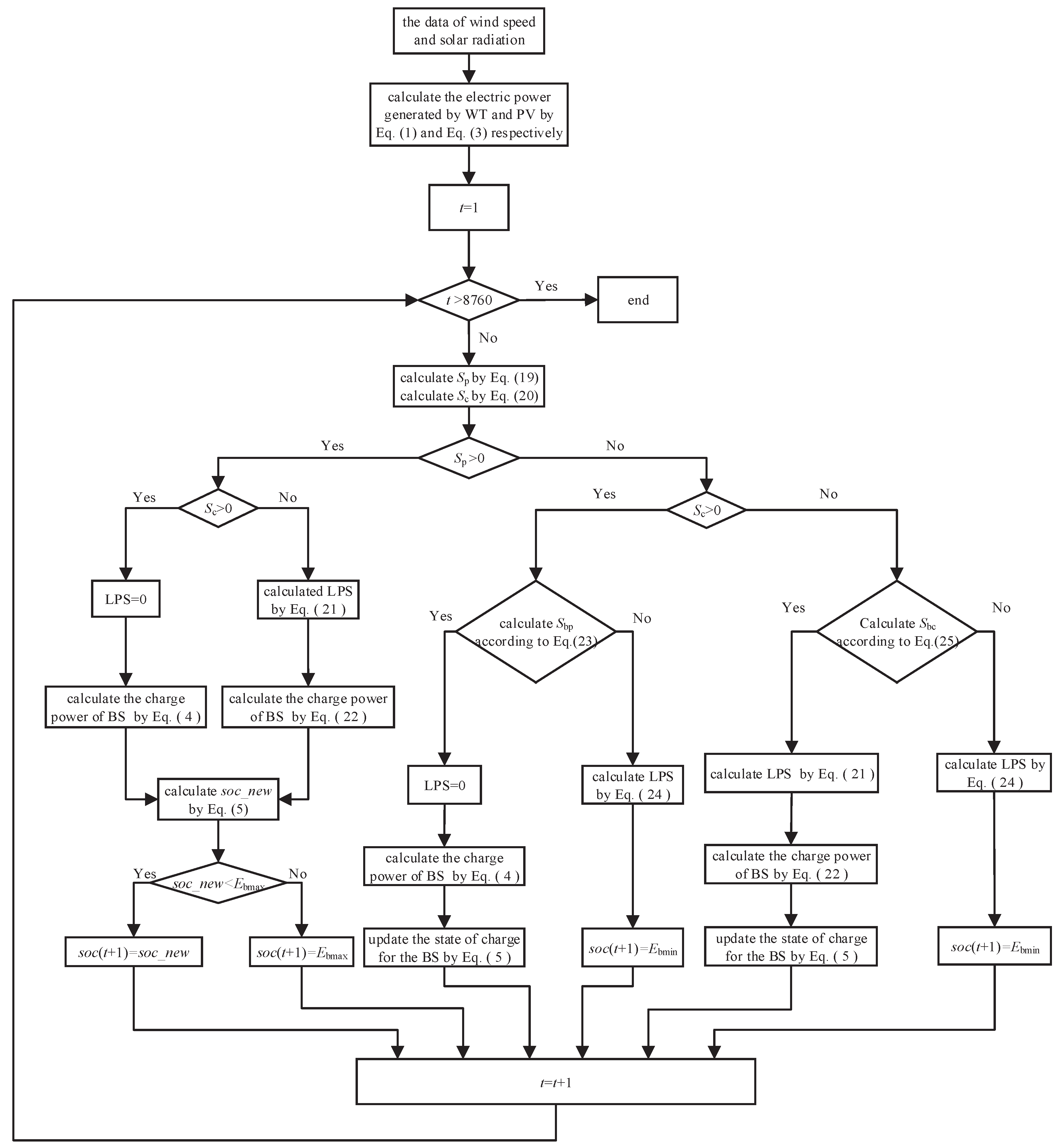
2.6. Rule-Based Energy Management Strategy
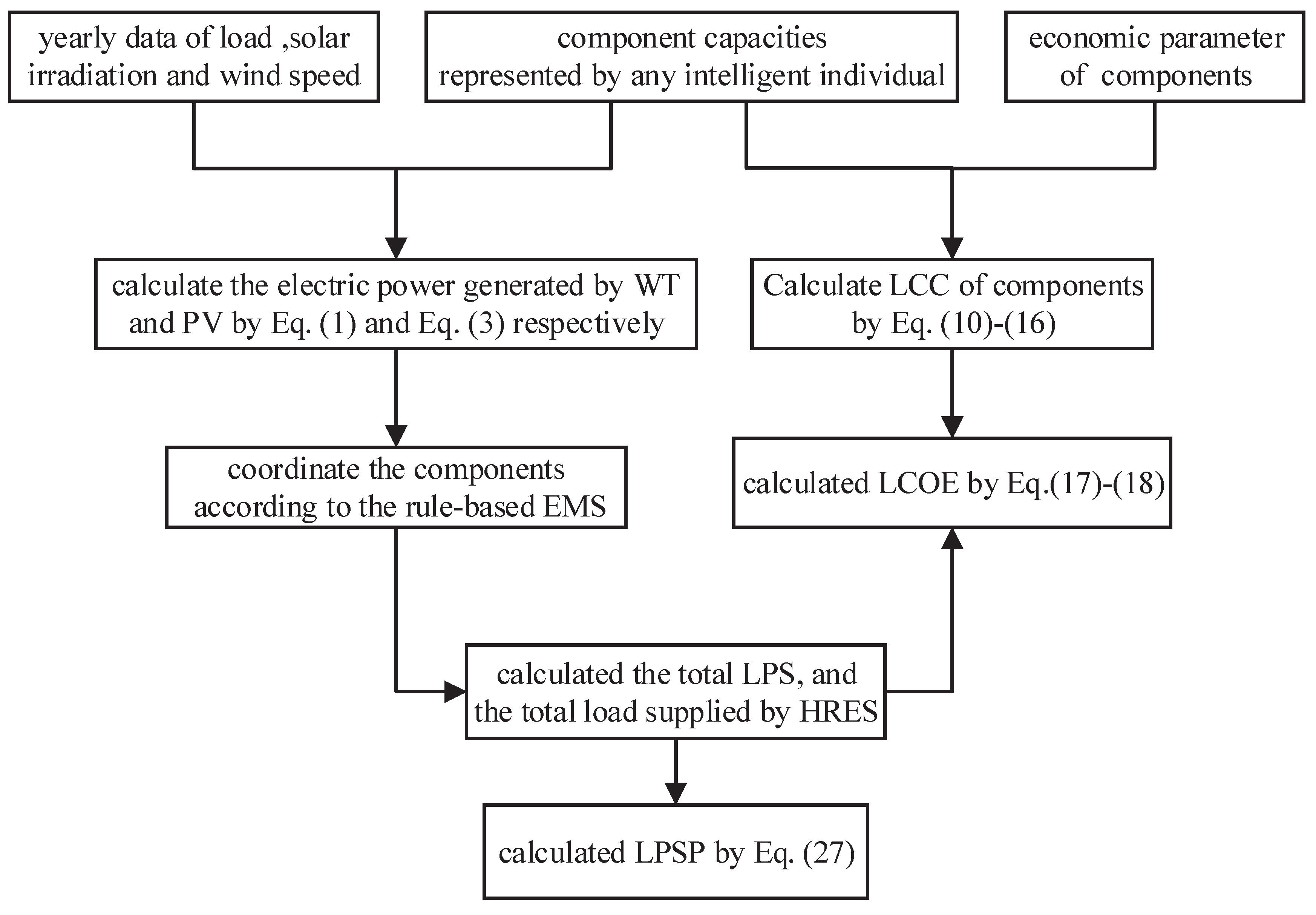
2.7. Objective Function and Constraints
3. Optimization Algorithm
3.1. MOEA/DADE
3.1.1. Differential Evolution Mechanism
3.1.2. Parameter Adaptive Mechanism
3.2. Algorithm Contrast
4. Case Study
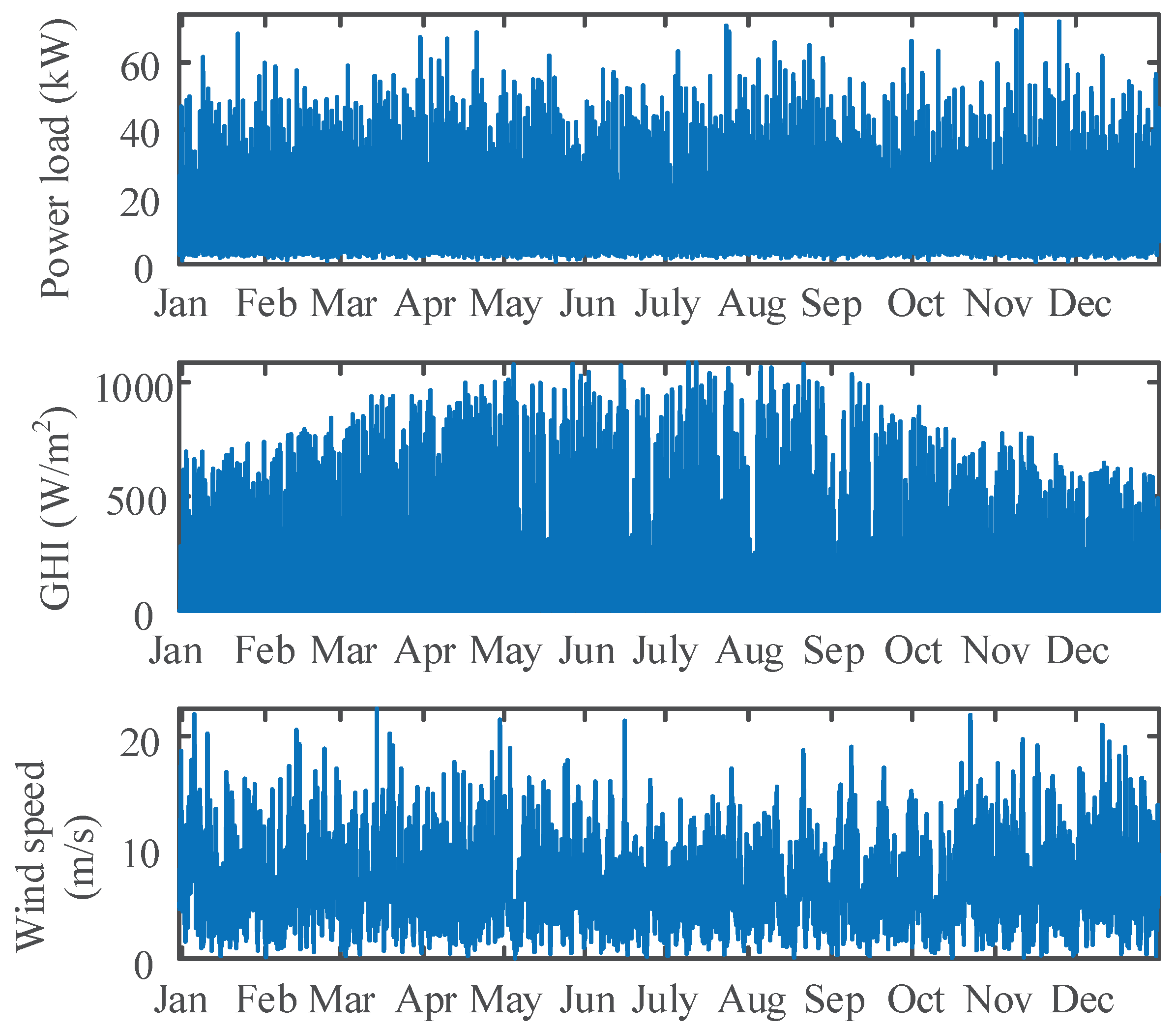
4.1. Data
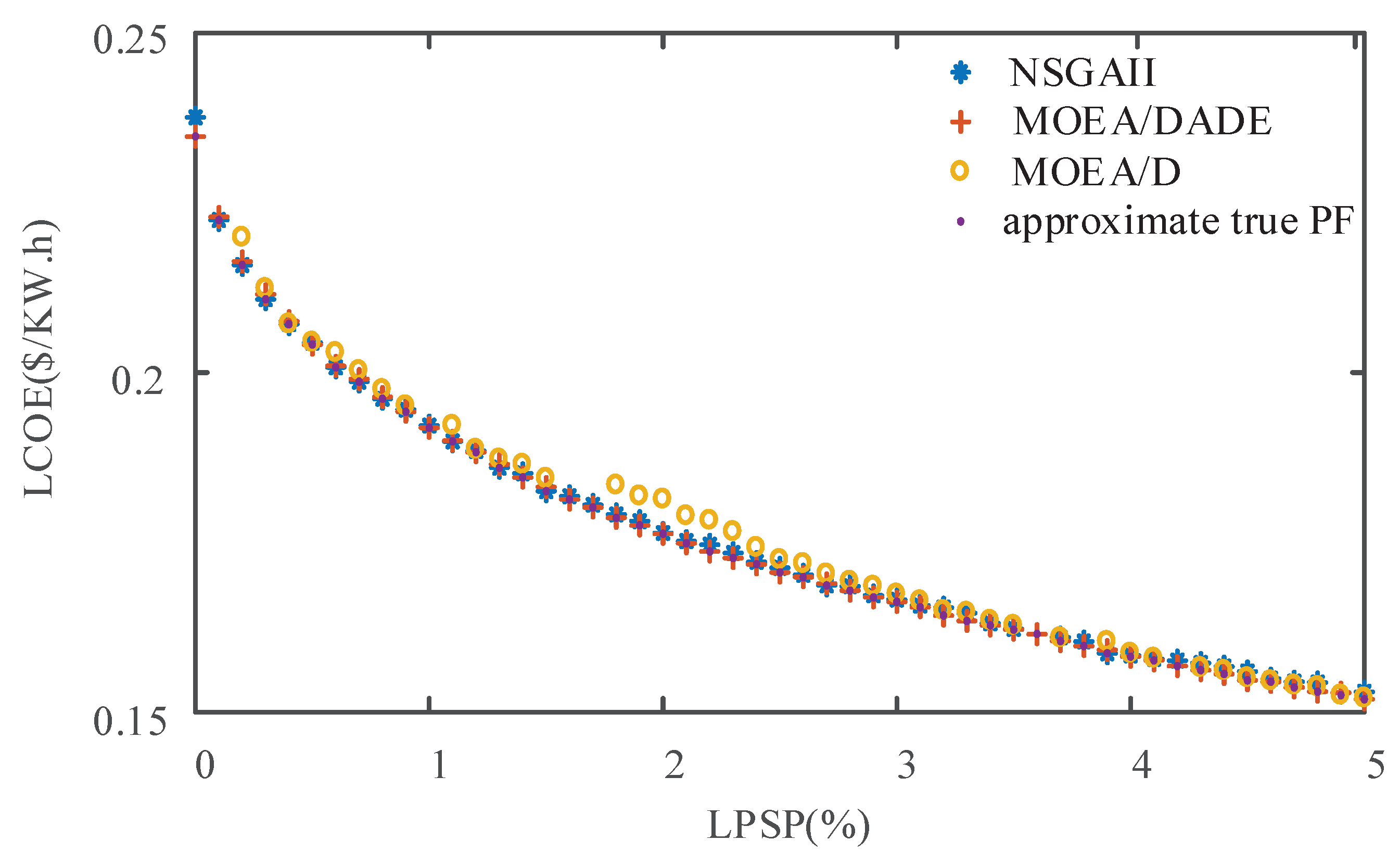
4.2. Techno-Economic Analysis
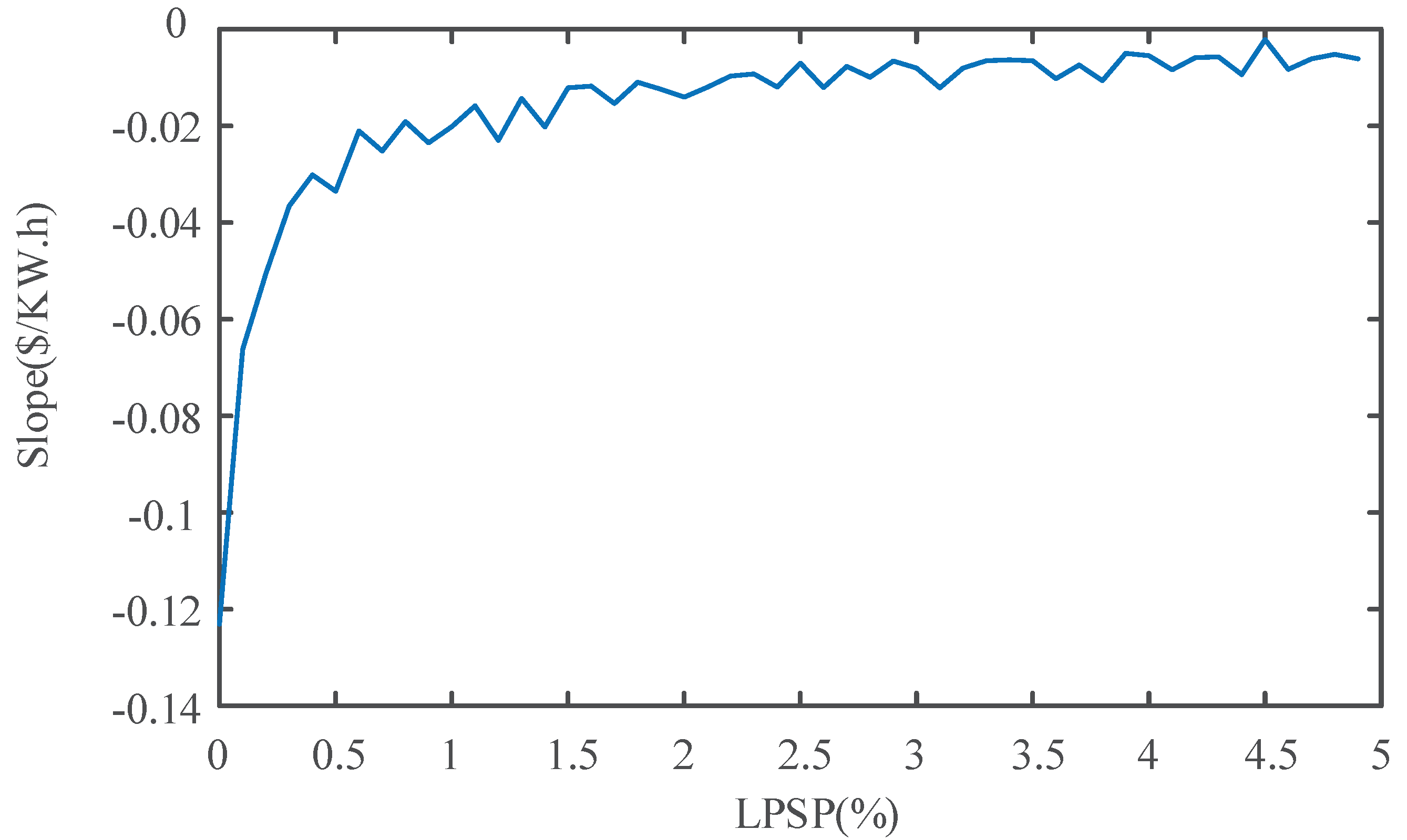
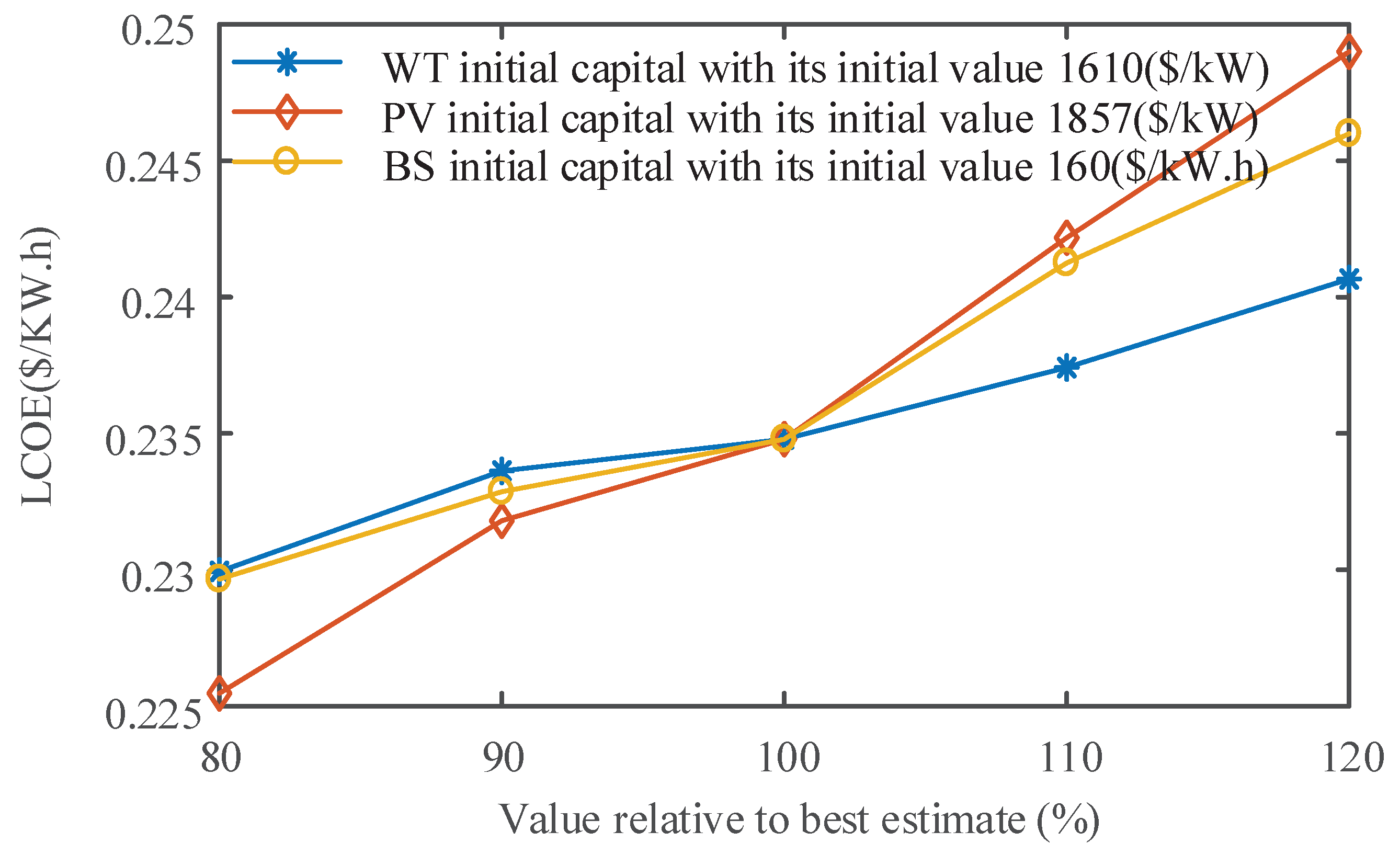
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| DOD | BS’s allowable depth of discharge |
| PV derating factor (%) | |
| solar incident radiation on the PV (kW/m2) | |
| solar radiation under standard test conditions ( = 1 kW/m2) | |
| turbine hub altitude (m) | |
| anemometer altitude (m) | |
| initial capital cost ($/kW) | |
| real discount rate (%) | |
| perturbation factor of load | |
| maintenance and operation cost ($/kW) | |
| electrical load (kW) | |
| output power of PV (kW) | |
| rated output power of WT (kW) | |
| output power of WT (kW) | |
| nominal discount rate (%) | |
| replacement cost ($/kW) | |
| salvage value($/kW) | |
| a binary variable denoting whether the converter capacity is sufficient | |
| a binary variable denoting whether the electric power generated is sufficient | |
| SOC BS’s state of charge | |
| u | expected inflation rate (%) |
| wind speed at the turbine hub altitude (m/s) | |
| cut-in speed (m/s) | |
| cut-out speed (m/s) | |
| nominal speed (m/s) | |
| wind speed measured by anemometer (m/s) | |
| daily variation percent of load | |
| hourly variation percent of load | |
| charge efficiency of BS | |
| discharge efficiency of BS | |
| converter efficiency |
Abbreviation
| BS | battery system |
| CRF | capital recovery factor |
| DG | diesel system |
| EMS | energy management strategy |
| HRES | hybrid renewable energy systems |
| LCC | life cycle cost |
| LCOE | levelized cost of electricity |
| LPSP | loss of power supply probability |
| WT | wind turbine |
| PF | Pareto frontier |
| PS | Pareto set |
References
- Huang, Y.; Li, S.; Ding, P.; Zhang, Y.; Yang, K.; Zhang, W. Optimal Operation for Economic and Exergetic Objectives of a Multiple Energy Carrier System Considering Demand Response Program. Energies 2019, 12, 3995. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, S.; Liu, D.; Li, R.; Chu, Y. Operation optimization strategy for wind-concentrated solar power hybrid power generation system. Energy Convers. Manag. 2018, 160, 243–250. [Google Scholar] [CrossRef]
- Kyritsis, A.; Voglitsis, D.; Papanikolaou, N.; Tselepis, S.; Christodoulou, C.; Gonos, I.; Kalogirou, S.A. Evolution of PV systems in Greece and review of applicable solutions for higher penetration levels. Renew. Energy 2017, 109, 487–499. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Zahraee, S.M.; Khalaji Assadi, M.; Saidur, R. Application of Artificial Intelligence Methods for Hybrid Energy System Optimization. Renew. Sustain. Energy Rev. 2016, 66, 617–630. [Google Scholar] [CrossRef]
- Nogueira, C.E.C.; Vidotto, M.L.; Niedzialkoski, R.K.; de Souza, S.N.M.; Chaves, L.I.; Edwiges, T.; dos Santos, D.B.; Werncke, I. Sizing and simulation of a photovoltaic-wind energy system using batteries, applied for a small rural property located in the south of Brazil. Renew. Sustain. Energy Rev. 2014, 29, 151–157. [Google Scholar] [CrossRef]
- Malheiro, A.; Castro, P.M.; Lima, R.M.; Estanqueiro, A. Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems. Renew. Energy 2015, 83, 646–657. [Google Scholar] [CrossRef]
- Li, J.L.; Guo, B.Q.; Niu, M.; Xiu, X.Q.; Tian, L.T. Optimal Configuration Strategy of Energy Storage Capacity in Wind/PV/Storage Hybrid System. Trans. China Electrotech. Soc. 2018, 33, 1189–1196. [Google Scholar]
- Smaoui, M.; Abdelkafi, A.; Krichen, L. Optimal sizing of stand-alone photovoltaic/wind/hydrogen hybrid system supplying a desalination unit. Sol. Energy 2015, 120, 263–276. [Google Scholar] [CrossRef]
- Bhuiyan, F.A.; Yazdani, A.; Primak, S.L. Optimal sizing approach for islanded microgrids. IET Renew. Power Gener. 2015, 9, 166–175. [Google Scholar] [CrossRef]
- Al-falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- HOMER Pro Version 3.7 User Manual. Available online: https://www.homerenergy.com (accessed on 15 December 2019).
- Lambert, T.; Gilman, P.; Lilienthal, P. Micropower System Modeling with HOMER. 2006. Available online: http://homerenergy.com/documents/MicropowerSystemModelingWithHOMER.pdf (accessed on 15 December 2019).
- Shahzad, M.K.; Zahid, A.; ur Rashid, T.; Rehan, M.A.; Ali, M.; Ahmad, M. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software. Renew. Energy 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Olatomiwa, L.; Hazelton, J. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia. Energy Convers. Manag. 2017, 144, 322–339. [Google Scholar] [CrossRef]
- Hossain, M.; Mekhilef, S.; Olatomiwa, L. Performance evaluation of a stand-alone PV-wind-diesel-battery hybrid system feasible for a large resort center in South China Sea, Malaysia. Sustain. Cities Soc. 2017, 28, 358–366. [Google Scholar] [CrossRef]
- Li, C.; Zhou, D.; Wang, H.; Lu, Y.; Li, D. Techno-economic performance study of stand-alone wind/diesel/battery hybrid system with different battery technologies in the cold region of China. Energy 2020, 192, 116702. [Google Scholar] [CrossRef]
- Park, E.; Kwon, S.J. Towards a Sustainable Island: Independent optimal renewable power generation systems at Gadeokdo Island in South Korea. Sustain. Cities Soc. 2016, 23, 114–118. [Google Scholar] [CrossRef]
- Rajbongshi, R.; Borgohain, D.; Mahapatra, S. Optimization of PV-biomass-diesel and grid base hybrid energy systems for rural electrification by using HOMER. Energy 2017, 126, 461–474. [Google Scholar] [CrossRef]
- Singh, A.; Baredar, P.; Gupta, B. Techno-economic feasibility analysis of hydrogen fuel cell and solar photovoltaic hybrid renewable energy system for academic research building. Energy Convers. Manag. 2017, 145, 398–414. [Google Scholar] [CrossRef]
- Zahboune, H.; Zouggar, S.; Krajacic, G.; Varbanov, P.S.; Elhafyani, M.; Ziani, E. Optimal hybrid renewable energy design in autonomous system using Modified Electric System Cascade Analysis and Homer software. Energy Convers. Manag. 2016, 126, 909–922. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Singh, S.; Kaushik, S.C. Optimal sizing of grid integrated hybrid PV-biomass energy system using artificial bee colony algorithm. IET Renew. Power Gener. 2016, 10, 642–650. [Google Scholar] [CrossRef]
- Shivaie, M.; Mokhayeri, M.; Kiani-Moghaddam, M.; Ashouri-Zadeh, A. A reliability-constrained cost-effective model for optimal sizing of an autonomous hybrid solar/wind/diesel/battery energy system by a modified discrete bat search algorithm. Sol. Energy 2019, 189, 344–356. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M.; Putrus, G.A. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Nasiraghdam, H.; Jadid, S. Optimal hybrid PV/WT/FC sizing and distribution system reconfiguration using multi-objective artificial bee colony (MOABC) algorithm. Sol. Energy 2012, 86, 3057–3071. [Google Scholar] [CrossRef]
- Mazzeo, D.; Baglivo, C.; Matera, N.; Congedo, P.M.; Oliveti, G. A novel energy-economic-environmental multi-criteria decision-making in the optimization of a hybrid renewable system. Sustain. Cities Soc. 2020, 52, 101780. [Google Scholar] [CrossRef]
- Qingfu, Z.; Hui, L. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Xinye, C.; Yexing, L.; Zhun, F.; Qingfu, Z. An External Archive Guided Multiobjective Evolutionary Algorithm Based on Decomposition for Combinatorial Optimization. IEEE Trans. Evol. Comput. 2015, 19, 508–523. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Coello, C.A.; Cortés, N.C. Solving multiobjective optimization problems using an artificial immune system. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- 2019 ATB. Available online: https://atb.nrel.gov/electricity/2019/ (accessed on 12 March 2020).

| Algorithm | Parameters |
|---|---|
| NSGA-II | Pc = 0.9, Pm = 1/D, ηc = 20, ηm = 20 |
| MOEA/D | T = 10, Pc = 0.9, Pm = 1/D, ηc = 20, ηm = 20 |
| MOEA/DADE | T = 10, , , δ = 0.9 |
| Function | NSGA-II Mean (std) | MOEA/D Mean (std) | MOEA/DADE Mean (std) |
|---|---|---|---|
| ZDT1 | 1.7218 × 10−1 (1.10 × 10−1) − | 1.6737 × 10−1 (5.91 × 10−2) − | 4.7928 × 10−2 (1.62 × 10−2) |
| ZDT 2 | 5.5298 × 10−1 (1.01 × 10−1) − | 3.2507 × 10−1 (1.88 × 10−1) − | 1.2261 × 10−1 (1.63 × 10−1) |
| ZDT 3 | 1.3700 × 10−1 (8.06 × 10−2) − | 2.1748 × 10−1 (1.12 × 10−1) − | 6.6407 × 10−2 (3.45 × 10−2) |
| ZDT 4 | 1.4230 × 101 (4.08 × 100) + | 1.4189 × 101 (4.79 × 100) + | 3.8489 × 101 (9.88 × 100) |
| ZDT 6 | 3.8877 × 100 (3.78 × 10−1) − | 2.3380 × 100 (4.81 × 10−1) − | 1.8724 × 100 (3.83 × 10−1) |
| +/-/= | 1/4/0 | 1/4/0 |
| Factor | Value | Factor | Value | ||
|---|---|---|---|---|---|
| Project | Lifetime (year) | 25 | Battery | Lifetime (year) | 10 |
| Discount rate (%) | 6 | Initial capital ($/kW∙h) | 160 | ||
| Inflation rate (%) | 2 | Replacement ($/kW∙h) | 128 | ||
| PV | Lifetime (year) | 25 | O&M ($/year/kW∙h) | 1 | |
| Initial capital ($/kW) | 1857 | Round trip efficiency (%) | 80 | ||
| Replacement ($/kW) | 1486 | Converter | Lifetime (year) | 15 | |
| O&M ($/year/kW) | 18 | Initial capital ($/kW) | 890 | ||
| Wind Turbine | Lifetime (year) | 20 | Replacement ($/kW) | 800 | |
| Initial capital ($/kW) | 1610 | O&M ($/year/kW) | 10 | ||
| Replacement ($/kW) | 1288 | Efficiency (%) | 95 | ||
| O&M ($/year/kW) | 32 |
| Algorithm | NSGA-II | MOEA/D | MOEA/DADE |
|---|---|---|---|
| IGD | 4.7809 × 10−4 | 1.3926 × 10−3 | 7.5655 × 10−5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, R. Techno-Economic Optimization of an Off-Grid Solar/Wind/Battery Hybrid System with a Novel Multi-Objective Differential Evolution Algorithm. Energies 2020, 13, 1585. https://doi.org/10.3390/en13071585
Yang Y, Li R. Techno-Economic Optimization of an Off-Grid Solar/Wind/Battery Hybrid System with a Novel Multi-Objective Differential Evolution Algorithm. Energies. 2020; 13(7):1585. https://doi.org/10.3390/en13071585
Chicago/Turabian StyleYang, Yong, and Rong Li. 2020. "Techno-Economic Optimization of an Off-Grid Solar/Wind/Battery Hybrid System with a Novel Multi-Objective Differential Evolution Algorithm" Energies 13, no. 7: 1585. https://doi.org/10.3390/en13071585
APA StyleYang, Y., & Li, R. (2020). Techno-Economic Optimization of an Off-Grid Solar/Wind/Battery Hybrid System with a Novel Multi-Objective Differential Evolution Algorithm. Energies, 13(7), 1585. https://doi.org/10.3390/en13071585





